Submitted:
21 August 2023
Posted:
23 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Theoretical Background
2.1. Standard Cosmological Model
2.2. Flat-Constant-wCDM Model
2.3. w0waCDM Model or CPL Parametrization
3. Data and Methodology
4. Results
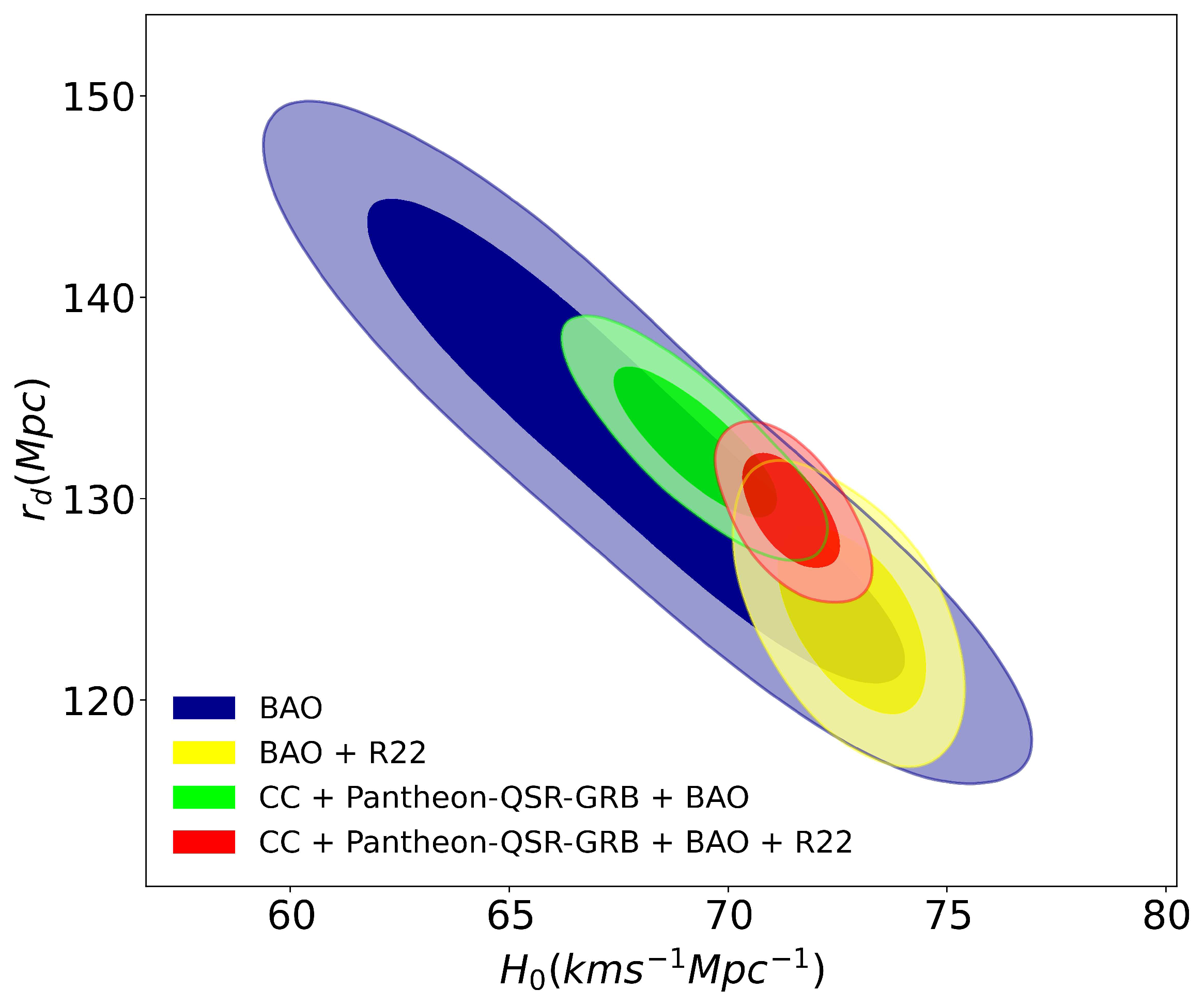
4.1. Standard Cosmological Model
4.2. Models Beyond Standard Model
4.2.1. wCDM Model
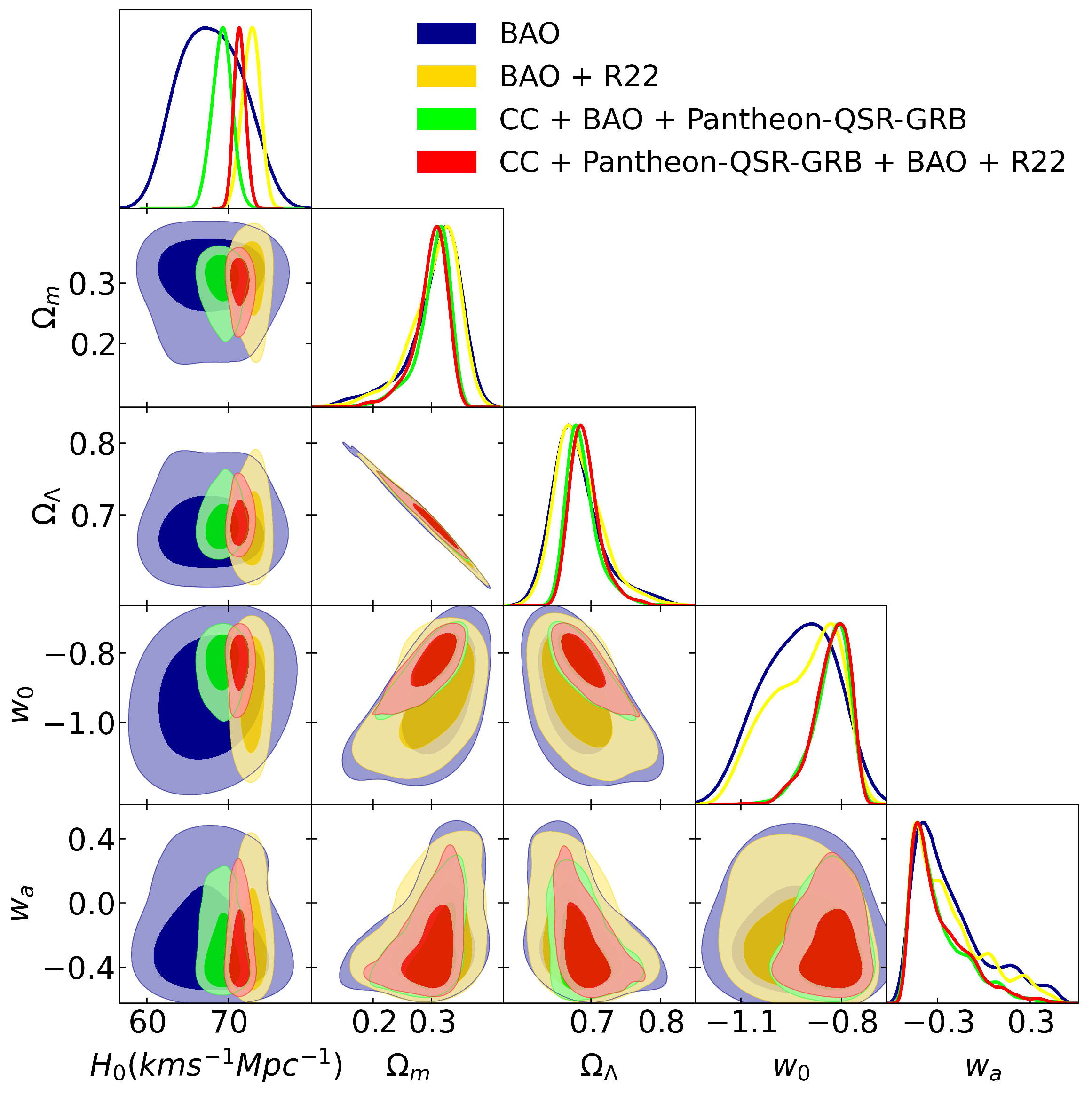
4.2.2. w0waCDM Model
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Planck Collaboration. Planck 2018 results - VI. Cosmological parameters. A&A 2020, A6, 641.
- C. L. Bennett et al. Nine-year Wilkinson microwave anisotropy probe (WMAP) observations: final maps and results. ApJS 2013, 208, 20. [CrossRef]
- Adam G. Riess et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. ApJ 1998, 116, 1009. [CrossRef]
- Adam G. Riess et al. A 3% solution: determination od the Hubble constant with the Hubble space telescope and wide field camera 3. ApJ 2011, 730, 119.
- Adam G. Riess et al. A 2.4% determination of the local value of the Hubble constant. ApJ 2016, 826, 56. [CrossRef]
- Adam G. Riess et al. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. ApJ 2019, 876, 55.
- Adam G. Riess et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team. ApJL 2022, 934, L7. [CrossRef]
- Huang, QG.; Wang, K. How the dark energy can reconcile Planck with local determination of the Hubble constant. Eur. Phys. J. 2016, C 76, 506. [CrossRef]
- E. Di Valentino; A. Melchiorri; J. Silk. Reconciling Planck with the local value of H0 in extended parameter space. Physics Letters B 2016, 761, 242-246. [CrossRef]
- Xu, L.; Huang, QG. Detecting the neutrinos mass hierarchy from cosmological data. Sci. China Phys. Mech. Astron. 2018, 61, 039521. [CrossRef]
- W. Yang; S. Pan; E. Di Valentino; E. N. Saridakis; S. Chakraborty. Observational constraints on one-parameter dynamical dark-energy parametrizations and the H0 tension. Phys. Rev. D 2019, 99, 043543.
- V. Poulin; Tristan L. Smith; T. Karwal; M. Kamionkowsk. Early Dark Energy can Resolve the Hubble Tension. Phys. Rev. Lett. 2019, 122, 221301. [CrossRef]
- Sunny Vagnozzi. New physics in light of the H0 tension: An alternative view. Phys. Rev. D 2020, 102, 023518.
- Liu, M.; Huang, Z.; Luo, X. et al. Can non-standard recombination resolve the Hubble tension?. Sci. China Phys. Mech. Astron. 2020, 63, 290405. [CrossRef]
- Ding, Q.; Nakama, T.; and Wang, Y. A gigaparsec-scale local void and the Hubble tension.Sci. China Phys. Mech. Astron. 2020, 63, 290403. [CrossRef]
- Joseph Ryan; Yun Chen; Bharat Ratra. Baryon acoustic oscillation, Hubble parameter, and angular size measurement constraints on the Hubble constant, dark energy dynamics, and spatial curvature. MNRAS 2019, 488, 3844–3856. [CrossRef]
- Zhao, GB.; Raveri, M.; Pogosian, L. et al. Dynamical dark energy in light of the latest observations. Nat Astron 2017, 1, 627–632. [CrossRef]
- Xiaolei Li; Arman Shafieloo. A Simple Phenomenological Emergent Dark Energy Model can Resolve the Hubble Tension. ApJL 2019,883, L3. [CrossRef]
- Eleonora Di Valentino. Investigating Cosmic Discordance. ApJL 2021, 908, L9. [CrossRef]
- Haitao M.; Zhiqi H. The H0 Tension in Non-flat QCDM Cosmology. ApJ 2018, 868, 20.
- M. Millon et al. An exploration of systematic uncertainties in the inference of H0 from time-delay cosmography. A& A 2020, 639, A101.
- Kenneth C. Wong et al. H0LiCOW – XIII. A 2.4 per cent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. MNRAS 2019, 498, 1420–1439. [CrossRef]
- Mooley, K.P.; Deller, A.T.; Gottlieb, O. et al. Superluminal motion of a relativistic jet in the neutron-star merger GW170817. Nature 2018, 561, 355–359. [CrossRef]
- The LIGO Scientific Collaboration and The Virgo Collaboration.; The 1M2H Collaboration.; The Dark Energy Camera GW-EM Collaboration; the DES Collaboration et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88.
- Hotokezaka, K.; Nakar, E.; Gottlieb, O. et al. A Hubble constant measurement from superluminal motion of the jet in GW170817. Nat Astron 2019, 3, 940–944. [CrossRef]
- Qin Wu et al. An 8 per cent determination of the Hubble constant from localized fast radio bursts. MNRAS:Letters 2022, 515, L1–L5. [CrossRef]
- C. W. James et al. A measurement of Hubble’s Constant using Fast Radio Bursts. MNRAS 2022, 516, 4862–4881. [CrossRef]
- D. W. Pesce et al. The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints ApJL 2020, 891, L1.
- J. Reid et al. An Improved Distance to NGC 4258 and Its Implications for the Hubble Constant. ApJL 2019, 886, L27.
- C. Y. Kuo et al. The Megamaser Cosmology Project. VI. Observations of NGC 6323. ApJ 2015, 800, 26. [CrossRef]
- Wendy L. Freedman et al. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. ApJ 2019, 882, 34. [CrossRef]
- Wendy L. Freedman et al. Calibration of the Tip of the Red Giant Branch. ApJ 2020, 891, 57. [CrossRef]
- Wendy L. Freedman. Measurements of the Hubble Constant: Tensions in Perspective. ApJ 2021, 919, 16. [CrossRef]
- G. E. Addison et al. Elucidating ΛCDM: Impact of Baryon Acoustic Oscillation Measurements on the Hubble Constant Discrepancy. ApJ 2021, 853, 119.
- Moresco, M.; Amati, L.; Amendola, L. et al. Unveiling the Universe with emerging cosmological probes. Living Rev Relativ 2022, 25, 6. [CrossRef]
- S. H. Suyu et al. H0LiCOW – I. H0 Lenses in COSMOGRAIL’s Wellspring: program overview. MNRAS 2017, 468, 2590–2604.
- Kenneth C. Wong et al. H0LiCOW – XIII. A 2.4 per cent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. MNRAS 2020, 498, 1420–1439. [CrossRef]
- The LIGO Scientific Collaboration and The Virgo Collaboration.; The 1M2H Collaboration.; The Dark Energy Camera GW-EM Collaboration; the DES Collaboration et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88.
- Zhang, X.; Huang, Q.G.; Measuring H0 from low-z datasets. Sci. China Phys. Mech. Astron. 2020, 63, 290402. [CrossRef]
- Florian Beutler et al. The 6dF Galaxy Survey: baryon acoustic oscillations and the local Hubble constant. MNRAS 2011, 416, 3017–3032. [CrossRef]
- Eyal A. Kazin et al. The WiggleZ Dark Energy Survey: improved distance measurements to z = 1 with reconstruction of the baryonic acoustic feature. MNRAS 2014, 441, 3524–3542. [CrossRef]
- Ashley J. Ross et al. The clustering of the SDSS DR7 main Galaxy sample – I. A 4 per cent distance measure at z = 0.15. MNRAS 2015, 449, 835–847.
- Shadab Alam et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: cosmological analysis of the DR12 galaxy sample. MNRAS 2017, 470, 2617–2652. [CrossRef]
- Srivatsan Sridhar et al. Clustering of LRGs in the DECaLS DR8 Footprint: Distance Constraints from Baryon Acoustic Oscillations Using Photometric Redshifts. ApJ 2020, 904, 69. [CrossRef]
- Héctor Gil-Marín et al. The Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: measurement of the BAO and growth rate of structure of the luminous red galaxy sample from the anisotropic power spectrum between redshifts 0.6 and 1.0. MNRAS 2020, 498, 2492–2531. [CrossRef]
- Anand Raichoor et al. The completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: large-scale structure catalogues and measurement of the isotropic BAO between redshift 0.6 and 1.1 for the Emission Line Galaxy Sample. MNRAS 2021, 500, 3254–3274. [CrossRef]
- Jiamin Hou et al. The completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: BAO and RSD measurements from anisotropic clustering analysis of the quasar sample in configuration space between redshift 0.8 and 2.2. MNRAS 2021, 500, 1201–1221. [CrossRef]
- Hélion du Mas des Bourboux et al. he Completed SDSS-IV Extended Baryon Oscillation Spectroscopic Survey: Baryon Acoustic Oscillations with Lyα Forests. ApJ 2020, 901, 153.
- E. de Carvalho; A. Bernui; F. Avila; C. P. Novaes; J. P. Nogueira-Cavalcante. BAO angular scale at zeff = 0.11 with the SDSS blue galaxies. A& A 2021, 649, A20. [CrossRef]
- T. M. C. Abbott et al. (DES Collaboration). Dark Energy Survey Year 3 results: A 2.7% measurement of baryon acoustic oscillation distance scale at redshift 0.835. Phys. Rev. D 2022, 105, 043512. [CrossRef]
- Lavrentios Kazantzidis; Leandros Perivolaropoulos. Evolution of the fσ8 tension with the Planck15/ΛCDM determination and implications for modified gravity theories Phys. Rev. D 2018, 97, 103503.
- Eric V. Linder. Probing gravitation, dark energy, and acceleration Phys. Rev. D 2004, 70, 023511.
- M. Chevallier; D. Polarski. Accelerating universes with scaling dark matter. International Journal of Modern Physics D 2001, 10:02, 213-223. [CrossRef]
- Eric V. Linder. Exploring the Expansion History of the Universe. Phys. Rev. Lett. 2003, 90, 091301. [CrossRef]
- W. J. Handley et al. POLYCHORD: nested sampling for cosmology. MNRAS:Letters 2015, 450, L61–L65. [CrossRef]
- D. M. Scolnic et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. ApJ 2018, 859, 101. [CrossRef]
- Michele Moresco. Raising the bar: new constraints on the Hubble parameter with cosmic chronometers at z≈2. MNRAS:Letters 2015, 450, L16–L20. [CrossRef]
- G. Risaliti; E. Lusso. A Hubble diagram for quasars. ApJ 2015, 815, 33. [CrossRef]
- Marek Demianski; Ester Piedipalumbo; Disha Sawant; Lorenzo Amati. Cosmology with gamma-ray bursts - I. The Hubble diagram through the calibrated Ep,i–Eiso correlation. A& A 2017, 598, A112.
- Licia Verde et al. The length of the low-redshift standard ruler. MNRAS 2017, 467, 731–736. [CrossRef]
- José Luis Bernal et al. The trouble with H0. JCAP 2016, 10, 019.
- Nunes, R.C.; Bernui, A. BAO signatures in the 2-point angular correlations and the Hubble tension. Eur. Phys. J. C 2020, 80, 1025. [CrossRef]
- Lemos, T. et al. Low-redshift estimates of the absolute scale of baryon acoustic oscillations. Eur. Phys. J. C 2023, 83, 495. [CrossRef]
- Andrew R. Liddle. Information criteria for astrophysical model selection. MNRAS:Letters 2007, 377, L74–L78. [CrossRef]
- Fotios K. Anagnostopoulos; Spyros Basilakos; Emmanuel N. Saridakis. Bayesian analysis of f(T) gravity using fσ8 data. Phys. Rev. D 2019, 100, 083517.
- Burnham, K. P.; Anderson, D. R. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociological Methods and Research 2004, 33(2), 261–304.
- H. Akaike. A new look at the statistical model identification. IEEE Transactions on Automatic Control 1974, 19(6), 716-723. [CrossRef]
- Gideon Schwarz. Estimating the Dimension of a Model. Ann. Statist. 1978, 6(2), 461-464. [CrossRef]
- Shadab Alam et al. Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory. Phys. Rev. D 2021, 103, 083533. [CrossRef]
- Radosław Wojtak ; Adriano Agnello. The Hubble–Lemaître constant and sound horizon from low-redshift probes. MNRAS 2019, 486, 5046–5051.
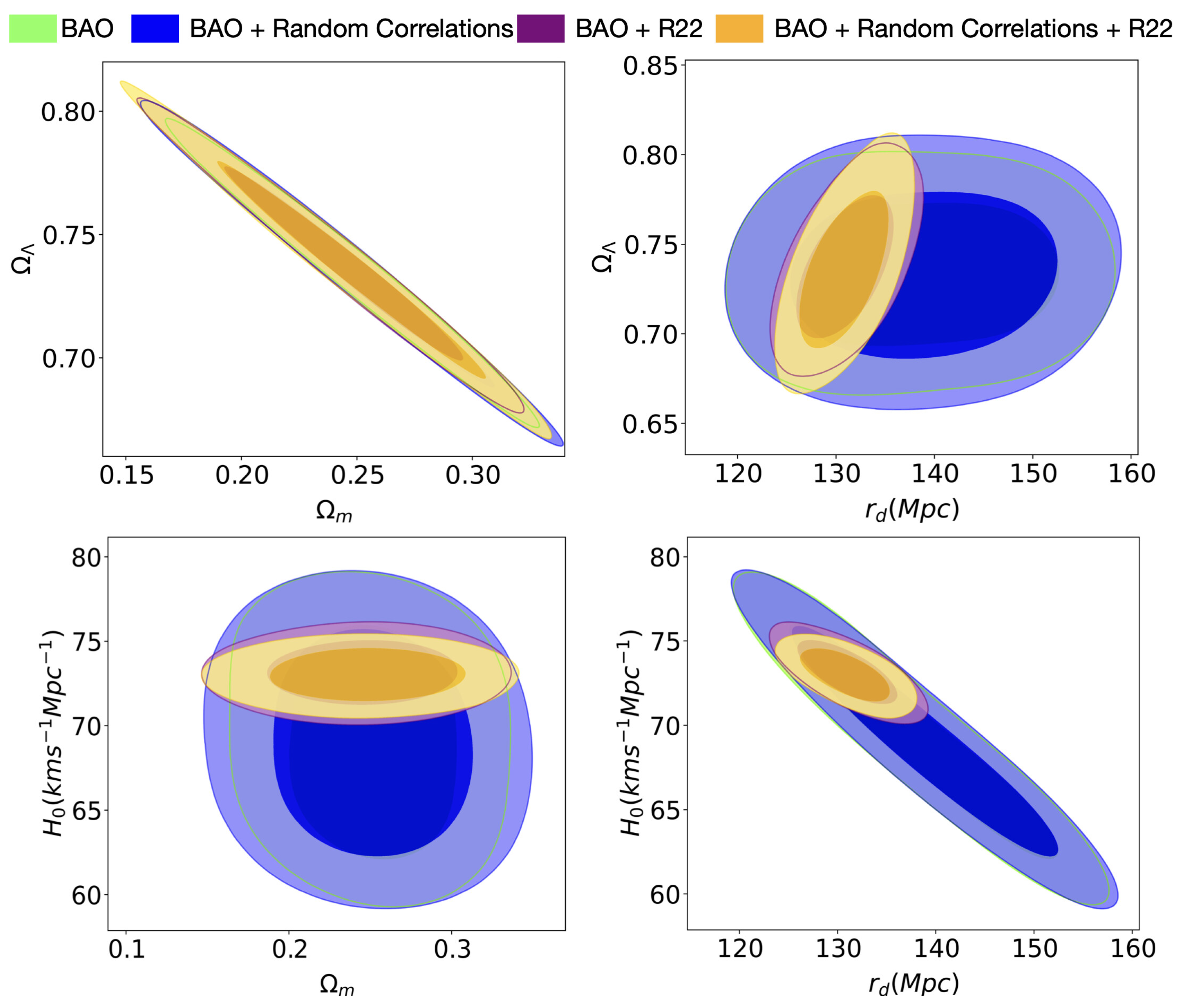
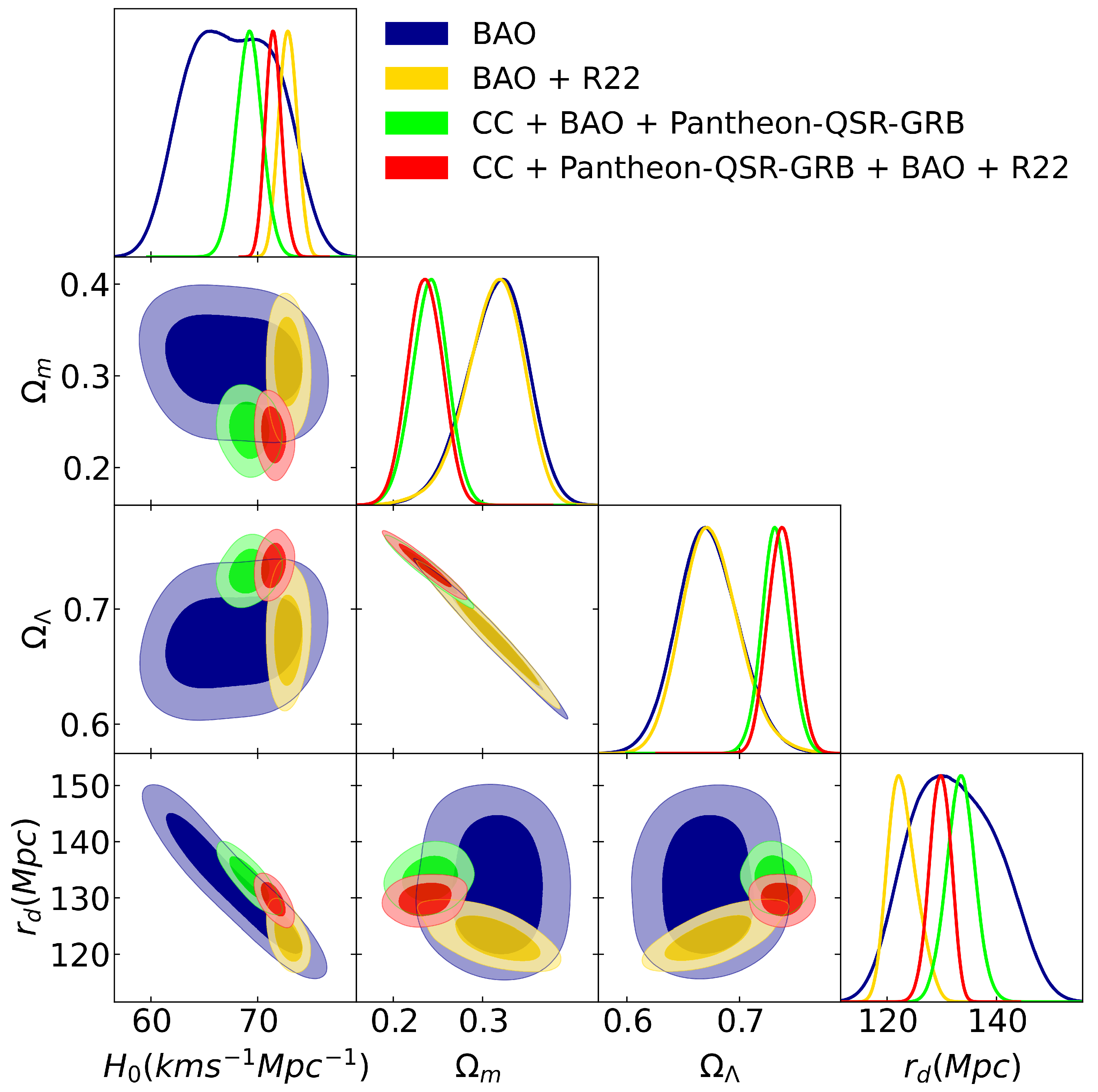
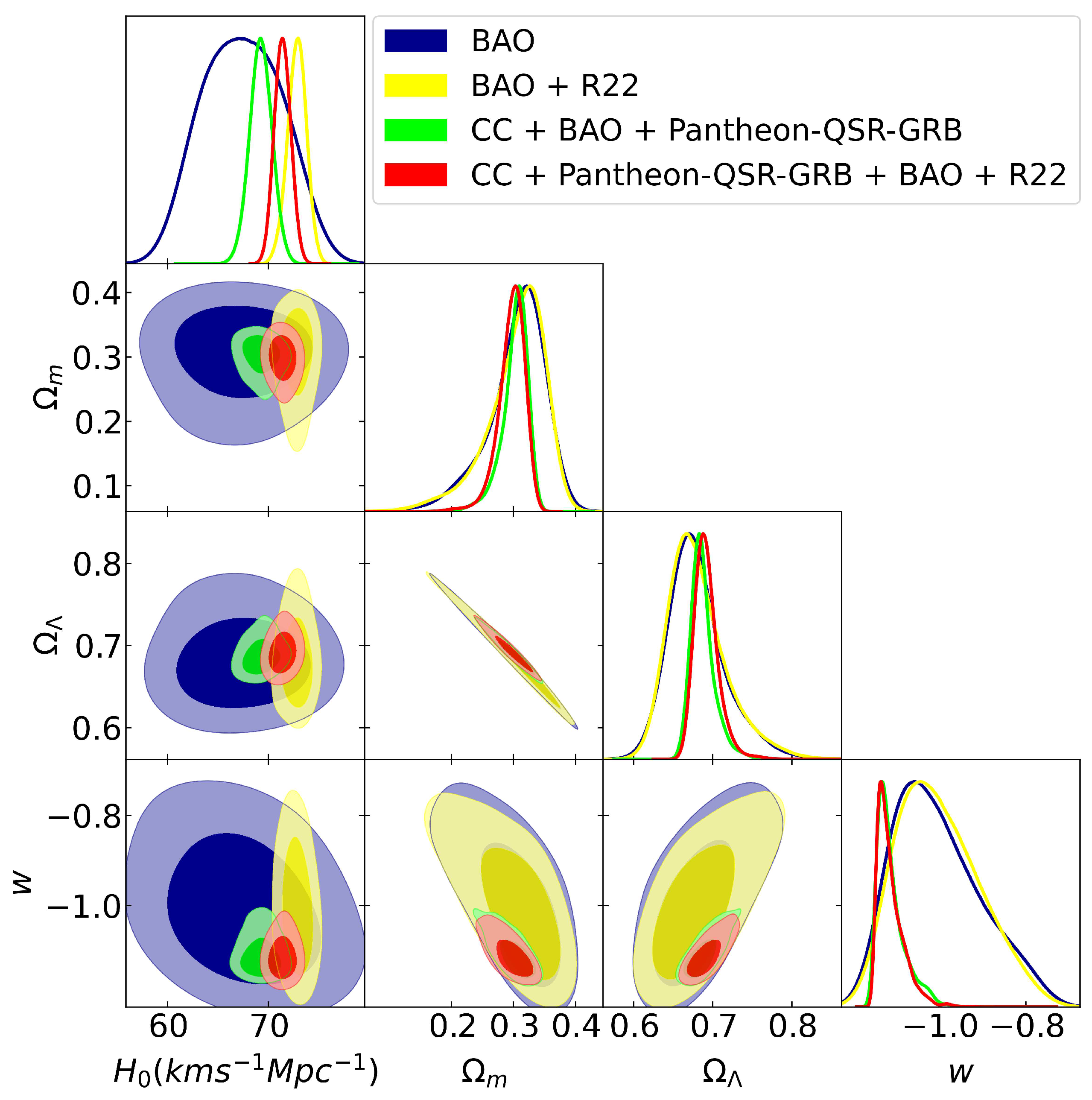
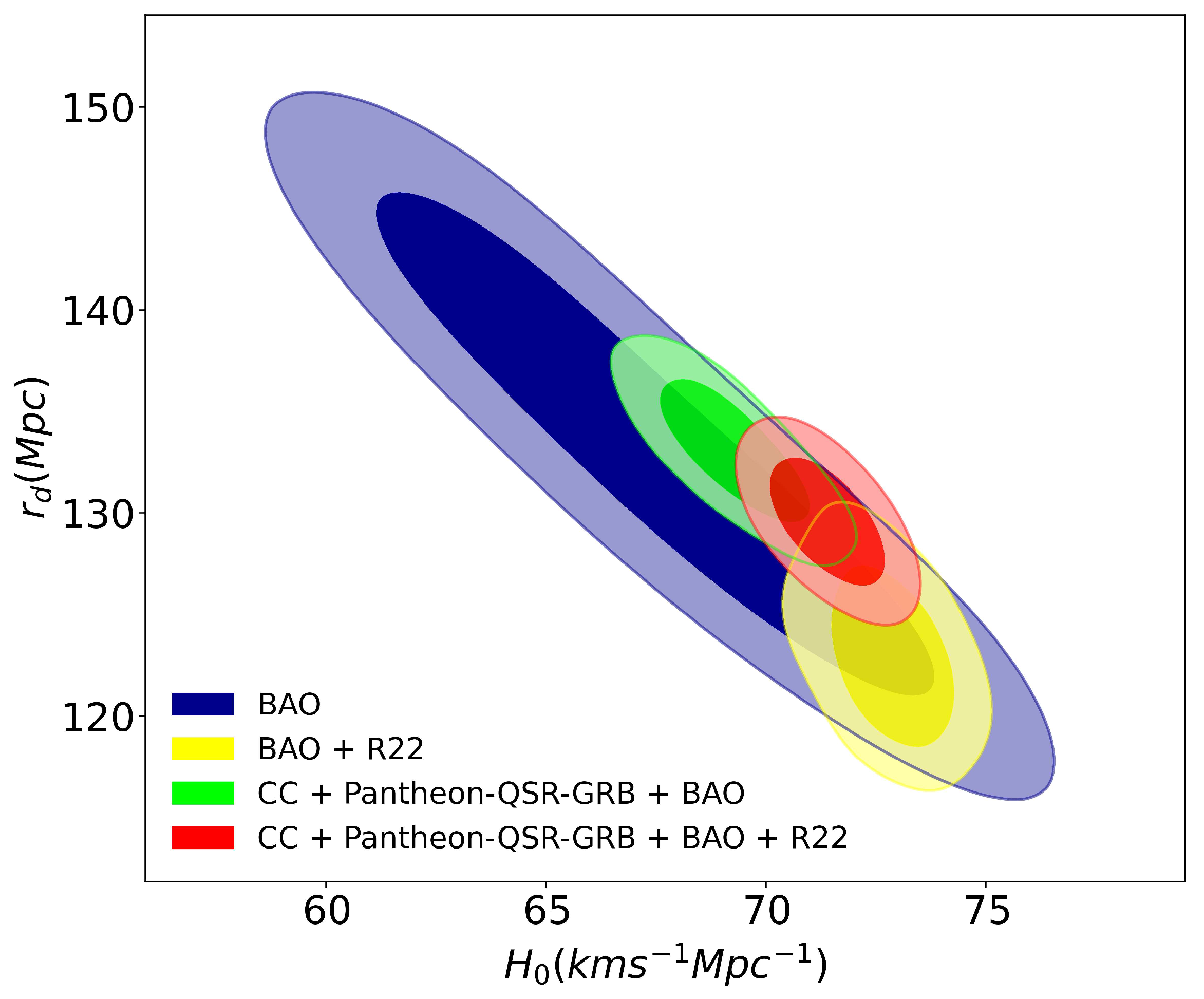
| Observable | Measurement | Error | Year | Data Set Survey | Reference | |
|---|---|---|---|---|---|---|
| 0.106 | 0.3366 | 0.015 | 2011 | 6dFGS BAO | [40] | |
| 0.11 | 2.607 | 0.138 | 2021 | SDSS Blue Galaxies sample | [49] | |
| 0.15 | 664 | 25 | 2015 | SDSS Main Galaxy Sample | [42] | |
| 0.38 | 1477 | 16 | 2017 | BOSS DR12 Galaxies | [43] | |
| 0.44 | 1716 | 83 | 2014 | WiggleZ Dark Energy Survey | [41] | |
| 0.51 | 1877 | 19 | 2017 | BOSS DR12 Galaxies | [43] | |
| 0.6 | 2221 | 101 | 2014 | WiggleZ Dark Energy Survey | [41] | |
| 0.61 | 2140 | 22 | 2017 | BOSS DR12 Galaxies | [43] | |
| 0.697 | 1529 | 73 | 2020 | DECaLS DR8 Footprint LRG Sample | [44] | |
| 0.698 | 19.77 | 0.47 | 2020 | eBOSS DR16 LRG Sample | [45] | |
| 0.73 | 2516 | 86 | 2014 | WiggleZ Dark Energy Survey | [41] | |
| 0.835 | 18.92 | 0.51 | 2022 | DES Year 3 | [50] | |
| 0.845 | 18.32 | 0.58 | 2020 | eBOSS DR16 LRG Sample | [46] | |
| 0.874 | 1674 | 102 | 2020 | DECaLS DR8 Footprint LRG Sample | [44] | |
| 1.48 | 13.11 | 0.52 | 2020 | eBOSS DR16 Quasar Sample | [47] | |
| 2.33 | 37.5 | 1.1 | 2020 | eBOSS DR16 Ly-Quasar | [48] | |
| 2.33 | 8.99 | 0.19 | 2020 | eBOSS DR16 Ly-Quasar | [48] |
| n correlated pairs | BAO | BAO + R22 |
|---|---|---|
| n=0 | = 0.2502 ± 0.0321 | = 0.2474 ± 0.0381 |
| = 0.7338 ± 0.0257 | = 0.7359 ± 0.0280 | |
| n=12 | = 0.2587 ± 0.0178 | = 0.2571 ± 0.0290 |
| = 0.7355 ± 0.0274 | = 0.7371 ± 0.0239 |
| Parameters | BAO | BAO + R22 | BAO+CC+Pantheon-QSR-GRB | BAO+R22+CC+Pantheon-QSR-GRB |
|---|---|---|---|---|
| [Km s Mpc] | 67.74 ± 4.40 | 72.85 ± 1.21 | 69.21 ± 1.22 | 71.50 ± 1.096 |
| 0.3157 ± 0.0341 | 0.3132 ± 0.0310 | 0.2411 ± 0.0290 | 0.2358 ± 0.0281 | |
| 0.6724 ± 0.0254 | 0.6748 ± 0.0243 | 0.7325 ± 0.0121 | 0.7376 ± 0.0125 | |
| [Mpc] | 132.28 ± 8.66 | 122.85 ± 2.58 | 133.46 ± 2.49 | 129.72 ± 2.90 |
| 0.9932 ± 0.0647 | 0.9218 ± 0.0141 | 0.9913 ± 0.0179 | 0.9620 ± 0.0102 |
| Parameters | BAO | BAO + R22 | BAO+CC+Pantheon-QSR-GRB | BAO+R22+CC+Pantheon-QSR-GRB |
|---|---|---|---|---|
| [Km s Mpc] | 67.43 ± 4.36 | 72.82 ± 1.47 | 69.25 ± 1.06 | 71.39 ± 1.11 |
| 0.3062 ± 0.0433 | 0.3055 ± 0.0447 | 0.3026 ± 0.0197 | 0.2974 ± 0.0187 | |
| 0.6799 ± 0.0325 | 0.6803 ± 0.0346 | 0.6871 ± 0.0134 | 0.6918 ± 0.0147 | |
| w | -1.006 ± 0.107 | -1.003 ± 0.101 | -1.111 ± 0.030 | -1.112 ± 0.0286 |
| [Mpc] | 133.29 ± 8.30 | 122.95 ± 2.74 | 133.08 ± 2.29 | 129.57 ± 2.64 |
| 0.9999 ± 0.0637 | 0.9231 ± 0.0164 | 0.9939 ± 0.0151 | 0.9663 ± 0.0106 |
| Parameters | BAO | BAO + R22 | BAO+CC+Pantheon-QSR-GRB | BAO+R22+CC+Pantheon-QSR-GRB |
|---|---|---|---|---|
| [Km s Mpc] | 67.88 ± 4.32 | 72.82 ± 1.20 | 69.25 ± 1.24 | 71.43 ± 1.01 |
| 0.3074 ± 0.0403 | 0.3058 ± 0.0408 | 0.3033 ± 0.0250 | 0.2989 ± 0.0268 | |
| 0.6802 ± 0.0331 | 0.6826 ± 0.0315 | 0.6871 ± 0.0216 | 0.6914 ± 0.0213 | |
| -0.926 ± 0.126 | -0.910 ± 0.123 | -0.830 ± 0.0925 | -0.828 ± 0.095 | |
| -0.214 ± 0.230 | -0.225 ± 0.227 | -0.292 ± 0.167 | -0.285 ± 0.169 | |
| [Mpc] | 132.68 ± 8.66 | 124.09 ± 2.94 | 132.79 ± 2.21 | 129.33 ± 2.71 |
| 1.000 ± 0.062 | 0.9334 ± 0.0202 | 0.9961 ± 0.0162 | 0.9680 ± 0.0109 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




