Submitted:
05 July 2023
Posted:
21 July 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Problem Formulation and Analysis
3. Analytical Expression of the Temperature using Akbari-Ganji’s method
4. Previous analytical results
4.1. Homotopy analysis method
4.2. Perturbation method
5. Discussion
5.1. Numerical Simulation
6. Limiting case
| Exact solution |
AGM Eq. (12) |
Error% | Exact solution |
AGM Eq. (12) |
Error% | Exact solution |
AGM Eq. (12) |
Error% | |
| 0 | 0.0522 | 0.0527 | 0.9578 | 0.1733 | 0.1795 | 3.5776 | 0.3290 | 0.3474 | 5.5927 |
| 0.2 | 0.0501 | 0.0505 | 0.7984 | 0.1661 | 0.1689 | 1.6857 | 0.3148 | 0.3246 | 3.1131 |
| 0.4 | 0.0436 | 0.0439 | 0.6881 | 0.1443 | 0.1440 | 0.2079 | 0.2728 | 0.2768 | 1.4663 |
| 0.6 | 0.0329 | 0.0330 | 0.3039 | 0.1085 | 0.1087 | 0.1843 | 0.2040 | 0.2060 | 0.9804 |
| 0.8 | 0.0180 | 0.0180 | 0.0000 | 0.0590 | 0.0590 | 0.0000 | 0.1102 | 0.1102 | 0.0000 |
| 1 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Average error (%) | 0.4580 | Average error (%) | 0.9426 | Average error (%) | 1.8587 | ||||
7. Influence of the parameters on temperature
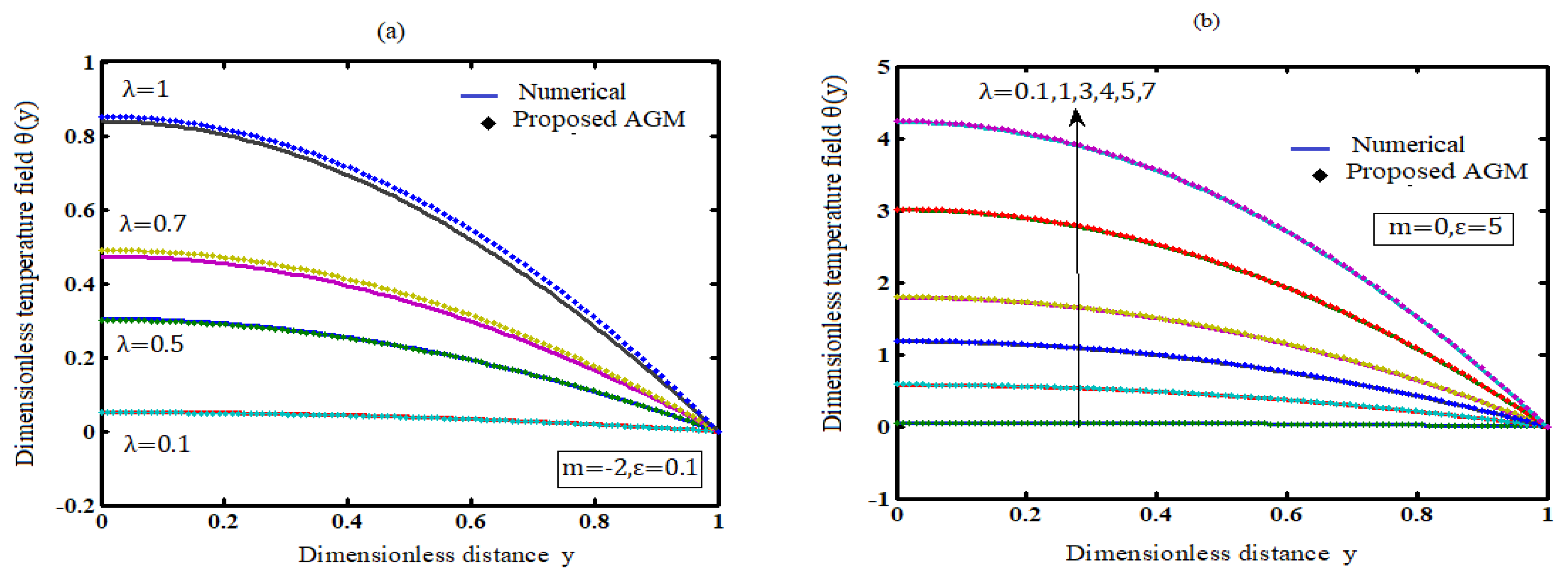
7.1. Effect of the Frank-Kamenetskii parameter on temperature
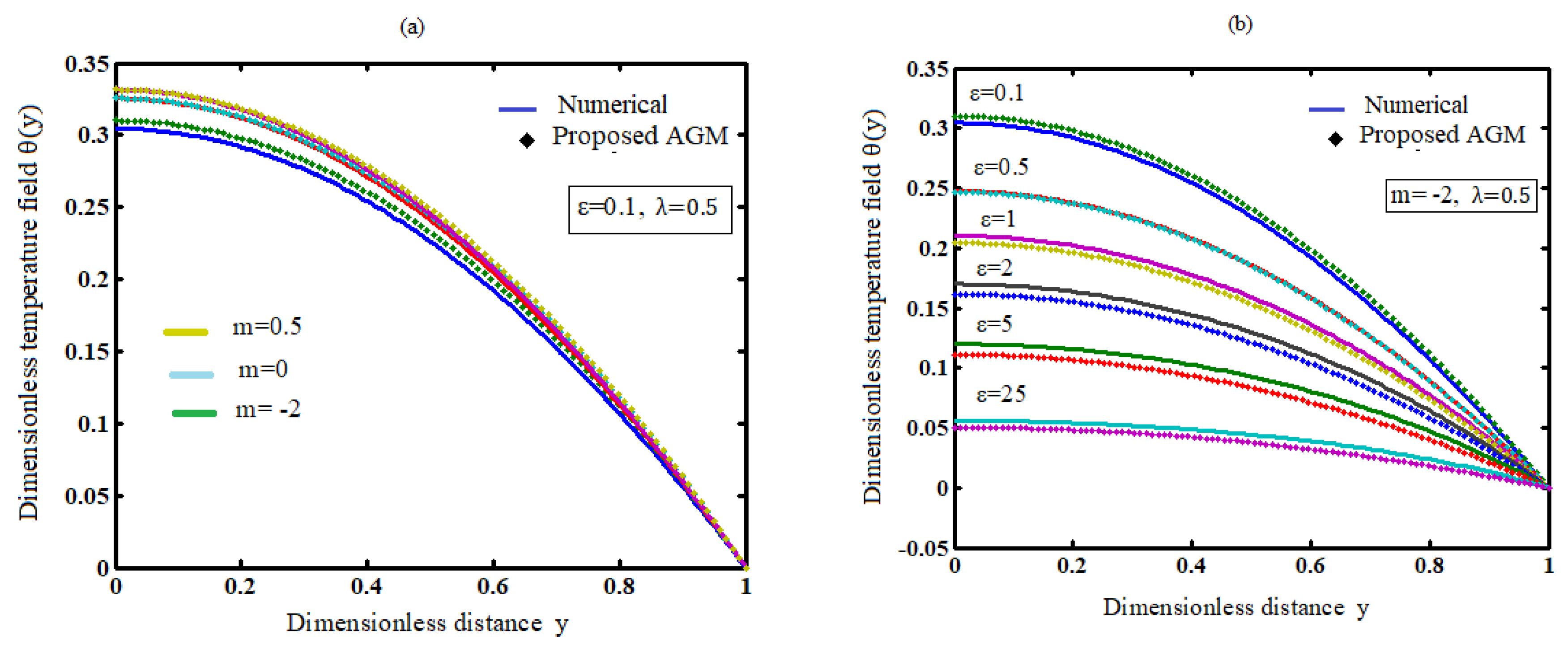
7.2. Effect of the numerical exponent m on temperature
7.3. Effect of the activation energy parameter (ε) on temperature
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Hatchard, T.D.; MacNeil, D.D.; Basu, A.; Dahn, J.R. Thermal model of cylindrical and prismatic lithium-ion cells. J. Electrochem. Soc 2001, 148, A755–A761. [Google Scholar] [CrossRef]
- Kim, G.H.; Pesaran, A.; Spotnitz, R. A three-dimensional thermal abuse model for lithium-ion cells. J. Power Sources 2007, 170, 476–489. [Google Scholar] [CrossRef]
- Peng, P.; Sun, Y.; Jiang, F. Thermal analyses of LiCoO2 lithium-ion battery during oven tests. Heat Mass Transf 2014, 50, 1405–1416. [Google Scholar] [CrossRef]
- Peng, P.; Sun, Y.; Jiang, F. Numerical simulations and thermal behavior analysis for oven thermal abusing of LiCoO2 lithium-ion battery. CIESC J 2014, 65, 647–657. [Google Scholar]
- Chiu, K.C.; Lin, C.H.; Yeh, S.F.; Lin, Y.H.; Chen, K.C. An electrochemical modeling of lithium-ion battery nail penetration. J. Power Sources 2014, 251, 254–263. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Sun, J. Catastrophe analysis of cylindrical lithium ion battery. Nonlinear Dyn 2010, 61, 763–772. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Lisbona, D.; Snee, T. A review of hazards associated with lithium and lithium-ion batteries. Process Saf. Environ. Prot 2011, 89, 434–442. [Google Scholar] [CrossRef]
- Abraham, D.P.; Roth, E.P.; Kostecki, R.; McCarthy, K.; MacLaren, S.; Doughty, D.H. Diagnostic examina tion of thermally abused high-power lithium-ion cells. J. Power Sources 2006, 161, 648–657. [Google Scholar] [CrossRef]
- Ziebert, C.; Melcher, A.; Lei, B.; Zhao, W.; Rohde, M.; Seifert, H.J. Chapter Six - Electrochemical–Thermal Characterization and Thermal Modeling for Batteries, Emerging Nanotechnologies in Rechargeable Energy Storage Systems. Micro and Nano Technologies 2017, 195–229. [Google Scholar]
- Guo, G.; Long, B.; Cheng, B.; Zhou, S.; Cao, B. Three-dimensional thermal finite element modeling of lithium-ion battery in thermal abuse application. J. Power Sources 2010, 195, 2393–2398. [Google Scholar] [CrossRef]
- Frank-Kamenetskii, D.A. Diffusion and Heat Transfer in Chemical Kinetics; Plenum Press: New York, NY, USA, 1969. [Google Scholar]
- Boddington, T.; Gray, P.; Robinson, C. Thermal explosions and the disappearance of criticality at small activation energies: Exact results for the slab. Proc. R. Soc. Lond 1979, 368, 441–461. [Google Scholar]
- Boddington, T.; Feng, C.G.; Gray, P. Thermal explosions, criticality and the disappearance of criticality in systems with distributed temperatures. I. arbitrary biot number and general reaction rate laws. Proc. R. Soc. Lond 1983, 390, 247–264. [Google Scholar]
- Boddington, T.; Gray, P.; Wake, G.C. Theory of thermal explosions with simultaneous parallel reactions. I. foundations and the one-dimensional case. Proc. R. Soc. Lond 1984, 393, 85–100. [Google Scholar]
- Graham-Eagle, J.G.; Wake, G.C. Theory of thermal explosions with simultaneous parallel reactions. II. The two- and three-dimensional cases and the variational method. Proc. R. Soc. Lond. A 1820, 401, 195–202. [Google Scholar]
- Graham-Eagle, J.G.; Wake, G.C. The theory of thermal explosions with simultaneous parallel reactions.III. Disappearance of critical behaviour with one exothermic and one endothermic reaction. Proc. R. Soc. Lond A 1986, 407, 183–198. [Google Scholar]
- Gelfand, I.M.; Fomin, S.V. Calculus of Variations; Prentice Hall: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
- Ajadi, S.O.; Gol’dshtein, V. Critical behaviour in a three-step reaction kinetics model. Combust. Theory Model 2009, 13, 1–16. [Google Scholar] [CrossRef]
- Balakrishnan, E.; Swift, A.; Ke, G.C. Critical values for some nonclass A geometries in thermal ignition theory. Mathl. Comput. Modelling 1996, 24, 1–10. [Google Scholar] [CrossRef]
- Makinde, O.D. Exothermic explosions in a slab: A case study of series summation technique. Int. Commun. Heat Mass Transf. 2004, 31, 1227–1231. [Google Scholar] [CrossRef]
- Ananthaswamy, V.; Subha, M. Analytical expressions for exothermic explosions in a slab. Int. J. Res. Granthaalayah 2014, 1, 22–33. [Google Scholar] [CrossRef]
- Er-Riani, M.; Chetehouna, K. On the critical behaviour of exothermic explosions in class A geometries. Math. Probl. Eng 2011, 536056, 1–14. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int J Non-Linear Mech 2000, 35, 37–43. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput 2003, 135, 73–79. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for solving boundary value problems. Phys. Lett. A 2006, 350, 87–88. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Kannan, M.; Rajendran, L. Approximate analytical solutions of biofilm reactor problem in applied biotechnology. Theor. Found. Chem. Eng 2021, 55, 851–861. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Rajendran, L.; Abukhaled, M.; Kannan, M. Semi-analytical expressions for the concentrations and effectiveness factor for the three general catalyst shapes. React. Kinet. Mech. Catal. 2022, 1–16. [Google Scholar] [CrossRef]
- Abukhaled, M. Variational iteration method for nonlinear singular two-point boundary value problems arising in human physiology. J. Math 2013, 1–4. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Variational iteration method: New development and applications. Comput. Math. with Appl 2007, 54, 881–894. [Google Scholar] [CrossRef]
- Vinolyn Sylvia, S.; Joy Salomi, R.; Rajendran, L.; Abukhaled, M. Solving nonlinear reaction–diffusion problem in electrostatic interaction with reaction-generated pH change on the kinetics of immobilized enzyme systems using Taylor series method. J. Math. Chem 2019, 59, 1332–1347. [Google Scholar] [CrossRef]
- He, J.H. Taylor series solution for a third order boundary value problem arising in Architectural Engineering. Ain Shams Eng. J. 2022, 11, 1411–141. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Rajendran, L.; Lyons, M.E.G.; Abukhaled, M. Theoretical Analysis of Mass Transfer Behavior in Fixed-Bed Electrochemical Reactors: Akbari-Ganji’s Method. Electrochem 2022, 3, 699–712. [Google Scholar] [CrossRef]
- Joy Salomi, R.; Vinolyn Sylvia, S.; Rajendran, L.; Abukhaled, M. Electric potential and surface oxygen ion density for planar, spherical and cylindrical metal oxide grains. Sens. Actuators B Chem 2020, 321, 128576. [Google Scholar] [CrossRef]
- Manimegalai, B.; Lyons, M.E.G.; Rajendran, L. A kinetic model for amperometric immobilized enzymes at planar, cylindrical and spherical electrodes: The Akbari-Ganji method. J Electroanal Chem 2021, 880, 114921. [Google Scholar] [CrossRef]
- Mary, M.; Chitra Devi, M.; Meena, A.; Rajendran, L.; Abukhaled, M. Mathematical modeling of immobilized enzyme in porous planar, cylindrical, and spherical particle: A reliable semi-analytical approach. React. Kinet. Mech. Catal 2021, 1–11. [Google Scholar] [CrossRef]
- Jeyabarathi, P.; Rajendran, L.; Lyons, M.E.G. Reaction-diffusion in a packed-bed reactors: Enzymatic isomerization with Michaelis-Menten kinetics. J Electroanal Chem 2022, 910, 11618. [Google Scholar] [CrossRef]
- Akbari, M.R.; Ganji, D.D.; Goltabar, A.R. Solving nonlinear differential equations of Vanderpol, Rayleigh and Duffing by AGM. Front. Mech. Eng 2014, 9, 177–190. [Google Scholar] [CrossRef]
- Rostami, A.K.; Akbari, M.R.; Ganji, D.D.; Heydari, S. Investigating Jeff ery-Hamel flow with high magnetic field and nanoparticle by HPM and AGM. Cent. Eur. J. Eng 2014, 4, 357–370. [Google Scholar]
- Meresht, N.B.; Ganji, D.D. Solving nonlinear differential equation arising in dynamical systems by AGM. Int. J. Appl. Comput. Math 2017, 3, 1507–1523. [Google Scholar] [CrossRef]
- Manimegalai, B.; Swaminathan, R.; Lyons, M.E.G.; Rajendran, L. Application of Taylor’s series with Ying Buzu Shu algorithm for the nonlinear problem in amperometric biosensors. Int. J. Electrochem. Sci. 2022, 17, 22074. [Google Scholar] [CrossRef]
| Num. | AGM Eq. (12). This work |
HAM [11] Eq. (14) |
PM [10] Eq. (15) |
Error % AGM Eq. (12) This work |
Error % HAM [11] Eq. (14) |
Error % PM [10] Eq. (15) |
|
| 0 | 0.0517 | 0.0517 | 0.0517 | 0.0516 | 0.0000 | 0.0000 | 0.1934 |
| 0.2 | 0.0496 | 0.0496 | 0.0496 | 0.0495 | 0.0000 | 0.0000 | 0.2016 |
| 0.4 | 0.0432 | 0.0436 | 0.0434 | 0.0433 | 0.9259 | 0.0230 | 0.4629 |
| 0.6 | 0.0327 | 0.0324 | 0.0330 | 0.0329 | 0.9174 | 0.0303 | 0.6116 |
| 0.8 | 0.0179 | 0.0180 | 0.0185 | 0.0185 | 0.5586 | 3.3519 | 3.3519 |
| 1 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Average error (%) | 0.3493 | 0.5675 | 0.8036 | ||||
| Num. | AGM Eq. (12). This work |
HAM [11] Eq. (14) |
PM [10] Eq. (15) |
Error % AGM Eq. (12) This work |
Error % HAM [11] Eq. (14) |
Error % PM [10] Eq. (15) |
||
| 0 | 0.3045 | 0.3201 | 0.2951 | 0.2823 | 4.8133 | 3.0870 | 7.2906 | |
| 0.2 | 0.2916 | 0.3001 | 0.2829 | 0.2707 | 2.8000 | 2.9835 | 7.1673 | |
| 0.4 | 0.2532 | 0.2548 | 0.2466 | 0.2363 | 0.6319 | 2.5671 | 6.6745 | |
| 0.6 | 0.1899 | 0.1893 | 0.1869 | 0.1792 | 0.3159 | 1.5798 | 5.6334 | |
| 0.8 | 0.1031 | 0.1030 | 0.1041 | 0.1002 | 0.0970 | 0.9699 | 2.8128 | |
| 1 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Average error (%) | 1.4430 | 1.8645 | 4.9298 | |||||
| Num. | AGM Eq. (12). This work |
HAM [11] Eq. (14) |
PM [10] Eq. (16) |
Error % AGM Eq. (12) This work |
Error % HAM [11] Eq. (14) |
Error % PM [10] Eq. (16) |
||
| 0 | 0.0522 | 0.0523 | 0.0521 | 0.0522 | 0.1916 | 0.1916 | 0.0000 | |
| 0.2 | 0.0501 | 0.0501 | 0.0500 | 0.0501 | 0.0000 | 0.1996 | 0.0000 | |
| 0.4 | 0.0436 | 0.0437 | 0.0437 | 0.0438 | 0.2294 | 0.2294 | 0.4587 | |
| 0.6 | 0.0329 | 0.0331 | 0.0332 | 0.0333 | 0.6079 | 0.9118 | 1.2158 | |
| 0.8 | 0.0180 | 0.0181 | 0.0188 | 0.0187 | 0.5555 | 4.4444 | 3.8889 | |
| 1 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Average error (%) | 0.2641 | 0.9961 | 0.9272 | |||||
| Num. | AGM Eq. (12). This work |
HAM [11] Eq. (14) |
PM [10] Eq. (16) |
Error % AGM Eq. (12) This work |
Error % HAM [11] Eq. (14) |
Error % PM [10] Eq. (16) |
|
| 0 | 0.3255 | 0.3208 | 0.3192 | 0.3172 | 1.4439 | 1.9355 | 2.5499 |
| 0.2 | 0.3116 | 0.3077 | 0.3059 | 0.3040 | 1.2516 | 1.8292 | 2.4390 |
| 0.4 | 0.2701 | 0.2684 | 0.2662 | 0.2646 | 0.6294 | 1.4439 | 2.0363 |
| 0.6 | 0.2021 | 0.2030 | 0.2011 | 0.1994 | 0.4433 | 0.4948 | 1.3360 |
| 0.8 | 0.1093 | 0.1113 | 0.1117 | 0.1110 | 1.8230 | 2.1958 | 1.5553 |
| 1 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Average error (%) | 0.9319 | 1.3163 | 1.6527 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





