Detailed Comparative Analysis of Structural Stability and Electron-Phonon Properties of ZrO₂: Mechanism of Water Adsorption on t-ZrO₂ (101) and t-YSZ (101) Surfaces

1. Introduction

Zirconium ceramics have been extensively studied in recent years because of their excellent electrical, optical and mechanical properties. They are also biocompatible and have a wide range of biomedical applications. Tetragonal phase yttria stabilized zirconia (Y-TZP) has been used in various medical applications since the 1980s, particularly for dental crowns [1,2]. In addition, bulk materials and nanocomposites based on ZrO₂ are used in electrochemical cells because of their high oxide ion conductivity and catalytic activity, low thermal conductivity and mechanical/chemical stability, as well as compatibility with electrolytes [3,4], which makes them from a structural point of view [3,4].

One of the most remarkable properties of ceramics based on zirconia is the presence of three crystalline forms with different properties [5,6,7,8,9]. There are the most stable monoclinic (mineral baddeleyite; m-ZrO₂), metastable tetragonal (medium temperature) and unstable cubic structure of zirconium dioxide (high temperature). High-pressure induced zirconium phases in the form of brookite (orthorhombic-I) and cotunnite (orthorhombic-II) are also known [10,11].

Pure zirconium dioxide undergoes a phase transformation from monoclinic to tetragonal (about 1173°C), and then to cubic (about 2370°C), accompanied by a change in volume and, accordingly, their strength [12,13,14]:

For the application of zirconia in advanced zirconia ion-conducting ceramic devices, it is important that the stabilized material has an adequate level of conductivity and the desired mechanical-chemical stability in both oxidizing and reducing atmospheres. Obtaining a stable material from zirconia is difficult due to a noticeable change in volume during the phase transition. Stabilization of zirconium dioxide is achieved by replacing some Zr4+ ions with larger ions in the crystal lattice [15,16,17,18]. For example, numerous studies have shown that doping with polyvalent oxides, including certain concentrations of yttrium oxide, stabilizes the high-temperature cubic and tetragonal phases of ZrO₂ at room temperature. This also leads to an increase in the concentration of oxygen vacancies and oxygen-ion conductivity, which makes it possible to use stabilized ZrO₂ as an electrolyte in fuel cells [17]). The ionic conductivity of ZrO₂ strongly depends on the phase modification and the content of stabilizing additives in the system, which is also evidenced by the phase diagram given in [18].

Many technological applications of zirconia (pure ZrO₂ or their stabilized alloys) are directly related to interaction with water. Examples are internal steam reforming in solid oxide fuel cells [19], catalysis [20], gas sensors [21], or their use as a biocompatible material [22]. ZrO₂ surfaces are also proposed as suitable materials for hydrogen storage [21,22,23]. However, little is known about the interaction of water with ZrO₂ surfaces at a fundamental level, which is mainly due to the lack of suitable samples. This is quite different for other oxide substrates [23,24,25]. Water is weakly adsorbed on many defect-free oxide surfaces; in ultrahigh vacuum, then stripped at a temperature below room temperature. Usually, at 160–250 K [26], water can bind more strongly to surfaces with defects, as was shown for rutile TiO₂ (110) [27]. In these cases, H₂O dissociates into an OH group, which fills the oxygen vacancy, and into a hydrogen atom, which binds to surface oxygen and forms a second OH group. On TiO₂, these OH groups are stable up to 490 K [28]. On a defect-free surface oxide (a-Cr2O₃(001) [29], a-Fe₂O₃(012) [30] and oxides of alkaline earth metals, including Ca₃Ru₂O₇(001) [31]), water can be strongly bound if the end of the surface includes highly active cations. Then it can easily dissociate. On the surface of RuO₂(110), PdO(101), and Fe₃O₄(001), water binds coordinatively unsaturated cations and partially dissociated forms of the structure stabilized by hydrogen bonds [32,33,34]. Very high enthalpy adsorption of low H₂O powder materials (≥ 2 eV on monoclinic and ≈ 1.5 eV on tetragonal ZrO₂) has been reported decreasing to liquid-water binding (0.45 eV) at coverages of approximately 2–4 H₂O/nm² [35]. In another work, Droshkevich A.S. and others [36] reported on the chemoelectric conversion of water adsorption energy into electricity on the surface of zirconium dioxide nanopowders when doped with 3 mol. %Y₂O₃, which were synthesized with sizes of 7.5 nm.

However, despite numerous works in this direction, such detailed studies of water adsorption on the ZrO₂ surface have not yet been carried out, and only a few reports on H₂O adsorption can be found in the literature. In particular, studies of H₂O adsorption on well-defined monoclinic surfaces of zirconia (m-ZrO₂ (101) and m-ZrO₂ (101) and their doped structures) have not yet been carried out. For example, it is especially difficult to study experimentally pure ZrO₂ single crystals grown from a melt; they exhibit phase transformations upon cooling; therefore, their doped structures (eg YSZ) are usually investigated. However, the surface chemistry of YSZ is much more complex than that of pure ZrO₂, as shown for CO and CO₂ adsorption [37]. In another work, Kobayashi et al. [38] found that YSZ slowly decomposed at about 250°C due to the t-m transformation. This t-m transformation is accompanied by microcracks and loss of material strength in a humid atmosphere, and this discovery cooled the excitement caused by the discovery of PPT in zirconia-based ceramics. This t-m transformation due to the presence of water or a humid environment in zirconia-based ceramic materials has been termed low-temperature degradation or aging of ZrO₂ crystals. A lot of work has been done on this topic over the past couple of decades, including many hypotheses and discussions, and the most reliable hypothesis on the topic of YSZ is based on filling oxygen vacancies that were present in the matrix to maintain a stable t-YSZ phase. Thus, the filling of these O-vacancies with water radicals, either O₂ or OH, destabilizes the t-YSZ phase. However, the YSZ stabilization mechanism itself has not been fully studied and is still the subject of numerous discussions. Therefore, the theoretical study and modeling of water adsorption on these surfaces is necessary as a starting point for a good understanding of the ongoing processes and phenomena from a fundamental point of view. On the other hand, aspects of the shift of the Fermi level after doping with yttrium oxide in ZrO₂, as well as under the influence of water adsorption, are still not clear due to the difficulty of their detection in the experiment.

For these reasons, in order to obtain detailed information on the process of adsorption of water molecules on the surface of ZrO₂ and YSZ, as well as on the effect of doping on their electronic and structural properties, quantum chemical calculations were carried out in this work within the framework of the DFT.

2. Modeling details

Ab initio quantum chemical calculations were carried out on the basis of the density functional theory [39]. All three modifications of ZrO₂ (Figure 1a–c) were first relaxed using the GGA functionals (PBE) [40] and strictly bounded normalized potential (SCAN) [41]. To obtain the most accurate value of the ground state energy, the total energy was calculated within the framework of the GGA exchange-correlation potential, and SCAN was used to correctly estimate the lattice parameters. The calculations were carried out using the Vienna Ab-initio Simulation Package (VASP 6.3.2) [42]. By comparing the total energy in the unit cell, a stable ZrO₂ phase was found, and for stabilization to room temperature, a 2x2x2 supercell was created to simulate the effect of 3.23, 6.67, 10.34 and 16.15 mol. %Y₂O₃ on the stability of ZrO₂ and evaluate influence of Y₂O₃ doping on the position of the Fermi level. An orbital analysis was performed by summing the contributions of the individual atomic species in the unit cell and showing the contributions of the main atoms at the meeting point of the valence and conduction bands. Vacancies were taken into account by removing one O atom with each subsequent substitution of 2 Y³⁺ ions to the Zr⁴⁺ position. The atomic orbitals H (1^s), O (2^s, 2^p), Zr (4^d, 5^s), and Y (4^s, 4^p, 4^d, 5^s) were considered valence electrons, while the remaining electrons were considered nuclear electrons and remained frozen. The PAW method has been used to describe the interaction between valence electrons and electrons in the nucleus. The kinetic energy cutoff was fixed at the level of 600 eV, and all calculations were carried out taking into account spin-polarized effects.

Next, ab initio calculations were carried out to study the mechanism of adsorption of a water molecule on the surface of ZrO₂ and ZrO₂ by stabilized Y₂O₃, where the adsorption energies of a water molecule on the surface of ZrO₂ and YSZ were found, as well as an orbital analysis was carried out and the shift of the Fermi level was estimated.

For such specific problems, the choice of an adsorbed surface is very important, and in order to obtain results consistent with experiment, we must accurately select a surface suitable for us, with the lowest density of surface broken bonds and electrostatic repulsion of neighboring layers, taking into account the thermodynamic stability of this surface. The higher the surface energy, the more thermodynamically unstable it is [43] and the more difficult it is to create the corresponding surface, namely, the surface energy is closely related to the number of atoms in the surface structure and the depth of the vacuum layer.

In this work, in order to select a suitable optimal surface for water adsorption and study its behavior on this surface, we also calculated the surface energy (σ) using equation 1 taken from [44]:

$$\sigma =\frac{1}{2}\frac{\left[E_{slab}-\left(\raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$n$}\right.\right)E_{bulk}\right]}{S},$$

(1)

where S — total surface area of the plate, $E_{slab}$ — total plate energy, $E_{bulk}$ – total energy of an optimized bulk structure. N and n respectively represent the total number of atoms in the surface structure and unit cell, and 2 represents the two surfaces of the calculated structure in the direction of the Z axis.

Models of the crystal wafer surface were constructed based on an extended 2 × 2 supercell with a vacuum space of 35 Å along the z direction to minimize the interaction of neighboring layers. Taking into account the accuracy and calculation time, the lower layers of the surface plate were frozen, and the upper part was allowed to relax. Monkhorst-Pack grids with a 3 × 3 × 1 k-point grid were used to sample the reciprocal space for 2 × 2 plate calculations. Each molecule in the gas phase was placed in a large box (11 × 13 × 10 Å3) to avoid side interactions.

Single H₂O molecules were initially located at a height of 2.5 Å above the chosen surface, and different orientations, relaxing H₂O molecules, and the upper layers of the plate were compared for each initial adsorption site. For each molecule, four initial adsorption centers were tested (above the Zr atom, above the terminal oxygen Ou (top) or Od (bottom), and also in the center above the Zr position (see Figure 1d)). For the YSZ surface model, various initial adsorption sites were also investigated: above the Zr atom, the extreme oxygen Ou (top), Od (bottom), in the oxygen vacancy position, the yttrium atom and the Ou-Od-Zr center (see Figure 1e) to find the most favorable adsorption sites leading to stable configurations. Nonequivalent initial adsorption sites have not been studied in detail.

The adsorption energy ($E_{ads}$) was calculated as the difference between the energy of the plate with adsorbed water ($E_{H2О/surface}$) and the sum of the energies of the surface ($E_{surface}$) and the H₂O molecule ($E_{H2О}$), according to the following equation:

$$E_{ads}=E_{H2О/surface}-(E_{surface}+E_{H2О})$$

(2)

To take into account long-range uncoupled interactions, the van der Waals effects were taken into account as the difference between the calculated van der Waals energy of a plate with adsorbed H₂O molecules ($E_{H2О/surface}^{vdW}$) and the sum of the calculated van der Waals energies of the surface ($E_{surface}^{vdW}$) and H₂О molecules ($E_{H2О}^{vdW}$):

$$E_{ads}^{vdW}=E_{H2О/surface}^{vdW}-(E_{surface}^{vdW}+E_{H2О}^{vdW})$$

(3)

where the interaction energy $vdW$ is taken into account by the Leonard-Jones potential.

3. Results and discussion

3.1. Structural stability and electron-phonon properties of ZrO₂

At the first stage of modeling, the structural-energy relaxation of pure ZrO₂ phases was carried out using the VASP package. To find the optimal cutoff energy for the ENCUT plane wave basis functions and the corresponding number of k-points in the Brillouin zone, we tested the convergence of the total unit cell energy as a function of ENCUT and KPOINTS.

The results of the k-point convergence test for ZrO₂ cubic phases are shown in Figure 3, 2 and performed to build a grid from k-point data with an initial value of ENCUT = 1.3*ENMAX. Based on the results obtained, it can be concluded that for a 4x4x4 k-point grid with the Monkhrost-Pack scheme, it is optimal for the geometric relaxation of ZrO2. However, when calculating the electronic structure of these compounds, the number of k-points was at least doubled in order to obtain a better density of states (DOS).

Figure 2. The total energy of the c-ZrO₂ unit cell as a function of the number of k-points under the condition ENCUT=1.3*ENMAX.

Figure 2. The total energy of the c-ZrO₂ unit cell as a function of the number of k-points under the condition ENCUT=1.3*ENMAX.

Similar tests were carried out to establish the cutoff energy, which shows that the choice of 600 eV is suitable for calculations, and a further increase in this energy increases the cost of the calculation without affecting its accuracy (Figure 3). Therefore, all further calculations were carried out at ENCUT = 600 eV.

Similar convergence tests were also carried out for the tetragonal and monoclinic phases of ZrO₂ using the GGA potential. In Table 1 compares the calculated values of the crystal lattice constants of the ZrO₂ phase, obtained from two exchange-correlation potentials, with the literature results.

According to the results given in Table 1, it can be seen that during the transition from the high-temperature phase to the low-temperature phase, the lattice distortion leads to a displacement of O ions in the c direction by the value of dz, expressed in relative units. As a result of distortion in the tetragonal phase, all Zr-O bonds will become nonequivalent. According to Table 3, the SCAN functionality describes the geometry much better than the standard GGA-PBE. However, it is also seen from the available data that GGA and SCAN almost identically describe the energy difference between the monoclinic and tetragonal phases of ZrO₂. Since the SCAN exchange-correlation functional describes the structural properties well, we decided to use this functional in the future when describing the geometry of other systems.

Table 2 compares the total energies calculated by the GGA method for systems of the monoclinic, tetragonal, and cubic phases of ZrO₂. It can be seen that among all systems, the most stable phase with the lowest energy is m-ZrO₂, that is, in fact, in terms of the field energy at low temperatures, the stable phase is monoclinic with the space group P21/c.

Table 2. GGA- calculated total electronic energies of c-ZrO₂, t-ZrO_2, m-ZrO₂.

System	Energy	ΔE
m-ZrO2	-115.179	0
t-ZrO2	-114.754	0.425
c-ZrO2	-114.346	0.833

Table 2. GGA- calculated total electronic energies of c-ZrO₂, t-ZrO_2, m-ZrO₂.

System	Energy	ΔE
m-ZrO2	-115.179	0
t-ZrO2	-114.754	0.425
c-ZrO2	-114.346	0.833

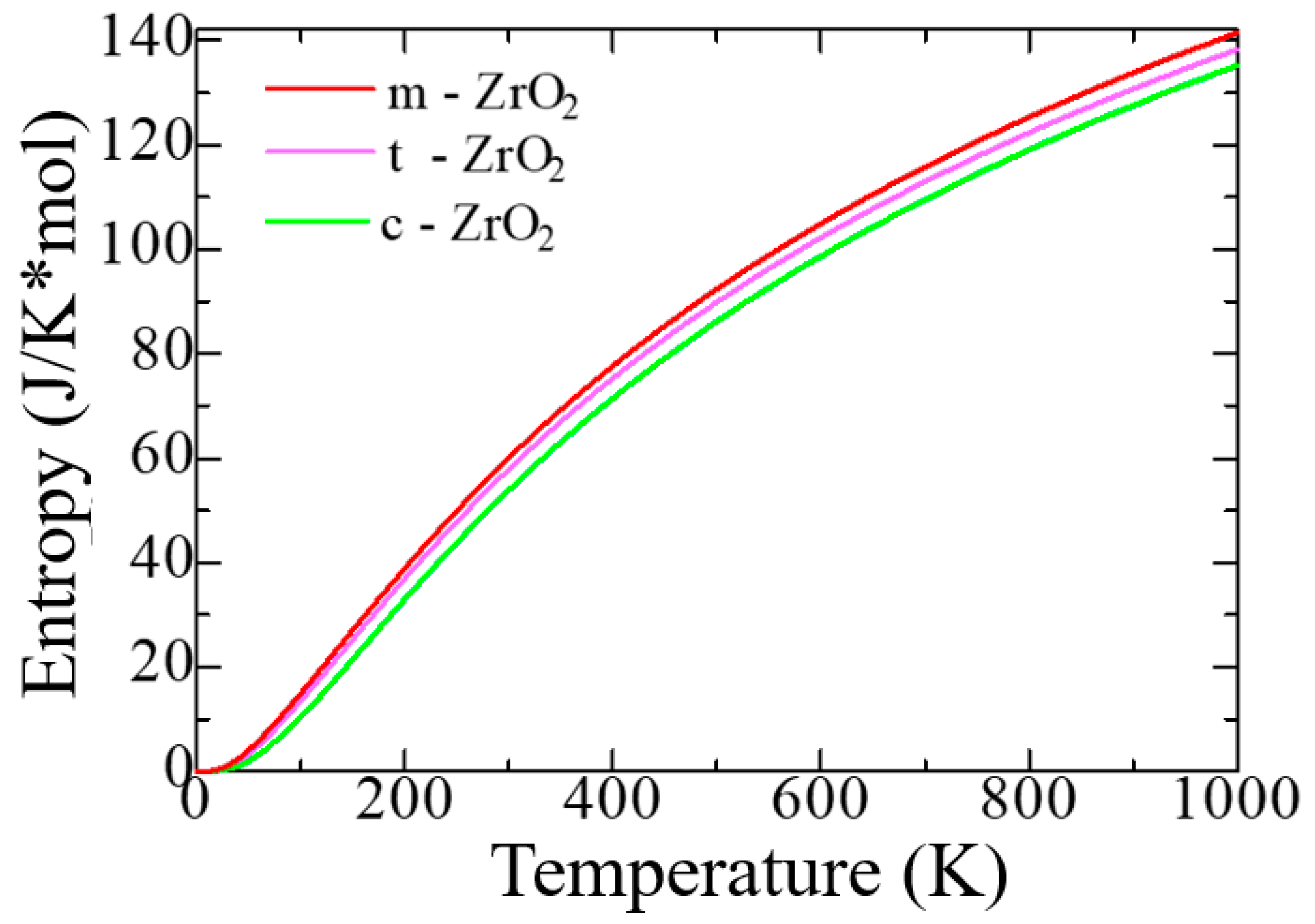
Further, using the Phonopy code in the VASP package, the thermodynamic properties and phonon spectra of the ZrO₂ phase were calculated for a more detailed discussion and substantiation of the structural stability of the ZrO₂ monoclinic phase. Figure 4 shows the change in the entropy of the unit cells of the ZrO₂ phase as a function of temperature.

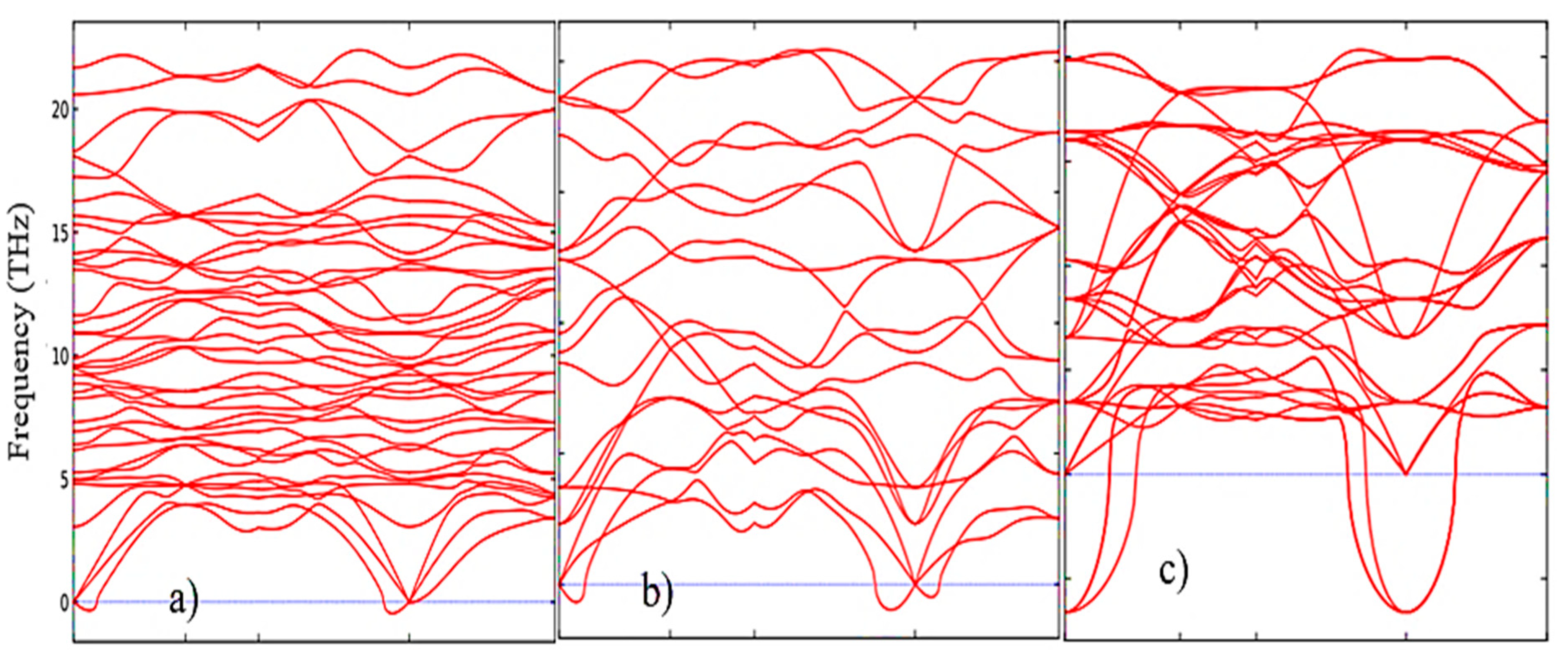
According to Figure 4, as the transition from monoclinic to tetragonal and cubic phases, the entropy of these compounds decreases, which corresponds to the criterion of inverse dependence of enthalpy or direct dependence of entropy and stability of solid systems [53]. Thus, the monoclinic phase is the most stable with the highest entropy among other ZrO₂ phases. This pattern can be clearly observed after analyzing the pattern of phonon frequencies of the three phases of ZrO₂ (Figure 5a–c), from which it is clearly seen that the monoclinic phase has the smallest negative modes than the other two phases.

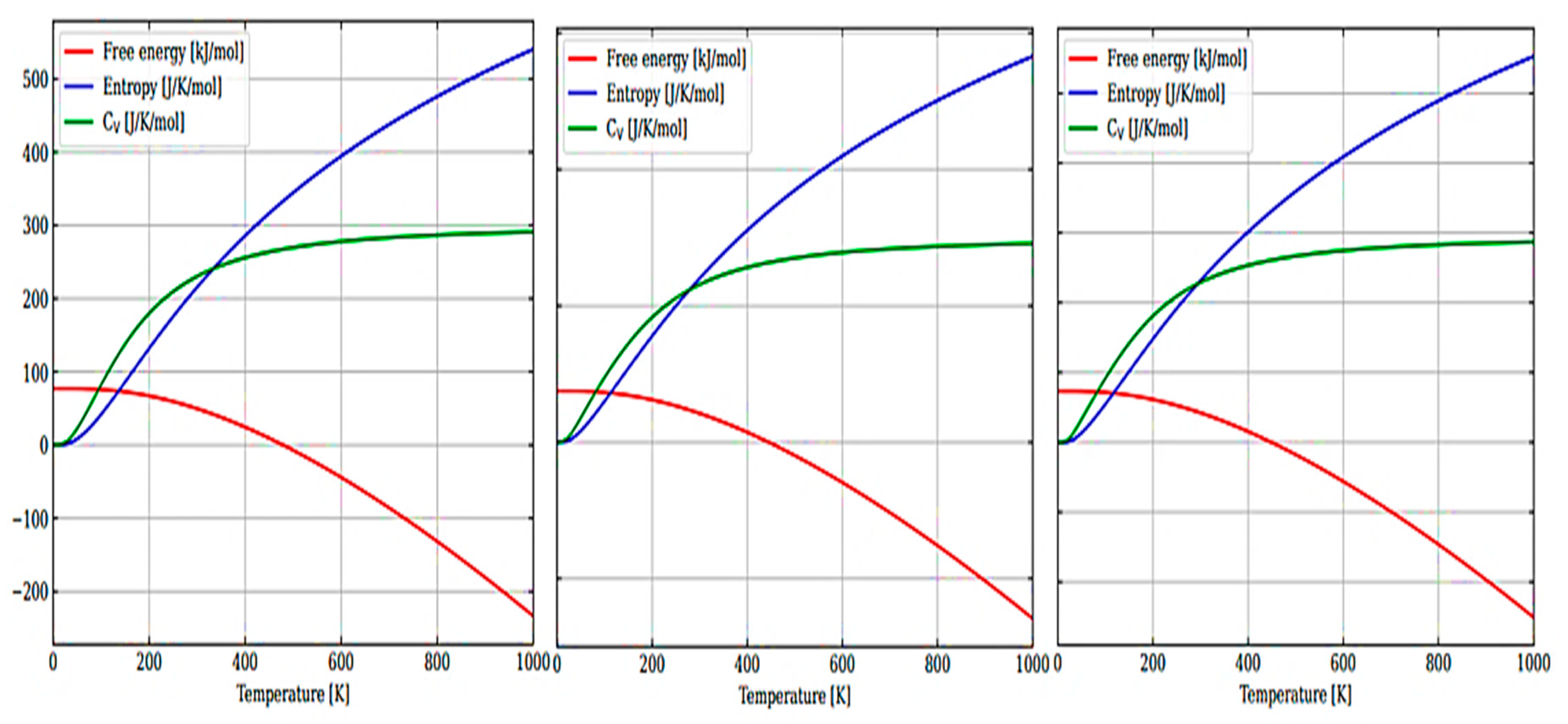
Figure 6a–c shows the temperature dependence of the free energy, entropy, and heat capacity of a 12-atom supercell for m-ZrO₂, t-ZrO₂, and m-ZrO₂.

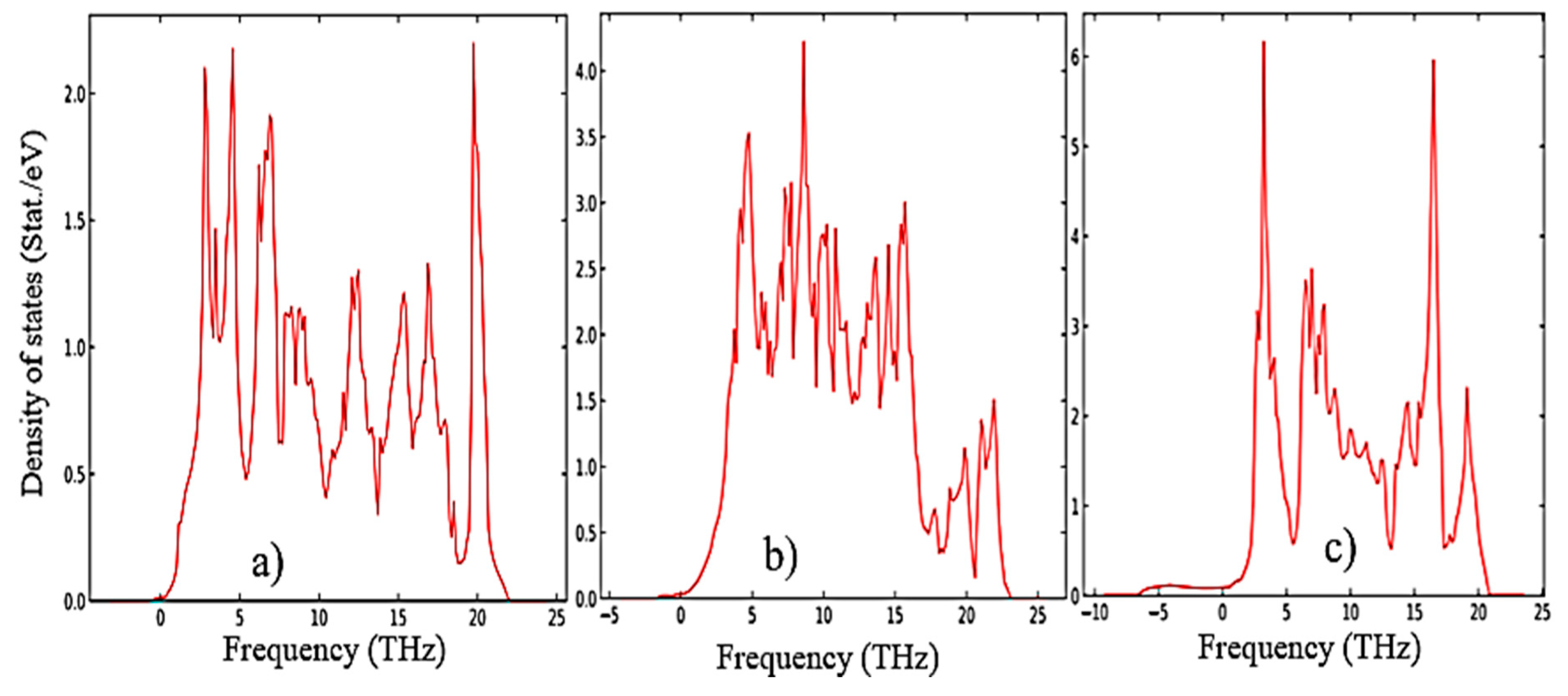
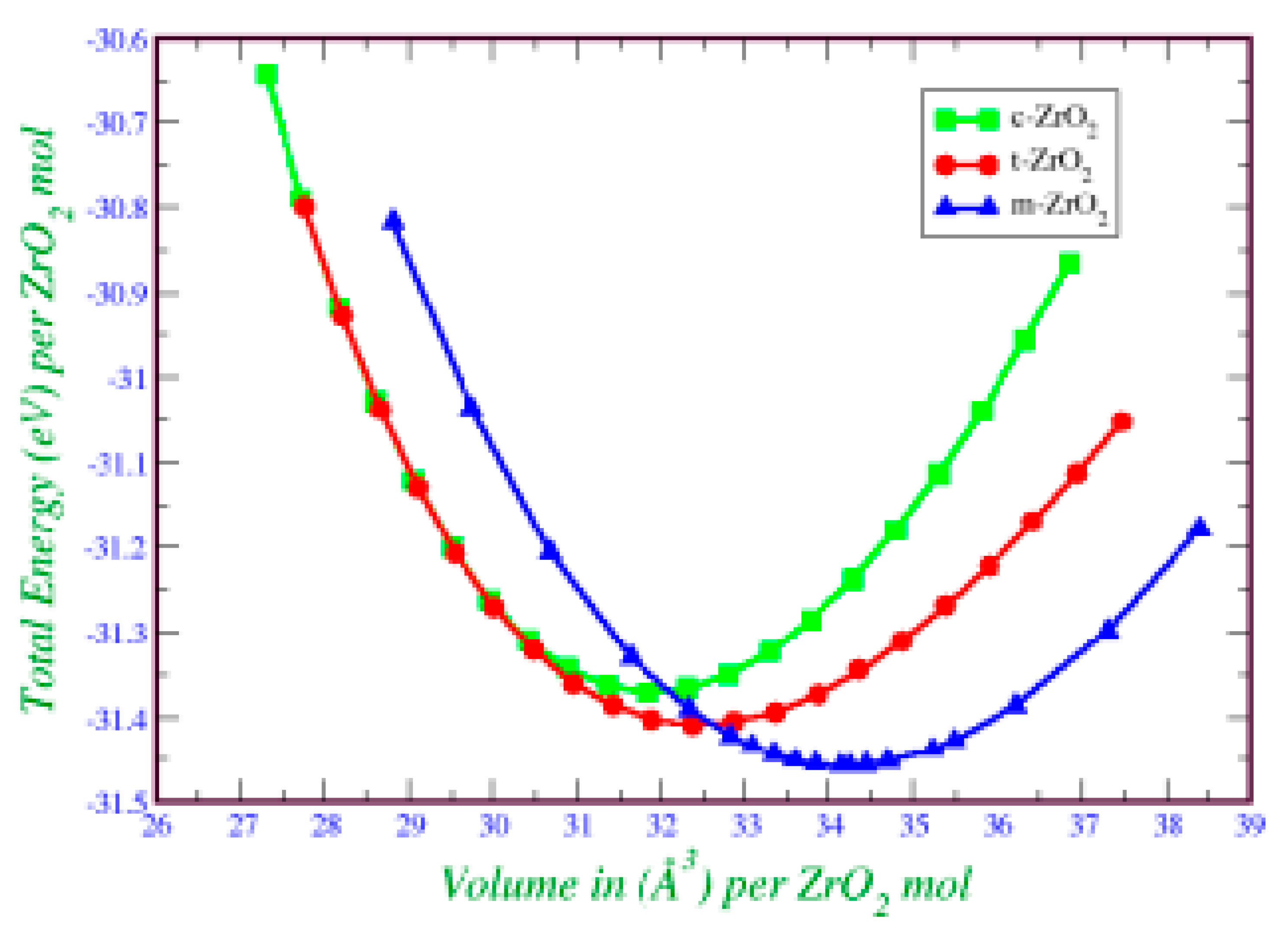
The results of calculations of the density of phonon states presented in Figure 7a–c indicate that as the transition from monoclinic to tetragonal and cubic phases, the density of electronic states increases, and they also agree well with the results shown in Figure 5 and confirm that the monoclinic phase is the most stable among the other phases of ZrO₂. This is also confirmed by the result of the Energy/Volume diagram presented in Figure 8. Therefore, for further stabilization by doping with Y₂O₃, it is reasonable to choose a monoclinic phase.

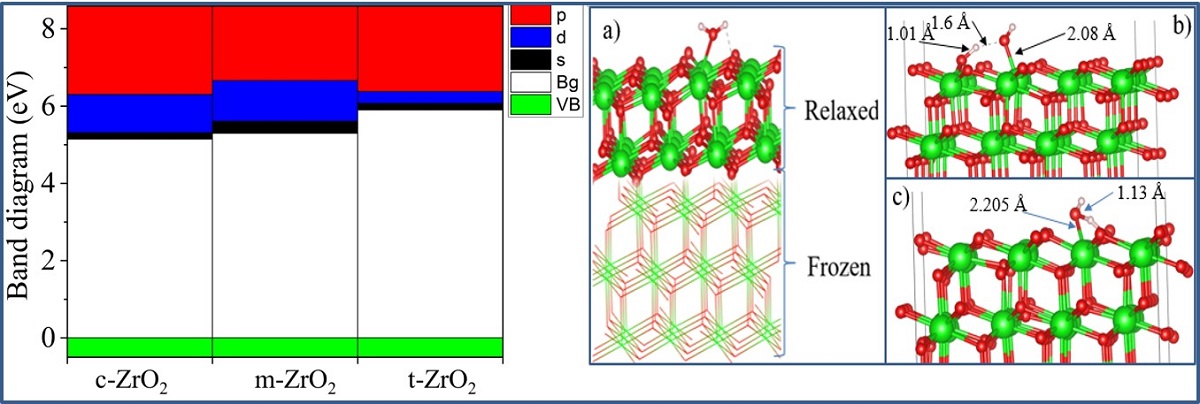
Next, using the well-optimized structures of the three phases of ZrO₂, we performed calculations to study their electronic properties. Using the GGA and SCAN functionals and the HSE06 hybrid functional, we found the band gaps of these systems (Table 3), analyzed their orbital structure, and modeled the change in the position of the Fermi level in these systems.

Table 3. Calculated and experimental band gap of c-ZrO₂, t-ZrO_2, m-ZrO₂ in eV.

System	This work			Experiment [55]
	GGA	SCAN	HSE06	VUV
m-ZrO2	3.9	3.8	5.288	5.78
t-ZrO2	4.42	4.37	5.898	5.83
c-ZrO2	4.03	3.93	5.140	6.10

Table 3. Calculated and experimental band gap of c-ZrO₂, t-ZrO_2, m-ZrO₂ in eV.

System	This work			Experiment [55]
	GGA	SCAN	HSE06	VUV
m-ZrO2	3.9	3.8	5.288	5.78
t-ZrO2	4.42	4.37	5.898	5.83
c-ZrO2	4.03	3.93	5.140	6.10

According to the results presented in Table 3, the GGA and SCAN functionals showed a rather small band gap compared to the HSE06 hybrid functional [56], which makes it possible to overcome the underestimation of the band gap. On the other hand, it is obvious that the standard SCAN and GGA functionals greatly underestimate the band gap. Given the suitability of HSE06 for estimating the band gap energy, we further used this hybrid functional to describe all the problems associated with the electronic properties of the systems under study.

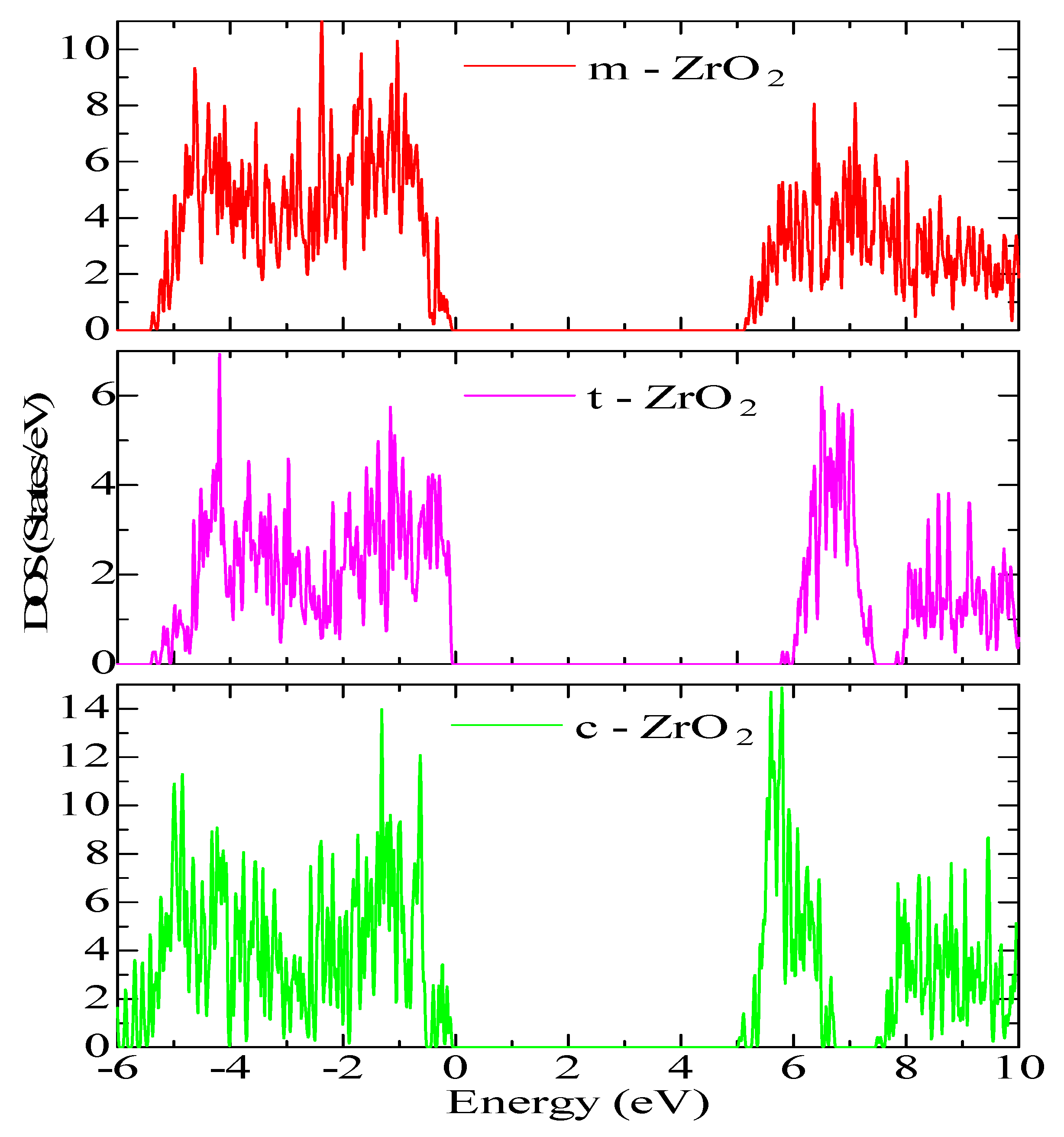
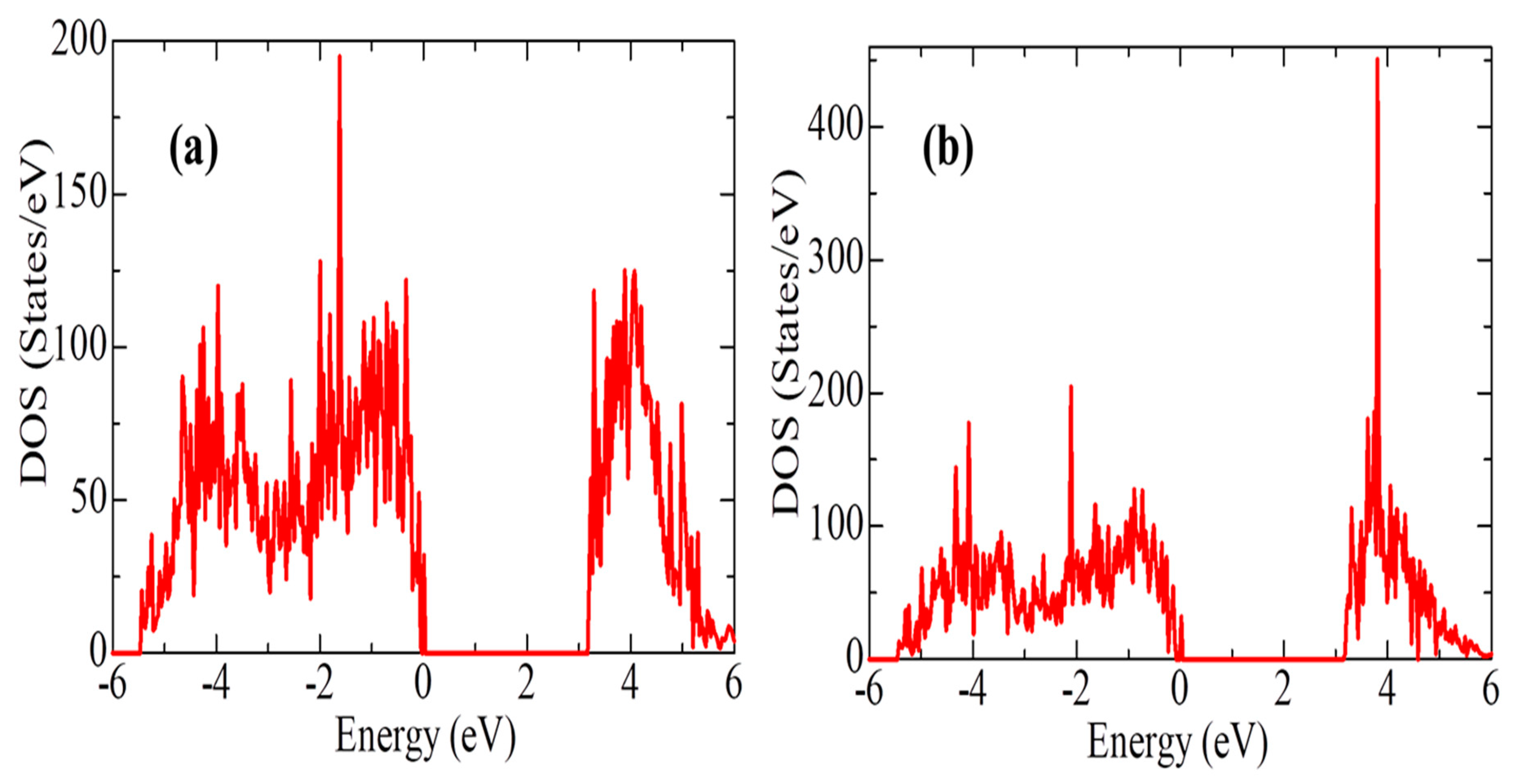
Next, for ZrO₂ structures relaxed using the SCAN functional, calculations were made of the density of available electronic states at the Fermi level (Figure 9), which is crucial for interpreting the electronic properties of ZrO₂ and the transport characteristics of electronic devices based on this.

According to Figure 9, the density of electronic states for c-ZrO₂ is somewhat overestimated compared to other phases. In addition, secondary energy gaps are observed in the energy diagram of the tetragonal and cubic phases. Also, this gap increases during the transition from the tetragonal to the cubic phase.

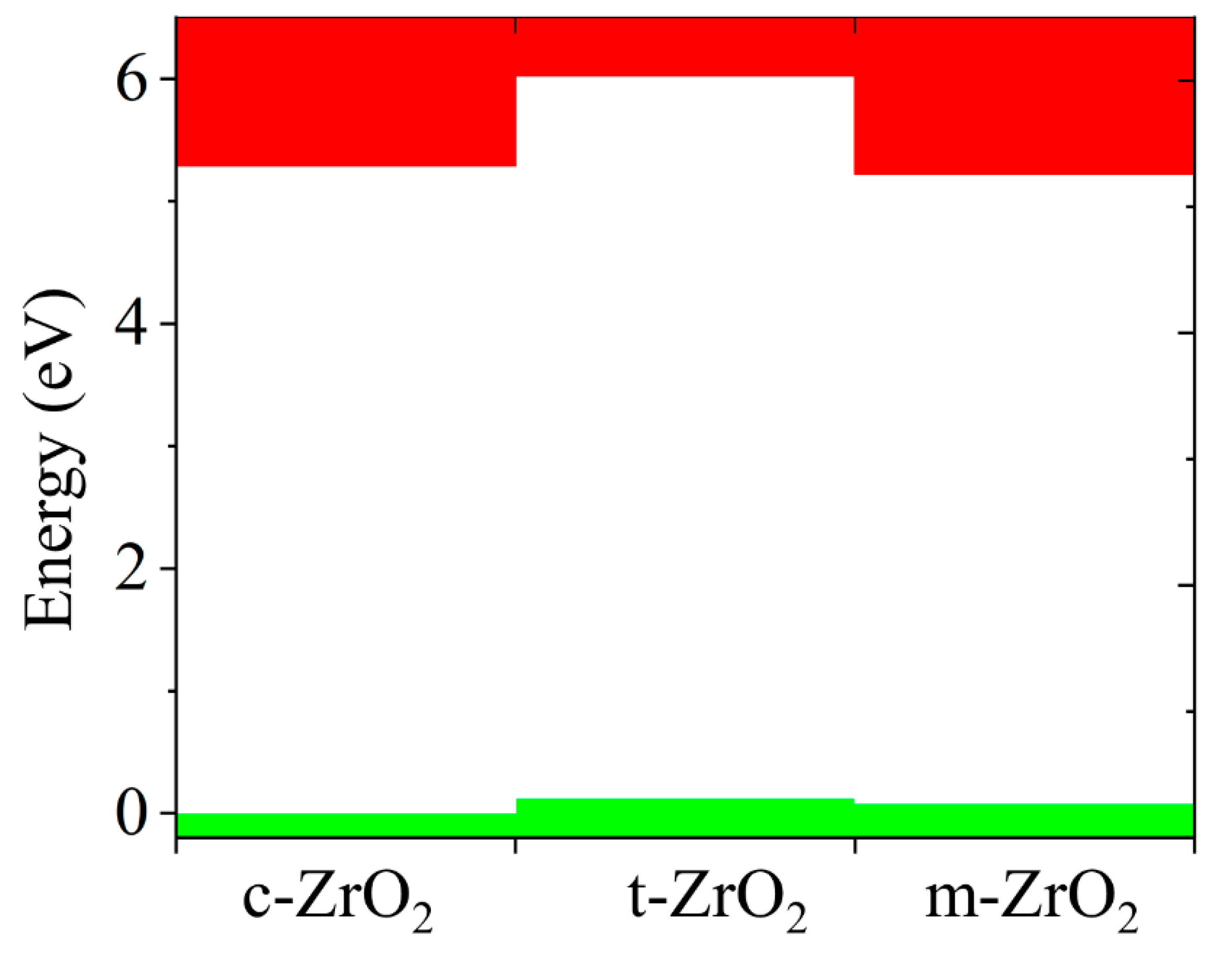
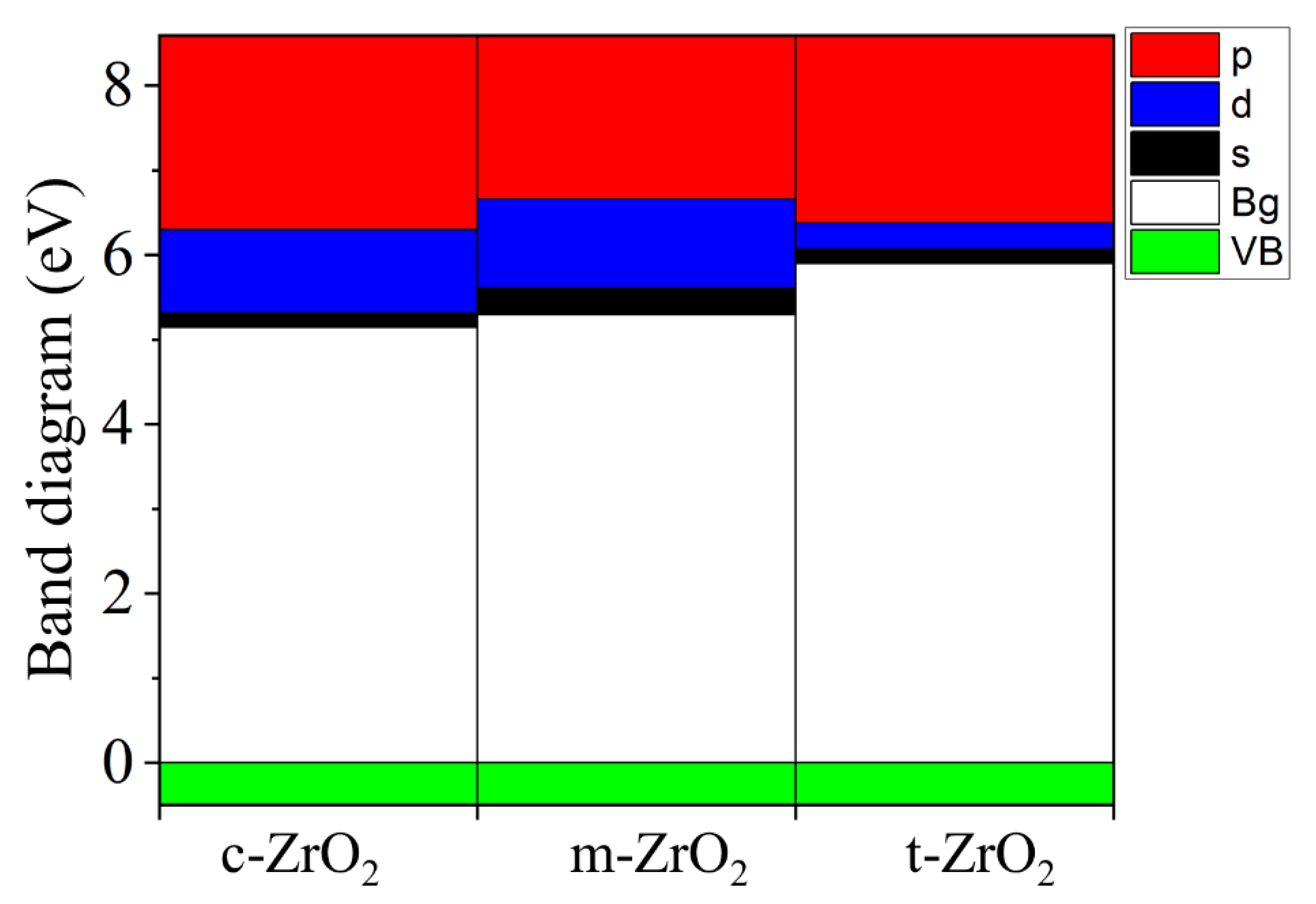
Next, the position of the Fermi level in ZrO₂ crystals and the shift of this level during their phase transformation were determined. As can be seen from Figure 10, if we take the position of the Fermi level (maximum of the valence band) for the monoclinic phase as a reference point, then during the m-t phase transformation of ZrO₂, this level first shifts by 0.125 eV towards higher energies (towards the valence band), and then , in the t-c section, decrease by 0.08 eV. This is also observed in detail from the band stacking results for the orbital analysis, which are shown in Figure 11 for the three phases of ZrO₂.

It can be seen that as the transition from the monoclinic to the tetragonal and cubic phases, the contribution of the p orbitals becomes more significant in CB, and the s orbitals make a small contribution, while the d state shows a different trend. It is assumed that this behavior may be associated with a change in the crystal field and covalence of ZrO₂ during the phase transformation.

3.2. Structural and energy properties of Y₂O₃ doped with m-ZrO₂. Electronic properties of YSZ.

Next, supercells with a size of 2x2x2 of 96 atoms were created to simulate the effect of Y₂O₃ on the stability and electronic properties of the most stable (monoclinic) modification of ZrO₂. To dope yttrium, it was necessary to replace some formula units of Y₂O₃ with ZrO₂ in a 2x2x2 supercell, with each replacement creating one oxygen vacancy. A schematic description of the generation of YSZ structures is given below:

$${xZrO}_2+k{Y}_2{O}_3\to {Zr}_x{Y}_{2k}{O}_{2x+3k}+V_{o_k}$$

$$\%Y_2{O}_3=\frac{k}{x+k}\times 100\%,$$

which can be considered as the union of x ZrO₂ formula units with k Y₂O₃ formula units located on the initial lattice of x + k ZrO₂ units, which leads to the formation of m oxygen defects. Based on this, we determine the percentage of vacancies equal to the percentage of yttrium units in the final structure. Thus, starting with a pure 96-atom ZrO₂ supercell, we mainly focused on 4 different concentrations of Y₂O₃ in our calculations (Table 4).

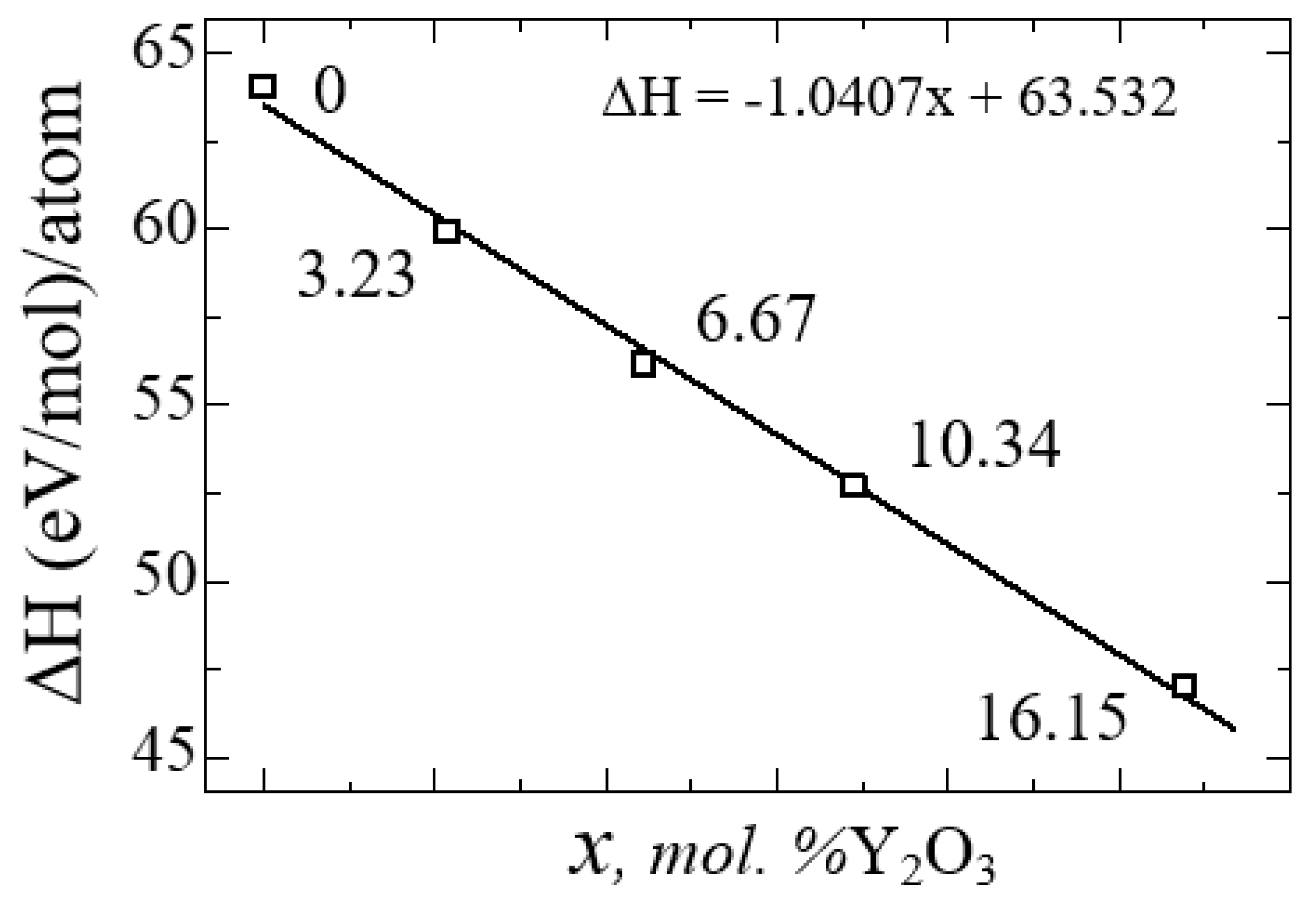
After the final preparation of the YSZ structures, geometric optimization and doping relaxation of the Y₂O₃ supercell were performed using the GGA and SCAN potentials. Figure 12 shows a diagram of the dependence of the change in the enthalpy of formation of YSZ on the concentration of Y₂O₃, calculated by formula 4:

$$\Delta H=\frac{E_{YSZ}-[x{E}_{Zr{O}_2}+k{E}_{Y_2{O}_3}]}{x+k}$$

(4)

from which it is clearly seen that doping with Y₂O₃ reduces the enthalpy and leads to the stabilization of zirconium dioxide. The empirical formula obtained by the least squares method says that the enthalpy of formation energy decreases linearly according to the law ΔН = -1.0407x + 63.532, where x is the concentration of Y₂O₃ in YSZ.

Thus, with an increase in the Y₂O₃ concentration, the number of oxygen vacancies in YSZ increases, and the growth of these O vacancies is considered as a stabilizing mechanism of the monoclinic zirconium phase, as evidenced by a decrease in the enthalpy of formation.

Numerical values of the enthalpy formation energy are given in Table 6. Table 5 shows the geometric parameters of the ZrO₂ and YSZ supercells at various Y₂O₃ concentrations after thorough relaxation using the SCAN functional.

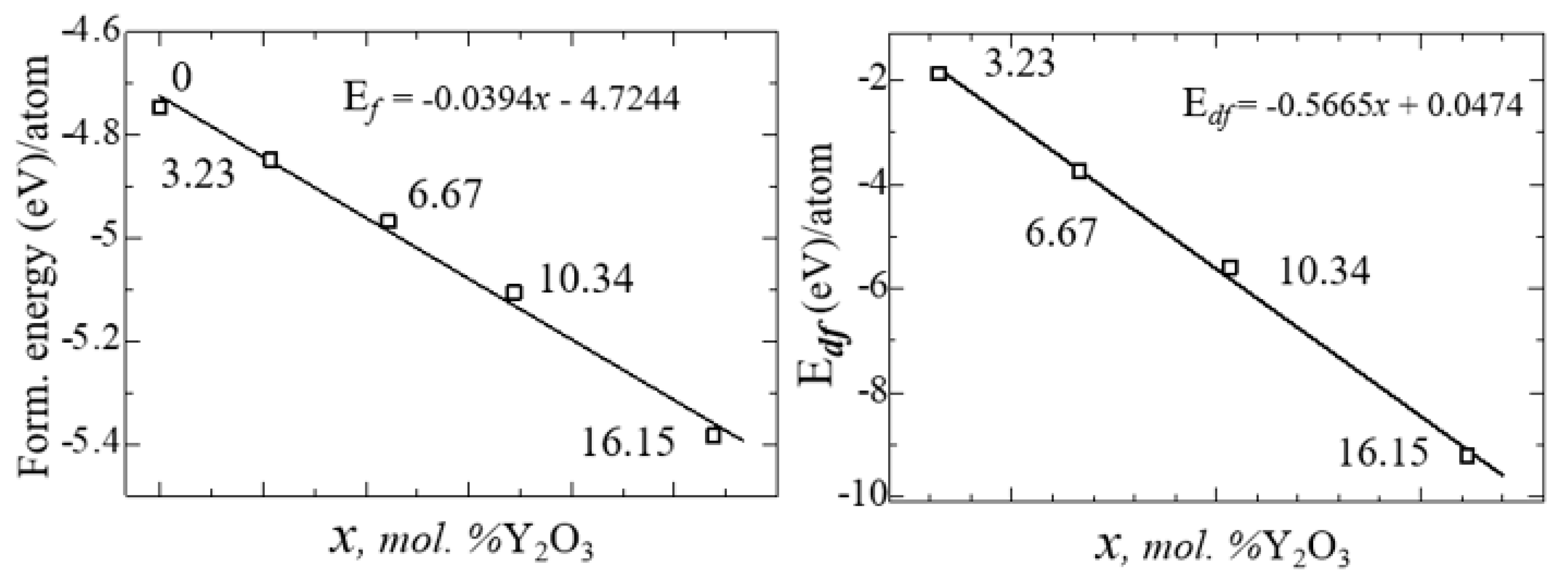
After obtaining the optimized structures, the energy of formation (Ef) for ZrO₂ and YSZ and the energy of formation of vacancies (Ev) for YSZ were calculated as:

$$E_f=E_{tot}-{\sum }_x{E}_{tot}\left(x\right)$$

$$E_{df}=E_{tot}^{{Zr}_{32-x}{Y}_x{O}_{64-\delta }}-E_{tot}^{{Zr}_{32}{O}_{64}}+\delta \ast E_{tot}^O$$

where $E_{tot}$- total energy of the system, $E_{tot}\left(x\right)$ – total energy of individual components, δ is the number of vacancies (defects) in the crystal. The calculated values of $E_f$and $E_{df}$for each atom are given in Table 6.

Table 6. GGA-calculated value of enthalpy (ΔН) and energy of formation ($E_f$) for ZrO₂ and YSZ. Oxygen vacancy formation energy ($E_{df}$) for YSZ.

System	ΔН	${\mathit{E}}_{\mathit{f}}$	${\mathit{E}}_{\mathit{d}\mathit{f}}$
0	64.02917222	-4.747216667	0
3.23 mol. %Y2O3	59.91124404	-4.848422632	-1.874577368
6.67 mol. %Y2O3	56.13271879	-4.967857447	-3.739875532
10.35 mol. %Y2O3	52.7041267	-5.106527419	-5.596013441
16.15 mol. %Y2O3	47.00229139	-5.384704945	-9.220196154

Table 6. GGA-calculated value of enthalpy (ΔН) and energy of formation ($E_f$) for ZrO₂ and YSZ. Oxygen vacancy formation energy ($E_{df}$) for YSZ.

System	ΔН	${\mathit{E}}_{\mathit{f}}$	${\mathit{E}}_{\mathit{d}\mathit{f}}$
0	64.02917222	-4.747216667	0
3.23 mol. %Y2O3	59.91124404	-4.848422632	-1.874577368
6.67 mol. %Y2O3	56.13271879	-4.967857447	-3.739875532
10.35 mol. %Y2O3	52.7041267	-5.106527419	-5.596013441
16.15 mol. %Y2O3	47.00229139	-5.384704945	-9.220196154

Figure 13 shows the nature of the change in $E_f$and $E_{df}$from the concentration of yttrium oxide, from which the regularity of their linear decrease is clearly visible.

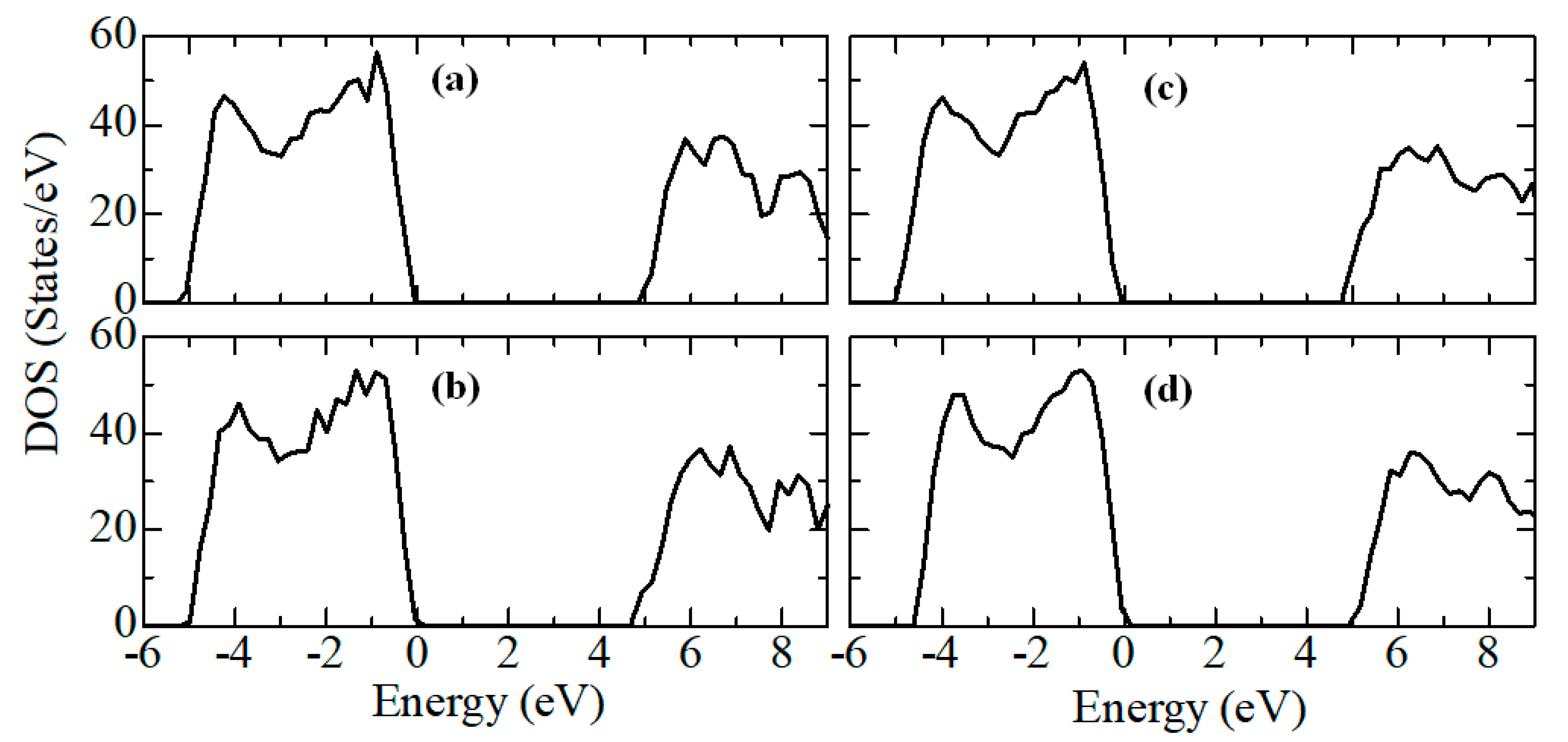
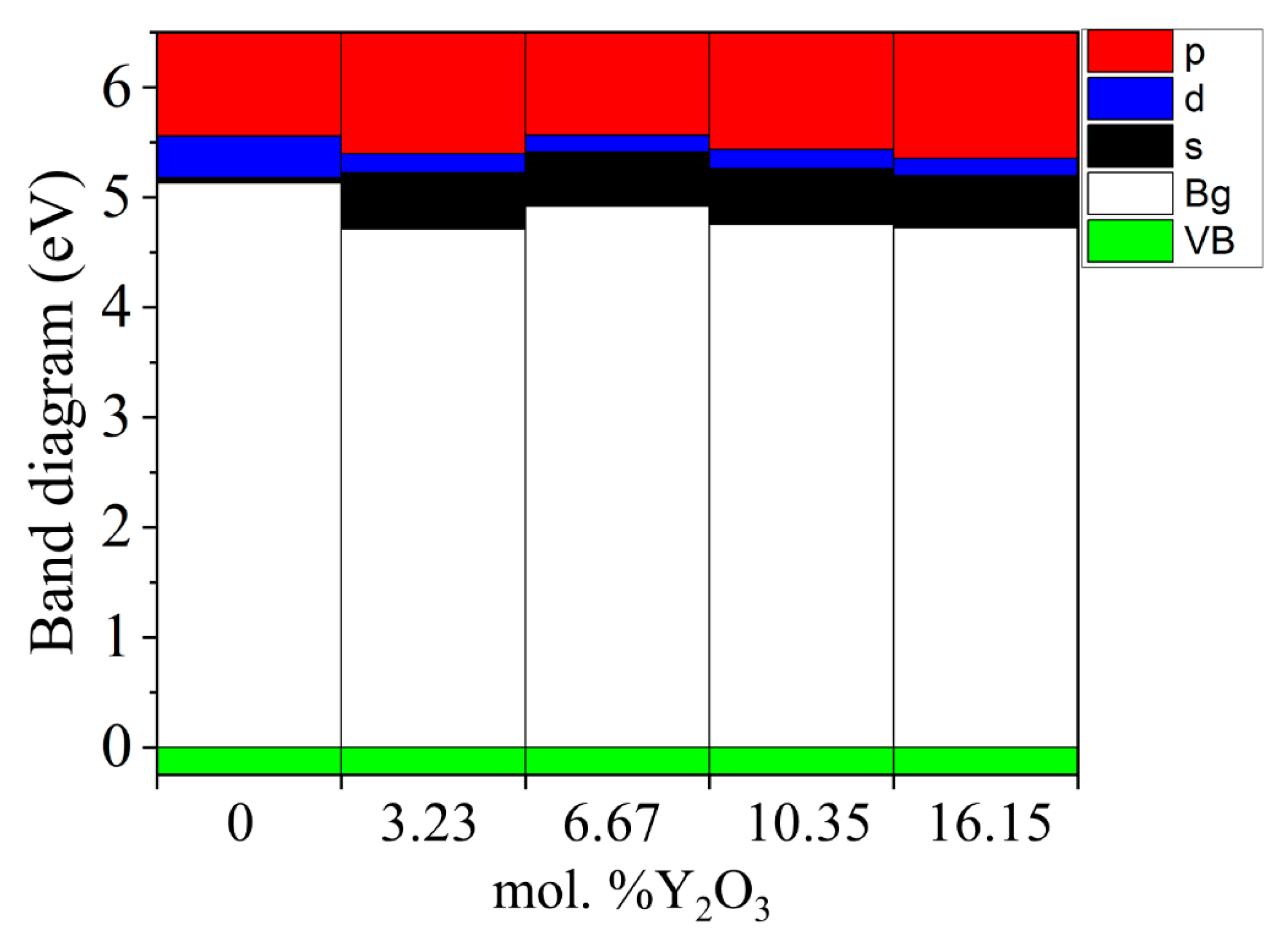
Next, calculations were performed to study the electronic structure of Y₂O₃-stabilized ZrO₂ supercells to reveal the effect of doping on the density of states, the behavior of the Fermi energy, and the orbital components. Figure 14 shows plots of changes in the density of electronic states YSZ for all doping concentrations of Y₂O₃.

According to the results presented in Figure 14, it can be noted that after doping with Y₂O₃, new energy states do not appear in the TDOS patterns due to the introduction of defects, that is, there are no noticeable changes, except for a decrease in the band gap , which can be understood in detail after orbital analysis (Figure 16) and Fermi level mixing estimates (Figure 15). The band gap is 4.71 eV, 4.92 eV, 4.75 eV, and 4.72 eV, respectively, for ZrO₂ doped with 3.23, 6.67, 10.34, and 16.15 mol. %Y₂O₃.

According to Figure 15, after doping with 3.23 mol. %Y₂O₃ into pure m-ZrO₂, the Fermi level drops by 0.067 eV and then shifts by 0.007 eV towards the conduction band upon doping with 6.67 mol. %Y2O3. Then, at a doping concentration of 10.34 mol. %Y₂O₃, it still increases by 0.01 eV, which is 0.017 eV more than in the case of 3.23 mol. %Y2O3. However, after doping with 16.15 mol. %Y₂O₃, it drops to 0.012 eV. The PDOS diagram also interprets the stepped conduction band pattern in terms of the contribution of the s, p, and d orbitals. Understanding these features makes it possible to tune the Fermi energies in the band structure to solve the most important problems of materials science and instrumentation.

The problems of studying the influence of doping of yttrium oxide on the properties and stability of tetragonal and cubic zirconia remain the subject of our future research.

3.3. Water adsorption on ZrO₂ and YSZ surfaces

As already mentioned, the most important point is the choice of the surface with the lowest surface energy in order to correctly model the mechanism of water adsorption on the corresponding surface. To select the optimal adsorbed surface, we calculated the surface energy (σ) for several different surface models according to the equation after their geometric relaxation. The calculated value of the surface energy for ZrO₂ is shown in Table 7.

According to the results presented in Table 7, it can be seen that the most stable surfaces can be obtained due to the tetragonal and monoclinic phases, namely, t-ZrO₂ (101) and m-ZrO₂ (111). The results obtained are in qualitative agreement with the work of Maliki et al. [57], who report that the most stable surface can be obtained from t-ZrO₂ (101). As for the comparison of the results with experimental data, there were no data for comparison in the literature. This is due to the fact that the surface energy of solid metal oxides is difficult to measure experimentally. In total, the measurement of the surface energy of some types of zirconium dioxide surfaces by the method of multiphase balancing at high temperatures was reported [58]. Based on the results obtained, the t-ZrO₂ (101) surface was chosen for this study as the most stable surface for the adsorption of water molecules.

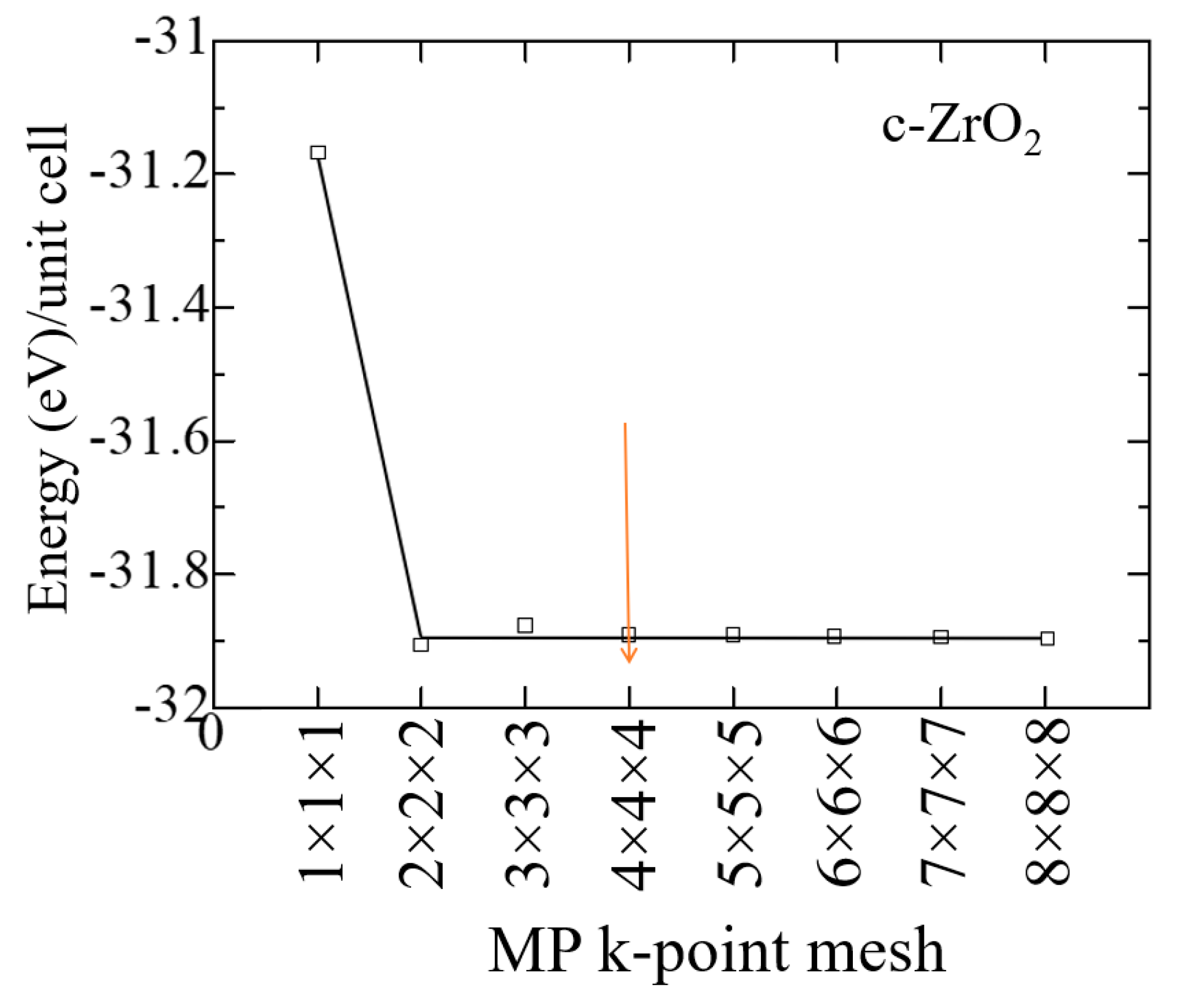
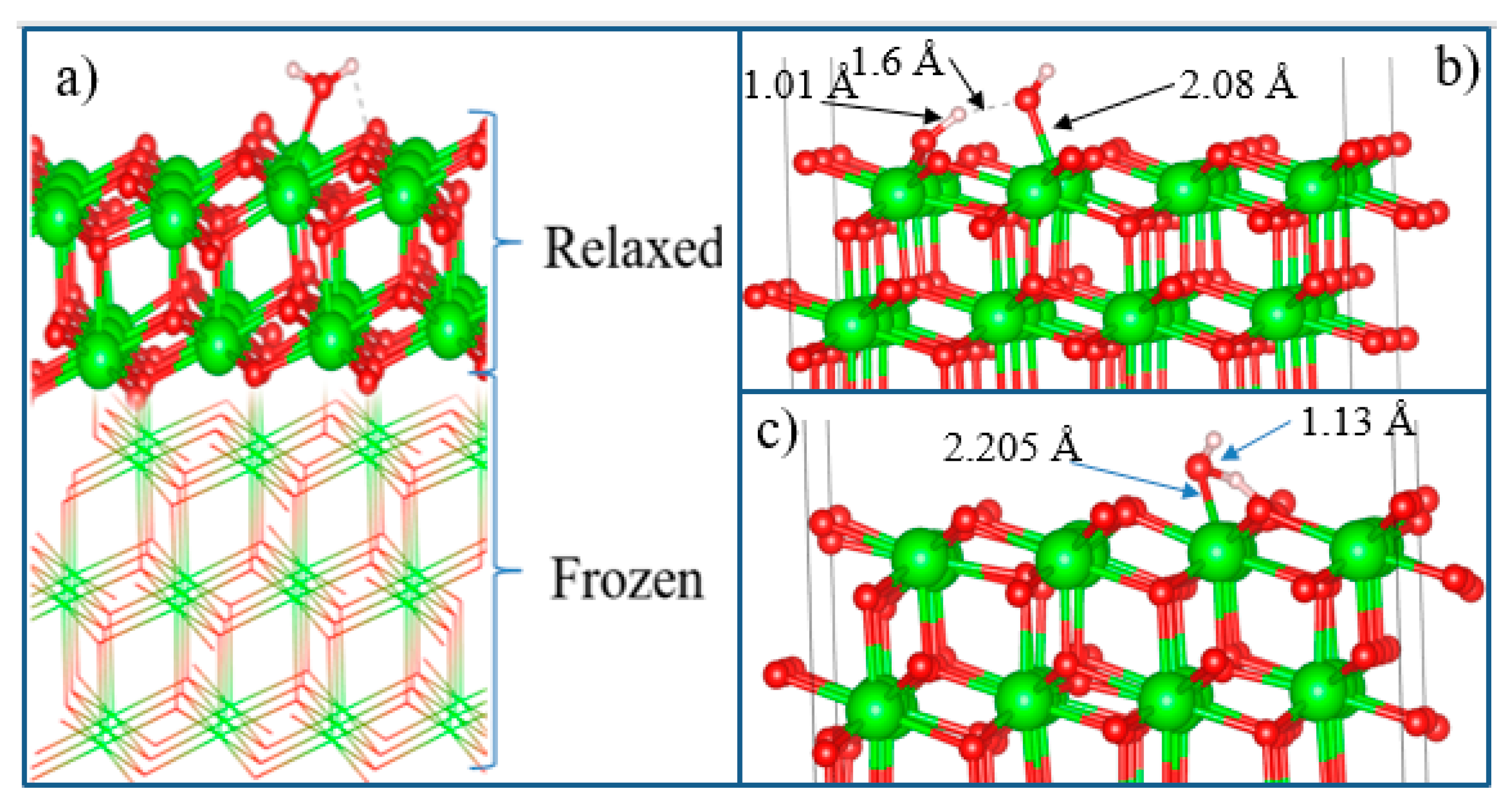
After the final surface preparation, single H₂O molecules were initially located at a height of 2.5 Å above the selected surface with different orientations, which is greater than the bond distance between Zr and O (2.12 Å) in the solid state. The structures were then optimized by freezing the bottom layers of the wafer (Figure 17a).

The optimized structure of the H₂O + t-ZrO₂ (101) system is shown in Figure 17b, which shows that the H₂O molecule is dissociatively adsorbed with an energy of -1.221 eV even in the most favorable region (where the system has the minimum energy of the stable configuration). Dissociative adsorption of water on ZrO₂ was also observed by Korhonen et al. [59], where it was experimentally and theoretically proven that water dissociates on the surface of m-ZrO₂ at low coverage, and the adsorption energy calculated by us on t-ZrO₂ (101) for [H+OH]-ZrO₂(101) is similar to their results for monoclinic (111) and (101) surfaces with energy -1.20 eV. It was also found that water is adsorbed on this surface by the method of molecular chemisorption, in which water oxygen coordinates the surface cation, and a slight elongation of one O–H water bond (1.13 Å) occurs in the form of hydrogen bonding water with the surface oxygen ion (Figure 17c). In this case, the adsorption energy is 0.69 eV, and the distance between the oxygen of the water molecule and the surface zirconium atom is 2.205 Å. In this case, the proton (H) in the water molecule and oxygen from the surface of the plate form a hydrogen bond with a bond length of 1.01 Å.

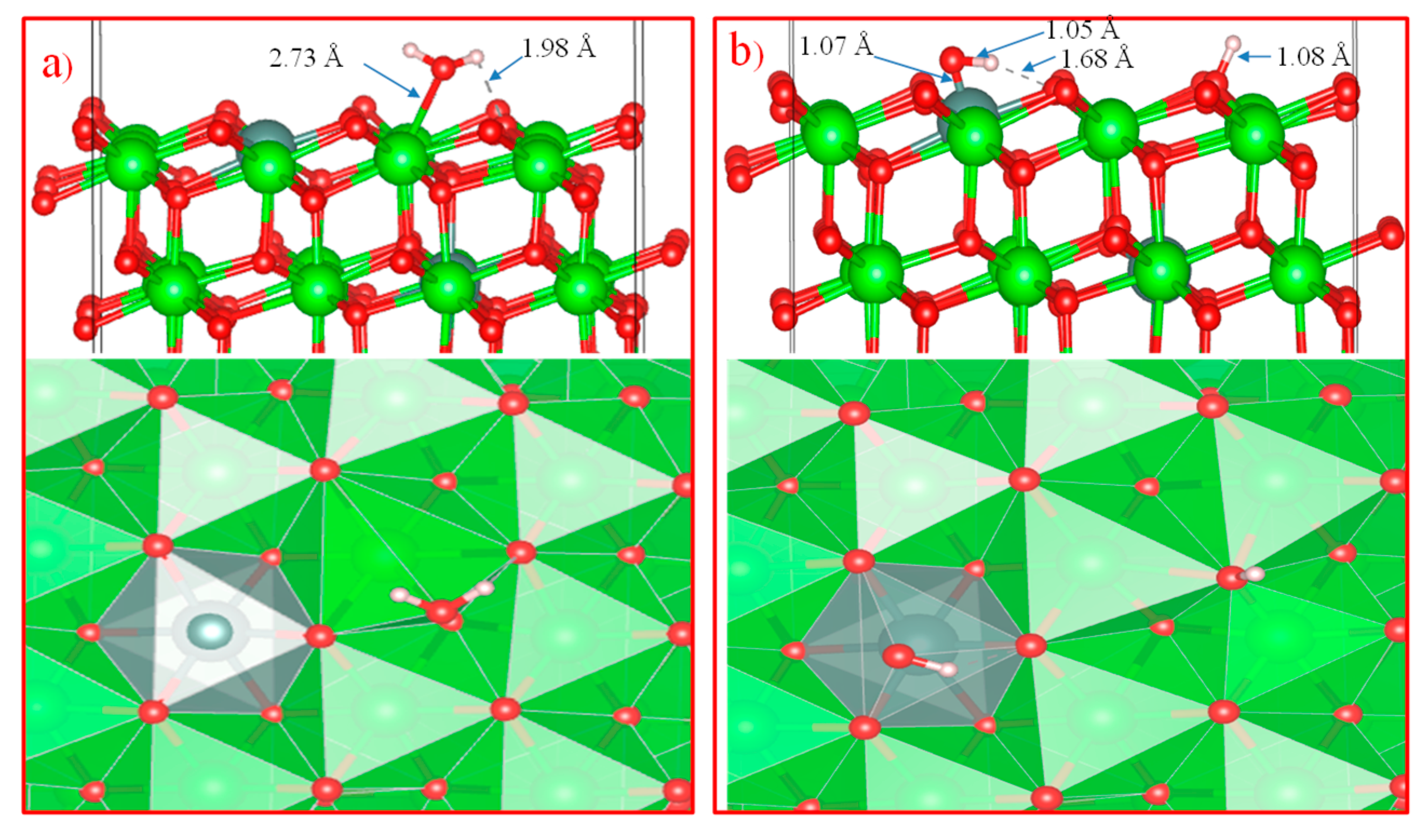
Further, in order to study the mechanism of water adsorption on the surface of t-YSZ, we replaced two Zr (from the uppermost and subsurface O-Zr-O trilayers by Y with the removal of one oxygen from the third atomic layer nearest neighbor of Y atoms) to obtain a surface similar to t-YSZ(101). The results showed that the water molecule is molecularly adsorbed and also dissociated on the t-YSZ(101) surface. Molecular adsorption of water at the most optimal configuration occurs from an energy of -1.84 eV, and the bond length of water with the t-YSZ (101) surface increases to 2.73 Å (Figure 18a). In this case, the O-H distance in water molecules will remain unchanged.

The dissociative adsorption of water was accompanied by the movement of oxygen in the area of the plate vacancies, which leads to a very strong adsorption of -1.23 eV, blocking surface areas for oxygen activation. In both cases, H₂O is adsorbed near the yttrium atom (Figure 18b).

Unlike water adsorption on t-ZrO₂(101), H₂O is more stably adsorbed on t-YSZ(101), since the adsorption energy of H₂O-YSZ(101) is more favorable than that of (H+OH)-YSZ(101).

Doping with Y₂O₃ stabilizes t-ZrO₂(101) and is accompanied by large relaxations of O atoms. Calculations based on the GGA functional greatly underestimate the band gap of the system (3.24 eV for the H₂O-ZrO₂(101) system and 3.21 eV for H₂O-YSZ(101 )), however, despite the presence of the Oth vacancy, the average gap energy states did not appear in the t-YSZ band diagram, as is observed in the systems under study. A comparative analysis of the electronic structure of the H₂O-ZrO₂(101) and H₂O-YSZ(101) systems indicates that the interaction of H₂O practically does not change the electronic configuration of the system (with the exception of an increase in the density of state) during the transition of the system to being modified by Y impurities (Figure 19). However, water molecules are predominantly prone to molecular adsorption on the t-YSZ (101) surface, and more often dissociatively on t-ZrO₂(101). Table 8 lists some key data obtained by modeling water adsorption on t-ZrO₂(101) and t-YSZ surfaces.

In such studies, it is also important to take into account the hydrophilic nature of ZrO₂. Studies show that, in addition to physically adsorbed water, the substrate surface contains terminal, bibridging, and triple bridging OH groups, which are actively involved in the surface reaction [60,61]. Surface hydroxyl groups and H₂O adsorbed on the surface can partially block active sites (lattice oxygen ions on the surface) of YSZ oxidation. 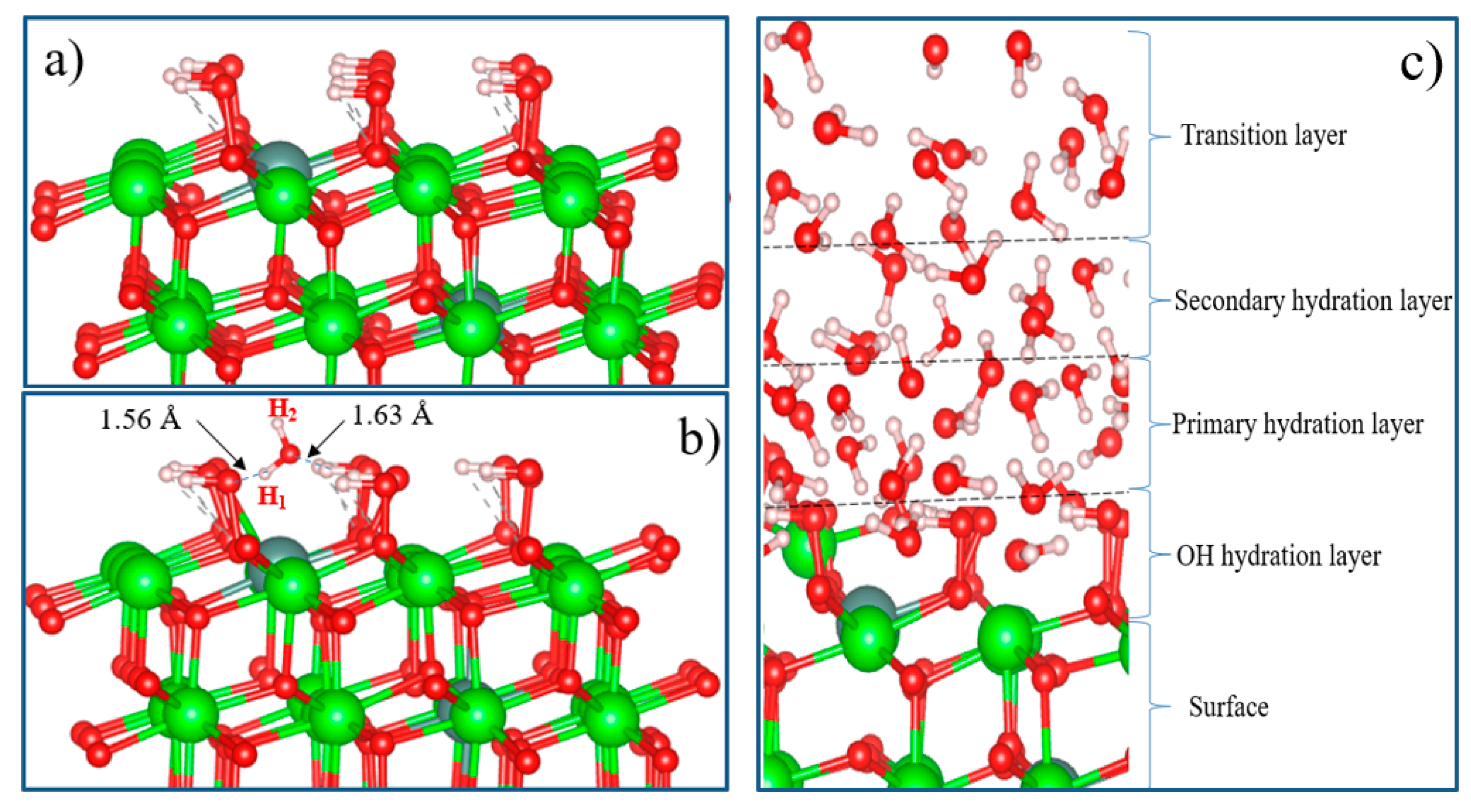The surface configuration model for fully hydroxylated t-YSZ(101) is shown in Figure 20a. The results show that the OH groups form strong bonds on the surface. Figure 20b shows the adsorption structure of a single water molecule on a fully hydroxylated YSZ surface.

It can be seen that the repulsive forces of oxygen and hydrogen atoms in a water molecule and OH atoms on a completely hydroxylated surface do not prevent the adsorption of an H₂O molecule on t-YSZ (101). When water is adsorbed on a hydroxylated surface, two strong hydrogen bonds are formed at a distance of 1.56 and 1.63 Å from each other. In this case, water is adsorbed with an adsorption energy of 0.34 eV. The adsorption model of a single water molecule and other similar systems will help in the future to study in detail more complex models, including the multilayer hydration structure of the interface (Figure 20). Although this model requires large computational power for DFT calculations, nevertheless, it can be assumed that in the layer closest to the surface (hydroxyl hydration layer), most of the water molecules can be adsorbed dissociatively. Further, due to hydrogen bonds, H₂O molecules will continue to be adsorbed and regularly located on the hydroxylated surface, forming primary and secondary hydrated layers. The regular arrangement of H₂O molecules in the outer layer can be considered as a transition layer, and the hydration structure of the first three H₂O layers located near the surface can be considered as a group of water molecules capable of being stably adsorbed and existing on the m-NSC surface (101). However, a detailed study of the complete model of t-YSZ(101) surface hydration remains the subject of our future research.