Apple-Like Shape of Freezing Paraffin Wax Droplets and its Origin

1. Introduction

Freezing the droplets leads to a surprising variety of shapes, ranging from the shapes of the metamorphic snowflakes [1,2] to the paradoxical pointed “freezing tip” observed for frozen water and germanium droplets [3,4,5,6,7]. The sharp tip registered during the cooling of water droplets exhibits a remarkable universality in its shape, independent of the cooling regime and physical properties of the substrate [4,5,6,7,8,9], which has been attributed to the jump in water density during freezing. Dendrite-like morphology has recently been observed on the outer shell of oil-coated frozen droplets [10].

We investigated paraffin wax freezing and observed a centrally concave, apple-like shape, which can be seen as the opposite of a freezing tip shape. Typically, centrally concave shapes are observed when water droplets impact cold solid surfaces [11,12,13,14]. The resulting shape is due to a combination of impact dynamics and the freezing process [11,12,13,14]. The formation of a central dimple is explained by the additional internal circular freezing front advancing both upwards and towards the periphery of the droplet [11].

Our experiments, in which a centrally concave shape of solidified paraffin wax droplets was observed, were almost static. Therefore, the observed shape of the solidified droplet is not related to the impact of the droplet on the solid plate. The centrally concave shape of solidified paraffin droplets was reported in ref. [15], in which it was noted that these shapes resemble those inherent to spreading oceanic ridges.

It should be noted that understanding the solidification process of paraffin wax is important for engineering applications. Like other phase change materials (abbreviated PCM), paraffin wax stores energy in the form of latent heat at a nearly constant temperature during melting and releases this energy during solidification. This effect is used in industrial energy storage [16,17,18,19,20]. The latent thermal energy storage mechanisms used in PCM are attracting increasing attention for solar energy storage because of their environmental friendliness and sustainability. Paraffin wax is one of the most popular PCM materials used for energy storage.

2. Materials and Methods

2.1. Materials

The following materials were used in the experiment: paraffin wax poly(dimethylsiloxane) (PDMS) Sylgard 184, supplied by Dow Corning, USA. Some properties of the material are the following: melting point $46℃-50℃$, specific heat capacity of the solid material is $2.95 \mathrm{k}\mathrm{J}/\mathrm{k}\mathrm{g}\mathrm{K}$, specific heat capacity of the liquid material – $2.51 \mathrm{k}\mathrm{J}/\left(\mathrm{k}\mathrm{g}\mathrm{K}\right)$, density of the solid material – 818$\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$, density of the liquid material – 760$\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$, thermal conductivity of solid and liquid material – 0.24$\mathrm{W}/\left(\mathrm{m}\mathrm{K}\right)$.

2.2. Experimental Procedure

First, the solid beads of paraffin wax were melted in a metal container at 150$℃$. Then using a micro-syringe, liquid paraffin wax was placed on a glass slide as shown in Figure 1. The glass slide was at room temperature (22$℃$). The total time to place a droplet on a glass slide from the metal container is $5\pm 2 \mathrm{s}.$ Molten droplets were gently placed on the glass slide to minimize the droplet impact. 10 µl to 100 µl droplets were used to study the formation of the eventual shape of the droplet under its solidification. The change in the shape of the droplet is illustrated with Figure 1. The temperature of different positions of the wax droplets (50 µl and 100 µl) were measured using a TM-902C Lutron Digital Thermometer with a chromel–alumel thermocouple with an error of $\pm 1℃$ as shown in Fig. 4S. The top surface temperature of 50 µl droplets were measured using a Therm-App Pro TAS19AV-M25A-HZ LWIR 7.5−14 μm infrared camera as shown in Figure 5S. The resolution, sensitivity, and frame rate of the camera were 640 × 480 pixels (>300 000 pixels), noise equivalent differential temperature (NEDT) <0.03°C, and 18 frames/s, respectively.

Figure 1. Solidification of molten paraffin wax. (a) Schematic representation of the solidification of a liquid paraffin wax droplet where θ is the contact angle, and h and w are the height and maximum width of the droplet, respectively. (b) Images of a 10 µl droplet before and after solidification on a glass slide at ${\tau }_{sub}=22 ℃$ where aspect ratio, $r=\frac{w}{h}$ and $\tau$ is the glass slide temperature.

Figure 1. Solidification of molten paraffin wax. (a) Schematic representation of the solidification of a liquid paraffin wax droplet where θ is the contact angle, and h and w are the height and maximum width of the droplet, respectively. (b) Images of a 10 µl droplet before and after solidification on a glass slide at ${\tau }_{sub}=22 ℃$ where aspect ratio, $r=\frac{w}{h}$ and $\tau$ is the glass slide temperature.

The experiments were carried out at room temperature $\tau =22°\mathrm{C}$ and relative humidity 40-58 %. In order to check the effect of gravity on the solidification of molten wax droplets, an experiment was performed on a rotating platform, as shown in Figure 3S. A 10 µl molten paraffin wax droplet was placed on a glass slide and immediately rotated 180° about horizontal axis, so the droplet was hanging vertically on the glass slide.

A replica of the solidified droplets was taken using PDMS to analyse the freezing dimple. A mixture of PDMS and its curing agent in a weight ratio of 10:1 was prepared for replication via stirring using a glass rod for 15 min and degassing in a low-pressure chamber for 30 min. After that, liquid PDMS mixture was poured on the solidified droplet and cured the PDMS at ambient conditions for 5 days. After curing, solid PDMS was peeled from the wax droplet, as shown in Figure 2. A cross-section was taken from the cured PDMS to analyse the freezing dimple.

A digital microscope BW1008-500X was used to capture the solidification process. The optical resolution of the microscope was $640\times 480$ pixels. Apparent contact angles (APCA), denoted θ were measured using ImageJ from the images captured using the digital microscope BW1008-500X with an accuracy $\mathsf{\Delta }\theta =0.5°$. Ten measurements were performed under ambient conditions; results were averaged.

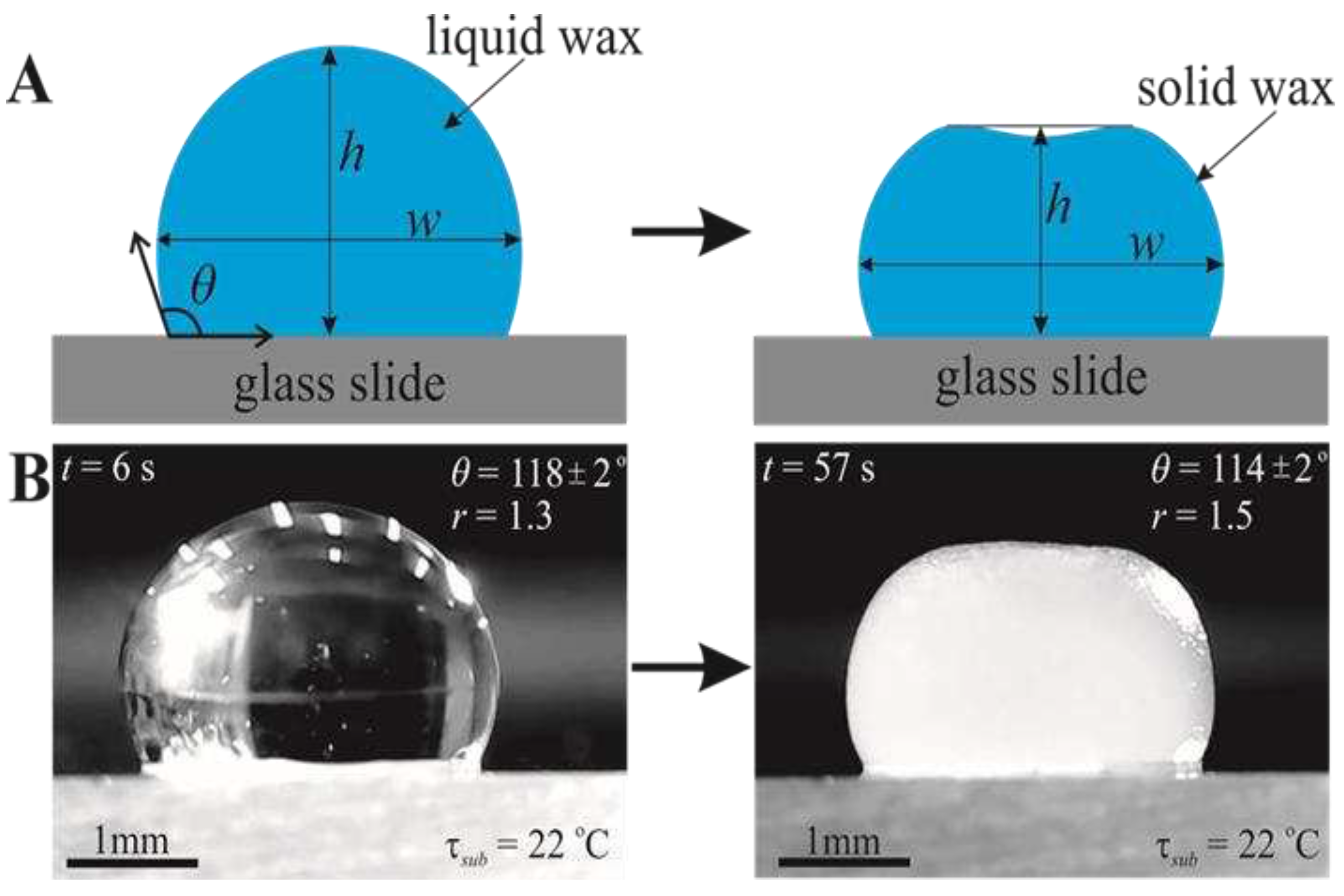
3. Results

3.1. In Situ Study of the Shape of Heated and Cooled Paraffin Wax Droplets

Droplets ($V=10-100 \mathsf{\mu }\mathrm{l}$) were placed on the heated from below glass slides, melted and frozen. The maximal temperature of the droplets was $\tau =150\pm 1℃$. The eventual temperature of the droplets was $\tau =22\pm 1℃$. The heating/freezing cycle was carried out over a period of time $t_c=t_{heating}+t_{freezing}$; $t_{heating}\cong 10-20 \mathrm{s}; t_{feezing}\cong 25-60 \mathrm{s}$, depending in the volume of the droplet. The shape of the droplet, which changed during the heating/freezing cycle, was constantly monitored. The droplet, the top surface of which was originally close to spherical, took the shape shown in Fig. 1. Under the action of gravity, the droplet changed its shape even before it began to solidify (see Videos 1S, 2S, and 3S in Supplementary Materials). The shape of its upper surface became like an oblate spheroid (see refs. [21,22]). Solidified droplets of volume 10 µl and 20 µl have an axisymmetric dimple on their upper surfaces, as shown in Figure 1.

The shape of the dimple was studied with the PDMS replica method (also called “soft lithography” [23]), illustrated in Figure 2 and described in detail in the Experimental procedure section. Soft lithography enabled a detailed study of the dimple shape; in particular, the opening angle of the dimple, denoted β, was determined, as shown in Figure 1S (Supplementary Materials).

The initial apparent contact angle denoted $\theta$ for the paraffin/air system was established at ambient conditions as $\theta =118\pm 2°$. Note that the value of θ depends strongly on the temperature of the substrate. Thus, the entire process of heating and solidification of the droplets depends crucially on the initial temperature of the substrate, as illustrated in Figure 2S. The apparent contact angle decreases with increasing substrate temperature; starting from substrate temperature ${\tau }_{\mathrm{s}\mathrm{u}\mathrm{b}}=60°\mathrm{C}$ full wettability of the glass plate with paraffin wax was observed, as shown in Figure 2S (inset c).

Interestingly, the solidification processes for small and larger droplets are markedly different. In Video S1 for a 10 µl droplet, the solidifying lower layer of the droplet first becomes opaque and then the zone of opacity (though not so pronounced) spreads from bottom to top covering the whole lateral surface of the droplet. As will be shown below in the computational-theoretical section, partial loss of transparency of paraffin occurs when the so-called mushy zone is formed, in which the paraffin wax is no longer liquid, but also not completely solidified. In Video S2 a thin opaque layer of paraffin wax can be seen on a 20 µl droplet, appearing on the upper surface of the droplet while the middle part of the droplet is still transparent. This effect is much stronger with a 50 µl droplet (see Video S3) where the two areas of opacity in the lower and upper part of the droplet extend and meet in the middle of the droplet. This change of solidification pattern towards larger droplets is accompanied by the disappearance of a dimple on the upper surface already at 50 µl droplet volume. The below presented computational analysis of the unsteady temperature field in a solidifying droplet explains the physical cause of the observed phenomenon.

In order to clarify the role of gravity we also performed the experiments hanging upside down, as shown in Figure 3S and Video S4. In these experiments, the formation of the dimple on the upper surface of the droplet was not observed. As one might expect, the effect of gravity is more significant for large droplets: such droplets, placed on the upper surface of a glass plate, are compressed more strongly along the vertical axis. The flattening effect of gravity on the droplet shape leads to a small increase in the contact radius and a decrease in droplet height (as shown in refs. 21-22), with these effects being more pronounced at larger values of the Bond number, which will be explicitly calculated below. The shape of the droplet was characterized by the aspect ratio, introduced according to Eq. 1:

$$r=\frac{w}{h},$$

(1)

where h and w are the height and maximum width of the droplet correspondingly, as shown in Figure 1. Time evolution $r\left(t\right)$ for different volumes of the droplet is depicted in Figure 3. The aspect ratio of the droplets grew under their heating and came to saturation under their solidification (all of the droplets were heated to $\tau =150°\mathrm{C}$ and cooled to $\tau =22°\mathrm{C}).$

Figure 3. Change of wax droplets shape with time. (A) Variation of aspect ratio (r) vs. time (t) for different paraffin wax droplets placed on a glass surface at τ_sub=22℃. (B) Variation of aspect ratio (r) vs. droplet volume (V).

Figure 3. Change of wax droplets shape with time. (A) Variation of aspect ratio (r) vs. time (t) for different paraffin wax droplets placed on a glass surface at τ_sub=22℃. (B) Variation of aspect ratio (r) vs. droplet volume (V).

The aspect ratio does not exhaust geometrical characterization of the droplet shape; the double logarithmic dependence of the eventual value of the maximal dimple depth $h_d$ on the initial volume of the droplet is presented in Figure 4.

Figure 4. Variation of dimple depth and tip angle with volume. (A) Logarithmic plot of freezing dimple depth vs. different initial molten wax droplet volume, where V₀=10 μl and h₀=66±5 μm. (B) Variation of tip angle with different molten wax droplet volumes.

Figure 4. Variation of dimple depth and tip angle with volume. (A) Logarithmic plot of freezing dimple depth vs. different initial molten wax droplet volume, where V₀=10 μl and h₀=66±5 μm. (B) Variation of tip angle with different molten wax droplet volumes.

The double-logarithmic dependence is reasonably approximated by the linear fitting:

$$y=kx+b,$$

(2)

where $y=ln\frac{h_d}{h_0}$, $x=ln\frac{V}{V_0}$, $k=0.58, b=0.1 , h_0=66 \mathsf{\mu }\mathrm{m}, V_0=10 \mathsf{\mu }\mathrm{l}$. This means that the dimensionless dimple depth $\overline{h}=\frac{h_d}{h_0}$ and initial volume of the droplet ${\overline{V}}_0=\frac{V}{V_0}$ are related by the following scaling relationship:

$$\overline{h}~{\overline{V}}_0^{0.58}$$

(3)

The physical basis for this dependence will be clarified in the last section of the paper.

The temperature of the substrate and paraffin wax droplet was monitored as described in detail in the Experimental procedure section. The time-varying temperature of the bottom and side of the droplet was measured with a thermocouple (see Figure 5 and Figure 4S), while infrared pyrometric measurements were used for the temperature of the top surface of the droplet (see Figure 6 and Figure 5S, and Video 5S). The results of these temperature measurements are used below in the computational analysis of the transient temperature field in the paraffin wax droplet.

Figure 5. Variation of the surface temperature of wax droplets with time.

Figure 5. Variation of the surface temperature of wax droplets with time.

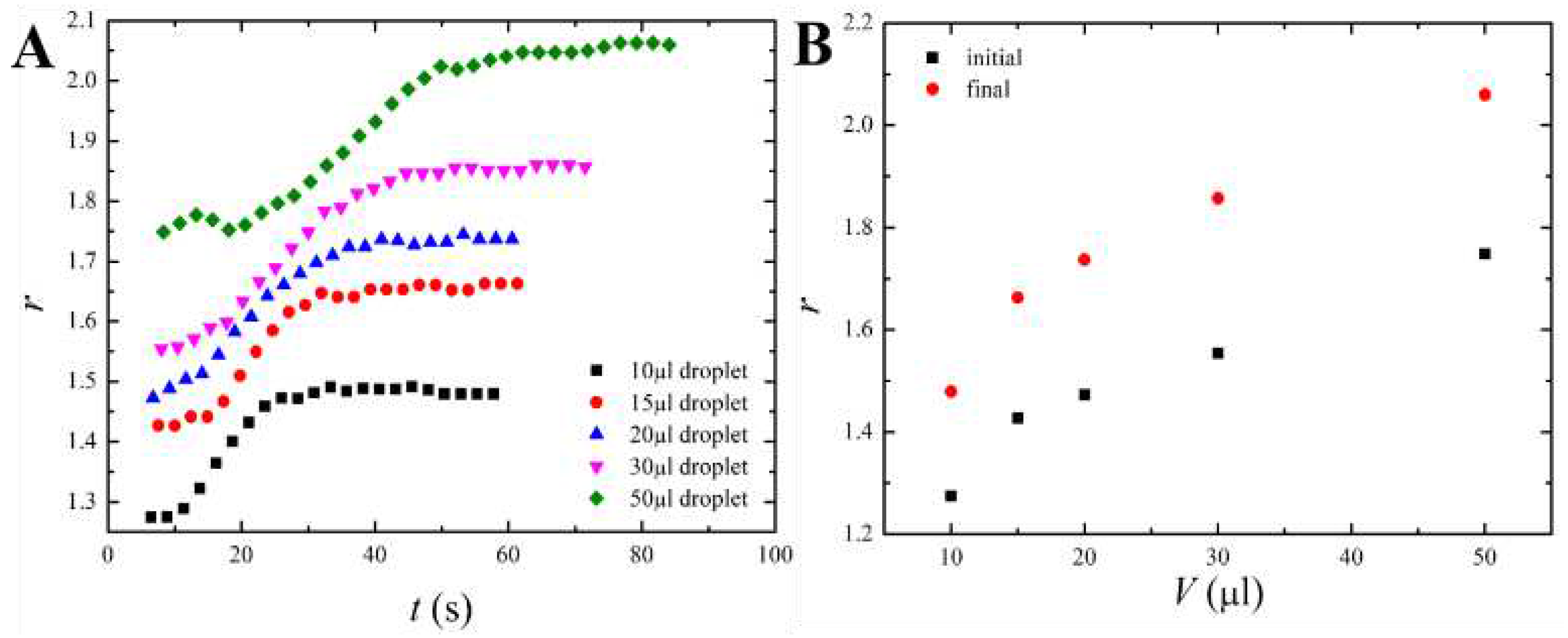
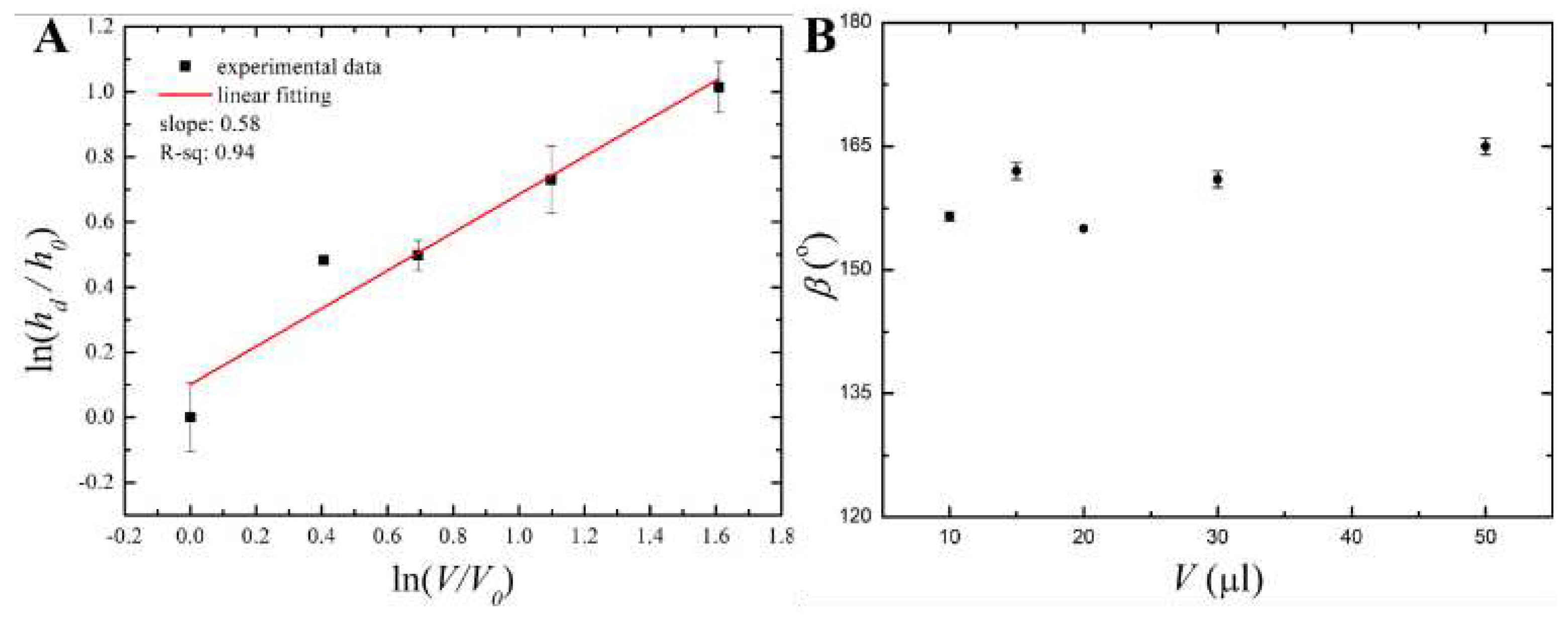
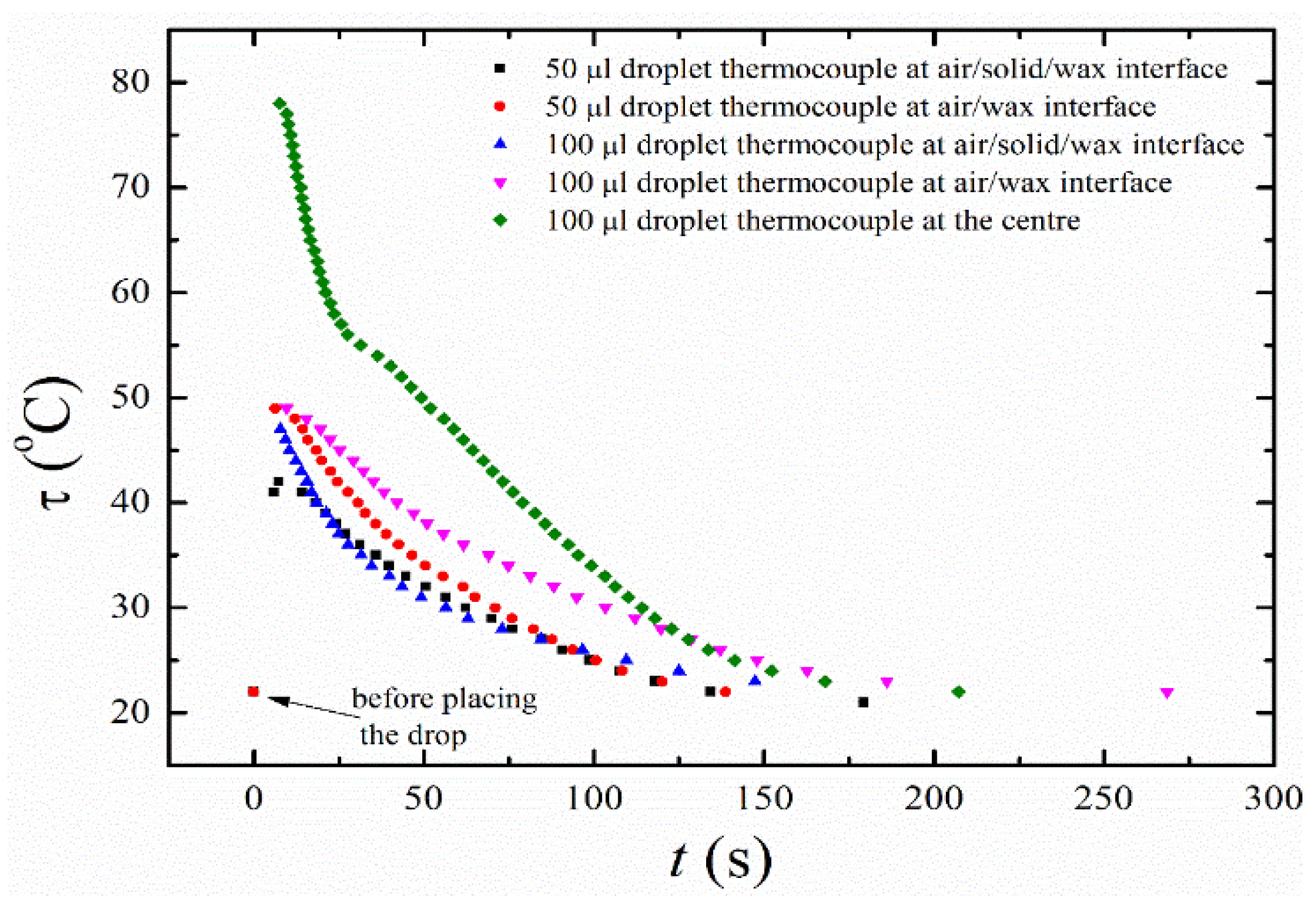
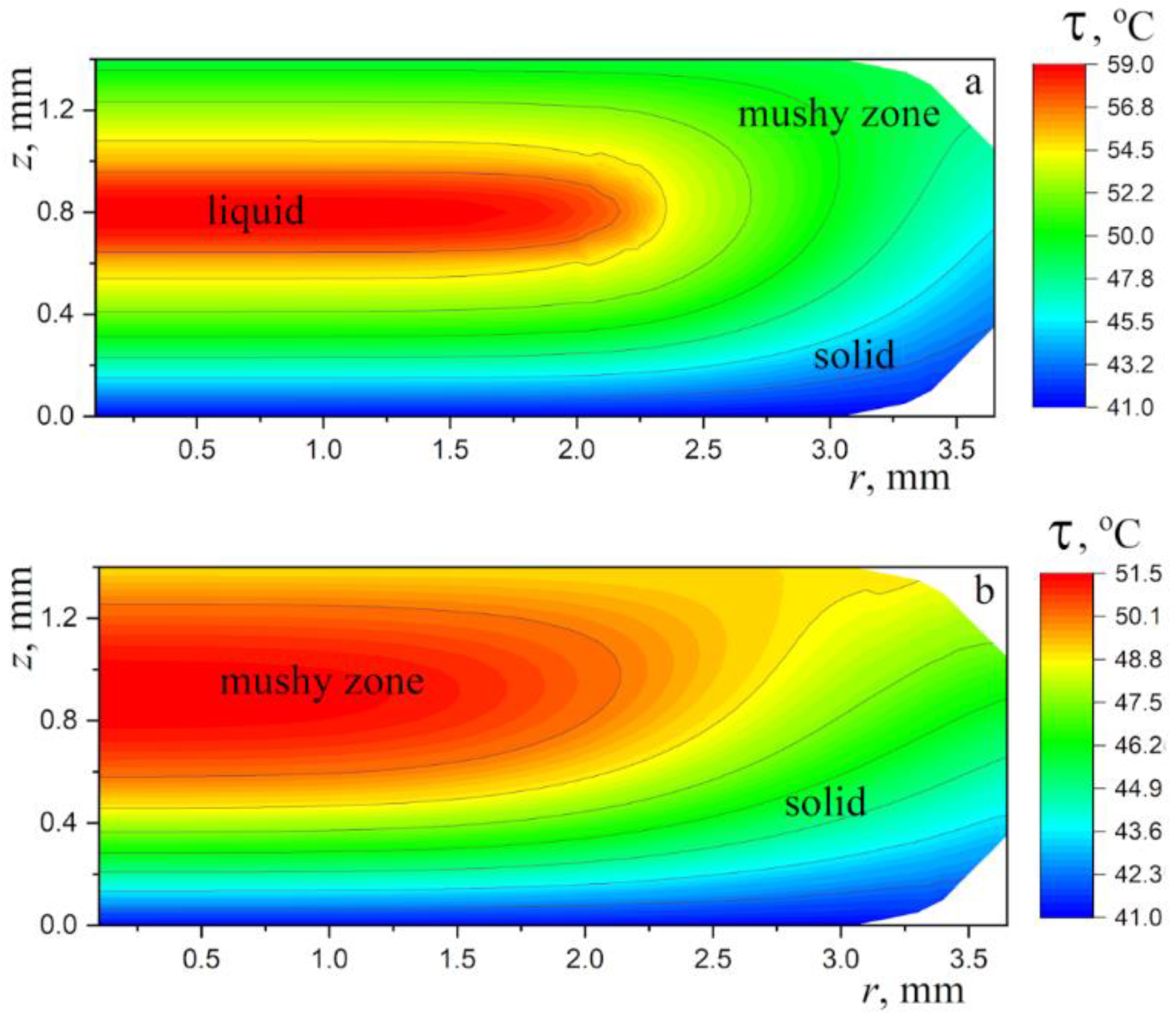
4. Discussion

4.1. Qualitative Analysis

Let us start with dimensionless numbers, relevant to the reported experiments. The Bond number, describing the interrelation between the gravity and surface tension-inspired effects:

$$\mathrm{B}\mathrm{o}=\frac{\rho g{d}^2}{\gamma },$$

(4)

where $\gamma$ and $\rho$ are the surface tension and density and paraffin wax, respectively, g is the acceleration of gravity, and d is the characteristic dimension of the droplet. Assuming for a sake of o rough estimation $\cong 8.0\times {10}^2\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^3}$ , $\gamma \cong 20.0\times {10}^{-3}\frac{\mathrm{J}}{{\mathrm{m}}^2}$ (see ref. 24) and $d\cong 1.0-2.0 \mathrm{m}\mathrm{m}$ yields $\mathrm{B}\mathrm{o}=0.8-3.2$. This means that the effects due to gravity and surface tension are comparable. The Reynolds number is given, in turn by Eq. 5:

$$\mathrm{R}\mathrm{e}=\frac{\rho vd}{\eta },$$

(5)

where v is the characteristic velocity of the paraffin flow in a course of the droplet deformation, $\eta$ is the dynamic viscosity. The dynamic viscosity of paraffin wax is varied in a very broad range, namely $\eta \left(\tau ={29}^0\mathrm{C}\right)\cong 10^{10}\mathrm{P}\mathrm{a}\times \mathrm{s}; \eta \left(\tau ={52}^{0}C\right)\cong 10 \mathrm{P}\mathrm{a}\times \mathrm{s}$ (see ref. 25). The characteristic velocity was estimated experimentally as $v\cong {10}^{-5}\frac{\mathrm{m}}{\mathrm{s}}.$ Substitution of aforementioned values of physical parameters yields $\mathrm{R}\mathrm{e}<{10}^{-6}.$ This means that inertial effects are negligible in the deformation of the paraffin wax droplet.

4.2. A Model of Cooling and Solidification of a Paraffin Wax Droplet

The above observations of the changing shape and the gradual solidification of the paraffin wax droplet show that these processes are interrelated in a rather complex way. Nevertheless, an initial relatively rapid deformation of the droplet by gravity, when the droplet is not yet cooled, can be distinguished. Experiments have shown that the deformation of the droplet continues throughout the cooling and solidification of the droplet, but this deformation is much slower.

When the lower layer of the droplet solidifies and a solid-liquid mushy zone is formed in the entire surface layer of the droplet (see Videos 1S, 2S, and 3S in Supplementary Materials), the surface tension can no longer hold the same shape of the droplet and the height of the droplet begins to decrease considerably. A similar effect was observed when cooling from the bottom of water marbles covered with a dense layer of fine powder (see ref. 26), but with a surface ice layer instead of the mushy zone. Of course, a droplet of higher-viscosity paraffin wax deforms much more slowly. The exponential increase in viscosity of liquid paraffin wax with decreasing temperature (this can be found in ref. 27) makes it difficult to estimate the rate of deformation using the ratio $\nu /\left(Rg\right)$ for the characteristic time of the process (here $\nu$ is the kinematic viscosity of the material, $R$ is the radius of an initially nearly spherical drop, $g$ is the acceleration of gravity). It should be noted that a slow decrease in droplet height continues for some time during the droplet solidification.

The slight increase in the density of paraffin wax during its solidification (only 9%) simplifies the estimation of the height of the solidified droplet. We will assume an approximate representation of the initial shape of the droplet as a hemisphere and assume that the top surface of the solidified droplet is flat (see Figure 7).

Assuming the material density remains unchanged, determine the height of the compressed droplet from the equality of the initial and final volumes with Eq.6:

$$\frac{2}{3}\pi R^3=\pi R^{2}H+\pi {\left(\frac{H}{2}\right)}^2\times 2\pi R$$

(6)

Equation (6) gives the following formula for the relative height of the compressed droplet:

$$\overline{H}=\frac{H}{R}=\frac{2}{\pi }\left(\sqrt{1+2\pi /3}-1\right)\approx 0.48$$

(7)

Taking into account the increase in the material density with solidification, we obtain $\overline{H}\approx 0.44$. This value is slightly less than that in the experiment, but it is not important for an approximate computational model.

Since the formation of a dimple in the center of the upper surface of a solidified droplet is of the main physical interest, we will focus on solving the problem of cooling and solidification of the droplet. It is natural to assume that the dimple formed before the full solidification of the droplet is due to a small volume of liquid paraffin wax remaining under the more viscous part of the mushy zone near the upper surface of the droplet. Volume reduction during the solidification of viscous paraffin wax in this area causes the surface layer to subside. In order to check this assumption, we should solve a 2D axisymmetric problem of transient heat conduction taking into account the latent heat of phase transition.

Considering the difficulty of quantifying the change in droplet shape when solving the thermal problem, we restrict ourselves to a simpler calculation, assuming that the droplet shape remains unchanged and is the same as the final shape. This relatively simple model is acceptable due to the very low thermal conductivity of paraffin wax: this value for liquid paraffin wax is 3.4 times lower than that of water, and the thermal conductivity of solid paraffin wax is 6.4 times lower than that of ice. Therefore, when cooling from below, the temperature field in most of the droplet volume is almost independent of the deformation of the upper surface of the droplet.

The temperature field in a droplet is determined as a solution to a transient heat transfer problem in the axisymmetric computational region with the cross-section shown in red in Fig. 7. The axial coordinate $z$ is measured from the glass plate, and the contact area of the droplet with the plate is a circle of radius $R$. The conduction equation for the temperature field $\tau \left(t,r,z\right)$ is as follows:

$$\rho c\frac{\partial \tau }{\partial t}=\frac{1}{r}\left(kr\frac{\partial \tau }{\partial r}\right)+\frac{\partial }{\partial z}\left(k\frac{\partial \tau }{\partial z}\right)$$

(8)

where $\rho$, $c$, and $k$ are the density, specific heat capacity, and thermal conductivity of paraffin wax, respectively. To take into account the latent heat $L_{\mathrm{m}}$ of phase change for substances whose phase change is characterized by the melting/solidification point $\tau ={\tau }_{\mathrm{m}}$ one can use an equivalent additional capacity in the temperature range of ${\tau }_{\mathrm{m}}-\mathsf{\Delta }\tau <\tau <{\tau }_{\mathrm{m}}+\mathsf{\Delta }\tau$, where $\mathsf{\Delta }\tau \ll {\tau }_{\mathrm{m}}$, as it was done if refs. 28-30:

$$\mathsf{\Delta }c=\frac{L_{\mathrm{m}}}{\mathsf{\Delta }T}\left(1-\frac{\left|{\tau }_{\mathrm{m}}-\tau \right|}{\mathsf{\Delta }\tau }\right)$$

(9)

When paraffin wax solidifies, a mushy zone is formed in the region of the temperature between the liquidus and solidus (see refs. 31, 32): ${\tau }_{\mathrm{s}\mathrm{o}\mathrm{l}}<\tau <{\tau }_{\mathrm{l}\mathrm{i}\mathrm{q}}$. In our case, the values of ${\tau }_{\mathrm{m}}$ and $\mathsf{\Delta }\tau$ in Eq. (9) should be replaced by $\left({\tau }_{\mathrm{l}\mathrm{i}\mathrm{q}}+{\tau }_{\mathrm{s}\mathrm{o}\mathrm{l}}\right)/2$ and $\left({\tau }_{\mathrm{l}\mathrm{i}\mathrm{q}}-{\tau }_{\mathrm{s}\mathrm{o}\mathrm{l}}\right)/2$, respectively. We will also assume that the density, specific heat capacity, and thermal conductivity depend linearly on the temperature in the mushy zone.

The initial condition and the boundary conditions for Eq. (8) are:

$$\tau \left(0,r,z\right)={\tau }_0$$

(10)

$$\frac{\partial \tau }{\partial r}=0 \mathrm{at} r=0; \tau ={\tau }_{\mathrm{g}}\left(t\right) \mathrm{at} z=0;$$

$$\tau ={\tau }_{\mathrm{a}}\left(t\right)\text{on other surfaces}$$

(11)

where ${\tau }_{\mathrm{g}}\left(t\right)$ and ${\tau }_{\mathrm{a}}\left(t\right)$ are the measured surface temperature of the droplet at the contact zone with the glass plate and at the surface surrounded by air. According to infrared pyrometric measurements of the brightness temperature of paraffin wax droplets, we assume that the temperature of the upper surface of the droplet is independent of the radial coordinate.

The above heat conduction problem was solved numerically using an implicit finite-difference scheme of the second order of approximation on an orthogonal grid with splitting the operator in the right side of Eq. (8) as it was done in ref. 33, 34. The thermo-physical properties of the different types of paraffin wax are essentially different (see refs. 35–37). The following values have been assumed for the calculations: ${\rho }_{\mathrm{liq}}=790$ kg/m³, ${\rho }_{\mathrm{sol}}=916$ kg/m³, $c_{\mathrm{liq}}=3.26$ kJ/(kg K), $c_{\mathrm{sol}}=1.92$ kJ/(kg K), $k_{\mathrm{liq}}=0.167$ W/(m K), $k_{\mathrm{sol}}=0.346$ W/(m K), ${\tau }_{\mathrm{liq}}=329$ K, ${\tau }_{\mathrm{sol}}=322$ K, and $L_{\mathrm{m}}=174$ kJ/kg. The results of the temperature field calculations for a typical paraffin wax droplet are presented in Figure 8 and 9.

It can be seen that by the time the lower layer, about a quarter of the droplet height, has solidified, the rest of the droplet volume is occupied by the mushy medium. In this case, the hottest zone, dominated by liquid paraffin wax, has the appearance of a lens close to the upper surface of the droplet. This result confirms the assumption made above about the physical nature of the dimple on the upper surface of the paraffin wax droplet.

Obviously, the relative width of the hot lens below the upper surface of the droplet depends on the droplet size. In very small droplets this zone cannot be as wide and almost flat as in Figure 9, and in very large droplets the hot lens, on the contrary, is almost flat and its width is only a little less than the diameter of the upper surface of the droplet. In both cases, there are no conditions for the formation of a dimple on the upper surface. A derivation of the two-dimensional heat transfer problem for large droplets where the temperature field in most of the droplet volume can be calculated by solving a one-dimensional problem considering heat transfer only in the axial direction is an extreme case showing that the appearance of a non-wide hot lens and the resulting formation of a dimple is possible only for small (but not too small) droplets. This conclusion, based on a consideration of the heat transfer characteristics of the paraffin wax droplet, explains the observed change in the solidification pattern of the droplet as its size changes (see Videos S1, S2, and S3). The suggested approximate computational model does not give accurate temperature values in each element of the droplet volume at each point in time for several obvious reasons. One source of systematic error is the simplified representation of the shape of the computational region; another is the natural uncertainty in the values of the thermo-physical parameters, which in addition are different for different types of paraffin. However, this by no means prevents one from obtaining a physically correct picture of the thermal process and correctly understanding the features of solidification of paraffin wax droplets and other phase change materials.

The above computational analysis enables us to understand the dimple formation on the upper surface of the solidified droplet. This stage of the process begins when the paraffin wax on the surface of the droplet is close to solidification and there is a hot mushy zone with high liquid paraffin wax content below it, near the axis of the droplet. Continued cooling causes the volume of the initial liquid lens to decrease, resulting in a thin crust of paraffin wax descending and forming a dimple on the surface of the solidified droplet.

The results of numerical modelling agree well with the laboratory observations. One can see in Videos 1S and 2S from the Supplementary Materials that at first only the solidified thin bottom layer of the droplet becomes white (opaque), then the image of the rest of the droplet of paraffin wax gradually becomes turbid (when the mushy zone extends to the whole volume of the droplet) and finally the dimple of interest appears on the top surface of the droplet.

Theoretical estimation of the final dip height can be based on the following simple considerations. First, the measurements demonstrate that the growth of the dip preserves the self-similarity to a large extent, since the aspect ratio and the angle are volume-independent (cf. Figs. 2D and 4B). Then, assuming the shape of the dip as spherical segment, its volume is expressed as follows:

$$V_{\mathrm{d}}=\frac{\pi h_{\mathrm{d}}^3}{3}\frac{2+\mathit{sin}(\beta /2)}{1-\mathit{sin}(\beta /2)}$$

(12)

Then, we assume that the dip grows in accordance with the dynamics of the bulk volume relaxation in the course of freezing. We assume that this process is characterized by some characteristic time $t_{\mathrm{r}}$ for the bulk, and only the part of the volume that is “relaxed out” actively participates in the process. Thus, the following empiric estimation is in order:

$$\frac{d{V}_{\mathrm{d}}}{dt}\approx \frac{{\rho }_{\mathrm{s}\mathrm{o}\mathrm{l}}-{\rho }_{\mathrm{l}\mathrm{i}\mathrm{q}}}{t_{\mathrm{r}}{\rho }_{\mathrm{s}\mathrm{o}\mathrm{l}}}V$$

(13)

The process of the dip growth stops when the droplet freezes; we assume that it happens after some characteristic time $t_f$. In all cases, the volume of the dip is much smaller than the volume of the droplet, and it is possible to estimate:

$$V_{\mathrm{d}}~\frac{{\rho }_{\mathrm{s}\mathrm{o}\mathrm{l}}-{\rho }_{\mathrm{l}\mathrm{i}\mathrm{q}}}{t_{\mathrm{r}}{\rho }_{\mathrm{s}\mathrm{o}\mathrm{l}}}V{t}_{\mathrm{f}}$$

(14)

The characteristic freezing time depends on the size of the droplet and on the thermal conductivity:

$$t_{\mathrm{f}}~\frac{\rho c{R}^2}{k}\sim \frac{\rho c{V}^{2/3}}{k}$$

(15)

The indices related to solid or liquid phase in Eq. (15) are omitted, since at this level of qualitative estimation there is no need to distinguish between them. Also, there is no need to distinguish between the running droplet volume V and the initial volume $V_0$ With account of Eqs. (12), (14), and (15) one arrives to the following estimation for the dip height:

$$h_{\mathrm{d}}~{\left(\frac{1-\mathit{sin}(\beta /2)}{2+\mathit{sin}(\beta /2)}\frac{{\rho }_{\mathrm{s}\mathrm{o}\mathrm{l}}-{\rho }_{\mathrm{l}\mathrm{i}\mathrm{q}}}{t_r{\rho }_{\mathrm{s}\mathrm{o}\mathrm{l}}}\frac{c\rho }{k}\right)}^{1/3}{V}_0^{5/9}$$

(16)

The exponent in Eq. (16) is in good agreement with numeric estimation (3). If we substitute the measured value of the angle $\beta \approx 160^0$, average values for the heat capacity, density and heat conductivity, and assume $t_{\mathrm{r}}~100$ s in accordance with our experimental observations (cf. Figure 5), then for the droplet volume $V_0=50$ µl one obtains the estimation $h_d~340$ µm, in reasonable qualitative agreement with the experimental findings.

5. Conclusions

Paraffin wax is a phase change material, exerted to intensive research recently. Paraffin wax stores energy in the form of latent heat at a nearly constant temperature during melting and releases this energy during solidification. This effect is used in industrial energy storage. An experimental and theoretical study of the unusual deformation of a droplet of paraffin wax placed on a relatively cold glass plate was carried out. Deformation of the droplet by gravity begins before the droplet cooling and continues, but at a much slower rate, as the droplet cools and solidifies. At the final stage of the process, a dimple is formed on the upper surface of the droplet. The mechanism of formation of this dimple has been the subject of special consideration by the authors.

In laboratory experiments, video recording of the droplet was used, which not only showed different stages of the droplet deformation but also, due to the transparency of liquid paraffin in the visible spectral range, allowed to observe solidification of the lower part of the droplet and formation of the mushy zone between the liquidus and solidus of paraffin wax at the side surface of the droplet. Infrared pyrometry of the upper surface of the droplet in the spectral range of the paraffin wax opacity showed insignificant temperature changes of the upper, almost isothermal, droplet surface during the whole process. Thermocouple measurements on the side and bottom surfaces and pyrometric measurements of the upper surface temperature of the droplet gave the necessary information for thermal calculations.

The theoretical part of the paper contains the physical model of transient heat transfer and calculations of the axisymmetric temperature field in the solidifying droplet of paraffin taking into account the latent heat of the phase transition and variable thermo-physical properties of the material in the mushy zone. The calculations showed that a relatively hot “lens” formed in a small droplet moves towards the central part of its upper surface. The solidification of the paraffin wax in the lens causes its volume to decrease and a thin surface layer of nearly solid material descends to form the central dimple. Heat transfer analysis has shown that such a dimple cannot be formed on very small or too large droplets of paraffin wax. The latter is confirmed by the observed patterns of solidification of droplets of different sizes. The studied effect is important for understanding of behavior of the phase change materials, used for energy storage.