On Structural Identifiability of System with Nonsymmetric Nonlinearities

1. Introduction

Nonsymmetric nonlinear systems used to control various objects [1,2,3,4,5]. A genetic procedure [1] proposed for the nonsymmetric hysteresis identification. In [2], an extended Prandtl-Ishlinskii model based on the application of the asymmetric reproduction operator proposed. Its analogue is used in [1]. In [3,4], models propose considering the influence of the excitation frequency on the hysteresis. A generalized Bouc-Wen model [5] proposed to describe strongly asymmetric hysteresis. Inverse motion control scheme [6] proposes for estimates of dynamic surface. The effect of nonsymmetric hysteresis compensates by the introduction of an estimated compensator.

The nonsymmetric Bouc-Wen model proposes to improve the accuracy of hysteresis modelling in [7]. The recursive least squares method used to identify the BWM parameters in real time. Other approaches to the nonsymmetric Bouc-Wen hysteresis identification consider in [8]. A nonsymmetric switching element used [9] to reduce its own losses in optical waveguides. A phenomenological hysteresis model studies to scribe a magnetostrictive actuator in [11]. The analysis of nonsymmetric oscillations described by polynomial functions in a resonant circuit is given in [12]. Closed systems with various nonsymmetric nonlinearities consider in [13]. Control systems with variable dead zones scribes in [14,15].

So, the analysis shows that nonsymmetric nonlinearities (NN) applied to implement non-standard control laws. Standard synthesis methods use for the analysis and construction of systems with NN. The input effect on properties of nonlinear systems has not been studied. This also applies to the analysis of the systems identifiability with nonsymmetric nonlinearities. The nonlinear systems (NS) identifiability estimation guarantees to implement control laws considering NS capabilities. As a rule, various approximation methods used to estimate the NS identifiability [16]. They level out the nonlinearity form and are applicable only under a priori certainty. Using these methods requires additional research. The NS identifiability is related to structural identification [16]. In contrast to parametric identifiability, the structural identifiability bases on the analysis of structures special class [16,17]. SI conditions get for symmetric nonlinearities in [16,17]. Nonsymmetric nonlinearities have features and require of the proposed method modification. We give a development and generalization of the results obtained in [16,17].

2. Problem Statement

Consider the system

$$\begin{array}{l}\dot{X}=AX+B_{\phi }\phi \left(y,\tilde{A}\right)+B_{u}u,\\ y=C^{T}X,\end{array}$$

(1)

where $u\in ℝ$, $y\in ℝ$  are input and output; $A\in {ℝ}^{q\times q}$, $B_{\phi }\in {ℝ}^q$, $C\in {ℝ}^q$ ; $\phi \left(y,\tilde{A}\right)$  is scalar nonlinear function; matrix $A$ ; $\tilde{A}\in {ℝ}^k$  is vector of nonlinearity parameters; $B_{\phi }=B_u=I={\left[0,0,\dots ,0,1\right]}^T$, $C={\left[1,0,\dots ,0\right]}^T$, $\phi ={\phi }_a={\phi }_a\left(y,A_a\right)$  is nonsymmetric nonlinearity.

Remark 1. In general, vector $A_a$ elements may not coincide. It reflects the ${\phi }_a\left(y,A_a\right)$ asymmetry.

Symmetric nonlinearity is denoted as ${\chi }_s={\phi }_s\left(y,A_s\right)$ . Various assumptions are made about the function structure. They determine by the level of a priori information. They determine by the level of a priori information. Linearization procedures [18] applied under a priori certainty. Often believe

$$\chi \in \left\{\phi (\xi )\xi \ge {\xi }^2,\hspace{0.17em}\hspace{0.17em}\xi \ne 0,\hspace{0.17em}\hspace{0.17em}\phi (0)=0\right\}$$

(2)

or

$$\chi \in {\mathbb{F}}_{\phi }=\left\{{\gamma }_1{\xi }^2\le \phi \left(y\right)\xi \le {\gamma }_2{\xi }^2,\hspace{0.17em}\hspace{0.17em}\xi \ne 0,\hspace{0.17em}\hspace{0.17em}\phi \left(0\right)=0,\hspace{0.17em}\hspace{0.17em}{\gamma }_1\ge 0,\hspace{0.17em}{\gamma }_2<\infty \right\}$$

(3)

where $\xi \in ℝ$  is nonlinear element input, $\xi =\xi \left(X\right)$ .

We assume that the nonlinear part of the system (1) described by static dependence. Function $\chi$  is smooth. Information set for (1)

$$\mathbb{I}{}_o=\left\{u(t),\hspace{0.17em}y(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\in \mathbb{J}=\left[t_0,t_k\right]\right\}$$

Problem: evaluate the structural identifiability of the system (1) nonlinear part based on the analysis and processing $\mathbb{I}{}_o$ .

The problem solution gives an answer to the question on the possibility of the system (1) structure evaluating. The use of parametric identification methods does not give the SI problem solution under uncertainty. Apply the approach to the structural identification proposed in [16]. It is based on the transition to a special structural space and the framework's $S_{ey}$ construction reflecting the nonlinear part (1) properties. The $S_{ey}$  analysis relates to the SI problem solution of the system (1). Describe the constructing method the $S_{ey}$ -framework.

3. Design $S_{ey}$ -frameworks

The $S_{ey}$ -framework design requires the preliminary formation of the set $\mathbb{I}{}_{N,g}$  containing information about the function $\phi (y)$ . Apply the differentiation operation to $y(t)$  and designate the resulting variable as $x_1$ . Get an extension $\mathbb{I}{}_{ent}=\left\{\mathbb{I}{}_o,x_1\right\}$ of the information set $\mathbb{I}{}_o$ .

Select the subset $\mathbb{I}{}_g\subset \mathbb{I}{}_{ent}$  corresponding to a system (1) particular solution. The set data $\mathbb{I}{}_g=\mathbb{I}{}_{ent}\backslash \mathbb{I}{}_{tr}$  contains not data about the transition process in the system (1). Apply the mathematical model

$${\widehat{x}}_1^l(t)=H^T{\left[1\hspace{0.17em}\hspace{0.17em}u(t)\hspace{0.17em}\hspace{0.17em}y(t)\right]}^T$$

(4)

to estimate the linear component in $x_1$ . The variable $x_1$ is defined on the interval ${\mathbb{J}}_g=\mathbb{J}\backslash {\mathbb{J}}_{tr}$ . $H\in {ℝ}^3$  is a vector of model parameters. Determine the vector $H\in {ℝ}^3$  as

$$\underset{H}{\min }Q(e){|}_{e={\widehat{x}}_1^l-x_1}\to H_{opt}$$

where  $Q(e)=0.5e^2$ .

Find the forecast for the variable $x_1$  based on the model (4) and generate the error  $e(t)={\widehat{x}}_1^l(t)-x_1(t)$ . $e(t)$  depends on the $\phi (y)$  in the system (1). So, the set $\mathbb{I}{}_{N,g}=\left\{y(t),\hspace{0.17em}\hspace{0.17em}e(t)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\in {\mathbb{J}}_g\right\}$  obtain. Next, we apply the notation $y(t)$, assuming that $y(t)\in \mathbb{I}{}_{N,g}$ .

The phase portrait $S$  application described by the function $\Gamma :\left\{y\right\}\to \left\{y^{\prime }\right\}$  is not always effective under uncertainty. Consider the set ${\mathbb{I}}_{N,g}$  and move to the space ${\mathcal{P}}_{ye}=(y,e)$, which you call structural. Consider the function ${\Gamma }_{ey}:\left\{y\right\}\to \left\{e\right\}$ $\forall t\in {\mathbb{J}}_g$  which describes the framework $S_{ey}$  on the plane $(y,e)$ . ${\mathbb{I}}_{N,g}$  contains information about $\phi (y)$  so $S_{ey}$  generalizes the change of a nonlinear function. This is true if the input of system (1) satisfies certain conditions. Such input guarantees the closure of the framework $S_{ey}$ . The model (45) application gives a new representation for the system (1).

$$\begin{array}{l}{S}_y:\{\begin{array}{l}\dot{\tilde{X}}=A\tilde{X}+I\zeta ,\\ \tilde{y}=C^T\tilde{X},\end{array}\\ S_{\phi }:e=f\left(y,x_1\right),\end{array}$$

(5)

where $\tilde{X}\in {ℝ}^q$  is a variable describing the general solution of the system (1); $\zeta \in ℝ$  is limited perturbation emerging as the result of the variable $e$  define.

Consider the system $S_{\phi }$  identifiability problem. The system $S_y$  identifiability is studied in [17].

4. h-Identifiability and S-Synchronizability

Consider the major results on the $h$ -identifiable of the system (1) with symmetric nonlinearity ${\chi }_s\in {\mathbb{F}}_{\phi }$  [16,21].

Input plays an important role in nonlinear systems. It affects S-synchronizability, $h$ -identifiability, and the appearance of "insignificant" $S_{ey}$ -structures in the system.

Assumptions.

B1. The input is extremely non-degenerate (constant excited) on the interval

$$\mathcal{P}{\mathcal{E}}_{\alpha ,\overline{\alpha }}^S:\hspace{0.17em}\hspace{0.17em}\left(\alpha I_l\le B_P(t)\le \overline{\alpha }{I}_l\right)\&\left({\Omega }_u(\omega )\subseteq {\Omega }_S(\omega )\right)\forall t\ge t_0,$$

(6)

where $\left(\alpha ,\overline{\alpha }\right)>0$  is some numbers, ${\Omega }_S(\omega )$  is the set of allowable input frequencies providing SI systems, ${\Omega }_u(\omega )$  is the frequencies $u(t)$  set.

B2. Input $u(t)$  provides an informative structure $S_{ey}\left({\mathrm{II}}_{N,g}\right)$ .

Definition 1. An input $u(t)$ is presentative if it satisfies conditions B1, B2.

Denote the framework $S_{ey}$  with asymmetric nonlinearity as $S_{ey}^s$ .

Let the framework $S_{ey}^s$  be closed, and its area is not zero. Denote the height $S_{ey}^s$  as $h\left(S_{ey}^s\right)$  where height is the distance between two points on opposite sides of the structure $S_{ey}^s$ .

Notations.

1. ${\mathcal{D}}_y=\mathrm{dom}\hspace{0.17em}\left(S_{ey}^s\right)$  is definitional domain $S_{ey}^s$ .

2. $D_y=D_y\left({\mathcal{D}}_y\right)=\underset{t}{\max }y(t)-\underset{t}{\min }y(t)$  is diameter ${\mathcal{D}}_y$ .

3. $u(t)\in \mathbb{U}$, where $\mathbb{U}$  is the allowed set of inputs for the system (1). The set $\mathbb{U}$  contains representative inputs.

Definition 2. If the definition domain ${\mathcal{D}}_y$ of the framework $S_{ey}^s$ has a maximum diameter $D_y$ on the set $\left\{y(t),t\in \right\}$ , then the input $u(t)\in {\mathbb{U}}_S\subseteq \mathbb{U}$ is the S-synchronizing system (1).

Let $S_{ey}={\mathcal{F}}_{S_{ey}}^l\cup {\mathcal{F}}_{S_{ey}}^r$, where ${\mathcal{F}}_{S_{ey}}^l,{\mathcal{F}}_{S_{ey}}^r$  are the left and right fragments $S_{ey}^s$ . Define secant

$${\gamma }_S^{r,s}={\alpha }^{r,s}y,{\gamma }_S^{l,s}={\alpha }^{l,s}y,$$

(7)

for ${\mathcal{F}}_{S_{ey}}^l,{\mathcal{F}}_{S_{ey}}^r$, where ${\alpha }^l$, ${\alpha }^l$  are positive numbers.

Theorem 1 [21]. Let 1) the framework $S_{ey}^s$ has the form $S_{ey}^s={\mathcal{F}}_{S_{ey}}^{l,s}\cup {\mathcal{F}}_{S_{ey}}^{r,s}$ ; 2) secants described by equations (7) for ${\mathcal{F}}_{S_{ey}}^{l,s},{\mathcal{F}}_{S_{ey}}^{r,s}$ . Then $S_{ey}^s$ is an $\mathcal{N}{S}_{ey}^s$ -framework if

$$\left|\left|{\alpha }^{l,s}\right|-\left|{\alpha }^{r,s}\right|\right|>{\delta }_h,$$

(8)

where ${\delta }_h>0$  is some set value.

Consider the reference framework $S_{ey}^{ref}$  reflecting all the properties of the function $\phi (y)$ . Let $D_y^{ref}$  be the $D_y\left(S_{ey}^{ref}\right)$  diameter. $D_y^{ref}$  exists for system (1) with S-synchronizing input.

Definitions 1, 2 show that if $S_{ey}^s\cong S_{ey}^{ref}$, then $\left|D_y-D_y^{ref}\right|\le {\epsilon }_y$, where ${\epsilon }_y\ge 0$, $\cong$  is a sign of proximity. Subset ${\mathbb{U}}_S$  elements have the property

$$S_{h_{\delta }}:\left|D_y\left(S_{ey}^s\left(u(t){|}_{u\in {\mathrm{U}}_S}\right)\right)-D_y^{ref}\right|\le {\epsilon }_y$$

(9)

We interpret the choice $u_h(t)\in$  as synchronization between the structures of the model and the system. Therefore, the condition ${\mathcal{d}}_{h,y}=\underset{u_h}{\max }{D}_y$  fulfillment guarantees the system $h$ -identifiability. $h$ -identifiability condition

$$\left|D_y\left(S_{ey}^s\left(u(t){|}_{u\in {\mathrm{U}}_S}\right)\right)-{\mathcal{d}}_{h,y}\right|\le {\epsilon }_y$$

(10)

Remark 2. Treat the condition (10) as an almost homotheticity of the structure $S_{ey}^s$ . The word "almost" emphasizes the computational aspects influence of structure obtaining. The homothety concept given in [22].

Let the input $u_h(t)$  synchronize the set ${\mathcal{D}}_y$ . If $u(t)$  is S-synchronizing, then we will write $u_h(t)\in S$ . A finite set $\left\{u_h(t)\right\}\in S$  exists for the system (1). The optimal $u_h(t)$  choice depends on ${\mathcal{d}}_{h,y}$  and (10). The condition (10) fulfillment is the basis for the SI (identification) of the system (1).

Definition 3. If condition (10) holds for ${\mathcal{F}}_{S_{ey}}^{l,s},{\mathcal{F}}_{S_{ey}}^{r,s}$ , then the $S_{ey}^s$ -framework is almost homothetic (AH) or $\epsilon$ -homothetic (EH).

Theorem 2. Let (i) $\left\{u_h(t)\right\}\in S$ ; (ii) condition (10) is hold; (iii) framework $S_{ey}^s$ (system (1)) is h-identifiable; (iv) condition

$$\left|\left|{\alpha }^{l,s}\right|-\left|{\alpha }^{r,s}\right|\right|\le {\delta }_h$$

(11)

is satisfied. Then system (1) (  $S_{ey}^s$  -framework) is structurally identifiable or $h_{{\delta }_h}$  -identifiable.

The Theorem 2 proof based on the conditions AH or EH (conditions (10), (11)) fulfillment for fragments $\left({\mathcal{F}}_{S_{ey}}^{l,s},{\mathcal{F}}_{S_{ey}}^{r,s}\right)\subset S_{ey}^s$ . Condition (11) says that lines (7) are almost parallel. Apply the Theorem 3 [17] proof and get that the condition $\left|{с}_S-{с}_{D_y}\right|\le \epsilon$, where $\epsilon \ge 0$, holds for the framework $S_{ey}^s$  with center ${с}_S$  and the domain ${\mathcal{D}}_y$  with the center ${с}_{D_y}$ . Hence, (i) the $S_{ey}^s$ -structure is almost symmetric or $S_{ey}^s\in {\mathcal{S}}_{ey}^H\left(\chi \right)$  on the plane $\left(y,e\right)$, where ${\mathcal{S}}_{ey}^H\left(\chi \right)$  is a homothetic structures class for symmetric nonlinear systems.; (ii) diameters of fragments $\left({\mathcal{F}}_{S_{ey}}^{l,s},{\mathcal{F}}_{S_{ey}}^{r,s}\right)\subset S_{ey}^s$  determination regions coincide accurate within value ${\epsilon }_{\mathcal{F}}\ge 0$  on $\left\{y(t)\right\}$ 

$$\left|D_{{\mathcal{F}}_S^l}\left({\mathcal{D}}_{{\mathcal{F}}_S^l}\right)-D_{{\mathcal{F}}_S^r}\left({\mathcal{D}}_{{\mathcal{F}}_S^r}\right)\right|\le {\epsilon }_{\mathcal{F}},$$

(12)

where ${\mathcal{D}}_{{\mathcal{F}}_S^l},{\mathcal{D}}_{{\mathcal{F}}_S^r}$  are determination regions ${\mathcal{F}}_{S_{ey}}^{l,s},{\mathcal{F}}_{S_{ey}}^{r,s}$ . Obtain from (12)

$$u(t)=u_h(t)\Rightarrow u(t)\in S\Rightarrow {\mathcal{d}}_{h,y}=\underset{u_h}{\max }{D}_y,$$

(13)

Conditions (12), (13) guarantee SI [16] ( $h_{{\delta }_h}$ -identifiability) of the system (1).

The asymmetry ${\chi }_a$  leads to $S_{ey}^s(\chi )$ -framework deformation in comparison with nonlinearities ${\chi }_s$ . Denote the structure corresponding to ${\chi }_a$  as $S_{ey}^a=S_{ey}\left({\chi }_a\right)$ .

Let the input $u(t)$  satisfy B1, B2 conditions. Hence, a subset $\left\{u_h(t)\right\}\in S$  that guarantees the system (1) $h$ -identifiability exists. Structure $S_{ey}^a\left({\chi }_a\right)\in {\mathcal{S}}_{ey}^{H_a}\left({\chi }_a\right)$  defined on ${\mathrm{II}}_h=\left\{y(t),u(t){|}_{u_h(t)\in S}\right\}$ . Structural differences between ${\chi }_a$  and ${\chi }_s$  belonging a class $ℱ(\chi )$  caused by the following condition

$${\chi }_a\ne {\chi }_s\Rightarrow \dim A_a\ge \dim A_s,A_a\in {\text{ℝ}}^k,A_s\in {\text{ℝ}}^m$$

(14)

We believe that $\left({\chi }_a,{\chi }_s\right)\in ℱ$  and ${\chi }_a,{\chi }_s$  have different parametric content.

Theorem 3. Let (i) $\left\{u_h(t)\right\}\in S$ ; (ii) $S_{ey}^a\in ℱ$ for almost everyone $y(t)$ . Then the structure $S_{ey}^a\in ℱ$ is $h_{{\delta }_h}^a$ -identifiable or ${\epsilon }_a$ -homothetic it ${\mathcal{F}}_{S_{ey}}^{l,a}\cong {\mathcal{F}}_{S_{ey}}^{r,a}$ is true for almost $\forall \left(y,u_h\right)\in {\mathrm{II}}_o$ excluding fragments areas ${\mathcal{F}}_{S_{ey}}^{l,a},{\mathcal{F}}_{S_{ey}}^{r,a}$ where (14) hold.

Theorem 3 proof. $u_h(t)\in S$  and therefore, the framework $S_{ey}^a\in ℱ$  has a maximum diameter. The condition $\left|{с}_{{\mathcal{F}}_{l,a}}-{с}_{{\mathcal{F}}_{r,a}}\right|\le {\epsilon }_a$  satisfied for centers ${\mathcal{F}}_{S_{ey}}^{l,a},{\mathcal{F}}_{S_{ey}}^{r,a}$, where ${\epsilon }_a\ge 0$ . Hence, fragments ${\mathcal{F}}_{S_{ey}}^{l,a},{\mathcal{F}}_{S_{ey}}^{r,a}$  are ${\epsilon }_a$ -homothetic, and the system (1) is $h_{{\delta }_{\approx }}^a$  identifiable for almost all $y(t)\in {\mathrm{II}}_h$ .■

Let 1) $\left({\chi }_a,{\chi }_s\right)\in ℱ$ ; 2) $\left|{\mathrm{a}}_{i,a}-a_{k,a}\right|\le \upsilon$  valid for some elements subset ${\mathcal{A}}_a\in A_a$, where $\upsilon \ge 0$, ${\mathrm{a}}_{i,a}\in {\mathcal{A}}_a$, $i$  belongs to some interval of integers, $i$  can coincide with $k$  when $\dim A_a\to \dim A_s$, $a_{k,a}\in A_s$ .

Consider a subdomain ${\mathcal{F}}_{S_{ey,i}}^{q,a}$  of the fragment ${\mathcal{F}}_{S_{ey}}^{q,a}$, $q=l,r$ . Select sub-domains ${\mathcal{F}}_{S_{ey,i}}^{l,a}$  and ${\mathcal{F}}_{S_{ey,i}}^{l,a}$, which are structurally similar (property $s_{\approx }$ ), as ${\chi }_a\in ℱ$ . Mark the ${\mathcal{F}}_{S_{ey,i}}^{l,a}$  and ${\mathcal{F}}_{S_{ey,i}}^{l,a}$  similarity as ${\epsilon }_{\approx }$ . If the function ${\chi }_a\in ℱ$  has the property $s_{\approx }$, then we write ${\chi }_a\in {ℱ}_{s_{\approx }}$, and the corresponding property $S_{ey}^a$ -framework denote as $S_{ey}^a\in {\mathcal{S}}_{{\epsilon }_{\approx }}$ .

Definition 4. The structure $S_{ey}^a\in ℱ$ is almost ${\epsilon }_a$ -homothetic or $h_{{\delta }_{\approx }}^a$ -identifiable, if $S_{ey}^a$ is ${\epsilon }_a$ -homothetic, and the regions ${\mathcal{F}}_{S_{ey,i}}^{q,a}\subset {\mathcal{F}}_{S_{ey}}^{q,a}$ have the property ${\mathcal{F}}_{S_{ey,i}}^{q,a}\in {ℱ}_{s_{\approx }}$ .

Theorem 4. Let (i) $\left\{u_h(t)\right\}\in S$ ; (ii) framework ${\chi }_a\in ℱ$ ; (iii) condition $\left|\left|a^{l,a}\right|-\left|a^{r,a}\right|\right|\le {\delta }_{h,a}$ ( ${\delta }_{h,a}\ge 0$ ) holds almost for all $y(t)$ for secant fragments $\left({\mathcal{F}}_{S_{ey}}^{l,a},{\mathcal{F}}_{S_{ey}}^{r,a}\right)\subset S_{ey}^a$ ; (iv) condition $\left|{\mathrm{a}}_{i,a}-a_{k,a}\right|\le \vartheta$ holds for the domain ${\mathcal{F}}_{S_{ey,i}}^{q,a}\subset {\mathcal{F}}_{S_{ey}}^{q,a}$ $(q=i,r)$ with parameters ${\mathcal{A}}_a\in A_a$ , where $\vartheta \ge 0$ , ${\mathrm{a}}_i\in {\mathcal{A}}_a$ , $a_k\in A_s$ . Then the framework $S_{ey}^a$ is ${\epsilon }_a$ -homothetic or $h_{{\delta }_{\approx }}^a$ -identifiable.

Theorem 4 proof. Apply theorem 3 and obtain the ${\epsilon }_a$ -homotheticity of the $S_{ey}^a$ -framework. If the theorem 4 condition (iv) satisfied, then the region ${\mathcal{F}}_{S_{ey,i}}^{q,a}\subset {\mathcal{F}}_{S_{ey}}^{q,a}$  is almost ${\epsilon }_a$ -homothetic to the corresponding region ${\mathcal{F}}_{S_{ey,i}}^{q,s}$  of the framework $S_{ey}^s$  at $\Vert {\mathcal{A}}_a-{\mathcal{A}}_s\Vert \le {\delta }_{\mathcal{A}}$, where ${\mathcal{A}}_s\subset A_s$ . Hence, $S_{ey}^a$  corresponds to some $S_{ey}^s\in ℱ$ . ■

So, if theorem 4 conditions fulfilled for $S_{ey}^a$, then we make decision on the system identifiability with $S_{ey}^a\in ℱ$  on the analysis base $S_{ey}^s\in ℱ$ .

As $u(t)\in \mathcal{P}{\mathcal{E}}_{\alpha ,\overline{\alpha }}^S$, the $\zeta (t)$  perturbation in (5) is limited due to the construction of the $S_{\phi }$ -system. Therefore, the $S_y$ -system is stable and recoverable. Therefore, the variable $y^{\prime }(t)$  is detectable. The system $S_y$  recoverability follows from the system $S_{\phi }$  detectability, any recoverable state is stable. This conclusion shows that the framework $S_{ey}^a$  is detectable and recoverable. The system input is representative and synchronizing on $u(t)\in S$, since the system is recoverable. The system (1) is almost structural identifiable ( $h_{{\delta }_{\approx }}^a$ -identifiable), and structure $S_{ey}^a$  is almost ${\epsilon }_a$ -homothetic. Its followers on theorem 4. So,

Theorem 5. Let (a) $\left(u(t)\in \mathcal{P}{\mathcal{E}}_{\alpha ,\overline{\alpha }}^S\right)\&\left(u(t)\in S\right)$ ; (b) the $S_y$ system is stable and recoverable. Then the system $S_{\phi }$ (structure $S_{ey}^a$ ) is detectable, recoverable and $h_{{\delta }_{\approx }}^a$ -identifiable, and the structure  $S_{ey}^a$ is almost  ${\epsilon }_a$  -homothetic.

Let $\left({\chi }_a,{\chi }_s\right)\in ℱ$ . Therefore, the function ${\chi }_a$  structurally coincides with ${\chi }_s$ . They belong to the same class of structures, excluding regions ${\mathcal{F}}_{S_{ey,i}}^{q,a}$ . At the level of sets, this means $S_{ey}^a\approx S_{ey}^s$, i.e., frameworks are close, excluding the regions ${\mathcal{F}}_{S_{ey,i}}^{q,a}$ .

Introduce frameworks $S_{ey}^a,S_{ey}^s$  defined on sets ${\mathbb{S}}_{ey}^a,{\mathbb{S}}_{ey}^s$  and the proximity index as $d\left({\mathbb{S}}_{ey}^a\backslash {\mathbb{S}}_{ey}^s\right)$, understanding it as $d(t)=\left|e_{ey}^a-e_{ey}^s(t)\right|\le {\delta }_e$ $\forall y(t)\in {\mathcal{D}}_y\left(S_{ey}^i\right)$, where ${\delta }_e>0$, $i=a,s$ . Obtain a set $\mathbb{D}\left({\mathbb{S}}_{ey}^a\backslash {\mathbb{S}}_{ey}^s\right)$  whose elements correspond to the asymmetry areas of the framework $S_{ey}^a$  with $d(t)>{\delta }_e$ . Let structures definition areas ${\mathcal{D}}_y\left(S_{ey}^i\right)$  coincide. The set $\mathbb{D}\left({\mathbb{S}}_{ey}^a\backslash {\mathbb{S}}_{ey}^s\right)$  is finite in construction.

So, if the reference $S_{ey}^s$  is known for ${\chi }_s\in ℱ$, then the asymmetry structure of the function ${\chi }_a\in ℱ$  estimating by $d\left({\mathbb{S}}_{ey}^a\backslash {\mathbb{S}}_{ey}^s\right)$ . The filling of the set $\mathbb{D}\left({\mathbb{S}}_{ey}^a\backslash {\mathbb{S}}_{ey}^s\right)$  depends on the condition (14) fulfilment.

Theorem 6. Let (i) $u(t)\in S$ ; (ii) the reference symmetric function ${\chi }_s\in ℱ$  is given; (iii) the -framework  $S_{ey}^s$  obtained for  ${\chi }_s$  ; (iv) condition (14) satisfied for the function  ${\chi }_a\in ℱ$  . Then the structure  $S_{ey}^a$  is almost  ${\epsilon }_a$  -homothetic for almost all  $t\ge t_0$  , and the system (1) is  $h_{{\delta }_{\approx }}^a$  -identifiable.

Theorem 6 proof. Consider the system (5) with ${\chi }_s\in ℱ$ . As $u(t)\in S$, there exists $u_h(t)\in S$ such that the $h_{{\delta }_h}$ -identifiability of system (5) guaranteed. The $S_{ey}^s$ -framework is $h_{{\delta }_h}$ -identifiable. For system (5) with ${\chi }_a\in {ℱ}_a$, according to theorem 5, there is an input $u_h(t)\in S$  such that $S_{ey}^a\approx S_{ey}^s$  is valid. So, the set $\mathbb{D}\left({\mathbb{S}}_{ey}^a\backslash {\mathbb{S}}_{ey}^s\right)$, whose elements correspond to the asymmetry areas of the framework for $\forall d(t)>{\delta }_e$, exists. According to theorem 5, domains ${\mathcal{F}}_{S_{ey,i}}^{l,a}$  and ${\mathcal{F}}_{S_{ey,i}}^{r,a}$  are almost homothetic. So, the $S_{ey}^a$ -framework is almost ${\epsilon }_a$ -homothetic, and the system is $h_{{\delta }_{\approx }}^a$ -identifiable. <

Consider the function ${\chi }_a\in {ℱ}_a$, which is a combination of continuous functions ${\chi }_{a,i}\left(A_{a,i}\right)$  ( ${\chi }_{a,i}\left(A_{a,i}\right)$  defines the framework ${\chi }_a$ ), parameters $A_{a,i}$  of which may not coincide with $A_{a,i+1}$, where $i\in {\text{ℤ}}_A$  is an integer. Class ${ℱ}_a$  contains functions with different structures.

Definition 5. If the system (1) input $u(t)\in S$ and $\left({\mathcal{F}}_{S_{ey}}^{l,a},{\mathcal{F}}_{S_{ey}}^{r,a}\right)\subset S_{ey}^a$ has a full diameter, then the framework $S_{ey}^a$ is structurally complete.

Theorem 7. Let (i) $u(t)\in S$ ; (ii) ${\chi }_a\in {ℱ}_a$ ; (iii) fragments ${\chi }_{a,i}\left(A_{a,i}\right)\in {\chi }_a$ are continuous functions; (iv) fragments $\left({\mathcal{F}}_{S_{ey}}^{l,a},{\mathcal{F}}_{S_{ey}}^{r,a}\right)\subset S_{ey}^a$ are structurally complete. Then the $S_{ey}^a$ -framework is detectable and recoverable.

Theorem 7 proof. Consider the system (5) with ${\chi }_s\in ℱ$ . The input $\left(u(t)\in \mathcal{P}{\mathcal{E}}_{\alpha ,\overline{\alpha }}^S\right)\&\left(u(t)\in S\right)$ . Hence, the input is an S-synchronizing. These properties of the input guarantee the closeness of the structure $S_{ey}^a$ . Detectability and recoverability follow from Theorem 5. The input is representative and guarantees the system identifiability. The continuity property ${\chi }_{a,i}\left(A_{a,i}\right)\in {\chi }_a$, $i>1$  can lead to non-fulfillment of almost ${\epsilon }_a$ -homotheticity $S_{ey}^a$ . Consequently, not all structural parameters  ${\chi }_a$  can be identified. <

Remark 3. The stated approach to SI assessment is general. Therefore, consider the features of specific nonlinear systems in the S1 analysis. It demands the proposed approach modification.

5. Examples

1. Consider the engine operation stabilization system described by the equation:

$$\{\begin{array}{l}{\dot{x}}_1=x_2,\\ {\dot{x}}_2=-a_1{x}_1-a_2{x}_2+kf\left(g(t)-x_1\right),\end{array}$$

(15)

$$f(z)=\{\begin{array}{l}{d}_1{z}^{\alpha },\mathrm{if}\hspace{0.17em}z\ge b,\\ d_{2}z,\hspace{0.17em}\hspace{0.17em}\mathrm{if}\hspace{0.17em}z\ge b,\end{array}$$

(16)

where $x_i$  is the state variable ( $i=1;2$ ); $g(t)$  is input; $a_1,a_2,k,d_1,d_2,b,\alpha$  are constant parameters.

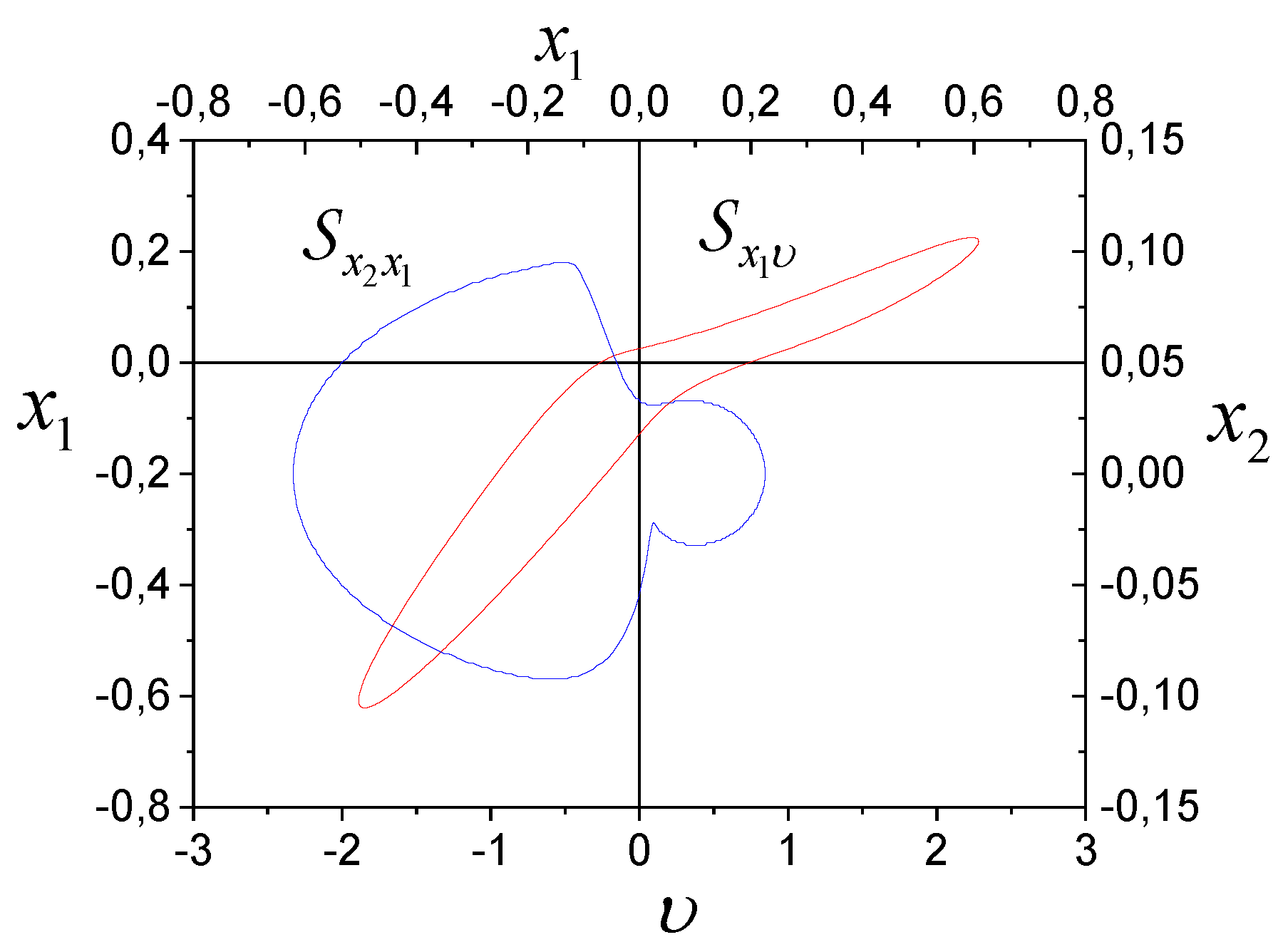
The system (15), (16) modeled with $a_1=3,\hspace{0.17em}{a}_2=4,\hspace{0.17em}k=5$, $\alpha =1.5$, $d_1=2,\hspace{0.17em}{d}_2=1,\hspace{0.17em}b=0$, $g(t)=2.5\sin \left(0.05\pi t\right)$ . The integration step is 2s. The set ${\mathbb{I}}_o$  and the phase portrait $S_{x_2{x}_1}$  of the system (Figure 1) are obtained for steady-state mode. The relationship analysis in the system showed that the variable $x_2$  does not depend on $x_1$, $g(t)$ . We use $x_1$  for SI analysis, because it has close connections with $g(t)$  and $\upsilon =g-x_1$ . The framework $S_{x_1\upsilon }$  reflecting the connection $x_1=x_1\left(\upsilon \right)$  shows in Figure 1.

As follows from Figure1, the framework left part has a larger diameter than the right one. Explain it is not an adequate choice of input. The framework $S_{x_2{x}_1}$  is not ${\epsilon }_a$ -homothetic and symmetric. We cannot obtain an adequate $S_{e{x}_2}$ -framework. The $S_{x_1\upsilon }$ -framework gives a more complete performance on system nonlinear properties. We see (Figure 1) that the nonlinearity consists of two sections with different slope of fragments. Fragment ${\mathcal{F}}_{S_{ey}}^{l,a}$  is almost ${\epsilon }_a$ -homothetic to fragment ${\mathcal{F}}_{S_{ey}}^{r,a}$ . Linear secants have an adequacy degree of 74% for ${\mathcal{F}}_{S_{ey}}^{r,a}$  and 82% for ${\mathcal{F}}_{S_{ey}}^{l,a}$ . Nonlinear secants do not increase the adequacy of models. The switching of the nonlinearity occurs in the origin, which coincides with the original dry friction model (16).

Remark 4. The variables mutual influence redistribution explains by the feedback influence in the system. This causes an emphasis shift in the analysis of system properties.

So, we decide about the system (15), (16) structural identifiability based on the analysis $S_{x_1\upsilon }$ . The mathematical structure choice for the nonlinear system SI analysis determines the final result.

2. Consider a control system with external and internal feedbacks.

$$\{\begin{array}{l}{\dot{x}}_1=x_2,\\ {\dot{x}}_2=-a_2{x}_2+k\left(g(t)-x_1-k_{os}f\left(x_1\right)\right),\end{array}$$

(17)

$$f(z)=\{\begin{array}{l}\hspace{0.17em}c,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}z\ge 0,\\ \hspace{0.17em}0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}z=0,\\ -c_1,if\hspace{0.17em}z<0,\end{array}$$

(18)

where $f\left(z\right)$  is a signed function with different clipping levels; $a_2>0,k>0,c>0,c_1>0,k_{os}>0$ .

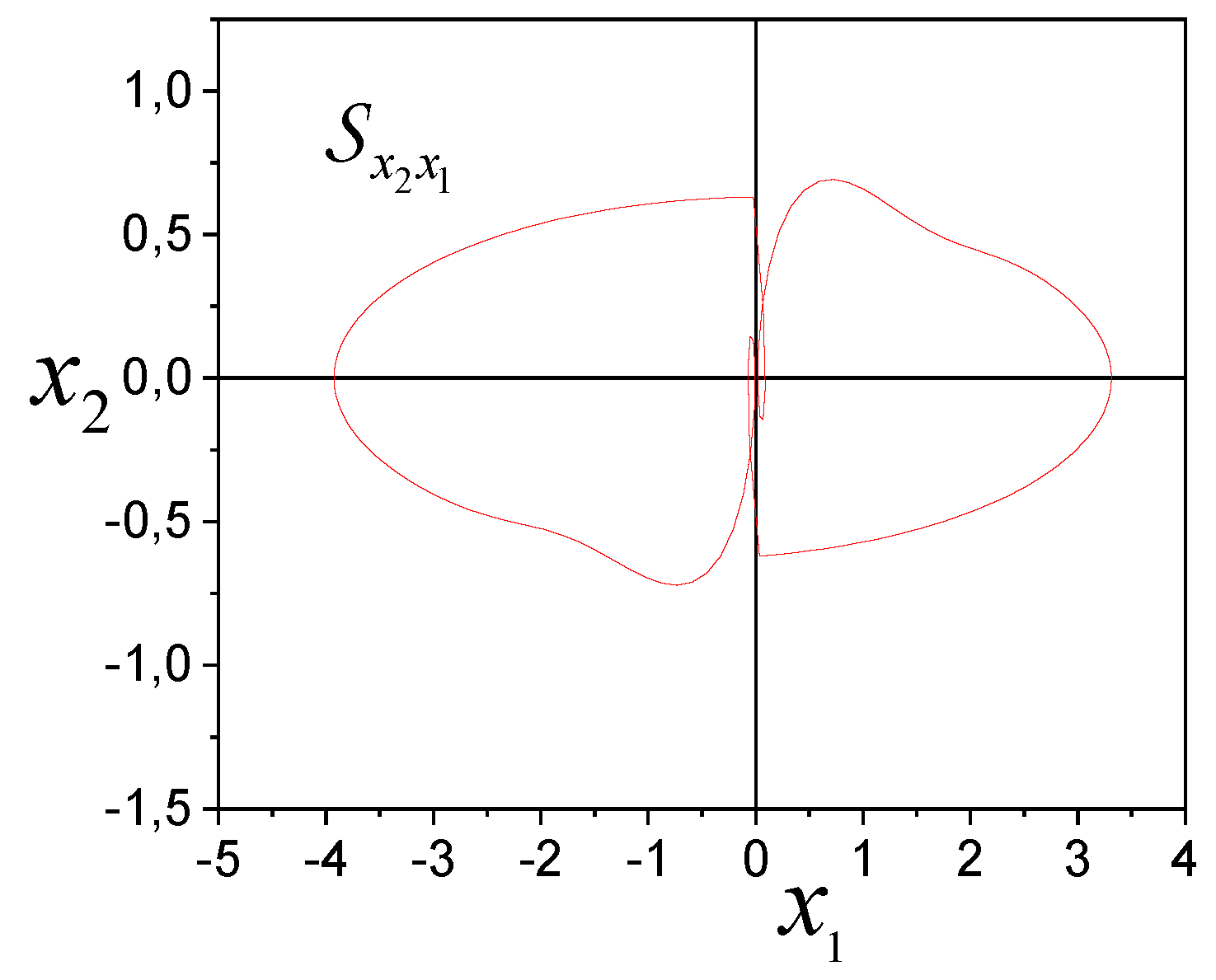
The system (17), (18) modeled with $a_2=2$, $k_{os}=3.5$, $c=2$, $c_1=0.25$, $g(t)=4\sin \left(0.05\pi t\right)$ . The system phase portrait $S_{x_2{x}_1}$  (steady-state mode) showed in Figure 2. The analysis $S_{x_2{x}_1}$  shows that a switching is in the nonlinear system in the region 0. $S_{x_2{x}_1}$  is almost ${\epsilon }_a$ -homothetic. The function $f\left(z\right)$  is asymmetric with relation to zero.

The approach described in the previous section is not applicable to $S_{x_2{x}_1}$, since the model (4) is inadequate. Therefore, consider the virtual structure (VS) $S_{x_1{\epsilon }_1}$  (Figure 3) described by the function $x_1=x_1\left({\epsilon }_1\right)$, where ${\epsilon }_1=g(t)-x_1-k_{os}f\left(x_1\right)$ . We see that the framework $S_{x_2{x}_1}$  (Figure 3) is asymmetric. Apply the approach described in section 4, construct the secant ${\gamma }_{x_1{\epsilon }_1}$  and calculate the residual ${\upsilon }_1=x_1-{\gamma }_{x_1{\epsilon }_1}$ . As a result, we get $S_{x_1{\epsilon }_1}$, which is a $S_{ey}$ -structure analog from section 3.

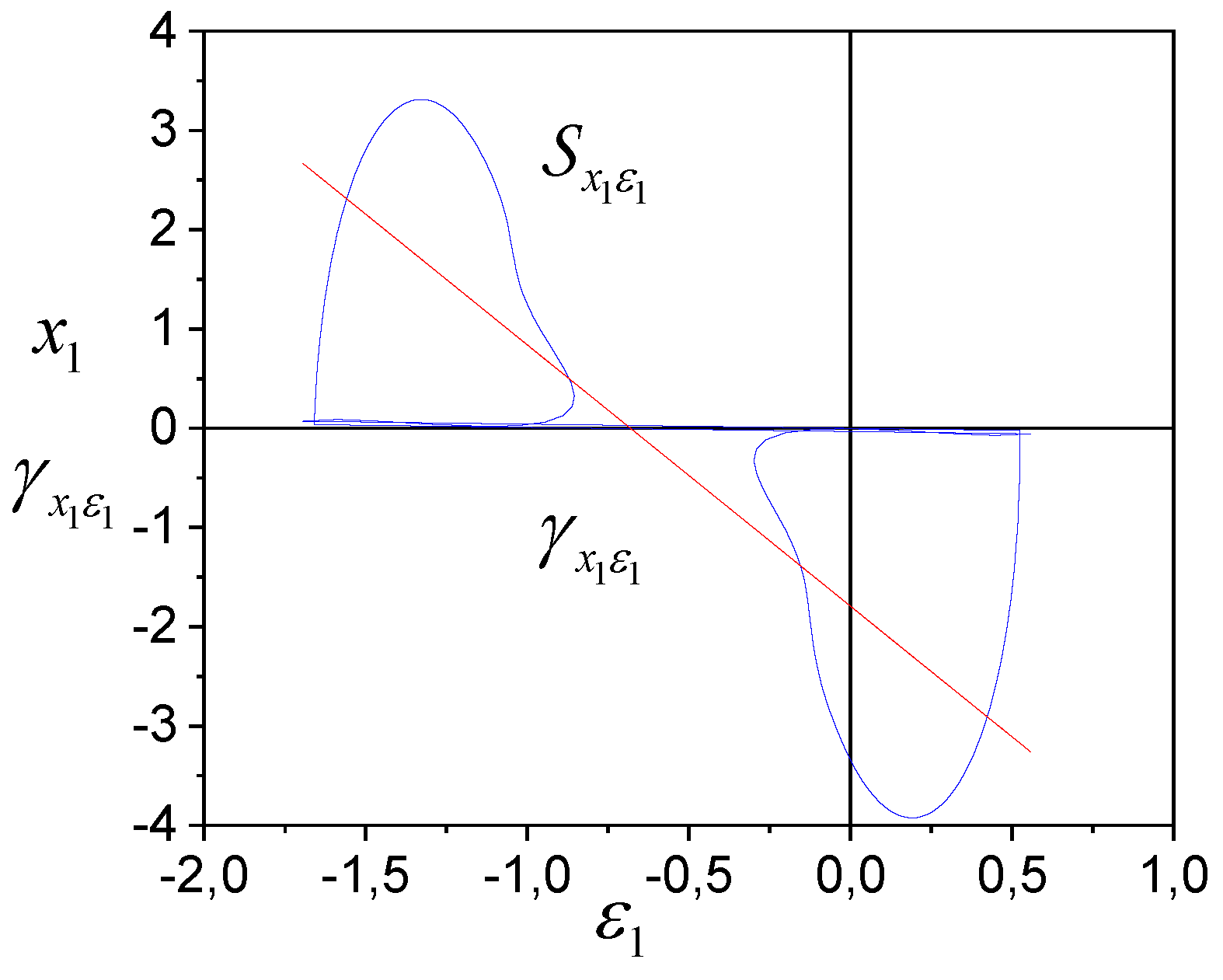
The structure $S_{{\upsilon }_1{\epsilon }_1}$  (Figure 4) describes by the function ${\upsilon }_1={\upsilon }_1\left({\epsilon }_1\right)$  and is almost ${\epsilon }_a$ -homothetic. The homothety process of the left fragment $S_{{\upsilon }_1{\epsilon }_1}$  into the right also shown in Figure 4. The point (0.327; 0.012) is a marker for switching from the left fragment $S_{{\upsilon }_1{\epsilon }_1}$ -framework to the right. This result confirms conclusions based on Figure 2.

So, the system (17), (18) is ${\epsilon }_a$ -homothetic and $h_{{\delta }_{\approx }}^a$ -identifiable, and the framework $S_{{\upsilon }_1{\epsilon }_1}$  is detectable and recoverable. The conclusion bases on the analysis and processing of the set ${\mathbb{I}}_o$  and the theorem 4, 7 applications.

3. Consider the engine stabilization system with external feedback

$$\begin{array}{l}{\dot{x}}_1=-a_1{x}_1+k_1\left(g-x_2\right),\\ {\dot{x}}_2=-a_2{x}_2+k_2{f}_a\left(x_1-k_{os}{x}_2\right),\end{array}$$

(19)

$$f_a\left(z\right)=\{\begin{array}{l}\alpha z,if\hspace{0.17em}d\le z<b,\\ c,if\hspace{0.17em}z\ge b,\\ {\alpha }_{1}z,\hspace{0.17em}if-b<z\le d,\hspace{0.17em}\\ -c_1,\hspace{0.17em}\hspace{0.17em}if\mathrm{z}\le -b_1,\end{array}$$

(20)

where $a_1,k_1$  are amplifier parameters; $g$  is input; $a_2,k_2$  are engine parameters; $\alpha ,{\alpha }_1,c,c_1,d,b,b_1$  are positive numbers; $k_{os}$ is a feedback coefficient.

System parameters (19), (20): $a_1=2$, $k_1=5$, $a_2=0.67$, $k_2=1.17$, $k_{os}=0.5$, $\alpha =1$, ${\alpha }_1=0.167$, $c=2$, $c_1=0.5$, $b=2$, $b_1=1.5$, $d=1.5$, $g(t)=2.5\sin \left(0.5\pi t\right)$ . As the simulation showed, there are many synchronizing inputs for the system. But reducing the input frequency changes the response time of the nonlinear element. This complicates the identifiability analysis.

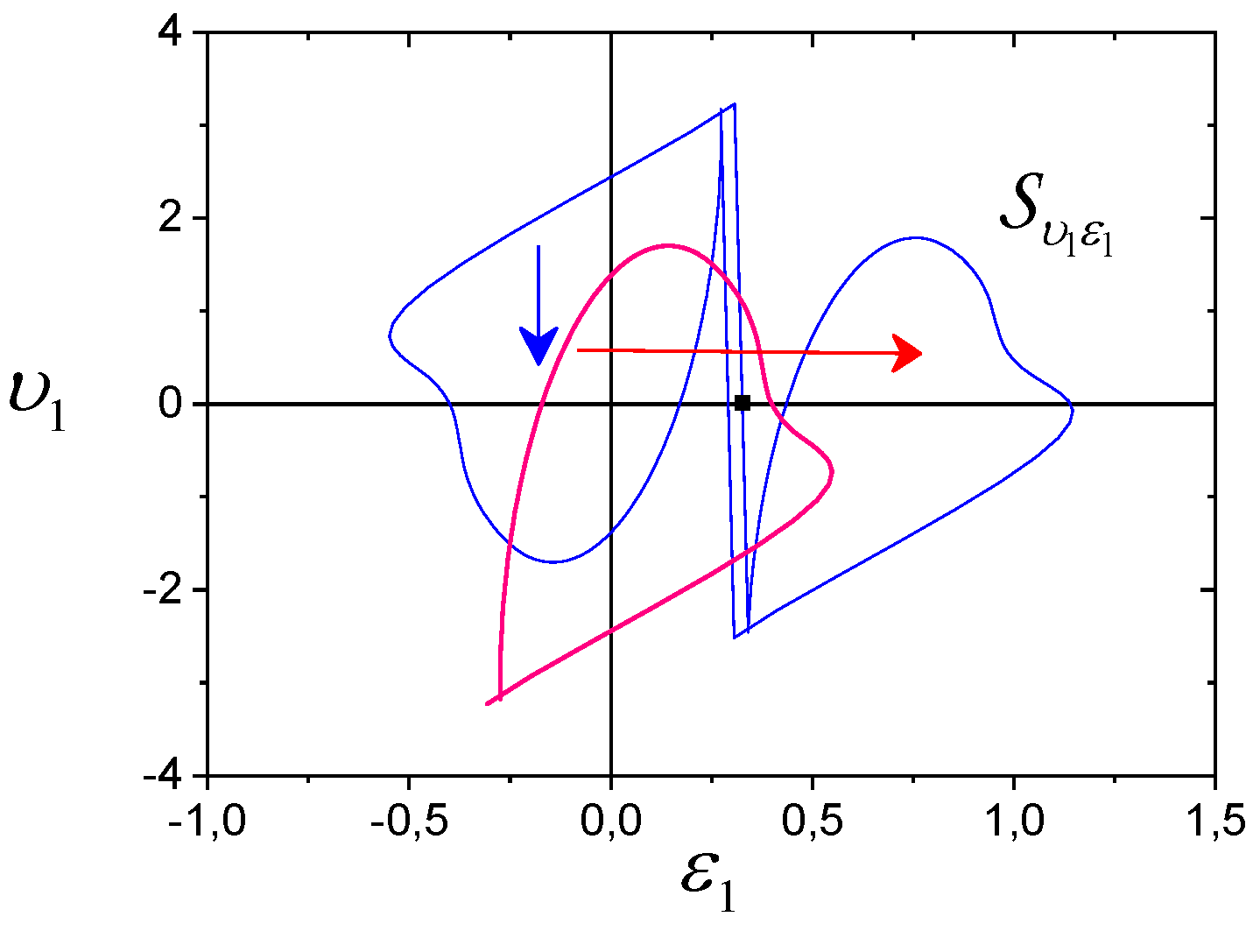
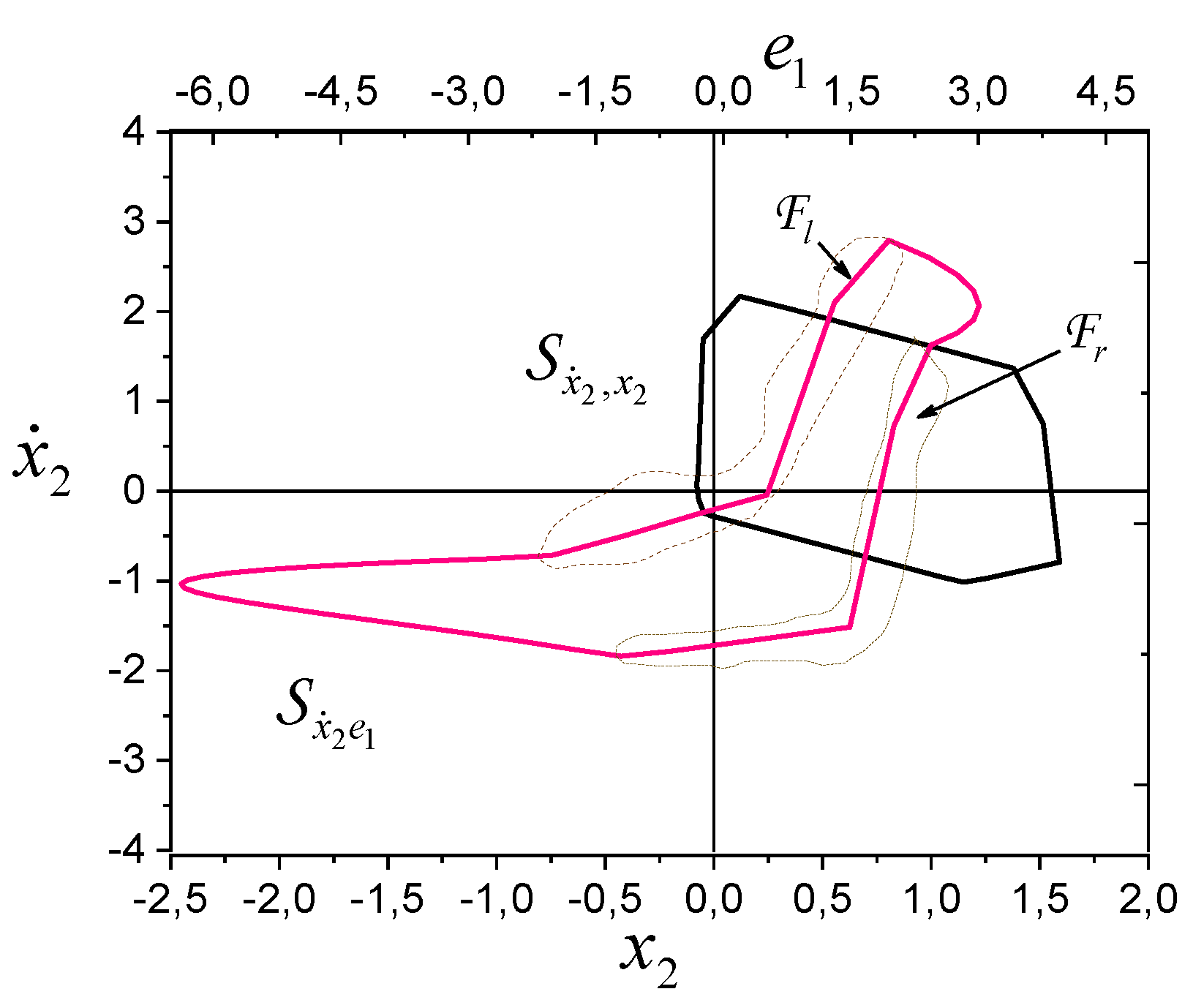
The phase portrait $S_{{\dot{x}}_2{x}_2}$  and the framework $S_{{\dot{x}}_2{e}_1}$  of the system (for steady state) show in Figure 5. Structures have an asymmetrical form. Since there is a closer relationship between $e_1$  and ${\dot{x}}_2$, then use the $S_{{\dot{x}}_2{e}_1}$  framework for analysis, where $e_1=x_1-k_{os}{x}_2$ . We conclude about the asymmetry $f_a\left(z\right)$  based on the right side $S_{{\dot{x}}_2{e}_1}$  analysis. Fragment ${\mathcal{F}}_l$  is almost G2-homothetic to fragment ${\mathcal{F}}_r$  (Figure 5). Therefore, the $S_{{\dot{x}}_2{e}_1}$ -framework is detectable and recoverable, and the system (19), (20) is ${\epsilon }_a$ -homothetic and $h_{{\delta }_{\approx }}^a$ -identifiable.

Remark 5. Feedbacks perform the signal $e_1$ adulteration. In this case, the choice $u_h(t)=g(t),g(t)\in S$ has a certain problem. The system phase portrait can be used as an indicator of such an effect.

6. Conclusion

The identifiability problem of dynamical systems with nonsymmetric nonlinearities consider. We propose requirements for system input guaranteed an assessment of the nonlinear system structural identifiability. The input must be constantly excited and S-synchronizing. The problem solution based on the construction and analysis of virtual structures reflecting the nonlinear properties of the system. ${\epsilon }_a$ -homothety and structural identifiability conditions obtained for a system with nonsymmetric nonlinearities. The detectability and recoverability of virtual structures under uncertainty conditions proved. Conditions obtain under which a nonsymmetric nonlinearity can be a hypothetical symmetric nonlinearity.