Submitted:
14 April 2023
Posted:
17 April 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Data accepted for analysis
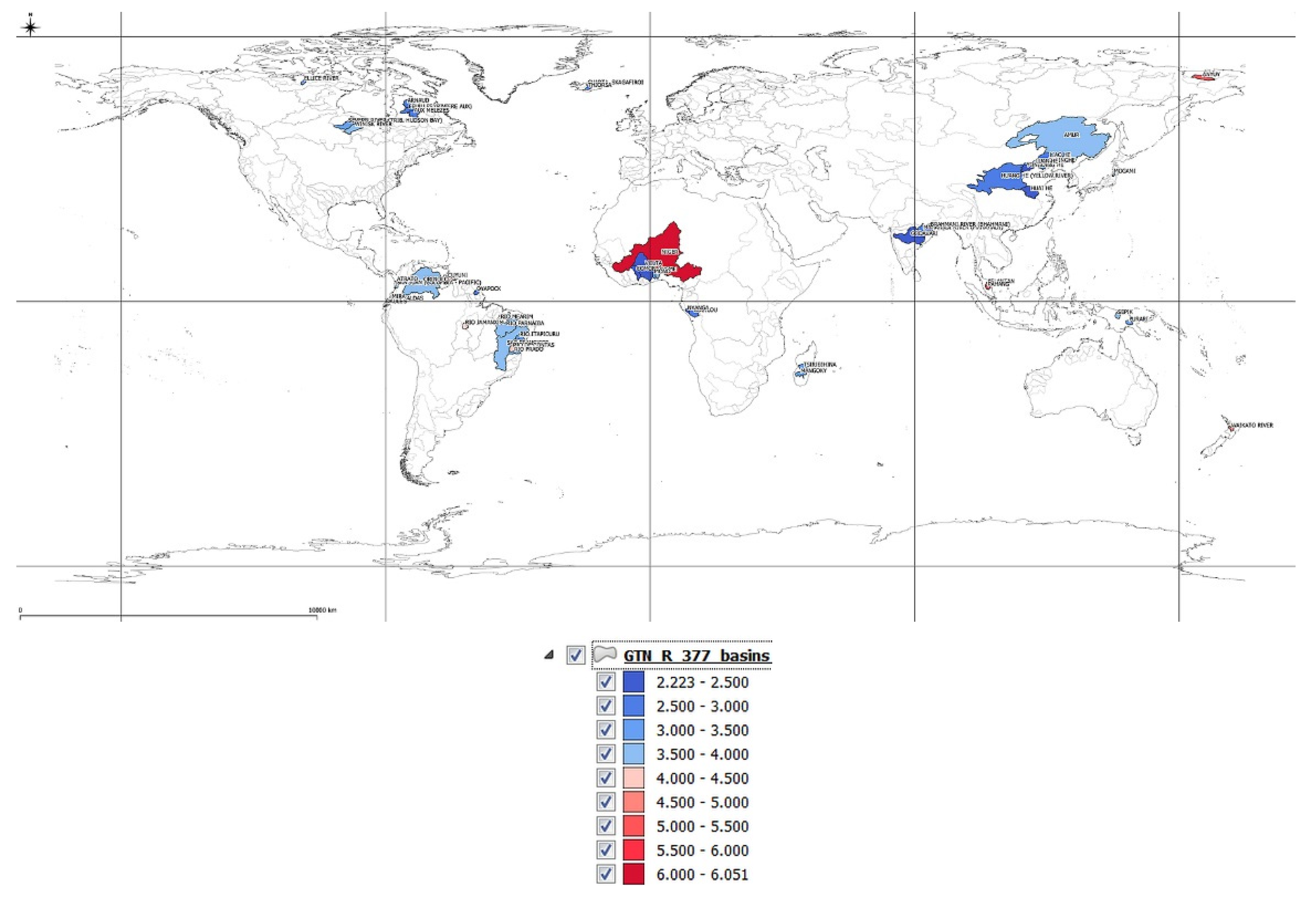
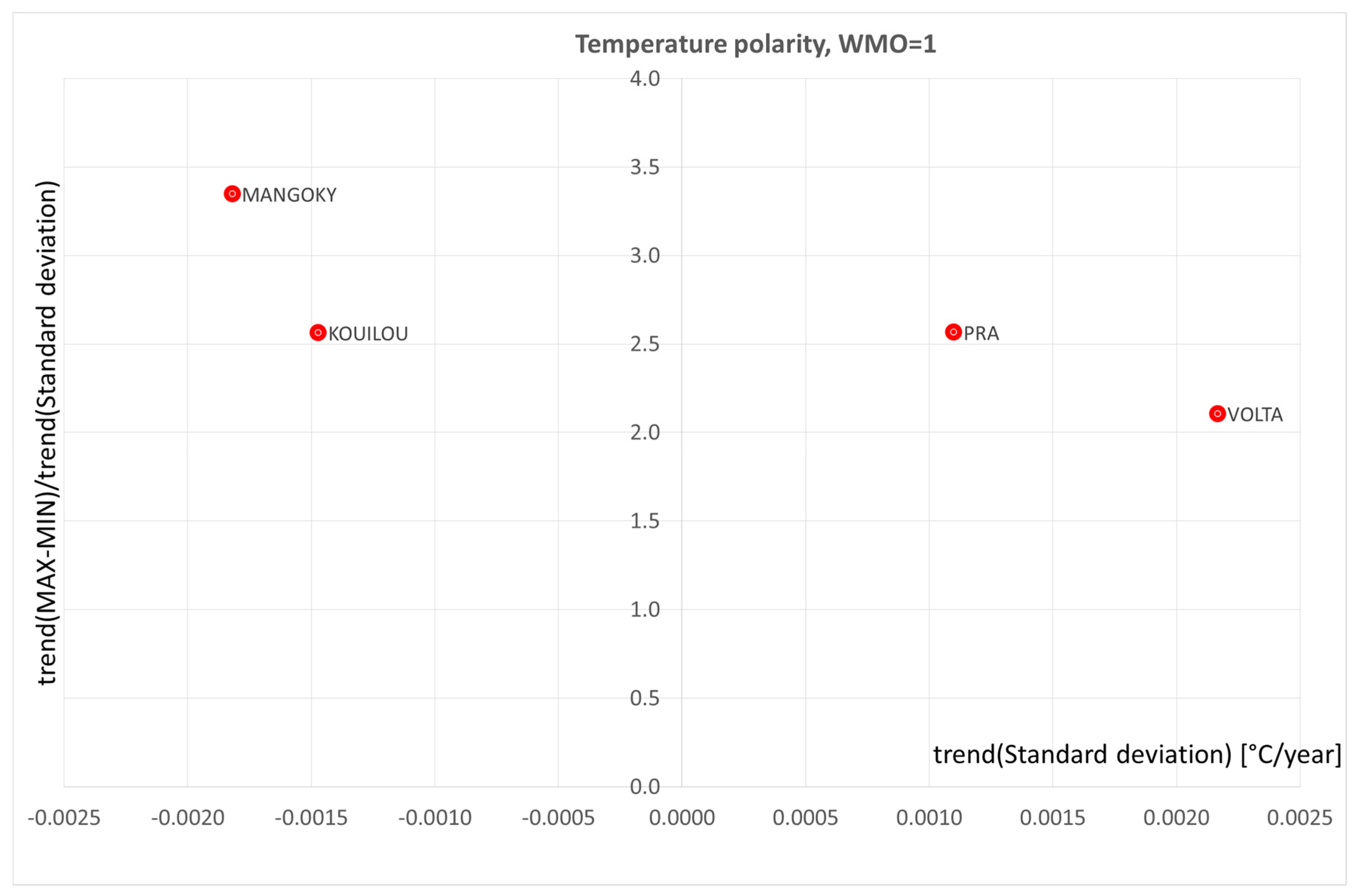
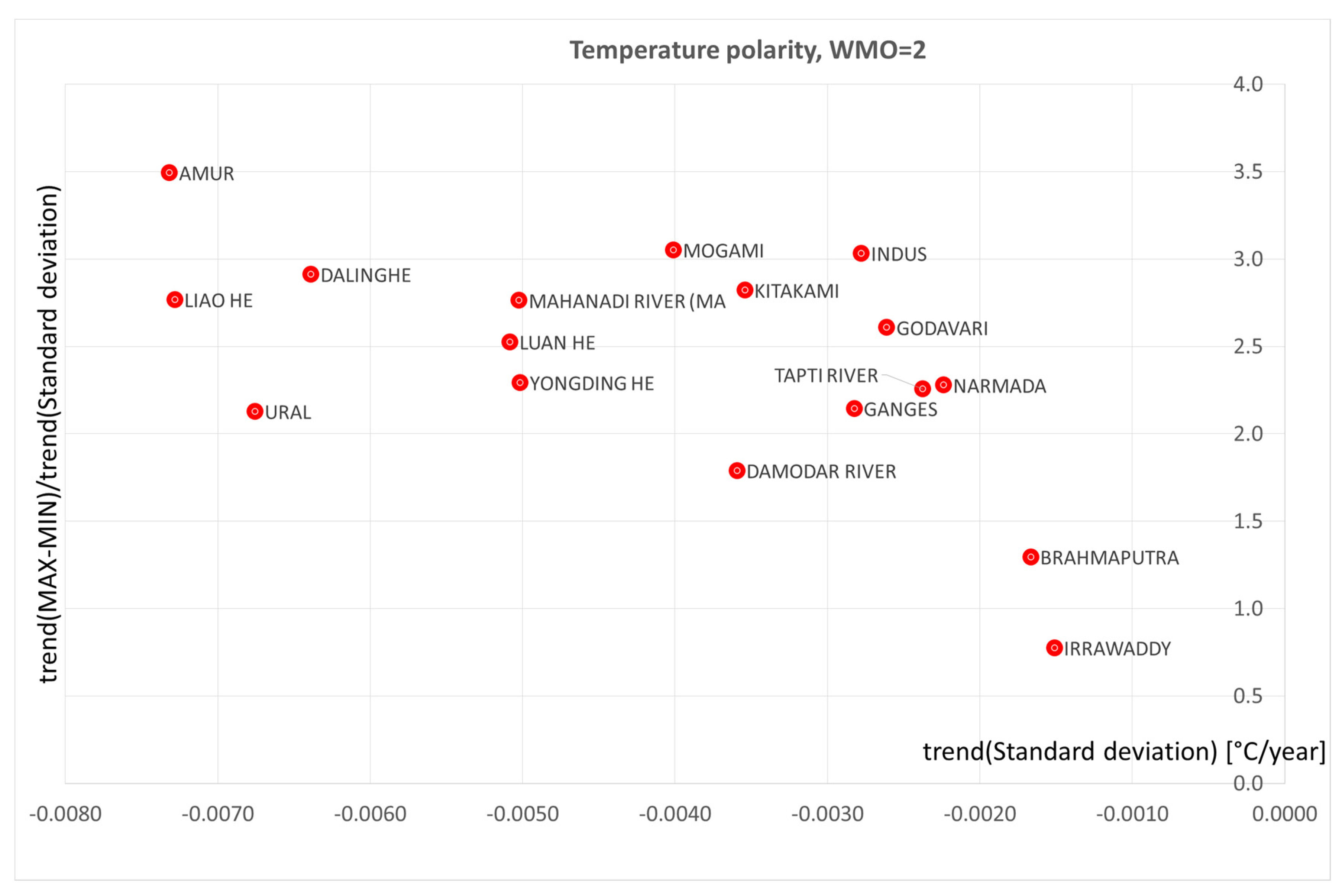
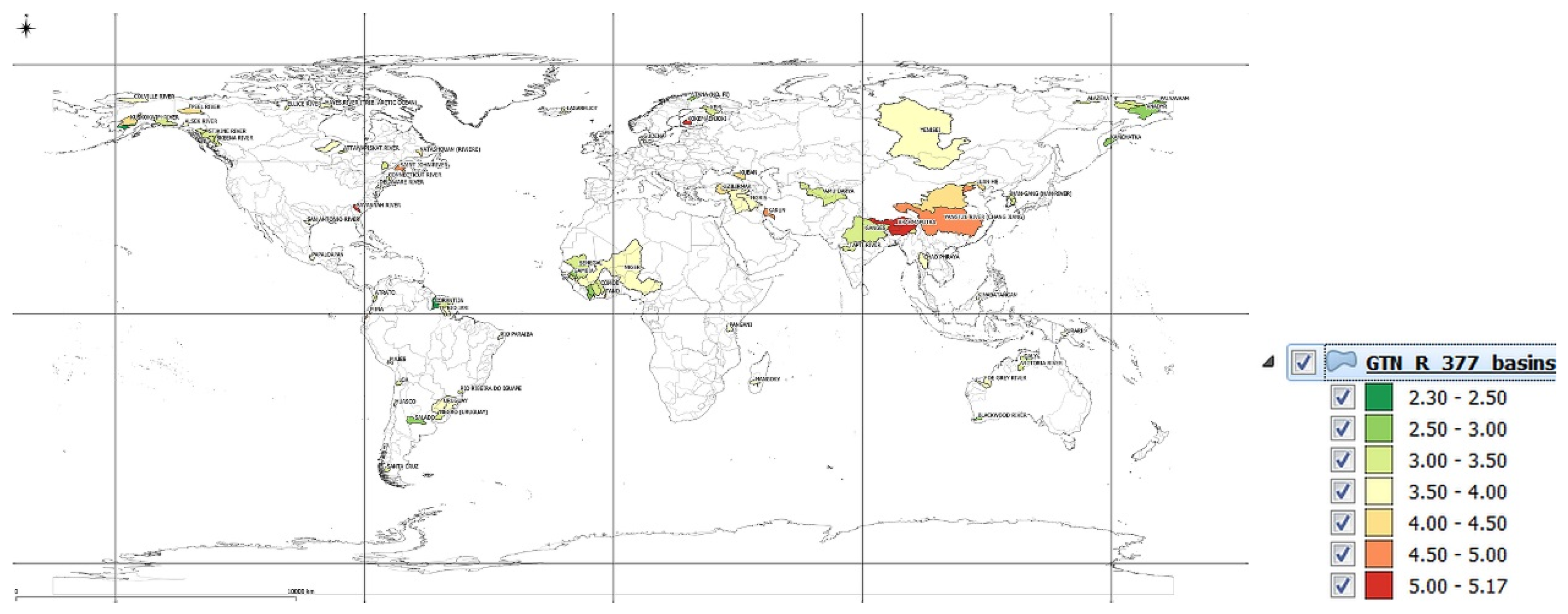
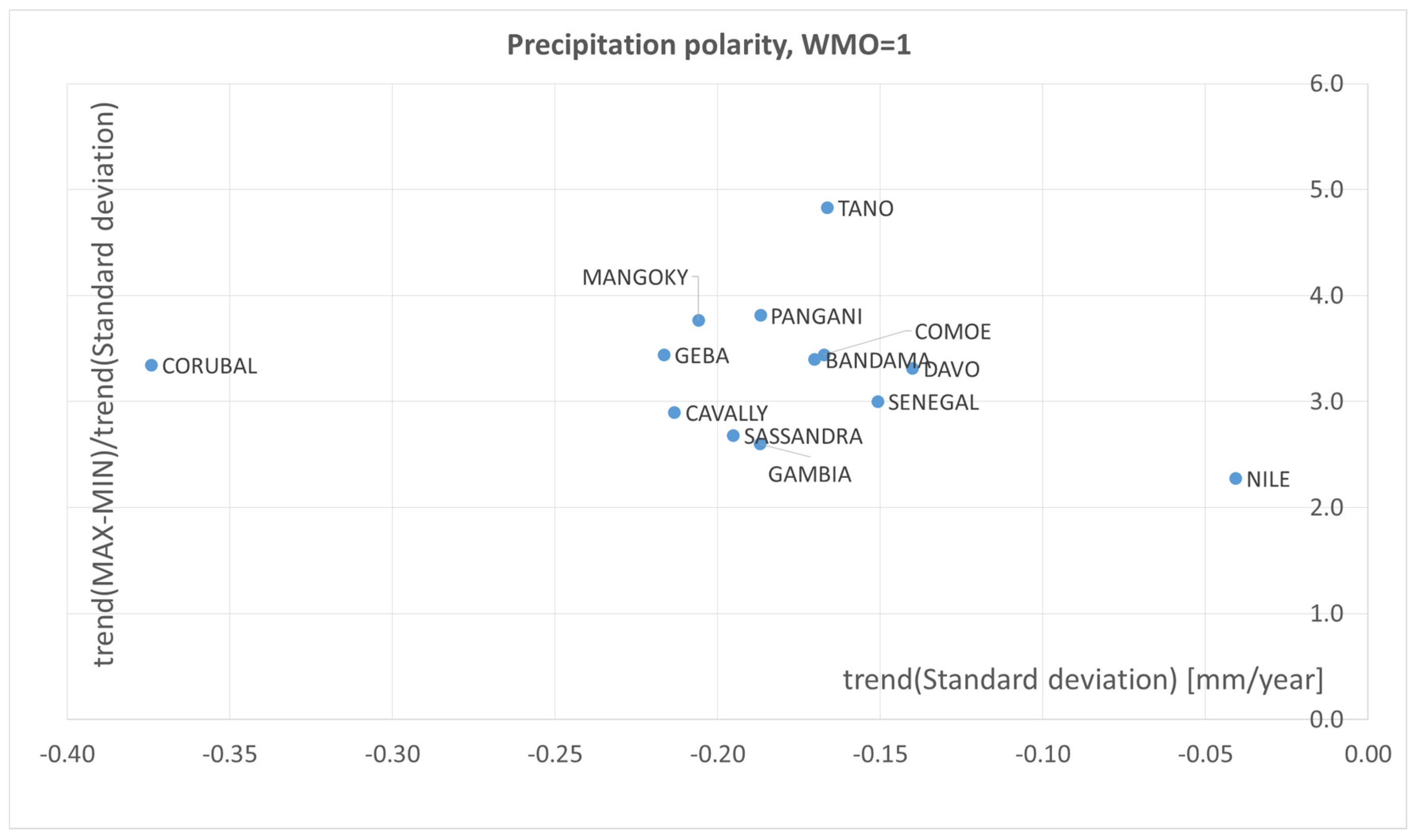
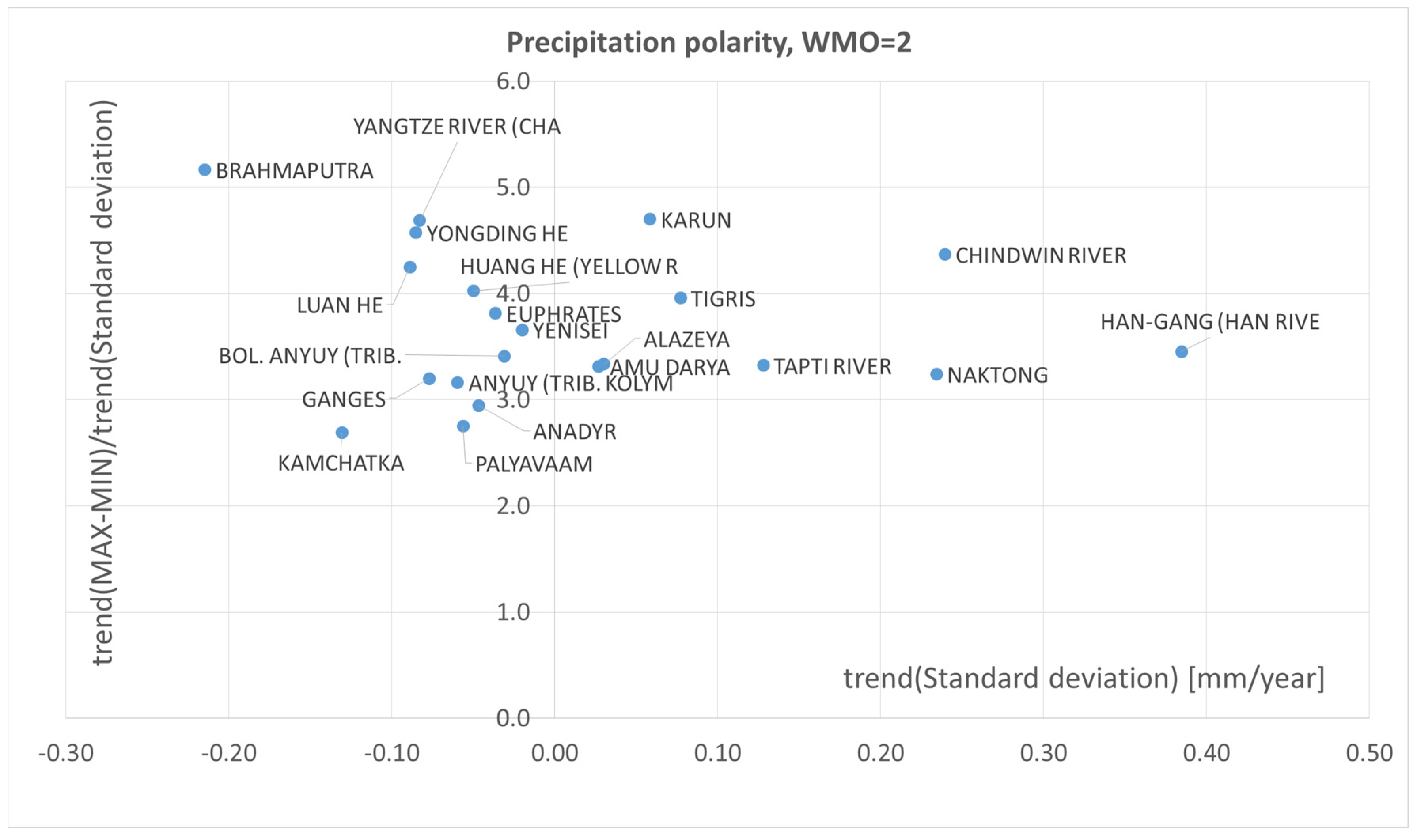
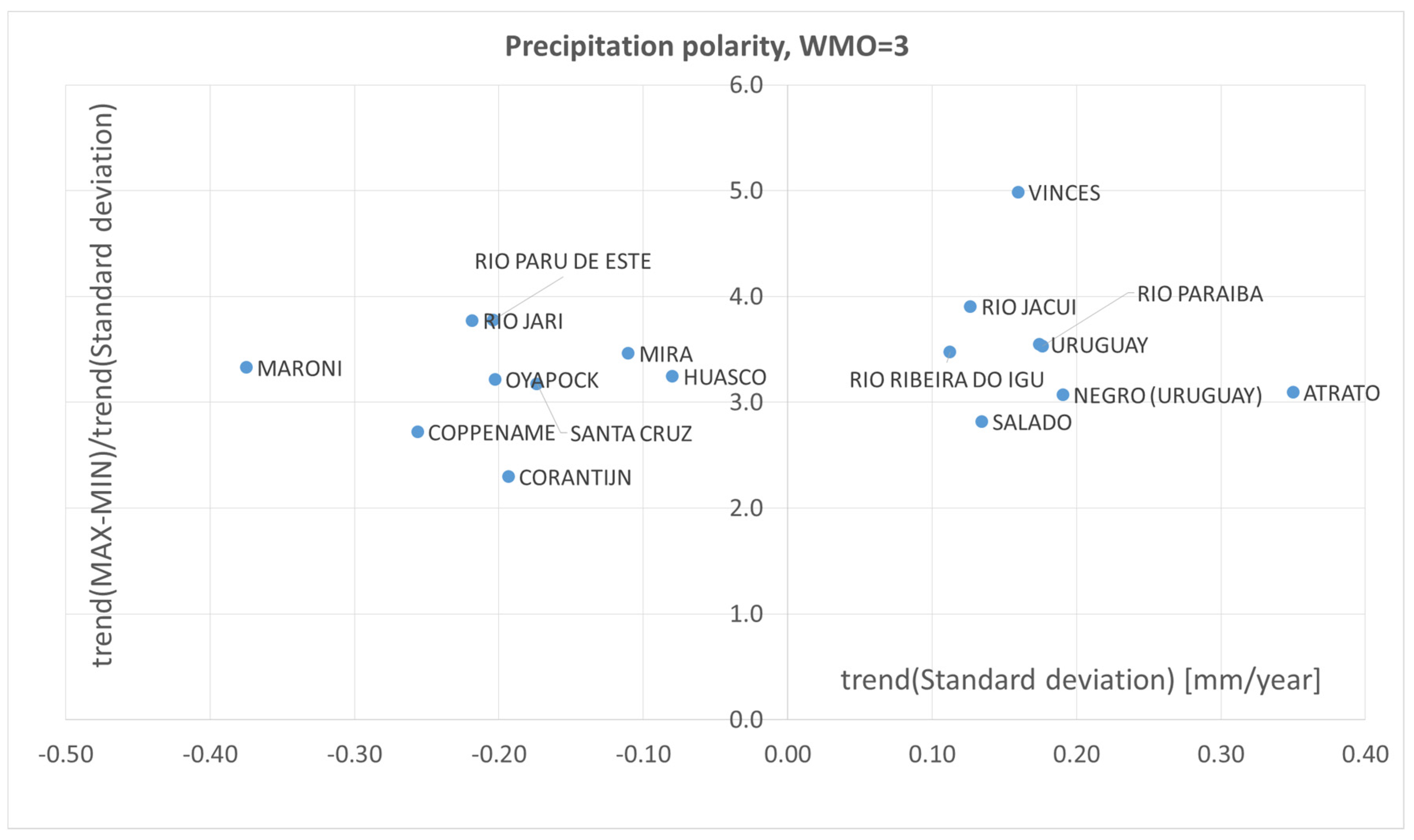
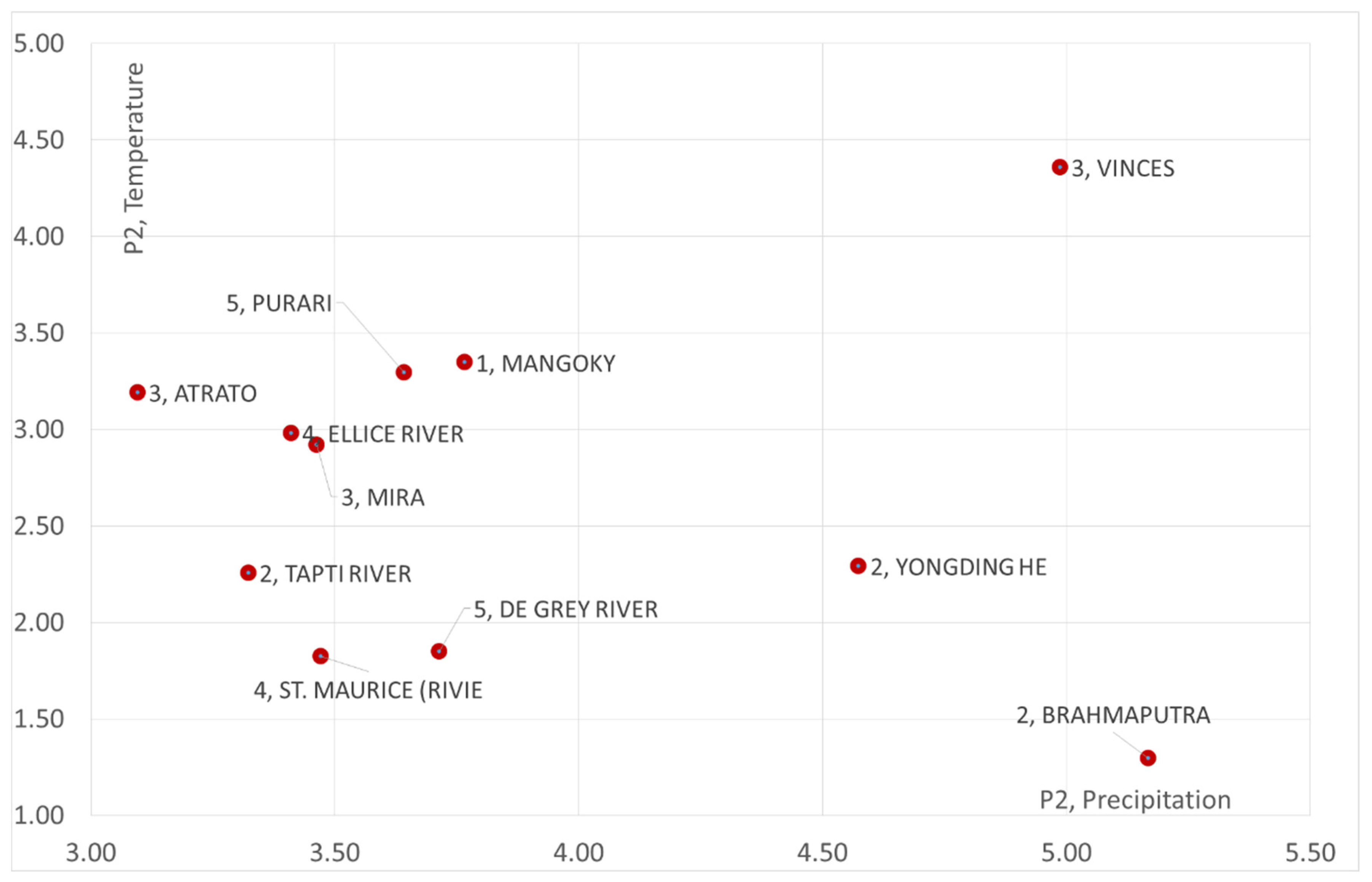
4. Polarization of precipitation and temperature phenomena
5. The concept of polarization measure
- The concentration ratio [80], which determines the degree of concentration of values at one end of the distribution, similar to the Gini coefficient. However, it should be noted that the Gini coefficient may be less useful in analyzing asymmetric distributions, which means that other indicators such as the concentration ratio or Lorenz curve should be considered in such cases.
- The GMD (Gini Mean Difference) index [81] is an inequality measure used in statistical and econometric analysis to measure polarization or inequality in a sample distribution. Unlike the Gini coefficient, which measures unevenness, the GMD index allows for the analysis of unevenness in the distribution of any variable, such as income, age, weight, height, precipitation, or temperature. The GMD index ranges from zero to one, where zero indicates complete evenness in the distribution, and one indicates concentration of all values in one class. The higher the GMD index value, the greater the unevenness in the variable distribution.
- Lorenz indicator [74,77] - is an inequality indicator in a distribution, which is based on the Lorenz curve. It is often used to measure income inequality but can also be used to measure inequality in other quantitative variables, including climate change studies. Higher values of the Lorenz curve indicate greater inequality in the occurrence of climate change effects such as droughts, floods, or sea level rise, meaning that some regions or social groups are more vulnerable to the effects of climate change than others.
- Atkinson index [73] - is a measure of inequality in the distribution of quantitative variables, which is based on the idea of absolute deviations. It takes into account the differences between groups of values in the distribution, similar to the Gini index, but focuses more on average values than extreme values.
- Range - values calculated as max-min usually refer to the difference between the maximum and minimum values of a given variable in a given period of time. In the case of assessing the polarization of precipitation and temperature, max-min can be used as a measure of the amplitude of these variables in a given period.
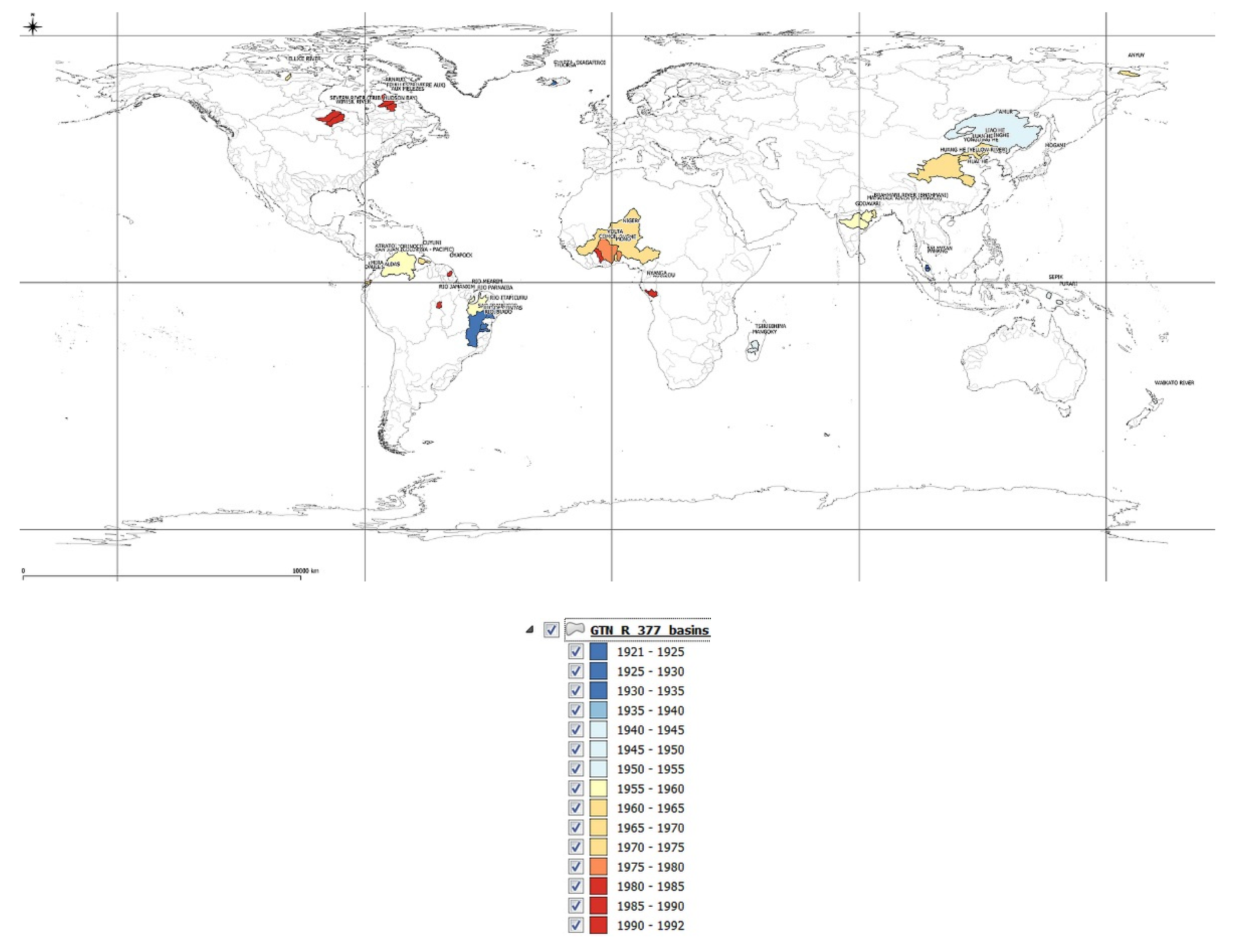
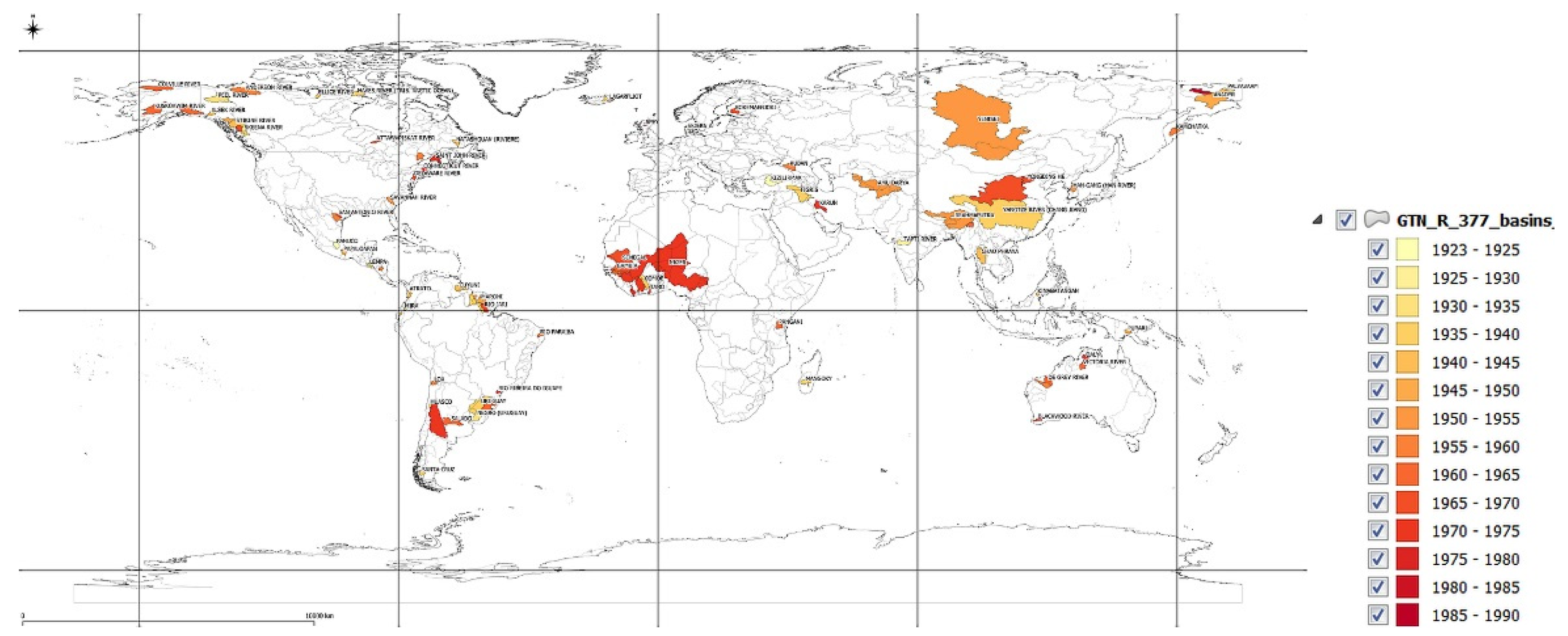
6. Detecting a change point in the trend
7. Trend test
9. Results and Discussion
- the values of long-term sequences of 110 years in monthly cross sections were determined,
- statistics were calculated: average values for each calendar month, minimum value, maximum value, mean value, standard deviation (Table 2),
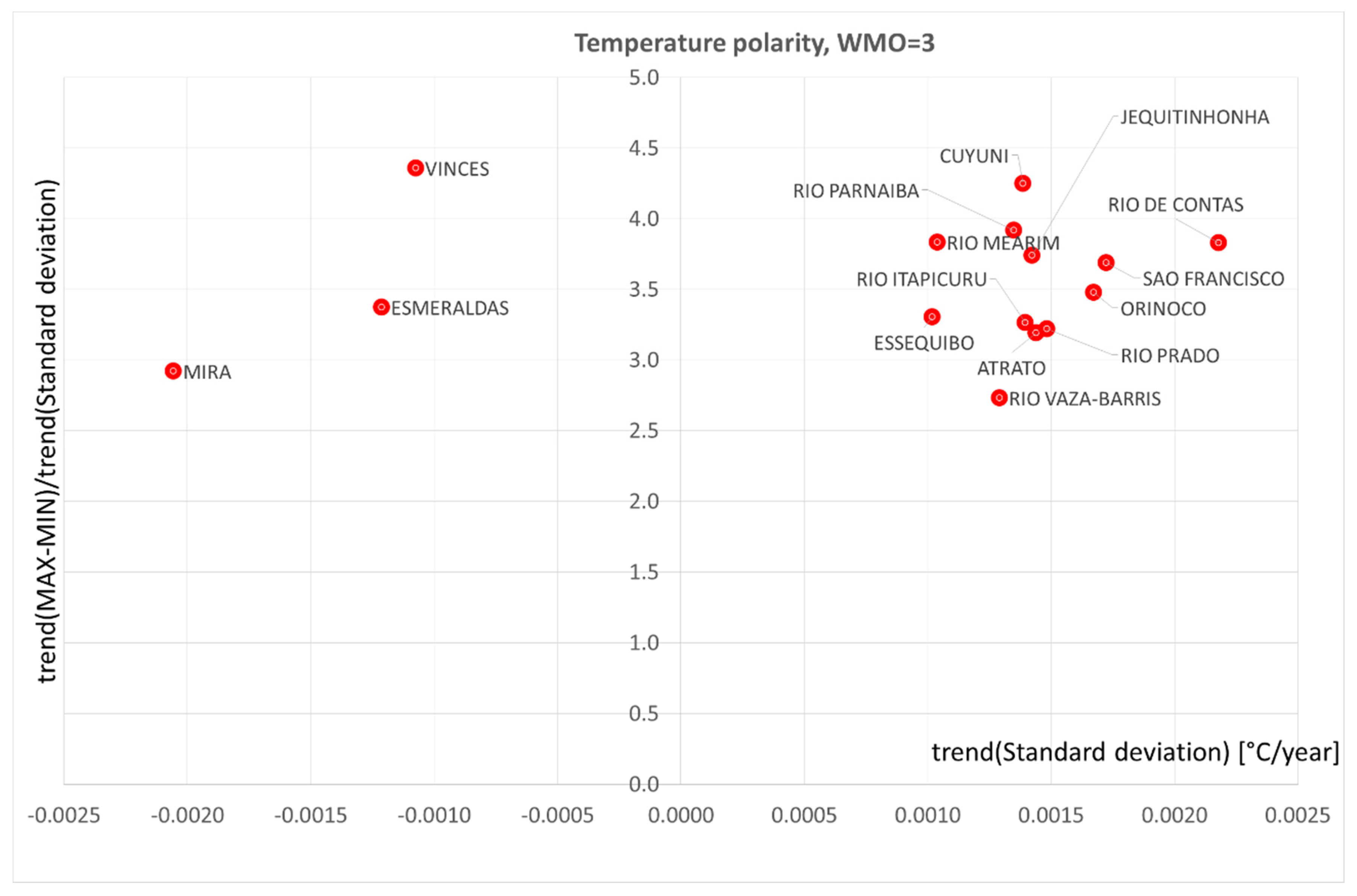
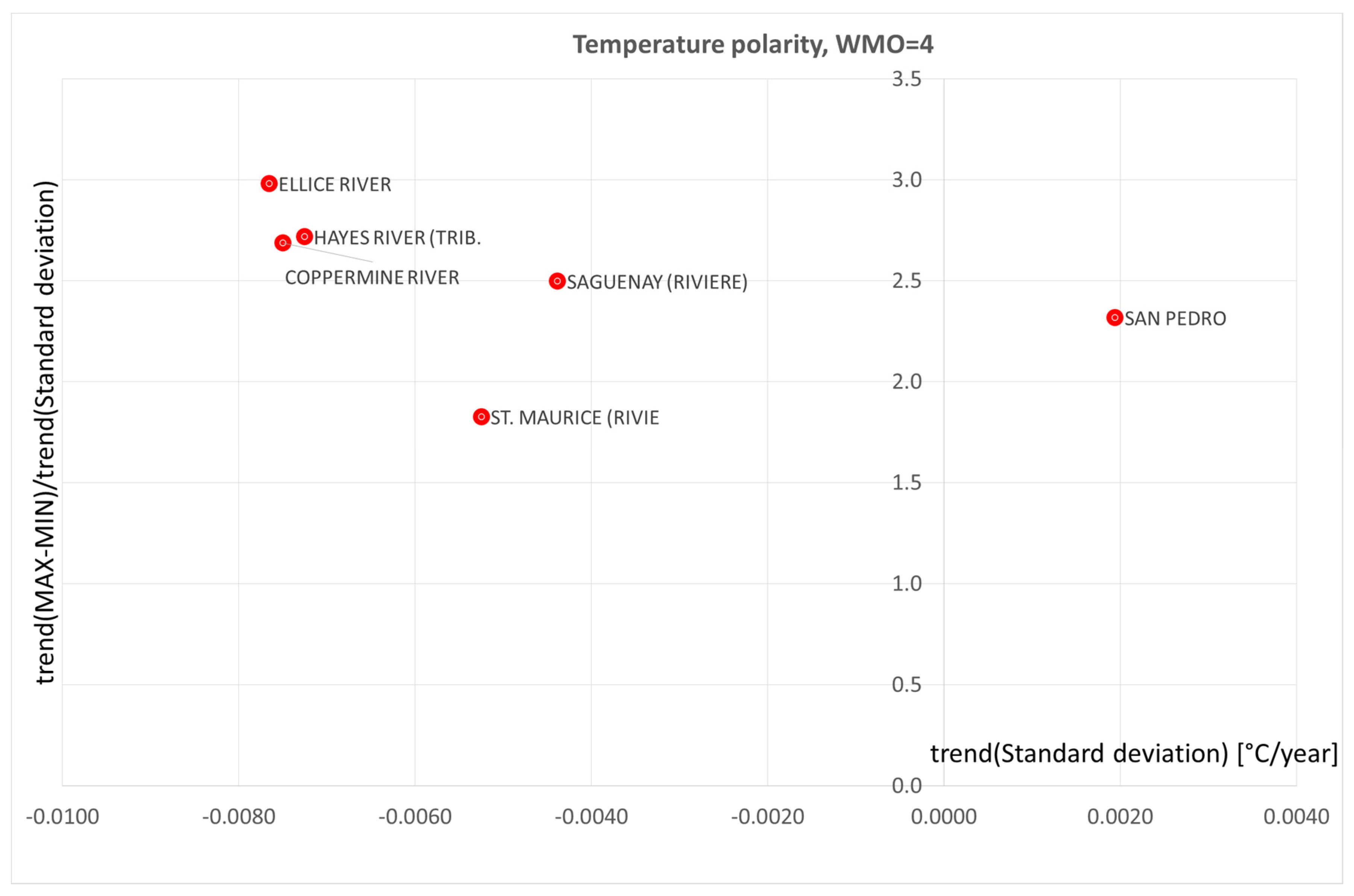
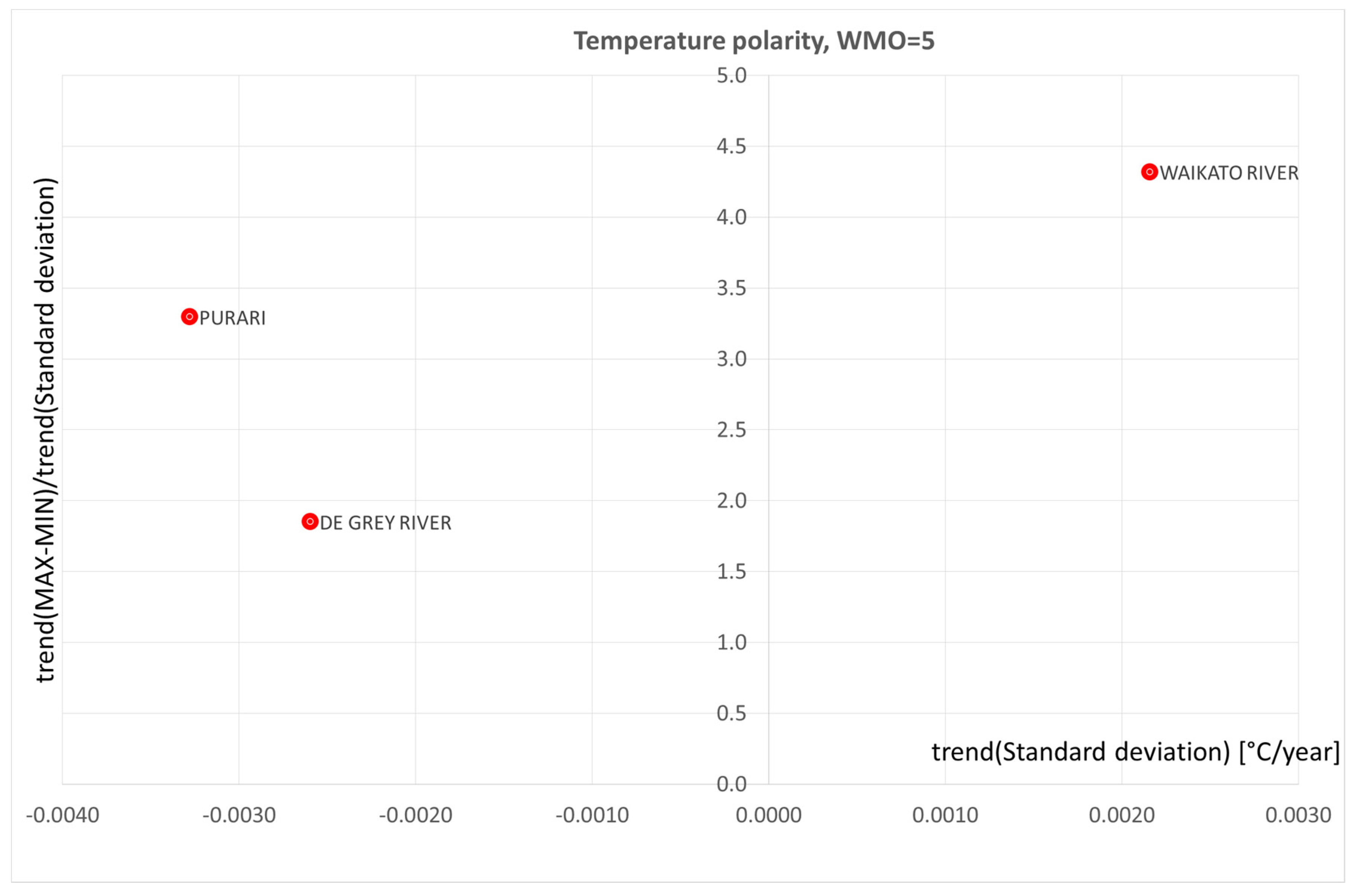
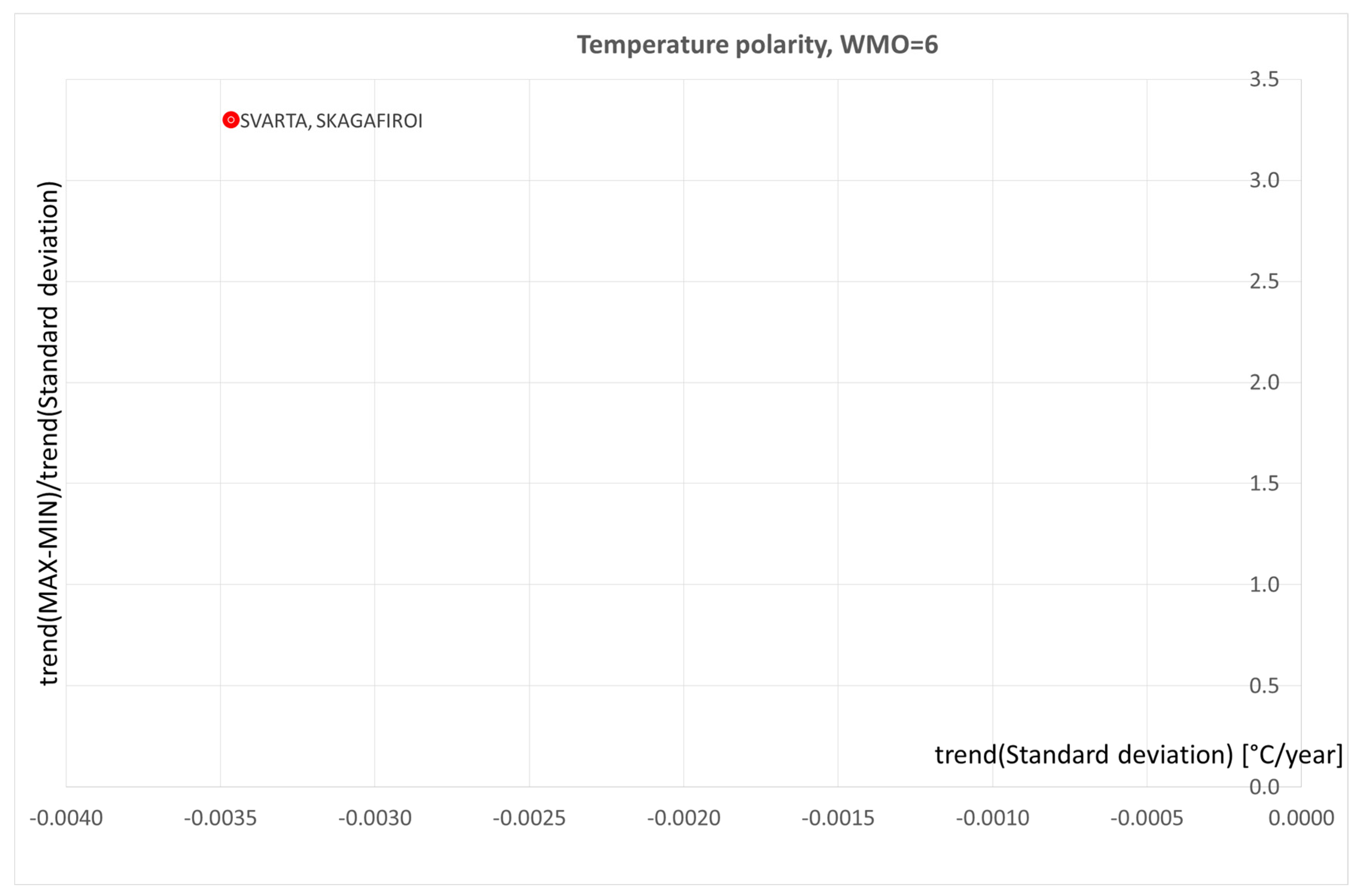
9. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- R. J. Romanowicz et al., “Climate Change Impact on Hydrological Extremes: Preliminary Results from the Polish-Norwegian Project,” Acta Geophys., vol. 64, no. 2, pp. 477–509, 2016. [CrossRef]
- S. Palaniswami and K. Muthiah, “Change point detection and trend analysis of rainfall and temperature series over the vellar river basin,” Polish J. Environ. Stud., vol. 27, no. 4, pp. 1673–1682, 2018. [CrossRef]
- D. G. Groves, D. Yates, and C. Tebaldi, “Developing and applying uncertain global climate change projections for regional water management planning,” Water Resour. Res., vol. 44, no. 12, pp. 1–16, 2008. [CrossRef]
- R. Katz, “Statistics of Extremes in Climatology and Hydrology,” Adv. Water Resour., vol. 25, pp. 1287–1304, 2002.
- R. W. Herschy, “The world’s maximum observed floods,” Flow Meas. Instrum., vol. 13, no. 5–6, pp. 231–235, 2002. [CrossRef]
- G. Blöschl et al., “Twenty-three unsolved problems in hydrology (UPH)–a community perspective,” Hydrol. Sci. J., vol. 64, no. 10, pp. 1141–1158, 2019. [CrossRef]
- S. C. Lewis and A. D. King, “Evolution of mean, variance and extremes in 21st century temperatures,” Weather Clim. Extrem., vol. 15, no. July 2016, pp. 1–10, 2017. [CrossRef]
- R. K. Jaiswal, A. K. Lohani, and H. L. Tiwari, “Statistical Analysis for Change Detection and Trend Assessment in Climatological Parameters,” Environ. Process., vol. 2, no. 4, pp. 729–749, 2015. [CrossRef]
- R. R. Heim, “An overview of weather and climate extremes - Products and trends,” Weather Clim. Extrem., vol. 10, pp. 1–9, 2015. [CrossRef]
- J. Sillmann et al., “Understanding, modeling and predicting weather and climate extremes: Challenges and opportunities,” Weather Clim. Extrem., vol. 18, no. August, pp. 65–74, 2017. [CrossRef]
- D. Młyński, M. Cebulska, and A. Wałȩga, “Trends, variability, and seasonality of maximum annual daily precipitation in the Upper Vistula Basin, Poland,” Atmosphere (Basel)., vol. 9, no. 8, pp. 1–14, 2018. [CrossRef]
- D. Młyński, A. Wałȩga, A. Petroselli, F. Tauro, and M. Cebulska, “Estimating maximum daily precipitation in the Upper Vistula Basin, Poland,” Atmosphere (Basel)., vol. 10, no. 2, 2019. [CrossRef]
- C. M. Twardosz R., “Temporal variability of maximum monthly precipitation totals in the Polish Western Carpathian Mts during the period 1951 – 2005,” pp. 123–134, 2012. [CrossRef]
- A. Ziernicka-Wojtaszek and J. Kopcińska, “Variation in atmospheric precipitation in Poland in the years 2001-2018,” Atmosphere (Basel)., vol. 11, no. 8, 2020. [CrossRef]
- N. Venegas-Cordero, Z. W. Kundzewicz, S. Jamro, and M. Piniewski, “Detection of trends in observed river floods in Poland,” J. Hydrol. Reg. Stud., vol. 41, Jun. 2022. [CrossRef]
- Z. W. Kundzewicz and M. Radziejewski, “Methodologies for trend detection,” IAHS-AISH Publ., no. 308, pp. 538–549, 2006.
- Z. W. Kundzewicz and A. Robson, “Detecting Trend and Other Changes in Hydrological Data,” World Clim. Program. - Water, no. May, p. 158, 2000, [Online]. Available: http://water.usgs.gov/osw/wcp-water/detecting-trend.pdf.
- T. Berezowski et al., “CPLFD-GDPT5: High-resolution gridded daily precipitation and temperature data set for two largest Polish river basins,” Earth Syst. Sci. Data, vol. 8, no. 1, pp. 127–139, 2016. [CrossRef]
- B. Twaróg, “Characteristics of multi-annual variation of precipitation in areas particularly exposed to extreme phenomena. Part 1. the upper Vistula river basin,” E3S Web Conf., vol. 49, 2018. [CrossRef]
- Y. Yu et al., “Climatic factors and human population changes in Eurasia between the Last Glacial Maximum and the early Holocene,” Glob. Planet. Change, vol. 221, p. 104054, Feb. 2023. [CrossRef]
- T. Chen, L. Zou, J. Xia, H. Liu, and F. Wang, “Decomposing the impacts of climate change and human activities on runoff changes in the Yangtze River Basin: Insights from regional differences and spatial correlations of multiple factors,” J. Hydrol., vol. 615, p. 128649, Dec. 2022. [CrossRef]
- E. Szolgayova, J. Parajka, G. Blöschl, and C. Bucher, “Long term variability of the Danube River flow and its relation to precipitation and air temperature,” J. Hydrol., vol. 519, no. PA, pp. 871–880, 2014. [CrossRef]
- I. G. Pechlivanidis, J. Olsson, T. Bosshard, D. Sharma, and K. C. Sharma, “Multi-basin modelling of future hydrological fluxes in the Indian subcontinent,” Water (Switzerland), vol. 8, no. 5, pp. 1–21, 2016. [CrossRef]
- M. Mudelsee, M. Börngen, G. Tetzlaff, and U. Grünewald, “Extreme floods in central Europe over the past 500 years: Role of cyclone pathway ‘Zugstrasse Vb,’” J. Geophys. Res. D Atmos., vol. 109, no. 23, pp. 1–21, 2004. [CrossRef]
- S. J. Vavrus, M. Notaro, and D. J. Lorenz, “Interpreting climate model projections of extreme weather events,” Weather Clim. Extrem., vol. 10, pp. 10–28, 2015. [CrossRef]
- O. Angélil et al., “Comparing regional precipitation and temperature extremes in climate model and reanalysis products,” Weather Clim. Extrem., vol. 13, pp. 35–43, 2016. [CrossRef]
- S. Michaelides, V. Levizzani, E. Anagnostou, P. Bauer, T. Kasparis, and J. E. Lane, “Precipitation: Measurement, remote sensing, climatology and modeling,” Atmos. Res., vol. 94, no. 4, pp. 512–533, Dec. 2009. [CrossRef]
- N. Das, R. Bhattacharjee, A. Choubey, A. Ohri, S. B. Dwivedi, and S. Gaur, “Time series analysis of automated surface water extraction and thermal pattern variation over the Betwa river, India,” Adv. Sp. Res., vol. 68, no. 4, pp. 1761–1788, Aug. 2021. [CrossRef]
- R. F. Reinking, “An approach to remote sensing and numerical modeling of orographic clouds and precipitation for climatic water resources assessment,” Atmos. Res., vol. 35, no. 2–4, pp. 349–367, Jan. 1995. [CrossRef]
- C. López-Bermeo, R. D. Montoya, F. J. Caro-Lopera, and J. A. Díaz-García, “Validation of the accuracy of the CHIRPS precipitation dataset at representing climate variability in a tropical mountainous region of South America,” Phys. Chem. Earth, Parts A/B/C, vol. 127, p. 103184, Oct. 2022. [CrossRef]
- A. Becker et al., “A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901-present,” Earth Syst. Sci. Data, vol. 5, no. 1, pp. 71–99, 2013. [CrossRef]
- J. D. Gómez, J. D. Etchevers, A. I. Monterroso, C. Gay, J. Campo, and M. Martínez, “Spatial estimation of mean temperature and precipitation in areas of scarce meteorological information,” Atmosfera, vol. 21, no. 1, pp. 35–56, 2008.
- D. R. Easterling, K. E. Kunkel, M. F. Wehner, and L. Sun, “Detection and attribution of climate extremes in the observed record,” Weather Clim. Extrem., vol. 11, pp. 17–27, 2016. [CrossRef]
- G. Guimares Nobre, B. Jongman, J. Aerts, and P. J. Ward, “The role of climate variability in extreme floods in Europe,” Environ. Res. Lett., vol. 12, no. 8, 2017. [CrossRef]
- T. Petrow and B. Merz, “Trends in flood magnitude, frequency and seasonality in Germany in the period 1951–2002,” J. Hydrol., vol. 371, no. 1–4, pp. 129–141, Jun. 2009. [CrossRef]
- P. Singh, A. Gupta, and M. Singh, “Hydrological inferences from watershed analysis for water resource management using remote sensing and GIS techniques,” Egypt. J. Remote Sens. Sp. Sci., vol. 17, no. 2, pp. 111–121, 2014. [CrossRef]
- X. Zhang, L. A. Vincent, W. D. Hogg, and A. Niitsoo, “Temperature and precipitation trends in Canada during the 20th century,” Atmos. - Ocean, vol. 38, no. 3, pp. 395–429, 2000. [CrossRef]
- N. N. Karmeshu Supervisor Frederick Scatena, “Trend Detection in Annual Temperature & Precipitation using the Mann Kendall Test – A Case Study to Assess Climate Change on Select States in the Northeastern United States,” Mausam, vol. 66, no. 1, pp. 1–6, 2015, [Online]. Available: http://repository.upenn.edu/mes_capstones/47.
- R. Dankers and R. Hiederer, “Extreme Temperatures and Precipitation in Europe: Analysis of a High-Resolution Climate Change Scenario,” JRC Sci. Tech. Reports, p. 82, 2008.
- R. W. Katz and M. B. Parlange, “Overdispersion phenomenon in stochastic modeling of precipitation,” J. Clim., vol. 11, no. 4, pp. 591–601, 1998. [CrossRef]
- S. Sen Roy and R. C. Balling, “Trends in extreme daily precipitation indices in India,” Int. J. Climatol., vol. 24, no. 4, pp. 457–466, 2004. [CrossRef]
- A. Colmet-Daage et al., “Evaluation of uncertainties in mean and extreme precipitation under climate change for northwestern Mediterranean watersheds from high-resolution Med and Euro-CORDEX ensembles,” Hydrol. Earth Syst. Sci., vol. 22, no. 1, pp. 673–687, 2018. [CrossRef]
- G. Y. Lenny Bernstein, Peter Bosch, Osvaldo Canziani, Zhenlin Chen, Renate Christ, Ogunlade Davidson, William Hare, Saleemul Huq, David Karoly, Vladimir Kattsov, Zbigniew Kundzewicz, Jian Liu, Ulrike Lohmann, Martin Manning, Taroh Matsuno, Bettina Menne, Bert M, “Climate Change 2007 : An Assessment of the Intergovernmental Panel on Climate Change,” Change, vol. 446, no. November, pp. 12–17, 2007, [Online]. Available: http://www.ipcc.ch/pdf/assessment-report/ar4/syr/ar4_syr.pdf.
- J. Chapman, “A nonparametric approach to detecting changes in variance in locally stationary time series,” no. April 2019, pp. 1–12, 2020. [CrossRef]
- M. H. and A. J. C. Philp K. Thornton, Pplly J. Ericksen, “Climate variability and vulnerability to climate change : A review,” pp. 3313–3328, 2014. [CrossRef]
- K. L. Swanson and A. A. Tsonis, “Has the climate recently shifted ?,” vol. 36, no. January, pp. 2–5, 2009. [CrossRef]
- S. Balhane, F. Driouech, O. Chafki, R. Manzanas, A. Chehbouni, and W. Moufouma-Okia, “Changes in mean and extreme temperature and precipitation events from different weighted multi-model ensembles over the northern half of Morocco,” Clim. Dyn., vol. 58, no. 1–2, pp. 389–404, 2022. [CrossRef]
- T. Mesbahzadeh, M. M. Miglietta, M. Mirakbari, F. Soleimani Sardoo, and M. Abdolhoseini, “Joint Modeling of Precipitation and Temperature Using Copula Theory for Current and Future Prediction under Climate Change Scenarios in Arid Lands (Case Study, Kerman Province, Iran),” Adv. Meteorol., vol. 2019, 2019. [CrossRef]
- D. Gerten, S. Rost, W. von Bloh, and W. Lucht, “Causes of change in 20th century global river discharge,” Geophys. Res. Lett., vol. 35, no. 20, pp. 1–5, 2008. [CrossRef]
- D. E. Walling, “Human impact on land–ocean sediment transfer by the world’s rivers,” Geomorphology, vol. 79, no. 3–4, pp. 192–216, Sep. 2006. [CrossRef]
- T. S. Hunter, A. H. Clites, K. B. Campbell, and A. D. Gronewold, “Development and application of a North American Great Lakes hydrometeorological database — Part I: Precipitation, evaporation, runoff, and air temperature,” J. Great Lakes Res., vol. 41, no. 1, pp. 65–77, Mar. 2015. [CrossRef]
- Y. Chai et al., “Homogenization and polarization of the seasonal water discharge of global rivers in response to climatic and anthropogenic effects,” Sci. Total Environ., vol. 709, p. 136062, 2020. [CrossRef]
- Z. Li, Y. Shi, A. A. Argiriou, P. Ioannidis, A. Mamara, and Z. Yan, “A Comparative Analysis of Changes in Temperature and Precipitation Extremes since 1960 between China and Greece,” Atmosphere (Basel)., vol. 13, no. 11, 2022. [CrossRef]
- M. Jahn, “Economics of extreme weather events: Terminology and regional impact models,” Weather Clim. Extrem., vol. 10, pp. 29–39, 2015. [CrossRef]
- X. Zhang et al., “Indices for monitoring changes in extremes based on daily temperature and precipitation data,” Wiley Interdiscip. Rev. Clim. Chang., vol. 2, no. 6, pp. 851–870, Nov. 2011. [CrossRef]
- R. P. Allan and B. J. Soden, “Atmospheric warming and the amplification of precipitation extremes,” Science (80-. )., vol. 321, no. 5895, pp. 1481–1484, 2008. [CrossRef]
- J. H. Christensen et al., “Climate phenomena and their relevance for future regional climate change,” Clim. Chang. 2013 Phys. Sci. Basis Work. Gr. I Contrib. to Fifth Assess. Rep. Intergov. Panel Clim. Chang., vol. 9781107057, pp. 1217–1308, 2013. [CrossRef]
- B. Rudolf, C. Beck, J. Grieser, and U. Schneider, “Global Precipitation Analysis Products of the GPCC,” Internet Pbulication, pp. 1–8, 2005, [Online]. Available: ftp://ftp-anon.dwd.de/pub/data/gpcc/PDF/GPCC_intro_products_2008.pdf.
- T. C. P. and R. S. Vose, “An overview of the global historical climatology network-daily database,” Bull. Am. Meteorol. Soc., vol. 78, no. 12, pp. 897–910, 1997. [CrossRef]
- M. G. Donat et al., “Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 dataset,” J. Geophys. Res. Atmos., vol. 118, no. 5, pp. 2098–2118, 2013. [CrossRef]
- J. Persson et al., “No polarization-expected values of climate change impacts among European forest professionals and scientists,” Sustain., vol. 12, no. 7, 2020. [CrossRef]
- B. Arheimer et al., “Global catchment modelling using World-Wide HYPE (WWH), open data, and stepwise parameter estimation,” Hydrol. Earth Syst. Sci., vol. 24, no. 2, pp. 535–559, 2020. [CrossRef]
- L. R. Iverson and D. McKenzie, “Tree-species range shifts in a changing climate: Detecting, modeling, assisting,” Landsc. Ecol., vol. 28, no. 5, pp. 879–889, 2013. [CrossRef]
- J. Franklin, “Mapping Species Distributions: Spatial Inference and Prediction,” Oryx, vol. 44, no. 4, pp. 615–615, 2010. [CrossRef]
- D. Viner, M. Ekstrom, M. Hulbert, N. K. Warner, A. Wreford, and Z. Zommers, “Understanding the dynamic nature of risk in climate change assessments—A new starting point for discussion,” Atmos. Sci. Lett., vol. 21, no. 4, pp. 1–8, 2020. [CrossRef]
- M. Rosenzweig, C., Parry, “Potential impact of climate change on world food supply,” Nature, vol. 367, pp. 133–138, 1992. [CrossRef]
- T. M. Smith, R. W. Reynolds, T. C. Peterson, and J. Lawrimore, “Improvements to NOAA’s historical merged land-ocean surface temperature analysis (1880-2006),” J. Clim., vol. 21, no. 10, pp. 2283–2296, 2008. [CrossRef]
- A. Kosanic, K. Anderson, S. Harrison, T. Turkington, and J. Bennie, “Changes in the geographical distribution of plant species and climatic variables on the west cornwall peninsula (south west UK),” PLoS ONE, vol. 13, no. 2, pp. 1–18, 2018. [CrossRef]
- L. Chen and S. Guo, Copulas and its application in hydrology and water resources. 2019.
- W. Hou, P. Yan, G. Feng, and D. Zuo, “A 3D Copula Method for the Impact and Risk Assessment of Drought Disaster and an Example Application,” Front. Phys., vol. 9, no. April, pp. 1–14, 2021. [CrossRef]
- S. M. Ross, Introduction to Probability and Statistics, no. 5. Academic Press is an imprint ofElsevier, 2014.
- J. D. Santos-Gómez, J. S. Fontalvo-García, and J. D. Giraldo Osorio, “Validating the University of Delaware’s precipitation and temperature database for northern South America,” Dyna, vol. 82, no. 194, pp. 86–95, 2015. [CrossRef]
- Y. Amiel and F. Cowell, Thinking about Inequality, no. December 1999. 1999.
- M. O. Lorenz, “Methods of Measuring the Concentration of Wealth,” Publ. Am. Stat. Assoc., vol. 9, no. 70, pp. 209–219, 1905, [Online]. Available: https://www.jstor.org/stable/2276207. [CrossRef]
- M. G. and F. V. F. Francesco Nicolli, “Inequality and Climate Change: Two Problems, One Solution,” no. 2022, 2023, [Online]. Available: https://www.jstor.org/stable/resrep44832.
- T. Ogwang, “Calculating a standard error for the Gini coefficient: Some further results: Reply,” Oxf. Bull. Econ. Stat., vol. 66, no. 3, pp. 435–437, 2004. [CrossRef]
- C. Damgaard and J. Weiner, “Describing Inequality in Plant Size or Fecundity,” Ecology, vol. 81, no. 4, p. 1139, 2000. [CrossRef]
- T. Panek, “Polaryzacja ekonomiczna w Polsce,” Wiadomości Stat., vol. 1, no. 1, pp. 41–62, 2017.
- T. Sitthiyot and K. Holasut, “A simple method for measuring inequality,” Palgrave Commun., vol. 6, no. 1, pp. 1–9, 2020. [CrossRef]
- P.-M. Samson, Concentration of measure principle and entropy-inequalities. 2017.
- S. Yitzhaki, “Gini ’ s Mean Difference : A Superior Measure of Variability for Non-Normal Gini ’ s Mean difference : A superior measure of variability for non-normal distributions,” no. November, 2016.
- P. F. Pedro Conceição, “Young Person’s Guide to the Theil Index: Suggesting Intuitive Interpretations and Exploring Analytical Applications,” World, pp. 1–54, 2000, [Online]. Available: https://hal.science/hal-01365314. http://doi.org/10.2139/ssrn.228703.
- T. A. Buishand, “Some methods for testing the homogeneity of rainfall records,” J. Hydrol., vol. 58, no. 1–2, pp. 11–27, Aug. 1982. [CrossRef]
- A. K. Gupta, Jie Chen, “Parametric Statistical Change Point Analysis,” Angew. Chemie Int. Ed. 6(11), 951–952., pp. 2013–2015, 2021. [CrossRef]
- M. Radziejewski, A. Bardossy, and Z. W. Kundzewicz, “Détection de changements dans les séries de débits utilisant la randonisation de phase,” Hydrol. Sci. J., vol. 45, no. 4, pp. 547–558, 2000. [CrossRef]
- M. Salarijazi, “Trend and change-point detection for the annual stream-flow series of the Karun River at the Ahvaz hydrometric station,” African J. Agric. Reseearch, vol. 7, no. 32, pp. 4540–4552, 2012. [CrossRef]
- A. N. Pettitt, “A Non-Parametric Approach to the Change-Point Problem,” J. R. Stat. Soc. Ser. C (Applied Stat., vol. 28, no. 2, pp. 126–135, Apr. 1979. [CrossRef]
- G. Verstraeten, J. Poesen, G. Demarée, and C. Salles, “Long-term (105 years) variability in rain erosivity as derived from 10-min rainfall depth data for Ukkel (Brussels, Belgium): Implications for assessing soil erosion rates,” J. Geophys. Res. Atmos., vol. 111, no. 22, pp. 1–11, 2006. [CrossRef]
- L. C. Conte, D. M. Bayer, and F. M. Bayer, “Bootstrap Pettitt test for detecting change points in hydroclimatological data: Case study of Itaipu Hydroelectric Plant, Brazil,” Hydrol. Sci. J., vol. 64, no. 11, pp. 1312–1326, 2019. [CrossRef]
- H. B. Mann, “Nonparametric Tests Against Trend,” Econometrica, vol. 13, no. 3, pp. 245–259, Apr. 1945. [CrossRef]
- S. Yue, P. Pilon, B. Phinney, and G. Cavadias, “The influence of autocorrelation on the ability to detect trend in hydrological series,” Hydrol. Process., vol. 16, no. 9, pp. 1807–1829, 2002. [CrossRef]
- K. Sen, “Estimates of the Regression Coefficient Based on Kendall’s Tau,” J. Am. Stat. Assoc., vol. 63, no. 324, pp. 1379–1389, Dec. 1968. [CrossRef]
- M. Hirsch, J. R. Slack, and R. A. Smith, “Techniques of trend analysis for monthly water quality data,” Water Resour. Res., vol. 18, no. 1, pp. 107–121, Feb. 1982. [CrossRef]
| Region | Continent | Lands area | Area catchment | Coverage of the continents |
| WMO | 106 km2 | 106 km2 | % | |
| 2 | Asia | 44.3 | 20.3 | 45.86% |
| 1 | Africa | 30.3 | 8.43 | 27.83% |
| 4 | North America | 24.2 | 13.0 | 53.87% |
| 3 | South America | 17.8 | 12.6 | 70.57% |
| Antarctica | 13.1 | 0.0 | 0.00% | |
| 6 | Europe | 10.5 | 6.7 | 64.10% |
| 5 | Australia and Oceania | 8.5 | 1.1 | 13.07% |
| Lands together | 148.7 | 65.1 | 43.77% | |
| Earth, total | 509.9 | 65.1 | 12.76% |
| No | GRDC | WMO | RIVER | COUNTRY | AREA | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC | MIN | MAX | MEAN | STD |
| 1 | 1104150 | 1 | CHELIF | DZ | 43750 | 54.9 | 43.2 | 41.0 | 37.8 | 34.1 | 11.3 | 3.8 | 7.4 | 26.8 | 40.3 | 48.3 | 56.0 | 0.2 | 209.6 | 33.7 | 30.54 |
| 2 | 1147010 | 1 | CONGO | CD | 3475000 | 122.7 | 123.2 | 158.3 | 152.1 | 105.9 | 71.0 | 70.2 | 97.6 | 129.9 | 161.9 | 163.5 | 146.5 | 45.2 | 227.2 | 125.2 | 36.04 |
| 3 | 1159100 | 1 | ORANGE | ZA | 850530 | 58.5 | 59.4 | 56.9 | 31.4 | 13.5 | 6.7 | 5.2 | 7.0 | 11.6 | 26.9 | 38.0 | 44.8 | 0.2 | 166.1 | 30.0 | 27.57 |
| 4 | 1160580 | 1 | GROOT-VIS | ZA | 29745 | 50.5 | 58.3 | 65.2 | 38.8 | 24.9 | 17.0 | 15.9 | 19.9 | 27.5 | 40.2 | 47.9 | 46.9 | 0.5 | 226.6 | 37.8 | 30.28 |
| 5 | 1160880 | 1 | TUGELA | ZA | 28920 | 147.7 | 127.5 | 102.6 | 46.1 | 20.6 | 12.5 | 13.1 | 23.0 | 41.2 | 83.4 | 113.0 | 131.5 | 0.2 | 351.2 | 71.9 | 60.10 |
| 6 | 1286900 | 1 | RUFIJI | TZ | 158200 | 176.3 | 154.7 | 196.3 | 155.0 | 41.8 | 7.9 | 5.1 | 4.1 | 6.2 | 15.3 | 55.9 | 152.7 | 0.1 | 380.9 | 80.9 | 84.20 |
| 7 | 1289200 | 1 | PANGANI | TZ | 25110 | 68.9 | 74.1 | 115.9 | 197.3 | 124.1 | 33.2 | 20.0 | 19.2 | 20.6 | 37.3 | 78.5 | 82.3 | 1.2 | 436.6 | 72.6 | 69.59 |
| 8 | 1289450 | 1 | RUVU | TZ | 15190 | 113.9 | 101.3 | 181.6 | 250.1 | 107.4 | 31.0 | 20.9 | 19.2 | 36.1 | 53.2 | 98.6 | 119.5 | 0.0 | 695.0 | 94.4 | 83.42 |
| 9 | 1309700 | 1 | SEBOU | MA | 17250 | 78.2 | 81.1 | 77.7 | 72.4 | 41.0 | 17.1 | 4.0 | 5.8 | 20.6 | 53.3 | 82.9 | 94.5 | 0.1 | 287.0 | 52.4 | 51.53 |
| 10 | 1336500 | 1 | CROSS | CM | 6810 | 23.9 | 51.3 | 144.4 | 194.9 | 241.0 | 311.6 | 379.4 | 398.6 | 425.5 | 312.4 | 90.5 | 25.0 | 0.0 | 1085.2 | 216.5 | 164.78 |
| 11 | 1338050 | 1 | SANAGA | CM | 131520 | 13.0 | 24.4 | 89.9 | 144.1 | 193.2 | 188.0 | 205.0 | 237.2 | 280.7 | 246.0 | 61.8 | 15.0 | 0.0 | 478.2 | 141.5 | 101.62 |
| 12 | 1339100 | 1 | NYONG | CM | 26400 | 29.8 | 51.4 | 135.6 | 178.5 | 224.5 | 160.6 | 96.3 | 136.0 | 265.5 | 303.0 | 127.0 | 36.4 | 0.0 | 1064.1 | 145.4 | 100.71 |
| 13 | 1340500 | 1 | NTEM | CM | 18100 | 50.8 | 72.3 | 152.4 | 182.1 | 198.2 | 123.1 | 56.1 | 63.4 | 212.0 | 281.4 | 166.5 | 61.3 | 0.0 | 1067.8 | 135.0 | 95.45 |
| 14 | 1362100 | 1 | NILE | EG | 2900000 | 10.3 | 13.9 | 27.1 | 45.9 | 64.1 | 74.5 | 110.9 | 123.9 | 86.3 | 52.0 | 26.0 | 14.7 | 3.3 | 167.5 | 54.2 | 38.6 |
| 15 | 1389090 | 1 | MANGOKY | MG | 53225 | 229.6 | 178.8 | 90.7 | 41.7 | 22.5 | 11.8 | 12.1 | 10.9 | 16.3 | 31.9 | 85.5 | 161.0 | 0.0 | 562.4 | 74.4 | 92.63 |
| 16 | 1389230 | 1 | TSIRIBIHINA | MG | 45000 | 293.6 | 215.3 | 142.3 | 58.7 | 24.7 | 12.1 | 14.2 | 12.6 | 18.0 | 48.3 | 107.0 | 198.6 | 0.0 | 613.7 | 95.5 | 110.17 |
| 17 | 1425500 | 1 | CAVALLY | CI | 28800 | 31.9 | 69.1 | 144.0 | 173.2 | 228.5 | 274.1 | 154.5 | 177.9 | 296.3 | 245.2 | 126.6 | 59.3 | 1.2 | 672.2 | 165.0 | 102.46 |
| 18 | 1426380 | 1 | BANDAMA | CI | 95500 | 12.3 | 32.4 | 80.5 | 117.4 | 142.3 | 153.8 | 129.8 | 159.0 | 192.3 | 123.5 | 40.7 | 16.6 | 0.0 | 434.6 | 100.1 | 71.48 |
| 19 | 1427500 | 1 | SASSANDRA | CI | 62000 | 14.2 | 40.8 | 96.6 | 130.3 | 154.1 | 185.4 | 175.4 | 222.9 | 250.6 | 157.2 | 52.5 | 18.5 | 0.0 | 624.8 | 124.9 | 90.50 |
| 20 | 1427600 | 1 | DAVO | CI | 6600 | 26.9 | 60.7 | 131.0 | 153.1 | 184.9 | 207.8 | 93.8 | 93.3 | 172.9 | 153.9 | 89.0 | 39.4 | 0.0 | 597.4 | 117.2 | 77.62 |
| 21 | 1428500 | 1 | COMOE | CI | 69900 | 6.8 | 20.0 | 58.4 | 104.0 | 136.8 | 150.1 | 147.2 | 177.8 | 187.4 | 115.3 | 33.6 | 9.4 | 0.0 | 388.7 | 95.6 | 73.07 |
| 22 | 1445100 | 1 | KOUILOU | CG | 55010 | 160.5 | 150.9 | 192.5 | 203.9 | 126.1 | 7.7 | 2.2 | 4.9 | 19.7 | 119.5 | 251.4 | 192.7 | 0.0 | 467.0 | 119.3 | 98.86 |
| 23 | 1526300 | 1 | PRA | GH | 22714 | 20.3 | 59.9 | 124.2 | 146.6 | 182.1 | 221.1 | 119.8 | 73.2 | 153.5 | 175.3 | 91.9 | 38.4 | 0.0 | 428.0 | 117.2 | 74.41 |
| 24 | 1530100 | 1 | TANO | GH | 15800 | 19.6 | 53.3 | 119.1 | 140.1 | 201.9 | 253.5 | 125.8 | 73.7 | 155.9 | 177.6 | 91.1 | 38.5 | 0.0 | 568.5 | 120.8 | 86.63 |
| 25 | 1531700 | 1 | VOLTA | GH | 394100 | 3.6 | 10.3 | 32.6 | 64.8 | 101.9 | 136.4 | 167.4 | 207.6 | 182.3 | 80.4 | 16.6 | 6.2 | 0.0 | 333.8 | 84.2 | 74.34 |
| 26 | 1643100 | 1 | OGOOUE | GA | 205000 | 120.8 | 135.6 | 202.3 | 200.2 | 185.3 | 52.2 | 17.1 | 28.4 | 118.8 | 267.1 | 249.9 | 151.6 | 0.4 | 770.6 | 144.1 | 90.22 |
| 27 | 1644100 | 1 | NYANGA | GA | 20000 | 164.0 | 162.4 | 200.6 | 192.2 | 108.3 | 6.4 | 1.6 | 2.5 | 18.7 | 162.2 | 278.9 | 192.0 | 0.0 | 562.6 | 124.2 | 110.57 |
| 28 | 1732100 | 1 | MONO | BJ | 21575 | 10.8 | 26.5 | 73.0 | 113.0 | 141.1 | 165.5 | 178.2 | 174.9 | 195.0 | 116.7 | 25.5 | 14.3 | 0.1 | 370.9 | 102.9 | 77.29 |
| 29 | 1733600 | 1 | OUEME | BJ | 46990 | 7.1 | 15.2 | 50.1 | 92.7 | 137.8 | 157.3 | 179.8 | 184.9 | 194.0 | 108.5 | 16.4 | 6.2 | 0.0 | 404.4 | 95.8 | 80.01 |
| 30 | 1789300 | 1 | TANA | KE | 42220 | 34.4 | 25.8 | 77.8 | 181.4 | 76.3 | 17.9 | 14.4 | 15.9 | 15.2 | 82.2 | 168.3 | 77.2 | 2.5 | 527.0 | 65.6 | 73.02 |
| 31 | 1812100 | 1 | SENEGAL | SN | 268000 | 0.7 | 0.9 | 1.8 | 6.1 | 21.9 | 65.2 | 128.4 | 178.6 | 118.5 | 34.5 | 4.2 | 1.5 | 0.0 | 310.4 | 46.9 | 62.73 |
| 32 | 1813200 | 1 | GAMBIA | SN | 42000 | 0.6 | 0.9 | 2.5 | 7.7 | 44.9 | 151.1 | 240.1 | 314.0 | 259.8 | 90.9 | 12.8 | 2.0 | 0.0 | 482.6 | 93.9 | 117.80 |
| 33 | 1814070 | 1 | GEBA | SN | 7340 | 0.3 | 0.7 | 0.4 | 1.8 | 25.8 | 137.9 | 225.4 | 343.0 | 287.0 | 106.0 | 9.1 | 0.9 | 0.0 | 653.1 | 94.9 | 128.2 |
| 34 | 1815020 | 1 | CORUBAL | SN | 23840 | 0.9 | 1.5 | 4.4 | 16.2 | 70.8 | 205.9 | 324.4 | 429.2 | 364.3 | 172.0 | 33.6 | 4.1 | 0.0 | 796.7 | 135.6 | 160.32 |
| 35 | 1834101 | 1 | NIGER | NG | 575500 | 1.6 | 2.4 | 10.0 | 27.5 | 58.0 | 85.7 | 133.1 | 169.2 | 118.0 | 43.0 | 5.9 | 1.6 | 0.1 | 236.1 | 54.7 | 57.78 |
| 36 | 1878100 | 1 | SHEBELLE | SO | 278000 | 9.0 | 16.7 | 38.5 | 105.4 | 93.7 | 35.5 | 49.8 | 63.4 | 58.1 | 85.4 | 39.0 | 9.8 | 0.2 | 268.1 | 50.4 | 39.91 |
| 37 | 1880100 | 1 | JUBA | SO | 179520 | 10.9 | 18.3 | 50.1 | 142.6 | 111.9 | 30.1 | 35.6 | 43.1 | 61.6 | 108.6 | 48.8 | 14.2 | 0.2 | 396.8 | 56.3 | 49.87 |
| 38 | 1891500 | 1 | ZAMBEZI | MZ | 940000 | 208.8 | 183.3 | 141.2 | 39.8 | 6.0 | 1.3 | 0.6 | 1.1 | 4.7 | 28.5 | 101.4 | 190.5 | 0.1 | 390.0 | 75.6 | 84.92 |
| 39 | 1894200 | 1 | BUZI | MZ | 26314 | 240.1 | 215.0 | 174.1 | 58.3 | 24.7 | 19.8 | 17.9 | 17.0 | 19.1 | 43.4 | 107.8 | 195.1 | 0.6 | 769.3 | 94.4 | 107.3 |
| 40 | 1895500 | 1 | SAVE | MZ | 100885 | 152.1 | 136.7 | 97.6 | 32.2 | 12.4 | 8.9 | 7.1 | 5.7 | 9.9 | 29.2 | 82.6 | 138.8 | 0.2 | 589.7 | 59.4 | 75.1 |
| 41 | 1896500 | 1 | LIMPOPO | MZ | 342000 | 105.6 | 89.2 | 67.7 | 29.0 | 11.3 | 5.2 | 4.1 | 4.4 | 11.7 | 37.0 | 74.0 | 91.1 | 0.1 | 344.5 | 44.2 | 48.27 |
| 42 | 1897500 | 1 | INCOMATI | MZ | 37600 | 137.7 | 124.4 | 100.4 | 48.3 | 19.7 | 10.9 | 10.6 | 12.2 | 29.9 | 63.2 | 111.4 | 124.6 | 0.0 | 504.0 | 66.1 | 64.89 |
| 43 | 1899100 | 1 | MAPUTO | MZ | 28500 | 132.7 | 110.3 | 91.4 | 47.4 | 20.3 | 12.4 | 11.6 | 16.4 | 36.0 | 80.0 | 117.1 | 129.3 | 0.1 | 462.8 | 67.1 | 62.04 |
| 44 | 1992900 | 1 | SHIRE | MW | 149500 | 236.8 | 209.6 | 218.0 | 125.7 | 38.6 | 13.6 | 9.9 | 8.3 | 7.6 | 15.0 | 72.1 | 191.1 | 1.0 | 390.7 | 95.5 | 97.09 |
| 45 | 2178300 | 2 | YONGDING HE | CN | 42500 | 3.0 | 3.6 | 10.2 | 16.7 | 33.2 | 56.0 | 111.7 | 87.4 | 50.7 | 19.1 | 8.5 | 2.8 | 0.1 | 249.5 | 33.6 | 42.12 |
| 46 | 2178400 | 2 | DALINGHE | CN | 17687 | 2.1 | 2.8 | 8.6 | 19.3 | 42.7 | 80.2 | 148.2 | 120.3 | 46.9 | 23.8 | 8.3 | 3.2 | 0.0 | 474.1 | 42.2 | 58.50 |
| 47 | 2178500 | 2 | LUAN HE | CN | 44100 | 2.7 | 3.2 | 8.6 | 16.4 | 37.3 | 71.3 | 142.6 | 109.0 | 50.7 | 19.9 | 7.6 | 2.6 | 0.0 | 315.9 | 39.3 | 51.49 |
| 48 | 2179100 | 2 | LIAO HE | CN | 120764 | 2.5 | 3.0 | 8.8 | 15.1 | 36.7 | 71.3 | 130.1 | 99.7 | 39.5 | 20.7 | 7.6 | 3.2 | 0.0 | 315.0 | 36.5 | 47.52 |
| 49 | 2180800 | 2 | HUANG HE (YELLOW R | CN | 730036 | 3.8 | 5.4 | 12.7 | 22.4 | 36.4 | 55.0 | 83.8 | 87.0 | 61.1 | 28.6 | 8.9 | 2.9 | 0.0 | 209.2 | 34.0 | 34.22 |
| 50 | 2181900 | 2 | YANGTZE RIVER (CHA | CN | 1705383 | 24.4 | 35.6 | 60.0 | 93.6 | 127.9 | 170.2 | 162.9 | 144.9 | 107.7 | 70.6 | 37.1 | 20.0 | 3.0 | 310.0 | 87.9 | 58.10 |
| 51 | 2181950 | 2 | HUAI HE | CN | 121330 | 24.1 | 28.9 | 48.7 | 63.2 | 77.0 | 110.7 | 194.6 | 134.8 | 81.7 | 49.2 | 35.5 | 19.1 | 0.0 | 523.6 | 72.3 | 68.36 |
| 52 | 2186800 | 2 | XI JIANG | CN | 329705 | 27.7 | 36.9 | 53.7 | 96.6 | 194.1 | 248.5 | 230.2 | 204.9 | 116.2 | 80.5 | 46.1 | 26.6 | 2.9 | 393.4 | 113.5 | 90.27 |
| 53 | 2186901 | 2 | BEI JIANG | CN | 38363 | 58.1 | 91.0 | 148.1 | 220.7 | 276.0 | 268.3 | 168.0 | 172.2 | 102.1 | 60.2 | 50.6 | 44.2 | 0.3 | 582.7 | 138.3 | 105.60 |
| 54 | 2186950 | 2 | DONG JIANG | CN | 25325 | 45.9 | 79.9 | 130.3 | 202.2 | 278.0 | 315.5 | 219.9 | 219.5 | 143.0 | 52.8 | 37.8 | 37.4 | 0.1 | 749.8 | 146.8 | 126.69 |
| 55 | 2260100 | 2 | CHINDWIN RIVER | MM | 27420 | 19.5 | 36.8 | 73.1 | 146.7 | 227.2 | 641.4 | 820.6 | 637.6 | 448.1 | 187.0 | 32.1 | 15.1 | 0.0 | 1284.9 | 273.8 | 289.55 |
| 56 | 2260500 | 2 | IRRAWADDY | MM | 117900 | 15.8 | 31.4 | 52.9 | 84.2 | 145.1 | 342.1 | 393.4 | 363.5 | 250.6 | 147.0 | 37.3 | 13.8 | 0.3 | 624.1 | 156.4 | 145.75 |
| 57 | 2261500 | 2 | SITTANG RIVER | MM | 14660 | 6.1 | 3.4 | 5.1 | 31.4 | 159.9 | 196.5 | 234.0 | 250.8 | 212.9 | 139.4 | 40.6 | 8.6 | 0.0 | 451.6 | 107.4 | 106.79 |
| 58 | 2335950 | 2 | INDUS | PK | 832418 | 31.1 | 36.1 | 43.7 | 31.3 | 23.7 | 28.4 | 90.5 | 86.6 | 41.8 | 12.0 | 7.8 | 17.8 | 0.6 | 184.2 | 37.6 | 31.84 |
| 61 | 2423450 | 2 | KARKHEH | IR | 45882 | 79.7 | 66.5 | 83.6 | 59.1 | 23.0 | 1.8 | 0.9 | 0.6 | 1.3 | 18.0 | 60.0 | 71.3 | 0.0 | 265.6 | 38.8 | 39.95 |
| 62 | 2423500 | 2 | KARUN | IR | 60769 | 111.2 | 88.2 | 108.4 | 57.8 | 16.3 | 1.0 | 1.1 | 0.8 | 1.2 | 14.3 | 60.5 | 109.5 | 0.0 | 302.8 | 47.5 | 51.62 |
| 63 | 2569005 | 2 | MEKONG | KH | 635000 | 11.4 | 18.5 | 37.5 | 77.2 | 176.9 | 228.6 | 278.5 | 288.9 | 234.4 | 113.6 | 41.1 | 15.4 | 1.2 | 445.9 | 126.8 | 108.40 |
| 64 | 2587100 | 2 | ISHIKARI | JP | 12697 | 89.0 | 66.1 | 58.8 | 59.3 | 75.5 | 76.6 | 111.1 | 135.1 | 140.4 | 111.9 | 114.0 | 105.6 | 13.7 | 535.8 | 95.3 | 46.34 |
| 65 | 2588200 | 2 | YODO | JP | 7281 | 98.7 | 92.9 | 117.5 | 135.7 | 149.6 | 222.3 | 207.8 | 155.8 | 214.7 | 145.7 | 99.7 | 94.6 | 20.5 | 574.2 | 144.6 | 78.17 |
| 66 | 2588301 | 2 | KISO | JP | 4684 | 74.6 | 78.3 | 115.3 | 136.0 | 143.1 | 211.1 | 214.6 | 154.9 | 215.1 | 139.9 | 89.0 | 73.1 | 17.4 | 560.6 | 137.1 | 81.42 |
| 67 | 2588320 | 2 | TENRYU | JP | 4880 | 56.1 | 67.6 | 112.2 | 132.3 | 141.2 | 206.6 | 197.5 | 162.0 | 206.9 | 143.5 | 82.9 | 55.9 | 3.5 | 538.5 | 130.4 | 82.86 |
| 68 | 2588551 | 2 | TONE | JP | 12458 | 50.4 | 57.1 | 80.5 | 108.6 | 132.2 | 179.9 | 194.4 | 221.1 | 232.9 | 164.2 | 77.7 | 53.4 | 9.7 | 576.8 | 129.4 | 86.95 |
| 69 | 2588700 | 2 | KITAKAMI | JP | 7869 | 74.8 | 67.1 | 86.1 | 103.8 | 110.2 | 124.9 | 168.7 | 168.7 | 175.7 | 130.3 | 105.0 | 85.3 | 11.9 | 453.3 | 116.7 | 60.45 |
| 70 | 2589200 | 2 | GONO (GO) | JP | 3807 | 81.9 | 84.1 | 108.3 | 127.2 | 131.4 | 208.4 | 214.6 | 113.9 | 191.5 | 113.5 | 86.9 | 81.3 | 8.5 | 537.0 | 128.6 | 80.46 |
| 71 | 2589500 | 2 | SHINANO, CHIKUMA | JP | 9719 | 116.8 | 92.5 | 95.4 | 93.3 | 104.8 | 153.2 | 177.7 | 155.1 | 187.4 | 140.2 | 109.7 | 120.5 | 19.8 | 403.3 | 128.9 | 54.78 |
| 72 | 2589700 | 2 | MOGAMI | JP | 6271 | 131.5 | 98.2 | 91.9 | 89.0 | 91.2 | 119.2 | 173.9 | 155.8 | 155.7 | 132.2 | 130.6 | 150.0 | 16.5 | 461.0 | 126.6 | 53.82 |
| 73 | 2595400 | 2 | EUPHRATES | IQ | 274100 | 49.7 | 46.6 | 46.0 | 44.6 | 29.9 | 10.0 | 4.5 | 4.0 | 5.4 | 24.2 | 40.0 | 48.5 | 0.0 | 147.1 | 29.4 | 24.81 |
| 74 | 2595700 | 2 | TIGRIS | IQ | 134000 | 78.1 | 82.7 | 87.1 | 77.3 | 41.1 | 7.6 | 2.7 | 2.7 | 4.4 | 28.0 | 65.6 | 76.3 | 0.1 | 232.3 | 46.1 | 40.99 |
| 75 | 2651100 | 2 | BRAHMAPUTRA | BD | 636130 | 15.2 | 28.3 | 53.1 | 107.3 | 163.8 | 274.8 | 313.0 | 272.4 | 194.2 | 85.0 | 16.4 | 9.1 | 1.3 | 651.4 | 127.7 | 120.00 |
| 76 | 2677100 | 2 | HAN-GANG (HAN RIVE | KR | 25046 | 28.6 | 32.1 | 47.5 | 76.9 | 90.9 | 134.3 | 311.7 | 254.4 | 153.2 | 49.2 | 45.0 | 28.4 | 0.5 | 757.3 | 104.3 | 113.63 |
| 77 | 2694510 | 2 | NAKTONG | KR | 22916 | 29.0 | 34.1 | 50.6 | 89.6 | 91.7 | 155.4 | 253.2 | 204.3 | 138.0 | 47.8 | 36.4 | 23.5 | 0.2 | 627.2 | 96.1 | 96.62 |
| 78 | 2846800 | 2 | GANGES | IN | 835000 | 20.6 | 22.3 | 19.7 | 18.3 | 36.6 | 136.1 | 315.6 | 307.2 | 181.9 | 42.0 | 8.9 | 9.3 | 0.4 | 441.1 | 93.2 | 115.61 |
| 79 | 2853150 | 2 | MAHI RIVER | IN | 33670 | 2.7 | 1.6 | 1.9 | 1.6 | 7.1 | 96.6 | 283.9 | 246.4 | 153.9 | 21.2 | 8.4 | 2.1 | 0.0 | 678.1 | 69.0 | 118.18 |
| 80 | 2853200 | 2 | NARMADA | IN | 89345 | 13.5 | 12.4 | 9.9 | 5.1 | 10.5 | 144.6 | 360.4 | 328.4 | 201.5 | 38.8 | 15.6 | 7.9 | 0.0 | 626.0 | 95.7 | 138.52 |
| 81 | 2853300 | 2 | TAPTI RIVER | IN | 61575 | 6.8 | 5.3 | 5.7 | 3.8 | 11.5 | 139.3 | 253.2 | 197.8 | 161.0 | 45.9 | 22.2 | 6.6 | 0.0 | 461.8 | 71.6 | 97.95 |
| 82 | 2854050 | 2 | DAMODAR RIVER | IN | 19220 | 17.2 | 24.2 | 18.7 | 17.7 | 48.3 | 189.2 | 329.8 | 312.8 | 228.1 | 80.7 | 12.0 | 5.7 | 0.0 | 652.8 | 107.0 | 132.09 |
| 84 | 2854300 | 2 | KRISHNA | IN | 251355 | 3.1 | 3.5 | 6.8 | 21.0 | 45.0 | 120.2 | 193.1 | 149.8 | 153.3 | 96.4 | 32.2 | 6.7 | 0.0 | 324.1 | 69.3 | 74.57 |
| 85 | 2854500 | 2 | PENNER RIVER | IN | 53290 | 6.2 | 3.9 | 6.4 | 20.7 | 54.4 | 56.3 | 81.5 | 93.9 | 125.6 | 123.0 | 71.4 | 19.8 | 0.0 | 324.5 | 55.3 | 59.23 |
| 86 | 2854800 | 2 | CAUVERY RIVER | IN | 74004 | 9.9 | 7.6 | 14.9 | 55.8 | 107.8 | 103.1 | 159.7 | 129.5 | 122.7 | 173.8 | 98.4 | 30.8 | 0.0 | 390.3 | 84.5 | 69.53 |
| 87 | 2855800 | 2 | MAHANADI RIVER (MA | IN | 132090 | 14.5 | 21.5 | 19.0 | 17.4 | 25.1 | 203.2 | 399.4 | 386.4 | 224.3 | 62.2 | 11.9 | 5.8 | 0.0 | 626.7 | 115.9 | 152.84 |
| 88 | 2856900 | 2 | GODAVARI | IN | 299320 | 8.3 | 11.3 | 13.1 | 18.1 | 24.5 | 168.9 | 321.4 | 280.1 | 202.0 | 70.5 | 20.8 | 6.8 | 0.0 | 487.2 | 95.5 | 119.05 |
| 89 | 2901202 | 2 | ANADYR | RU | 156000 | 19.5 | 13.6 | 12.3 | 11.2 | 11.8 | 25.1 | 51.5 | 51.4 | 30.5 | 24.6 | 23.1 | 17.6 | 0.0 | 200.2 | 24.3 | 20.78 |
| 90 | 2902850 | 2 | KAMCHATKA | RU | 51600 | 42.6 | 35.4 | 29.8 | 35.4 | 33.8 | 39.3 | 66.3 | 73.3 | 52.8 | 47.6 | 46.5 | 44.4 | 0.0 | 263.9 | 45.6 | 30.77 |
| 91 | 2903420 | 2 | LENA | RU | 2430000 | 11.2 | 8.2 | 8.8 | 14.2 | 28.1 | 49.0 | 61.0 | 61.8 | 39.9 | 26.2 | 17.5 | 13.2 | 1.8 | 96.2 | 28.3 | 20.66 |
| 92 | 2906900 | 2 | AMUR | RU | 1730000 | 5.4 | 4.8 | 9.4 | 22.5 | 42.7 | 78.3 | 119.7 | 109.8 | 60.9 | 26.4 | 13.6 | 7.8 | 0.6 | 188.5 | 41.8 | 41.71 |
| 93 | 2909150 | 2 | YENISEI | RU | 2440000 | 15.7 | 11.2 | 12.4 | 19.0 | 33.8 | 55.6 | 70.9 | 69.1 | 44.3 | 30.9 | 24.6 | 19.4 | 3.5 | 95.8 | 33.9 | 21.73 |
| 94 | 2912600 | 2 | OB | RU | 2949998 | 21.2 | 16.6 | 19.1 | 25.5 | 42.2 | 56.3 | 68.4 | 62.1 | 45.7 | 39.7 | 32.7 | 25.5 | 4.5 | 99.5 | 37.9 | 19.01 |
| 96 | 2917100 | 2 | AMU DARYA | UZ | 450000 | 33.7 | 38.3 | 54.6 | 49.0 | 32.5 | 10.2 | 5.6 | 3.4 | 3.3 | 12.6 | 21.5 | 29.7 | 0.2 | 103.8 | 24.5 | 20.30 |
| 97 | 2919200 | 2 | URAL | KZ | 190000 | 20.8 | 16.5 | 19.4 | 22.9 | 33.6 | 39.4 | 43.2 | 31.9 | 27.5 | 32.5 | 26.9 | 25.2 | 0.7 | 107.7 | 28.3 | 17.40 |
| 99 | 2964998 | 2 | MAE KLONG | TH | 26449 | 5.6 | 16.2 | 36.7 | 83.3 | 210.3 | 283.8 | 294.4 | 324.9 | 292.3 | 186.5 | 46.5 | 6.2 | 0.0 | 653.6 | 148.9 | 135.25 |
| 100 | 2998110 | 2 | YANA | RU | 224000 | 5.8 | 6.0 | 5.2 | 7.3 | 16.8 | 36.9 | 45.5 | 39.8 | 24.0 | 13.7 | 9.2 | 7.1 | 0.0 | 99.7 | 18.1 | 17.00 |
| 101 | 2998150 | 2 | OMOLOY | RU | 10800 | 5.3 | 5.4 | 5.0 | 6.7 | 14.1 | 28.8 | 36.0 | 32.7 | 19.2 | 9.7 | 7.4 | 5.6 | 0.0 | 102.8 | 14.7 | 14.95 |
| 102 | 2998400 | 2 | INDIGIRKA | RU | 305000 | 8.2 | 7.9 | 5.8 | 6.5 | 13.7 | 34.7 | 49.1 | 44.8 | 24.4 | 15.0 | 12.0 | 9.2 | 0.0 | 107.1 | 19.3 | 17.39 |
| 103 | 2998450 | 2 | ALAZEYA | RU | 29000 | 12.7 | 11.2 | 8.2 | 6.5 | 10.3 | 27.0 | 37.4 | 34.9 | 22.5 | 18.7 | 16.8 | 13.2 | 0.0 | 113.1 | 18.3 | 15.44 |
| 104 | 2998510 | 2 | KOLYMA | RU | 526000 | 14.6 | 12.9 | 9.7 | 8.3 | 13.6 | 32.6 | 50.7 | 47.8 | 29.7 | 20.9 | 19.5 | 14.6 | 0.0 | 106.5 | 22.9 | 18.12 |
| 105 | 2998702 | 2 | ANYUY (TRIB. KOLYM | RU | 30000 | 12.7 | 8.4 | 7.3 | 5.4 | 6.9 | 22.4 | 44.7 | 36.2 | 20.7 | 15.0 | 13.5 | 11.7 | 0.0 | 212.2 | 17.1 | 17.64 |
| 106 | 2998720 | 2 | BOL. ANYUY (TRIB. | RU | 49600 | 12.7 | 9.0 | 7.4 | 6.2 | 8.0 | 23.2 | 45.1 | 36.1 | 22.5 | 16.2 | 14.7 | 12.1 | 0.0 | 175.0 | 17.8 | 16.77 |
| 107 | 2998800 | 2 | PALYAVAAM | RU | 6810 | 15.6 | 10.8 | 8.8 | 8.1 | 9.6 | 18.2 | 40.3 | 41.4 | 29.9 | 23.4 | 18.8 | 13.6 | 0.0 | 207.4 | 19.9 | 18.69 |
| 108 | 2999150 | 2 | ANABAR | RU | 78800 | 7.8 | 6.6 | 8.1 | 11.0 | 19.0 | 33.5 | 42.3 | 39.2 | 29.0 | 19.5 | 11.5 | 8.8 | 0.0 | 160.5 | 19.7 | 17.54 |
| 109 | 2999200 | 2 | NADYM | RU | 48000 | 21.4 | 15.7 | 20.9 | 23.7 | 38.9 | 56.9 | 70.6 | 68.1 | 58.2 | 45.5 | 30.5 | 24.2 | 0.5 | 172.1 | 39.6 | 25.50 |
| 110 | 2999250 | 2 | TAZ | RU | 100000 | 24.0 | 18.0 | 21.9 | 28.0 | 37.2 | 57.3 | 62.7 | 68.9 | 57.5 | 52.7 | 37.5 | 27.8 | 1.1 | 144.1 | 41.1 | 23.93 |
| 111 | 2999500 | 2 | PUR | RU | 95100 | 21.6 | 16.9 | 21.6 | 25.6 | 37.3 | 55.9 | 67.0 | 69.9 | 59.3 | 48.1 | 33.8 | 24.9 | 2.6 | 148.6 | 40.2 | 24.71 |
| 112 | 2999850 | 2 | KHATANGA | RU | 275000 | 9.4 | 8.2 | 8.5 | 12.4 | 18.9 | 38.9 | 43.6 | 48.0 | 30.4 | 21.5 | 13.3 | 11.3 | 0.0 | 129.4 | 22.0 | 18.74 |
| 113 | 2999910 | 2 | OLENEK | RU | 198000 | 10.2 | 8.6 | 9.7 | 12.0 | 21.0 | 36.6 | 44.9 | 44.1 | 31.2 | 23.6 | 14.5 | 12.1 | 0.9 | 114.7 | 22.4 | 16.82 |
| 114 | 3102500 | 3 | ATRATO | CO | 9432 | 405.2 | 329.2 | 357.8 | 495.4 | 555.8 | 511.6 | 516.5 | 554.1 | 502.5 | 507.8 | 512.8 | 480.6 | 48.5 | 1065.2 | 477.4 | 118.18 |
| 115 | 3103300 | 3 | MAGDALENA | CO | 257438 | 73.1 | 87.6 | 131.8 | 204.6 | 237.8 | 181.0 | 159.6 | 176.0 | 207.2 | 261.7 | 213.5 | 112.9 | 22.0 | 400.0 | 170.6 | 69.09 |
| 118 | 3178800 | 3 | LIMARI | CL | 11343 | 0.6 | 1.6 | 1.9 | 5.1 | 30.5 | 43.0 | 47.6 | 30.1 | 7.8 | 3.7 | 1.8 | 1.3 | 0.0 | 275.6 | 14.6 | 27.87 |
| 119 | 3178900 | 3 | HUASCO | CL | 7187 | 0.9 | 1.7 | 1.5 | 3.8 | 14.4 | 22.1 | 20.5 | 12.3 | 2.7 | 2.0 | 1.0 | 0.7 | 0.0 | 202.2 | 7.0 | 17.27 |
| 120 | 3179250 | 3 | RAPEL | CL | 13186 | 5.0 | 3.8 | 11.1 | 35.9 | 121.5 | 170.2 | 163.8 | 113.4 | 55.2 | 33.9 | 20.3 | 9.9 | 0.0 | 473.6 | 62.0 | 77.45 |
| 121 | 3179500 | 3 | BIOBIO | CL | 24029 | 23.5 | 22.2 | 44.3 | 91.9 | 210.0 | 234.6 | 207.6 | 163.8 | 96.9 | 69.0 | 49.6 | 44.1 | 0.1 | 611.1 | 104.8 | 98.00 |
| 122 | 3181500 | 3 | BAKER | CL | 23736 | 38.1 | 34.0 | 48.7 | 57.2 | 75.9 | 71.3 | 69.5 | 68.8 | 44.2 | 44.1 | 36.2 | 37.8 | 0.0 | 333.4 | 52.1 | 41.99 |
| 123 | 3206720 | 3 | ORINOCO | VE | 836000 | 39.1 | 51.9 | 83.6 | 185.2 | 293.6 | 340.5 | 342.0 | 294.4 | 229.5 | 197.7 | 140.8 | 76.6 | 9.8 | 501.6 | 189.6 | 112.18 |
| 124 | 3258200 | 3 | SALADO | AR | 29000 | 101.6 | 88.7 | 104.5 | 63.6 | 34.6 | 20.1 | 20.8 | 22.1 | 40.8 | 76.9 | 91.0 | 102.5 | 0.1 | 256.3 | 63.9 | 47.61 |
| 125 | 3265601 | 3 | PARANA | AR | 2346000 | 178.4 | 153.9 | 142.4 | 88.9 | 63.1 | 38.9 | 28.0 | 29.5 | 60.3 | 104.6 | 131.7 | 168.3 | 3.1 | 264.1 | 99.0 | 57.62 |
| 126 | 3275750 | 3 | COLORADO (ARGENTIN | AR | 223000 | 33.9 | 30.1 | 30.4 | 19.6 | 24.3 | 25.1 | 22.9 | 19.9 | 19.6 | 22.7 | 23.5 | 28.5 | 1.4 | 101.7 | 25.0 | 15.31 |
| 127 | 3275990 | 3 | NEGRO (ARGENTINIA) | AR | 95000 | 19.1 | 19.2 | 30.1 | 42.8 | 82.9 | 95.3 | 85.2 | 63.3 | 40.7 | 33.3 | 25.5 | 25.2 | 0.7 | 299.0 | 46.9 | 39.77 |
| 128 | 3276200 | 3 | CHUBUT | AR | 16400 | 18.5 | 21.8 | 27.9 | 43.6 | 74.2 | 85.0 | 67.8 | 58.9 | 36.8 | 27.6 | 23.7 | 21.4 | 0.4 | 224.1 | 42.3 | 34.18 |
| 129 | 3276800 | 3 | SANTA CRUZ | AR | 15550 | 28.4 | 20.6 | 34.5 | 41.6 | 44.2 | 33.4 | 36.4 | 32.1 | 26.4 | 20.6 | 21.4 | 25.5 | 0.0 | 176.4 | 30.4 | 26.02 |
| 130 | 3308400 | 3 | CUYUNI | GY | 53400 | 128.9 | 82.7 | 90.1 | 116.5 | 201.9 | 246.2 | 233.3 | 196.6 | 130.8 | 107.6 | 121.6 | 160.0 | 6.4 | 471.4 | 151.3 | 79.96 |
| 131 | 3308600 | 3 | ESSEQUIBO | GY | 66600 | 102.2 | 82.5 | 109.4 | 177.3 | 328.6 | 365.9 | 307.5 | 199.3 | 94.6 | 64.6 | 75.0 | 111.6 | 2.2 | 624.3 | 168.2 | 124.29 |
| 132 | 3410500 | 3 | CORANTIJN | SR | 51600 | 143.5 | 132.8 | 170.5 | 228.4 | 359.2 | 318.8 | 260.5 | 155.0 | 65.0 | 48.3 | 64.1 | 116.7 | 0.0 | 567.5 | 171.9 | 118.72 |
| 133 | 3411300 | 3 | COPPENAME | SR | 12300 | 210.7 | 170.5 | 207.4 | 261.6 | 374.6 | 341.8 | 273.7 | 158.0 | 71.8 | 53.4 | 82.1 | 167.8 | 0.1 | 631.5 | 197.8 | 121.59 |
| 134 | 3412800 | 3 | MARONI | SR | 63700 | 223.8 | 204.7 | 266.8 | 314.8 | 379.1 | 268.9 | 203.0 | 122.6 | 52.9 | 46.1 | 81.8 | 180.7 | 0.3 | 1246.6 | 195.4 | 132.88 |
| 135 | 3469050 | 3 | URUGUAY | UY | 244000 | 143.2 | 133.3 | 128.6 | 150.1 | 132.6 | 119.6 | 110.8 | 100.6 | 141.1 | 157.8 | 129.0 | 127.0 | 19.0 | 439.2 | 131.2 | 58.78 |
| 136 | 3469100 | 3 | NEGRO (URUGUAY) | UY | 63000 | 98.5 | 100.1 | 118.0 | 103.4 | 105.8 | 94.2 | 99.9 | 91.4 | 106.9 | 99.3 | 92.8 | 91.0 | 1.6 | 623.3 | 100.1 | 59.64 |
| 137 | 3514800 | 3 | OYAPOCK | GF | 25120 | 295.7 | 275.4 | 309.3 | 375.9 | 414.8 | 273.0 | 177.5 | 103.1 | 51.6 | 45.2 | 90.8 | 222.6 | 0.0 | 1870.9 | 219.6 | 166.35 |
| 138 | 3629000 | 3 | AMAZONAS | BR | 4640300 | 240.9 | 230.4 | 253.3 | 223.5 | 193.7 | 145.8 | 120.6 | 106.5 | 125.1 | 165.9 | 186.6 | 222.0 | 69.5 | 333.9 | 184.5 | 53.88 |
| 139 | 3629150 | 3 | RIO TAPAJOS | BR | 358657 | 347.4 | 324.9 | 313.1 | 182.6 | 58.8 | 16.2 | 9.5 | 24.7 | 84.8 | 174.3 | 227.5 | 310.5 | 0.0 | 540.7 | 172.9 | 133.97 |
| 140 | 3629204 | 3 | RIO JAMANXIM | BR | 40400 | 347.0 | 342.2 | 357.3 | 259.1 | 92.2 | 21.2 | 14.4 | 27.8 | 105.4 | 195.4 | 240.0 | 313.0 | 0.0 | 629.1 | 192.9 | 146.18 |
| 141 | 3630050 | 3 | XINGU | BR | 446570 | 312.6 | 301.7 | 294.3 | 192.9 | 73.3 | 22.4 | 12.7 | 24.5 | 78.3 | 166.6 | 200.0 | 268.1 | 0.0 | 483.5 | 162.3 | 119.37 |
| 142 | 3630300 | 3 | RIO MAICURU | BR | 17072 | 182.6 | 218.0 | 294.5 | 296.9 | 270.2 | 176.4 | 132.9 | 85.7 | 78.5 | 61.4 | 66.0 | 100.4 | 0.0 | 1051.9 | 163.6 | 113.08 |
| 143 | 3631050 | 3 | RIO ARAGUARI | BR | 23373 | 307.1 | 333.5 | 355.5 | 392.4 | 379.8 | 242.5 | 160.4 | 77.2 | 33.3 | 30.1 | 56.1 | 172.0 | 0.0 | 1972.8 | 211.7 | 169.92 |
| 144 | 3631100 | 3 | RIO JARI | BR | 51343 | 243.4 | 245.0 | 276.6 | 325.6 | 362.4 | 224.5 | 177.2 | 102.1 | 51.2 | 37.8 | 51.7 | 127.6 | 0.0 | 1758.9 | 185.4 | 140.04 |
| 145 | 3631210 | 3 | RIO PARU DE ESTE | BR | 30945 | 203.1 | 199.0 | 259.2 | 309.7 | 355.7 | 219.5 | 176.1 | 100.8 | 57.3 | 38.9 | 46.0 | 103.8 | 0.0 | 1444.9 | 172.4 | 129.07 |
| 146 | 3649950 | 3 | TOCANTINS | BR | 742300 | 277.6 | 248.8 | 257.7 | 140.6 | 44.2 | 9.6 | 6.8 | 12.3 | 47.3 | 133.9 | 201.6 | 269.1 | 0.0 | 528.5 | 137.5 | 116.47 |
| 147 | 3650150 | 3 | RIO CAPIM | BR | 38178 | 267.6 | 306.1 | 424.7 | 322.1 | 165.5 | 51.2 | 29.4 | 22.5 | 26.9 | 49.6 | 81.0 | 162.7 | 0.0 | 907.2 | 159.1 | 149.44 |
| 148 | 3650202 | 3 | RIO GURUPI | BR | 31850 | 234.7 | 254.5 | 375.0 | 309.1 | 182.8 | 69.3 | 40.8 | 33.2 | 28.0 | 41.3 | 62.4 | 125.4 | 0.5 | 682.5 | 146.4 | 130.83 |
| 149 | 3650285 | 3 | RIO PINDARE | BR | 34300 | 218.9 | 244.5 | 332.6 | 248.1 | 121.9 | 31.4 | 15.8 | 10.9 | 19.3 | 40.0 | 80.5 | 123.6 | 0.0 | 709.3 | 124.0 | 121.43 |
| 150 | 3650335 | 3 | RIO MEARIM | BR | 25500 | 185.2 | 200.8 | 248.2 | 182.1 | 76.8 | 17.4 | 10.1 | 7.8 | 20.3 | 49.8 | 91.4 | 122.9 | 0.0 | 566.7 | 101.1 | 98.89 |
| 151 | 3650359 | 3 | RIO ITAPECURU | BR | 50800 | 190.0 | 211.0 | 266.6 | 223.4 | 89.9 | 21.6 | 11.4 | 8.2 | 19.3 | 50.1 | 84.8 | 129.0 | 0.0 | 538.8 | 108.8 | 104.80 |
| 152 | 3650481 | 3 | RIO PARNAIBA | BR | 322823 | 154.3 | 162.2 | 186.5 | 127.6 | 40.5 | 8.7 | 5.1 | 3.6 | 12.5 | 51.8 | 99.1 | 128.7 | 0.0 | 435.8 | 81.7 | 78.86 |
| 153 | 3650525 | 3 | RIO ACARAU | BR | 11160 | 74.3 | 129.8 | 208.1 | 190.2 | 93.5 | 26.8 | 11.6 | 4.1 | 1.7 | 2.6 | 6.2 | 24.7 | 0.0 | 504.5 | 64.5 | 89.02 |
| 154 | 3650649 | 3 | RIO JAGUARIBE | BR | 48200 | 94.3 | 133.5 | 192.7 | 150.7 | 69.3 | 27.5 | 13.6 | 5.4 | 5.5 | 10.3 | 18.5 | 43.9 | 0.1 | 450.4 | 63.8 | 77.52 |
| 155 | 3650885 | 3 | RIO PARAIBA | BR | 19244 | 36.5 | 60.9 | 100.2 | 96.9 | 70.3 | 67.3 | 53.9 | 28.5 | 13.8 | 8.2 | 10.4 | 21.2 | 0.0 | 362.8 | 47.3 | 51.21 |
| 156 | 3651900 | 3 | SAO FRANCISCO | BR | 622600 | 155.5 | 129.3 | 134.4 | 65.1 | 21.3 | 10.9 | 8.7 | 7.1 | 20.8 | 68.3 | 141.2 | 184.8 | 0.0 | 430.0 | 78.9 | 76.93 |
| 157 | 3652039 | 3 | RIO ITAPICURU | BR | 35150 | 55.2 | 59.0 | 72.6 | 64.3 | 58.6 | 51.8 | 47.6 | 32.4 | 21.0 | 25.6 | 54.5 | 66.1 | 0.0 | 331.8 | 50.7 | 44.64 |
| 158 | 3652050 | 3 | RIO VAZA-BARRIS | BR | 15740 | 46.4 | 53.4 | 69.1 | 65.1 | 69.5 | 61.0 | 58.8 | 37.2 | 21.4 | 21.3 | 35.8 | 49.1 | 0.0 | 314.5 | 49.0 | 41.96 |
| 159 | 3652135 | 3 | RIO PARAGUACU | BR | 53866 | 77.2 | 76.6 | 87.6 | 68.4 | 44.7 | 41.9 | 39.0 | 26.7 | 22.6 | 39.3 | 88.1 | 98.7 | 0.0 | 435.8 | 59.2 | 55.48 |
| 160 | 3652220 | 3 | RIO DE CONTAS | BR | 42245 | 102.1 | 81.0 | 87.3 | 51.3 | 17.8 | 12.0 | 9.8 | 9.8 | 15.6 | 55.6 | 124.4 | 129.6 | 0.0 | 445.2 | 58.0 | 66.71 |
| 161 | 3652320 | 3 | RIO PRADO | BR | 30360 | 112.6 | 86.5 | 100.2 | 59.5 | 30.9 | 26.1 | 27.4 | 21.7 | 28.5 | 69.2 | 141.3 | 144.4 | 0.5 | 461.8 | 70.7 | 68.93 |
| 162 | 3652455 | 3 | JEQUITINHONHA | BR | 67769 | 153.8 | 104.1 | 112.5 | 49.8 | 22.5 | 13.1 | 14.7 | 11.8 | 26.4 | 83.8 | 165.6 | 189.3 | 0.0 | 519.1 | 79.0 | 83.82 |
| 163 | 3652500 | 3 | MUCURI | BR | 14174 | 151.6 | 104.8 | 122.5 | 68.3 | 36.3 | 25.9 | 34.2 | 24.0 | 36.0 | 91.4 | 167.8 | 169.5 | 0.0 | 542.7 | 86.0 | 80.73 |
| 164 | 3652600 | 3 | RIO DOCE | BR | 78456 | 220.3 | 129.5 | 142.6 | 63.6 | 26.9 | 18.3 | 16.6 | 17.3 | 37.8 | 107.4 | 204.3 | 249.6 | 0.0 | 565.9 | 102.9 | 101.32 |
| 165 | 3652890 | 3 | PARAIBA DO SUL | BR | 55083 | 248.4 | 174.6 | 166.0 | 76.6 | 42.1 | 30.9 | 24.3 | 27.7 | 64.2 | 118.1 | 179.2 | 241.7 | 0.1 | 449.3 | 116.2 | 93.15 |
| 166 | 3653120 | 3 | RIO RIBEIRA DO IGU | BR | 12450 | 208.6 | 169.6 | 134.8 | 80.8 | 99.4 | 86.6 | 75.4 | 68.9 | 106.9 | 130.2 | 113.7 | 155.8 | 0.2 | 429.6 | 119.2 | 67.57 |
| 167 | 3653400 | 3 | RIO JACUI | BR | 71454 | 144.5 | 129.0 | 116.7 | 132.4 | 122.0 | 137.7 | 141.0 | 133.6 | 160.3 | 151.8 | 125.5 | 127.6 | 4.0 | 381.8 | 135.2 | 60.48 |
| 168 | 3843100 | 3 | MIRA | EC | 4960 | 117.3 | 116.2 | 128.5 | 148.5 | 111.7 | 69.2 | 41.9 | 42.2 | 71.7 | 117.7 | 131.3 | 116.9 | 13.3 | 330.4 | 101.1 | 50.87 |
| 169 | 3844100 | 3 | ESMERALDAS | EC | 18800 | 244.9 | 274.0 | 293.9 | 289.1 | 183.1 | 95.9 | 45.8 | 46.8 | 83.2 | 91.9 | 88.6 | 137.4 | 8.0 | 555.1 | 156.2 | 105.90 |
| 170 | 3844400 | 3 | DAULE | EC | 8690 | 275.5 | 318.2 | 333.5 | 267.3 | 128.4 | 56.6 | 22.3 | 16.3 | 29.5 | 31.9 | 32.3 | 90.2 | 0.2 | 677.7 | 133.5 | 140.59 |
| 171 | 3844450 | 3 | VINCES | EC | 4400 | 360.3 | 384.3 | 400.9 | 363.2 | 183.7 | 78.7 | 25.8 | 24.0 | 45.7 | 53.5 | 55.0 | 143.3 | 1.3 | 777.4 | 176.5 | 166.87 |
| 174 | 3948800 | 3 | CANETE | PE | 4900 | 93.5 | 90.0 | 105.7 | 36.3 | 11.0 | 4.3 | 4.1 | 5.2 | 15.8 | 26.7 | 31.3 | 62.5 | 0.0 | 229.4 | 40.5 | 40.69 |
| 176 | 4101500 | 4 | COLVILLE RIVER | US | 53535 | 10.3 | 8.7 | 7.5 | 6.6 | 6.2 | 20.1 | 28.1 | 34.7 | 19.0 | 18.1 | 11.0 | 9.9 | 0.0 | 112.9 | 15.0 | 15.59 |
| 177 | 4101800 | 4 | NOATAK RIVER | US | 31080 | 16.0 | 15.0 | 15.9 | 11.5 | 9.5 | 19.8 | 48.4 | 60.9 | 47.8 | 37.3 | 19.6 | 20.0 | 0.2 | 158.6 | 26.8 | 22.28 |
| 178 | 4101900 | 4 | KOBUK RIVER | US | 24657 | 18.1 | 15.9 | 19.0 | 11.3 | 11.0 | 25.5 | 50.9 | 61.9 | 43.3 | 28.4 | 18.9 | 18.4 | 0.2 | 184.7 | 26.9 | 23.10 |
| 179 | 4102100 | 4 | KUSKOKWIM RIVER | US | 80549 | 24.8 | 21.6 | 22.2 | 22.2 | 24.6 | 50.1 | 78.6 | 89.9 | 59.4 | 39.1 | 28.8 | 29.1 | 0.5 | 195.3 | 40.9 | 30.65 |
| 180 | 4102710 | 4 | COPPER RIVER | US | 62678 | 46.5 | 46.7 | 35.0 | 31.7 | 41.9 | 55.9 | 74.7 | 81.4 | 97.5 | 88.3 | 65.9 | 63.6 | 2.5 | 553.6 | 60.7 | 43.12 |
| 181 | 4102740 | 4 | NUSHAGAK RIVER | US | 25512 | 31.6 | 28.4 | 30.6 | 28.1 | 31.2 | 47.5 | 75.3 | 106.6 | 83.1 | 61.7 | 42.3 | 39.7 | 0.0 | 318.6 | 50.5 | 36.89 |
| 182 | 4102800 | 4 | SUSITNA RIVER | US | 50246 | 43.9 | 38.6 | 33.3 | 25.4 | 27.4 | 47.2 | 73.8 | 96.3 | 93.4 | 64.1 | 43.7 | 53.9 | 2.8 | 222.9 | 53.4 | 35.55 |
| 183 | 4103200 | 4 | YUKON RIVER | US | 831390 | 19.7 | 16.1 | 15.0 | 11.6 | 19.3 | 37.9 | 52.7 | 54.1 | 38.9 | 27.6 | 21.3 | 20.0 | 2.9 | 98.8 | 27.9 | 16.67 |
| 184 | 4115201 | 4 | COLUMBIA RIVER | US | 665371 | 70.3 | 52.5 | 49.4 | 39.7 | 45.3 | 43.6 | 22.2 | 23.3 | 31.4 | 44.2 | 67.6 | 73.2 | 3.7 | 165.5 | 46.9 | 24.62 |
| 185 | 4126700 | 4 | OUACHITA RIVER | US | 39622 | 114.4 | 107.1 | 129.3 | 130.6 | 131.7 | 101.3 | 105.3 | 83.3 | 89.8 | 91.4 | 112.7 | 126.7 | 3.1 | 416.2 | 110.3 | 59.04 |
| 186 | 4126800 | 4 | RED RIVER | US | 174825 | 50.9 | 54.4 | 69.0 | 84.6 | 112.9 | 94.2 | 72.6 | 69.0 | 78.7 | 77.6 | 62.7 | 60.5 | 3.9 | 219.4 | 73.9 | 39.91 |
| 187 | 4127800 | 4 | MISSISSIPPI RIVER | US | 2964255 | 38.8 | 36.2 | 53.8 | 67.5 | 88.3 | 92.6 | 78.4 | 71.3 | 64.9 | 51.0 | 43.9 | 40.1 | 10.6 | 148.7 | 60.6 | 24.95 |
| 188 | 4145081 | 4 | SKAGIT RIVER | US | 7089 | 241.5 | 171.4 | 154.5 | 96.7 | 72.5 | 57.7 | 33.4 | 39.2 | 79.2 | 160.5 | 245.7 | 257.6 | 1.0 | 609.5 | 134.2 | 102.81 |
| 189 | 4145900 | 4 | ROGUE RIVER | US | 10202 | 157.4 | 121.5 | 105.5 | 65.7 | 49.5 | 28.6 | 9.4 | 12.6 | 28.7 | 73.7 | 146.8 | 166.2 | 0.1 | 517.3 | 80.5 | 73.94 |
| 190 | 4146110 | 4 | KLAMATH RIVER | US | 31339 | 129.3 | 104.9 | 87.8 | 52.2 | 37.6 | 23.4 | 8.1 | 10.5 | 19.4 | 53.2 | 110.1 | 133.5 | 0.0 | 425.3 | 64.2 | 64.29 |
| 191 | 4146180 | 4 | EEL RIVER (CALIF.) | US | 8063 | 272.6 | 225.2 | 175.0 | 91.2 | 46.1 | 15.9 | 2.4 | 6.3 | 18.7 | 81.0 | 184.6 | 262.0 | 0.0 | 841.9 | 115.1 | 135.02 |
| 192 | 4146280 | 4 | SACRAMENTO RIVER | US | 60886 | 158.8 | 137.7 | 114.0 | 64.2 | 38.1 | 18.6 | 4.1 | 6.1 | 16.1 | 49.4 | 104.8 | 145.4 | 0.0 | 564.3 | 71.4 | 81.19 |
| 193 | 4146360 | 4 | SAN JOAQUIN RIVER | US | 35058 | 100.8 | 89.8 | 80.5 | 42.4 | 19.8 | 6.1 | 2.1 | 2.2 | 8.4 | 25.2 | 54.5 | 84.1 | 0.0 | 354.1 | 43.0 | 53.95 |
| 194 | 4146400 | 4 | SALINAS RIVER | US | 10764 | 82.1 | 76.2 | 60.3 | 29.3 | 9.3 | 1.6 | 0.6 | 1.1 | 5.1 | 15.1 | 39.6 | 66.9 | 0.0 | 304.7 | 32.3 | 46.22 |
| 195 | 4147011 | 4 | PENOBSCOT RIVER | US | 19464 | 78.6 | 66.0 | 79.3 | 82.7 | 86.1 | 97.5 | 99.3 | 89.9 | 96.4 | 99.7 | 98.5 | 87.9 | 12.6 | 267.7 | 88.5 | 36.70 |
| 196 | 4147060 | 4 | ST. CROIX RIVER | US | 3559 | 89.6 | 74.2 | 89.0 | 85.3 | 86.5 | 89.3 | 87.6 | 81.5 | 94.3 | 101.1 | 106.8 | 101.6 | 9.3 | 279.7 | 90.6 | 39.23 |
| 197 | 4147380 | 4 | MERRIMACK RIVER | US | 12005 | 82.8 | 75.9 | 91.8 | 92.1 | 91.0 | 95.8 | 97.5 | 91.1 | 93.0 | 90.6 | 99.2 | 94.4 | 6.3 | 355.5 | 91.3 | 40.96 |
| 198 | 4147460 | 4 | CONNECTICUT RIVER | US | 25019 | 76.3 | 68.1 | 82.8 | 85.9 | 92.6 | 99.5 | 102.7 | 98.2 | 96.4 | 91.6 | 93.4 | 84.5 | 10.5 | 296.2 | 89.3 | 35.85 |
| 199 | 4147500 | 4 | HUDSON RIVER | US | 20953 | 78.8 | 70.2 | 84.8 | 86.0 | 92.1 | 98.0 | 101.1 | 95.0 | 95.8 | 90.1 | 91.3 | 86.6 | 8.6 | 224.7 | 89.2 | 35.14 |
| 200 | 4147600 | 4 | DELAWARE RIVER | US | 17560 | 82.1 | 72.9 | 89.7 | 96.9 | 101.6 | 106.9 | 113.3 | 109.4 | 103.4 | 93.9 | 91.9 | 90.5 | 8.2 | 361.8 | 96.0 | 42.11 |
| 201 | 4147703 | 4 | SUSQUEHANNA RIVER | US | 70189 | 70.4 | 61.0 | 82.4 | 87.3 | 96.4 | 102.2 | 102.5 | 96.7 | 91.7 | 82.2 | 77.7 | 74.3 | 6.3 | 304.1 | 85.4 | 35.44 |
| 202 | 4147900 | 4 | POTOMAC RIVER | US | 29940 | 71.2 | 60.7 | 84.0 | 83.8 | 96.1 | 102.3 | 98.7 | 97.3 | 86.5 | 76.7 | 68.8 | 71.5 | 4.0 | 260.3 | 83.1 | 38.87 |
| 203 | 4148050 | 4 | JAMES RIVER | US | 17503 | 80.8 | 71.2 | 91.8 | 84.4 | 97.5 | 98.8 | 108.3 | 104.2 | 91.1 | 83.3 | 75.8 | 79.8 | 3.5 | 287.8 | 88.9 | 42.61 |
| 204 | 4148090 | 4 | ROANOKE RIVER | US | 21715 | 85.8 | 79.0 | 98.0 | 87.9 | 97.2 | 101.8 | 114.9 | 110.5 | 96.5 | 82.9 | 73.5 | 84.6 | 1.1 | 296.1 | 92.7 | 45.14 |
| 205 | 4148232 | 4 | CAPE FEAR RIVER | US | 13611 | 89.5 | 90.2 | 99.4 | 85.6 | 94.6 | 113.7 | 142.5 | 130.9 | 106.0 | 77.5 | 71.9 | 85.5 | 1.5 | 414.8 | 98.9 | 49.17 |
| 206 | 4148300 | 4 | PEE DEE RIVER | US | 22870 | 91.7 | 92.2 | 105.9 | 88.8 | 94.5 | 111.5 | 131.1 | 124.3 | 99.6 | 81.5 | 72.7 | 89.7 | 0.2 | 334.5 | 98.6 | 47.06 |
| 207 | 4148550 | 4 | SANTEE RIVER | US | 38073 | 101.1 | 102.4 | 116.7 | 90.8 | 93.9 | 110.4 | 125.9 | 125.3 | 98.9 | 83.1 | 75.5 | 100.8 | 0.3 | 361.6 | 102.1 | 49.80 |
| 208 | 4148650 | 4 | SAVANNAH RIVER | US | 25512 | 112.5 | 116.0 | 127.7 | 95.9 | 95.0 | 112.2 | 128.5 | 118.0 | 97.0 | 78.9 | 78.2 | 109.4 | 2.3 | 329.0 | 105.8 | 51.50 |
| 209 | 4148720 | 4 | ALTAMAHA RIVER | US | 35224 | 106.6 | 111.5 | 126.8 | 90.7 | 89.2 | 107.9 | 130.5 | 117.8 | 92.2 | 68.2 | 72.0 | 101.4 | 1.4 | 348.9 | 101.2 | 50.97 |
| 210 | 4148851 | 4 | ST. JOHNS RIVER | US | 22922 | 66.1 | 74.3 | 88.7 | 65.1 | 98.4 | 175.6 | 180.9 | 173.6 | 169.3 | 97.3 | 50.5 | 63.5 | 2.9 | 415.9 | 108.6 | 70.66 |
| 211 | 4149120 | 4 | PEARL RIVER | US | 17024 | 135.0 | 132.6 | 148.0 | 133.5 | 118.3 | 103.6 | 132.5 | 106.5 | 87.5 | 76.9 | 104.4 | 141.4 | 0.5 | 373.6 | 118.3 | 61.59 |
| 212 | 4149400 | 4 | ALABAMA RIVER | US | 56895 | 128.3 | 131.6 | 153.9 | 119.0 | 104.4 | 104.0 | 131.5 | 104.7 | 91.2 | 72.2 | 95.5 | 129.2 | 1.0 | 428.2 | 113.8 | 56.31 |
| 213 | 4149413 | 4 | TOMBIGBEE RIVER | US | 47700 | 135.1 | 131.9 | 149.3 | 124.0 | 114.4 | 102.5 | 124.6 | 98.4 | 88.1 | 76.8 | 105.8 | 134.1 | 0.9 | 416.5 | 115.4 | 57.70 |
| 214 | 4149632 | 4 | APALACHICOLA RIVER | US | 49728 | 116.2 | 123.1 | 141.4 | 106.2 | 95.5 | 112.8 | 146.3 | 120.5 | 97.9 | 67.1 | 82.8 | 114.6 | 1.4 | 424.8 | 110.4 | 53.88 |
| 215 | 4149781 | 4 | SUWANNEE RIVER | US | 24320 | 96.2 | 97.5 | 113.9 | 81.6 | 84.5 | 151.5 | 170.7 | 161.2 | 119.7 | 68.3 | 56.6 | 85.1 | 2.4 | 425.7 | 107.2 | 61.43 |
| 216 | 4150283 | 4 | NUECES RIVER | US | 43823 | 28.7 | 32.6 | 36.3 | 52.8 | 79.2 | 70.3 | 56.0 | 53.9 | 79.2 | 62.7 | 38.3 | 31.5 | 0.1 | 292.5 | 51.8 | 43.22 |
| 217 | 4150330 | 4 | SAN ANTONIO RIVER | US | 10155 | 43.0 | 47.6 | 50.2 | 70.4 | 90.8 | 84.2 | 68.3 | 58.1 | 88.1 | 80.2 | 56.0 | 48.3 | 0.6 | 351.5 | 65.4 | 51.21 |
| 218 | 4150450 | 4 | COLORADO RIVER (CA | US | 108788 | 25.1 | 30.0 | 31.7 | 49.1 | 74.8 | 63.3 | 52.4 | 53.7 | 69.2 | 58.9 | 34.3 | 27.6 | 0.4 | 256.0 | 47.5 | 35.52 |
| 219 | 4150500 | 4 | BRAZOS RIVER | US | 116827 | 36.0 | 41.0 | 46.1 | 63.7 | 91.6 | 76.2 | 56.4 | 58.0 | 71.4 | 68.5 | 47.9 | 42.2 | 0.9 | 220.1 | 58.3 | 37.49 |
| 220 | 4150600 | 4 | TRINITY RIVER (TEX | US | 44512 | 63.5 | 69.0 | 76.8 | 96.4 | 119.2 | 89.7 | 63.7 | 57.9 | 79.4 | 89.6 | 77.7 | 75.7 | 3.2 | 319.2 | 79.9 | 48.67 |
| 221 | 4150700 | 4 | SABINE RIVER | US | 24162 | 102.5 | 99.9 | 106.1 | 112.1 | 124.9 | 101.8 | 92.1 | 76.8 | 85.4 | 95.5 | 105.9 | 118.9 | 5.1 | 377.8 | 101.8 | 55.10 |
| 222 | 4152050 | 4 | COLORADO RIVER (PA | US | 618715 | 25.0 | 25.2 | 25.8 | 19.3 | 16.6 | 13.0 | 35.6 | 41.4 | 29.3 | 25.7 | 20.2 | 25.0 | 0.9 | 106.5 | 25.2 | 15.52 |
| 223 | 4202100 | 4 | ALSEK RIVER | CA | 16200 | 40.6 | 27.5 | 24.9 | 21.0 | 25.4 | 36.7 | 51.2 | 50.8 | 45.3 | 55.1 | 49.2 | 42.0 | 0.0 | 268.5 | 39.1 | 31.82 |
| 224 | 4202601 | 4 | TAKU RIVER | CA | 17700 | 90.0 | 64.1 | 58.9 | 47.6 | 49.8 | 51.0 | 72.1 | 94.5 | 129.0 | 146.1 | 105.6 | 96.1 | 3.1 | 392.0 | 83.7 | 54.50 |
| 225 | 4204900 | 4 | STIKINE RIVER | US | 51593 | 65.2 | 41.0 | 37.7 | 29.8 | 30.5 | 40.9 | 62.0 | 69.4 | 79.9 | 84.8 | 70.5 | 68.5 | 0.2 | 437.8 | 56.7 | 46.36 |
| 226 | 4206100 | 4 | NASS RIVER | CA | 19200 | 158.4 | 106.6 | 90.7 | 73.1 | 50.4 | 55.4 | 68.9 | 96.6 | 144.0 | 216.1 | 161.5 | 167.5 | 3.0 | 681.1 | 115.8 | 79.49 |
| 227 | 4206250 | 4 | SKEENA RIVER | CA | 42200 | 78.6 | 49.4 | 42.5 | 36.1 | 40.6 | 51.8 | 56.3 | 57.5 | 77.3 | 99.1 | 83.0 | 84.5 | 0.8 | 409.9 | 63.1 | 37.34 |
| 228 | 4207900 | 4 | FRASER RIVER | CA | 217000 | 60.6 | 39.8 | 37.2 | 29.5 | 39.7 | 55.2 | 51.5 | 47.8 | 49.0 | 55.7 | 62.9 | 64.0 | 6.5 | 130.1 | 49.4 | 20.05 |
| 229 | 4208025 | 4 | MACKENZIE RIVER | CA | 1660000 | 21.8 | 17.7 | 17.8 | 16.1 | 29.7 | 47.5 | 58.9 | 52.6 | -415.7 | -426.5 | -428.3 | -432.1 | 6.4 | 89.8 | 31.7 | 16.35 |
| 230 | 4208040 | 4 | PEEL RIVER (TRIB. | CA | 70600 | 22.2 | 20.5 | 17.9 | 15.2 | 22.2 | 45.1 | 59.8 | 54.1 | 41.8 | 35.7 | 26.3 | 26.0 | 3.4 | 107.6 | 32.2 | 18.48 |
| 231 | 4209150 | 4 | ANDERSON RIVER | CA | 56300 | 13.0 | 11.8 | 13.3 | 12.0 | 14.2 | 20.3 | 31.8 | 40.1 | 26.6 | 24.5 | 18.0 | 14.1 | 0.0 | 138.1 | 20.0 | 14.62 |
| 232 | 4209402 | 4 | COPPERMINE RIVER | CA | 50700 | 9.7 | 8.3 | 12.4 | 13.0 | 16.6 | 23.8 | 37.6 | 50.1 | 36.1 | 26.3 | 16.0 | 12.3 | 0.0 | 182.3 | 21.8 | 17.97 |
| 233 | 4209600 | 4 | ELLICE RIVER | CA | 16900 | 5.6 | 6.7 | 7.1 | 8.3 | 11.7 | 19.9 | 27.3 | 35.8 | 25.4 | 21.0 | 11.6 | 7.8 | 0.0 | 154.8 | 15.7 | 15.25 |
| 234 | 4209800 | 4 | BACK RIVER | CA | 98200 | 7.9 | 8.4 | 9.6 | 12.1 | 14.8 | 24.9 | 33.6 | 43.6 | 34.4 | 26.3 | 16.2 | 10.9 | 0.0 | 141.9 | 20.2 | 16.80 |
| 235 | 4209850 | 4 | HAYES RIVER (TRIB. | CA | 18100 | 7.4 | 8.3 | 10.1 | 14.6 | 14.7 | 19.0 | 30.1 | 40.3 | 30.4 | 24.4 | 15.5 | 10.8 | 0.0 | 118.2 | 18.8 | 16.72 |
| 236 | 4213711 | 4 | NELSON RIVER | CA | 1060000 | 20.7 | 16.8 | 23.2 | 28.9 | 51.0 | 78.4 | 71.6 | 62.4 | -303.6 | -323.3 | -330.4 | -333.4 | 4.0 | 147.2 | 40.2 | 24.76 |
| 237 | 4214025 | 4 | HAYES RIVER (TRIB. | CA | 103000 | 19.8 | 16.7 | 22.5 | 24.2 | 37.8 | 60.2 | 76.2 | 69.3 | 60.1 | 41.2 | 34.0 | 23.6 | 0.0 | 159.8 | 40.5 | 27.91 |
| 238 | 4214035 | 4 | AUX MELEZES | CA | 42700 | 31.8 | 27.5 | 29.0 | 27.3 | 34.1 | 53.2 | 67.0 | 71.9 | 69.9 | 55.8 | 48.6 | 38.9 | 0.0 | 233.1 | 46.2 | 27.37 |
| 239 | 4214040 | 4 | CANIAPISCAU | CA | 86800 | 43.2 | 34.3 | 40.9 | 41.0 | 45.1 | 70.0 | 95.9 | 90.1 | 83.1 | 71.9 | 59.9 | 45.9 | 0.0 | 315.8 | 60.1 | 33.32 |
| 240 | 4214051 | 4 | THELON RIVER | CA | 152000 | 10.0 | 8.9 | 11.0 | 14.4 | 16.2 | 28.6 | 40.3 | 44.2 | 39.1 | 27.7 | 17.8 | 12.0 | 0.0 | 164.7 | 22.5 | 18.20 |
| 241 | 4214070 | 4 | THLEWIAZA RIVER | CA | 27000 | 13.2 | 9.7 | 13.9 | 17.3 | 22.5 | 35.0 | 55.4 | 49.9 | 46.5 | 31.3 | 19.7 | 14.0 | 0.1 | 156.3 | 27.4 | 22.37 |
| 242 | 4214075 | 4 | FERGUSON RIVER | CA | 12400 | 8.9 | 8.4 | 11.2 | 15.4 | 13.4 | 24.6 | 36.6 | 48.0 | 41.0 | 26.9 | 18.5 | 11.2 | 0.0 | 114.7 | 22.0 | 19.91 |
| 243 | 4214080 | 4 | ATTAWAPISKAT RIVER | CA | 36000 | 27.6 | 21.6 | 28.1 | 36.9 | 49.1 | 74.4 | 90.6 | 83.6 | 80.5 | 57.4 | 44.2 | 29.8 | 0.0 | 245.3 | 52.0 | 35.36 |
| 244 | 4214090 | 4 | KAZAN RIVER | CA | 72300 | 8.2 | 7.6 | 10.7 | 14.5 | 14.5 | 25.7 | 41.8 | 43.5 | 40.8 | 27.7 | 16.7 | 10.9 | 0.0 | 155.9 | 21.9 | 19.61 |
| 245 | 4214100 | 4 | QUOICH RIVER | CA | 30100 | 8.0 | 8.1 | 10.9 | 15.3 | 13.7 | 21.6 | 38.2 | 41.7 | 38.6 | 26.6 | 19.5 | 11.1 | 0.0 | 145.8 | 21.1 | 19.54 |
| 246 | 4214105 | 4 | SEAL RIVER | CA | 48100 | 20.0 | 13.8 | 18.6 | 19.1 | 30.4 | 48.0 | 69.8 | 60.4 | 55.7 | 36.0 | 28.3 | 19.8 | 0.2 | 226.7 | 35.0 | 26.20 |
| 247 | 4214270 | 4 | CHURCHILL RIVER | CA | 287000 | 20.5 | 16.9 | 20.5 | 23.1 | 39.8 | 64.3 | 80.3 | 67.3 | 53.3 | 31.8 | 28.2 | 22.1 | 2.9 | 149.1 | 39.0 | 25.63 |
| 248 | 4214440 | 4 | SEVERN RIVER (TRIB | CA | 94300 | 23.8 | 19.1 | 24.8 | 28.4 | 45.1 | 70.5 | 88.8 | 81.0 | 72.5 | 50.1 | 41.8 | 27.3 | 1.0 | 183.7 | 47.8 | 31.36 |
| 249 | 4214450 | 4 | WINISK RIVER | CA | 50000 | 29.0 | 24.4 | 29.8 | 36.2 | 53.6 | 77.6 | 95.5 | 86.7 | 80.1 | 55.9 | 46.8 | 32.0 | 3.1 | 195.6 | 54.0 | 32.90 |
| 250 | 4214520 | 4 | ALBANY RIVER | CA | 118000 | 42.2 | 36.7 | 38.8 | 45.2 | 63.4 | 82.5 | 87.4 | 79.8 | 82.9 | 63.4 | 62.1 | 45.7 | 6.3 | 189.3 | 60.8 | 28.34 |
| 251 | 4214551 | 4 | MOOSE RIVER (TRIB. | CA | 60100 | 52.1 | 40.2 | 47.6 | 48.3 | 67.1 | 76.7 | 87.0 | 79.1 | 89.6 | 70.2 | 67.2 | 57.0 | 5.1 | 173.4 | 65.2 | 27.61 |
| 252 | 4214650 | 4 | NOTTAWAY | CA | 57500 | 58.3 | 41.5 | 49.7 | 53.7 | 72.6 | 96.2 | 113.7 | 101.4 | 110.1 | 85.9 | 75.8 | 62.9 | 11.6 | 202.4 | 76.8 | 33.79 |
| 253 | 4214680 | 4 | RUPERT RIVER | CA | 40900 | 55.0 | 49.9 | 50.3 | 43.3 | 63.3 | 81.6 | 99.9 | 100.7 | 98.3 | 74.3 | 74.2 | 59.9 | 1.6 | 234.7 | 70.9 | 33.99 |
| 254 | 4214700 | 4 | EASTMAIN | CA | 44300 | 36.1 | 29.3 | 36.2 | 36.1 | 52.4 | 77.7 | 97.8 | 99.3 | 105.1 | 79.6 | 64.6 | 46.4 | 0.3 | 213.0 | 63.4 | 34.85 |
| 255 | 4214770 | 4 | GRANDE RIVIERE | CA | 96300 | 31.3 | 23.7 | 32.1 | 33.9 | 48.3 | 76.7 | 96.1 | 99.2 | 106.5 | 80.8 | 61.2 | 43.0 | 0.0 | 218.4 | 61.1 | 36.00 |
| 256 | 4214800 | 4 | GRANDE RIVIERE DE | CA | 42200 | 27.9 | 22.4 | 26.1 | 29.3 | 42.1 | 66.9 | 84.3 | 92.2 | 101.5 | 75.2 | 60.2 | 43.4 | 0.0 | 189.3 | 56.0 | 35.02 |
| 257 | 4214900 | 4 | BALEINE, GRANDE RI | CA | 29800 | 34.5 | 27.6 | 27.0 | 24.6 | 29.3 | 50.6 | 76.3 | 68.3 | 70.1 | 50.6 | 41.4 | 33.1 | 0.0 | 285.4 | 44.5 | 30.85 |
| 258 | 4214930 | 4 | ARNAUD | CA | 26900 | 17.6 | 16.2 | 19.0 | 16.5 | 21.3 | 34.5 | 42.7 | 51.3 | 47.9 | 38.8 | 33.5 | 27.9 | 0.0 | 152.1 | 30.6 | 22.36 |
| 259 | 4214940 | 4 | FEUILLES (RIVIERE | CA | 41700 | 23.5 | 21.2 | 23.4 | 21.5 | 27.8 | 42.4 | 53.7 | 63.2 | 62.3 | 50.4 | 44.0 | 33.5 | 0.0 | 140.1 | 38.9 | 24.58 |
| 260 | 4214950 | 4 | GEORGE RIVER | CA | 35200 | 38.7 | 31.4 | 33.4 | 30.6 | 31.7 | 53.1 | 87.0 | 74.3 | 71.0 | 53.6 | 45.0 | 36.1 | 0.0 | 284.9 | 48.8 | 33.07 |
| 261 | 4231630 | 4 | SAINT JOHN RIVER | CA | 39900 | 74.5 | 61.0 | 69.9 | 71.0 | 81.9 | 95.1 | 105.2 | 94.5 | 94.0 | 92.5 | 86.6 | 82.9 | 10.4 | 242.3 | 84.1 | 31.69 |
| 263 | 4243300 | 4 | ST. MAURICE (RIVIE | CA | 42000 | 63.3 | 55.3 | 59.6 | 56.2 | 70.6 | 91.2 | 106.1 | 93.0 | 99.0 | 74.6 | 74.8 | 71.9 | 6.9 | 220.9 | 76.3 | 31.58 |
| 264 | 4243400 | 4 | SAGUENAY (RIVIERE) | CA | 73000 | 53.8 | 42.2 | 47.3 | 52.5 | 70.3 | 97.8 | 117.0 | 99.4 | 100.5 | 81.3 | 76.0 | 60.7 | 3.3 | 199.8 | 74.9 | 34.81 |
| 265 | 4243610 | 4 | MANICOUAGAN (RIVIE | CA | 45800 | 54.0 | 44.6 | 57.0 | 54.6 | 70.1 | 97.7 | 125.0 | 107.0 | 107.1 | 85.3 | 81.9 | 65.1 | 2.5 | 329.2 | 79.1 | 37.35 |
| 266 | 4244500 | 4 | CHURCHILL, FLEUVE | CA | 92500 | 56.3 | 44.9 | 53.6 | 50.0 | 51.7 | 81.6 | 104.1 | 92.9 | 88.0 | 75.7 | 66.9 | 56.1 | 0.0 | 284.1 | 68.5 | 32.55 |
| 267 | 4244635 | 4 | NATASHQUAN (RIVIER | CA | 15600 | 62.4 | 53.6 | 65.2 | 52.7 | 67.1 | 82.5 | 94.0 | 99.5 | 84.5 | 88.0 | 73.0 | 64.4 | 0.1 | 254.6 | 73.9 | 35.23 |
| 268 | 4244660 | 4 | LITTLE MECATINA RI | CA | 19100 | 70.5 | 56.7 | 68.7 | 60.6 | 70.0 | 86.5 | 97.1 | 100.1 | 91.1 | 94.7 | 84.6 | 76.0 | 0.0 | 241.1 | 79.7 | 34.00 |
| 269 | 4351900 | 4 | BRAVO | MX | 450902 | 15.2 | 14.6 | 14.6 | 21.0 | 33.7 | 39.9 | 56.9 | 58.8 | 60.4 | 35.0 | 17.4 | 16.2 | 0.9 | 148.2 | 32.0 | 24.79 |
| 270 | 4353300 | 4 | YAQUI | MX | 57908 | 29.9 | 22.0 | 15.9 | 7.4 | 7.2 | 33.1 | 139.5 | 120.6 | 58.3 | 29.4 | 21.3 | 33.4 | 0.2 | 258.9 | 43.2 | 46.84 |
| 271 | 4355300 | 4 | FUERTE | MX | 34247 | 36.1 | 23.6 | 13.4 | 8.3 | 8.9 | 65.1 | 185.4 | 170.1 | 109.3 | 45.6 | 23.8 | 47.0 | 0.1 | 313.0 | 61.4 | 66.52 |
| 272 | 4356080 | 4 | SAN PEDRO | MX | 25800 | 17.1 | 11.0 | 4.3 | 3.8 | 11.4 | 73.7 | 145.1 | 144.9 | 110.6 | 35.8 | 15.0 | 16.4 | 0.0 | 643.5 | 49.1 | 62.52 |
| 273 | 4356100 | 4 | SANTIAGO | MX | 128943 | 16.9 | 10.2 | 7.3 | 8.0 | 24.8 | 118.6 | 177.4 | 153.0 | 119.2 | 42.8 | 13.4 | 13.8 | 0.2 | 348.4 | 58.8 | 67.46 |
| 274 | 4356280 | 4 | ARMERIA | MX | 9744 | 20.0 | 12.5 | 7.4 | 8.3 | 23.6 | 141.7 | 181.6 | 147.8 | 155.7 | 70.3 | 25.5 | 20.9 | 0.0 | 420.9 | 67.9 | 76.15 |
| 275 | 4356700 | 4 | VERDE | MX | 17617 | 8.3 | 10.5 | 12.4 | 30.8 | 108.7 | 231.9 | 222.0 | 225.9 | 248.9 | 113.9 | 23.8 | 11.6 | 0.0 | 522.1 | 104.1 | 108.63 |
| 276 | 4358300 | 4 | PANUCO | MX | 58115 | 23.5 | 22.7 | 26.0 | 45.3 | 76.3 | 145.4 | 152.3 | 138.3 | 184.0 | 93.7 | 39.0 | 23.2 | 0.4 | 592.5 | 80.8 | 73.16 |
| 277 | 4359220 | 4 | PAPALOAPAN | MX | 21419 | 46.7 | 41.7 | 43.6 | 60.4 | 124.1 | 326.9 | 375.4 | 348.3 | 361.2 | 201.1 | 100.5 | 65.4 | 2.4 | 1003.3 | 174.6 | 153.14 |
| 278 | 4362201 | 4 | GRISALVA | MX | 37702 | 16.7 | 16.1 | 16.4 | 37.5 | 120.8 | 266.5 | 208.5 | 223.4 | 272.1 | 145.6 | 43.2 | 24.4 | 0.0 | 556.6 | 115.9 | 112.02 |
| 279 | 4362600 | 4 | USUMACINTA | MX | 50743 | 104.0 | 72.1 | 66.5 | 77.5 | 170.9 | 362.0 | 346.2 | 325.4 | 380.1 | 294.3 | 169.9 | 127.6 | 6.1 | 621.9 | 208.0 | 134.59 |
| 280 | 4664800 | 4 | LEMPA | SV | 18176 | 11.3 | 8.7 | 13.2 | 42.6 | 148.2 | 272.4 | 218.7 | 236.7 | 279.2 | 170.7 | 37.7 | 16.1 | 0.0 | 568.1 | 121.3 | 117.29 |
| 281 | 4772300 | 4 | GRANDE DE MATAGALP | NI | 14646 | 78.4 | 42.1 | 32.2 | 44.1 | 176.6 | 323.3 | 325.3 | 298.0 | 271.9 | 243.2 | 135.5 | 100.7 | 0.0 | 714.0 | 172.6 | 129.74 |
| 282 | 4773800 | 4 | SAN JUAN | NI | 28600 | 53.2 | 30.4 | 20.3 | 35.7 | 170.9 | 269.5 | 237.4 | 232.7 | 281.6 | 273.3 | 135.1 | 82.5 | 0.2 | 728.7 | 151.9 | 119.67 |
| 283 | 5101201 | 5 | BURDEKIN | AU | 129760 | 137.0 | 128.6 | 83.4 | 37.2 | 25.9 | 25.6 | 17.8 | 14.2 | 13.8 | 27.0 | 52.9 | 87.2 | 0.1 | 597.5 | 54.2 | 66.25 |
| 284 | 5101301 | 5 | FITZROY | AU | 135757 | 106.8 | 100.5 | 67.0 | 39.0 | 34.2 | 34.8 | 28.0 | 21.8 | 24.9 | 44.4 | 66.6 | 94.9 | 0.2 | 531.4 | 55.2 | 54.76 |
| 285 | 5109170 | 5 | GILBERT RIVER | AU | 11800 | 207.7 | 183.3 | 106.0 | 25.6 | 12.7 | 12.3 | 6.7 | 4.8 | 6.3 | 18.7 | 53.8 | 119.1 | 0.0 | 907.4 | 63.1 | 91.86 |
| 286 | 5109200 | 5 | MITCHELL RIVER (N. | AU | 45872 | 233.7 | 230.1 | 160.7 | 43.3 | 16.6 | 13.0 | 6.8 | 5.6 | 6.9 | 18.6 | 59.8 | 143.3 | 0.1 | 639.7 | 78.2 | 105.72 |
| 287 | 5141100 | 5 | BRANTAS | ID | 8650 | 353.9 | 314.6 | 327.4 | 224.7 | 157.6 | 96.0 | 73.9 | 45.1 | 56.5 | 137.0 | 238.6 | 314.1 | 0.0 | 684.7 | 195.0 | 137.15 |
| 288 | 5141200 | 5 | SOLO (BENGAWAN SOL | ID | 12804 | 321.7 | 298.8 | 304.5 | 203.2 | 137.6 | 82.4 | 52.7 | 36.7 | 48.6 | 114.2 | 214.6 | 282.9 | 0.0 | 578.7 | 174.8 | 128.36 |
| 289 | 5223100 | 5 | KELANTAN | MY | 11900 | 209.1 | 108.3 | 136.7 | 151.9 | 193.5 | 179.6 | 158.2 | 197.2 | 245.1 | 303.5 | 350.8 | 412.0 | 4.0 | 875.8 | 220.5 | 119.37 |
| 290 | 5224500 | 5 | PAHANG | MY | 19000 | 195.5 | 127.9 | 163.4 | 204.0 | 208.8 | 159.9 | 141.7 | 171.8 | 215.0 | 278.0 | 293.0 | 322.3 | 18.4 | 876.1 | 206.8 | 93.08 |
| 291 | 5230300 | 5 | RAJANG | MY | 34053 | 382.7 | 298.7 | 324.5 | 286.9 | 272.8 | 253.2 | 211.2 | 280.2 | 290.3 | 358.1 | 341.8 | 438.5 | 51.1 | 957.2 | 311.6 | 119.93 |
| 292 | 5231700 | 5 | KINABATANGAN | MY | 10800 | 268.2 | 204.4 | 196.1 | 183.4 | 245.7 | 214.2 | 191.6 | 206.8 | 221.5 | 214.6 | 237.8 | 248.7 | 7.2 | 1035.7 | 219.4 | 84.96 |
| 294 | 5550500 | 5 | SEPIK | PG | 40922 | 353.8 | 342.3 | 404.8 | 341.9 | 305.7 | 231.0 | 214.4 | 265.7 | 266.1 | 278.0 | 275.6 | 331.3 | 16.4 | 841.7 | 300.9 | 108.33 |
| 295 | 5553100 | 5 | PURARI | PG | 11100 | 290.3 | 302.7 | 359.8 | 264.9 | 255.6 | 170.8 | 154.9 | 174.2 | 226.3 | 245.4 | 247.8 | 287.4 | 0.0 | 984.9 | 248.3 | 110.02 |
| 296 | 5606100 | 5 | BLACKWOOD RIVER | AU | 20500 | 13.2 | 14.0 | 21.1 | 33.1 | 70.7 | 90.4 | 91.2 | 73.5 | 54.0 | 38.5 | 21.5 | 14.3 | 0.1 | 244.3 | 44.6 | 38.03 |
| 297 | 5607100 | 5 | MURCHISON RIVER | AU | 82300 | 23.3 | 27.3 | 25.8 | 18.1 | 26.5 | 32.1 | 26.7 | 17.1 | 6.2 | 5.5 | 6.6 | 11.0 | 0.1 | 192.5 | 18.9 | 23.28 |
| 298 | 5607200 | 5 | GASCOYNE RIVER | AU | 73400 | 28.5 | 39.4 | 29.6 | 19.7 | 25.9 | 29.5 | 20.9 | 11.1 | 3.3 | 3.8 | 5.1 | 11.1 | 0.1 | 255.4 | 19.0 | 27.32 |
| 299 | 5607400 | 5 | ASHBURTON RIVER | AU | 70200 | 48.5 | 58.8 | 41.0 | 20.5 | 22.8 | 24.4 | 14.2 | 9.1 | 2.5 | 3.4 | 7.4 | 19.5 | 0.0 | 240.5 | 22.7 | 33.21 |
| 300 | 5607450 | 5 | FORTESCUE RIVER | AU | 48900 | 60.9 | 71.7 | 53.7 | 22.8 | 21.3 | 21.5 | 12.2 | 7.6 | 2.6 | 4.1 | 8.5 | 31.8 | 0.0 | 277.1 | 26.6 | 40.25 |
| 301 | 5607500 | 5 | DE GREY RIVER | AU | 49600 | 61.3 | 70.3 | 51.4 | 18.0 | 19.4 | 20.4 | 11.0 | 5.6 | 1.7 | 4.1 | 7.9 | 30.0 | 0.0 | 331.6 | 25.1 | 41.87 |
| 302 | 5608024 | 5 | FITZROY RIVER | AU | 45300 | 169.3 | 151.2 | 84.7 | 21.9 | 11.2 | 7.4 | 5.1 | 2.1 | 4.4 | 16.6 | 39.2 | 97.8 | 0.0 | 488.1 | 50.9 | 74.18 |
| 303 | 5608090 | 5 | ORD | AU | 46100 | 162.8 | 153.2 | 92.5 | 19.2 | 9.0 | 5.1 | 4.1 | 1.6 | 4.9 | 21.5 | 47.3 | 103.5 | 0.0 | 475.2 | 52.1 | 75.50 |
| 304 | 5608400 | 5 | DURACK RIVER | AU | 4150 | 192.2 | 192.2 | 110.0 | 25.7 | 13.1 | 7.2 | 4.5 | 1.6 | 6.8 | 26.7 | 58.4 | 127.3 | 0.0 | 537.1 | 63.8 | 87.66 |
| 305 | 5608500 | 5 | DRYSDALE | AU | 14000 | 239.5 | 213.0 | 164.3 | 37.5 | 11.6 | 6.1 | 4.2 | 1.5 | 4.7 | 27.5 | 76.7 | 174.6 | 0.0 | 673.3 | 80.1 | 104.96 |
| 306 | 5708110 | 5 | VICTORIA RIVER | AU | 44900 | 148.5 | 160.2 | 101.2 | 17.8 | 6.4 | 3.3 | 3.3 | 1.0 | 4.8 | 21.5 | 53.9 | 111.3 | 0.0 | 482.8 | 52.8 | 77.09 |
| 307 | 5708145 | 5 | DALY | AU | 47000 | 245.4 | 235.7 | 172.3 | 35.2 | 6.1 | 2.6 | 1.5 | 1.3 | 6.0 | 31.9 | 92.7 | 191.7 | 0.0 | 583.0 | 85.2 | 111.58 |
| 308 | 5709100 | 5 | ROPER RIVER | AU | 47400 | 189.7 | 191.0 | 149.8 | 34.0 | 6.2 | 4.4 | 1.7 | 1.5 | 4.1 | 21.3 | 60.4 | 148.3 | 0.0 | 563.6 | 67.7 | 93.81 |
| 309 | 5709110 | 5 | MACARTHUR RIVER | AU | 10400 | 174.3 | 169.7 | 118.6 | 22.1 | 7.0 | 5.3 | 2.7 | 0.9 | 6.1 | 23.9 | 40.0 | 104.1 | 0.0 | 615.0 | 56.2 | 87.07 |
| 310 | 5803180 | 5 | SOUTH ESK RIVER | AU | 3278 | 48.6 | 42.9 | 48.9 | 58.8 | 64.1 | 71.1 | 74.3 | 74.6 | 67.9 | 67.2 | 55.7 | 61.0 | 1.1 | 218.0 | 61.3 | 34.09 |
| 311 | 5865300 | 5 | WAIKATO RIVER | NZ | 11395 | 102.9 | 100.4 | 102.5 | 111.9 | 138.8 | 154.5 | 154.5 | 144.5 | 132.5 | 135.2 | 115.5 | 127.9 | 6.2 | 405.0 | 126.8 | 55.64 |
| 312 | 5868100 | 5 | CLUTHA | NZ | 20306 | 91.9 | 71.7 | 92.7 | 81.1 | 82.1 | 74.8 | 67.3 | 71.8 | 85.9 | 92.3 | 84.7 | 90.8 | 5.1 | 271.8 | 82.3 | 40.61 |
| 313 | 6112090 | 6 | DOURO | PT | 91491 | 65.8 | 60.0 | 58.6 | 56.1 | 61.4 | 42.6 | 19.4 | 17.0 | 39.9 | 66.7 | 73.7 | 76.9 | 0.4 | 216.5 | 53.2 | 38.97 |
| 314 | 6113050 | 6 | TEJO | PT | 67490 | 75.7 | 71.5 | 67.5 | 62.4 | 59.5 | 36.6 | 11.2 | 12.0 | 40.3 | 75.1 | 86.4 | 88.0 | 0.2 | 275.9 | 57.2 | 46.61 |
| 315 | 6116200 | 6 | GUADIANA | PT | 60883 | 58.4 | 59.2 | 57.3 | 54.1 | 45.6 | 28.3 | 5.7 | 7.0 | 30.8 | 60.5 | 69.2 | 70.3 | 0.1 | 247.3 | 45.5 | 39.80 |
| 316 | 6122100 | 6 | SEINE | FR | 65000 | 63.3 | 53.3 | 54.4 | 53.0 | 62.0 | 60.9 | 62.6 | 61.2 | 58.6 | 65.9 | 68.3 | 70.1 | 1.7 | 180.5 | 61.1 | 29.14 |
| 317 | 6123100 | 6 | LOIRE | FR | 110000 | 64.5 | 56.9 | 59.1 | 60.1 | 73.3 | 63.5 | 59.1 | 61.5 | 65.0 | 73.1 | 75.2 | 73.0 | 3.0 | 188.9 | 65.4 | 29.90 |
| 318 | 6125100 | 6 | GARONNE | FR | 52000 | 74.4 | 66.6 | 72.7 | 81.1 | 90.2 | 70.9 | 52.9 | 63.7 | 72.7 | 82.0 | 81.4 | 87.7 | 1.4 | 236.2 | 74.7 | 36.17 |
| 319 | 6139100 | 6 | RHONE | FR | 95590 | 77.1 | 71.4 | 79.0 | 80.6 | 91.4 | 87.6 | 72.7 | 86.4 | 92.9 | 101.6 | 99.4 | 89.8 | 6.5 | 278.0 | 85.8 | 39.95 |
| 320 | 6217100 | 6 | GUADALQUIVIR | ES | 46995 | 61.9 | 65.2 | 67.2 | 59.1 | 46.0 | 24.0 | 4.4 | 5.8 | 30.5 | 61.9 | 71.8 | 76.3 | 0.1 | 270.0 | 47.9 | 44.12 |
| 321 | 6226800 | 6 | EBRO | ES | 84230 | 48.2 | 44.0 | 51.3 | 61.5 | 72.4 | 55.8 | 32.3 | 36.2 | 55.4 | 63.8 | 63.4 | 59.4 | 2.3 | 192.9 | 53.6 | 27.88 |
| 322 | 6229500 | 6 | VAENERN-GOETA (GOE | SE | 46886 | 48.7 | 33.9 | 36.2 | 39.5 | 47.8 | 63.9 | 77.3 | 82.7 | 70.2 | 70.5 | 64.6 | 52.2 | 3.6 | 180.0 | 57.3 | 30.02 |
| 323 | 6233650 | 6 | ANGERMANAELVEN | SE | 30638 | 49.2 | 38.8 | 39.5 | 32.9 | 40.8 | 57.4 | 81.6 | 76.4 | 68.8 | 58.0 | 54.4 | 50.1 | 3.9 | 187.3 | 54.0 | 27.76 |
| 324 | 6233750 | 6 | LULEAELVEN | SE | 24924 | 43.3 | 35.1 | 32.9 | 29.7 | 35.7 | 51.8 | 75.5 | 72.4 | 61.3 | 56.7 | 49.3 | 44.6 | 2.5 | 155.8 | 49.0 | 24.79 |
| 325 | 6233850 | 6 | KALIXAELVEN | SE | 23103 | 31.0 | 26.6 | 26.9 | 27.8 | 33.5 | 48.5 | 70.5 | 69.0 | 53.6 | 47.8 | 43.5 | 33.7 | 2.5 | 168.1 | 42.7 | 24.95 |
| 326 | 6233900 | 6 | MUONIO | SE | 14409 | 26.5 | 22.4 | 21.7 | 21.1 | 27.2 | 46.9 | 67.1 | 64.0 | 46.9 | 38.6 | 34.0 | 25.9 | 1.8 | 155.7 | 36.9 | 23.44 |
| 327 | 6335020 | 6 | RHINE RIVER | DE | 159300 | 74.0 | 64.0 | 66.6 | 67.2 | 79.4 | 88.8 | 92.0 | 90.9 | 75.3 | 73.1 | 78.4 | 80.5 | 7.4 | 202.3 | 77.5 | 33.15 |
| 328 | 6337200 | 6 | WESER | DE | 37720 | 61.8 | 50.8 | 50.8 | 52.3 | 61.3 | 69.1 | 78.9 | 73.9 | 58.6 | 58.3 | 62.3 | 65.4 | 2.3 | 186.6 | 62.0 | 28.94 |
| 329 | 6340110 | 6 | ELBE RIVER | DE | 131950 | 44.3 | 38.4 | 41.1 | 45.2 | 60.3 | 69.7 | 77.7 | 72.5 | 51.1 | 46.0 | 47.3 | 47.9 | 2.1 | 183.9 | 53.5 | 25.72 |
| 330 | 6348800 | 6 | PO | IT | 70091 | 55.2 | 55.4 | 76.8 | 90.8 | 111.6 | 87.8 | 72.8 | 86.0 | 88.6 | 113.9 | 94.1 | 69.1 | 1.7 | 311.3 | 83.5 | 47.78 |
| 331 | 6401090 | 6 | OELFUSA | IS | 5678 | 100.2 | 96.6 | 86.9 | 70.1 | 58.1 | 65.5 | 68.1 | 80.9 | 100.5 | 112.3 | 95.3 | 101.4 | 3.9 | 345.2 | 86.3 | 45.50 |
| 332 | 6401120 | 6 | THJORSA | IS | 7380 | 103.9 | 97.5 | 86.5 | 76.3 | 63.2 | 73.0 | 77.4 | 97.7 | 110.2 | 120.6 | 99.8 | 115.6 | 4.4 | 312.8 | 93.5 | 42.93 |
| 333 | 6401601 | 6 | SVARTA, SKAGAFIROI | IS | 393 | 41.6 | 39.4 | 36.4 | 27.4 | 25.4 | 33.8 | 39.3 | 47.5 | 49.7 | 53.3 | 42.5 | 44.3 | 0.0 | 170.0 | 40.0 | 21.62 |
| 334 | 6401701 | 6 | JOEKULSA A FJOELLU | IS | 7074 | 53.2 | 39.6 | 40.9 | 36.1 | 34.6 | 40.3 | 53.6 | 58.8 | 63.9 | 62.7 | 51.3 | 52.8 | 0.1 | 200.0 | 49.0 | 26.39 |
| 335 | 6401800 | 6 | LAGARFLJOT | IS | 2782 | 107.6 | 74.8 | 69.6 | 56.1 | 44.5 | 44.8 | 52.6 | 64.1 | 89.9 | 101.1 | 93.8 | 100.4 | 0.0 | 439.4 | 75.0 | 51.17 |
| 336 | 6421100 | 6 | MAAS | NL | 29000 | 76.0 | 64.0 | 65.1 | 60.8 | 63.9 | 72.7 | 79.7 | 79.7 | 69.6 | 73.8 | 76.2 | 82.9 | 1.6 | 212.9 | 72.0 | 33.23 |
| 337 | 6457010 | 6 | ODER RIVER | PL | 109729 | 38.2 | 33.2 | 36.7 | 41.8 | 61.4 | 69.8 | 83.5 | 75.7 | 50.9 | 44.3 | 45.1 | 42.5 | 4.1 | 214.6 | 51.9 | 26.18 |
| 338 | 6458010 | 6 | WISLA | PL | 194376 | 34.2 | 30.0 | 33.2 | 42.1 | 61.3 | 76.9 | 88.0 | 78.6 | 52.9 | 43.4 | 44.3 | 38.5 | 2.2 | 178.0 | 52.0 | 27.49 |
| 339 | 6604650 | 6 | SPEY | GB | 2861 | 89.1 | 64.1 | 64.6 | 52.7 | 58.0 | 56.4 | 65.9 | 73.2 | 70.3 | 90.6 | 89.7 | 81.6 | 11.8 | 223.9 | 71.3 | 32.25 |
| 340 | 6604750 | 6 | TWEED | GB | 4390 | 88.1 | 62.7 | 66.4 | 54.9 | 64.1 | 62.9 | 75.4 | 85.3 | 74.9 | 94.8 | 88.3 | 84.7 | 3.6 | 218.0 | 75.2 | 34.53 |
| 341 | 6605600 | 6 | TRENT | GB | 7486 | 70.1 | 55.3 | 53.8 | 55.9 | 58.8 | 59.9 | 68.8 | 74.4 | 63.5 | 79.7 | 74.7 | 74.9 | 3.9 | 175.3 | 65.8 | 31.03 |
| 342 | 6607650 | 6 | THAMES | GB | 9948 | 64.9 | 47.3 | 50.8 | 49.7 | 54.9 | 50.4 | 57.1 | 60.5 | 53.8 | 71.7 | 70.9 | 70.5 | 0.9 | 184.5 | 58.5 | 31.36 |
| 343 | 6688150 | 6 | SAKARYA | TR | 55322 | 52.1 | 45.4 | 45.2 | 45.5 | 49.4 | 36.3 | 19.7 | 15.1 | 22.7 | 38.4 | 46.2 | 61.6 | 0.8 | 172.4 | 39.8 | 24.31 |
| 344 | 6688600 | 6 | KIZILIRMAK | TR | 75121 | 51.4 | 40.6 | 43.1 | 49.3 | 54.5 | 36.9 | 17.8 | 12.6 | 22.0 | 36.1 | 45.4 | 54.7 | 0.3 | 230.1 | 38.7 | 26.44 |
| 345 | 6730500 | 6 | TANA (NO, FI) | NO | 14165 | 24.5 | 21.5 | 20.1 | 19.8 | 23.5 | 43.3 | 57.7 | 54.5 | 41.3 | 35.7 | 30.1 | 24.7 | 3.3 | 149.3 | 33.1 | 19.86 |
| 346 | 6731310 | 6 | DRAMSELV | NO | 16020 | 49.7 | 35.1 | 38.1 | 36.9 | 50.0 | 67.1 | 85.6 | 90.4 | 68.5 | 75.4 | 61.4 | 51.5 | 2.6 | 257.2 | 59.2 | 34.96 |
| 347 | 6731400 | 6 | GLOMA | NO | 40243 | 45.3 | 33.8 | 33.8 | 32.4 | 43.4 | 63.4 | 77.3 | 81.5 | 62.2 | 63.9 | 53.8 | 47.3 | 3.0 | 172.6 | 53.2 | 26.92 |
| 348 | 6742900 | 6 | DANUBE | RO | 807000 | 45.7 | 42.4 | 47.4 | 59.2 | 78.1 | 93.9 | 86.0 | 77.4 | 63.6 | 59.3 | 61.0 | 54.9 | 5.5 | 156.7 | 64.1 | 25.79 |
| 349 | 6854100 | 6 | KOKEMAENJOKI | FI | 26025 | 41.3 | 31.4 | 32.3 | 33.7 | 41.2 | 57.8 | 70.5 | 77.6 | 65.1 | 60.1 | 52.5 | 45.0 | 1.2 | 164.3 | 50.7 | 27.40 |
| 350 | 6854500 | 6 | OULUJOKI | FI | 22841 | 39.4 | 34.7 | 32.4 | 33.3 | 44.1 | 61.9 | 74.0 | 80.7 | 62.4 | 56.0 | 50.9 | 41.2 | 5.9 | 155.0 | 50.9 | 26.50 |
| 351 | 6854600 | 6 | IIJOKI | FI | 14191 | 39.2 | 35.4 | 34.2 | 31.5 | 42.8 | 60.3 | 73.6 | 76.2 | 60.4 | 56.0 | 49.4 | 42.0 | 5.6 | 143.9 | 50.1 | 25.29 |
| 352 | 6854700 | 6 | KEMIJOKI | FI | 50686 | 30.7 | 30.0 | 28.9 | 26.9 | 35.9 | 57.3 | 67.0 | 69.8 | 52.7 | 47.8 | 40.6 | 32.9 | 3.5 | 137.1 | 43.4 | 23.61 |
| 353 | 6855200 | 6 | KYMIJOKI | FI | 36275 | 42.1 | 33.6 | 34.1 | 34.4 | 40.6 | 59.7 | 73.1 | 80.7 | 64.2 | 59.8 | 51.8 | 44.5 | 0.8 | 183.7 | 51.5 | 27.99 |
| 354 | 6855400 | 6 | VUOKSI | FI | 61061 | 41.9 | 35.3 | 34.0 | 35.1 | 42.6 | 64.3 | 71.2 | 80.1 | 66.2 | 58.3 | 54.3 | 45.7 | 4.6 | 152.7 | 52.4 | 26.03 |
| 355 | 6934100 | 6 | SKJERN A | DK | 1040 | 70.0 | 49.4 | 52.3 | 43.6 | 48.3 | 60.4 | 68.7 | 79.7 | 83.5 | 89.1 | 84.9 | 77.2 | 0.0 | 255.5 | 67.3 | 35.14 |
| 356 | 6934250 | 6 | GUDENA | DK | 1290 | 61.7 | 44.5 | 47.2 | 39.8 | 46.0 | 54.9 | 64.5 | 70.1 | 70.5 | 74.6 | 73.5 | 66.4 | 0.6 | 196.8 | 59.5 | 30.81 |
| 357 | 6970100 | 6 | ONEGA | RU | 55770 | 33.9 | 26.7 | 30.4 | 33.6 | 46.0 | 62.3 | 63.0 | 72.9 | 62.9 | 57.7 | 47.6 | 41.6 | 3.0 | 175.2 | 48.2 | 24.28 |
| 358 | 6970250 | 6 | NORTHERN DVINA(SEV | RU | 348000 | 35.2 | 26.4 | 29.3 | 34.7 | 47.9 | 64.2 | 68.8 | 68.9 | 62.0 | 57.8 | 47.6 | 40.7 | 3.6 | 132.2 | 48.6 | 21.95 |
| 359 | 6970500 | 6 | MEZEN | RU | 56400 | 31.3 | 24.1 | 27.7 | 32.7 | 44.4 | 61.2 | 64.4 | 68.7 | 61.8 | 55.1 | 42.4 | 35.7 | 3.8 | 150.6 | 45.8 | 23.54 |
| 360 | 6970700 | 6 | PECHORA | RU | 312000 | 32.0 | 25.5 | 27.9 | 31.1 | 40.1 | 51.6 | 60.7 | 69.6 | 62.5 | 54.3 | 44.3 | 35.1 | 5.8 | 131.9 | 44.6 | 20.32 |
| 361 | 6971130 | 6 | TULOMA | RU | 17500 | 26.4 | 24.4 | 24.3 | 26.4 | 36.3 | 55.9 | 67.9 | 64.8 | 50.9 | 44.9 | 34.6 | 29.6 | 6.3 | 148.8 | 40.5 | 22.57 |
| 362 | 6971450 | 6 | PONOY | RU | 15200 | 26.2 | 22.6 | 25.3 | 26.0 | 34.0 | 50.7 | 53.7 | 57.9 | 53.1 | 43.5 | 35.0 | 32.6 | 1.8 | 193.8 | 38.4 | 22.01 |
| 363 | 6971600 | 6 | VARZUGA | RU | 7940 | 25.9 | 21.7 | 23.9 | 26.6 | 37.2 | 49.5 | 58.6 | 65.1 | 54.0 | 46.5 | 38.7 | 31.5 | 2.3 | 139.2 | 39.9 | 22.93 |
| 364 | 6972130 | 6 | NIZHNY VYG (SOROKA | RU | 27000 | 30.4 | 26.2 | 27.4 | 31.0 | 40.3 | 62.7 | 63.6 | 76.1 | 63.9 | 56.4 | 45.9 | 36.4 | 4.9 | 162.8 | 46.7 | 25.87 |
| 365 | 6972350 | 6 | NARVA | EE | 56000 | 37.1 | 30.5 | 32.1 | 35.7 | 48.4 | 71.4 | 80.1 | 82.6 | 64.6 | 55.6 | 51.8 | 43.9 | 3.8 | 167.7 | 52.8 | 28.59 |
| 366 | 6972430 | 6 | NEVA | RU | 281000 | 38.5 | 31.9 | 33.5 | 36.1 | 46.6 | 67.7 | 75.4 | 78.6 | -3385.3 | -3391.6 | -3397.8 | -3406.0 | 5.1 | 162.2 | 52.9 | 25.00 |
| 367 | 6972800 | 6 | KEM | RU | 27900 | 30.7 | 27.6 | 27.3 | 29.4 | 42.4 | 60.2 | 67.9 | 71.3 | 59.7 | 49.6 | 43.2 | 34.2 | 3.8 | 149.6 | 45.3 | 24.19 |
| 368 | 6972860 | 6 | KOVDA | RU | 25900 | 29.7 | 26.7 | 27.1 | 28.5 | 41.5 | 56.3 | 65.8 | 67.3 | 54.8 | 46.8 | 40.2 | 31.7 | 0.4 | 149.9 | 43.0 | 24.35 |
| 369 | 6973300 | 6 | WESTERN DVINA (DAU | LV | 64500 | 39.2 | 34.4 | 36.2 | 39.7 | 56.0 | 78.4 | 89.3 | 78.3 | 60.8 | 52.4 | 48.9 | 44.6 | 0.5 | 228.3 | 54.9 | 29.97 |
| 370 | 6974150 | 6 | NEMAN | LT | 81200 | 39.2 | 32.0 | 35.0 | 41.7 | 56.0 | 74.4 | 86.6 | 77.0 | 56.4 | 49.7 | 49.5 | 46.2 | 1.4 | 178.0 | 53.6 | 28.24 |
| 371 | 6977100 | 6 | VOLGA | RU | 1360000 | 34.1 | 27.2 | 28.8 | 32.0 | 45.7 | 63.2 | 70.6 | 61.5 | 54.0 | 52.1 | 44.2 | 39.2 | 2.4 | 113.7 | 46.1 | 20.54 |
| 372 | 6978250 | 6 | DON | RU | 378000 | 34.4 | 28.5 | 28.4 | 32.7 | 42.6 | 55.2 | 57.3 | 45.8 | 39.3 | 38.9 | 41.3 | 40.7 | 2.1 | 111.4 | 40.4 | 19.74 |
| 373 | 6980300 | 6 | SOUTHERN BUG | UA | 46200 | 33.4 | 31.9 | 29.4 | 41.4 | 53.5 | 77.9 | 80.3 | 60.3 | 42.9 | 37.2 | 40.1 | 38.1 | 0.5 | 174.7 | 47.2 | 29.07 |
| 374 | 6980800 | 6 | DNIEPR | UA | 463000 | 36.8 | 32.7 | 33.6 | 41.5 | 53.6 | 74.4 | 82.5 | 64.6 | 49.3 | 44.2 | 46.4 | 43.0 | 3.0 | 142.5 | 50.2 | 24.20 |
| 375 | 6981800 | 6 | DNIESTR | MD | 66100 | 33.4 | 33.4 | 33.9 | 48.4 | 68.9 | 90.3 | 90.9 | 72.5 | 52.8 | 43.9 | 42.3 | 37.6 | 3.6 | 195.4 | 54.0 | 30.97 |
| 376 | 6983350 | 6 | KUBAN | RU | 48100 | 70.2 | 58.3 | 62.0 | 69.4 | 84.7 | 95.9 | 82.0 | 76.0 | 74.4 | 77.7 | 82.8 | 82.3 | 3.1 | 203.9 | 76.3 | 33.93 |
| 377 | 6990700 | 6 | KURA | AZ | 178000 | 27.8 | 30.4 | 41.4 | 58.5 | 76.1 | 63.4 | 38.9 | 33.5 | 36.6 | 46.3 | 37.9 | 28.1 | 3.1 | 141.6 | 43.2 | 22.09 |
| No | GRDC | WMO | RIVER | COUNTRY | POL/STD | sen_SD | sen_POL | P1 | LOC_SD | LOC_POL | pvalP_SD | pvalP_POL | pval_SD_n | pval_POL_n | sen_SD_n | sen_POL_n | P2 |
| 7 | 1289200 | 1 | PANGANI | TZ | 6.26 | -0.187 | -0.712 | 3.81 | 1964 | 1964 | 0.01 | 0.00 | 0.37 | 0.23 | -0.164 | -0.762 | 4.64 |
| 14 | 1362100 | 1 | NILE | EG | 4.26 | -0.041 | -0.093 | 2.28 | 1964 | 1967 | 0.00 | 0.00 | 0.57 | 0.94 | -0.029 | -0.021 | 0.73 |
| 15 | 1389090 | 1 | MANGOKY | MG | 6.07 | -0.206 | -0.776 | 3.77 | 1939 | 1939 | 0.01 | 0.01 | 0.46 | 0.48 | 0.083 | 0.305 | 3.66 |
| 17 | 1425500 | 1 | CAVALLY | CI | 6.55 | -0.213 | -0.618 | 2.90 | 1963 | 1971 | 0.00 | 0.02 | 0.51 | 0.79 | -0.104 | -0.210 | 2.02 |
| 18 | 1426380 | 1 | BANDAMA | CI | 6.08 | -0.170 | -0.578 | 3.40 | 1929 | 1974 | 0.00 | 0.00 | 0.07 | 0.99 | -0.089 | -0.037 | 0.42 |
| 19 | 1427500 | 1 | SASSANDRA | CI | 6.90 | -0.195 | -0.523 | 2.68 | 1967 | 1960 | 0.01 | 0.06 | 0.91 | 0.70 | 0.027 | -0.163 | -6.05 |
| 20 | 1427600 | 1 | DAVO | CI | 7.70 | -0.140 | -0.464 | 3.31 | 1964 | 1964 | 0.00 | 0.01 | 0.12 | 0.49 | 0.170 | 0.314 | 1.85 |
| 21 | 1428500 | 1 | COMOE | CI | 5.32 | -0.167 | -0.576 | 3.44 | 1938 | 1938 | 0.00 | 0.00 | 0.19 | 0.11 | -0.077 | -0.323 | 4.20 |
| 24 | 1530100 | 1 | TANO | GH | 6.56 | -0.166 | -0.804 | 4.83 | 1968 | 1968 | 0.00 | 0.00 | 0.12 | 0.11 | -0.180 | -0.797 | 4.44 |
| 31 | 1812100 | 1 | SENEGAL | SN | 4.95 | -0.151 | -0.453 | 3.00 | 1967 | 1967 | 0.00 | 0.00 | 0.54 | 0.37 | 0.070 | 0.441 | 6.29 |
| 32 | 1813200 | 1 | GAMBIA | SN | 4.10 | -0.187 | -0.486 | 2.60 | 1965 | 1965 | 0.00 | 0.00 | 0.40 | 0.54 | 0.176 | 0.467 | 2.65 |
| 33 | 1814070 | 1 | GEBA | SN | 5.09 | -0.217 | -0.745 | 3.44 | 1965 | 1965 | 0.00 | 0.00 | 0.29 | 0.43 | 0.240 | 0.616 | 2.57 |
| 34 | 1815020 | 1 | CORUBAL | SN | 4.97 | -0.374 | -1.251 | 3.35 | 1967 | 1965 | 0.00 | 0.00 | 0.23 | 0.60 | 0.240 | 0.363 | 1.51 |
| 45 | 2178300 | 2 | YONGDING HE | CN | 5.92 | -0.085 | -0.391 | 4.57 | 1979 | 1967 | 0.09 | 0.03 | 0.24 | 0.09 | -0.198 | -0.619 | 3.12 |
| 47 | 2178500 | 2 | LUAN HE | CN | 6.13 | -0.089 | -0.378 | 4.25 | 1979 | 1978 | 0.07 | 0.06 | 0.51 | 0.13 | -0.147 | -1.077 | 7.31 |
| 49 | 2180800 | 2 | HUANG HE (YELLOW R | CN | 6.11 | -0.050 | -0.201 | 4.02 | 1968 | 1968 | 0.14 | 0.04 | 0.87 | 0.43 | -0.010 | -0.154 | 15.31 |
| 50 | 2181900 | 2 | YANGTZE RIVER (CHA | CN | 5.28 | -0.083 | -0.388 | 4.69 | 1932 | 1939 | 0.00 | 0.00 | 0.81 | 0.94 | -0.007 | 0.010 | -1.38 |
| 55 | 2260100 | 2 | CHINDWIN RIVER | MM | 4.44 | 0.239 | 1.046 | 4.37 | 1962 | 1963 | 0.02 | 0.02 | 0.52 | 0.39 | -0.188 | -1.537 | 8.17 |
| 62 | 2423500 | 2 | KARUN | IR | 5.87 | 0.058 | 0.274 | 4.70 | 1973 | 1973 | 0.00 | 0.00 | 0.33 | 0.24 | -0.205 | -0.842 | 4.10 |
| 73 | 2595400 | 2 | EUPHRATES | IQ | 5.93 | -0.037 | -0.139 | 3.81 | 1976 | 1977 | 0.16 | 0.12 | 0.09 | 0.22 | -0.113 | -0.322 | 2.85 |
| 74 | 2595700 | 2 | TIGRIS | IQ | 5.67 | 0.077 | 0.306 | 3.96 | 1937 | 1937 | 0.00 | 0.00 | 0.61 | 0.76 | -0.024 | 0.048 | -2.03 |
| 75 | 2651100 | 2 | BRAHMAPUTRA | BD | 5.42 | -0.215 | -1.109 | 5.17 | 1955 | 1955 | 0.00 | 0.00 | 0.29 | 0.11 | -0.142 | -0.677 | 4.76 |
| 76 | 2677100 | 2 | HAN-GANG (HAN RIVE | KR | 6.66 | 0.385 | 1.329 | 3.46 | 1962 | 1953 | 0.00 | 0.00 | 0.50 | 0.13 | 0.208 | 1.268 | 6.09 |
| 77 | 2694510 | 2 | NAKTONG | KR | 6.49 | 0.234 | 0.759 | 3.24 | 1952 | 1973 | 0.07 | 0.08 | 0.05 | 0.05 | 0.384 | 2.653 | 6.91 |
| 78 | 2846800 | 2 | GANGES | IN | 3.81 | -0.077 | -0.247 | 3.20 | 1978 | 1982 | 0.13 | 0.22 | 0.25 | 0.14 | -0.305 | -1.259 | 4.12 |
| 81 | 2853300 | 2 | TAPTI RIVER | IN | 4.71 | 0.128 | 0.426 | 3.32 | 1929 | 1929 | 0.01 | 0.00 | 0.62 | 0.53 | -0.036 | -0.159 | 4.37 |
| 89 | 2901202 | 2 | ANADYR | RU | 9.64 | -0.047 | -0.138 | 2.95 | 1950 | 1950 | 0.01 | 0.04 | 0.29 | 0.58 | -0.036 | -0.058 | 1.59 |
| 90 | 2902850 | 2 | KAMCHATKA | RU | 8.57 | -0.131 | -0.351 | 2.69 | 1956 | 1956 | 0.00 | 0.00 | 0.14 | 0.09 | -0.075 | -0.264 | 3.52 |
| 93 | 2909150 | 2 | YENISEI | RU | 4.25 | -0.020 | -0.074 | 3.66 | 1975 | 1954 | 0.01 | 0.01 | 0.09 | 0.54 | 0.081 | -0.051 | -0.62 |
| 96 | 2917100 | 2 | AMU DARYA | UZ | 5.10 | 0.027 | 0.089 | 3.31 | 1947 | 1951 | 0.00 | 0.01 | 0.11 | 0.07 | -0.052 | -0.230 | 4.42 |
| 103 | 2998450 | 2 | ALAZEYA | RU | 7.33 | 0.030 | 0.101 | 3.34 | 1995 | 1995 | 0.09 | 0.10 | 0.56 | 0.34 | 0.282 | 1.207 | 4.29 |
| 105 | 2998702 | 2 | ANYUY (TRIB. KOLYM | RU | 12.03 | -0.060 | -0.189 | 3.16 | 1986 | 1990 | 0.00 | 0.00 | 0.56 | 0.49 | -0.066 | 0.160 | -2.41 |
| 106 | 2998720 | 2 | BOL. ANYUY (TRIB. | RU | 10.43 | -0.031 | -0.105 | 3.41 | 1990 | 1990 | 0.03 | 0.07 | 0.00 | 0.06 | 0.215 | 0.635 | 2.96 |
| 107 | 2998800 | 2 | PALYAVAAM | RU | 11.10 | -0.056 | -0.155 | 2.75 | 1930 | 1930 | 0.00 | 0.01 | 0.48 | 0.91 | -0.014 | -0.011 | 0.78 |
| 114 | 3102500 | 3 | ATRATO | CO | 8.60 | 0.350 | 1.084 | 3.10 | 1941 | 1941 | 0.00 | 0.00 | 0.68 | 0.61 | 0.086 | 0.300 | 3.49 |
| 119 | 3178900 | 3 | HUASCO | CL | 11.71 | -0.080 | -0.259 | 3.25 | 1944 | 1944 | 0.00 | 0.00 | 0.72 | 0.54 | 0.013 | 0.092 | 6.96 |
| 124 | 3258200 | 3 | SALADO | AR | 5.38 | 0.134 | 0.379 | 2.82 | 1965 | 1965 | 0.00 | 0.00 | 0.22 | 0.88 | 0.153 | 0.121 | 0.79 |
| 129 | 3276800 | 3 | SANTA CRUZ | AR | 6.78 | -0.174 | -0.552 | 3.18 | 1941 | 1940 | 0.00 | 0.00 | 1.00 | 0.90 | 0.000 | 0.020 | -71.56 |
| 132 | 3410500 | 3 | CORANTIJN | SR | 4.78 | -0.193 | -0.444 | 2.30 | 1938 | 1938 | 0.00 | 0.03 | 0.97 | 0.82 | -0.004 | 0.073 | -16.82 |
| 133 | 3411300 | 3 | COPPENAME | SR | 5.19 | -0.256 | -0.697 | 2.72 | 1955 | 1955 | 0.00 | 0.01 | 0.56 | 0.50 | -0.097 | -0.322 | 3.31 |
| 134 | 3412800 | 3 | MARONI | SR | 9.38 | -0.375 | -1.247 | 3.33 | 1949 | 1950 | 0.00 | 0.00 | 0.81 | 0.73 | -0.040 | -0.168 | 4.23 |
| 135 | 3469050 | 3 | URUGUAY | UY | 7.15 | 0.174 | 0.618 | 3.55 | 1945 | 1940 | 0.00 | 0.01 | 0.13 | 0.07 | 0.155 | 0.558 | 3.59 |
| 136 | 3469100 | 3 | NEGRO (URUGUAY) | UY | 10.43 | 0.191 | 0.586 | 3.07 | 1933 | 1933 | 0.00 | 0.01 | 0.27 | 0.28 | 0.087 | 0.324 | 3.71 |
| 137 | 3514800 | 3 | OYAPOCK | GF | 11.25 | -0.203 | -0.653 | 3.22 | 1958 | 1949 | 0.12 | 0.05 | 0.08 | 0.31 | 0.463 | 0.709 | 1.53 |
| 144 | 3631100 | 3 | RIO JARI | BR | 12.56 | -0.219 | -0.825 | 3.78 | 1958 | 1969 | 0.06 | 0.01 | 0.85 | 0.68 | -0.029 | -0.460 | 15.65 |
| 145 | 3631210 | 3 | RIO PARU DE ESTE | BR | 11.19 | -0.204 | -0.771 | 3.78 | 1940 | 1945 | 0.04 | 0.04 | 0.94 | 0.90 | -0.013 | 0.084 | -6.52 |
| 155 | 3650885 | 3 | RIO PARAIBA | BR | 7.08 | 0.177 | 0.624 | 3.53 | 1959 | 1959 | 0.04 | 0.05 | 0.33 | 0.22 | 0.124 | 0.659 | 5.30 |
| 166 | 3653120 | 3 | RIO RIBEIRA DO IGU | BR | 6.36 | 0.112 | 0.390 | 3.47 | 1981 | 1979 | 0.00 | 0.00 | 0.12 | 0.09 | 0.400 | 1.198 | 3.00 |
| 167 | 3653400 | 3 | RIO JACUI | BR | 6.25 | 0.126 | 0.494 | 3.91 | 1945 | 1962 | 0.03 | 0.03 | 0.56 | 0.53 | 0.059 | 0.434 | 7.38 |
| 168 | 3843100 | 3 | MIRA | EC | 6.23 | -0.110 | -0.382 | 3.46 | 1930 | 1929 | 0.00 | 0.00 | 0.30 | 0.99 | 0.047 | -0.001 | -0.02 |
| 171 | 3844450 | 3 | VINCES | EC | 4.65 | 0.160 | 0.796 | 4.99 | 1920 | 1946 | 0.14 | 0.01 | 0.89 | 0.95 | 0.017 | 0.041 | 2.45 |
| 176 | 4101500 | 4 | COLVILLE RIVER | US | 7.24 | -0.041 | -0.146 | 3.59 | 1967 | 1965 | 0.04 | 0.02 | 0.86 | 0.85 | 0.010 | 0.029 | 2.98 |
| 179 | 4102100 | 4 | KUSKOKWIM RIVER | US | 6.36 | -0.068 | -0.275 | 4.06 | 1955 | 1963 | 0.00 | 0.00 | 0.38 | 0.44 | -0.054 | -0.204 | 3.79 |
| 180 | 4102710 | 4 | COPPER RIVER | US | 12.78 | -0.174 | -0.532 | 3.06 | 1961 | 1961 | 0.00 | 0.00 | 0.46 | 0.58 | 0.047 | 0.157 | 3.36 |
| 181 | 4102740 | 4 | NUSHAGAK RIVER | US | 8.64 | -0.091 | -0.216 | 2.38 | 1951 | 1967 | 0.00 | 0.08 | 0.61 | 0.65 | -0.031 | 0.192 | -6.22 |
| 196 | 4147060 | 4 | ST. CROIX RIVER | US | 6.89 | 0.076 | 0.262 | 3.44 | 1956 | 1956 | 0.03 | 0.05 | 0.91 | 0.81 | 0.009 | -0.081 | -9.44 |
| 197 | 4147380 | 4 | MERRIMACK RIVER | US | 8.52 | 0.088 | 0.307 | 3.50 | 1976 | 1977 | 0.00 | 0.01 | 0.48 | 0.70 | 0.149 | 0.323 | 2.17 |
| 198 | 4147460 | 4 | CONNECTICUT RIVER | US | 7.97 | 0.056 | 0.191 | 3.42 | 1971 | 1971 | 0.01 | 0.03 | 0.81 | 0.95 | 0.050 | 0.034 | 0.68 |
| 200 | 4147600 | 4 | DELAWARE RIVER | US | 8.40 | 0.081 | 0.298 | 3.70 | 1970 | 1967 | 0.02 | 0.02 | 0.74 | 0.93 | 0.045 | 0.089 | 1.98 |
| 208 | 4148650 | 4 | SAVANNAH RIVER | US | 6.34 | -0.073 | -0.364 | 5.00 | 1945 | 1953 | 0.07 | 0.01 | 0.72 | 0.99 | -0.022 | -0.004 | 0.18 |
| 217 | 4150330 | 4 | SAN ANTONIO RIVER | US | 6.85 | 0.142 | 0.493 | 3.48 | 1964 | 1966 | 0.00 | 0.00 | 0.38 | 0.87 | 0.169 | 0.113 | 0.67 |
| 223 | 4202100 | 4 | ALSEK RIVER | CA | 8.44 | -0.087 | -0.320 | 3.68 | 1943 | 1943 | 0.00 | 0.00 | 0.13 | 0.25 | 0.053 | 0.134 | 2.54 |
| 224 | 4202601 | 4 | TAKU RIVER | CA | 7.14 | -0.165 | -0.524 | 3.18 | 1948 | 1948 | 0.00 | 0.00 | 0.64 | 0.96 | 0.050 | 0.006 | 0.12 |
| 225 | 4204900 | 4 | STIKINE RIVER | US | 9.44 | -0.276 | -0.903 | 3.27 | 1941 | 1942 | 0.00 | 0.00 | 0.84 | 0.75 | 0.011 | 0.048 | 4.31 |
| 226 | 4206100 | 4 | NASS RIVER | CA | 8.53 | -0.204 | -0.694 | 3.41 | 1967 | 1966 | 0.00 | 0.00 | 0.50 | 0.78 | 0.147 | 0.146 | 0.99 |
| 227 | 4206250 | 4 | SKEENA RIVER | CA | 10.96 | -0.122 | -0.423 | 3.46 | 1926 | 1936 | 0.00 | 0.00 | 0.30 | 0.52 | -0.032 | -0.100 | 3.08 |
| 230 | 4208040 | 4 | PEEL RIVER (TRIB. | CA | 5.64 | 0.038 | 0.153 | 4.01 | 1935 | 1935 | 0.01 | 0.00 | 0.49 | 0.24 | 0.014 | 0.080 | 5.73 |
| 233 | 4209600 | 4 | ELLICE RIVER | CA | 10.15 | -0.043 | -0.148 | 3.41 | 1939 | 1939 | 0.00 | 0.00 | 0.61 | 0.54 | -0.013 | -0.048 | 3.62 |
| 235 | 4209850 | 4 | HAYES RIVER (TRIB. | CA | 7.07 | -0.037 | -0.140 | 3.75 | 1937 | 1937 | 0.00 | 0.00 | 0.16 | 0.26 | 0.033 | 0.104 | 3.19 |
| 243 | 4214080 | 4 | ATTAWAPISKAT RIVER | CA | 6.94 | 0.078 | 0.250 | 3.20 | 1965 | 1965 | 0.00 | 0.00 | 0.60 | 0.53 | -0.060 | -0.315 | 5.22 |
| 248 | 4214440 | 4 | SEVERN RIVER (TRIB | CA | 5.83 | 0.045 | 0.160 | 3.58 | 1967 | 1937 | 0.08 | 0.06 | 0.26 | 0.68 | 0.097 | 0.084 | 0.86 |
| 261 | 4231630 | 4 | SAINT JOHN RIVER | CA | 7.32 | 0.054 | 0.254 | 4.68 | 1975 | 1975 | 0.12 | 0.02 | 0.71 | 0.56 | 0.044 | 0.255 | 5.84 |
| 263 | 4243300 | 4 | ST. MAURICE (RIVIE | CA | 6.78 | 0.076 | 0.265 | 3.47 | 1956 | 1956 | 0.00 | 0.00 | 0.76 | 0.95 | 0.020 | 0.026 | 1.30 |
| 267 | 4244635 | 4 | NATASHQUAN (RIVIER | CA | 7.22 | -0.049 | -0.199 | 4.03 | 1940 | 1944 | 0.00 | 0.01 | 0.55 | 0.70 | 0.017 | 0.057 | 3.40 |
| 277 | 4359220 | 4 | PAPALOAPAN | MX | 6.54 | 0.160 | 0.591 | 3.71 | 1950 | 1950 | 0.05 | 0.01 | 0.46 | 0.14 | -0.203 | -1.280 | 6.30 |
| 292 | 5231700 | 5 | KINABATANGAN | MY | 12.11 | -0.130 | -0.560 | 4.32 | 1947 | 1947 | 0.00 | 0.00 | 0.03 | 0.05 | 0.247 | 0.864 | 3.50 |
| 295 | 5553100 | 5 | PURARI | PG | 8.95 | -0.365 | -1.331 | 3.64 | 1950 | 1950 | 0.00 | 0.00 | 0.11 | 0.17 | 0.238 | 0.814 | 3.43 |
| 296 | 5606100 | 5 | BLACKWOOD RIVER | AU | 6.42 | -0.068 | -0.202 | 2.95 | 1968 | 1970 | 0.00 | 0.01 | 0.85 | 0.85 | 0.011 | -0.067 | -6.31 |
| 300 | 5607450 | 5 | FORTESCUE RIVER | AU | 6.88 | 0.111 | 0.399 | 3.60 | 1959 | 1959 | 0.03 | 0.02 | 0.31 | 0.50 | 0.181 | 0.445 | 2.46 |
| 301 | 5607500 | 5 | DE GREY RIVER | AU | 7.92 | 0.144 | 0.536 | 3.72 | 1972 | 1965 | 0.04 | 0.01 | 0.29 | 0.26 | 0.414 | 0.981 | 2.37 |
| 306 | 5708110 | 5 | VICTORIA RIVER | AU | 6.26 | 0.221 | 0.664 | 3.01 | 1971 | 1964 | 0.02 | 0.05 | 0.05 | 0.11 | 0.541 | 1.304 | 2.41 |
| 307 | 5708145 | 5 | DALY | AU | 5.22 | 0.209 | 0.717 | 3.43 | 1973 | 1972 | 0.03 | 0.03 | 0.13 | 0.06 | 0.618 | 2.309 | 3.74 |
| 308 | 5709100 | 5 | ROPER RIVER | AU | 6.01 | 0.238 | 0.680 | 2.86 | 1973 | 1973 | 0.02 | 0.05 | 0.15 | 0.13 | 0.556 | 1.940 | 3.49 |
| 334 | 6401701 | 6 | JOEKULSA A FJOELLU | IS | 7.58 | -0.116 | -0.401 | 3.45 | 1937 | 1937 | 0.00 | 0.00 | 0.71 | 0.34 | -0.013 | -0.095 | 7.47 |
| 335 | 6401800 | 6 | LAGARFLJOT | IS | 8.59 | -0.136 | -0.533 | 3.92 | 1953 | 1953 | 0.00 | 0.00 | 0.00 | 0.00 | 0.310 | 0.889 | 2.86 |
| 339 | 6604650 | 6 | SPEY | GB | 6.58 | 0.126 | 0.433 | 3.44 | 1973 | 1973 | 0.00 | 0.00 | 0.69 | 0.98 | -0.048 | 0.014 | -0.29 |
| 344 | 6688600 | 6 | KIZILIRMAK | TR | 8.69 | -0.062 | -0.260 | 4.16 | 1925 | 1925 | 0.00 | 0.00 | 0.40 | 0.94 | 0.015 | 0.004 | 0.24 |
| 345 | 6730500 | 6 | TANA (NO, FI) | NO | 7.35 | 0.040 | 0.113 | 2.80 | 1963 | 1950 | 0.04 | 0.07 | 0.95 | 0.79 | -0.002 | 0.031 | -14.31 |
| 349 | 6854100 | 6 | KOKEMAENJOKI | FI | 5.95 | 0.037 | 0.186 | 5.03 | 1976 | 1968 | 0.18 | 0.05 | 0.80 | 0.45 | -0.024 | 0.186 | -7.89 |
| 355 | 6934100 | 6 | SKJERN A | DK | 7.27 | 0.096 | 0.309 | 3.21 | 1958 | 1930 | 0.00 | 0.02 | 0.58 | 0.17 | 0.051 | 0.202 | 3.96 |
| 356 | 6934250 | 6 | GUDENA | DK | 6.37 | 0.070 | 0.207 | 2.97 | 1931 | 1931 | 0.03 | 0.08 | 0.34 | 0.63 | 0.035 | 0.067 | 1.94 |
| 367 | 6972800 | 6 | KEM | RU | 6.03 | -0.037 | -0.127 | 3.45 | 1941 | 1941 | 0.11 | 0.11 | 0.66 | 0.44 | -0.012 | -0.062 | 4.99 |
| 376 | 6983350 | 6 | KUBAN | RU | 5.92 | 0.058 | 0.241 | 4.13 | 1959 | 1960 | 0.03 | 0.03 | 0.22 | 0.72 | 0.075 | 0.110 | 1.46 |
| Lp | GRDC_NO | WMO | RIVER | COUNTRY | P1 | sen_SD | sen_POL | P2 | LOC_SD | LOC_POL | pvalP_SD | pvalP_POL | pval_SD_n | pval_POL_n | sen_SD_n | sen_POL_n | sen_POL1_n |
| 15 | 1389090 | 1 | MANGOKY | MG | 3.64 | -0.00182 | -0.00609 | 3.35 | 1947 | 1942 | 0.003 | 0.001 | 0.520 | 0.365 | -0.00067 | 0.00288 | -4.282 |
| 22 | 1445100 | 1 | KOUILOU | CG | 5.36 | -0.00147 | -0.00377 | 2.56 | 1983 | 1983 | 0.002 | 0.009 | 0.260 | 0.066 | -0.00479 | -0.01666 | 3.481 |
| 23 | 1526300 | 1 | PRA | GH | 6.35 | 0.00110 | 0.00282 | 2.57 | 1968 | 1971 | 0.054 | 0.204 | 0.900 | 0.898 | -0.00020 | -0.00152 | 7.721 |
| 25 | 1531700 | 1 | VOLTA | GH | 4.67 | 0.00217 | 0.00457 | 2.11 | 1968 | 1978 | 0.000 | 0.008 | 0.090 | 0.840 | 0.00413 | -0.00260 | -0.628 |
| 45 | 2178300 | 2 | YONGDING HE | CN | 3.51 | -0.00502 | -0.01150 | 2.29 | 1972 | 1972 | 0.008 | 0.005 | 0.981 | 0.200 | 0.00064 | 0.02979 | 46.785 |
| 46 | 2178400 | 2 | DALINGHE | CN | 3.42 | -0.00639 | -0.01860 | 2.91 | 1971 | 1970 | 0.000 | 0.003 | 0.522 | 0.745 | -0.00509 | -0.01123 | 2.207 |
| 47 | 2178500 | 2 | LUAN HE | CN | 3.44 | -0.00508 | -0.01284 | 2.53 | 1972 | 1969 | 0.002 | 0.004 | 0.753 | 0.965 | -0.00311 | -0.00066 | 0.211 |
| 48 | 2179100 | 2 | LIAO HE | CN | 3.47 | -0.00728 | -0.02015 | 2.77 | 1957 | 1970 | 0.000 | 0.001 | 0.107 | 0.991 | -0.00856 | -0.00164 | 0.192 |
| 56 | 2260500 | 2 | IRRAWADDY | MM | 3.37 | -0.00151 | -0.00117 | 0.78 | 1983 | 1983 | 0.009 | 0.298 | 0.119 | 0.061 | -0.00827 | -0.02844 | 3.439 |
| 58 | 2335950 | 2 | INDUS | PK | 3.34 | -0.00278 | -0.00842 | 3.03 | 1950 | 1973 | 0.007 | 0.045 | 0.076 | 0.227 | -0.00378 | -0.01879 | 4.970 |
| 69 | 2588700 | 2 | KITAKAMI | JP | 3.58 | -0.00354 | -0.00999 | 2.82 | 1952 | 1955 | 0.009 | 0.044 | 0.440 | 0.416 | -0.00268 | -0.01211 | 4.525 |
| 72 | 2589700 | 2 | MOGAMI | JP | 3.59 | -0.00401 | -0.01224 | 3.05 | 1952 | 1952 | 0.004 | 0.020 | 0.472 | 0.333 | -0.00263 | -0.01563 | 5.947 |
| 75 | 2651100 | 2 | BRAHMAPUTRA | BD | 3.39 | -0.00167 | -0.00216 | 1.30 | 1983 | 1985 | 0.027 | 0.240 | 0.138 | 0.134 | -0.01091 | -0.02456 | 2.252 |
| 78 | 2846800 | 2 | GANGES | IN | 3.74 | -0.00282 | -0.00605 | 2.14 | 1962 | 1965 | 0.007 | 0.142 | 0.485 | 0.955 | -0.00178 | 0.00090 | -0.507 |
| 80 | 2853200 | 2 | NARMADA | IN | 4.00 | -0.00224 | -0.00510 | 2.28 | 1954 | 1962 | 0.056 | 0.101 | 0.496 | 0.924 | -0.00182 | 0.00107 | -0.592 |
| 81 | 2853300 | 2 | TAPTI RIVER | IN | 4.05 | -0.00237 | -0.00536 | 2.26 | 1975 | 1955 | 0.062 | 0.112 | 0.470 | 0.949 | -0.00379 | -0.00123 | 0.323 |
| 82 | 2854050 | 2 | DAMODAR RIVER | IN | 4.01 | -0.00359 | -0.00643 | 1.79 | 1962 | 1962 | 0.008 | 0.185 | 0.883 | 0.737 | -0.00078 | 0.00390 | -5.015 |
| 87 | 2855800 | 2 | MAHANADI RIVER (MA | IN | 4.38 | -0.00502 | -0.01388 | 2.76 | 1961 | 1955 | 0.000 | 0.000 | 0.150 | 0.109 | -0.00447 | -0.01622 | 3.629 |
| 88 | 2856900 | 2 | GODAVARI | IN | 4.29 | -0.00261 | -0.00681 | 2.61 | 1955 | 1955 | 0.015 | 0.040 | 0.425 | 0.772 | -0.00198 | -0.00316 | 1.600 |
| 92 | 2906900 | 2 | AMUR | RU | 3.42 | -0.00732 | -0.02556 | 3.49 | 1956 | 1954 | 0.000 | 0.000 | 0.425 | 0.250 | -0.00359 | -0.01835 | 5.117 |
| 97 | 2919200 | 2 | URAL | KZ | 3.87 | -0.00675 | -0.01437 | 2.13 | 1957 | 1977 | 0.011 | 0.312 | 0.474 | 0.700 | -0.00676 | 0.01863 | -2.754 |
| 114 | 3102500 | 3 | ATRATO | CO | 6.56 | 0.00144 | 0.00459 | 3.19 | 1939 | 1939 | 0.002 | 0.000 | 0.942 | 0.973 | -0.00009 | -0.00008 | 0.894 |
| 123 | 3206720 | 3 | ORINOCO | VE | 6.10 | 0.00167 | 0.00582 | 3.48 | 1957 | 1957 | 0.001 | 0.001 | 0.720 | 0.788 | -0.00051 | -0.00153 | 3.025 |
| 130 | 3308400 | 3 | CUYUNI | GY | 6.30 | 0.00139 | 0.00589 | 4.25 | 1983 | 1971 | 0.000 | 0.000 | 0.567 | 0.096 | 0.00272 | 0.01479 | 5.440 |
| 131 | 3308600 | 3 | ESSEQUIBO | GY | 6.04 | 0.00102 | 0.00337 | 3.30 | 1971 | 1971 | 0.043 | 0.011 | 0.173 | 0.159 | 0.00322 | 0.00913 | 2.837 |
| 150 | 3650335 | 3 | RIO MEARIM | BR | 5.66 | 0.00104 | 0.00398 | 3.83 | 1958 | 1958 | 0.048 | 0.004 | 0.777 | 0.112 | -0.00045 | -0.01061 | 23.601 |
| 152 | 3650481 | 3 | RIO PARNAIBA | BR | 5.65 | 0.00135 | 0.00529 | 3.92 | 1958 | 1958 | 0.010 | 0.001 | 0.730 | 0.921 | 0.00056 | -0.00078 | -1.389 |
| 156 | 3651900 | 3 | SAO FRANCISCO | BR | 5.24 | 0.00172 | 0.00636 | 3.69 | 1932 | 1932 | 0.033 | 0.011 | 0.383 | 0.097 | 0.00088 | 0.00511 | 5.782 |
| 157 | 3652039 | 3 | RIO ITAPICURU | BR | 4.22 | 0.00140 | 0.00456 | 3.27 | 1932 | 1933 | 0.031 | 0.043 | 0.629 | 0.296 | 0.00037 | 0.00216 | 5.855 |
| 158 | 3652050 | 3 | RIO VAZA-BARRIS | BR | 4.47 | 0.00129 | 0.00353 | 2.73 | 1933 | 1933 | 0.035 | 0.161 | 0.938 | 0.599 | 0.00008 | 0.00157 | 18.577 |
| 160 | 3652220 | 3 | RIO DE CONTAS | BR | 5.76 | 0.00218 | 0.00834 | 3.83 | 1930 | 1930 | 0.008 | 0.002 | 0.451 | 0.235 | 0.00086 | 0.00414 | 4.834 |
| 161 | 3652320 | 3 | RIO PRADO | BR | 5.23 | 0.00148 | 0.00478 | 3.22 | 1930 | 1930 | 0.068 | 0.035 | 0.582 | 0.880 | 0.00044 | 0.00055 | 1.247 |
| 162 | 3652455 | 3 | JEQUITINHONHA | BR | 4.52 | 0.00142 | 0.00533 | 3.74 | 1980 | 1937 | 0.078 | 0.054 | 0.395 | 0.385 | 0.00358 | 0.00300 | 0.839 |
| 168 | 3843100 | 3 | MIRA | EC | 5.65 | -0.00206 | -0.00601 | 2.92 | 1977 | 1977 | 0.000 | 0.000 | 0.066 | 0.116 | -0.00499 | -0.01346 | 2.699 |
| 169 | 3844100 | 3 | ESMERALDAS | EC | 6.97 | -0.00121 | -0.00409 | 3.37 | 1970 | 1970 | 0.002 | 0.007 | 0.694 | 0.465 | -0.00057 | -0.00407 | 7.160 |
| 171 | 3844450 | 3 | VINCES | EC | 6.24 | -0.00107 | -0.00468 | 4.36 | 1962 | 1955 | 0.014 | 0.000 | 0.750 | 0.362 | 0.00065 | -0.00279 | -4.298 |
| 232 | 4209402 | 4 | COPPERMINE RIVER | CA | 3.45 | -0.00750 | -0.02014 | 2.69 | 1976 | 1976 | 0.016 | 0.087 | 0.495 | 0.650 | -0.01386 | -0.02472 | 1.784 |
| 233 | 4209600 | 4 | ELLICE RIVER | CA | 3.99 | -0.00765 | -0.02281 | 2.98 | 1976 | 1966 | 0.005 | 0.015 | 0.182 | 0.080 | -0.01694 | -0.05337 | 3.150 |
| 237 | 4214025 | 4 | HAYES RIVER (TRIB. | CA | 3.64 | -0.00725 | -0.01971 | 2.72 | 1976 | 1984 | 0.011 | 0.044 | 0.074 | 0.453 | -0.03471 | -0.05878 | 1.693 |
| 263 | 4243300 | 4 | ST. MAURICE (RIVIE | CA | 3.72 | -0.00524 | -0.00957 | 1.83 | 1924 | 1925 | 0.062 | 0.452 | 0.714 | 0.952 | -0.00100 | -0.00094 | 0.940 |
| 264 | 4243400 | 4 | SAGUENAY (RIVIERE) | CA | 3.67 | -0.00438 | -0.01094 | 2.50 | 1949 | 1935 | 0.155 | 0.447 | 0.817 | 0.644 | 0.00170 | -0.00713 | -4.183 |
| 272 | 4356080 | 4 | SAN PEDRO | MX | 4.32 | 0.00195 | 0.00451 | 2.32 | 1927 | 1979 | 0.170 | 0.879 | 0.529 | 0.661 | 0.00093 | 0.01016 | 10.943 |
| 295 | 5553100 | 5 | PURARI | PG | 6.38 | -0.00328 | -0.01081 | 3.30 | 1946 | 1946 | 0.000 | 0.000 | 0.180 | 0.412 | 0.00100 | 0.00191 | 1.905 |
| 301 | 5607500 | 5 | DE GREY RIVER | AU | 3.66 | -0.00260 | -0.00480 | 1.85 | 1939 | 1939 | 0.064 | 0.342 | 0.576 | 0.865 | -0.00095 | 0.00070 | -0.737 |
| 311 | 5865300 | 5 | WAIKATO RIVER | NZ | 4.05 | 0.00216 | 0.00933 | 4.32 | 1953 | 1953 | 0.044 | 0.004 | 0.737 | 0.851 | -0.00090 | -0.00160 | 1.781 |
| 333 | 6401601 | 6 | SVARTA, SKAGAFIROI | IS | 5.17 | -0.00347 | -0.01143 | 3.30 | 1920 | 1920 | 0.016 | 0.081 | 0.907 | 0.430 | 0.00019 | -0.00539 | -28.674 |
| Lp | GRDC_NO | WMO | RIVER | CNT | AREA | JAN | FEB | MAR | APR | MAY | JUN | JUL | AUG | SEP | OCT | NOV | DEC | MIN | MAX | MEAN | STD | Cv |
| 2 | 1147010 | 1 | CONGO | CD | 3475000 | 23.7 | 24.1 | 24.4 | 24.2 | 23.9 | 23.0 | 22.6 | 23.2 | 23.9 | 24.0 | 23.7 | 23.5 | 21.5 | 26.0 | 23.69 | 0.67 | 0.03 |
| 3 | 1159100 | 1 | ORANGE | ZA | 850530 | 24.2 | 23.5 | 21.5 | 18.0 | 13.9 | 10.6 | 10.3 | 12.8 | 16.4 | 19.7 | 21.6 | 23.5 | 7.8 | 26.3 | 18.01 | 4.97 | 0.28 |
| 4 | 1160580 | 1 | GROOT-VIS | ZA | 29745 | 20.8 | 20.6 | 18.9 | 16.0 | 12.7 | 9.9 | 9.4 | 11.4 | 13.6 | 15.8 | 17.8 | 19.8 | 7.5 | 22.6 | 15.56 | 4.02 | 0.26 |
| 5 | 1160880 | 1 | TUGELA | ZA | 28920 | 20.7 | 20.4 | 19.0 | 16.6 | 13.2 | 10.4 | 10.3 | 13.0 | 15.7 | 17.7 | 18.8 | 20.2 | 7.6 | 22.6 | 16.34 | 3.73 | 0.23 |
| 6 | 1286900 | 1 | RUFIJI | TZ | 158200 | 22.9 | 22.8 | 22.6 | 22.1 | 20.9 | 19.6 | 18.9 | 19.8 | 21.3 | 22.9 | 23.8 | 23.5 | 17.6 | 26.2 | 21.78 | 1.66 | 0.08 |
| 7 | 1289200 | 1 | PANGANI | TZ | 25110 | 22.5 | 22.8 | 22.5 | 21.6 | 20.0 | 18.8 | 18.0 | 18.5 | 19.8 | 21.1 | 22.0 | 22.3 | 16.1 | 24.9 | 20.83 | 1.77 | 0.09 |
| 8 | 1289450 | 1 | RUVU | TZ | 15190 | 26.8 | 26.8 | 26.6 | 25.5 | 24.4 | 22.8 | 22.2 | 22.8 | 23.8 | 25.0 | 26.1 | 26.9 | 20.7 | 28.5 | 24.99 | 1.75 | 0.07 |
| 9 | 1309700 | 1 | SEBOU | MA | 17250 | 7.0 | 8.2 | 10.3 | 12.6 | 15.6 | 19.9 | 23.9 | 24.3 | 20.7 | 16.1 | 11.0 | 7.9 | 4.2 | 27.0 | 14.81 | 6.08 | 0.41 |
| 10 | 1336500 | 1 | CROSS | CM | 6810 | 22.9 | 23.6 | 23.8 | 23.1 | 22.9 | 22.1 | 20.9 | 20.5 | 21.3 | 21.4 | 22.3 | 22.5 | 18.7 | 25.5 | 22.27 | 1.16 | 0.05 |
| 11 | 1338050 | 1 | SANAGA | CM | 131520 | 23.7 | 24.7 | 24.9 | 24.4 | 23.7 | 22.9 | 22.1 | 22.2 | 22.5 | 23.0 | 23.4 | 23.3 | 20.9 | 26.3 | 23.40 | 1.02 | 0.04 |
| 12 | 1339100 | 1 | NYONG | CM | 26400 | 23.9 | 24.6 | 24.8 | 24.5 | 24.2 | 23.4 | 22.6 | 22.6 | 23.1 | 23.4 | 23.7 | 23.8 | 21.1 | 26.2 | 23.70 | 0.87 | 0.04 |
| 13 | 1340500 | 1 | NTEM | CM | 18100 | 23.9 | 24.4 | 24.4 | 24.4 | 24.1 | 23.3 | 22.4 | 22.5 | 23.2 | 23.4 | 23.5 | 23.7 | 20.9 | 26.4 | 23.58 | 0.86 | 0.04 |
| 14 | 1362100 | 1 | NILE | EG | 2900000 | 21.9 | 23.1 | 25.2 | 27.0 | 27.8 | 27.5 | 26.4 | 26.1 | 26.4 | 26.1 | 24.2 | 22.2 | 19.4 | 29.5 | 25.32 | 2.08 | 0.08 |
| 15 | 1389090 | 1 | MANGOKY | MG | 53225 | 25.4 | 25.2 | 24.7 | 23.5 | 20.5 | 18.5 | 18.1 | 19.3 | 21.6 | 24.0 | 25.6 | 25.5 | 16.7 | 27.0 | 22.65 | 2.83 | 0.12 |
| 16 | 1389230 | 1 | TSIRIBIHINA | MG | 45000 | 23.3 | 23.1 | 22.9 | 22.0 | 19.6 | 17.7 | 17.1 | 18.2 | 20.2 | 22.3 | 23.3 | 23.2 | 15.8 | 24.9 | 21.07 | 2.37 | 0.11 |
| 18 | 1426380 | 1 | BANDAMA | CI | 95500 | 26.5 | 28.2 | 28.5 | 28.2 | 27.3 | 26.1 | 25.1 | 24.8 | 25.4 | 26.1 | 26.5 | 25.9 | 23.6 | 30.5 | 26.55 | 1.29 | 0.05 |
| 19 | 1427500 | 1 | SASSANDRA | CI | 62000 | 24.7 | 26.6 | 26.9 | 26.9 | 26.3 | 25.3 | 24.3 | 24.1 | 24.7 | 25.3 | 25.3 | 24.3 | 22.7 | 28.5 | 25.40 | 1.10 | 0.04 |
| 20 | 1427600 | 1 | DAVO | CI | 6600 | 26.0 | 27.2 | 27.2 | 27.2 | 26.6 | 25.6 | 24.7 | 24.5 | 25.1 | 25.9 | 26.1 | 25.7 | 23.4 | 28.7 | 25.96 | 1.02 | 0.04 |
| 21 | 1428500 | 1 | COMOE | CI | 69900 | 26.4 | 28.5 | 29.4 | 29.0 | 28.1 | 26.6 | 25.5 | 25.1 | 25.7 | 26.7 | 27.1 | 26.1 | 23.8 | 31.0 | 27.01 | 1.44 | 0.05 |
| 22 | 1445100 | 1 | KOUILOU | CG | 55010 | 24.7 | 25.2 | 25.5 | 25.5 | 24.8 | 22.7 | 21.5 | 22.1 | 23.4 | 24.6 | 24.7 | 24.6 | 19.8 | 27.4 | 24.11 | 1.42 | 0.06 |
| 23 | 1526300 | 1 | PRA | GH | 22714 | 26.1 | 27.2 | 27.4 | 27.3 | 26.9 | 25.7 | 24.8 | 24.4 | 25.2 | 25.9 | 26.4 | 26.1 | 22.3 | 29.4 | 26.11 | 1.13 | 0.04 |
| 24 | 1530100 | 1 | TANO | GH | 15800 | 26.0 | 27.2 | 27.4 | 27.1 | 26.6 | 25.3 | 24.4 | 24.0 | 24.7 | 25.5 | 26.1 | 25.9 | 22.1 | 29.4 | 25.85 | 1.18 | 0.05 |
| 25 | 1531700 | 1 | VOLTA | GH | 394100 | 26.1 | 28.4 | 30.3 | 30.7 | 29.7 | 27.7 | 26.3 | 25.7 | 26.2 | 27.6 | 27.6 | 26.2 | 24.1 | 32.2 | 27.70 | 1.75 | 0.06 |
| 26 | 1643100 | 1 | OGOOUE | GA | 205000 | 24.1 | 24.5 | 24.8 | 24.9 | 24.4 | 23.0 | 22.0 | 22.4 | 23.5 | 24.0 | 23.9 | 23.9 | 20.6 | 26.5 | 23.80 | 1.03 | 0.04 |
| 27 | 1644100 | 1 | NYANGA | GA | 20000 | 25.0 | 25.3 | 25.6 | 25.7 | 24.9 | 22.7 | 21.6 | 21.9 | 23.1 | 24.5 | 24.6 | 24.7 | 19.9 | 27.4 | 24.12 | 1.47 | 0.06 |
| 28 | 1732100 | 1 | MONO | BJ | 21575 | 26.3 | 27.9 | 28.2 | 27.7 | 26.9 | 25.5 | 24.5 | 24.3 | 24.9 | 25.7 | 26.6 | 26.1 | 23.2 | 29.9 | 26.22 | 1.35 | 0.05 |
| 29 | 1733600 | 1 | OUEME | BJ | 46990 | 27.0 | 28.6 | 29.1 | 28.6 | 27.5 | 26.1 | 25.0 | 24.5 | 25.1 | 26.1 | 27.0 | 26.6 | 23.6 | 30.5 | 26.78 | 1.53 | 0.06 |
| 30 | 1789300 | 1 | TANA | KE | 42220 | 22.7 | 23.7 | 24.2 | 23.8 | 23.0 | 21.8 | 21.0 | 21.3 | 22.4 | 23.4 | 23.1 | 22.3 | 19.8 | 26.0 | 22.72 | 1.12 | 0.05 |
| 31 | 1812100 | 1 | SENEGAL | SN | 268000 | 23.4 | 26.1 | 29.0 | 31.8 | 33.4 | 32.4 | 29.9 | 28.5 | 29.0 | 29.6 | 27.1 | 23.8 | 20.3 | 35.5 | 28.67 | 3.13 | 0.11 |
| 32 | 1813200 | 1 | GAMBIA | SN | 42000 | 25.2 | 27.7 | 30.1 | 31.8 | 31.5 | 29.0 | 26.8 | 26.1 | 26.3 | 27.1 | 26.4 | 24.8 | 21.5 | 33.5 | 27.73 | 2.35 | 0.08 |
| 33 | 1814070 | 1 | GEBA | SN | 7340 | 23.4 | 26.2 | 28.9 | 30.5 | 30.7 | 28.8 | 26.9 | 26.5 | 26.4 | 27.1 | 26.0 | 23.5 | 20.0 | 32.6 | 27.09 | 2.36 | 0.09 |
| 34 | 1815020 | 1 | CORUBAL | SN | 23840 | 24.1 | 26.1 | 28.1 | 29.3 | 28.7 | 27.0 | 25.5 | 25.2 | 25.4 | 25.8 | 25.3 | 23.6 | 20.7 | 30.9 | 26.18 | 1.79 | 0.07 |
| 37 | 1880100 | 1 | JUBA | SO | 179520 | 24.1 | 25.0 | 25.7 | 24.9 | 24.3 | 23.9 | 23.1 | 23.3 | 24.0 | 23.6 | 23.3 | 23.3 | 19.9 | 28.2 | 24.05 | 1.09 | 0.05 |
| 38 | 1891500 | 1 | ZAMBEZI | MZ | 940000 | 22.9 | 22.8 | 22.5 | 21.7 | 19.2 | 16.8 | 16.6 | 19.0 | 22.6 | 24.8 | 24.2 | 23.1 | 14.5 | 26.7 | 21.35 | 2.77 | 0.13 |
| 39 | 1894200 | 1 | BUZI | MZ | 26314 | 25.2 | 24.9 | 24.0 | 22.9 | 20.7 | 18.6 | 18.3 | 19.9 | 22.2 | 24.3 | 24.9 | 25.0 | 15.5 | 27.3 | 22.57 | 2.63 | 0.12 |
| 40 | 1895500 | 1 | SAVE | MZ | 100885 | 24.2 | 23.9 | 23.0 | 21.7 | 19.1 | 16.8 | 16.5 | 18.3 | 21.2 | 23.5 | 24.2 | 24.1 | 14.8 | 26.9 | 21.37 | 2.98 | 0.14 |
| 41 | 1896500 | 1 | LIMPOPO | MZ | 342000 | 24.3 | 23.8 | 22.6 | 20.2 | 16.9 | 14.1 | 13.9 | 16.4 | 20.0 | 22.7 | 23.5 | 24.1 | 11.6 | 27.2 | 20.21 | 3.89 | 0.19 |
| 42 | 1897500 | 1 | INCOMATI | MZ | 37600 | 22.9 | 22.6 | 21.6 | 19.8 | 16.9 | 14.5 | 14.3 | 16.2 | 18.7 | 20.7 | 21.4 | 22.5 | 11.9 | 25.4 | 19.34 | 3.14 | 0.16 |
| 43 | 1899100 | 1 | MAPUTO | MZ | 28500 | 21.6 | 21.5 | 20.4 | 18.4 | 15.7 | 13.2 | 13.1 | 15.0 | 17.3 | 19.2 | 20.1 | 21.2 | 10.3 | 23.7 | 18.06 | 3.12 | 0.17 |
| 44 | 1992900 | 1 | SHIRE | MW | 149500 | 23.0 | 22.8 | 22.6 | 21.9 | 20.1 | 18.0 | 17.7 | 19.0 | 21.4 | 24.0 | 24.6 | 23.6 | 15.4 | 26.9 | 21.55 | 2.38 | 0.11 |
| 45 | 2178300 | 2 | YONGDING HE | CN | 42500 | -11.6 | -8.3 | -0.9 | 7.3 | 14.3 | 19.1 | 21.3 | 19.6 | 14.1 | 6.8 | -2.5 | -9.7 | -16.1 | 24.8 | 5.79 | 11.68 | 2.02 |
| 46 | 2178400 | 2 | DALINGHE | CN | 17687 | -11.9 | -7.8 | -0.4 | 9.3 | 16.3 | 21.3 | 23.9 | 22.9 | 16.6 | 9.3 | -0.7 | -8.9 | -16.2 | 26.9 | 7.48 | 12.58 | 1.68 |
| 47 | 2178500 | 2 | LUAN HE | CN | 44100 | -13.9 | -10.0 | -2.7 | 6.9 | 13.5 | 18.6 | 21.1 | 19.7 | 13.7 | 6.3 | -3.3 | -11.4 | -17.8 | 24.5 | 4.87 | 12.31 | 2.53 |
| 48 | 2179100 | 2 | LIAO HE | CN | 120764 | -14.9 | -11.2 | -2.8 | 7.1 | 14.1 | 19.8 | 22.8 | 21.2 | 14.6 | 6.9 | -3.5 | -12.2 | -20.3 | 25.7 | 5.15 | 13.24 | 2.57 |
| 49 | 2180800 | 2 | HUANG HE (YELLOW R | CN | 730036 | -9.3 | -5.5 | 0.9 | 7.5 | 13.2 | 17.4 | 19.5 | 18.2 | 13.1 | 6.8 | -1.2 | -7.7 | -14.4 | 21.4 | 6.07 | 10.04 | 1.66 |
| 50 | 2181900 | 2 | YANGTZE RIVER (CHA | CN | 1705383 | 0.3 | 2.3 | 6.6 | 11.6 | 16.0 | 19.0 | 21.3 | 20.9 | 17.3 | 12.3 | 6.6 | 1.8 | -2.4 | 23.0 | 11.34 | 7.40 | 0.65 |
| 51 | 2181950 | 2 | HUAI HE | CN | 121330 | 1.5 | 3.4 | 8.5 | 15.3 | 20.7 | 25.3 | 27.6 | 26.8 | 22.0 | 16.4 | 9.6 | 3.4 | -3.0 | 31.0 | 15.05 | 9.25 | 0.61 |
| 52 | 2186800 | 2 | XI JIANG | CN | 329705 | 9.8 | 11.3 | 15.1 | 19.5 | 22.8 | 24.5 | 25.3 | 25.0 | 23.3 | 19.7 | 15.3 | 11.3 | 5.9 | 26.6 | 18.56 | 5.66 | 0.31 |
| 53 | 2186901 | 2 | BEI JIANG | CN | 38363 | 9.1 | 10.8 | 14.0 | 18.9 | 23.5 | 25.8 | 27.6 | 27.3 | 25.4 | 20.9 | 15.8 | 11.1 | 4.8 | 29.6 | 19.19 | 6.66 | 0.35 |
| 55 | 2260100 | 2 | CHINDWIN RIVER | MM | 27420 | 12.4 | 14.3 | 17.8 | 20.4 | 22.9 | 24.0 | 24.3 | 24.3 | 23.9 | 21.7 | 17.9 | 13.2 | 10.9 | 25.8 | 19.76 | 4.38 | 0.22 |
| 56 | 2260500 | 2 | IRRAWADDY | MM | 117900 | 10.7 | 12.6 | 16.1 | 19.1 | 21.3 | 21.9 | 22.0 | 21.8 | 21.6 | 19.3 | 15.6 | 11.6 | 9.3 | 23.4 | 17.79 | 4.19 | 0.24 |
| 57 | 2261500 | 2 | SITTANG RIVER | MM | 14660 | 20.3 | 22.5 | 26.2 | 29.1 | 28.1 | 26.1 | 25.7 | 25.5 | 25.9 | 25.7 | 23.6 | 20.5 | 18.0 | 31.9 | 24.93 | 2.69 | 0.11 |
| 58 | 2335950 | 2 | INDUS | PK | 832418 | 4.4 | 7.0 | 12.2 | 17.9 | 22.9 | 25.8 | 25.5 | 24.4 | 22.2 | 17.5 | 11.4 | 6.3 | 1.7 | 27.3 | 16.46 | 7.65 | 0.47 |
| 61 | 2423450 | 2 | KARKHEH | IR | 45882 | 3.7 | 4.7 | 8.4 | 12.8 | 18.2 | 24.1 | 28.2 | 28.2 | 24.3 | 18.6 | 12.3 | 6.7 | -3.6 | 30.2 | 15.86 | 8.74 | 0.55 |
| 62 | 2423500 | 2 | KARUN | IR | 60769 | 2.6 | 4.6 | 8.6 | 13.6 | 19.5 | 24.9 | 28.1 | 27.6 | 23.9 | 18.1 | 11.5 | 5.4 | -3.1 | 30.5 | 15.69 | 8.95 | 0.57 |
| 63 | 2569005 | 2 | MEKONG | KH | 635000 | 15.1 | 17.2 | 20.1 | 22.3 | 23.2 | 23.5 | 23.4 | 23.0 | 22.3 | 20.6 | 17.9 | 15.3 | 12.5 | 24.8 | 20.33 | 3.09 | 0.15 |
| 65 | 2588200 | 2 | YODO | JP | 7281 | 2.2 | 2.6 | 5.6 | 11.3 | 16.1 | 20.3 | 24.9 | 25.8 | 21.9 | 15.6 | 9.9 | 4.9 | -0.5 | 28.1 | 13.43 | 8.29 | 0.62 |
| 66 | 2588301 | 2 | KISO | JP | 4683.8 | -1.7 | -0.8 | 2.8 | 9.2 | 13.9 | 18.2 | 22.5 | 23.3 | 19.4 | 12.8 | 6.8 | 1.4 | -4.7 | 25.2 | 10.65 | 8.73 | 0.82 |
| 67 | 2588320 | 2 | TENRYU | JP | 4880 | -3.3 | -2.1 | 1.4 | 7.4 | 12.1 | 16.1 | 20.5 | 20.9 | 17.1 | 11.0 | 5.3 | 0.0 | -6.3 | 23.2 | 8.86 | 8.40 | 0.95 |
| 68 | 2588551 | 2 | TONE | JP | 12458 | 0.3 | 1.0 | 4.3 | 10.3 | 15.0 | 19.0 | 23.4 | 24.2 | 20.6 | 14.2 | 8.5 | 3.1 | -2.8 | 26.6 | 11.98 | 8.38 | 0.70 |
| 69 | 2588700 | 2 | KITAKAMI | JP | 7869.4 | -3.7 | -2.9 | 0.8 | 7.2 | 12.7 | 17.1 | 21.6 | 22.9 | 18.3 | 11.6 | 5.5 | -0.5 | -7.3 | 25.7 | 9.23 | 9.21 | 1.00 |
| 72 | 2589700 | 2 | MOGAMI | JP | 6270.9 | -2.0 | -1.5 | 1.6 | 8.1 | 13.9 | 18.5 | 22.9 | 24.1 | 19.4 | 12.7 | 6.6 | 1.0 | -5.9 | 27.0 | 10.45 | 9.16 | 0.88 |
| 73 | 2595400 | 2 | EUPHRATES | IQ | 274100 | 3.2 | 5.2 | 9.4 | 15.2 | 20.6 | 25.4 | 28.9 | 28.6 | 24.5 | 18.4 | 11.2 | 5.3 | -1.6 | 32.0 | 16.33 | 9.12 | 0.56 |
| 74 | 2595700 | 2 | TIGRIS | IQ | 134000 | 2.8 | 4.4 | 8.5 | 13.9 | 19.9 | 25.5 | 29.5 | 29.4 | 25.0 | 18.6 | 11.2 | 5.2 | -2.6 | 32.1 | 16.17 | 9.54 | 0.59 |
| 75 | 2651100 | 2 | BRAHMAPUTRA | BD | 636130 | 0.2 | 2.2 | 5.8 | 9.0 | 12.0 | 14.6 | 15.1 | 14.8 | 13.5 | 9.8 | 5.0 | 1.2 | -1.7 | 16.5 | 8.60 | 5.38 | 0.63 |
| 78 | 2846800 | 2 | GANGES | IN | 835000 | 12.7 | 15.2 | 20.2 | 25.3 | 28.5 | 28.4 | 25.7 | 24.9 | 24.6 | 22.1 | 17.4 | 13.6 | 10.3 | 30.8 | 21.56 | 5.47 | 0.25 |
| 79 | 2853150 | 2 | MAHI RIVER | IN | 33670 | 19.1 | 21.7 | 26.4 | 30.7 | 33.2 | 31.5 | 27.9 | 26.7 | 27.2 | 26.8 | 22.9 | 20.2 | 16.7 | 35.7 | 26.18 | 4.37 | 0.17 |
| 80 | 2853200 | 2 | NARMADA | IN | 89345 | 18.7 | 21.0 | 25.7 | 30.3 | 33.2 | 30.9 | 26.8 | 25.9 | 26.2 | 25.2 | 21.4 | 18.6 | 16.3 | 34.8 | 25.31 | 4.63 | 0.18 |
| 81 | 2853300 | 2 | TAPTI RIVER | IN | 61575 | 20.9 | 23.1 | 27.3 | 31.3 | 33.2 | 30.5 | 27.0 | 26.2 | 26.4 | 26.1 | 22.3 | 20.5 | 18.7 | 34.8 | 26.24 | 3.97 | 0.15 |
| 82 | 2854050 | 2 | DAMODAR RIVER | IN | 19220 | 17.3 | 20.1 | 25.5 | 30.2 | 31.9 | 30.4 | 27.7 | 27.4 | 27.3 | 25.4 | 21.1 | 17.8 | 14.8 | 34.2 | 25.18 | 4.84 | 0.19 |
| 84 | 2854300 | 2 | KRISHNA | IN | 251355 | 22.9 | 24.9 | 28.0 | 30.1 | 30.5 | 27.6 | 25.7 | 25.3 | 25.5 | 25.6 | 23.6 | 22.2 | 20.5 | 31.9 | 25.99 | 2.58 | 0.10 |
| 85 | 2854500 | 2 | PENNER RIVER | IN | 53290 | 23.4 | 25.8 | 28.9 | 31.2 | 31.7 | 29.5 | 28.0 | 27.4 | 27.2 | 26.5 | 24.4 | 22.9 | 21.5 | 33.2 | 27.24 | 2.78 | 0.10 |
| 86 | 2854800 | 2 | CAUVERY RIVER | IN | 74004 | 22.1 | 24.0 | 26.2 | 27.6 | 27.3 | 25.4 | 24.6 | 24.5 | 24.4 | 24.3 | 23.1 | 22.0 | 20.7 | 28.9 | 24.63 | 1.78 | 0.07 |
| 87 | 2855800 | 2 | MAHANADI RIVER (MA | IN | 132090 | 19.7 | 22.5 | 26.9 | 31.1 | 34.0 | 31.2 | 27.1 | 26.8 | 27.0 | 25.7 | 21.7 | 19.1 | 16.8 | 36.7 | 26.07 | 4.53 | 0.17 |
| 88 | 2856900 | 2 | GODAVARI | IN | 299320 | 21.1 | 23.6 | 27.6 | 31.1 | 33.2 | 30.2 | 26.6 | 26.1 | 26.2 | 25.6 | 22.3 | 20.3 | 18.6 | 35.3 | 26.16 | 3.89 | 0.15 |
| 89 | 2901202 | 2 | ANADYR | RU | 156000 | -26.3 | -26.2 | -23.5 | -15.3 | -3.9 | 6.7 | 10.0 | 7.8 | 2.0 | -8.2 | -17.9 | -24.2 | -38.6 | 13.0 | -9.92 | 13.84 | -1.40 |
| 90 | 2902850 | 2 | KAMCHATKA | RU | 51600 | -19.8 | -17.1 | -12.4 | -5.2 | 1.7 | 8.0 | 11.7 | 10.8 | 5.7 | -1.3 | -10.3 | -17.2 | -27.6 | 14.9 | -3.77 | 11.19 | -2.96 |
| 91 | 2903420 | 2 | LENA | RU | 2430000 | -36.3 | -31.5 | -20.7 | -8.1 | 2.9 | 11.8 | 15.3 | 11.8 | 3.8 | -8.7 | -25.3 | -34.2 | -44.5 | 18.1 | -9.93 | 18.48 | -1.86 |
| 92 | 2906900 | 2 | AMUR | RU | 1730000 | -25.1 | -20.4 | -10.7 | 1.2 | 9.4 | 15.9 | 19.1 | 17.1 | 10.0 | 0.5 | -12.7 | -22.8 | -32.2 | 21.4 | -1.56 | 15.67 | -10.07 |
| 93 | 2909150 | 2 | YENISEI | RU | 2440000 | -27.7 | -24.4 | -14.8 | -4.4 | 4.2 | 12.0 | 15.4 | 12.3 | 5.3 | -4.4 | -17.2 | -25.4 | -36.2 | 18.8 | -5.75 | 15.32 | -2.66 |
| 94 | 2912600 | 2 | OB | RU | 2949998 | -19.0 | -17.5 | -9.9 | 0.3 | 8.4 | 15.2 | 17.9 | 14.9 | 8.9 | 0.3 | -9.6 | -16.6 | -30.1 | 20.7 | -0.59 | 13.30 | -22.69 |
| 96 | 2917100 | 2 | AMU DARYA | UZ | 450000 | -6.0 | -3.7 | 1.9 | 8.9 | 14.4 | 19.2 | 21.8 | 20.4 | 15.0 | 8.2 | 1.7 | -3.6 | -13.5 | 24.2 | 8.17 | 9.72 | 1.19 |
| 97 | 2919200 | 2 | URAL | KZ | 190000 | -14.7 | -14.4 | -7.7 | 5.1 | 13.9 | 19.0 | 21.0 | 18.9 | 12.5 | 3.7 | -4.6 | -11.5 | -25.7 | 25.8 | 3.44 | 13.30 | 3.87 |
| 99 | 2964998 | 2 | MAE KLONG | TH | 26449 | 22.3 | 24.4 | 26.3 | 27.5 | 26.5 | 25.5 | 25.0 | 24.8 | 24.8 | 24.5 | 23.3 | 21.7 | 19.1 | 29.5 | 24.72 | 1.77 | 0.07 |
| 100 | 2998110 | 2 | YANA | RU | 224000 | -44.7 | -41.1 | -30.3 | -15.8 | -1.1 | 9.1 | 12.0 | 8.3 | 0.1 | -16.0 | -34.8 | -41.8 | -51.5 | 17.0 | -16.34 | 20.91 | -1.28 |
| 101 | 2998150 | 2 | OMOLOY | RU | 10800 | -47.3 | -43.3 | -31.5 | -16.4 | -1.9 | 8.7 | 11.6 | 7.6 | -0.7 | -16.9 | -36.9 | -44.2 | -54.7 | 17.2 | -17.61 | 21.63 | -1.23 |
| 102 | 2998400 | 2 | INDIGIRKA | RU | 305000 | -43.8 | -40.5 | -30.3 | -16.1 | -1.0 | 9.5 | 12.1 | 8.6 | 0.4 | -15.8 | -33.6 | -41.6 | -50.1 | 17.3 | -16.00 | 20.71 | -1.29 |
| 103 | 2998450 | 2 | ALAZEYA | RU | 29000 | -37.7 | -35.2 | -27.4 | -15.6 | -0.9 | 10.7 | 13.2 | 9.5 | 2.5 | -11.7 | -27.3 | -35.1 | -44.4 | 18.9 | -12.92 | 18.75 | -1.45 |
| 104 | 2998510 | 2 | KOLYMA | RU | 526000 | -37.5 | -34.3 | -26.3 | -13.9 | 0.3 | 10.4 | 12.9 | 9.4 | 2.0 | -12.5 | -28.1 | -35.6 | -44.4 | 17.9 | -12.77 | 18.61 | -1.46 |
| 105 | 2998702 | 2 | ANYUY (TRIB. KOLYM | RU | 30000 | -35.0 | -33.9 | -28.4 | -18.3 | -4.0 | 7.7 | 10.4 | 7.0 | -0.2 | -13.9 | -27.1 | -33.4 | -47.1 | 15.1 | -14.09 | 17.16 | -1.22 |
| 106 | 2998720 | 2 | BOL. ANYUY (TRIB. | RU | 49600 | -35.4 | -34.0 | -27.6 | -16.8 | -2.4 | 8.8 | 11.1 | 7.8 | 0.7 | -12.9 | -26.6 | -33.4 | -47.0 | 16.0 | -13.39 | 17.49 | -1.31 |
| 107 | 2998800 | 2 | PALYAVAAM | RU | 6810 | -26.2 | -26.4 | -25.3 | -17.3 | -8.9 | 0.9 | 3.7 | 3.6 | -0.1 | -7.0 | -15.9 | -22.6 | -34.8 | 8.7 | -11.79 | 11.77 | -1.00 |
| 108 | 2999150 | 2 | ANABAR | RU | 78800 | -38.5 | -35.4 | -27.3 | -16.0 | -4.5 | 7.7 | 12.7 | 8.8 | 1.2 | -13.3 | -30.0 | -35.6 | -47.9 | 17.8 | -14.19 | 18.49 | -1.30 |
| 109 | 2999200 | 2 | NADYM | RU | 48000 | -23.7 | -22.7 | -14.8 | -7.5 | 0.2 | 10.3 | 15.8 | 12.2 | 6.1 | -4.1 | -14.8 | -21.0 | -34.2 | 20.4 | -5.33 | 14.03 | -2.63 |
| 110 | 2999250 | 2 | TAZ | RU | 100000 | -26.0 | -24.3 | -16.6 | -8.2 | 0.2 | 10.6 | 16.0 | 12.3 | 5.7 | -5.4 | -17.7 | -24.1 | -39.5 | 20.1 | -6.46 | 15.08 | -2.33 |
| 111 | 2999500 | 2 | PUR | RU | 95100 | -24.5 | -23.3 | -16.0 | -8.3 | -0.1 | 10.5 | 16.0 | 12.4 | 6.0 | -4.4 | -16.2 | -22.4 | -37.1 | 20.1 | -5.87 | 14.53 | -2.48 |
| 112 | 2999850 | 2 | KHATANGA | RU | 275000 | -36.0 | -33.9 | -26.9 | -16.4 | -5.9 | 5.0 | 11.7 | 8.6 | 0.8 | -13.3 | -27.8 | -32.7 | -46.1 | 16.3 | -13.90 | 17.18 | -1.24 |
| 113 | 2999910 | 2 | OLENEK | RU | 198000 | -39.1 | -35.5 | -26.1 | -14.6 | -2.9 | 8.5 | 13.1 | 9.3 | 1.7 | -12.5 | -29.8 | -35.9 | -48.7 | 17.7 | -13.64 | 18.77 | -1.38 |
| 114 | 3102500 | 3 | ATRATO | CO | 9432 | 24.6 | 24.9 | 25.1 | 25.0 | 24.9 | 24.8 | 24.5 | 24.7 | 24.5 | 24.3 | 24.4 | 24.4 | 22.6 | 27.3 | 24.67 | 0.72 | 0.03 |
| 115 | 3103300 | 3 | MAGDALENA | CO | 257438 | 22.7 | 23.0 | 23.1 | 23.1 | 23.0 | 22.9 | 22.9 | 22.9 | 22.8 | 22.5 | 22.2 | 22.4 | 20.6 | 24.9 | 22.79 | 0.69 | 0.03 |
| 119 | 3178900 | 3 | HUASCO | CL | 7187 | 2.8 | 2.8 | 1.2 | -1.2 | -3.1 | -4.9 | -5.2 | -4.4 | -3.2 | -1.6 | -0.3 | 1.8 | -7.5 | 5.4 | -1.27 | 2.94 | -2.31 |
| 122 | 3181500 | 3 | BAKER | CL | 23736 | 13.2 | 13.0 | 11.2 | 8.6 | 5.9 | 4.0 | 3.6 | 4.2 | 6.2 | 8.3 | 10.1 | 12.1 | -1.4 | 17.6 | 8.36 | 3.60 | 0.43 |
| 123 | 3206720 | 3 | ORINOCO | VE | 836000 | 24.9 | 25.5 | 25.8 | 25.3 | 24.7 | 24.0 | 23.7 | 24.1 | 24.5 | 24.8 | 24.9 | 24.8 | 22.1 | 27.7 | 24.75 | 0.92 | 0.04 |
| 124 | 3258200 | 3 | SALADO | AR | 29000 | 23.7 | 22.5 | 19.9 | 16.0 | 12.1 | 8.7 | 8.4 | 10.0 | 13.1 | 16.3 | 19.8 | 22.4 | 4.7 | 26.0 | 16.08 | 5.47 | 0.34 |
| 125 | 3265601 | 3 | PARANA | AR | 2346000 | 25.0 | 24.6 | 23.7 | 21.4 | 18.7 | 16.9 | 16.6 | 18.5 | 20.7 | 22.5 | 23.7 | 24.7 | 13.1 | 26.4 | 21.43 | 3.10 | 0.14 |
| 126 | 3275750 | 3 | COLORADO (ARGENTIN | AR | 223000 | 19.8 | 18.6 | 15.8 | 11.6 | 7.7 | 4.4 | 4.1 | 6.0 | 9.0 | 12.6 | 15.9 | 18.8 | 1.3 | 21.5 | 12.03 | 5.61 | 0.47 |
| 127 | 3275990 | 3 | NEGRO (ARGENTINIA) | AR | 95000 | 18.1 | 17.0 | 14.0 | 9.9 | 6.3 | 3.5 | 2.9 | 4.2 | 6.9 | 10.4 | 13.7 | 16.6 | 0.1 | 20.4 | 10.30 | 5.38 | 0.52 |
| 128 | 3276200 | 3 | CHUBUT | AR | 16400 | 14.7 | 14.1 | 11.7 | 7.9 | 4.4 | 1.4 | 0.9 | 2.6 | 5.1 | 7.9 | 10.8 | 13.3 | -4.5 | 17.8 | 7.90 | 4.91 | 0.62 |
| 129 | 3276800 | 3 | SANTA CRUZ | AR | 15550 | 9.1 | 8.6 | 6.5 | 3.8 | 0.1 | -2.2 | -2.6 | -1.3 | 1.1 | 4.0 | 6.2 | 8.0 | -6.1 | 11.5 | 3.46 | 4.25 | 1.23 |
| 130 | 3308400 | 3 | CUYUNI | GY | 53400 | 24.2 | 24.4 | 24.9 | 25.5 | 25.4 | 24.9 | 24.8 | 25.4 | 25.8 | 25.8 | 25.4 | 24.5 | 22.6 | 27.9 | 25.08 | 0.83 | 0.03 |
| 131 | 3308600 | 3 | ESSEQUIBO | GY | 66600 | 25.6 | 25.6 | 25.9 | 25.9 | 25.7 | 25.5 | 25.7 | 26.3 | 27.0 | 27.3 | 27.0 | 25.9 | 24.1 | 28.8 | 26.10 | 0.77 | 0.03 |
| 132 | 3410500 | 3 | CORANTIJN | SR | 51600 | 25.7 | 25.8 | 26.0 | 26.3 | 26.1 | 26.0 | 26.2 | 26.8 | 27.6 | 28.0 | 27.4 | 26.5 | 24.6 | 29.3 | 26.52 | 0.86 | 0.03 |
| 133 | 3411300 | 3 | COPPENAME | SR | 12300 | 25.1 | 25.2 | 25.5 | 25.7 | 25.7 | 25.6 | 25.8 | 26.5 | 27.1 | 27.4 | 26.9 | 25.8 | 23.9 | 28.8 | 26.02 | 0.86 | 0.03 |
| 134 | 3412800 | 3 | MARONI | SR | 63700 | 24.9 | 25.0 | 25.2 | 25.6 | 25.5 | 25.4 | 25.5 | 26.1 | 26.5 | 26.8 | 26.5 | 25.6 | 23.6 | 28.6 | 25.72 | 0.78 | 0.03 |
| 135 | 3469050 | 3 | URUGUAY | UY | 244000 | 23.9 | 23.3 | 21.8 | 18.4 | 15.3 | 13.3 | 12.8 | 14.1 | 15.9 | 18.1 | 20.6 | 22.9 | 9.6 | 25.6 | 18.35 | 4.07 | 0.22 |
| 136 | 3469100 | 3 | NEGRO (URUGUAY) | UY | 63000 | 23.8 | 23.0 | 21.3 | 17.4 | 13.8 | 11.3 | 11.0 | 12.3 | 14.0 | 16.7 | 19.6 | 22.2 | 7.2 | 26.0 | 17.20 | 4.66 | 0.27 |
| 137 | 3514800 | 3 | OYAPOCK | GF | 25120 | 24.5 | 24.4 | 24.6 | 24.9 | 24.8 | 24.8 | 24.9 | 25.4 | 25.8 | 26.0 | 25.8 | 25.0 | 23.0 | 29.0 | 25.07 | 0.80 | 0.03 |
| 138 | 3629000 | 3 | AMAZONAS | BR | 4640300 | 25.1 | 25.0 | 25.0 | 24.8 | 24.3 | 23.8 | 23.7 | 24.6 | 25.3 | 25.6 | 25.5 | 25.3 | 22.4 | 26.9 | 24.84 | 0.76 | 0.03 |
| 139 | 3629150 | 3 | RIO TAPAJOS | BR | 358657 | 24.8 | 25.0 | 24.9 | 24.9 | 24.7 | 24.3 | 24.0 | 24.8 | 25.4 | 25.5 | 25.2 | 25.0 | 21.7 | 28.0 | 24.89 | 0.87 | 0.03 |
| 140 | 3629204 | 3 | RIO JAMANXIM | BR | 40400 | 25.6 | 25.6 | 25.9 | 26.1 | 26.3 | 26.0 | 25.9 | 26.8 | 26.8 | 26.5 | 26.3 | 25.8 | 24.3 | 29.5 | 26.14 | 0.75 | 0.03 |
| 141 | 3630050 | 3 | XINGU | BR | 446570 | 24.6 | 24.6 | 24.7 | 24.7 | 24.4 | 23.8 | 23.8 | 24.7 | 25.3 | 25.2 | 25.0 | 24.8 | 22.0 | 27.6 | 24.63 | 0.76 | 0.03 |
| 142 | 3630300 | 3 | RIO MAICURU | BR | 17072 | 24.7 | 24.3 | 24.3 | 24.5 | 24.5 | 24.4 | 24.4 | 25.2 | 25.8 | 26.2 | 26.0 | 25.4 | 22.8 | 28.2 | 24.98 | 0.86 | 0.03 |
| 143 | 3631050 | 3 | RIO ARAGUARI | BR | 23373 | 24.8 | 24.6 | 24.7 | 24.9 | 25.0 | 25.3 | 25.5 | 26.1 | 26.6 | 26.8 | 26.6 | 25.8 | 23.2 | 28.9 | 25.58 | 0.94 | 0.04 |
| 144 | 3631100 | 3 | RIO JARI | BR | 51343 | 25.2 | 25.0 | 25.1 | 25.4 | 25.4 | 25.5 | 25.6 | 26.2 | 26.7 | 26.9 | 26.8 | 26.1 | 23.6 | 28.7 | 25.81 | 0.84 | 0.03 |
| 145 | 3631210 | 3 | RIO PARU DE ESTE | BR | 30945 | 25.2 | 25.0 | 25.1 | 25.3 | 25.3 | 25.4 | 25.4 | 26.0 | 26.6 | 27.1 | 26.8 | 26.0 | 23.7 | 28.7 | 25.77 | 0.86 | 0.03 |
| 146 | 3649950 | 3 | TOCANTINS | BR | 742300 | 24.5 | 24.4 | 24.4 | 24.5 | 24.0 | 23.2 | 23.1 | 24.5 | 25.7 | 25.5 | 24.9 | 24.5 | 21.0 | 28.3 | 24.43 | 1.00 | 0.04 |
| 147 | 3650150 | 3 | RIO CAPIM | BR | 38178 | 25.8 | 25.6 | 25.7 | 26.0 | 26.3 | 26.3 | 26.3 | 26.8 | 27.0 | 27.1 | 26.9 | 26.4 | 24.1 | 28.8 | 26.36 | 0.71 | 0.03 |
| 148 | 3650202 | 3 | RIO GURUPI | BR | 31850 | 25.4 | 25.2 | 25.1 | 25.2 | 25.4 | 25.2 | 25.1 | 25.7 | 26.2 | 26.3 | 26.3 | 26.0 | 23.6 | 27.8 | 25.58 | 0.70 | 0.03 |
| 149 | 3650285 | 3 | RIO PINDARE | BR | 34300 | 25.4 | 25.3 | 25.3 | 25.5 | 25.5 | 25.1 | 25.0 | 25.9 | 26.9 | 26.8 | 26.5 | 26.0 | 23.7 | 28.7 | 25.76 | 0.85 | 0.03 |
| 150 | 3650335 | 3 | RIO MEARIM | BR | 25500 | 25.2 | 25.0 | 25.0 | 25.1 | 25.0 | 24.6 | 24.5 | 25.7 | 27.0 | 27.0 | 26.6 | 26.0 | 22.9 | 29.0 | 25.55 | 1.07 | 0.04 |
| 151 | 3650359 | 3 | RIO ITAPECURU | BR | 50800 | 25.4 | 25.0 | 25.0 | 25.1 | 25.2 | 24.9 | 24.7 | 25.9 | 27.4 | 27.1 | 26.6 | 26.3 | 22.6 | 29.2 | 25.71 | 1.06 | 0.04 |
| 152 | 3650481 | 3 | RIO PARNAIBA | BR | 322823 | 25.4 | 25.2 | 25.1 | 25.2 | 25.1 | 24.7 | 24.7 | 25.8 | 27.2 | 27.3 | 26.7 | 26.0 | 23.2 | 29.2 | 25.71 | 1.06 | 0.04 |
| 153 | 3650525 | 3 | RIO ACARAU | BR | 11160 | 26.0 | 25.3 | 24.6 | 24.5 | 24.5 | 24.5 | 24.6 | 25.2 | 25.8 | 26.1 | 26.3 | 26.4 | 22.8 | 27.6 | 25.31 | 1.00 | 0.04 |
| 154 | 3650649 | 3 | RIO JAGUARIBE | BR | 48200 | 26.8 | 25.9 | 25.2 | 24.9 | 24.6 | 24.2 | 24.3 | 25.2 | 26.3 | 27.0 | 27.3 | 27.3 | 22.2 | 28.7 | 25.75 | 1.31 | 0.05 |
| 155 | 3650885 | 3 | RIO PARAIBA | BR | 19244 | 25.0 | 24.8 | 24.7 | 24.1 | 23.1 | 22.0 | 21.2 | 21.4 | 22.6 | 23.8 | 24.5 | 24.8 | 19.8 | 26.6 | 23.50 | 1.44 | 0.06 |
| 156 | 3651900 | 3 | SAO FRANCISCO | BR | 622600 | 24.4 | 24.4 | 24.2 | 23.7 | 22.4 | 21.1 | 20.7 | 21.9 | 23.8 | 24.8 | 24.5 | 24.3 | 19.2 | 27.1 | 23.35 | 1.52 | 0.07 |
| 157 | 3652039 | 3 | RIO ITAPICURU | BR | 35150 | 25.3 | 25.3 | 25.1 | 24.4 | 23.0 | 21.6 | 20.6 | 21.0 | 22.5 | 24.3 | 25.0 | 25.4 | 19.5 | 27.2 | 23.63 | 1.83 | 0.08 |
| 158 | 3652050 | 3 | RIO VAZA-BARRIS | BR | 15740 | 25.7 | 25.7 | 25.6 | 24.9 | 23.5 | 22.1 | 21.2 | 21.5 | 22.9 | 24.6 | 25.5 | 25.8 | 19.9 | 28.0 | 24.07 | 1.80 | 0.07 |
| 160 | 3652220 | 3 | RIO DE CONTAS | BR | 42245 | 24.2 | 24.4 | 24.1 | 23.5 | 22.2 | 21.2 | 20.4 | 21.2 | 22.9 | 24.1 | 23.6 | 24.1 | 18.8 | 27.8 | 22.99 | 1.56 | 0.07 |
| 161 | 3652320 | 3 | RIO PRADO | BR | 30360 | 23.7 | 23.8 | 23.4 | 22.6 | 21.0 | 19.8 | 19.0 | 20.2 | 21.6 | 22.9 | 22.8 | 23.4 | 17.7 | 26.8 | 22.02 | 1.74 | 0.08 |
| 162 | 3652455 | 3 | JEQUITINHONHA | BR | 67769 | 23.5 | 23.6 | 23.2 | 22.2 | 20.4 | 19.0 | 18.4 | 19.6 | 21.5 | 22.9 | 22.7 | 23.1 | 17.0 | 25.7 | 21.67 | 1.93 | 0.09 |
| 163 | 3652500 | 3 | MUCURI | BR | 14174 | 24.7 | 24.6 | 24.4 | 23.2 | 21.4 | 19.8 | 19.0 | 19.8 | 21.7 | 23.3 | 23.7 | 24.3 | 17.5 | 26.6 | 22.48 | 2.11 | 0.09 |
| 164 | 3652600 | 3 | RIO DOCE | BR | 78456 | 23.2 | 23.2 | 22.9 | 21.4 | 19.3 | 17.9 | 17.1 | 18.2 | 19.9 | 21.4 | 22.0 | 22.6 | 15.4 | 25.3 | 20.77 | 2.26 | 0.11 |
| 166 | 3653120 | 3 | RIO RIBEIRA DO IGU | BR | 12450 | 21.7 | 21.7 | 21.0 | 19.0 | 16.1 | 14.8 | 14.2 | 15.3 | 16.5 | 17.9 | 19.6 | 21.0 | 10.6 | 24.2 | 18.23 | 2.91 | 0.16 |
| 168 | 3843100 | 3 | MIRA | EC | 4960 | 17.1 | 16.9 | 17.4 | 17.4 | 17.5 | 16.9 | 16.1 | 15.9 | 16.8 | 17.2 | 17.2 | 17.4 | 14.1 | 23.9 | 16.99 | 1.73 | 0.10 |
| 169 | 3844100 | 3 | ESMERALDAS | EC | 18800 | 18.2 | 18.4 | 18.6 | 18.6 | 18.5 | 17.9 | 17.7 | 17.7 | 17.9 | 17.9 | 17.9 | 18.1 | 15.1 | 20.3 | 18.11 | 0.75 | 0.04 |
| 170 | 3844400 | 3 | DAULE | EC | 8690 | 25.1 | 25.4 | 25.6 | 25.7 | 25.1 | 24.2 | 23.7 | 23.6 | 23.9 | 24.1 | 24.2 | 24.8 | 20.7 | 27.5 | 24.62 | 1.02 | 0.04 |
| 171 | 3844450 | 3 | VINCES | EC | 4400 | 23.4 | 23.7 | 23.9 | 24.0 | 23.5 | 22.5 | 22.0 | 22.2 | 22.6 | 22.7 | 22.9 | 23.3 | 20.0 | 25.8 | 23.06 | 0.93 | 0.04 |
| 174 | 3948800 | 3 | CANETE | PE | 4900 | 8.7 | 8.9 | 8.7 | 8.0 | 6.4 | 5.2 | 4.7 | 5.1 | 6.0 | 6.9 | 7.4 | 7.9 | 2.7 | 12.3 | 6.99 | 1.64 | 0.23 |
| 176 | 4101500 | 4 | COLVILLE RIVER | US | 53535.3 | -28.2 | -27.4 | -25.3 | -15.5 | -2.8 | 7.7 | 10.5 | 7.0 | 0.0 | -11.6 | -21.6 | -26.7 | -40.0 | 13.5 | -11.15 | 14.66 | -1.31 |
| 177 | 4101800 | 4 | NOATAK RIVER | US | 31080 | -25.9 | -23.4 | -21.3 | -12.0 | 0.0 | 9.0 | 10.8 | 7.5 | 1.1 | -9.5 | -19.3 | -23.6 | -38.7 | 14.7 | -8.89 | 13.71 | -1.54 |
| 178 | 4101900 | 4 | KOBUK RIVER | US | 24656.8 | -24.8 | -22.7 | -19.0 | -9.9 | 2.1 | 10.5 | 12.2 | 9.1 | 2.9 | -8.0 | -18.3 | -23.4 | -37.7 | 14.9 | -7.44 | 14.02 | -1.88 |
| 179 | 4102100 | 4 | KUSKOKWIM RIVER | US | 80549 | -19.2 | -15.0 | -11.3 | -2.6 | 5.4 | 11.2 | 12.8 | 10.6 | 5.3 | -3.9 | -13.1 | -17.9 | -29.8 | 15.3 | -3.16 | 11.84 | -3.75 |
| 180 | 4102710 | 4 | COPPER RIVER | US | 62678 | -21.8 | -17.2 | -12.6 | -4.7 | 2.1 | 7.1 | 8.9 | 7.1 | 2.1 | -5.8 | -15.8 | -20.2 | -33.9 | 12.9 | -5.91 | 11.19 | -1.89 |
| 181 | 4102740 | 4 | NUSHAGAK RIVER | US | 25511.5 | -12.9 | -10.5 | -8.4 | -1.9 | 4.8 | 10.0 | 11.9 | 10.9 | 6.6 | -0.8 | -7.6 | -11.9 | -23.3 | 14.8 | -0.81 | 9.44 | -11.67 |
| 182 | 4102800 | 4 | SUSITNA RIVER | US | 50246 | -17.2 | -14.2 | -10.8 | -3.7 | 3.5 | 9.1 | 10.9 | 9.0 | 3.9 | -4.4 | -12.6 | -16.2 | -28.3 | 14.3 | -3.57 | 10.44 | -2.92 |
| 183 | 4103200 | 4 | YUKON RIVER | US | 831390 | -24.9 | -21.0 | -15.7 | -5.5 | 4.3 | 11.2 | 12.7 | 9.8 | 3.6 | -6.3 | -17.7 | -22.7 | -37.4 | 14.9 | -6.02 | 13.80 | -2.29 |
| 184 | 4115201 | 4 | COLUMBIA RIVER | US | 665371 | -5.1 | -2.8 | 0.8 | 5.0 | 9.3 | 13.2 | 17.4 | 16.7 | 12.1 | 6.2 | -0.2 | -4.4 | -13.8 | 20.5 | 5.68 | 7.90 | 1.39 |
| 185 | 4126700 | 4 | OUACHITA RIVER | US | 39621.8 | 6.3 | 8.1 | 12.5 | 17.2 | 21.4 | 25.6 | 27.4 | 27.1 | 23.8 | 17.7 | 11.8 | 7.2 | 0.2 | 30.2 | 17.17 | 7.74 | 0.45 |
| 186 | 4126800 | 4 | RED RIVER | US | 174825 | 5.1 | 7.2 | 11.7 | 16.6 | 21.0 | 25.6 | 27.8 | 27.5 | 23.5 | 17.5 | 11.0 | 6.1 | -1.0 | 30.7 | 16.72 | 8.24 | 0.49 |
| 187 | 4127800 | 4 | MISSISSIPPI RIVER | US | 2964255 | -4.2 | -2.2 | 3.1 | 9.5 | 15.0 | 20.0 | 23.0 | 22.1 | 17.4 | 11.0 | 3.5 | -2.4 | -11.0 | 26.5 | 9.64 | 9.67 | 1.00 |
| 188 | 4145081 | 4 | SKAGIT RIVER | US | 7088.8 | -3.8 | -2.1 | 0.1 | 3.5 | 7.1 | 10.0 | 13.3 | 13.3 | 10.2 | 4.8 | -0.4 | -3.4 | -12.5 | 17.0 | 4.38 | 6.27 | 1.43 |
| 189 | 4145900 | 4 | ROGUE RIVER | US | 10202 | 2.2 | 3.8 | 5.4 | 7.7 | 11.2 | 14.6 | 18.6 | 18.3 | 15.3 | 10.3 | 5.1 | 2.2 | -3.5 | 21.5 | 9.55 | 5.95 | 0.62 |
| 191 | 4146180 | 4 | EEL RIVER (CALIF.) | US | 8062.7 | 5.1 | 6.6 | 8.1 | 10.3 | 13.4 | 16.8 | 20.6 | 20.1 | 17.8 | 13.4 | 8.4 | 5.4 | 1.1 | 22.7 | 12.16 | 5.55 | 0.46 |
| 192 | 4146280 | 4 | SACRAMENTO RIVER | US | 60885.7 | 3.2 | 4.7 | 6.7 | 9.3 | 13.5 | 17.6 | 21.5 | 20.7 | 17.8 | 12.7 | 7.0 | 3.3 | -3.1 | 24.1 | 11.49 | 6.60 | 0.57 |
| 193 | 4146360 | 4 | SAN JOAQUIN RIVER | US | 35058.2 | 5.8 | 7.4 | 9.4 | 11.9 | 15.9 | 20.0 | 23.5 | 22.8 | 20.1 | 15.2 | 9.7 | 5.9 | 0.7 | 26.9 | 13.96 | 6.39 | 0.46 |
| 194 | 4146400 | 4 | SALINAS RIVER | US | 10764 | 8.2 | 9.3 | 10.9 | 12.7 | 15.6 | 18.7 | 21.2 | 21.0 | 19.3 | 15.8 | 11.4 | 8.3 | 3.6 | 23.9 | 14.35 | 4.83 | 0.34 |
| 195 | 4147011 | 4 | PENOBSCOT RIVER | US | 19463.9 | -10.9 | -9.8 | -3.7 | 3.5 | 10.4 | 15.8 | 18.8 | 17.6 | 13.0 | 6.9 | 0.3 | -7.3 | -16.9 | 21.7 | 4.56 | 10.50 | 2.30 |
| 196 | 4147060 | 4 | ST. CROIX RIVER | US | 3558.7 | -9.5 | -8.4 | -2.6 | 4.2 | 10.7 | 15.8 | 18.9 | 18.0 | 13.4 | 7.3 | 1.3 | -6.0 | -15.4 | 22.3 | 5.24 | 10.03 | 1.91 |
| 197 | 4147380 | 4 | MERRIMACK RIVER | US | 12004.7 | -6.2 | -5.5 | -0.2 | 6.4 | 12.7 | 17.7 | 20.5 | 19.3 | 15.0 | 9.0 | 2.9 | -3.8 | -11.8 | 22.9 | 7.31 | 9.55 | 1.31 |
| 198 | 4147460 | 4 | CONNECTICUT RIVER | US | 25019.4 | -8.4 | -7.5 | -1.8 | 5.1 | 11.7 | 16.6 | 19.3 | 18.1 | 13.9 | 7.7 | 1.4 | -5.5 | -14.4 | 21.7 | 5.88 | 9.90 | 1.68 |
| 199 | 4147500 | 4 | HUDSON RIVER | US | 20953 | -7.2 | -6.8 | -1.2 | 5.9 | 12.6 | 17.4 | 19.9 | 18.8 | 14.8 | 8.6 | 2.3 | -4.5 | -13.7 | 22.8 | 6.71 | 9.86 | 1.47 |
| 200 | 4147600 | 4 | DELAWARE RIVER | US | 17560.2 | -4.4 | -3.9 | 1.3 | 7.5 | 13.6 | 18.4 | 20.9 | 19.8 | 16.0 | 9.9 | 3.8 | -2.3 | -10.5 | 23.7 | 8.40 | 9.16 | 1.09 |
| 201 | 4147703 | 4 | SUSQUEHANNA RIVER | US | 70189 | -3.9 | -3.3 | 1.7 | 8.1 | 14.0 | 18.7 | 21.1 | 20.2 | 16.4 | 10.2 | 4.1 | -1.9 | -10.3 | 23.8 | 8.79 | 9.13 | 1.04 |
| 202 | 4147900 | 4 | POTOMAC RIVER | US | 29940.4 | -0.8 | 0.1 | 5.0 | 10.6 | 15.8 | 20.3 | 22.5 | 21.7 | 18.1 | 11.9 | 6.1 | 0.6 | -7.6 | 24.9 | 11.00 | 8.50 | 0.77 |
| 203 | 4148050 | 4 | JAMES RIVER | US | 17503.2 | 0.9 | 2.0 | 6.6 | 11.9 | 16.7 | 21.0 | 23.1 | 22.4 | 18.8 | 12.7 | 7.0 | 2.1 | -5.6 | 25.4 | 12.10 | 8.11 | 0.67 |
| 204 | 4148090 | 4 | ROANOKE RIVER | US | 21714.6 | 3.1 | 4.1 | 8.6 | 13.7 | 18.5 | 22.7 | 24.7 | 24.0 | 20.5 | 14.4 | 8.9 | 4.1 | -3.4 | 26.8 | 13.96 | 7.94 | 0.57 |
| 205 | 4148232 | 4 | CAPE FEAR RIVER | US | 13610.5 | 5.5 | 6.5 | 10.9 | 15.8 | 20.2 | 24.3 | 26.0 | 25.4 | 22.3 | 16.3 | 10.8 | 6.4 | -1.0 | 28.1 | 15.86 | 7.58 | 0.48 |
| 206 | 4148300 | 4 | PEE DEE RIVER | US | 22869.7 | 4.9 | 6.1 | 10.6 | 15.3 | 19.8 | 23.9 | 25.5 | 25.0 | 21.8 | 15.9 | 10.4 | 5.9 | -1.5 | 28.0 | 15.42 | 7.60 | 0.49 |
| 207 | 4148550 | 4 | SANTEE RIVER | US | 38073 | 5.8 | 6.9 | 11.1 | 15.7 | 20.3 | 24.2 | 25.8 | 25.2 | 22.2 | 16.3 | 10.7 | 6.4 | -0.4 | 28.4 | 15.86 | 7.45 | 0.47 |
| 208 | 4148650 | 4 | SAVANNAH RIVER | US | 25511.5 | 6.7 | 8.0 | 12.0 | 16.5 | 21.0 | 24.8 | 26.3 | 25.8 | 22.9 | 17.0 | 11.6 | 7.4 | 0.3 | 28.8 | 16.66 | 7.30 | 0.44 |
| 209 | 4148720 | 4 | ALTAMAHA RIVER | US | 35224 | 8.2 | 9.5 | 13.6 | 17.6 | 22.0 | 25.7 | 27.0 | 26.6 | 24.0 | 18.3 | 12.9 | 8.9 | 1.8 | 29.3 | 17.86 | 7.03 | 0.39 |
| 211 | 4149120 | 4 | PEARL RIVER | US | 17024.1 | 8.4 | 9.9 | 14.0 | 18.0 | 22.0 | 25.7 | 27.0 | 26.8 | 24.2 | 18.4 | 13.0 | 9.2 | 0.7 | 28.8 | 18.06 | 6.98 | 0.39 |
| 212 | 4149400 | 4 | ALABAMA RIVER | US | 56894.5 | 6.7 | 8.2 | 12.3 | 16.7 | 21.0 | 24.8 | 26.2 | 26.0 | 23.2 | 17.1 | 11.5 | 7.5 | -0.4 | 28.7 | 16.76 | 7.30 | 0.44 |
| 213 | 4149413 | 4 | TOMBIGBEE RIVER | US | 47700 | 6.7 | 8.2 | 12.5 | 16.9 | 21.3 | 25.3 | 26.8 | 26.5 | 23.6 | 17.4 | 11.7 | 7.5 | -1.0 | 29.5 | 17.03 | 7.51 | 0.44 |
| 215 | 4149781 | 4 | SUWANNEE RIVER | US | 24320.1 | 11.4 | 12.7 | 16.1 | 19.5 | 23.4 | 26.3 | 27.3 | 27.1 | 25.3 | 20.5 | 15.5 | 12.0 | 5.6 | 28.8 | 19.76 | 6.03 | 0.31 |
| 216 | 4150283 | 4 | NUECES RIVER | US | 43822.8 | 11.4 | 13.4 | 17.4 | 21.5 | 25.0 | 28.1 | 29.2 | 29.4 | 26.6 | 21.9 | 16.2 | 12.0 | 6.9 | 31.3 | 21.01 | 6.66 | 0.32 |
| 217 | 4150330 | 4 | SAN ANTONIO RIVER | US | 10155.4 | 10.7 | 12.6 | 16.5 | 20.3 | 23.9 | 27.1 | 28.4 | 28.5 | 25.8 | 21.1 | 15.6 | 11.5 | 5.9 | 30.4 | 20.17 | 6.57 | 0.33 |
| 218 | 4150450 | 4 | COLORADO RIVER (CA | US | 108788 | 7.1 | 9.2 | 13.3 | 17.9 | 22.1 | 26.1 | 27.5 | 27.3 | 23.7 | 18.4 | 12.1 | 7.8 | 2.1 | 29.8 | 17.70 | 7.51 | 0.42 |
| 219 | 4150500 | 4 | BRAZOS RIVER | US | 116827.1 | 6.7 | 8.7 | 12.9 | 17.6 | 21.9 | 26.2 | 27.9 | 27.8 | 24.0 | 18.4 | 12.2 | 7.6 | 0.9 | 30.3 | 17.65 | 7.77 | 0.44 |
| 220 | 4150600 | 4 | TRINITY RIVER (TEX | US | 44511.7 | 7.9 | 9.8 | 14.0 | 18.5 | 22.7 | 26.9 | 28.8 | 28.9 | 25.2 | 19.6 | 13.6 | 8.8 | 2.0 | 31.8 | 18.73 | 7.67 | 0.41 |
| 221 | 4150700 | 4 | SABINE RIVER | US | 24162.1 | 8.3 | 10.2 | 14.2 | 18.4 | 22.5 | 26.3 | 28.0 | 27.9 | 24.7 | 19.2 | 13.4 | 9.2 | 2.0 | 30.9 | 18.53 | 7.24 | 0.39 |
| 222 | 4152050 | 4 | COLORADO RIVER (PA | US | 618715 | 0.1 | 2.3 | 5.9 | 10.1 | 15.0 | 20.2 | 23.4 | 22.3 | 18.4 | 12.2 | 5.4 | 0.6 | -6.8 | 25.8 | 11.33 | 8.28 | 0.73 |
| 223 | 4202100 | 4 | ALSEK RIVER | CA | 16200 | -22.4 | -18.2 | -12.3 | -4.6 | 2.3 | 7.2 | 9.1 | 7.3 | 2.7 | -4.6 | -14.7 | -20.8 | -35.0 | 12.4 | -5.75 | 11.50 | -2.00 |
| 224 | 4202601 | 4 | TAKU RIVER | CA | 17700 | -15.6 | -12.8 | -6.8 | -0.8 | 4.3 | 8.4 | 9.7 | 8.9 | 5.2 | -0.1 | -7.9 | -12.9 | -26.3 | 12.8 | -1.70 | 9.16 | -5.40 |
| 225 | 4204900 | 4 | STIKINE RIVER | US | 51592.8 | -16.5 | -12.7 | -7.4 | -1.6 | 3.5 | 7.6 | 9.5 | 8.7 | 4.5 | -1.2 | -9.7 | -14.8 | -27.6 | 12.3 | -2.51 | 9.35 | -3.72 |
| 226 | 4206100 | 4 | NASS RIVER | CA | 19200 | -9.9 | -7.2 | -3.7 | 0.7 | 5.2 | 8.8 | 10.7 | 10.3 | 6.5 | 1.2 | -4.8 | -8.5 | -20.6 | 13.4 | 0.79 | 7.45 | 9.49 |
| 227 | 4206250 | 4 | SKEENA RIVER | CA | 42200 | -12.8 | -9.0 | -4.5 | 0.5 | 5.1 | 8.7 | 10.9 | 10.4 | 6.2 | 0.8 | -6.0 | -10.9 | -27.6 | 14.2 | -0.05 | 8.40 | -156.82 |
| 228 | 4207900 | 4 | FRASER RIVER | CA | 217000 | -11.4 | -7.6 | -3.1 | 2.1 | 6.9 | 10.5 | 13.0 | 12.4 | 8.1 | 2.5 | -4.4 | -9.5 | -27.3 | 16.4 | 1.63 | 8.63 | 5.28 |
| 229 | 4208025 | 4 | MACKENZIE RIVER | CA | 1660000 | -24.2 | -20.8 | -14.8 | -4.1 | 4.8 | 11.3 | 14.0 | 12.1 | 6.1 | -1.7 | -13.6 | -21.2 | -33.9 | 16.4 | -4.35 | 13.77 | -3.16 |
| 230 | 4208040 | 4 | PEEL RIVER (TRIB. | CA | 70600 | -27.4 | -24.6 | -19.5 | -8.7 | 1.8 | 9.9 | 11.9 | 8.7 | 2.0 | -8.8 | -20.3 | -24.9 | -41.5 | 14.4 | -8.31 | 14.50 | -1.74 |
| 231 | 4209150 | 4 | ANDERSON RIVER | CA | 56300 | -28.6 | -26.9 | -23.6 | -11.7 | 0.0 | 9.5 | 12.9 | 10.1 | 3.4 | -6.6 | -19.2 | -25.5 | -37.5 | 16.8 | -8.84 | 15.33 | -1.73 |
| 232 | 4209402 | 4 | COPPERMINE RIVER | CA | 50700 | -29.3 | -28.7 | -24.6 | -15.1 | -4.4 | 5.8 | 10.7 | 8.7 | 2.3 | -6.8 | -19.0 | -25.9 | -36.9 | 13.9 | -10.52 | 14.72 | -1.40 |
| 233 | 4209600 | 4 | ELLICE RIVER | CA | 16900 | -24.6 | -24.2 | -20.4 | -11.9 | -2.5 | 6.8 | 12.0 | 10.4 | 4.0 | -4.5 | -15.7 | -22.1 | -38.3 | 15.7 | -7.72 | 13.57 | -1.76 |
| 234 | 4209800 | 4 | BACK RIVER | CA | 98200 | -30.0 | -29.2 | -25.0 | -15.3 | -4.7 | 6.2 | 11.7 | 9.7 | 2.8 | -6.6 | -18.8 | -26.4 | -38.1 | 15.0 | -10.46 | 15.21 | -1.45 |
| 235 | 4209850 | 4 | HAYES RIVER (TRIB. | CA | 18100 | -34.7 | -35.2 | -30.6 | -20.8 | -10.1 | 0.4 | 6.7 | 4.8 | -1.8 | -11.3 | -22.8 | -30.3 | -44.3 | 11.6 | -15.47 | 15.17 | -0.98 |
| 236 | 4213711 | 4 | NELSON RIVER | CA | 1060000 | -17.1 | -14.1 | -7.3 | 2.4 | 9.7 | 14.8 | 17.9 | 16.6 | 10.9 | 4.4 | -5.5 | -13.7 | -28.0 | 21.3 | 1.58 | 12.45 | 7.87 |
| 237 | 4214025 | 4 | HAYES RIVER (TRIB. | CA | 103000 | -24.4 | -21.5 | -14.3 | -3.6 | 5.2 | 11.9 | 16.6 | 14.8 | 8.6 | 1.3 | -10.1 | -19.9 | -32.9 | 19.6 | -2.96 | 14.43 | -4.88 |
| 238 | 4214035 | 4 | AUX MELEZES | CA | 42700 | -24.9 | -23.4 | -17.3 | -8.9 | -0.2 | 6.6 | 10.8 | 9.9 | 5.5 | -0.7 | -8.6 | -18.8 | -32.7 | 14.8 | -5.84 | 12.68 | -2.17 |
| 239 | 4214040 | 4 | CANIAPISCAU | CA | 86800 | -24.2 | -22.4 | -15.7 | -7.0 | 1.3 | 8.5 | 12.6 | 11.3 | 6.1 | -0.5 | -8.8 | -18.8 | -30.9 | 14.7 | -4.79 | 12.91 | -2.70 |
| 240 | 4214051 | 4 | THELON RIVER | CA | 152000 | -30.6 | -29.4 | -24.0 | -14.4 | -3.3 | 6.6 | 12.4 | 10.7 | 3.6 | -5.8 | -18.1 | -26.1 | -39.2 | 16.1 | -9.86 | 15.51 | -1.57 |
| 241 | 4214070 | 4 | THLEWIAZA RIVER | CA | 27000 | -28.4 | -26.2 | -20.0 | -9.9 | 0.8 | 8.4 | 13.6 | 12.4 | 5.4 | -3.2 | -14.9 | -23.7 | -37.0 | 16.8 | -7.14 | 15.03 | -2.10 |
| 242 | 4214075 | 4 | FERGUSON RIVER | CA | 12400 | -32.0 | -31.5 | -26.1 | -16.5 | -6.3 | 3.6 | 9.9 | 9.0 | 2.7 | -6.2 | -18.7 | -26.8 | -41.0 | 13.9 | -11.57 | 15.26 | -1.32 |
| 243 | 4214080 | 4 | ATTAWAPISKAT RIVER | CA | 36000 | -22.5 | -20.2 | -12.7 | -2.0 | 5.9 | 13.3 | 16.7 | 14.7 | 9.1 | 2.2 | -7.3 | -17.2 | -29.9 | 20.2 | -1.66 | 13.73 | -8.27 |
| 244 | 4214090 | 4 | KAZAN RIVER | CA | 72300 | -31.3 | -30.3 | -24.8 | -15.2 | -4.6 | 5.2 | 11.7 | 10.1 | 3.4 | -6.0 | -18.7 | -26.6 | -39.6 | 15.4 | -10.58 | 15.46 | -1.46 |
| 245 | 4214100 | 4 | QUOICH RIVER | CA | 30100 | -33.3 | -33.2 | -29.0 | -18.1 | -8.7 | 3.0 | 8.0 | 6.7 | 0.2 | -7.7 | -20.2 | -29.2 | -43.5 | 13.3 | -13.46 | 15.31 | -1.14 |
| 246 | 4214105 | 4 | SEAL RIVER | CA | 48100 | -23.4 | -21.4 | -14.8 | -4.7 | 4.1 | 11.8 | 15.7 | 14.3 | 8.3 | 0.6 | -10.5 | -19.6 | -32.5 | 18.3 | -3.31 | 14.11 | -4.26 |
| 247 | 4214270 | 4 | CHURCHILL RIVER | CA | 287000 | -22.5 | -18.9 | -11.9 | -1.3 | 6.7 | 12.8 | 16.1 | 14.6 | 8.4 | 1.5 | -9.8 | -18.8 | -33.6 | 18.4 | -1.93 | 13.72 | -7.11 |
| 248 | 4214440 | 4 | SEVERN RIVER (TRIB | CA | 94300 | -22.0 | -19.4 | -12.1 | -2.1 | 6.0 | 12.8 | 16.8 | 15.4 | 9.3 | 2.7 | -7.8 | -17.8 | -30.9 | 20.0 | -1.52 | 13.78 | -9.06 |
| 249 | 4214450 | 4 | WINISK RIVER | CA | 50000 | -21.7 | -19.0 | -11.6 | -1.8 | 6.3 | 13.1 | 17.0 | 15.3 | 9.4 | 2.6 | -7.6 | -17.3 | -29.6 | 20.4 | -1.28 | 13.59 | -10.62 |
| 250 | 4214520 | 4 | ALBANY RIVER | CA | 118000 | -20.0 | -17.5 | -10.6 | -0.6 | 7.2 | 13.7 | 16.8 | 15.2 | 9.8 | 3.3 | -6.1 | -15.2 | -27.9 | 20.3 | -0.34 | 12.96 | -37.68 |
| 251 | 4214551 | 4 | MOOSE RIVER (TRIB. | CA | 60100 | -18.1 | -16.1 | -9.3 | 0.1 | 8.2 | 14.2 | 17.0 | 15.5 | 10.6 | 4.2 | -4.4 | -13.6 | -25.8 | 20.6 | 0.70 | 12.44 | 17.89 |
| 252 | 4214650 | 4 | NOTTAWAY | CA | 57500 | -18.4 | -16.7 | -9.2 | -0.4 | 7.6 | 13.6 | 16.3 | 14.9 | 10.1 | 4.0 | -4.2 | -13.6 | -26.5 | 20.2 | 0.32 | 12.28 | 37.93 |
| 253 | 4214680 | 4 | RUPERT RIVER | CA | 40900 | -19.7 | -17.8 | -10.8 | -1.8 | 6.5 | 12.9 | 15.9 | 14.6 | 9.9 | 3.4 | -4.6 | -14.7 | -27.8 | 19.4 | -0.52 | 12.61 | -24.15 |
| 254 | 4214700 | 4 | EASTMAIN | CA | 44300 | -21.2 | -19.7 | -12.7 | -3.5 | 4.8 | 11.4 | 14.7 | 13.4 | 8.5 | 2.1 | -5.9 | -16.0 | -28.6 | 18.1 | -2.01 | 12.73 | -6.33 |
| 255 | 4214770 | 4 | GRANDE RIVIERE | CA | 96300 | -23.3 | -21.8 | -14.9 | -5.4 | 2.9 | 10.0 | 13.6 | 12.3 | 7.2 | 0.8 | -7.2 | -17.8 | -30.5 | 16.8 | -3.63 | 13.05 | -3.60 |
| 257 | 4214900 | 4 | BALEINE, GRANDE RI | CA | 29800 | -24.5 | -23.2 | -16.9 | -8.5 | 0.0 | 7.0 | 11.4 | 10.2 | 5.2 | -1.0 | -8.9 | -18.3 | -31.6 | 14.1 | -5.62 | 12.64 | -2.25 |
| 258 | 4214930 | 4 | ARNAUD | CA | 26900 | -22.5 | -22.3 | -18.0 | -10.1 | -2.3 | 3.5 | 8.0 | 7.7 | 3.8 | -1.2 | -7.7 | -16.0 | -33.4 | 12.8 | -6.42 | 11.12 | -1.73 |
| 259 | 4214940 | 4 | FEUILLES (RIVIERE | CA | 41700 | -22.7 | -22.2 | -17.2 | -9.1 | -1.3 | 4.6 | 8.7 | 8.2 | 4.6 | -0.6 | -7.6 | -16.4 | -31.7 | 13.4 | -5.91 | 11.40 | -1.93 |
| 260 | 4214950 | 4 | GEORGE RIVER | CA | 35200 | -23.9 | -22.6 | -16.2 | -8.0 | -0.3 | 6.5 | 10.8 | 9.6 | 4.7 | -1.6 | -9.2 | -17.7 | -30.8 | 13.3 | -5.67 | 12.13 | -2.14 |
| 263 | 4243300 | 4 | ST. MAURICE (RIVIE | CA | 42000 | -16.5 | -15.1 | -8.0 | 0.8 | 8.4 | 14.0 | 16.6 | 15.1 | 10.5 | 4.4 | -3.4 | -12.6 | -23.7 | 20.1 | 1.18 | 11.80 | 10.00 |
| 264 | 4243400 | 4 | SAGUENAY (RIVIERE) | CA | 73000 | -19.3 | -17.3 | -10.1 | -1.0 | 6.8 | 13.0 | 15.8 | 14.3 | 9.5 | 3.1 | -4.8 | -14.7 | -26.3 | 19.1 | -0.39 | 12.36 | -31.44 |
| 265 | 4243610 | 4 | MANICOUAGAN (RIVIE | CA | 45800 | -20.6 | -18.2 | -11.6 | -3.2 | 4.2 | 11.0 | 14.3 | 12.8 | 7.6 | 1.1 | -6.7 | -16.3 | -26.7 | 16.4 | -2.13 | 12.17 | -5.71 |
| 267 | 4244635 | 4 | NATASHQUAN (RIVIER | CA | 15600 | -18.6 | -17.0 | -10.2 | -2.5 | 3.7 | 10.0 | 14.2 | 13.3 | 8.4 | 1.6 | -5.5 | -14.6 | -25.3 | 18.2 | -1.43 | 11.50 | -8.01 |
| 268 | 4244660 | 4 | LITTLE MECATINA RI | CA | 19100 | -17.9 | -16.4 | -10.3 | -3.0 | 2.9 | 8.6 | 12.9 | 12.4 | 7.8 | 1.6 | -5.0 | -13.5 | -24.7 | 15.4 | -1.66 | 10.79 | -6.48 |
| 269 | 4351900 | 4 | BRAVO | MX | 450902 | 6.5 | 8.7 | 12.3 | 16.5 | 20.6 | 24.2 | 25.0 | 24.5 | 21.6 | 16.8 | 10.9 | 6.8 | 3.7 | 27.1 | 16.21 | 6.82 | 0.42 |
| 270 | 4353300 | 4 | YAQUI | MX | 57908 | 8.5 | 10.1 | 12.9 | 16.5 | 20.5 | 24.9 | 24.7 | 23.5 | 22.4 | 18.2 | 12.7 | 8.9 | 5.5 | 26.9 | 17.00 | 6.07 | 0.36 |
| 272 | 4356080 | 4 | SAN PEDRO | MX | 25800 | 10.8 | 12.4 | 14.5 | 17.3 | 20.1 | 21.8 | 20.4 | 20.0 | 19.0 | 17.2 | 13.8 | 11.3 | 7.4 | 23.8 | 16.55 | 3.80 | 0.23 |
| 273 | 4356100 | 4 | SANTIAGO | MX | 128943 | 13.2 | 14.7 | 16.9 | 19.1 | 21.1 | 21.2 | 19.8 | 19.7 | 19.2 | 18.0 | 15.6 | 13.8 | 10.4 | 23.3 | 17.68 | 2.77 | 0.16 |
| 275 | 4356700 | 4 | VERDE | MX | 17617 | 16.0 | 17.4 | 18.9 | 20.2 | 20.8 | 20.2 | 19.5 | 19.6 | 19.3 | 18.5 | 17.1 | 16.4 | 13.9 | 23.1 | 18.66 | 1.71 | 0.09 |
| 276 | 4358300 | 4 | PANUCO | MX | 58115 | 13.1 | 14.6 | 16.8 | 18.7 | 19.8 | 19.5 | 18.7 | 18.8 | 18.1 | 16.8 | 14.7 | 13.5 | 10.6 | 22.3 | 16.92 | 2.45 | 0.14 |
| 277 | 4359220 | 4 | PAPALOAPAN | MX | 21419 | 16.6 | 17.6 | 19.4 | 21.4 | 22.3 | 21.7 | 20.8 | 21.0 | 20.7 | 19.6 | 18.0 | 17.1 | 14.3 | 24.6 | 19.67 | 2.03 | 0.10 |
| 278 | 4362201 | 4 | GRISALVA | MX | 37702 | 19.4 | 20.4 | 22.1 | 23.7 | 24.4 | 23.4 | 23.0 | 23.1 | 22.7 | 22.0 | 20.5 | 19.7 | 17.6 | 26.5 | 22.04 | 1.74 | 0.08 |
| 279 | 4362600 | 4 | USUMACINTA | MX | 50743 | 20.1 | 20.9 | 22.6 | 23.9 | 24.9 | 24.4 | 23.6 | 23.9 | 23.8 | 22.9 | 21.5 | 20.5 | 18.1 | 27.1 | 22.75 | 1.78 | 0.08 |
| 280 | 4664800 | 4 | LEMPA | SV | 18176 | 20.8 | 21.7 | 23.0 | 24.0 | 23.9 | 23.2 | 23.0 | 23.2 | 22.6 | 22.4 | 21.4 | 20.8 | 18.3 | 26.6 | 22.50 | 1.35 | 0.06 |
| 281 | 4772300 | 4 | GRANDE DE MATAGALP | NI | 14646 | 23.5 | 24.1 | 25.1 | 25.9 | 26.4 | 25.3 | 25.0 | 25.2 | 25.3 | 25.0 | 24.3 | 23.8 | 20.3 | 28.5 | 24.91 | 1.14 | 0.05 |
| 283 | 5101201 | 5 | BURDEKIN | AU | 129760 | 27.1 | 26.5 | 25.3 | 22.9 | 19.6 | 16.8 | 16.0 | 17.8 | 20.7 | 23.8 | 26.0 | 27.1 | 14.0 | 29.5 | 22.47 | 4.06 | 0.18 |
| 285 | 5109170 | 5 | GILBERT RIVER | AU | 11800 | 27.3 | 26.8 | 25.9 | 24.2 | 21.5 | 19.1 | 18.4 | 19.9 | 22.9 | 26.2 | 27.8 | 28.0 | 15.7 | 30.2 | 24.01 | 3.51 | 0.15 |
| 287 | 5141100 | 5 | BRANTAS | ID | 8650 | 24.2 | 24.3 | 24.4 | 24.5 | 24.4 | 23.9 | 23.5 | 23.7 | 24.4 | 24.9 | 24.9 | 24.5 | 21.7 | 26.6 | 24.30 | 0.72 | 0.03 |
| 289 | 5223100 | 5 | KELANTAN | MY | 11900 | 24.6 | 25.1 | 25.9 | 26.4 | 26.5 | 26.2 | 25.9 | 25.9 | 25.7 | 25.6 | 25.3 | 24.8 | 22.5 | 28.0 | 25.64 | 0.71 | 0.03 |
| 290 | 5224500 | 5 | PAHANG | MY | 19000 | 23.7 | 24.3 | 24.9 | 25.3 | 25.4 | 25.1 | 25.0 | 24.8 | 24.7 | 24.6 | 24.3 | 23.8 | 21.7 | 27.2 | 24.65 | 0.68 | 0.03 |
| 291 | 5230300 | 5 | RAJANG | MY | 34053 | 23.9 | 24.1 | 24.4 | 24.8 | 25.1 | 24.9 | 24.8 | 24.8 | 24.6 | 24.4 | 24.4 | 24.1 | 22.3 | 26.6 | 24.52 | 0.56 | 0.02 |
| 292 | 5231700 | 5 | KINABATANGAN | MY | 10800 | 23.7 | 23.8 | 24.3 | 24.9 | 25.0 | 24.8 | 24.5 | 24.6 | 24.5 | 24.3 | 24.2 | 23.9 | 22.2 | 27.2 | 24.38 | 0.60 | 0.02 |
| 294 | 5550500 | 5 | SEPIK | PG | 40922 | 24.0 | 23.7 | 24.0 | 24.4 | 24.4 | 24.1 | 23.7 | 23.6 | 23.9 | 24.2 | 24.4 | 24.2 | 15.3 | 25.8 | 24.04 | 1.01 | 0.04 |
| 295 | 5553100 | 5 | PURARI | PG | 11100 | 20.7 | 20.7 | 20.7 | 20.8 | 20.5 | 19.6 | 19.2 | 19.3 | 19.8 | 20.1 | 20.5 | 20.7 | 17.2 | 22.5 | 20.22 | 0.84 | 0.04 |
| 296 | 5606100 | 5 | BLACKWOOD RIVER | AU | 20500 | 21.8 | 21.6 | 19.8 | 16.6 | 13.3 | 11.1 | 10.2 | 10.6 | 12.0 | 14.2 | 17.4 | 20.1 | 8.5 | 24.9 | 15.74 | 4.31 | 0.27 |
| 297 | 5607100 | 5 | MURCHISON RIVER | AU | 82300 | 30.1 | 29.6 | 27.2 | 22.8 | 17.7 | 14.1 | 13.0 | 14.5 | 17.6 | 21.1 | 24.9 | 28.2 | 10.8 | 32.7 | 21.73 | 6.12 | 0.28 |
| 299 | 5607400 | 5 | ASHBURTON RIVER | AU | 70200 | 32.5 | 31.4 | 29.8 | 26.2 | 21.0 | 17.4 | 16.4 | 18.4 | 21.8 | 25.5 | 28.8 | 31.3 | 14.4 | 34.7 | 25.05 | 5.70 | 0.23 |
| 300 | 5607450 | 5 | FORTESCUE RIVER | AU | 48900 | 31.7 | 30.6 | 29.1 | 25.5 | 20.4 | 16.8 | 16.0 | 18.1 | 21.9 | 25.8 | 29.0 | 31.1 | 13.6 | 34.1 | 24.67 | 5.70 | 0.23 |
| 301 | 5607500 | 5 | DE GREY RIVER | AU | 49600 | 32.4 | 31.4 | 30.3 | 26.9 | 21.9 | 18.4 | 17.6 | 19.7 | 23.5 | 27.2 | 30.3 | 32.0 | 15.0 | 34.9 | 25.98 | 5.42 | 0.21 |
| 302 | 5608024 | 5 | FITZROY RIVER | AU | 45300 | 30.4 | 29.6 | 29.0 | 26.9 | 23.1 | 20.2 | 19.6 | 21.9 | 26.0 | 29.6 | 31.4 | 31.2 | 16.8 | 33.6 | 26.58 | 4.30 | 0.16 |
| 303 | 5608090 | 5 | ORD | AU | 46100 | 30.5 | 29.8 | 29.1 | 27.2 | 23.7 | 20.8 | 20.3 | 22.7 | 26.8 | 30.1 | 31.4 | 31.1 | 17.5 | 33.7 | 26.96 | 4.08 | 0.15 |
| 304 | 5608400 | 5 | DURACK RIVER | AU | 4150 | 29.5 | 28.7 | 28.3 | 26.7 | 23.4 | 20.5 | 20.1 | 22.3 | 26.3 | 29.4 | 30.6 | 30.1 | 17.5 | 32.6 | 26.33 | 3.79 | 0.14 |
| 306 | 5708110 | 5 | VICTORIA RIVER | AU | 44900 | 30.2 | 29.6 | 28.7 | 26.7 | 23.4 | 20.3 | 20.0 | 22.3 | 26.6 | 29.8 | 31.1 | 30.9 | 17.1 | 33.1 | 26.63 | 4.10 | 0.15 |
| 307 | 5708145 | 5 | DALY | AU | 47000 | 28.9 | 28.5 | 28.4 | 27.4 | 24.9 | 22.3 | 22.2 | 24.0 | 27.8 | 30.4 | 30.7 | 29.8 | 18.8 | 32.3 | 27.11 | 3.03 | 0.11 |
| 308 | 5709100 | 5 | ROPER RIVER | AU | 47400 | 29.7 | 29.1 | 28.5 | 27.1 | 24.4 | 21.6 | 21.3 | 23.2 | 26.9 | 30.0 | 31.1 | 30.6 | 18.5 | 33.1 | 26.97 | 3.51 | 0.13 |
| 309 | 5709110 | 5 | MACARTHUR RIVER | AU | 10400 | 29.7 | 29.3 | 28.3 | 26.7 | 23.7 | 20.5 | 20.2 | 22.0 | 25.4 | 28.7 | 30.4 | 30.6 | 17.4 | 32.9 | 26.30 | 3.83 | 0.15 |
| 310 | 5803180 | 5 | SOUTH ESK RIVER | AU | 3278 | 15.9 | 15.9 | 14.1 | 11.3 | 8.8 | 6.6 | 6.1 | 7.0 | 8.7 | 10.5 | 12.5 | 14.3 | 4.4 | 18.2 | 10.97 | 3.53 | 0.32 |
| 311 | 5865300 | 5 | WAIKATO RIVER | NZ | 11395 | 16.4 | 16.7 | 14.9 | 12.2 | 9.6 | 7.1 | 6.3 | 7.3 | 9.2 | 11.1 | 13.0 | 14.8 | 4.8 | 19.5 | 11.55 | 3.64 | 0.32 |
| 312 | 5868100 | 5 | CLUTHA | NZ | 20306 | 12.6 | 12.4 | 10.5 | 7.5 | 3.8 | 1.2 | 0.4 | 2.5 | 5.2 | 7.6 | 9.4 | 11.3 | -2.6 | 15.4 | 7.03 | 4.26 | 0.61 |
| 313 | 6112090 | 6 | DOURO | PT | 91491 | 3.2 | 4.4 | 7.0 | 9.1 | 12.7 | 16.9 | 19.9 | 19.9 | 16.6 | 11.6 | 6.6 | 3.8 | -0.8 | 23.1 | 10.97 | 6.11 | 0.56 |
| 314 | 6113050 | 6 | TEJO | PT | 67490 | 5.6 | 6.8 | 9.4 | 11.6 | 15.2 | 19.9 | 23.3 | 23.2 | 19.4 | 14.2 | 9.1 | 6.1 | 2.0 | 25.9 | 13.65 | 6.44 | 0.47 |
| 315 | 6116200 | 6 | GUADIANA | PT | 60883 | 6.7 | 8.1 | 10.7 | 13.0 | 16.7 | 21.6 | 25.2 | 25.0 | 21.3 | 15.8 | 10.5 | 7.3 | 3.4 | 27.9 | 15.15 | 6.65 | 0.44 |
| 316 | 6122100 | 6 | SEINE | FR | 65000 | 2.3 | 3.3 | 6.1 | 9.2 | 13.3 | 16.2 | 18.3 | 17.8 | 14.8 | 10.4 | 5.6 | 3.1 | -5.8 | 22.6 | 10.05 | 5.93 | 0.59 |
| 317 | 6123100 | 6 | LOIRE | FR | 110000 | 2.8 | 3.8 | 6.5 | 9.3 | 13.3 | 16.4 | 18.5 | 18.1 | 15.3 | 10.9 | 6.1 | 3.6 | -5.3 | 23.3 | 10.38 | 5.82 | 0.56 |
| 318 | 6125100 | 6 | GARONNE | FR | 52000 | 3.0 | 4.1 | 6.8 | 9.3 | 13.1 | 16.6 | 19.0 | 18.8 | 15.9 | 11.6 | 6.7 | 3.8 | -4.8 | 23.7 | 10.72 | 5.86 | 0.55 |
| 319 | 6139100 | 6 | RHONE | FR | 95590 | -0.1 | 1.1 | 4.4 | 7.7 | 11.9 | 15.3 | 17.7 | 17.2 | 13.9 | 9.2 | 4.0 | 0.8 | -7.8 | 22.2 | 8.59 | 6.46 | 0.75 |
| 320 | 6217100 | 6 | GUADALQUIVIR | ES | 46995 | 7.1 | 8.6 | 11.0 | 13.3 | 17.0 | 21.7 | 25.3 | 25.3 | 21.6 | 16.3 | 11.1 | 7.8 | 3.9 | 27.8 | 15.51 | 6.53 | 0.42 |
| 321 | 6226800 | 6 | EBRO | ES | 84230 | 3.5 | 4.8 | 7.5 | 9.7 | 13.4 | 17.4 | 20.3 | 20.3 | 17.0 | 12.3 | 7.2 | 4.1 | -1.8 | 24.0 | 11.46 | 6.10 | 0.53 |
| 322 | 6229500 | 6 | VAENERN-GOETA (GOE | SE | 46886 | -5.6 | -5.2 | -1.8 | 3.1 | 8.8 | 13.1 | 15.3 | 14.0 | 9.7 | 4.9 | -0.3 | -4.1 | -14.6 | 19.5 | 4.31 | 7.70 | 1.79 |
| 323 | 6233650 | 6 | ANGERMANAELVEN | SE | 30638 | -10.4 | -9.7 | -5.7 | -0.4 | 5.3 | 10.5 | 13.2 | 11.4 | 6.7 | 1.1 | -4.9 | -8.6 | -19.7 | 16.3 | 0.71 | 8.55 | 12.04 |
| 324 | 6233750 | 6 | LULEAELVEN | SE | 24924 | -13.0 | -12.7 | -8.7 | -3.0 | 2.9 | 8.6 | 11.9 | 9.9 | 4.9 | -1.3 | -7.8 | -11.6 | -22.7 | 15.1 | -1.66 | 9.06 | -5.45 |
| 326 | 6233900 | 6 | MUONIO | SE | 14408.5 | -14.1 | -13.9 | -9.5 | -3.6 | 2.9 | 9.4 | 12.6 | 10.3 | 5.0 | -1.9 | -8.5 | -12.2 | -24.1 | 16.1 | -1.95 | 9.73 | -4.98 |
| 327 | 6335020 | 6 | RHINE RIVER | DE | 159300 | -0.4 | 0.6 | 3.9 | 7.6 | 12.2 | 15.2 | 17.0 | 16.4 | 13.2 | 8.6 | 3.7 | 0.7 | -9.6 | 21.6 | 8.21 | 6.43 | 0.78 |
| 328 | 6337200 | 6 | WESER | DE | 37720 | -0.3 | 0.4 | 3.5 | 7.4 | 12.2 | 15.0 | 16.8 | 16.2 | 13.0 | 8.5 | 3.8 | 0.8 | -9.9 | 21.2 | 8.12 | 6.42 | 0.79 |
| 329 | 6340110 | 6 | ELBE RIVER | DE | 131950 | -1.4 | -0.5 | 3.0 | 7.3 | 12.5 | 15.5 | 17.3 | 16.6 | 13.0 | 8.1 | 3.1 | -0.1 | -11.4 | 21.7 | 7.87 | 6.95 | 0.88 |
| 332 | 6401120 | 6 | THJORSA | IS | 7380 | -5.0 | -5.0 | -3.9 | -1.7 | 2.2 | 5.6 | 7.4 | 6.6 | 3.8 | -0.1 | -2.7 | -4.4 | -12.8 | 9.6 | 0.24 | 4.74 | 19.59 |
| 333 | 6401601 | 6 | SVARTA, SKAGAFIROI | IS | 393 | -5.7 | -5.7 | -4.7 | -2.5 | 1.9 | 5.5 | 7.1 | 6.3 | 3.6 | -0.6 | -3.4 | -5.0 | -15.8 | 10.1 | -0.24 | 5.00 | -21.05 |
| 334 | 6401701 | 6 | JOEKULSA A FJOELLU | IS | 7074 | -5.5 | -5.2 | -4.3 | -2.0 | 2.1 | 5.7 | 7.6 | 6.8 | 4.1 | -0.1 | -3.1 | -4.7 | -15.0 | 10.5 | 0.10 | 5.01 | 47.92 |
| 336 | 6421100 | 6 | MAAS | NL | 29000 | 1.2 | 2.0 | 4.9 | 8.0 | 12.5 | 15.1 | 16.9 | 16.4 | 13.7 | 9.5 | 4.9 | 2.3 | -7.9 | 22.4 | 8.96 | 5.89 | 0.66 |
| 337 | 6457010 | 6 | ODER RIVER | PL | 109729 | -2.2 | -1.2 | 2.7 | 7.8 | 13.1 | 16.1 | 18.2 | 17.2 | 13.5 | 8.4 | 3.2 | -0.5 | -12.9 | 22.5 | 8.01 | 7.48 | 0.93 |
| 338 | 6458010 | 6 | WISLA | PL | 194376 | -3.8 | -2.9 | 1.4 | 7.6 | 13.2 | 16.3 | 18.3 | 17.4 | 13.2 | 8.0 | 2.6 | -1.8 | -14.3 | 21.5 | 7.45 | 8.15 | 1.09 |
| 341 | 6605600 | 6 | TRENT | GB | 7486 | 3.5 | 3.7 | 5.5 | 7.8 | 10.9 | 14.0 | 15.9 | 15.5 | 13.2 | 9.7 | 6.2 | 4.0 | -2.2 | 19.4 | 9.16 | 4.67 | 0.51 |
| 342 | 6607650 | 6 | THAMES | GB | 9948 | 4.1 | 4.2 | 6.1 | 8.4 | 11.8 | 14.7 | 16.6 | 16.3 | 13.9 | 10.4 | 6.7 | 4.5 | -2.7 | 20.6 | 9.83 | 4.77 | 0.49 |
| 345 | 6730500 | 6 | TANA (NO, FI) | NO | 14165 | -14.6 | -14.6 | -10.3 | -4.3 | 2.1 | 8.5 | 11.9 | 9.8 | 4.8 | -2.2 | -8.9 | -12.8 | -24.8 | 15.8 | -2.54 | 9.75 | -3.84 |
| 346 | 6731310 | 6 | DRAMSELV | NO | 16020 | -9.0 | -8.1 | -4.4 | 0.4 | 5.8 | 10.2 | 12.5 | 11.0 | 6.7 | 1.4 | -4.1 | -8.0 | -16.7 | 16.4 | 1.20 | 7.85 | 6.54 |
| 347 | 6731400 | 6 | GLOMA | NO | 40243 | -9.6 | -8.7 | -4.8 | 0.2 | 5.8 | 10.1 | 12.5 | 10.9 | 6.6 | 1.3 | -4.2 | -8.4 | -17.8 | 16.9 | 0.97 | 8.05 | 8.31 |
| 349 | 6854100 | 6 | KOKEMAENJOKI | FI | 26025 | -7.4 | -7.8 | -3.9 | 2.1 | 8.4 | 13.3 | 16.3 | 14.4 | 9.5 | 4.0 | -1.0 | -5.0 | -19.7 | 20.5 | 3.58 | 8.68 | 2.42 |
| 350 | 6854500 | 6 | OULUJOKI | FI | 22841 | -11.1 | -11.4 | -6.8 | -0.1 | 6.3 | 12.2 | 15.4 | 12.9 | 7.6 | 1.3 | -4.1 | -8.6 | -23.1 | 18.9 | 1.14 | 9.61 | 8.46 |
| 354 | 6855400 | 6 | VUOKSI | FI | 61061 | -10.1 | -10.3 | -5.5 | 1.0 | 7.7 | 13.4 | 16.4 | 14.1 | 8.8 | 2.9 | -2.6 | -7.5 | -21.7 | 20.8 | 2.36 | 9.60 | 4.07 |
| 355 | 6934100 | 6 | SKJERN A | DK | 1040 | 0.1 | -0.1 | 1.9 | 5.9 | 10.8 | 14.0 | 15.9 | 15.4 | 12.2 | 8.1 | 4.0 | 1.2 | -7.3 | 19.6 | 7.47 | 6.07 | 0.81 |
| 357 | 6970100 | 6 | ONEGA | RU | 55770 | -12.6 | -11.5 | -6.1 | 1.1 | 7.8 | 13.6 | 16.3 | 13.9 | 8.3 | 1.9 | -4.4 | -9.5 | -22.8 | 21.9 | 1.55 | 10.33 | 6.68 |
| 358 | 6970250 | 6 | NORTHERN DVINA(SEV | RU | 348000 | -14.8 | -13.1 | -6.7 | 1.2 | 7.9 | 14.0 | 16.6 | 13.7 | 7.9 | 0.9 | -6.2 | -11.8 | -24.6 | 20.8 | 0.79 | 11.12 | 14.00 |
| 359 | 6970500 | 6 | MEZEN | RU | 56400 | -16.6 | -14.5 | -8.6 | -1.1 | 5.2 | 12.1 | 15.4 | 12.3 | 6.5 | -0.5 | -7.8 | -13.5 | -27.5 | 20.0 | -0.94 | 11.24 | -12.01 |
| 360 | 6970700 | 6 | PECHORA | RU | 312000 | -18.9 | -17.6 | -11.9 | -4.6 | 1.8 | 9.7 | 13.8 | 11.0 | 5.5 | -2.3 | -10.5 | -15.9 | -29.7 | 18.9 | -3.32 | 11.66 | -3.52 |
| 361 | 6971130 | 6 | TULOMA | RU | 17500 | -12.7 | -12.7 | -8.3 | -2.3 | 3.7 | 9.9 | 13.2 | 11.0 | 5.9 | -0.6 | -6.6 | -10.4 | -22.6 | 18.1 | -0.82 | 9.39 | -11.42 |
| 364 | 6972130 | 6 | NIZHNY VYG (SOROKA | RU | 27000 | -11.7 | -11.4 | -6.6 | -0.2 | 6.3 | 12.5 | 15.6 | 13.3 | 7.9 | 1.8 | -4.0 | -9.1 | -22.6 | 20.3 | 1.20 | 9.83 | 8.18 |
| 365 | 6972350 | 6 | NARVA | EE | 56000 | -7.4 | -7.1 | -2.8 | 4.3 | 10.8 | 15.0 | 17.2 | 15.7 | 10.7 | 5.1 | -0.5 | -4.9 | -17.6 | 22.2 | 4.69 | 9.08 | 1.94 |
| 366 | 6972430 | 6 | NEVA | RU | 281000 | -9.6 | -9.0 | -4.3 | 2.7 | 9.4 | 14.3 | 16.8 | 14.8 | 9.6 | 3.8 | -1.9 | -6.8 | -21.3 | 22.2 | 3.31 | 9.56 | 2.89 |
| 367 | 6972800 | 6 | KEM | RU | 27900 | -12.3 | -12.1 | -7.4 | -1.1 | 5.2 | 11.8 | 14.9 | 12.4 | 7.1 | 0.9 | -4.9 | -9.7 | -24.5 | 18.6 | 0.40 | 9.77 | 24.70 |
| 369 | 6973300 | 6 | WESTERN DVINA (DAU | LV | 64500 | -8.0 | -7.2 | -2.7 | 4.9 | 11.8 | 15.6 | 17.3 | 15.9 | 10.9 | 5.0 | -0.8 | -5.6 | -18.2 | 22.7 | 4.75 | 9.39 | 1.98 |
| 370 | 6974150 | 6 | NEMAN | LT | 81200 | -5.4 | -4.9 | -0.9 | 6.0 | 12.4 | 15.7 | 17.6 | 16.5 | 11.9 | 6.6 | 1.3 | -3.2 | -16.1 | 21.6 | 6.13 | 8.58 | 1.40 |
| 371 | 6977100 | 6 | VOLGA | RU | 1360000 | -12.5 | -11.6 | -5.5 | 3.9 | 11.5 | 16.4 | 18.4 | 16.2 | 10.3 | 3.1 | -4.1 | -9.8 | -22.0 | 23.4 | 3.02 | 11.28 | 3.74 |
| 372 | 6978250 | 6 | DON | RU | 378000 | -8.3 | -7.8 | -2.3 | 7.5 | 14.9 | 19.0 | 21.1 | 19.7 | 13.7 | 6.5 | -0.3 | -5.6 | -19.1 | 26.4 | 6.50 | 10.97 | 1.69 |
| 373 | 6980300 | 6 | SOUTHERN BUG | UA | 46200 | -5.2 | -4.1 | 0.6 | 8.2 | 14.7 | 17.9 | 19.5 | 18.9 | 14.0 | 8.0 | 2.0 | -2.5 | -15.5 | 24.3 | 7.67 | 9.18 | 1.20 |
| 374 | 6980800 | 6 | DNIEPR | UA | 463000 | -6.3 | -5.4 | -0.6 | 7.4 | 14.0 | 17.3 | 19.0 | 17.9 | 12.9 | 6.8 | 0.9 | -3.7 | -16.3 | 23.5 | 6.69 | 9.39 | 1.40 |
| 375 | 6981800 | 6 | DNIESTR | MD | 66100 | -4.6 | -3.2 | 1.3 | 8.0 | 14.0 | 17.1 | 18.8 | 18.1 | 13.7 | 8.2 | 2.4 | -2.1 | -13.9 | 22.8 | 7.64 | 8.59 | 1.12 |
| 377 | 6990700 | 6 | KURA | AZ | 178000 | -3.6 | -2.4 | 1.8 | 8.0 | 13.0 | 17.1 | 20.5 | 20.2 | 16.0 | 10.1 | 4.2 | -1.1 | -9.3 | 23.7 | 8.67 | 8.62 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




