The Mass of Our Observable Universe

1. Introduction

The standard cosmological model ([1,2]), also called LCDM, assumes that our Universe correspond to a global space-time that began in a hot Big Bang (BB) expansion at the very beginning time. Such initial conditions seem to violate the classical concept of energy conservation and are very unlikely ([3,4,5,6]). According to this singular start BB model, the full observable Universe came out of (macroscopic) nothing, resulting from some Quantum Gravity vacuum fluctuations that we can only speculate about. We will never be able to test experimentally these ideas because of the enormous energies involved (${10}^{19}GeV$) and here is no direct evidence that this ever occurred. The BB model also requires three more exotic patches: Cosmic Inflation, Dark Matter and Dark Energy (DE), for which we have no direct evidence or understanding at any fundamental level.

Despite these shortfalls, the LCDM model seems very successful in explaining most observations by fitting just a handful of free cosmological parameters. Here we how how the Black Hole Universe (BHU) can be an alternative paradigm to the LCDM and elaborate that the main difference between these two approaches reside in whether the mass-energy of our Universe is finite or not.

The fact that the universe might be generated from the inside of a BH has been studied extensively in the literature. [7] and [8] proposed that the FLRW metric could be the interior of a BH. But these early proposals were not proper GR solutions, but just incomplete analogies (see [9]). [10] presented a more rigorous demonstration within classical GR that that the FLRW metric could be inside a BH, something that was also clear from the works of [11]. Many of the previous approaches ([12,13,14,15,16,17,18]) involve modifications to Classical GR. There are also some simple scalar field $\phi \left(x\right)$ examples (e.g. [14]) which presented models within the scope of a classical GR and classical field theory with a false vacuum interior. A particular case are Bubble or Baby Universe solutions where the BH interior is de-Sitter metric ([19,20,21,22,23,24,25,26]). In the BHU solution ([27,28,29,30]) and also in the previously cite works of [11] and [10], no surface terms (or Bubble) are needed and the inside is not filled with a false vacuum, but with regular matter and radiation. The difference between the recent BHU and the earlier FLRW metric solutions inside a BH is the role of the $\Lambda$ term as a boundary condition ([29]). The model by [31] has the same name and similar features as the BHU, but the model is proposed as a new postulate to GR and not as a classical solution.

Here, we will start by reviewing in §Section 2 the classical GR solutions to the problem of a uniform spherical ball with fixed mass. In §Section 3 we will interpret what we mean by a fixed mass and we will then focus in §Section 4 on the corresponding BH solutions to show that the observed cosmic expansion is consistent with the BHU idea. We end with some conclusion and discussion of how the BHU form in §Section 5.

2. A uniform spherical ball of fixed mass

The most general metric with spherical symmetry in spherical coordinates and proper time $d{x}^{\mu }=(d\tau ,d\chi ,d\theta ,d\varphi )$ has the form ([11,32,33]):

$$d{s}^2=-d{\tau }^2+e^{\lambda (\tau ,\chi )}d{\chi }^2+r^2(\tau ,\chi )d{\Omega }^2,$$

(1)

where we use units of speed of light $c=1$ and the radial coordinate $\chi$ will be taken here to be comoving with the matter content. This metric is sometimes called the Lemaitre-Tolman metric ([32,34]) or the Lemaitre-Tolman-Bondi (LTB) metric. This is a metric localized around a reference central point in space which we have set to be the origin ($\overrightarrow{r}=0$) for simplicity.

For an observer moving with a perfect fluid the energy-momentum tensor is diagonal: $T_{\mu }^{\nu }=diag[-\rho ,p,p,p]$, where $\rho =\rho (\tau ,\chi )$ is the energy density and $p=p(\tau ,\chi )$ is the pressure. The off-diagonal terms of the field equation are zero, e.g.: $8\pi G{T}_0^1=G_0^1=0$, which translates into:

$$\left({\partial }_{\tau }\lambda \right)\left({\partial }_{\chi }r\right)=2{\partial }_{\tau }\left({\partial }_{\chi }r\right)$$

(2)

This equation can be solved as: $e^{\lambda }=C{\left({\partial }_{\chi }r\right)}^2$, where ${\partial }_{\tau }C=0$. The case $C=1$ corresponds a flat geometry:

$$d{s}^2=-d{\tau }^2+{\left[{\partial }_{\chi }r\right]}^{2}d{\chi }^2+r^{2}d{\Omega }^2,$$

(3)

so that there is only one function we need to solve: $r=r(\tau ,\chi )$ which corresponds to the radial proper distance. The field equations for r (with $\Lambda =0$) are:

$$\begin{array}{ccc}\hfill H^2& \equiv & r_H^{-2}\equiv {\left(\frac{\dot{r}}{r}\right)}^2=\frac{2GM}{r^3}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill M& \equiv & {\int }_0^{\chi }\rho 4\pi r^2\left({\partial }_{\chi }r\right)d\chi =M(\tau ,\chi )\hfill \end{array}$$

(5)

where the dot here is $\dot{r}\equiv {\partial }_{\tau }r$. When $\rho =\rho \left(\tau \right)$ is uniform, we have $M=\rho \frac{4\pi }{3}{r}^3$ and $r=a\left(\tau \right)\chi$, so that Eq.3 reproduces the flat (global) FLRW metric and Eq.4 is the corresponding solution: $3H^2\left(\tau \right)=8\pi G\rho \left(\tau \right)$, which corresponds to a global solution (any point can be choosen as to be the center of the metric $\overrightarrow{r}=0$). The non flat case can also be reproduced if we consider the more general case $e^{\lambda }={\left({\partial }_{\chi }r\right)}^2/[1+K\left(r\right)]$.

But the solution in Eq.4- can also be used to solve non-homogeneous cases. The simplest is the case of an expanding (or collapsing) uniform spherical ball inside a comoving coordinate ${\chi }_{*}$ and empty outside:

$$\rho (\tau ,\chi )=\left\{\begin{array}{cc}\rho \left(\tau \right)\hfill & \mathrm{for}\chi \le {\chi }_{*}\hfill \\ 0\hfill & \mathrm{for}\chi >{\chi }_{*}\hfill \end{array}\right.$$

(6)

which reproduces the exact same FLRW metric and solution $r=a\chi$ with the same mass inside ${\chi }_{*}$ as in the infinite FLRW case:

$$M=\frac{4}{3}\pi R^3\rho \left(\tau \right)$$

(7)

where $R\equiv a{\chi }_{*}$. The only difference is that this is now a local solution with empty space outside ${\chi }_{*}$. The Hubble-Lemaitre expansion law: $\dot{r}=H\left(\tau \right)r$ of Eq.4 with $3H^2\left(\tau \right)=8\pi G\rho \left(\tau \right)$ is the same for the global or the local FLRW solution inside ${\chi }_{*}$. This is a consequence of Birkhoff’s theorem (see [35,36]), since a sphere cut out of an infinite uniform distribution has the same spherical symmetry. Thus, the FLRW metric is both a solution to a global homogeneous (i.e. infinite M) uniform background and also to the inside of a local (finite mass) uniform sphere centered around one particular point. The local solution is called the FLRW cloud ([29]).

3. Relativistic mass

The Misner and Sharp ([33]) mass-energy $M_{MS}$ inside a spatial hypersurface $\Sigma$ of Eq.1, given by $\chi <{\chi }_{*}$, is:

$$M_{MS}={\int }_{\Sigma }\rho {\left(1+\frac{{\dot{r}}^2}{c^2}-\frac{2G{M}_{MS}}{c^{2}r}\right)}^{1/2}d{V}_3$$

(8)

where $d{V}_3=d^{3}y\sqrt{-h}=4\pi r^2{e}^{\lambda /2}d\chi$ is the 3D spatial volume element of the metric in $\Sigma$ (we recover here units if $c\ne 1$ to check the non relativistic limit). The first term is the material or passive mass (which we call here M):

$$M={\int }_{\Sigma }\rho d{V}_3={\int }_0^{{\chi }_{*}}\rho 4\pi r^2\left({\partial }_{\chi }r\right)d\chi$$

(9)

and corresponds to Eq.. We can then interpret the next two terms in Eq.8 as the contribution to mass energy from the kinetic and potential energy (see also [37] for a more general description). In the non relativistic limit ($c=\infty$) these two terms are negligible and $M_{MS}=M$. But in general, as indicated by Eq.8, $M_{MS}$ can not be expressed as a sum of individual energies as $M_{MS}$ also appears inside the integral, reflecting the non-linear nature of gravity. But in the case of Eq.4, the kinetic and potential energy terms cancel for $M=M_{MS}$ and we can interpret M as the total mass-energy of the system.

For the case in Eq.4-, the mass inside $\chi$ is constant for matter dominated fluid when $\rho \sim a^{-3}$. But in the early stages of the expansion, when the Energy-density is dominated by radiation or a fluid with a different equation of state the mass inside $\chi$ is a function $\tau$. If we want M to be constant throughout its evolution we need the junction ${\chi }_{*}$ to be a function of time $\tau$. In the case of mass-energy dominated by $\rho ={\rho }_0{a}^{-3+\beta }$ inside ${\chi }_{*}$ (and empty outside) we have $r=a\chi$ and from Eq.:

$$M=\rho a^3{\int }_0^{{\chi }_{*}}4\pi {\chi }^{2}d\chi =\frac{4\pi }{3}{\rho }_0{a}^{\beta }{\chi }_{*}^3$$

(10)

where $\beta =-1$ corresponds to radiation and $\beta =0$ to matter domination. So we need ${\chi }_{*}\sim a^{-\beta /3}$ to find a physical solution with fixed mass M. More generally, for a fluid with several components $i=1,2,\cdots$:

$$\rho =\sum _i{\rho }_i=\sum _i{\rho }_{0i}{a}^{-3+{\beta }_i}$$

(11)

we have

$$M=\frac{4\pi }{3}{\chi }_{*}^3\sum _i{\rho }_{0i}{a}^{{\beta }_i}=\frac{4\pi }{3}{\chi }_{*}^3{a}^3\rho$$

(12)

Thus, a solution with constant M requires:

$$R^3\equiv a^3{\chi }_{*}^3=\frac{3M}{4\pi \rho }$$

(13)

Note that both R and ${\chi }_{*}$ here are just radial coordinates and not proper distances between events.

4. Black Hole solution

For the local top-hat distribution of Eq.6, if all the mass M is contained within $R<r_S=2GM$ the solution correspond to a Black Hole (BH, see [38]). In the limit where the exterior is empty, the gravitational radius $r_S$ should be interpreted as a boundary that separates the interior ($r<r_S$) from the exterior manifold. This creates and isolated Universe inside with a boundary condition at $r_S$. As detailed in [28,29], starting from the general case with $\Lambda =0$, the corresponding GHY boundary term ([39,40,41]) to the Einstein-Hilbert action requieres an effective $\Lambda$ term: $\Lambda =3/r_S^2$, which changes the field equations Eq.4 into:

$$H^2=\frac{2GM}{r^3}+\frac{1}{r_S^2}=\frac{8\pi G}{3}\sum _i{\rho }_i^0{a}^{-3+{\beta }_i}+\frac{1}{r_S^2}$$

(14)

where in the last step we have use $r=a{\chi }_{*}$ and M given by Eq.12. Note that Eq. does not change and we still have $M=M_{MS}$. The $r_S$ boundary adds another contribution to $M_{MS}$ in Eq.8:

$$M_{MS}={\int }_{\Sigma }\rho {\left(1+\frac{{\dot{r}}^2}{c^2}-\frac{2G{M}_{MS}}{c^{2}r}-\frac{r^2}{r_S^2}\right)}^{1/2}d{V}_3$$

(15)

which also cancels out with the new Hubble law in Eq.14. In terms of ${\Omega }_i={\rho }_i/{\rho }_c$, where ${\rho }_c=3H_0^2/\left(8\pi G\right)$:

$$H^2=H_0^2\left[\sum _i{\Omega }_i{a}^{-3+{\beta }_i}\right]+\frac{1}{r_S^2}$$

(16)

where typically we have $i=\{1,2\}$ with ${\beta }_1=0$ for matter and ${\beta }_2=-1$ for radiation. This is exactly what we measure in cosmological surveys. It shows how we can interpret the observed cosmic expansion as being a local BH solution, the BHU (instead of a global LCDM model with $\Lambda$ or DE). If there is also dark energy (DE) we have to add an additional term:

$$H^2=H_0^2\left[\sum _i{\Omega }_i{a}^{-3+{\beta }_i}+{\Omega }_{DE}{a}^{-3(1+{\omega }_{DE})}\right]+\frac{1}{r_S^2},$$

(17)

where ${\omega }_{DE}=p_{DE}/{\rho }_{DE}$ is the DE equation of state. Given that the last 2 terms are approximately constant (for ${\omega }_{DE}=-1$) there is no way to distinguish them using measurements of the Hubble-Lemaitre law. Current observations tell us that indeed ${\omega }_{DE}\simeq -1$ ([42]) and the sum of the 2 terms is an effective $\Lambda$ term such that ${\Omega }_{\Lambda }\equiv \frac{\Lambda }{3H_0^2}\simeq 0.7$ or, in other words:

$$\Lambda \equiv 3/r_{\Lambda }^2\equiv 3{\Omega }_{\Lambda }{H}_0^2\equiv 8\pi G{\rho }_{DE}+3/r_S^2\simeq 2.1H_0^2,$$

(18)

If ${\rho }_{DE}=0$, we have that $r_S=r_{\Lambda }$ and the mass of our Universe is:

$$M=\frac{c^2}{2G}\sqrt{3/\Lambda }=\frac{c^2}{2G}{\Omega }_{\Lambda }^{-1/2}{H}_0^{-1}\simeq 6\times {10}^{22}{M}_{\odot }$$

(19)

where we have returned to units of $c\ne 1$ here to be more explicit. This corresponds to the BHU. In the other limit, if $r_S=\infty$ we recover the infinite LCDM model with $M=\infty$ and ${\Omega }_{\Lambda }={\Omega }_{DE}\simeq 0.7$. Both models have a future Event Horizon (E.H.) R::

$$R\left(a\right)=a{\int }_a^{\infty }\frac{da}{H{a}^2}<r_{\Lambda }$$

(20)

which is bounded by $R<r_{\Lambda }$ ([29]): anything that is at $r>R\left(a\right)$ is outside causal reach. Here $R\left(a\right)$ is the maximum proper distance that a photon can travel. Fig.Figure 1 shows a comparison of the two possible interpretations.

We could also have an intermediate situation, but it would be quite unnatural that $r_S$ (from M) and $r_{\Lambda }$ (from DE) are fine tuned to both contribute to the observed cosmic acceleration. We therefore have to choose one of the two interpretations. Given that $M=\infty$ is a non physical (and not causally possible) solution and that we do not know what DE is, it seems more plausible and simpler to interpret cosmic acceleration as a measurement for the mass M of our Universe. In this case ${\rho }_{DE}\simeq 0$ and the raw value of $\Lambda$ is also $\Lambda \simeq 0$. Our Universe is therefore inside a local BHU.

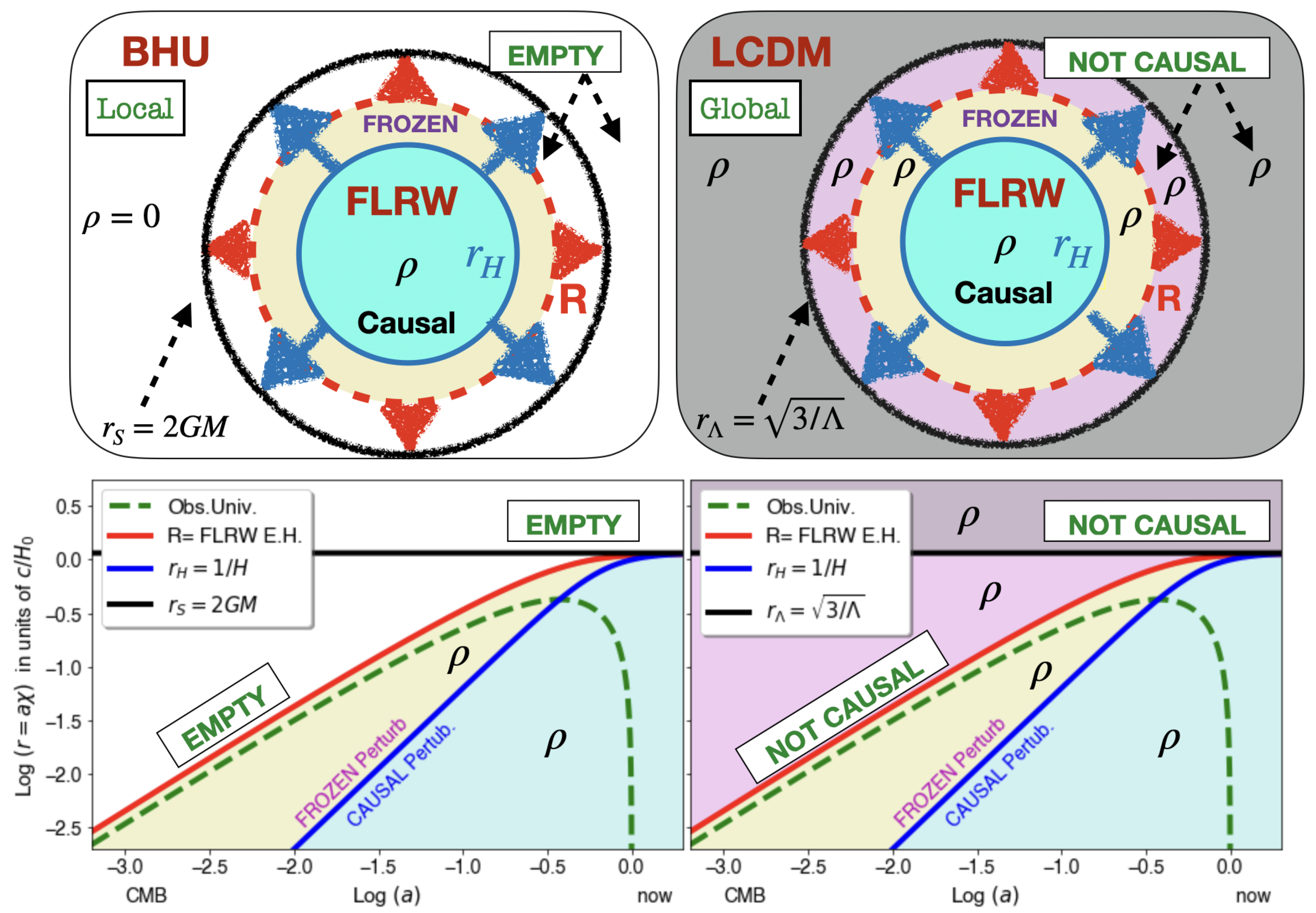
5. Conclusion

We have interpreted the observed $\Lambda$ to be an effective term that corresponds to the gravitational radius $r_S=\sqrt{3/\Lambda }=2GM$ of our local Universe. This has several implications:

• The mass of our Universe can be estimated to be: $M\simeq 6\times {10}^{22}{M}_{\odot }$ (see Eq.19), which agrees well with what we have observed in the largest Galaxy Surveys, such as [42].
• Our Universe is a local solution inside its gravitational radius $r_S$. It is therefore a Black Hole Universe (BHU).
• The dynamical time associated to M in our Universe is $\tau \sim GM\sim 14Gyr$, which is close to the measured age of the oldest galaxies and stars that we observe.
• An observer placed anywhere within the local BHU measures the same background as one within the LCDM ([29]).
• The smoking gun of the BHU is a cut-off in the scale of the largest perturbations which has already been measured in CMB maps ([43,44]).
• Our BHU might not be unique: there could also exist other Universes, like ours, elsewhere. This is part of the The Copernican Revolution: our place is not special.

How did such a BHU form? Here we enter the more speculative grounds of the Big Bang theories. The BHU could have formed in a similar way as the standard LCDM universe: out of one of the many existing models of Cosmic Inflation ([46,47,48,49,50]) or from some of the Quantum Gravity alternatives (e.g. [6,13,16,51,52]).

The BHU could have also formed in a much simpler way, just like the first stars: collapsing and exploding in a Supernova following the known laws of Physics ([30]). Left panel of Figure 2 shows the Crab Nebula, a remnant of a Supernova, which can be thought as a small version of our Universe today. In such case, Cosmic Inflation or Quantum Gravity explanations are not needed to understand the origin of our cosmic expansion. Such beginning would provide us with an anthropic explanation for the observed value of $r_S$ and the coincidence problem. It also yields new candidates for Dark Matter in the form of compact remnants of the collapse and bouncing phases, such as primordial BHs and primordial Neutron Stars ([30]).

The BHU exists within a larger background that may or may not be totally empty outside. In the later case, $r_S$ will increase if there is accretion from outside. This case is more speculative and needs to be studied in more detail, but it would result in an effective $\Lambda$ term that decreases with time (${\omega }_{DE}>-1$). The alternative interpretation is that M (and therefore $r_S$) are infinite so that the measured $\Lambda$ can only be attributed to DE. This is the standard (LCDM) interpretation. In our view, this alternative is less appealing because it involves non physical infinite, non causal structure ([53,54]) and new components, DE or $\Lambda$, which are not really needed.