Preprint

Article

The Morphology of the Active Galactic Nucleus and its Impact on Accretion Flows and Relativistic Jets

Altmetrics

Downloads

1079

Views

1252

Comments

A peer-reviewed article of this preprint also exists.

Mohammed Al-Fadhli^*

This version is not peer-reviewed

Submitted:

11 January 2023

Posted:

12 January 2023

You are already at the latest version

Alerts

Abstract

The G2 gas cloud motion data and the scarcity of observations on the event horizon-scale distances have challenged the comprehensiveness of the central supermassive black hole model. In addition, the Planck Legacy 2018 release has preferred a positively curved early Universe with a confidence level higher than 99%. This study investigates the impact of the background curvature and its evolution over the conformal time on the formation and morphological evolution of central compact objects and the consequent effect on their host galaxies. The formation of a galaxy from the collapse of a supermassive gas cloud in the early Universe is modeled based on interaction field equations as a 4D relativistic cloud-world that flows and spins through a 4D conformal bulk of a primordial positive curvature considering the preference of the Planck release. Owing to the curved background, this scenario of galaxy formation reveals that the core of the galaxy undergoes a forced vortex formation with a central event horizon leading to opposite vortices (traversable wormholes) that spatially shrink while evolving in the conformal time. It indicates that the galaxy and its core are formed in the same process whereas the surrounding gas clouds form the spiral arms due to the frame-dragging induced by the fast-rotating core. It demonstrates that the accretion flow onto the central supermassive compact object only occurs at the central event horizon of the two opposite vortices while their other ends eject the relativistic jets. This can elucidate the relativistic jet formation and explain the G2 gas cloud motion if its orbit is around one of the vortices but at a distance from the central event horizon. The gravitational potential of the early curved bulk could contribute to galaxy formation while the present spatial flatness deprives the potential of bulk which could lead to galaxy quenching. The formation of a galaxy and its core simultaneously could explain the growth of the supermassive compact galaxy core to a mass of ~10⁹ M_⊙ at just 6% of the current Universe age.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

Relativistic jets are extended beams of ionized matter emitted in opposite directions along the axis of rotation of active galaxies, quasars, stellar black holes, neutron stars and pulsars at speeds that approach the speed of light. Their radiative signatures and kinetic luminosity can be immensely powerful and such jets can exceed thousandths to millions of parsecs in length. The precise mechanisms by which the relativistic jets are produced are under ongoing debate in the scientific community [1,2,3].

Recently, the G2 gas cloud orbit around the galactic centre and lack of observations on the event horizon-scale distances have challenged the completeness of the supermassive black hole model [4,5]. In addition, the PL18 release confirmed the existence of an enhanced lensing amplitude in the cosmic microwave background power spectra, which prefers a positively curved early Universe with a confidence level greater than 99% [6,7]. This study presents a new galaxy formation scenario by utilizing interaction field equations in which celestial objects are considered as 4D relativistic cloud-worlds that flow and spin through a 4D conformal bulk of a primordial curvature considering the preference of the Planck release. The derived model reveals a new mechanism of relativistic jet generation.

2. Interaction Field Equations

The PL18 release has preferred a positively curved early Universe, that is, is a sign of a primordial background curvature or a curved bulk. To incorporate the bulk curvature and its evolution over the conformal time, a modulus of spacetime deformation,

E_{D}

in terms of energy density, is introduced based on the theory of elasticity [8]. The modulus can be expressed in terms of the resistance of the bulk to the localized curvature induced by celestial objects by using Einstein field equations or in terms of the field strength of the bulk by using the Lagrangian formulation of the energy density existing in the bulk as a manifestation of the vacuum energy density as follows

E_{D} = \frac{{- F}_{λ ρ} F^{λ ρ}}{4 μ_{0}}

(1)

where

F_{λ ρ}

is the field strength tensor of the bulk and

μ_{0}

is vacuum permeability. By incorporating the bulk influence, the Einstein–Hilbert action can be extended to

S = E_{D} \int_{C}^{} [\frac{R}{R} + \frac{L}{L}] {\sqrt{- g} d}^{4} ρ

(2)

where

R = R_{μ ν} g^{μ ν}

is Ricci scalar curvature representing a localized curvature induced in the bulk by a celestial object that is regarded as a 4D relativistic cloud-world of metric

g_{u v}

and Lagrangian density

L = L_{μ ν} g^{μ ν}

R = R_{μ ν} {\tilde{g}}^{μ ν}

is the scalar curvature of the 4D bulk of metric

{\tilde{g}}_{μ ν}

whereas

L = L_{μ ν} {\tilde{g}}^{μ ν}

is the bulk’s Lagrangian density as an indication of its internal stresses and momenta reflecting its curvature. A dual-action concerning the conservation of energy on global (bulk) and local (cloud-world) scales can be introduced as

S = \int_{B}^{} [\frac{- F_{λ ρ} {\tilde{g}}^{λ γ} F_{γ α} {\tilde{g}}^{ρ α}}{4 μ_{0}}] \sqrt{- \tilde{g}} \int_{C}^{} [\frac{R_{μ ν} g^{μ ν}}{R_{μ ν} {\tilde{g}}^{μ ν}} + \frac{L_{μ ν} g^{μ ν}}{L_{μ ν} {\tilde{g}}^{μ ν}}] \sqrt{- g} d^{4} ρ d^{4} σ

(3)

By applying the principle of stationary action in [9] yields

\frac{R_{μ ν}}{R} - \frac{1}{2} \frac{R}{R} g_{μ ν} - \frac{R R_{μ ν}}{R^{2}} + \frac{R (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν}) - R (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν})}{R^{2}} = \frac{{\hat{T}}_{μ ν}}{T_{μ ν}}

(4)

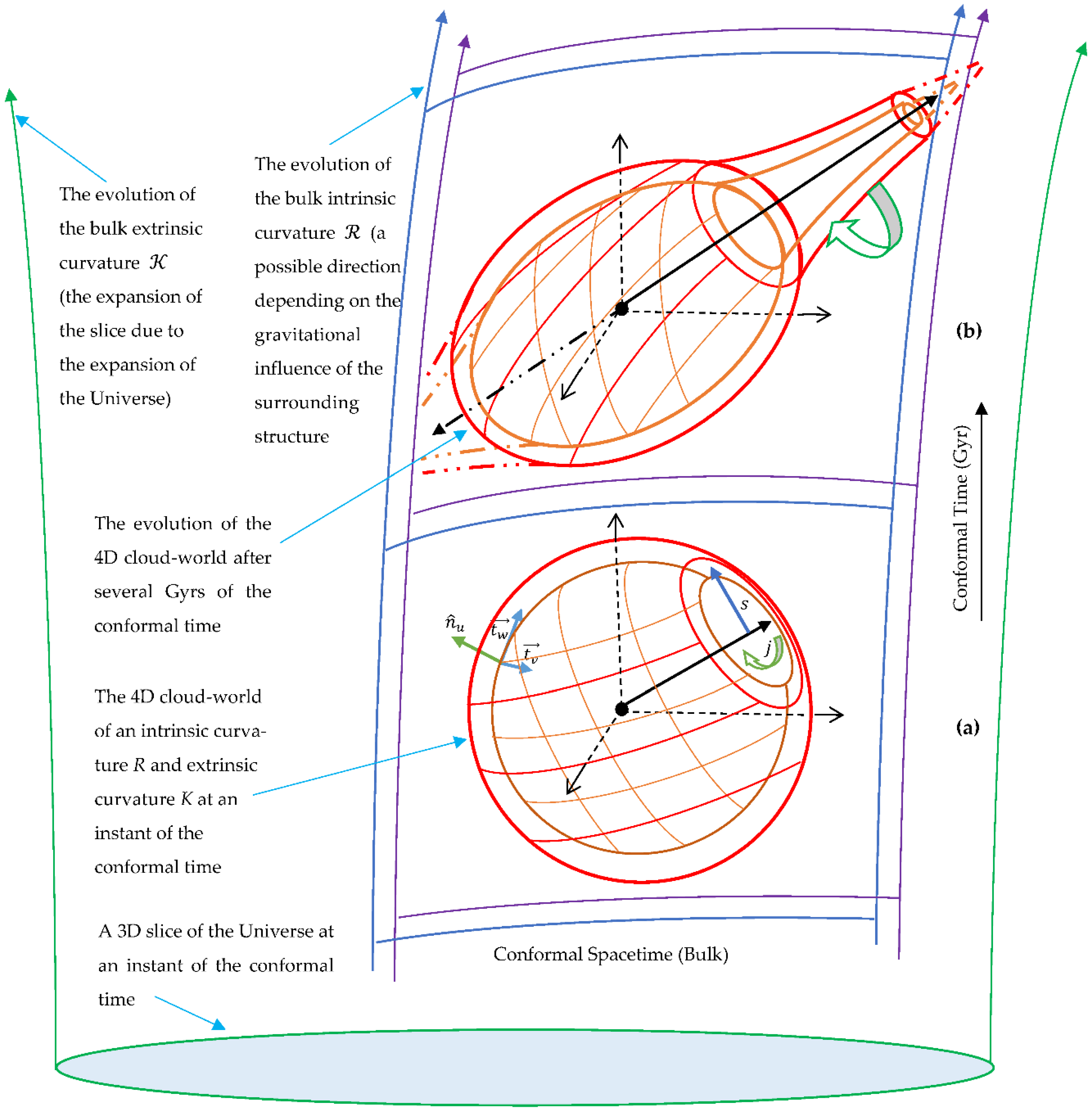
The interaction field equations can be interpreted as indicating that the cloud-world’s induced curvature over the bulk’s existing curvature equals the ratio of the cloud-world’s imposed energy density and its flux to the bulk’s vacuum energy density and its flux through the expanding/contracting Universe. The equations can describe the interaction of a 4D relativistic cloud-world of intrinsic

R_{μ ν}

and extrinsic

K_{μ ν}

curvatures with a stress-energy

{\hat{T}}_{μ ν}

and the 4D bulk of intrinsic

R_{μ ν}

and extrinsic

K_{μ ν}

curvatures with a stress-energy

T_{μ ν}

(as visualized in Figure 2). By utilizing Equation (1) that states

T_{μ ν} ≔ E_{D} = R c^{4} / {8 π G}_{R}

, the field equations can be simplified to

R_{μ ν} - \frac{1}{2} R {\hat{g}}_{μ ν} - (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν}) = \frac{{8 π G}_{R}}{c^{4}} {\hat{T}}_{μ ν}

(5)

where

{{\hat{g}}_{μ ν} = g}_{μ ν} + 2 R_{μ ν} / R + 2 {\overset{̿}{g}}_{μ ν}

or can be simplified to

{{\hat{g}}_{μ ν} = g}_{μ ν} + 2 {\tilde{g}}_{μ ν} + 2 {\overset{̿}{g}}_{μ ν}

is the conformally transformed metric tensor counting for the contributions of the cloud-world metric,

g_{μ ν},

in addition to the contribution from intrinsic and extrinsic curvatures of the bulk, whereas Einstein spaces are a subclass of conformal spaces [10]. The evolution in

G_{R}

reflects the field strength of the bulk and depends on the bulk or background curvature.

3. Galaxy Formation and Relativistic Jet Generation

The entire contribution comes from the boundary term when calculating the black hole entropy using the semiclassical approach [11,12]. By applying this concept and re-arranging the field equations for this setting as

R_{μ ν} - \frac{1}{2} R {\hat{g}}_{μ ν} = \frac{8 π G_{R}}{c^{4}} {\hat{T}}_{μ ν} - \frac{R (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν}) - R (K_{μ ν} - \frac{1}{2} K {\hat{q}}_{μ ν})}{R} = 0

(6)

The field equations can describe the interaction between a 4D relativistic cloud-world of intrinsic

R_{μ ν}

and extrinsic

K_{μ ν}

curvatures with a stress-energy

{\hat{T}}_{μ ν}

and the 4D bulk of intrinsic

R_{μ ν}

and extrinsic

K_{μ ν}

curvatures with a stress-energy

T_{μ ν}

. From Equation (6), the field equations yield

R_{μ ν} = \frac{1}{2} R {\hat{g}}_{μ ν} = \frac{1}{2} R g_{μ ν} + \frac{R_{μ ν}}{R} R = \frac{1}{2} R (g_{μ ν} + 2 {\tilde{g}}_{μ ν}) = \frac{1}{2} R g_{μ ν} (1 + 2 Ω^{2}) = 0

(7)

where

{\hat{g}}_{μ ν} = g_{μ ν} + 2 {\tilde{g}}_{μ ν}

and

{{\tilde{g}}_{μ ν} = R}_{μ ν} / R = R_{μ ν} / R_{μ ν} {\tilde{g}}^{μ ν}

is the conformal bulk metric, which can be expressed as proportional to cloud-world metric

g_{μ ν}

{\tilde{g}}_{μ ν} = g_{μ ν} Ω^{2}

by utilizing

Ω^{2}

, the conformal transformation function. The conformally transformed metric

{\hat{g}}_{μ ν} = g_{μ ν} (1 + 2 Ω^{2})

can be expressed as

d s^{2} = - A (r) (1 + 2 Ω^{2} (r, r)) c^{2} d t^{2} + S^{2} (B (r) (1 + 2 Ω^{2} (r, r)) d r^{2} + r^{2} d θ^{2} + r^{2} {s i n}^{2} θ d ϕ^{2})

(8)

where

A^{}

and

B

are functions of the cloud-world radius

r

S^{2}

is a dimensionless conformal scale factor. By performing the coordinate transformation as follows

d s^{2} = - (A (λ) + 2 A (λ) Ω^{2} (λ, r)) c^{2} d t^{2} + (B (λ) + 2 B (λ) Ω^{2} (λ, r)) d λ^{2} + λ^{2} d θ^{2} + λ^{2} {s i n}^{2} θ d ϕ^{2}

(9)

where the conformal function

Ω^{2}

is a function of the bulk radius of curvature

r

and it can be influenced by the cloud-world radius.

The Christoffel symbols of this metric are

Γ_{00}^{1} = \frac{\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω}}{2 (B + 2 B Ω^{2})}, Γ_{01}^{0} = \frac{\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω}}{2 (A + 2 A Ω^{2})}, Γ_{11}^{1} = \frac{\dot{B} (1 + 2 Ω^{2}) + 4 B \dot{Ω}}{2 (B + 2 B Ω^{2})} Γ_{22}^{1} = \frac{- λ}{(B + 2 B Ω^{2})}, Γ_{33}^{1} = \frac{- λ {s i n}^{2} θ}{(B + 2 B Ω^{2})}, Γ_{21}^{2} = Γ_{12}^{2} = \frac{1}{λ} Γ_{33}^{2} = - s i n θ c o s θ, Γ_{32}^{3} = Γ_{23}^{3} = \frac{c o s θ}{s i n θ}

(10)

where the sign

\dot{}

is a total derivative of the function. The Ricci tensor components are

R_{t t}^{} = - \frac{\frac{d}{d λ} (\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω})}{2 (B + 2 B Ω^{2})} - \frac{\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω}}{2 (B + 2 B Ω^{2})} \frac{\dot{B} (1 + 2 Ω^{2}) + 4 B \dot{Ω}}{2 (B + 2 B Ω^{2})} + \frac{\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω}}{2 (B + 2 B Ω^{2})} \frac{\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω}}{2 (A + 2 A Ω^{2})} - \frac{1}{λ} \frac{\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω}}{2 (B + 2 B Ω^{2})}

(11)

R_{t t}^{} = - \frac{\ddot{A} (1 + 2 Ω^{2} + 4 \dot{Ω}) + 4 A \ddot{Ω} + 4 \dot{Ω} \dot{A}}{2 (B + 2 B Ω^{2})} + \frac{(\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω}) (\dot{B} (1 + 2 Ω^{2}) + 4 B \dot{Ω})}{4 {(B + 2 B Ω^{2})}^{2}} + \frac{{(\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω})}^{2}}{4 (A + 2 A Ω^{2}) (B + 2 B Ω^{2})} - \frac{1}{λ} \frac{\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω}}{(B + 2 B Ω^{2})}

(12)

R_{r r}^{} = \frac{1}{2} (\frac{\ddot{A} (1 + 2 Ω^{2} + 4 \dot{Ω}) + 4 A \ddot{Ω} + 4 \dot{Ω} \dot{A}}{(A + 2 A Ω^{2})} - \frac{{(\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω})}^{2}}{2 {(A + 2 A Ω^{2})}^{2}}) - \frac{{(\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω}) (\dot{B} (1 + 2 Ω^{2}) + 4 B \dot{Ω})}^{}}{4 (A + 2 A Ω^{2}) (B + 2 B Ω^{2})} - \frac{1}{λ} \frac{\dot{B} (1 + 2 Ω^{2}) + 4 B \dot{Ω}}{B + 2 B Ω^{2}}

(13)

R_{θ θ}^{} = \frac{1}{(B + 2 B Ω^{2})} - \frac{λ}{2 (B + 2 B Ω^{2})} (\frac{\dot{B} (1 + 2 Ω^{2}) + 4 B \dot{Ω}}{{(B + 2 B Ω^{2})}^{}} - \frac{\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω}}{{(A + 2 A Ω^{2})}^{}}) - 1

(14)

R_{ϕ ϕ}^{} = \frac{{s i n}^{2} θ}{(B + 2 B Ω^{2})} - \frac{λ {s i n}^{2} θ}{2 (B + 2 B Ω^{2})} (\frac{\dot{B} (1 + 2 Ω^{2}) + 4 B \overset{´}{Ω}}{{(B + 2 B Ω^{2})}^{}} - \frac{\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω}}{{(A + 2 A Ω^{2})}^{}}) - {s i n}^{2} θ

(15)

By substituting Ricci tensor components to Equation (7) gives

(\dot{A} (1 + 2 Ω^{2}) + 4 A \dot{Ω}) (B + 2 B Ω^{2}) + (A + 2 A Ω^{2}) (\dot{B} (1 + 2 Ω^{2}) + 4 B \dot{Ω}) = 0

(16)

Equation (16) yields

B + 2 B Ω^{2} = \frac{k}{A + 2 A Ω^{2}}

(17)

where

k = 1 + 4 Ω^{2} + Ω^{4}

for the conformal metric by considering the bulk curvature.

By applying the weak-field limit:

{\hat{g}}_{μ ν} \approx η_{μ ν} + {\hat{h}}_{μ ν}

, as follows

Γ_{t t}^{i} = \frac{1}{2} \int \partial_{i} {\hat{h}}_{t t} = \frac{1}{c^{2}} \int \partial_{i} φ

(18)

where

φ

is the Newtonian gravitational potential. By integrating both sides

{\hat{g}}_{t t} = - A (1 + 2 Ω^{2}) = - (η_{t t} + \frac{2 φ_{c}}{c^{2}} + \frac{2 φ_{p}}{c^{2}})

(19)

where

φ_{c} = - G M / λ

is the gravitational potential of the cloud-world’s spherical mass and

φ_{p}

that arises from the integration can be interpreted as the gravitational potential resulting from the bulk curvature, which can be expressed, using the same Newtonian analogue, in terms of the mass,

M_{p}

, of the early Universe plasma of preferred positive curvature and the bulk curvature radius

r

φ_{p} = - G_{p} M_{p} / r

. The metric should yield only the gravitational potential of the cloud-world when there is no bulk curvature

(Ω^{2} = 0)

and (

φ_{b} = 0)

; hence,

A = (1 + 2 φ_{c} / c^{2})

; consequently, the conformal function is

Ω^{2} = φ_{p} / A c^{2}

By performing the coordinate retransformation and combining Equations (17 - 19) yield

Ω^{2} = - \frac{G_{p} M_{p}}{r c^{2}} {(1 - \frac{2 G M}{r c^{2}})}^{- 1}, A = 1 - \frac{2 G M}{r c^{2}}, B = {(1 - \frac{2 G M}{r c^{2}})}^{- 1}

(20)

where the conformal function

Ω^{2}

relies on the gravitational potential of the bulk while its influence is inversely proportional to cloud-world potential. In the case of PI18’s preferred early Universe positive curvature, the gravitational potential of the bulk can be expressed in terms of the early Universe plasma of mass,

M_{p}

, and

r

denoting the radius of curvature of the bulk, where the bulk’s potential decreases with the Universe expansion and vanishes in the flat spacetime background (

r \to \infty)

. The minus sign of

Ω^{2}

reveals a spatial shrinking through evolving in the conformal time, which agrees with the vortex model that can occur due to high-speed spinning. By substituting Equation (20) to Equation (8), the conformally metric

{\hat{g}}_{μ ν} = g_{μ ν} + 2 {\tilde{g}}_{μ ν} = g_{μ ν} (1 + 2 Ω^{2})

d s^{2} = (1 - \frac{r_{s}}{r} - \frac{r_{p}}{r}) (- c^{2} d t^{2} + S^{2} (\frac{d r^{2}}{1 + \frac{{r_{s}}^{2}}{r^{2}} - 2 \frac{r_{s}}{r}} + \frac{r^{2} d θ^{2} + r^{2} {s i n}^{2} θ d ϕ^{2}}{1 - \frac{r_{s}}{r} - \frac{r_{p}}{r}}))

(21)

This metric reduces to the Schwarzschild metric in a flat background (

r_{} \to \infty)

, where

r

is the background or bulk curvature radius,

r_{s}

is Schwarzschild radius,

r_{p} = 2 G_{p} M_{p} / c^{2}

is early Universe gravitational radius and

S^{2}

is a dimensionless spatial scale factor. The denominator of the radial dimension can be interpreted as an intrinsic curvature term where the metric on the radial and two-sphere is warped by the bulk and cloud-world radii. The metric can be visualized through evolving in the conformal time by using Flamm's approach as follows

w (r, r) = \mp \int \frac{\sqrt{(\frac{r_{s}}{r} - \frac{{r_{s}}^{2}}{r^{2}} - \frac{r_{p}}{r})}}{{(1 - \frac{r_{s}}{r})}^{}} d r = \mp \sqrt{r_{s} (r - {r_{s}}^{}) - r_{p} \frac{r^{2}}{r}} + O + C

(22)

where

C

is a constant and

O

denotes less significant terms. By choosing an appropriate

C

, Figure 1 shows the proper distances, and their corresponding proper areas are increasing as they are evolving in the conformal time while the radius decreases.

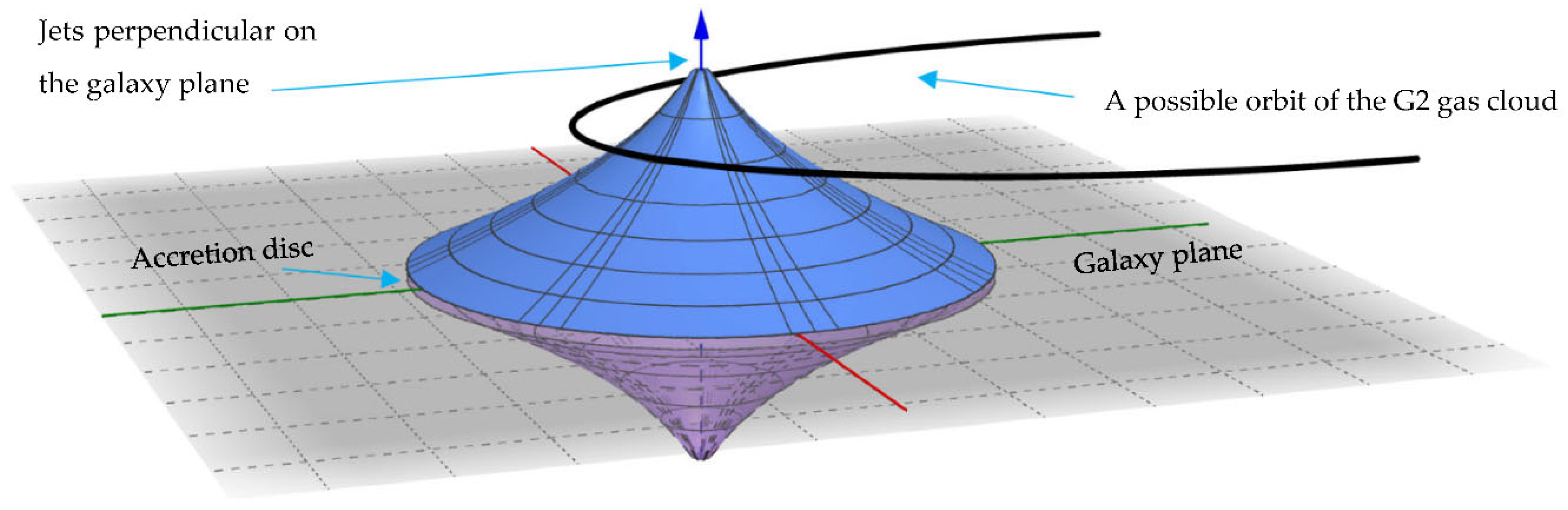
The increase in the proper distances and their corresponding proper areas as the radius decreases agree with the vortex model while the positive and negative solutions of Equation (22) indicate the evolution of the vortex in opposite directions, i.e., forming a dual vortex perpendicular on the galaxy plane. The 4D cloud-world of metric

g_{μ ν}

through its travel and spin in the conformal space-time of the 4D bulk of metric

{\tilde{g}}_{μ ν}

The G2 cloud has only faced drag forces [4,5], where orbiting a vortex could explain these observations if its orbit is at a distance from the central event horizon. In addition, the observations of the superluminal motion in the x-ray jet of M87 [14] could be travelled through these two opposite traversable wormholes.

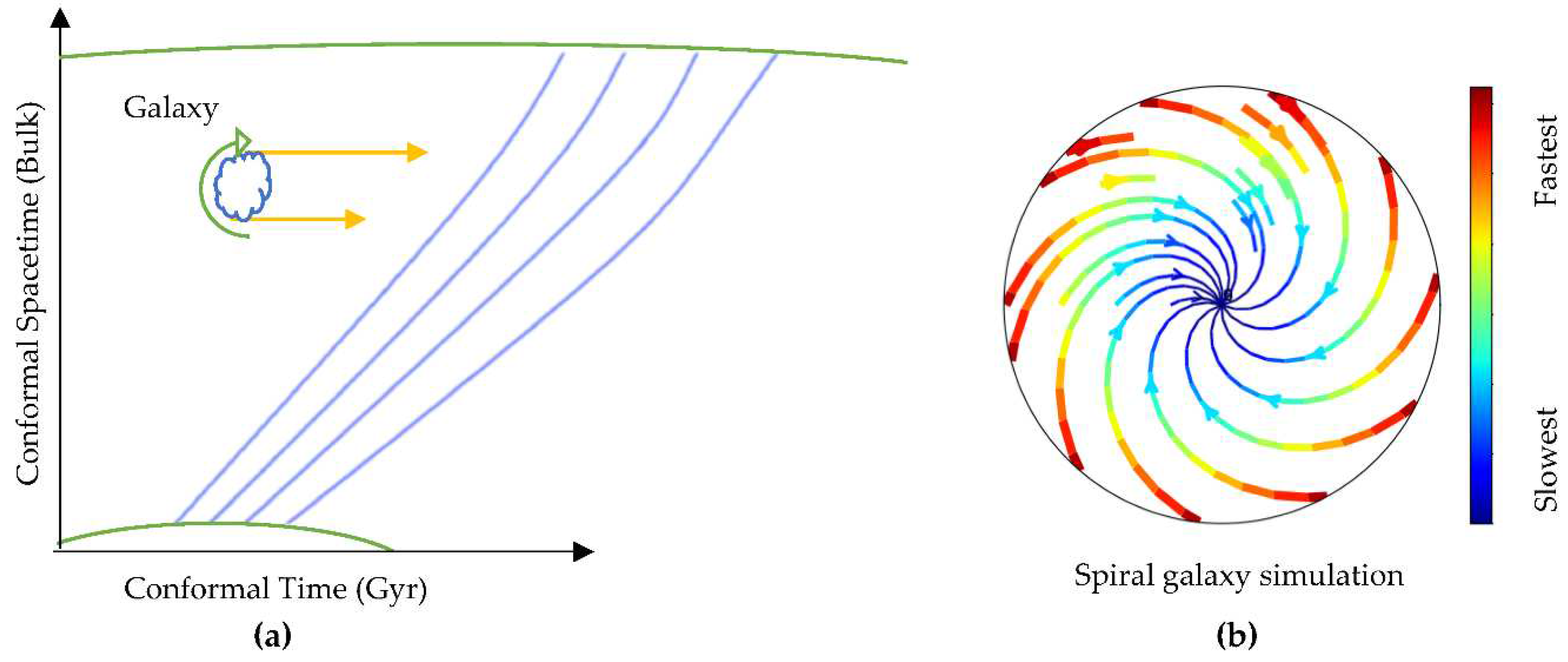
To evaluate the influence of the spinning and the curvature of the bulk on the core of the galaxy and the surrounding gas clouds (the spiral arms), a fluid simulation was performed based on Newtonian dynamics by using the Fluid Pressure and Flow software [13]. In this simulation, the fluid was deemed to represent the spacetime continuum throughout incrementally flattening curvature paths representing conformal curvature evolution to analyze the external momenta exerted on objects flowing throughout the incrementally flattening curvatures. The momenta yielded by the fluid simulation were used to simulate a spiral galaxy as a forced vortex as shown in Figure 3.

The simulation shows that the tangential speeds of the outer parts of the spiral galaxy are rotating faster in comparison with the rotational speeds of the inner parts, which resembles observations of galaxy rotation except the simulation used an ideal fluid.

4. Conclusions and Future Works

In this study, interaction field equations are derived in which the curvature of the background or the 4D conformal bulk evolves over the conformal time based on the PL18 recent release which has preferred a positively curved early Universe with a confidence level higher than 99%. Throughout this bulk, 4D relativistic cloud-worlds flow and spin.

Owing to the curved background, the findings of galaxy formation showed that the core of the galaxy undergoes a forced vortex formation with a central event horizon leading to opposite traversable wormholes that are spatially shrinking through evolving in the conformal time. It revealed that the galaxy and its core form in the same process, while the surrounding gas clouds can form spiral arms due to the fast-rotating core. These findings demonstrated that the accretion flow onto the central supermassive compact object only occurs at the central event horizon of the two opposite vortices while their other ends eject the relativistic jets. The formation of the galaxy and its core at the same process can explain the formation of supermassive compact galaxy cores with a mass of ~10⁹ M_⊙ at just 6% of the current Universe age and could solve the black hole hierarchy problem.

Conflicts of Interest

The author declares no conflict of interest.

References

Beall J H, Beall and H. J 2015 A Review of Astrophysical Jets mbhe 58.
Kundt W A Uniform Description of All the Astrophysical Jets.
Beall J H 2014 A review of astrophysical jets Frascati Work. 2013 - 10th Int. Work. Multifrequency Behav. High Energy Cosm. Sources 259–64.
Burkert A, Schartmann M, Alig C, Gillessen S, Genzel R, Fritz T K and Eisenhauer F 2012 Physics of the galactic center cloud G2, on its way toward the supermassive black hole Astrophys. J. 750 58. [CrossRef]
Becerra-Vergara E A, Argüelles C R, Krut A, Rueda J A and Ruffini R 2021 Hinting a dark matter nature of Sgr A* via the S-stars Mon. Not. R. Astron. Soc. Lett. 505 L64–8. [CrossRef]
Di Valentino E, Melchiorri A and Silk J 2020 Planck evidence for a closed Universe and a possible crisis for cosmology Nat. Astron. 4 196–203. [CrossRef]
Handley W 2021 Curvature tension: Evidence for a closed universe Phys. Rev. D 103 L041301. [CrossRef]
Landau L D 1986 Theory of Elasticity (Elsevier).
Al-Fadhli M B 2023 Celestial and Quantum Propagation, Spinning, and Interaction as 4D Relativistic Cloud-Worlds Embedded in a 4D Conformal Bulk: From String to Cloud Theory.
Kozameh C, Newman E, gravitation K T-G relativity and and 1985 Conformal Einstein spaces Springer.
Dyer E and Hinterbichler K 2009 Boundary terms, variational principles, and higher derivative modified gravity Phys. Rev. D - Part. Fields, Gravit. Cosmol. 79. [CrossRef]
Brown J D and York J W 1993 Microcanonical functional integral for the gravitational field Phys. Rev. D 47 1420–31. [CrossRef]
Reid S, Podolefsky H and Pual A 2013 Fluid Pressure and Flow, PhET Interactive Simulations.
Snios B, Nulsen P E J, Kraft R P, Cheung C C, Meyer E T, Forman W R, Jones C and Murray S S 2019 Detection of Superluminal Motion in the X-Ray Jet of M87.

Figure 1. The metric of the supermassive compact object as a central event horizon leading to opposite vortices with two jets that are perpendicular on the rotation plane.

Figure 2. The hypersphere of a compact core of a galaxy (the red-orange 4D cloud-world) along with its travel and spin through the conformal spacetime (the blue-purple 4D bulk representing the bulk of distinctive curvature evolving over the conformal time.

Figure 3. (a) External fields exerted on a galaxy due to the spacetime conformal curvature evolution. Green curves represent the curvature of spacetime worldlines. Blue curves represent the simulated spacetime continuum. (b) Simulation of spiral galaxy rotation. Blue represents the slowest tangential speeds and red represents the fastest speeds.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.