Thermal-Dependent Intermolecular Forces in Gases: A New Analytical Approach Based on Experimental Evidence

1. Introduction

The behavior of gases under gravitational fields is traditionally described through classical Newtonian gravity and kinetic theory principles, where intermolecular forces in the gaseous state are commonly assumed to be negligible. Under such approximations, buoyancy and thermal expansion are sufficient to explain most vertical gas and vapor motions observed in the atmosphere and engineered systems.

However, certain laboratory and natural observations reported in a series of previous studies [1,2,3,4] have indicated upward movement of matter that may not be fully accounted for by standard buoyancy and diffusion alone. The findings forwarded in this paper, together with experimental results [2,3,4] from previous studies, motivated the development of an analytical approach that considers potential, energy-dependent interactions influencing gas behavior in gravitational environments.

This study of gravitation forces in gases has been conducted modelling them as two distinct forces of repulsion and attraction acting on gaseous matter. The gravitational repulsion concept presented in the series of publications [1,2,3,4] emanating from this research program, are based on experimental observations and natural phenomena; making neither abstruse assumptions nor explanations. The model has been validated using experimentally determined and established data utilized in practical thermodynamic applications of mechanical engineering industries. It is a self-standing model, which requires no fitting into existing models. The presented alternative model could more effectively describe the nature of the Universe at both micro and macro levels.

The current understanding of fundamental interactions - gravitational, electromagnetic, and the strong and weak nuclear forces [Table S1 in supplementary information] does not include any explicitly temperature-dependent (hence energy dependent) component. Yet, many macroscopic physical phenomena such as pressure development, phase change behavior, and thermal expansion are inherently linked to temperature which is a manifestation of the thermal energy content. This raises a scientific question of whether temperature-dependent effects could contribute in subtle ways to the motion and distribution of matter under gravity.

Historical discussions of non-attractive gravitational effects can be found dating back to Newton’s Principia [5], published by Isaac Newton in 1687; see Prepositions XLIII-XLV of Book 1, pp171-182, and more recent theoretical explorations have occasionally entertained similar concepts [6,7,8,9,10]. Additionally, recent discussions suggest that some interstellar objects, such as comets (e.g., 1I/ʻOumuamua and 3I/ATLAS), have exhibited non-gravitational accelerations that are not fully explained within the standard fundamental interaction models.

Although many natural and cosmological phenomena—such as pressure, expansion, and phase transitions - depend on temperature, which reflects the system’s thermal energy content, none of the four fundamental forces in classical theory are considered to be directly dependent on thermal energy or temperature. As presented below, and supported by both analytical and experimental evidence, a gravitational repulsive force dependent on thermal energy offers a potential mechanism to bridge the critical gap between energy and the fundamental forces.

In some literature [7,8,9,10], the gravitational repulsion force is referred to as the antigravitational force. Therefore, we use both these words in our text to mean the same concept.

Presenting a new scientific revelation that fundamentally challenges our understanding of the Universe, requires examining the foundations of our present understanding, viz., Newtonian and Einsteinian gravity concepts. The Author would, for the benefit of those interested in contextual knowledge, in the supplementary information (supplementary information: Section A), briefly note the following:

• Newtonian and Einsteinian gravity concepts, thus highlighting foundations of our present understanding
• Early notions of the gravitational repulsion force and its recent revelations

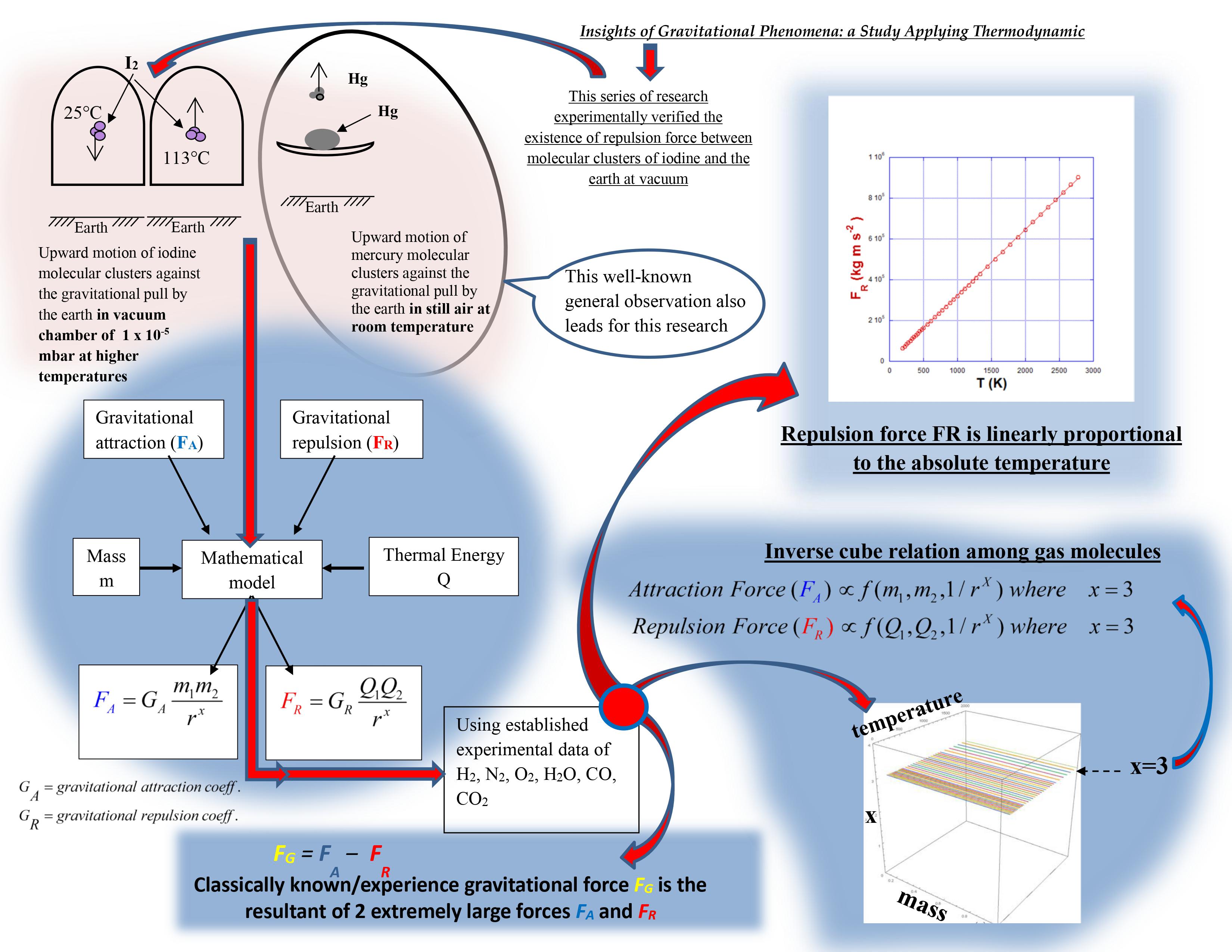
1.1. Motivation from Recent Experimental Observations; the Gravitational Repulsion Force

Experiments previously reported by the author [1,2,3,4] demonstrated displacement against the gravitational attraction in systems such as iodine vapor [3] (briefly presented in Section C) in a partial vacuum and suspended water droplets [2,4] in air.

The observations suggested that the magnitude of these motions against the gravitational attraction scaled with the internal thermal energy of the observed material. Additional experimental work highlighted upward tendencies in mercury molecular clusters [11], despite their significantly higher density compared to ambient air at room temperature.

These findings indicate a possible non-classical contribution to motions against the gravitational attraction that warrants deeper investigation. In particular, an improved theoretical description may support better interpretation of processes involving condensation, aerosol aggregation, and accumulative (flocking together) nature of clouds - phenomena occurring both microscopically and macroscopically.

The discussion thus far suggests that a broader conceptual framework is required beyond the conventional gravitational models, such as Newton’s Law of Universal Gravitation and Einstein’s Einstein Field Equations. We also need to revisiting the key idealized assumptions of the kinetic theory of gases, as discussed in the following section. Our aim is to develop a relationship that offers a deeper understanding of gas-molecule behavior under a proposed repulsive interaction acting on matter.

1.2. Revisiting Key Ideal Gas Theory Assumptions

To formulate a framework capable of evaluating these observations, it is important to revisit certain core assumptions [12] used in classical gas models. The kinetic theory of gases typically assumes:

(i)

negligible intermolecular forces

(ii)

perfectly elastic collisions

(iii)

negligible molecular volume

In deriving the ideal gas equation, one of the most fundamental forces—gravitational interaction among matter - has been largely overlooked, both in terms of molecule–molecule interactions and the interaction between gas molecules and the Earth. Such a sweeping assumption is difficult to justify within the framework of fundamental science. Even though a gas molecule contains only a minute amount of mass, it is still subject to gravitational forces exerted by surrounding matter. Therefore, neglecting gravitational interactions on gas molecules, regardless of the scale of the interacting bodies, may not be a prudent assumption.

It is well established that Earth’s atmosphere is retained due to the planet’s gravitational attraction, which constitutes the dominant force acting on air molecules. Mars, despite its weaker gravitational field, maintains a thin atmosphere of about 0.6% (610 Pa) of Earth’s atmospheric pressure [13]. Conversely, planets with stronger gravitational fields, such as Jupiter and Saturn, possess dense atmospheres capable of retaining even light gases like hydrogen and helium [14].

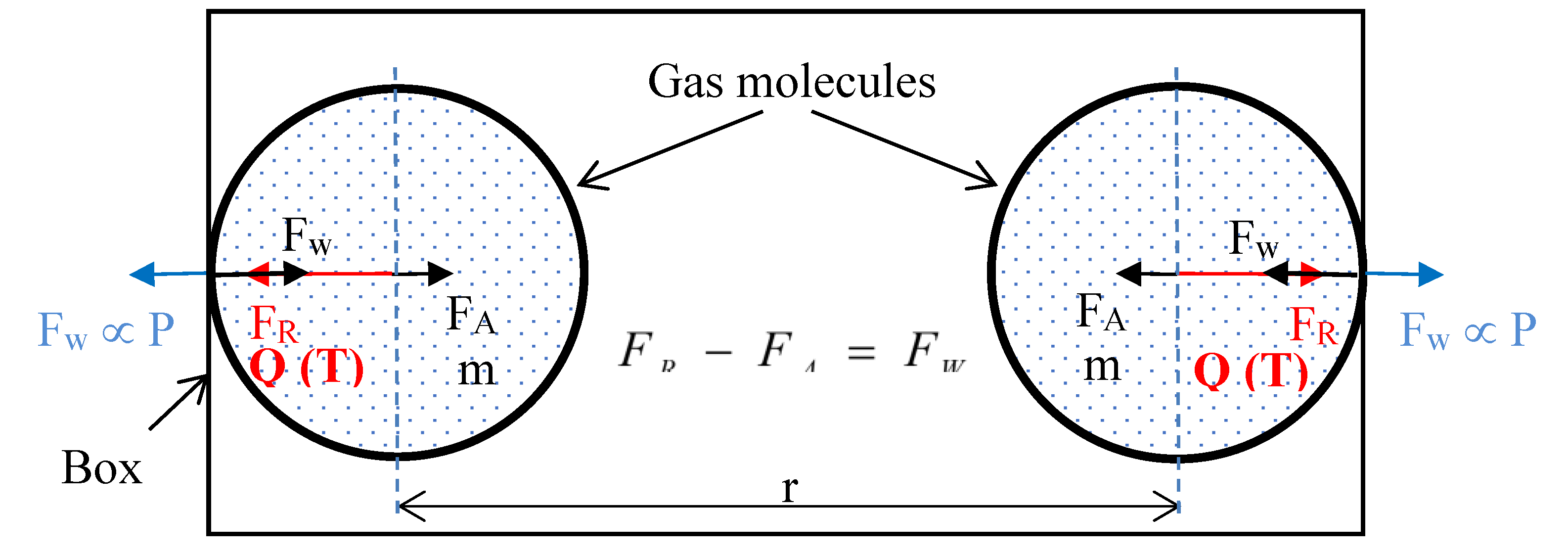
Another assumption in kinetic theory that prompts scrutiny is the notion of “perfectly elastic collisions” between gas molecules and container walls when defining pressure under static conditions. This definition becomes problematic when the wall itself moves under the influence of pressure. Any displacement of the wall requires the transfer of momentum (energy) from gas molecules, which contradicts the premise of a perfectly elastic collision. The mass of an average air molecule (~4.8 × 10⁻²⁶ kg) is negligible compared with the mass of a rigid wall, making the idea that gas-molecule impacts can realistically move such a massive object questionable under Newton’s Third Law. Furthermore, the detailed mechanism by which momentum or energy is transferred through fundamental forces remains unclear.

The postulates of the kinetic molecular theory also neglect the finite volume occupied by gas molecules. Real gases, however, exhibit significant deviations from ideal behavior [15], as reflected in models such as the van der Waals equation. A brief discussion on real-gas behavior is included in Supplementary Information – Section B.

Rather than relying on assumptions with such limitations, this research program considers experimentally established forces. The following section highlights several previous experiments conducted in this program, in which a Gravitational Repulsion force was discovered alongside the well-known Gravitational Attraction force.

2. First Experimental Observation of Gravitational Repulsion:

The first experiment on gravitational repulsion conducted by the Author [1] demonstrated the upward motion of heavy particles (iodine) in a vacuum. Details of the experimental setup are provided in Supplementary Information, Section C. In this design, all conventional mechanisms that might cause upward particle motion in air—such as buoyancy and convective currents - were eliminated.

At room temperature (≈ 25 °C), iodine particles detached from the sample moved downward under the Earth’s gravitational attraction and accumulated at the bottom of the paper jacket. However, when the iodine sample was heated, the particles were observed to move upward in the vacuum, against gravitational pull, as shown in Supplementary Information Figure S1. Paper [1] also references a similar phenomenon in electronic vacuum tubes, where evaporated tungsten and thorium particles from heated filaments rise and deposit at the top of the glass tube despite both gravity and strong radial electric fields. These observations collectively suggest the presence of a gravitational repulsion force acting on matter, analogous in significance to gravitational attraction.

2.1. Key Takeaways from the Iodine Experiment

In the experimentally observed gravitational repulsion described above, the interacting bodies are the iodine particles and the Earth. The main findings can be summarized as follows:

• A repulsive force acts on iodine particles in a direction opposite to the Earth’s gravitational attraction.
• This repulsive force depends on the thermal energy of the particle, as indicated by its temperature T, which reflects the system’s thermal energy Q.

Note: Heat is a form of thermal energy. Classically, thermal energy corresponds to the net potential energy of a system, while internal energy includes both potential and kinetic components. The virial theorem states that for a stable system of particles bound by potential forces, the time-averaged kinetic energy is proportional to the time-averaged potential energy [16]. It also outlines mechanisms contributing to stellar contraction due to gravitational attraction [17]. In contrast, the current discussion focuses solely on a thermally dependent repulsive force arising from potential energy; thus, kinetic energy considerations are not pursued further in this paper.

Subsequent stages of this research program have also experimentally demonstrated a repulsive interaction between water droplets and the Earth. Specifically, the time-of-fall of a water droplet in still air increases with the droplet’s temperature [1,2]. A comparable concept has been proposed for a hypothetical quantum fluid, where temperature differences could generate a preferred spatial direction that enables flow even against gravity [17] p1950184-1.

Overall, these experiments motivate exploration of an energy-dependent gravitational response acting among matter.

2.2. Conceptual Model: Forces Between Two Entities of Matter:

To generalize the phenomena, a conceptual representation is provided in Figure 1, illustrating interactions between two arbitrary masses m₁ and m₂ at temperatures T₁ and T₂, with thermal energy contents Q₁ and Q₂, respectively.

From this conceptualization (Figure 1), two relationships are considered:

(1)

Based on the conventional gravitational law:

$$attractionforce\propto mass(m_1,m_2)$$

(1)

(2)

Experimentally inferred energy-dependent gravitational response [2]:

$$repulsionforce\propto thermalenergy(Q_1,Q_2)$$

(2)

Thermal energy, Q is expressed by definition [18] as:

$$Q=mcT$$

(3)

where c is the specific heat capacity and T is the absolute temperature.

The purpose of the present study is not to challenge classical gravitational theory, but to investigate whether including an additional temperature-dependent term may help describe certain unexplained behaviors in systems.

Rationale for Focusing on Gases

The subsequent modeling effort concentrates on gaseous matter due to two reasons:

In summary, the above conceptual and experimental basis provides justification for developing a thermodynamic analytical model incorporating both conventional gravitational attraction and a hypothesized energy-dependent gravitational response.

This framework is introduced in the following section.

• Atmospheric relevance — Gas-phase interactions contribute to cloud microphysics, pollutant lifting, and vapor transport, where similar anomalous motion has been observed [1,2].
• Scalability of forces — Interactions at the molecular scale may produce emergent effects detectable at macroscopic scales, potentially informing cosmological distribution models.

3. Theoretical Framework for an Energy-Dependent Gravitational Repulsion in Gases:

3.1. Motivation and Scope:

To investigate whether the gravitational repulsion described in Section 2 (Figure 1- two distinct forces acting between two arbitrary masses) could be captured in a mathematical form, an analytical framework was developed incorporating both:

(a)

the conventional gravitational attraction proportional to mass, and

(b)

a temperature-dependent gravitational repulsion proportional to thermal energy.

The purpose of this framework is to determine whether such a dual-term formulation can reproduce measured macroscopic behavior of gases using established thermodynamic data [19]. In particular, the model seeks to estimate:

• coefficients for the hypothesized energy-dependent term and the classical gravitational term,
• orders of magnitude of the respective forces at the molecular scale,
• the relative importance of each contribution under standard gas conditions.

Throughout, the derivation avoids strong idealizations highlighted in Section 1.2 and uses directly measurable quantities where possible.

3.2. Representation of Forces Between Two Gas Molecules:

To focus on the underlying interaction mechanism, a conceptual representation is shown in Figure 2, involving two identical gas molecules separated by distance r, each with mass m and thermal energy Q.

The model assigns:

a gravitational attraction force F_A that scales with mass, and

a gravitational response term F_R that scales with thermal energy, as motivated by Section 2.

Both are assumed to be inversely proportional to the separation distance r^x, with an initially unknown exponent x:

3.3. Mathematical Model for Gravitational Repulsion and Attraction Coefficient:

For the mathematical analysis, consider only these two molecules exist confined within a box at a distance r apart (Figure 3), at a certain pressure (i.e., outward force F_W exists). The two molecules, hence, are at rest touching the walls of the box, under the gravitational repulsion force (F_R), the gravitational attraction (F_A) and the F_W exerted by the wall. Existence of pressure on the box walls imply that the repulsion force between molecules is greater than the attraction force (F_R > F_A).

For equilibrium of forces on gas molecules depicted in Figure 3:

$$F_R-F_A=F_W$$

(4)

In this situation, Pressure P on the wall (by the two gas molecules) results from the outward force F_W of the system on a unit area; thus: P ∝ F_W

In reality, any small quantity of gas molecules exhibits same pressure regardless of the number of molecules enclosed. This implies that pressure at any point in the gas is caused by the very basic building block; intermolecular forces.

The intensity of the gravitational attraction force is proportional to the mass m (Equation 1). Under the proposed concept [2], the intensity of the gravitational repulsion force is proportional to the thermal energy Q (Equation 2).

Isotropic distribution of the force field from an entity of matter could be considered same irrespective of the type of force; whether gravitational repulsion force or gravitational attraction force. The distance r between the two entities of matter, is in the denominator of the relationships for both the intensity of the gravitational repulsion force, as well as the intensity of the gravitational attraction force. In the denominator, the power of r is denoted by x, because the distribution of force field around the molecule with the distance is assumed unknown in the context of gravitational attraction and repulsion. The value of the exponent x is to be derived with established experimental data. For the two identical molecules with mass m given in Figure 3, gravitational attraction force F_A is defined (Equation 1 is modified) as:

$$F_A=G_A{\displaystyle \frac{mm}{r^x}}=G_A{\displaystyle \frac{m^2}{r^x}}$$

(5)

where, G_A is defined as the ‘Gravitational Attraction Coefficient’.

For the two identical molecules with thermal energy Q in given Figure 3, gravitational repulsion force, F_R is also defined as:

$$F_R=G_R{\displaystyle \frac{QQ}{r^x}}=G_R{\displaystyle \frac{Q^2}{r^x}}$$

(6)

where, G_R is defined as the ‘Gravitational Repulsion Coefficient’.

Thermal energy Q (which contributes to the repulsion force) is defined (Equation 3 is modified) for the calculation of F_R as:

$$Q=mc{T}^y$$

(7)

where, c (Note 1 below) is the Specific Heat Capacity, T (Note 2 below) is the absolute temperature and y is the exponent of T (the effect of absolute temperature on the thermal energy of an entity is not known in the context of gravitational repulsion). Introducing the exponent y allows the model to accommodate unknown nonlinear radiation–temperature relationships, such as in the Stefan–Boltzmann T⁴ law [20], recognizing that gas molecules exchange thermal radiation even as isolated entities [21]. The value of the exponent y is to be derived with established experimental data.

Note 1: c is further defined for gases [18] as: c_v (Specific Heat Capacity at constant volume) and c_p (Specific Heat Capacity at constant pressure).

Note 2: In the classical theories, the thermal energy of a single molecule is considered as its kinetic energy (translational, vibrational, rotational etc.), and no temperature term is associated. Nevertheless, any matter, regardless of its size, absorbs and emits energy (infrared radiation in the case of thermal energy); Stefan–Boltzmann Law [20]. Gas molecule in the space is also an individual entity having its own characteristic mass and temperature, thus absorbs and emits radiation corresponding to its temperature regardless of its size [21].

Solutions for parameters x, y, G_R, G_A, F_R and F_A in Equations (5), (6) and (7) are obtained, considering 3 Situations i, ii and iii (Figure S2 and Section D in supplementary information), pertaining to Figure 3, to yield Equations (8), (9), (10), (11) and (12). Details are given in supplementary information: Section D.2.

3.4. Solutions for Parameters x, G_R, G_A, F_R and F_A:

Equations (5), (6) and (7) gives the solution for x as follows:

$$x=Log\left({\displaystyle \frac{\alpha m^2-\beta Q_1^2}{\alpha m^2-\beta Q_2^2}}\right)/Log\left({\displaystyle \frac{r_1}{r_3}}\right)$$

(8)

where: $\alpha ={\displaystyle \frac{\beta Q_1^2-(P_1/N_f)}{m^2}}$ and $\beta ={\displaystyle \frac{P_2-P_1}{N_f(Q_2^2-Q_1^2)}}$General solutions for G_R, G_A, F_R and F_A are given as:

$$G_R=\beta r^x$$

(9)

$$G_A=\alpha r^x$$

(10)

$$F_R={\displaystyle \frac{G_R{Q}^2}{r^x}}$$

(11)

$$F_A={\displaystyle \frac{G_A{m}^2}{r^x}}$$

(12)

To determine numerical values for x, y, G_R, G_A, F_R and F_A it is necessary to consider established experimental values of mass, specific heat capacity (either c_v or c_p discussed later in this paper), molecular distance, and pressure of gases at different T and y. As a sample calculation of the said analysis, established experimental data on thermodynamic properties [22] of nitrogen N₂ are utilized and presented in this paper. Analysis was repeated utilizing established experimental data on thermodynamic properties [22] of hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide as well, and all information is available on request.

Details of analysis of nitrogen is presented in supplementary information: Section G.

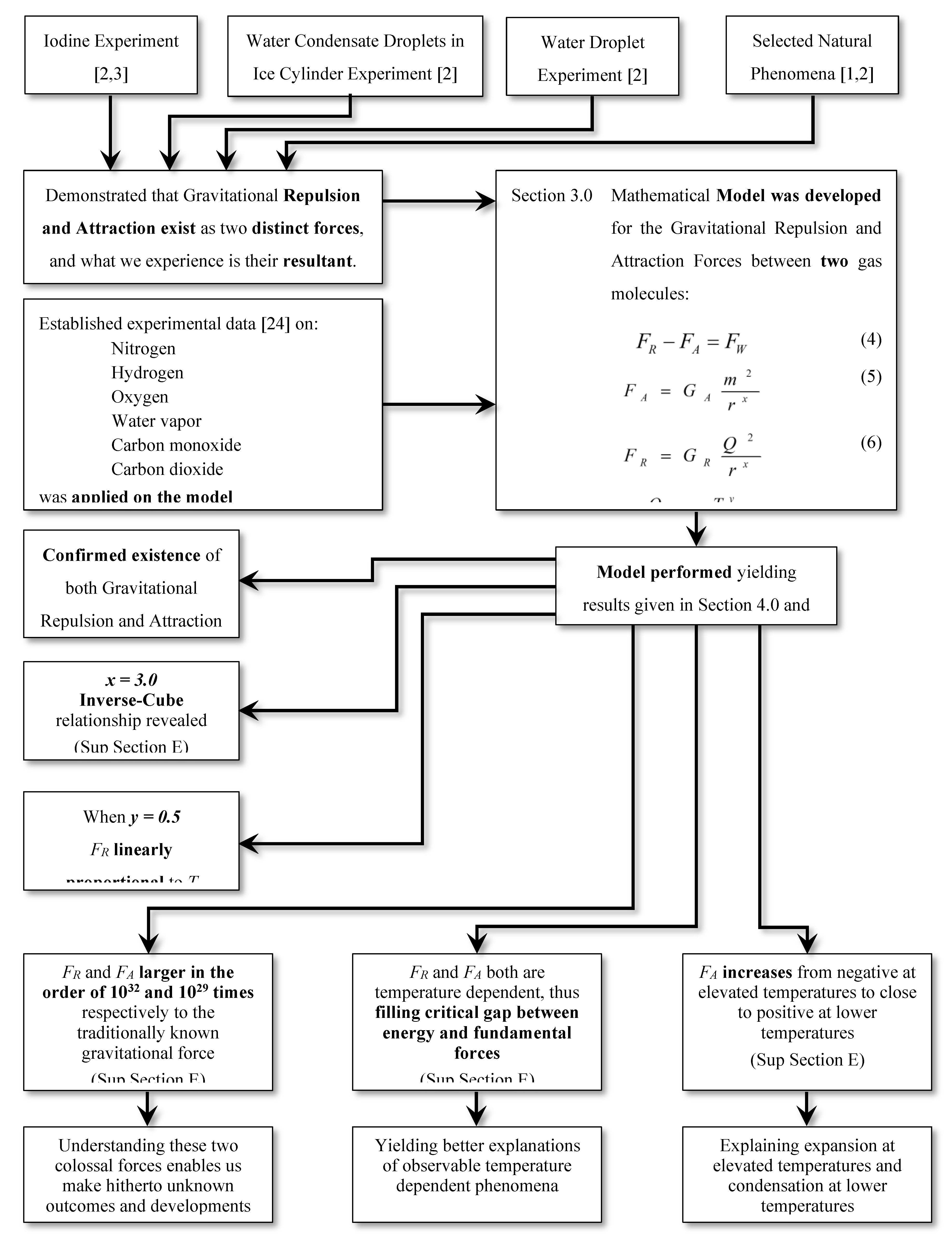
4. Quantitative Evaluation of Parameters x, y, G_R, G_A, F_R and F_A Based on Thermodynamic Properties of Gas:

This section aims to provide a qualitative and quantitative evaluation of the proposed interaction model as applied to gaseous matter. Using established thermodynamic properties, the combined effects of the hypothesized thermal-energy-dependent repulsive force and the conventional mass-dependent attractive force are explored. Nitrogen gas is selected as a representative working medium due to the extensive availability of verified property datasets.

Published experimental data for nitrogen thermodynamic properties [22] (see Supplementary Information, SF1) were applied to Equations (8) - (12) to compute values of the exponent x, temperature exponent y, gravitational repulsion coefficient G_R, gravitational attraction coefficient G_A, and the corresponding force magnitudes F_R and F_A. Nitrogen properties were evaluated across the temperature range 146.65–2888.9 K using a molecular mass of 28.016×1.66054×10⁻²⁷ kg. Specific heats at constant volume c_v and constant pressure c_p were extracted for each condition. Full computational steps are available in Supplementary Information, Section E.

Based on this analysis, the following key results were established (see Supplementary Information, Section E.2):

• The exponent x is equal to 3, independent of temperature and y (Figure S4a, Supplementary Information Section E.2)

This suggests an inverse-cube spatial dependence, distinct from the inverse-square form of classical gravity. The implications are examined in the Discussion.

2.

The temperature exponent y = 0.5 emerges as a characteristic value (Figure S4b,c, Supplementary Information Section E.2)

This value yields stable and physically interpretable coefficients in the model.

3.

F_R is linearly proportionate to temperature T (Figure S4d)

This is consistent with the analytical form of Equation (2) and is aligned with the previously reported experimental observation [2] that heated droplets exhibit increased suspension times in air - summarized in Ref. [2], p.148:

In experiment 2, t_f (time-of-fall) of a water-droplet in still air increases with the temperature of the droplet. That is: “The hotter the water-droplet, the slower it falls”.

4.

The F_R Vs T relationship extrapolates close to the origin when y ≈ 0.5 (Figure S7, Supplementary Information)

This suggests that at low thermal energy, the repulsive contribution approaches zero smoothly.

These computational outcomes are further interpreted in Supplementary Information, Section F, and key points are synthesized in the Discussion.

4.1. The Gist of the Model and the Outcomes:

An alternative framework describing thermal-energy-dependent repulsive interactions, coexisting with mass-dependent attraction between gaseous molecules, has been developed in Section 3. The evaluation using thermodynamic properties of six common gases - nitrogen, hydrogen, oxygen, water vapor, carbon monoxide, and carbon dioxide - indicates that the model produces internally consistent and physically meaningful trends.

For reader clarity, the essential structure of the model and its main results are summarized schematically in Figure 4.

5. Discussion

Certain observations in laboratory settings - such as the upward movement of heated iodine particles in vacuum, upward motion of mercury in room temperature and natural behavior of matter, for example condensation and aggregation of water droplets in clouds and accelerating expansion of the Universe, motivate continued examination of how energy, particularly thermal energy, which has been the focus of this research series, interacts with gravity [1,2,3,4]. Classical Newtonian gravity and General Relativity do not generally include thermal energy as a factor in gravitational interactions. Similarly, gravitational forces among gas molecules are traditionally neglected in kinetic theory and in derivations of the ideal gas law. These gaps suggest value in exploring alternative formulations that incorporate interactions between mass and energy, particularly thermal energy, which has been the focus of this research series.

The alternative model considering both gravitational repulsion and attraction, presented in this paper, is self-standing; independent of existing idealistic models. This model has been built without idealistic assumptions such as: “intermolecular force in gaseous state is zero”, “perfectly elastic collisions”, “consists of a large number of molecules”, “volume of the molecules is negligibly small” and so on. In fact, there are no idealistic assumptions involved in this model; hence it is closer to reality.

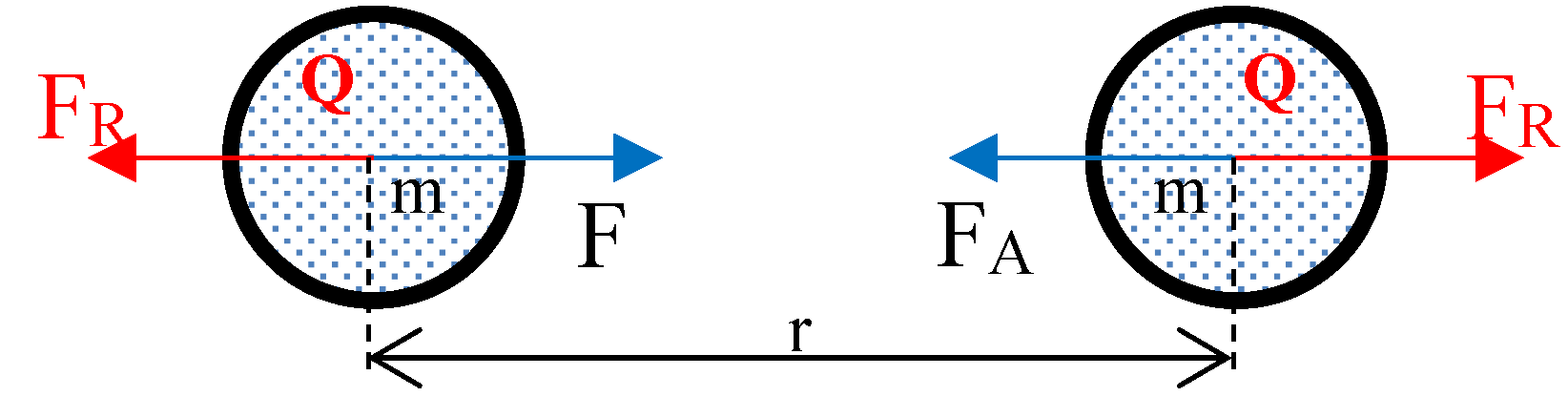
The entire mathematical model presented in this paper was derived considering the forces of gravitational repulsion and attraction between just two gaseous molecules; the basic building blocks of the gas. Force (net repulsive) between individual gas molecules represents the pressure in the system; a significant deviation from the kinetic theory’s concept of momentum transfer. Hence, pressure does not depend on the rate of change of momentum of a number of molecules in a certain mass or volume of the gas, as assumed in the kinetic theory in the derivation of the ideal gas equation. The two gaseous molecule model justifies that any small quantity of gas molecules would exhibit same pressure (independent of the tag of rate of change of momentum) as a large quantity at the same temperature and molecular number density. In short, even a small quantity of gas could produce the same pressure as a large quantity.

It should be noted that the above relationships (Equations S11, S12 and 8–12) are developed for the matter in the gaseous state. It is, hence, recommended that future research should focus on analysis of matter in other states, viz., solid, liquid and plasma.

The model has been validated using experimentally determined and established data [22] utilized in practical thermodynamic applications of mechanical engineering industries. The data has been published in 1948, by Joseph Henry Keenan and Joseph Kaye. Applying these data to Equations 8-12, behavior of x, G_R, G_A, F_R and F_A with respect to T and y were derived and presented in 3D graphs (a), (b), (c), (d) and (e) in Figure S4 in supplementary information (Section E2).

The result x = 3.0 as presented in the 3D graph Figure S4 (a) contributes new scientific information on distribution of gravitational force fields that fill up the volume in free space, at the length scale of intermolecular distances for gas molecules. The relationship of gravitational repulsion and attraction forces being inversely proportional to the cube of the distance, interprets the gravitational force distributions as volumetric or solid spherical distributions (4/3 πr³) in free space, rather than the area or surface distributions (4πr²) considered in the classical model. This is a significant departure from the Inverse-Square Law. Inverse-Square Law describes wave front propagation of energy. In contrast, force fields fill up volume in the free space. The volumetric distribution or fill-up the free space by the force is more appropriate in understanding; as a force field always exists in a 3D space rather than on a 2D surface.

In literature on force fields, the inverse proportionality to cube (Inverse-Cube Law) with the distance is not new. An extra force besides gravity, that is obeying the Inverse-Cube Law, has been mentioned in ‘Principia Mathematica’ [5] published by Isaac Newton in 1687; see Prepositions XLIII-XLV of Book 1, pp171-182. It has also been demonstrated [23] experimentally that, in magnetostatic fields where both poles geometrically coincide, attraction and repulsion forces obey the Inverse-Cube Law with the distance. Future research should focus on discerning where inverse proportionality to the cube of the distance is more appropriate in applications of fundamental physics.

The analysis presented in this paper signifies that y = 0.5 as a characteristic temperature exponent for all tested gases, is a very special value when considering behaviors of G_R, G_A, F_R and F_A. Most noteworthy points were that, for both c_v and c_p, when y ≈ 0.5:

• Linear extrapolation of graphs F_R vs. T crosses (0,0)
• The attraction term, F_A approaches zero from negative values as T approaches 0 K

This was found to be true for all gases considered: nitrogen, hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide; yielding similar results irrespective of atomic mass m. How these results resonate with other empirically established models such as Boyle’s Law, Charles’ Law and Amontons’ Law/Gay-Lussac’s Law will be discussed in a future publication.

In the 3D graphs Figure S4 (b) and (c), both Gravitational Repulsion Coefficient and Gravitational Attraction Coefficient appeared dependent on the temperature T. This result is unexpected, as temperature dependency of G_A was not previously known. Further to that, as presented in 3D graphs Figure S4 (d) and (e), both F_R and F_A are temperature dependent; being gravitational forces, they are fundamental interactions in nature. Significant departure from the existing knowledge is that, the four fundamental interactions (fundamental forces) in classical theory are not defined to be temperature dependent. Existing theories, nevertheless, state that increase of thermal energy increases the potential energy of the gas molecules; with no mention that a relationship exists between thermal energy (classically known as potential energy) and gravitational forces. Results showed that, increase of thermal energy increased repulsion (Equations 2 and 11) between gas molecules. See graphs of F_R vs. T and F_A vs. T, where, as T increases:

• positive value of F_R increases
• negative value of F_A increases

That implies that thermal energy is directly proportional to the resultant of F_R and F_A, confirming the relationship between energy and fundamental forces. With this revelation, the critical gap between energy and fundamental forces has been filled. Fundamental forces could be more readily linked with observable temperature dependent phenomena (e.g.: pressure, expansion, and so on) in the nature/Universe; thus, enabling better explanations.

In the 3D graph Figure S4 (d) (supplementary information (Section E2).), gravitational repulsion force appeared linearly proportionate to the temperature. This vindicated the experiment conducted in this research program by the Author, presented in paper [2]. The said experiment demonstrated that the time-of-fall of water droplets is linearly proportionate to the temperature (Figure S6 in supplementary information).

Negative values of F_A at elevated temperatures [Figure S4 (e)], together with F_R, cause the gas to have only repulsive forces among molecules. This gives rise to the property that real gases expand infinitely as the available space increases. Such circumstances of all repulsive forces were observed in other gases studied (hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide) as well (information available on request).

Analysis presented in this paper further shows that as temperature decreases, repulsion forces decrease and attraction forces increase (from negative at elevated temperatures to close to positive at lower temperatures) between gaseous molecules, thus causing aggregation of atoms/molecules together, i.e., causing condensation of the gas. This finding is significant in a context where exact fundamental mechanism of condensation has so far not been explained by classical theories.

This program of research has shown that, the so called ‘weak’ gravitational force (Table S1 in supplementary information), is actually the resultant of two extremely large forces, i.e., gravitational repulsion and gravitational attraction, which distinctly act on matter. Newly determined gravitational repulsion and attraction forces between two nitrogen molecules at 305 K are in the order of 10³⁰ times (supplementary information: Section F) greater than the classically calculated gravitational attraction force. It thus reveals that gravitational repulsion and attraction forces in fact are of similar orders of magnitude as the other three forces in the nature. Even though, gravitational repulsion and attraction forces are colossal, they are nearly equal, thus nearly in equilibrium in nature; hence always observed to be a weak force.

An experiment was referred to in Section 02, where heated iodine particles moved upwards in vacuum against the Earth’s gravitational pull. This is a groundbreaking experiment where the said phenomenon occurred in a situation where all factors which are believed to be causing the upward movement of particles in air against the gravitational pull, viz., buoyancy and convective forces, are eliminated by experimental design. Initially, at the room temperature (≈ 25°C), the iodine particles detached from the iodine sample moved downward under gravitational attraction force with the Earth, and deposited in the bottom part of the paper jacket. When the iodine sample was heated, the experiment revealed that iodine particles move against gravitational pull in the vacuum and deposited in the top part of the paper jacket. In electronic vacuum tubes (called electronic valves) also, evaporated tungsten and thorium particles from the filament moves upwards in the absence of air, despite the gravitational pull and the strong radial electric fields, and deposit at the top of the glass tube.

The above was a laboratory experiment at a micro scale. The antigravity concept could also be extended to macro level phenomena in the nature such as clouds and the accelerating expansion of the Universe. Review paper by the Author [1] on the previous papers in this research program states:

In addition to attractive and repulsive forces of water-droplets of a cloud with earth, there exist attractive and repulsive forces among water droplets within the cloud. These forces acting inside the cloud explain the accumulative (flocking together) nature of the cloud which has not been explained by the classical theories. The equilibrium of these two forces will confine the droplets to a certain area as a floccule. The repulsiveness does not allow shrinking and finally collapsing the cloud while the attractive force keeps the droplets together without dispersion. [1] p4

The above is an ideal example where there is no net outward force (no net pressure exerted outward) among flocculent water droplets. Water droplets behave as a flock under the equilibrium of gravitational repulsion and gravitational attraction forces. The paper [2] dispelled the classical belief that clouds float due to convection currents, and showed that the force that holds the flocculent water droplets up in the air is “antigravity”. Coexistence of repulsive and attractive forces considered in theoretical derivations presented in this paper are supported by the mechanism for existence of clouds deduced in the paper [2].

Considering both gravitational repulsion and gravitational attraction on matter and filling the critical gap between energy and fundamental forces, opens the doors for more research enabling stronger scientific explanations of observable temperature dependent phenomena, e.g.:

• Heavy gas molecules (such as CFC) in the upper atmosphere
• Brownian Motion
• Condensation/evaporation/sublimation
• Expansion/contraction of gas/liquid/solid
• and more

The concept of gravitational repulsion and gravitational attraction forces could be further applied at macro level to explain the accelerating expansion of the Universe. Even in our solar system:

… the distance of the Earth’s [sic] from the sun. Various measurements indicate that this distance (or at least the length of the Earth’s semimajor axis) is increasing at the rate of 15 cm per year (plus or minus 4 cm). [24,25]

Galaxies and other interstellar objects are not in a state of equilibrium as a result of increasing thermal energy content due to various reasons including atomic fission and fusion causing mass-energy conversion (E = mc²). The effect of increasing thermal energy on (a) expanding gas, i.e., at the microscopic level, and (b) expanding universe [1], i.e., at the macroscopic level, should be similar. Such mass-energy conversion has dual effects on equilibria in the Universe: (1) increasing thermal energy increases gravitational repulsion forces, while (2) decreasing mass decreases gravitational attraction forces. Gravitational repulsion forces, hence, keep exceeding gravitational attraction forces, thus causing outward expansion of the Universe with acceleration [26]. In essence, gravitational repulsion is a significant force between gas molecules (microscopic level), and could be generalized to explain macroscopic level phenomena, e.g., behavior of the universe [27,28,29,30], existence of clouds [1].

In conclusion, the analytical framework developed in this study demonstrates that intermolecular forces in gases exhibit a measurable and systematic dependence on thermal conditions, extending beyond the assumptions of purely temperature-independent interactions. By grounding the analysis in experimental evidence, the results highlight the necessity of incorporating thermal energy as an active parameter influencing molecular behavior, rather than treating it solely as a statistical descriptor. This thermal-dependent perspective provides a more comprehensive understanding of gas-phase interactions, offers improved consistency with observed non-ideal behavior, and opens new avenues for refining existing models of molecular dynamics. Ultimately, the approach presented here lays a foundation for future experimental and theoretical investigations aimed at unifying thermal effects with intermolecular force descriptions in gaseous systems.

6. Conclusions

A self-standing alternative mathematical model for gravitational repulsion and attraction forces has been developed, built entirely without idealized assumptions. The model is based on interactions between just two gaseous molecules, the fundamental building blocks of a gas. When applied to established experimental data for nitrogen, hydrogen, oxygen, water vapor, carbon monoxide, and carbon dioxide, the model successfully describes observed behaviors and remains consistent with empirical thermodynamic laws.

Key findings of the model include:

• Inverse-Cube Dependence: Both gravitational repulsion and attraction forces are inversely proportional to the cube of the distance between gaseous molecules, indicating volumetric distribution of force fields and a departure from the classical Inverse-Square Law.
• Temperature Dependence: The gravitational repulsion force is linearly proportional to the thermal energy content (temperature) of the molecules, confirming previous experimental observations. Gravitational attraction is also found to vary with temperature, revealing a previously unrecognized link between energy and fundamental forces.
• Magnitude of Forces: The calculated magnitudes of gravitational repulsion and attraction between gas molecules are colossal, on the order of 10³⁰ times greater than the traditionally calculated gravitational force, yet nearly balanced, which may explain why classical measurements perceive gravity as weak.

These results suggest that energy, particularly thermal energy, which has been the focus of this research series. may play a direct role in modulating fundamental forces, bridging a critical gap in understanding the relationship between energy and gravitation. While the model has been applied successfully at the molecular (microscopic) level, it also provides a framework to explore macro-scale phenomena, including cloud formation and potentially the accelerating expansion of the Universe.

Future research should focus on further experimental validation, exploration of other states of matter (solid, liquid, plasma), and understanding how these colossal forces could be controlled or harnessed. Careful study could open new avenues for explaining temperature-dependent physical phenomena and potentially enable applications previously considered beyond reach.