Unifying Environmental Stress Cracking and Mechano-Sorptive Creep Under the Umbrella of Mechano-Sorptive Phenomena

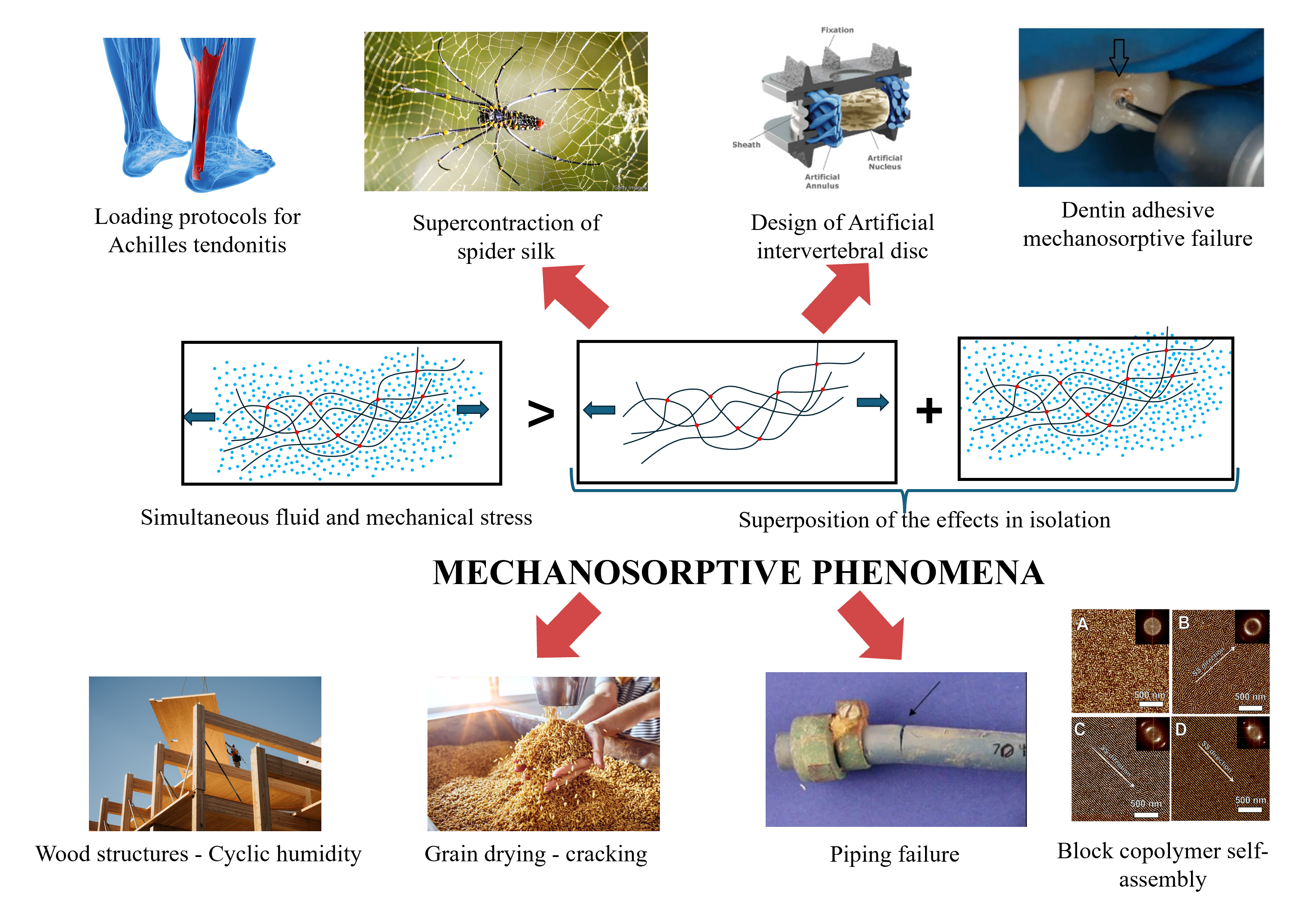
1. Introduction

The term mechano-sorptive phenomena (MSP) is introduced as the mechanical response of a polymer to the simultaneous action of mechanical stress and interaction with an adsorbing or absorbing fluid. MSP can range from brittle cracking to ductile yielding with large reversible or irreversible deformation. The mechanical failure caused by the MSP depends on the effect of mechanical stress on the polymer-fluid interaction and the consequent proximity of the polymer’s state to its glass transition for the specified testing temperature, mechanical stress state, loading frequency, and fluid concentration. In the present review, the term MSP describes only the effects of physically active fluids in polymers. Chemically active fluids which cause irreversible chemical degradation of the polymer are not considered although they may be just as important, or more so [1], especially for biomedical materials and devices. Physical interaction between the polymer and the fluid involves dissociation of intermolecular non-covalent bonds in the polymer and manifests as bulk plasticization or reduced surface energy in the case of strong solvents. A distinctive feature of MSP is that the effect of the simultaneous action of mechanical stress and solvent ingress is greater than the sum of the effects of each factor in isolation [2].

MSP can encompass a wide spectrum of chemo-mechanical behaviors as evidenced by the extensive research on environmental stress cracking (ESC) [3,4] and mechano-sorptive creep (MSC) [5]. ESC is often described as the reduced time-to-failure of polymers in an aggressive agent by cracking or crazing at stresses much lower than the stresses that cause detectable damage in air. ESC is a reduced time-to-failure for a creep test performed on a notched sample in an aggressive agent as compared to the same test performed in air. An ESC failure typically happens with pseudo-brittle fracture involving fibrillation and crazing but lacking secondary and tertiary creep.

While large ductile deformations can be observed in ESC testing, the results are typically not classified as ESC, i.e. one research group has termed such phenomena environmental stress yielding (ESY) [6,7,8]. The phenomenon associated with ESY most closely resembles mechano-sorptive creep (MSC). The term ESY has been applied when the stresses cause large plastic deformation. In comparison, MSC shows features resembling secondary creep with recoverable deformation under sufficiently low stress magnitudes but progresses rapidly to tertiary creep and rupture when stress magnitudes are sufficiently large.

ESC and MSC are both MSP and as such share commonalities in terms of underlying mechanisms and experimental methods. Interestingly, despite the commonalities, research on these two phenomena have occurred in isolation. As a result, knowledge that was gained through experimentation and modeling of ESC and MSC has not been integrated. Integrating knowledge and understanding of the two phenomena offers significant promise for improving the predictability of material models for MSP. Potentially, MSP can be predicted solely from fundamental physical and chemical descriptors of the polymer and fluid [9].

This review provides a detailed examination of ESC, MSC and other MSP under one umbrella. The goal of this approach is to initiate the critical process of knowledge exchange across the phenomena. A schematic of four possible outcomes of a MSP on a crosslinked polymer has been shown in Figure 1.

Figure 1(a) shows the well-known free swelling case while Figure 1(b) shows the increased swelling and strain when a pre-saturated sample is subjected to tensile stress. Figure 1(c) shows the increased swelling and strain when a dry sample under tension is subjected to solvent saturation. Figure 1(d) shows an example of brittle fracture which occurs when tensile stress is applied to a polymer in the presence of a poorly compatible solvent. All these cases have been covered in existing literature under various terminologies such as free swelling, strain-driven swelling, mechanosorptive creep, and environmental stress cracking for cases (a), (b), (c) and (d), respectively. Cases (a) and (b) are mostly relevant to applications where the polymer is initially saturated, e.g. hydrogels used as soft actuators, sensors, drug delivery systems, and numerous other applications. Cases (c) and (d) are more relevant to conditions where the polymer is initially in a dry state but may contact fluids in the application process. For example, thermoplastics in aerospace components exposed to paint strippers and jet fuels, cable jacketing and automotive parts exposed to cleaning agents or lubricants, timber structures exposed to moisture, and so forth. There are cases such as dentin adhesives and food grains which may undergo MSP involving all cases (a) through (d). Although both ESC [10] and MSC [11] have been identified as potential failure mechanisms for dentin adhesives and other dental materials, they are not typically examined from a mechano-sorptive perspective. Therefore, this review is relevant to the durability of polymeric dental materials including composite restorative materials from the perspective of MSPs. This review provides guidelines for such investigations.

2. Commonalities in the Molecular Phenomena Underlying ESC and MSC

The term mechano-sorptive creep (MSC) has been mostly used for the partially reversible creep of polymers under moisture cycling. It is characterized by a “molecular Velcro” mechanism where hydrogen bonds between polymer chains are disrupted by solvation and mechanical stress causes partially irreversible slippage between the corresponding polymer chains. Depending on the stress level, the hydrogen bonds may be partially or completely reformed after the removal of the stimulus leading to augmented anomalous creep beyond that of fully saturated polymer samples. Under sufficiently high stress, MSC transitions into secondary and tertiary creep leading to creep rupture [12,13,14]. MSC has been mostly studied for different types of wood and wood-based cellulosic polymers and the solvent has generally been water or water vapor [15]. ESC, on the other hand, has been studied for a wide variety of amorphous and semi-crystalline polymers including crosslinked polymers. Like MSC, ESC also involves the disruption of non-covalent interactions between polymer segments of the amorphous phase. In ESC, the non-covalent interactions are usually tie molecule entanglements in the case of semi-crystalline polymers and hydrogen bonds in the case of amorphous polymers, while for MSC they are often hydrogen bonds. In addition, ESC also reflects the effect of the fluid on the surface energy of the polymer.

The molecular level mechanisms underlying both MSC and ESC, as all MSP, are inherently time-dependent by virtue of the viscoelastic nature of the polymer as well as diffusion of the fluid molecules in the polymer. Both mechanisms happen primarily in the amorphous region of the polymer, which is accessible for fluid diffusion. The crystalline regions do not participate in any major way in MSP. For example, MSC as studied in wood and cellulose shows that only the non-crystalline portions are accessible to moisture [16,17]. Similarly, the underlying mechanism behind ESC is primarily polymer-fluid interaction in the amorphous regions and the consequent void formation followed by fibrillation, drawing and failure.

Despite resulting in visually different macroscopic failures, ESC and MSC overlap significantly. Under sufficiently high stress, MSC progresses to Mechano-sorptive Creep Rupture (MSCR) [13,18,19]. ESC caused by moderately strong solvents interacting with amorphous polymers can induce a gel layer at the crack tip which prevents crack propagation [3,20], leading to a ductile failure which is not unlike what is observed for MSCR [13]. Researchers have postulated that the brittle failure associated with ESC in amorphous polymers is caused by localized swelling due to non-solvents or weak solvents that induce tension in the material subjacent to the swollen gel layer. On the other hand, MSC and MSCR are observed for good to moderately good solvents due to bulk sorption [21]. Further details are provided in sections 3.3 and 4.

3. Evidence That ESC and MSC(R) Are Variants of the Same Underlying Phenomenon

By applying Flory’s statistical thermodynamics of polymer solvent interaction [22] to the case of swelling under hydrostatic tension, Gent [23] hypothesized that ESC in amorphous polymers was caused by increased swelling in zones of stress concentrations which caused tensile stress in underlying regions still in the glassy state. Following Flory in writing the free energy of a polymer-solvent system, it is straightforward to show that hydrostatic tension decreases the Gibbs free energy of the polymer-solvent system further below that of a stress-free condition, with reference to the pure solvent, while pressure increases it closer to that of the pure solvent.

$$\mu ={{\displaystyle \frac{\partial G}{\partial n}}|}_{T,P}={{\displaystyle \frac{\partial U}{\partial n}}|}_{T,P}+{P{\displaystyle \frac{\partial V}{\partial n}}|}_{T,P}-{T{\displaystyle \frac{\partial S}{\partial n}}|}_{T,P}$$

(1)

where G is the Gibbs free energy, U is the internal energy, n is the number of moles of the solvent, V is the volume of the polymer-solvent system, T is the temperature of the system (held constant) and P is the external pressure on the system (held constant). Gent’s relationship, reproduced from [23] is shown in Figure 2. Gent’s relationship shows the dramatic increase in sorption when hydrostatic tension is sufficiently high. Gent’s predictions have been corroborated by several researchers, e.g. Tynnyi [24] and Wolf [25,26,27].

Section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

3.1. Swelling and Diffusion Responses Driven by Chemical Potential Gradients

It is understood that equilibrium between the swollen polymer and the solvent is achieved when the chemical potential inside the polymer-solvent system becomes equal to that of the pure solvent in the surrounding environment. The Smoluchowksi equation [28] fundamentally derives that the rate of diffusion of the solvent into the polymer is driven by the gradient of the chemical potential across the polymer-solvent boundary. Therefore, from Eq. (1) it follows that hydrostatic tension would cause an increase in swelling and hydrostatic pressure would decrease swelling. Gent argued similarly and derived equations for uniaxial tension originally explored by Flory [29] and Gee [30] and for biaxial cases studied by Urayama [31] and others. Lejcuś and colleagues [32], reported that external loads (such as soil pressure) significantly suppressed the swelling rate and the final equilibrium swelling capacity. As the soil load increased, both the swelling rate and the equilibrium swelling capacity showed a clear decrease.

Using Eq. (1), it also follows that the rate of solvent diffusion into the polymer should be greatly increased by the presence of hydrostatic tension since the diffusion rate is a function of the chemical potential gradient. This increase was observed for polyether ether ketone (PEEK) using several solvents. The increase in rate of diffusion and solubility with uniaxial tension and residual stress was termed SEDS (stress enhanced diffusion and solubility/swelling) by Wolf’s research group [6,7,8]. A similar increase in the rates of diffusion of kerosene and acetone in polytetrafluoroethylene (PTFE or Teflon) under uniaxial tension has been reported by Tynni’s research group [33]. Wolf and colleagues reported that the induction period for initial swelling via toluene into unstressed PEEK was five to six orders of magnitude larger than that into PEEK under uniaxial tension greater than 25 MPa [34]. The increase in diffusion rates under tension can also be understood in terms of Eyring’s theory where bond dissociation and association rates are functions of the chain force [35,36]. The solubility data provided by Wolf agree with the theory proposed by Treloar [37,38]; Treloar’s theory is applicable to solubility, but it is not suitable for diffusion processes. There has been limited research on MSC and ESY for amorphous polymers. In distinct contrast, there has been an extensive investigation of MSC in wood and wood-related materials, and ESC for amorphous and semicrystalline polymers. Singh and colleagues(11) studied MSC/ESY in methacrylate-based polymers interacting with water. Toratti [39] has studied MSCR which parallels ESY in wood. Fukumori and colleagues [40] used nuclear magnetic resonance (NMR) to show that tensile strain enhanced the increase in molecular mobility of an acrylonitrile-butadiene copolymer rubber matrix under carbon tetrachloride sorption [41].

For simple cross-linked networks, MSC has not, to the best of our knowledge, been explicitly studied through experiments. In several studies, MSC is treated as a separate strain component, distinct from swelling-induced strain and viscoelastic strain. However, as we elaborate in the following section, and as noted by Reichel and Kaliske [19], the reversible part of the anomalous strain observed under simultaneous tensile stress and solvent diffusion for sufficiently small stresses can be fully explained in the framework of gel thermodynamics. If all the anomalous strain is reversible, mechano-sorptive creep is not an independent strain mode but is inherently included in the swelling-induced strain. The orders of magnitude difference in diffusion rates between swollen gels and initially dry gels could be why MSC is mistakenly regarded as being entirely independent from swelling-induced strain. For materials like wood, which possess a complex hierarchical structure, the manifestation of MSP is more nuanced.

3.2. Path-Independence of Loading and Swelling

The swelling behavior of polymers, including hydrogels, originates from a thermodynamic balance between osmotic pressure and the elastic restoring force of the polymer network. This understanding is rooted in the principle of thermodynamic equilibrium, where the final state is determined by minimizing the system’s free energy, regardless of the loading path. For a thermodynamically reversible process where the final equilibrium or steady state reached by a system should be independent of the order in which boundary conditions are applied, Gent’s hypothesis leads to the conclusion that a polymer will reach the same equilibrium condition for the cases (b) and (c) from Figure 1(b) and 1(c). We note that the equilibrium thermodynamics-based Flory-Rehner theory considers all solvent molecules as free and does not account for the bound portion of solvent molecules. Therefore, if all the solvent is free and the stress is sufficiently low, cases (b) and (c) should reach the same equilibrium sorption and creep strain. However, when the bound solvent content is significant, case (c) is likely to lead to much higher creep strains and possibly greater equilibrium sorption as compared to case (b). This is because only the bound solvent, distinct from “bulk” free solvent, is irreversibly bonded to the polymer chains and is involved in irreversible deformation under simultaneous stress and sorption associated with MSC – all interactions with “bulk” free solvent are necessarily reversible as per polymer-solvent equilibrium thermodynamics. The sorption kinetics for case (c) are expected to be orders of magnitude faster than case (b) since a dry polymer creates a higher chemical potential gradient against pure solvent, as compared to an initially saturated sample. This difference makes it difficult to separate the deformation caused by non-equilibrium thermodynamic processes from comparison of cases (b) and (c). However, the reversible component of the deformation from case (c) is expected to match case (b). A schematic of this argument is shown in Figure 3, which shows a comparison between cases (b) and (c) when all the solvent is free, and when a portion of the solvent is bound.

Experiments paralleling cases (b) and (c) can be found in the literature. For example, in the case of Norway spruce wood loaded in four-point bending, it was reported that after enough cycles, the response is independent of the humidity condition at initial loading. Montero and colleagues reported this observation after comparing initially dry and initially saturated specimens [41]. The compliance of the wet loaded samples tended to catch up with the response of the dry loaded samples. Furthermore, the responses of the initially dry and initially saturated samples were closely matched after several moisture cycles. Since bound water is expected to be effectively saturated within the first cycle, this observation indicates that the relatively small change in bound water in subsequent loading cycles leads to the convergence in the behavior of wet and dry loaded samples. This effect can be investigated further from the results of Singh et al [42] who demonstrated a marked difference in the creep between stored dry-tested wet and stored wet-tested wet methacrylate-based dentin adhesive polymer samples. Even after accounting for the orders of magnitude difference in sorption kinetics between these samples, the difference in the results from the creep testing is likely driven, in part, by non-equilibrium thermodynamics. In partial support of this explanation, samples of this composition were found by Parthasarathy et al [43] to have a relatively high content of bound water compared to polymers with significantly reduced crosslink density. The classification of total water or solvent into free and bound components as well as the decomposition of MSC into reversible and irreversible parts is therefore an important step in understanding the nature of the MSC – this point has not been sufficiently appreciated in the literature. The results from Montero and Singh have been reproduced in Figure 4(a) and (b) respectively. These observations suggest that the reversible part of MSC is explained by equilibrium theory of polymer swelling and does not require the rate of solvent sorption as a constitutive variable in the material model.

Further evidence is available from the work of Armstrong and Christensen [44] on MSC of eucalyptus and pine wood under bending, where two points are clear: (a) there is a significant recovery of the sample upon unloading under wet conditions, (b) MSC decreases with subsequent absorption cycles, and (c) final deflection of the sample when saturation was reached did not depend on the rate of sorption, but did depend on the gradient of vapor pressure. This indicates that a significant portion of the MSC which was reversible under wet conditions happened with respect to free water, especially with increasing number of cycles, once the bound water was saturated.

Future work is required to provide thorough, experimental validation of the arguments that are presented in this section. Experiments resembling Case (b) have been performed for Poly(acrylamide) gels [45,46] and rubber vulcanates [40,47,48], demonstrating increased swelling under tension. Similarly, numerous researchers [49,50,51,52,53,54,55] have thoroughly investigated the mechanical response of polymers under axial stretching in swollen states, most of these studies were conducted under fully swollen unstressed equilibrium prior to deformation, i.e. corresponding to Case (b). As an example, the results from Fujine [45] and colleagues have been reproduced in Figure 5a,b.

The figures show that axial tensile strain on a hydrogel immersed in water causes increased swelling in the lateral direction and stress relaxation in the directions of strain application. Experiments like Case (c) have been performed for a wide variety of polymers, e.g. references [25,26,27,56,57,58,59,60,61,62]. As examples, the results of Soshko [24] and Wolf [25] have been reproduced in Figure 6(a) and (b).

They show how tensile stress greatly increases the equilibrium sorption and accelerates the sorption kinetics for (a) Teflon-3 in acetone [24], and (b) 29% crystalline PEEK in toluene [25], respectively. However, experimental results explicitly comparing polymers tested under cases (b) and (c) are limited and considerable work is required in this direction to better understand MSP. Given the similarity in causative stimuli, it is highly noteworthy that the above points are strongly relevant for ESC as well and need to be appropriately incorporated into any constitutive theories modeling ESC.

Irreversibility can also arise when stress-driven plastic yielding occurs for a particular solvent saturation. It is likely that the stress limit of linearity proposed by Reichel and Kaliske [63] is related to this yield stress. When the applied stress is greater than the yield stress, which depends on the solvent fraction and the temperature, the equilibrium deformation of Case (c) is expected to exceed that of Case (b). This observation is explained as follows: when the stress exceeds the yield stress under the conditions specified for case (c), there will be significant plastic deformation in the polymer, which reaches a maximum for conditions where the plasticization is sufficient for the glass transition temperature to drop below the testing temperature. This plastic deformation is termed pseudo-plasticity [64] since it is reversible with an increase in temperature. This plastic deformation adds to the tension-induced swelling thereby increasing the overall deformation in Case (c) as compared to Case (b). It must be noted that in MSC experiments, the yield stress will not be a uniform value across the volume of the sample, but rather vary with the spatial distribution of the solvent. The extent of MSP is strongly dependent on the macroscopic sample size. The regions with greater amounts of solvent will be more plasticized and have a lower yield stress.

For conditions involving very low concentrations of solvent either due to low compatibility or low concentrations of a compatible solvent, there are two phenomena possible (a) ESC or (b) antiplasticization. In the case of ESC, as described in section 2 and in Figure 1(d), the mechanism is primarily due to high tensile stress in regions underlying localized swelling, with reduced surface energy for fracture propagation also playing a role. Antiplasticization happens when at low concentrations, solvent molecules in a bound condition act as bridges between polymer chains whereby some polymers experience increases in stiffness, glass transition temperature and tensile strength accompanied by lowered fracture strain since certain segmental motions of polymer chains could be restricted by these bridges [65]. With increasing solvent amounts, the transition to free solvent clusters and therefore “full plasticization” takes place. This transition has been observed and traced back to the presence of bound water for dentin adhesive polymers [43], although a feeble reduction in stiffness and strength, rather than clear antiplasticization was observed prior to the onset of “full plasticization”.

3.3. Experimental Studies Spanning the ESC–MSC Transition

Despite the vast amount of literature on both ESC and MSC, there are very few investigations that demonstrate both ESC and MSC for the same polymer under different conditions of solvent compatibility, exposure time, mechanical stress and temperature. Such investigations are however crucial in qualitatively and quantitatively describing ESC and MSC as particular cases in a generalized spectrum of MSP. Rudakova [66,67] was one of the first authors to explicitly state that the simultaneous action of mechanical stress and the aggressive medium could lead to failure resembling either ESC or MSC. Results pertaining to this philosophy have been compiled in Table 1. Table 1 details conditions that led to either a ESC or a ESY/MSCR type of failure for the same polymer under different testing conditions.

It is apparent from Table 1 that for a given polymer, when the fluid only causes localized swelling, either due to low fluid solubility or insufficient diffusion times, a brittle failure associated with ESC results, while large deformation and ductile failure may result in an MSC or MSCR/ESY in the case of significant absorption. In the case of a compatible solvent, the behavior is controlled by either bulk plasticization or surface energy reduction [75]. Therefore, ESC and MSC can be unified under a single common umbrella of MSP, which can have far reaching consequences on enriching both experimental and modeling studies of polymers, particularly in applications involving biomedical materials and devices.

4. Requirements of Constitutive Models for MSP

The primary characteristics required in any constitutive model for an MSP are:

• Validity across the glass transition: To capture the viscoelastic, viscoplastic and fracture behavior across the glass transition as a function of mechanical stress, loading frequency, temperature, and crucially, the fluid concentration.
• Volume change independence: The polymer-fluid system volume is not equal to the sum of the volumes of the dry polymer and the solvent during the dry-to-wet transition, in contrast to the case of a hydrogel whose free volume is already saturated.
• Fluid concentration dependent properties: Both viscous and elastic properties evolve strongly across the glass transition during the dry-to-wet transition of the polymer. The model should incorporate the effect of fluid sorption on viscoplasticity, damage and fracture. The model should also incorporate the appropriate plastic behavior to capture the irreversible part of MSC associated with bound solvent.
• Built from a molecular basis: The model parameters can be traced back to the fundamental physical and chemical descriptors of the polymer and fluid.
• Fit into a computational framework capable of handling both fracture and large deformation: To be able to seamlessly transition from an ESC type brittle fracture to an ESY/MSCR type ductile failure.

The development of constitutive models for MSP must necessarily begin with amorphous polymers because it is well-established that the amorphous phase of semi-crystalline polymers (SCPs) accounts almost entirely for the MSP including both ESC and MSC. There is a large body of literature on polyethylene, polystyrene, polyamide and other SCPs showing that ESC is associated with interlamellar deformation in the amorphous phase between the crystalline lamellae [9,21,76,77].

Among constitutive models for amorphous polymers, phenomenological viscoelastic constitutive models such as the standard linear solid intrinsically span the glass transition across frequency. If the Time-temperature superposition is valid, such models can be extended to span the glass transition across temperature. Constitutive laws to specifically span the glass transition across temperature have been developed by Buckley and Jones [64], Dupaix and Boyce [78], Srivastava and colleagues [79], Das and colleagues [80], Chen and Schweizer [81], and Liu and colleagues [82], among others. Such models formulate the free energy of the polymer as a sum of energetic and entropic contributions accounting for each micromechanism of deformation of the polymer. Constitutive models incorporating volume change independence between polymer and fluid, and accounting for the change in mechanical properties due to fluid-induced glass transition were first addressed by Govindjee and Simo [83] in their constitutive model to describe Case II coupled stress-diffusion, and by Weitsman [84,85,86]. While their models are well-suited to describe MSP, they have unfortunately not been utilized for this purpose. The Tube-Junction model by Simon and Ploehn has been explicitly designed to span the glass transition across temperature, frequency, and plasticizer fraction by accounting for cohesive, frictional and entropic forces. While molecular simulations can be used in the glassy regime, and statistical mechanics accounting for molecular structure in the rubbery regime, the viscoelastic regime is inaccessible to molecular simulations and requires mesoscale modeling [87,88,89,90].

Experiments revealing the dependence of dynamical mechanical properties on solvent concentration, temperature and frequency, for example temperature-solvent sweep experiments using DMA, greatly aid in calibrating such constitutive models and in the understanding of MSP. Although there is a large body of data available comparing the isochronal temperature sweeps of dry and saturated polymers, there are only a few examples of solvent-sweep data in the literature. Bonnaillie and Tomalusa [91] performed humidity-temperature sweep using dynamic mechanical analysis (DMA) on moisture sensitive edible casein films: part of their results has been reproduced in Figure 7.

Constitutive models which can model MSP across the spectrum from ESC to MSCR/ESY must necessarily model the MSP within a viscoelastic fracture mechanics framework due to rate-dependent fracture toughness, the existence of discontinuous and continuous crack propagation modes [92,93], and rate dependent features of the damage and crack tip [94,95]. Analytical solutions for mode I fracture developed by Schapery [96,97,98] and Chudnovsky [93] are extremely valuable in understanding the failure process of MSP. Simulation of viscoelastic fracture mechanics of MSP for arbitrary geometries and boundary conditions involves simultaneous handling of the sharp or diffuse swelling front with large deformations behind the crack tip in addition to fracture propagation. As explained in section 3, the stress concentration behind the crack tip will induce rapid diffusion and localized swelling, thus reducing relaxation times. To regularize the problem, accurately represent chemomechanical evolution and avoid mesh-dependent solutions, a non-local formulation is required. Numerical methods that are most promising to address these challenges include the phase field method (PFM) [99,100,101,102,103,104,105,106,107,108,109], peridynamics [110,111,112] and strain-gradient based damage modeling. Further details regarding constitutive models ideally suited for MSP will be discussed in a follow up article to this review.

5. Applications of MSP for Biomimetic Materials

The biomechanical functionality of several natural tissues e.g. tendons and cartilage involve MSP. Poroelasticity of cartilage and other tissues is primarily controlled by free water while viscoelasticity is controlled by bound water [113,114,115,116]. Accordingly, controlling the proportions of bound and free water in unloaded and loaded conditions has been identified as a key parameter in mimicking natural extracellular matrix (ECM), e.g. using hydrogels, especially for replicating poroviscoelastic properties [117,118]. Replication of these properties is also a crucial aspect of developing biomaterials for annulus fibrosus rupture repair [119]. Results from successful treatment protocols for tendinopathy have also used stress relaxation for healing and applied bound and free water contents as part of a set of benchmarks to evaluate tissue recovery [120]. Thus, a deeper understanding of MSP in native and biomimetic materials using the theoretical arguments and experimental protocols presented in this review is expected to significantly aid the development of synthetic biomimetic materials for biomechanical applications.

Waterborne biodegradable polyurethanes have been successfully explored to simultaneously mimic the hydration state, low modulus, and structural stability of hydrogel mimics for the EMC of central nervous system soft tissue [121]. In the synthesis, structural stability was achieved after several loading-unloading and saturation cycles. However, the explicit contributions of bound and free water for elastic and poroviscoelastic properties were not quantitatively leveraged. In previous work, we have shown the dramatic reduction in modulus with free water [43]. The discussion presented in this review on MSP is expected to significantly enhance the controllability and predictability of the mechanical behaviour of synthesized scaffolds in a wet environment. It is also similarly useful to guide the simultaneous achievement of tunable mechanical properties, controlled swelling, dissolution behaviour, and sustained release in the development of wound dressings [122].

Several biomimetic materials rely on bound water for functionality e.g. biomimetic bone scaffolds, aquaporin-based membranes, hygro-responsive textiles, zwitterionic hydrogels, and artificial cartilage. Spider silk has generated high research interest due to its outstanding mechanical properties and toughness. It is formed by molecular alignment during web spinning, which is achieved by simultaneous deformation and loss of water. Supercontraction of spider silk is a phenomenon where this process is essentially reversed, resulting in loss of the oriented structure between crystalline regions [123,124,125]. During supercontraction, the interaction between the pre-stress in the “frozen” glassy state and the moisture influx is by definition a MSP. Although it is recognized that the synthesized glassy state is not a ground state [126], the phenomenon is yet to be analyzed from the perspective presented in this review. Peptide-cellulose reactions have been used to tune water sensitivity and mechanical performance in biomimetic analogs of spider silk [127]. This review is expected to strongly inform such design. Similarly, several sea-cucumber inspired smart hydrogels [128] have been developed which are responsive to various types of stimuli including stress, light, and chemical changes. The concepts presented in this review can be leveraged to pre-condition the hydrogels to specific proportions of bound and free water, to tune the resulting viscoelastic properties.

Solvent vapor annealing assisted by soft shear (SVA-SS) is a method which leverages the synergistic effects of solvent induced mobility and mechanical stress to aid the alignment of nanodomains in block polymer thin films (BCPs) [129,130,131]. BCPs have been demonstrated to serve as a general platform for patterning of supramolecular structures that are known to assemble at solid–liquid interfaces. They have been used to prepare templates for biomimetic mineral synthesis [132]. Although the terminology used in SVA-SS does not mention MSP, the underlying mechanism shows substantial overlap with MSP. Therefore, the insights into MSP presented in this review can be utilized to guide self-assembly in BCPs from a more predictable standpoint. For further optimizing such self-assembly as well as predicting yet undiscovered exotic programmable material behaviour incorporating MSP, a spiralling Kuhn paradigm, such as the one designed by dell’Isola and Misra for metamaterials [133] can be utilized.

6. Discussion

The following points, important to the experimental, theoretical, and computational investigation of MSP, most of which have been explicitly identified for the first time, have been discussed in this review:

• For the first time, several seemingly disparate mechanosorptive phenomena from a variety of applications have been brought together under a single review. The interrelationship between several terminologies used in literature including MSC, MSCR, ESY, SEDS, and ESC have been explained.
• MSCR and ESC have been identified as two extremes of the same underlying phenomenon with supporting evidence from a large body of studies from a variety of fields. Several experimental results which show responses resembling ESC and MSCR/ESY for the same polymer for different solvents or different sorption of the same solvent have been reproduced here to justify this conclusion.
• For the first time, it has been hypothesized that the reversible parts of MSC, ESY or SEDS can be explained by the equilibrium swelling of polymer networks. Only the irreversible part of the MSC necessitates the rate of solvent sorption as a constitutive variable. Irreversibility can also arise from plastic yielding. Once proven, this hypothesis is expected to greatly simplify constitutive modelling of MSP.

Finally, several applications for biomimetic materials where mechanosorptive phenomena can be leveraged have been identified in this review.