Viscosity Analysis of Electron-Beam Degraded Gellan in Dilute Aqueous Solution

1. Introduction

Polymers are distinctive materials characterized by a wide range of high molar masses and corresponding solution viscosities [1]. They are composed of chain molecules formed by repeating organic units called monomers, where each pair of monomers is covalently bonded [2].

In solution, the length of the covalent bond (b) is usually referred to as the chain segment; the length of a single polymer chain corresponds to a specific number of segments (N) and degree of polymerization (DP), where N is equal to 2 DP; the degree of polymerization, also called the number of monomers, is equal to the chain molar mass (M) divided by the monomer molar mass Mu [1]. Both are represent average values due to the varying chain lengths of polymeric substances.

In a diluted solution, polymer chains exist as individual coils and behave ether as a random walk coils or self-avoiding walk coils [3,4,5]. In a good solvent, these coils adopt irregular and dynamic shapes due to segmental perturbations, behaving like a real chain that is fully dissolved and conforming to the self-avoiding walk (SAW) model [4,5]. However, electrolyte chains tend to adopt stretched conformations unless a small amount of neutralizing salt is added, which causes the chains to collapse back into the coil shapes [1].

In contrast, in a theta (θ) solvent, the coil assumes a static, spherical shape due to its unperturbed segments, following the random walk (RW) model or freely rotating chain (FRC) model [3,4,5]. In this case, the chain behaves like an ideal chain, neither completely dissolved nor precipitate.

Polymers in infinitely diluted solutions (IDS) exhibit specific intrinsic properties (Ps) such as intrinsic viscosity ([η]), radius of gyration (Rg), chain end-to-end distance (Re), hydrodynamic radius (Rh), and interaction parameter (A2). Their relationships play a critical role in the viscosity analysis of polymers in solution [1,4,5,6,7].

Polysaccharides are natural polymer, composed of glycosidic-linked mono-saccharide units, and commonly utilized in numerous industrial and biomedical contexts [8]. A key task in these applications is controlling the M- P relationships of polysaccharides. Radiation degradation methods, such as electron beam (EB) techniques, are effective, eco-friendly ways to regulate these relationships. When irradiated polysaccharides are dissolved in a solution, their viscosity behavior often differs from that of the native polysaccharides, see for example Ref. [9,10,11,12].

In dilute solutions, polysaccharides exhibit a range of M-P relationships, which are typically analyzed Flory [4,13] scaling laws and theoretical models such as the FRC and SAW models, as previously discussed [3,4,5]. Additionally, the transition state theory (TST) and the worm-like chain (W-LC) model, covered in References [6,14] and [1,8,15], provide further insight into their behavior.

Gellan is a linear, water-soluble polysaccharide obtained through bacterial fermentation [15,16]. It functions as an anionic polysaccharide and is composed of repeating monomeric units, as shown in Figure 1 [16].

Gellan gum, utilized in solutions across a variety of molar masses, serves multiple purposes, including as a food, antioxidant activities, in drug delivery systems, and plant growth regulators [16,17].

In the literature, relevant studies have primarily explored the formulation of the Mark–Houwink equation [18], the structural and conformational properties of polysaccharides in organic solvents [19], and the impact of radiation on the molar mass-viscosity relationship [20]. However, our research specifically examines radiation-induced M-P modifications in diluted gellan within an aqueous solution, a topic that has not yet been addressed in previous studies.

This study seeks to offer scientists and engineers working with polymers and polysaccharides an efficient approach to modifying gellan in aqueous solution for targeted applications. The objectives of the study are categorized into three main areas: examining radiation degradation kinetics, establishing scaling laws, and analyzing changes in chain flexibility following modification.

2. Experimental

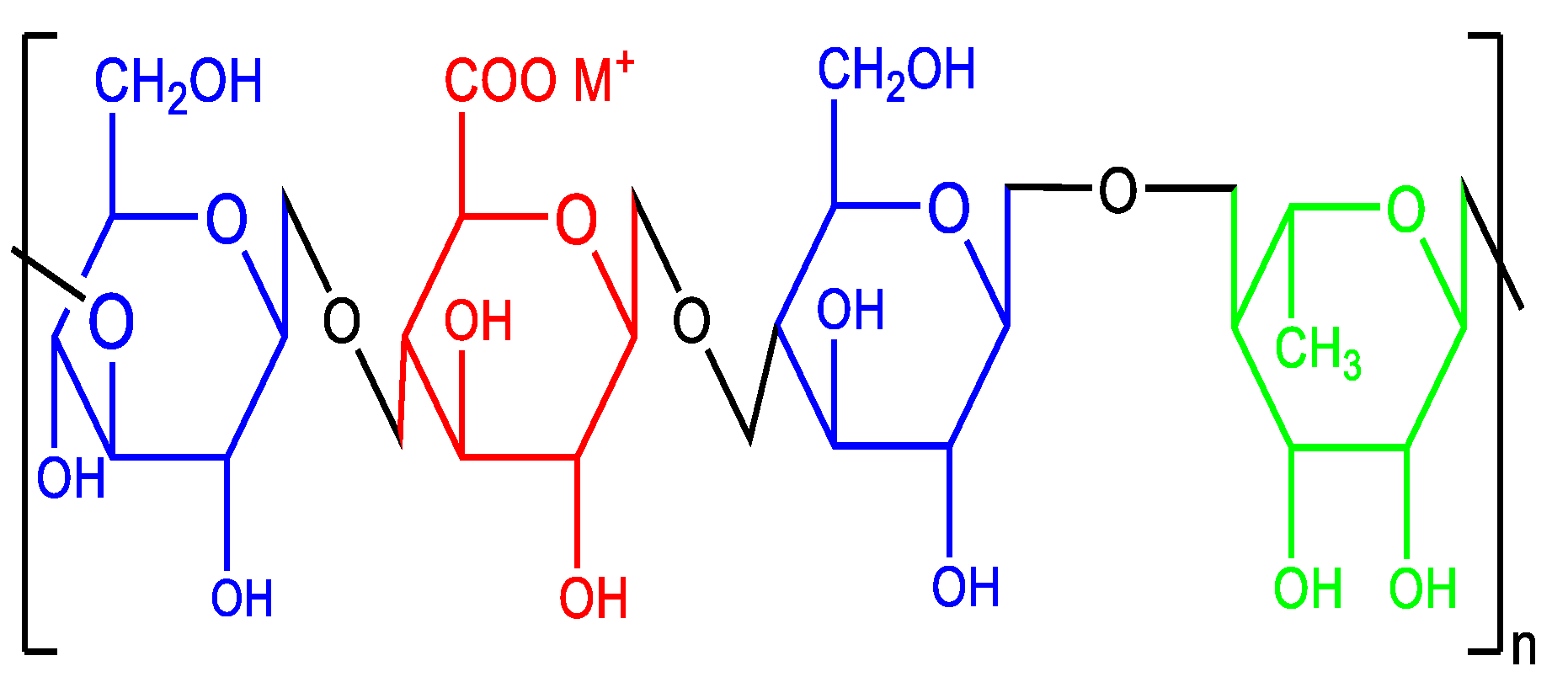
2.1. Materials

Gellan was supplied as commercial-grade powder by Glentham Life Sciences Ltd at UK. The Potassium Chloride (KCl) powered was supplied as Commercial-grade powder by Surechem products ltd, Needham market, Suffolk, UK.

2.2. Solution preparations

Potassium chloride, KCl, was dissolved in double-distilled water to obtain a stock solvent up to 0.1M. Gellan gum, GG, was then dissolved in the solvent to obtain a stock solution up to 0.05 g/cm³. In both dissolution proses, the mixture was gently stirred using a magnetic stirrer to ensure complete dissolution.

2.3. Viscosity measurements

Viscosity measurements were performed using a thermostated water bath (TCB-7-Viscometer Bath, 230V/50-60Hz, PSL-Rheotek) maintained at a temperature of 24.99 ± 0.01°C. The measurements utilized an Ostwald viscometer (YUCHENGTECH) with a capillary diameter of 0.5 mm and a water flow time ranging from 100 to 150 seconds. Flow times for both the solvent and the solution were measured in triplicate, and their averages were calculated using Eq. 1[1,6]:

η_r = t / t_o , η_sp = η_r -1

(1)

Here, t, t₀, ηᵣ, and ηₛ represent the solution flow time, solvent flow time, relative viscosity, and specific viscosity, respectively.

2.4. E-beam irradiation

The solution samples were irradiated using a digital linear accelerator manufactured by Elekta Infinity Company in Sweden, situated at the National Oncology Center in Benghazi, Libya. The irradiation process was conducted in an air atmosphere at room temperature, with electron energy of 6 MeV. The chosen absorbed dose ranged from 50 to 500 Gy, and changes in each sample were assessed through viscosity analysis immediately after irradiation and at various intervals.

2.5. Intrinsic viscosity and molar mass determinations

For the native and degraded 0.05 g/cm³ GG solutions, the intrinsic viscosity ([η]) was determined by the single-concentration method, using the Solomon–Ciuta equation [21]:

$$\left[\eta \right]=(2{\eta }_{\mathrm{s}\mathrm{p}}-{2\mathrm{l}\mathrm{n} \eta }_{\mathrm{r}}{)}^{0.5}/C$$

(2)

The molar masses Ms of the native and degraded gellan were calculated, using Mark-Houwink equation (Eq.3) relating to intrinsic viscosity $\left[\eta \right]$ as [22,23]:

[η] = K_[η] M_r^a

(3)

where the M-H constantans of the used polymer-solvent system were given in the literature as [18]: K_[η] = 7.48 × 10⁻³ cm³ /g anda = 0.91.

2.6. Characterizations

2.6.1. Degradation kinetics

The degradation rate (k) of GL in the diluted solution was graphically obtained by using Eq.4 [10,24]:

1/M_D – 1/M_O = k D/M_u

(4)

where: M_D is GL molar mass at specific radiation dose, M_O is the initial GL molar masses, and M_u is the monomeric GL molar mass. Furthermore, the rate constant k is related to the first order lifetime (τ) as:

1/k = τ

(5)

2.6.2. Scaling laws

The scaling parameters, including Rg and A2, were determined using calculations based on Eq.( 6) and (7), respectively [1,4,13]:

$$R_{\mathrm{g}}={{\displaystyle \frac{M\left[\eta \right]}{{\mathsf{\Phi }}_{\mathsf{\theta }}}})}^{1/3}, {\mathsf{\Phi }}_{\mathsf{\theta }}=3.7\mathrm{X}{10}^{24}{\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$$

(6)

$$A_2\approx {\displaystyle \frac{\left[\eta \right]}{M}}$$

(7)

Then, the scaling coefficients ($\nu$ and ${\nu }_{\mathrm{A}2}$ ) were respectively deduced from the scaling laws [4,13]:

$$\ln R_{\mathrm{g}}={\mathrm{K}}_{\mathrm{R}\mathrm{g}}+\nu \ln M_{\mathrm{r}},$$

(8)

$$\ln A_2={\mathrm{K}}_{\mathrm{A}2}+{\nu }_{\mathrm{A}2}\ln M_{\mathrm{r}}$$

(9)

where ${\mathrm{K}}_{\mathrm{R}\mathrm{g}}$ and ${\mathrm{K}}_{\mathrm{A}2}$ are the equations proportionality constants.

2.6.3. Chain flexibility

The chain flexibility parameters under non-theta conditions, including the shape parameter (${\rho }_{\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}}$), activation energy ($E_{\left[\mathsf{\eta }\right]}$), and solution entropy ($∆S$), were determined using equations (10), (11), and (12), respectively [1,6,14]:

$${\rho }_{\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}}={\displaystyle \frac{R_{\mathrm{g}}}{R_{\mathrm{h}}}}$$

(10)

$$\mathrm{l}\mathrm{n}\left[\mathsf{\eta }\right]=\mathrm{l}\mathrm{n}{A}_{\left[\mathsf{\eta }\right]}+{\displaystyle \frac{E_{\left[\mathsf{\eta }\right]}}{\mathrm{R}T}}$$

(11)

$${∆S}_{\mathrm{o}}+\ln {\displaystyle \frac{{\eta }_{\mathrm{r}}}{{\mathrm{N}}_{\mathrm{A}}\mathrm{h}}}=-{\displaystyle \frac{∆S}{\mathrm{R}}}+{\displaystyle \frac{{∆H}_{\mathrm{r}}}{\mathrm{R}T}}$$

(12)

In the above equations $R_{\mathrm{h}}$ was computed from the relation:

$$R_{\mathrm{h}}=({{\displaystyle \frac{3\left[\eta \right]M}{10\mathsf{\pi }{\mathrm{N}}_{\mathrm{A}}}})}^{1/3}$$

(13)

where ${\mathrm{N}}_{\mathrm{A}}$ is the Avogadro constant; $A_{\left[\mathsf{\eta }\right]}$ , $R,$ and T are respectively the activation energy, Arrhenius–like constant, gas constant, and the temperature in Kelvin; ${∆S}_{\mathrm{o}}$ , $∆S,$ ${∆H}_{\mathrm{r}},$ and $\mathrm{h}$ are the solvent entropy, solution entropy, relative enthalpy, and the Plank constant, respectively.

The equations (14), (15), and (16) were utilized to determine the characteristic ratio ($C_{\mathrm{\infty }}$), end-to-end distance ($R_{\mathsf{\theta }}$), and persistence length ($l_{\mathrm{p}}$), respectively, to assess chain flexibility under theta conditions [1,4,5,8]:

$$C_{\mathrm{\infty }}={\displaystyle \frac{N{b}^2}{{R_{\mathsf{\theta }}}^2}}$$

(14)

$$R_{\mathsf{\theta }}= {( {\displaystyle \frac{{\left[\mathsf{\eta }\right]}_{\mathsf{\theta }}M }{\mathsf{\Phi }}} )}^{1/3}$$

(15)

$$l_{\mathrm{p}}={\displaystyle \frac{b{C}_{\mathrm{\infty }}}{2}}$$

(16)

The following relationships were considered during the application of the above equations[1,25,26]:

$$N =2 M/M_u$$

(17)

$$\mathsf{\Phi }\approx 2.5\mathrm{X}{10}^{23}{\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$$

(18)

$${\left[\eta \right]}_{\mathsf{\theta }}={\displaystyle \frac{\left[\mathsf{\eta }\right][1-\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{C}{C^{*}}\left)\right]}{\frac{{0.77}^3{\rho }_{\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{i}\mathrm{n}}}{C^{*}}-\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{C}{C^{*}})}}$$

(19)

$${\rho }_{\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{i}\mathrm{n}} ={\displaystyle \frac{2.5}{\left[\eta \right]}}$$

(20)

$$C^{*}\approx {\displaystyle \frac{0.77}{\left[\eta \right]}}$$

(21)

where$\mathsf{\Phi }$, ${\left[\eta \right]}_{\mathsf{\theta }}$, ${\rho }_{\mathrm{e}\mathrm{c}\mathrm{u}}$, and $C^{*}$ are known as the Flory constant, intrinsic viscosity at theta condition, chain density, and its critical concentration, respectively.

3. Results and discussion

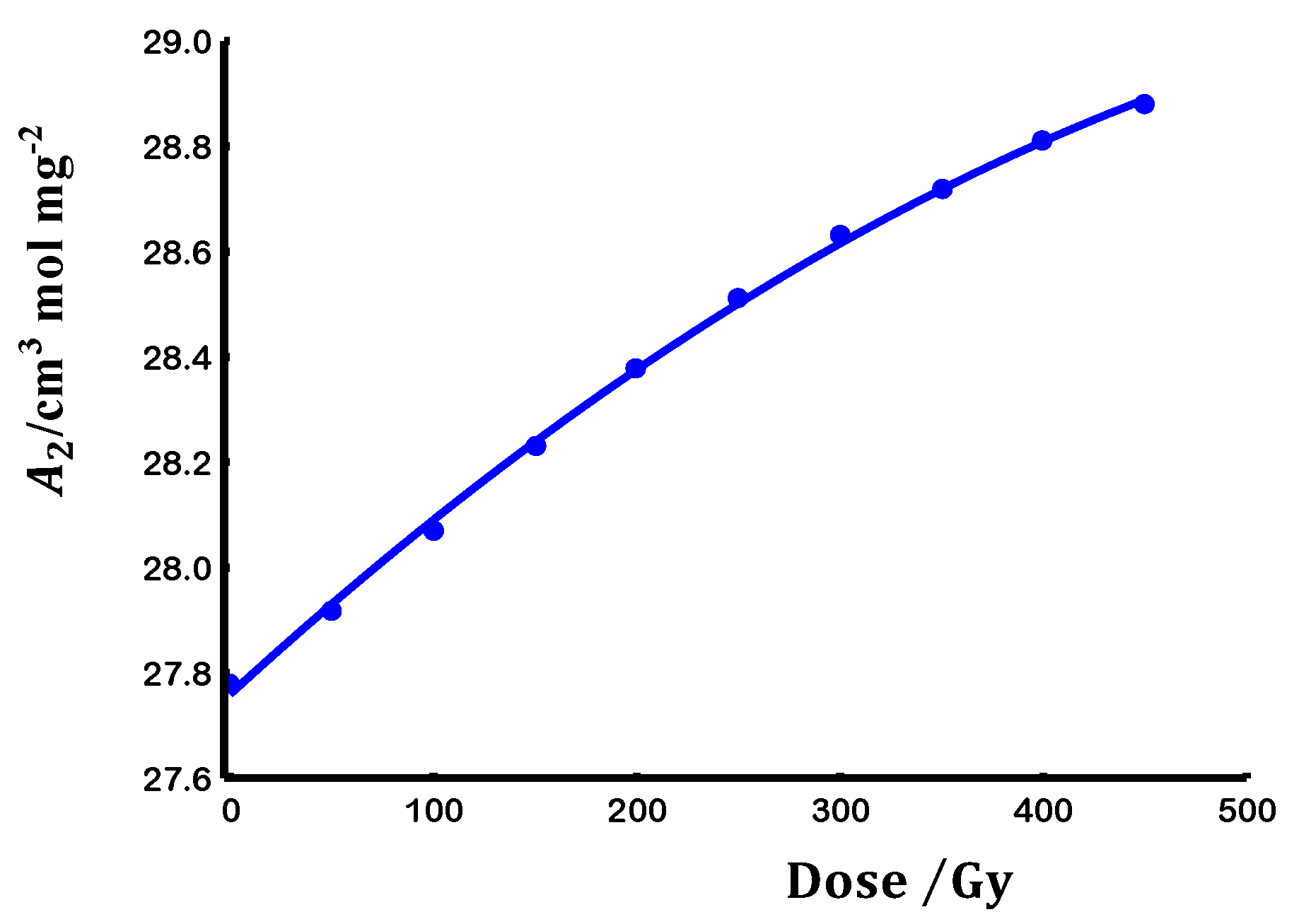
3.1. Degradation kinetics

Figure 2 shows how EB-radiation affects gellan when it is in a solution. The observed rapid decrease indicates a strong molar mass reduction up to an absorbed dose of 200 Gy. After that point the no major reduction were seen. This behavior happens because of random chain breaks, which are likely to occur at a steady rate during the fast decline part. According to Figure 2, the rate constant was found to be a 1.03 x 10^-5 Gy⁻¹ and the lifetime was 97 x 10³ Gy.

Figure 2. Progress of E-beam degraded molar mass for gellan samples at 25°C.

Figure 2. Progress of E-beam degraded molar mass for gellan samples at 25°C.

Figure 3. First order degradation law of native gellan sample by E-beam at 25°C.

Figure 3. First order degradation law of native gellan sample by E-beam at 25°C.

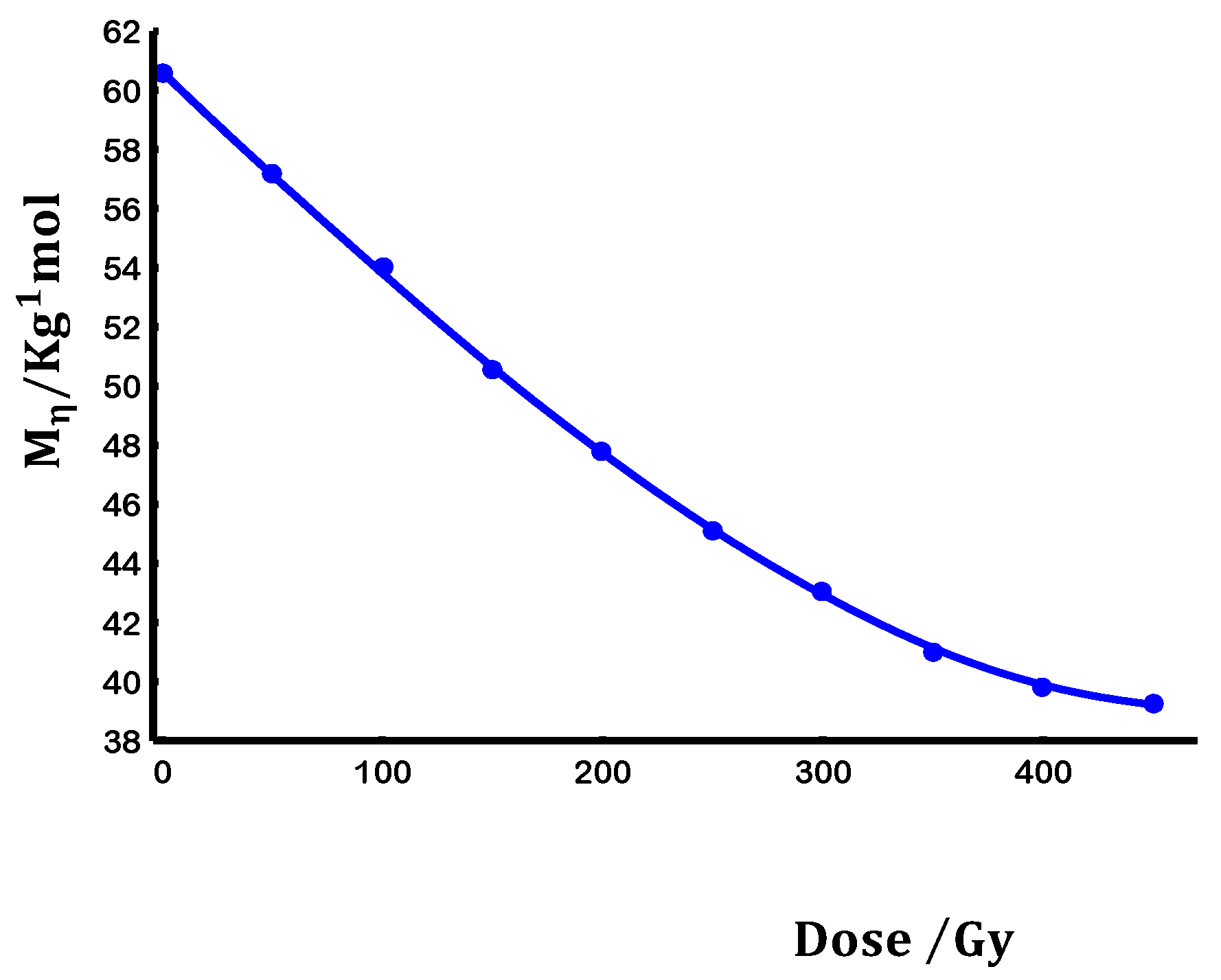
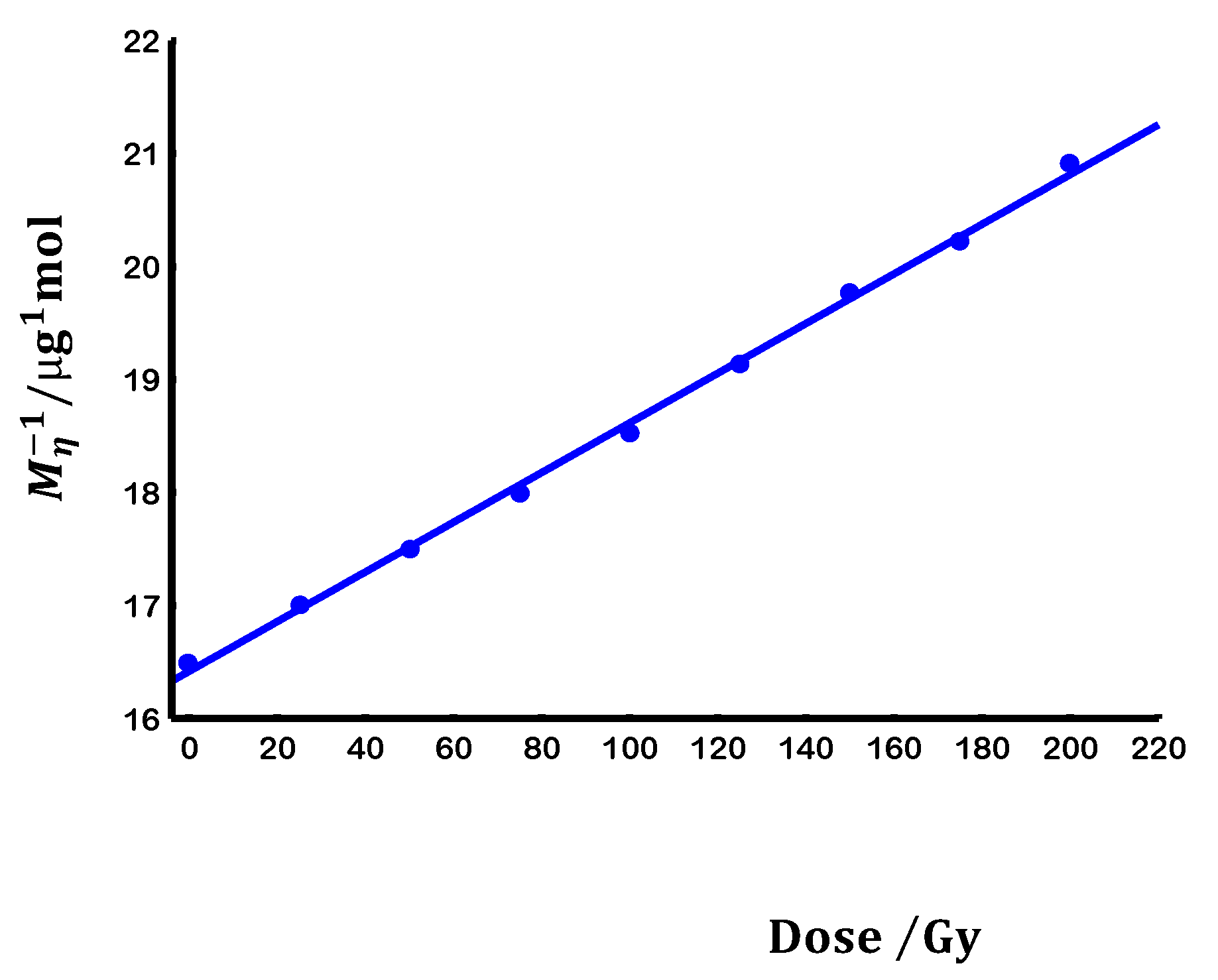
3.2. Scaling laws

Similar to the degraded molar masses (Ms) shown in Figure 2, Figure 4 illustrates the effect of EB-radiation on the size parameter$R_{\mathrm{g}}$ of the polymer–solvent system. A logarithmic plot in Figure 4 was then utilized to derive the corresponding scaling law.

Figure 4. Progress of E-beam degraded radius of gyration for gellan samples at 25°C.

Figure 4. Progress of E-beam degraded radius of gyration for gellan samples at 25°C.

Figure 5. The logarithmic forms of radius of gyration vs molar mass for gellan samples at 25$°\mathrm{C}.$

Figure 5. The logarithmic forms of radius of gyration vs molar mass for gellan samples at 25$°\mathrm{C}.$

In contrast to the reduction in size observed in Figure 4, Figure 6 highlights the increase in solvation parameters $A_2$ caused by the EB-radiation, which was used to determine the solvation scaling law through its logarithmic representation Figure 7

The above scaling laws offer valuable frameworks for tailoring the desired $R_{\mathrm{g}}$ and${ A}_2$ using EB-radiation. Additionally, their coefficients $\nu$ and${\nu }_{A_2}$, along with the M-H scaling coefficient a, which was calculated as a = 3$\nu$ – 1[1,4,5], were employed to predict the real perturbed chain, as summarized in Table 1.

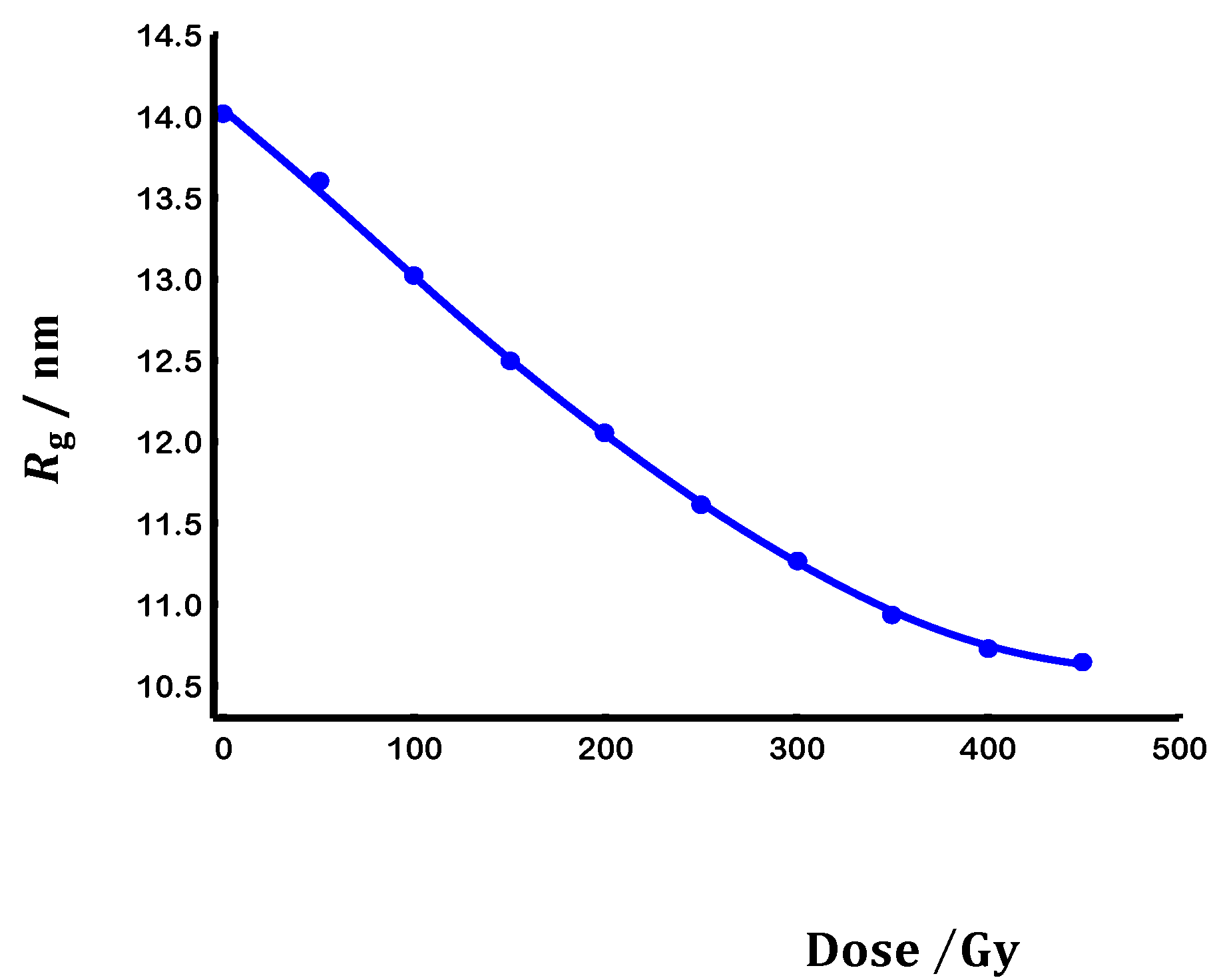
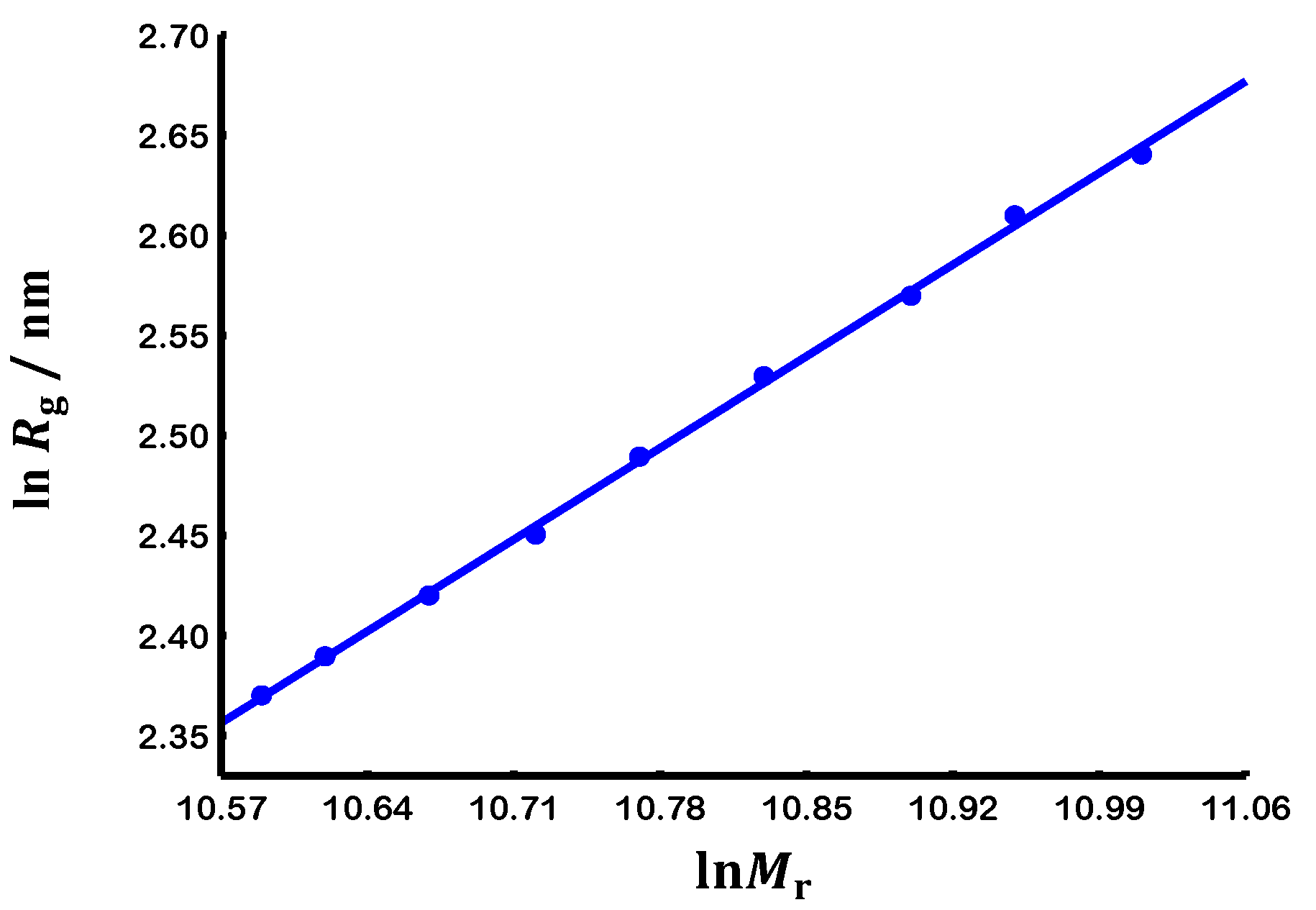
3.3. Chain flexibility

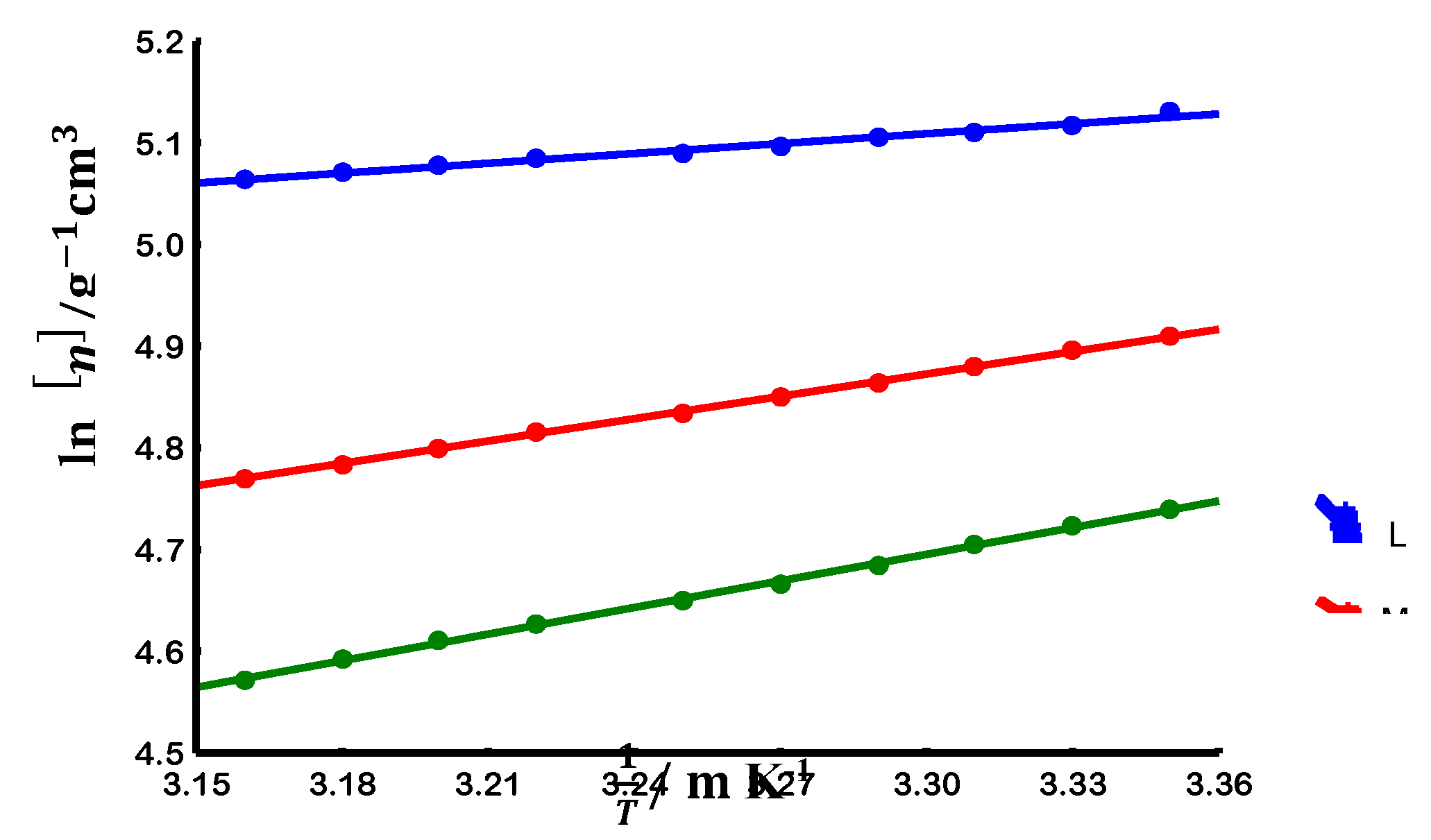
3.3.1. Evaluation at non-theta conditions

Figure 8 and Figure 9 illustrate Eq. 10 and 11, respectively, for large (L), medium (M), and small (S) molar masses of diluted gellan in the solvent used. These are represented by the linear plots shown in the figures.

The linear plots in Figure 8 and Figure 9 were utilized to calculate $E_{\left[\mathsf{\eta }\right]}$ and $∆S$ values, respectively. These values, along with their corresponding${\rho }_{\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}}$values, are summarized in Table 2 to assess the effect of EB radiation on them and, consequently, on gellan flexibility.

As in Table 2, EB radiation led to a decrease in Ms and $E_{\left[\mathsf{\eta }\right]}$s of gellan in solution, while it increased $∆S$ of gellan in solution. This reduction in $E_{\left[\mathsf{\eta }\right]}$ caused a decrease in the flexibility of the gellan chain [6,14]. Conversely, the solvent quality (SQ) was enhanced by EB radiation due to the increase in its $∆S$[6]. However, the ideal random coiled structure of gellan, as defined by it’s${\rho }_{\mathrm{s}\mathrm{h}\mathrm{a}\mathrm{p}\mathrm{e}}$, remained unaffected by EB-radiation.

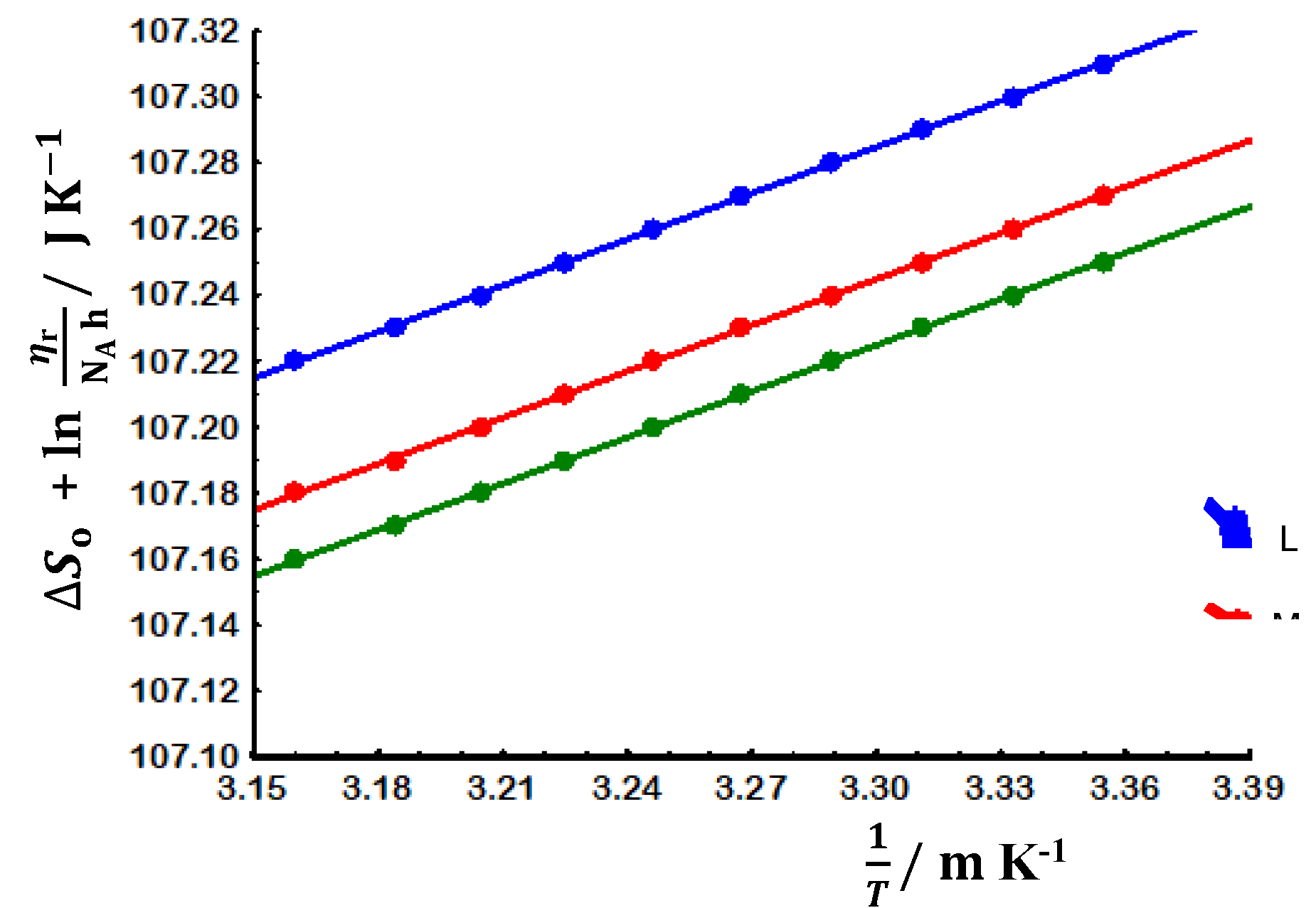
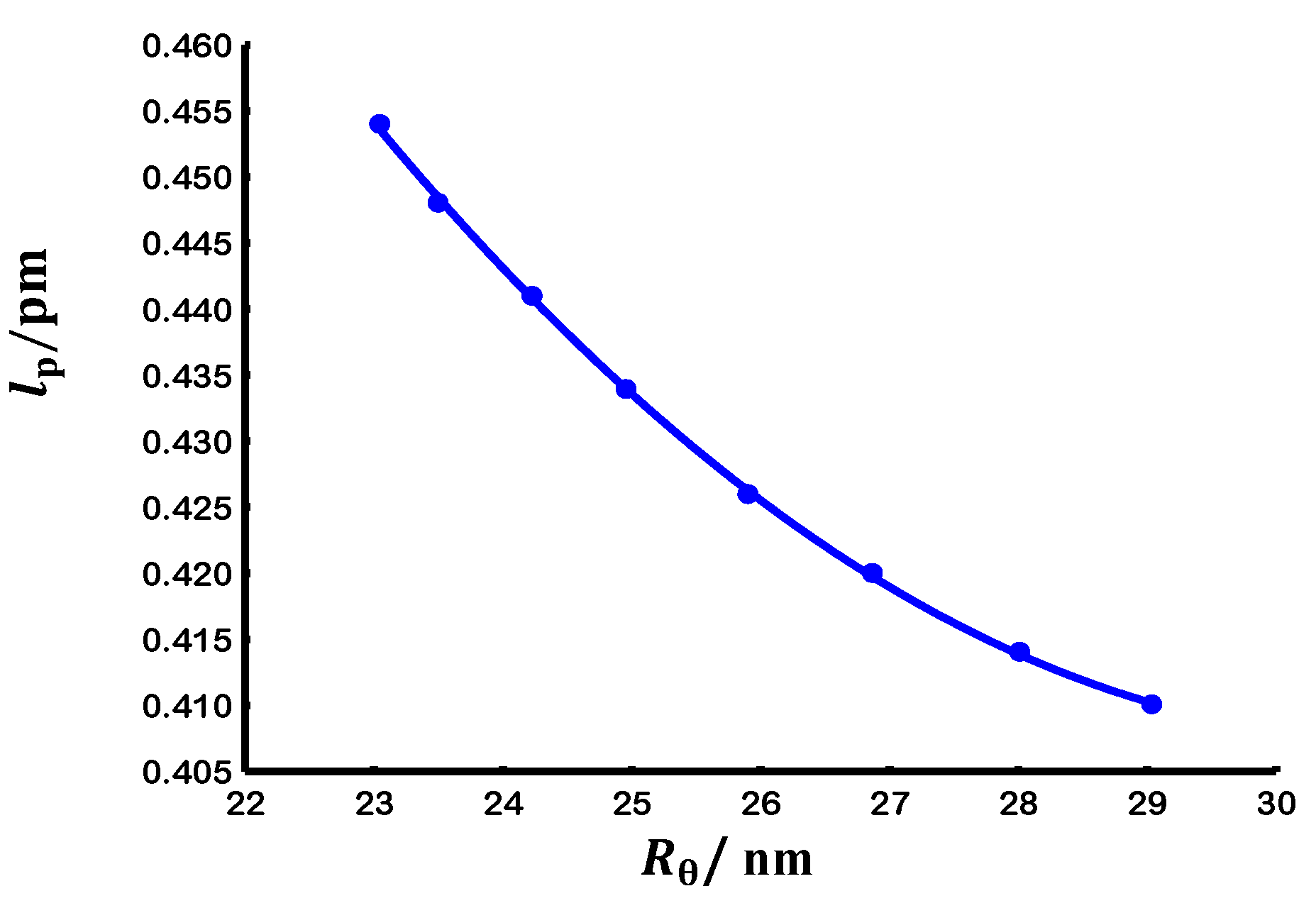
3.3.2. Evaluation at theta conditions

Figure 10 and Figure 11 illustrate the relationships between $C_{\mathrm{\infty }}$ and $l_{\mathrm{p}}$ with${ R}_{\mathsf{\theta }}$, which represents the chain size, for both native and degraded gellan samples. As expected, these characteristics are influenced by the gellan chain length and related molar mass M, particularly at high values of${ R}_{\mathsf{\theta }}$.

The M dependencies of these characteristics are summarized in Table 3. As shown in Table 3, EB radiation resulted in a reduction in Ms and ${ R}_{\mathsf{\theta }}$of the GL samples, while increasing$l_{\mathrm{p}}$ . This increase led to a decrease in CF and an increase in SQ of the gellan samples, as discussed in section 3.3.1. Additionally, the data in Table 3 indicate no deviation from chain ideality, as reflected by${ C}_{\mathrm{\infty }}$, at the molar masses listed in Table 3.

4. Concluding remarks

(1) Viscometry serves as an effective technique for analyzing radiation-modified gellan in diluted aqueous solutions.

(2) Electron beam (E-beam) degradation enables precise control over the applicability of gellan solutions, by modifying the relationship between molar mass and viscosity.

(3) Gellan scaling laws have practical significance for users, allowing them to tailor the polymer’s molar mass to achieve desired properties and vice versa.

(4) Activation parameters, including activation energy and activation entropy, can be utilized to assess the flexibility of both native and modified gellan through relative viscosity measurements.

(5)The flexibility characteristics of native and E-beam-degraded gellan chains, such as end-to-end distance and persistence length, can be determined using the Mark-Houwink relationship under theta conditions.