Development of a 1D Finite-Volume Model for the Simulation of Solid Oxide Fuel Cells

1. Introduction

Solid oxide fuel cells (SOFCs) and solid oxide electrolysis cells (SOECs) are emerging energy conversion technologies that can support the energy transition. Their use can improve the efficiency of existing energy conversion concepts, like in the case of an SOFC used for cogeneration applications, or prompt the development of new concepts, like multi-energy systems based on reversible solid oxide cells (rSOCs) [1], or hybrid power generation systems integrating an SOFC with gas or steam cycles [2]. Modern SOCs operate at a high temperature between 600 °C-800 °C using in most cases a solid yttria-stabilized zirconia (YSZ) electrolyte. On the one hand, the high temperatures bring several advantages compared to similar electrochemical devices based on polymeric or alkaline electrolytes, including higher efficiency, the possibility of thermal integration at system level, fuel flexibility, and absence of expensive catalysts. On the other hand, the main drawbacks include a faster degradation of the cell main components and the need to carefully manage internal thermal gradients.

Using accurate models to predict the performance of SOFC (or SOEC) is a crucial aspect for the development of energy systems based on this technology. In general, a stationary SOFC model includes mass and energy balances to find the internal gas composition and temperature profiles, and an electro-chemical model to calculate the local rate of electrochemical and chemical reactions. The model dimensionality and complexity can vary substantially, including 1D approaches developed along the main direction of the gas flows [3], 1D+1D or 2D models with a refined description of the processes occurring within the electrodes [4] and at the cell layer boundaries, and 3D models of the solid oxide cell (or stack) using commercial software like COMSOL [5] and CFD (computational fluid-dynamics) approach. The review work of Wu et al. [6] provides an in-depth description of the available SOFC models, highlighting strengths, weaknesses, and field of application for each of them. In particular, 1D models can be more easily integrated into wider system simulations due to the significant computational burden of 2D and 3D models, allowing the system optimization while retaining a good description of physical processes occurring within the stack. Two- and three-dimensional models provide additional insights on the stack internal operating conditions and can improve the performance estimation, especially at high current density [7].

This work presents an updated version of a 1D, co-flow, finite-volume model for the simulation of planar SOFCs, that has been already validated and used in several works [3,8]. Differently from previous versions, the model is developed to allow running within Aspen Plus^® for wider system and process simulations; the Aspen environment provides built-in functions for the calculation of physical and thermodynamic properties of gases and facilitates the model integration.

The model developed is calibrated and validated using experimental polarization curves of an SOFC, covering a wide range of operating conditions in terms of H₂ and H₂O molar fraction in the fuel, temperature, and fuel utilization factor (exceeding 90%), which is not common for relatively simple 1D models. The experimental data are reported in ref. [4], which also includes a numerical investigation using a 1D+1D model integrating the dusty gas model (DGM) for species diffusion in the electrode, and a distributed electrochemical model applied throughout the electrode thickness. One of the aims of this work is to demonstrate that the same set of data can be described by a simpler 1D model over a wide range of operating conditions, drastically reducing complexity and computational time, facilitating the grid convergence, while retaining a good accuracy.

2. Model Description

The model developed is designed for the simulation of standard solid oxide cells using Y-doped zirconia as electrolyte. The electrochemical reactions (1) and (2), representing the hydrogen oxidation reaction (HOR) and the oxygen reduction reaction (ORR), occur at the fuel and air electrode, respectively. In fuel cell mode, H₂ is oxidized to H₂O, consuming an oxygen ion in the electrolyte and producing two electrons in the electronic-conducting phase (e.g., nickel). Electrons flow through an external resistance towards the positive electrode (air electrode), where they combine with oxygen to produce an oxygen ion in the electrolyte. The HOR and the ORR proceed forward and backward in fuel cell and electrolysis mode, respectively.

$${\mathrm{H}}_2+{\mathrm{O}}^{2-}\leftrightarrow {\mathrm{H}}_2\mathrm{O}+2{\mathrm{e}}^{-}$$

(1)

$${{\displaystyle \frac{1}{2}}\mathrm{O}}_2+2{\mathrm{e}}^{-}\leftrightarrow {\mathrm{O}}^{2-}$$

(2)

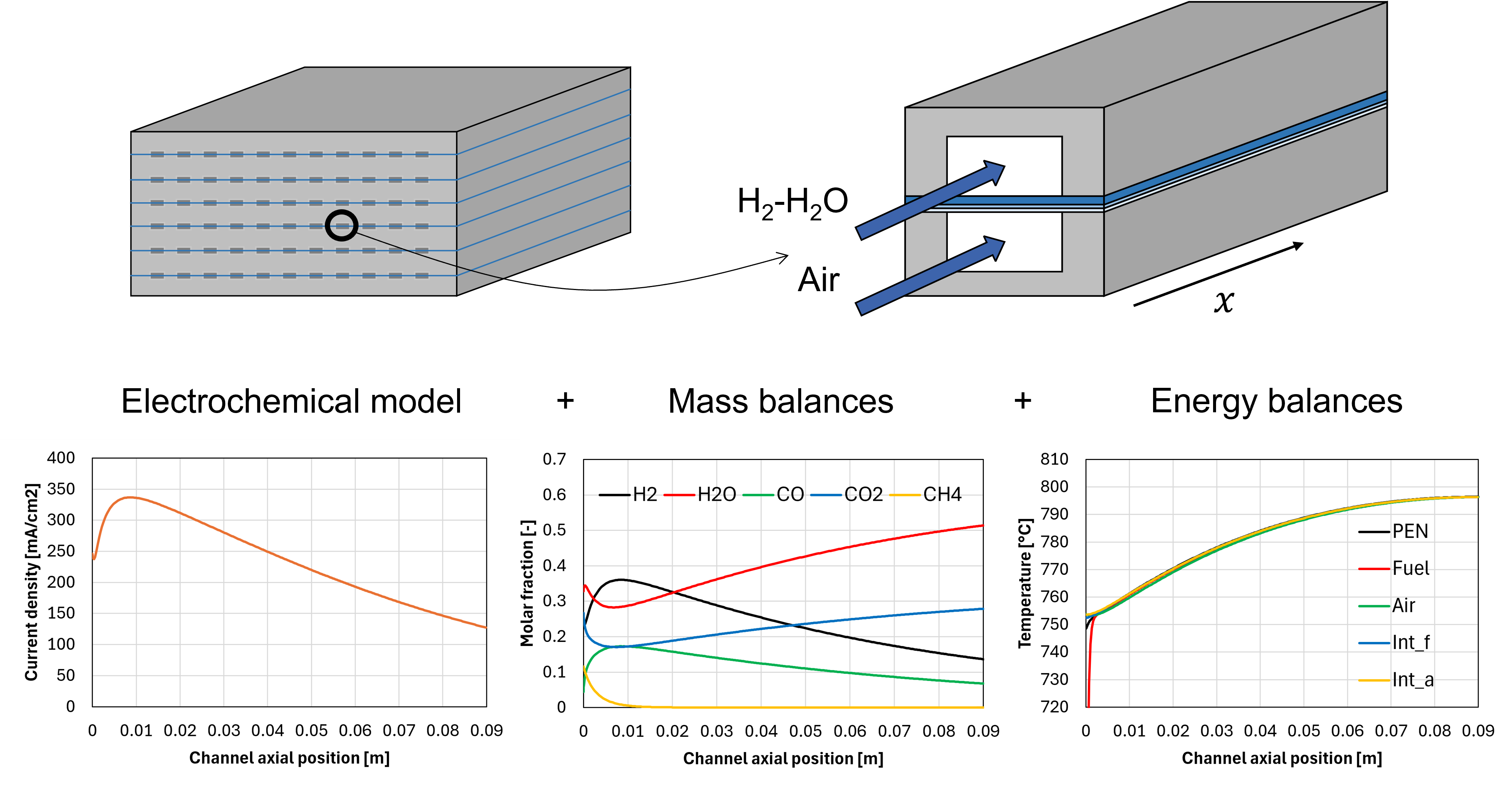
Figure 1 (left) shows a generic solid oxide cell stack made of multiple planar cells stacked on top of each other, each cell containing several gas channels as the one shown in the right-hand side of Figure 1. The model developed in this work considers a single channel as geometric domain, assuming that the whole stack (or cell) can be represented by a number of identical channels, which significantly limits the model complexity. The finite-volume model developed is one-dimensional in the direction of the channel; it assumes steady-state operation, co-flow arrangement, and it can be used to model both fuel cell and electrolyzer modes. The model is implemented in Aspen Plus^® environment, which allows exploiting a built-in equations solver and accurate datasets for the calculation of thermodynamic and physical properties of gas mixtures.

The model inputs are the channel geometry, the conditions of the inlet streams (temperature, composition, pressure, and mass flow rate), several parameters required to model the physical processes, and the cell voltage, which is assumed to be constant throughout the channel (electrode equipotential assumption). The main outputs of the 1D model are the distribution along the axial direction of:

• The composition ($x_i$) and temperatures ($T_f$ and $T_a$) of the gas streams;

• The temperature ($T_{PEN}$) of the Positive-Electrolyte-Negative (PEN) structure (i.e., assembly including the electrodes and the electrolyte);

• The temperature of the interconnect at the fuel side and air side ($T_{int,f}$ and $T_{int,a}$);
• The current density ($i_{O^{2-}}$) and the electrochemical overpotentials (${\eta }_k$).

Figure 2 shows the main dimensions defining the channel geometry, which also allow to define the relevant geometrical parameters shown in Table 1.

The finite-volume solution algorithm includes the division of the channel in N small pieces as the one shown in Figure 3 (left), which will be called control volume (CV). Assuming that the cell voltage is fixed throughout the channel, the electrochemical model allows to calculate the local current density $i_{O^{2-}}$, which is equal to the small (but finite) current ($\Delta I$) flowing through the interconnects of the CV divided by the active area contained in it ($\Delta A_{act}$), as shown in Eq. (3).

$$i_{O^{2-}}={\displaystyle \frac{\Delta I}{\Delta A_{act}}}={\displaystyle \frac{\Delta I}{l_{act}·\Delta x}}$$

(3)

The electrochemical model developed is zero-dimensional, meaning that electrochemical reactions are assumed to only occur at the interface between the electrode and the bulk of the electrolyte. Coherently with the use YSZ as electrolyte, short-circuit electronic currents in the electrolyte are neglected, hence the current collected by the interconnects is equal to the ionic current flowing in the electrolyte.

As shown in Figure 3 (right), each CV is further divided into 5 sub-volumes enclosing the fuel and air channels, the interconnects, and the PEN structure. Mass and energy balances are solved for each of these 5 x N sub-volumes to find the temperature and gas composition along the channel. A uniform temperature is defined for the solid parts (interconnects and PEN sub-volumes) of each CV, resulting in 3 x N unknown temperatures. The fuel and air temperatures at the outlet interface of each CV are also unknown, resulting in 5 x N unknown temperatures in total, which is equal to the number of energy balance equations.

Axial heat conduction in the $x$ direction is considered for the PEN and the interconnects, while it is neglected for gas streams due to the low thermal conductivity of the gases. In the $y$ direction, only the convective heat exchange between gases and interconnects is considered (with exchange area per unit length equal to $4·h_{ch}$). The heat exchange in the $z$ direction includes the convective heat transfer between gases and solid parts, the conductive heat transfer between PEN and interconnects, and the heat loss which is assumed to be uniformly distributed on the external interconnect surfaces. The radiative heat exchange between PEN and interconnects is neglected since the temperature of the solid parts are always found to be very similar in the $z$ and $y$ directions even when radiative heat exchange is not considered, while the view factors are very small in the $x$ direction.

The main equation used for the calculation of the local current density is the voltage balance shown in Eq. (4). The cell voltage ($V_{cell}$) is fixed (if the total current is fixed, instead of the voltage, the same model can be run iteratively to find the voltage which matches the required current), and $E_{H_2}$ is the ideal maximum (minimum) cell voltage in fuel cell (electrolysis) mode. The term $E_{H_2}^0$ depends on temperature, and a simple correlation can be derived by fitting thermodynamic data [3]. The partial pressures of hydrogen and steam ($p_{H_2}$ and $p_{H_{2}O})$ used in Equation (5) are those found locally in the fuel channel; similarly, the local oxygen partial pressure in the air channel ($p_{O_2}$) is used. The overpotentials ${\eta }_k$ shift the cell voltage from the ideal value, decreasing its performance. In the model developed, both the overpotentials and the current density are positive in fuel cell mode and negative in electrolysis mode. All the overpotentials depend on the current density, and Eq. (4) is used to implicitly calculate $i_{O^{2-}}$.

$$V_{cell}=E_{H_2}-{\eta }_{conc}-{\eta }_{ohm}-{\eta }_{act}-{\eta }_{leakage}$$

(4)

$$E_{H_2}=E_{H_2}^0+{\displaystyle \frac{R{·T}_{PEN}}{2·F}}\mathit{ln}\left({\displaystyle \frac{p_{H_2}·p_{O_2}^{1/2}}{p_{H_{2}O}}}\right)$$

(5)

Equation (6) is used to calculate ${\eta }_{leakage}$, which accounts for the fact that the measured open-circuit voltage (OCV) is typically slightly lower compared to the ideal value calculated with Equation (5), even if the external current is null [4,9]. This might be due to small gas leaks or a short-circuit electronic current within the electrolyte. In fuel cell (or electrolysis) mode the maximum current density $i_{max}$ is calculated assuming that all the equivalent hydrogen (or steam) is consumed, generating a corresponding faradaic current. Therefore, the leakage loss is important near the OCV and tends to zero when the current density is large (in absolute value).

$${\eta }_{leakage}=\left(E_{H_2}-OCV\right)·\left(1-{\displaystyle \frac{i_{O^{2-}}}{i_{max}}}\right)$$

(6)

The concentration overpotential, which is calculated with Eq. (7), accounts for the fact that the ideal voltage should be calculated using the species partial pressures in the proximity of the reaction site (i.e., $p_{H_2,r}$, $p_{H_{2}O,r}$, and $p_{O_2,r}$), here assumed located at the electrode-electrolyte interface. Assuming that the total pressure is constant throughout the electrodes, the partial pressures in Eq. (7) can be replaced by molar fractions.

$${\eta }_{conc}={\displaystyle \frac{R·T_{PEN}}{2·F}}\mathit{ln}\left({\displaystyle \frac{ p_{H_2}}{p_{H_2,r}}}·{\displaystyle \frac{ p_{H_{2}O,r}}{p_{H_{2}O}}}·{\displaystyle \frac{ p_{O_2}^{1/2}}{p_{O_2,r}^{1/2}}}\right)$$

(7)

The molar fractions of H₂, H₂O, and O₂ at the electrode-electrolyte interfaces are calculated using Eqs. (8), (9), and (10) [10]. The coefficient $l_{act}/w_{ch}$ is included to account for the fact that the reference surface for the diffusion process is lower than the active area.

$$x_{H_2,r}=x_{H_2}-{\displaystyle \frac{i_{O^{2-}}·R·T_{PEN}·t_{fe}}{2·F·p·D_{H_2,p}}}·{\displaystyle \frac{l_{act}}{w_{ch}}}$$

(8)

$$x_{H_{2}O,r}=x_{H_{2}O}+{\displaystyle \frac{i_{O^{2-}}·R·T_{PEN}·t_{fe}}{2·F·p·D_{H_{2}O,p}}}·{\displaystyle \frac{l_{act}}{w_{ch}}}$$

(9)

$$x_{O_2,r}=1-\left(1-x_{O_2}\right)·\mathit{exp}\left({\displaystyle \frac{i_{O^{2-}}·R·T_{PEN}·t_{ae}}{4·F·p·D_{O_2,p}}}·{\displaystyle \frac{l_{act}}{w_{ch}}}\right)$$

(10)

The binary diffusion coefficients $D_{ij}$ are calculated according to the Fuller method, which is valid for pressures below 35 bar [11]. The effective molecular diffusion coefficients in the gas mixture are then calculated with Eq. (11), which assumes that the species $i$ diffuses in subsequent gas layers, where each layer $j$ has a thickness proportional to $x_j$ and a binary diffusion coefficient $D_{ij}$. The effective Knudsen diffusion coefficient is calculated with Eq. (12), and the overall diffusion coefficient in the porous electrode $D_{i,p}$ is calculated using Eq. (13), which assumes that molecular and Knudsen diffusion occur in series. The parameter $r_p$ is the average pore radius, and $M{M}_i$ is the molar mass of species $i$.

$$D_{i,mix}^e={\displaystyle \frac{\epsilon }{\tau }}·\left(1-x_i\right)·{\left(\sum _{j\ne i}^{NS}{\displaystyle \frac{x_j}{D_{ij}}}\right)}^{-1}$$

(11)

$$D_{K,i}^e={\displaystyle \frac{\epsilon }{\tau }}·{\displaystyle \frac{2}{3}}·r_p·\sqrt{{\displaystyle \frac{8·R·T_{PEN}}{\pi ·M{M}_i}}}$$

(12)

$$D_{i,p}={\left({\displaystyle \frac{1}{D_{K,i}^e}}+{\displaystyle \frac{1}{D_{i,mix}^e}}\right)}^{-1}$$

(13)

The ohmic loss is calculated with Eq. (14), where the main contribution is due to the oxygen ion conductivity ($\sigma$) along the electrolyte thickness ($t_{ely}$), and $r_{contact}$ is a calibration parameter that can be used to fit the data, representing an additional electric contact resistance which includes the effect of the interconnects (material electric resistance and contact resistance) and other contributions that are not (or cannot be) explicitly considered in the model.

$${\eta }_{ohm}=i_{O^{2-}}·\left({\displaystyle \frac{t_{ely}}{\sigma }}+r_{contact}\right)$$

(14)

$$\sigma ={\displaystyle \frac{{\sigma }_0}{T_{PEN}}}·\mathit{exp}\left(-{\displaystyle \frac{E_{act,\sigma }}{R·T_{PEN}}}\right)$$

(15)

The activation overpotentials in the fuel electrode (${\eta }_{act,fe}$) and air electrode (${\eta }_{act,ae}$) are calculated using Butler-Volmer equations (16) and (18), and their sum is equal to the overall activation overpotential (${\eta }_{act}$). The form of the Butler-Volmer equations is taken from [4], and both $k_{HOR}$ and $k_{ORR}$ are referred to the active area of the cell.

$$i_{O^{2-}}=i_{0,fe}·\left[\mathit{exp}\left({\alpha }_{fe}{\displaystyle \frac{2·F·{\eta }_{act,fe}}{R·T_{PEN}}}\right)-\mathit{exp}\left(-\left(1-{\alpha }_{fe}\right) {\displaystyle \frac{2·F·{\eta }_{act,fe}}{R·T_{PEN}}}\right)\right]$$

(16)

$$i_{0,fe}=k_{HOR}·p_{H_2,r}^a·p_{H_{2}O,r}^b·\mathit{exp}\left(-{\displaystyle \frac{E_{act,fe}}{R·T_{PEN}}}\right)$$

(17)

$$i_{O^{2-}}=i_{0,ae}·\left[\mathit{exp}\left({\alpha }_{ae}{\displaystyle \frac{2·F·{\eta }_{act,ae}}{R·T_{PEN}}}\right)-\mathit{exp}\left(-(1-{\alpha }_{ae}){\displaystyle \frac{2·F·{\eta }_{act,ae}}{R·T_{PEN}}}\right)\right]$$

(18)

$$i_{0,ae}=k_{ORR}·p_{O_2,r}^c·\mathit{exp}\left(-{\displaystyle \frac{E_{act,ae}}{R·T_{PEN}}}\right)$$

(19)

The mass balance equation for each species $i$ can be written in differential form as shown in Equation (20), accounting for $NR$ possible chemical or electrochemical reactions and the stoichiometric coefficient ${\nu }_{ij}$ of species $i$ in reaction $j$. The reaction rate $r_j$ (mol s^-1 m^-2) is specific to the active area of the cell. The sum of the HOR and the ORR can be considered as a single overall reaction whose reaction rate is calculated as in Eq. (21), with stoichiometric coefficients equal to -1, 1, and -0.5 for H₂, H₂O, and O₂, respectively.

Concerning water gas shift (WGS) and methane steam reforming (MSR) reactions, a global reaction approach described by Eqs. (22) and (23) is used. In this work, the WGS reaction is assumed to be equilibrated throughout the channel. In particular, the forward kinetic constant $k_f^{WGS}$ is fixed to an arbitrarily large value, the partial pressures in Eq. (22) are those at the outlet of each CV, and $K_{eq}^{WGS}$ is calculated using the fuel temperature at the outlet of each CV. In this way, the species partial pressures are guaranteed to satisfy the WGS equilibrium condition throughout the channel. Assuming that the inlet fuel composition is already in equilibrium, which is typically the case for pre-reformed gas mixtures, using the fuel temperature to calculate $K_{eq}^{WGS}$ also allows to avoid a step-wise change in composition that would arise in case the PEN temperature was used.

Regarding the MSR reaction, the kinetic model reported by Timmermann et al. is selected [12]. This model is valid in the range 600 °C-750 °C, which is in line with the operating temperature of modern SOFCs; the temperature at cell outlet might be even larger, but methane is typically consumed near the inlet section of the cell. The pre-exponential factor appearing in the kinetic constant $k_f^{MSR}$, which is equal to 1483 mol s^-1 m^-2 in the original reference, is scaled by a factor 1.73 to refer to the active area instead of the surface touched by the gas. The scaling factor is derived from the channel width ($w_{ch}$) and interconnect thickness ($t_{int}$) stated in ref. [12], equal to 1.5 mm and 0.55 mm, respectively. Note that both $K_{eq}^{MSR}$ and $k_f^{MSR}$ are calculated using the local PEN temperature.

$${\displaystyle \frac{1}{l_{act}}}{\displaystyle \frac{d{\dot{n}}_i}{dx}}=\sum _j^{NR}{r}_j·{\nu }_{ij}$$

(20)

$$r_{HOR+ORR}={\displaystyle \frac{i_{O^{2-}}}{2·F}}$$

(21)

$$r_{WGS}=k_f^{WGS}·p_{CO}·p_{H_{2}O}·\left(1-{\displaystyle \frac{p_{H_2}·p_{C{O}_2}}{K_{eq}^{WGS}·p_{CO}·p_{H_{2}O}}}\right)$$

(22)

$$r_{MSR}=k_f^{MSR}·p_{C{H}_4}·\left(1-{\displaystyle \frac{p_{H_2}^3·p_{CO}}{K_{eq}^{MSR}·p_{C{H}_4}·p_{H_{2}O}}}\right)$$

(23)

$$k_f^{MSR}=856·exp\left(-{\displaystyle \frac{61000}{R·T_{PEN}}}\right)$$

(24)

Equations (24)-(28) represent the energy balances for the fuel channel, air channel, PEN assembly, fuel-side interconnect, and air-side interconnect, respectively. The energy exchanges between gas and solid parts are further detailed in Table 2. The left-hand side of Eqs. (24) and (25) represents the variation of enthalpy flow along the axial coordinate, where ${\dot{n}}_f$ and ${\dot{n}}_a$ are the overall molar flow rate at the fuel and air side, respectively, and the specific enthalpy, which is calculated using Peng-Robinson correlations imported from Aspen Plus^®, is a function of the local gas composition and temperature. The left-hand side of Eqs. (26), (27), and (28) accounts for the axial conduction of the solid parts. A heat loss term $q_{loss}$, expressed in W m^-2, is also included in Eqs. (28) and (29), and it is specific to the interconnects surfaces facing adjacent cells. All other external surfaces of the channel are assumed to be adiabatic.

$${\displaystyle \frac{d({\dot{n}}_f·h_f)}{dx}}={\dot{Q}}_{f-PEN}+{\dot{H}}_{f-PEN}+{\dot{Q}}_{f-in{t}_f}$$

(25)

$${\displaystyle \frac{d({\dot{n}}_a·h_a)}{dx}}={\dot{Q}}_{a-PEN}+{\dot{H}}_{a-PEN}+{\dot{Q}}_{a-in{t}_a}$$

(26)

$$A_{PEN}·k_{PEN}·{\displaystyle \frac{d^2{T}_{PEN}}{d{x}^2}}={\dot{Q}}_{f-PEN}+{\dot{Q}}_{a-PEN}+{\dot{Q}}_{PEN-in{t}_f}+{\dot{Q}}_{PEN-in{t}_a}+{\dot{H}}_{f-PEN}+{\dot{H}}_{a-PEN}+l_{act}·i_{O^{2-}}·V_{cell}$$

(27)

$$A_{int}·k_{int}·{\displaystyle \frac{d^2{T}_{in{t}_f}}{d{x}^2}}={\dot{Q}}_{f-in{t}_f}-{\dot{Q}}_{PEN-in{t}_f}+q_{loss}·l_{act}$$

(28)

$$A_{int}·k_{int}·{\displaystyle \frac{d^2{T}_{in{t}_a}}{d{x}^2}}={\dot{Q}}_{a-in{t}_a}-{\dot{Q}}_{PEN-in{t}_a}+q_{loss}·l_{act}$$

(29)

The local convective heat transfer coefficients ($h_{conv}$) for the fuel and air streams are calculated from the local gas thermal conductivity and the hydraulic diameter of the channels, and assuming constant Nusselt numbers. The PEN thermal conductivity is calculated as shown in Eq. (30).

$$k_{PEN}={\displaystyle \frac{k_{fe}·A_{fe}+k_{ae}·A_{ae}+k_{ely}·A_{ely}}{A_{PEN}}}$$

(30)

3. Results and Discussion

3.1. Model Calibration and Validation

The experimental data on commercial 5 x 5 cm² (4 x 4 cm² active area) cells, reported by Neri et al. [4], is used to validate the model. The cell is manufactured by Elcogen and it is composed by a thick Ni-YSZ composite electrode (400 μm), a thin YSZ electrolyte (1.5 μm), a GDC (Ce_0.9Gd_0.1O_2-δ) barrier layer (1.6 μm), and a LSC (La_0.6Sr_0.4CoO_3-δ) single-phase cathode (15 μm). The experimental polarization curves used for the model validation cover a wide range of operating conditions:

• 7% humidified fuel gas mixtures with 21%-93% H₂ fraction and N₂ balance at 750 °C;
• 50% H₂ fuel gas mixtures with 10%-50% steam content and N₂ balance at 750 °C;
• 7% humidified fuel gas mixture with 93% H₂ fraction at 550 °C-700 °C.

A large excess of air (assumed composition is 21% O₂ and 79% N₂) is always used at the cathode side of the cell. Note that the limiting current density is approached when the H₂ fraction is low, allowing to evaluate the model performance at large fuel utilization factors typical of real applications. More detailed information on the cells, the experimental setup, and the experimental procedures are available in ref. [4].

Since the cell was placed in a furnace with a fixed setpoint temperature, the temperature distribution is assumed uniform throughout the channel length for all gas and solid parts. As demonstrated by Neri et al., this hypothesis can be justified by the inconsistent results stemmed from the assumption of adiabaticity, and the large thermal conductivity of the nickel current collector, which efficiently dissipates the heat produced by electrochemical reactions.

Table 3 summarizes the main parameters used for model validation. Most of the values are derived from ref. [4], while several parameters are calibrated. The ohmic parameters ${\sigma }_0$ and $E_{act,\sigma }$ are calibrated from EIS data shown in ref. [4]; note that the contact resistance grew significantly as a consequence of a blackout (15 min) when passing from experiments at low temperature to 750 °C, therefore, two values of ${\sigma }_0$ are calculated (the blackout only affected the ohmic resistance of the cell). The remaining 8 parameters are calibrated using the polarization curves, and include the activation loss parameters, the anode tortuosity, and the inlet fuel flow rate. Note that there is uncertainty about the fuel flow rate that actually reaches the cell due to leakages on the fuel pathway and in the fuel distributor (the experimental setup avoids using sealings, which may damage the cells during disassembling), which justifies its inclusion in the set of calibrated variables. The calibrated inlet fuel flow rate is equal to 5.486 Nml min^-1 cm^-2, which is similar to the 6.25 Nml min^-1 cm^-2 value indicated in ref. [4].

Figure 4 shows the experimental polarization curves and the model predictions for different H₂ and H₂O concentrations (panels a and b), and different temperatures (panel c). At each cell voltage, the average current density is calculated by the model with Eq. (31).

$$i_{av}={\displaystyle \frac{1}{L_{ch}}}·{\int }_0^{L_{ch}}{i}_{O^{2-}}dx$$

(31)

Considering the wide range of operating conditions investigated in terms of reactants concentrations, temperature, and fuel utilization, the good matching between model and experiments demonstrates the generality of the model developed. Notably, the model accuracy is not significantly worse compared to the results shown in ref. [4], where the same set of data is described using a 1D+1D model which couples the dusty gas model with a distributed electrochemical model along the electrode thickness for a better representation of ohmic and activation overpotentials.

The measured OCV is always 6-24 mV lower compared to the theoretical value $E_{H_2}$. Therefore, the leakage loss calculated with Eq. (6) is limited. The limiting current is approached for the case with 21% H₂, as 95.6% of the available hydrogen is consumed near 0.7 V. Notably, the model correctly predicts the cell performance also in this extreme case, where concentration losses plays a major role.

Figure 5 shows the average overpotentials, calculated using Eq. (32), in different selected operating conditions. Note that since the overpotentials represent the exergy lost per unit charge (J C^-1), they are weighted by the local current produced. The oxygen concentration loss is not shown in the figure since it is negligible in all cases, and the anode concentration loss includes contributions from both H₂O and H₂ diffusion processes in the electrode.

$${\eta }_{k,av}={\displaystyle \frac{1}{i_{av}·L_{ch}}}·{\int }_0^{L_{ch}}{i}_{O^{2-}}·{\eta }_k·dx$$

(32)

Panel a shows the overpotentials for the case with 7% H₂O and 21% H₂ (N₂ balance) at 750 °C, and suggests that the concentration loss always dictates the cell performance. Although it is not shown, most of the anode concentration loss is due to steam diffusion in the low current density region since its concentration in the channel is low compared to hydrogen. In other words, if $p_{H_{2}O}$ or $p_{H_2}$ in the channel are low, $p_{H_{2}O,r}$ or $p_{H_2,r}$ can be very different from their channel values percentage-wise, significantly increasing the concentration polarization (see Eqs. (7), (8), and (9)). The H₂ concentration polarization becomes dominant only above 125 mA cm^-2 due to the fuel depletion, and it grows exponentially at larger current densities. Since the calibrated H₂ exponent (coefficient $a$ in Table 3) is equal to 0.5, the anode activation loss grows significantly at large current densities. The anode tortuosity has been calibrated by closely matching the cell performance at low current densities due to the dominance of concentration losses in this region.

Panel b shows the overpotentials calculated for the case with 50% H₂ and 50% H₂O at 750 °C. Concentration losses are limited due to the large channel concentration of both H₂ and H₂O. Hydrogen and steam diffusion processes contribute approximately equally to the anode concentration loss, since $p_{H_{2}O}$ is large even at low current densities, and the H₂ utilization factor is limited in the high current region (78% at 0.7 V). Anode activation and ohmic overpotentials have the greatest impact on the cell performance.

Panel c shows the polarization losses for the case with 93% H₂ and 7% H₂O at 550 °C. The concentration overpotential gives the smallest contribution to the cell polarization due to the relatively weak dependence of diffusion processes on temperature. Contrarily, the cathode activation overpotential grows significantly, being the most important contributor together with the anode activation loss.

In general, the trends discussed and the overpotentials calculated are similar to those shown in ref. [4], suggesting that both models can be used for the simulation of solid oxide fuel cells.

Note that there are instances where the sum of the molar fractions of steam ($x_{H_{2}O,r}$) and hydrogen ($x_{H_2,r}$) in the reaction site is above 1 (e.g., in the case with 50% H₂ and 50% H₂O at high current density), which could raise concerns on the modified Fick’s model used (Eqs. (8) and (9)) compared to the rigorous dusty gas model approach employed in more sophisticated SOFC models. Nevertheless, the model remains consistent since $x_{H_{2}O,r}$ and $x_{H_2,r}$ shall not be intended as accurate estimations of the molar fractions in the reaction site, but only be used to calculate the partial pressures $p_{H_{2}O,r}$ and $p_{H_2,r}$. The sum of the partial pressures at the reaction site is indeed allowed to exceed the total pressure in the channel (i.e., the total pressure in the electrode can be larger compared to the channel value), and their values are in good agreement with those found with the DGM model, as discussed with more detail in the Appendix A.

3.2. Adiabatic Model with Reformate Fuel

In order to test the adiabatic model (which also includes energy balances) in a condition representative of a real application, the operating conditions calculated in ref. [2] are considered. In particular, Table 4 shows the operating conditions of an SOFC integrated in a hybrid power generation system which also includes a bottoming steam cycle.

The global heat loss assumption is used to calculate $q_{loss}$ (see Eqs. (28) and (29)), which is equal to 40 W m^-2. The investigated operating conditions are peculiar because of the low inlet fuel temperature equal to 521 °C, which might cause significant thermal gradients near the SOFC entrance. All parameters shown in Table 3 are used for the simulation, with some exceptions:

• The inlet fuel and air mass flow rates at channel inlet are derived to match the fuel utilization factor and the outlet cell temperature stated in Table 4;
• The channel length is set to 9 cm, which is a value in line with applicative cells, the channel width is fixed to 3 mm for the same reason;

The parameter ${\sigma }_0$

• is fixed to 464167 S K m^-1 (used for the simulations in Figure 4c).

The thermal conductivity of the anode, cathode, and electrolyte ($k_{fe}$, $k_{ae}$, $k_{ely}$) is fixed to 2 W m^-1 K^-1, while the interconnect conductivity ($k_{int}$) is equal to 20 W m^-1 K^-1. The Nusselt number is fixed to 3.6 and 5.0 in the fuel and air channels, respectively [3].

Figure 6 shows the results of the adiabatic simulation. Panel a shows the temperature profiles calculated for the PEN, interconnects, and gas streams. Although the fuel inlet temperature is equal to 521 °C, the minimum value of the temperature axis is fixed to 720 °C for clarity.

The fuel reaches a temperature close to that of the air stream almost instantly, which is due to its relatively low thermal inertia (the inlet air molar flow rate is 5.42 times larger). The PEN temperature near the channel inlet seems to be the only one slightly affected by the low fuel temperature; this is attributed to its relatively large resistance to axial conduction, since the temperature of the fuel interconnect is higher despite having a larger contact surface with the fuel stream. The PEN temperature remains large due to the heat exchange with the air stream and the interconnects, but there is a very small region where the PEN temperature gradient reaches 4 °C mm^-1, which is a large value if compared with the one calculated in the middle of the channel, equal to 0.5 °C mm^-1.

Panel b shows that the current density reaches a maximum value near the channel entrance, which corresponds to the H₂ concentration peak shown in panel c. After this point, the current density decreases due to H₂ depletion and H₂O formation, despite the increasing temperature trend. Panel c shows that methane is rapidly consumed producing H₂, overcompensating the H₂ consumed by electrochemical reactions up to the peak already mentioned. The existence of a H₂ concentration peak near the channel inlet is typical of SOFCs operating with reformate, as also demonstrated in other modelling works [3,8].

Panel d shows the effect of grid refinement on the PEN temperature distribution. Since the PEN temperature frequently appears both in the electrochemical, chemical, and energy balance models, it is considered representative of the status of all other calculated variables. The sensitivity analysis suggests that dividing the channel into 100 control volumes is sufficient to achieve the grid independence.

Overall, the model developed correctly simulates the most relevant physical processes occurring within a SOFC, elucidating the internal operating conditions like the temperature, current density, and gas composition profiles.

It shall be noted that the model is also flexible by the point of view of the cell operating mode, since its extension to the case of electrolysis operation (not sown here for brevity) is straightforward and does not require any mathematical modification; in the electrolysis case, the cell voltage assigned in input is larger than the Nernst voltage, resulting in a negative current density calculated by the electrochemical model.

4. Conclusions

This work presented the development and validation of a 1D, co-flow, finite-volume model for the simulation of planar SOFCs. The model is developed to facilitate the SOFC simulation in wider system and process simulations in Aspen Plus^®, which provides built-in functions for the calculation of physical and thermodynamic properties of gases.

The model allows to simulate the most relevant physical processes occurring within an SOFC and to investigate its internal operating conditions in terms of temperature, current density, and gas composition profiles. The model is calibrated and validated using experimental SOFC polarization curves covering a wide range of operating conditions in terms of H₂ and H₂O molar fraction in the fuel, temperature, and fuel utilization factor. The discussion demonstrates that the dataset can be described by the 1D model over a wide range of operating conditions, drastically reducing complexity and computational time compared to more complex multi-dimensional models, facilitating the grid convergence, while retaining a good accuracy. The same model can also be used in the case of electrolysis operation without substantial modifications.