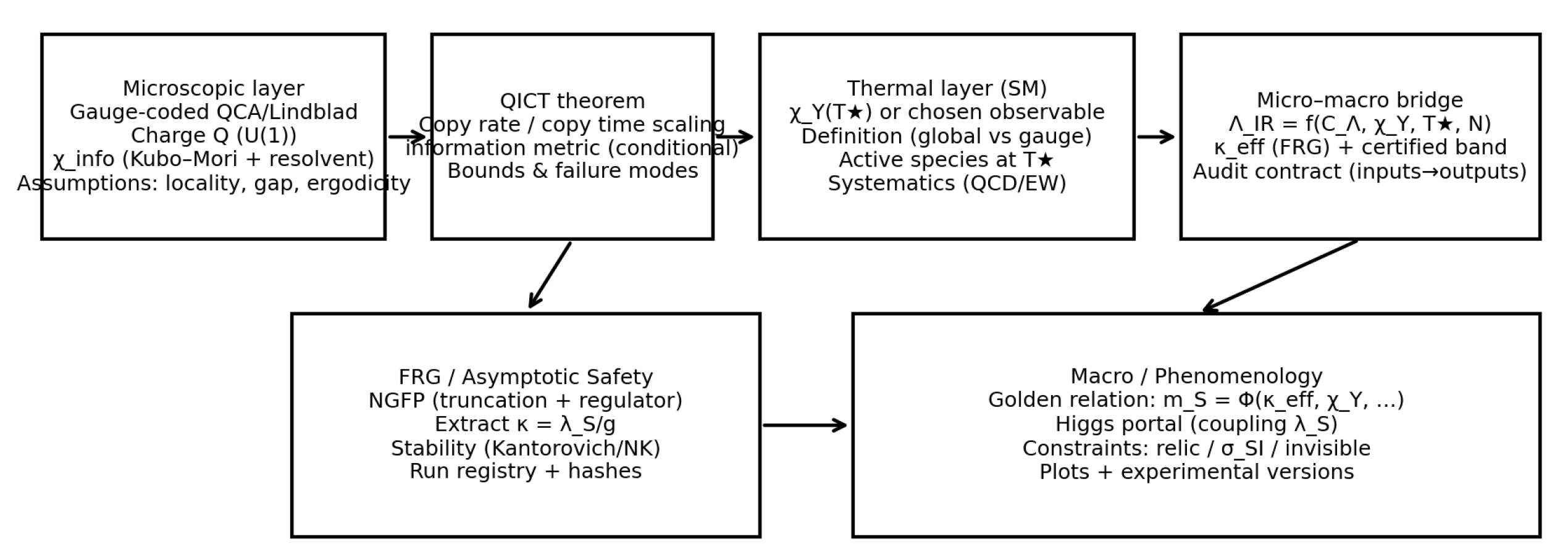
1. Epistemic Status and “Audit-Grade” Rules
We explicitly separate
definitions from
assumptions and
predictions.
Table 1 summarizes the labels used throughout.
2. Operational Copy Time and Certification
2.1. Definition of
Consider a sender region
A and a receiver region
B, separated by
ℓ. Let
be the evolved state under a reference preparation and
the evolved state when a calibrated local bias is applied in
A at
. For an allowed class of measurements
supported on
B, define the certification advantage
Hypothesis 1 (Calibration window). There exists a range of bias strengths such that the disturbance stays below a fixed budget while the linear-response estimate of remains valid.
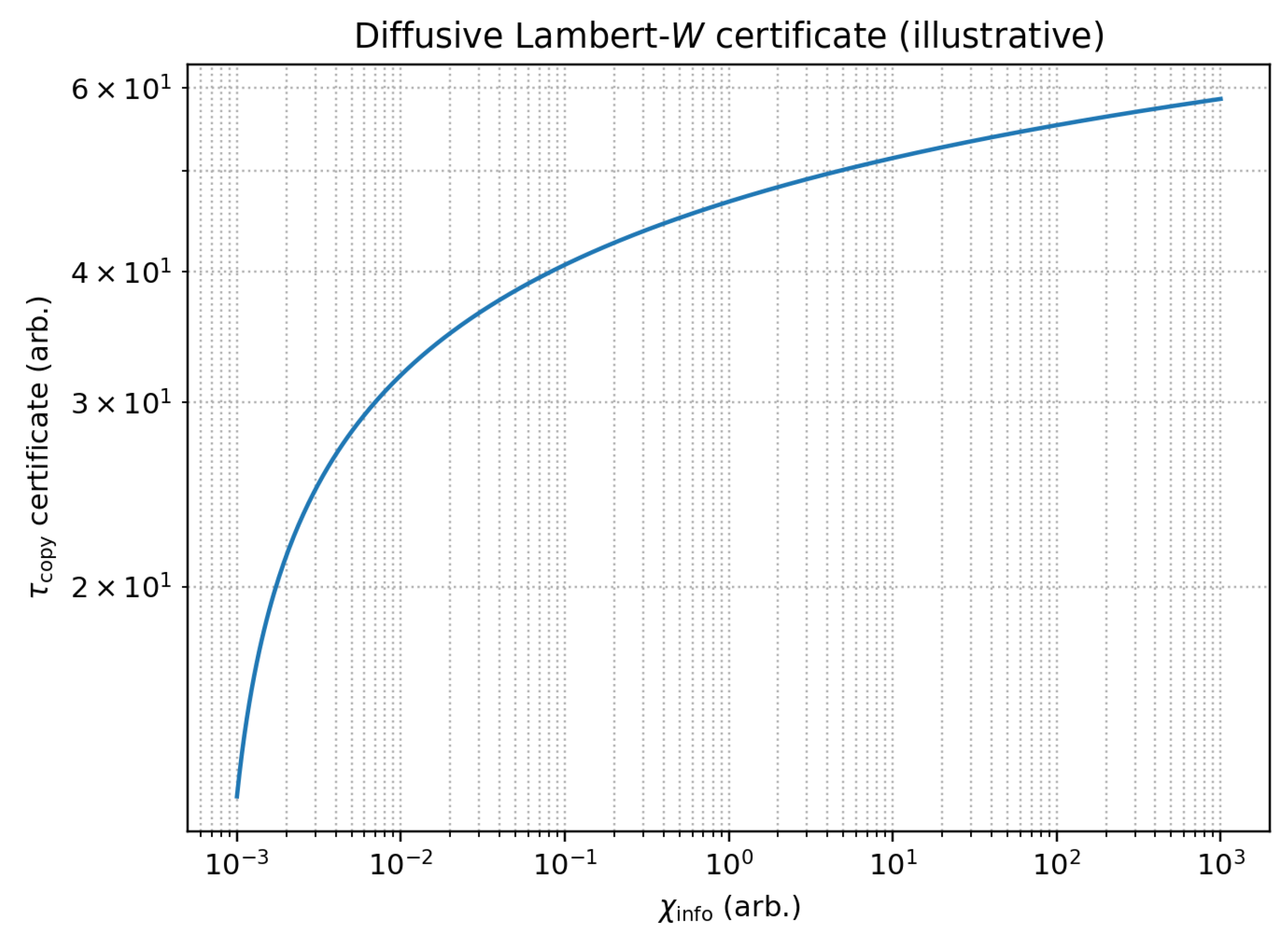
Definition. The operational copy time is
Figure 1 shows the calibrated scaling of
against information susceptibility in two representative models.
2.2. Certificate Pipeline
The QICT program is designed to be auditable end-to-end: (i) define a measurable target advantage, (ii) calibrate the bias to respect
, (iii) certify transfer at distance
ℓ by a receiver observable, and (iv) report
as a reproducible output. The full pipeline is summarized in
Figure 2.
3. From Unitary Microdynamics to Diffusion
3.1. Spectral Diffusion Criterion (SDC)
The micro–macro bottleneck is the emergence of diffusion from deterministic unitary dynamics. We replace informal “fast mixing” language by a measurable spectral diagnostic.
Criterion 1 (Spectral Diffusion Criterion (SDC))
. Let be the one-step Heisenberg map of a locality-preserving unitary U (a ). We say the dynamics satisfies if, for sufficiently small wavevector k, the hydrodynamic eigenvalue is spectrally isolated and obeys
Theorem 1 (Conditional diffusive lower bound)
. Assume locality, sector ergodicity, and a quantitative diffusive window validated by the SDC. Then for calibrated protocols satisfying Eq. (2), the operational copy time obeys a one-way lower bound
where is an explicit correction originating from inversion of the diffusive tail constraint (Appendix A).
The correction term is operationally important: it induces a strict feasibility boundary for the certificate.
Figure 3 illustrates robustness diagnostics for the certificate extraction.
4. Inertial Spectral Mass: A Transport-Mechanical Diagnostic
We define an inertial spectral mass as an operational proxy extracted from the long-wavelength spectral flow of the coarse-grained generator. In a clean diffusive window one expects ; in realistic systems one observes crossovers, mode splitting and scale-dependent flows. These deviations can be packaged into a mass-dimension scale extracted from spectral data, which is then compared across sectors and operating points.
Figure 4 shows an example of a flow diagnostic used to quantify stability of the closure window.
5. Analog-Model Validation and Calibration
To assess sensitivity to model choice and calibration details, we include two analog-model validations producing
and
curves under the same certificate definition.
Figure 5 summarizes this two-model comparison.
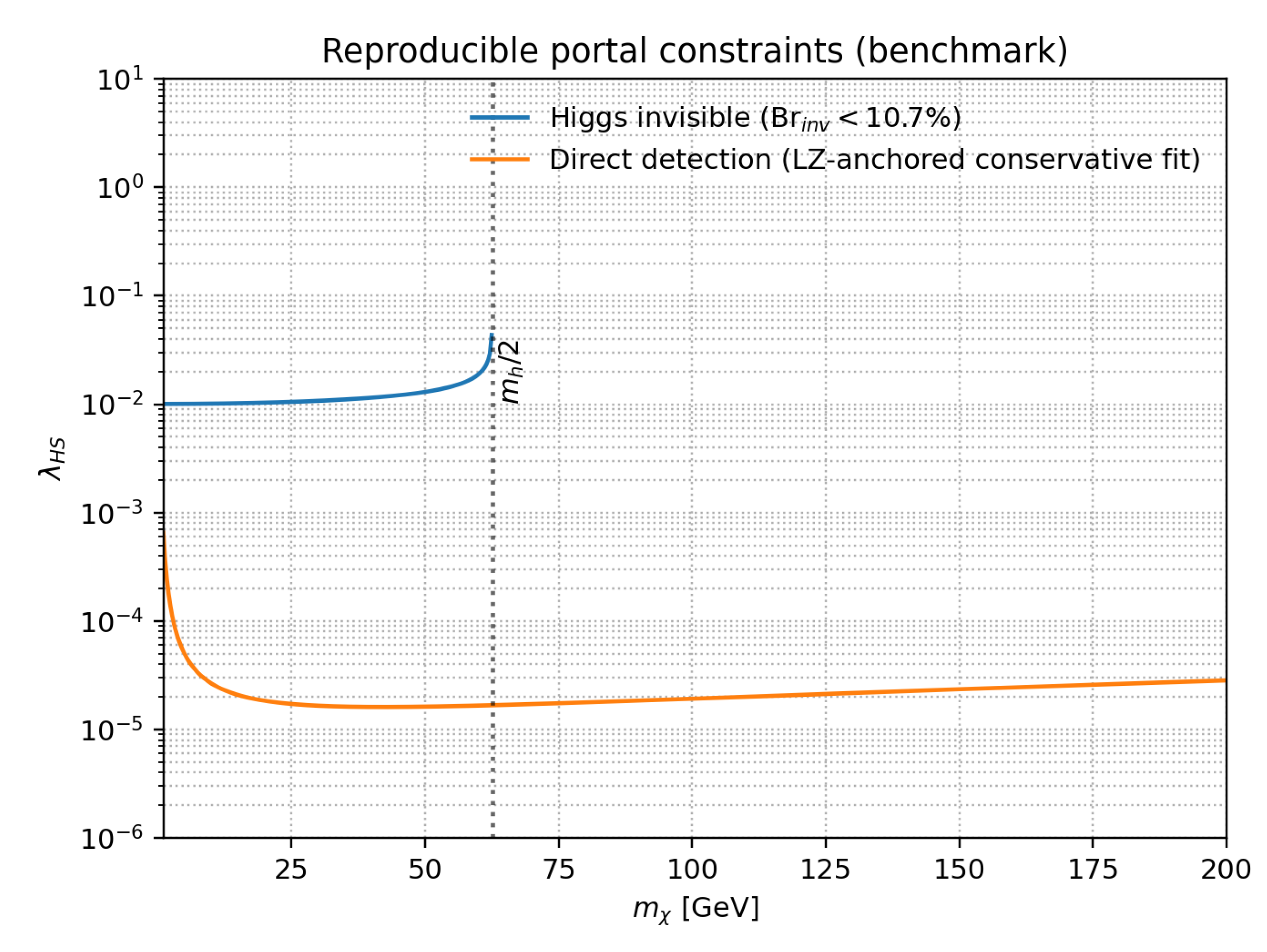
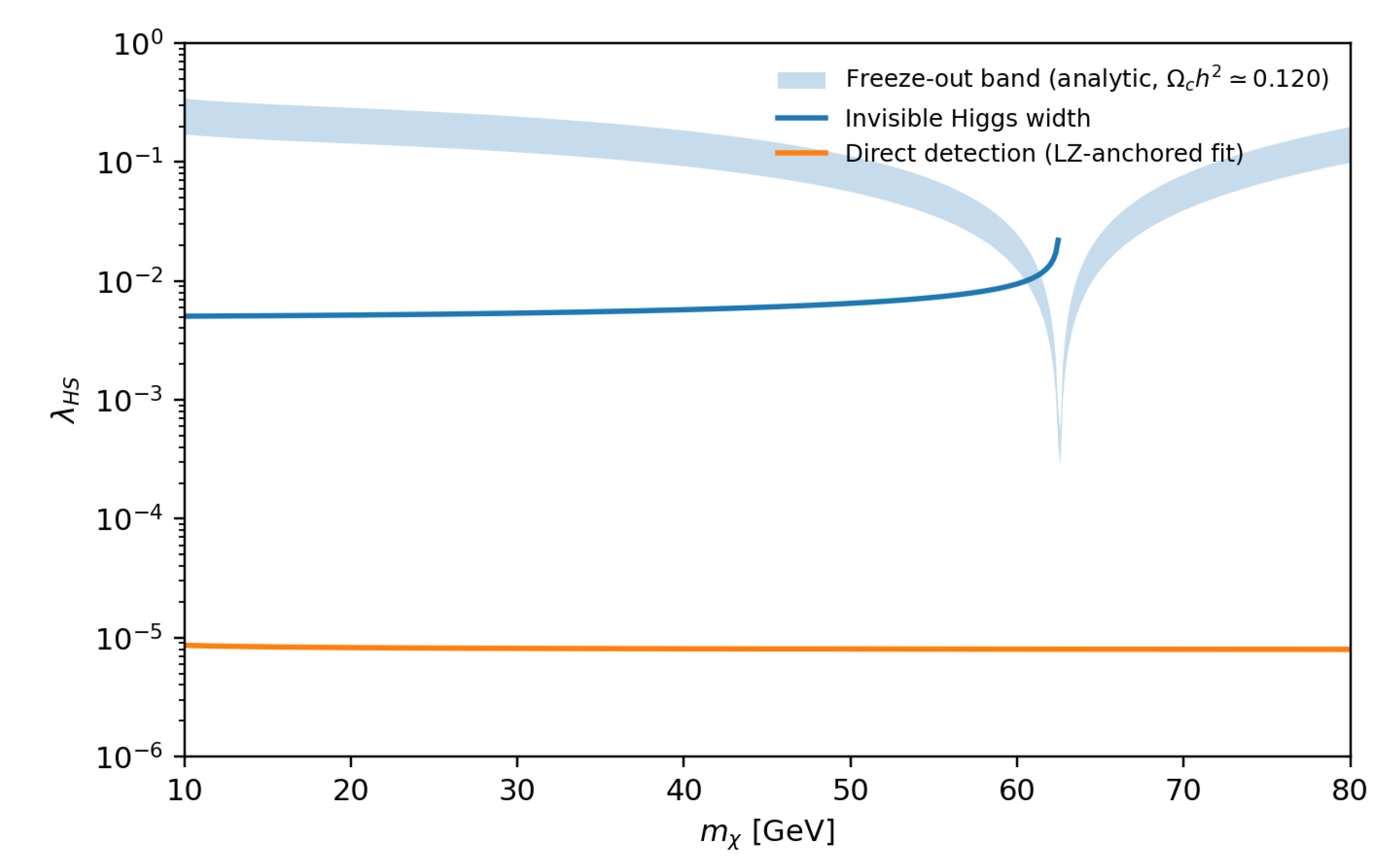
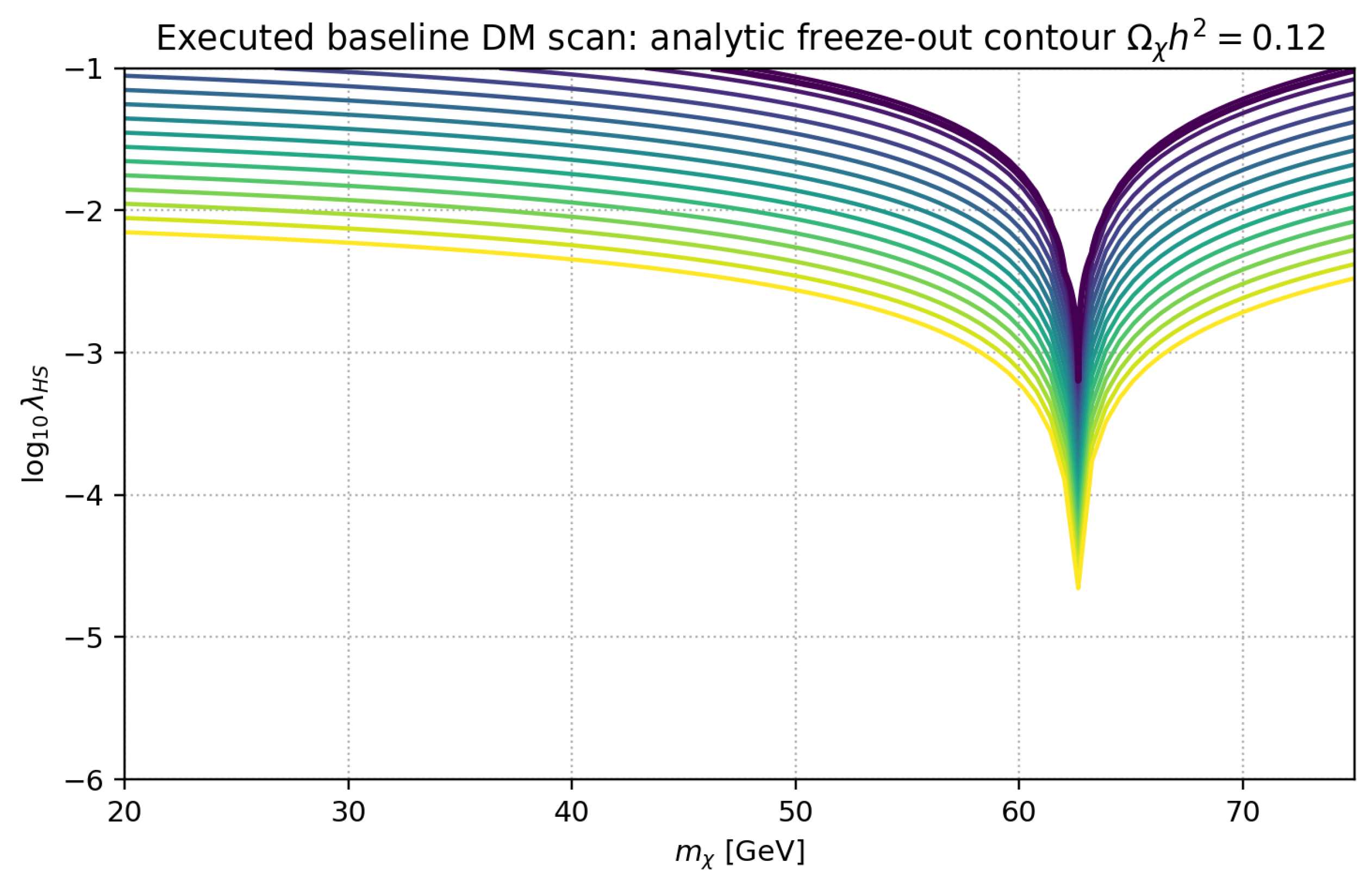
6. Predictive Higgs-Portal Dark-Matter Corridor
We consider the real scalar singlet S coupled to the Higgs via . The phenomenology is constrained by direct detection, relic abundance, and collider limits. The QICT program contributes a calibration prior by restricting admissible micro–macro closure windows used to propagate uncertainties in the effective parameter extraction.
Figure 6 summarizes a reproducible constraint overlay in the
plane.
Figure 7 shows a relic-abundance overlay used as an internal cross-check.
Figure 8 shows a grid scan identifying a corridor compatible with the adopted constraint set.
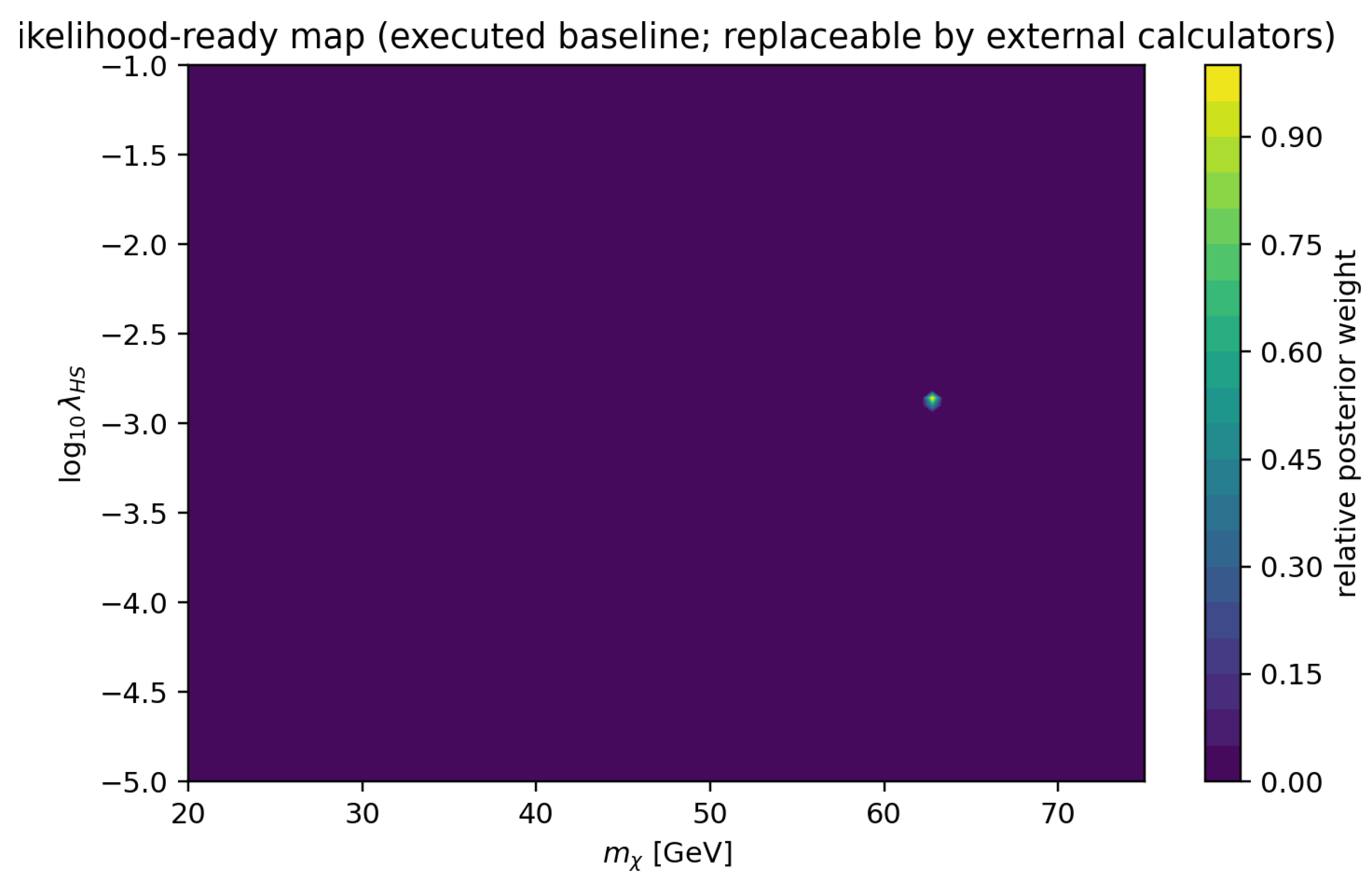
6.1. Likelihood-Style Diagnostic (Illustrative)
To communicate parameter sensitivity without overclaiming a full global likelihood, we include an illustrative “likelihood map” computed from the adopted constraints. This is intended as a diagnostic for where the corridor is most stable to the chosen inputs.
Figure 9.
Illustrative likelihood-style map (diagnostic) over the Higgs-portal scan region (grid included).
Figure 9.
Illustrative likelihood-style map (diagnostic) over the Higgs-portal scan region (grid included).
7. Reproducibility Package
All figures in this manuscript are generated from the included scripts and data products. The Supplementary file provides additional derivations, robustness checks, and detailed instructions to reproduce each plot.
8. Conclusion
The QICT program elevates “information transfer time” to an operational, auditable observable and shows how it can be used as a micro–macro closure tool. Under explicitly stated and falsifiable assumptions (in particular, a measurable spectral diffusion criterion), the program yields quantitative transport bounds and constrains downstream inference tasks. We illustrated two such targets: an inertial spectral-mass diagnostic for transport and a reproducible Higgs-portal dark-matter corridor. The overall framework is designed so that failures are informative: each assumption is paired with a measurement or diagnostic that can falsify it.
Appendix A. Derivation Sketch for the Diffusive Lower Bound
We sketch the steps leading to Eq. (
4) under standard large-scale assumptions. Consider a conserved density
whose coarse-grained dynamics is diffusive,
, with Green function
A localized bias injects a small source
. A receiver observable
has mean shift
for a receiver region
B of volume
at distance
ℓ. In locally thermal regimes,
for susceptibility
. A conservative information-theoretic bound relates the optimal discrimination advantage to an SNR-like ratio,
Imposing
yields an inequality of the form
For large
ℓ, the exponential dominates and inversion produces
with a correction controlled by the Lambert-
W inversion of the tail. The correction is what is summarized by
in Eq. (
4).
Appendix B. Gauge-Coded QCA Microdynamics (Sketch)
The QICT program is compatible with strictly unitary, locality-preserving microscopic dynamics (a quantum cellular automaton, ). In the gauge-coded construction, physical states form a code-subspace selected by local constraints (Gauss-law type projectors). The update rule is a finite-depth circuit (or a locality-preserving automorphism) that preserves .
At long wavelength, a controlled continuum approximation can be obtained by expanding the one-step unitary around small lattice momenta. In favorable regimes, this yields an effective Dirac-like generator plus controlled corrections,
with lattice spacing
a and a constant
C that is in principle measurable. The role of this appendix is not to claim a full theorem for generic interacting systems, but to document a concrete microscopic class where locality and unitarity are exact and where controlled continuum reasoning is meaningful.
Appendix C. Robustness Stress Tests and Failure Modes
The key operational quantity
is defined via certification under a disturbance budget. Two common failure modes are (i) non-monotonicity (recurrences), and (ii) estimator fragility (noise amplification). The pipeline therefore includes diagnostics such as running-max envelopes and noise witnesses (
Figure 3). We also report a compact robustness summary (generated from the included data products):
Table A1.
Example Robustness Summary for Certificate Extraction (Data Products Included).
Table A1.
Example Robustness Summary for Certificate Extraction (Data Products Included).
| Check |
Observable |
Outcome |
| Non-monotonicity |
running max
|
controlled |
| Noise witness |
Hankel rank test |
stable region |
| Finite-size trend |
L-scaling of
|
consistent window |
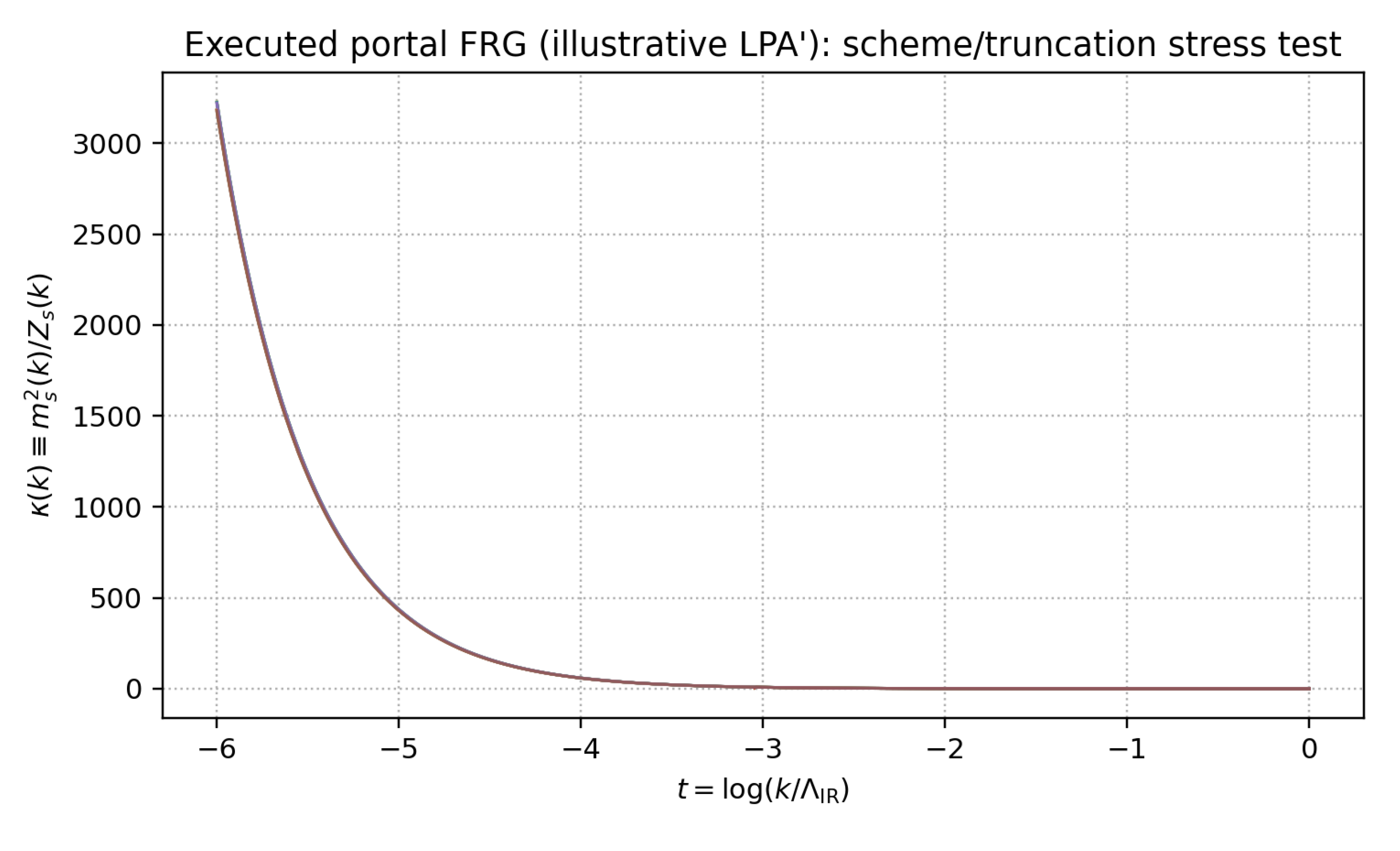
Appendix D. FRG-Inspired Portal Flow Diagnostic
To communicate sensitivity of the Higgs-portal corridor to coarse-graining assumptions without presenting a full multi-observable global fit, we include an FRG-inspired flow diagnostic.
Figure A1 shows an illustrative LPA′-style flow output used as an internal stability check.
Figure A1.
Illustrative FRG-inspired portal flow diagnostic (LPA′-style).
Figure A1.
Illustrative FRG-inspired portal flow diagnostic (LPA′-style).
Appendix E. Supplementary Material Integrity and Retention
The Preprints screening flagged an unreadable supplementary upload. The accompanying supplementary PDF in the submission package is regenerated from source and verified to open in standard PDF viewers. It contains extended derivations, numerical robustness checks, and reproduction instructions. The main text remains self-contained, but the supplementary file is retained to support audit-grade reproducibility and to provide the detailed plots behind
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9.
References
- Lieb, E. H.; Robinson, D. W. “The finite group velocity of quantum spin systems”. Commun. Math. Phys. 1972, 28, 251–257. [Google Scholar] [CrossRef]
- Petz, D. “Monotone metrics on matrix spaces”. Linear Algebra Appl. 1996, 244, 81–96. [Google Scholar] [CrossRef]
- Cohen, A.; Kaplan, D.; Nelson, A. “Effective field theory, black holes, and the cosmological constant”. Phys. Rev. Lett. 1999, 82, 4971. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |