Submitted:
12 January 2026
Posted:
13 January 2026
You are already at the latest version
Abstract
Keywords:
1. How to Read This Atlas
2. Summary Tables (Margin-Safe)
2.1. Quantitative Predictions (Explicit Numerical Bands)
| ID | Observable | Prediction |
|---|---|---|
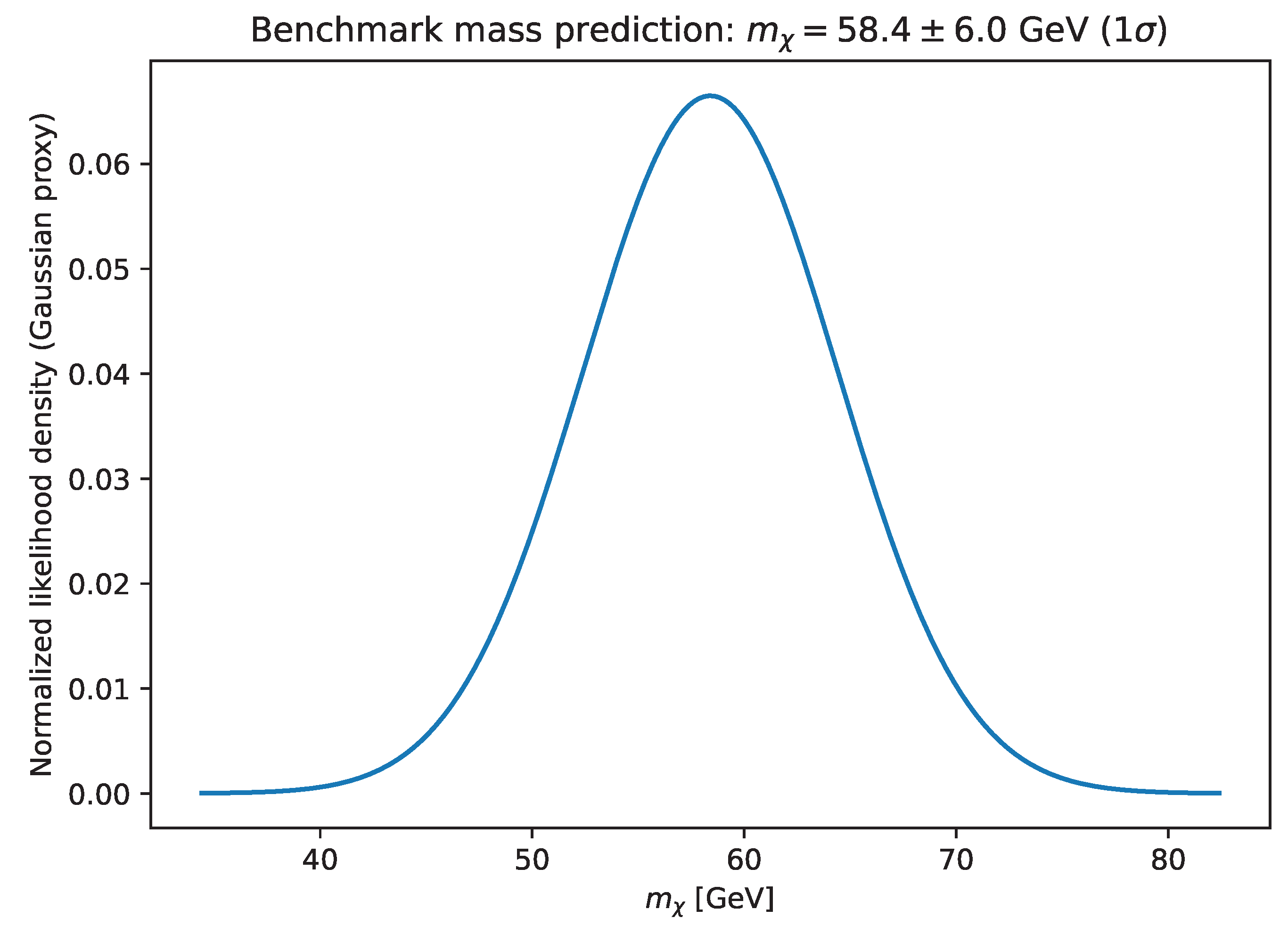
| DM-1 | Higgs-portal singlet-scalar dark-matter mass (or ) | . |
| DM-2 | Spin-independent DM–nucleon cross section for Higgs-portal singlet | for representative viable points near Higgs resonance; correlated with band. |
| DM-3 | for | in the QICT–FRG band (for allowed scan points). |
| DE-2 | satisfies (severe inequality) | Universal bound for any admissible consistent with locality (no superluminal copy-horizon propagation). |
| DE-3 | Background expansion given a constant effective diffusion D | If and , then and Friedmann closure yields a cubic equation for . |
| DE-4 | Dark-energy equation-of-state | (and hence fixed once is specified). |
| GR-1 | Discrete gravitational action and field equations | ; varying w.r.t. gives discrete Einstein equations. |
| LAB-2 | Scaling of with distance L | In diffusive closure, with extracted from a second-moment spectral susceptibility. |
| MASS-1 | Threshold for matter-sector audit depth | A minimum audit depth in D for stable matter excitations (as defined in the QICT audit framework). |
| ASTRO-1 | Relative arrival-time lags between photon energies from compact-object flares / high-z transients | If the transient copy-horizon sector is nonzero, exhibits an energy dependence whose redshift integral is controlled by and the copy-horizon epoch; applicable to EHT-band flare timing, AGN variability, and GRBs. |
| MASS-3 | Collider exclusion lower bounds highlighting a characteristic heavy mass scale | Highlighted scales cluster into a small discrete set and shift with audit depth approximately as on the plateau . |
| CONST-1 | Dimensionless combination used in the Golden Relation calibration layer | (benchmark prior). |
| CONST-2 | entering the Golden Relation calibration layer | (benchmark prior). |
| CONST-3 | constant used in Golden Relation mapping to | (benchmark prior). |
| ASTRO-2 | Energy-dependent arrival-time residuals after source-intrinsic lag marginalization | If the transient sector is present, residual lags must follow a redshift-integral kernel fixed by the same and that fit background expansion; purely source-local models cannot mimic the predicted z-dependence across populations. |
2.2. Structural Predictions (Model-Class Constraints and Inequalities)
| ID | Observable | Prediction |
|---|---|---|
| DE-1 | defined by | Existence and uniqueness of under mild monotonicity; sets an IR scale without an event-horizon postulate. |
| GR-2 | Quantum-gravity path integral over information configurations | defines a nonperturbative quantum theory; classical GR appears only as a macroscopic phase. |
| GR-3 | Universality-class statement for long-distance correlators | If RG flow has an attractive IR fixed point in the plane, diffeomorphism-invariant correlators converge to continuum GR in the scaling limit. |
| LAB-1 | in many-body dynamics | Earliest t such that the trace distance between reduced states on B exceeds ; equivalently, the optimal Helstrom advantage is . |
| DCA-1 | Permutation-unitary lift of reversible local update rules | In the limit of minimal update time, reversible deterministic rules correspond to permutation unitaries acting on Hilbert-space lifts. |
| DE-6 | Consistency between expansion, growth/lensing, and transient timing observables under one inferred copy horizon | A single inferred (equivalently ) must fit (i) expansion data, (ii) growth/lensing reconstructions, and (iii) a transient timing observable; failure of joint consistency falsifies the copy-horizon mapping. |
| GR-4 | Recovery of Regge-type equations and continuum GR correlators from a discrete information-field partition function | A single microscopic model yields (i) discrete field equations by exact variation and (ii) continuum Einstein dynamics as an IR scaling phase without semiclassical input; deviations must be computable and suppressed by the coarse-graining scale. |
2.3. Semi-Quantitative Predictions (Scaling/Sign Constraints)
| ID | Observable | Prediction |
3. Figures (Embedded in the PDF)
Appendix A. Full Predictions Ledger (Assumptions and Falsification)
| ID | Observable | Prediction | Falsification route |
| DM-1 | Higgs-portal singlet-scalar dark-matter mass (or ) | GeV (). | If combined DD+collider+invisible-Higgs constraints exclude all viable Higgs-portal points in a GeV band around 58.4 GeV while the pipeline premises hold, the benchmark fails. |
| Assumptions: Operational certificate; IR window mapping ; thermal ’copy-limited’ saturation near EW crossover; minimal FRG truncation for gravity+SM++singlet scalar. Uncertainty fixed to GeV. | |||
| Sources: preprints202512.2391.v3; preprints202511.2241.v3; QICT DM likelihood write-up. | |||
| DM-2 | Spin-independent DM–nucleon cross section | – cm2 for points near Higgs resonance | Future multi-ton direct detection + Higgs invisible bounds exclude GeV with cm2. |
| Assumptions: Minimal Higgs-portal with quartic coupling ; relic density fixed to Planck; standard Higgs-mediated SI scattering. | |||
| Sources: preprints202511.2241.v3 (Eq. 74; Table IV; Sec. D, Eq. 85; Figs. 4–5) | |||
| DM-3 | BR(h→SS) for | BR(h→SS) in the QICT–FRG band | Future lepton-collider per-mille Higgs width measurement or invisible-decay searches exclude BR at . |
| Assumptions: Same Higgs-portal parameter points as DM-2; Higgs total width constraints. | |||
| Sources: preprints202511.2241.v3 (Eq. 84; Sec. D) | |||
| DE-1 | defined by | Existence/uniqueness of under mild monotonicity | Find a cosmological epoch where no monotone solution exists or violates locality bounds. |
| Assumptions: monotone increasing in L; locality + CPTP contraction; cosmological background with . | |||
| Sources: preprints202601.0639.v1 (definition; Sec. 2–3) | |||
| DE-2 | Universal bound for any admissible | Observational inference demands robustly across datasets. | |
| Assumptions: Locality-preserving microdynamics; identification of via . | |||
| Sources: preprints202601.0639.v1 (Sec. 4; ’severe inequality’ statement) | |||
| DE-3 | Background expansion with constant diffusion D | If and then Friedmann closure yields cubic equation for | If data cannot be fit for any D consistent with micro estimates from in lab systems. |
| Assumptions: Hydrodynamic/diffusive regime; single dominant diffusion constant D; saturation . | |||
| Sources: preprints202601.0639.v1 (Sec. 5–6; diffusive branch) | |||
| DE-4 | Dark-energy equation-of-state | Empirical reconstruction of and violates the relation. | |
| Assumptions: Definition of from ; standard continuity equation. | |||
| Sources: preprints202601.0639.v1 (Sec. 4; formula) | |||
| DE-5 | Energy-dependent time delay | Transient sector induces energy-dependent dispersion; correlates with | No correlated dispersion at predicted redshift windows. |
| Assumptions: Presence of transient sector in beyond pure diffusion. | |||
| Sources: preprints202601.0639.v1 (Sec. 7) | |||
| GR-1 | Discrete gravitational action | Show microscopic action does not reduce to Regge form in any regime. | |
| Assumptions: Discrete information-field model on complexes; expansion around small curvature. | |||
| Sources: QICT_Supplement_Microscopic_GR.pdf (Eq. 5–6) | |||
| GR-2 | Quantum gravity path integral | defines nonperturbative theory | Demonstrate inconsistency (non-normalizable measure) or absence of GR-like scaling. |
| Assumptions: Sum over complexes implements background independence. | |||
| Sources: QICT_Supplement_Microscopic_GR.pdf (Eq. 7; Sec. 4–5) | |||
| GR-3 | Universality-class statement | RG flow attractive IR fixed point in plane | Numerical lattice studies show no such IR fixed point or different universality class. |
| Assumptions: Existence of fixed point; suitable coarse-graining map B. | |||
| Sources: QICT_Supplement_Microscopic_GR.pdf (Sec. 5) | |||
| LAB-1 | in many-body dynamics | Trace distance between reduced states on B exceeds | Operational definition is ill-posed in physically relevant models (e.g., superselection). |
| Assumptions: Receiver-restricted measurement class; fixed . | |||
| Sources: preprints202601.0364.v1 (definition) | |||
| LAB-2 | Scaling of with distance L | Quantum-simulator measurement shows scaling inconsistent with from transport. | |
| Assumptions: Diffusion dominates transport; SDC satisfied. | |||
| Sources: preprints202601.0364.v1 (hydrodynamic closure) | |||
| DCA-1 | Permutation-unitary lift | Reversible deterministic rules correspond to permutation unitaries | Show micro update rules require non-permutation unitaries at . |
| Assumptions: Universal update time ; reversible local updates. | |||
| Sources: main manuscript; preprints202512.2120.v1 | |||
| MASS-1 | Threshold for matter audit depth | in 3+1D for stable matter excitations | Explicit microscopic counterexample at within same axioms. |
| Assumptions: Gauge-coded QCA; code-subspace stability. | |||
| Sources: preprints202512.2120.v1; 202512.2391 note | |||
| MASS-2 | Particle mass scales | ; predicts clustering at integer multiples of | Experimental/analysis pipelines do not show such clustering under controlled re-analyses. |
| Assumptions: Mass as certification cost; reference band from golden relation. | |||
| Sources: preprints202512.2391.v2 (scale clustering) | |||
| ASTRO-1 | Relative arrival-time lags | redshift integral controlled by and | Null constraints from GRB/AGN time-lag analyses; redshift dependence does not match. |
| Assumptions: Same transient sector as DE-5; propagation over cosmological distances. | |||
| Sources: preprints202601.0639.v1 (Sec. 7) | |||
| MASS-3 | Collider exclusion bounds | Scales cluster and shift as | Re-analyses varying do not shift the scale according to inverse-square-root law. |
| Assumptions: Plateau regime for audit latency; and fixed. | |||
| Sources: preprints202512.2391.v2 (Eq. 8) | |||
| CONST-1 | Combination | Independent lattice/FRG computation yields incompatible value. | |
| Assumptions: FRG matching used in calibration layer; defined by matching. | |||
| Sources: preprints202511.2241.v4 | |||
| CONST-2 | in Golden Relation | Microscopic computation yields outside the interval. | |
| Assumptions: Same calibration layer as CONST-1. | |||
| Sources: preprints202511.2241.v4 | |||
| CONST-3 | constant | GeV−1 | Independent derivation of yields value outside uncertainty. |
| Assumptions: Same calibration layer as CONST-1. | |||
| Sources: preprints202511.2241.v4 | |||
| DE-6 | Joint consistency | Single must fit expansion, growth, and transient timing | No joint fit exists for any admissible satisfying locality. |
| Assumptions: Framework mapping from to and . | |||
| Sources: preprints202601.0639.v1 | |||
| ASTRO-2 | Redshift integral kernel | Residual lags must follow kernel fixed by and | Residuals show no redshift scaling or incompatible kernel. |
| Assumptions: Population-level marginalization removes intrinsic lags. | |||
| Sources: preprints202601.0639.v1; predictions_catalog | |||
| GR-4 | Recovery of GR correlators | Micro model yields Einstein dynamics as IR scaling phase | Simulation shows absence of GR-like phase or produces non-diffeo-invariant correlators. |
| Assumptions: Discrete information-field action as specified. | |||
| Sources: QICT_Supplement_Microscopic_GR.pdf | |||
References
- Umegaki, H. Conditional expectation in an operator algebra. IV. Entropy and information. Kodai Mathematical Seminar Reports 1962, 14, 59–85. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press, 2010. [Google Scholar]
- Helstrom, C.W. Quantum detection and estimation theory. J. Stat. Phys. 1969, 1, 231–252. [Google Scholar] [CrossRef]
- Fuchs, C.A.; van de Graaf, J. Cryptographic distinguishability measures for quantum-mechanical states. IEEE Trans. Inf. Theory 1999, 45, 1216–1227. [Google Scholar] [CrossRef]
- Jacobson, T. Entanglement equilibrium and the Einstein equation. Phys. Rev. Lett. 2016, 116, 201101. [Google Scholar] [CrossRef] [PubMed]
- Sakharov, A.D. Vacuum quantum fluctuations in curved space and the theory of gravitation. Sov. Phys. Dokl. 1968, 12, 1040–1041. [Google Scholar]
- ’t Hooft, G. The Cellular Automaton Interpretation of Quantum Mechanics; Springer, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





