Real-Now-Front Cosmology: A Generative Framework for Spacetime, Expansion, and Dark Matter

1. Introduction

1.1. Motivation

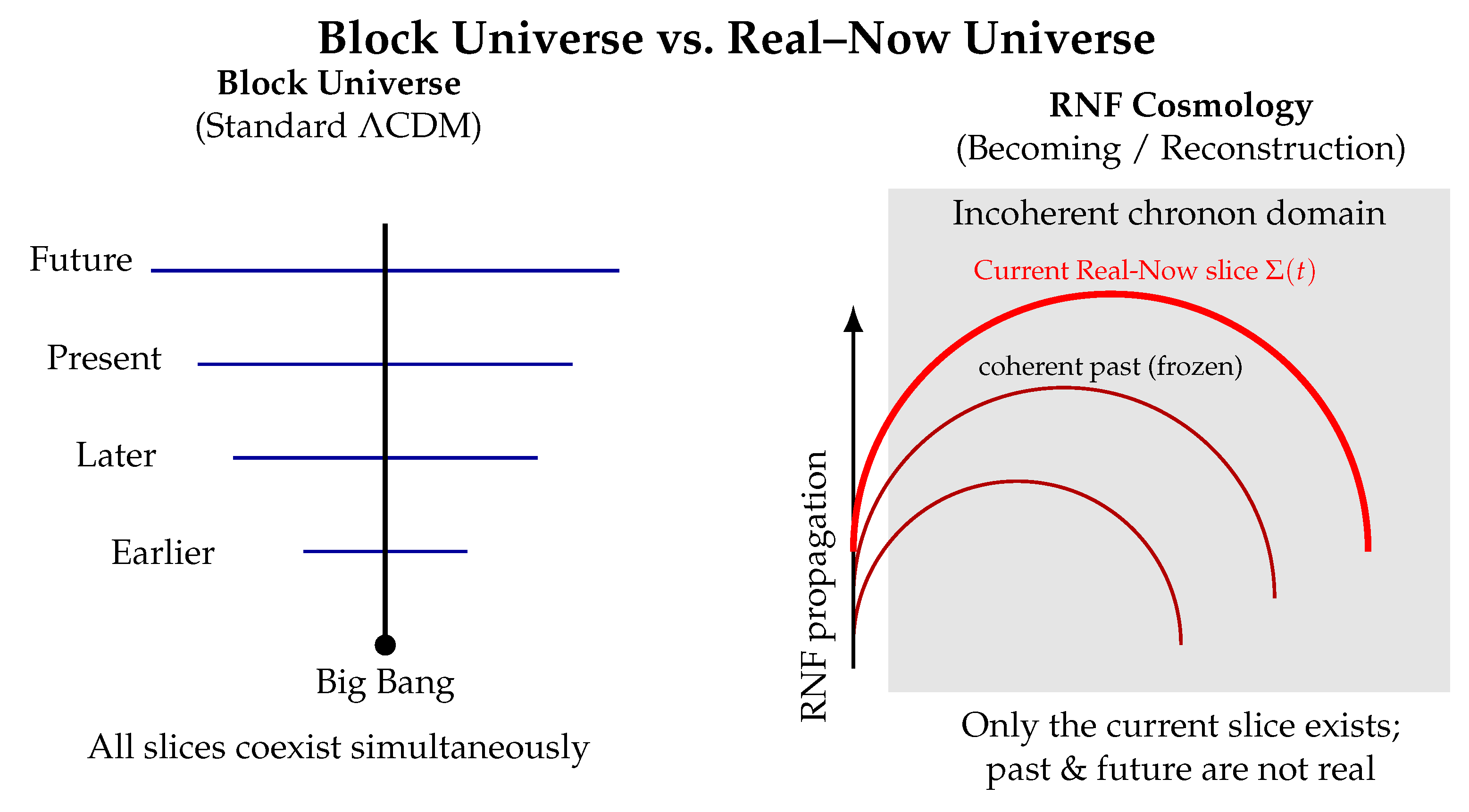
Standard cosmology begins with a fully formed four-dimensional spacetime equipped with a Lorentzian metric. In this block-universe picture, the entire manifold already exists, with no distinguished present, and with spacetime geometry postulated rather than generated. Although empirically successful, this framework leaves several foundational questions unresolved: the origin of large-scale smoothness and near-flat curvature [1,2], the horizon problem and the associated need for an inflationary scalar [3,4,5], the extreme fine-tuning implied by dark energy, and the unexplained microphysical nature of dark matter [6,7].

A deeper conceptual issue underlies these puzzles: spacetime symmetries are assumed a priori, rather than explained as emergent properties of an underlying physical structure. Lorentz invariance, causal cones, elastic curvature response, and universal propagation speeds are all imposed at the level of the metric, even though the metric itself is not associated with identifiable microscopic degrees of freedom.

A more physical perspective is therefore to treat spacetime as an emergent medium. In every other domain of physics, robust symmetries, propagation speeds, elastic response, large-scale coherence, defect formation, and domain growth arise from ordered phases of underlying microstructures. By contrast, $\Lambda$CDM assigns these properties directly to the metric, leading to several longstanding conceptual tensions:

• The invariance of c is postulated rather than derived from a microscopic alignment or ordering mechanism.
• Curvature behaves like an elastic strain, yet no underlying degrees of freedom exist to carry or regulate such strain.
• Cosmic expansion is driven by a constant vacuum energy whose origin remains obscure.
• The observed near-flat geometry and horizon-scale correlations require either fine-tuned initial conditions or an inflationary field whose own initial conditions are left unspecified.

These considerations motivate a framework in which spacetime geometry and its symmetries are generated dynamically from a microscopic alignment field, much as elastic, optical, and transport properties emerge from the ordering of constituents in condensed phases.

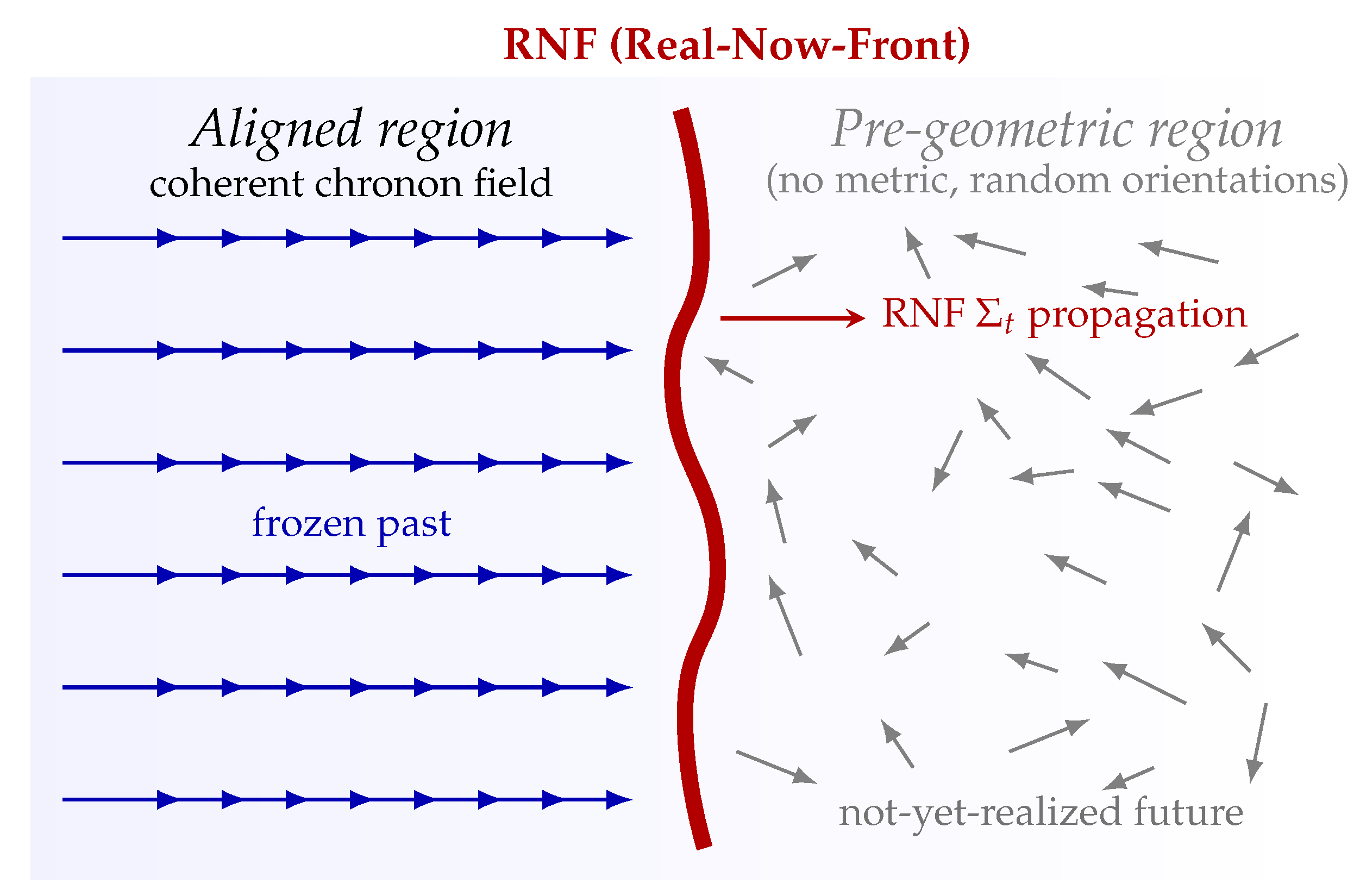
Real–Now–Front (RNF) cosmology develops precisely such a generative picture. The Universe does not begin as a pre-existing spacetime but as a pre-geometric chronon medium. Aligned regions nucleate and merge; their boundary—the Real–Now–Front (RNF)—propagates through the unaligned domain, constructing new spatial slices. From within the Universe, this advancing hypersurface is experienced as the evolving physical present. The central organizing principle is the Temporal Coherence Principle (TCP), which governs chronon alignment, reconstructs matter patterns, and induces the emergent Lorentzian metric [8]. Crucially, TCP drives each newly reconstructed region toward a preferred coherence–curvature density, so that cosmic expansion, structure formation, void growth, and local collapse arise as distinct local responses of a single coherence-restoration mechanism.

A second microphysical ingredient is the Chronon Exclusivity Principle (CEP), which forbids curvature concentrations from overlapping within a single causal cell. Near this bound the medium becomes effectively incompressible and forms finite-density, nonsingular cores with universal scaling $R_{\mathrm{core}}\propto M^{1/3}$. Small cores behave as horizonless cold dark matter candidates (Micro Chronon Condensates, MCCs), while massive cores reproduce the exterior geometry of GR black holes with CEP-regulated interiors. A single TCP–CEP dynamical process therefore accounts for compact objects across the entire mass range [7,9,10,11].

Within this framework, cosmic expansion, late-time acceleration, void dynamics, and the dark sector all emerge not from added fields or finely tuned initial conditions, but from the local, self-tuning response of the chronon medium as the Real–Now–Front advances.

1.2. Why Spacetime Should Be an Emergent Medium

The introduction of an underlying medium is motivated by physical necessity. Several key features of modern cosmology become more natural, and in some cases only intelligible, when geometry arises from microphysical alignment dynamics:

Universality of c.

A single invariant propagation speed c for all locations, observers, and all types of probes (photons, gravitational waves, massless neutrinos) is difficult to justify in a stage-only picture. In RNF, the light cone is the characteristic cone of pattern-preserving chronon alignment dynamics. Lorentz invariance then emerges as the symmetry of an ordered phase, rather than a primitive axiom.

Curvature as elastic response.

Einstein’s equation,

$$G_{\mu \nu }=8\pi G{T}_{\mu \nu },$$

treats the metric as if it could be deformed by energy–momentum. But how can an abstract geometric field, with no physical microstructure, respond elastically to stress? In RNF, curvature is not imposed on a mathematical stage but arises as the coarse-grained strain of aligned chronon configurations, making Einstein’s equation a constitutive relation of an underlying medium [12,13].

Late-time accelerated expansion.

Unlike $\Lambda$CDM, where acceleration is imposed by a constant vacuum energy, RNF cosmology allows it to emerge kinematically. As vacuum-rich regions come to dominate cosmic volume, TCP-driven metric stretching approaches a steady rate, yielding an accelerated, de Sitter–like phase without dark energy.

Early-universe smoothing.

Near-flatness and large-scale uniformity arise from TCP-driven relaxation during RNF percolation, rather than from fine-tuned initial conditions or inflation.

Arrow of time.

A block universe lacks an ontological distinction between past and future. RNF provides a physical advancing present: aligned slices form the past, unaligned regions constitute the future, and the RNF itself generates new spacetime.

Becoming and the physical present.

A stage-only spacetime cannot explain why a single definite outcome appears in quantum measurements: the block universe contains all events at once and provides no mechanism of `becoming.” In RNF cosmology the advancing Real–Now–Front is a physical process that creates new slices by selecting a single coherent continuation of chronon patterns. Outcome selection is therefore tied to the generative construction of spacetime itself, giving a concrete physical meaning to the present.

These considerations together make a strong physical case that cosmology requires a microphysical substrate. RNF cosmology provides one concrete realization of such a substrate, introducing no additional fields beyond the chronon medium and its alignment dynamics. It is built on three coupled ingredients:

• The Real–Now–Front (RNF): An advancing three-surface that generates spacetime. Behind the RNF lies the aligned, metric-bearing region; ahead lies a non-geometric domain. From within the Universe the RNF is experienced as the advancing present.
• The chronon field ${\Phi }_{\mu }$: A unit timelike covector whose alignment induces both the emergent metric and the temporal direction. Unaligned regions carry no geometry. Early alignment proceeds through defect formation and coarsening [14,15].
• The Temporal Coherence Principle (TCP): A local variational rule that aligns chronons as the RNF advances, reconstructing matter patterns and inducing $g_{\mu \nu }\left[\Phi \right]$. TCP drives each reconstructed region toward a preferred coherence–curvature density ${\rho }^{*}$, which is central to the dynamics described below.

A key geometric consequence follows directly from the generative nature of the RNF:

Advancing the RNF forces each newly formed slice to rescale its geometry.

TCP requires every reconstructed patch to maintain the characteristic coherence density ${\rho }^{*}$(See Section 6.2) while RNF propagation continually increases the aligned four-volume behind the front. To satisfy both constraints, the induced spatial metric must either stretch or shrink. This produces a local TCP bifurcation with three regimes:

• Stretching branch (${\rho }_{\mathrm{curv}}<{\rho }^{*}$): Under-curved regions lower their TCP energy by expanding the metric, generating the familiar Hubble flow. Because RNF propagation depends on local chronon structure, the expansion rate becomes self-tuning: voids stretch more rapidly, and regions near massive objects or MCCs stretch more slowly.
• Near-equilibrium branch (${\rho }_{\mathrm{curv}}\approx {\rho }^{*}$): Mild adjustments produce GR and FRW-like behavior.
• Shrinking branch (${\rho }_{\mathrm{curv}}>{\rho }^{*}$): Over-curved regions lower their TCP energy by metric contraction, initiating collapse into chronon condensates (MCCs).

Chronon soliton condensates formed during early alignment behave as stable, compact, lensing dark-matter objects. Their properties follow from the Chronon Exclusivity Principle (CEP), which forbids curvature knots from overlapping within a causal cell and thereby enforces a finite-density, nonsingular core with $R_{\mathrm{core}}\propto M^{1/3}$ (Appendix D). Small CEP-saturated objects serve as horizonless cold dark matter; large ones reproduce the exterior geometry of GR black holes while avoiding singularities.

RNF cosmology thus ties the emergence of geometry, cosmic expansion, the arrow of time, and the dark sector to a single generative mechanism: the propagation of the RNF through the chronon medium.

Recent advances in Chronon Field Theory (ChFT) supply the mathematical foundation. Lorentzian signature emerges dynamically from chronon ordering [12], and Einstein–Yang–Mills structure appears as the long-wavelength limit of chronon alignment [13]. RNF cosmology extends these results by identifying RNF propagation as the engine that constructs spacetime itself.

Summary of Contributions

Conceptually, RNF cosmology builds on the Evolving Block Universe (EBU) perspective introduced by Ellis [26,27], providing a concrete microphysical mechanism by which spacetime itself is generated slice by slice. Building on this foundation, this paper develops Real–Now–Front (RNF) cosmology as a generative framework and establishes the following main advances:

• Generative origin of spacetime: Spacetime is created slice by slice as the RNF advances into an unaligned chronon domain, rather than being assumed as a pre-existing four-dimensional manifold.
• Local geometric mechanism for cosmic expansion: RNF propagation forces the induced spatial metric to stretch in order to restore temporal coherence, producing the Hubble law and late-time acceleration without invoking dark energy. Expansion is intrinsically local and self-tuning.
• Unified origin of dark energy and dark matter: The stretching branch yields cosmic expansion (phenomenologically replacing dark energy), while the shrinking branch forms CEP-regulated chronon cores ($R_{\mathrm{core}}\propto M^{1/3}$) that serve as cold dark matter and compact objects.
• Early-universe smoothing without inflation: Alignment-domain growth in the pre-geometric chronon medium naturally produces large-scale isotropy and near-flatness without requiring an inflationary scalar field.
• Mild two-metric phenomenology: Photon and matter excitations couple to slightly different chronon-based effective metrics, leading to small but testable deviations in cosmological distance–redshift relations.

Together these elements yield a unified microphysical picture in which geometry, expansion, compact objects, and the dark sector all emerge from a single generative process: the propagation of the Real–Now–Front through the chronon medium.

Scope and limitations.

The present work is intended as a conceptual and theoretical foundation rather than a precision cosmological fit. Quantitative confrontation with CMB anisotropies, large-scale structure statistics, and detailed numerical simulations of RNF alignment dynamics are identified as important future directions. The framework is constructed to be compatible with the large-scale phenomenology of $\Lambda$CDM while addressing its foundational limitations at the level of microphysics and spacetime ontology, rather than to replace standard cosmological modeling tools at this stage.

2. RNF as a Physical Theory of the Present

2.1. Why the Present is Dynamical

Standard cosmology assumes a fully formed four-dimensional manifold with a pre-existing metric. In this traditional “block-universe” view [23,25], the entire cosmic history is embedded in a fixed spacetime geometry with no physically privileged present. Large-scale smoothness, near-flat curvature, and correlated matter distribution must therefore be imposed as initial conditions on the entire four-dimensional structure at once [24,25].

A generative alternative, introduced most prominently by Ellis in the Evolving Block Universe (EBU) framework [26,27], is to treat the present as a physically meaningful and dynamically advancing entity. In the EBU and related becoming-based approaches [26,27,28,29], the Universe is constructed slice by slice as an advancing hypersurface actualizes new regions of spacetime. This perspective aligns naturally with our direct experience that only the present is physically accessible, and that decisions and actions are made now, influencing a future that is not yet realized.

RNF cosmology provides a concrete microphysical implementation of this idea. The Real-Now-Front (RNF) is a codimension-one surface whose propagation is governed by the Temporal Coherence Principle (TCP). Geometry, effective causal description, and matter fields are reconstructed only in the region through which the RNF has passed; ahead of the front the chronon field is unaligned and lacks metric structure. Spacetime is therefore built dynamically rather than assumed from the outset, supplying a microphysical realization of Ellis’ dynamical present within an emergent-spacetime framework.

A viable emergent-spacetime picture must also specify how geometry is generated. The RNF provides a definite boundary between realized geometry and a pre-geometric domain, together with a natural ordering that sequences the construction of successive slices. The following sections analyze the quantitative consequences of this mechanism, while Appendices Appendix A and Appendix C present the mathematical formulation of RNF propagation and its homogeneous expansion law.

2.2. Definition of the Real–Now–Front

The RNF is a smooth, spacelike hypersurface $\Sigma \left(t\right)$ that advances monotonically through an underlying pre-geometric chronon domain. At the RNF, the chronon field ${\Phi }_{\mu }$ undergoes alignment, and the patterns inherited from earlier slices are reconstructed into a newly actualized three-dimensional slice. The induced metric $g_{\mu \nu }\left[\Phi \right]$ and effective matter fields arise as part of this reconstruction, while the aligned region left behind constitutes the frozen past. All apparent physical processes—including cosmological evolution—emerge from the ordered reconstruction of patterns across successive RNF advances.

Ahead of the RNF lies a region that is not spacetime in the usual sense: the chronon field is unaligned, and no metric, distances, or causal structure exist. This domain resembles Wheeler’s pregeometry and modern emergent-gravity precursors [19]. When the RNF reaches such a region, the Temporal Coherence Principle aligns ${\Phi }_{\mu }$ and incorporates the region into the reconstructed sequence of physical slices.

In this way the RNF functions as the physical present: the generative boundary at which new spacetime slices are instantiated. The future remains non-metric until the RNF arrives, while the past consists of the stack of previously reconstructed, frozen slices.

2.3. Forest-Fire Analogy

To illustrate the unfamiliar role of the RNF, consider a forest fire advancing across a landscape. Ahead of the fireline lies unburned forest with no flame or temperature structure; at the fireline local chemistry ignites combustion; behind it lies a coherent thermal region.

The RNF picture parallels this:

• the unaligned domain resembles unburned forest, lacking geometric structure;
• the RNF front corresponds to the fireline, activating local degrees of freedom;
• the aligned spacetime corresponds to the burned region, where coherent chronon alignment defines geometry;
• the copying of persistent chronon patterns resembles the replication of flame structure at the fireline.

This analogy highlights two points. First, the RNF selects a preferred generative direction, similar to the irreversible transition from unburned to burned states. Second, the RNF does not generate coherence from nothing: it reconstructs alignment by copying persistent chronon patterns from previous slices. This copying mechanism underlies the expansion behavior derived in Section 8 and Appendix A.

2.4. Pre-Geometric Domain

The domain ahead of the RNF lacks metric structure: although a manifold topology may exist, there is no notion of distance, curvature, or volume. Without volume, there is no meaningful sense in which the RNF could “run out’’ of unaligned region; such questions require geometry, which only appears after alignment.

This also reframes the cosmological beginning. The RNF has a finite past consisting of earlier aligned slices, but the pre-geometric domain need not possess a beginning or boundary. The Big Bang corresponds not to a geometric singularity but to the first slice on which the chronon field achieved self-sustaining alignment, a view consistent with nonsingular emergent-gravity perspectives [19].

2.5. Temporal Coherence Principle

The Temporal Coherence Principle (TCP) governs chronon alignment and determines the propagation of the RNF [8]. Intuitively, the TCP aligns the chronon field so as to minimize local misalignment gradients, akin to order-parameter dynamics in nonequilibrium systems [30]. This behavior parallels domain-wall motion under gradient flow and pattern formation in condensed-matter systems [31,32].

Two consequences are central:

• Alignment Rule. As the RNF encounters an unaligned region, the chronon field is driven into a coherent configuration, inducing the local metric and reconstructing matter fields.
• Propagation Rule. The RNF advances because misaligned regions ahead of the front are favored sites for further alignment. Geometry grows outward as the RNF sweeps through the pre-geometric domain.

The TCP field Equation (3) and well-posedness conditions appear in Section 4 and Appendix A, and the resulting homogeneous expansion law in Appendix C.

In summary, the RNF provides the physical present, the TCP supplies the law that generates spacetime, and the pre-geometric domain provides the substrate through which this generative process unfolds. Together these ingredients form the conceptual and dynamical foundation of RNF cosmology. See Figure 1 for a schematic illustration of RNF propagation. The RNF is the physical present: the three–dimensional slice on which all fields and measurements exist, advancing irreversibly as new spacetime is generated.

3. RNF Propagation and Operational Lorentz Invariance

3.1. Effective Spacetime Description and RNF Reconstruction

Before discussing propagation and Lorentz invariance, it is important to clarify the role of standard spacetime language within the RNF/ChFT framework. In RNF cosmology, an RNF slice is not a dynamical arena in which processes unfold. No physical motion, signal transmission, or causal influence occurs within a slice. Instead, all apparent dynamics arise from the reconstruction of patterns across successive RNF advances.

Nevertheless, once reconstructed, the slice-by-slice dynamics admits an operationally equivalent description in the familiar block-universe language. Concepts such as signal propagation, light cones, worldlines, and Lorentz invariance may therefore be used throughout as effective descriptors of RNF reconstruction dynamics, provided it is kept in mind that they are not ontologically fundamental. This effective description is fully adequate for observational and phenomenological analysis, and it is only when the generative role of the RNF itself is under consideration —such as in front propagation or measurement selection—that RNF-native language becomes essential.

With this understanding, we proceed using conventional spacetime terminology while interpreting it as an emergent and operationally equivalent description of RNF reconstruction.

3.2. RNF Advance and Microscopic Alignment Scale

A central property of RNF cosmology is that the Real–Now–Front (RNF) advances into the pre-geometric chronon domain at a fixed microscopic alignment scale. This advance is not defined relative to any spacetime metric—no metric exists ahead of the RNF—but reflects the intrinsic rate at which chronon alignment relaxes in the underlying medium.

From the hyperbolic TCP field equation (Appendix A, Section 4), the characteristic alignment scale is

$$C=c_{\Phi }=\sqrt{{\displaystyle \frac{J}{{\lambda }_{\mathrm{eff}}}}},$$

which may be described, in effective language, as the maximal rate at which coherent patterns can be reconstructed across RNF advances in a nonlinear order-parameter medium [30].

Importantly, this microphysical scale governs only the generative process by which aligned slices and their induced metrics come into existence. It has no operational meaning for observers, who exist only on already-aligned RNF slices and have access solely to the emergent geometry.

3.3. Meta-Time and the Generative Order of Slices

The RNF does not move within physical time; instead, physical time is defined only after a slice has been aligned and endowed with a metric $g_{\mu \nu }\left[\Phi \right]$. Ahead of the RNF there are no rods, clocks, or causal structure. The advance of the RNF is therefore parametrized by a more primitive meta-time, a bookkeeping variable that orders the creation of successive slices.

Meta-time is not an additional physical dimension. It labels discrete generative steps of RNF reconstruction, much as an iteration parameter labels updates in lattice relaxation or domain-growth models. All physical observers exist strictly within the aligned region and have access only to the emergent Lorentzian geometry. Consequently, the microphysical direction of RNF advance is operationally unobservable.

This remains true even when a slice contains matter, curvature, or defect-induced structure. After each reconstruction step, the TCP ensures that all chronon patterns—including “defect + curved vacuum” configurations—are fully equilibrated on that slice. The emergent metric therefore already incorporates the curvature required for local coherence, and no trace of the generative ordering survives within the observable description.

3.4. Co-moving Concealment Principle

These considerations lead to the:

Co-moving Concealment Principle (CCP). All observable physics occurs on fully aligned RNF slices whose local geometry has already been TCP-stabilized. Because reconstruction precedes the existence of clocks, signals, or causal ordering, the microphysical direction and scale of RNF advance cannot be detected by observers within spacetime. Observable phenomena are governed solely by the induced Lorentzian metric $g_{\mu \nu }\left[\Phi \right]$.

The CCP is strengthened by the three-regime structure of TCP reconstruction: whether a patch stretches, adjusts curvature, or collapses into a Micro Chronon Condensate, the outcome is always a locally equilibrated geometric structure. Any geometric adjustment associated with RNF reconstruction is completed before the slice becomes part of the observable universe. As a result, no measurement can access the generative asymmetry.

3.5. Compatibility with Lorentz symmetry Tests

The decoupling between microphysical generative ordering and emergent Lorentz invariance parallels mechanisms in analogue-gravity systems, condensed-matter emergence models, Einstein–Æther frameworks, and Hořava–Lifshitz constructions [17,33,34,35]. In each case, a preferred microstructure exists but remains concealed by the equilibrated effective geometry.

RNF cosmology must satisfy stringent empirical bounds on Lorentz violation. Observational constraints from multi-messenger observations [36], high-energy neutrinos [37], ultra–high-energy cosmic rays [38], and the SME program [39] require any violations to be below ${10}^{-15}$–${10}^{-20}$. The CCP ensures compliance: the only geometry accessible to observation is the fully TCP-stabilized metric, not the microphysical reconstruction dynamics that produced it.

Even in regions where TCP actively adjusts curvature—such as near solitons, MCCs, or mild coherence deficits—this adjustment is completed at reconstruction. Once a slice is formed, both massive and massless excitations admit a consistent effective spacetime description with no memory of the RNF ordering. Lorentz invariance is therefore preserved to all experimentally accessible precision.

3.6. Summary

The distinction between meta-time and emergent time, together with slice-by-slice TCP equilibration, ensures that:

• a preferred generative ordering exists at the microphysical level,
• all observable physics admits a fully Lorentz-invariant effective description,
• coherence-driven geometric adjustments leave no operational imprint of the RNF,
• and no experiment within the aligned region can detect the RNF or infer a preferred frame.

RNF cosmology therefore contains a microphysical generative ordering associated with chronon alignment, but this structure is completely concealed by the TCP-stabilized effective geometry, leaving observable physics strictly Lorentz invariant.

4. Chronon Field and TCP: Minimal Mathematical Formulation

RNF cosmology is based on a single structural hypothesis: spacetime geometry is induced by the alignment of a smooth unit-timelike covector field ${\Phi }_{\mu }$, the chronon field. The Temporal Coherence Principle (TCP) governs this alignment and supplies the restoring dynamics that selects, stabilizes, and preserves geometric patterns. As in other ordering phenomena in condensed-matter or statistical systems [14,30], coherence of an order-parameter field controls the emergence of macroscopic structure. Here, the chronon medium plays this role for geometry itself, including its curvature, causal structure, and matter content.

4.1. Chronon Field ${\Phi }_{\mu }$

The chronon field ${\Phi }_{\mu }$ is the fundamental pre-geometric field of the theory: a smooth covector on the underlying manifold whose alignment creates spacetime. It is not a particle, not a time quantum, and not a scalar “clock’’ field. Rather, it is an order-parameter–like orientation field whose coherent domains generate the emergent metric.

When the RNF aligns a region, ${\Phi }_{\mu }$ enters an ordered phase satisfying

$${\Phi }_{\mu }{\Phi }^{\mu }=-1,$$

(1)

and small gradients ${\nabla }_{\mu }{\Phi }_{\nu }$ encode a well-defined temporal direction and induce the emergent Lorentzian metric $g_{\mu \nu }[\Phi ]$ [8,12]. Where ${\Phi }_{\mu }$ is highly sheared or disordered, the region is pre-geometric: the manifold exists, but no physical metric or causal structure has yet formed.

Similar unit-timelike fields occur in Einstein–Æther theory [34], ADM formulations [40], and analogue-gravity systems [17]. But in RNF cosmology, ${\Phi }_{\mu }$ is not auxiliary: its alignment creates the spacetime manifold and determines the microscopic origin of causal cones, curvature, matter, and gauge fields.

4.2. The Temporal Coherence Principle (TCP)

The Temporal Coherence Principle (TCP) specifies the local dynamical rule by which the ontological chronon field ${\Phi }_{\mu }$ aligns and relaxes as the Real–Now–Front (RNF) advances. TCP is not a phenomenological postulate but a local variational principle governing chronon ordering on an underlying smooth manifold. Its role is to suppress misalignment, stabilize curvature-bearing structures, and enforce a preferred ordered phase from which spacetime geometry emerges.

A minimal effective action capturing these requirements is

$$S_{\mathrm{TCP}}=\int d^{4}x\sqrt{-g_{\mathrm{eff}}}\left[{\displaystyle \frac{J}{2}}\left({\nabla }_{\mu }{\Phi }_{\nu }\right)\left({\nabla }^{\mu }{\Phi }^{\nu }\right)+{\displaystyle \frac{\kappa }{4}}{\left(\left({\nabla }_{\mu }{\Phi }_{\nu }\right)\left({\nabla }^{\mu }{\Phi }^{\nu }\right)\right)}^2-{\displaystyle \frac{\lambda }{2}}({\Phi }_{\mu }{\Phi }^{\mu }+1)\right],$$

(2)

where:

• $J>0$ penalizes chronon misalignment and large gradients;
• $\kappa >0$ stabilizes finite-size curvature concentrations and prevents Derrick-type collapse;
• $\lambda$ enforces the unit timelike normalization ${\Phi }_{\mu }{\Phi }^{\mu }=-1$.

The effective measure $\sqrt{-g_{\mathrm{eff}}}$ reflects the coarse-grained volume element induced by aligned chronons; its precise form is not required here.

Varying (2) yields the local TCP equation of motion,

$$J{\nabla }_{\nu }{\nabla }^{\nu }{\Phi }_{\mu }-\lambda {\Phi }_{\mu }+\kappa {\mathcal{N}}_{\mu }(\Phi ,\nabla \Phi )=0,$$

(3)

where ${\mathcal{N}}_{\mu }$ collects quartic-gradient corrections responsible for soliton stabilization and curvature saturation. Equation (3) is hyperbolic, with characteristic speed

$$c_{\Phi }=\sqrt{{\displaystyle \frac{J}{\lambda }}},$$

(4)

which governs chronon-pattern relaxation in the pre-geometric medium. This speed is not the physical speed of light; causal structure and null cones emerge only after coherent alignment has produced an effective metric.

TCP as a coherence-restoration principle.

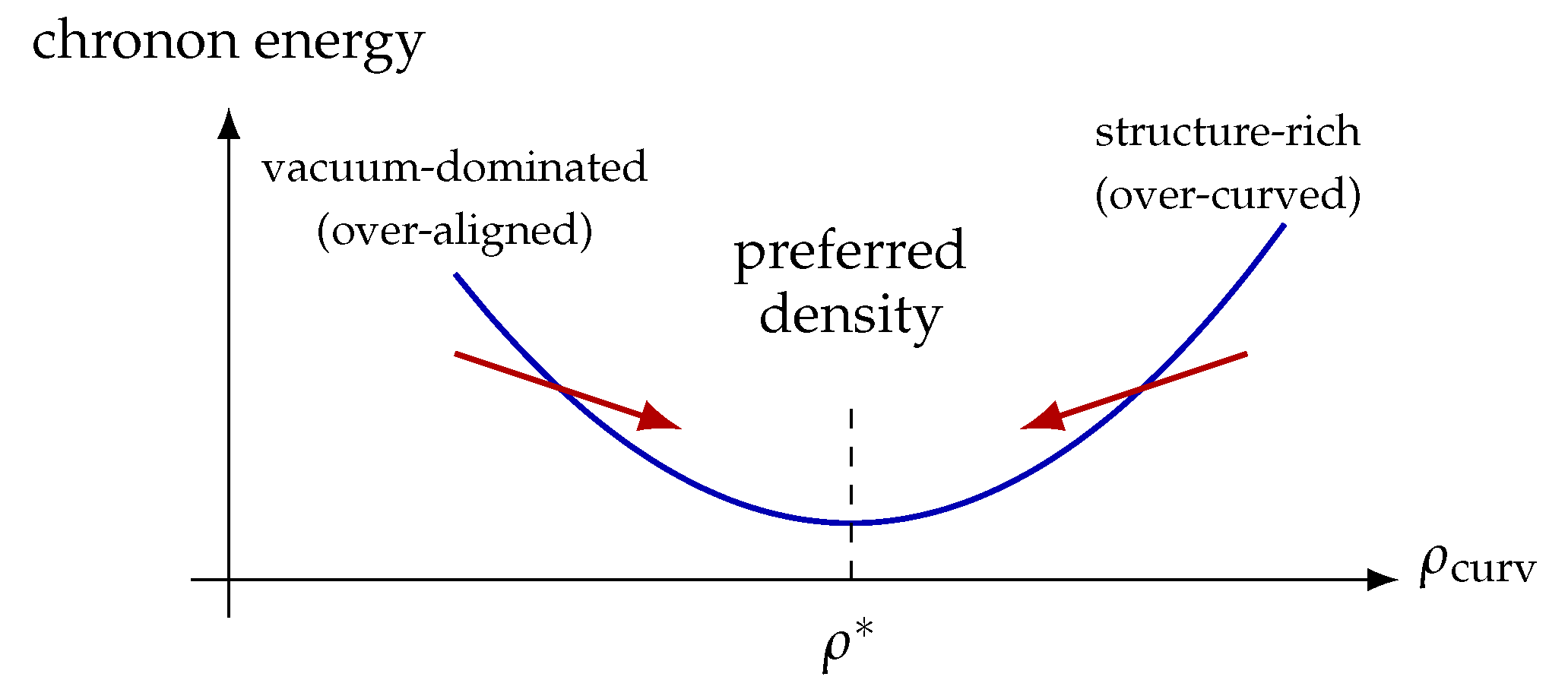
A crucial consequence of (2) is that TCP does not favor either perfect vacuum alignment or arbitrarily dense curvature. Excessive homogeneity increases the energetic cost of perturbations through the quartic term, while excessive curvature raises the quadratic gradient energy. The competition between these contributions selects a preferred local coherence–curvature density ${\rho }^{★}$, corresponding to a stable “defect + curved vacuum” pattern. This preferred density is not imposed externally; it is an intrinsic property of the chronon medium.

During RNF reconstruction, the internal chronon pattern of a comoving patch is copied from slice to slice. To leading order, TCP therefore cannot modify the pattern itself on the reconstruction timescale; instead, it acts by adjusting the geometric assignment to that pattern. As shown in Section 6.2 and Section 8.5, deviations of the inherited coherence density from ${\rho }^{★}$ force TCP to respond geometrically: metric stretching when coherence is too high, metric shrinking when it is too low, and curvature redistribution near equilibrium.

Thus the same local TCP equation (3) underlies: (i) early-universe smoothing and near-flatness, (ii) the local Hubble law from RNF kinematics, (iii) the stretching–equilibrium–shrinking bifurcation, and (iv) the formation of CEP-saturated solitonic cores.

4.3. Metric Emergence and Curvature as Part of the Pattern

When ${\Phi }_{\mu }$ is aligned on an RNF slice, a Lorentzian metric emerges as a functional of the chronon field:

$$g_{\mu \nu }[\Phi ]=-{\Phi }_{\mu }{\Phi }_{\nu }+h_{\mu \nu }[\Phi ],$$

(5)

with $h_{\mu \nu }$ defined by

$$h_{\mu \nu }{\Phi }^{\nu }=0.$$

(6)

This parallels ADM decompositions but arises here from chronon alignment rather than from an assumed manifold structure.

Crucially, $h_{\mu \nu }$ is not arbitrary: it is selected by TCP so that the local defect + curved vacuum structure has the correct coherent pattern density. Curvature is therefore not an independent geometric field but the self-consistent spatial distortion required for TCP coherence. A soliton with insufficient curvature induces further curvature via TCP; a soliton with excess curvature induces stretching to reduce curvature density. This logic underlies the geometric bifurcation between expansion, curvature equilibria, and collapse.

Where ${\Phi }_{\mu }$ is not aligned, $g_{\mu \nu }$ is undefined, consistent with the pre-geometric interpretation of Section 2.

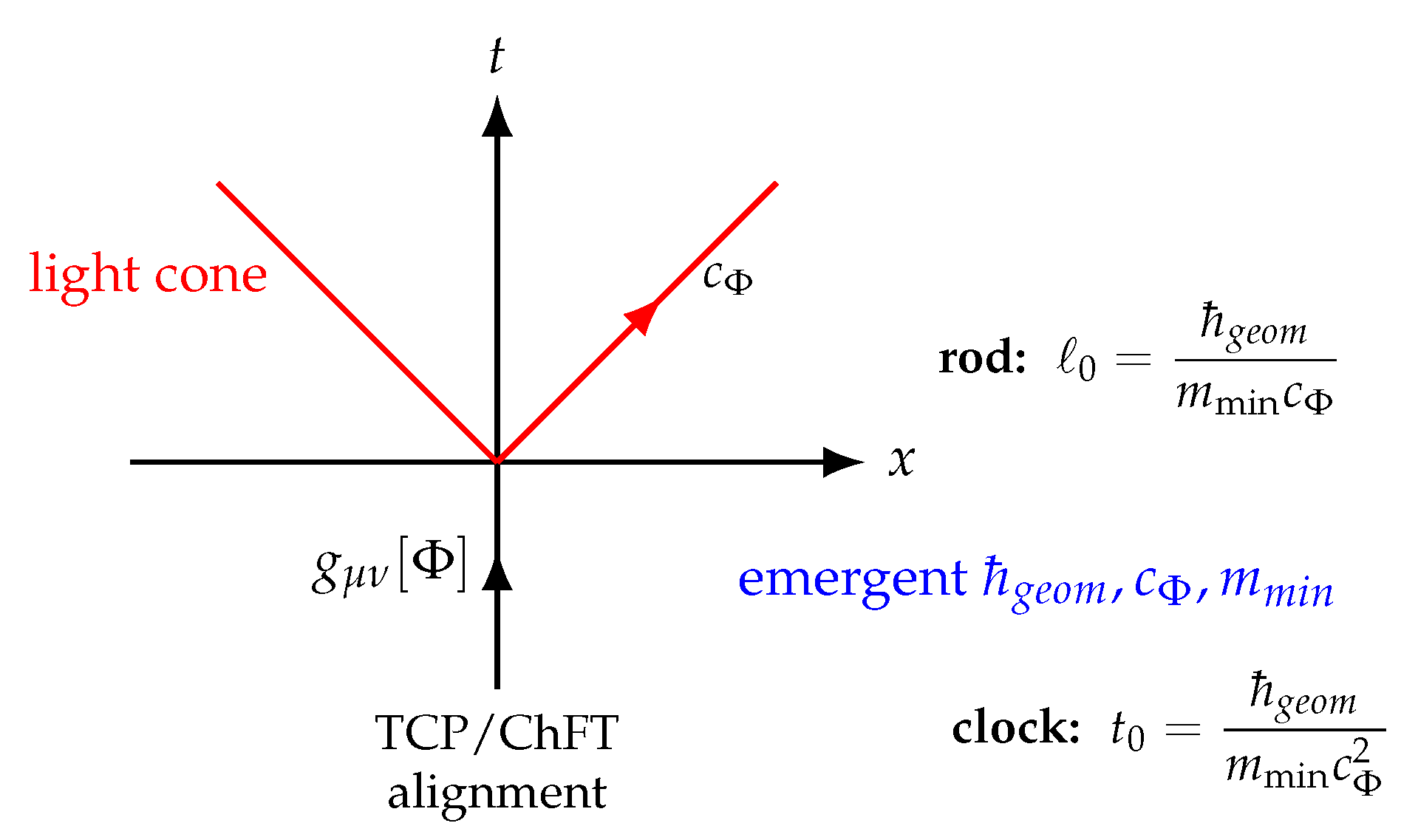
4.4. Invariant Standards and Operational Geometry

A metric becomes operational only when invariant physical standards of length and phase exist. In RNF cosmology these standards arise dynamically: alignment at the Planck correlation scale generates a fixed quantum of symplectic flux, the minimal quantum of action ${\hslash }_{\mathrm{geom}}$ [8]. Relations such as

$$E={\hslash }_{\mathrm{geom}}\omega ,p={\displaystyle \frac{{\hslash }_{\mathrm{geom}}}{{\lambda }_{\mathrm{dB}}}},$$

(7)

provide the clocks and rods needed to measure the emergent metric. Thus the chronon field not only produces geometry but also supplies the measurement standards that make geometry physical.

4.5. RNF Propagation as an Energy-Reducing Solution of TCP

An RNF slice $\Sigma \left(t\right)$ is characterized by:

• fully aligned ${\Phi }_{\mu }$,
• a TCP-stabilized metric $g_{\mu \nu }[\Phi ]$,
• a boundary beyond which ${\Phi }_{\mu }$ remains misaligned.

Because misalignment carries higher TCP energy, the front advances by aligning regions ahead of it—exactly analogous to advancing phase boundaries in non-equilibrium pattern-forming systems [31]. A key property is copying invariance: once TCP stabilizes a “defect + curvature” pattern on $\Sigma \left(t\right)$, the RNF copies that pattern into $\Sigma (t+\Delta t)$, where only the metric embedding may adjust to restore the preferred coherence density. This copying mechanism underlies matter persistence, gauge reconstruction, and the slice-by-slice geometric responses (stretching, curvature adjustment, or shrinking) discussed in Section 8.6.

4.6. Emergent GR, Gauge Fields, and Matter

Chronon Field Theory (ChFT) provides a unified microphysical origin for spacetime geometry, gauge interactions, and matter fields. Only a brief summary is provided here; detailed derivations are given in Refs. [8,13].

Emergent Einstein dynamics.

In the aligned phase, coarse-graining the TCP alignment equation yields an effective metric theory whose long-wavelength limit reproduces Einstein dynamics. Specifically, variations of the chronon alignment energy with respect to the induced metric give

$$G_{\mu \nu }\left[g\right]=8\pi G_{\Phi }{T}_{\mu \nu }^{(\Phi )}+O({\nabla }^3\Phi ),$$

(8)

where $G_{\Phi }$ is determined by chronon stiffness parameters and $T_{\mu \nu }^{(\Phi )}$ encodes alignment stress. General relativity thus appears as the hydrodynamic limit of chronon ordering rather than a fundamental postulate.

Emergent gauge structure.

Internal rotations and twists of the chronon polarization bundle induce effective gauge connections. At long wavelengths these reduce to standard Abelian and non-Abelian gauge fields, with curvature two-forms $F_{\mu \nu }$ arising from chronon twist modes [13]. Gauge invariance is therefore emergent, reflecting redundancy in the description of aligned chronon configurations rather than an imposed symmetry principle.

Bosons as transverse excitation modes.

Small-amplitude transverse fluctuations of the aligned chronon field act as propagating bosonic degrees of freedom. In particular, the normalization constraint ${\Phi }_{\mu }{\Phi }^{\mu }=-1$ implies gapless transverse modes that propagate within each RNF slice along null directions of the photon metric:

$$g_{\mu \nu }^{\left(\gamma \right)}{k}^{\mu }{k}^{\nu }=0.$$

(9)

These modes preserve the internal pattern and therefore do not undergo slice-by-slice reconstruction.

Matter as topological solitons.

Fermionic matter arises as localized, topologically protected solitonic excitations of the chronon alignment field. Quartic-gradient (Skyrme-like) terms stabilize these defects, whose combined “defect + curved vacuum” configuration represents a local TCP energy minimum. Mass corresponds to the integrated curvature and misalignment energy of the soliton core, while internal topological structure accounts for charge and chirality. Because solitons carry intrinsic curvature, they must be reconstructed at each RNF advance, naturally coupling them to the reconstruction metric.

Emergent physical constants and operational geometry.

A key consequence of ChFT is that the fundamental constants required for an operational spacetime geometry are not imposed but emerge dynamically. As shown in Ref. [8], the effective Planck constant ${\hslash }_{\mathrm{geom}}$ arises from the symplectic flex and minimum action associated with stable chronon solitons, while the characteristic propagation speed $c_{\Phi }$ emerges from the TCP alignment dynamics. The lightest stable soliton is identified with the electron, whose mass $m_{min}(=m_e)$, charge e, and coupling strengths follow from integrated curvature and polarization structure of the soliton core.

Together, ${\hslash }_{\mathrm{geom}}$, $m_{min}$, and $c_{\Phi }$ define natural operational units: a fundamental length (rod)

$${\ell }_0={\displaystyle \frac{{\hslash }_{\mathrm{geom}}}{m_{min}{c}_{\Phi }}},$$

and a fundamental time (clock)

$$t_0={\displaystyle \frac{{\hslash }_{\mathrm{geom}}}{m_{min}{c}_{\Phi }^2}},$$

corresponding to the Compton wavelength and period of the minimal soliton. These emergent rods and clocks provide the physical basis for Lorentzian metric measurements. Accordingly, the spacetime metric used in RNF cosmology is not merely a geometric construct but an operationally grounded structure, anchored in the same chronon microphysics that generates matter and interactions.

Cosmological relevance.

RNF cosmology therefore requires no additional matter or interaction sector beyond the chronon field itself. It inherits:

• GR-like dynamics from aligned chronon hydrodynamics,
• Standard Model–like gauge interactions from polarization geometry,
• photons as transverse excitation modes,
• matter as solitonic curvature concentrations,
• and persistent worldlines via RNF reconstruction.

Together, these results establish the chronon field ${\Phi }_{\mu }$ as the single microphysical substrate underlying geometry, interactions, and matter, providing a closed and self-consistent foundation for the cosmological framework developed in this paper.

Figure 2 is a schematic illustration of the emergent metric structure.

5. Propagation of the RNF as Local 4D Reconstruction

In RNF cosmology, the advance of the Real–Now–Front (RNF) is the fundamental generative process by which spacetime is created. Nothing evolves within a pre-existing 4D manifold. Instead, when the RNF encounters unaligned chronon regions, those chronons align to the incoming “defect + curved vacuum” pattern and thereby acquire metric structure. The universe is thus built slice-by-slice: the RNF is a propagating 3-surface that continuously reconstructs spacetime one infinitesimal layer at a time.

This section formulates RNF propagation directly from the TCP equation and clarifies how continuity, motion, curvature, and matter arise from strictly local chronon alignment dynamics.

5.1. Local Reconstruction from the TCP Equation

The leading-order TCP equation in an already-aligned region is

$$J{\nabla }_{\nu }{\nabla }^{\nu }{\Phi }_{\mu }+\lambda {\Phi }_{\mu }=O\left(\kappa \right),$$

(10)

subject to the unit-norm constraint ${\Phi }_{\mu }{\Phi }^{\mu }=-1$. All geometric quantities—curvatures, covariant derivatives, and the induced spatial Laplacian—are defined only on the aligned side of the RNF; the unaligned domain carries no metric and no notion of 4D geometry.

Let $\Sigma (\ell )$ denote slices displaced by proper distance ℓ along the aligned normal $n^{\mu }\simeq {\Phi }^{\mu }$, with $\ell =0$ at the RNF. In Gaussian normal coordinates on the aligned side,

$$g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }=-d{\ell }^2+h_{ij}(\ell ,x)d{x}^{i}d{x}^j,{\partial }_{\ell }=n^{\mu }{\partial }_{\mu },$$

and the d’Alembertian decomposes as

$${\nabla }_{\nu }{\nabla }^{\nu }{\Phi }_{\mu }=-{\partial }_{\ell }^2{\Phi }_{\mu }-K{\partial }_{\ell }{\Phi }_{\mu }+{\Delta }_h{\Phi }_{\mu }+(\mathrm{connection}\mathrm{terms}).$$

In the slow-front regime relevant for cosmology, chronon alignment relaxes much more rapidly than the RNF advances. Hence

$$|{\partial }_{\ell }{\Phi }_{\mu }|\ll |{\nabla }_i{\Phi }_{\mu }|,$$

and Equation (10) reduces on each slice to the elliptic equation

$$J{\Delta }_h{\Phi }_{\mu }-\lambda {\Phi }_{\mu }\simeq 0,$$

(11)

which determines the TCP-smoothing of boundary alignment data.

Let ${\Sigma }_0$ be the current slice and ${\Sigma }_{\delta \ell }$ the slice created after an RNF advance $\delta \ell$. Because ${\Phi }_{\mu }$ is continuous on the aligned side,

$${\Phi }_{\mu }(0^{+},x)={\Phi }_{\mu }(0^{-},x)+O\left(\kappa \right),$$

the newly created slice inherits the same alignment pattern up to small smoothing corrections. Solving (11) yields the first-order reconstruction law

$${\Phi }_{\mu }(\delta \ell ,x)={\Phi }_{\mu }(0,x)+\delta \ell {\partial }_{\ell }{\Phi }_{\mu }(0,x)+O\left(\delta {\ell }^2\right).$$

(12)

Copying invariance and curvature inheritance.

Equation (11) implies that the RNF does not create new structure; instead it copies the existing “defect + curved vacuum” pattern onto the next slice and then allows TCP to restore the preferred coherence density. This is the microscopic origin of

• persistence of matter (soliton cores reconstruct),
• persistence of gauge fields (twist modes reconstruct),
• persistence of curvature patterns (spatial geometry reconstructs),
• and the local geometric responses—stretching, curvature equilibration, shrinking—described in Section 8.6.

Thus RNF propagation is local 4D reconstruction: chronon alignment copies the entire coherent pattern into the next infinitesimal layer of spacetime, while TCP provides the metric adjustment needed to maintain the preferred coherence density.

These features, illustrated in Figure 3, ensure that as the RNF advances, solitons, gauge twists, curvature distributions, and vacuum structure are reinstantiated with high fidelity, yielding a smooth and dynamically consistent emergent spacetime.

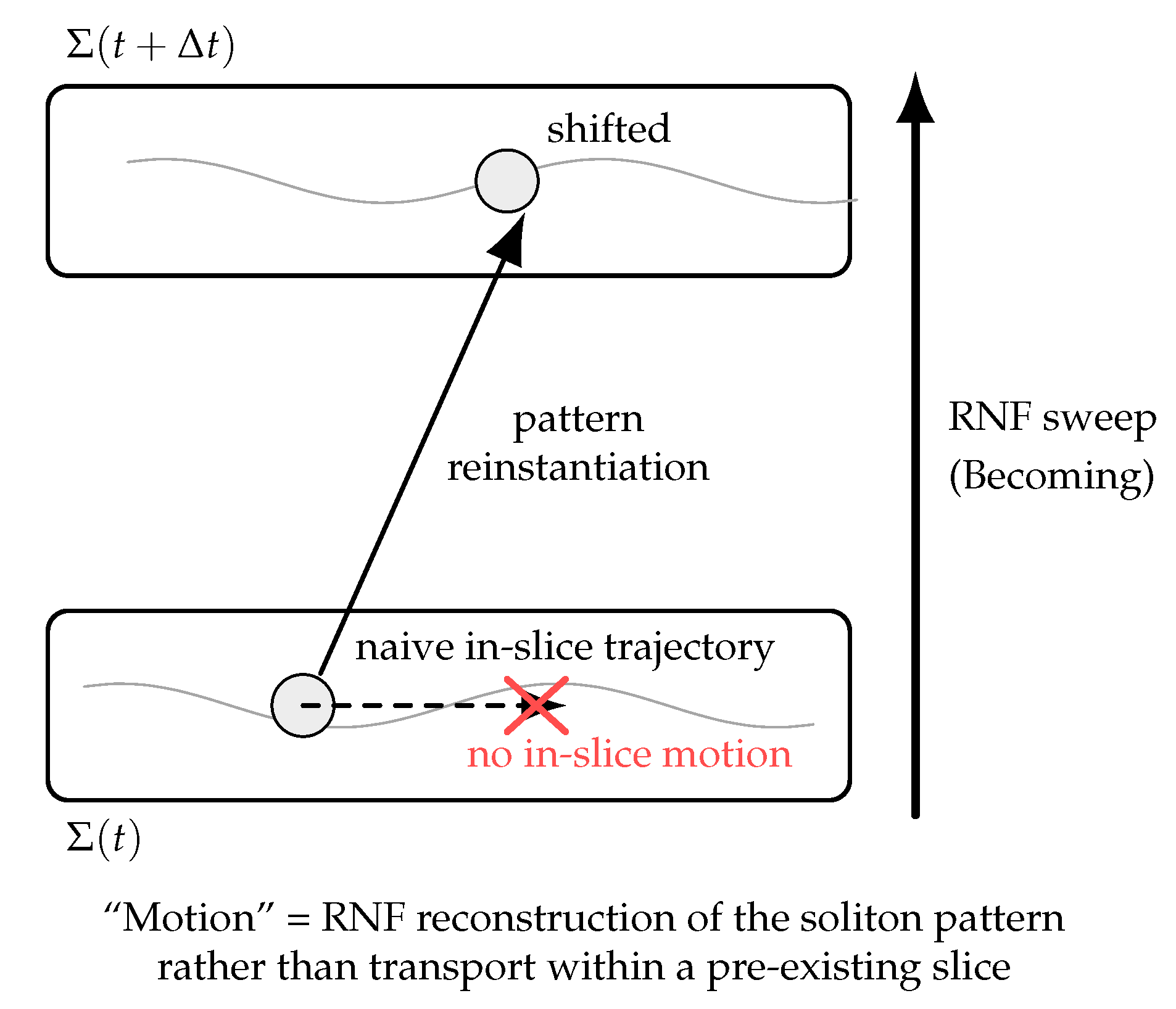
5.2. Motion and Interactions as Reconstruction Dynamics

Because nothing moves within a fixed RNF slice, all apparent motion arises from where a given pattern is re-instantiated when the next slice is created. Let $\mathcal{P}[\Phi ]$ denote the solitonic pattern corresponding to a particle. On $\Sigma (t+\Delta t)$ the RNF places this pattern at the position $x^i(t+\Delta t)$ that minimizes the local TCP spatial energy:

$$E_{\mathrm{TCP}}[\Phi ]={\int }_{\Sigma (t+\Delta t)}\left[J\left({\nabla }_i{\Phi }_{\mu }\right)\left({\nabla }^i{\Phi }^{\mu }\right)+\lambda (1+{\Phi }_{\mu }{\Phi }^{\mu })\right]\sqrt{h}{d}^{3}x.$$

(13)

Small spatial displacements $\mathcal{P}[\Phi ](x^i-v^i)$ give

$$\delta x^i=\underset{v^i}{arg\; min}{E}_{\mathrm{TCP}}\left[\mathcal{P}[\Phi ](x^i-v^i)\right],$$

(14)

so the effective velocity is

$$v_{\mathrm{eff}}^i={\displaystyle \frac{\delta x^i}{\Delta t}}\propto -{\left.{\displaystyle \frac{\partial E_{\mathrm{TCP}}}{\partial v_i}}\right|}_{v=0}+O\left(\Delta t\right).$$

(15)

5.2.0.16. Interpretation.

From within $\Sigma \left(t\right)$ this may appear as global optimization, but in the chronon ontology it is completely local: each chronon aligns with the chronon “above’’ it (in meta-time), while neighboring aligned chronons exert small tilting biases. These tiny biases accumulate slice by slice into what observers interpret as inertia and forces.

For the remainder of this paper, and for notational simplicity, we use “RNF copying” to denote both exact copying and copying accompanied by TCP-guided pattern shifts; this distinction is immaterial because such shifts preserve the coherence content and do not affect the subsequent coherence-restoration analysis.

Interactions.

Different distortions of ${\nabla }_i{\Phi }_{\mu }$ correspond to:

• curvature gradients ⇒ geodesic motion,
• gauge twists ⇒ electromagnetic forces,
• soliton overlap distortions ⇒ mutual forces.

Photons are special: as pattern-preserving excitations they propagate along the chronon-induced null cone $g_{\mu \nu }^{\left(\gamma \right)}$, producing the two-metric phenomenology of Section 10.

Thus motion and interaction arise entirely from the slice-by-slice reconstruction of chronon patterns.

Figure 4. Illustration of motion as reconstruction in the RNF framework. The lower and upper rectangles represent successive slices $\Sigma \left(t\right)$ and $\Sigma (t+\Delta t)$. The soliton does not move within a pre-existing slice; instead, the RNF generates the next slice with the soliton pattern reinstantiated at a shifted location. Conventional trajectories (dashed arrow) are effective descriptions of this underlying reconstruction process.

Figure 4. Illustration of motion as reconstruction in the RNF framework. The lower and upper rectangles represent successive slices $\Sigma \left(t\right)$ and $\Sigma (t+\Delta t)$. The soliton does not move within a pre-existing slice; instead, the RNF generates the next slice with the soliton pattern reinstantiated at a shifted location. Conventional trajectories (dashed arrow) are effective descriptions of this underlying reconstruction process.

5.3. Geometric Volume Response from RNF Reconstruction

A defining feature of RNF cosmology is that the unaligned chronon domain carries no geometric structure. When the Real–Now–Front advances, TCP induces a spatial metric on the newly aligned patch so that the inherited chronon pattern attains the preferred coherence density ${\rho }^{★}$ (Section 6.2).

Crucially, RNF advancement does not imply universal volume increase. Because the internal “defect + curved vacuum” pattern is copied across slices, TCP can restore coherence only by adjusting the metric volume assigned to that pattern. This leads to three generic local geometric responses:

• Vacuum-rich regions (${\rho }_{\mathrm{coh}}>{\rho }^{★}$) undergo metric stretching and local expansion;
• Near-equilibrium regions (${\rho }_{\mathrm{coh}}\approx {\rho }^{★}$) exhibit GR-like behavior with slowly varying volume;
• Curvature-rich regions (${\rho }_{\mathrm{coh}}<{\rho }^{★}$) undergo metric contraction, potentially leading to collapse and MCC formation.

In statistically homogeneous vacuum-dominated regions, this local response becomes uniform and yields an FRW-like expansion law. The full mathematical formulation of metric stretching, coherence-density scaling, TCP bifurcation, and the resulting Hubble law is developed in Section 8 and Section 8.5.

6. Early Universe: Smoothness, Flatness, and Horizon Resolution

In RNF cosmology, the large-scale smoothness, near-flatness, and uniformity of the early Universe arise from the statistical properties of the pre-geometric chronon medium and from chronon alignment under the Temporal Coherence Principle (TCP). Before alignment, the chronon substrate possesses no metric, no causal cones, and no horizons. Nevertheless, its microphysics is statistically homogeneous: every region of the unaligned medium has the same local chronon statistics by symmetry. Geometry appears only after RNF alignment imposes coherent structure; the classical puzzles of standard cosmology—horizon, flatness, and initial-condition tuning—are therefore reframed. Smoothness does not require superluminal expansion or horizon-spanning correlations; it reflects the uniformity of the substrate from which geometry is later constructed.

This behaviour parallels ordering phenomena in nonlinear media [30,31], where an initially featureless state undergoes coarsening, defect formation, and relaxation toward a characteristic defect density. In RNF cosmology the analogue is TCP-driven relaxation toward a preferred coherence density ${\rho }^{★}$, which sets the equilibrium balance between aligned vacuum and localized curvature.

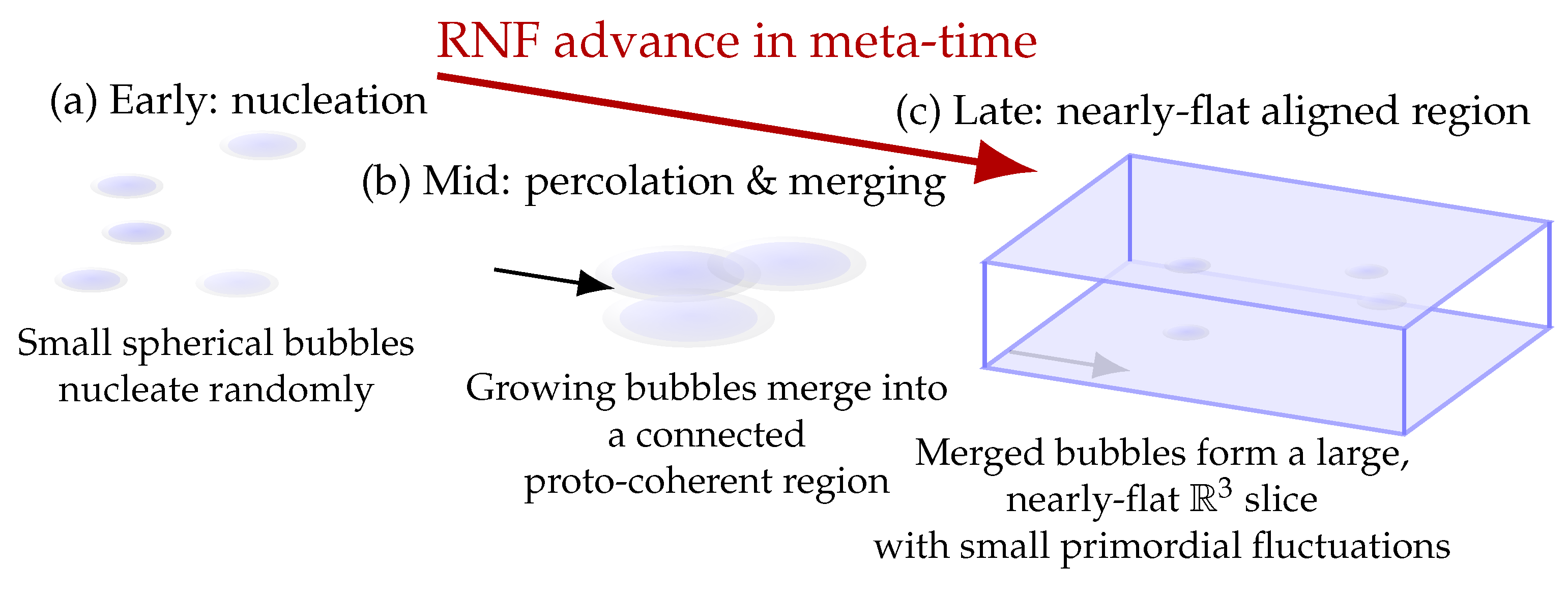
6.1. RNF Foam and the Emergence of Global Coherence

The chronon medium begins in an unaligned, pre-geometric phase. Small aligned patches nucleate stochastically, creating a multi-domain network—an RNF foam. These domains expand, merge, and eliminate misaligned interfaces in the same manner as phase-ordering dynamics [32,44]. TCP penalizes large gradients and deviations from the preferred coherence density, gradually steering each region toward a stable “defect + aligned-vacuum” configuration.

Three processes structure this epoch:

• domain coarsening through TCP suppression of strong gradients,
• defect capture and annihilation at domain collisions,
• percolation of aligned domains into a single connected region.

Once percolation is achieved, the RNF becomes a single coherent three-surface. At this moment the Universe first acquires a global geometric structure. Because the pre-geometric medium was statistically homogeneous, each region entering the aligned phase inherits effectively identical local structure.

The Universe becomes smooth because the substrate it is built from is uniform, not because distant regions ever required causal contact.

Thus the horizon problem never arises: smoothness and isotropy follow from substrate homogeneity plus TCP alignment, not from inflationary stretching of a causally connected patch.

6.2. Preferred Coherence Density in the Early Universe

A central microphysical ingredient of RNF cosmology is the existence of a preferred coherence–curvature density ${\rho }^{*}$ selected by chronon dynamics. This density determines the equilibrium balance between vacuum alignment and localized curvature (defects, solitons) in an ordered chronon medium. Its existence is generic and follows from simple energetic considerations; a formal derivation from coarse-grained Chronon Field Theory is given in Appendix B.

Competing microscopic tendencies.

Chronon alignment energetically favors coherent, low-entropy regions, but perfect alignment is not optimal. If the medium becomes too homogeneous, any perturbation produces large gradients in ${\Phi }_{\mu }$, increasing the Skyrme-type quartic term in the chronon energy functional. Thus extremely aligned vacuum carries a coherence penalty. Conversely, excessive curvature or defect concentration also raises the energy by increasing local misalignment. Between these two extremes lies an energetically preferred density ${\rho }^{*}$ of “defect + curved vacuum” content that minimizes the local chronon free energy.

Early-universe condensation.

During the initial ordering of the chronon medium, alignment fronts nucleate and expand. As defects form and smooth out, the medium naturally relaxes toward the preferred density ${\rho }^{*}$. This process mirrors defect-mediated ordering in condensed-matter quenches, where gradient and quartic terms balance to produce a stable density of vortices, disclinations, or topological textures.

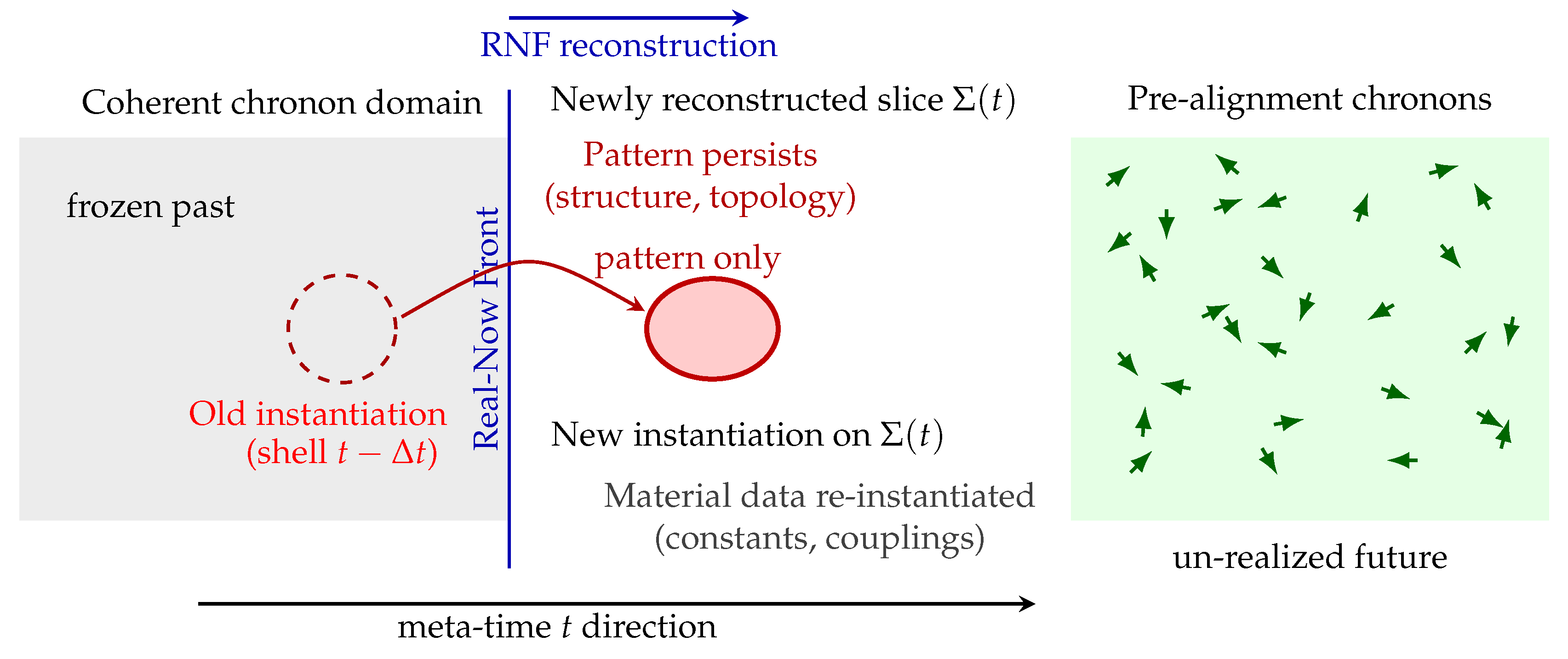
Why newly aligned regions must copy the previous slice.

When the RNF invades an unaligned region, that region can no longer form its own defect population dynamically—unaligned chronons lack geometric structure and cannot sustain curvature. Instead, the TCP reconstruction process copies the pattern of the previously aligned layer, preserving its coherence density. Thus ${\rho }^{*}$ is not only a microphysical optimum but also a dynamical attractor: every newly formed slice inherits its structure from the advancing RNF and then relaxes locally toward the same preferred density. See Figure 5 for a schematic demonstration.

Implications for cosmic evolution.

Once the Universe becomes largely aligned, local deviations from the preferred density directly determine the response of the induced metric:

• ${\rho }_{\mathrm{curv}}<{\rho }^{*}$: under-curved, coherence too high ⇒ TCP expands (stretches) the metric.
• ${\rho }_{\mathrm{curv}}\approx {\rho }^{*}$: balanced configuration ⇒ supports local gravity and yields FRW-like evolution.
• ${\rho }_{\mathrm{curv}}>{\rho }^{*}$: over-curved, coherence too low ⇒ TCP contracts (shrinks) the metric into MCCs.

These three regimes underpin the TCP bifurcation discussed in later sections.

6.3. Flatness from TCP Coherence-Equilibration

After percolation, the Universe consists of an almost uniformly aligned chronon field, but with small spatial variations: trapped twists, incipient solitonic cores, and mild deviations from the preferred coherence density ${\rho }^{★}$.

The TCP functional,

$$\left({\nabla }_{\mu }{\Phi }_{\nu }\right)\left({\nabla }^{\mu }{\Phi }^{\nu }\right),$$

measures departures from the locally optimal “defect + aligned-vacuum’’ pattern and drives each region toward the coherence density ${\rho }^{★}$ that minimizes the chronon free energy. This produces the three-regime behaviour of Section 8.6:

• Stretching branch: vacuum-rich (over-coherent) regions expand.
• Equilibrium branch: regions with ${\rho }_{\mathrm{coh}}\simeq {\rho }^{★}$ adjust their curvature with minimal change in volume.
• Shrinking branch: structure-rich (under-coherent) regions contract.

In the early Universe the equilibrium branch dominates. Misalignment gradients and small curvature irregularities are efficiently damped, and each RNF slice relaxes toward a nearly flat metric. Subsequent RNF copying preserves this low-curvature pattern, while mild global stretching in vacuum-rich regions dilutes any remaining variations.

Flatness is therefore not a fine-tuned initial condition and not an inflationary attractor; it emerges naturally from TCP coherence-restoration acting during and shortly after alignment. The metric is generated only after large-scale smoothness is already statistically encoded in the homogeneous chronon substrate, and TCP equilibration ensures that the first geometric slices are nearly flat.

6.4. Origin of Primordial Perturbations

TCP smoothing ensures large-scale uniformity, but small fluctuations are unavoidable in any nonlinear alignment medium. In RNF cosmology they originate from deviations from the preferred coherence density ${\rho }^{★}$ through two microphysical channels:

• Defect and quasi-defect remnants. During RNF-foam evolution, domain collisions trap twists and create localized curvature distortions. These structures persist on the curvature-equilibrium branch and seed density perturbations once the metric becomes well defined.
• Stochastic chronon-alignment noise. In the aligned region immediately behind the RNF, local alignment relaxes quasi-critically and exhibits intrinsic stochasticity [31,44]. TCP then restores the coherence density toward ${\rho }^{★}$, converting alignment fluctuations into small curvature perturbations. Coarse-graining across many domains yields an approximately Gaussian scalar spectrum, with controlled non-Gaussian contributions from defect capture.

RNF reconstruction preserves these features slice by slice, so once imprinted the perturbations remain stable and coherent.

Near scale invariance and spectral tilt.

During early coarsening, the alignment pattern exhibits a single growing correlation length,

$$L\left(\tau \right)\propto {\tau }^{\zeta },$$

with dynamic exponent $\zeta$ set by chronon microphysics. Curvature fluctuations generated at scale L satisfy

$${\Delta }^2\left(k\right)\propto k^{3-1/\zeta },(k\sim L^{-1}),$$

yielding a spectrum that is naturally close to scale invariant for $\zeta \approx 1$, as expected for relativistic ordering dynamics. A small red tilt would arise if $\zeta <1$, but determining the precise value of $\zeta$ requires a dedicated RNF/ChFT calculation that remains to be carried out.

Tensor perturbations require long-range transverse-traceless modes of ${\Phi }_{\mu }$, but these are strongly suppressed both before and after alignment. RNF cosmology therefore predicts a very small primordial tensor amplitude ($r\approx 0$).

Summary.

RNF cosmology naturally produces:

• nearly scale-invariant scalar perturbations from alignment-domain coarsening,
• a plausibly slight red tilt depending on the coarsening exponent $\zeta$ (not yet derived microscopically),
• negligible primordial tensor modes ($r\approx 0$),
• small, physical non-Gaussianities associated with defect formation and capture.

These perturbations arise from chronon microphysics—not from inflaton potentials, vacuum fluctuations, or superluminal expansion.

6.5. Comparison with Inflation

In standard cosmology, inflation solves the early-universe puzzles by stretching pre-existing geometry. In RNF cosmology these puzzles do not arise: geometry is generated after the chronon substrate has already become statistically homogeneous and after TCP alignment has eliminated misaligned gradients.

• Horizon problem: Inflation stretches correlations; RNF cosmology inherits homogeneity from the pre-geometric substrate.
• Flatness: Inflation drives curvature toward zero; RNF cosmology drives curvature toward the TCP equilibrium density ${\rho }^{★}$.
• Perturbations: Inflation sources them from quantum vacuum modes; RNF cosmology sources them from defect remnants and alignment stochasticity.
• Tensor modes: Inflation allows $r>0$; RNF cosmology predicts $r\approx 0$.
• Late-time acceleration: Inflation is separate from dark-energy dynamics; RNF cosmology produces acceleration through geometric stretching in vacuum-rich regions (the stretching branch), without dark energy.

Thus RNF cosmology offers a microphysical, generative alternative to inflation: smoothness and near-flatness reflect the properties of the chronon substrate and TCP equilibration, not exponential expansion driven by a scalar field. Figure 6 is a schematic illustration of the early universe.

7. Structure Formation in the RNF Framework

RNF cosmology reproduces the large-scale phenomenological successes of the $\Lambda$CDM structure–formation paradigm while grounding its ingredients in a generative microphysical model of spacetime, coherence, and dark matter. Differences arise from three structural features of the chronon–TCP system:

• the origin and scaling of primordial perturbations from TCP coherence-equilibration dynamics during RNF-domain coarsening,
• the microphysical nature of dark matter as coherence-regulated solitonic structures (MCCs),
• a mild two-metric structure arising from the distinct ways photons and matter propagate through RNF slices.

At cosmological scales these differences leave the standard linear-growth picture almost unchanged; deviations appear primarily on small scales and in precision distance and growth measurements.

Primordial perturbations from RNF percolation and TCP coherence dynamics.

As described in Section 6, the Universe transitions from an initially unaligned chronon medium to a single connected aligned region as the RNF percolates. Throughout this epoch, the TCP coherence-restoration rule drives each domain toward the preferred coherence density ${\rho }^{★}$. Departures from ${\rho }^{★}$—whether excess coherence (vacuum-rich) or deficient coherence (structure-rich)—generate local geometric distortions once a metric appears.

Two microphysical channels robustly produce scalar perturbations:

• Defect remnants from domain mergers. Domain collisions during RNF-foam evolution trap twists and pockets of misalignment. Relative to ${\rho }^{★}$ these manifest as localized under- or over-coherent regions. Once geometry emerges, they seed scalar curvature perturbations.
• Stochastic alignment variations on each newly reconstructed slice. In the aligned region immediately behind the advancing RNF, chronon alignment relaxes quasi-critically and exhibits intrinsic stochasticity [31,44]. TCP then restores the local coherence density toward ${\rho }^{★}$, mapping alignment fluctuations into curvature perturbations. Coarse-graining over many domains produces an approximately Gaussian scalar spectrum, with controlled non-Gaussianities from defect capture.

Because the chronon substrate is already statistically homogeneous before the metric exists, long-range coherence is imprinted prior to the emergence of light cones. Thus the horizon problem does not arise: homogeneity is inherited from the pre-metric substrate, not generated by superluminal expansion.

TCP coherence-equilibrium then damps large gradients while preserving the scaling behaviour of fluctuations. Tensor modes remain extremely suppressed, since long-range transverse–traceless excitations of ${\Phi }_{\mu }$ are energetically disfavored.

RNF reconstruction preserves these perturbations slice by slice, ensuring their fidelity until they re-enter causal horizons.

Linear growth under emergent Einstein dynamics.

Once the RNF has produced a sufficiently coherent and nearly flat region, metric perturbations evolve according to the emergent Einstein equation obtained from chronon hydrodynamics [12,13]. At linear order the matter overdensity satisfies

$$\ddot{\delta }+2H\dot{\delta }-4\pi G_{\Phi }{\rho }_m\delta =0,$$

where $G_{\Phi }$ depends on chronon stiffness parameters $(J,\lambda )$ that govern how the medium responds to coherence-density deviations.

Corrections to GR scale as ${\left(k{\xi }_{\Phi }\right)}^2$, where ${\xi }_{\Phi }$ is the chronon coherence length (Appendix E). Thus for modes with $k{\xi }_{\Phi }\ll 1$—the cosmologically relevant regime—RNF cosmology recovers standard linear growth. Departures appear only at high precision or at small physical scales.

Micro Chronon Condensates (MCCs) as dark matter.

Within TCP microphysics, stable solitonic structures appear whenever a localized chronon distortion plus its self-consistent aligned vacuum minimizes the coherence energy. These objects—Micro Chronon Condensates (MCCs)—play the role of cold dark matter.

Key properties follow directly from coherence-density physics:

• Cold and collisionless: MCCs form nonrelativistically and interact almost exclusively through the emergent gravitational field, reproducing CDM-like clustering.
• Finite core radius from TCP equilibrium: TCP stabilization at coherence density ${\rho }^{★}$ gives

  $$R_{\mathrm{core}}\propto M^{1/3},$$

  producing naturally cored halo profiles and alleviating the cusp problem.
• Granularity at small scales: For modes with $k\gtrsim {\xi }_{\Phi }^{-1}$, MCC discreteness and coherence-equilibrium effects suppress power, while large-scale ($k\ll {\xi }_{\Phi }^{-1}$) behaviour remains CDM-like.
• Black-hole mimicry for high mass: Massive MCCs approximate GR black-hole exteriors with high accuracy, consistent with strong-lensing and shadow measurements, while maintaining CEP-regulated interiors.

Thus RNF cosmology preserves the large-scale clustering success of CDM while predicting distinctive microphysical structure in dark-matter halos.

Two-metric effects from RNF reconstruction.

As shown in Appendix E, photons and matter couple to slightly different emergent metrics:

$$g_{\mu \nu }^{\left(\gamma \right)}\ne g_{\mu \nu }^{\left(m\right)},$$

because photons propagate as transverse chronon waves within each slice, whereas matter solitons are reconstructed across slices under TCP.

This produces subtle but testable phenomenology:

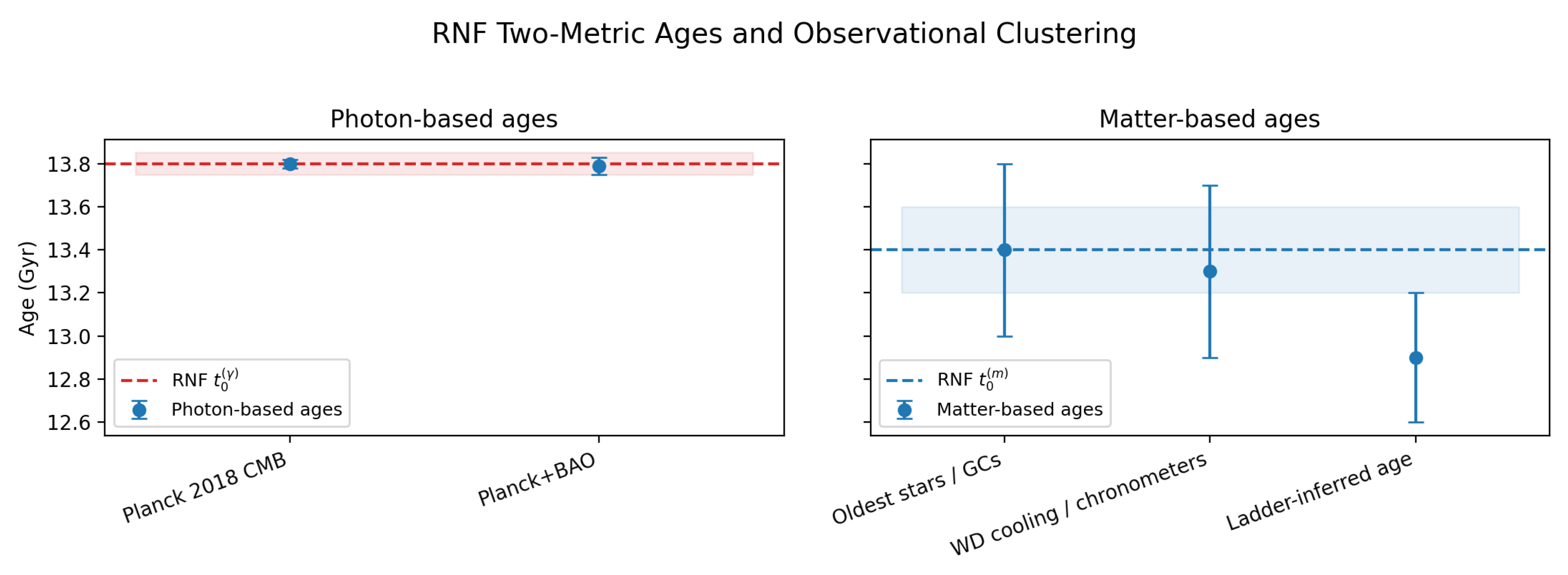
• BAO–SN distance offset: BAO relies on $g_{\mu \nu }^{\left(\gamma \right)}$, while SN luminosity distances trace $g_{\mu \nu }^{\left(m\right)}$, generating a small redshift-dependent mismatch.
• Growth-rate shifts:$f{\sigma }_8$ probes matter geodesics, whereas CMB and BAO infer expansion from photon geodesics.
• Lorentz invariance preserved: The Co-moving Concealment Principle ensures both metrics share identical local inertial frames, consistent with observational bounds.

These effects are cosmologically small but offer sharp discriminants between RNF and $\Lambda$CDM.

Summary.

Structure formation in RNF cosmology rests on four pillars:

• Primordial perturbations sourced by TCP coherence dynamics during RNF-domain coarsening, not by inflaton fluctuations.
• GR-like linear evolution emerging from the hydrodynamic limit of chronon alignment.
• A cold MCC dark-matter sector that matches CDM on large scales while predicting microphysical halo structure at small scales.
• Two-metric phenomenology yielding subtle but testable redshift-dependent differences between matter- and light-based observables.

Accordingly, RNF cosmology reproduces the large-scale successes of $\Lambda$CDM while providing a microphysical and generative origin for perturbations, coherence, dark matter, and small but measurable departures from the standard model. A full quantitative comparison will ultimately require Boltzmann codes adapted to RNF hypersurface propagation and chronon-based perturbation evolution.

8. Cosmic Expansion as a Local Geometric Response to TCP Curvature Restoration

In RNF cosmology, a spatial slice $\Sigma \left(t\right)$ is not a pre-existing three-dimensional manifold but the instantaneously reconstructed boundary of the newly aligned chronon domain. The Real–Now–Front (RNF) is a propagating 3D hypersurface in a 4D pre-geometric medium; the induced spatial metric ${\gamma }_{ij}\left(t\right)$ arises from chronon alignment obeying the Temporal Coherence Principle (TCP). Geometry, curvature, and local scale are therefore outputs of the alignment process, not background structures.

This viewpoint is aligned with ADM hypersurface geometry [23,40,42] and with emergent-gravity approaches in which curvature is a collective, pattern-dependent response of a microscopic medium [16,17,18,19].

Crucially:

Cosmic expansion is not driven by stress–energy or vacuum pressure, but arises whenever the curvature density of the aligned pattern lies below the preferred TCP value ${\rho }^{★}$.

TCP always attempts to restore the local “defect + curved vacuum” structure to the coherence–curvature density ${\rho }^{★}$ associated with a stable chronon pattern. Thus:

• If the reconstructed slice is under-curved (${\rho }_{\mathrm{curv}}<{\rho }^{★}$), TCP lowers its energy by stretching the metric: cosmic expansion.
• If the curvature is near ${\rho }^{★}$, TCP produces only mild adjustments, yielding equilibrium GR and FRW-like evolution.
• If the curvature is too large (${\rho }_{\mathrm{curv}}>{\rho }^{★}$), TCP lowers its energy by shrinking the metric: collapse into MCCs.

These three responses constitute the TCP bifurcation that governs the global evolution of the Universe.

We now derive the corresponding geometric law of expansion and show that accelerated expansion emerges generically from the stretching branch.

8.1. Local Reconstruction and the TCP Curvature–Density Condition

When the RNF advances by a normal distance $\delta \ell$ into an unaligned region, a thin new layer of chronons becomes aligned. Because the pre-geometric domain carries no metric, the induced metric on the new layer is selected by TCP so as to minimize the local alignment energy.

A central consequence is that TCP drives each newly reconstructed slice toward a preferred coherence–curvature density ${\rho }^{★}$. In the language developed later (Sec. Section 8.5), this density is a coarse-grained quantity obtained by dividing the integrated local coherence content of the inherited chronon pattern by the assigned spatial volume:

$${\rho }_{\mathrm{coh}}\left(t\right)⟶{\rho }^{★}.$$

(16)

Because RNF reconstruction copies the internal chronon pattern while allowing the metric volume to adjust, deviations from ${\rho }^{★}$ are corrected primarily through local volume rescaling. Schematically, for a comoving patch of physical volume $V_3\left(t\right)$,

$${\rho }_{\mathrm{coh}}\sim {\displaystyle \frac{\mathrm{coherence}\mathrm{content}\mathrm{of}\mathrm{the}\mathrm{local}\mathrm{pattern}}{V_3\left(t\right)}}.$$

Accordingly:

• if ${\rho }_{\mathrm{coh}}<{\rho }^{★}$, TCP restores coherence by metric stretching ($V_3$ increases);
• if ${\rho }_{\mathrm{coh}}>{\rho }^{★}$, TCP restores coherence by metric shrinking ($V_3$ decreases).

RNF advancement therefore induces a local rescaling

$$V_3(t+\delta t)=s\left(t\right)V_3\left(t\right),s\left(t\right)>1\left(\mathrm{stretching}\right),s\left(t\right)<1\left(\mathrm{shrinking}\right).$$

The stretching branch underlies cosmic expansion, while the shrinking branch leads to local collapse and the formation of Micro Chronon Condensates (MCCs). A quantitative formulation of coherence density, metric rescaling, and the associated TCP bifurcation is developed in Sec. Section 8.5.

8.2. Hubble Law from Hypersurface Kinematics

Let ${\gamma }_{ij}\left(t\right)$ be the induced metric on $\Sigma \left(t\right)$. When the RNF advances by $\delta \ell$ along its normal $n^{\mu }$, the ADM evolution identity gives

$${\gamma }_{ij}(t+\delta t)={\gamma }_{ij}\left(t\right)+2K_{ij}\left(t\right)\delta \ell +O\left(\delta {\ell }^2\right),$$

(17)

where $K_{ij}$ is the extrinsic curvature.

In homogeneous and isotropic regions:

$${\gamma }_{ij}=a^2\left(t\right){\delta }_{ij},K_{ij}=H\left(t\right){\gamma }_{ij}.$$

Substituting into (17) yields

$$a(t+\delta t)=a\left(t\right)[1+H(t)\delta \ell ],$$

implying the Hubble relation

$${\displaystyle \frac{\dot{a}}{a}}=H\left(t\right).$$

(18)

Thus the FRW expansion law is a geometric identity arising solely from the motion of the RNF hypersurface.

8.3. Why Expansion is Generic in the Large-Scale Universe

The early Universe after percolation (Section 6) is extremely smooth and nearly flat due to TCP curvature smoothing. Such a region is typically under-curved relative to the preferred curvature density ${\rho }^{★}$ because curvature associated with defects has been diluted.

Thus the large-scale Universe enters the stretching branch:

$${\rho }_{\mathrm{curv}}\left(t\right)<{\rho }^{★}⟹s\left(t\right)>1⟹a(t+\delta t)>a\left(t\right).$$

Cosmic expansion is therefore not an exotic dynamical phenomenon—it is the default response of the chronon medium to under-curvature. No vacuum energy or negative-pressure fluid is required [20,21].

8.4. Local RNF Expansion Theorem

Theorem 8.1

(Local RNF Expansion Theorem). Let $\Sigma \left(t\right)$ be an RNF slice with metric ${\gamma }_{ij}\left(t\right)$ and extrinsic curvature $K_{ij}\left(t\right)$. Assume:

• the RNF advances by $\delta \ell >0$ during $\delta t$,
• TCP drives the curvature density to the preferred value ${\rho }^{★}$,
• the patch is isotropic: ${\gamma }_{ij}=a^2\left(t\right){\delta }_{ij}$.

Then the induced scale factor satisfies:

$${\displaystyle \frac{\dot{a}\left(t\right)}{a\left(t\right)}}=H\left(t\right),$$

where $H\left(t\right)$ is one-third the trace of $K_{ij}$:

$$K_{ij}\left(t\right)=H\left(t\right){\gamma }_{ij}\left(t\right).$$

Proof. 

Insert isotropy into the ADM evolution law

$${\gamma }_{ij}(t+\delta t)={\gamma }_{ij}\left(t\right)+2H\left(t\right){\gamma }_{ij}\left(t\right)\delta \ell .$$

This gives

$$a(t+\delta t)=a\left(t\right)[1+H(t)\delta \ell ].$$

Taking $\delta t\to 0$ yields the differential identity

$$\dot{a}/a=H\left(t\right).$$

TCP curvature restoration guarantees that this rescaling is required to bring ${\rho }_{\mathrm{curv}}\to {\rho }^{★}$, completing the proof. □

Interpretation.

The FRW expansion law is not a dynamical equation—it is the local kinematic imprint of RNF propagation plus TCP curvature restoration.

8.5. Metric Stretching/Shrinking as Coherence-Density Restoration

1. A local coherence scalar and its density.

Let ${\Phi }_{\mu }$ be the ontological chronon alignment field on the underlying smooth manifold, and let $\Sigma$ be an RNF slice with induced spatial metric $h_{ij}$ and volume element $\sqrt{h}{d}^{3}x$. Introduce a nonnegative coherence functional density $\mathcal{C}\left(x\right)$ built from local chronon structure (one convenient choice is the simplest quadratic alignment measure)

$$\mathcal{C}\left(x\right):=\mathcal{C}\left({\nabla }_i{\Phi }_{\mu },{\Omega }_{ij},\dots \right)\ge 0,\mathrm{e}.\mathrm{g}.\mathcal{C}\left(x\right)=1-\alpha {\nabla }_i{\Phi }_{\mu }{\nabla }^i{\Phi }^{\mu }+\dots ,$$

(19)

where ${\Omega }_{ij}$ denotes the (coarse-grained) symplectic/vorticity two-form associated with the aligned phase and $\alpha >0$ sets units.

For any comoving domain $\mathcal{D}\subset \Sigma$, define the coherence content

$$Q_{\mathcal{D}}:={\int }_{\mathcal{D}}\mathcal{C}\left(x\right)\sqrt{h}{d}^{3}x,$$

(20)

the physical volume

$$V_{\mathcal{D}}:={\int }_{\mathcal{D}}\sqrt{h}{d}^{3}x,$$

(21)

and the coherence density

$${\rho }_{\mathrm{coh}}:={\displaystyle \frac{Q_{\mathcal{D}}}{V_{\mathcal{D}}}}.$$

(22)

2. The RNF copying constraint: “pattern fixed, volume adjustable.”

RNF reconstruction copies the internal chronon pattern slice-by-slice. To leading order in a single RNF step, this means that the comoving distribution of $\mathcal{C}\left(x\right)$ is inherited, so $Q_{\mathcal{D}}$ is approximately conserved across the step,

$$Q_{\mathcal{D}}(t+\Delta t)\simeq Q_{\mathcal{D}}\left(t\right).$$

(23)

TCP therefore restores ${\rho }_{\mathrm{coh}}$ primarily by changing the metric volume $V_{\mathcal{D}}$ assigned to the fixed pattern.

3. Metric stretching/shrinking and the density scaling law.

Model the immediate TCP response within $\mathcal{D}$ as an (approximately) isotropic rescaling of the induced 3-metric,

$$h_{ij}⟶h_{ij}^{\prime }=s^2{h}_{ij},s=s(x,t)>0.$$

(24)

Then

$$\sqrt{h}⟶\sqrt{h^{\prime }}=s^3\sqrt{h},V_{\mathcal{D}}^{\prime }=s^3{V}_{\mathcal{D}}.$$

(25)

Using $Q_{\mathcal{D}}^{\prime }\simeq Q_{\mathcal{D}}$ from Equation (23), the coherence density transforms as

$${\rho }_{\mathrm{coh}}^{\prime }={\displaystyle \frac{Q_{\mathcal{D}}^{\prime }}{V_{\mathcal{D}}^{\prime }}}\simeq {\displaystyle \frac{Q_{\mathcal{D}}}{s^3{V}_{\mathcal{D}}}}={\displaystyle \frac{{\rho }_{\mathrm{coh}}}{s^3}}.$$

(26)

Hence metric stretching ($s>1$) dilutes coherence density, while metric shrinking ($s<1$) concentrates it:

$$s>1\Rightarrow {\rho }_{\mathrm{coh}}^{\prime }<{\rho }_{\mathrm{coh}},s<1\Rightarrow {\rho }_{\mathrm{coh}}^{\prime }>{\rho }_{\mathrm{coh}}.$$

(27)

4. Preferred density and the TCP “restoration” rule.

TCP selects a preferred value ${\rho }^{★}$ (set by chronon microphysics), implemented as minimization of a local effective potential $U\left({\rho }_{\mathrm{coh}}\right)$ with a minimum at ${\rho }^{★}$:

$$U^{\prime }\left({\rho }^{★}\right)=0,U^{\prime \prime }\left({\rho }^{★}\right)>0.$$

(28)

Given ${\rho }_{\mathrm{coh}}$ on the inherited pattern, the instantaneous TCP rescaling chooses s so that ${\rho }_{\mathrm{coh}}^{\prime }$ moves toward ${\rho }^{★}$:

$${\rho }_{\mathrm{coh}}^{\prime }={\displaystyle \frac{{\rho }_{\mathrm{coh}}}{s^3}}\approx {\rho }^{★}⟹s\approx {\left({\displaystyle \frac{{\rho }_{\mathrm{coh}}}{{\rho }^{★}}}\right)}^{1/3}.$$

(29)

Therefore:

$${\rho }_{\mathrm{coh}}>{\rho }^{★}\Rightarrow s>1\left(\mathrm{stretching}/\mathrm{expansion}\right),{\rho }_{\mathrm{coh}}<{\rho }^{★}\Rightarrow s<1\left(\mathrm{shrinking}/\mathrm{collapse}\right),$$

(30)

while ${\rho }_{\mathrm{coh}}\approx {\rho }^{★}$ yields $s\approx 1$ (near-equilibrium, GR and FRW-like evolution).

5. Connection to extrinsic curvature and the local Hubble law.

In Gaussian normal slicing, ${\partial }_{\ell }ln\sqrt{h}=-K$ so the local volume-creation rate $\Gamma :=V^{-1}dV/d\ell$ satisfies $\Gamma =-\langle K\rangle$. For an isotropic scaling $h_{ij}\propto a^2$, one has $\Gamma =3a^{-1}da/d\ell$, and therefore $H=\dot{a}/a=\Gamma /3$ (Appendix C). The sign of $\Gamma$ matches the TCP branch:

$$s>1\Rightarrow \Gamma >0\Rightarrow H>0,s<1\Rightarrow \Gamma <0\Rightarrow H<0.$$

(31)

Interpretation.

The coherence density ${\rho }_{\mathrm{coh}}$ measures the amount of aligned chronon structure per unit physical volume on an RNF slice. Metric rescaling changes only the denominator of Equation (22) during reconstruction, while the numerator is fixed by RNF pattern copying. Thus expansion and contraction are not dynamical responses to stress–energy, but purely geometric operations required to restore coherence density toward its preferred value ${\rho }^{★}$.

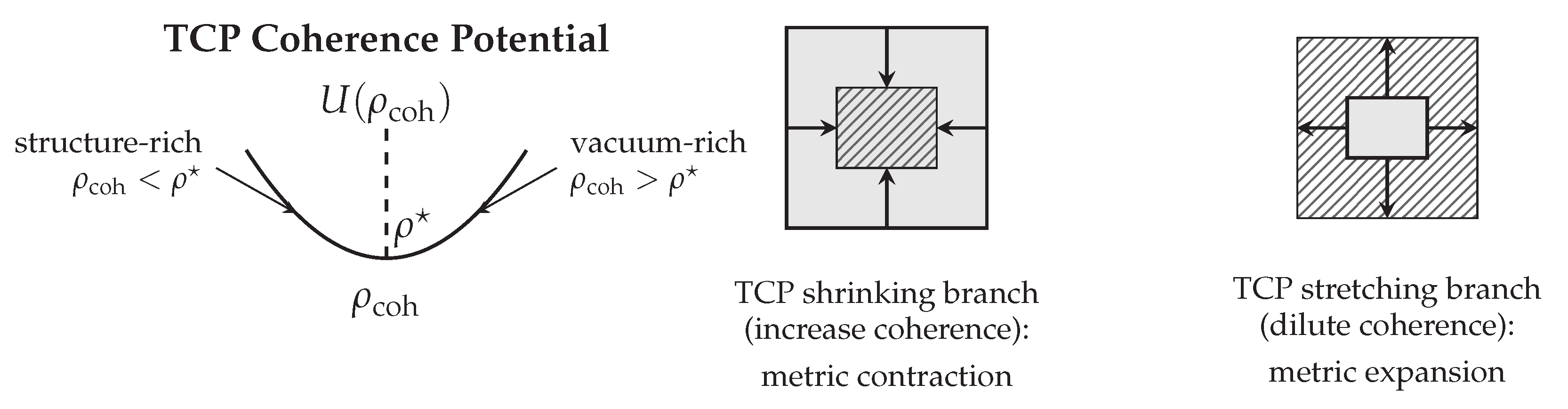
8.6. TCP Bifurcation: Stretching, Equilibrium, and Collapse

The Temporal Coherence Principle admits three distinct local responses, depending on the coherence density ${\rho }_{\mathrm{coh}}$ inherited by a comoving patch during RNF reconstruction:

• Stretching branch (${\rho }_{\mathrm{coh}}>{\rho }^{★}$). The copied patch is vacuum-rich and therefore over-coherent. TCP restores coherence by diluting ${\rho }_{\mathrm{coh}}$ through metric expansion ($s>1$). This branch produces local Hubble-like expansion and dominates void regions.
• Equilibrium branch (${\rho }_{\mathrm{coh}}\approx {\rho }^{★}$). Coherence density is near its preferred value. TCP does not drive significant volume change ($s\simeq 1$) and instead acts primarily through redistribution of curvature within an approximately fixed volume. This regime yields standard GR-like dynamics and FRW evolution.
• Shrinking branch (${\rho }_{\mathrm{coh}}<{\rho }^{★}$). The patch is structure-rich and under-coherent. TCP increases ${\rho }_{\mathrm{coh}}$ by contracting the metric ($s<1$), amplifying curvature until CEP saturation halts collapse. The endpoint is a stable Micro Chronon Condensate (MCC) or, at higher mass, a CEP-regulated black-hole interior.

These three responses form a genuine TCP bifurcation. Cosmic expansion, ordinary gravity, and compact-object formation therefore arise as different local geometric responses of the same chronon medium to coherence-density restoration.

8.7. Late-Time Acceleration from RNF Propagation

At late cosmic times, large-scale regions are expected to be increasingly vacuum-dominated as structure formation localizes coherence into compact objects. Such regions generically satisfy ${\rho }_{\mathrm{coh}}>{\rho }^{★}$ and therefore lie on the stretching branch of TCP.

As a result, RNF reconstruction continues to induce metric expansion in these regions. Whether this expansion asymptotically approaches a constant-rate (de Sitter–like) behavior or exhibits slow evolution depends on the chronon stiffness parameters governing the effective potential $U\left({\rho }_{\mathrm{coh}}\right)$ and the relaxation timescale of TCP restoration.

Thus RNF cosmology predicts late-time acceleration as a geometric response to vacuum dominance, without invoking vacuum energy. Determining the precise functional form of $H\left(z\right)$ requires a quantitative derivation of chronon microphysics and is deferred to future work.

8.8. Summary

In RNF cosmology, cosmic expansion follows directly from chronon microphysics and RNF reconstruction:

• RNF advancement continuously generates newly aligned spatial slices with no preset physical scale.
• RNF copying preserves the internal chronon pattern of each patch, fixing its coherence content while leaving its metric volume adjustable.
• The Temporal Coherence Principle restores the local coherence density toward a preferred value ${\rho }^{★}$ by metric stretching (${\rho }_{\mathrm{coh}}>{\rho }^{★}$) or shrinking (${\rho }_{\mathrm{coh}}<{\rho }^{★}$).
• In near-equilibrium regions this produces GR-like/FRW-like expansion as a geometric consequence of hypersurface kinematics.
• Vacuum-dominated regions preferentially lie on the stretching branch, while over-structured regions collapse into CEP-regulated solitonic objects (MCCs).

Cosmic expansion, compact-object formation, and late-time acceleration thus emerge as distinct local geometric responses of a single mechanism: TCP-driven coherence-density restoration during RNF hypersurface propagation.

Figure 7 illustrates how the Temporal Coherence Principle (TCP) determines whether a comoving patch expands or collapses as the RNF advances.

9. Collapsed Objects and Cold Dark Matter in RNF Cosmology

Cosmic expansion and the formation of collapsed objects originate from the same local TCP reconstruction mechanism. As shown in Section 8, when the RNF aligns a new layer of chronons, TCP compares the inherited curvature density of the copied pattern to the preferred value ${\rho }^{★}$ fixed by chronon microphysics. This comparison determines whether the induced metric must stretch or shrink:

$$\left(\mathrm{i}\right)\mathrm{Stretching}\mathrm{branch}\text{:}{\rho }_{\mathrm{curv}}\left(t\right)<{\rho }^{★},\left(\mathrm{ii}\right)\mathrm{Shrinking}\mathrm{branch}\text{:}{\rho }_{\mathrm{curv}}\left(t\right)>{\rho }^{★}.$$

The stretching branch yields cosmic expansion. The shrinking branch produces local collapse: a comoving region is assigned a smaller metric volume on the next RNF slice, raising its curvature density until the Chronon Exclusivity Principle (CEP) halts compression. This mechanism is analogous to curvature focusing in GR [63] and to pattern collapse in nonlinear media [31,32].

Cosmic expansion and solitonic dark matter are two outcomes of a single TCP curvature–restoration bifurcation.

This section develops the microphysics of the shrinking branch, the CEP regulator, and the resulting spectrum of collapsed, dark, nonsingular objects.

9.1. TCP Shrinking Branch and the Onset of Collapse

If the inherited chronon pattern in a local patch carries excess curvature relative to the preferred density ${\rho }^{★}$, TCP must shrink the induced metric to raise the curvature density toward its target:

$$s\left(t\right)<1⟹V_3(t+\delta t)<V_3\left(t\right).$$

The reduced metric volume increases curvature and gradient energy, driving the patch into a collapse regime reminiscent of GR curvature focusing [63]. As curvature increases, the patch eventually encounters a microphysical limit: the Chronon Exclusivity Principle.

Collapse in RNF cosmology is therefore:

• a local, microphysical effect of TCP reconstruction,
• triggered purely by geometric mismatch (${\rho }_{\mathrm{curv}}>{\rho }^{★}$),
• regulated by CEP at high curvature.

This mechanism mirrors soliton formation in nonlinear field theories [72,75], but arises here from the microscopic alignment dynamics of spacetime itself.

9.2. Chronon Exclusivity Principle (CEP)

Chronon Field Theory assigns each solitonic pattern element a quantized symplectic-curvature flux. The Chronon Exclusivity Principle states that a finite spacetime cell cannot support curvature density beyond a fixed microphysical limit:

$${\displaystyle \frac{1}{V_{\mathrm{cell}}}}{\int }_{V_{\mathrm{cell}}}\Omega \le {\Omega }_{max}={\displaystyle \frac{\hslash }{v_0}},$$

(32)

where $\Omega$ is the symplectic curvature density and $v_0$ the chronon stiffness scale.

As TCP-driven collapse raises ${\rho }_{\mathrm{curv}}$, the curvature density approaches ${\Omega }_{max}$. Once this saturation occurs, further compression becomes impossible: the chronon medium transitions to an effectively incompressible, finite-density state. The result is a minimal-radius chronon core—the CEP analog of a topological soliton core in other nonlinear systems [72].

This replaces the singular interior of GR collapse [63] with a nonsingular, microphysically regulated structure.

9.3. Core Radius and the Universal $M^{1/3}$ Law

A CEP-saturated core contains N curvature quanta, with $N\propto M$ because mass corresponds to integrated curvature content in ChFT. Since each quantum occupies a minimal cell,

$$V_{\mathrm{core}}\propto N\propto M,$$

implying the universal scaling law

$$R_{\mathrm{core}}\left(M\right)\propto M^{1/3}.$$

(33)

This $M^{1/3}$ behavior parallels the scaling of solitonic and condensate cores in several nonlinear systems [66]. A key implication is

$$R_{\mathrm{core}}\ll R_{\mathrm{S}}\left(M\right)\mathrm{for}\mathrm{sufficiently}\mathrm{large}M,R_{\mathrm{core}}\gg R_{\mathrm{S}}\left(M\right)\mathrm{for}\mathrm{sufficiently}\mathrm{small}M,$$

which determines whether the final object is an MCC or a CEP black hole.

9.4. MCCs vs. Black Holes: Two Outcomes of the Same Soliton Core

A CEP core forms first. Whether a horizon develops is governed by the standard Schwarzschild condition:

1. Micro Chronon Condensates (MCCs).

If

$$R_{\mathrm{core}}\left(M\right)>R_{\mathrm{S}}\left(M\right),$$

the configuration is horizonless. MCCs are:

• nonsingular solitonic objects,
• extremely compact (near Planck scale for minimal mass),
• absolutely stable,
• completely dark (Section 9.5).

2. CEP-regulated black holes.

If

$$R_{\mathrm{core}}\left(M\right)<R_{\mathrm{S}}\left(M\right),$$

the exterior geometry is standard Schwarzschild/Kerr, but the interior is non-singular and saturated by a finite-density CEP core. This resembles gravastar-like interiors [76] but with a microphysical, not phenomenological, origin.

9.5. Gauge Freezing and Electromagnetic Darkness

Gauge fields in ChFT arise from twist modes of the chronon-alignment bundle. Inside a CEP-saturated core, alignment collapses to a single orientation and all twist modes vanish:

$$F_{\mu \nu }{|}_{\mathrm{core}}=0.$$

This resembles gauge-structure freezing in certain condensed phases [16,17] and implies:

• no electromagnetic or Yang–Mills charge can be supported,
• no flux or radiation can escape from the core,
• gauge fields cannot propagate through the interior.

Thus MCCs are intrinsically dark without hidden sectors or new particles, consistent with observational constraints on compact dark matter [68].

9.6. Stability and Absence of Evaporation

Because quantum vacuum fluctuations do not exist in the chronon medium, Hawking radiation—which relies on vacuum-mode excitation near a horizon [77]—works differently [8]. The emission is exponentially suppressed leakage of curvature waves:

$$P_{\mathrm{emit}}\propto exp\left[-\alpha {\displaystyle \frac{R_{\mathrm{core}}}{{\xi }_{\Phi }}}\right],\alpha >0.$$

Both MCCs and CEP black holes are therefore stable over cosmological times, much like solitonic compact objects in other theories [78].

9.7. Formation of MCCs During RNF Alignment

During early RNF percolation:

• domain boundaries trap symplectic curvature, similar to defect formation in quenched phase transitions [15],
• over-curved TCP patches enter the shrinking branch,
• CEP saturation produces minimal-radius cores,
• these cores become MCCs.

Even extremely small trapping fractions,

$$f_{\mathrm{trap}}\sim {10}^{-60}--{10}^{-50},$$

naturally yield the observed dark-matter density, paralleling estimates for primordial compact objects [68].

Thus MCCs form automatically during spacetime genesis.

9.8. MCCs as Cold, Collisionless Dark Matter

MCCs satisfy all criteria for cold dark matter (CDM) [56,58,59]:

• Compactness: minimal radii near the Planck scale for low-mass cores.
• Electromagnetic darkness:$F_{\mu \nu }=0$ inside the core.
• Collisionlessness:${\sigma }_{\mathrm{self}}\sim R_{\mathrm{core}}^2$ is far below observational limits.
• Gravitational clustering: identical to standard CDM on large scales.

No new matter species or hidden sectors are required.

9.9. Unified Family of Collapsed Objects

RNF cosmology predicts a continuous spectrum of collapsed configurations:

• MCCs: horizonless dark-matter solitons.
• Chronon stars: intermediate, horizonless compact objects stabilized by CEP.
• Astrophysical black holes: GR exterior with a CEP-regulated, nonsingular interior.

All arise from the same microphysical pathway:

$$\mathrm{TCP}\mathrm{shrinking}⟶\mathrm{CEP}\mathrm{saturation}.$$

9.10. Cosmological Summary

• TCP curvature comparison yields two branches: stretching (expansion) and shrinking (collapse).
• The shrinking branch raises curvature until CEP saturation.
• CEP produces a minimal finite-density core with $R_{\mathrm{core}}\propto M^{1/3}$.
• If $R_{\mathrm{core}}>R_{\mathrm{S}}$, an MCC forms; if $R_{\mathrm{core}}<R_{\mathrm{S}}$, a CEP black hole forms.
• MCCs are stable, cold, collisionless, and electromagnetically inert.
• Thus dark matter, black holes, and expansion share a single origin: TCP–CEP microphysics of the chronon field.

RNF cosmology provides a unified, generative account of collapse, compact-object formation, and dark matter without invoking new particles or exotic fields.

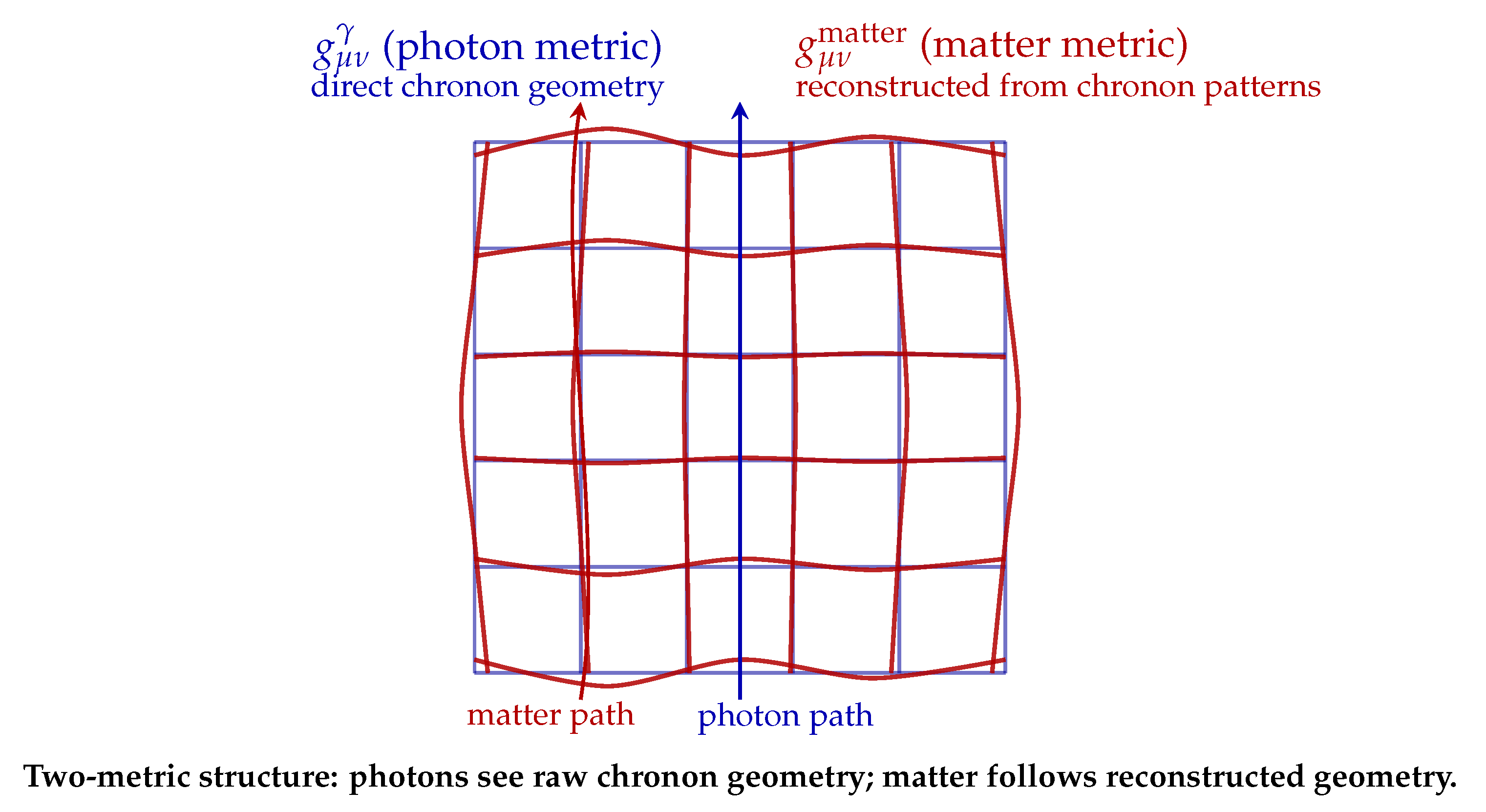
10. Photon vs. Matter Geometry: A Two-Metric Framework

A distinctive prediction of RNF cosmology is that photons and massive matter probe slightly different effective geometries. The origin is microphysical: photons propagate as pattern-preserving excitations within each RNF slice, while massive matter is reconstructed slice-by-slice from persistent internal chronon patterns. Because these two classes of excitations couple differently to chronon curvature and to RNF advancement, their long-distance propagation is governed by two closely related but not identical metrics.

Crucially, the two-metric structure is not imposed. It emerges generatively from the chronon field and its TCP dynamics. On local scales the two metrics coincide to extremely high precision, ensuring operational Lorentz invariance and complete agreement with laboratory, solar-system, and binary-pulsar tests [38,39]. Small differences arise only through gradients of the chronon field and accumulate only over cosmological distances.

10.1. Suppression of Photon–Matter Cone Differences

To leading order, the difference between the photon and matter metrics can be written as

$$g_{\mu \nu }^{\left(\gamma \right)}-g_{\mu \nu }^{\left(m\right)}={ϵ}_{\mu \nu },{ϵ}_{\mu \nu }\propto {\displaystyle \frac{({\nabla }_{\mu }\Phi )({\nabla }_{\nu }\Phi )}{{\Lambda }_{\mathrm{TCP}}^2}},$$

(34)

where ${\Lambda }_{\mathrm{TCP}}$ is the chronon stiffness scale controlling curvature restoration under TCP. Thus:

$${ϵ}_{\mu \nu }\sim {|\nabla \Phi |}^2,$$

showing that photon–matter cone differences are quadratically suppressed in chronon-misalignment gradients.

In an FRW background,

$${\nabla }_i\Phi =0,$$

so the mismatch vanishes identically:

$$g_{\mu \nu }^{\left(\gamma \right)}=g_{\mu \nu }^{\left(m\right)}(\mathrm{exact}\mathrm{in}\mathrm{FRW}).$$

Nonzero differences arise only in regions with large-scale alignment gradients—primarily voids, early-time defects, or remnant domain boundaries [14,31,46]. Even in such regions, typical magnitudes satisfy

$$|{ϵ}_{\mu \nu }|\lesssim {10}^{-6}--{10}^{-7},$$

well below multimessenger bounds [36,37].

Thus the two-metric structure is fully compatible with Lorentz invariance tests and astrophysical timing constraints.

10.2. Photon Metric from Pattern-Preserving Propagation

Photon excitations are transverse, pattern-preserving fluctuations of the aligned chronon field. Linearizing the TCP evolution equation around a smoothly aligned background yields the null condition

$$g_{\mu \nu }^{\left(\gamma \right)}{k}^{\mu }{k}^{\nu }=0,$$

(35)

where $g_{\mu \nu }^{\left(\gamma \right)}$ is determined by the local chronon alignment texture and the chronon signal speed $c_{\Phi }$.

Because photons do not undergo RNF-mediated pattern reconstruction, they propagate along the “bare” chronon null cone. All photon-based cosmological observables therefore probe $g_{\mu \nu }^{\left(\gamma \right)}$: CMB anisotropies [58,59], photon-based BAO distances [56,60], and luminosity distances from Type Ia supernovae [61].

10.3. Matter Metric from RNF Reconstruction

Massive matter corresponds to persistent chronon patterns whose internal structure is copied forward by RNF advancement. Their coarse-grained trajectories follow an emergent timelike metric

$$g_{\mu \nu }^{\left(m\right)}{u}^{\mu }{u}^{\nu }=-1,$$

(36)

whose coefficients incorporate:

• the accumulation of small reconstruction biases over many RNF slices;
• renormalization effects from pattern persistence;
• suppressed sensitivity to residual curvature gradients.

Each effect is individually tiny ($\lesssim {10}^{-7}$ on Mpc scales) but can accumulate over Gpc distances, producing measurable offsets between photon and matter distance indicators in principle.

10.4. Why Observations Do Not Rule This Out

(1) FRW symmetry eliminates the difference at the background level.

Because ${\nabla }_i\Phi =0$ in FRW evolution, the two metrics coincide to better than one part in ${10}^{15}$. Hence all standard cosmological analyses— CMB [58,59], BAO [56,60], and SNe Ia [61]— are unchanged at leading order.

(2) Deviations arise only in void-scale curvature gradients.

Chronon alignment gradients primarily occur in cosmic voids, where RNF curvature restoration operates most strongly. Even there, the photon–matter cone offset satisfies

$${\displaystyle \frac{\Delta c}{c}}\lesssim {10}^{-6},$$

well below timing constraints from GRBs, TeV blazars, and joint gravitational-wave–gamma-ray observations [36,37].

(3) Current cosmological precision is insufficient to detect RNF-level differences.

DESI, Planck, and SH0ES analyses assume a single metric and are sensitive only to $\gtrsim {10}^{-3}$ variations in distance–redshift relations. RNF predicts effects at the ${10}^{-5}$–${10}^{-6}$ level—below current detection thresholds but within reach of future high-precision surveys.

Thus the RNF two-metric framework is observationally viable, theoretically natural, and provides concrete, testable predictions for next-generation cosmology.

Figure 8 is a schematic illustration of the two-metric structure.

10.5. Cosmological Consequences

The small separation between $g_{\mu \nu }^{\left(\gamma \right)}$ and $g_{\mu \nu }^{\left(m\right)}$ produces three main observational consequences:

• Photon vs. matter redshift. Redshift inferred from photon geodesics differs slightly from that implied by matter kinematics.
• Sandage–Loeb redshift drift. The photon redshift drift ${\dot{z}}_{\gamma }$ probes the photon metric, leading to a characteristic offset from $\Lambda$CDM expectations [51].
• BAO–SN offset. BAO scales follow matter geodesics [60], while SNe Ia probe photon luminosity distances [61]. A mild two-metric difference naturally produces the observed small BAO–SN discrepancy.

These effects do not affect local Lorentz invariance but become noticeable after Gpc-scale propagation.

10.6. Empirical Age Clustering as Evidence for the Two-Metric Structure

Photon-based cosmic age estimates (CMB and BAO) [2,58,59] cluster around

$$t_0^{\left(\gamma \right)}\simeq 13.8\mathrm{Gyr},$$

while matter-based age indicators— white-dwarf cooling [65], cosmic chronometers [64], globular cluster dating [62], and ladder-based ages [61]— form a second cluster around

$$t_0^{\left(m\right)}\simeq 13.3--13.4\mathrm{Gyr}.$$

This persistent offset is precisely the signature expected from a gradient-suppressed but cosmologically cumulative difference between photon and matter metrics.

These observational patterns do not signal tension but instead constitute a natural prediction of RNF’s two-metric cosmological framework.

As shown in Figure 9, the persistent $\sim 0.4$–$0.5$ Gyr offset between the two groups is precisely the qualitative signature predicted by RNF’s two-metric structure. Rather than indicating tension, the observed age clustering is naturally explained by RNF cosmology.

11. Non-Exhaustion and the Fate of Expansion

A natural question for RNF cosmology is whether the advancing Real–Now–Front (RNF) might eventually “run out’’ of pre-geometric domain. This section shows that such depletion is conceptually impossible. In emergent-spacetime frameworks—including analogue-gravity systems [66], thermodynamic gravity [55], and superfluid-inspired models [33]—geometric quantities exist only after ordering. RNF cosmology follows the same principle: ahead of the RNF the chronon field is unaligned and therefore carries no metric. Without a metric there is no notion of size, extent, or volume; the unaligned domain cannot be “used up’’ because nothing in it is geometrically measurable.

Thus the depletion concern is ill-posed: cosmic expansion persists for as long as the RNF propagates.

11.1. Metric-Free Pre-Geometric Domain

Ahead of the alignment front, the chronon field has not yet acquired coherent orientation and cannot support spatial geometry. The pre-geometric domain possesses:

• no metric or volume element,
• no curvature tensors or extrinsic geometry,
• no diffeomorphism-invariant notion of distance or extent.

It is not an “empty region of space’’ but a differentiable manifold without geometric structure, consistent with emergent-gravity paradigms [16,55]. Only when the RNF arrives does the Temporal Coherence Principle (TCP) assign a metric $g_{ij}[\Phi ]$ through chronon alignment [12,13].

Because geometry does not exist ahead of the RNF, the claim that the RNF might “run out of domain’’ is not meaningful. Exhaustion presupposes a geometric measure, which is absent here.

Because the metric is emergent, the pre-geometric domain has no quantifiable size and therefore cannot be exhausted.

11.2. Non-Exhaustion Theorem

Theorem 11.1

(Non-Exhaustion of the Pre-Geometric Domain).

Let $\mathcal{U}$ denote the unaligned domain ahead of the RNF, and let $\Sigma \left(t\right)$ be an aligned slice with induced metric $g_{ij}\left(t\right)$. Assume:

(a)

$\mathcal{U}$ carries no metric or volume form prior to alignment;

(b)

alignment induces $g_{ij}\left(t\right)$ via TCP dynamics;

(c)

RNF propagation maps regions of $\mathcal{U}$ into new aligned slices $\Sigma (t+\Delta t)$.

Then:

(i)

no volume function exists on $\mathcal{U}$ prior to alignment;

(ii)

volumes defined on aligned slices cannot be extended to $\mathcal{U}$;

(iii)

depletion of $\mathcal{U}$ is undefined and therefore impossible.

Conclusion.The RNF can always advance into $\mathcal{U}$; “running out of domain’’ is not a well-posed physical concept.

Thus the intuitive image of the Universe “hitting a boundary’’ results from mistakenly assigning geometric properties to a non-geometric region.

11.3. Eternal Expansion

Non-exhaustion has an immediate cosmological implication: as long as the RNF propagates, the Universe expands.

The expansion law derived in Section 8 shows that the Hubble parameter is determined by the extrinsic curvature of the advancing hypersurface:

$$H\left(t\right)={\displaystyle \frac{\dot{a}}{a}}=(\mathrm{mean}\mathrm{curvature}\mathrm{of}\mathrm{the}\mathrm{RNF}\mathrm{slice}).$$

Whenever the RNF advances outward into the pre-geometric domain, the induced 3D geometry stretches, and $a\left(t\right)$ increases. Since the pre-geometric region cannot be depleted, this stretching can continue indefinitely.

The late-time behavior depends on the asymptotic statistics of RNF propagation:

• If the RNF velocity approaches a constant$c_{\Phi }$, then the mean curvature saturates and

  $$H\left(t\right)⟶H_{\infty }>0,$$

  producing late-time accelerated expansion without invoking vacuum energy.
• If RNF microphysics slow the front, the expansion rate gradually decreases, but cannot reach zero unless the front completely halts.
• Expansion cannot end due to exhaustion: since the pre-geometric domain has no intrinsic measure, RNF propagation is never limited by geometric depletion.

Thus RNF cosmology predicts that cosmic expansion is not driven by stress–energy or vacuum pressure, but is a purely kinematic consequence of the advancing generative boundary of spacetime.

As long as the RNF advances, the Universe expands; as long as the asymptotic propagation rate remains positive, the expansion accelerates.

12. A Self-Tuning Universe and the Unified Dark Sector

RNF cosmology, combined with the TCP reconstruction law, reveals a new feature of cosmic evolution: the Universe dynamically self-tunes its local geometry and expansion rate according to the local chronon curvature pattern. This single geometric response simultaneously explains (i) cosmic expansion, (ii) accelerated expansion, (iii) void formation and their enhanced growth, (iv) local collapse into compact chronon condensates, and (v) the cold dark-matter sector.

All five phenomena arise from the same microphysical origin: the bifurcation of TCP curvature restoration into stretching and shrinking branches.

This stands in contrast to $\Lambda$CDM, where expansion, dark energy, void dynamics, and dark matter originate from independent, phenomenological components[5].

12.1. Local TCP Bifurcation and Self-Tuning Dynamics

The Temporal Coherence Principle enforces a preferred curvature density ${\rho }_{\mathrm{curv}}^{★}$ determined by chronon microphysics. When the RNF advances into unaligned domain, the local reconstruction law forces a rescaling of the induced spatial volume:

$$V_3(t+\delta t)=s\left(t\right)V_3\left(t\right),$$

with $s\left(t\right)$ determined by the mismatch between inherited curvature and the TCP-preferred value.

Two branches arise:

$$\begin{array}{cc}\hfill s\left(t\right)>1& ⟹\mathrm{metric}\mathrm{stretching}(\mathrm{local}\mathrm{expansion}),\hfill \\ \hfill s\left(t\right)<1& ⟹\mathrm{metric}\mathrm{shrinking}(\mathrm{local}\mathrm{collapse}).\hfill \end{array}$$

This gives spacetime an intrinsic local elasticity: curvature-poor (vacuum-rich) regions stretch, while curvature-rich regions contract—mirroring the observed spatial heterogeneity of the cosmic web [79,80].

Consequences.

Each local patch independently selects its TCP branch. Thus spacetime is not globally rigid but locally self-tuning:

• vacuum regions expand fastest,
• mildly curved regions expand slowly,
• strongly curved regions collapse into compact objects.

This differs from $\Lambda$CDM, where the Hubble rate is imposed globally and void dynamics appear only as a secondary effect of density contrasts [81,82].

12.2. The Stretching Branch: Local Expansion and Accelerated Voids

Vacuum-dominated patches carry low curvature and minimal gradient energy. TCP can restore the preferred curvature only by adding vacuum volume, placing them firmly in the $s\left(t\right)>1$ stretching branch. As they expand, their RNF surface area grows, and the compounding mechanism of Section 8 drives accelerated expansion.

Because voids occupy the majority of cosmic volume at late times, the effective expansion rate becomes:

$$H_{\mathrm{eff}}\left(t\right)={\langle H_{\mathrm{local}}(x,t)\rangle }_{\mathrm{vol}},$$

with low-density regions dominating the average.

This gives a microphysical origin for:

• rapid expansion in voids,
• the suppression of expansion in filament and cluster regions,
• global late-time acceleration without vacuum energy.

This matches the observed fact that voids expand faster than the mean background [80,81] and that the Universe accelerates as it becomes increasingly empty [56,58,59].

12.3. The Shrinking Branch: Local Collapse and MCC Formation

In curvature-rich regions, TCP cannot restore the preferred curvature by stretching and must instead shrink the metric. These $s\left(t\right)<1$ patches contract, amplifying curvature in a manner similar to GR focusing [63]. Once the CEP curvature bound is reached, collapse halts and a finite-density chronon condensate forms:

$$\mathrm{TCP}\mathrm{shrinking}⟹\mathrm{CEP}-\mathrm{saturated}\mathrm{soliton}\left(\mathrm{MCC}\right).$$

Thus TCP-driven collapse parallels defect concentration in nonlinear ordering systems [14,31,46].

Interpretation.

The Universe organizes itself into:

• expanding low-curvature domains (voids),
• collapsed high-curvature solitons (MCC dark matter),
• intermediate filamentary regions where stretching and shrinking compete.

From one mechanism emerge:

• cosmic expansion,
• accelerated expansion,
• cold dark matter,
• nonsingular black holes,
• the void–filament morphology of large-scale structure.

12.4. Restoring GR at Large Scales

RNF cosmology modifies the microphysics of expansion and collapse while preserving standard GR phenomenology in two ways:

• Collapsed objects obey GR externally. MCCs and CEP black holes reproduce the Schwarzschild/Kerr metric outside the CEP core [63], ensuring classical gravitational consistency.
• Large-scale expansion is the volume-average of local stretching. Coarse-graining over many patches yields an effective FRW scale factor consistent with CMB, BAO, and SN Ia data [56,58,59].

Thus RNF cosmology adds microphysical richness without spoiling the successes of GR and $\Lambda$CDM.

12.5. Unified Dark Sector from a Single Mechanism

The TCP bifurcation naturally reproduces the entire dark sector:

• Cold Dark Matter: MCCs behave as cold, collisionless solitons identical to CDM at large scales [58,79].
• Dark Energy (effective): Global accelerated expansion arises because $s\left(t\right)>1$ vacuum patches dominate cosmic volume—no cosmological constant is required.
• Dark Structure: CEP-regulated black holes and other compact objects arise from the same shrinking branch[76].

Thus the dark sector is not a multiplicity of unknown fields but the emergent expression of one microphysical geometric rule.

12.6. Cosmological Picture

RNF cosmology produces a self-organizing Universe:

• The RNF advances, aligning chronons and reconstructing each slice.
• Each patch selects the stretching or shrinking branch of TCP.
• Stretching patches dominate cosmic volume → expansion.
• Increasing vacuum dominance → late-time acceleration.
• Shrinking patches → MCCs and CEP black holes.
• Coarse-graining over all patches → FRW-like geometry.

The cosmic web, dark matter, black holes, voids, and cosmic acceleration all emerge from a single microphysical mechanism.

12.7. Void Formation as a TCP-Driven Dilution Process

In $\Lambda$CDM, voids arise from the passive evolution of small initial underdensities. In RNF cosmology they have a microphysical origin.

During early chronon ordering, RNF propagation and defect formation [14,44] create strong spatial curvature variations. Regions where alignment succeeds rapidly acquire low curvature and undergo TCP-driven rarefaction, diluting curvature and forming proto-voids.

Because stretching factors are larger in such regions, they expand more rapidly than their surroundings, matching observed void-enhanced expansion rates and ISW signatures [58].

Meanwhile, shrinking-branch patches collapse into MCCs—giving a unified origin for voids and compact dark-matter structures.

12.8. Metric Shrinking and GR Focusing as the Same Process

Regions on the shrinking branch satisfy ${\partial }_{\ell }\sqrt{h}<0$ with positive extrinsic curvature K, implying local geometric contraction. This is the microscopic analogue of curvature focusing in GR [63].

Once contraction reaches the CEP bound, a nonsingular chronon core forms, analogous to proposed nonsingular black-hole interiors [76].

Externally the metric remains GR; internally the CEP regulates curvature.

Summary

RNF cosmology describes a Universe governed not by a single global expansion rate but by a field of locally self-adjusting chronon domains. Cosmic acceleration, void growth, MCC formation, and black-hole interiors all emerge from the same TCP bifurcation. The dark sector is unified, geometrical, and economical: the stretching branch drives expansion and acceleration; the shrinking branch produces dark matter; and GR reappears at large scales through coarse-graining.

13. RNF Cosmology vs. $\Lambda$CDM

The $\Lambda$CDM model remains the standard framework for precision cosmology [59]. RNF cosmology does not dispute its empirical successes; rather, it offers a different microphysical foundation for the observed cosmic expansion, dark matter, and large-scale structure—one based on chronon alignment, TCP coherence restoration, and slice-by-slice propagation of the Real–Now–Front (RNF).

The central conceptual shift is that cosmic expansion in RNF cosmology is a local, self-tuning response of each spacetime patch. TCP compares the patch’s coherence density to the preferred value ${\rho }^{★}$: vacuum-rich (over-coherent) regions stretch; structure-rich (under-coherent) regions shrink; near-equilibrium regions evolve GR and FRW-like. The globally observed Hubble flow is therefore an average over locally determined expansion rates. Despite this microscopic heterogeneity, large-scale homogeneity ensures that RNF cosmology reproduces FRW-like behaviour on cosmic scales.

This section contrasts RNF and $\Lambda$CDM both conceptually and phenomenologically.

13.1. Conceptual Comparison

$\Lambda$CDM begins with a pre-existing four-dimensional Lorentzian manifold and treats the metric as fundamental. Cosmic evolution is governed by the Friedmann equation with a cosmological constant.

RNF cosmology adopts a generative and microscopically grounded ontology:

• Advancing present vs. block universe. RNF defines a physically meaningful advancing present. Spacetime is generated slice-by-slice; ahead of the RNF, no metric yet exists.
• Emergent vs. fundamental geometry. In RNF, the metric $g_{\mu \nu }$ emerges from chronon alignment [12,13]. In $\Lambda$CDM, geometry is given a priori.
• Expansion mechanism. RNF: expansion is kinematic, arising from TCP restoration of coherence density as the RNF advances (Section 8). $\Lambda$CDM: expansion is dynamical, sourced by $\Lambda$.
• Locality and self-tuning. RNF: each patch expands or contracts depending on whether it is vacuum-rich, near-equilibrium, or structure-rich. $\Lambda$CDM: a single global Hubble rate applies everywhere.
• Dark matter origin. RNF: structure-rich $s<1$ patches collapse into MCCs and CEP-regulated cores (Section 9); no new particles are introduced. $\Lambda$CDM: requires new non-baryonic particle species [67].

Thus RNF cosmology reframes expansion, structure formation, and dark matter as different expressions of a single microphysical mechanism, rather than independent theoretical assumptions.

13.2. Phenomenology: Agreements and Differences

Although the ontologies differ, RNF cosmology qualitatively reproduces many observational features of the standard model while predicting additional signatures arising from chronon microphysics.

• Horizon-scale coherence.$\Lambda$CDM resolves the horizon problem via inflation [3,4,5]. RNF resolves it because large-scale smoothness arises from the uniform pre-geometric chronon substrate during early RNF percolation, before spacetime geometry—and hence horizons or causal scales—are defined (Section 6).
• Near-flat geometry. RNF: TCP coherence restoration damps early curvature variations and drives slices toward near-flatness. Precise matching to ${\Omega }_k$ remains a target for future analysis.
• Cosmic and accelerated expansion.$\Lambda$CDM: requires a cosmological constant. RNF: accelerated expansion emerges when vacuum-rich, over-coherent regions dominate the cosmic volume (stretching branch of TCP). The global $H\left(z\right)$ is a spatial average of local stretching rates. Quantitative matching will require RNF-adapted Boltzmann codes.
• Dark matter phenomenology. RNF: MCCs behave as cold, collisionless dark matter with natural finite-density cores. Small-scale structure may differ from CDM, potentially addressing cusp or diversity problems, while large-scale clustering remains CDM-like.
• Void dynamics and inhomogeneous expansion. RNF: voids expand faster because they are extremely over-coherent and thus lie deep on the stretching branch of TCP. $\Lambda$CDM: reproduces void behaviour numerically but lacks a microphysical mechanism for differential expansion.
• Two-metric effects. RNF generically predicts $g_{\mu \nu }^{\left(\gamma \right)}\ne g_{\mu \nu }^{\left(m\right)}$ due to slice-based vs. reconstruction-based propagation:

  -

  BAO vs. SN distance offsets,

  -

  mild shifts in growth indicators,

  -

  small deviations in redshift drift.

  These effects remain below current precision but offer targets for next-generation observatories.

RNF cosmology therefore qualitatively reproduces the principal empirical successes of $\Lambda$CDM while offering a new microphysical foundation. Quantitative predictions and precision tests will be developed in future work.

13.3. Summary Table

RNF cosmology therefore provides a unified and microphysically grounded framework in which cosmic expansion, late-time acceleration, dark matter, void dynamics, and compact objects all emerge from a single local mechanism: TCP-driven coherence restoration in the chronon field. A complete quantitative comparison with $\Lambda$CDM will require perturbation theory, Boltzmann solvers, and N-body simulations adapted to RNF dynamics.

Table 1. Conceptual and phenomenological comparison between RNF cosmology and $\Lambda$CDM. RNF entries describe microphysics-driven predictions that remain to be quantitatively calibrated against cosmological data.

Feature	RNF Cosmology	$\mathit{\Lambda }$CDM
Ontology	Advancing present; slice-by-slice generation	Static block-universe
Geometry	Emergent from chronon alignment	Fundamental metric
Expansion Mechanism	Local TCP coherence restoration; self-tuning	Friedmann dynamics with $\Lambda$
Horizon/Flatness	Pre-metric uniformity; TCP smoothing	Inflation
Dark Matter Origin	MCCs and CEP cores (no new fields)	New non-baryonic particles
Locality of Expansion	Patch-dependent $H_{\mathrm{local}}\left(x\right)$; voids expand fastest	Uniform global Hubble rate
Photon vs. Matter Geometry	Two-metric structure (tiny but generic)	Single metric
Small-Scale Structure	Cored solitonic halos; granular MCC effects	Cuspy CDM unless modified

Table 1. Conceptual and phenomenological comparison between RNF cosmology and $\Lambda$CDM. RNF entries describe microphysics-driven predictions that remain to be quantitatively calibrated against cosmological data.

Feature	RNF Cosmology	$\mathit{\Lambda }$CDM
Ontology	Advancing present; slice-by-slice generation	Static block-universe
Geometry	Emergent from chronon alignment	Fundamental metric
Expansion Mechanism	Local TCP coherence restoration; self-tuning	Friedmann dynamics with $\Lambda$
Horizon/Flatness	Pre-metric uniformity; TCP smoothing	Inflation
Dark Matter Origin	MCCs and CEP cores (no new fields)	New non-baryonic particles
Locality of Expansion	Patch-dependent $H_{\mathrm{local}}\left(x\right)$; voids expand fastest	Uniform global Hubble rate
Photon vs. Matter Geometry	Two-metric structure (tiny but generic)	Single metric
Small-Scale Structure	Cored solitonic halos; granular MCC effects	Cuspy CDM unless modified

Figure 10 schematically compares RNF cosmology with the block-universe picture.

14. Conclusions

Real–Now–Front (RNF) cosmology provides a microphysically grounded and geometrically unified framework in which spacetime, cosmic expansion, compact-object formation, and the dark sector all emerge from the alignment dynamics of an underlying chronon field. Building on Chronon Field Theory—where smooth chronon alignment reproduces Lorentzian signature, Einstein dynamics, and Yang–Mills structure at long wavelengths [12,13]—the present work applies these mechanisms to cosmology by treating the advancing Real–Now–Front as the generative engine of spacetime.

The central finding is that cosmic expansion is not driven by vacuum pressure or exotic stress–energy sources but arises kinematically from hypersurface geometry. As the RNF advances into an unaligned chronon medium, the Temporal Coherence Principle (TCP) forces each newly reconstructed slice to adjust its induced metric so that the local chronon coherence density is restored toward its preferred microscopic value ${\rho }^{★}$. This coherence-restoration mechanism leads to a local bifurcation: vacuum-rich, over-coherent regions lie on a stretching branch ($s>1$), while structure-rich, under-coherent regions lie on a shrinking branch ($s<1$). The local Hubble law follows directly from this geometric adjustment, and accelerated expansion arises whenever stretching-branch regions fill most of the cosmic volume.

Chronon microphysics further imposes the Chronon Exclusivity Principle (CEP), which enforces a universal upper bound on symplectic curvature. When TCP places a region on the shrinking branch, contraction amplifies curvature until the CEP threshold is reached. This halts collapse and produces finite-density chronon cores: horizonless Micro Chronon Condensates (MCCs) at small masses and CEP-regulated black holes at higher masses. These objects are cold, stable, and electromagnetically dark, supplying a single non-particle microphysical origin for the dark sector. A mild two-metric structure—arising from slice-confined photon propagation versus reconstruction-based matter propagation—leads to small, testable differences in cosmological distance relations.

Altogether, RNF cosmology demonstrates that a single microphysical mechanism—chronon alignment under TCP and its branching into stretching and shrinking responses—can simultaneously generate spacetime geometry, cosmic expansion, compact-object structure, void evolution, and dark-matter phenomenology while remaining broadly consistent with the observational successes of $\Lambda$CDM.

14.1. Empirical Signatures

RNF cosmology leads to several qualitative, microphysics-driven signatures that distinguish it from $\Lambda$CDM and provide clear targets for future tests:

• Compact dark objects with finite cores. Chronon collapse on the shrinking TCP branch produces horizonless, finite-density compact objects (MCCs). Their lensing behavior can differ from that of pointlike primordial black holes due to CEP-stabilized core structure.
• Locally self-tuning expansion. Because expansion arises from local TCP curvature restoration rather than a global cosmological constant, deviations from the standard $\Lambda$CDM expansion history are possible, especially in void-dominated or low-redshift regimes. Quantitative predictions require RNF-specific perturbation theory.
• Photon–matter consistency tests. RNF generically allows a small distinction between photon-based and matter-based distance measures due to slice propagation versus reconstruction. This may manifest as subtle discrepancies between different cosmological distance indicators in future precision data.

These signatures follow directly from the generative mechanism of RNF cosmology. Deriving their precise magnitudes is an important goal for future theoretical and numerical work.

14.2. Future Directions

Elevating RNF cosmology to a precision framework will require significant theoretical and computational advances:

• Quantum chronon theory. A quantum formulation of chronon excitations is needed to compute primordial power spectra, stochastic fluctuations, and gravitational-wave signatures.
• Numerical RNF simulations. Simulations of TCP-mediated alignment, RNF propagation, and percolation are essential for validating the local expansion law and predicting initial perturbation statistics.
• MCC-based structure formation. Incorporating MCC granular microphysics into N-body and hydrodynamic simulations will allow precise predictions for halo profiles, substructure, and Lyman-$\alpha$ constraints.
• Two-metric cosmological pipelines. A unified analysis framework distinguishing photon- from matter-based observables is required for BAO, lensing, SN Ia, and redshift-drift analyses.

Concluding Remarks

RNF cosmology offers a unified and microphysically motivated alternative to the standard cosmological paradigm. By deriving geometry, expansion, compact objects, and the dark sector from a single generative process—chronon alignment under TCP—it resolves several foundational tensions of $\Lambda$CDM while retaining its broad empirical successes.

The framework is intentionally falsifiable. Upcoming lensing surveys, high-precision expansion measurements, and photon–matter consistency tests will provide decisive opportunities to confirm or refute RNF predictions. Future advances in chronon microphysics and RNF dynamics will determine whether this generative approach ultimately complements, extends, or replaces the standard cosmological model.

Appendix A.1. TCP Action, Assumptions, and Variation

On each aligned RNF slice, the chronon field ${\Phi }_{\mu }$ is treated as a unit-timelike vector encoding the local orientation of the aligned configuration. The emergent metric $g_{\mu \nu }[\Phi ]$ is defined via coarse-graining of chronon interfaces as in Refs. [12,13]. For the purposes of this appendix, we hold $g_{\mu \nu }$ fixed during the variation and study the dynamics of ${\Phi }_{\mu }$ generated by the TCP functional.

The TCP action is

$$S_{\mathrm{TCP}}[\Phi ]=\int d^{4}x\sqrt{-g}\left[{\displaystyle \frac{J}{2}}{\nabla }_{\mu }{\Phi }_{\nu }{\nabla }^{\mu }{\Phi }^{\nu }+{\displaystyle \frac{\lambda }{2}}({\Phi }_{\mu }{\Phi }^{\mu }+1)+{\displaystyle \frac{\kappa }{4}}{\left({\nabla }_{\mu }{\Phi }_{\nu }{\nabla }^{\mu }{\Phi }^{\nu }\right)}^2\right],$$

(A1)

where $J>0$ is the alignment stiffness, $\lambda$ is the Lagrange multiplier enforcing the fixed-norm constraint ${\Phi }_{\mu }{\Phi }^{\mu }=-1$, and $\kappa \ge 0$ provides Skyrme-type quartic regularization [72].

Assumptions.

We assume:

• smooth $\left(C^2\right)$ fields on each RNF slice;
• bounded curvature on relevant scales;
• a fully aligned background satisfying ${\overline{\Phi }}_{\mu }{\overline{\Phi }}^{\mu }=-1$ and ${\nabla }_{\mu }{\overline{\Phi }}_{\nu }=0$;
• small fluctuations ${\phi }_{\mu }$ obeying the linearized constraint

  $${\overline{\Phi }}^{\mu }{\phi }_{\mu }=0,$$

  obtained from varying ${\Phi }_{\mu }{\Phi }^{\mu }=-1$ to first order.

Variation.

Varying (A1) with respect to ${\Phi }_{\mu }$ while holding the metric fixed gives

$$\delta S_{\mathrm{TCP}}=\int d^{4}x\sqrt{-g}\left[J\left({\nabla }_{\mu }{\Phi }_{\nu }\right)\left({\nabla }^{\mu }\delta {\Phi }^{\nu }\right)+\lambda {\Phi }_{\nu }\delta {\Phi }^{\nu }+\kappa \left({\nabla }_{\alpha }{\Phi }_{\beta }\right)\left({\nabla }^{\alpha }{\Phi }^{\beta }\right)\left({\nabla }_{\mu }{\Phi }_{\nu }\right)\left({\nabla }^{\mu }\delta {\Phi }^{\nu }\right)\right].$$

Integrating by parts and discarding boundary terms yields the Euler–Lagrange equation

$$J{\nabla }_{\mu }{\nabla }^{\mu }{\Phi }_{\nu }+\lambda {\Phi }_{\nu }+\kappa {\nabla }_{\mu }\left[\left({\nabla }_{\alpha }{\Phi }_{\beta }\right)\left({\nabla }^{\alpha }{\Phi }^{\beta }\right){\nabla }^{\mu }{\Phi }_{\nu }\right]=0.$$

(A2)

The quartic term vanishes at linear order around an aligned background, since it is cubic in gradients of ${\Phi }_{\mu }$. Thus the principal symbol is governed entirely by the quadratic part.

Leading-order propagation.

To first order in fluctuations,

$$J{\nabla }_{\mu }{\nabla }^{\mu }{\Phi }_{\nu }+\lambda {\Phi }_{\nu }=0+O\left(\kappa \right),$$

(A3)

which determines the emergent causal structure.

Appendix A.2. Linearization and Characteristic Cones

Let $({\overline{g}}_{\mu \nu },{\overline{\Phi }}_{\mu })$ denote a fully aligned background, and write perturbations as

$${\Phi }_{\mu }={\overline{\Phi }}_{\mu }+{\phi }_{\mu },{\overline{\Phi }}^{\mu }{\phi }_{\mu }=0.$$

Linearizing (A3) gives

$$J{\overline{\nabla }}_{\alpha }{\overline{\nabla }}^{\alpha }{\phi }_{\mu }+\lambda {\phi }_{\mu }=0.$$

(A4)

In a local inertial frame of ${\overline{g}}_{\mu \nu }$, ${\overline{\nabla }}_{\alpha }{\overline{\nabla }}^{\alpha }\to \square =-{\partial }_t^2+{\nabla }^2$, so

$${\phi }_{\mu }\sim e^{i(\mathbf{k}·\mathbf{x}-\omega t)}$$

satisfies

$$J(-{\omega }^2+{\mathbf{k}}^2)+\lambda =0.$$

(A5)

Characteristic surfaces.

The principal symbol of the operator is

$$P\left(k\right)=J{\overline{g}}^{\mu \nu }{k}_{\mu }{k}_{\nu },$$

so the characteristic surfaces satisfy

$${\overline{g}}^{\mu \nu }{k}_{\mu }{k}_{\nu }=0.$$

(A6)

The $\lambda$ term does not affect characteristics because it is lower order. Thus perturbations propagate on the null cones of the emergent metric, as in [12] and in analogue-gravity systems [33,66].

Propagation speed c Φ .

From (A5),

$${\omega }^2={\mathbf{k}}^2+{\displaystyle \frac{\lambda }{J}}.$$

The constraint ensures that $\lambda$ acts effectively as a curvature term rather than a physical mass, leading to a propagation speed

$$c_{\Phi }=\sqrt{{\displaystyle \frac{J}{{\lambda }_{\mathrm{eff}}}}},$$

(A7)

where ${\lambda }_{\mathrm{eff}}$ is the second derivative of the constraint potential. In the fully aligned phase, $c_{\Phi }$ coincides with the physical speed of light, ensuring that Standard-Model fields propagate on the emergent metric [13].

Appendix D.1. Chronon Solitons as Quantized Curvature Excitations

The chronon polarization field ${\Phi }_{\mu }$ defines a coarse-grained symplectic 2-form ${\Omega }_{\mu \nu }$, representing the vorticity of the alignment field. Localized excitations correspond to compact domains of nonzero ${\Omega }_{\mu \nu }$ whose total curvature flux satisfies the quantization rule

$${\int }_{\Sigma }\Omega =\hslash ,$$

(A27)

for any two-surface $\Sigma$ linking the defect. This arises because ${\Phi }_{\mu }$ defines a map $S^2\to \mathcal{P}$ into the polarization manifold with nontrivial ${\pi }_2\left(\mathcal{P}\right)$, exactly as in Skyrme-type or sigma-model solitons [72].

Appendix D.4.4.52. Energy functional and stability.

Near alignment the chronon energy reduces to a quadratic-plus-Skyrme form:

$$E[\Phi ]=\int d^{3}x\sqrt{\gamma }\left[{\displaystyle \frac{J}{2}}{\gamma }^{ij}{\nabla }_i{\Phi }_{\mu }{\nabla }_j{\Phi }^{\mu }+{\displaystyle \frac{\kappa }{4}}{\left({\gamma }^{ij}{\nabla }_i{\Phi }_{\mu }{\nabla }_j{\Phi }^{\mu }\right)}^2\right].$$

(A28)

The quartic term stabilizes the soliton and prevents Derrick collapse, yielding a characteristic soliton radius

$$R_{\mathrm{sol}}\sim \sqrt{{\displaystyle \frac{\kappa }{J}}},$$

up to order-unity factors. Chronon solitons are thus finite-sized, topologically protected curvature excitation packets.

Appendix D.2. Chronon Exclusivity Principle (CEP): A Bound on Curvature Density

The aligned chronon medium contains a minimal causal cell volume $v_0$, associated with the local alignment scale. Because each soliton carries a single curvature-flux quantum ℏ, no causal cell can host more than one unit of topological flux. For any region V,

$${\int }_V\mathcal{Q}\le {\displaystyle \frac{V}{v_0}},$$

(A29)

where $\mathcal{Q}$ is the topological charge density sourced by ${\Omega }_{\mu \nu }$. Equivalently,

$${\displaystyle \frac{1}{V}}{\int }_V\Omega \le {\displaystyle \frac{\hslash }{v_0}}.$$

(A30)

This is the Chronon Exclusivity Principle (CEP):

• curvature flux is hard-core excluded;
• curvature density is universally bounded;
• compression toward the CEP bound induces a rapidly rising geometric exclusion pressure $P_{\Omega }$ independent of thermodynamic assumptions.

Because curvature cannot exceed a finite limit, collapse cannot proceed to arbitrarily high density. CEP therefore provides the microphysical origin of the nonsingular interiors of MCCs.

Appendix D.3. Gauge Freezing in CEP-Saturated Regions

In chronon field theory, internal gauge fields arise as twist modes of the polarization bundle [13]. These require transverse directions in the tangent space of the polarization manifold.

Inside a CEP-saturated region:

• the polarization manifold collapses effectively to one direction;
• transverse directions vanish;
• twist modes cannot be supported.

Thus the gauge curvature is forced to zero:

$$F_{\mu \nu }\to 0(\mathrm{CEP}-\mathrm{saturated}\mathrm{interior}).$$

(A31)

Consequences:

• no electric charge or dipole structure can exist inside the core,
• electromagnetic fields cannot propagate,
• the interior is perfectly dark and effectively collisionless.

This mechanism explains the cold, inert behavior of MCC dark matter.

Appendix D.4. Packing Solitons and the Emergence of CEP Cores

As curvature solitons accumulate, CEP forbids their topological flux from overlapping. If N solitons occupy volume V, then

$$V_{min}\approx N{v}_0.$$

This determines a purely geometric core density:

$${\rho }_{\mathrm{core}}\approx {\displaystyle \frac{m_{\mathrm{sol}}}{v_0}},$$

independent of environmental conditions or collapse history.

The mass–radius relation follows immediately:

$$R_{\mathrm{core}}={\left({\displaystyle \frac{3M}{4\pi {\rho }_{\mathrm{core}}}}\right)}^{1/3}.$$

(A32)

Key properties:

• $R\propto M^{1/3}$: a universal geometric scaling;
• a minimal-radius MCC composed of a single soliton: $R_{\mathrm{core},\min }\sim v_0^{1/3}$;
• complete independence from thermal or hydrodynamic assumptions.

Appendix D.5. Stability and Horizon Avoidance

Compression toward the CEP bound encounters a divergent exclusion pressure $P_{\Omega }$. For a stable core one requires

$$P_{\Omega }\left(R_{\mathrm{core}}\right)\gtrsim {\displaystyle \frac{G{M}^2}{R_{\mathrm{core}}^4}},$$

i.e., the geometric exclusion pressure must counteract gravitational compression.

Because $P_{\Omega }\to \infty$ as $R\to R_{min}$, collapse halts before the Schwarzschild radius is reached:

$$R_{\mathrm{core}}>2GM.$$

Thus:

• light and intermediate-mass objects form stable, horizonless MCCs;
• sufficiently massive collapse yields a GR horizon outside a nonsingular CEP core.

This agrees with the exterior Schwarzschild/Kerr behavior discussed in the main text.

Appendix D.6. Expected MCC Mass Spectrum from RNF Fragmentation

During early RNF alignment, the chronon medium undergoes a rapid quench from disorder to ordered alignment. Front collisions trap curvature in pockets determined by percolationlike fragmentation. Such quenches generically produce power-law mass spectra

$${\displaystyle \frac{dN}{dM}}\propto M^{-\tau },2.5\lesssim \tau \lesssim 3,$$

(A33)

matching many nonlinear ordering systems.

Consequences:

• abundant light ($N=1$ or few-soliton) MCCs;
• progressively rarer heavy MCCs from merger histories;
• a high-mass tail corresponding to “chronon stars.’’

The total dark-matter abundance is naturally

$${\Omega }_{\mathrm{MCC}}\sim f_{\mathrm{trap}}{\displaystyle \frac{m_{\mathrm{sol}}}{v_0{\rho }_c}},$$

with modest trapping fractions giving the observed ${\Omega }_{\mathrm{DM}}$ without fine tuning.

Appendix D.7. Observational Constraints and Allowed MCC Masses

The mass–radius scaling (A32) enables comparison with existing compact-dark-matter bounds:

• Microlensing (EROS, OGLE, Subaru/HSC). MCCs evade constraints when extremely compact or very light ($M\lesssim {10}^{-12}{M}_{\odot }$) due to small Einstein radii.
• Dynamical bounds. MCCs behave as cold, collisionless objects with negligible self-interaction.
• Structure formation. MCCs cluster like CDM because their free-streaming length is microscopic.
• Galactic cores. The $M^{1/3}$ scaling yields natural constant-density halo cores, easing small-scale tensions [73].

A broad MCC mass range remains observationally viable.

Appendix D.8. Summary: Solitons → CEP → MCCs

• Chronon solitons are topologically quantized, finite-size curvature excitations stabilized by Skyrme-like terms.
• CEP imposes a universal curvature-flux bound, yielding geometric incompressibility.
• Packing solitons produces finite-density, nonsingular, CEP-saturated cores.
• Gauge freezing within CEP cores enforces $F_{\mu \nu }=0$, ensuring electromagnetic darkness.
• MCCs obey $R\propto M^{1/3}$ and remain horizonless unless extremely massive.
• RNF fragmentation yields a power-law mass spectrum with index $2.5\lesssim \tau \lesssim 3$.
• Observational constraints allow MCCs to constitute the full dark sector.

These results provide the microphysical basis for the dark-matter phenomenology developed in Section 9.

Appendix E.1. Chronon-Based Construction of the Two Metrics

Let ${\Phi }_{\mu }$ denote the chronon alignment field, and ${\overline{\Phi }}_{\mu }$ the background aligned configuration on an RNF slice $\Sigma \left(t\right)$. The emergent metric $g_{\mu \nu }[\Phi ]$ is defined as in Refs. [12,13]. A perturbation decomposes uniquely into transverse and longitudinal parts:

$${\phi }_{\mu }={\phi }_{\mu }^{\perp }+\left({\overline{\Phi }}^{\alpha }{\phi }_{\alpha }\right){\overline{\Phi }}_{\mu },{\overline{\Phi }}^{\mu }{\phi }_{\mu }^{\perp }=0.$$

Two independent projection procedures act on $g_{\mu \nu }[\Phi ]$ and yield the two emergent metrics.

1. Photon metric: transverse propagation within a slice.

Define the transverse projector:

$${P_{\mu }}^{\alpha }={{\delta }_{\mu }}^{\alpha }+{\overline{\Phi }}_{\mu }{\overline{\Phi }}^{\alpha },{P_{\mu }}^{\alpha }{\overline{\Phi }}_{\alpha }=0.$$

The effective metric governing photon propagation is:

$$g_{\mu \nu }^{\left(\gamma \right)}={P_{\mu }}^{\alpha }{P_{\nu }}^{\beta }{g}_{\alpha \beta }[\Phi ].$$

(A34)

This metric controls the dynamics of transverse modes ${\phi }_{\mu }^{\perp }$ and defines the null cone for emergent electromagnetism.

2. Matter metric: TCP reconstruction across the RNF.

Localized matter excitations must be reinstantiated at every RNF advance. Let $\mathcal{R}$ denote the TCP reconstruction map that transports a local pattern from $\Sigma \left(t\right)$ to $\Sigma (t+\Delta t)$. The induced effective metric for matter is:

$$g_{\mu \nu }^{\left(m\right)}:={\displaystyle \frac{\partial x_{\mu }^{\prime }}{\partial x_{\alpha }}}{\displaystyle \frac{\partial x_{\nu }^{\prime }}{\partial x_{\beta }}}{g}_{\alpha \beta }[\Phi ]\mathrm{with}{x}^{\prime }=\mathcal{R}\left(x\right).$$

(A35)

Thus photons and matter probe different aspects of the same chronon geometry: photons probe the in-slice propagation geometry, while massive excitations probe the slice-to-slice reconstruction geometry.

Appendix E.2. Photon Sector: Propagation-Induced Geometry

Transverse chronon fluctuations behave as an emergent gauge field with quadratic action:

$$S_{\gamma }=-{\displaystyle \frac{1}{4}}\int d^{4}x\sqrt{-g}{Z}^{\mu \nu \alpha \beta }\left(\overline{\Phi }\right)F_{\mu \nu }{F}_{\alpha \beta }.$$

(A36)

Chronon alignment symmetry restricts the tensor $Z^{\mu \nu \alpha \beta }$ to the Maxwell form with the replacement $g\to g^{\left(\gamma \right)}$:

$$Z^{\mu \nu \alpha \beta }={\displaystyle \frac{1}{2}}\left(g^{\left(\gamma \right)\mu \alpha }{g}^{\left(\gamma \right)\nu \beta }-g^{\left(\gamma \right)\mu \beta }{g}^{\left(\gamma \right)\nu \alpha }\right).$$

Photon trajectories therefore satisfy:

$$g_{\mu \nu }^{\left(\gamma \right)}{k}^{\mu }{k}^{\nu }=0.$$

(A37)

They depend only on the geometry of each completed slice, not on the RNF reconstruction mechanism.

Appendix E.3. Matter Sector: Reconstruction-Induced Geometry

Matter excitations (curvature knots, MCCs, solitons) cannot propagate through a metric-free domain and thus must be reconstructed during RNF advancement. Coarse-graining this process yields the standard matter action:

$$S_m=\int d^{4}x\sqrt{-g^{\left(m\right)}}{\mathcal{L}}_m(\psi ,g_{\mu \nu }^{\left(m\right)}).$$

Geodesics for massive bodies follow $g_{\mu \nu }^{\left(m\right)}$, consistent with reconstruction rather than propagation.

This structure is closely analogous to condensed-matter systems where:

• small-amplitude waves follow a propagation metric, while
• topological defects and textures follow reconstruction rules derived from energy minimization.

Appendix E.4. Magnitude and Structure of Metric Differences

The two emergent metrics differ by:

$$g_{\mu \nu }^{\left(\gamma \right)}=g_{\mu \nu }^{\left(m\right)}+\delta g_{\mu \nu },|\delta g_{\mu \nu }|\ll |g_{\mu \nu }^{\left(m\right)}|.$$

(A38)

Sources of δg μν .

• Partial alignment near the RNF introduces small anisotropies in the reconstruction geometry.
• Higher-order TCP gradient terms contribute suppressed corrections depending on ${|\nabla \Phi |}^2$.
• Repeated reconstruction accumulates tiny distortions over cosmological distances.

To leading order, symmetry allows:

$$\delta g_{\mu \nu }\simeq ϵ\left({\overline{\Phi }}_{\mu }{\overline{\Phi }}_{\nu }-{\displaystyle \frac{1}{3}}{g}_{\mu \nu }^{\left(m\right)}\right),\left|ϵ\right|\ll 1.$$

(A39)

Local Lorentz-symmetry tests [39,74] require $ϵ$ to be essentially zero on small scales.

Appendix E.5. Cosmological Limit: Two Scale Factors

In an FLRW background the two metrics reduce to:

$$d{s}_{\gamma }^2=-d{t}^2+a_{\gamma }^2\left(t\right)d{\mathbf{x}}^2,d{s}_m^2=-d{t}^2+a_m^2\left(t\right)d{\mathbf{x}}^2.$$

Equation (A39) implies:

$${\displaystyle \frac{a_{\gamma }\left(t\right)-a_m\left(t\right)}{a_m\left(t\right)}}=ϵ\left(t\right),\left|ϵ\left(t\right)\right|\ll 1.$$

(A40)

Consequences.

• BAO and growth-of-structure observables trace $a_m\left(t\right)$.
• SN Ia luminosity distances trace $a_{\gamma }\left(t\right)$.
• Redshift drift depends on ${\dot{a}}_{\gamma }\left(t\right)$.
• Weak-lensing distances follow null geodesics of $g^{\left(\gamma \right)}$.

These signatures are small but accumulate over cosmological baselines and are detectable with next-generation distance probes.