Operational Copy Time and Audited Closure: A Locality–Mixing Separation Diagnostic for Open Quantum Dynamics

1. Introduction

Many effective descriptions are justified heuristically, while practical certification requires explicit, verifiable error budgets tied to operational tasks. We propose a minimal framework based on (i) audited closure and (ii) receiver-region copy time. The manuscript is deliberately modest: it provides a technically explicit pipeline for one controlled class (quasi-free fermions) and introduces a signature diagnostic for open-system dynamics that is not reducible to locality alone.

2. Framework: Audited Closure and Bridge Maps

Let O_* be a declared set of bounded observables and D a declared domain of admissible initial states/protocols. Audited closure holds up to tolerance ε on a time window [0,T_*] if sup_{ρ∈D} sup_{t≤T_*} sup_{O∈O_*} |Tr[ρ_micro(t)O] − Tr[ρ_eff(t)O]| ≤ ε.

Bridge map formalism (Dirac surrogate example). Domain D_{kmax} is the set of gauge-invariant quasi-free, translation-invariant, band-diagonal, band-limited states specified by symbols N(k) with support |k|≤kmax. Codomain consists of time-indexed quasi-free states. The bridge B acts by dynamics substitution: given ρ(N) and an effective one-particle propagator U_eff(t), define ρ_eff(t) as the quasi-free state with symbol N_eff(t)=U_eff(t) N U_eff(t)†.

3. Receiver-Region Copy Time and Locality Lower Bounds

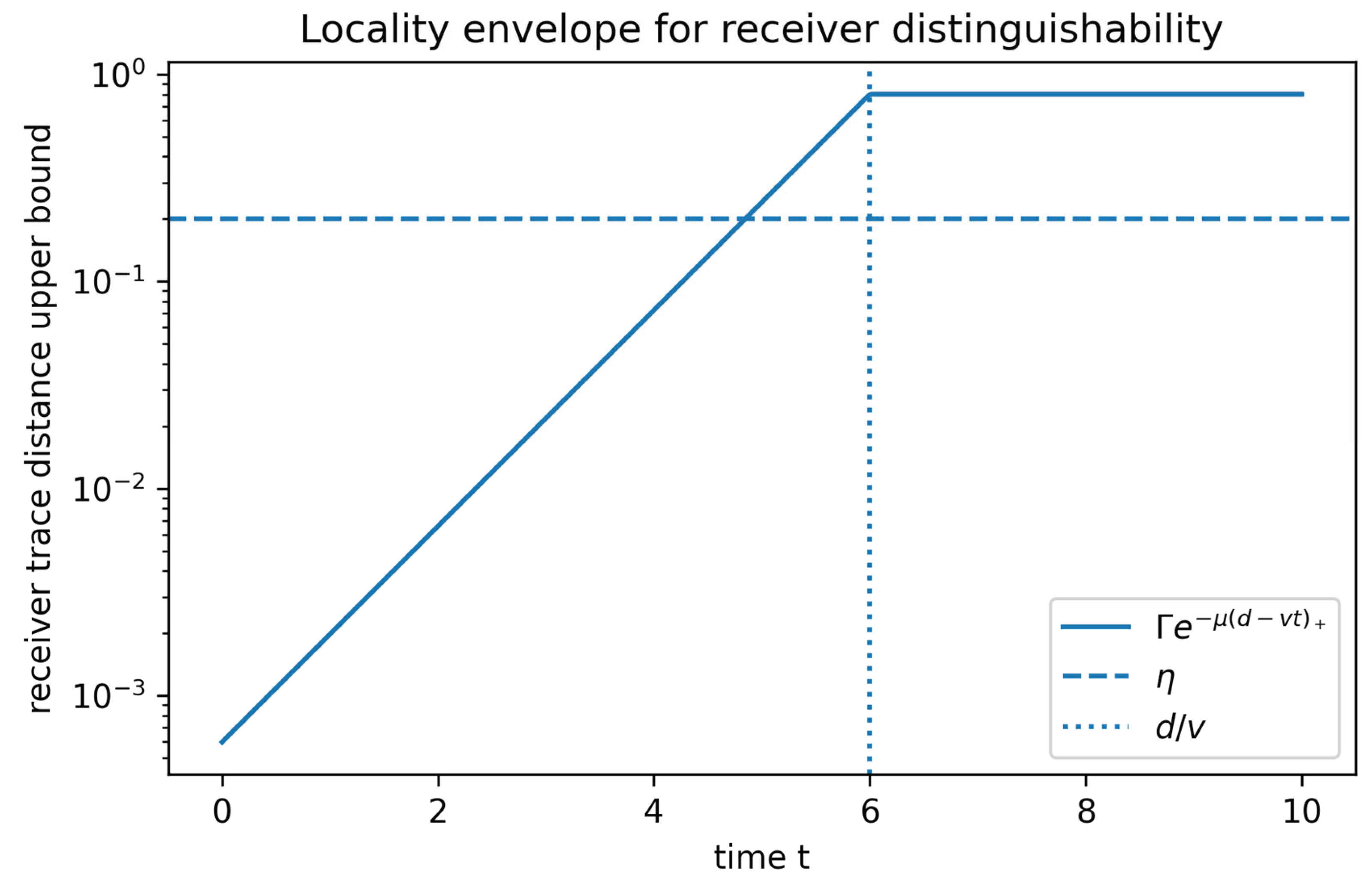
For disjoint regions A,B and threshold η∈(0,1), define τ_copy(η;A→B)=inf{t≥0: ½||ρ_1^{(B)}(t)−ρ_0^{(B)}(t)||_1 ≥ η}, with τ_copy=+∞ if the set is empty. For an exponential tilting perturbation ρ_1 ∝ e^{εQ_A} ρ_0 e^{εQ_A}, and under a Lieb–Robinson commutator bound ||[X(t),Y]|| ≤ C||X||||Y|| exp(−μ(d(A,B)−v_LR t)_+), we obtain the receiver envelope: ½||ρ_1^{(B)}(t)−ρ_0^{(B)}(t)||_1 ≤ Γ(ε,Q_A) exp(−μ(d−v_LR t)_+), with Γ(ε,Q_A)=2ε||Q_A|| e^{2ε||Q_A||}C. In particular, if η≥Γ and d(A,B)>0 then τ_copy=+∞.

Figure 1. Locality envelope for receiver distinguishability (log scale).

Figure 1. Locality envelope for receiver distinguishability (log scale).

4. Signature Result: Locality–Mixing Separation for Primitive Lindbladians

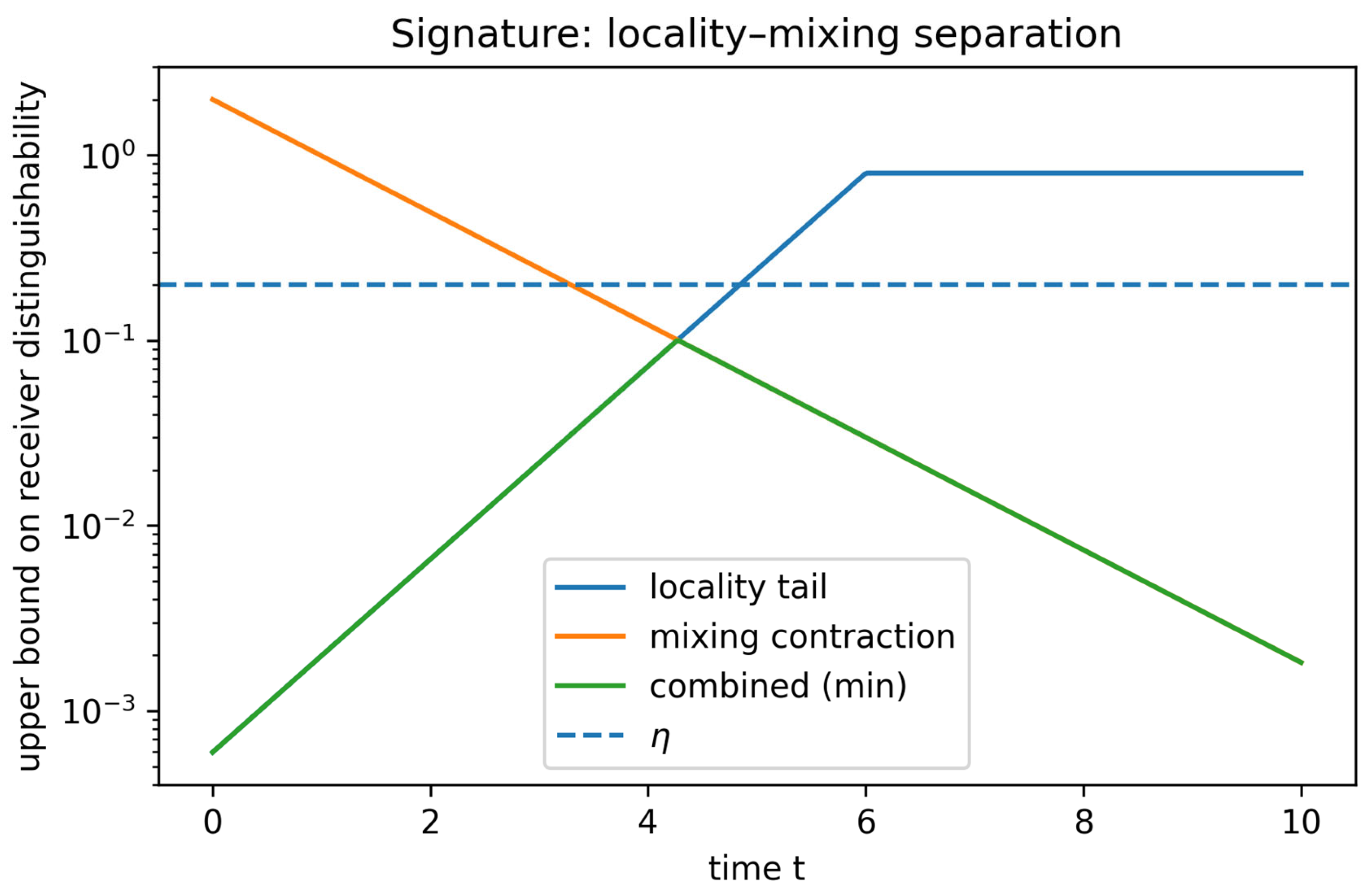
New contribution. For a primitive Lindbladian semigroup with mixing rate λ (e.g., via a log-Sobolev or spectral-gap inequality implying trace-norm contraction toward the unique fixed point), one has global contraction ½||Φ_t(ρ)−Φ_t(σ)||_1 ≤ e^{−λ t}·½||ρ−σ||_1. Combining this with the receiver-region LR envelope yields a strictly stronger operational bound on receiver distinguishability:

½||ρ_1^{(B)}(t)−ρ_0^{(B)}(t)||_1 ≤ min{ Γ exp(−μ(d−v_LR t)_+), 2 e^{−λ t} }.

This produces a crossover time t× at which locality-limited growth yields to mixing-limited suppression, and an operational separation between unitary evolution (λ=0) and dissipative cooling (λ>0) that is testable by receiver discrimination protocols.

Figure 2. Signature bound: minimum of a locality tail and mixing contraction.

Figure 2. Signature bound: minimum of a locality tail and mixing contraction.

5. Numerical Demonstration: Operational Gap and Mixing-Rate Constraint

We provide a minimal numerical illustration of the signature locality–mixing separation. We consider a one-dimensional split-step quantum walk (unitary transport) and a dissipative variant in which each step is followed by a primitive depolarizing channel, serving as a finite-dimensional proxy for a mixing Lindbladian. For a sender region A and a spatially separated receiver region B at distance d(A,B)=d, we monitor the receiver-accessible distinguishability

d_B(t) := (1/2)|| E_B(ρ1(t)) − E_B(ρ0(t)) ||_1,

where E_B denotes the CPTP “receiver reduction” (erasure outside B). Figure 4 plots d_B(t) for the unitary and dissipative dynamics together with the two envelopes entering the analytic certificate: the Lieb–Robinson tail Γ exp[−μ(d−vt)_+] and the mixing contraction 2 exp[−λ t].

In the dissipative case, the post-arrival tail is well fit by an exponential, yielding an estimate of the effective mixing rate λ. The resulting crossover window provides an operational constraint on λ (equivalently a mixing time t_mix≈λ^{-1}) that is not implied by locality alone. The dataset (data/numerics_gap.csv), the plotting script (code/numerics_demo.py), and the figure sources are included in the submission package to enable straightforward reproduction.

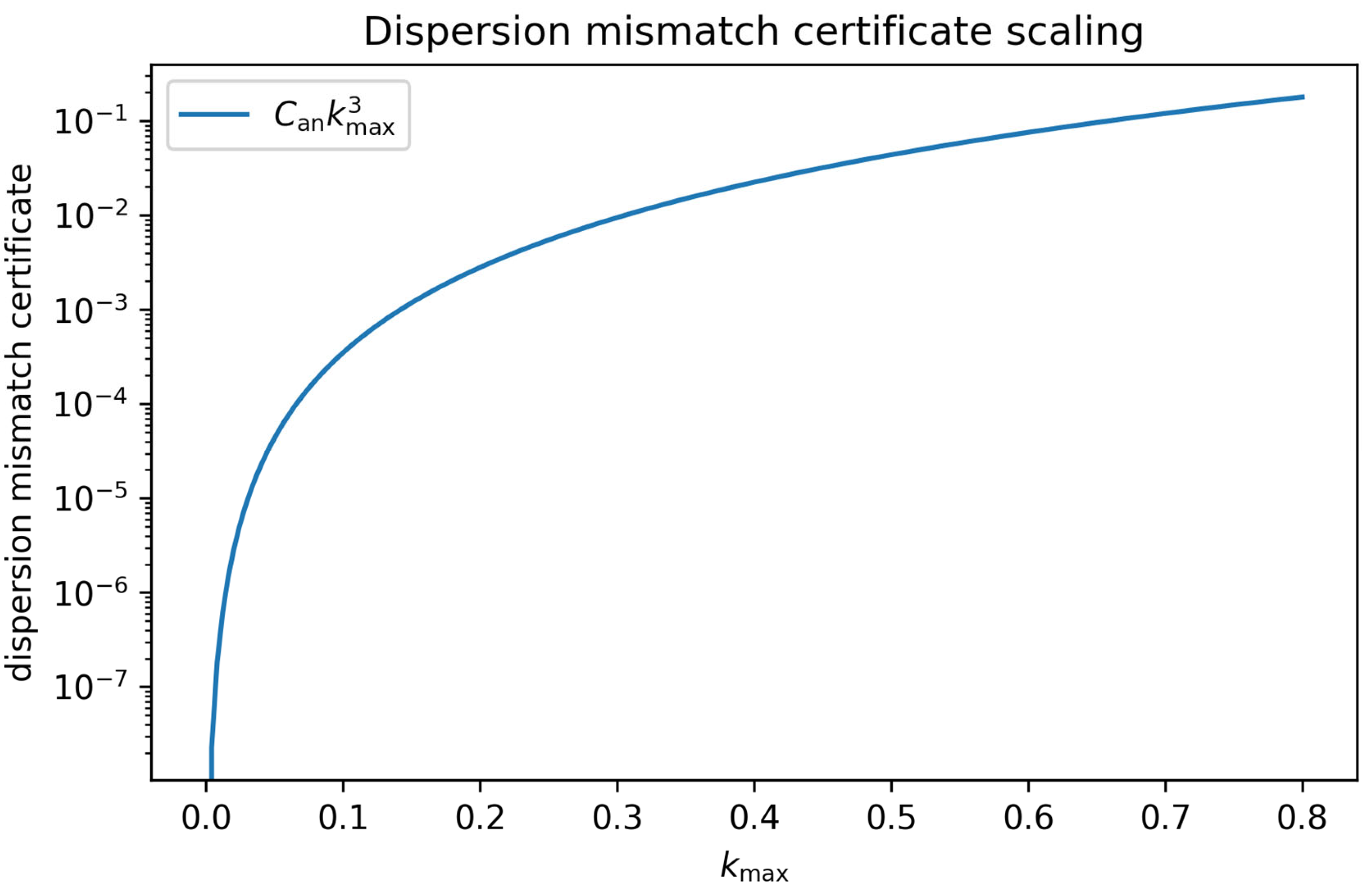
Figure 3. Dispersion mismatch certificate scaling (log scale).

Figure 3. Dispersion mismatch certificate scaling (log scale).

6. Achieved Closure Example: Split-Step Walk → Dirac Surrogate in Quasi-Free Fermions

We consider a split-step quantum walk (parameters θ1, θ2) on a 1D lattice, lifted to a quasi-free fermionic many-body system by second quantization. On the declared quasi-free band-limited domain, we match the effective Dirac surrogate dispersion to the microscopic dispersion through second order at k=0. Under an explicit gap condition |A cos k + B| ≤ 1−δ on |k|≤kmax, we bound the third derivative of ε(k)=arccos(A cos k + B) and obtain a computable constant C_an such that sup_{|k|≤kmax} |ε_micro(k)−ε_eff(k)| ≤ C_an kmax^3.

Two-point closure. For centered two-point density observables O_{f,g} built from smeared densities n_f, n_g (kernels f,g∈ℓ¹), we prove a complete quasi-free bound via Wick reduction and phase Lipschitz control:

|Tr[ρ_micro(t)O_{f,g}]−Tr[ρ_eff(t)O_{f,g}]| ≤ 4 ||f||₁||g||₁ t sup_{|k|≤kmax}|Δε(k)|.

All steps and constants are given in the Supplementary Material.

7. Weak-Interaction Extension (g≠0): Stability of Audited Closure

To move beyond the Gaussian setting, we add a weak interaction gV with local interaction norm ||V||_μ finite. Using a Duhamel expansion around the quasi-free generator plus locality control, we obtain a perturbative bound showing that audited closure degrades additively by O(|g| t) on bounded-time windows, with explicit constants in terms of ||V||_μ and the same locality parameters (C, μ, v_LR). This constitutes a controlled non-Gaussian stability statement (full derivation in Supplement S5).

8. Statistical Audit Layer

For bounded observables and independent shots, Hoeffding + union bounds yield explicit sample complexity for auditing a finite suite with confidence 1−δ. Because two-point observables may suffer correlated shot noise, we also provide a conservative correlation-robust bound based on bounded average covariance, which can be used as a worst-case fallback (Supplement S4).

9. Concrete Use Case: Cooling Lindbladian on a Defected Fermionic Chain

We include a realistic model: a tight-binding fermionic chain with a localized defect and Lindblad cooling. We provide a complete certified budget: interaction norm ||I||_μ, explicit v_LR ~ ||I||_μ/μ, Γ(ε) for tilting perturbations, the achieved closure horizon T_* from the dispersion/two-point bounds, and a concrete experiment-facing observable (coarse-grained density–density correlator). The signature locality–mixing separation applies directly because λ>0 is expected for primitive cooling (assumption stated and discussed).

10. Discussion and Conclusions

The work provides a verifiable certification pipeline for a controlled domain and introduces a signature locality–mixing separation diagnostic for dissipative dynamics that goes beyond locality alone. Extensions to strongly interacting or non-primitive open systems remain future work.