Submitted:
30 December 2025
Posted:
05 January 2026
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Unified Electro-Gravity Theory of a Static UEG Electron
- (a) The mass m and its associated energy of a given body is assumed to be inversely proportional to the relative permittivity , or directly proportional to the inverse-relative permittivity , of the surrounding medium. This is in consistency with the energy of a spherical surface charge q of radius , placed in a medium with permittivity . The is the permittivity of an “ideal free-space” having an ideal unit relative permittivity , which is assumed to exist far away from any gravitating body .
2.1. Energy Density in a Non-Linear Medium
2.2. Series Solution for the Inverse-Relative Permittivity Function
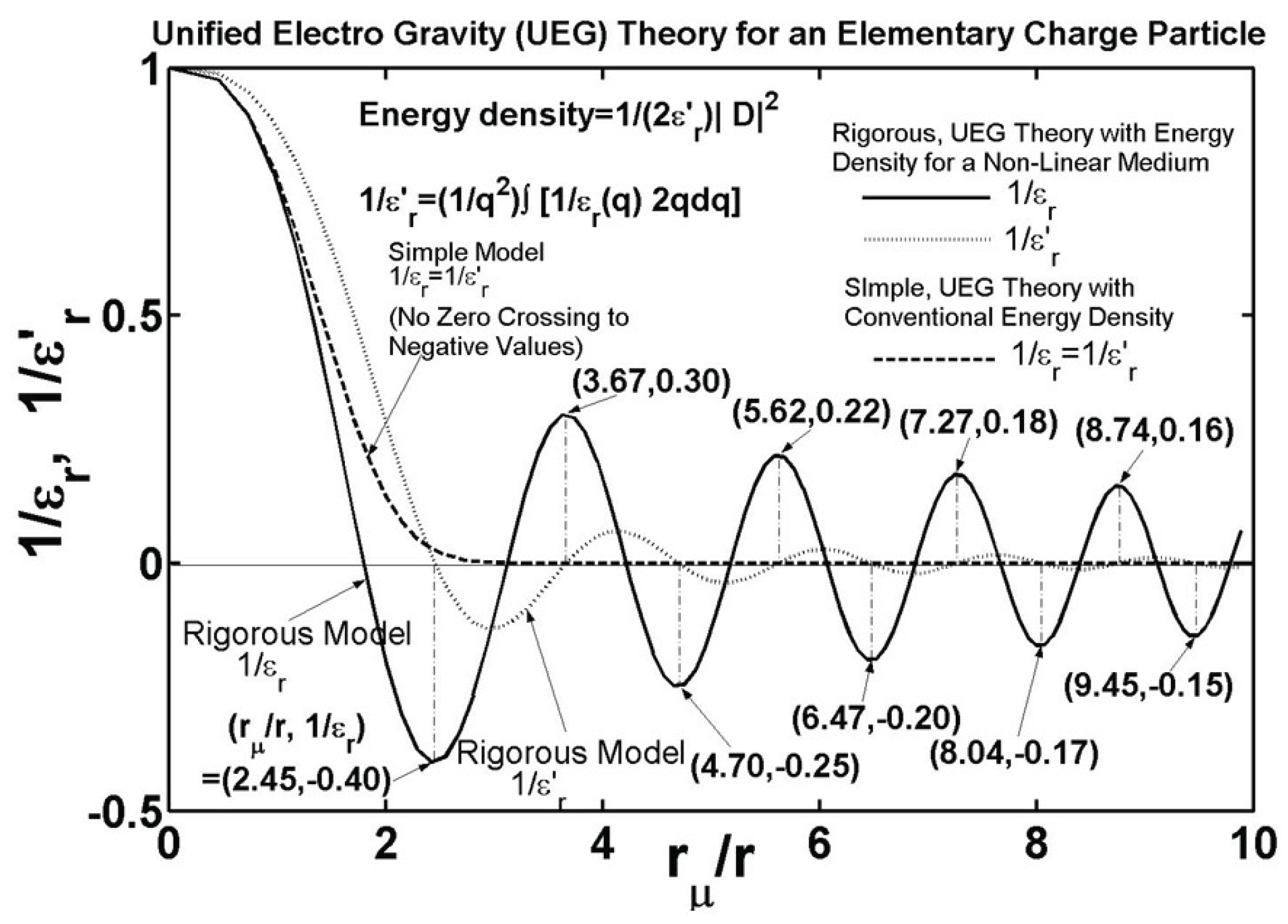
2.3. Particle Energy and Mass, as a Function of the Charge Radius
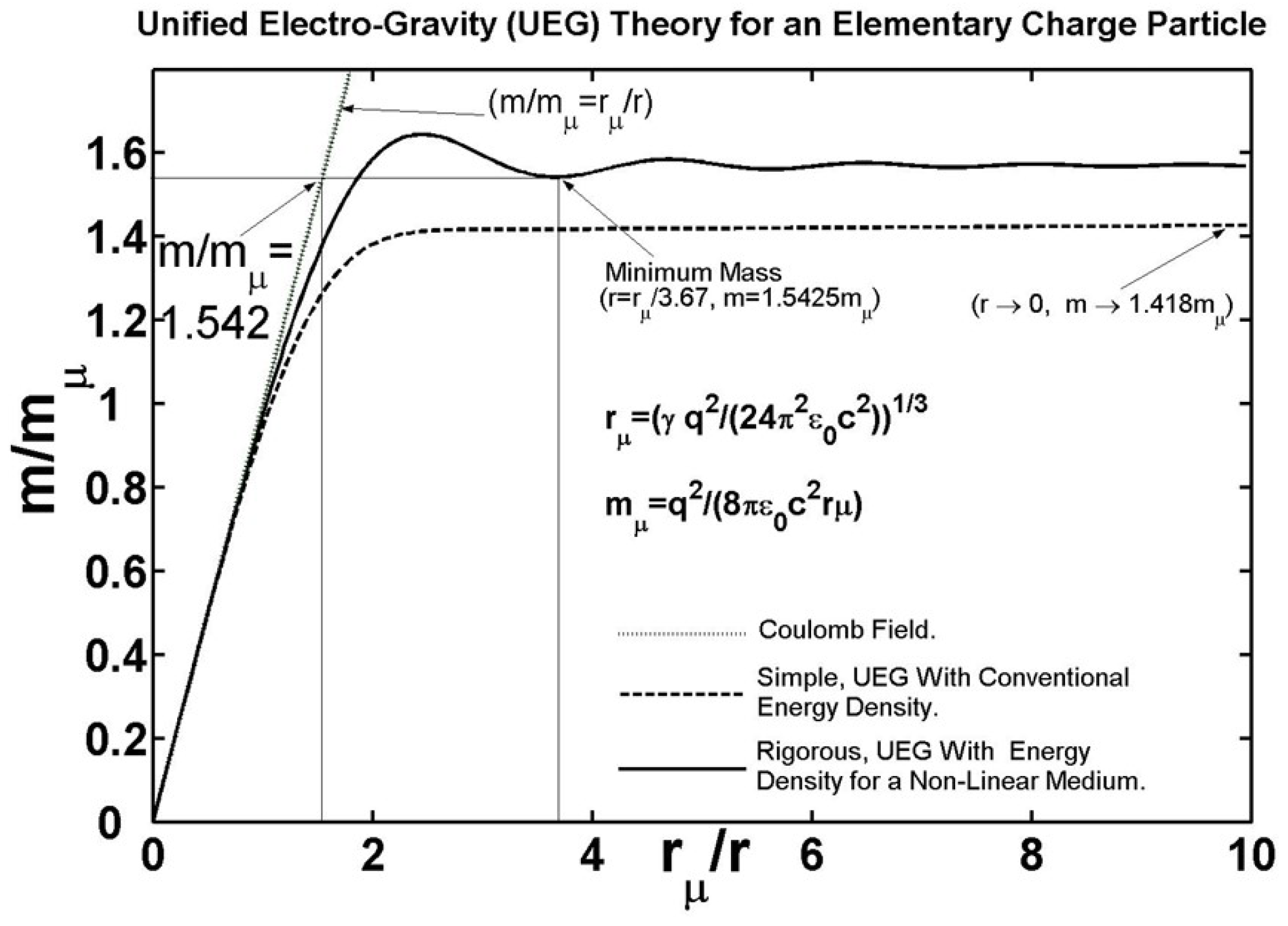
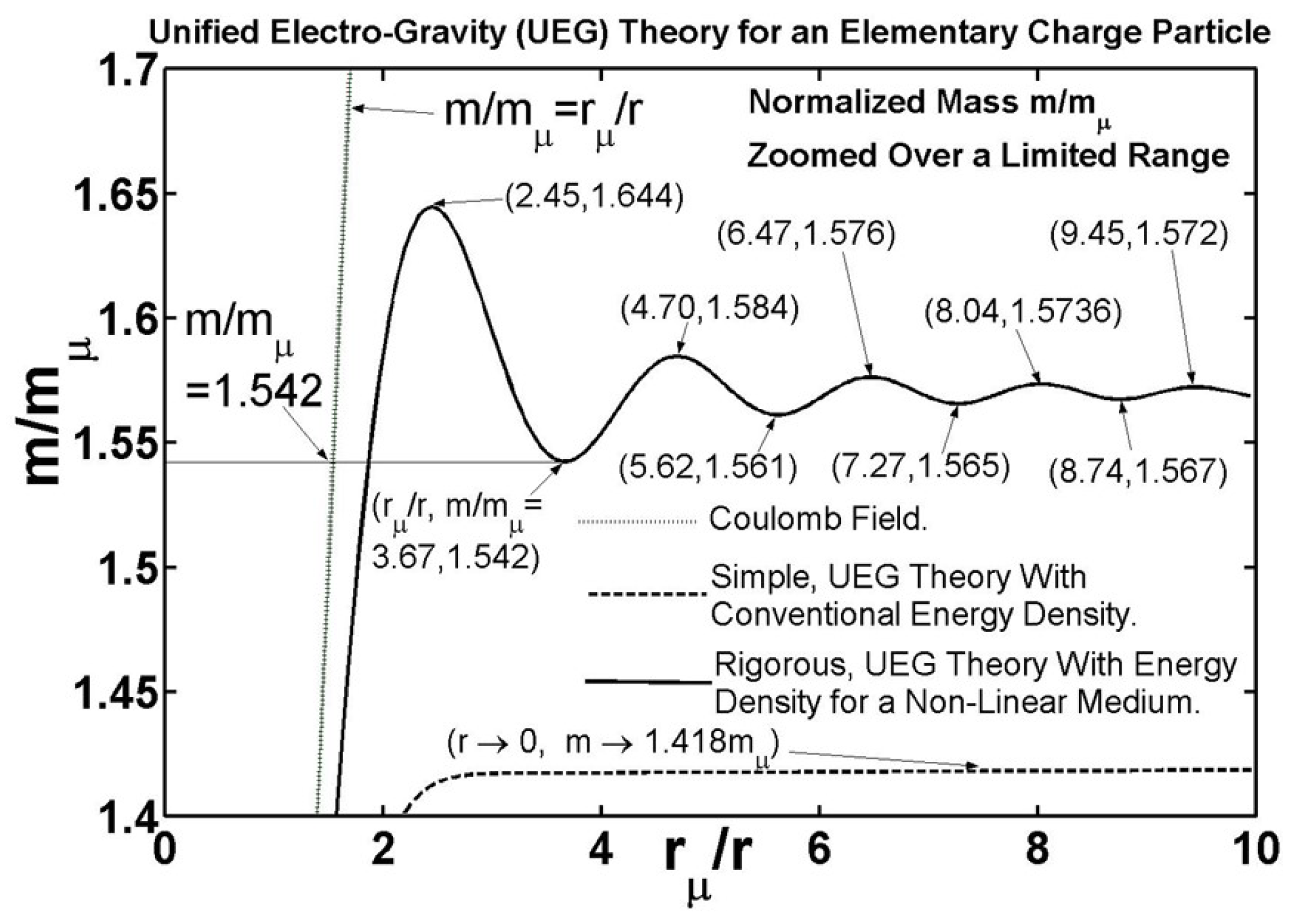
2.4. General Relationship Between the UEG Constant , the Particle Mass and Classical Radius
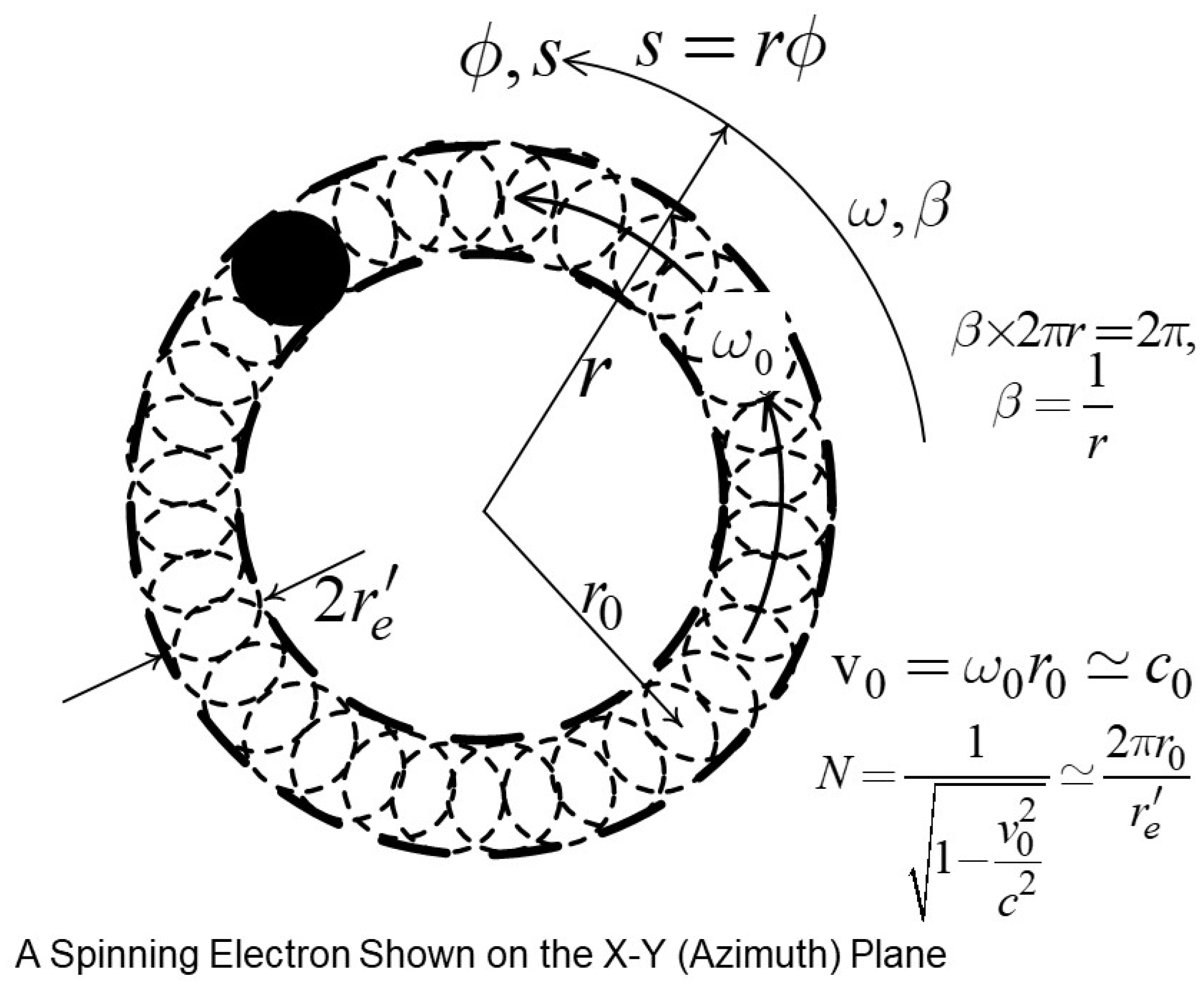
3. Electron Spin Modeled as Orbiting of a Static UEG Electron, Around its Own Fields
4. UEG Acceleration Components that Support the Spinning Central Motion)
5. Planck’s and Fine Structure Constants Related to the UEG Constant Using the Spin Model
5.1. Closer Relationship Between the UEG and Quantum Electrodynamics
6. The UEG Acceleration Due to the Magnetic Field, and the UEGM (UEGravito-Magnetic) Acceleration Due to the Field Momentum
7. Quantum Mechanical Wave is a Ripple in the “Non-Linear” Free-Space Medium, With the Quantum Frequency Close to the Spin Frequency
7.1. Electron g-Factor Related to Relativistic Boost factor, and to the Spin and Quantum Wave Frequencies
7.2. Estimating g-Factor from the Fine Structure and UEG Constants, Based on the Spin Model
7.3. Higher Order Corrections to the g-factor
8. Discussion: Fundamental Implications from the UEG Theory of a Spinning Electron
8.1. Quantization of Charge and Angular Momentum as Complementary, Emergent Concepts
8.2. Wave-Particle Duality
8.3. Electrodynamic Scattering, Photoelectric Effect, and the Photon Concept
References
- Thomson, J.J. Cathode Rays. Philosophical Magazine Series 5 1897, 44, 293–316. [Google Scholar] [CrossRef]
- Cottingham, N.; Greenwood, D. An Introduction to the Standard Model of Particle Physics (2Ed); Cambridge University Press, 2007. [Google Scholar]
- Wikipedia. Leptons, Table of Leptons. 2013. Available online: http://en.wikipedia.org/wiki/Lepton.
- Rotherford, E. Scattering of α and β Particles by Matter and the Structure of the Atom. Philosophical Magazine Series 6 1911, 21, 669–688. [Google Scholar] [CrossRef]
- Bohr, N. Nobel Lecture: The Structure of the Atom. Nobel Foundation: (Retrieved August 2017). 1922. Available online: http://www.nobelprize.org/nobel_prizes/physics/laureates/1922/bohr-lecture.html.
- Mohr, P.J.; Taylor, B.N.; Newell, D.B. The 2014 CODATA Recommended Values of the Fundamental Physical Constants. Review of Modern Physics 2016, 88, 1–73. [Google Scholar] [CrossRef]
- Millikan, R.A. The Isolation of an Ion, A Precision Measurement of its Charge, and the Correction off Stoke’s Law. Physical Review (Series I) 1911, 32, 349–397. [Google Scholar] [CrossRef]
- Gabrielse, G.; Hanneke, D. Precision pins down the electron’s magnetism. CERN Courier 2006, 46, 35–37. [Google Scholar]
- Schrodinger, E. Quantisierung als Eigenwertproblem. Annalen der Physik 1926, 384, 361–376. [Google Scholar] [CrossRef]
- de L. Kronig, R.; Penney, W.G. Quantum Mechanics of Electrons in Crystal Lattices. Proceedings of the Royal Society A 1931, 130, 499–513. [Google Scholar]
- Dirac, P.A.M. Quantum Theory of the Electron. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 1928, 117, 610–624. [Google Scholar] [CrossRef]
- Feynman, R.P. Mathematical Formulation of the Quantum Theory of Electromagnetic Interction. Physical Review 1950, 80, 440–457. [Google Scholar] [CrossRef]
- Eichten, E.J.; Peskin, M.E.; Peskin, M. New Tests for Quarks and Lepton Substructure. Physical Review Letters 1983, 50, 811–814. [Google Scholar] [CrossRef]
- Feynman, R.P.; Leighton, R.B.; Sands, M. Lectures on Physics Vol.II, Ch.28; Addision Wesley, 1964. [Google Scholar]
- Das, N. A New Unified Electro-Gravity Theory for the Electron. Preprints 2019, 2019070052. [Google Scholar] [CrossRef]
- Das, N. A New Unified Electro-Gravity Theory for the Electron, and the Fundamental Origin of the Fine Structure Constant and the Casimir Effect. Journal of High Energy Physics, Gravitation and Cosmology 2021, 7, 66–87. [Google Scholar] [CrossRef]
- Newton, S.I. Principia: Mathematical Principles of Natural Philosophy. I. B. Cohen, A. Whitman and J. Budenz, English Translators from 1726 Original; University of California Press, 1999. [Google Scholar]
- Einstein, A. Zur Elektrodynamik bewegter Körper (On the Electrodynamics of Moving Bodies). Annalen der Physik 1905, 322, 891–921. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, Vol. I and II (Reprint from 1873); Dover Publications, 2007. [Google Scholar]
- Einstein, A. Grundlage der allgemeinen Relativitätstheorie (The Foundation of the General Theory of Relativity). Annalen der Physik 1916, 354, 769–822. [Google Scholar] [CrossRef]
- Planck, M. On the Law of Distribution of Energy in the Normal Spectrum. Annalen der Physik 1901, 309, 553–563. [Google Scholar] [CrossRef]
- Sommerfeld, A. Atomic Structure and Spectral Lines. (Translated by H. L. Brose); Methuen, 1923. [Google Scholar]
- Feynman, R.P. QED: The Strange Theory of Light and Matter (p. 129); Princeton University Press, 1985. [Google Scholar]
- Brodsky, S.; Franke, V.; Hiller, J.; McCartor, G.; Paston, S.; and, E.P. A Nonperturbative Calculation of the Electron’s Magnetic Moment. Nuclear Physics B 2004, 46, 353–362. [Google Scholar]
- Wikipedia. g-factor. 2017. Available online: http://en.wikipedia.org/wiki/G-factor_(physics).
- Wikipedia. Fine-Structure Constant. 2017. Available online: http://en.wikipedia.org/wiki/Fine_structure_constant.
- Mashhoon, B.; Gronwald, F.; Lichtenegger, H.I.M. Gravitomagnetism and Clock Effect. Gyros, Clocks, Interferometers. Testing Relativistic Gravity in Space 2001, 562, 83–110. [Google Scholar]
- McGregor, M.H. The Power of Alpha (p. 69); World Scientific, 2007. [Google Scholar]
- Lederman, L.M.; Teresi, D. The God Particle: If the Universe is the Answer, What is the Question (ch.2); Dell Publishing, 1993. [Google Scholar]
- Pauli, W. Quantum Mechanics of the Magnetic Electron. Journal of Physics 1927, 43, 601–623. [Google Scholar]
- de Broglie, L. La mecanique ondulatoire et la structure atomique de la matiere et du rayonnement. Journal de Physique et le Radium 1927, 8, 225–241. [Google Scholar] [CrossRef]
- Bohm, D. A Suggested Interpretation of the Quantum Theory in Terms of Hidden Variables. Physical Review 1952, 85, 166–179. [Google Scholar] [CrossRef]
- Couder, Y.; Fort, E. Single Particle Diffraction and Interference at a Macroscopic Scale. Physical Review Letters 2006, 97. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 2nd Edition; John Wiley and Sons, 1998. [Google Scholar]
- Compton, A.H. A Quantum Theory of the Scattering of X-Rays by Light Elements. Physical Review 1923, 21, 483–502. [Google Scholar] [CrossRef]
- Raman, C.V.; Krishnan, K.S. A New Type of Secondary Radiation. Nature 1928, 121, 501–502. [Google Scholar] [CrossRef]
- Einstein, A. Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (On a Heuristic Point of View about the Creation and Conversion of Light). Annalen der Physik 1905, 17, 132–148. [Google Scholar] [CrossRef]
- Wikipedia. Angular Momentum of Light. 2018. Available online: http://en.wikipedia.org/wiki/Spin_angular_momentum_of_light.
- Stewart, A.M. Angular momentum of the electromagnetic field: the plane wave paradox resolved. arXiv:physics. class-ph, physics/0504082v3 2005. [Google Scholar] [CrossRef]
- Kuhn, T.S. Black-Body Theory and Quantum Discontinuity; Clarendon Press: Oxford, 1978. [Google Scholar]
- Kragh, H. Max Planck: The Reluctant Revolutionary 1894-1912. PhysicsWorld.com. 2000. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




