Receiver-Centric Hypothesis-Parallel Message Passing for Unit-Rate Transmission

1. Introduction

The era of channel coding began with linear block codes, in which codewords are represented as vectors in an n-dimensional space generated by a set of linearly independent rows of a generator matrix. Classical decoding methods for such codes, including syndrome-based lookup decoding and bounded-distance decoding, identify the most probable error pattern consistent with the received syndrome [1]. While these techniques are optimal for short block lengths, their computational complexity grows exponentially with code dimension or the number of parity constraints, which makes them impractical for moderate and long codes [2]. Maximum-likelihood (ML) decoding provides optimal error performance, but its complexity of $O\left(2^k\right)$ is prohibitive for most real-time applications.

Iterative message-passing decoding, most notably belief propagation (BP) and the sum-product algorithm, offers a scalable alternative by performing probabilistic inference on the Tanner-graph representation of a code [3,4]. The computational complexity of message passing grows linearly with the number of graph edges, and when applied to sparse parity-check matrices, it enables decoding performance that approaches the Shannon limit [5]. These properties have established message-passing decoding as a core technique in modern communication systems.

Despite these advances, conventional coded systems rely on the transmission of redundancy, and the channel code rate $R=k/n$ is necessarily smaller than one. Improvements in minimum distance or iterative convergence typically require additional parity symbols, which reduce effective throughput. This paper examines a different operating regime: only the uncoded information bits are transmitted over the channel, while the receiver alone introduces code structure and performs decoding within an n-dimensional code space. From the channel perspective, the transmission operates at unit rate ($R_{\mathrm{eff}}=1$).

Scope and interpretation. The proposed framework should be interpreted as constrained hypothesis testing rather than probabilistic inference under a modified channel model. The physical channel is unchanged: the only random observation is the channel output $\mathbf{y}$ associated with the transmitted information symbols. Code structure is used at the receiver to restrict and score candidate hypotheses. In particular, the parity-related terms used within the decoder are deterministic, hypothesis-conditioned constraints and are not treated as additional channel observations or side information. Consequently, the method makes no claim of increasing channel capacity; instead, it explicitly trades receiver-side computational complexity against decision reliability in a finite-hypothesis regime.

The main contributions of this work are summarized as follows:

• A receiver-centric framework for unit-rate transmission is formulated as hypothesis-parallel, constrained decision-making in an n-dimensional code space.
• Message passing is employed as a one-shot soft refinement operator for each hypothesis, followed by an orthogonality-based constraint metric for final selection.
• The role of parity-related metric weighting is clarified: it controls constraint hardness and influences bit-error-rate (BER) curve presentation, without implying a physical signal-to-noise ratio (SNR) change or a capacity gain.

The rest of the paper is organized as follows. Section 2 introduces the system model and notation. Section 3 presents the receiver architecture, including hypothesis-conditioned constraint weighting and the selection rule. Section 4 clarifies the relationship to channel capacity and conditional entropy. Section 5 analyzes computational complexity. Section 6 reports simulation results. Section 7 concludes the paper.

2. System Model and Preliminaries

2.1. Linear Block Code Representation

We consider a binary linear block code $\mathcal{C}$ of length n and dimension k, denoted as a $(k,n)$ code. The code can be specified by a generator matrix $G\in {0,1}^{k\times n}$ and a parity-check matrix $H\in {0,1}^{(n-k)\times n}$ such that

$$H{G}^{\top }=0\mathrm{over}\mathbb{F}*2.$$

(1)

We focus on systematic generator matrices of the form

$$G=[I_k;P],$$

(2)

where $I_k$ is the $k\times k$ identity matrix and P is a $k\times (n-k)$ parity matrix. A corresponding systematic parity-check matrix is

$$H=[P^{\top };I*n-k].$$

(3)

The Tanner graph associated with H is a bipartite graph with variable nodes corresponding to codeword symbols and check nodes corresponding to parity constraints.

2.2. Channel Model and Information-Symbol LLRs

The transmitter sends k uncoded information bits

$$\mathbf{u}=(u_1,\dots ,u_k)\in {0,1}^k.$$

(4)

These bits are binary-phase shift-keying (BPSK) modulated as

$$x_i=1-2u_i\in -1,+1,i=1,\dots ,k,$$

(5)

and are transmitted over an additive white Gaussian noise (AWGN) channel:

$$y_i=x_i+n_i,n_i\sim \mathcal{N}(0,{\sigma }^2),i=1,\dots ,k.$$

(6)

No parity symbols are transmitted; the effective information rate over the physical channel is therefore $R_{\mathrm{eff}}=1$.

At the receiver, log-likelihood ratios (LLRs) are computed for each received information symbol:

$$L_i=log{\displaystyle \frac{p\left(y_i\right|x_i=+1)}{p\left(y_i\right|x_i=-1)}}={\displaystyle \frac{2y_i}{{\sigma }^2}},i=1,\dots ,k.$$

(7)

These k LLRs constitute the only probabilistic soft information derived from the physical channel.

2.3. Remark on Noise-Variance Bookkeeping

In traditional coded communication, all n symbols of a codeword are transmitted and independently corrupted by noise. The familiar relation

$${\sigma }_{\mathrm{trad}}^2={\displaystyle \frac{1}{2R(E_b/N_0)}},R={\displaystyle \frac{k}{n}}$$

(8)

reflects that $E_b$ is spread across n channel uses. In the present unit-rate setting, only k channel uses occur, hence

$${\sigma }^2={\displaystyle \frac{1}{2(E_b/N_0)}}$$

(9)

is the relevant physical-noise relation for the transmitted information symbols. Any additional reliability parameters used inside the receiver act on the decision rule and are not part of the physical channel model.

3. Proposed Receiver and Hypothesis-Parallel Decoding

3.1. Receiver-Only Code Embedding

The receiver is equipped with a $(k,n)$ linear block code $\mathcal{C}$ with known matrices $G=[I_k;P]$ and $H=[P^{\top };I_{n-k}]$. All $2^k$ information hypotheses are considered,

$${\mathbf{u}}^{\left(m\right)}\in {0,1}^k,m=1,\dots ,2^k,$$

(10)

and each hypothesis uniquely determines a candidate codeword

$${\mathbf{c}}^{\left(m\right)}={\mathbf{u}}^{\left(m\right)}G\in {0,1}^n.$$

(11)

In particular, the parity pattern of ${\mathbf{c}}^{\left(m\right)}$ is a deterministic function of the hypothesis ${\mathbf{u}}^{\left(m\right)}$.

3.2. Hypothesis-Conditioned Constraint Weighting

To enable message passing over the Tanner graph for each hypothesis, an n-dimensional initialization vector is formed. For the information positions, the initialization is given by the channel-derived LLRs ${L_i}_{i=1}^k$. For the parity positions, the receiver introduces deterministic constraint weights that are conditioned on the hypothesis. These weights are not interpreted as channel observations. Instead, they control the hardness with which the parity consistency implied by ${\mathbf{c}}^{\left(m\right)}$ is enforced within the decision rule.

For numerical convenience, a constraint-weight magnitude $L_p>0$ may be represented on an “LLR-like” scale. This is purely an internal parameter of the decoder metric and should not be interpreted as implying a reduced physical noise variance for untransmitted symbols.

3.3. Parallel Message Passing Across Hypotheses

For each hypothesis m, one iteration of message passing is executed on the Tanner graph with the above initialization. The goal of this single iteration is soft refinement of the hypothesis-conditioned estimate, not iterative convergence under a probabilistic channel model.

Let ${\widehat{\mathbf{x}}}^{\left(m\right)}$ denote the refined soft estimate after the single message-passing step for hypothesis m.

3.4. Orthogonality-Based Constraint Metric and Selection Rule

Each refined estimate is scored by an orthogonality-based constraint metric defined with respect to the candidate codeword. Specifically, an energy functional is computed as

$${\mathcal{E}}^{\left(m\right)}=\sum _{i=1}^n\widehat{x}*i^{\left(m\right)},\neg c_i^{\left(m\right)},$$

(12)

where $\neg c_i^{\left(m\right)}$ denotes the complement (in the chosen bipolar or binary representation) of the i-th component of the hypothesis-induced codeword. The decoded hypothesis is

$$\widehat{m}=argmin*m\in 1,\dots ,2^k{\mathcal{E}}^{\left(m\right)},$$

(13)

with the decoded information vector $\widehat{\mathbf{u}}={\mathbf{u}}^{\left(\widehat{m}\right)}$.

4. Relation to Channel Capacity and Conditional Entropy

This section clarifies why the proposed receiver-centric framework does not break established information-theoretic principles.

4.1. No Change to the Physical Channel or Mutual Information

The physical channel is the AWGN channel used to transmit the k information symbols. The only random observation available to the receiver is $\mathbf{y}$. The decoder does not obtain additional channel outputs, and it does not modify the channel law $p\left(\mathbf{y}\right|\mathbf{x})$. Therefore, the mutual information between the transmitted information symbols and the channel output, $I(X;Y)$, is unchanged by any internal decoder parameter.

It is important to mention that the observed reduction in the required $E_b/N_0$ for a given target BER does not indicate an increase in channel capacity. The physical channel remains unchanged, and the mutual information $I(X;Y)$ is fixed by the AWGN channel law. The improved performance reflects a reduction in the decoding gap to capacity achieved through a more powerful decision rule, rather than a shift of the capacity limit itself. In particular, the proposed receiver approaches ML decision behavior in a finite-hypothesis regime by enumerating and scoring all candidate information hypotheses under strong structural constraints. This improved hypothesis resolution is obtained at the expense of increased receiver-side computational complexity, which scales exponentially with the number of information bits k. Such a trade-off between complexity and reliability is fully consistent with information-theoretic principles and does not rely on transmitting additional redundancy or side information through the channel. Consequently, the apparent leftward shift of BER curves should be interpreted as a reduction of the decoder-induced performance gap to capacity, not as evidence of capacity enhancement, especially in short-block, unit-rate transmission scenarios.

4.2. Reliability via Constrained Hypothesis Testing and Complexity

The proposed method reduces decision uncertainty by restricting and scoring hypotheses using code-structure constraints. In information-theoretic terms, improved reliability corresponds to reducing the conditional uncertainty of the decision given the observation, i.e., reducing the effective ambiguity in $H\left(X\right|Y)$ through a more powerful decision rule (here, an explicit enumeration over a finite hypothesis set combined with constraint-based scoring). This reduction is achieved by computational complexity (scaling with $2^k$ for hypothesis enumeration) rather than by transmitting redundancy. No claim is made of exceeding capacity; rather, the framework highlights a complexity–reliability trade-off in a finite-hypothesis regime.

4.3. Interpretation of Metric Weighting and BER Presentation

The constraint-weight magnitude $L_p$ influences how strongly parity consistency is enforced inside the decision metric. Because $L_p$ is an internal metric parameter, varying $L_p$ can produce apparent horizontal displacements of BER curves when performance is plotted against $E_b/N_0$. Such displacements reflect changes in the decision rule and metric scaling, not a physical reduction of channel noise. Any “compensation” applied in plots should therefore be interpreted as a plotting/normalization device to compare decision rules, not as a claim of physical equivalence between systems.

The magnitude of $L_p$, causes a horizontal displacement of the BER curves when performance is plotted versus $E_b/N_0$. This effect arises because representing the parity constraint on an LLR-like scale implicitly corresponds to assuming an effective noise variance for the parity positions, even though no physical channel observations exist for those symbols. To enable fair comparison across different values of $L_p$, a deterministic horizontal normalization is applied. Under the standard AWGN LLR normalization $L=2y/{\sigma }^2$ with normalized constellation values, the corresponding horizontal offset is given by

$${\Delta }_{\mathrm{SNR}}=10{log}_{10}\left({\displaystyle \frac{L_p}{2}}\right).$$

(14)

This normalization compensates for the model-induced metric scaling only and does not represent a physical SNR gain or any change in the underlying channel conditions.

5. Complexity Considerations

A naive ML decoder over all $2^k$ hypotheses has complexity $O\left(k{2}^k\right)$. A standard BP decoder for a length-n code, when all n symbols are transmitted, requires iterative processing with complexity on the order of

$$O(I·E),$$

(15)

where I is the number of iterations and E is the number of edges in the Tanner graph.

In the proposed architecture, two observations alter the complexity profile. First, the number of hypotheses $2^k$ is fixed and small in the targeted regime (e.g., $2^8=256$). Second, each hypothesis requires only a single message-passing iteration. Thus, the total effort is dominated by

$$C_{\mathrm{total}}(k,n)\approx 2^k·C_{\mathrm{BP}}^{\left(1\right)}\left(n\right),$$

(16)

where $C_{\mathrm{BP}}^{\left(1\right)}\left(n\right)$ denotes the cost of one BP iteration on the graph. For fixed k, complexity scales essentially linearly with n.

6. Simulation Setup and Illustrative Results

6.1. Code Family

We consider a family of $(k,n)$ codes with:

• fixed information dimension $k=8$;
• block length $n=24$;
• minimum distance $d_{min}=3$;
• systematic generator matrix of the form $G=[I_8;P_n]$;
• parity-check matrix $H=[P_n^{\top };I_{n-8}]$ constructed via a progressive edge-growth (PEG)-like procedure;
• sparse parity-check structure (low-density parity-check (LDPC) type), limited column and row weights;
• Tanner graph girth at least six (no four-cycles);
• no zero rows or zero columns in H.

These codes are generated using a PEG-style construction to ensure large girth and good graph connectivity [6].

6.2. Channel and Decoder Parameters

For each $(k,n)$ code and each SNR point, the simulation procedure is as follows:

• Random information vectors $\mathbf{u}\in {0,1}^8$ are generated.
• The bits are BPSK-modulated and transmitted over an AWGN channel with noise variance

  $${\sigma }^2={\displaystyle \frac{1}{2(E_b/N_0)}},$$

  (17)

  corresponding to unit-rate transmission.
• LLRs for the information positions are computed from the received symbols.
• A hypothesis-conditioned constraint-weight magnitude $L_p$ is selected (varied from 25 to 100 in the reported experiments) to control the hardness of parity consistency in the internal decision metric. This parameter is not a channel observation and does not modify the physical noise model.
• Hypothesis-parallel message passing is executed over all $2^8=256$ hypotheses, with each hypothesis refined through a single BP iteration.
• The orthogonality-based constraint metric is computed for each candidate, and the hypothesis minimizing the metric is selected.
• BER is estimated over a large number of trials (e.g., 1000 packet errors per SNR point).

6.3. Results and Interpretations

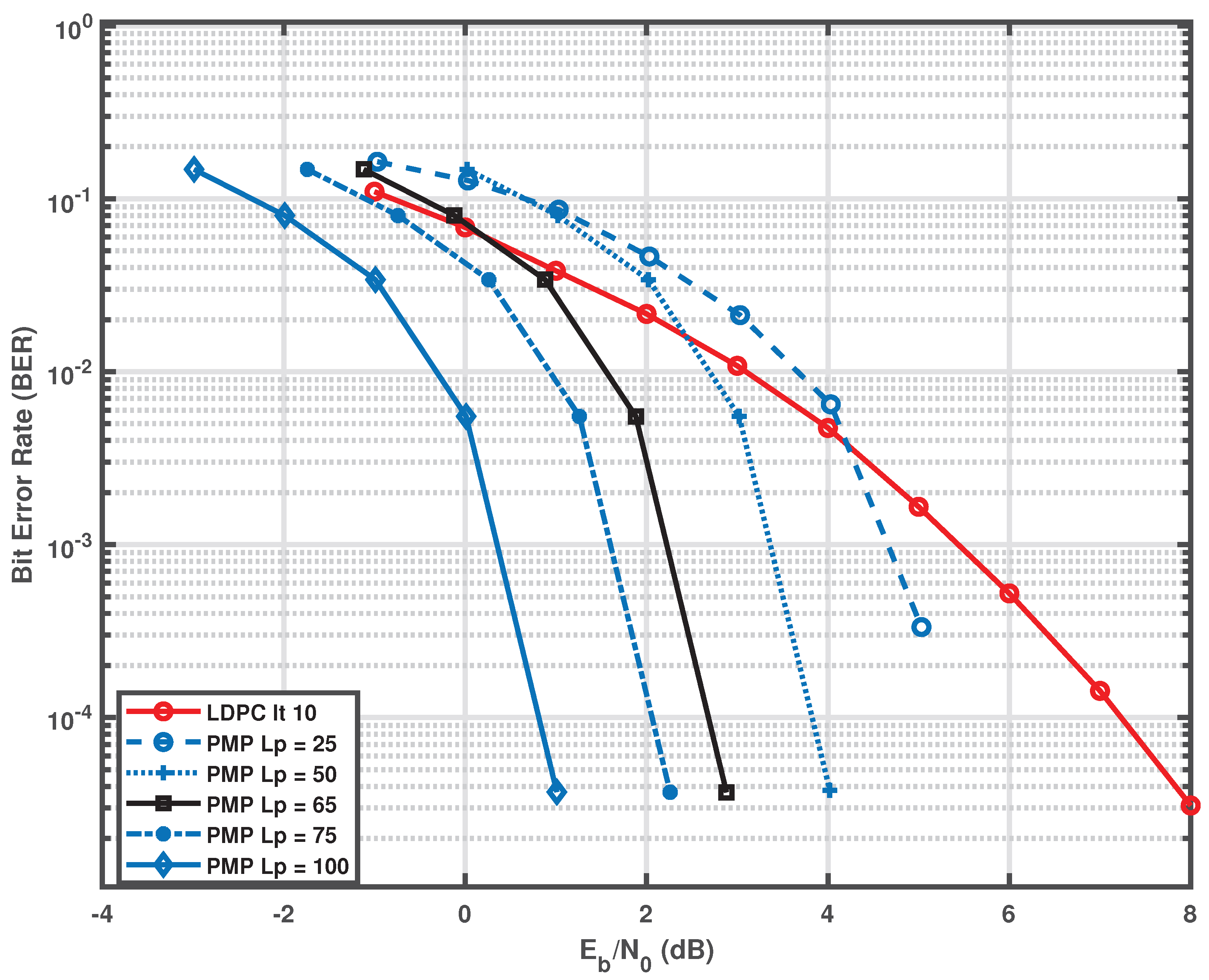
Figure 1 presents the BER performance of a conventional iterative LDPC decoder for the $(8,24)$ code and the proposed receiver for different values of the constraint-weight magnitude $L_p$. The curves labeled LDPC correspond to the standard iterative LDPC decoder operated with its maximum allowed number of iterations. The curves labeled PMP correspond to the proposed hypothesis-parallel message-passing framework.

As $L_p$ increases, hypothesis discrimination becomes sharper, producing a steeper waterfall region. Because $L_p$ changes the internal metric scaling, BER curves may exhibit horizontal displacements when plotted versus $E_b/N_0$. Such displacements reflect decision-rule parameterization rather than physical SNR changes; accordingly, any horizontal normalization applied to the plots should be interpreted as a comparison aid between decision rules, not as an attempt to claim physical equivalence.

It is observed that around $L_p\approx 65$ (in the chosen parameterization), the proposed scheme approaches the performance of the conventional LDPC decoder, and for larger $L_p$ it can yield lower BER in the tested short-block regime. Beyond a certain $L_p$, the curve shape saturates and further improvement requires increasing code length while keeping k fixed.

7. Conclusions

This paper investigated a receiver-centric framework for unit-rate transmission in which no redundancy is conveyed through the physical channel. By embedding each candidate information hypothesis into a higher-dimensional linear block code at the receiver and applying hypothesis-parallel message passing followed by an orthogonality-based constraint metric, reliable decisions can be approached in a finite-hypothesis regime.

The parity-related quantities used inside the decoder act as deterministic, hypothesis-conditioned constraint weights and are not interpreted as additional channel observations. Accordingly, the method does not alter the physical channel model, does not introduce additional mutual information beyond the channel output, and does not claim any channel-capacity gain. Instead, it highlights a complexity–reliability trade-off: improved decision performance is obtained by increased receiver-side computation and structured constraint enforcement.