1. Introduction
The Additive White Gaussian Noise (AWGN) channel serves as a foundational model in the analysis and design of digital communication systems. Despite the existence of more sophisticated models that capture fading, interference, and non-linearities, the AWGN channel remains a critical benchmark for evaluating the performance of coding and decoding techniques.
Among the most widely adopted techniques for decoding over AWGN channels are iterative decoding schemes, such as the Viterbi algorithm for convolutional codes and Belief Propagation (BP) for Low-Density Parity-Check (LDPC) codes. These methods iteratively refine symbol estimates using local message passing or state evaluation to achieve near optimal decoding. In particular, LDPC and Turbo codes (both decoded iteratively) have demonstrated remarkable performance, approaching the Shannon limit in AWGN environments [
1]. However, while these algorithms are effective, their convergence speed remains a practical limitation, especially in low-latency or power-constrained applications.
To address this, recent research has explored enhancing iterative decoding through machine learning (ML) and deep learning (DL) frameworks. For instance, DeepTurbo integrates recurrent neural networks into the Turbo decoding process, improving convergence in the low-SNR regime [
2]. Similarly, recent studies have explored the use of deep learning to model and enhance decoding dynamics through end-to-end optimization [
3]. These techniques reflect a growing trend toward data-driven improvements in classical decoding frameworks. Additionally, hybrid architectures such as the Attention Turbo-Autoencoder [
4] and deep unfolding networks [
5] combine the structural advantages of traditional iterative decoding with the adaptability of neural networks. These methods often yield faster or more stable convergence under AWGN conditions by learning optimal update schedules, message weights, or stopping criteria.
The main aim of this work is to speed up the convergence of the traditional iterative decoding algorithms such as LDPC or product codes. To this end, re–scaled Gaussian observations are multiplied together in order to satisfy the Bayes’ theorem and reflect the channel coding memory on the observation side of the factor graph. This is followed by a bit log–liklihood ratio (LLR) correction procedure which selects and updates the provided bit LLRs to the decoder. The algorithm will accumulate the value of a bit LLR only if it was in the ambiguity region, i.e., the region close to zero. The length of the region is adjusted during the simulations. The algorithm applies the sum–product algorithm (SPA) on factor graphs. At every iteration, the receiver makes hard decisions on the received symbols using extrinsic information provided by the decoder. At the first iteration, receiver applies Kullback–Leibler (KL) divergence to the observations prior to re–scaling and multiplying procedures. Te reach the maximum performance of the algorithm, iterating strategy uses a unique scheduling procedure. This guarantees that the first iteration of the receiver equals the traditional decoding algorithm. The simulation results demonstrate significant gains of the proposed algorithm.
The paper is organized as follows:
Section 2 introduces the system model.
Section 3 discusses the corresponding factor graph and its SPA equations. Receiver implementations are detailed in
Section 4, with performance analysis provided in
Section 5. Finally, conclusions are drawn in
Section 6.
2. System Model
In a modern wireless communication system, the data bits are encoded using an LDPC encoder. This is followed by a Gray encoder and an
M–ary digital modulator. The sequence of the coded modulation symbols
is then transmitted over an AWGN channel. The baseband equivalent of the received samples can be described by
where
is a sequence of independent and identically distributed (i.i.d.), complex circularly symmetric Gaussian noise components, i.e.,
.
3. Factor Graph
According to the Bayes’ theorem, the receiver can be implemented by factorizing the posterior distribution of data bits
given the observation samples
and applying the SPA to the corresponding factor graph. It is assumed that the encoding function
maps the information sequence
to the codeword
. The factorization yields
where
is the code indicator function which equals to 1 if
is the codeword corresponding to
and zero otherwise. Equation (
2) ends with the product of Gaussian observations. To achieve this, re–scaling of distributions is necessary. The re–scaled observation at time epoch
k is shown below.
According to the Gaussian product rule, the product of re–scaled distributions provides a single Gaussian distribution which contains the memory of the channel coder in its mean. It should be mentioned that we employed the product of two re–scaled Gaussian distributions at every time epoch prior to bit LLR computations in our last work on multipath mitigation [
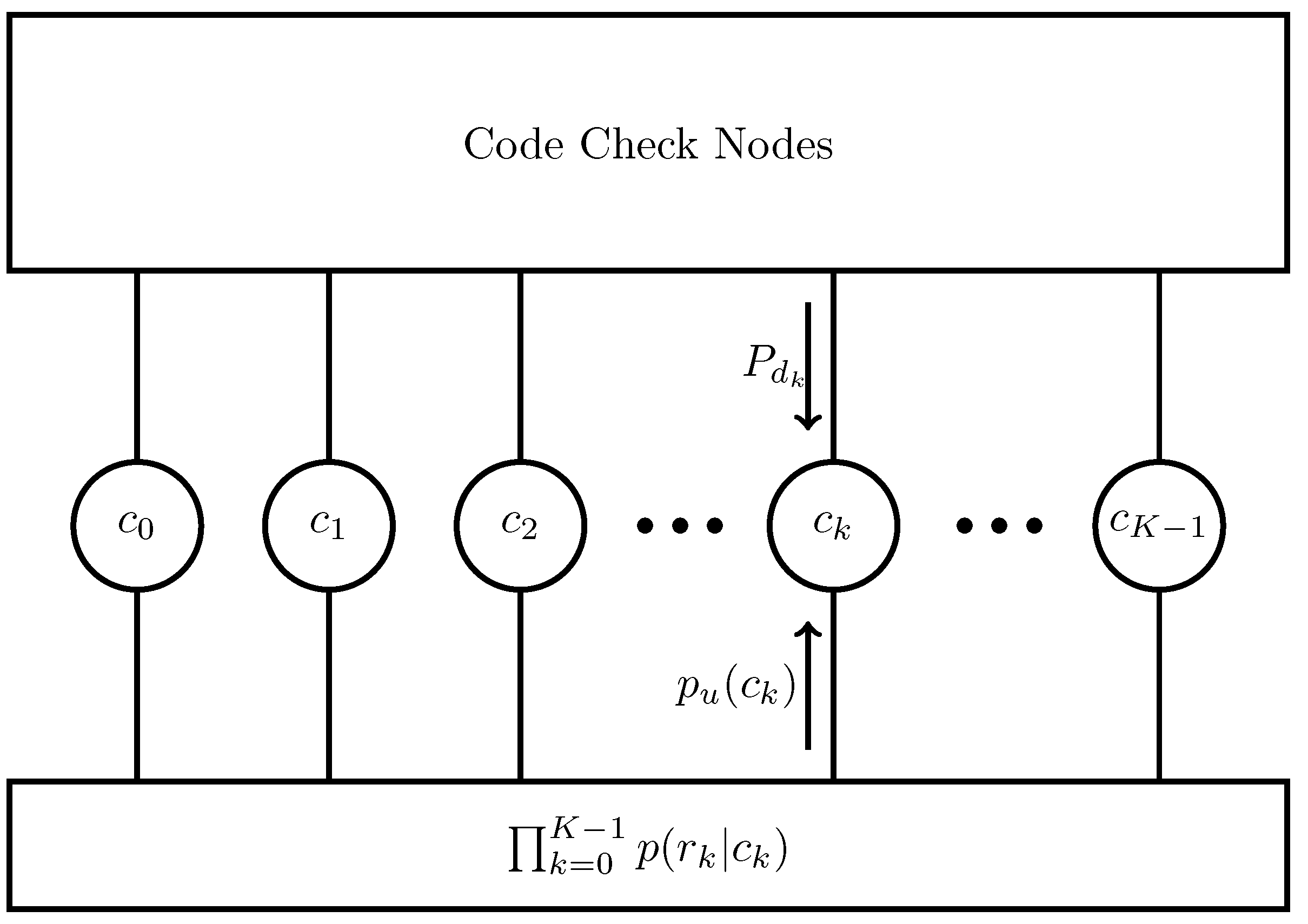
6]. The corresponding factor graph is depicted in Fig.
Figure 1.
4. Implementation Strategies
At every iteration, the receiver performs hard decisions on the received bits,
. This is accomplished by using the extrinsic information provided by the LDPC decoder. Consequently, a set of
M–ary modulation symbols
is also detected. At the time epoch
k, we perform message passing on the corresponding factor graph to compute the belief about the symbol
provided by the rest of the factor graph. The message
is a Gaussian distribution whose mean and variance are computed by
This is followed by computations of bit LLR for every bit associated with the constellation symbol in the Gray ordering. When the bit LLR value falls in the ambiguity region, whose length is adjusted during simulations, its value will be accumulated by the obtained LLR at the current iteration. At the first iteration of the receiver, KL divergence is applied to each observation prior to the Gaussian multiplication. In this way, only at the first iteration, the receiver works like the traditional decoders. The performance of the receiver is maximized by employing a proper scheduling procedure as elaborated on extensively in the next section.
5. Simulation Results
To assess the performance of the proposed algorithm in AWGN environments, computer simulations were conducted. Specifically, bit error rate (BER) curves were plotted as a function of the signal-to-noise ratio (SNR). We used a
-regular LDPC code with a block length of 4000 bits. Binary and quadrature phase shift keying (BPSK and QPSK) modulation schemes were used as the modulation schemes. Since a bit error rate (BER) of
is considered sufficient for performance evaluation in practical applications, the curves were plotted down to this error level. To enhance clarity and better visualize the differences, the BER curves were also plotted as a function of
.
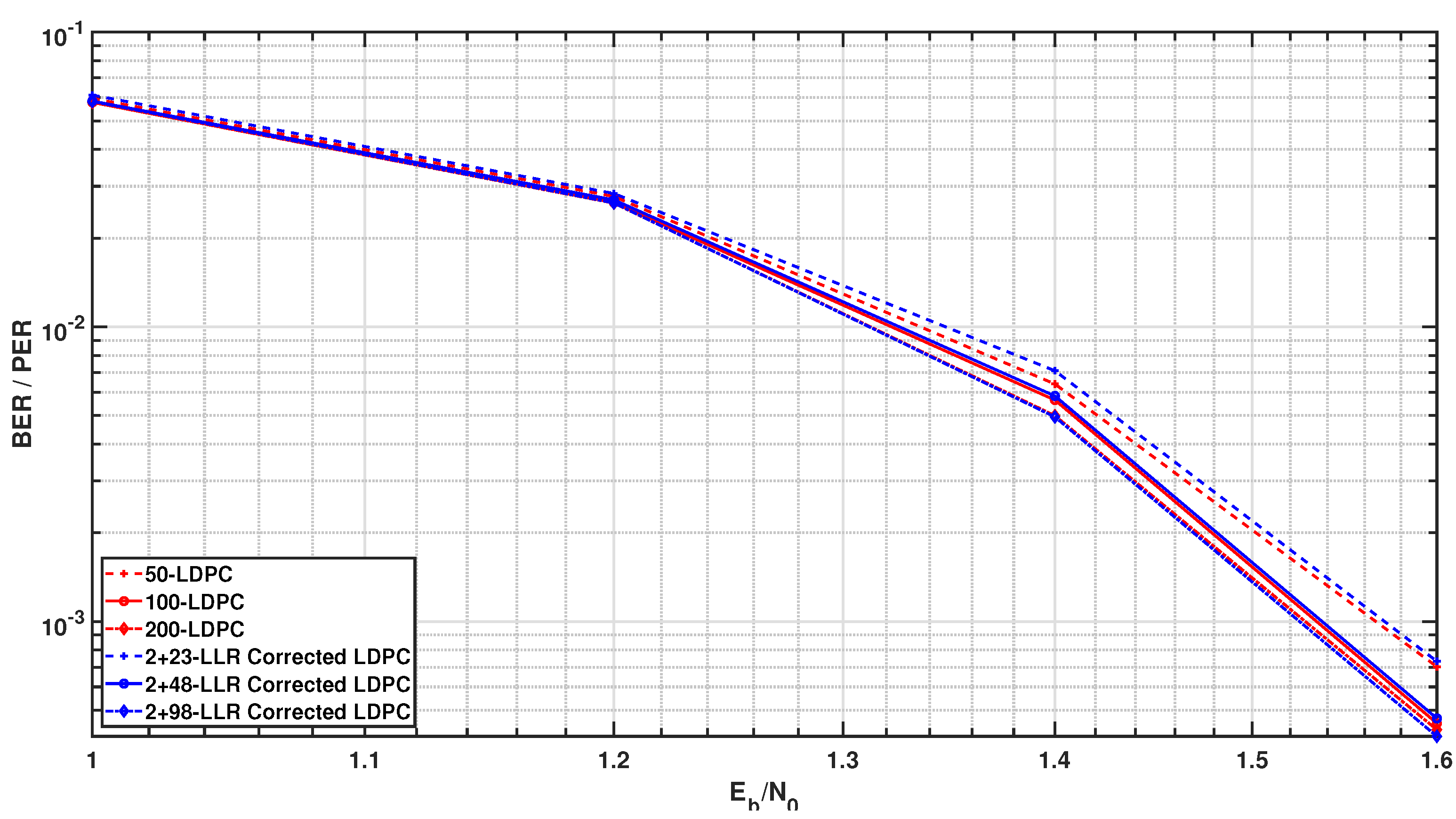
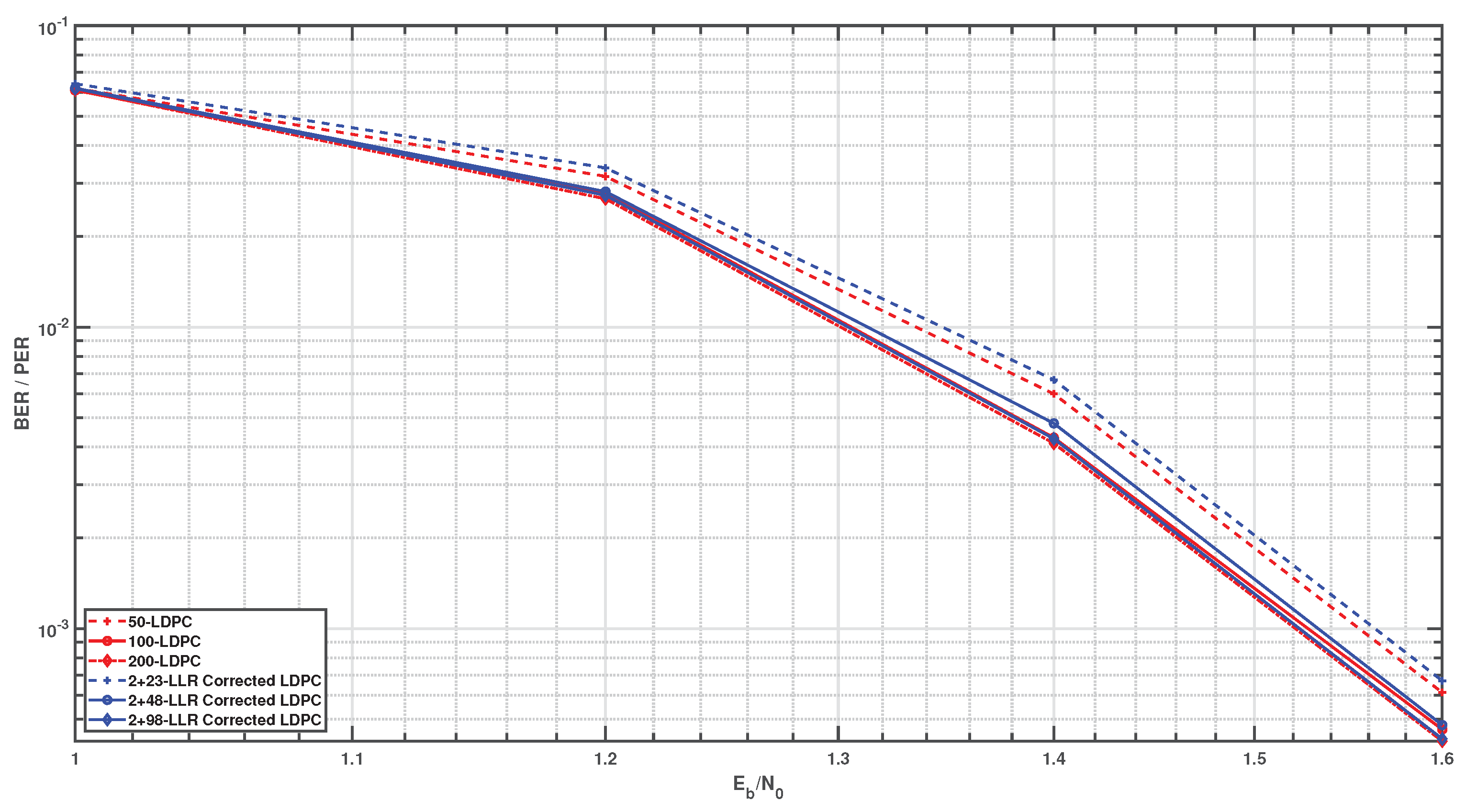
Figure 2 and
Figure 3 show the simulation results for BPSK and QPSK modulation formats, respectively. The red curves are associated with the original LDPC codes, named by their maximum number of decoder iterations, e.g., 200–LDPC. The blue curves correspond to the proposed joint bit LLR correction and decoding algorithms. Their names reflect the employed scheduling strategy that assumes a single receiver iteration. In this iteration, the LDPC decoder first performs 2 internal iterations, followed by the bit LLR correction step. Afterward, the LDPC decoder continues until the maximum number of decoding iterations is reached, i.e., it performs a total of the maximum number of LDPC iterations. The length of the decision region for LLR correction algorithm is set to 1 for BPSK modulation format and
for QPSK one.
A preliminary analysis of the results indicates that increasing the maximum number of iterations leads to improved convergence speed with the proposed algorithm, yielding approximately a gain. Furthermore, a comparison of convergence regions and receiver iteration counts reveals a trade-off between the ambiguity region length and the constellation size. Specifically, the decision region for higher-order constellations can be determined by dividing the binary region by the constellation size (M).
6. Conclusion and Future Work
The proposed method achieves faster communication performance compared to existing approaches. This represents a significant advancement for satellite communications and low–power communication systems. To address this, the memory of channel coding schemes has first been reflected in the observation part of the receiver. This has been obtained by re–scaling the independent observations and computing their product in line with the SPA algorithm on factor graphs. Then, a novel bit LLR correction has been proposed to increase the convergence speed of the decoder. For future work in this context, the receiver might also be implemented by applying KL divergence to the symbols whose LLRs fall in the ambiguity region. In such a scenario, the exact computation of the KL divergence is unachievable (even by using cell function in the MATLAB simulations) due to the large number of the calculations. Therefore, the KL divergence can only be applied to the extreme situations, e.g., all bits being zeros or ones.
Author Contributions
Conceptualization, A.M. and A.Z.; methodology, A.M. and A.Z.; software, A.M. and A.Z.; validation, A.M. and A.Z.; formal analysis, A.M. and A.Z.; investigation, A.M. and A.Z.; resources, A.M. and A.Z.; data curation, A.M. and A.Z.; writing—original draft preparation, A.M. and A.Z.; writing—review and editing, A.M. and A.Z.; visualization, A.M. and A.Z.; supervision, A.M. and A.Z.; project administration, A.M. and A.Z.; funding acquisition, A.M. and A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Richardson, T.J.; Urbanke, R.L. Modern Coding Theory; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Jiang, Y.; Kim, H.; Asnani, H.; Kannan, S.; Oh, S.; Viswanath, P. DEEPTURBO: Deep Turbo Decoder. In Proceedings of the 2019 IEEE 20th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Cannes, France, 2–5 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Nachmani, E.; Marciano, E.; Lugosch, L.; Gross, W.J.; Burshtein, D.; Be’ery, Y. Deep Learning Methods for Improved Decoding of Linear Codes. IEEE J. Sel. Top. Signal Process. 2018, 12, 119–131. [Google Scholar] [CrossRef]
- Lu, M.; Zhou, B.; Bu, Z. Attention-Empowered Residual Autoencoder for End-to-End Communication Systems. IEEE Commun. Lett. 2023, 27, 1140–1144. [Google Scholar] [CrossRef]
- Gruber, T.; Cammerer, S.; Hoydis, J.; ten Brink, S. On Deep Learning-Based Channel Decoding. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Mirbadin, A.; Zaraki, A. Partial Path Overlapping Mitigation: An Initial Stage for Joint Detection and Decoding in Multipath Channels Using the Sum–Product Algorithm. Appl. Sci. 2024, 14, 9175. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).