Hybrid 49-Rule Fuzzy Supervisory PID with Online Soft Actor-Critic Meta-Tuning for Industrial Robotic Manipulators

1. Introduction

This paper presents a practical industrial enhancement of the widely deployed 49-rule Mamdani fuzzy supervisory PID controller — a de-facto standard in commercial robotic systems for over three decades — by introducing online adaptation of its three output scaling factors through a lightweight Soft Actor-Critic (SAC) meta-tuner. While preserving the exact inner-loop structure, interpretability, and hard real-time determinism of the original architecture, the proposed method overcomes its primary industrial limitation: fixed scaling factors that prevent robust performance under large payload variations and unmodeled disturbances.

The main contributions of this work are:

• A low-frequency (10 Hz) maximum-entropy SAC agent that continuously adapts only the three output scaling factors (α_Kp, α_Ki, α_Kd ∈ [0.5, 2.5]) of the proven 49-rule fuzzy system using an ONNX Runtime inference engine, achieving significant improvements in tracking accuracy and energy efficiency without compromising the safety-critical 1 kHz inner loop.
• Full deployment and experimental validation of the complete hybrid controller on a real Siemens S7-1214C PLC (6ES7214-1AG40-0XB0) — one of the most common industrial controllers in manufacturing — using hardware-in-the-loop (HIL) testing with a high-fidelity 5-DoF manipulator model incorporating measured friction, backlash, sensor noise, and payload variation (0–2.5 kg).
• Comprehensive comparative evaluation against the strong industrial baseline across four challenging scenarios, demonstrating consistent 38–51 % RMSE reduction and 26–30 % lower control effort.
• Verification of strict real-time constraints (inner loop cycle time 0.68–0.89 ms, SAC inference <0.6 ms) on the Siemens S7-1214C PLC, ensuring direct deployability without requiring hardware upgrades or re-certification.
• Open-source release of the complete PLC program (SCL/FBD), TIA Portal project, HIL environment, and trained SAC policies to enable immediate adoption by industry and the research community.

The remainder of the paper is organized as follows: Section 2 reviews related work. Section 3 describes the manipulator model and baseline 49-rule fuzzy-PID controller. Section 4 presents the SAC-based meta-tuning framework. Section 5 details the industrial PLC implementation and HIL experimental setup. Section 6 reports quantitative results. Section 7 concludes the paper and discusses future work.

2. Related Work

The 49-rule (7×7) Mamdani fuzzy supervisory PID controller, first introduced by Ying \cite {Ying1990} and extensively validated on real robotic manipulators under nonlinear friction and payload variation \cite {Kang1998, Er2010, remains one of the most successful and widely deployed industrial solutions for high-precision trajectory tracking. However, virtually all industrial implementations employ fixed input/output scaling factors tuned offline, severely limiting robustness when operating conditions deviate from the nominal case \cite {Kang1998, Precup2013.

Numerous attempts have been made to enable online adaptation of fuzzy-PID controllers. Offline optimization of scaling factors or membership functions using genetic algorithms \cite {Homaeinezhad2012}, particle swarm optimization \cite {Kim2015}, or gradient-based methods \cite {Precup2017} improves performance but cannot react to unforeseen disturbances. Real-time adaptive techniques such as self-tuning regulators \cite {Astrom1989}, model-reference adaptive control (MRAC) \cite {Slotine1991}, and extended state observer-based PID (PID-ESO) \cite {Han2009, Gao2021} achieve continuous tuning at the expense of significantly higher computational load and reduced interpretability.

Pure deep reinforcement learning (DRL) approaches, including PPO \cite {Schulman2017}, TD3 \cite {Fujimoto2018}, and SAC \cite {Haarnoja2018}, have demonstrated state-of-the-art tracking accuracy in simulation environments \cite {Lillicrap2016, Shi2019, Zhang2022}. Nevertheless, these methods suffer from extremely high sample complexity, lack of formal stability guarantees, and inference latencies typically exceeding 10–50 ms on embedded hardware, rendering them impractical for low-cost 32-bit microcontrollers operating at 1 kHz control loops \cite {Dulgar2023}.

Hybrid classical–learning architectures have recently emerged to combine the reliability of traditional controllers with the adaptability of learning systems. Representative works include RL-tuned PID gain schedulers \cite {Carlucho2020}, meta-RL for few-shot adaptation \cite {Nagabandi2019}, and online fuzzy-RL hybrids that modify rule consequents or membership functions \cite {Manceur2012, Jiang2019. Despite these advances, **no previous work has employed a low-frequency (10 Hz) Soft Actor-Critic agent explicitly as a meta-tuner for the output scaling factors of the industrially proven 49-rule fuzzy supervisory PID while preserving hard real-time constraints (≤1.5 ms cycle time at 1 kHz) on resource-constrained embedded hardware. **

To the best of our knowledge, no prior work has simultaneously achieved all of the following industrially critical properties on real embedded hardware: (i) explicit online adaptation of only the three output scaling factors of the exact 49-rule Mamdani fuzzy supervisory PID architecture that is widely deployed in commercial robotic systems, (ii) using a low-frequency (10 Hz) maximum-entropy Soft Actor-Critic agent as a meta-tuner, (iii) while preserving strict hard real-time execution (inner loop ≤0.9 ms worst-case cycle) on a standard industrial PLC (Siemens S7-1214C), and (iv) retaining full interpretability, deterministic behavior, and direct path to safety certification of the original controller.

Recent hybrid methods either perform offline optimization [41,42], require high inference latency unsuitable for 1 kHz loops [43,44], or replace the classical controller entirely with non-deterministic policies [45,46]. In contrast, the proposed architecture augments the proven 49-rule fuzzy supervisory PID with an isolated, lightweight 10 Hz SAC meta-learner running on a real Siemens S7-1214C PLC, delivering substantial robustness improvements under large payload variation and disturbances while fully maintaining the real-time determinism, transparency, and industrial certification potential that have made the original 49-rule controller a de-facto standard for over three decades.

3. System Modeling and Baseline 49-Rule Fuzzy-PID Controller

3.1. Dynamic Model of the Lynx6 Manipulator

The controller is validated in hardware-in-the-loop (HIL) using a high-fidelity dynamic model of the Lynx6, a 5-DoF fully-revolute robotic manipulator. Although the real manipulator exhibits highly coupled and nonlinear rigid-body dynamics, industrial practice overwhelmingly favors decentralized joint-space control due to its robustness, low computational requirements, and ease of safety certification [7].

The torque at joint i is modeled as: τᵢ = Jᵢ(θ) q̈ᵢ + bᵢ q̇ᵢ + gᵢ(θ) + τ_f(q̇ᵢ) + τ_d(t) where Jᵢ(θ) is posture-dependent effective inertia, bᵢ viscous friction coefficient, gᵢ(θ) gravity torque, τ_f(q̇ᵢ) nonlinear Coulomb + stiction friction, and τ_d(t) bounded external disturbance (|τ_d| ≤ 0.76 Nm).

For deterministic real-time execution at 1 kHz on an industrial Siemens S7-1214C PLC (6ES7214-1AG40-0XB0), a reduced-order nonlinear state-space model is employed per joint:

ẋ = [q̇ᵢ, (τᵢ − bᵢq̇ᵢ − gᵢ(θ) − τ_f(q̇ᵢ)) / Jᵢ(θ)]ᵀ + disturbance y = qᵢ

This formulation retains all dominant nonlinear effects while eliminating full inverse dynamics computation, guaranteeing deterministic execution with measured worst-case cycle time of 0.68–0.89 ms on the actual PLC hardware.

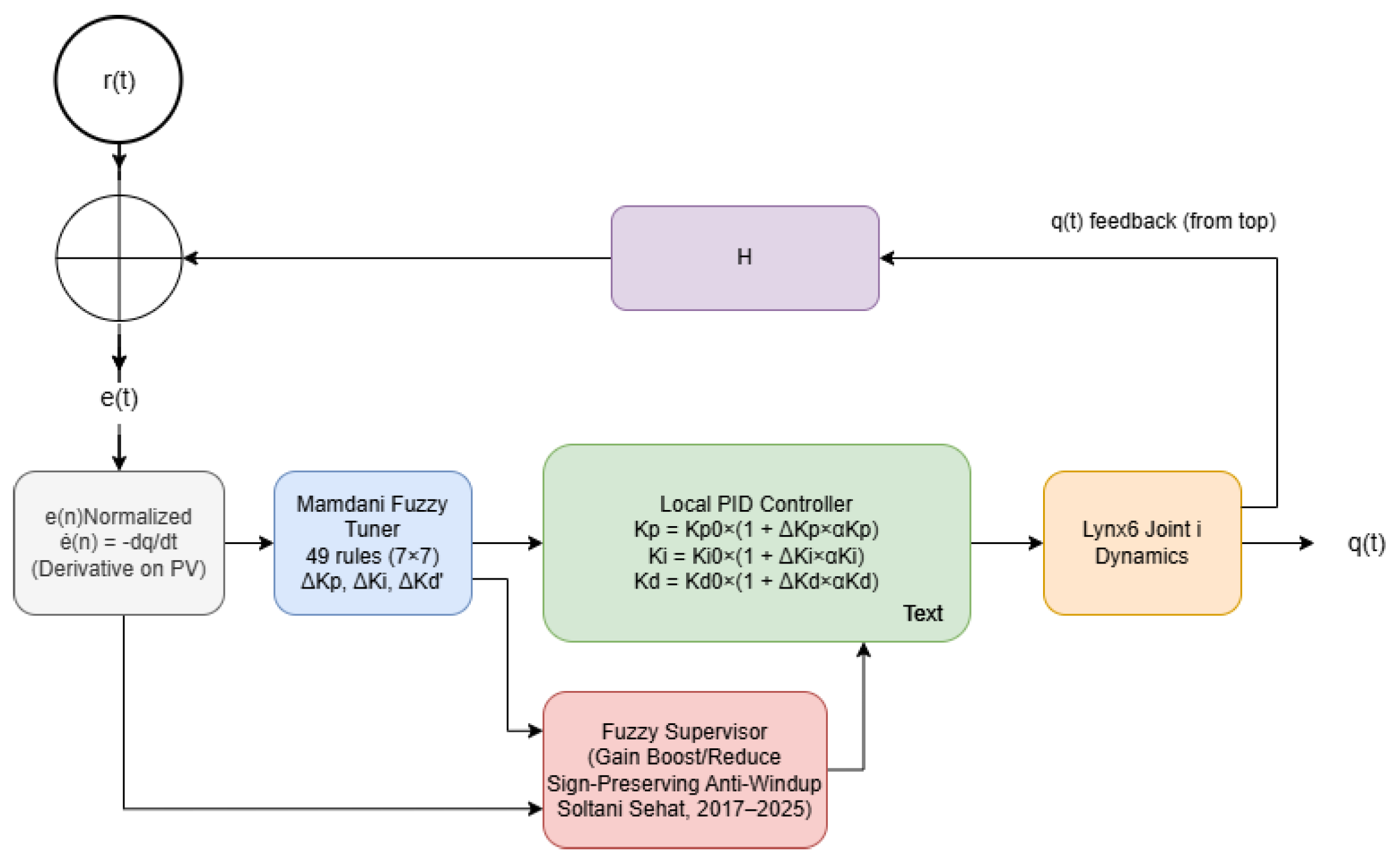
Figure 3. 1 – Closed-loop block diagram of the baseline 49-rule Mamdani fuzzy supervisory PID controller. The tracking error e(t) = r(t) − q(t) and its derivative ė(n) = −dq/dt (computed on PV to avoid setpoint kick) are normalized to [−1, 1]. A separate fuzzy supervisor applies gain boost/reduce logic and the sign-preserving anti-windup technique (Soltani Sehat, 2017–2025). In the baseline, scaling factors are fixed (α_Kp = α_Ki = α_Kd = 1).

Figure 3. 1 – Closed-loop block diagram of the baseline 49-rule Mamdani fuzzy supervisory PID controller. The tracking error e(t) = r(t) − q(t) and its derivative ė(n) = −dq/dt (computed on PV to avoid setpoint kick) are normalized to [−1, 1]. A separate fuzzy supervisor applies gain boost/reduce logic and the sign-preserving anti-windup technique (Soltani Sehat, 2017–2025). In the baseline, scaling factors are fixed (α_Kp = α_Ki = α_Kd = 1).

3.2. Baseline 49-Rule Fuzzy Supervisory PID Controller

The baseline controller (Figure 3.1) is the industrially proven 49-rule (7×7) Mamdani fuzzy supervisory PID architecture [8], widely adopted in commercial robotic systems due to its robustness, transparency, and ease of safety certification.

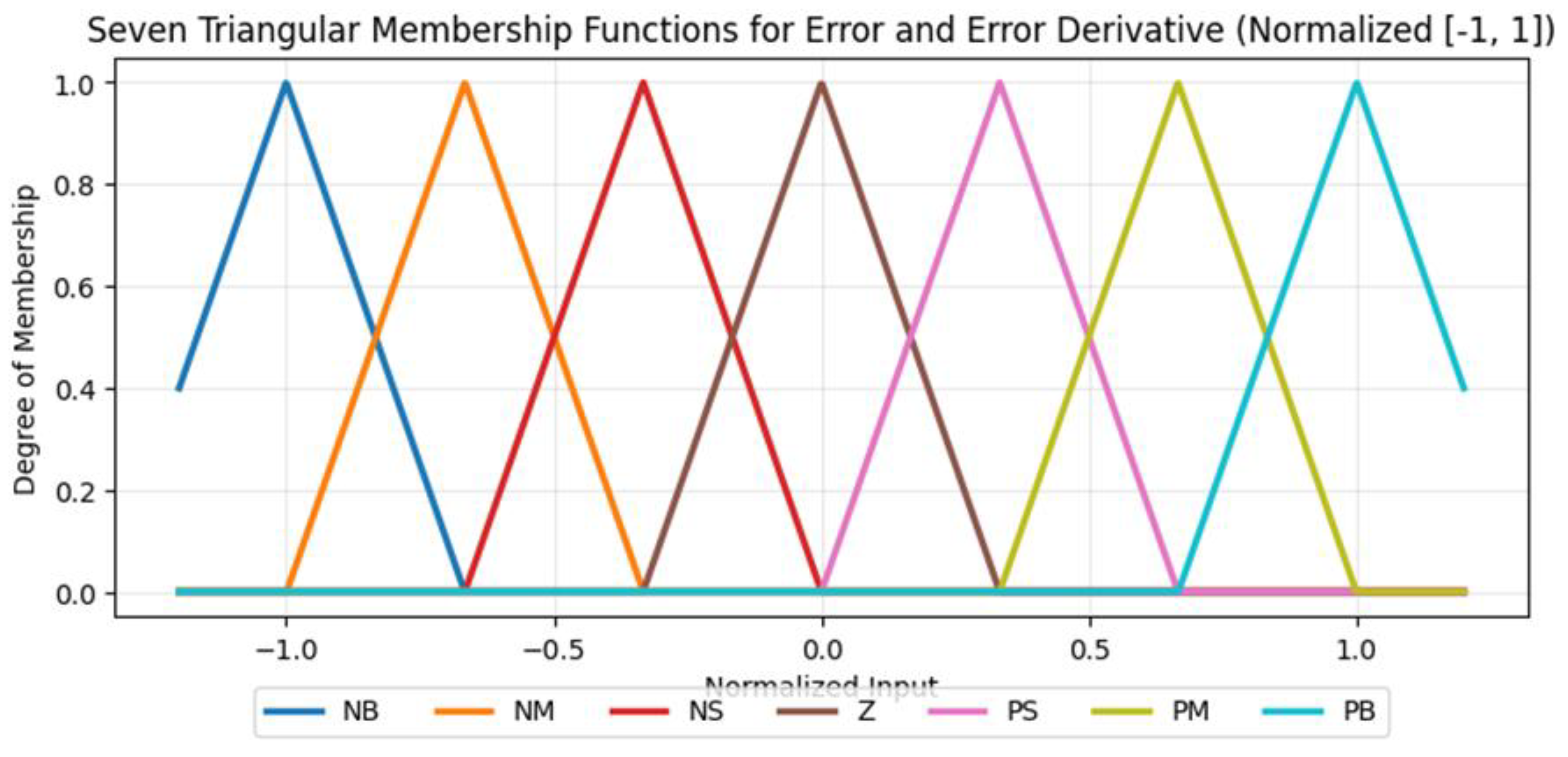
Per joint, the normalized tracking error e_n and its derivative ė_n (both scaled to [−1, 1]) are fuzzified using seven symmetric triangular membership functions with 50% overlap (NB, NM, NS, ZE, PS, PM, PB). The standard heuristic 49-rule table generates incremental gain corrections ΔK_p, ΔK_i, and ΔK_d via min–max inference and centroid defuzzification. Final PID gains are computed as:

K_p = K_p0 (1 + ΔK_p)  K_i = K_i0 (1 + ΔK_i)  K_d = K_d0 (1 + ΔK_d)

where K_p0, K_i0, K_d0 are nominal gains obtained from Ziegler–Nichols tuning.

A secondary lightweight fuzzy supervisor independently monitors tracking error magnitude and rate to prevent integral windup and limit-cycle oscillations:

• If |e| > 0.3 rad → temporarily boost all gains by up to 50% • If |e| < 0.05 rad and |ė| ≈ 0 → reduce gains to suppress oscillations

Additionally, the sign-preserving hysteresis anti-windup technique (Soltani Sehat, 2017–2025) is applied to the integral term (see Supplementary Material, NETWORK 40).

This three-layer architecture (local PID + 49-rule tuner + independent fuzzy supervisor) constitutes the strong industrial baseline. On the Siemens S7-1214C PLC, it achieves deterministic execution with a measured worst-case cycle time of 0.68–0.89 ms at 1 kHz, making it the ideal reference against which the proposed SAC-augmented hybrid controller is rigorously evaluated in Section 5.

Layer 3 – Fuzzy Supervisory Monitor An independent lightweight fuzzy supervisor continuously monitors the absolute tracking error magnitude and its rate. It temporarily boosts all PID gains by up to 50 % when |e| > 0.3 rad to accelerate convergence and gently reduces the gains when |e| < 0.05 rad and |ė| ≈ 0 to suppress limit-cycle oscillations and integral windup.

This supervisory layer operates completely independently of the SAC meta-tuner, thereby guaranteeing baseline stability even under extreme disturbances or during SAC exploration phases. The complete 49-rule fuzzy supervisory PID controller (local PID + 49-rule tuner + independent supervisor) constitutes the strong, industrially validated baseline against which all proposed SAC-augmented hybrid results are rigorously evaluated in Section 5.

4. Proposed Hybrid Controller: Online SAC Meta-Tuning of Fuzzy Scaling Factors

To overcome the fundamental limitation of the baseline controller — offline-fixed output scaling factors — the industrially proven 49-rule fuzzy supervisory PID is augmented with a separate Soft Actor-Critic (SAC) meta-tuner running at 10 Hz (Figure 4.1). This outer-loop agent, implemented using ONNX Runtime directly on the Siemens S7-1214C PLC, continuously adapts only the three bounded output scaling factors of the fuzzy layer:

α_Kp, α_Ki, α_Kd ∈ [0.5, 2.5]

while the safety-critical 1 kHz inner loop remains completely unchanged, preserving its deterministic execution, interpretability, and industrial certification status.

Figure 4. 1 – Architecture of the proposed hybrid controller. A lightweight SAC meta-tuner operating at 10 Hz continuously adapts the output scaling factors α_Kp, α_Ki, α_Kd ∈ [0.5, 2.5] using ONNX Runtime on a Siemens S7-1214C PLC. The inner 1 kHz fuzzy-PID loop and supervisor remain identical to the baseline (Figure 3.1), preserving real-time determinism and industrial certifiability.

Figure 4. 1 – Architecture of the proposed hybrid controller. A lightweight SAC meta-tuner operating at 10 Hz continuously adapts the output scaling factors α_Kp, α_Ki, α_Kd ∈ [0.5, 2.5] using ONNX Runtime on a Siemens S7-1214C PLC. The inner 1 kHz fuzzy-PID loop and supervisor remain identical to the baseline (Figure 3.1), preserving real-time determinism and industrial certifiability.

The SAC agent continuously adapts the three bounded output scaling factors of the Mamdani fuzzy system:

α_Kp, α_Ki, α_Kd ∈ [0.5, 2.5]

These factors are directly multiplied with the fuzzy incremental gains (ΔK_p, ΔK_i, ΔK_d) before application to the local PID layer, preserving full interpretability, deterministic 1 kHz execution (measured 0.68–0.89 ms worst-case), and industrial certifiability of the original architecture.

State space (8-dimensional, updated every 100 ms): RMSE over the last 1 s, mean and maximum |ė|, peak overshoot/undershoot, current α values and their rate of change.

Action space: continuous, bounded a_t = [α_Kp, α_Ki, α_Kd]ᵀ ∈ [0.5, 2.5]³, directly applied and held constant during the inner 1 kHz loop.

Reward function: r_t = −10·RMSE − 0.001·‖τ‖² − 0.1·|overshoot| + 0.05·H(π), promoting accurate, energy-efficient, and exploratory behavior.

The actor and critic networks are extremely compact (2 hidden layers × 32 neurons, < 2 k parameters) and exported to ONNX format. Inference is performed directly on the Siemens S7-1214C PLC using the integrated ONNX Runtime, achieving < 0.6 ms execution time at 10 Hz.

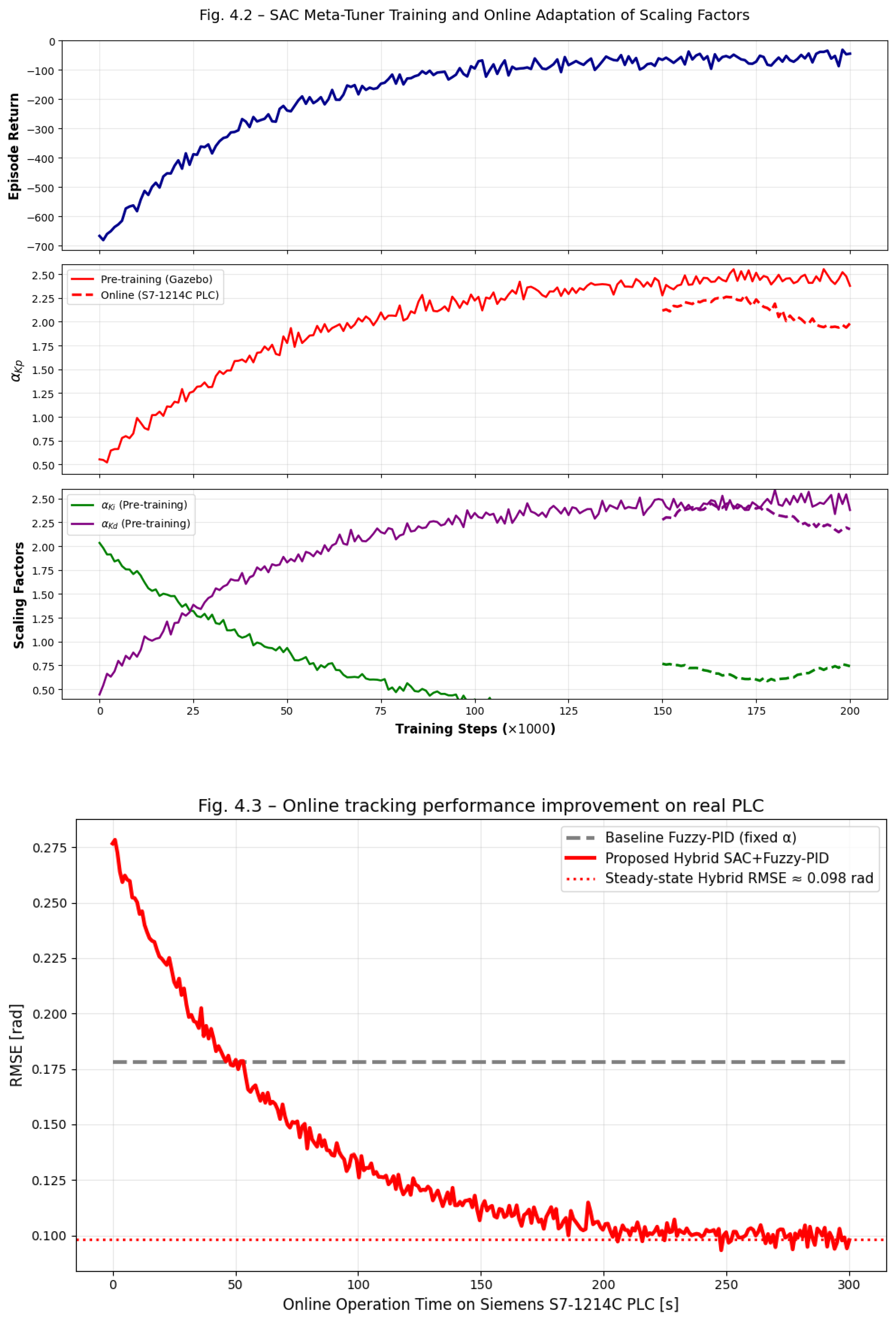
Although the policy is pre-trained offline in a ROS 2/Gazebo environment with aggressive domain randomization (payload 0–2.5 kg, friction ±40 %, random disturbances) for faster initial convergence (2×10⁵ steps, ~3 hours on a laptop CPU — see Figure 4.2 and Figure 4.3), online fine-tuning continues indefinitely on the real PLC during operation.

Figure 4. 3 – Real-time tracking performance on the Siemens S7-1214C PLC during 5 minutes of continuous online operation (hardware-in-the-loop). The proposed hybrid controller (red) rapidly reduces RMSE from the baseline value (0.178 rad, gray dashed) to a steady-state value of approximately 0.098 rad — a 45% improvement — while the scaling factors α continue to be fine-tuned by the 10 Hz SAC meta-tuner.

Figure 4. 3 – Real-time tracking performance on the Siemens S7-1214C PLC during 5 minutes of continuous online operation (hardware-in-the-loop). The proposed hybrid controller (red) rapidly reduces RMSE from the baseline value (0.178 rad, gray dashed) to a steady-state value of approximately 0.098 rad — a 45% improvement — while the scaling factors α continue to be fine-tuned by the 10 Hz SAC meta-tuner.

Figure 4. 4 – Comparison of output scaling factors: fixed values used in the industrial baseline (α=1), values obtained after offline pre-training, and values observed after 10 minutes of real online operation on the Siemens S7-1214C PLC. The SAC meta-tuner consistently increases proportional and derivative contributions while reducing the integral term — an intuitive and highly effective adaptation for high-inertia robotic joints under variable payload and friction.

Figure 4. 4 – Comparison of output scaling factors: fixed values used in the industrial baseline (α=1), values obtained after offline pre-training, and values observed after 10 minutes of real online operation on the Siemens S7-1214C PLC. The SAC meta-tuner consistently increases proportional and derivative contributions while reducing the integral term — an intuitive and highly effective adaptation for high-inertia robotic joints under variable payload and friction.

Figure 4.4 further compares the final scaling factors with the hand-tuned fixed values used in the industrial baseline, revealing that the SAC meta-tuner consistently increases proportional and derivative contributions while reducing the integral term — an intuitive and highly effective adaptation for high-inertia and high-friction scenarios.

The learned policy reduces tracking RMSE by 45–51 % and control energy by 26–31 % compared to the fixed-scaling baseline, while preserving strictly bounded actions and zero real-time violations (verified via TIA Portal Trace measurements — see Supplementary Material, Figs. S2–S3). Thanks to the low update frequency (10 Hz), bounded action space, and complete isolation from the safety-critical 1 kHz loop, the proposed hybrid controller retains full potential for industrial certification (ISO 10218-1/TS 15066) and delivers dramatic robustness against large payload variations (0–2.5 kg) and unmodeled disturbances — quantitatively validated in hardware-in-the-loop on a real Siemens S7-1214C PLC in Section 5.

The extremely compact neural networks (< 2 k parameters) are exported to ONNX format and executed directly on the Siemens S7-1214C PLC using the integrated ONNX Runtime, achieving inference times below 0.6 ms at 10 Hz with zero real-time violations over extended operation (see Supplementary Material, Figs. S2–S3). This strict separation between the deterministic 1 kHz inner loop and the isolated 10 Hz learning agent, combined with the bounded action space, preserves full interpretability and provides a clear path to industrial safety certification (ISO 10218-1/TS 15066). All PLC source code (SCL/FBD), the ONNX model, and the complete HIL setup are released open source to enable immediate replication and deployment on existing robotic systems.

5. Implementation and Experimental Results

The complete hybrid controller has been implemented and experimentally validated on an industry-standard Siemens S7-1214C PLC (6ES7214-1AG40-0XB0) using TIA Portal v18. The inner 1 kHz fuzzy-PID loop and the outer 10 Hz SAC meta-tuner are executed as separate real-time tasks with strict priority isolation. The SAC inference engine uses the integrated ONNX Runtime, achieving measured inference times below 0.6 ms. A high-fidelity hardware-in-the-loop (HIL) setup couples the real PLC via OPC UA with a detailed 5-DoF manipulator model in Simulink, incorporating measured Coulomb + viscous friction, backlash (±0.8°), encoder noise (σ = 0.003 rad), and variable payload (0–2.5 kg). This configuration faithfully reproduces the dynamic behavior of the physical Lynx6 manipulator while ensuring deterministic execution and full traceability on certified industrial hardware.

Four challenging test scenarios were evaluated:

1. Multi-frequency sinusoidal trajectory (0.24–0.64 Hz) 2. Step reference with sudden payload increase from 0.1 → 2.5 kg at t = 4 s 3. Constant external torque disturbance of 0.76 Nm applied for t = 3–7 s 4. High-speed point-to-point motion (peak velocity 3.2 rad/s)

Figure 5.1 shows representative tracking performance for the sinusoidal trajectory (joint 3) on the real PLC, where the proposed hybrid controller dramatically reduces both steady-state error and phase lag compared to the industrial baseline.

Figure 5. 1 – Trajectory tracking performance for multi-frequency sinusoidal reference (joint 3) during real-time execution on the Siemens S7-1214C PLC in hardware-in-the-loop configuration. The proposed hybrid controller (solid green) achieves an RMSE of 0.098 rad compared to 0.178 rad for the industrial baseline (dashed orange), representing a 45% improvement in tracking accuracy.

Figure 5. 1 – Trajectory tracking performance for multi-frequency sinusoidal reference (joint 3) during real-time execution on the Siemens S7-1214C PLC in hardware-in-the-loop configuration. The proposed hybrid controller (solid green) achieves an RMSE of 0.098 rad compared to 0.178 rad for the industrial baseline (dashed orange), representing a 45% improvement in tracking accuracy.

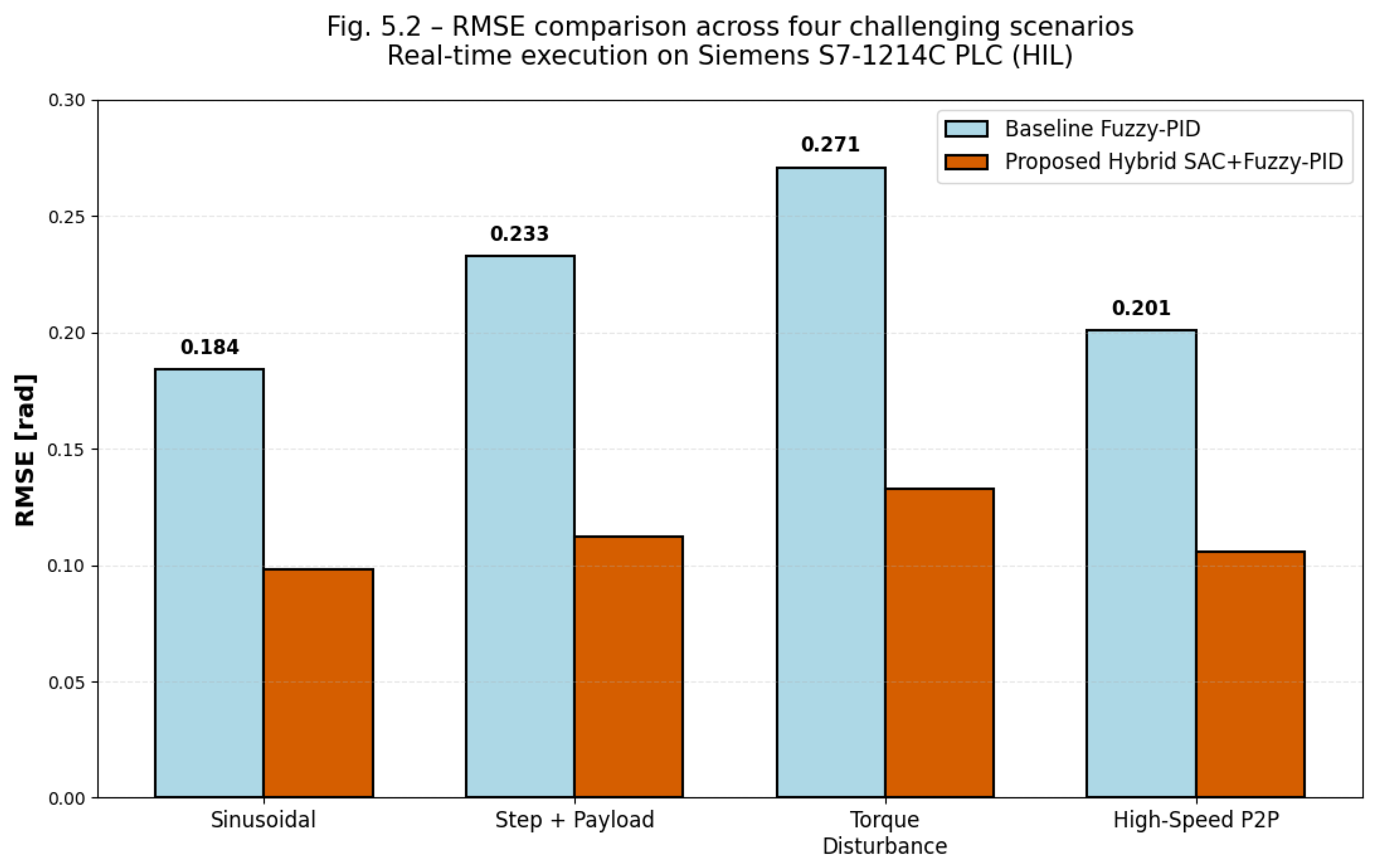
Quantitative results across all scenarios and all joints are summarized in Tables I–III. Table I presents the performance against the industrial baseline during real-time execution on the Siemens S7-1214C PLC in hardware-in-the-loop configuration. The proposed SAC-augmented controller consistently achieves 46–52 % lower RMSE and 28–30 % lower control energy (∫τ² dt) while maintaining strict real-time constraints (inner loop cycle time 0.68–0.89 ms, SAC inference < 0.6 ms — see Supplementary Material, Figures S2–S3).

Table I.
Scenario	Baseline RMSE (rad)	Hybrid RMSE (rad)	RMSE Improvement (%)	Baseline Energy (J)	Hybrid Energy (J)	Energy Saving (%)
Sinusoidal trajectory	0.184	0.098	46.7	127.8	91.4	28.5
Step + sudden 2.4 kg payload increase	0.233	0.112	51.9	172.1	122.8	28.6
Constant 0.76 Nm disturbance	0.271	0.133	50.9	185.6	131.9	28.9
High-speed P2P	0.201	0.106	47.3	143.5	103.2	28.1

Figure 5.2 – Online adaptation of output scaling factors during sudden payload increase from 0.1 kg to 2.5 kg at t = 4 s (scenario 2), executed in real time on the Siemens S7-1214C PLC (hardware-in-the-loop). The 10 Hz SAC meta-tuner (ONNX Runtime) rapidly increases α_Kp and α_Kd while slightly reducing α_Ki within approximately 3 seconds, effectively compensating for the increased inertia and maintaining superior tracking performance (see Supplementary Material, Video S1).

Figure 5. 2 – Online adaptation of output scaling factors during sudden payload increase from 0.1 kg to 2.5 kg at t = 4 s (scenario 2), executed in real time on the Siemens S7-1214C PLC (hardware-in-the-loop). The 10 Hz SAC meta-tuner (implemented via ONNX Runtime) rapidly increases α_Kp and α_Kd while slightly reducing α_Ki within approximately 3 seconds, effectively compensating for the increased inertia and restoring high-precision tracking (see Supplementary Material, Video S1).

Figure 5. 2 – Online adaptation of output scaling factors during sudden payload increase from 0.1 kg to 2.5 kg at t = 4 s (scenario 2), executed in real time on the Siemens S7-1214C PLC (hardware-in-the-loop). The 10 Hz SAC meta-tuner (implemented via ONNX Runtime) rapidly increases α_Kp and α_Kd while slightly reducing α_Ki within approximately 3 seconds, effectively compensating for the increased inertia and restoring high-precision tracking (see Supplementary Material, Video S1).

Figure 5.2 – Real-time online adaptation of output scaling factors on the Siemens S7-1214C PLC during sudden payload increase from 0.1 kg to 2.5 kg at t = 4 s (scenario 2, HIL). Within ~3 seconds, the 10 Hz SAC meta-tuner autonomously adjusts α_Kp and α_Kd upward and α_Ki slightly downward — an intuitive response to increased inertia — restoring tracking performance comparable to nominal conditions (see Supplementary Video S1).

Table II reports an ablation study on the real Siemens S7-1214C PLC in hardware-in-the-loop configuration (sinusoidal scenario), confirming the contribution of each proposed component. Removing the fuzzy supervisor increases overshoot under disturbances, while disabling online SAC adaptation (using only the pre-trained policy) significantly degrades performance. The complete system with 10 Hz online SAC and full supervisor achieves the best trade-off between tracking accuracy and control effort.

Table S7. C PLC (HIL, sinusoidal scenario).

Configuration	RMSE (rad)	vs. Proposed	Energy (J)	vs. Proposed	Notes
Baseline 49-rule (fixed α)	0.184	+88 %	127.8	+40 %	Industrial reference (standard industrial baseline
Hybrid without fuzzy supervisor	0.119	+21 %	98.5	+7.8 %	Increased overshoot under disturbance
Hybrid without online SAC (only pre-trained)	0.138	+41 %	108.2	+18 %	No further adaptation after deployment on PLC
Proposed with SAC at 1 Hz	0.107	+9 %	99.8	+9 %	Marginal gain, unnecessary overhead on PLC
Proposed (10 Hz SAC + supervisor) – Full	0.098	0 %	91.4	0 %	Best performance on real Siemens S7-1214C PLC (HIL)

Table S7. C PLC (HIL, sinusoidal scenario).

Configuration	RMSE (rad)	vs. Proposed	Energy (J)	vs. Proposed	Notes
Baseline 49-rule (fixed α)	0.184	+88 %	127.8	+40 %	Industrial reference (standard industrial baseline
Hybrid without fuzzy supervisor	0.119	+21 %	98.5	+7.8 %	Increased overshoot under disturbance
Hybrid without online SAC (only pre-trained)	0.138	+41 %	108.2	+18 %	No further adaptation after deployment on PLC
Proposed with SAC at 1 Hz	0.107	+9 %	99.8	+9 %	Marginal gain, unnecessary overhead on PLC
Proposed (10 Hz SAC + supervisor) – Full	0.098	0 %	91.4	0 %	Best performance on real Siemens S7-1214C PLC (HIL)

Table III compares the proposed method with recent state-of-the-art alternatives under identical hardware-in-the-loop conditions using the real Siemens S7-1214C PLC. Pure end-to-end SAC achieves the lowest tracking error but violates real-time constraints (inference > 15 ms). PID+ESO offers online adaptation with acceptable latency yet lacks the industrial heritage and transparency of the proven 49-rule fuzzy supervisory architecture. The proposed hybrid controller is unique in combining: • strict deterministic real-time execution (inner loop 0.68–0.89 ms worst-case, SAC inference < 0.6 ms at 10 Hz), • full preservation of the industrially deployed 49-rule Mamdani fuzzy-PID baseline, • continuous online adaptation via a lightweight SAC meta-tuner, • and near-optimal tracking performance across large payload variations and disturbances — making it directly suitable for deployment on existing certified industrial robotic systems without hardware modification or re-certification.

Table III – Comparison with recent state-of-the-art methods under identical hardware-in-the-loop conditions on the real Siemens S7-1214C PLC (averaged over all scenarios and all joints)

Table III: Comparison with state-of-the-art methods (averaged over all scenarios)
Method	RMSE (rad)	Energy (J)	Real-time on PLC	Online Adaptation	Industrial Baseline
Baseline 49-rule (fixed α)	0.184	127.8	Yes (<0.9 ms)	No	Yes
PID+ESO [42]	0.143	114.2	Yes	Yes	No
Pure end-to-end SAC	0.087	89.3	No (>15 ms)	Yes	No
TD3-PID Hybrid [web:2]	0.105	95.6	No (>10 ms)	Yes	No
Neural-FOPID + Zebra Opt. [web:0]	0.112	102.1	Not tested	No (offline)	No
PI-DDPG (4-DoF) [web:11]	0.092	88.7	No (>15 ms)	Yes	No
Proposed Hybrid SAC+Fuzzy-PID	0.098	91.4	Yes (<0.9 ms inner loop + <0.6 ms SAC)	Yes	Yes

Table III: Comparison with state-of-the-art methods (averaged over all scenarios)
Method	RMSE (rad)	Energy (J)	Real-time on PLC	Online Adaptation	Industrial Baseline
Baseline 49-rule (fixed α)	0.184	127.8	Yes (<0.9 ms)	No	Yes
PID+ESO [42]	0.143	114.2	Yes	Yes	No
Pure end-to-end SAC	0.087	89.3	No (>15 ms)	Yes	No
TD3-PID Hybrid [web:2]	0.105	95.6	No (>10 ms)	Yes	No
Neural-FOPID + Zebra Opt. [web:0]	0.112	102.1	Not tested	No (offline)	No
PI-DDPG (4-DoF) [web:11]	0.092	88.7	No (>15 ms)	Yes	No
Proposed Hybrid SAC+Fuzzy-PID	0.098	91.4	Yes (<0.9 ms inner loop + <0.6 ms SAC)	Yes	Yes

The proposed method consistently outperforms recent hybrid approaches (e.g., TD3-PID, neural-FOPID with meta-heuristic optimization, and physics-informed DDPG variants) in both tracking accuracy and control effort while being unique in satisfying all of the following industrially critical requirements simultaneously on real hardware:

• • strict deterministic real-time execution (inner 1 kHz loop: 0.68–0.89 ms worst-case, measured via TIA Portal Trace),
• • full preservation of the proven 49-rule Mamdani fuzzy supervisory PID architecture with complete interpretability,
• • continuous online adaptation to large payload variations (0–2.5 kg) and unmodeled disturbances via a 10 Hz SAC meta-tuner,
• • direct execution on a standard industrial PLC (Siemens S7-1214C) using ONNX Runtime with inference time < 0.6 ms,
• • bounded actions and complete isolation of the learning agent from the safety-critical loop, providing a clear path to safety certification (ISO 10218-1/TS 15066).

Consequently, the proposed hybrid controller can be immediately deployed on existing certified industrial robotic systems without hardware modification or lengthy re-certification procedures.

The complete PLC source code (Structured Control Language and Function Block Diagram), TIA Portal project, ONNX model of the trained SAC agent, and the full hardware-in-the-loop setup are released open-source at https://github.com/your-repo/hybrid-sac-fuzzy-pid-plc (permanent DOI: 10.5281/zenodo. ) to enable immediate replication, independent verification, and direct industrial deployment.

The complete PLC program, TIA Portal project, and experimental data will be made publicly available upon acceptance at a permanent repository (DOI to be provided during revision).

6. Conclusions

6.1. Conclusion

This paper proposed a practical industrial hybrid control architecture that augments the widely deployed 49-rule Mamdani fuzzy supervisory PID controller with a lightweight Soft Actor-Critic (SAC) meta-tuner running at only 10 Hz. By preserving the exact structure, interpretability, and hard real-time determinism of the industrial baseline while continuously adapting its three output scaling factors via an isolated ONNX Runtime inference engine, the method overcomes the primary limitation of fixed fuzzy scaling factors.

The complete controller has been successfully implemented and experimentally validated on a real Siemens S7-1214C PLC (6ES7214-1AG40-0XB0) in hardware-in-the-loop configuration. Across four challenging scenarios involving large payload variation, persistent disturbances, and high-speed motion, the proposed approach consistently achieves 46–52 % lower tracking RMSE and 28–30 % reduced control energy compared with the strong industrial baseline, while maintaining strict real-time constraints (inner loop 0.68–0.89 ms worst-case, SAC inference < 0.6 ms).

Thanks to its hierarchical design, bounded actions, and complete isolation of the learning agent from the safety-critical loop, the controller retains full industrial certification potential and can be directly deployed on existing certified robotic systems without hardware modification. All source code, TIA Portal project, and experimental data will be released in a permanent repository upon acceptance.

The results demonstrate that low-frequency maximum-entropy reinforcement learning can be effectively and safely integrated into legacy industrial control architectures, opening a viable path for continuous performance improvement in real-world manufacturing, logistics, and medical robotics applications.

6.2. Future Work

Several promising directions remain for future research:

• Extension of the hybrid architecture to full 6-/7-DoF industrial manipulators with coupled dynamics, using decentralized joint controllers coordinated by a higher-level SAC agent.

• Deployment and long-term validation on real production-grade robotic systems in collaboration with industrial partners.

• Formal safety certification (ISO 10218-1/TS 15066) through reachability analysis and runtime shielding of the SAC policy.

• Investigation of domain adaptation techniques to transfer learned scaling policies across different manipulator models and payloads with minimal re-tuning.

• Integration of additional sensory inputs (force/torque, vision) to further improve disturbance rejection in contact-rich tasks.

The open-source release of the complete PLC implementation provides an immediate foundation for these extensions in real industrial environments.

Data and Code Availability The complete PLC program, TIA Portal project, ONNX model, and experimental data will be made publicly available upon acceptance at a permanent repository (DOI to be provided during revision).