Numerical Investigation of Vapor-Chamber Heat Spreading Using 3D Multiphysics Modeling

1. Introduction

The continual push for higher computational performance in microelectronics has led to a pronounced increase in both power consumption and heat flux densities at the chip level, posing a critical challenge for reliable thermal management in compact devices. Elevated junction temperatures accelerate failure mechanisms, degrade performance, and reduce service life; consequently, conventional air-cooled heat sinks are often insufficient for current and emerging power levels [1,2].

Two-phase passive cooling devices, such as heat pipes and vapor chambers, have therefore attracted extensive attention because of their very high effective thermal conductivity and lack of moving parts [7,36,37]. A heat pipe primarily transports heat along its longitudinal axis, whereas a vapor chamber functions as a planar heat spreader that distributes heat quasi-isotropically from a localized hot spot to a larger condenser area. This is particularly advantageous for microprocessors with non-uniform heat generation and compact form factors.

The design of vapor chambers is inherently multidisciplinary, involving conjugate heat transfer, vapor and liquid transport, porous-media flow in wicks, and interfacial phase change. Several recent studies have reported complementary insights into thermal transport and evaporation phenomena in micro- and nanoscale systems using both numerical and molecular approaches [9,10,11,12,13]. While experiments are essential for device qualification, computational modeling plays a key role in design exploration by enabling parametric studies of geometry, materials, and operating conditions. Existing models range from simplified thermal-resistance networks to fully resolved CFD formulations [16,21,22]. However, many reduced-order models lack spatial resolution of internal fields, whereas high-fidelity multiphase CFD can be computationally intensive for routine design.

In this context, the present work develops a three-dimensional multiphysics model of a copper–water vapor chamber in COMSOL Multiphysics^®. The model incorporates laminar compressible vapor flow, Brinkman flow in a porous wick, and conjugate heat transfer with latent heat effects represented through boundary conditions at the liquid–vapor interface. The main objectives are:

• to construct a computationally efficient yet physically representative 3D model of a vapor chamber using coupled flow and heat transfer physics;
• to quantify thermal spreading and peak temperature reduction under representative chip-level heating;
• to analyze internal temperature, velocity, and pressure fields for improved physical understanding; and
• to establish a modeling framework, with clearly stated assumptions, that can be extended for parametric studies involving geometry, wick properties, and working-fluid selection.

2. Methods and Materials

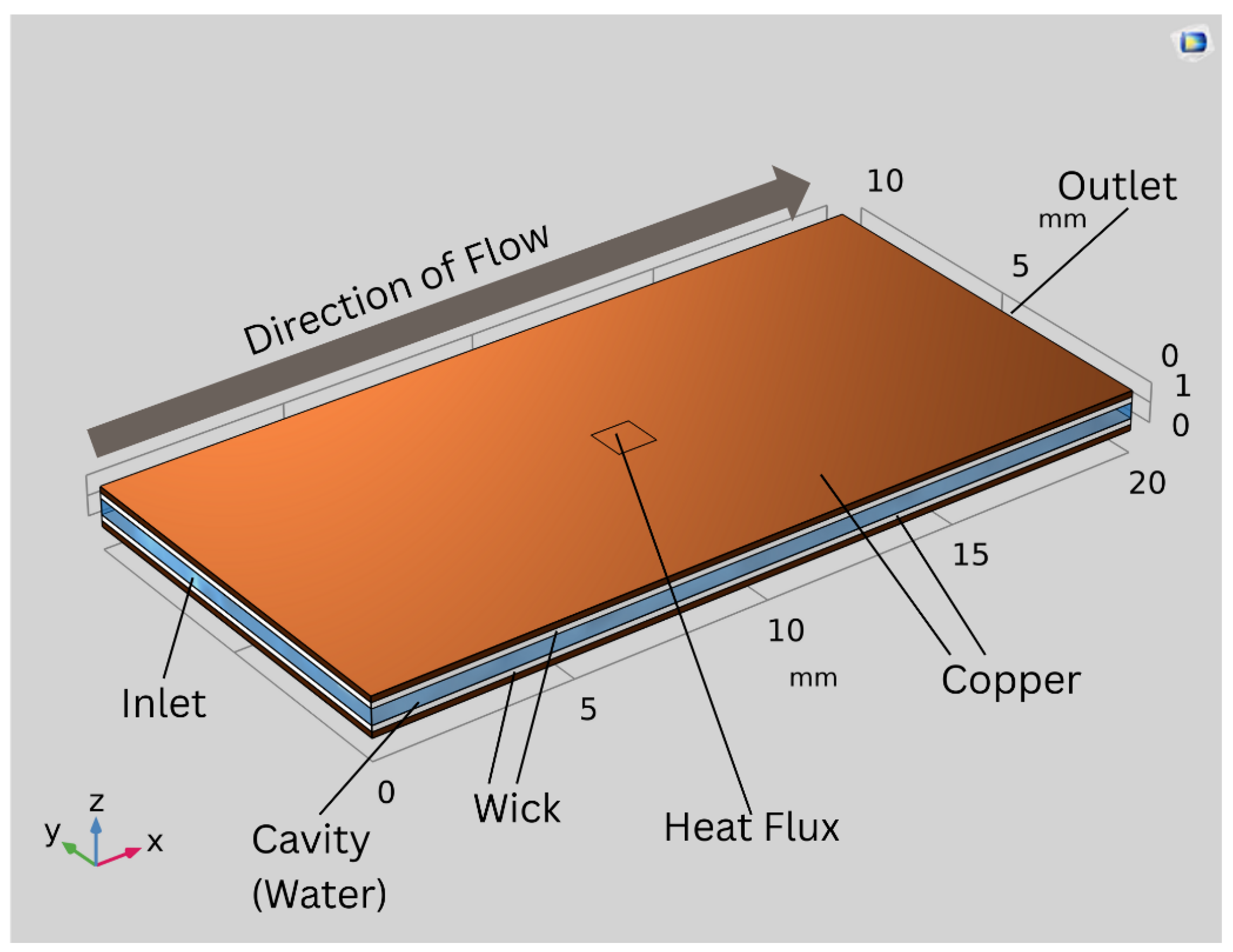
2.1. Model Geometry and Simplifications

A simplified 3D geometry representing the central body of a vapor chamber was constructed to reduce computational cost while retaining the dominant physics of two-phase heat spreading. The modeled dimensions are 10SImm × SI20mm × SI1mm. The assembly comprises three principal functional regions: (i) two solid copper plates forming the outer shell, (ii) porous copper wicks lining the inner walls, and (iii) a central cavity containing the working fluid in its vapor phase.

Owing to geometric symmetry about the y–z plane, only half of the chamber was modeled, thereby reducing the number of degrees of freedom. The overall geometry and layer arrangement used in the COMSOL model are illustrated in Figure 1.

Table 1. Geometry and materials of the vapor chamber model.

Quantity	Layer name	Material	Thickness (mm)
2	Copper shell	Copper (solid)	0.3
2	Wick	Porous copper (68% porosity)	0.3
1	Cavity	Water (vapor)	0.4

Table 1. Geometry and materials of the vapor chamber model.

Quantity	Layer name	Material	Thickness (mm)
2	Copper shell	Copper (solid)	0.3
2	Wick	Porous copper (68% porosity)	0.3
1	Cavity	Water (vapor)	0.4

A SI1mm×SI1mm region on the bottom copper plate serves as the heat source, representing a localized microprocessor hot spot. External fins and detailed air-side flow are not resolved explicitly. Instead, heat rejection at the condenser side is represented via an effective convective boundary condition (Section 2.3). This approach is common in compact device-level modeling when the focus is on internal vapor-chamber transport rather than detailed external aerothermal design.

2.2. Governing Equations

The steady-state behavior of the vapor chamber is governed by conservation of mass, momentum, and energy, solved using multiple physics interfaces in COMSOL.

2.2.1. Heat Transfer in Solids and Fluids

Energy conservation in each domain is written as

$$\rho C_p\mathbf{u}·\nabla T+\nabla ·\mathbf{q}=Q,$$

(1)

where $\rho$ is density, $C_p$ is specific heat capacity, $\mathbf{u}$ is velocity, T is temperature, $\mathbf{q}$ is heat flux, and Q is a volumetric heat source. The conductive heat flux follows Fourier’s law,

$$\mathbf{q}=-k\nabla T,$$

(2)

with k the thermal conductivity.

2.2.2. Laminar Flow in the Vapor Cavity

The vapor flow in the central cavity is assumed laminar and compressible. The governing equations are the steady-state Navier–Stokes equations:

$$\begin{array}{cc}\hfill \nabla ·\left(\rho \mathbf{u}\right)& =0,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \rho (\mathbf{u}·\nabla )\mathbf{u}& =\nabla ·\left[-p\mathbf{I}+\mu \left(\nabla \mathbf{u}+{(\nabla \mathbf{u})}^T\right)-{\displaystyle \frac{2}{3}}\mu (\nabla ·\mathbf{u})\mathbf{I}\right]+\mathbf{F},\hfill \end{array}$$

(4)

where p is pressure, $\mu$ is dynamic viscosity, $\mathbf{I}$ is the identity tensor, and $\mathbf{F}$ denotes body forces (e.g., gravity).

2.2.3. Brinkman Flow in the Porous Wick

The porous wick is modeled using the Brinkman equations, which augment Darcy’s law with viscous shear terms:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\rho }{\epsilon }}(\mathbf{u}·\nabla )\left({\displaystyle \frac{\mathbf{u}}{\epsilon }}\right)& =\nabla ·\left[-p\mathbf{I}+{\displaystyle \frac{\mu }{\epsilon }}\left(\nabla \mathbf{u}+{(\nabla \mathbf{u})}^T\right)-{\displaystyle \frac{2}{3}}{\displaystyle \frac{\mu }{\epsilon }}(\nabla ·\mathbf{u})\mathbf{I}\right]\hfill \\ \hfill & -{\kappa }^{-1}\mu \mathbf{u}+\mathbf{F},\hfill \end{array}$$

(5)

where $\epsilon$ is porosity and $\kappa$ is permeability. This formulation captures both Darcy drag and local viscous dissipation within the porous wick [32].

2.2.4. Effective Thermal Conductivity of the Wick

The effective thermal conductivity $k_{\mathrm{eff}}$ of a saturated porous wick is estimated using the Halpin–Tsai model:

$$\begin{array}{cc}\hfill k_{\mathrm{eff}}& =k_c{\displaystyle \frac{1+\zeta \eta (1-\epsilon )}{1-\eta (1-\epsilon )}},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \eta & ={\displaystyle \frac{k_d/k_c-1}{k_d/k_c+\zeta }},\hfill \end{array}$$

(7)

where $k_c$ and $k_d$ denote the conductivities of the continuous (copper) and dispersed (water) phases, respectively, and $\zeta$ is a shape factor related to pore morphology [33]. This provides a practical estimate for design-level modeling where detailed pore-scale reconstruction is not performed.

2.3. Multiphysics Couplings and Boundary Conditions

The physics interfaces are coupled through shared variables and explicit multiphysics features.

2.3.1. Nonisothermal Flow

The Nonisothermal Flow coupling links the Laminar Flow and Heat Transfer interfaces, ensuring that temperature-dependent fluid properties influence the velocity field and that convective transport contributes to the energy equation.

2.3.2. Heat Input and Phase-Change Treatment

A constant heat flux is applied to the SI1mm ² source area on the bottom copper surface to represent localized chip heating. Phase change between the wick-supplied liquid and the vapor cavity is not resolved using explicit interface-tracking techniques such as Level Set or VOF. Instead, latent heat exchange is incorporated via energy-conserving boundary conditions at the wick–vapor interface, following the common engineering approach used in heat-pipe style models [7,36].

At this interface, evaporation and condensation appear as heat sinks or sources:

• evaporation: liquid absorbs heat to form vapor, acting as a local heat sink in the wick;

  Table 2. Material properties used in the COMSOL model.

  Material	Property	Symbol	Value	Units	Source
  Copper (solid)	Density	$\rho$	8960	SIkg.m -3	[30]
  Copper (solid)	Specific heat	$C_p$	385	SIJ.kg-1.K-1	[30]
  Copper (solid)	Thermal conductivity	k	400	SIW.m-1.K-1	[30]
  Water (liquid)	Density	$\rho$	997	SIkg.m-3	[30]
  Water (liquid)	Specific heat	$C_p$	4180	SIJ.kg-1.K-1	[30]
  Water (liquid)	Thermal conductivity	k	0.6	SIW.m-1.K-1	[30]
  Water (liquid)	Dynamic viscosity	$\mu$	$8.9\times {10}^{-4}$	SIPa.s	[30]
  Water (vapor)	Density	$\rho$	0.554	SIkg.m-3	[30]
  Water (vapor)	Specific heat	$C_p$	2010	SIJ.kg-1.K-1	[30]
  Water (vapor)	Thermal conductivity	k	0.026	SIW.m-1.K-1	[30]
  Water (vapor)	Dynamic viscosity	$\mu$	$1.34\times {10}^{-5}$	SIPa.s	[30]
  Porous wick	Porosity	$\epsilon$	0.68	–	assumed/design value
  Porous wick	Permeability	$\kappa$	$1.2\times {10}^{-10}$	SIm2	estimated
  Porous wick	Effective conductivity	$k_{\mathrm{eff}}$	64.02	SIW.m-1.K-1	from Eq. (6)

  Table 2. Material properties used in the COMSOL model.

  Material	Property	Symbol	Value	Units	Source
  Copper (solid)	Density	$\rho$	8960	SIkg.m -3	[30]
  Copper (solid)	Specific heat	$C_p$	385	SIJ.kg-1.K-1	[30]
  Copper (solid)	Thermal conductivity	k	400	SIW.m-1.K-1	[30]
  Water (liquid)	Density	$\rho$	997	SIkg.m-3	[30]
  Water (liquid)	Specific heat	$C_p$	4180	SIJ.kg-1.K-1	[30]
  Water (liquid)	Thermal conductivity	k	0.6	SIW.m-1.K-1	[30]
  Water (liquid)	Dynamic viscosity	$\mu$	$8.9\times {10}^{-4}$	SIPa.s	[30]
  Water (vapor)	Density	$\rho$	0.554	SIkg.m-3	[30]
  Water (vapor)	Specific heat	$C_p$	2010	SIJ.kg-1.K-1	[30]
  Water (vapor)	Thermal conductivity	k	0.026	SIW.m-1.K-1	[30]
  Water (vapor)	Dynamic viscosity	$\mu$	$1.34\times {10}^{-5}$	SIPa.s	[30]
  Porous wick	Porosity	$\epsilon$	0.68	–	assumed/design value
  Porous wick	Permeability	$\kappa$	$1.2\times {10}^{-10}$	SIm2	estimated
  Porous wick	Effective conductivity	$k_{\mathrm{eff}}$	64.02	SIW.m-1.K-1	from Eq. (6)

• condensation: vapor releases heat upon liquefaction, acting as a local heat source at the condenser side.

The corresponding interfacial heat flux is

$$q_{\mathrm{pc}}=\dot{m}{h}_{fg},$$

(8)

where $\dot{m}$ is the phase-change mass flux and $h_{fg}$ is the latent heat of vaporization. This boundary-based formulation captures the dominant energetic effect of phase change without resolving microscopic interface dynamics.

2.3.3. Convective Cooling and Wall Conditions

To represent air-side heat rejection at the condenser, a convective boundary condition is imposed on a designated condenser surface region with an effective heat transfer coefficient $h=SI9.75W.m^{-2}.K^{-1}$, representative of low-to-moderate forced convection conditions in compact electronics enclosures. All solid walls are treated as impermeable with no-slip conditions for both vapor and porous domains.

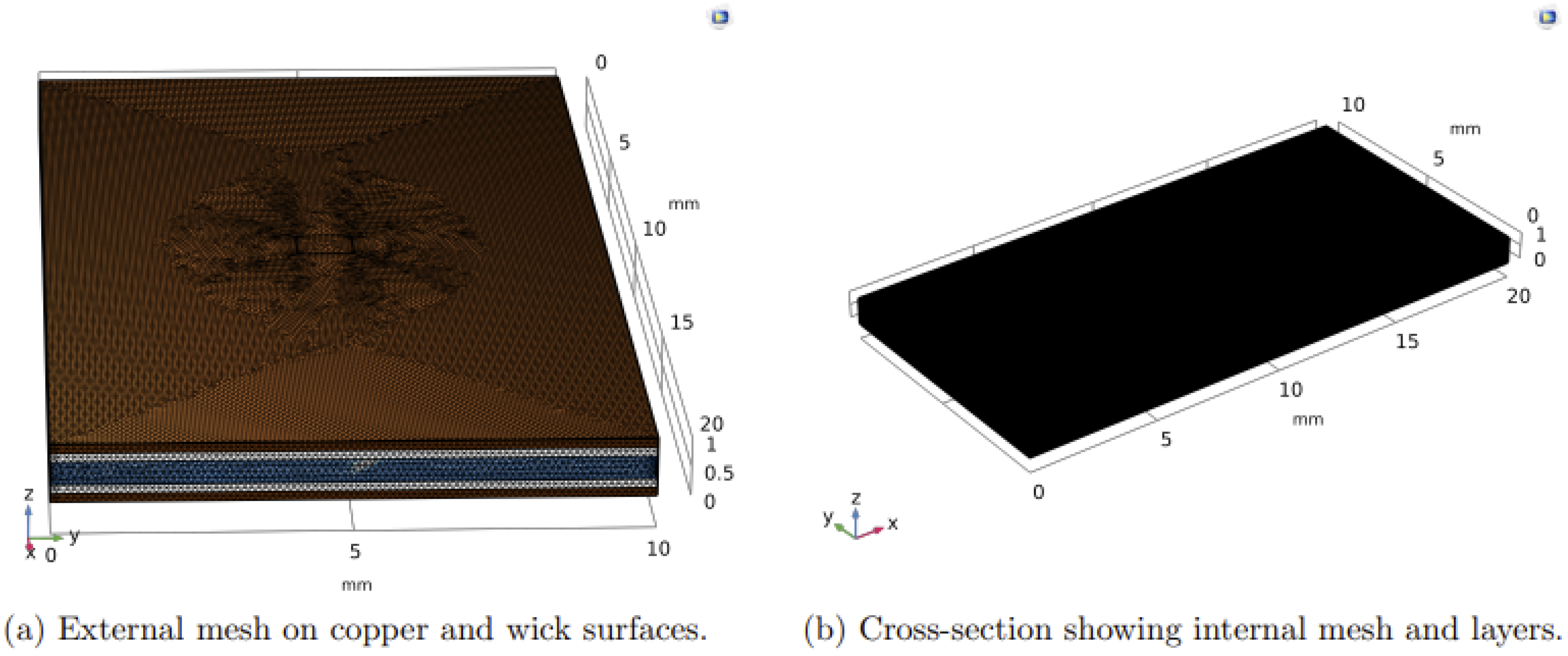
2.4. Mesh Configuration

A high-quality mesh is essential for capturing steep gradients in temperature and velocity near the wick–vapor interface. The mesh consists primarily of structured swept elements with a maximum element size of SI0.1mm, ensuring adequate resolution across layers. Boundary-layer elements are deployed adjacent to the wick–vapor interface to resolve near-wall gradients.

The resulting external and internal meshes are shown in Figure 2a and Figure 2b, respectively, while quantitative mesh-independence results are summarized in Table 3.

2.5. Solver Setup

The coupled nonlinear system is solved in steady state using COMSOL’s fully coupled stationary solver with the MUMPS direct linear solver. Convergence is declared when the relative residuals of all dependent variables fall below the specified tolerance. Mesh-independence tests confirm that further refinement produces negligible changes in peak temperature and the reported effective wick conductivity (Table 3).

3. Results and Discussion

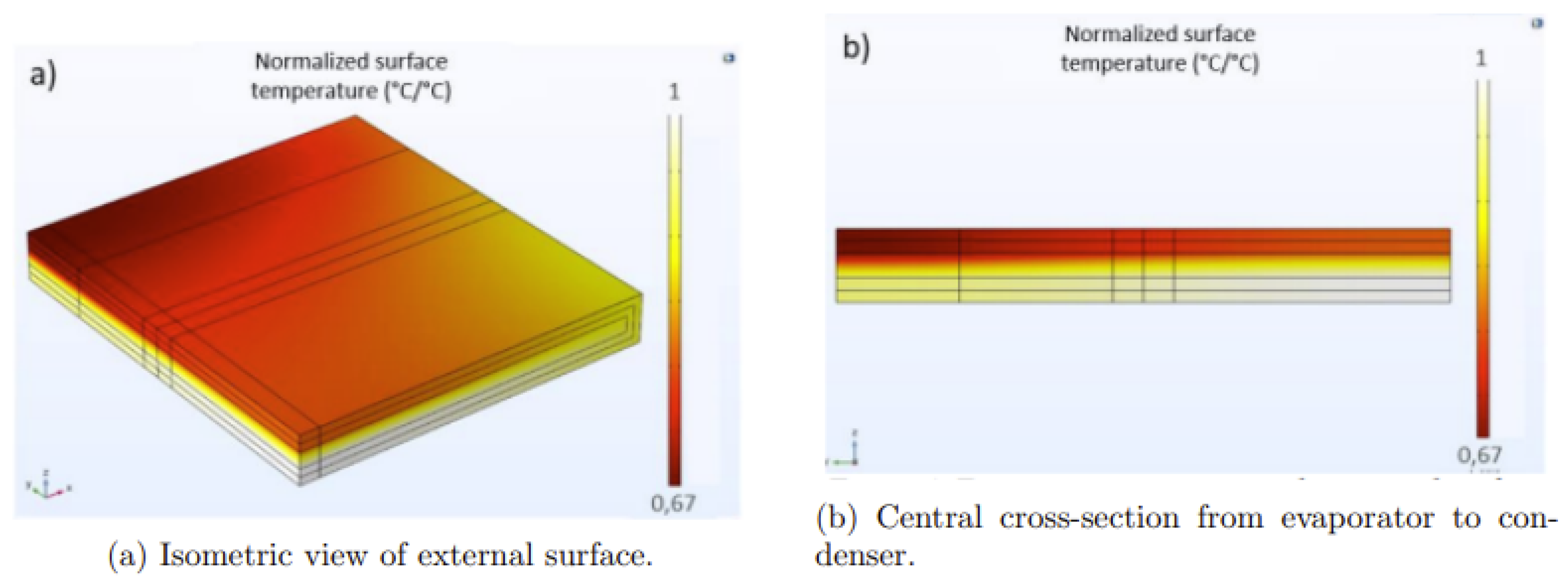
3.1. Surface Temperature Distribution

The normalized surface temperature distribution is plotted in Figure 3. The hottest region is localized beneath the evaporator at the center of the bottom surface, while temperatures decrease toward the condenser region, confirming effective two-dimensional heat spreading enabled by the vapor chamber architecture.

Axial temperature values at representative positions between evaporator and condenser are given in Table 4. The profile shows a smooth monotonic decline from the evaporator toward the condenser, consistent with the expected operation of a planar two-phase heat spreader.

3.2. Thermal Circuit Interpretation

For design interpretation, an equivalent resistance network can be constructed to partition the overall temperature rise into (i) junction-to-chamber resistance, (ii) internal spreading resistance within the vapor chamber, and (iii) condenser-to-ambient resistance. Within the present modeling assumptions, the internal spreading contribution is reduced by the two-phase mechanism, which promotes quasi-isothermal behavior in the vapor region and distributes heat over a larger condenser area. The largest sensitivity is typically associated with the external convection boundary condition and the wick transport parameters (porosity and permeability), indicating that accurate specification of air-side conditions and wick properties is important for predictive design studies.

3.3. Effective Thermal Conductivity

The modeled average effective thermal conductivity at the wick region is $k_{\mathrm{eff}}=SI64.02W.m^{-1}.K^{-1}$. This value is substantially higher than that of water and far lower than bulk copper, reflecting the composite nature of the wick: copper ligaments provide high-conductivity pathways, while water-filled pores enable latent-heat-driven redistribution through evaporation and condensation.

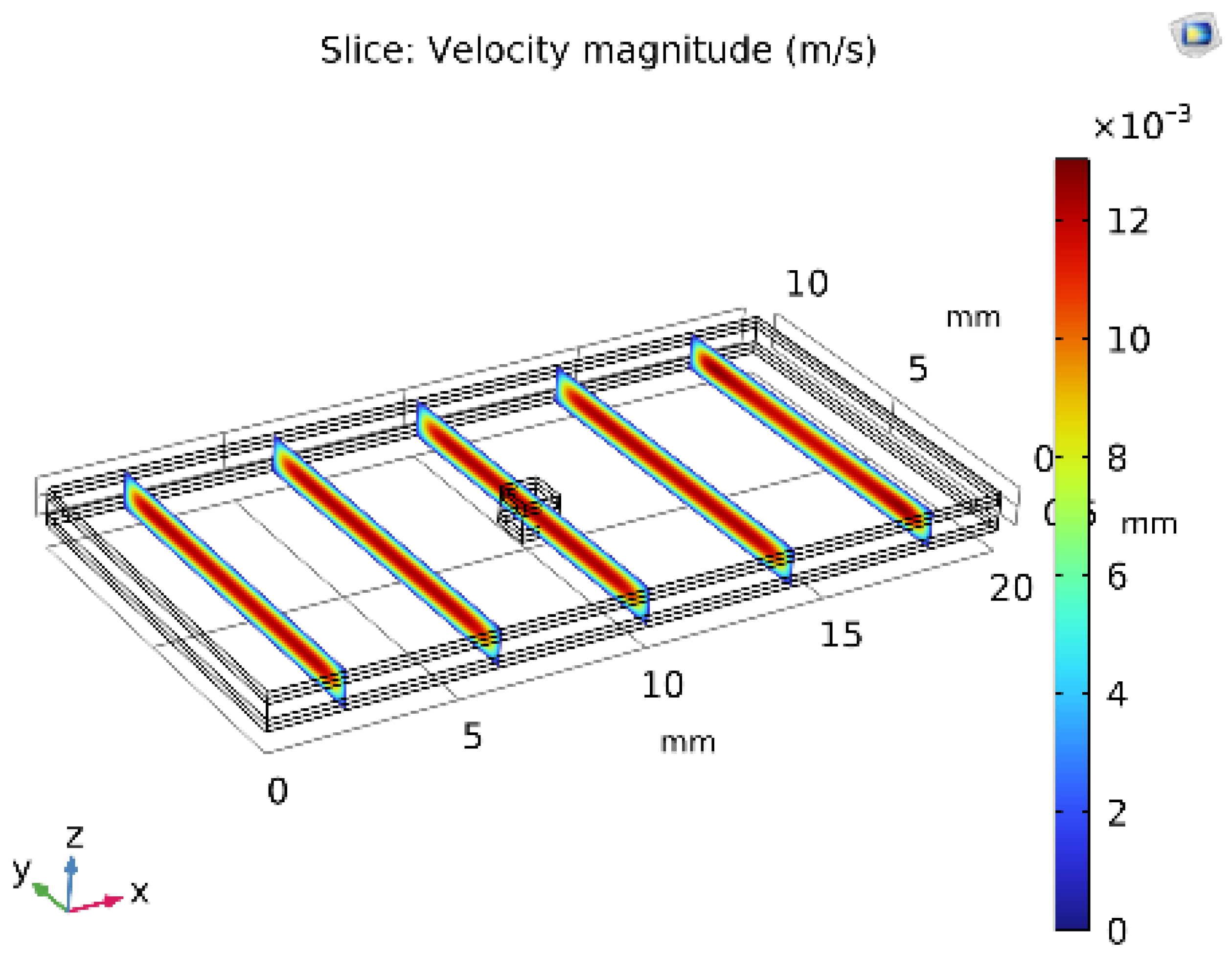
3.4. Velocity Field and Phase-Change-Driven Flow

The velocity field shows elevated vapor speeds in the cavity, driven by pressure gradients associated with net evaporation at the evaporator and condensation at the condenser. Vapor transport is directed from the evaporator toward the condenser, consistent with the physical operation of vapor chambers. Within the porous wick, velocities remain small because of high flow resistance, but the capillary-driven liquid return is sufficient to resupply the evaporator region under the imposed heat load.

The transverse velocity profile across the cavity thickness is summarized in Table 5. The near-parabolic shape, with maximum speed around mid-height and vanishing velocities at the walls, is characteristic of laminar shear-dominated internal flow.

3.5. Pressure Distribution

The predicted pressure field shows a modest high-pressure zone near the evaporator and a gradual decrease toward the condenser. Although the absolute variations are small on an ambient-scale reference, the gradient is sufficient to drive vapor flow across the cavity. The pressure distribution on the cavity surface is plotted in Figure 4.

Pressure vs. axial position along the cavity is given in Table 6.

4. Conclusions

A three-dimensional multiphysics model of a copper–water vapor chamber has been developed in COMSOL Multiphysics^® for electronics cooling applications. The model couples laminar compressible vapor flow, Brinkman flow in a porous wick, and conjugate heat transfer, with latent heat incorporated through energy-conserving interfacial boundary conditions.

The numerical results demonstrate strong in-plane thermal spreading and reduced peak temperature beneath the localized heat source compared with purely conductive transport. Internal fields indicate that net evaporation at the heated region establishes a pressure-driven vapor flow toward the condenser, while the porous wick provides a return pathway for liquid replenishment. The model predicts an effective wick conductivity on the order of SI64W.m^-1.K^-1, consistent with the expected intermediate behavior of a saturated porous composite.

The present modeling strategy provides a practical balance between physical fidelity and computational efficiency, making it suitable for design-oriented parametric studies involving geometry, wick properties, and boundary conditions. Future work will extend the framework to transient operation, higher heat fluxes, and more detailed phase-change kinetics and capillary-limit characterization.