Submitted:
10 April 2024
Posted:
11 April 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Mathematical Modeling
2.1. Lattice Boltzmann Method for Fluid Flow
2.2. Boussinesq Approach for Natural Convection
2.3. Lattice Boltzmann Method for Conjugate Heat-Transfer
3. Benchmark Tests
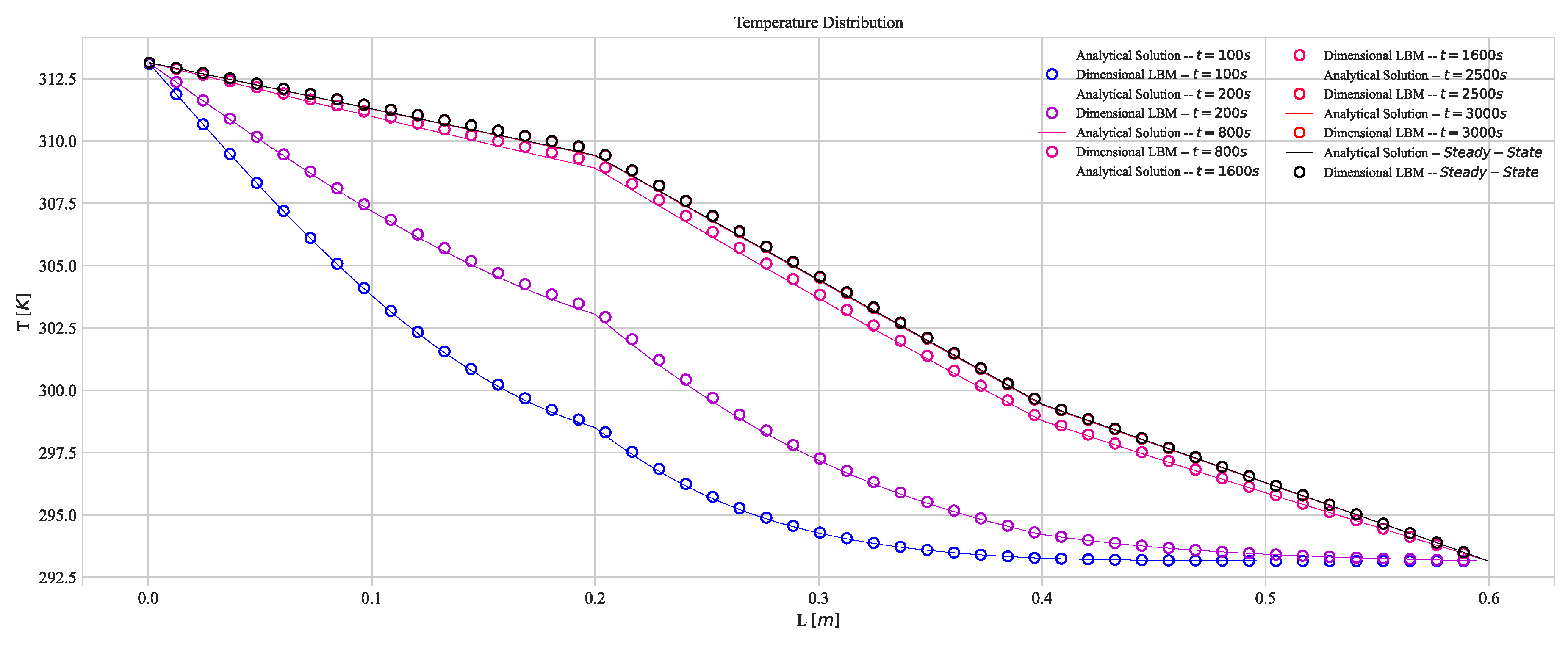
3.1. Heat Diffusion between Three Solids
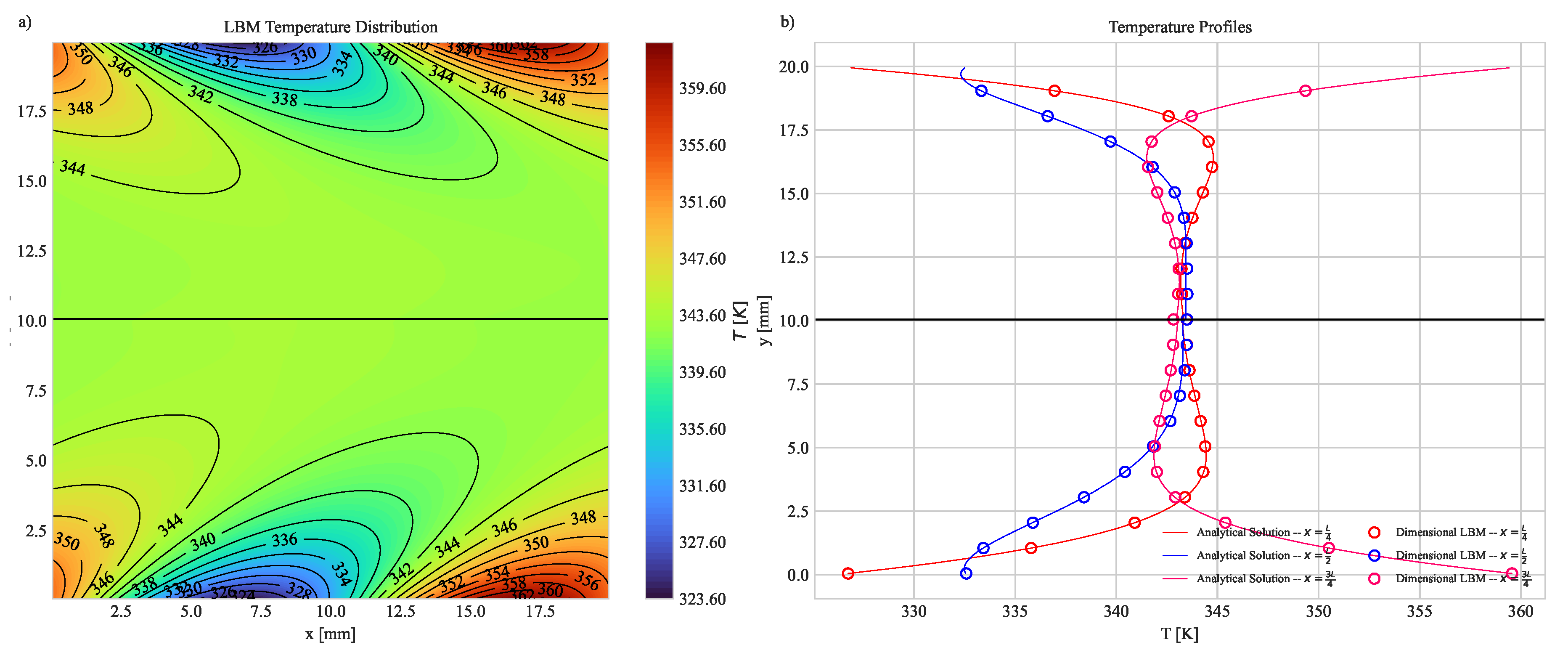
3.2. Convection-Diffusion with a Flat Interface
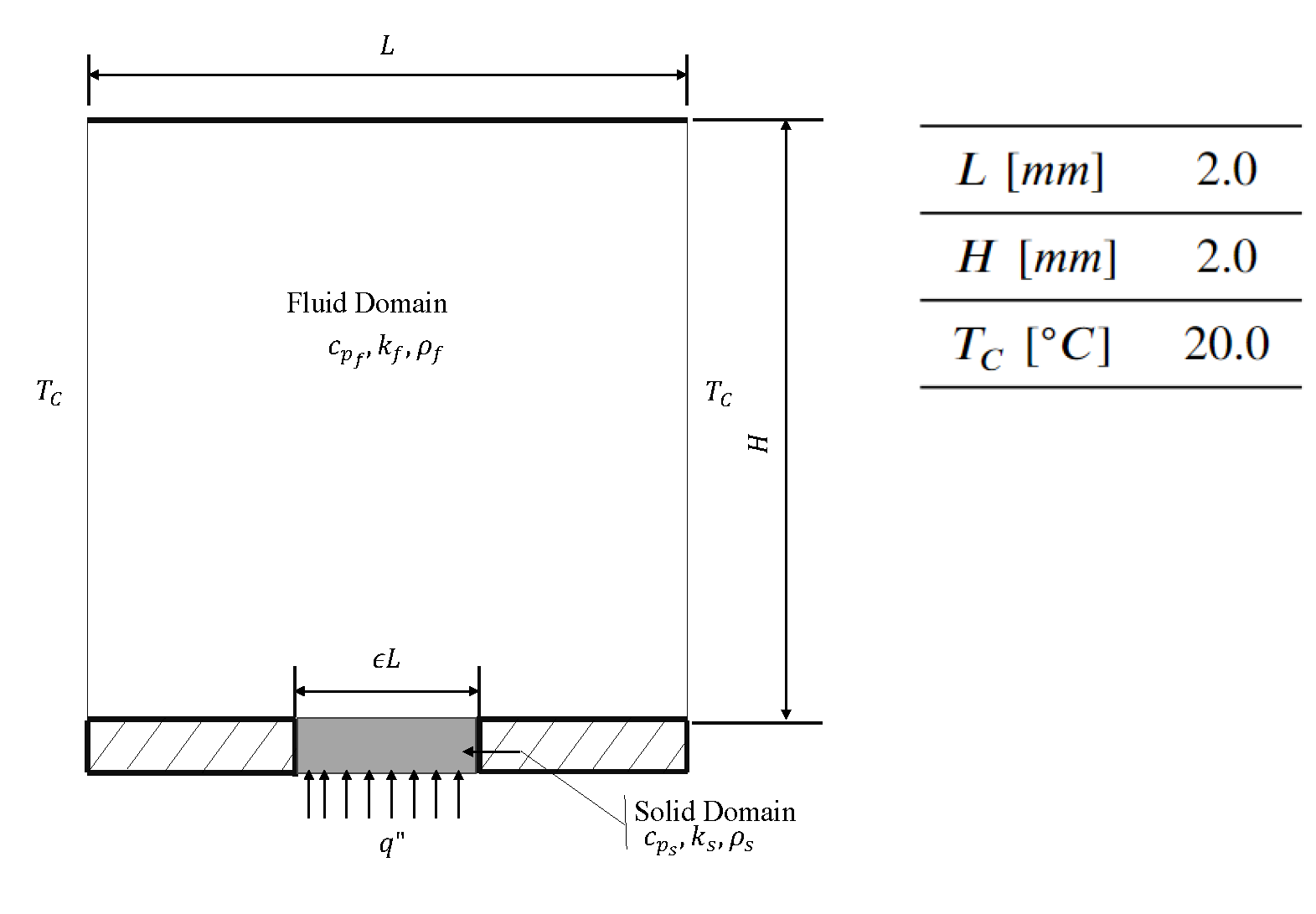
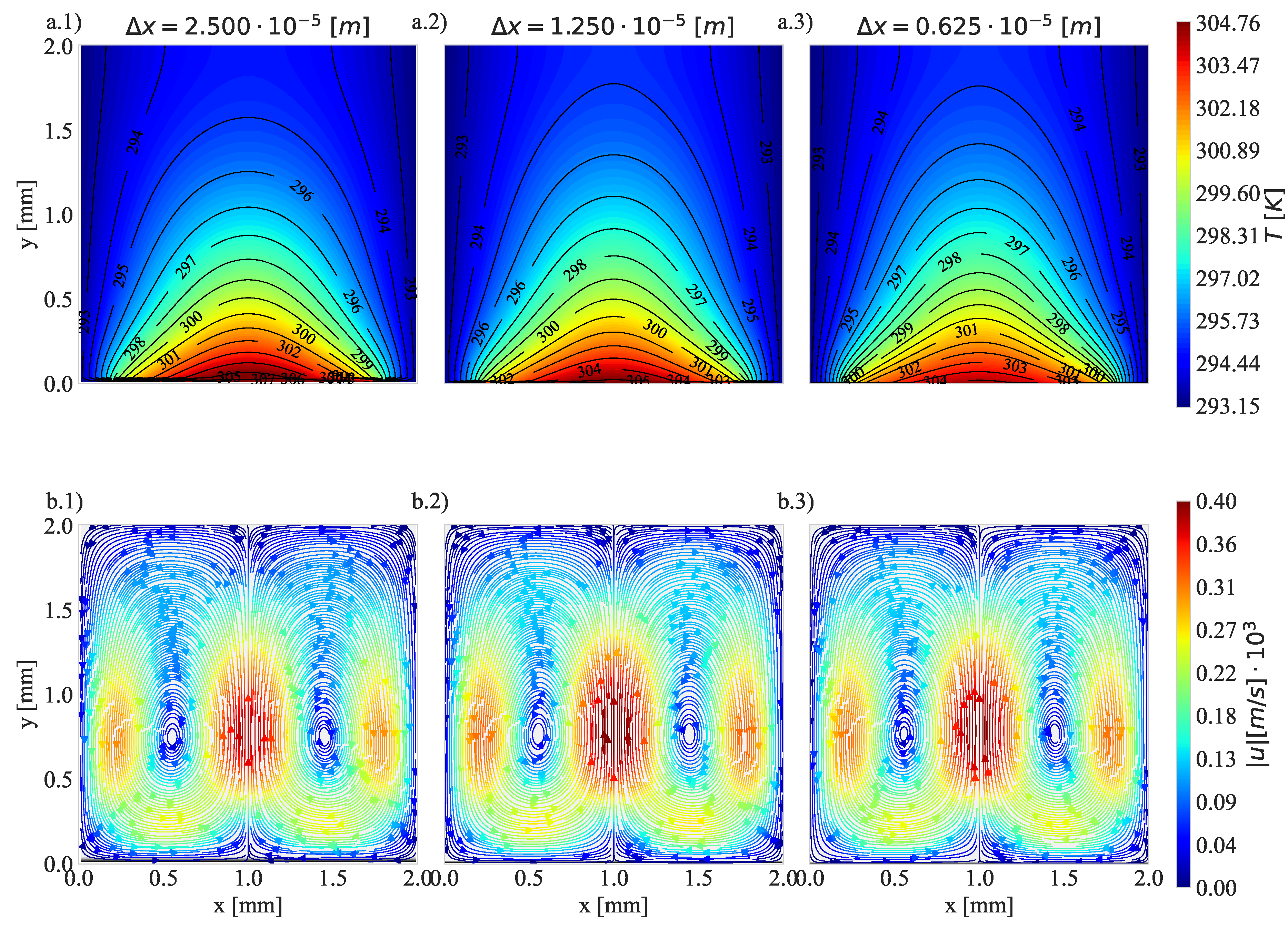
3.3. Natural Convection with a Fixed Heat Flux
4. Results for Natural Convection with Structured Cavities
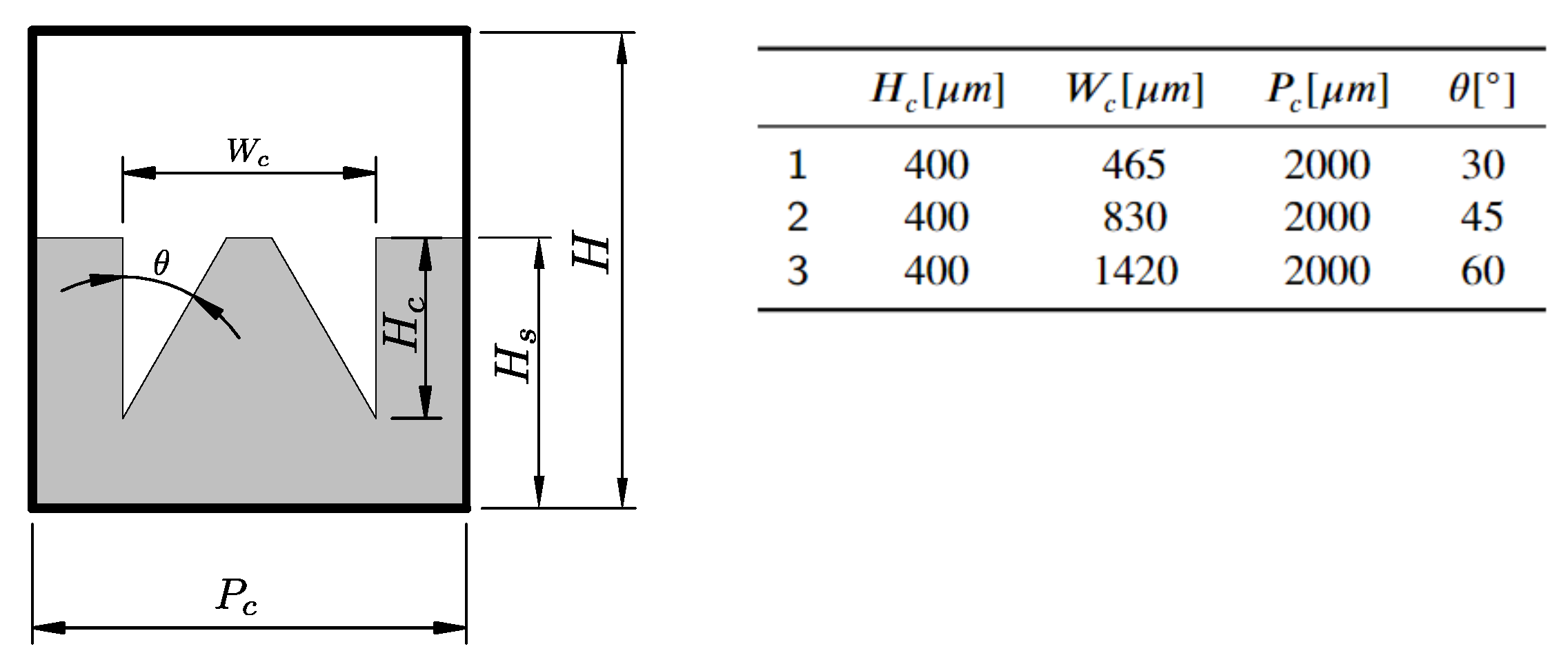
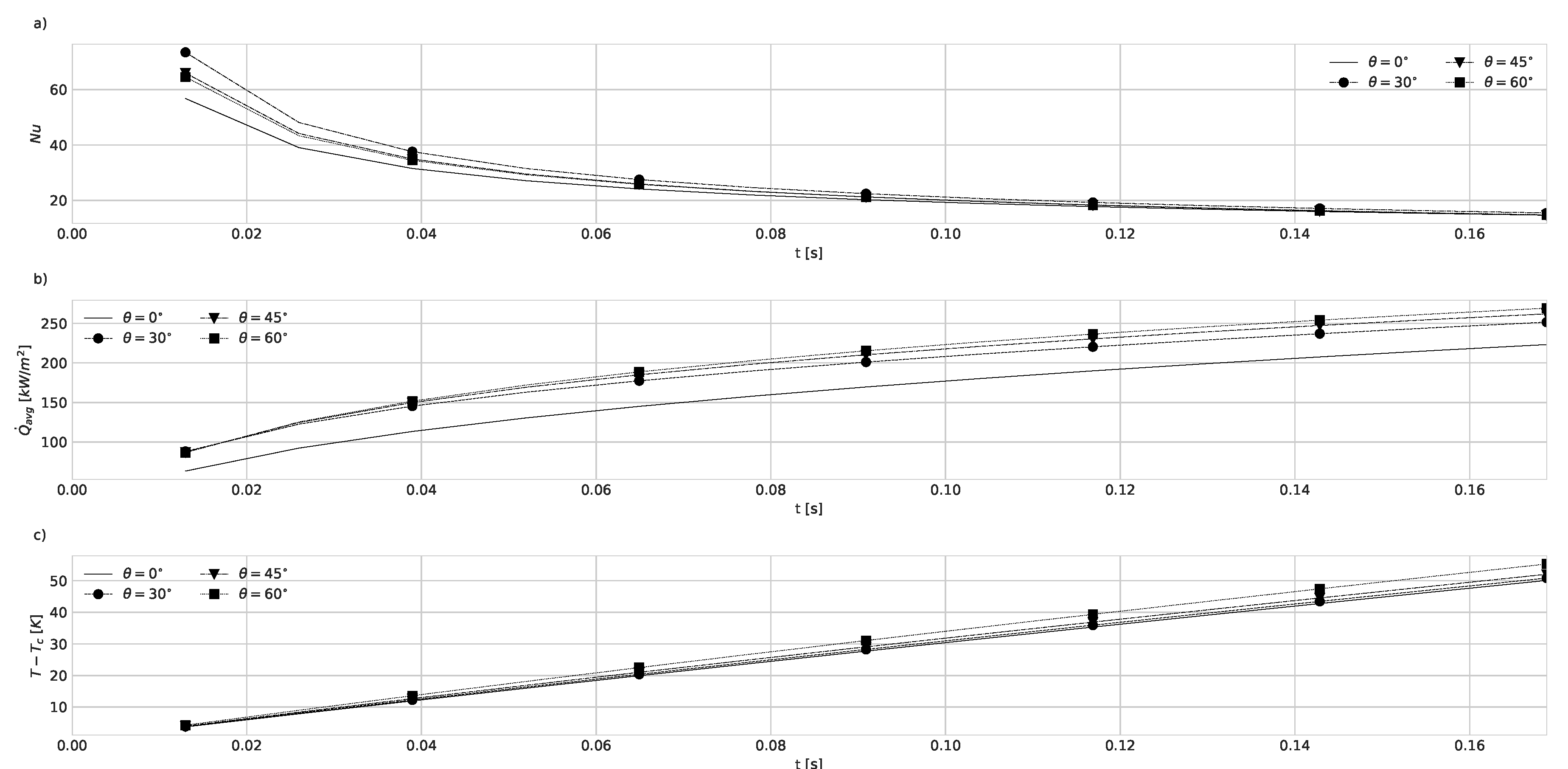
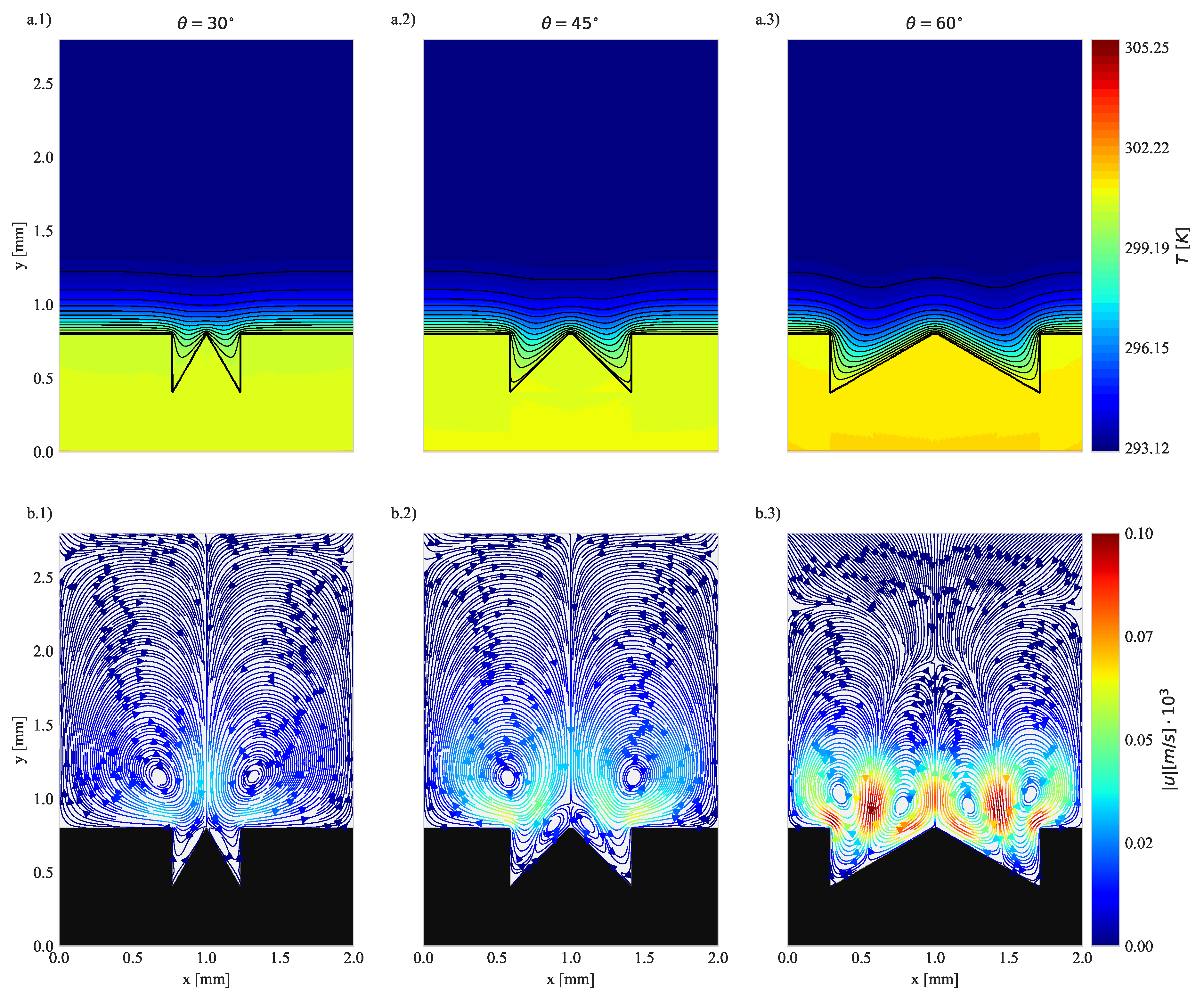
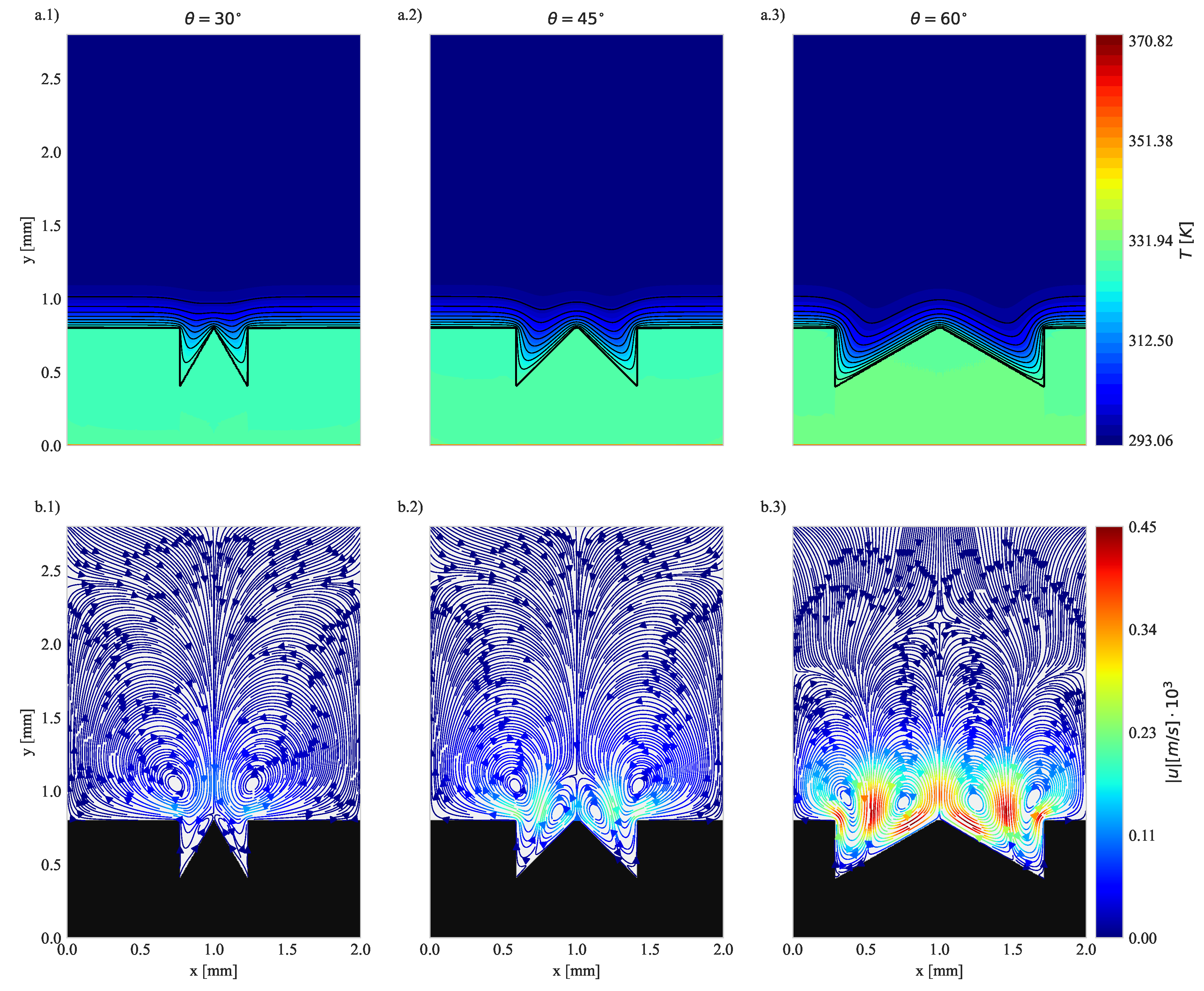
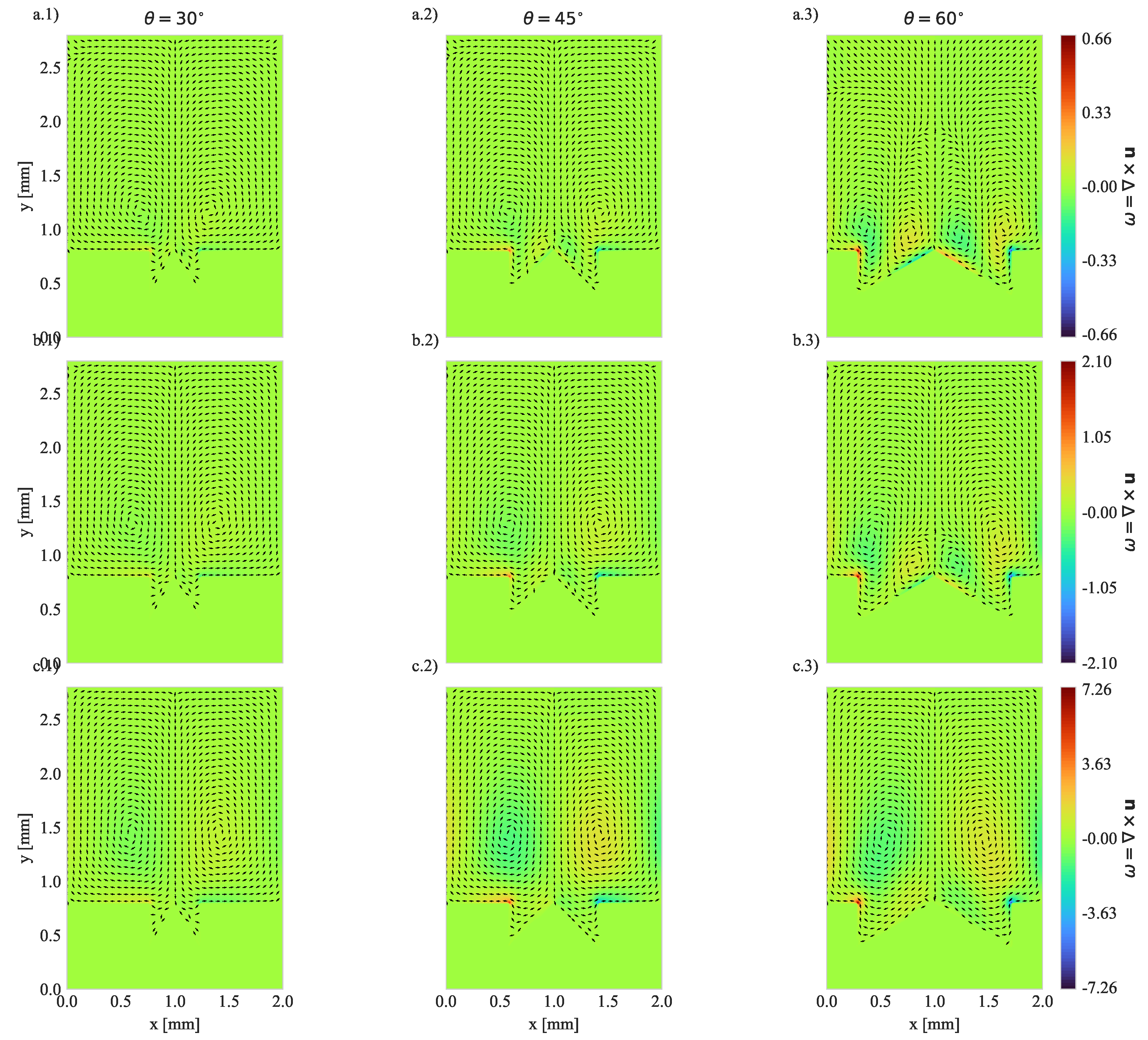
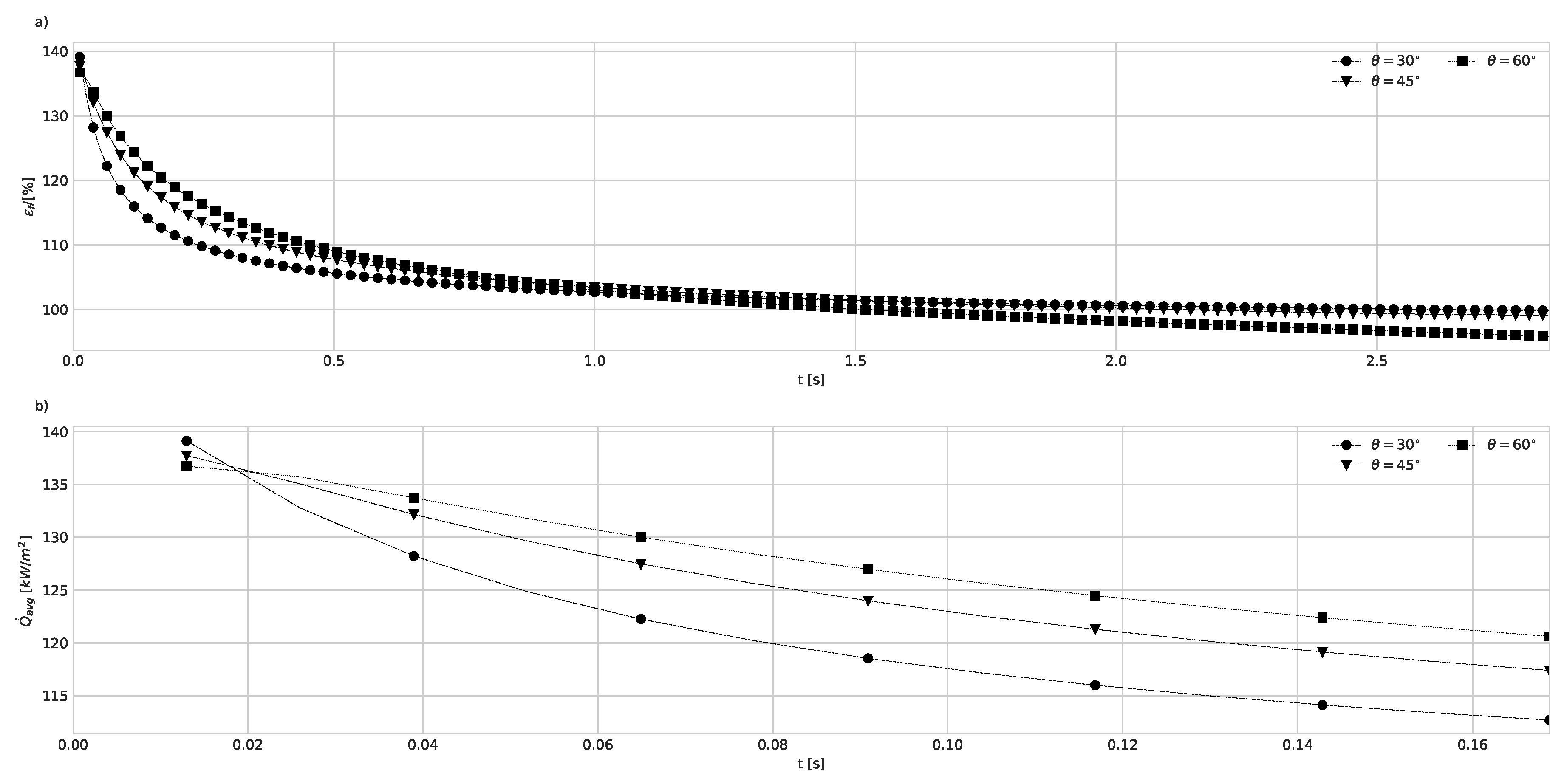
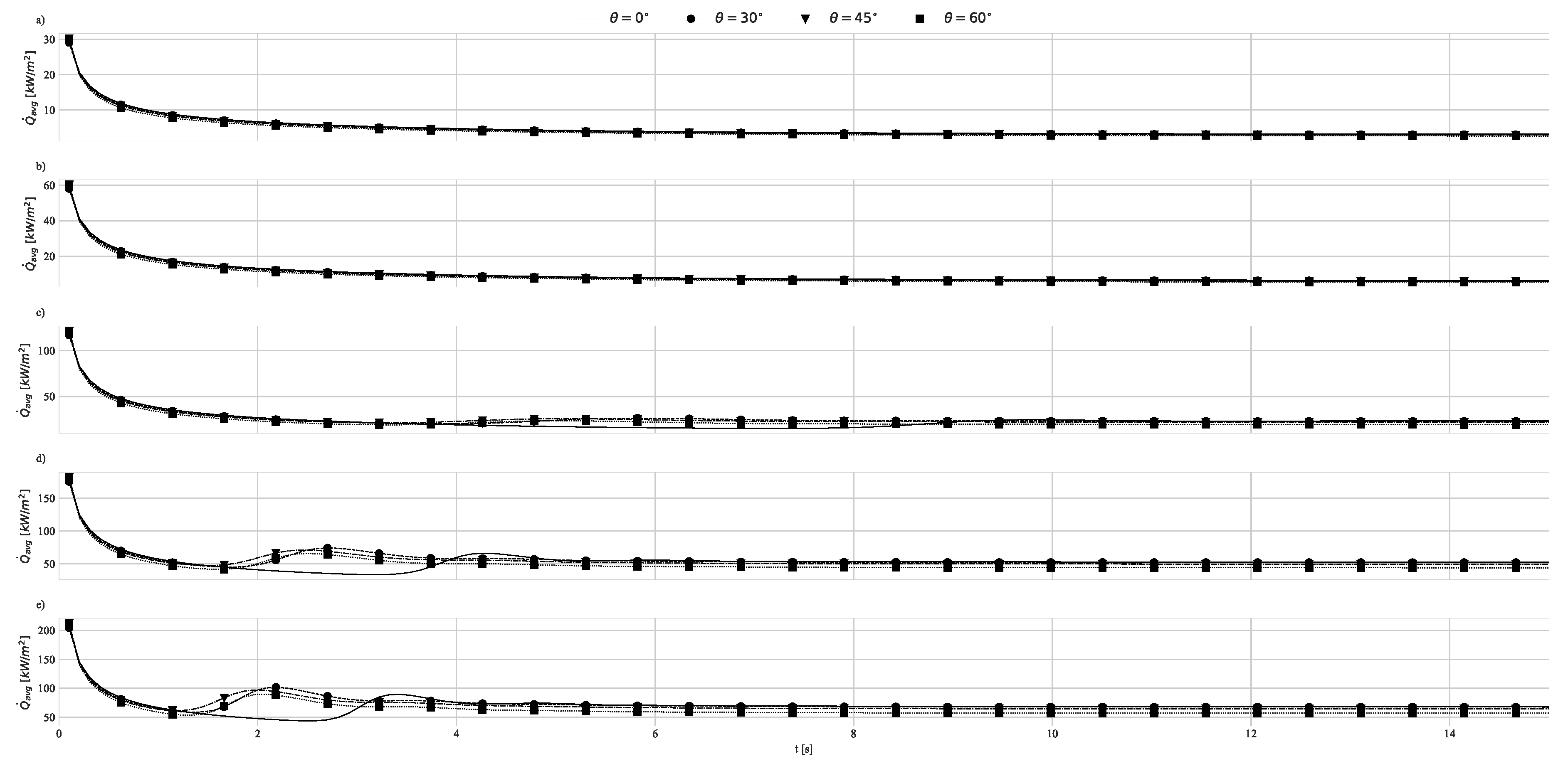
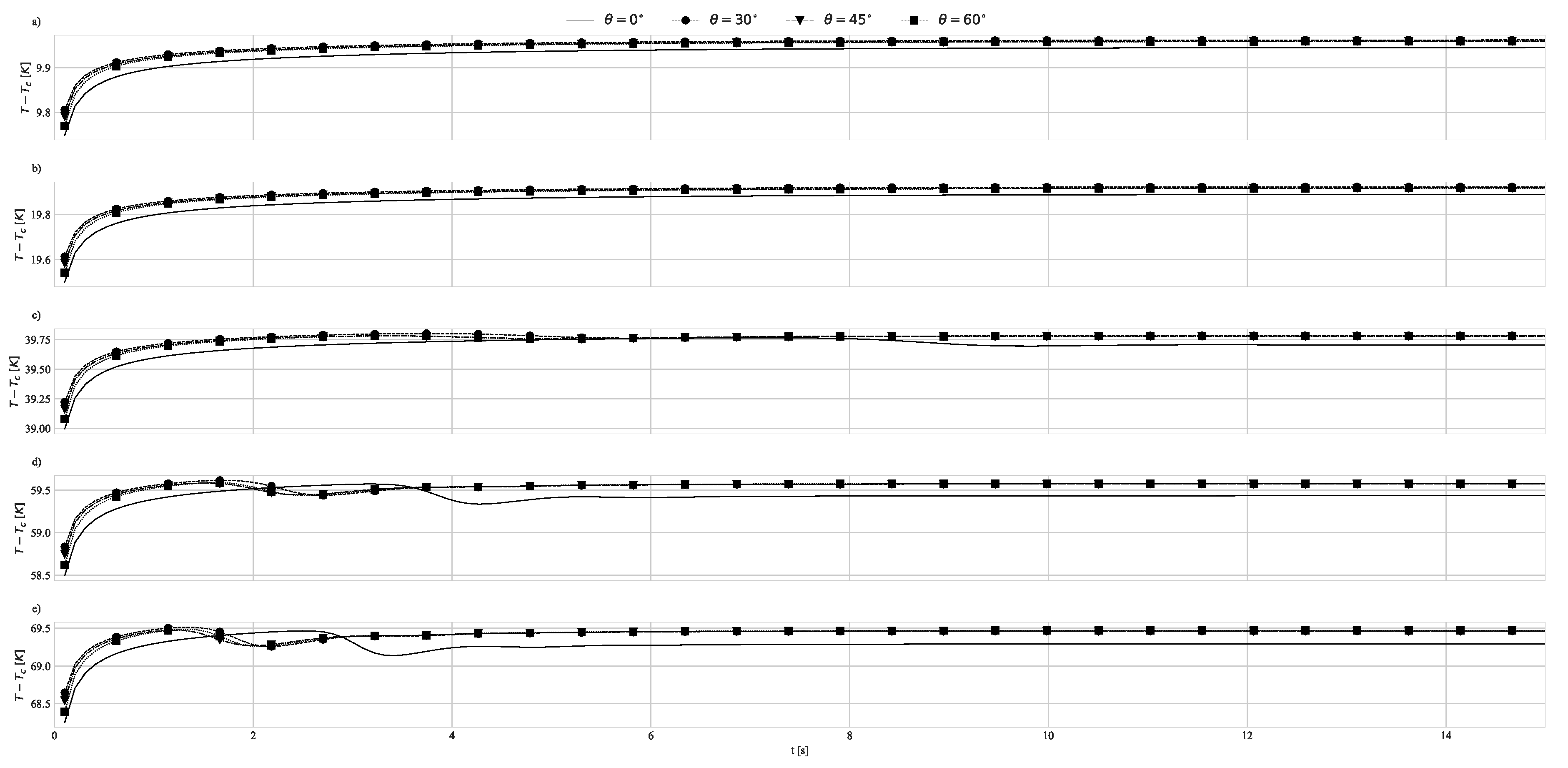
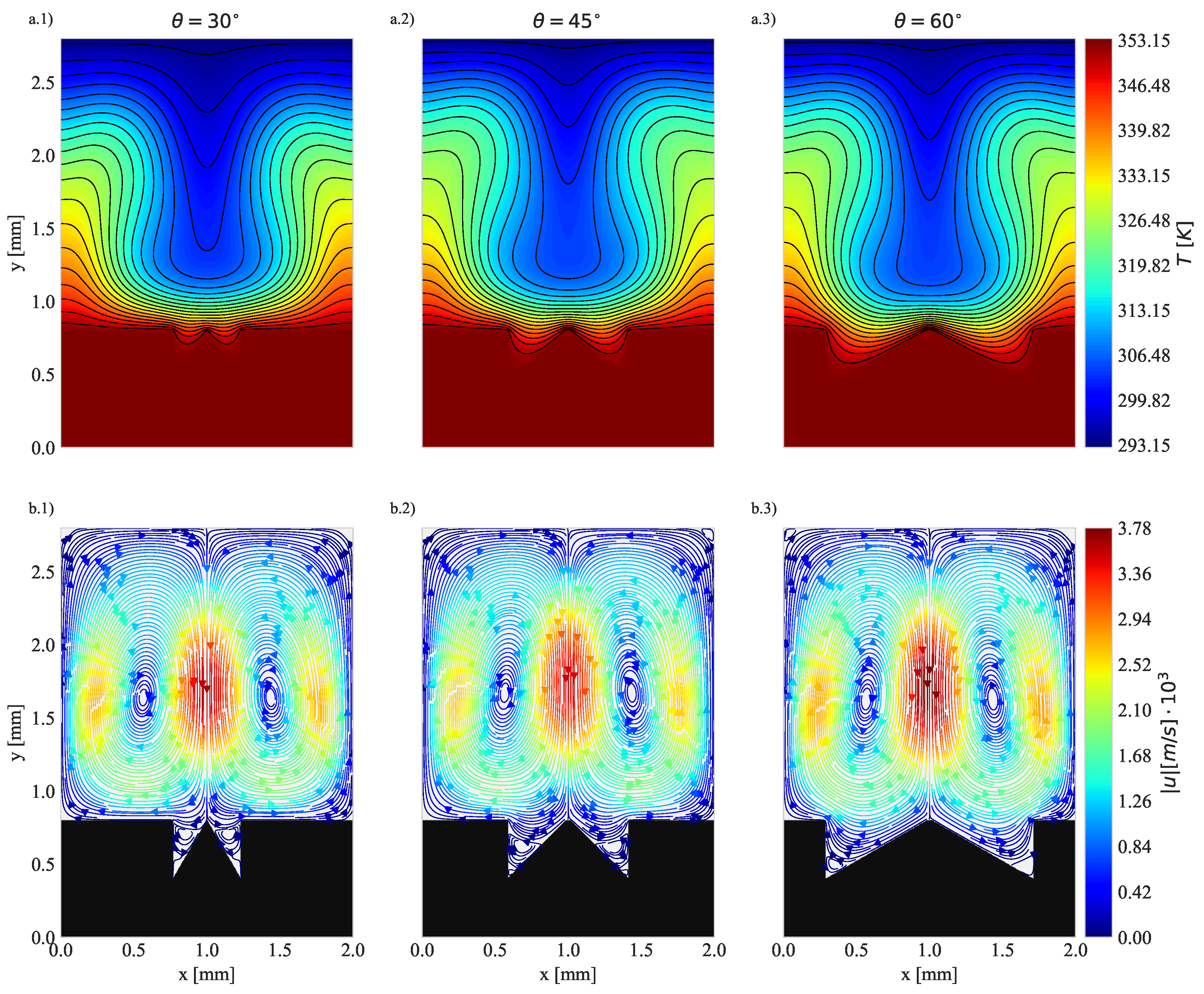
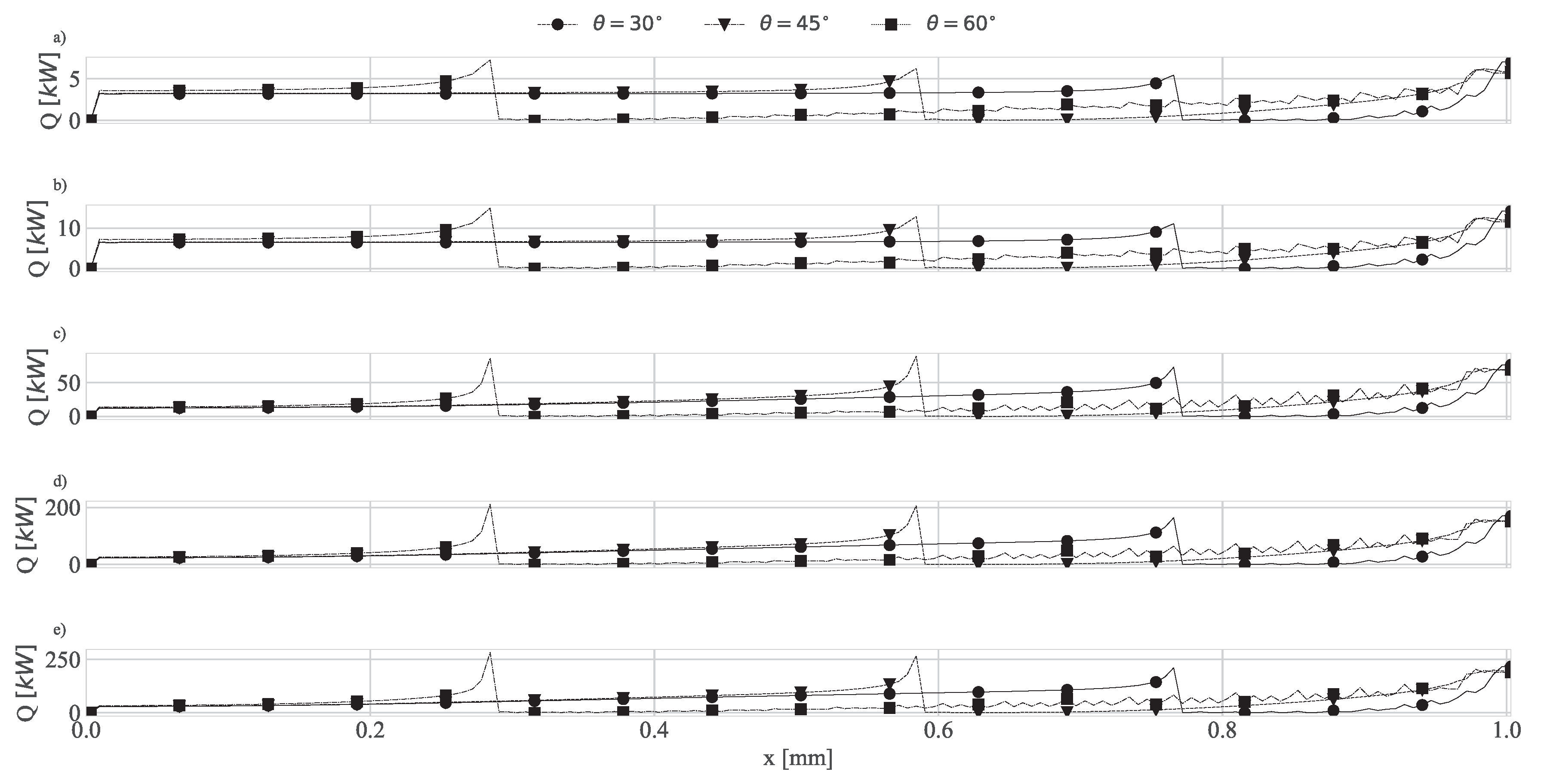
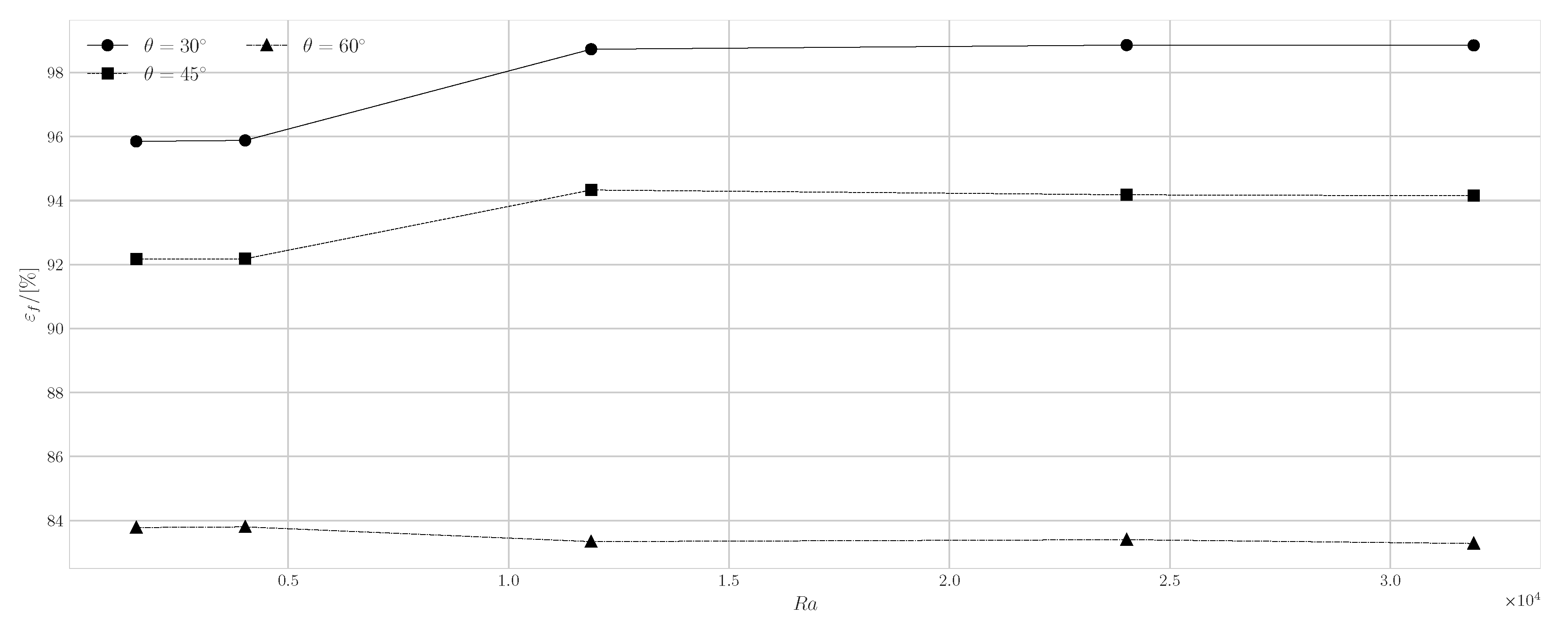
4.1. Geometry Impact on Natural Convection with Imposed Heat Flux
| 30 | 45 | 60 | 30 | 45 | 60 | |
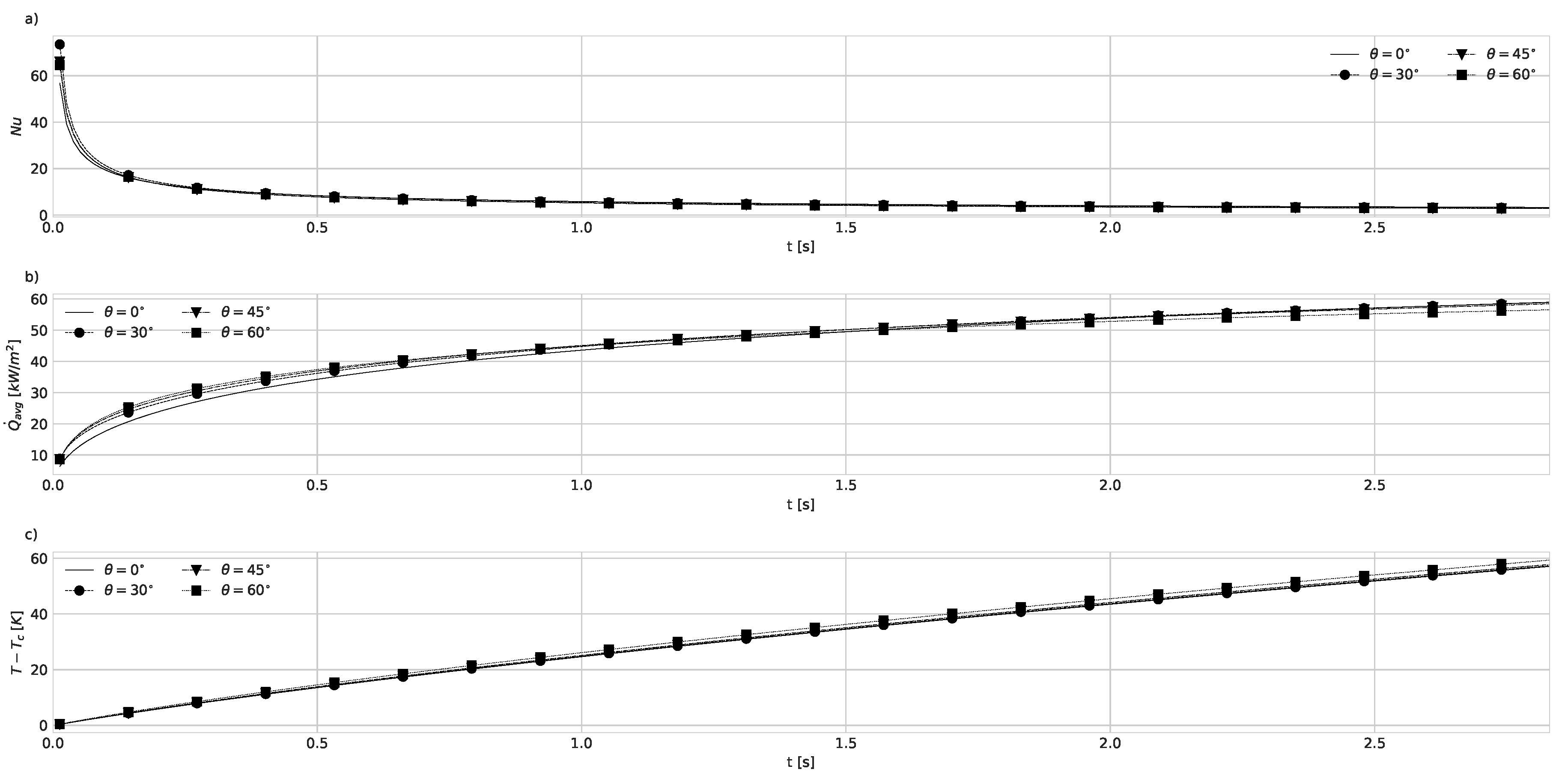
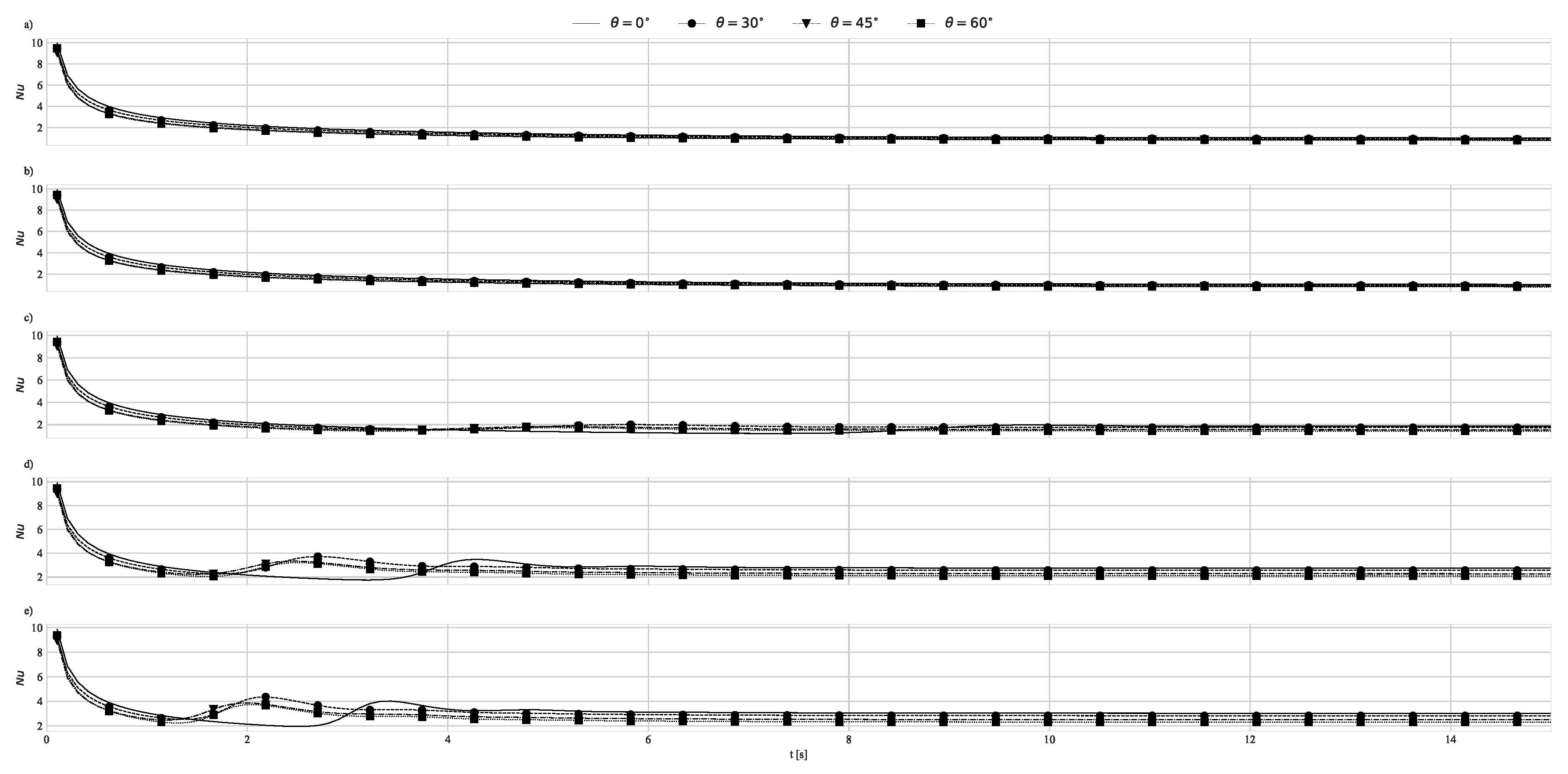
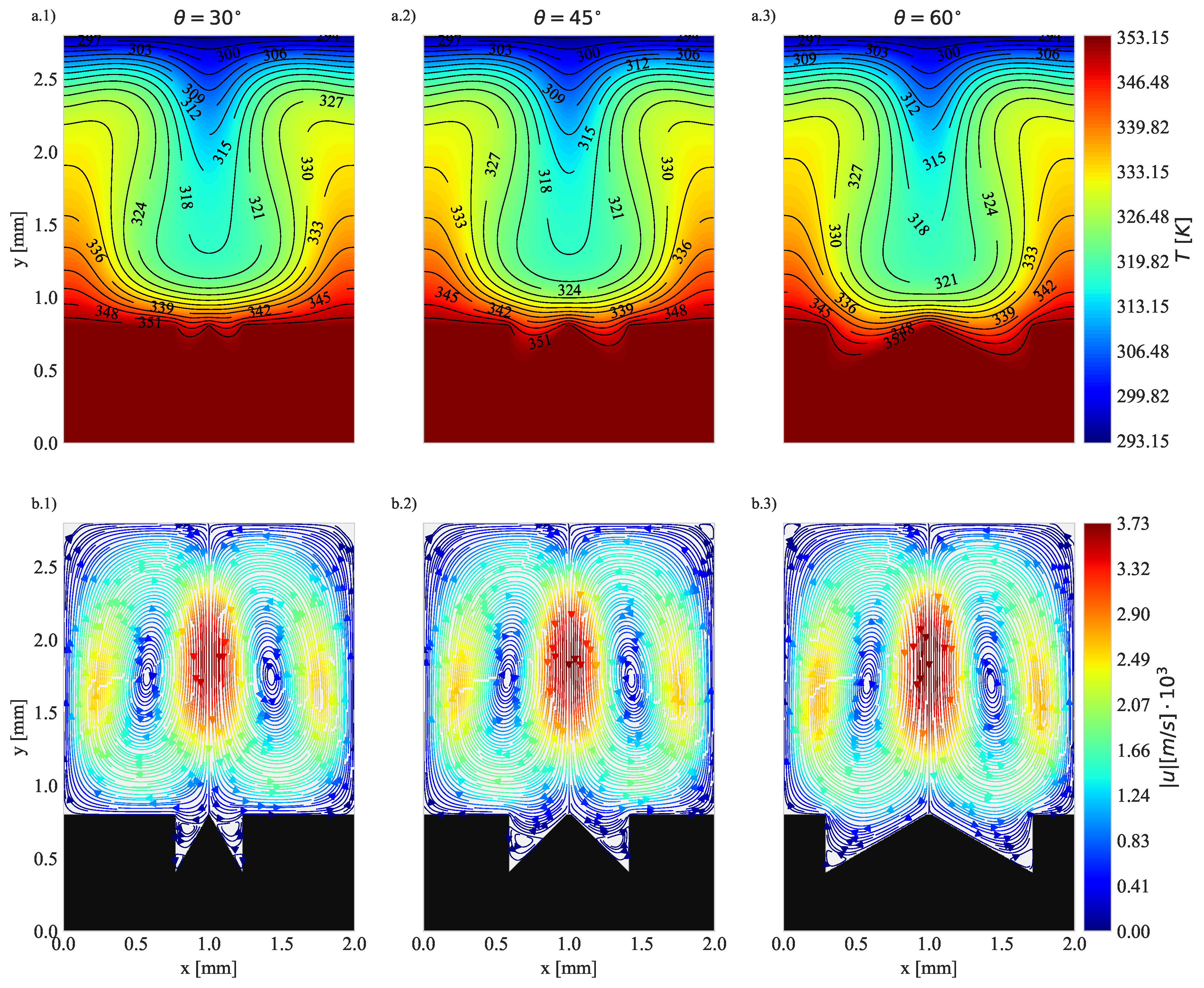
4.2. Natural Convection with Fixed Base Temperature
5. Conclusions
Acknowledgments

Appendix A Chapman-Enskog Analysis
Appendix B Analytical Solution Heat Diffusion between Three Solids
Appendix C Analytical Solution Convection-Diffusion with a Flat Interface
Appendix D Nusselt Number Calculation
References
- Bejan, A.; Kraus, A. Heat Transfer Handbook; Number v. 1 in Heat Transfer Handbook, Wiley, 2003.
- Aneesh, A.; Sharma, A.; Srivastava, A.; Vyas, K.; Chaudhuri, P. Thermal-hydraulic characteristics and performance of 3D straight channel based printed circuit heat exchanger. Applied Thermal Engineering 2016, 98, 474–482. [Google Scholar] [CrossRef]
- Buchberg, H.; Catton, I.; Edwards, D.K. Natural Convection in Enclosed Spaces—A Review of Application to Solar Energy Collection. Journal of Heat Transfer 1976, 98, 182–188. [Google Scholar] [CrossRef]
- Baïri, A.; Zarco-Pernia, E.; De María, J.M.G. A review on natural convection in enclosures for engineering applications. The particular case of the parallelogrammic diode cavity. Applied Thermal Engineering 2014, 63, 304–322. [Google Scholar] [CrossRef]
- Pretot, S.; Zeghmati, B.; Caminat, P. Influence of surface roughness on natural convection above a horizontal plate. Advances in Engineering Software 2000, 31, 793–801. [Google Scholar] [CrossRef]
- Oosthuizen, P.H. A numerical study of laminar and turbulent natural convective heat transfer from an isothermal vertical plate with a wavy surface. ASME International Mechanical Engineering Congress and Exposition, 2010, Vol. 44441, pp. 1481–1486. [CrossRef]
- Oosthuizen, P. Natural convective heat transfer from an inclined isothermal plate with a wavy surface. 42nd AIAA Thermophysics Conference, 2011, p. 3943.
- Oosthuizen, P.H.; Kalendar, A. A numerical study of the effect of spaced triangular surface waves on natural convective heat transfer from an upward facing heated horizontal isothermal surface. ASTFE Digital Library. Begel House Inc., 2020.
- Hussain, S.; Kalendar, A.; Rafique, M.Z.; Oosthuizen, P.H. Assessment of thermal characteristics of square wavy plates. Heat Transfer 2020, 49, 3742–3757. [Google Scholar] [CrossRef]
- Hossain, M.; Rees, D.A.S. Combined heat and mass transfer in natural convection flow from a vertical wavy surface. Acta Mechanica 1999, 136, 133–141. [Google Scholar] [CrossRef]
- Siddiqa, S.; Hossain, M.; Saha, S.C. The effect of thermal radiation on the natural convection boundary layer flow over a wavy horizontal surface. International Journal of Thermal Sciences 2014, 84, 143–150. [Google Scholar] [CrossRef]
- Siddiqa, S.; Hossain, M.A.; Gorla, R.S.R. Natural convection flow of viscous fluid over triangular wavy horizontal surface. Computers & Fluids 2015, 106, 130–134. [Google Scholar]
- Oosthuizen, P.H.; Paul, J.T. A numerical study of natural convective heat transfer from an inclined isothermal plate having a square wave surface. ASME International Mechanical Engineering Congress and Exposition, 2011, Vol. 54969, pp. 445–450.
- Perelman, T. On conjugated problems of heat transfer. International Journal of Heat and Mass Transfer 1961, 3, 293–303. [Google Scholar] [CrossRef]
- Armero, F.; Simo, J. A new unconditionally stable fractional step method for non-linear coupled thermomechanical problems. International Journal for numerical methods in Engineering 1992, 35, 737–766. [Google Scholar] [CrossRef]
- Giles, M.B. Stability analysis of numerical interface conditions in fluid–structure thermal analysis. International journal for numerical methods in fluids 1997, 25, 421–436. [Google Scholar] [CrossRef]
- Roe, B.; Jaiman, R.; Haselbacher, A.; Geubelle, P. Combined interface boundary condition method for coupled thermal simulations. International journal for numerical methods in fluids 2008, 57, 329–354. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, C.; Mao, Z.S. Unsteady conjugate mass transfer from a spherical drop in simple extensional creeping flow. Chemical engineering science 2012, 79, 29–40. [Google Scholar] [CrossRef]
- Succi, S. The lattice Boltzmann equation: for fluid dynamics and beyond; Oxford university press, 2001.
- Lee, T.; Liu, L. Lattice Boltzmann simulations of micron-scale drop impact on dry surfaces. Journal of Computational Physics 2010, 229, 8045–8063. [Google Scholar] [CrossRef]
- Fakhari, A.; Mitchell, T.; Leonardi, C.; Bolster, D. Improved locality of the phase-field lattice Boltzmann model for immiscible fluids at high density ratios. Physical Review E 2017, 96, 053301. [Google Scholar] [CrossRef]
- Liang, H.; Liu, H.; Chai, Z.; Shi, B. Lattice Boltzmann method for contact-line motion of binary fluids with high density ratio. Physical Review E 2019, 99, 063306. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, J.; Wu, H. Phase-field lattice Boltzmann model for two-phase flows with large density ratio. Physical Review E 2022, 105, 015304. [Google Scholar] [CrossRef]
- Safari, H.; Rahimian, M.H.; Krafczyk, M. Extended lattice Boltzmann method for numerical simulation of thermal phase change in two-phase fluid flow. Physical Review E 2013, 88, 013304. [Google Scholar] [CrossRef]
- Korba, D.; Wang, N.; Li, L. Accuracy of interface schemes for conjugate heat and mass transfer in the lattice Boltzmann method. International Journal of Heat and Mass Transfer 2020, 156, 119694. [Google Scholar] [CrossRef]
- Li, L.; Chen, C.; Mei, R.; Klausner, J.F. Conjugate heat and mass transfer in the lattice Boltzmann equation method. Phys. Rev. E 2014, 89, 043308. [Google Scholar] [CrossRef]
- Chen, S.; Yan, Y.; Gong, W. A simple lattice Boltzmann model for conjugate heat transfer research. International Journal of Heat and Mass Transfer 2017, 107, 862–870. [Google Scholar] [CrossRef]
- Hosseini, S.; Darabiha, N.; Thévenin, D. Lattice Boltzmann advection-diffusion model for conjugate heat transfer in heterogeneous media. International Journal of Heat and Mass Transfer 2019, 132, 906–919. [Google Scholar] [CrossRef]
- Kiani-Oshtorjani, M.; Kiani-Oshtorjani, M.; Mikkola, A.; Jalali, P. Conjugate heat transfer in isolated granular clusters with interstitial fluid using lattice Boltzmann method. International Journal of Heat and Mass Transfer 2022, 187, 122539. [Google Scholar] [CrossRef]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E. The Lattice Boltzmann Method: Principles and Practice; Springer International Publishing, 2017.
- Martins, I.T.; Alvariño, P.F.; Cabezas-Gómez, L. Dimensional lattice Boltzmann method for transport phenomena simulation without conversion to lattice units. arXiv preprint arXiv:2302.04120, arXiv:2302.04120 2023.
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Physical Review 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Qian, Y.H.; D’Humieres, D.; Lalleman, P. Lattice BGK Models for Navier-Stokes Equation. Europhysics Letters 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and its Applications in Engineering; World Scientific Publishing Co. Pte. Ltd., 2013.
- Guo, Z.; Zheng, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Physical Review E 2002, 65, 046308. [Google Scholar] [CrossRef] [PubMed]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-uniform Gases, 2nd ed.; Cambridge University Press, 1952.
- Klein, S.A. EES – Engineering Equation Solver Version 11.444 (2022-09-29) 2022. Computer Software.
- Rihab, H.; Moudhaffar, N.; Sassi, B.N.; Patrick, P. Enthalpic lattice Boltzmann formulation for unsteady heat conduction in heterogeneous media. International Journal of Heat and Mass Transfer 2016, 100, 728–736. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons, Inc, 2002.
- Seta, T. Implicit temperature correction-based immersed boundary-thermal lattice Boltzmannmethod for the simulation of natural convection. Physical Review E 2013, 87, 063304. [Google Scholar] [CrossRef]
- Karani, H.; Huber, C. Lattice Boltzmann formulation for conjugate heat transfer in heterogeneous media. Phys. Rev. E 2015, 91, 023304–10. [Google Scholar] [CrossRef]
- Chai, Z.; Zhao, T.S. Nonequilibrium scheme for computing the flux of the convection-diffusion equation in theframework of the lattice Boltzmann method. Phys. Rev. E 2014, 90, 013305. [Google Scholar] [CrossRef]
- Sun, Y.; Wichman, I.S. On transient heat conduction in a one-dimensional composite slab. International Journal of Heat and Mass Transfer 2004, 47, 1555–1559. [Google Scholar] [CrossRef]
- Cheikh, N.B.; Beya, B.B.; Lili, T. Influence of thermal boundary conditions on natural convection in a square enclosure partially heated from below. International communications in heat and mass transfer 2007, 34, 369–379. [Google Scholar] [CrossRef]
- Martins, I.T.; Matsuda, V.A.; Cabezas-Gómez, L. A new Neumann boundary condition scheme for the thermal lattice Boltzmann method. Preprint submited to the Journal: International Communications in Heat and Mass Transfer in 2023.
- Moreira, D.C.; Nascimento, V.; Ribatski, G.; Kandlikar, S. Combining liquid inertia and evaporation momentum forces to achieve flow boiling inversion and performance enhancement in asymmetric Dual V-groove microchannels. International Journal of Heat and Mass Transfer 2022, 194, 123009. [Google Scholar] [CrossRef]
- Kakac, S.; Bergles, A.; Mayinger, F.; Yuncu, H. Heat transfer enhancement of heat exchangers. Drying Technology 2000, 18, 837–838. [Google Scholar] [CrossRef]
- Lienhard, I.V.; Lienhard, V.J.H. A Heat Transfer Textbook, 5th ed.; Phlogiston Press: Cambridge, MA, 2020. [Google Scholar]
| Reference Nusselt Number : | ||
| [m] | Errors [%] | |
| 0 | 30 | 45 | 60 | 0 | 30 | 45 | 60 | 0 | 30 | 45 | 60 | 0 | 30 | 45 | 60 | 0 | 30 | 45 | 60 | |
| 1.03 | 0.94 | 0.84 | 0.8 | 1.03 | 0.94 | 0.84 | 0.8 | 1.86 | 1.74 | 1.55 | 1.43 | 2.75 | 2.56 | 2.28 | 2.1 | 3.04 | 2.84 | 2.52 | 2.32 | |
| 3.14 | 3.01 | 2.89 | 2.63 | 6.36 | 6.1 | 5.86 | 5.33 | 23.29 | 23.0 | 21.97 | 19.41 | 52.46 | 51.86 | 49.4 | 43.75 | 68.25 | 67.46 | 64.25 | 56.83 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





