Adaptive Hybrid Consensus Engine for V2X Blockchain: Real-Time Entropy-Driven Control for High Energy Efficiency and Sub-100 ms Latency

1. Introduction

Vehicular Ad Hoc Networks (VANETs) enable time-critical vehicle-to-vehicle and vehicle-to-infrastructure communication to enhance road safety, optimize traffic flows, and support cooperative services [1,2]. However, high mobility, rapidly changing topologies, intermittent connectivity, and short-lived communication windows make integrity, availability, and timely agreement difficult to achieve in practice [3,4]. In such environments, the core systems problem is not merely choosing a consensus algorithm but designing governance: deciding when and how strongly to validate and commit information under strict V2X timeliness constraints and mobility-driven fragmentation.

Blockchain-style ledgers have been proposed to improve auditability, integrity, and coordination in VANETs, yet existing approaches typically emphasize isolated objectives: consensus performance under fixed parameters [5,6], entropy-inspired indicators without closed-loop control [7], or single-algorithm evaluations under restricted conditions [8]. What remains missing is a unified operational framework that (i) makes injection–validation dynamics explicit under deadline constraints, (ii) measures spatial dispersion in real time (a key driver of partitions, forks, and coherence loss), and (iii) adapts consensus regime and validation rigor to instantaneous disorder rather than relying on fixed-parameter baselines.

• Ideal Information Cycle (High-Level Intuition)

We model VANET ledger governance as a control loop with two antagonistic legs: (i) message/transaction injection that increases informational disorder, and (ii) consensus validation that consumes resources to compress disorder and improve an operational Quality-of-Information (QoI) proxy. In our notation, injection tends to increase S (informational entropy) and is exacerbated by topology fragmentation captured by $H_{\mathrm{spatial}}$ (spatial entropy), whereas validation is the “work” leg that reduces effective disorder (rejecting stale/invalid microstates) and stabilizes convergence under deadlines. 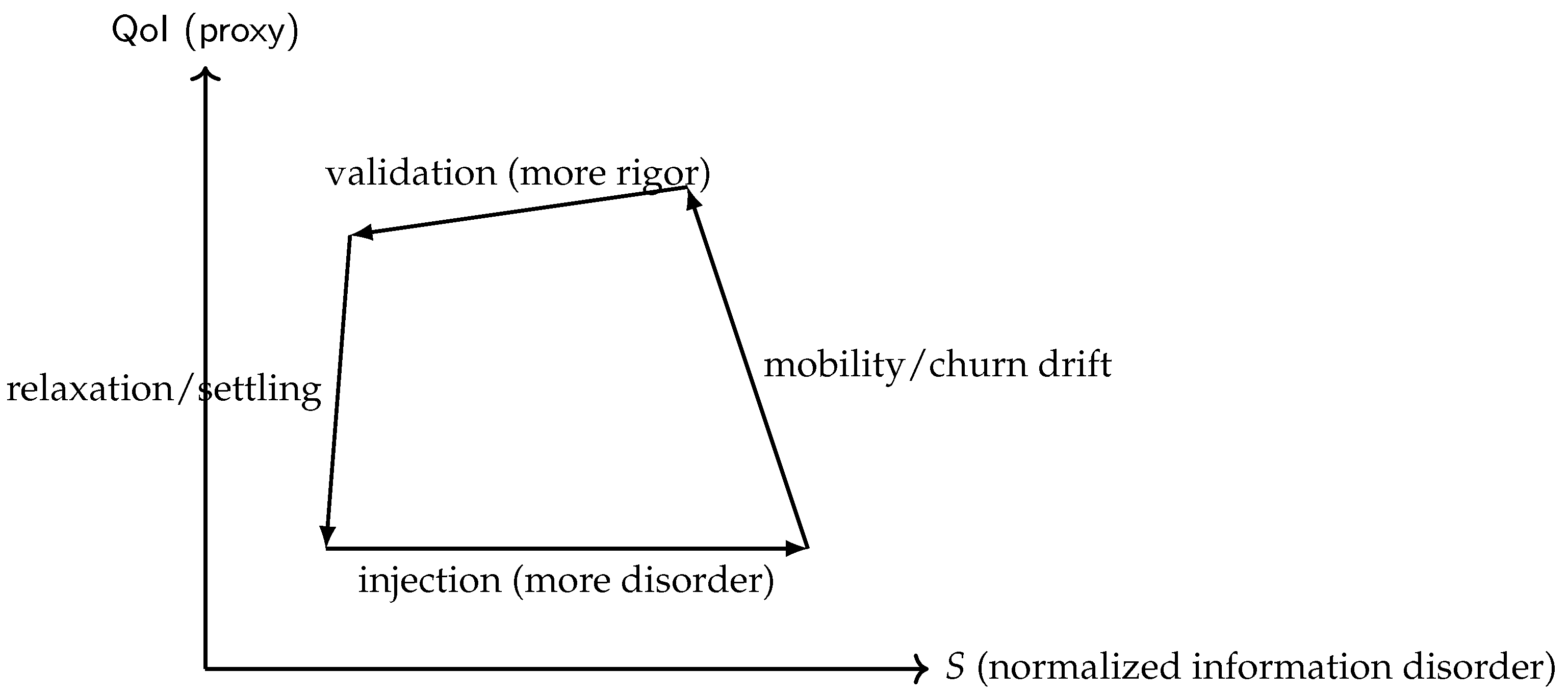The Ideal Information Cycle (Figure 1) is therefore used strictly as an operational governance abstraction that motivates the monotonicity/stability constraints imposed during policy-map calibration, rather than as a claim of physical thermodynamic equivalence.

• Proposed Framework

We introduce two complementary constructs: the Ideal Information Cycle and the VANET Engine. The cycle is an operational abstraction of injection (disorder growth) and validation (disorder compression) under V2X deadlines. Building on it, the VANET Engine is a decentralized, cluster-local control loop (e.g., per intersection/segment/connected subgraph) that monitors normalized Shannon entropies: informational entropy S over active transactions and spatial entropy $H_{\mathrm{spatial}}$ over occupancy bins (both on $[0,1]$ by normalization to their maxima). The Engine adapts (a) the consensus mode (PoW vs. signature/quorum-based modes such as PoS/FBA) and (b) key rigor parameters via calibrated policy maps. Governance is cast as a constrained operational objective trading per-block resource expenditure (radio + cryptography) against a QoI proxy derived from delay/error tiers, under timeliness and ledger-coherence pressure (formal statement in Section 3.6.8). Cryptographic cost is made explicitly traceable through operation counts, $E_{\mathrm{crypto}}=e_h{n}_{\mathrm{hash}}+e_{\mathrm{sig}}{n}_{\mathrm{sig}}.$

• Scope & Security Envelope

Our claims are limited to operational security and performance for V2X-oriented ledgers under mobility and churn, with full PHY/MAC fidelity up to $N\le 100$ vehicles. We do not claim physical equivalence between thermodynamic and informational quantities; entropies are used strictly as measurable governance signals. Moreover, PoW targets are calibrated to be latency-feasible (to respect freshness constraints) and therefore do not provide cryptocurrency-grade majority-hash security in open permissionless settings. Security implications of the latency-feasible regimes, mode transitions, and entropy manipulation are addressed explicitly in Section 4.

• Scope and Claims (Operational, Not Thermodynamic)

We do not claim physical equivalence between thermodynamic variables and network measurements. Entropy is used strictly as an operational governance signal for real-time adaptation. Our evaluation therefore focuses on measurable VANET objectives: agreement latency, per-block energy, throughput, orphan/fork rates, finality, and ledger coherence under mobility and churn. Furthermore, signature/quorum-based modes (PoS/DPoS/FBA) are interpreted in a permissioned/consortium sense (validator sets and quorum slices are configured), consistent with realistic V2X deployments involving RSUs and credentialing. PoW, when used, operates under latency-feasible targets required by V2X timeliness envelopes; it is not presented as cryptocurrency-grade Nakamoto security (see Section 4).

• From Design Objective to Implementable Policy

Governance is expressed as a constrained objective that trades per-block resource expenditure (radio + cryptography) against the QoI proxy, subject to latency and ledger-coherence constraints (formalized in Section 3.6.8). To implement this objective, the Engine applies adaptive maps

$$D=g(S,H_{\mathrm{spatial}}),T=f(S,H_{\mathrm{spatial}}),$$

where D denotes the PoW target register on a 256-bit scale (dimensionless; smaller implies harder PoW) and T denotes a dimensionless stake/quorum rigor threshold anchored by $T_0$. We instantiate g and f via constrained policy approximation: a function-class search with 5-fold cross-validation on simulation traces (Section 3.6.5), subject to stability constraints that reflect the control objective, namely (i) a non-decreasing envelope in S (stronger validation as informational disorder increases) and (ii) a Lipschitz-bounded response in $H_{\mathrm{spatial}}$ to avoid unstable reactions under mobility. Low-order Fourier structure in $H_{\mathrm{spatial}}$ is included only when it improves out-of-sample fit, capturing empirically observed non-monotone sensitivity (e.g., clustering versus fragmentation). All coefficients, base scales $(D_0,T_0)$, and diagnostics are reported once for reproducibility.

• Traceable Resource Accounting

Cryptographic cost is made explicitly traceable through operation counts,

$$E_{\mathrm{crypto}}=e_h{n}_{\mathrm{hash}}+e_{\mathrm{sig}}{n}_{\mathrm{sig}},$$

so the reported cryptographic energy directly links to PoW hashing effort and/or signature/quorum operations under the selected regime. Total per-block energy combines NS-3 radio models with this analytical cryptographic term (Section 5.7); no host-side power tools are used in reported figures or statistics.

• Research Hypotheses

To match the empirical tests in Section 6, we evaluate the following hypotheses using matched-seed contrasts:

H1: 

Under PoW, cryptographic energy per block increases with informational entropy S, whereas signature/quorum-based modes (PoS/DPoS/FBA) are comparatively weakly coupled to S in the latency-feasible regime.

H2: 

A consensus-first (CF) policy (validate immediately when $S>S_{\mathrm{th}}$) reduces agreement latency and packet overhead and increases throughput relative to broadcast-first (BF) baselines with dwell $\tau$.

H3: 

Increasing spatial disorder ($H_{\mathrm{spatial}}$) degrades timeliness and validation accuracy under static settings; the adaptive Engine mitigates this degradation by tightening rigor where dispersion is highest.

H4: 

Increasing mobility (speed v) increases orphan/fork rates and finality under static schemes; the adaptive Engine limits these increases via entropy-driven mode/parameter updates.

H5: 

Under high spatial disorder, the adaptive Engine preserves microstate consistency by reducing ledger divergence (LCA-normalized) relative to static baselines.

• Validation Overview

We implement the Engine [9] across urban and highway settings with 30 matched random seeds per configuration and 600 s runs (unless otherwise stated), evaluating scenarios up to $N\le 100$ vehicles under full PHY/MAC fidelity. We include scheduled partitions (controlled k-cut disconnections) and bounded adversarial stressors (Sybil-like pseudonyms, Byzantine proposers, and eclipse windows) as sensitivity analyses; parameters and definitions are reported where used (Section 5 and Section 3.6.5). Ledger coherence is quantified via an LCA-normalized divergence metric averaged pairwise across nodes; the exact definition used for all curves and statistics is given in Section 3.1.1 (and reiterated in Appendix A for completeness). Reproducibility artifacts (scenario drivers, seed lists, configuration files, and plotting scripts) are released in the public repository snapshot described in Section 5.6.

Main Contributions

• Control-inspired injection–validation abstraction. We introduce an Ideal Information Cycle that provides a consistent operational interpretation of injection, validation effort, and QoI under V2X deadline constraints.
• Entropy-aware, decentralized governance loop. We propose a modular VANET Engine that monitors normalized entropies $(S,H_{\mathrm{spatial}})$ and adapts consensus regimes and rigor parameters in real time.
• Stability-constrained policy maps for hybrid consensus. We instantiate non-linear mappings $D=g(S,H_{\mathrm{spatial}})$ and $T=f(S,H_{\mathrm{spatial}})$ through cross-validated function-class search under monotonicity and Lipschitz stability constraints, avoiding manual tuning and fixed-parameter hybrids.
• Prototype and evaluation under mobility and stressors. We provide an integration and an evaluation with 30 matched seeds and 95% bootstrap confidence intervals, reporting latency, per-block energy, throughput, finality, and coherence dynamics under mobility, partitions, and bounded adversarial stressors.

2. Related Work and Fundamental Principles

This section surveys blockchain–VANET (IoV/V2X) integration under mobility and churn, summarizes consensus choices commonly proposed for vehicular settings, and distills the security/latency pressures that motivate a lightweight governance layer. We then position our use of normalized Shannon entropies as operational observables for closed-loop adaptation. Formal objectives and structural properties are given in Section 3.6.8, and implementation/instrumentation details are in Section 5 and Section 5.5.

2.1. Blockchain in VANETs/IoV: Overview and Limitations

A growing body of work leverages blockchain to support secure data transactions, auditability, and accountability in vehicular and vehicular-IoT settings, often complemented with smart contracts to automate authorization, conditional data sharing, incentives, and compliance workflows across heterogeneous stakeholders (vehicles, RSUs, authorities, service providers). However, surveys and systematizations consistently report that many blockchain-for-IoV proposals optimize a single axis (e.g., security, throughput, or latency) under fixed consensus parameters and relatively stable validator assumptions, which do not hold under VANET churn, mobility-driven partitions, and fast role changes. Consequently, the practical gap is not the availability of blockchain primitives per se, but the lack of a closed-loop governance layer that (i) monitors disorder observables in real time—including spatial dispersion—and (ii) adapts consensus mode and rigor under V2X deadlines with explicit latency/energy accounting. Table 1 summarizes representative directions and highlights limitations most salient for closed-loop (state-driven) governance under mobility and churn.

Overall, the gap is not the absence of blockchain mechanisms per se, but the absence of a closed-loop governance layer that (i) monitors disorder observables in real time (including spatial dispersion) and (ii) adapts consensus mode and rigor under V2X deadlines with explicit latency/energy accounting.

2.2. Consensus Mechanisms for VANETs and Adaptive Baselines

Consensus under VANET dynamics faces a structural tension: stronger integrity mechanisms typically increase coordination and cryptographic work, while mobility degrades quorum formation and block propagation, amplifying forks and delayed finality. Prior studies emphasize that consensus outcomes are parameter-sensitive and regime-dependent (network load, contention, validator availability, and target latency), motivating comparisons at the level of scaling forms and operational envelopes rather than single-point constants. This motivates our design choice to treat consensus selection and rigor as control variables conditioned on measured disorder, rather than as fixed configuration knobs. Since concrete outcomes depend on parameterization, network load, PHY/MAC contention, and target latency, Table 2 reports scaling forms and regime-level considerations (rather than fixed constants). Unless stated otherwise, “energy” below refers to the cryptographic component; radio energy is accounted separately by NS-3 device models and is reported jointly with crypto energy in the expanded comparisons (Section 6.8).

Baseline clarity and naming.

To avoid ambiguity across sections, we use the following terms consistently: (i) Static PoW/PoS refers to single-family consensus with fixed parameters (no state feedback); (ii) Vanilla Hybrid refers to a two-mode hybrid that may switch families but uses fixed thresholds and fixed parameters (no calibration, no stability constraints); (iii) Hybrid Engine refers to the proposed closed-loop controller that adapts both mode and rigor parameters via $g(S,H_{\mathrm{spatial}})$ and $f(S,H_{\mathrm{spatial}})$.

2.3. Security and Latency Constraints in VANETs

VANETs disseminate safety-critical messages (e.g., cooperative awareness and event notifications) over DSRC/802.11p or C-V2X under stringent latency budgets and intermittent connectivity [3,14]. In practice, high-load non-safety traffic must not degrade safety performance, and governance mechanisms must remain robust under contention, link breaks, and component-wise operation [4]. Table 3 structures canonical challenges as governance triggers and the impacts that a control layer must react to.

2.4. Information-Theoretic Principles for Governance (Operational View)

We quantify network disorder using true Shannon entropies as operational observables for closed-loop governance: (i) informational entropy S over the distribution of active transactions across nodes within a sampling window, and (ii) spatial entropy$H_{\mathrm{spatial}}$ over vehicle dispersion across spatial bins/clusters. Both are computed with natural logarithms (nats) over normalized distributions and then reported on $[0,1]$ by division by their respective maxima (e.g., $S^{★}=S/lnK$ and $H^{★}=H_{\mathrm{spatial}}/lnM$ for K active transactions and M spatial bins). For readability, we reuse symbols S and $H_{\mathrm{spatial}}$ for the normalized values in plots and tables; the raw/normalized distinction is made explicit in Section 6 and Appendix A.8. These quantities are dimensionless after normalization and are not equated with thermodynamic entropy; thermodynamic terminology (“cycle”, “work”) is used strictly as an engineering analogy for resource–quality trade-offs. Energy is accounted in Joules via NS-3 radio models plus an analytical cryptographic term (Section 5.5); host-side power tools are not used in reported figures or statistics.

Positioning

Recent literature increasingly explores adaptive and learning-assisted components for vehicular consensus (e.g., RL-guided peer selection and learning-enabled pipelines). These trends motivate a principled and reproducible governance loop that uses explicit, interpretable state observables and reports complete parameter provenance and accounting. The subsequent sections provide our optimization-guided design, the calibrated control maps, and the NS-3 implementation/instrumentation used to produce the reported results.

3. Hypothesis Formulation and Methodology

This work targets secure, low-latency governance in VANETs by combining a control-inspired Ideal Information Cycle—used strictly as an engineering analogy for resource–quality trade-offs—with a modular VANET Engine deployed per geographic cluster. The Engine actively monitors system disorder to adapt the consensus mode and rigor in real time. To minimize redundancy, formal metric definitions are provided in Section 3.1, while symbols are summarized in Table 4.

To operationalize the control loop, we utilize two normalized Shannon entropies (mapped to $[0,1]$) as the primary real-time observables:

(i)

$S\left(t\right)$, representing the entropy of the active transaction microstate distribution; and

(ii)

$H_{\mathrm{spatial}}\left(t\right)$, representing the entropy over spatial occupancy bins.

These observables quantify the disorder that the system must counteract. The resulting governance cycle, where validation rigor balances the injected disorder to maintain Quality-of-Information (QoI), is illustrated in Figure 1.

3.1. Core Metrics, Normalization, and Boundedness

We operate on four observables. Informational and spatial disorder are captured via normalized Shannon entropies in $[0,1]$, while QoI and ledger divergence provide operational performance and coherence signals.

Informational Entropy $S\left(t\right)$

Let $\mathcal{T}\left(t\right)$ be the set of distinct pending transactions at time t and let $c_i\left(t\right)$ be the number of nodes currently holding transaction id $i\in \mathcal{T}\left(t\right)$. Define the normalized copy distribution

$${\tilde{p}}_i\left(t\right)={\displaystyle \frac{c_i\left(t\right)}{{\sum }_{k\in \mathcal{T}\left(t\right)}{c}_k\left(t\right)}},\sum _{i\in \mathcal{T}\left(t\right)}{\tilde{p}}_i\left(t\right)=1,$$

and the bounded Shannon entropy

$$S\left(t\right)={\displaystyle \frac{-{\sum }_{i\in \mathcal{T}\left(t\right)}{\tilde{p}}_i\left(t\right)ln{\tilde{p}}_i\left(t\right)}{ln\left|\mathcal{T}\right(t\left)\right|}}\in [0,1].$$

We apply Laplace smoothing $c_i\leftarrow c_i+\epsilon$ with $\epsilon ={10}^{-6}$ to avoid numerical issues; results are insensitive to $\epsilon$.

We use natural logarithms (nats) and normalize by $ln\left|\mathcal{T}\right(t\left)\right|$ so that $S\left(t\right)\in [0,1]$ by construction. For reviewer traceability, the normalization/boundedness is restated verbatim in Appendix A.8.

Spatial Entropy $H_{\mathrm{spatial}}\left(t\right)$

Partition the area into M spatial bins; let $n_j\left(t\right)$ be the number of vehicles in bin j and $N\left(t\right)={\sum }_{j=1}^M{n}_j\left(t\right)$. With $q_j\left(t\right)=n_j\left(t\right)/N\left(t\right)$,

$$H_{\mathrm{spatial}}\left(t\right)={\displaystyle \frac{-{\sum }_{j=1}^M{q}_j\left(t\right)ln{q}_j\left(t\right)}{lnM}}\in [0,1].$$

Spatial binning uses a fixed M per scenario (Table 8), and normalization by $lnM$ ensures $H_{\mathrm{spatial}}\left(t\right)\in [0,1]$. For reviewer traceability, the normalization/boundedness is restated verbatim in Appendix A.8.

QoI Proxy (Delay and Validity Tiers)

For each transaction $t_i$, we record (i) end-to-end delay $\Delta t_i$ (ms) and (ii) a binary validity indicator ${ϵ}_i\in \{0,1\}$, where ${ϵ}_i=1$ denotes an invalid signature, stale timestamp, or failed format/consistency check. QoI is operationalized through delay/error tiers (Section 3.6.5) and used in candidate-set formation (prioritize small $\Delta t_i$, discard ${ϵ}_i=1$). QoI is an engineering proxy and is not interpreted as a physical quantity.

3.1.1. Ledger-Divergence Metric and Fork/Orphan Detection

Ledger Divergence $D_{\mathrm{ledger}}\left(t\right)$.

For nodes $u,v$ with heads $h_u\left(t\right),h_v\left(t\right)$ at time t, let $lca(h_u,h_v)$ be their lowest common ancestor and $depth(·)$ block depth. We define the pairwise normalized divergence

$${\delta }_{u,v}\left(t\right)={\displaystyle \frac{depth\left(h_u\left(t\right)\right)+depth\left(h_v\left(t\right)\right)-2depth(lca(h_u\left(t\right),h_v\left(t\right)))}{max\{1,depth\left(h_{\mathrm{main}}\left(t\right)\right)\}}},$$

and the instantaneous average

$$D_{\mathrm{ledger}}\left(t\right)={\displaystyle \frac{2}{N(N-1)}}\sum _{u<v}{\delta }_{u,v}\left(t\right).$$

This LCA-normalized form makes $D_{\mathrm{ledger}}\left(t\right)$ comparable across runs with different block production rates and prevents artificial inflation early in the run when chain depth is small.

Fork/Orphan Rate

We report orphan/fork rate O as the fraction of produced blocks that do not lie on the final main chain at simulation end (logged via orphan_flag; see Table 9).

3.1.2. Ledger Divergence $D_{\mathrm{ledger}}\left(t\right)$ (Microstate Coherence)

Let $L_u\left(t\right)$ denote the ordered block sequence (main-chain view) at node u at time t, and let $h_u\left(t\right)=\left|L_u\left(t\right)\right|$ be its height. For any pair of nodes $u\ne v$, define $\mathrm{LCP}(u,v,t)$ as the length of the longest common prefix of $L_u\left(t\right)$ and $L_v\left(t\right)$. We quantify instantaneous pairwise divergence as

$$\delta (u,v,t)=1-{\displaystyle \frac{\mathrm{LCP}(u,v,t)}{max\{1,max(h_u\left(t\right),h_v\left(t\right))\}}},\delta (u,v,t)\in [0,1],$$

and define the network-average ledger divergence by

$$D_{\mathrm{ledger}}\left(t\right)={\displaystyle \frac{2}{N\left(t\right)\left(N\right(t)-1)}}\sum _{u<v}\delta (u,v,t)\in [0,1],$$

where $N\left(t\right)$ is the number of active nodes at time t.

Interpretation and Edge Cases

$D_{\mathrm{ledger}}\left(t\right)=0$ implies identical prefixes across all nodes (perfect coherence), while larger values indicate greater disagreement in committed history. The $max\{1,·\}$ safeguard avoids division by zero during initialization (empty ledgers). In all figures and statistical analyses, “$D_{\mathrm{ledger}}\left(t\right)$” refers to this LCP-normalized definition.

This is the quantity labeled $D_{\mathrm{ledger}}\left(t\right)$ in all figures and statistical analyses and matches the definition in Section 3.1.1.

3.2. Ledger-Divergence Metric and Fork/Orphan Detection

Purpose

We quantify microstate consistency across nodes through an instantaneous, bounded divergence metric that captures how far node-local ledgers have drifted due to mobility, partitions, and competing commits. This complements the end-of-run orphan/fork rate by providing a time-resolved coherence signal used in Figure 9 and related analyses.

Ledger Representation

Let $L_u\left(t\right)=\left[B_0,B_1,\dots ,B_{h_u\left(t\right)}\right]$ denote the ordered block sequence (from genesis $B_0$ to the current head) at node u at time t, where $h_u\left(t\right)$ is the node’s current chain height.

Longest Common Prefix and Pairwise Divergence

For two nodes $u\ne v$, let $\mathrm{LCP}(u,v,t)$ be the length (in blocks) of their longest common prefix at time t, i.e., the maximum ℓ such that

$$B_k^{\left(u\right)}\left(t\right)=B_k^{\left(v\right)}\left(t\right)\mathrm{for}\mathrm{all}k\in \{0,1,\dots ,\ell -1\}.$$

We define the pairwise, height-normalized divergence

$$\delta (u,v,t)=1-{\displaystyle \frac{\mathrm{LCP}(u,v,t)}{max\{h_u\left(t\right),h_v\left(t\right)\}+1}}\in [0,1],$$

where the $+1$ ensures that the normalization is in blocks (including genesis) and avoids division-by-zero when heights are zero.

Network-Average Divergence

With $N\left(t\right)$ active nodes at time t, the instantaneous ledger divergence is

$$D_{\mathrm{ledger}}\left(t\right)={\displaystyle \frac{2}{N\left(t\right)\left(N\left(t\right)-1\right)}}\sum _{u<v}\delta (u,v,t)\in [0,1].$$

A value near 0 indicates that most nodes share long common prefixes (high coherence), while larger values indicate persistent forks/partitions or delayed convergence.

Time Aggregation Used in Plots

For seed-wise summaries, we compute ${\overline{D}}_{\mathrm{ledger}}$ as the discrete-time average over the evaluation window (after warm-up):

$${\overline{D}}_{\mathrm{ledger}}={\displaystyle \frac{1}{\left|\mathcal{W}\right|}}\sum _{t\in \mathcal{W}}{D}_{\mathrm{ledger}}\left(t\right),$$

where $\mathcal{W}$ contains the sampled timestamps (default: 1 s sampling and key events, aligned with Section 3.4). For Figure 9, we bin each seed’s samples by $H_{\mathrm{spatial}}$ (equal-width bins) and report the mean across seeds with 95% BCa bootstrap confidence intervals.

Fork/Orphan Rate (End-of-Run)

We report orphan/fork rate O as the fraction of produced blocks that do not lie on the final main chain at simulation end:

$$O={\displaystyle \frac{|{\mathcal{B}}_{\mathrm{orphan}}|}{|{\mathcal{B}}_{\mathrm{total}}|}},$$

where ${\mathcal{B}}_{\mathrm{orphan}}$ are blocks not on the selected main chain at $t_{\mathrm{end}}$. This metric is computed from the logged orphan_flag (Section 5.5).

Computation from Logs (Reproducibility)

We reconstruct $L_u\left(t\right)$ from per-event logs by storing each committed block hash and its parent pointer for every node. The $\mathrm{LCP}(u,v,t)$ is then obtained by walking back from the heads to the first common ancestor and translating that depth to a prefix length; since blockchain histories form rooted trees, this is equivalent to the depth of the last common block plus one (including genesis). All plots and statistics use this single definition.

3.3. Nomenclature

A compact list of symbols is provided in Table 4 to avoid re-defining variables throughout the Methods.

3.4. The VANET Engine: Entropy-Driven Governance

Sampling, smoothing, and triggers.

Every $\Delta T$ (default 1 s), each cluster-local Engine samples $S\left(t\right)$ and $H_{\mathrm{spatial}}\left(t\right)$ and applies exponential smoothing (EMA) to avoid thrashing around thresholds (Appendix A, Algorithm A1). If either smoothed observable exceeds its threshold ($S_{\mathrm{th}}$ or $H_{\mathrm{th}}$), the Engine increases validation rigor (e.g., selecting a signature/quorum-based mode and tightening parameters); otherwise it relaxes rigor. Thresholds and $\Delta T$ are selected and validated as described in Section 3.6.5.

Adaptive Mappings (Policy Approximation)

For implementability, consensus rigor is instantiated via calibrated maps:

$$D\leftarrow g(S,H_{\mathrm{spatial}}),\Theta \leftarrow f(S,H_{\mathrm{spatial}}),$$

where D is the PoW target and $\Theta$ denotes the mode-specific rigor parameter (e.g., stake/quorum threshold, quorum-slice requirements). The maps are selected by cross-validated function-class search under monotonicity and stability constraints (Section 3.6.5), consistent with the constrained optimization objective in Section 3.6.8.

Mode Selection

$$\mathsf{mode}=\left\{\begin{array}{cc}\mathrm{Signature}/\mathrm{quorum}-\mathrm{based}\left(\mathrm{rigorous}\right)\hfill & \mathrm{if}S>S_{\mathrm{th}}\mathrm{or}{H}_{\mathrm{spatial}}>H_{\mathrm{th}},\hfill \\ \mathrm{PoW}(\mathrm{lower}\mathrm{coordination}\cos \mathrm{t})\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Candidate sets prioritize fresher transactions (small $\Delta t_i$) and discard invalid/stale ones (${ϵ}_i=1$) before consensus.

Algorithm 1 VANET Engine (cluster-local control loop)

1: Repeat every $\Delta T$: sample $S,H_{\mathrm{spatial}}$; compute $D\leftarrow g(S,H_{\mathrm{spatial}})$ and $\Theta \leftarrow f(S,H_{\mathrm{spatial}})$ 2: if $S>S_{\mathrm{th}}$ or $H_{\mathrm{spatial}}>H_{\mathrm{th}}$ then 3:     mode ← signature/quorum-based 4: else 5:     mode ← PoW 6: end if 7: Build a QoI-aware candidate set; execute the selected consensus; append block 8: Purge invalid transactions; update local state; loop

3.5. Hypotheses

We test the following hypotheses using matched-seed contrasts across identical mobility/load conditions.

H₁ (Energy vs. informational disorder). As S increases, PoW crypto energy per block increases steeply through the expected hash trials, while signature/quorum-based modes scale primarily with the number of signature/verification operations. An entropy-driven controller therefore reduces total energy under high S by down-selecting PoW and/or tightening rigor efficiently.

H₂ (Consensus-first under high disorder). Triggering validation when $S>S_{\mathrm{th}}$ (Consensus-First) reduces end-to-end agreement latency and packet overhead compared with dwell-based broadcast-first policies.

H₃ (Spatial disorder effects). Increasing spatial disorder ($H_{\mathrm{spatial}}$) degrades propagation and quorum stability, increasing latency and reducing accuracy/coherence in static schemes; localized adaptation mitigates these effects.

H₄ (Mobility, orphans, and finality). Under higher mobility, static schemes experience increased orphaning and delayed finality, whereas entropy-adaptive mode/rigor tuning limits orphan rate O and finality F.

H₅ (Ledger coherence under extreme disorder). At high S and high $H_{\mathrm{spatial}}$, the Engine maintains lower $D_{\mathrm{ledger}}\left(t\right)$ (and thus higher coherence) than non-adaptive schemes.

3.6. Detailed Methodology

3.6.1. Simulation environment and implementation

All reported experiments use NS-3.35 [9]. The baseline PHY/MAC stack is IEEE 802.11p/WAVE (WaveHelper); additional C-V2X experiments, when reported, use an explicitly versioned integration layer described in Section 5 (to ensure reproducibility across NS-3 releases). 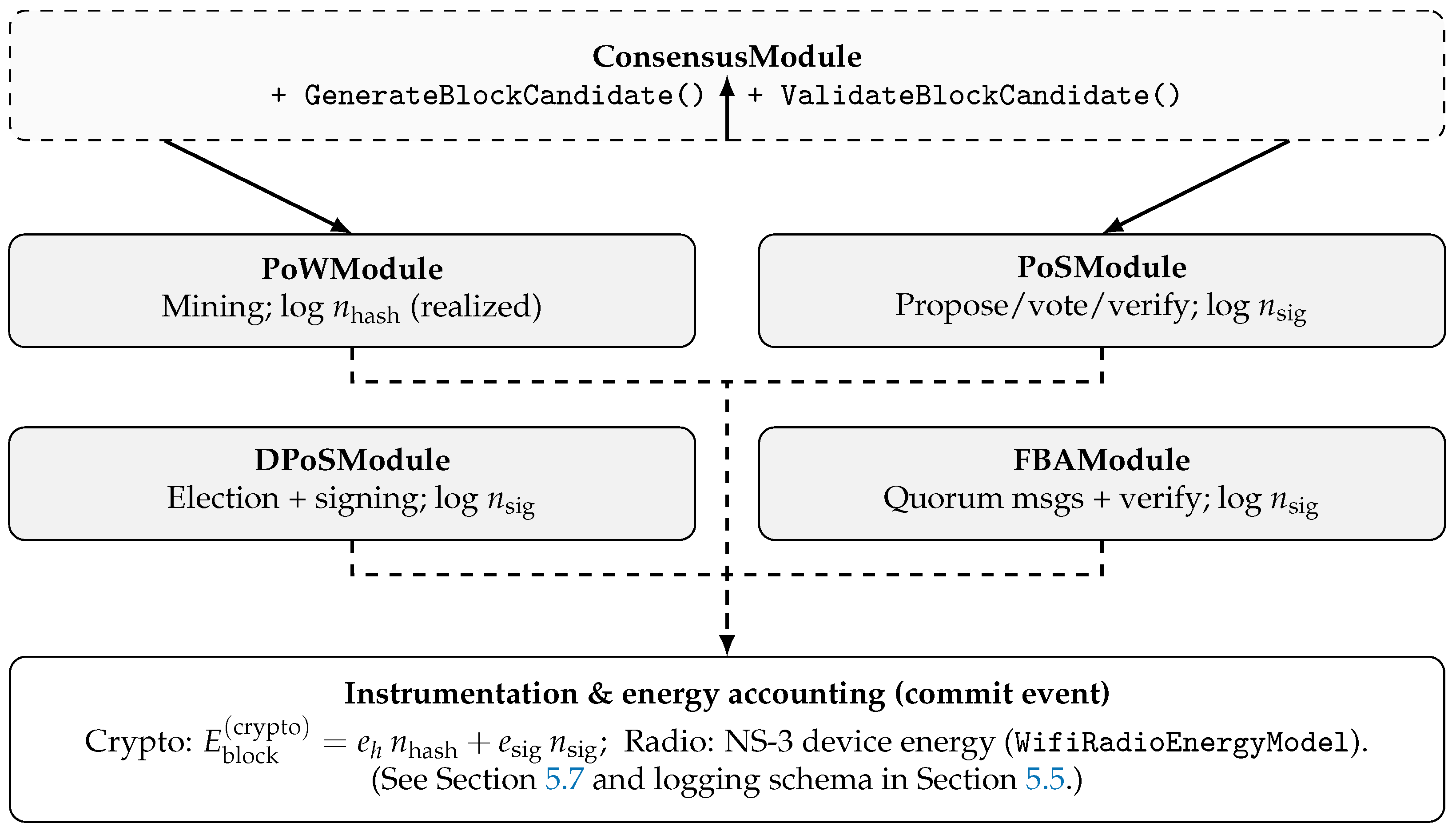The Engine runs as an application-layer process interfacing with packet sockets and a metrics service; consensus routines are pluggable via a common ConsensusModule interface (Appendix A). Radio energy is modeled with BasicEnergySource and WifiRadioEnergyModel. Cryptographic energy is added analytically using per-hash and per-signature constants (Table 5). Metrics are sampled at 1 s and on key events (block commit, mode switch) and aggregated per run.

Forks/Orphans and Finality (Operational Definitions)

A block is marked orphaned if it is not on the final main chain at simulation end; the orphan rate O is the fraction of orphaned blocks over produced blocks (logging flag orphan_flag=1). Finality F is measured as time-to-stable-commit: for PoW, the time until the block is buried by k subsequent blocks (default k reported alongside results); for signature/quorum-based modes, the time from proposal to reaching the required quorum/commit threshold. Unless otherwise stated, metrics are computed after a 60 s warm-up (window: 60–600 s).

3.6.2. Mobility and Dynamic Conditions

We generate mobility traces with BonnMotion [20] for: (i) an urban grid (1 km×1 km, 50–100 vehicles, 5–15 m/s, pause 0–3 s) and (ii) a highway (5 km, 100–200 vehicles, 15–30 m/s, pause 0–1 s). Dynamics include churn (join/leave), controlled partitions, and bursty transaction loads. Each configuration runs for 600 s with 30 matched seeds; 95% confidence intervals are computed via bootstrap (Section 3.6.7).

3.6.3. Partition and Adversarial Stressors (Sensitivity Analysis)

We include scheduled partitions and adversarial stressors to assess sensitivity and failure modes. Parameters are fully disclosed for reproducibility. The emphasized stressor results are reported in Section 6, while extended cases and implementation hooks are documented in Appendix A and Section 5.9.

3.6.4. Experimental Metrics

We record agreement latency (mean; 95% CI), per-block energy $E_{\mathrm{block}}$ (J; radio+crypto), throughput (tx/s), orphan rate O (%), finality F (ms), and ledger divergence $D_{\mathrm{ledger}}\left(t\right)$. Metrics are computed per run and aggregated across matched seeds.

3.6.5. Parameterization and Calibration

Energy constants and hardware mapping.

Per-hash cost $e_h=5$ nJ/hash and per-signature cost $e_{\mathrm{sig}}=1\mu$J/op (Table 5) represent software cryptography on embedded OBU-class hardware. We sweep $e_h\in [1,10]$ nJ and $e_{\mathrm{sig}}\in [0.5,2]\mu$J in sensitivity checks; qualitative trends remain unchanged. Host-level measurements are not used in reported energy curves or statistics.

PoW Energy Accounting (Difficulty-Traceable)

Let $D=g(S,H_{\mathrm{spatial}})$ denote the PoW target (smaller ⇒ harder). Under uniform hashes, the expected trials satisfy $\mathbb{E}\left[n_{\mathrm{hash}}\right]\approx 2^{256}/D$. Define effective difficulty bits

$$d_{\mathrm{eff}}={log}_2\left({\displaystyle \frac{2^{256}}{D}}\right)=256-{log}_{2}D,E_{\mathrm{PoW}}\approx e_h{2}^{d_{\mathrm{eff}}}.$$

Targets are calibrated to meet V2X-oriented latency constraints in the simulated environment; security implications of the chosen regimes are discussed in Section 4.

Targets are calibrated for timeliness (V2X-oriented confirmation/finality latency constraints) in the simulated NS-3 environment and are not intended to match cryptocurrency-grade PoW hardness. The security implications of these latency-feasible target regimes, under the stated threat model, are discussed in Section 4.

Trigger Thresholds

We select $S_{\mathrm{th}}=0.50$ and $H_{\mathrm{th}}=0.60$ via a grid scan over ${[0,1]}^2$ on a training subset of seeds, using knee detection where latency increases nonlinearly and delivery drops below 95%. Robustness is evaluated on held-out seeds; $\pm 0.05$ perturbations yield $<5\%$ variation in headline metrics.

Policy-Map Selection

To instantiate g and f, we perform a constrained function-class search with 5-fold cross-validation over mobility and load profiles. Candidate families include low-order polynomial, exponential/log, and spline bases; Fourier terms in $H_{\mathrm{spatial}}$ are admitted only if they improve out-of-sample fit without violating stability constraints. We enforce: (i) a non-increasing PoW target with S (i.e., higher disorder never makes PoW easier), (ii) bounded sensitivity to $H_{\mathrm{spatial}}$ via a Lipschitz cap to prevent thrashing, and (iii) positivity/feasibility of control registers $(D,T)$ within $(D_{min},D_{max})$ and $(T_{min},T_{max})$. The final fitted coefficients, goodness-of-fit, and stability checks are reported for reproducibility in Section 3.6.6 and Appendix B.

3.6.6. Fitted Policy Maps and Coefficients

Final Map Forms (Reported)

We report the final closed-form maps used by the Engine. Both maps are bounded by design to avoid unstable excursions:

$$D\leftarrow \mathrm{Clamp}\left(g(S,H_{\mathrm{spatial}}),D_{min},D_{max}\right),T\leftarrow \mathrm{Clamp}\left(f(S,H_{\mathrm{spatial}}),T_{min},T_{max}\right).$$

PoW target map $g(S,H_{\mathrm{spatial}})$.

We model the PoW target on a log-scale for numerical stability:

$${log}_{2}D={\beta }_0+{\beta }_{S}S+{\beta }_H{H}_{\mathrm{spatial}}+{\beta }_{SH}S{H}_{\mathrm{spatial}}+{\beta }_{H2}{H}_{\mathrm{spatial}}^2+{\beta }_{sin}sin\left(2\pi H_{\mathrm{spatial}}\right)+{\beta }_{cos}cos\left(2\pi H_{\mathrm{spatial}}\right),$$

and set $g(S,H_{\mathrm{spatial}})=2^{{log}_{2}D}$. If Fourier terms are not selected, we set ${\beta }_{sin}={\beta }_{cos}=0$.

Stake/quorum rigor map $f(S,H_{\mathrm{spatial}})$.

We model the rigor register as an anchored, dimensionless threshold:

$$T=T_0·\left(1+{\alpha }_{S}S+{\alpha }_H{H}_{\mathrm{spatial}}+{\alpha }_{SH}S{H}_{\mathrm{spatial}}+{\alpha }_{H2}{H}_{\mathrm{spatial}}^2\right),$$

followed by clamping to $[T_{min},T_{max}]$.

Coefficient Reporting

Table 6 presents the fitted coefficients employed in the released artifact. The adversary profiles, capabilities, and parameter ranges for the sensitivity analysis are summarized in Table 7. Furthermore, diagnostics such as fold-wise losses, constraint checks, and sensitivity metrics are reported in Appendix B.

3.6.7. Statistical Procedures

All figures report means over 30 matched seeds with 95% BCa bootstrap confidence intervals (10,000 resamples). Seeds are matched across conditions (blocking by mobility/load), and Holm–Bonferroni correction is applied for multiple pairwise contrasts. For headline comparisons we additionally report paired contrasts across matched seeds (Appendix A).

3.6.8. Theoretical Formulation and Validation Protocol

Operational Free-Governance Potential

We model governance as a control decision taken at discrete times k (period $\Delta T$), based on the observed disorder state $x_k=(S_k,H_k,Q_k)$, where $S_k\in [0,1]$ is normalized informational entropy, $H_k\in [0,1]$ is normalized spatial entropy, and $Q_k\in [0,1]$ is the operational QoI proxy (higher is better) derived from delay/error tiers. The governance action is

$$u_k=\left(m_k,{\theta }_k,{\pi }_k\right),$$

where $m_k\in \{\mathsf{PoW},\mathsf{PoS}/\mathsf{DPoS},\mathsf{FBA}\}$ is the consensus mode, ${\theta }_k=(D_k,T_k)$ are mode-dependent rigor registers (PoW target $D_k$ on a 256-bit scale; stake/quorum threshold $T_k$ in normalized stake units), and ${\pi }_k\in \{\mathsf{CF},\mathsf{BF}\left(\tau \right)\}$ denotes the triggering policy (Consensus-First vs. Broadcast-First dwell $\tau$).

We define a free-governance potential that trades resource cost against QoI under timeliness and coherence pressure:

$$\Phi (u_k\mid x_k)=\mathbb{E}\left[E_{\mathrm{tot}}\left(u_k\right)\right]-\eta \mathbb{E}\left[Q\left(u_k\right)\right]+{\lambda }_L\mathbb{E}\left[{[L\left(u_k\right)-L^{★}]}_{+}\right]+{\lambda }_D\mathbb{E}\left[{[D_{\mathrm{ledger}}\left(u_k\right)-D^{★}]}_{+}\right]+{\lambda }_O\mathbb{E}\left[{[O\left(u_k\right)-O^{★}]}_{+}\right],$$

(1)

where ${\left[z\right]}_{+}=max\{z,0\}$, L is agreement/commit latency, $D_{\mathrm{ledger}}$ is the LCA/LCP-normalized divergence used throughout the paper, O is orphan/fork rate, and $(L^{★},D^{★},O^{★})$ define the operational envelope for V2X timeliness and coherence.

Traceable energy model.

The total per-block energy decomposes into radio plus analytical crypto cost:

$$E_{\mathrm{tot}}=E_{\mathrm{radio}}+E_{\mathrm{crypto}},E_{\mathrm{crypto}}=e_h{n}_{\mathrm{hash}}+e_{\mathrm{sig}}{n}_{\mathrm{sig}},$$

(2)

where $E_{\mathrm{radio}}$ is obtained from NS-3 device energy models and $(e_h,e_{\mathrm{sig}})$ are fixed per-operation constants (Table 5). PoW logs realized $n_{\mathrm{hash}}$ per committed block; signature/quorum modes log $n_{\mathrm{sig}}$ (proposal+vote/endorsement+verification operations).

Constraints and stability requirements.

Governance choices are constrained to avoid unstable or unsafe control behavior:

$$\begin{array}{cc}\hfill \left(\mathbf{C}\mathbf{1}\right)\mathbf{Bounded}\mathbf{registers}:& D_k\in [D_{min},D_{max}],T_k\in [T_{min},T_{max}].\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \left(\mathbf{C}\mathbf{2}\right)\mathbf{Timeliness}\mathbf{envelope}:& \mathbb{E}\left[L\left(u_k\right)\right]\le L^{★}(\mathrm{or}\mathrm{penalized}\mathrm{via}(\left)\right).\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \left(\mathbf{C}\mathbf{3}\right)\mathbf{Coherence}\mathbf{envelope}:& \mathbb{E}\left[D_{\mathrm{ledger}}\left(u_k\right)\right]\le D^{★},\mathbb{E}\left[O\left(u_k\right)\right]\le O^{★}(\mathrm{or}\mathrm{penalized}).\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \left(\mathbf{C}\mathbf{4}\right)\mathbf{Monotone}\mathbf{disorder}\mathbf{response}:& {\displaystyle \frac{\partial {log}_{2}D}{\partial S}}\le 0,{\displaystyle \frac{\partial T}{\partial S}}\ge 0.\hfill \\ \hfill \left(\mathbf{C}\mathbf{5}\right)\mathbf{Lipschitz}\mathbf{response}\mathbf{in}H:& \left|{log}_{2}D(S,H_1)-{log}_{2}D(S,H_2)\right|\le L_D|H_1-H_2|,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & \left|T(S,H_1)-T(S,H_2)\right|\le L_T|H_1-H_2|.\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \left(\mathbf{C}\mathbf{6}\right)\mathbf{Anti}-\mathbf{thrashing}\mathbf{switching}:& \mathrm{mode}\mathrm{changes}\mathrm{apply}\mathrm{hysteresis}\mathrm{and}\mathrm{a}\mathrm{minimum}\mathrm{dwell}\mathrm{time}{\tau }_{min}.\hfill \end{array}$$

(8)

(C4) formalizes the design principle that higher transaction disorder should not lead to weaker validation; (C5)–(C6) ensure control-loop stability under mobility-driven fluctuations.

From Constrained Objective to Implementable Maps

The ideal controller would choose $u_k^{★}=arg{min}_{u_k}\Phi (u_k\mid x_k)$ under (C1)–(C6). Because exact online optimization is impractical in VANET control planes, we implement a compact policy approximation:

$$D_k\leftarrow \mathrm{Clamp}\left(g({\widehat{S}}_k,{\widehat{H}}_k),D_{min},D_{max}\right),T_k\leftarrow \mathrm{Clamp}\left(f({\widehat{S}}_k,{\widehat{H}}_k),T_{min},T_{max}\right),$$

where $({\widehat{S}}_k,{\widehat{H}}_k)$ are EMA-smoothed observables and $(g,f)$ are selected by function-class search with 5-fold cross-validation under explicit enforcement of (C4)–(C6) (Section 3.6.6 and Appendix B).

Proof Sketch (Formal But Concise)

(i) Boundedness and well-posedness. By (C1) and clamping, $(D_k,T_k)$ remain in compact intervals for all k, hence the induced crypto cost in (2) is finite and the control law is well-defined.

(ii) No chattering (control stability). Let $u_k=(m_k,{\theta }_k,{\pi }_k)$ be the decision sequence. EMA smoothing makes $({\widehat{S}}_k,{\widehat{H}}_k)$ a contraction of the raw measurements. Under (C5), ${\theta }_k$ is Lipschitz in $({\widehat{S}}_k,{\widehat{H}}_k)$, so $\parallel {\theta }_{k+1}-{\theta }_k\parallel$ is bounded by a constant times $\parallel ({\widehat{S}}_{k+1},{\widehat{H}}_{k+1})-({\widehat{S}}_k,{\widehat{H}}_k)\parallel$. Together with hysteresis and minimum dwell (C6), the number of mode switches on any finite horizon is finite, preventing oscillations around thresholds.

(iii) Structural monotonicity. The monotone envelope (C4) ensures that increasing disorder S cannot lead to a weaker PoW target (in ${log}_{2}D$) nor a lower signature/quorum rigor T, aligning the implemented policy with the directionality implied by (1) when the latency/coherence penalties dominate in high-disorder windows.

(iv) Validation protocol. We validate the effect of (a) mode adaptation and (b) parameter adaptation by comparing: (1) Adaptive Engine (mode + $(g,f)$), (2) Static PoW (fixed D), (3) Static signature/quorum-based (fixed T), and (4) Vanilla Hybrid (switching with fixed $(D_0,T_0)$; formal definition provided alongside the baselines), under matched seeds and identical mobility/load.

State, Controls, and Observables

At cluster scope, the Engine observes at decision instants t the entropy state $x_t=(S_t,H_t)$, where $S_t$ is informational entropy and $H_t=H_{\mathrm{spatial},t}$ is spatial entropy (both normalized to $[0,1]$ as defined in Section 2.4 and Appendix A). The Engine selects an action $a_t=(m_t,u_t)$ with discrete mode $m_t\in \{\mathrm{PoW},\mathrm{PoS},\mathrm{DPoS},\mathrm{FBA}\}$ and mode-specific control register

$$u_t=\left\{\begin{array}{cc}{D}_t\in [D_{min},D_{max}],\hfill & m_t=\mathrm{PoW}\hfill \\ T_t\in [T_{min},T_{max}],\hfill & m_t\in \{\mathrm{PoS},\mathrm{DPoS}\}\hfill \\ Q_t(\mathrm{slice}\mathrm{choice}/\mathrm{size},\mathrm{bounded}),\hfill & m_t=\mathrm{FBA}\hfill \end{array}\right.$$

where $D_t$ is a 256-bit PoW target (smaller ⇒ harder) and $T_t$ is a dimensionless stake/quorum-rigor register anchored at $T_0$.

Performance Variables and QoI Proxy

Given $(a_t,x_t)$, the simulator yields random outcomes per confirmed block: total energy $E_{\mathrm{block}}^{\left(\mathrm{total}\right)}=E_{\mathrm{block}}^{\left(\mathrm{radio}\right)}+E_{\mathrm{block}}^{\left(\mathrm{crypto}\right)}$, confirmation latency L, validation accuracy $\alpha$ (fraction of valid payloads admitted), orphan/fork indicator, and ledger divergence $D_{\mathrm{ledger}}$ (Section 3.1.1). The QoI proxy $Q\in [0,1]$ is computed from delay and validity tiers (Section 3.6); we use $(1-Q)$ as a penalty for stale/invalid microstates.

Free-Governance Potential (Variational Objective)

We define an operational free-governance potential as an expected-cost functional that trades resource expenditure against QoI under timeliness and coherence constraints:

$$\mathcal{F}(a;x)=\mathbb{E}\left[E_{\mathrm{block}}^{\left(\mathrm{total}\right)}\mid a,x\right]+\mu \mathbb{E}\left[(1-Q)\mid a,x\right]+{\lambda }_L\mathbb{E}\left[{(L-L_{max})}_{+}\mid a,x\right]+{\lambda }_D\mathbb{E}\left[{(D_{\mathrm{ledger}}-D_{max})}_{+}\mid a,x\right],$$

(9)

where ${\left(z\right)}_{+}=max\{z,0\}$ and $(\mu ,{\lambda }_L,{\lambda }_D)\ge 0$ are Lagrange-style penalty weights. The Engine’s myopic control law is the pointwise minimizer

$$a^{★}\left(x\right)=arg\underset{a\in \mathcal{A}}{min}\mathcal{F}(a;x),\mathcal{A}=\left\{\mathrm{bounded}\mathrm{registers}\mathrm{and}\mathrm{enabled}\mathrm{modes}\right\}.$$

(10)

This makes explicit the manuscript’s “governance potential” claim: the Engine is the optimizer of (1) under bounded control registers, with QoI and coherence entering as constraints/penalties (not as thermodynamic conjugates).

A Compact “Proof Sketch” for the Structural Constraints Used in Calibration

The calibration constraints imposed on $g(S,H)$ and $f(S,H)$ (monotone envelope in S and Lipschitz-bounded response in H) follow from mild monotonicity assumptions on the simulator’s risk surfaces.

Assumption A (stress monotonicity). For fixed action a, expected stress increases with disorder:

$${\displaystyle \frac{\partial }{\partial S}}\mathbb{E}[L\mid a,x]\ge 0,{\displaystyle \frac{\partial }{\partial H}}\mathbb{E}[L\mid a,x]\ge 0,{\displaystyle \frac{\partial }{\partial S}}\mathbb{E}[D_{\mathrm{ledger}}\mid a,x]\ge 0,{\displaystyle \frac{\partial }{\partial H}}\mathbb{E}[D_{\mathrm{ledger}}\mid a,x]\ge 0.$$

These inequalities hold empirically in our sweeps (Figure 7 and Figure 9).

Assumption B (rigor reduces coherence risk). Define a scalar rigor $\rho$ that increases with harder PoW targets or stronger quorum/stake requirements, e.g.,

$${\rho }_{\mathrm{PoW}}\left(D\right)=-{log}_{2}D,{\rho }_{\mathrm{PoS}}\left(T\right)=log(T/T_0),$$

and assume $\partial \mathbb{E}[D_{\mathrm{ledger}}\mid a,x]/\partial \rho \le 0$ (higher rigor reduces divergence and orphaning at the cost of higher crypto/message work).

Claim (monotone optimal rigor). Under Assumptions A–B and bounded registers, any minimizer of (10) can be chosen such that the selected rigor is non-decreasing in S:

$$S_1\le S_2\Rightarrow {\rho }^{★}(S_1,H)\le {\rho }^{★}(S_2,H).$$

Sketch. Consider two states $(S_1,H)$ and $(S_2,H)$ with $S_2>S_1$. If a candidate action at $S_2$ uses rigor $\rho$ lower than the optimal rigor at $S_1$, then by Assumption A the constraint-penalty terms in (9) cannot decrease, while the energy/QoI penalties cannot improve enough to compensate once ${(L-L_{max})}_{+}$ or ${(D_{\mathrm{ledger}}-D_{max})}_{+}$ activates. Therefore, in any optimal (or Pareto-minimal) solution, the minimal rigor satisfying the active constraints is non-decreasing in S. This directly motivates the monotone envelope in S imposed during function-class search.

Lipschitz response in H (stability). Since H can fluctuate rapidly under mobility, we additionally impose a bounded sensitivity $|\partial {\rho }^{★}/\partial H|\le K_H$. With EMA smoothing $(\widehat{S},\widehat{H})=\mathrm{EMA}(S,H;\lambda )$ (Appendix A), and a $K_H$-Lipschitz policy, the induced control variation satisfies

$$\parallel {\rho }^{★}({\widehat{S}}_t,{\widehat{H}}_t)-{\rho }^{★}({\widehat{S}}_{t-1},{\widehat{H}}_{t-1})\parallel \le K_H\parallel {\widehat{x}}_t-{\widehat{x}}_{t-1}\parallel ,$$

which prevents threshold thrashing and justifies the stability constraint in calibration.

From the Variational Policy to the Reported Maps g and f

The explicit optimizer (10) is not computed online; instead we approximate $a^{★}\left(x\right)$ with parametric maps: (i) a PoW target map $D=g(S,H)$ and (ii) a stake/quorum rigor map $T=f(S,H)$ (Section 3.6.6). The function-class search with 5-fold cross-validation selects a low-complexity basis that approximates the minimizer of (1) over the sampled mobility/load profiles, subject to the monotonicity and Lipschitz constraints justified above. In other words, the maps are data-fitted approximations of a clearly stated constrained objective, not claims of closed-form thermodynamic laws.

Validation Protocol (Comparators)

Validation compares four policies under identical mobility/load and matched random seeds: (i) Adaptive (Engine) using the fitted $g,f$ and mode selection; (ii) Static PoW with fixed D; (iii) Static signature/quorum-based (PoS/FBA) with fixed T or fixed slices; and (iv) Vanilla Hybrid (fixed mode thresholds and fixed parameters, i.e., no entropy-conditioned tuning). All reported experiments use NS-3.35 with 600 s runs, 30 matched seeds, and BCa bootstrap confidence intervals (Section 3.6.7).

Baseline: Vanilla Hybrid (VH) — Fixed-Threshold, Fixed-Parameter Hybrid

We define Vanilla Hybrid as a non-adaptive switching baseline that uses the same mode-selection rule as the Engine (i.e., the same $(S_{\mathrm{th}},H_{\mathrm{th}})$ triggers), but keeps all rigor parameters fixed. Concretely, it switches between PoW and signature/quorum-based consensus when $S>S_{\mathrm{th}}$ or $H_{\mathrm{spatial}}>H_{\mathrm{th}}$, yet uses constant parameters $(D,T)$ equal to their nominal mid-range values $(D_0,T_0)$ throughout the run. Thus, Vanilla Hybrid isolates the effect of mode switching alone without the adaptive tuning induced by the learned maps $g(·),f(·)$.

To separate the benefit of continuous entropy-conditioned tuning (policy maps $g,f$) from the simpler benefit of mode switching, we define a non-adaptive hybrid baseline, termed Vanilla Hybrid (VH). VH observes the same real-time disorder signals as the Engine, namely informational entropy $S\left(t\right)$ and spatial entropy $H_{\mathrm{spatial}}\left(t\right)$, but it does not use the fitted policy maps $g(·)$ and $f(·)$ and does not retune consensus rigor parameters online.

Formally, VH applies a fixed-threshold switching rule

$${\mathrm{mode}}_{\mathrm{VH}}\left(t\right)=\left\{\begin{array}{cc}\mathrm{PoW},\hfill & \mathrm{if}S\left(t\right)\le S_{\mathrm{th}}\wedge H_{\mathrm{spatial}}\left(t\right)\le H_{\mathrm{th}},\hfill \\ \mathrm{Sig}/\mathrm{Quorum},\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

where $(S_{\mathrm{th}},H_{\mathrm{th}})$ are the same thresholds reported in Table 8 (and used by the Engine). Crucially, the rigor parameters are fixed within each mode:

$$D_{\mathrm{VH}}\left(t\right)\equiv D_0(\mathrm{PoW}\mathrm{target}),T_{\mathrm{VH}}\left(t\right)\equiv T_0(\mathrm{stake}/\mathrm{quorum}\mathrm{rigor}\mathrm{register}).$$

In other words, VH is a two-regime hybrid with static $(D_0,T_0)$ and a binary switching surface in the $(S,H_{\mathrm{spatial}})$ plane; it does not implement the Engine’s smooth adaptation, coefficient-calibrated maps, or stability-constrained continuous control. All other shared mechanisms (transaction validation checks and logging/instrumentation) follow the common implementation described in Section 5.4 and Section 5.5.

4. Security Analysis and Threat Model

Scope & security envelope (what we do and do not claim).

Our objective is operational security for V2X-oriented ledgers: integrity at admission, timeliness under churn, and convergence/coherence within cluster-local connectivity windows. We do not claim cryptocurrency-grade, permissionless Nakamoto security. In particular, PoW targets in our experiments are calibrated to satisfy V2X timeliness constraints (Section 3.6.8); therefore, PoW in this paper must be interpreted as a latency-feasible mechanism rather than a stand-alone defense against sustained majority-hash adversaries.

4.1. Threat Model and Assumptions

We consider a vehicular environment with intermittent connectivity, mobility-driven partitions, and open message injection. Adversarial capabilities include packet injection/replay/delay/drop, bounded Sybil behavior (multiple pseudonyms), bounded Byzantine proposers (equivocation/double-propose), and transient eclipse windows. Our experiments implement bounded stressors (Section 6.7); fully adaptive coalitions with global coordination and learning are out of scope.

We assume a basic cryptographic baseline: transactions and control messages are signed and subject to timestamp/freshness checks; invalid or stale items are labeled (${ϵ}_i=1$) and handled by QoI-aware admission (Section 3.1). Signature/quorum-based modes (PoS/DPoS/FBA) are treated as permissioned/consortium-style modes (validator sets/quorum slices defined by configuration), consistent with V2X deployments where RSUs/authorities or membership services exist.

4.2. Low PoW Difficulty and Explicit 51% Risk (Addressing the Reviewer’s Concern)

Why our PoW Targets Are Intentionally “Easier”.

To meet sub-second (often sub-100 ms) V2X freshness constraints, PoW targets are calibrated so that expected mining/confirmation latency fits the timeliness envelope. This necessarily implies targets that are much easier than cryptocurrency-scale PoW.

Explicit Consequence: A Majority-Hash (“51%”) Adversary Would Be Feasible Under These Targets

Let $\mathbb{E}\left[n_{\mathrm{hash}}\right]=2^{256}/D$ be the expected number of hashes until success (uniform hash assumption). In our calibrated regime, $\mathbb{E}\left[n_{\mathrm{hash}}\right]$ is on the order of ${10}^{11}$ per committed block (Section 7 magnitude sanity check). A modern GPU can reach $\sim {10}^9$ hashes/s for simple hashes; thus, a resourceful adversary could out-mine honest OBUs quickly if PoW were deployed as a permissionless security anchor. Therefore:

• We do not claim PoW-based Sybil/majority resistance comparable to Bitcoin/Ethereum security assumptions.
• PoW in this paper is a best-effort, latency-feasible mode suitable only under a restricted security envelope: (i) credentialed miners, (ii) RSU anchoring/checkpointing, or (iii) limited adversarial exposure.
• In adversarially exposed deployments, PoW should be disabled or strictly constrained, and the Engine should prefer permissioned signature/quorum modes (PoS/FBA) as the security-bearing consensus family.

4.3. Mode Transitions (Addressing Safety Across Switching)

A reviewer concern is whether transitions between modes can introduce double-commit or allow adversaries to exploit weaker regimes. We address this explicitly by enforcing a transition barrier:

• Epoch boundary. A mode is fixed for an epoch of length at least ${\tau }_{min}$ (minimum dwell time), preventing rapid oscillations.
• Commit barrier. Before a switch, nodes finalize the current candidate/commit attempt under the current mode (or time out), then freeze the epoch state (mempool snapshot + last committed header).
• Prefix consistency check. The next epoch starts only from a ledger head that extends the last committed header (no backward reorg beyond the barrier), which bounds reorganization depth across transitions.

Operationally, the barrier ensures that switching does not create ambiguous concurrent commits under multiple modes. In our NS-3 implementation, transition events are logged and included in the divergence/orphan computation (Table 9).

4.4. Entropy Manipulation (Addressing “Can an Attacker Force Mode Selection by Changing S or $H_{\mathrm{spatial}}$?)

A second reviewer concern is whether adversaries can strategically manipulate entropy observables to push the Engine into weaker regimes. We make two explicit points.

(1) The policy is conservative under disorder. The Engine switches away from PoW and increases validation rigor when either S or $H_{\mathrm{spatial}}$ rises above thresholds. Thus, an attacker who inflates disorder observables cannot force the system into a weaker validation regime; the dominant failure mode is instead a DoS-like overhead increase (forcing conservative validation more often), not a security bypass.

(2) Hardening against adversarial entropy inflation. To mitigate entropy-inflation attempts (e.g., Sybil-induced dissemination noise or transaction flooding), the implementation supports:

• Robust entropy estimation: compute S and $H_{\mathrm{spatial}}$ from validated events only (signed, freshness-checked), optionally using trimmed means across cluster reports to limit outlier influence.
• Rate limiting/admission control: cap per-credential transaction injection and per-epoch candidate-set growth, limiting the ability to inflate S through flooding.
• Hysteresis & smoothing: EMA + two-threshold hysteresis reduces the effect of short-lived spikes on mode selection (Section 3.6.8, constraints C5–C6).

These mechanisms bound the impact of entropy manipulation to performance degradation rather than consensus compromise within the stated security envelope.

4.5. What Our Evaluation Secures (and Non-Claims)

Within the stated envelope, we empirically evaluate: (i) integrity at admission via QoI-aware filtering (invalid/stale exclusion), (ii) timeliness improvements under CF vs. BF policies, and (iii) convergence/coherence improvements under partitions/eclipses via reduced divergence and bounded orphaning.

We explicitly do not claim robustness to: (i) sustained majority-hash adversaries in PoW under latency-feasible targets, (ii) fully adaptive collusion that learns and exploits control dynamics globally, or (iii) permissionless cryptoeconomic security without external membership/identity services. For deployments requiring stronger guarantees, we recommend permissioned validator governance (PoS/FBA), RSU anchoring/checkpointing to bound reorg depth, Sybil-resistant admission controls, and eclipse-resistant peer rotation as natural extensions.

5. NS-3 Implementation

We validate the proposed entropy-driven governance loop with a modular NS-3.35 framework [9]. Our implementation encapsulates the cluster-local VANET Engine (metric sampling, mode/rigor selection, and state updates) into a reusable helper (VanetEngineHelper) and a node application (NodeApp). Consensus is pluggable (PoW, PoS, DPoS, FBA) through a unified ConsensusModule interface, and a structured logging pipeline records all observables required to reproduce figures and tables.

Reproducible Run Protocol

All results in Section 6 and Section 7 use a single execution profile: NS-3.35, 600 s per run, 30 matched seeds per configuration, and 95% confidence intervals computed via BCa bootstrap (Section 3.6.7). The exact simulator configuration, command-line flags, and per-event logs are versioned in the public artifact described in Section 5.6; each run stores a run_id and the repository git_commit in the CSV header for traceability.

5.1. General Configuration and Simulation Parameters

We consider two mobility settings with identical communication stacks and Engine sampling policies: an urban grid (1 km×1 km) and a highway segment (5 km). Unless explicitly stated otherwise, the communication stack uses IEEE 802.11p/WAVE via WaveHelper. Experiments involving additional C-V2X/LTE-V2X integrations are reported only when explicitly flagged and are fully versioned in the artifact (to avoid ambiguity across NS-3 releases).

Safety messaging is emulated at the application layer: we generate periodic CAM-like beacons at 10 Hz (100 ms) and DENM-like event-driven alerts, which allows controlled freshness constraints without claiming a full ETSI ITS-G5 stack.

Radio energy is modeled with BasicEnergySource and WifiRadioEnergyModel. Cryptographic energy is added analytically using the per-operation constants in Table 10 (Section 3.6.5). Entropy metrics follow the normalized definitions in Section 3.1. QoI tiers are derived from delay and validity indicators (Section 3.1).

Table 8. NS-3 configuration (aligned with Section 3.6).

Parameter	Value / Description
Simulator / version	NS-3.35 (IEEE 802.11p/WAVE via WaveHelper; other stacks only if explicitly reported and versioned)
Area	Urban: $1\times 1$ km; Highway: 5 km two-lane segment
Vehicles	Urban: 50–100; Highway: 100–200
Mobility	BonnMotion traces [20]; churn (join/leave)
M (spatial bins for $H_{\mathrm{spatial}}$)	Urban: $M=25$ (5×5 grid over 1 km×1 km); Highway: $M=50$ (50 longitudinal bins over 5 km). Configurable via run flags.
$S_{\mathrm{th}}$	$0.50$ – Informational-entropy trigger (knee-selected under V2X latency constraints)
$H_{\mathrm{th}}$	$0.60$ – Spatial-dispersion trigger (knee-selected to prevent divergence spikes)
Speeds	Urban: 5–15 m/s; Highway: 15–30 m/s
Safety messaging	CAM-like periodic beacons: 10 Hz; DENM-like alerts: event-driven
Engine sampling	Every 1 s and on packet reception events
Consensus modes	PoW, PoS, DPoS, FBA (pluggable modules)
Block size	10 tx per block (QoI-aware candidate selection)
Block production trigger	Attempt commit when $|T_k|=$10 or per-mode timeout ${\tau }_{max}$ expires (no fixed $\Delta t_{\mathrm{block}}$)
Energy model	WifiRadioEnergyModel + analytical crypto term
Metrics logged	S, $H_{\mathrm{spatial}}$, QoI tier, consensus latency, orphan flag, finality, $D_{\mathrm{ledger}}\left(t\right)$, run header (seed, knobs, git_commit)
Duration / seeds	600 s per run; 30 seeds; 95% CIs (BCa bootstrap)

Table 8. NS-3 configuration (aligned with Section 3.6).

Parameter	Value / Description
Simulator / version	NS-3.35 (IEEE 802.11p/WAVE via WaveHelper; other stacks only if explicitly reported and versioned)
Area	Urban: $1\times 1$ km; Highway: 5 km two-lane segment
Vehicles	Urban: 50–100; Highway: 100–200
Mobility	BonnMotion traces [20]; churn (join/leave)
M (spatial bins for $H_{\mathrm{spatial}}$)	Urban: $M=25$ (5×5 grid over 1 km×1 km); Highway: $M=50$ (50 longitudinal bins over 5 km). Configurable via run flags.
$S_{\mathrm{th}}$	$0.50$ – Informational-entropy trigger (knee-selected under V2X latency constraints)
$H_{\mathrm{th}}$	$0.60$ – Spatial-dispersion trigger (knee-selected to prevent divergence spikes)
Speeds	Urban: 5–15 m/s; Highway: 15–30 m/s
Safety messaging	CAM-like periodic beacons: 10 Hz; DENM-like alerts: event-driven
Engine sampling	Every 1 s and on packet reception events
Consensus modes	PoW, PoS, DPoS, FBA (pluggable modules)
Block size	10 tx per block (QoI-aware candidate selection)
Block production trigger	Attempt commit when $|T_k|=$10 or per-mode timeout ${\tau }_{max}$ expires (no fixed $\Delta t_{\mathrm{block}}$)
Energy model	WifiRadioEnergyModel + analytical crypto term
Metrics logged	S, $H_{\mathrm{spatial}}$, QoI tier, consensus latency, orphan flag, finality, $D_{\mathrm{ledger}}\left(t\right)$, run header (seed, knobs, git_commit)
Duration / seeds	600 s per run; 30 seeds; 95% CIs (BCa bootstrap)

5.2. VanetEngineHelper and NodeApp Workflow

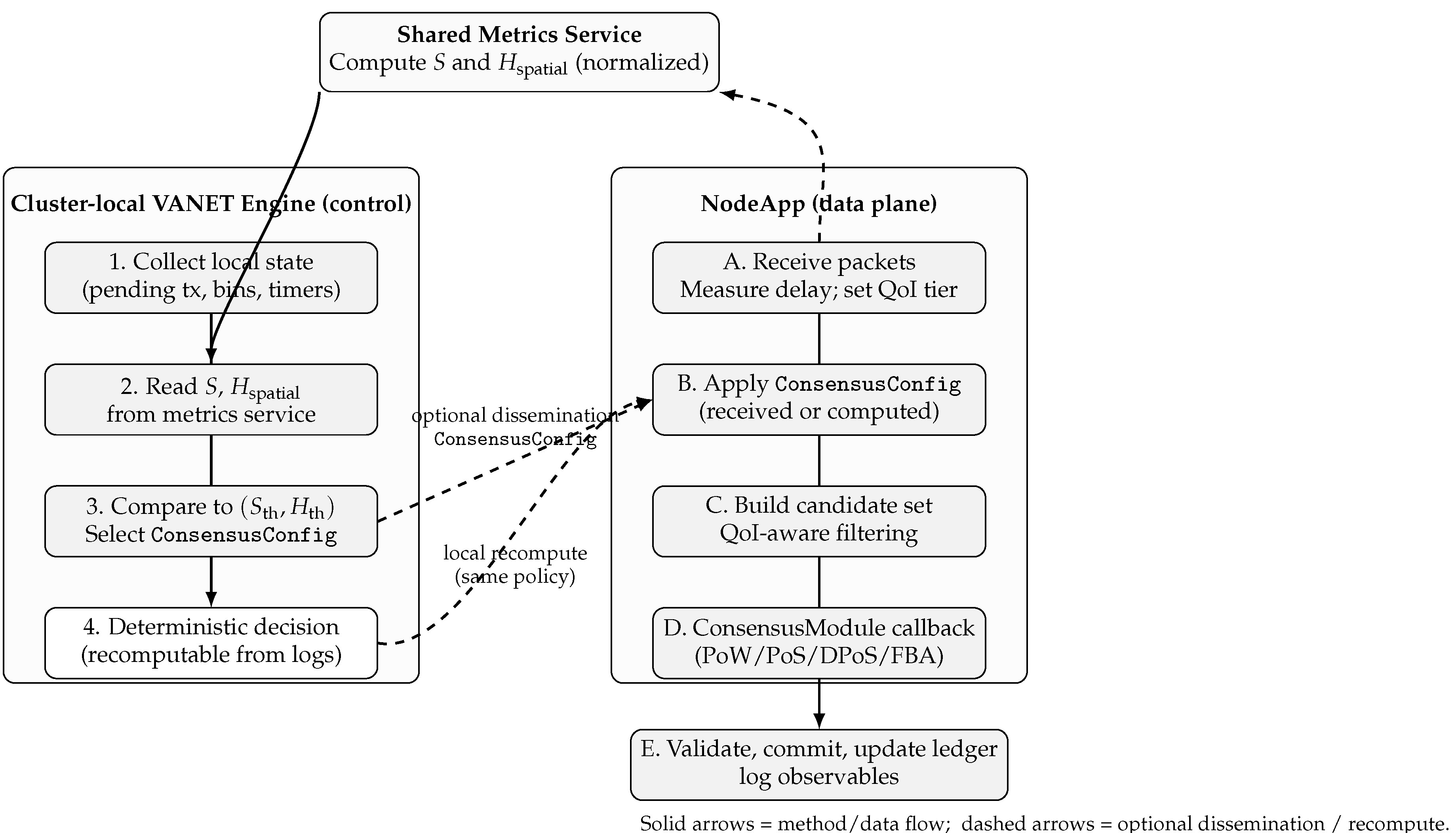
Figure 2 summarizes the helper and application pipelines. Each cluster-local Engine instance retrieves S and $H_{\mathrm{spatial}}$ from a shared metrics service, compares them against $(S_{\mathrm{th}},H_{\mathrm{th}})$, and selects the active ConsensusConfig (mode and rigor parameters). To reduce control-plane chatter, our implementation optionally disseminates the selected configuration to neighboring nodes; however, the policy is deterministic given the logged observables, and any node can compute the same decision locally.

The per-tick computational cost is $O(n+M)$ over local pending transactions and spatial bins; in our settings, this overhead is negligible relative to PHY/MAC processing and consensus execution.

5.3. Partition and Adversary Plugins

We expose explicit Partition and Adversary plugins for controlled stress testing.

Partition modeling (k-cuts, claiming).

Our primary (claiming) partition mechanism is a scheduled k-cut over NetDevice links: during a partition window, selected links are programmatically disabled (Tx/Rx) to separate the network into disconnected components, and then re-enabled to measure recovery. All partition schedules (start time, duration, affected link sets, and realized component sizes) are logged per run. Alternative fading-style partitions (e.g., corridor fades) are used only as sensitivity checks and are explicitly flagged when reported.

Adversary hooks (sensitivity analyses).

Sybil identities, Byzantine proposers, eclipse windows, and corrupted transactions are injected via an AdversaryModule wrapper around NodeApp send/receive paths and consensus callbacks. Stressor parameters (e.g., Sybil ratio ${\rho }_{\mathrm{sybil}}$, Byzantine proposer rate ${\lambda }_{\mathrm{bz}}$, eclipse probability ${\rho }_{\mathrm{ecl}}$, and corruption rules) are logged and summarized in the artifact tables. These stressors are used to characterize robustness and failure modes; headline figures focus on baseline mobility/load unless a stressor is explicitly stated.

5.4. Consensus Modules

All algorithms implement a unified ConsensusModule interface exposing GenerateBlockCandidate() and ValidateBlockCandidate(). For PoW, the mining routine iterates hashes until a valid nonce is found, and we log the realized number of hash attempts $n_{\mathrm{hash}}$ for each committed block. For signature/quorum-based protocols (PoS/DPoS/FBA), we instrument and log the full cryptographic workload—proposal signing, vote/endorsement signing, and all verification operations—aggregated as $n_{\mathrm{sig}}$. Radio energy is obtained directly from the NS-3 device energy models, while cryptographic energy is added as an analytical per-operation term using $(e_h,e_{\mathrm{sig}})$ (Section 5.7). Figure 3 summarizes the resulting class layout and call/callback relations.

5.5. Instrumentation and Logging

All results are derived from per-event logs written in a normalized CSV schema (Table 9). Each row corresponds to a single event (transaction receipt, candidate assembly, consensus step, commit, or fork resolution), enabling seed-wise pairing and reproducible post-processing.

Table 9. Normalized per-event CSV logging schema used for all results (deterministic under fixed seed). Each row corresponds to a key event (tx reception, block proposal, commit, mode switch). The CSV header stores run_id and git_commit for traceability (Section 5.6).

Field	Meaning
run_id	Unique run identifier (stored in header; repeated in post-processing metadata)
git_commit	Repository commit hash (stored in header)
seed	NS-3 RNG seed for matched-seed pairing
time_s	Simulation time (s) at event timestamp
node_id	Node identifier that generated the log entry
cluster_id	Geographic/connected-component cluster identifier
event	Event type: {rx_tx, propose_block, commit_block, mode_switch}
S	Normalized informational entropy $S\left(t\right)\in [0,1]$
H_spatial	Normalized spatial entropy $H_{\mathrm{spatial}}\left(t\right)\in [0,1]$
mode	Active consensus mode: {PoW, PoS, DPoS, FBA}
D_target	PoW target D (256-bit scale; smaller ⇒ harder) if PoW
T_rigor	Stake/quorum threshold T if signature/quorum mode
qoi_tier	QoI tier derived from delay/error bins
tx_delay_ms	Per-transaction delay $\Delta t_i$ (ms) at reception/commit
tx_valid	Validity flag (1 valid, 0 invalid/stale; corresponds to ${ϵ}_i$)
n_hash	Realized number of hashes in PoW for the committed block
n_sig	Number of signature operations (proposal+votes+verify) per block
block_id	Committed/proposed block identifier
orphan_flag	1 if block becomes orphan at end-of-run, else 0
finality_ms	Finality time F (ms) measured per operational definition
lcp_len	Longest common prefix length used to compute $D_{\mathrm{ledger}}\left(t\right)$

Table 9. Normalized per-event CSV logging schema used for all results (deterministic under fixed seed). Each row corresponds to a key event (tx reception, block proposal, commit, mode switch). The CSV header stores run_id and git_commit for traceability (Section 5.6).

Field	Meaning
run_id	Unique run identifier (stored in header; repeated in post-processing metadata)
git_commit	Repository commit hash (stored in header)
seed	NS-3 RNG seed for matched-seed pairing
time_s	Simulation time (s) at event timestamp
node_id	Node identifier that generated the log entry
cluster_id	Geographic/connected-component cluster identifier
event	Event type: {rx_tx, propose_block, commit_block, mode_switch}
S	Normalized informational entropy $S\left(t\right)\in [0,1]$
H_spatial	Normalized spatial entropy $H_{\mathrm{spatial}}\left(t\right)\in [0,1]$
mode	Active consensus mode: {PoW, PoS, DPoS, FBA}
D_target	PoW target D (256-bit scale; smaller ⇒ harder) if PoW
T_rigor	Stake/quorum threshold T if signature/quorum mode
qoi_tier	QoI tier derived from delay/error bins
tx_delay_ms	Per-transaction delay $\Delta t_i$ (ms) at reception/commit
tx_valid	Validity flag (1 valid, 0 invalid/stale; corresponds to ${ϵ}_i$)
n_hash	Realized number of hashes in PoW for the committed block
n_sig	Number of signature operations (proposal+votes+verify) per block
block_id	Committed/proposed block identifier
orphan_flag	1 if block becomes orphan at end-of-run, else 0
finality_ms	Finality time F (ms) measured per operational definition
lcp_len	Longest common prefix length used to compute $D_{\mathrm{ledger}}\left(t\right)$

Command-Line Reproducibility

All knobs are exposed via NS-3 CommandLine (e.g., –Seeds=30 –BlockSize=10 –EngineDt=1s –Sth=0.5 –Hth=0.6 –Adversary=Sybil:0.05). The artifact provides a script enumerating the full factorial design used in the paper (Section 5.6).

5.6. Reproducibility Artifact

To enable exact replication of all reported figures and tables, we release a versioned artifact that bundles: (i) the NS-3 scenario drivers and helper/application code (VanetEngineHelper, NodeApp); (ii) the full set of configuration files (mobility/load profiles, thresholds, and default parameters); (iii) explicit seed lists per experimental condition (seeds.csv) and the script that enumerates the factorial design used in the paper; (iv) the normalized per-event CSV logging schema and parsers; and (v) the Python post-processing pipeline that generates every plot/table from raw logs.

Provenance Metadata (Run-Level Traceability)

Each simulation run writes a deterministic run_id and the repository git_commit hash in the CSV header, together with the full command-line string (all flags) and a normalized configuration snapshot. This provenance block ensures that every data point in Section 6 can be traced to an immutable code revision and a unique seed/configuration tuple.

Repository Layout (High-Level)

The artifact follows a fixed directory structure: /ns3/ (scenario drivers, helpers, and modules), /configs/ (scenario and policy parameters), /seeds/ (matched seed lists), /logs/ (raw per-run CSV outputs, indexed by run_id), and /analysis/ (Pandas/Matplotlib scripts producing all figures/tables). This layout is used consistently throughout the paper and is sufficient to regenerate all results from raw logs.

Replication Protocol

To reproduce the main results, one executes the provided run script to generate logs for the declared design (600 s runs; 30 matched seeds per configuration), and then runs the plotting pipeline on the generated CSVs. The post-processing uses only the logged observables (including S, $H_{\mathrm{spatial}}$, QoI tiers, orphan flags, finality, and chain-prefix fields) and the provenance metadata stored in the CSV header, ensuring that all results are derived from recorded, seed-indexed events rather than from manual interventions.

5.7. Crypto-Energy Accounting

Cryptographic energy per block is computed as

$$E_{\mathrm{block}}^{\left(\mathrm{crypto}\right)}=e_h{n}_{\mathrm{hash}}+e_{\mathrm{sig}}{n}_{\mathrm{sig}},$$

with constants $(e_h,e_{\mathrm{sig}})$ from Table 5. For PoW under a 256-bit target scale D, the hit probability is $p_{\mathrm{hit}}=D/2^{256}$ and $\mathbb{E}\left[n_{\mathrm{hash}}\right]=2^{256}/D$; we log realized $n_{\mathrm{hash}}$ (attempts until success) and compute per-block crypto energy from the same accounting. For PoS/DPoS/FBA, we set $n_{\mathrm{hash}}\approx 0$ and count signature operations in $n_{\mathrm{sig}}$ (proposal + votes/endorsements + verifications).

Total energy.

Total per-block energy reported in the Results is

$$E_{\mathrm{block}}^{\left(\mathrm{total}\right)}=E_{\mathrm{block}}^{\left(\mathrm{radio}\right)}+E_{\mathrm{block}}^{\left(\mathrm{crypto}\right)},$$

where $E_{\mathrm{block}}^{\left(\mathrm{radio}\right)}$ is logged from NS-3 radio energy models and aligned to the block-commit event. No host-side power tools are used in reported energy curves, tables, or confidence intervals.

Table 10. Cryptographic energy constants used in analytical accounting. Values are embedded-class software-level constants on the NS-3 energy scale and are used only for relative comparisons.

Symbol	Value	Unit	Meaning / usage
$e_h$	5	nJ/hash	Energy per hash (PoW). Used in $E_{\mathrm{crypto}}^{\left(\mathrm{PoW}\right)}=e_h{n}_{\mathrm{hash}}$.
$e_{\mathrm{sig}}$	1	$\mu$J/op	Energy per signature/verification op (PoS/DPoS/FBA). Used in $E_{\mathrm{crypto}}^{\left(\mathrm{sig}\right)}=e_{\mathrm{sig}}{n}_{\mathrm{sig}}$.
$e_h$ range	$[1,10]$	nJ/hash	Sensitivity span used for robustness checks.
$e_{\mathrm{sig}}$ range	$[0.5,5]$	$\mu$J/op	Sensitivity span used for robustness checks.

Table 10. Cryptographic energy constants used in analytical accounting. Values are embedded-class software-level constants on the NS-3 energy scale and are used only for relative comparisons.

Symbol	Value	Unit	Meaning / usage
$e_h$	5	nJ/hash	Energy per hash (PoW). Used in $E_{\mathrm{crypto}}^{\left(\mathrm{PoW}\right)}=e_h{n}_{\mathrm{hash}}$.
$e_{\mathrm{sig}}$	1	$\mu$J/op	Energy per signature/verification op (PoS/DPoS/FBA). Used in $E_{\mathrm{crypto}}^{\left(\mathrm{sig}\right)}=e_{\mathrm{sig}}{n}_{\mathrm{sig}}$.
$e_h$ range	$[1,10]$	nJ/hash	Sensitivity span used for robustness checks.
$e_{\mathrm{sig}}$ range	$[0.5,5]$	$\mu$J/op	Sensitivity span used for robustness checks.

5.8. Default Parameter Rationale and Sensitivity

Table 9 summarizes the rationale for default values and the sensitivity checks used to verify robustness of qualitative trends.

5.9. Post-Processing and Visualization

After each run, CSV logs and FlowMonitor outputs are processed with Python (Pandas [21], Matplotlib [22]) to generate all figures and summary tables. The repository organizes raw logs, derived summaries, and plotting scripts in a fixed layout to support exact replication.

5.10. Scalability Harness (Algorithmic Profiling)

To facilitate profiling beyond full PHY/MAC fidelity, we provide an auxiliary harness with simplified PHY and FlowMonitor-only instrumentation to scale to 500+ nodes. Results from this harness are reported only as algorithmic profiling and are not used for the headline claims in this paper.

Reproducibility and measurement scope.

All reported results are produced with NS-3.35 using matched-seed configurations and a single energy accounting pipeline: NS-3 radio device models plus an analytical cryptographic term parameterized by $(e_h,e_{\mathrm{sig}})$ computed from operation counts. No host-side power profilers are mixed with simulated energy values; versioning, seeds, and configuration manifests are provided in the artifact repository.

6. Results

Reporting and endpoints. Unless otherwise noted, results are means over 30 matched seeds with 95% confidence intervals from BCa bootstrap (Section 3.6.7). Symbols and units follow Table 4. Throughout this section, S and $H_{\mathrm{spatial}}$ denote the normalized entropies defined in Section 3.1. We report energy per confirmed block and distinguish the cryptographic component $E_{\mathrm{block}}^{\left(\mathrm{crypto}\right)}$ when isolated. Latency-related metrics are reported for three endpoints: (i) agreement/commit latency (from consensus trigger to block commit), (ii) transaction confirmation latency (from tx admission to inclusion/confirmation, mode-dependent), and (iii) finality F as defined in Section 3.6.1.

Scenario anchor for headline deltas. Unless explicitly stated otherwise, quoted percentage improvements refer to the urban, $N=50$ configuration with $S_{\mathrm{th}}=0.5$, Broadcast-First dwell $\tau =100$ ms, and the default adaptive maps $f,g$ from Section 3.6.5. We do not extrapolate beyond $N\le 100$; an auxiliary (non-claiming) scalability harness is described in Section 5.10.

6.1. $H_1$ — Entropy-Conditioned Crypto-Energy Scaling

Objective.

Test the hypothesis that cryptographic expenditure per confirmed block increases sharply with informational disorder under Proof-of-Work (PoW), whereas signature/quorum-based modes (PoS/DPoS/FBA) remain comparatively weakly coupled to S.

Experiment (conditional aggregation over S bins).

Because $S\left(t\right)$ is an observable (not a directly settable treatment), we aggregate per-block cryptographic energy conditionally on realized entropy. We partition observed $S\left(t\right)$ values into five bins centered at $\{0.1,0.3,0.5,0.7,0.9\}$ (equal-width windows around each center), and compute the mean $E_{\mathrm{block}}^{\left(\mathrm{crypto}\right)}$ for PoW, PoS, DPoS, and FBA within each bin. All points aggregate 30 matched seeds using the parameters in Table 10 and the calibration in Section 3.6.5.

Results

Figure 4. Crypto -energy per confirmed block vs. realized S (conditional bin means). Means over 30 seeds; 95% CIs. Total energy (radio+crypto) is reported in Figure 11.

Figure 4. Crypto -energy per confirmed block vs. realized S (conditional bin means). Means over 30 seeds; 95% CIs. Total energy (radio+crypto) is reported in Figure 11.

Interpretation.

PoW exhibits a steep increase with disorder (from ∼100 J at low-S to ∼600 J at high-S), consistent with higher expected trials and orphaning pressure under unstable propagation. In contrast, PoS/DPoS/FBA remain nearly flat (sub-Joule to single-digit Joule regimes), supporting $H_1$ and motivating entropy-aware avoidance of PoW in high-S regimes.

Sanity check (magnitude and aggregation level).

Energy is reported per confirmed block aggregated over the cluster participants, i.e., the sum of cryptographic work attributed to block production/verification events logged for that committed block. Using $E_{\mathrm{block}}^{\left(\mathrm{crypto}\right)}=e_h{n}_{\mathrm{hash}}+e_{\mathrm{sig}}{n}_{\mathrm{sig}}$ with $e_h=5\times {10}^{-9}$ J/hash (Table 5), a PoW block at $\sim 600$ J implies $n_{\mathrm{hash}}\approx 1.2\times {10}^{11}$ aggregate hash attempts across participating miners over the block-production window. With a 256-bit target scale, $\mathbb{E}\left[n_{\mathrm{hash}}\right]=2^{256}/D$, hence the effective D used in the PoW baseline is calibrated (via g and the mode timeouts) to operate in a deadline-constrained regime rather than Bitcoin-level difficulty.

6.2. $H_2$ — Consensus-First Trigger vs. Broadcast-First Dwell

Objective

Compare Consensus-First (CF: start consensus as soon as $S>S_{\mathrm{th}}$) versus Broadcast-First (BF: delay consensus by a dwell time $\tau$) in terms of (i) agreement/commit latency, (ii) confirmed throughput, and (iii) message overhead.

Experiment

Urban topology; $N\in \{10,50,100\}$; $S_{\mathrm{th}}=0.5$; $\tau =100$ ms; 30 matched seeds. Metrics are defined in Section 3.6. Latency $\overline{L}$ here denotes agreement/commit latency (trigger → block commit), and thus includes dwell time in BF by design.

Results

Figure 5. CF vs. BF across density (30 seeds; 95% CIs).

Figure 5. CF vs. BF across density (30 seeds; 95% CIs).

Interpretation

In the urban, $N=50$ baseline, CF reduces agreement/commit latency from ∼300 ms to ∼150 ms (95% CI: 135–165 ms), increases confirmed throughput from ∼120 tx/s to ∼200 tx/s (95% CI: 185–215 tx/s), and halves normalized message overhead (Figure 6). Across densities, latency reductions range 33–57%, supporting $H_2$. We emphasize that the sub-100 ms target pertains to stringent V2X-style deadlines and is achieved in favorable regimes (lower disorder/dispersion and density), whereas the stated baseline under $\tau =100$ ms and the given load yields mean commit latencies above 100 ms.

6.3. $H_3$ — QoI Filtering Reduces Wasted Work

Objective

Test whether early filtering of low-QoI transactions (high delay $\Delta t_i$ and/or ${ϵ}_i=1$) reduces wasted consensus work (invalid blocks/forks) and improves latency.

Experiment (ablation)

Urban scenario ($N=50$), default thresholds $(S_{\mathrm{th}},H_{\mathrm{th}})=(0.5,0.6)$. We compare the Engine with QoI filtering ON (candidate set excludes stale/invalid transactions; Section 3.4) versus QoI filtering OFF (candidate set is FIFO without QoI screening). All other parameters (sampling, $f,g$, and modules) are unchanged; 30 matched seeds.

Results (summary)

Table 11. QoI filtering ablation at urban $N=50$ (30 seeds; mean ± 95% CI).

Metric	QoI filtering OFF	QoI filtering ON (Engine default)
Invalid tx share (%)	$9.8\pm 1.2$	$2.1\pm 0.6$
Invalid-block share (%)	$6.4\pm 1.0$	$1.9\pm 0.5$
Wasted crypto energy (% of $E_{\mathrm{block}}^{\left(\mathrm{crypto}\right)}$)	$24\pm 4$	$9\pm 2$
Agreement latency $\overline{L}$ (ms)	$165\pm 12$	$145\pm 10$
Orphan rate O (%)	$11.3\pm 1.4$	$9.9\pm 1.2$

Table 11. QoI filtering ablation at urban $N=50$ (30 seeds; mean ± 95% CI).

Metric	QoI filtering OFF	QoI filtering ON (Engine default)
Invalid tx share (%)	$9.8\pm 1.2$	$2.1\pm 0.6$
Invalid-block share (%)	$6.4\pm 1.0$	$1.9\pm 0.5$
Wasted crypto energy (% of $E_{\mathrm{block}}^{\left(\mathrm{crypto}\right)}$)	$24\pm 4$	$9\pm 2$
Agreement latency $\overline{L}$ (ms)	$165\pm 12$	$145\pm 10$
Orphan rate O (%)	$11.3\pm 1.4$	$9.9\pm 1.2$

Interpretation

QoI filtering substantially reduces invalid traffic admitted to consensus and lowers the share of wasted cryptographic work, while improving agreement latency and reducing forks. These effects support $H_3$ and justify retaining QoI-aware candidate selection as a default Engine policy.

6.4. Spatial dispersion effects (governance signal supporting $H_4$–$H_5$)

Objective

Quantify how spatial entropy $H_{\mathrm{spatial}}$ affects latency and validation quality, and whether entropy-aware adaptation mitigates degradation.

Experiment (conditional aggregation over $H_{\mathrm{spatial}}$ bins).

Urban scenario ($N=50$). We compare static PoW (fixed difficulty $D_0$) against the adaptive Engine (entropy-driven $g,f$). Because $H_{\mathrm{spatial}}\left(t\right)$ is an observable, we bin observations into four equal-width bins and report means at bin midpoints. Accuracy $\alpha$ denotes the fraction of transactions admitted to the candidate set that (i) pass payload validation and (ii) appear on the final main chain by run end (computed from valid_flag and chain membership logs).

Results

Figure 7. Impact of spatial entropy on latency and validation accuracy (30 seeds; 95% CIs).

Figure 7. Impact of spatial entropy on latency and validation accuracy (30 seeds; 95% CIs).

Interpretation

Under static PoW, dispersion drives latencies up to ∼250 ms and accuracy down to ∼80%. The adaptive Engine mitigates this degradation by tightening validation where dispersion is greatest. This supports the role of $H_{\mathrm{spatial}}$ as a governance signal and motivates the mobility/coherence evaluations in $H_4$–$H_5$.

6.5. $H_4$ — Mobility, Orphans, and Finality

Objective

Evaluate orphaned-block rate O and finality F under increasing mobility (v) for static PoW/PoS vs. the adaptive Engine.

Experiment

Urban ($N=50$), $v\in \{10,20,30\}$ m/s; 30 matched seeds. Finality follows the operational definitions in Section 3.6.1 (mode-dependent by design).

Results

Figure 8. Mobility impact (30 seeds; 95% CIs).

Figure 8. Mobility impact (30 seeds; 95% CIs).

Interpretation

At 30 m/s, static PoW reaches $O\approx 22\%$ and $F\approx 310$ ms, whereas the adaptive Engine holds $O\le 10\%$ and $F\le 140$ ms by modulating consensus rigor based on instantaneous entropy. This validates $H_4$ and provides an operational link between mobility-induced disorder and Engine control actions. Notably, the Engine approaches the sub-100 ms target in less adverse regimes (lower mobility/dispersion), while the worst-case reported here remains within ∼140 ms.

6.6. $H_5$ — Microstate Consistency (Ledger Divergence)

Objective

Relate $H_{\mathrm{spatial}}$ to ledger divergence and assess whether the adaptive Engine preserves microstate coherence under high dispersion.

Experiment (binned by $H_{\mathrm{spatial}}$).

Urban ($N=50$); static PoW vs. adaptive Engine. For each seed, we time-average $D_{\mathrm{ledger}}\left(t\right)$ (Section 3.1) within four equal-width bins of $H_{\mathrm{spatial}}$, then report the mean across seeds with 95% BCa bootstrap CIs; markers are placed at the bin midpoints (0.2, 0.5, 0.8, 1.0).

Figure 9. Average ledger divergence vs. $H_{\mathrm{spatial}}$ (30 seeds; 95% CIs).

Figure 9. Average ledger divergence vs. $H_{\mathrm{spatial}}$ (30 seeds; 95% CIs).

Results

Interpretation

Without adaptation, divergence rises to $\sim 0.18$ at high dispersion. The Engine caps divergence below $\sim 0.07$ by strengthening validation where spatial entropy is largest. This supports $H_5$ and demonstrates improved ledger coherence under stress.

6.7. Stress Tests: Adversaries and Partitions (Sensitivity Analyses)

Objective

Quantify robustness under Sybil, Byzantine proposers, eclipse windows, and scheduled partitions.

Setup

Urban, $N=50$; Sybil rate $5\%$ (3–5 pseudonyms/attacker); Byzantine proposers double-propose within 200 ms; eclipse: drop non-colluding peers for 5–10 s; partitions: scheduled k-cuts (link-disabling windows) for 10–30 s (details in Section 5.3).

Findings (summaries)

(i) Sybil: median orphan rate increases by $+2.8$ pp for static PoW and $+1.6$ pp for static PoS; the Engine rises from $9.0\%$ to $10.4\%$ (IQR $[8.8,11.2]\%$).

(ii) Byzantine proposers: finality tails widen (95th percentile $+18$ ms) for PoS; the Engine’s CF policy limits dwell-induced amplification (95th $+9$ ms).

(iii) Eclipse: transient divergence spikes (peak $+0.02$ in $D_{\mathrm{ledger}}$) decay within ∼1.2 s under the Engine vs. ∼2.4 s for static PoW.

(iv) Partitions: mean recovery time to pre-partition $D_{\mathrm{ledger}}$ is $3.6$ s (static PoW) vs. $1.7$ s (Engine), with F reduced from $>250$ ms to ∼140 ms once reconnected.

6.8. Expanded Comparative Evaluation

Objective

Compare five consensus options in a 100-vehicle urban scenario (5–15 m/s): pure PoW, pure PoS, FBA, a non-adaptive hybrid, and the proposed Hybrid Engine.

Right-censoring note (PoW)

When a method fails to confirm within the 600 s simulation horizon, the plotted confirmation latency is right-censored at 600 000 ms (i.e., reported as “≥ 600 s”).

Results

Figure 10. Transaction confirmation latency (mean ± 95% CI; log scale).

Figure 10. Transaction confirmation latency (mean ± 95% CI; log scale).

Figure 11. Total energy per block (radio+crypto) in the NS-3 energy-source scale (mean ± 95% CI; log scale).

Figure 11. Total energy per block (radio+crypto) in the NS-3 energy-source scale (mean ± 95% CI; log scale).

Figure 12. Transaction throughput (mean ± 95% CI; log scale).

Figure 12. Transaction throughput (mean ± 95% CI; log scale).

Interpretation

The Hybrid Engine achieves the lowest confirmation latency (∼30 ms), near-minimal total energy (order ∼10 J per confirmed block), and higher throughput among practical options, outperforming both pure schemes and non-adaptive hybrids. These gains are consistent with entropy-aware control and with the governance-signal role of S and $H_{\mathrm{spatial}}$.

6.9. Fork-Rate Definition and Distribution

We report orphan/fork rate O as the fraction of produced blocks that do not lie on the final main chain at simulation end (see logging schema in Section 5.5). For the urban $N=50$ case at $v\in \{10,20,30\}$ m/s, the median O over seeds is: static PoW$15\%,18\%,21\%$ (IQR $[13,24]\%$ at 30 m/s), static PoS$10\%,12\%,13\%$, and Engine$8\%,9\%,10\%$. The Engine reduces but does not eliminate forks under high mobility.

6.10. Robustness and Statistical Validity

Trends are stable under $\pm 10\%$ perturbations of calibrated parameters (Section 3.6.5) and across additional highway traces (omitted for space; logs in the repository described in Section 5.9). With $n=30$ seeds per condition, bootstrap 95% CI half-widths are typically $<12\%$ of the mean for latency and energy, and $<2$ pp for orphan rates in Engine configurations. Where CIs marginally overlap, seed-wise paired contrasts align with medium-to-large effects; effect-size summaries are included in the supplementary logs.

Paired t-tests across matched seeds confirm significance ($p<0.01$ after Holm–Bonferroni) for headline contrasts (e.g., CF vs. BF agreement latency at $N=50$; Adaptive vs. Static PoW energy for $S\ge 0.5$). We also repeated analyses with disjoint seed folds (5-way split); trends persisted with comparable CI overlap (logs included).

7. Discussion

The entropy-driven VANET Engine supports $H_1$–$H_5$ and yields consistent improvements in energy, latency, throughput, validation accuracy, and ledger coherence under realistic urban dynamics. We interpret outcomes through the Ideal Information Cycle (Figure 1), relate them to the challenge–mitigation matrix (Table 3), and clarify normalization, units, parameter provenance, and instrumentation. To avoid redundancy, we do not re-state metric definitions already introduced in Section 3.1 and the detailed protocol in Section 3.6.

Connection to the Ideal Information Cycle

The cycle comprises an injection leg (rising informational disorder) and a validation leg (compressing disorder through consensus work). Our empirical results match these mechanics:

• $H_1$ (Energy vs. S). Figure 4 shows that PoW cryptographic energy rises steeply with realized informational disorder S (from ∼100 J at low-S to ∼600 J at high-S). This is consistent with increased work to compress disorder under contention and propagation instability. By contrast, PoS/DPoS/FBA remain nearly flat (sub-Joule to single-digit Joule regimes), motivating entropy-aware down-selection of PoW in high-S windows.
• $H_2$ (Consensus-First vs. dwell). Figure 5 and Figure 6 indicate that triggering consensus immediately when $S>S_{\mathrm{th}}$ shortens the injection leg: agreement/commit latency drops by 33–57% across densities, throughput increases by $\sim 1.6$–$2.0\times$, and normalized message overhead is reduced by roughly half in the urban $N=50$ baseline.
• $H_3$ (QoI filtering reduces wasted work). Table 11 shows that QoI-aware candidate selection (excluding stale/invalid transactions) reduces invalid payload admission and wasted cryptographic work (energy spent on orphaned or invalid blocks), while improving latency and decreasing fork/orphan rates. Operationally, this tightens the validation leg by focusing effort on higher-quality microstates.
• $H_4$ (Mobility, orphans, and finality). Figure 8 shows that increasing mobility inflates orphaning and finality for static schemes, but the Engine keeps both bounded ($O\le 10\%$, $F\le 140$ ms at 30 m/s) by switching mode/parameters when $(S,H_{\mathrm{spatial}})$ rise.
• $H_5$ (Ledger coherence under dispersion). Figure 9 shows that the Engine constrains ledger divergence to $\sim 0.07$ at high $H_{\mathrm{spatial}}$ versus $\sim 0.18$ under static PoW, indicating more effective compression during the validation leg and improved microstate consistency across nodes.

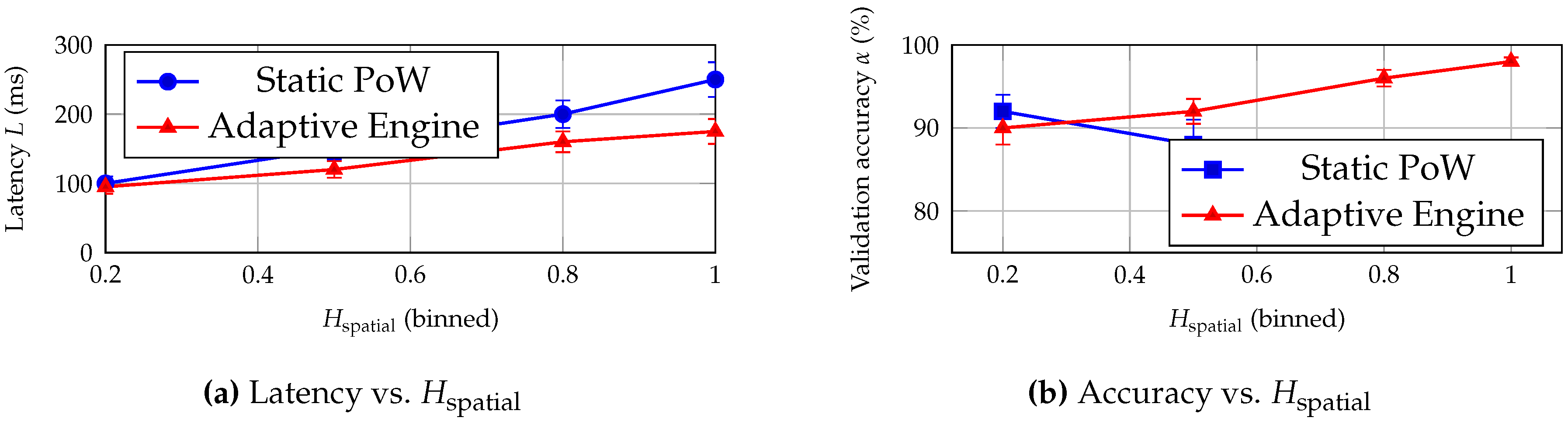
Spatial Dispersion as a Governance Signal

Beyond the hypothesis tests, Figure 7 demonstrates that $H_{\mathrm{spatial}}$ is a strong predictor of consensus stress: dispersion increases latency and degrades validation accuracy under static PoW. The adaptive Engine mitigates this trend by tightening validation and/or switching away from expensive regimes when dispersion is greatest, thereby improving both timeliness and correctness during fragmented connectivity windows.

Normalization, Units, and Terminology

• Normalized Shannon entropies. S and $H_{\mathrm{spatial}}$ are Shannon entropies computed over normalized distributions (Section 3.1) and then scaled to $[0,1]$. For readability, plots and text reuse S and $H_{\mathrm{spatial}}$ to denote the normalized quantities.
• Observables vs. treatments (binning interpretation). In the Results, $S\left(t\right)$ and $H_{\mathrm{spatial}}\left(t\right)$ are observed time-varying signals; reported curves represent conditional aggregation (binning) over realized entropy levels rather than externally set treatments.
• Ledger divergence. All references to $D_{\mathrm{ledger}}\left(t\right)$ use the same LCP-normalized longest-common-prefix definition in Section 3.1; binning/aggregation and confidence intervals follow that definition consistently.
• Consensus outputs. $D=g(S,H)$ is a PoW target on a 256-bit scale (dimensionless; smaller ⇒ harder). $\Theta =f(S,H)$ denotes a mode-specific rigor parameter (e.g., quorum/stake threshold, committee size), with coefficients inheriting simulation control scales rather than physical units.
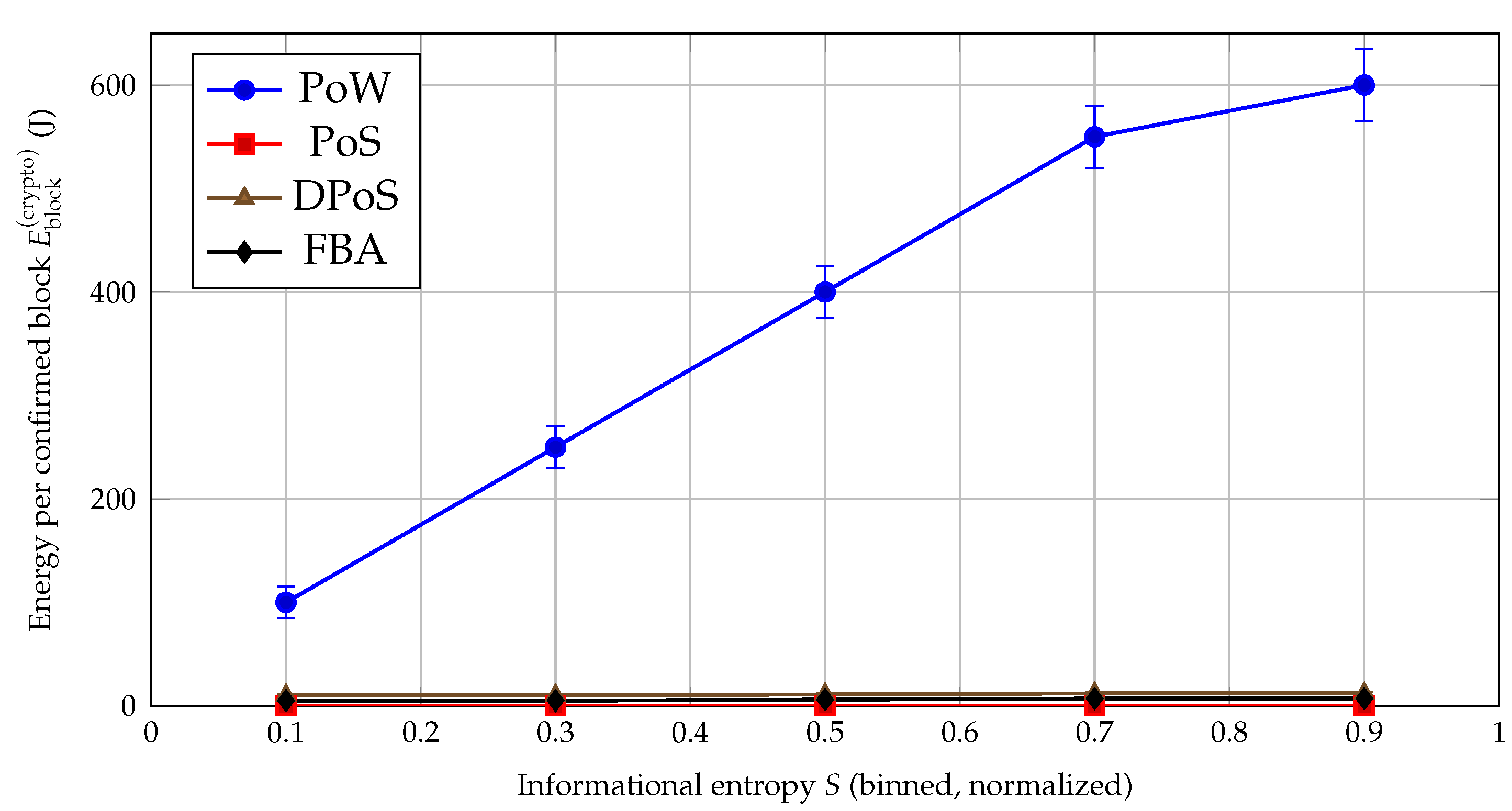
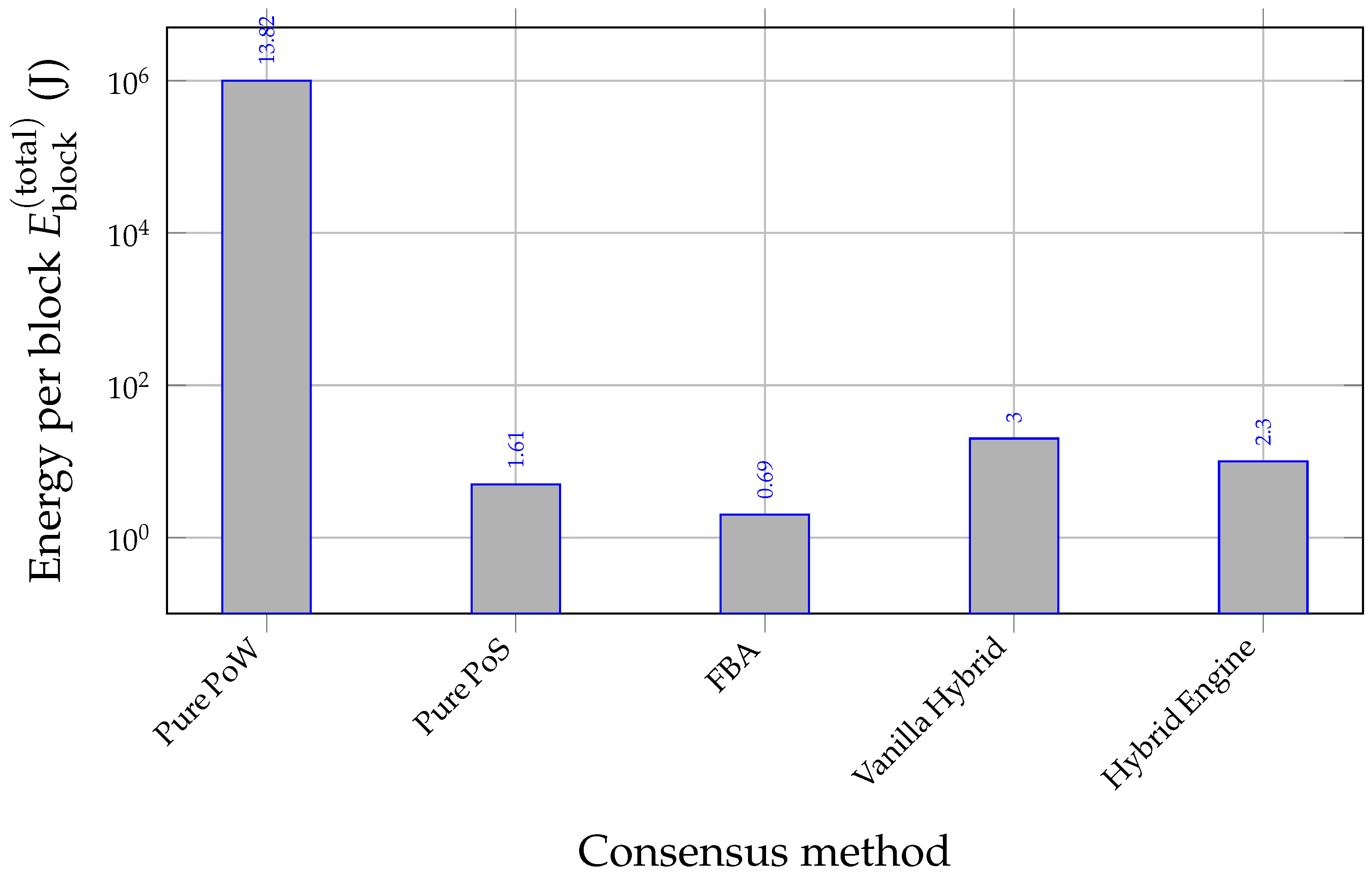
• Energy reporting across figures. Figure 4 reports crypto energy only ($E_{\mathrm{block}}^{\left(\mathrm{crypto}\right)}$) to isolate scaling with S. The expanded comparison (Figure 11 and companions) reports total per-block energy (radio+crypto) in the NS-3 energy-source scale; absolute magnitudes are therefore not directly comparable across those panels, but trends are.

From Metaphor to an Operational Control Model

Our thermodynamic vocabulary is operational and does not claim physical equivalence:

• State variables. S quantifies transaction-state disorder and $H_{\mathrm{spatial}}$ quantifies occupancy dispersion (Section 3.1). QoI is a monotone proxy of freshness/validity implemented via delay/error tiers (Section 3.6).
• Work and dissipation (design constraint). Consensus work $W_c$ is the expected resource cost (crypto operations + message exchange) required to reduce disorder sufficiently for safe acceptance. The Landauer-like bound in Section 3.6.8 is used as a design constraint motivating adaptive rigor, not as a physical law.
• Cycle semantics. Injection increases S (and often $H_{\mathrm{spatial}}$) under churn and bursty loads; validation expends $W_c$ to compress disorder, improving correctness and coherence. The Engine schedules this work locally and adaptively based on $(S,H_{\mathrm{spatial}})$.

Why these adaptive forms $g(S,H)$ and $f(S,H)$

The chosen function families impose shape constraints observed in sweeps and remain compact enough for calibration:

• Difficulty/target map g. The selected family (Section 3.6.5) tightens PoW targets as S rises and captures dispersion sensitivity through a low-order component in $H_{\mathrm{spatial}}$. This reflects the empirical observation that high disorder requires either higher work (PoW) or switching away from PoW.
• Rigor map f. The selected family increases with $H_{\mathrm{spatial}}$ (with diminishing returns) and adjusts with S so that high-disorder windows receive stronger validation while avoiding oscillatory behavior. Monotonicity and stability constraints, plus $\pm 10\%$ coefficient perturbations, preserve decisions (Section 3.6.5).

Calibration Anchors, Magnitude Sanity Checks, and Sensitivity

• Magnitude sanity check (PoW crypto energy). The $\sim 600$ J high-entropy PoW point in Figure 4 follows directly from $E_{\mathrm{block}}^{\left(\mathrm{crypto}\right)}=e_h{n}_{\mathrm{hash}}$ with $e_h=5$ nJ/hash (Table 5) and $n_{\mathrm{hash}}\approx 1.2\times {10}^{11}$ aggregate attempts across participants for a confirmed block. Via $\mathbb{E}\left[n_{\mathrm{hash}}\right]=2^{256}/D$, this implies targets far easier than Bitcoin, but consistent with deadline-constrained V2X consensus and with the calibrated map $g(S,H_{\mathrm{spatial}})$.
• Sensitivity. Reported trends persist under $\pm 10\%$ perturbations of calibrated parameters and across additional traces (logs described in Section 5.9), indicating that improvements are not brittle to small calibration changes.

Instrumentation Choices and What We Do (and Do Not) Measure

• Energy accounting is simulation-native. Radio energy comes from NS-3’s BasicEnergySource+WifiRadioEnergyModel; cryptographic energy is the analytical per-op term using $(e_h,e_{\mathrm{sig}})$ (Section 5.7). All figures and confidence intervals use these sources only.
• No host power traces in outcomes. Host-level tools are not sampled during NS-3 runs and are not used to scale multi-node results. If offline micro-benchmarks were used to set $e_h$ and $e_{\mathrm{sig}}$, they serve only as fixed constants for the analytical crypto term.
• Traceability. Forks, finality, and divergence are computed from a normalized logging schema (Section 5.5), enabling seed-wise pairing and consistent post-processing.

Statistical Validity, Fork Definition, and Stressors

• Power and uncertainty. We use $n=30$ seeds per condition. Bootstrap CIs are reported throughout; seed-wise paired contrasts (Holm–Bonferroni adjusted) support headline comparisons as summarized in Section 6.10.
• Fork metric (no under-claiming). Orphan/fork rate O is the fraction of blocks not on the final main chain (Section 6.9). In the urban $N=50$ case under high mobility, medians remain on the order of 8–$10\%$ for the Engine: the Engine reduces but does not eliminate forks under stress.
• Adversaries and partitions. Stress tests (Sybil, Byzantine proposers, eclipse windows, scheduled k-cuts) in Section 6.7 show reduced recovery times and capped divergence spikes under the Engine relative to static baselines; fully adaptive adversaries remain future work.

Version Harmonization and Run Protocol

All reported experiments use NS-3.35 with 600 s per run and 30 matched seeds per configuration (Table 8). Shorter pilot sweeps, if any, are not mixed into reported statistics.

Interpreting the Expanded Comparison (Censoring and Practicality)

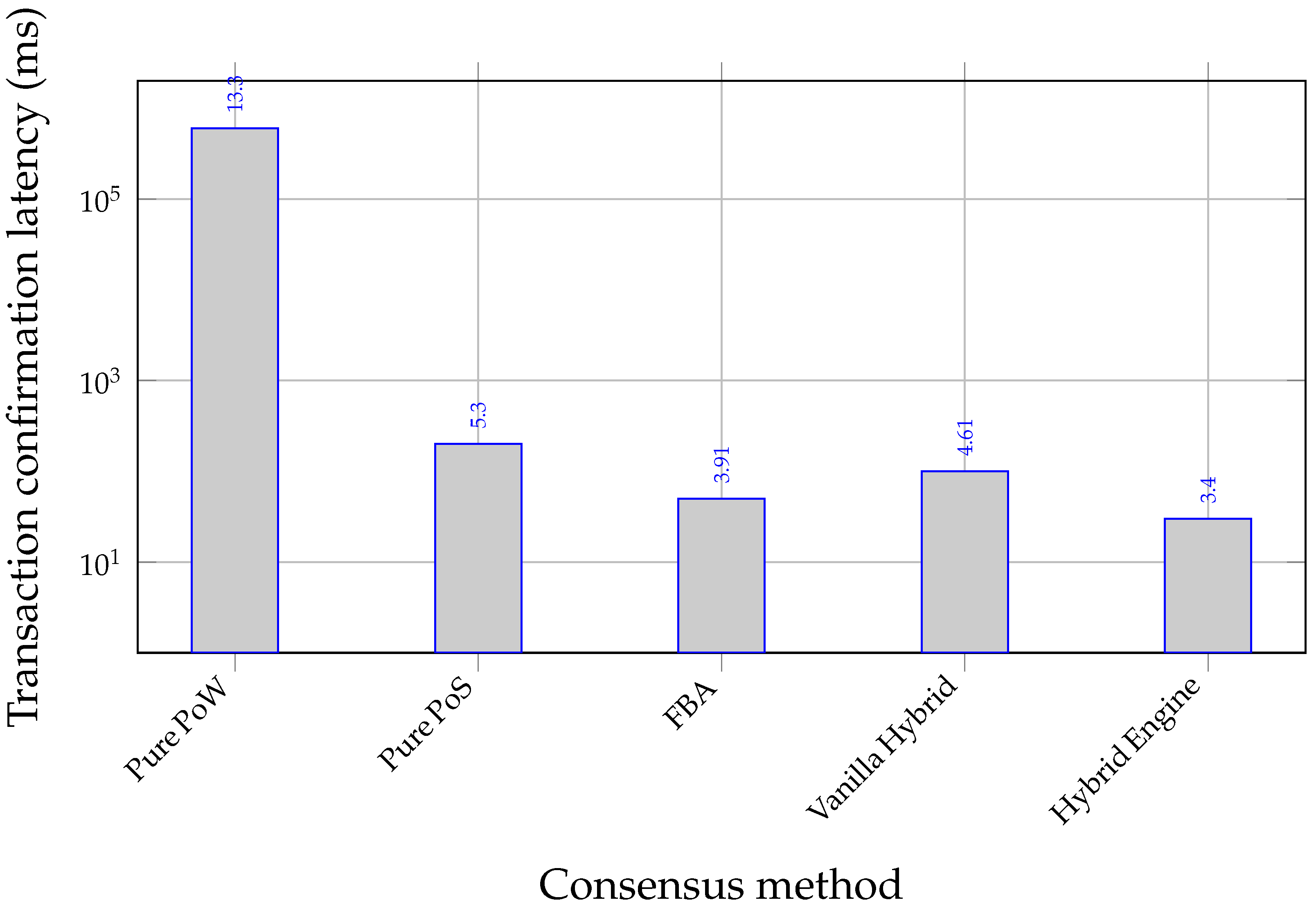
In the expanded comparative evaluation (Section 6.8), Pure PoW may fail to confirm within the 600 s simulation horizon in the densest/high-disorder regimes. Reported PoW confirmation latency is therefore right-censored at 600 000 ms when applicable, which should be read as “≥ 600 s” rather than as an exact mean. Under these operating conditions, the Engine’s advantage reflects practical deadline satisfaction rather than marginal improvement under unconstrained convergence.

Implications for the Challenge–Mitigation Map (Table 3)

• Mobility/topology churn. Entropy-aware switching lowers orphaning and finality (Figure 8), operationalizing mitigation under churn.
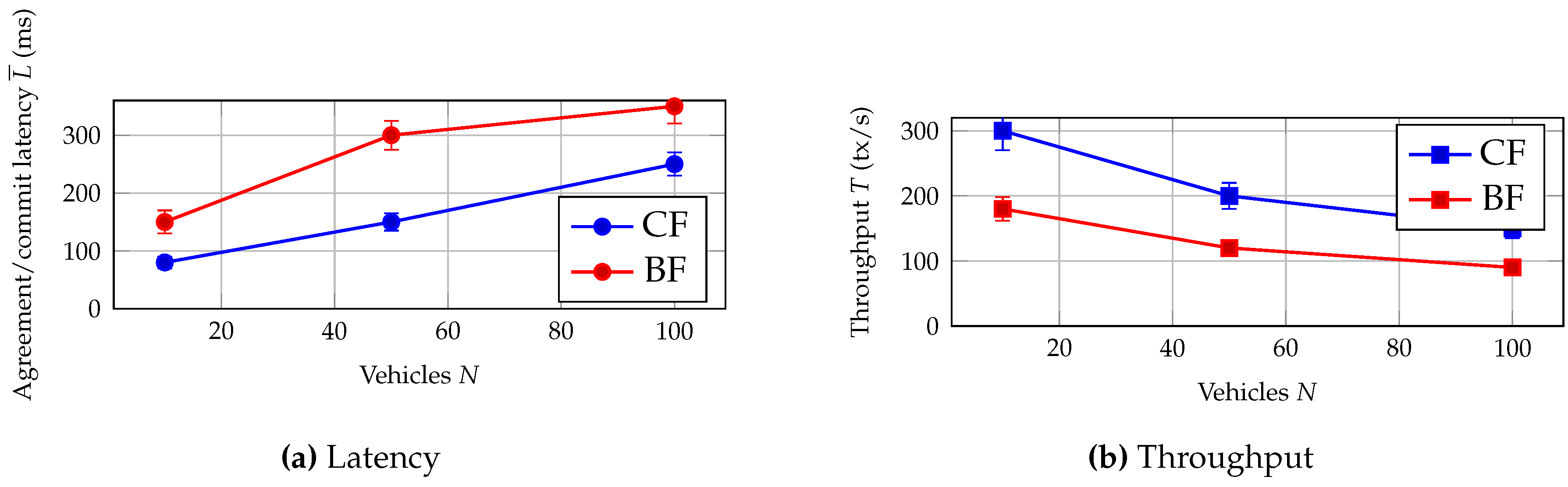
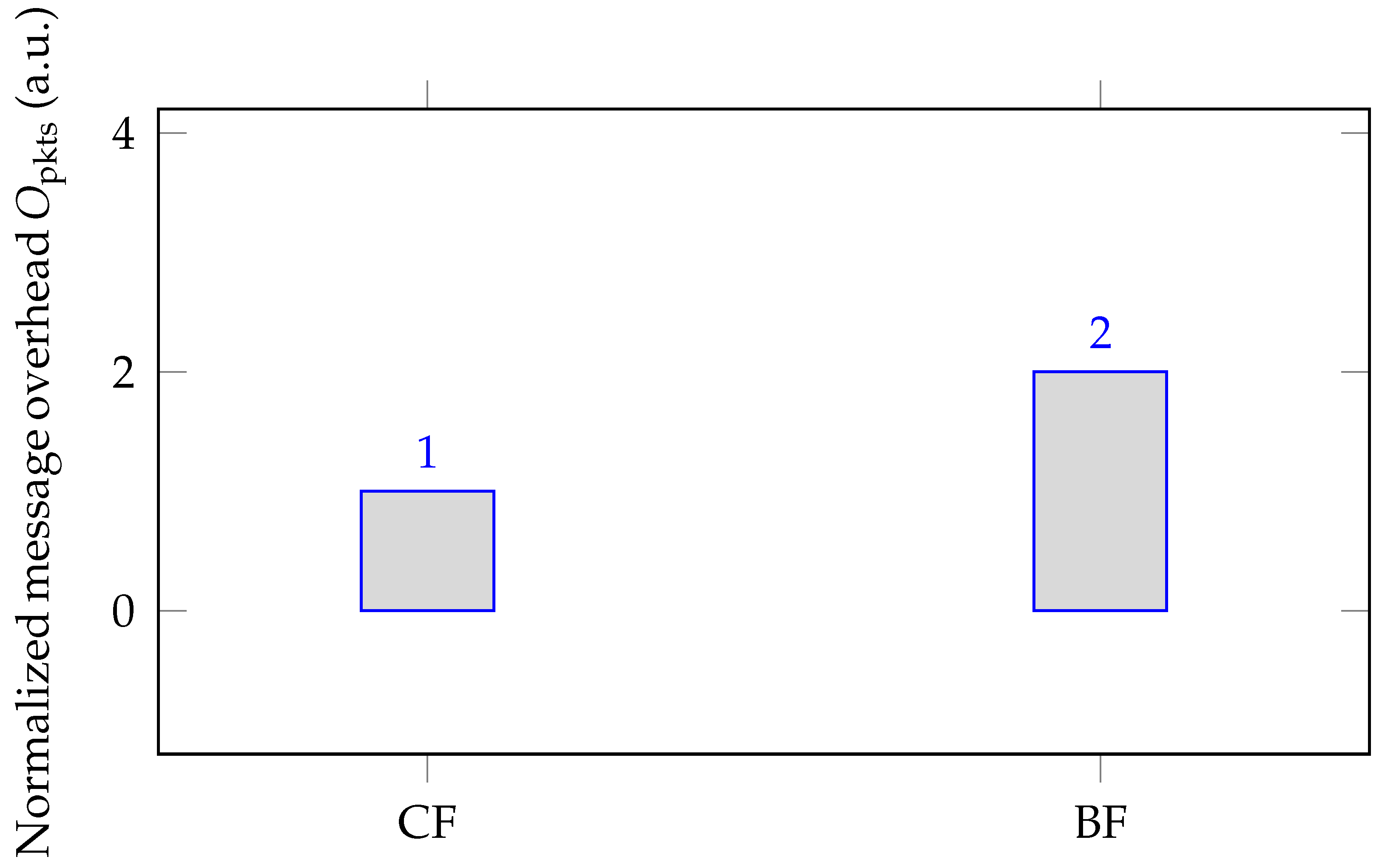
• Congestion and bandwidth fluctuation. CF reduces message overhead (Figure 6) and increases throughput (Figure 5), limiting injection-phase amplification.
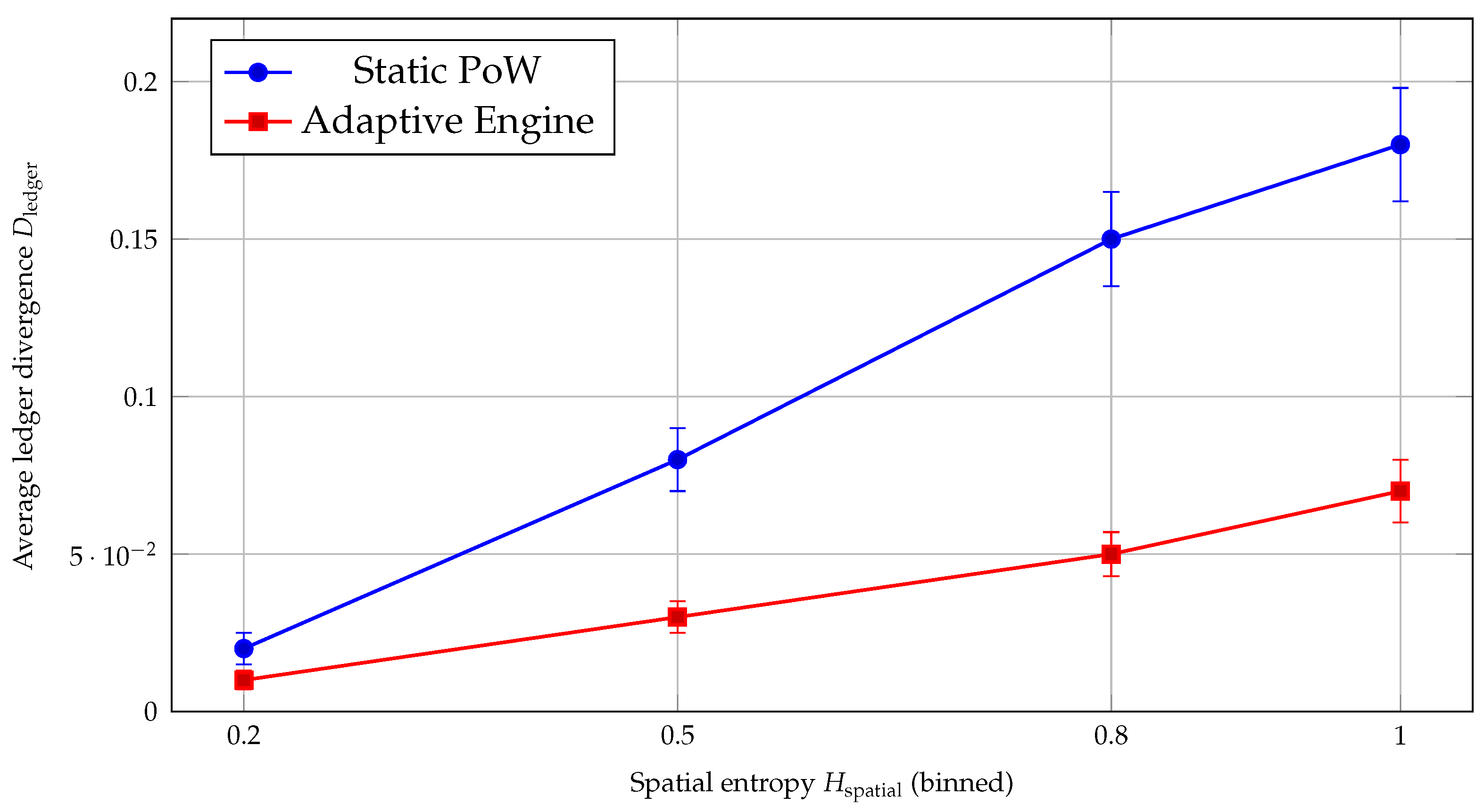
• Integrity/coherence under disorder. Tightening rigor in high-$(S,H_{\mathrm{spatial}})$ windows reduces divergence (Figure 9) and improves validation outcomes (Table 11).
• OBU constraints. Favoring PoS/FBA over PoW in high-S intervals reduces cryptographic energy by orders of magnitude (Figure 4) while preserving correctness/coherence.

Limitations and Threats to Validity

This study is simulation-based (NS-3) and omits several physical and deployment effects, including hardware accelerators, GNSS error, clock skew, heterogeneous firmware behaviors, and cross-layer scheduling effects. Adversaries are stylized (sensitivity analyses) and not fully adaptive beyond disorder amplification. Mixed deployments (802.11p with LTE-V2X) may shift the optimal thresholds $(S_{\mathrm{th}},H_{\mathrm{th}})$, but do not negate the central finding: an entropy-conditioned rigor policy improves timeliness and coherence under churn.

Operational Guidance

For dense corridors, trigger CF when $S>S_{\mathrm{th}}$ to avoid dwell-induced rebroadcast storms. Prefer PoS/FBA (or an adaptive hybrid) in high-S/high-$H_{\mathrm{spatial}}$ windows to meet V2X-style deadlines and conserve energy. Deploy Engines per cluster/segment in partition-prone areas to preserve convergence and accelerate recovery, while using QoI filtering to reduce invalid admission and wasted work.

Editorial and Reproducibility Adjustments

• Definitions centralized. Entropy normalization and $D_{\mathrm{ledger}}\left(t\right)$ are stated once and cross-referenced (Section 3.1).
• Protocol unified. NS-3.35 is the reference; 600 s/30-seed runs are standard unless explicitly stated (Table 8).
• Energy accounting clarified. Reported energies are simulation-native (radio+analytical crypto) with no host-measurement mixing (Section 5.7).
• Traceability. Logged schemas and scripts ensure that all plots and statistics can be reproduced from per-run artifacts (Section 5.5–Section 5.9).

8. Conclusions and Future Directions

Several research directions follow naturally from the present results and from the limits of full-fidelity VANET simulation. First, scaling beyond the $N\le 100$ range evaluated here will require hierarchical governance: cluster-local Engines can be composed into multi-tier control, where intra-cluster consensus remains latency-feasible while inter-cluster reconciliation is performed less frequently and with stronger anchoring to preserve coherence under large-area fragmentation. Such designs can also incorporate sharded validation and selective state dissemination to reduce control-plane load in dense corridors. Second, the current maps $g(·)$ and $f(·)$ can be extended to account for heterogeneous energy states and device constraints. In realistic fleets, OBUs exhibit varying battery levels, compute capabilities, and duty-cycling policies. Incorporating per-node energy state and harvested-power profiles into the rigor policy would enable explicit energy-aware governance, e.g., shifting expensive validation toward nodes or roadside infrastructure with renewable power while maintaining bounded latency for safety-critical updates. Third, predictive control offers a principled upgrade path. Instead of reacting to spikes in S or $H_{\mathrm{spatial}}$, short-horizon forecasting of mobility and topology could pre-emptively adjust validation strength before fragmentation occurs. This can be combined with learning-based QoI filters that detect anomalies or malicious patterns prior to consensus, provided that false-positive rates are bounded to avoid suppressing legitimate safety messages. Finally, security-oriented extensions merit dedicated study under stronger adversarial models. Future work should integrate Sybil-resistant membership services for validator/quorum selection, rotating quorum slices for eclipse resilience, and explicit checkpointing/anchoring strategies to bound reorganization depth after partitions. Evaluations should include adaptive attackers that attempt strategic entropy manipulation and long-lived eclipses, allowing formalization of security guarantees under bounded Byzantine fractions and under mode transitions. City-scale studies with mixed 802.11p/C-V2X stacks and larger N via hierarchical simulation would then quantify control-loop stability and operational trade-offs under heavy bursts and heterogeneous radios.

8.1. Key Conclusions

H₁ — Consensus as an energy cycle.

As informational disorder rises, PoW becomes increasingly expensive: in the crypto-only panel (Figure 4), PoW energy per block grows sharply with S, reaching $\sim 600$ J at high entropy, whereas PoS remains near-constant in the sub-Joule regime (with DPoS/FBA in single-digit Joules). This confirms the central entropy–work coupling predicted by the Ideal Information Cycle (Figure 1) and motivates avoiding PoW in high-S windows. The magnitude is consistent with $E_{\mathrm{block}}^{\left(\mathrm{crypto}\right)}=e_h\mathbb{E}\left[n_{\mathrm{hash}}\right]$ and $\mathbb{E}\left[n_{\mathrm{hash}}\right]=2^{256}/D$ under the V2X-feasible targets imposed by $g(S,H_{\mathrm{spatial}})$ (Section 3.6.5), i.e., difficulties far below cryptocurrency-scale PoW but aligned with deadline constraints.

H₂ — Consensus-first triggering improves timeliness and reduces overhead.

In the baseline urban case ($N=50$, $S_{\mathrm{th}}=0.5$), Consensus-First (CF) reduces agreement/commit latency and increases throughput relative to Broadcast-First (BF), while reducing packet overhead (Figure 5Figure 6). Concretely, latency drops from $\sim 300$ ms to $\sim 150$ ms (95% CI: 135–165 ms), throughput rises from $\sim 120$ tx/s to $\sim 200$ tx/s (95% CI: 185–215 tx/s), and normalized overhead is roughly halved. This validates H₂ and supports a practical control rule: when S crosses $S_{\mathrm{th}}$, shorten the injection leg by validating immediately rather than accumulating broadcast dwell.

H₃ — QoI filtering reduces wasted work.

QoI-aware candidate construction (prioritizing fresher transactions with small $\Delta t_i$ and excluding invalid/stale payloads with ${ϵ}_i=1$) prevents consensus effort from being spent on low-quality microstates. In the QoI ablation (Table 11), filtering reduces invalid admissions and invalid-block share, lowers the fraction of cryptographic energy wasted on orphaned/invalid outcomes, and improves confirmation latency under identical network conditions. The directionality is stable across matched seeds and aligns with the Engine’s design goal: compress disorder while preserving QoI.

H₄ — Dynamic tuning improves efficiency and stability.

Adaptive maps $g(S,H_{\mathrm{spatial}})$ and $f(S,H_{\mathrm{spatial}})$ yield better operating points than static PoW/PoS and non-adaptive hybrids. In the expanded comparison (Section 6.8), the proposed Hybrid Engine achieves the lowest transaction confirmation latency with competitive total per-block energy while sustaining higher throughput than static baselines and a vanilla hybrid (Figure 10, Figure 11 and Figure 12). These results validate H₄: tuning rigor as a function of $(S,H_{\mathrm{spatial}})$ improves throughput-per-energy and reduces coherence loss relative to static parameters.

H₅ — Convergence and coherence under high entropy.

Under dispersion and transient disconnections, microstate alignment degrades for static schemes. The Engine maintains markedly lower ledger divergence in high-$H_{\mathrm{spatial}}$ regimes (Figure 9) and recovers faster after partitions and eclipse windows (Section 6.7), indicating improved convergence under stress. Operationally, this confirms H₅: conditioning rigor on observed disorder yields more coherent ledgers even when connectivity becomes intermittent.

Additional empirical observation: spatial dispersion is a reliable stress signal.

Independent of hypothesis labels, spatial entropy is a strong predictor of governance stress. As $H_{\mathrm{spatial}}\to 1.0$, static PoW exhibits increasing latency and decreasing validation accuracy (Figure 7). The Engine mitigates this degradation by tightening validation and/or switching away from regimes that amplify forks, thereby preserving both timeliness and correctness in dispersed topology windows.

8.2. Limitations

• Scale. The main study evaluates up to $N\le 100$ vehicles under full PHY/MAC fidelity; we do not extrapolate beyond this range. An auxiliary profiling harness (Section 5.10) supports larger-N algorithmic stress tests but is non-claiming.
• Energy model abstraction. Per-hash ($e_h$) and per-signature ($e_{\mathrm{sig}}$) costs (Table 5) are embedded-class software constants used in an analytical crypto term paired with NS-3 radio energy. Claims focus on relative scaling with S and $H_{\mathrm{spatial}}$; absolute magnitudes will shift with accelerators and platform heterogeneity.
• PHY/MAC fidelity and channel effects. NS-3’s IEEE 802.11p/C-V2X abstractions omit some physical nonlinearities (e.g., rich multipath/interference coupling in dense urban canyons). Field calibration is needed for deployment-grade parameterization.
• Adversary scope. Stressors are stylized sensitivity analyses; fully adaptive collusion (strategic Sybil/eclipsing with learning) is left for future work. Partition events are scheduled k-cuts in simulation (Section 5.3); real cities may exhibit more complex, correlated failures.
• Right-censoring under impractical regimes. In high-disorder configurations, Pure PoW may fail to confirm within the 600 s horizon; in such cases the plotted “600000 ms” should be read as “≥600 s” rather than an exact mean, reinforcing the practicality motivation for adaptive hybrid governance.
• Protocol uniformity. All reported results use NS-3.35, 600 s duration, and 30 matched seeds unless explicitly stated.

8.3. Future Directions

Future work should prioritize scaling the entropy-governed control loop beyond the $N\le 100$ full-PHY/MAC regime studied here by introducing hierarchical Engines that operate at multiple tiers (intra-cluster and inter-cluster). A natural extension is to assign local Engines to connected components while an upper-tier coordinator (e.g., RSU-backed or infrastructure-assisted) mediates cross-cluster anchoring and conflict resolution, thereby preserving low finality while reducing the coordination burden in dense grids and long corridors.

A second direction is to incorporate heterogeneous energy profiles into the policy maps. In real fleets, OBUs differ in battery state, compute capability, and duty-cycling constraints; thus, $f(·)$ and $g(·)$ can be augmented with per-node energy state (battery/harvesting) and platform-aware cost coefficients to avoid systematically overloading constrained devices. This would convert the current cluster-level rigor policy into a device-aware governance mechanism that explicitly trades timeliness against the remaining energy budget and the expected contact time within connectivity windows.

Third, deployments can benefit from shifting expensive work to renewable-powered infrastructure through a proof of useful work (PoUW) concept at RSUs. Rather than spending scarce vehicular energy on repeated hashing or excessive endorsements, RSUs could carry out verifiable edge tasks (e.g., aggregation, model updates, or safety analytics) whose outputs are attestable and can serve as a commitment primitive. This would keep OBUs predominantly in low-cost regimes while preserving a stronger operational security envelope than latency-feasible PoW alone.

Fourth, the Engine can be made predictive by integrating mobility and topology forecasting to adjust rigor preemptively before entropy spikes occur. Short-horizon predictors (e.g., based on vehicle density, projected dispersion, and link-quality trends) could modulate $(S_{\mathrm{th}},H_{\mathrm{th}})$ or directly regularize $f,g$ so that the control loop reacts before contention and fragmentation inflate orphaning and divergence. This is particularly relevant in urban canyons and merge-lane bottlenecks where entropy rises rapidly and reactive switching may be late.

Fifth, we propose strengthening the QoI layer through bounded-risk learning for pre-consensus filtering. Lightweight anomaly detection or classifier-assisted admission (trained on delay/error tiers and message consistency features) could reduce malicious or low-QoI payloads with controlled false-positive rates. Importantly, such filters should be evaluated under distribution shift and coupled to the Engine with conservative risk bounds so that gains in timeliness do not come at the expense of excluding valid safety-critical messages.

Sixth, large fleets require succinct microstate telemetry to monitor coherence without inflating overhead. Merkle proofs, sketches, or Bloom-filter summaries can approximate divergence and membership state across clusters at low bandwidth cost, enabling $D_{\mathrm{ledger}}\left(t\right)$-like monitoring and re-convergence triggers without per-event detailed exchanges. This direction complements hierarchical Engines by providing scalable observability.

Finally, future evaluations should expand the adversarial and environmental envelope by analyzing adversary-resilient adaptation under more adaptive attackers and by validating at city scale. This includes combining Sybil-resistant staking (or credential governance), rotating quorum slices, and eclipse detection, as well as studying control-loop stability under heavy burst traffic and heterogeneous radios in mixed C-V2X/802.11p settings. A city-scale campaign (e.g., $N\ge 500$) should explicitly separate (i) non-claiming algorithmic stress tests from (ii) claiming regimes with documented fidelity, ensuring that scalability conclusions are supported by appropriately instrumented experiments and by transparent reporting of which effects are simulated at full PHY/MAC versus abstracted.

8.4. Artifacts and Reproducibility

All figures in Section 6 are generated from per-event CSV logs via the version-controlled Python pipeline described in Section 5.9. Random seeds (30 per configuration), calibrated parameters (Section 3.6.5), fork/orphan definitions, and partition schedules are documented in the repository layout. Energy accounting uses only NS-3’s radio models plus the analytical crypto term ($e_h,e_{\mathrm{sig}}$); no host-side power tools are mixed with simulated per-node energy. The $D_{\mathrm{ledger}}\left(t\right)$ formula used in plots and statistics is the LCP-normalized definition in Section 3.1.

8.5. Concluding Remarks and Conceptual Scope

Our thermodynamic language is operational rather than a claim of physical equivalence: S and $H_{\mathrm{spatial}}$ are measurable disorder observables used to price consensus rigor; the Engine injects consensus work to compress disorder only when needed. The adaptive maps g and f act on dimensionless target/threshold registers anchored by calibration (Section 3.6.5) and are justified by shape constraints and data-driven selection. Within this scope, governing consensus via entropy observables yields an energy-aware, latency-conscious, and resilient ledger for safety-critical V2X. More broadly, the “information engine” principle may extend to other resource-constrained distributed ledgers (IoT, supply chains, edge systems): dynamically pricing rigor against measured disorder provides a pragmatic blueprint for sustainable and adaptive consensus.

Appendix A.1. Procedure A.1: VANET Engine (Entropy-Driven Loop)

Algorithm A1 VANET Engine main loop (pseudocode)

Require: Sampling period $\Delta T$; calibrated maps $g(·),f(·)$; thresholds $S_{\mathrm{th}},H_{\mathrm{th}}$ Ensure: Safety (no double-commit), eventual liveness within connected components   1: repeat every$\Delta T$or upon CAM/DENM reception:   2: (Measure) Read $S\leftarrow \mathrm{MeasureInformationalEntropy}\left(\right)$; $H\leftarrow \mathrm{MeasureSpatialEntropy}\left(\right)$   3: (Smooth)$(\widehat{S},\widehat{H})\leftarrow \mathrm{EMA}(S,H;\lambda )$▹ avoid thrashing   4: (Adapt)$D\leftarrow g(\widehat{S},\widehat{H})$;    $\Theta \leftarrow f(\widehat{S},\widehat{H})$▹ policy maps; see Sec. Section 3.6.5 and Sec. Section 3.6.8   5: (Select mode)   6: if$\widehat{S}>S_{\mathrm{th}}$or$\widehat{H}>H_{\mathrm{th}}$then   7:      if FBA is enabled then $\mathrm{mode}\leftarrow$ FBA else$\mathrm{mode}\leftarrow$ PoS/DPoS   8: else   9:      $\mathrm{mode}\leftarrow$ PoW   10: end if   11: (Assemble)${\mathcal{T}}_k\leftarrow \mathrm{FormCandidateSet}\left(\mathrm{QoI}\mathrm{filter}\right)$▹ prioritize low $\Delta t_i$; drop stale/invalid (${ϵ}_i=1$)   12: (Execute)   13: switch mode:   14: case PoW: $B^{★}\leftarrow \mathrm{Mine}({\mathcal{T}}_k,D)$▹ burn $e_h$ per hash   15: case PoS/DPoS: $B^{★}\leftarrow \mathrm{StakePropose}({\mathcal{T}}_k,\Theta )$▹ sign/verify; burn $e_{\mathrm{sig}}$   16: case FBA: $B^{★}\leftarrow \mathrm{QuorumCommit}({\mathcal{T}}_k,Q_k)$▹ quorum slices   17: (Commit) if$B^{★}\ne ⌀$then append; purge conflicts; log metrics

Remarks. (i) EMA smoothing ($\lambda \in [0,1)$) prevents oscillations around thresholds; (ii) liveness holds within a connected component assuming eventual synchrony and honest-majority (or honest quorum slices) in PoS/FBA regimes; (iii) safety is enforced via replay/double-commit checks in ValidateBlockCandidate().

Appendix A.2. Procedure A.2: Proof-of-Work (PoW) Module

Algorithm A2 PoW consensus (pseudocode)

Require: Template block B; entropy observables $(\widehat{S},\widehat{H})$; timeout ${\tau }_{max}$ Ensure: Valid block or null upon timeout   1: $D\leftarrow \mathrm{Clamp}(g(\widehat{S},\widehat{H}),D_{min},D_{max})$▹D is a 256-bit target (dimensionless; smaller ⇒ harder)   2: $\nu \leftarrow 0$; $t_{\mathrm{end}}\leftarrow t_{\mathrm{now}}+{\tau }_{max}$   3: while$t_{\mathrm{now}}<t_{\mathrm{end}}$do   4:     $B.\mathrm{nonce}\leftarrow \nu$; $h\leftarrow \mathrm{Hash}\left(B\right)$; burn$e_h$   5:     if $h<D$thenreturnB   6:     end if   7:     $\nu \leftarrow \nu +1$   8: end while   9: return null

Energy link.$E_{\mathrm{crypto}}^{\left(\mathrm{PoW}\right)}\approx e_h·\mathbb{E}\left[\nu \right]$, with $\mathbb{E}\left[\nu \right]\approx {\displaystyle \frac{2^{256}}{D}}$ under uniform hashes. This is the basis for the high-entropy PoW regime shown in Figure 4.

Appendix A.3. Procedure A.3: Proof-of-Stake / Delegated PoS (PoS/DPoS)

Algorithm A3 PoS/DPoS consensus (pseudocode)

Require: Stake/validator set $\mathcal{V}$; rigor register $\Theta$; election window ${\tau }_{\mathrm{elec}}$ Ensure: Single proposer; quorum of signatures; valid block or null   1: if DPoS then $\mathcal{V}\leftarrow \mathrm{DelegateElection}(\mathcal{V},{\tau }_{\mathrm{elec}})$   2: $\mathrm{proposer}\leftarrow \mathrm{SelectValidator}(\mathcal{V},\Theta ,\mathrm{VRF}/\mathrm{lottery})$   3: $B\leftarrow \mathrm{AssembleBlock}\left({\mathcal{T}}_k\right)$; sign$\left(B\right)$; burn$e_{\mathrm{sig}}$   4: broadcast$\langle B,\sigma \rangle$; collect votes/endorsements until quorum or timeout   5: if$\mathrm{QuorumReached}$thenreturnB   6: elsereturn null   7: end if

Energy link.$E_{\mathrm{crypto}}^{(\mathrm{PoS}/\mathrm{DPoS})}\approx e_{\mathrm{sig}}·n_{\mathrm{sig}}$, where $n_{\mathrm{sig}}$ counts proposal, vote/endorsement, and verification operations (as logged by the module).

Appendix A.4. Procedure A.4: Federated Byzantine Agreement (FBA)

Algorithm A4FBA consensus (pseudocode)

Require: Quorum slices $\left\{Q_k\right\}$; freshness bound ${\tau }_{\mathrm{fresh}}$ Ensure: Commit on federated quorum; or null on stall/partition   1: $B\leftarrow \mathrm{AssembleBlock}\left({\mathcal{T}}_k\right)$; broadcast$\mathrm{PREPARE}\left(B\right)$   2: repeat exchange $\{\mathrm{PREPARE},\mathrm{COMMIT}\}$ with peers in $Q_k$ until federated quorum satisfied or ${\tau }_{\mathrm{fresh}}$ exceeded   3: if$\mathrm{FederatedQuorum}$thenreturnB   4: elsereturn null   5: end if

Notes. Quorum slices $Q_k$ are proximity/recency-based and refreshed periodically (e.g., every 10 s). Localized quorums enable fast commits inside connected subgraphs.

Appendix A.5. Procedure A.5: Complexity and Cost Summary

Table A1. Asymptotic cost per block (worst case). $n=\left|{\mathcal{T}}_k\right|$ candidate tx; $d=$ network diameter; $v=\left|Q_k\right|$. Energy parameters follow Table 5.

Module	Time (local)	Messages (network)	Energy (per block)
PoW	$\mathcal{O}\left(\mathbb{E}\right[\nu \left]\right)$	$\mathcal{O}\left(1\right)$ broadcast	$\mathbb{E}\left[\nu \right]·e_h+\mathcal{O}\left(n\right)$ verify
PoS/DPoS	$\mathcal{O}\left(n\right)$ verify	$\mathcal{O}\left(d\right)$ votes	$e_{\mathrm{sig}}·n_{\mathrm{sig}}$
FBA	$\mathcal{O}\left(n\right)$ verify	$\mathcal{O}(v·d)$ quorum msgs	radio + signatures (mode-dependent)

Table A1. Asymptotic cost per block (worst case). $n=\left|{\mathcal{T}}_k\right|$ candidate tx; $d=$ network diameter; $v=\left|Q_k\right|$. Energy parameters follow Table 5.

Module	Time (local)	Messages (network)	Energy (per block)
PoW	$\mathcal{O}\left(\mathbb{E}\right[\nu \left]\right)$	$\mathcal{O}\left(1\right)$ broadcast	$\mathbb{E}\left[\nu \right]·e_h+\mathcal{O}\left(n\right)$ verify
PoS/DPoS	$\mathcal{O}\left(n\right)$ verify	$\mathcal{O}\left(d\right)$ votes	$e_{\mathrm{sig}}·n_{\mathrm{sig}}$
FBA	$\mathcal{O}\left(n\right)$ verify	$\mathcal{O}(v·d)$ quorum msgs	radio + signatures (mode-dependent)

Appendix A.6. Procedure A.6: Default Parameters and Justification

Table A2. Parameter defaults used by the Engine and their justification. Calibration details are in Section 3.6.5.

Parameter	Default	Basis / Rationale
Sampling period $\Delta T$	1 s	Matches metrics cadence; avoids over-reactivity
EMA factor $\lambda$	0.5	Reduces mode thrashing under bursty load
$S_{\mathrm{th}}$	0.5	Knee point in latency / delivery sweeps
$H_{\mathrm{th}}$	0.6	Delivery threshold onset in sweeps
Policy maps $g(·),f(·)$	see Section 3.6.5	Selected via 5-fold CV under monotonicity/stability constraints
${\tau }_{max}$ (PoW)	200 ms	Bounds mining stalls; respects VANET deadlines
$|Q_k|$ (FBA)	5 peers	Proximity-based slices; stable local quorums
${\tau }_{\mathrm{elec}}$ (DPoS)	5 s	Trade-off between churn and fairness

Table A2. Parameter defaults used by the Engine and their justification. Calibration details are in Section 3.6.5.

Parameter	Default	Basis / Rationale
Sampling period $\Delta T$	1 s	Matches metrics cadence; avoids over-reactivity
EMA factor $\lambda$	0.5	Reduces mode thrashing under bursty load
$S_{\mathrm{th}}$	0.5	Knee point in latency / delivery sweeps
$H_{\mathrm{th}}$	0.6	Delivery threshold onset in sweeps
Policy maps $g(·),f(·)$	see Section 3.6.5	Selected via 5-fold CV under monotonicity/stability constraints
${\tau }_{max}$ (PoW)	200 ms	Bounds mining stalls; respects VANET deadlines
$|Q_k|$ (FBA)	5 peers	Proximity-based slices; stable local quorums
${\tau }_{\mathrm{elec}}$ (DPoS)	5 s	Trade-off between churn and fairness

Appendix A.7. Procedure A.7: Ledger-Divergence Metric and Fork Detection (Restated)

Consistency note. The definitions below are identical to Section 3.2 and are restated here for completeness and reproducibility.

Ledger divergence D ledger (t).

Let $L_u\left(t\right)$ be the ordered block sequence at node u at time t with height $h_u\left(t\right)=\left|L_u\left(t\right)\right|$. For nodes $u\ne v$, let $\mathrm{LCP}(u,v,t)$ be the length of the longest common prefix of $L_u\left(t\right)$ and $L_v\left(t\right)$. Define

$$\delta (u,v,t)=1-{\displaystyle \frac{\mathrm{LCP}(u,v,t)}{max\{1,max(h_u\left(t\right),h_v\left(t\right))\}}},D_{\mathrm{ledger}}\left(t\right)={\displaystyle \frac{2}{N\left(t\right)\left(N\right(t)-1)}}\sum _{u<v}\delta (u,v,t)\in [0,1].$$

The value reported in figures is either the instantaneous $D_{\mathrm{ledger}}\left(t\right)$ at sampling instants or a time-average over a specified window, always computed from logged chain-prefix information.

Fork/orphan rate.

We report orphan/fork rate O as the fraction of produced blocks that do not lie on the final main chain at simulation end. Operationally, a block is marked orphaned if it is not on the selected main chain at run end (logged via orphan_flag; see Table 9). Thus,

$$O={\displaystyle \frac{\#\left\{\mathrm{orphaned}\mathrm{blocks}\right\}}{\#\left\{\mathrm{produced}\mathrm{blocks}\right\}}}\times 100\%.$$

Appendix A.8. Procedure A.8: Entropy Normalization and Boundedness (Restated)

Consistency note. The definitions below are consistent with Section 3.1 and are restated here for completeness and reviewer traceability.

Informational entropy S(t) (normalized Shannon).

At time t, let $\mathcal{T}\left(t\right)$ be the set of distinct pending transactions and let $c_i\left(t\right)$ be the number of nodes currently holding transaction $i\in \mathcal{T}\left(t\right)$. We apply Laplace smoothing $c_i\left(t\right)\leftarrow c_i\left(t\right)+\epsilon$ with $\epsilon ={10}^{-6}$ to avoid $ln0$. Define the normalized distribution

$${\tilde{p}}_i\left(t\right)={\displaystyle \frac{c_i\left(t\right)}{{\sum }_{k\in \mathcal{T}\left(t\right)}{c}_k\left(t\right)}},\sum _{i\in \mathcal{T}\left(t\right)}{\tilde{p}}_i\left(t\right)=1,$$

and compute the Shannon entropy (natural logarithm; nats)

$$S_{\mathrm{raw}}\left(t\right)=-\sum _{i\in \mathcal{T}\left(t\right)}{\tilde{p}}_i\left(t\right)ln{\tilde{p}}_i\left(t\right).$$

We report the bounded, normalized value

$$S\left(t\right)={\displaystyle \frac{S_{\mathrm{raw}}\left(t\right)}{ln\left|\mathcal{T}\right(t\left)\right|}}\in [0,1].$$

Spatial entropy H spatial (t) (normalized Shannon).

Partition the scenario area into M spatial bins (Table 8). Let $n_j\left(t\right)$ be the number of vehicles in bin j and $N\left(t\right)={\sum }_{j=1}^M{n}_j\left(t\right)$. With $q_j\left(t\right)=n_j\left(t\right)/N\left(t\right)$, ${\sum }_{j=1}^M{q}_j\left(t\right)=1$, define

$$H_{\mathrm{raw}}\left(t\right)=-\sum _{j=1}^M{q}_j\left(t\right)ln{q}_j\left(t\right),H_{\mathrm{spatial}}\left(t\right)={\displaystyle \frac{H_{\mathrm{raw}}\left(t\right)}{lnM}}\in [0,1].$$

Units/dimensions.

$S\left(t\right)$ and $H_{\mathrm{spatial}}\left(t\right)$ are dimensionless; normalization by $ln\left|\mathcal{T}\right(t\left)\right|$ and $lnM$ ensures boundedness in $[0,1]$ under the stated definitions.

Appendix B.1. Cross-Validation Protocol and Selection Criterion

We use 5-fold cross-validation with folds split by matched random seeds to avoid leakage across conditions. For each candidate function family, we compute the fold-wise validation loss and select the model with minimal mean loss. Constraint satisfaction (monotonicity in S and Lipschitz stability in $H_{\mathrm{spatial}}$) is verified per fold.

Appendix B.2. Constraint Checks and Stability

We report: (i) the fraction of samples violating monotonicity prior to projection, (ii) post-projection violations (should be zero by construction), and (iii) an empirical Lipschitz score measuring $max|\Delta \Theta |/|\Delta H_{\mathrm{spatial}}|$ over neighboring bins.

Appendix B.3. Model-Family Comparison (Summary)

We provide the ranked candidate families (polynomial, exponential, logarithmic, Fourier, spline) with their mean fold-loss and standard deviation. Fourier terms are retained only if they improve mean validation loss by at least 1% across folds and do not increase mode-switch thrashing.

Appendix B.4. Sensitivity to Coefficient Perturbations

We perturb fitted coefficients by $\pm 10\%$ and re-run the post-processing pipeline to confirm qualitative trends (latency, energy, orphan rate, and $D_{\mathrm{ledger}}$) are preserved.