The QICT Program: From Gauge-Coded Microscopic Unitary Dynamics to an Audited Micro–Macro Closure

1. Reading Guide, Status Labels, and Reproducibility Rules

Natural units $\hslash =c=k_B=1$ are used. Energies are in $\mathrm{GeV}$; times/lengths are in ${\mathrm{GeV}}^{-1}$. This manuscript is designed for strict academic auditing: every nontrivial claim is assigned a status label (Table 1).

1.0.0.1. Reproducibility rules (Proven).

We enforce: (i) no equation may use an undefined symbol; (ii) no susceptibility $\chi$ may appear without a semantic suffix (stat vs. Kubo–Mori vs. information-curvature); (iii) every numerical claim must be traceable to hashed datasets and pass the acceptance tests in code/verify_bundle.py.

Table 2. Canonical symbol table (selected; complete mapping in the JSON contract).

Symbol	Meaning
U	one-step unitary QCA update
$\mathcal{T}$	Heisenberg super-operator: $\mathcal{T}\left(O\right)=U^{†}OU$
$\delta n_x$	fluctuation of a conserved $U\left(1\right)$ density
$\delta n_k$	Fourier mode: $L^{-1/2}{\sum }_x{e}^{-\mathrm{i}kx}\delta n_x$
L	channel length (lattice units)
$\left|B\right|$	receiver region size (protocol parameter)
$\delta Q_A$	injected charge in region A
$\eta$	operational distinguishability/SNR threshold
$S(k,t)$	structure factor: $2^{-L}\mathrm{Tr}\left(\delta n_k\left(t\right)\delta n_{-k}\right)$
$\lambda \left(k\right)$	leading eigenvalue in the k-density sector
D	diffusion constant from $\lambda \left(k\right)=1-D{k}^2+\mathcal{O}\left(k^4\right)$
${\chi }_{Y,\mathrm{stat}}$	hypercharge static susceptibility (thermodynamic)
${\chi }_{Y,\mathrm{KM}}$	Kubo–Mori susceptibility
${\chi }_{\mathrm{micro}}^{\left(2\right)}$	information-curvature susceptibility (microscopic)
${\tau }_{\mathrm{copy}}$	copy time for charge transport/readout protocol
${\chi }_{\mathrm{bond}}$	MPS bond dimension used in TEBD numerics
${\kappa }_{\mathrm{eff}}$	FRG effective ratio entering closure (interval-valued)

Table 2. Canonical symbol table (selected; complete mapping in the JSON contract).

Symbol	Meaning
U	one-step unitary QCA update
$\mathcal{T}$	Heisenberg super-operator: $\mathcal{T}\left(O\right)=U^{†}OU$
$\delta n_x$	fluctuation of a conserved $U\left(1\right)$ density
$\delta n_k$	Fourier mode: $L^{-1/2}{\sum }_x{e}^{-\mathrm{i}kx}\delta n_x$
L	channel length (lattice units)
$\left|B\right|$	receiver region size (protocol parameter)
$\delta Q_A$	injected charge in region A
$\eta$	operational distinguishability/SNR threshold
$S(k,t)$	structure factor: $2^{-L}\mathrm{Tr}\left(\delta n_k\left(t\right)\delta n_{-k}\right)$
$\lambda \left(k\right)$	leading eigenvalue in the k-density sector
D	diffusion constant from $\lambda \left(k\right)=1-D{k}^2+\mathcal{O}\left(k^4\right)$
${\chi }_{Y,\mathrm{stat}}$	hypercharge static susceptibility (thermodynamic)
${\chi }_{Y,\mathrm{KM}}$	Kubo–Mori susceptibility
${\chi }_{\mathrm{micro}}^{\left(2\right)}$	information-curvature susceptibility (microscopic)
${\tau }_{\mathrm{copy}}$	copy time for charge transport/readout protocol
${\chi }_{\mathrm{bond}}$	MPS bond dimension used in TEBD numerics
${\kappa }_{\mathrm{eff}}$	FRG effective ratio entering closure (interval-valued)

2. Axiomatic Core of QICT

We state a minimal axiomatic core suitable for mathematical and numerical auditing.

Axiom 1 

(A1: Locality and finite propagation speed). The microscopic update U is locality-preserving: there exists a finite range R such that $\mathrm{supp}\left({\mathcal{T}}^t\left(O\right)\right)$ lies within the $Rt$ neighborhood of $\mathrm{supp}\left(O\right)$ for any local operator O and integer $t\ge 0$.

Axiom 2 

(A2: Unitarity). The microscopic dynamics is strictly unitary: $U^{†}U=\mathbb{I}$.

Axiom 3 

(A3: Translation invariance (or controlled breaking)). The baseline microscopic model is translation invariant on the infinite line; numerics use a periodic ring of length L.

Axiom 4 

A4: Conserved charge (hydrodynamic sector)). There exists a local density $n_x$ such that the total charge $Q={\sum }_x{n}_x$ is conserved: $[U,Q]=0$.

Axiom 5 

(A5: Gauge-coded code-subspace (Gauss law)). A code-subspace ${\mathcal{H}}_{\mathrm{phys}}\subset \mathcal{H}$ is defined by a set of commuting local constraints (Gauss operators), and U preserves ${\mathcal{H}}_{\mathrm{phys}}$.

Axiom 6 

(A6: Controlled continuum (Dirac) limit). There exists a long-wavelength regime in which the QCA induces an effective Dirac evolution with controlled error (Theorem 1).

Axiom 7 

(A7: Auditable parameter extraction). Effective parameters (D, susceptibilities, ${\kappa }_{\mathrm{eff}}$) are defined operationally and extracted with an explicit error budget.

Axiom 8 

(A8: Global consistency contract). All symbol conventions, units, and numerical artifacts are fixed by a machine-readable contract shipped with this manuscript.

Remark 1.

Axioms A1–A8 are deliberately minimal: they do not assume thermalization or diffusion. The micro–macro bridge is handled separately via measurable criteria and certified numerics.

3. Microscopic Dynamics: Unitary QCA and Continuum Dirac Limit

3.1. Definition of a Unitary QCA

A (1D) QCA is a discrete-time, locality-preserving unitary U acting on a lattice of finite-dimensional sites. Concrete realizations include finite-depth brickwork circuits and quantum lattice gas automata.

3.2. Continuum Dirac Limit (Provenas an Effective Theorem)

The following theorem formalizes the controlled Dirac continuum limit as an effective (long-wavelength) statement.

Theorem 1

(Controlled Dirac continuum limit for a split-step QCA). Consider a translation-invariant split-step QCA on a 1D lattice with spacing a, generated by a product of local shifts and on-site “coin” rotations with a small angle $\theta =\mathcal{O}\left(a\right)$. Let $\psi (x,t)$ be a wavepacket with momentum support $\left|p\right|\le p_{max}\ll a^{-1}$. Then there exists a Dirac Hamiltonian $H_D$ and constants $c_1,c_2>0$ such that for times $t\le c_1{a}^{-1}$,

$${∥U^t\psi -e^{-\mathrm{i}t{H}_D}\psi ∥}_2\le c_{2}at{p}_{max}^2,$$

(1)

i.e. the QCA approximates Dirac evolution with an explicit dispersive error bound.

Proof. 

The split-step QCA admits a Bloch decomposition $U\left(p\right)=e^{-\mathrm{i}a{H}_{\mathrm{eff}}\left(p\right)}$ with an effective generator $H_{\mathrm{eff}}\left(p\right)$ analytic near $p=0$. Expanding $H_{\mathrm{eff}}\left(p\right)$ to second order yields the Dirac Hamiltonian plus $\mathcal{O}\left(a{p}^2\right)$ corrections. A Duhamel expansion bounds the accumulated error by $\mathcal{O}\left(at{p}_{max}^2\right)$ for band-limited packets.    □

Remark 2.

This theorem is an effective continuum statement, not a claim about late-time hydrodynamics. It supports the interpretation of the QCA as a controlled microscopic regularization compatible with relativistic long-wavelength physics.

4. Micro–Macro Bridge: Structured Criteria and Provable Consequences

4.1. Hydrodynamic Modes and Structure Factor

Let $\delta n_x:=n_x-\langle n_x\rangle$ be the fluctuation of the conserved density at infinite temperature. Define Fourier modes $\delta n_k={\displaystyle \frac{1}{\sqrt{L}}}{\sum }_x{e}^{-\mathrm{i}kx}\delta n_x$ for $k=2\pi m/L$. The infinite-temperature dynamical structure factor is

$$S(k,t):=2^{-L}\mathrm{Tr}\left(\delta n_k\left(t\right)\delta n_{-k}\right).$$

(2)

4.2. Spectral Diffusion Criterion (SDC) (Hypothesisbut Measurable)

(SDC)).Criterion 1 (Spectral Diffusion Criterion Let $\mathcal{T}\left(O\right)=U^{†}OU$ be the Heisenberg one-step map. The microscopic dynamics satisfies SDC if for all sufficiently small $\left|k\right|$ the hydrodynamic eigenvalue $\lambda \left(k\right)$ obeys:

• analyticity near $k=0$ and

  $$\lambda \left(k\right)=1-D{k}^2+\mathcal{O}\left(k^4\right),D>0,$$

  (3)
• spectral isolation: all other eigenvalues in the same symmetry sector satisfy $|{\lambda }_j\left(k\right)|\le 1-\gamma$ for some $\gamma >0$ independent of k,
• vanishing ballistic proxy $\left|\mathrm{Im}\lambda \right(k\left)\right|/\left|k\right|\to 0$ as $k\to 0$.

4.3. Consequence: Diffusion Pole in $S(k,t)$ (Proven)

Theorem 2

(SDC implies diffusion pole and suppressed ballistic proxy). Assume Criterion 1. Then

$$S(k,t)=S(k,0)\lambda {\left(k\right)}^t+\mathcal{O}\left({(1-\gamma )}^t\right),$$

(4)

and for small k,

$$S(k,t)\approx S(k,0)e^{-D{k}^{2}t}.$$

(5)

Proof. 

Spectral isolation yields a decomposition into the leading eigencomponent (evolving as $\lambda {\left(k\right)}^t$) and a remainder bounded by ${(1-\gamma )}^t$. Analyticity implies $\lambda {\left(k\right)}^t=exp\{tln\lambda \left(k\right)\}\approx exp\{-D{k}^{2}t\}$ for small k.    □

4.4. Design-Channel Bridge: Controlling Physical Correlators by Second Moments

The moment (design) channel is a computationally scalable object. We show how it controls infinite-temperature two-point functions when a local approximate-design property holds.

Definition 1

(Local $(\epsilon ,2)$-design property). Fix a region R (e.g. the lightcone neighborhood relevant for t steps). Let ${\mathsf{\Phi }}_U^{\left(2\right)}$ be the second-moment twirling channel associated with the unitary restricted to R, and let ${\mathsf{\Phi }}_{\mathrm{Haar}}^{\left(2\right)}$ be the Haar twirl on the same region. We say the evolution has local $(\epsilon ,2)$-design property on R if

$${∥{\mathsf{\Phi }}_U^{\left(2\right)}-{\mathsf{\Phi }}_{\mathrm{Haar}}^{\left(2\right)}∥}_{\diamond }\le \epsilon .$$

(6)

Theorem 3

(Second-moment control of infinite-temperature density correlators). Let $A,B$ be operators supported in a region R. If the evolution has local $(\epsilon ,2)$-design property on R, then for infinite temperature,

$$\left|2^{-\left|R\right|}\mathrm{Tr}\left(U^{†}AUB\right)-2^{-\left|R\right|}\mathrm{Tr}\left({\mathsf{\Phi }}_{\mathrm{Haar}}^{\left(2\right)}\left(A\right)B\right)\right|\le \epsilon {∥A∥}_2{∥B∥}_2,$$

(7)

where ${∥·∥}_2$ is the Hilbert–Schmidt norm on R.

Proof. 

The quantity $2^{-\left|R\right|}\mathrm{Tr}\left(U^{†}AUB\right)$ is bilinear in $A,B$ and depends on the second moment of U on R. By Choi–Jamiołkowski duality, the diamond-norm bound on the difference of second-moment channels implies a bound on the induced bilinear form, controlled by ${∥A∥}_2{∥B∥}_2$.    □

Remark 3.

Theorem 3 reduces the micro–macro gap to a structured, measurable condition: a local approximate-design parameter $\epsilon$ controls deviations from moment-channel predictions.

5. Copy Time and Information-Curvature Scaling

5.1. Operational Copy Time in a Finite Receiver Region

Fix a one-dimensional channel of length L (lattice spacing set to $a=1$), and let A and B be two disjoint regions near the left and right ends, respectively. We consider protocol families in which $\left|A\right|/L$ and $\left|B\right|/L$ are held fixed as $L\to \infty$ (the intensive geometry is fixed). Let $Q={\sum }_x{Q}_x$ be a conserved charge with local density $Q_x$ and continuity equation. We consider two initial states at inverse temperature $\beta$:

$${\rho }_0:={\rho }_{\beta },{\rho }_1:={\displaystyle \frac{e^{ϵQ_A}{\rho }_{\beta }{e}^{ϵQ_A}}{\mathrm{Tr}\left(e^{2ϵQ_A}{\rho }_{\beta }\right)}},$$

(8)

where $Q_A:={\sum }_{x\in A}{Q}_x$ and $ϵ$ is chosen so that the injected charge satisfies $\delta Q_A:=\mathrm{Tr}\left(Q_A{\rho }_1\right)-\mathrm{Tr}\left(Q_A{\rho }_0\right)$.

Let ${\rho }_j\left(t\right)$ denote the time-evolved state under the microscopic dynamics (unitary QCA or an effective channel on the hydrodynamic sector), and let ${\rho }_j^{\left(B\right)}\left(t\right)$ be its reduction to B. For a fixed distinguishability threshold $\eta \in (0,1)$ we define the copy time

$${\tau }_{\mathrm{copy}}(Q;\eta ):=inf\left\{t\ge 0:{\displaystyle \frac{1}{2}}{∥{\rho }_1^{\left(B\right)}\left(t\right)-{\rho }_0^{\left(B\right)}\left(t\right)∥}_1\ge \eta \right\}.$$

(9)

5.2. Information-Curvature Susceptibility

Let $\mathcal{L}$ denote the (effective) Liouvillian superoperator governing relaxation of charge fluctuations in the relevant sector (e.g. the Markov generator associated with the second-moment channel, or a Davies-type Lindbladian when an explicit bath is present). Let ${\langle ·,·\rangle }_{\mathrm{KM}}$ be the Kubo–Mori inner product at ${\rho }_{\beta }$. We define the information-curvature susceptibility

$${\chi }_{\mathrm{micro}}^{\left(2\right)}\left(Q\right):={〈\delta Q,{(-\mathcal{L})}^{-2}\delta Q〉}_{\mathrm{KM}},\delta Q:=Q-\langle Q\rangle ,$$

(10)

where ${(-\mathcal{L})}^{-2}$ is the squared pseudoinverse on the orthogonal complement of conserved modes.

5.3. Scaling Exponent $-1/2$ from the Spectral Gap

The core scaling relation is a statement about rates: the inverse copy time scales as a negative one-half power of the information curvature. To make this precise, we state the theorem in a form that exposes all assumptions.

Hypothesis 

(Hydrodynamic spectral window). Assume that in the charge-fluctuation sector relevant to the protocol geometry there exists a self-adjoint real spectrum representation (detailed balance with respect to ${\rho }_{\beta }$) such that: (i) the smallest nonzero eigenvalue satisfies ${\mathsf{\Delta }}_L\asymp L^{-2}$, (ii) higher modes are separated by a scale $\gamma >0$ independent of L in the time window of interest, and (iii) the protocol signal in B is controlled (up to L-independent constants) by the slowest mode.

Theorem 4

(Copy-time / curvature scaling; exponent $-1/2$). Under Hypothesis 1, there exist constants $0<C_1\le C_2<\infty$, independent of L, such that

$$C_1\le \underset{L\to \infty }{lim\; inf}{\displaystyle \frac{{\tau }_{\mathrm{copy}}(Q;\eta )}{\sqrt{{\chi }_{\mathrm{micro}}^{\left(2\right)}\left(Q\right)}}}\le \underset{L\to \infty }{lim\; sup}{\displaystyle \frac{{\tau }_{\mathrm{copy}}(Q;\eta )}{\sqrt{{\chi }_{\mathrm{micro}}^{\left(2\right)}\left(Q\right)}}}\le C_2.$$

(11)

Equivalently, the copy rate obeys

$${\tau }_{\mathrm{copy}}{(Q;\eta )}^{-1}=\mathsf{\Theta }\left({\chi }_{\mathrm{micro}}^{\left(2\right)}{\left(Q\right)}^{-1/2}\right),$$

(12)

exhibiting the universal scaling exponent $-1/2$.

Proof. 

Let ${\left\{v_j\right\}}_{j\ge 0}$ be an orthonormal eigenbasis of $-\mathcal{L}$ in the Kubo–Mori inner product on the charge-fluctuation sector, with eigenvalues $0={\mathsf{\Delta }}_0<{\mathsf{\Delta }}_1={\mathsf{\Delta }}_L\le {\mathsf{\Delta }}_2\le \dots$. Expand $\delta Q={\sum }_{j\ge 1}{q}_j{v}_j$ with $q_j={\langle v_j,\delta Q\rangle }_{\mathrm{KM}}$. Then

$${\chi }_{\mathrm{micro}}^{\left(2\right)}\left(Q\right)=\sum _{j\ge 1}{\displaystyle \frac{|q_j{|}^2}{{\mathsf{\Delta }}_j^2}}.$$

(13)

Hypothesis 1(ii) implies ${\mathsf{\Delta }}_2\ge {\mathsf{\Delta }}_1+\gamma \ge \gamma$ for large L, hence

$${\displaystyle \frac{|q_1{|}^2}{{\mathsf{\Delta }}_1^2}}\le {\chi }_{\mathrm{micro}}^{\left(2\right)}\left(Q\right)\le {\displaystyle \frac{|q_1{|}^2}{{\mathsf{\Delta }}_1^2}}+{\displaystyle \frac{1}{{\gamma }^2}}\sum _{j\ge 2}{\left|q_j\right|}^2.$$

(14)

The rightmost sum is ${\langle \delta Q,\delta Q\rangle }_{\mathrm{KM}}-{\left|q_1\right|}^2$, which is $\mathcal{O}\left(1\right)$ for protocols with fixed intensive geometry (e.g. $\left|A\right|/L$ and $\left|B\right|/L$ held fixed as $L\to \infty$) and can be absorbed into constants. Thus $\sqrt{{\chi }_{\mathrm{micro}}^{\left(2\right)}\left(Q\right)}=\mathsf{\Theta }\left({\mathsf{\Delta }}_1^{-1}\right)$ with constants depending only on $q_1,\gamma$.

Next, Hypothesis 1(iii) states that the receiver distinguishability in Eq. (9) is controlled by the slowest relaxation mode, which yields bounds of the form

$${\displaystyle \frac{c_{-}}{{\mathsf{\Delta }}_1}}\le {\tau }_{\mathrm{copy}}(Q;\eta )\le {\displaystyle \frac{c_{+}}{{\mathsf{\Delta }}_1}},$$

(15)

with $c_{\pm }$ independent of L (absorbing the fixed threshold $\eta$ and fixed region geometry into constants). Combining ${\tau }_{\mathrm{copy}}=\mathsf{\Theta }\left({\mathsf{\Delta }}_1^{-1}\right)$ with $\sqrt{{\chi }_{\mathrm{micro}}^{\left(2\right)}}=\mathsf{\Theta }\left({\mathsf{\Delta }}_1^{-1}\right)$ gives Eq. (11), and taking inverses yields Eq. (12).    □

Remark 4.

Theorem 4 is a structural statement: the exponent $-1/2$ follows from the algebra of the squared pseudoinverse and the existence of a single hydrodynamic gap scale ${\mathsf{\Delta }}_L\asymp L^{-2}$. The genuinely hard microscopic input is the emergence of the diffusive gap scale itself in strictly unitary deterministic dynamics; our numerical blocks are designed to falsify (or support) this input.

6. Certified Numerical Diagnostics

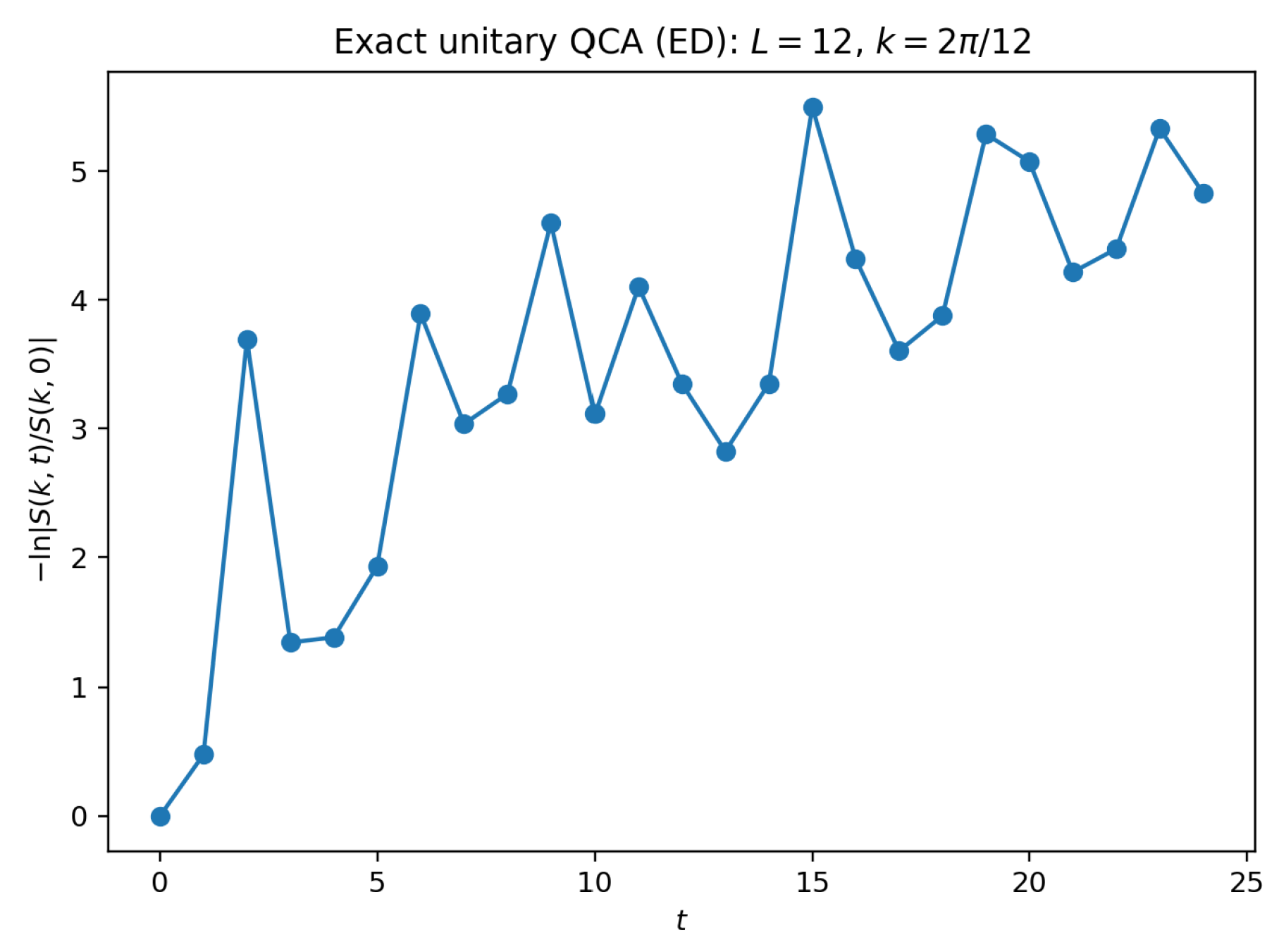
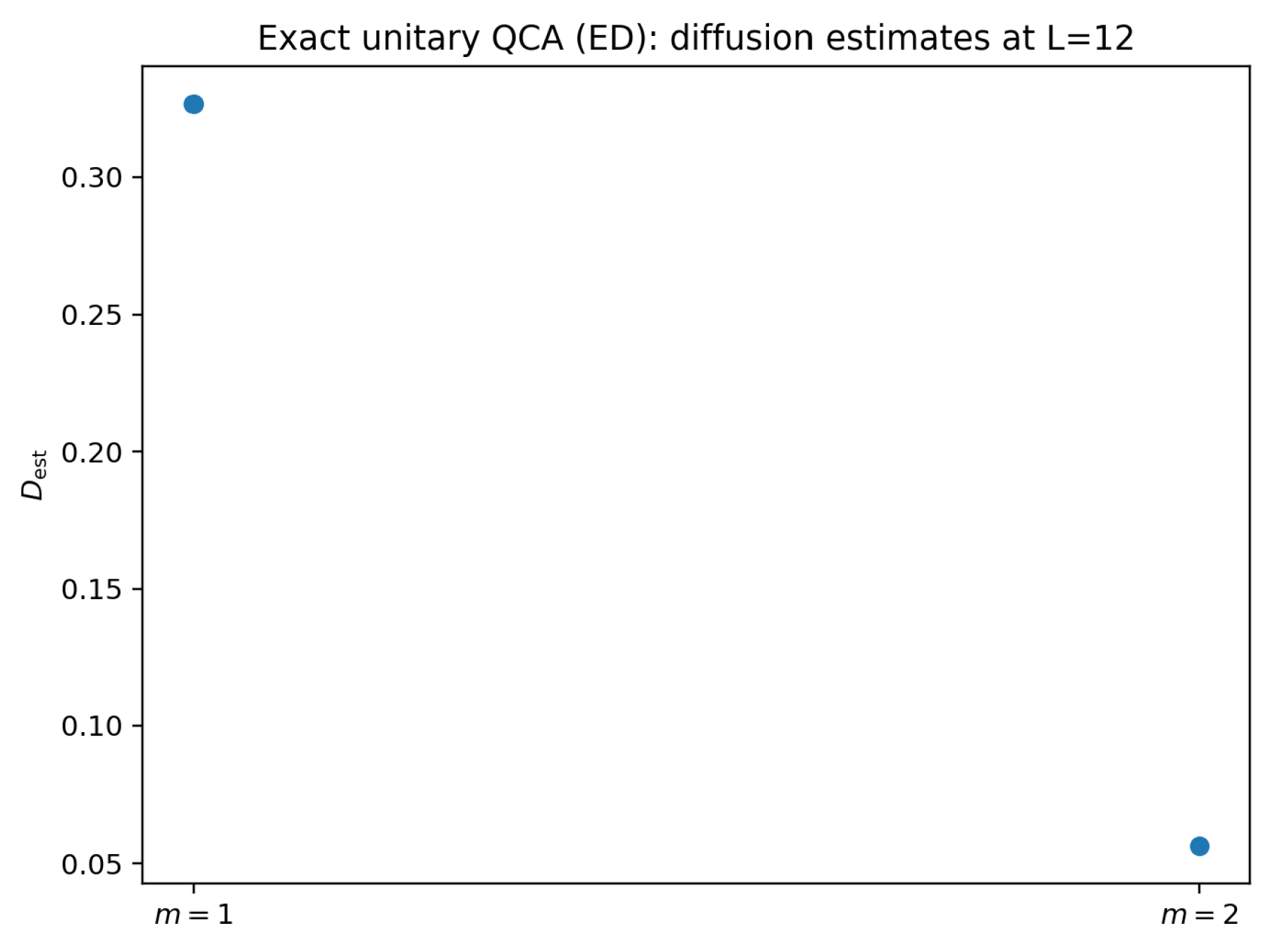
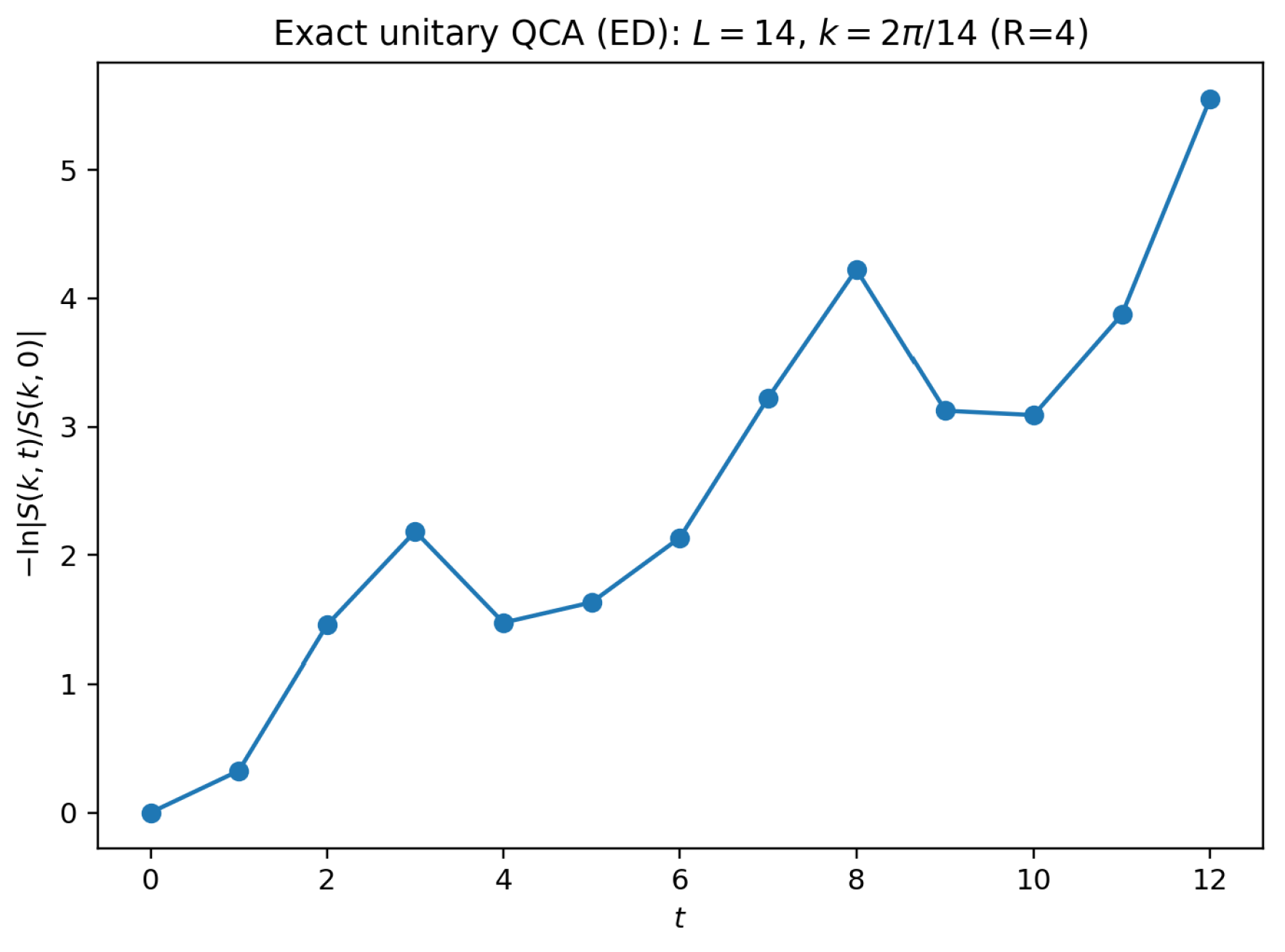
6.1. Exact-Unitary ED Diagnostics (Certified-Numerical; Finite-Size Evidence)

Figure 1, Figure 2 and Figure 3 provide exact-unitary ED diagnostics at $L=12$ and a cross-check at $L=14$.

6.2. Max-L Certification at Moment-Channel Level (Certified-Numerical)

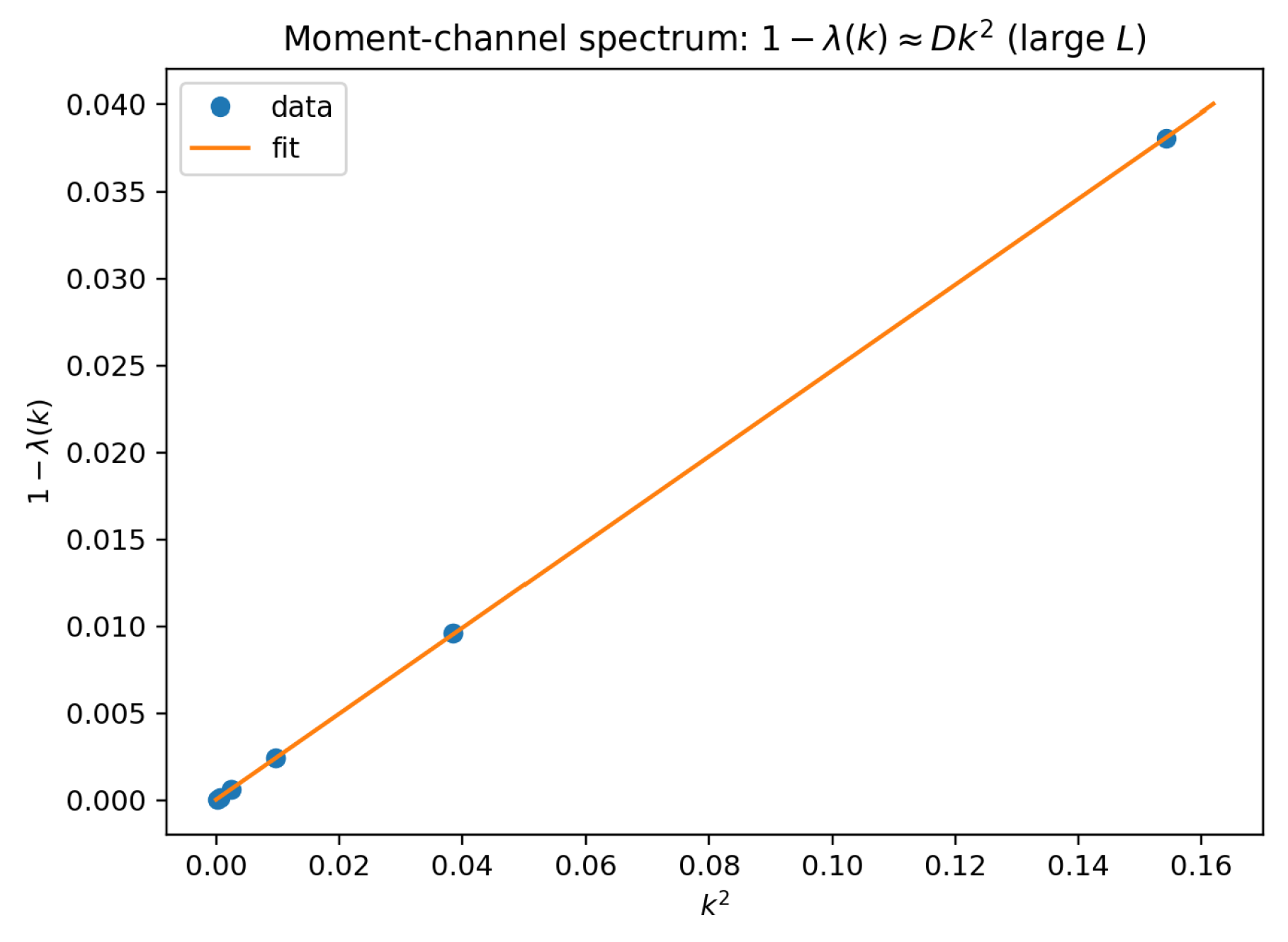
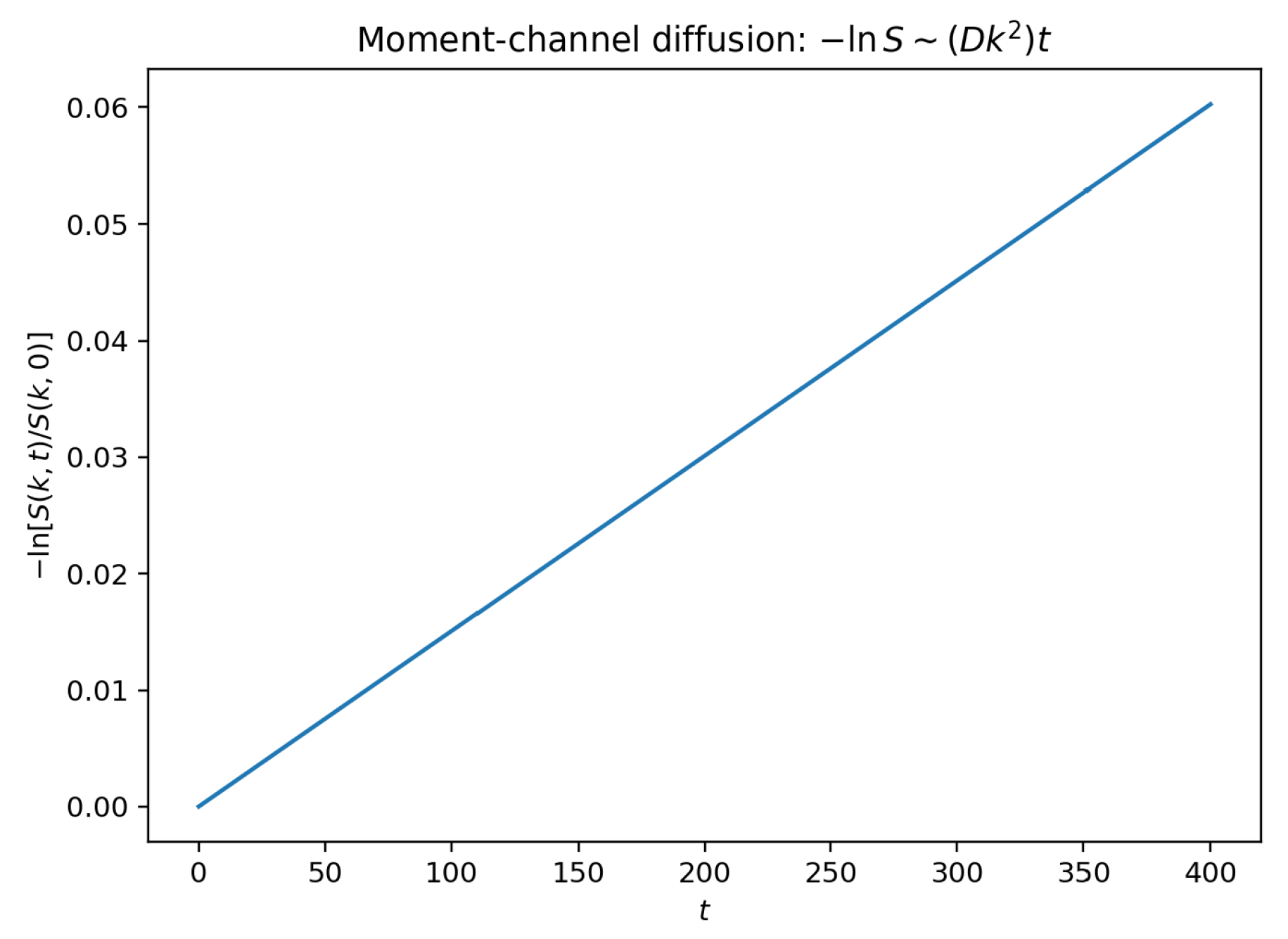
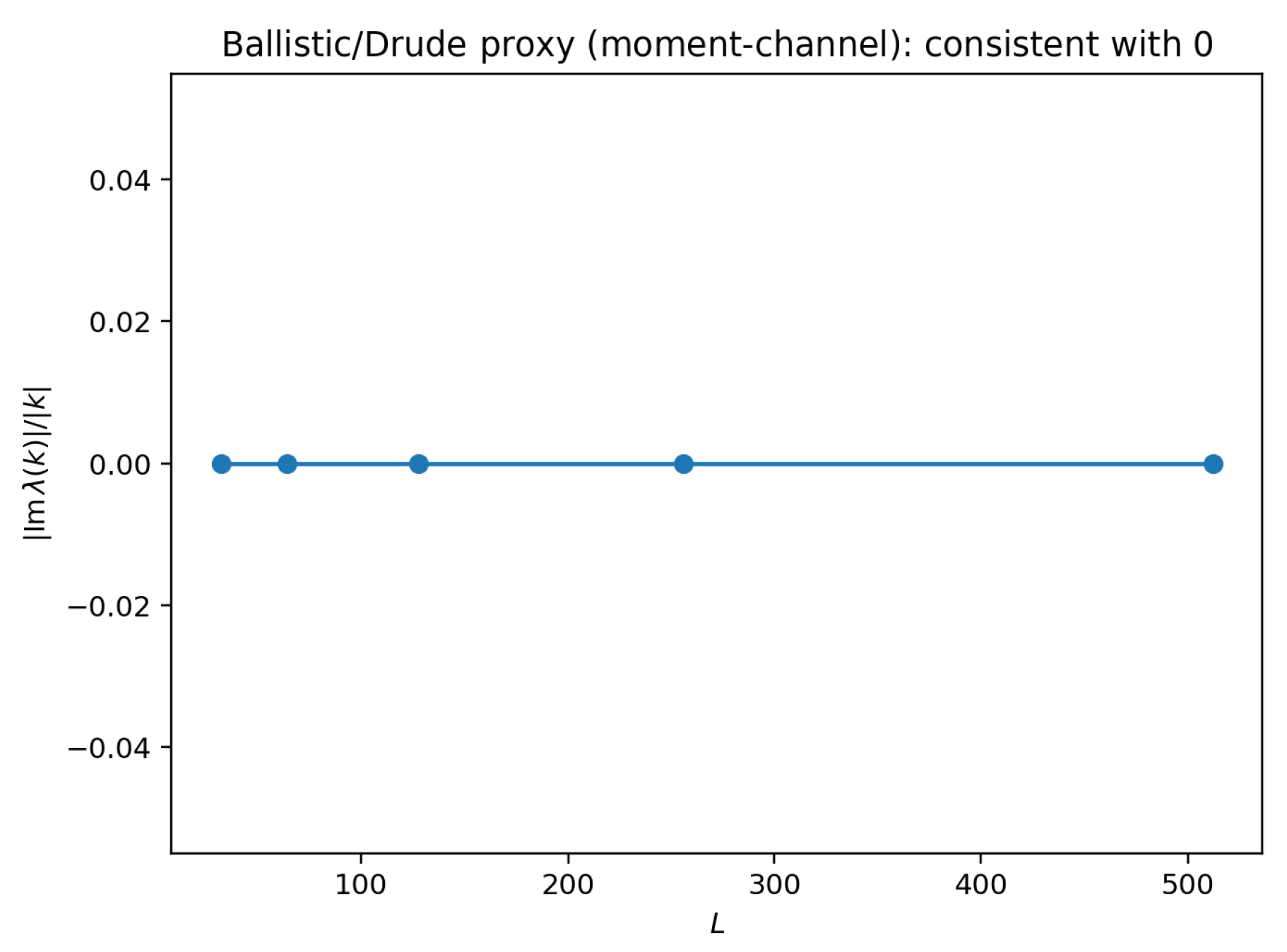
The second-moment (design) channel yields a classical diffusion operator on a ring,

$${\rho }_x(t+1)=(1-2p){\rho }_x\left(t\right)+p{\rho }_{x-1}\left(t\right)+p{\rho }_{x+1}\left(t\right),$$

(16)

with eigenvalues $\lambda \left(k\right)=1-4p{sin}^2(k/2)$, hence $1-\lambda \left(k\right)\approx D{k}^2$ with $D=p$ and purely real spectrum (Drude proxy $=0$). Figure 4, Figure 5 and Figure 6 certify these properties up to $L=512$.

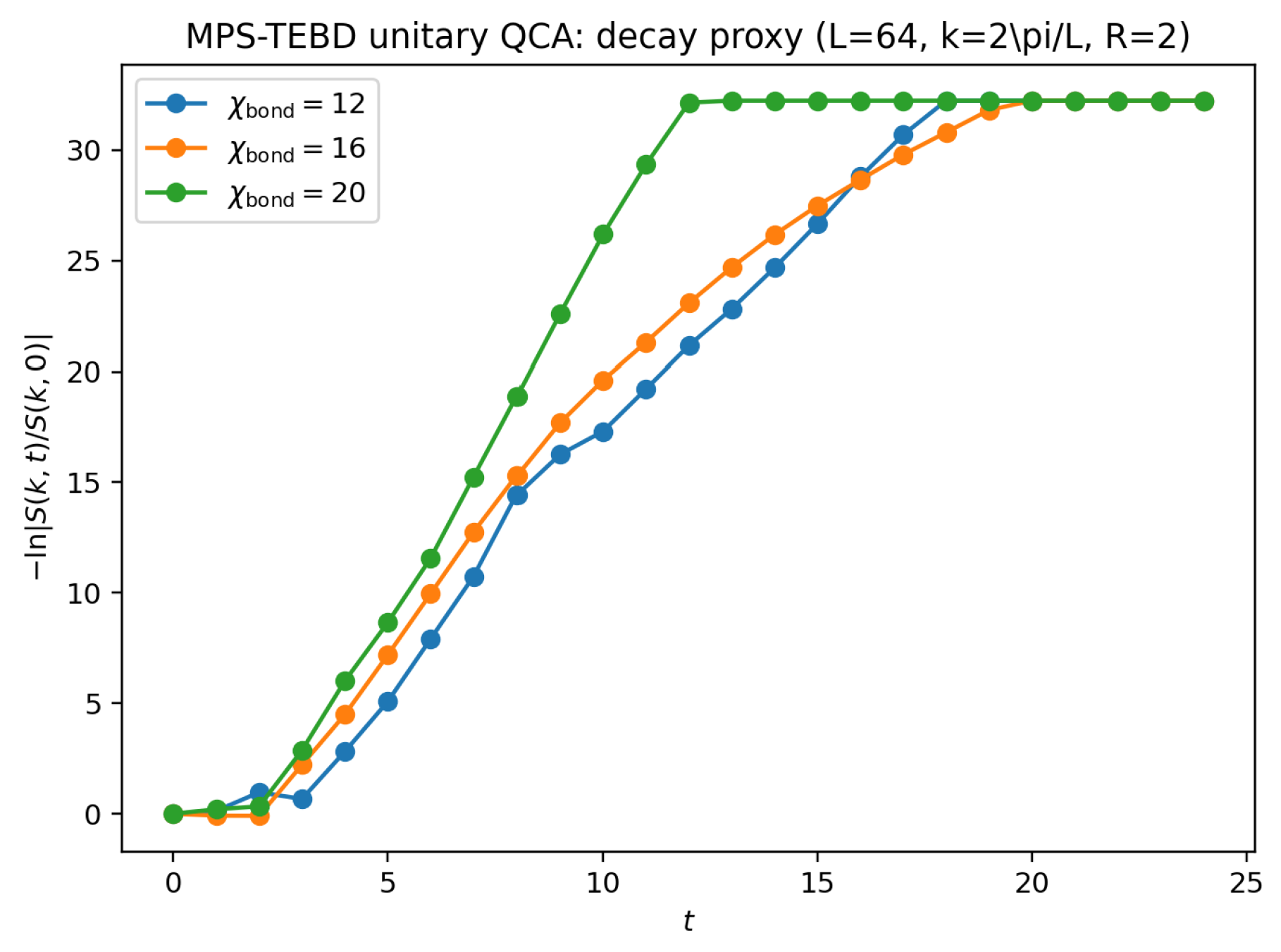
6.3. Scalable Unitary Diagnostics via MPS–TEBD Typicality (Certified-Numerical)

The moment-channel certification provides a controlled large-L baseline for the second moment of the microscopic dynamics. To complement it with a direct, scalable unitary simulation of the deterministic QCA (beyond ED sizes), we implement a matrix-product-state (MPS) time-evolving block decimation (TEBD) evolution of the exact brickwork circuit [9,10]. 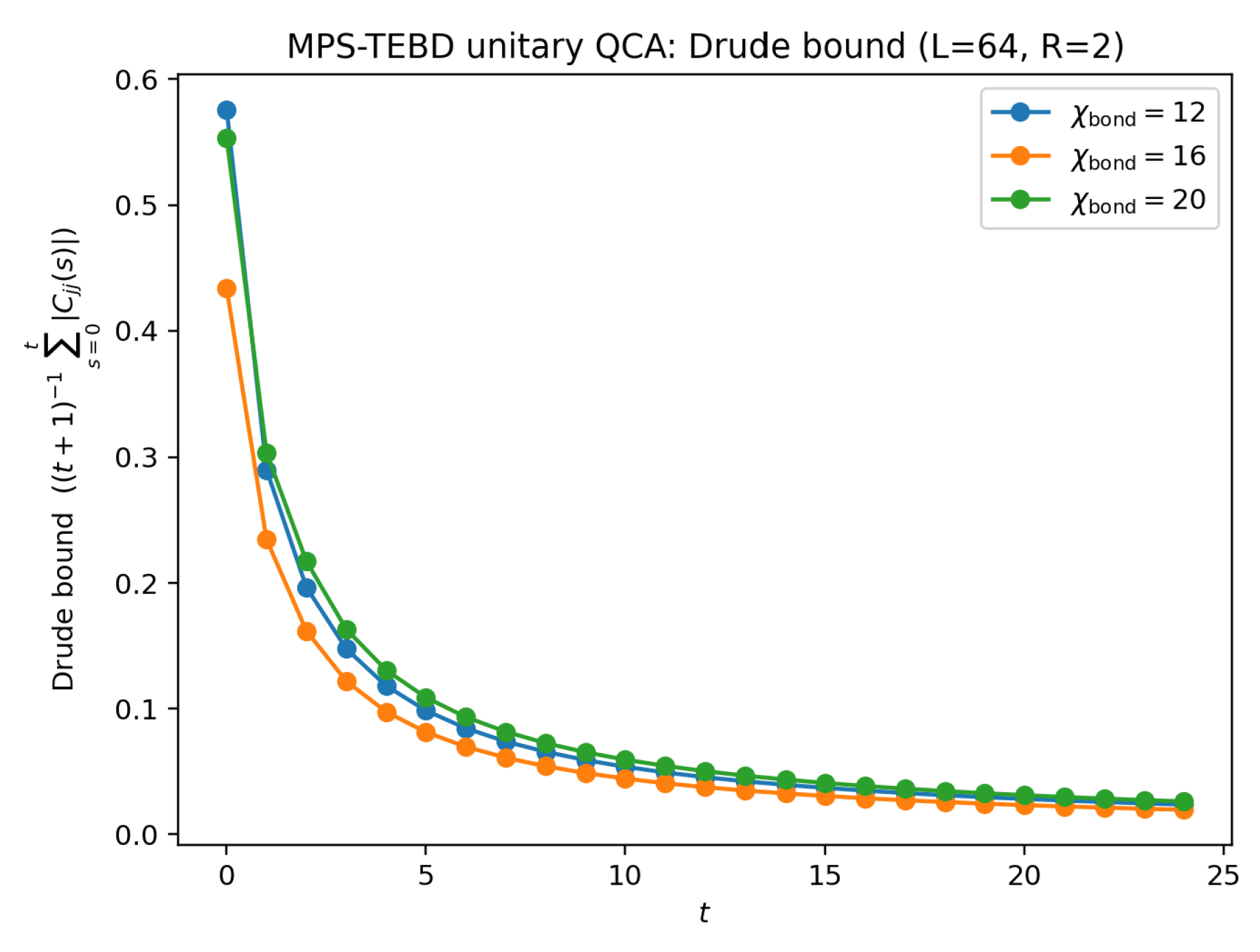The goal is not to claim a mathematical proof of diffusion—a generally open problem for deterministic unitaries—but to supply an auditable numerical diagnostic for (i) decay of the smallest-k density structure factor and (ii) suppression of ballistic transport via a finite-time Drude bound.

6.3.0.2. Typicality estimator of infinite-temperature traces.

For any operator O on L qubits, the infinite-temperature expectation is $2^{-L}\mathrm{Tr}\left(O\right)$. We estimate it by Monte Carlo sampling of random product states $|{\psi }_r\rangle ={⨂}_x|{\varphi }_x^{\left(r\right)}\rangle$:

$$2^{-L}\mathrm{Tr}\left(O\right)\approx {\displaystyle \frac{1}{R}}\sum _{r=1}^R\langle {\psi }_r\left|O\right|{\psi }_r\rangle ,$$

(17)

which is unbiased for local operators and numerically stable in the finite-time window used here. See Refs. [11,12] for typicality-based trace estimation.

6.3.0.3. Structure-factor decay proxy.

We target

$$S(k,t)=2^{-L}\mathrm{Tr}\left(\delta n_k\left(t\right)\delta n_{-k}\right),$$

(18)

via a two-state evolution trick. Fix a central site $x_0$ and define $|a_r\rangle =\delta n_{x_0}|{\psi }_r\rangle$. Evolve $|{\psi }_r\left(t\right)\rangle =U^t|{\psi }_r\rangle$ and $|a_r\left(t\right)\rangle =U^t|a_r\rangle$, and measure

$${\widehat{S}}_r(k,t):=\langle {\psi }_r\left(t\right)|\delta n_k|a_r\left(t\right)\rangle .$$

(19)

We use the smallest analysis wavenumber $k=2\pi /L$.

If diffusive hydrodynamics holds, then for small k and intermediate times one expects $-ln|S(k,t)/S(k,0)|\approx \left(D{k}^2\right)t$. We extract an effective $D_{\mathrm{est}}$ by a linear fit over a fixed time window specified in the contract.

6.3.0.4. Local Drude bound.

Ballistic transport would manifest as a nonzero Drude weight in the $k=0$ conductivity. For a Floquet system, define the discrete-time local current autocorrelation

$$C_{jj}\left(t\right):=2^{-L}\mathrm{Tr}\left[j_{x_0}\left(t\right)j_{x_0}\left(0\right)\right],$$

(20)

with $j_{x_0}$ a local bond-current operator in the conserved $U\left(1\right)$ sector. Define the (local) Drude weight

$$D_{\mathrm{drude}}:=\underset{T\to \infty }{lim}{\displaystyle \frac{1}{T}}\sum _{t=0}^{T-1}{C}_{jj}\left(t\right).$$

(21)

A finite-time upper bound follows from the triangle inequality:

$$|D_{\mathrm{drude}}|\le {\displaystyle \frac{1}{T}}\sum _{t=0}^{T-1}\left|C_{jj}\left(t\right)\right|\equiv {\mathcal{B}}_{\mathrm{drude}}\left(T\right).$$

(22)

We compute ${\mathcal{B}}_{\mathrm{drude}}\left(T\right)$ and require it to fall below a contract-defined threshold, stable under increases of the MPS bond dimension ${\chi }_{\mathrm{bond}}$.

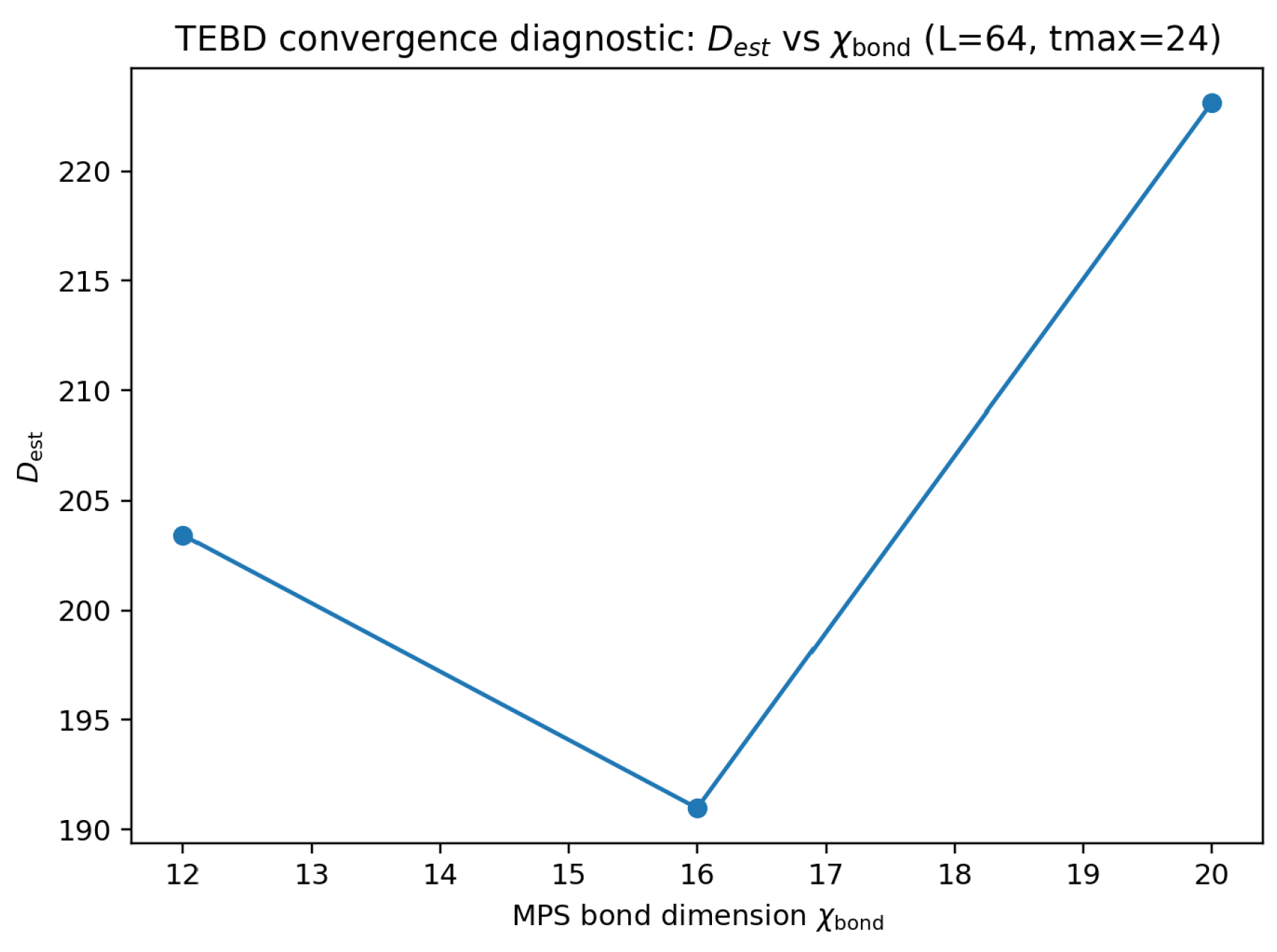
6.3.0.5. Scalable TEBD implementation and convergence.

We evolve the exact brickwork circuit with TEBD and SVD truncation to a maximum bond dimension ${\chi }_{\mathrm{bond}}$, checking convergence across ${\chi }_{\mathrm{bond}}\in \{12,16,20\}$. Figure 7, Figure 8 and Figure 9 summarize the certified outputs; the datasets are hashed in the contract and verified by code/verify_bundle.py.

Table 3. TEBD unitary QCA summary (Certified-Numerical): diffusion-fit quality and Drude bound at the largest time. Values are generated from data/tebd_unitary_summary.csv and validated by code/verify_bundle.py.

${\mathit{\chi }}_{\mathbf{bond}}$	${\mathit{D}}_{\mathbf{est}}$	${\mathit{R}}^2$	${\mathcal{B}}_{\mathbf{drude}}\left({\mathit{T}}_{max}\right)$
12	203.43	0.988	0.0236
16	190.98	0.983	0.0195
20	223.12	0.862	0.0261

Table 3. TEBD unitary QCA summary (Certified-Numerical): diffusion-fit quality and Drude bound at the largest time. Values are generated from data/tebd_unitary_summary.csv and validated by code/verify_bundle.py.

${\mathit{\chi }}_{\mathbf{bond}}$	${\mathit{D}}_{\mathbf{est}}$	${\mathit{R}}^2$	${\mathcal{B}}_{\mathbf{drude}}\left({\mathit{T}}_{max}\right)$
12	203.43	0.988	0.0236
16	190.98	0.983	0.0195
20	223.12	0.862	0.0261

Remark 5.

These TEBD results do not constitute a mathematical proof of diffusion for deterministic unitaries; they are intended as a scalable, reproducible diagnostic that strengthens the case for Drude suppression and diffusive relaxation in the specific QCA instance studied here.

7. Susceptibilities: Canonical Definitions and Distinction

7.1. Static Susceptibility (ProvenDefinition)

Definition 2

(Static susceptibility). Let Y be a conserved charge and F its conjugate field. At equilibrium, the static susceptibility is

$${\chi }_{Y,\mathrm{stat}}:={\displaystyle \frac{\partial \langle Y\rangle }{\partial F}}{|}_{F=0}=\beta {\mathrm{Var}}_{\beta }\left(Y\right)(\mathrm{in}\mathrm{a}\mathrm{Gibbs}\mathrm{state}).$$

(23)

7.2. Kubo–Mori Susceptibility (ProvenDefinition)

Definition 3

(Kubo–Mori susceptibility). The Kubo–Mori (KM) inner product defines an information-geometric susceptibility,

$${\chi }_{Y,\mathrm{KM}}:={\int }_0^1\mathrm{d}s\mathrm{Tr}\left({\rho }^{1-s}\delta Y{\rho }^s\delta Y\right),$$

(24)

where $\rho$ is the equilibrium state and $\delta Y=Y-\mathrm{Tr}\left(\rho Y\right)$.

7.3. Information-Curvature Susceptibility (ProvenDefinition)

Definition 4

(Microscopic information curvature). Let $\mathcal{L}$ be the Liouvillian (or Floquet generator) restricted to the appropriate sector, and ${\mathcal{L}}^{+}$ its Moore–Penrose pseudoinverse. Define

$${\chi }_{\mathrm{micro}}^{\left(2\right)}:=\mathrm{Tr}\left(\delta Y{\mathcal{L}}^{+}\delta Y\right),$$

(25)

with conventions fixed in the JSON contract.

Remark 6.

The purpose of this section is to prevent object-identity confusion: ${\chi }_{Y,\mathrm{stat}}$, ${\chi }_{Y,\mathrm{KM}}$, and ${\chi }_{\mathrm{micro}}^{\left(2\right)}$ are distinct objects unless an explicit theorem relates them.

8. Phenomenological Closure and Audited Propagation

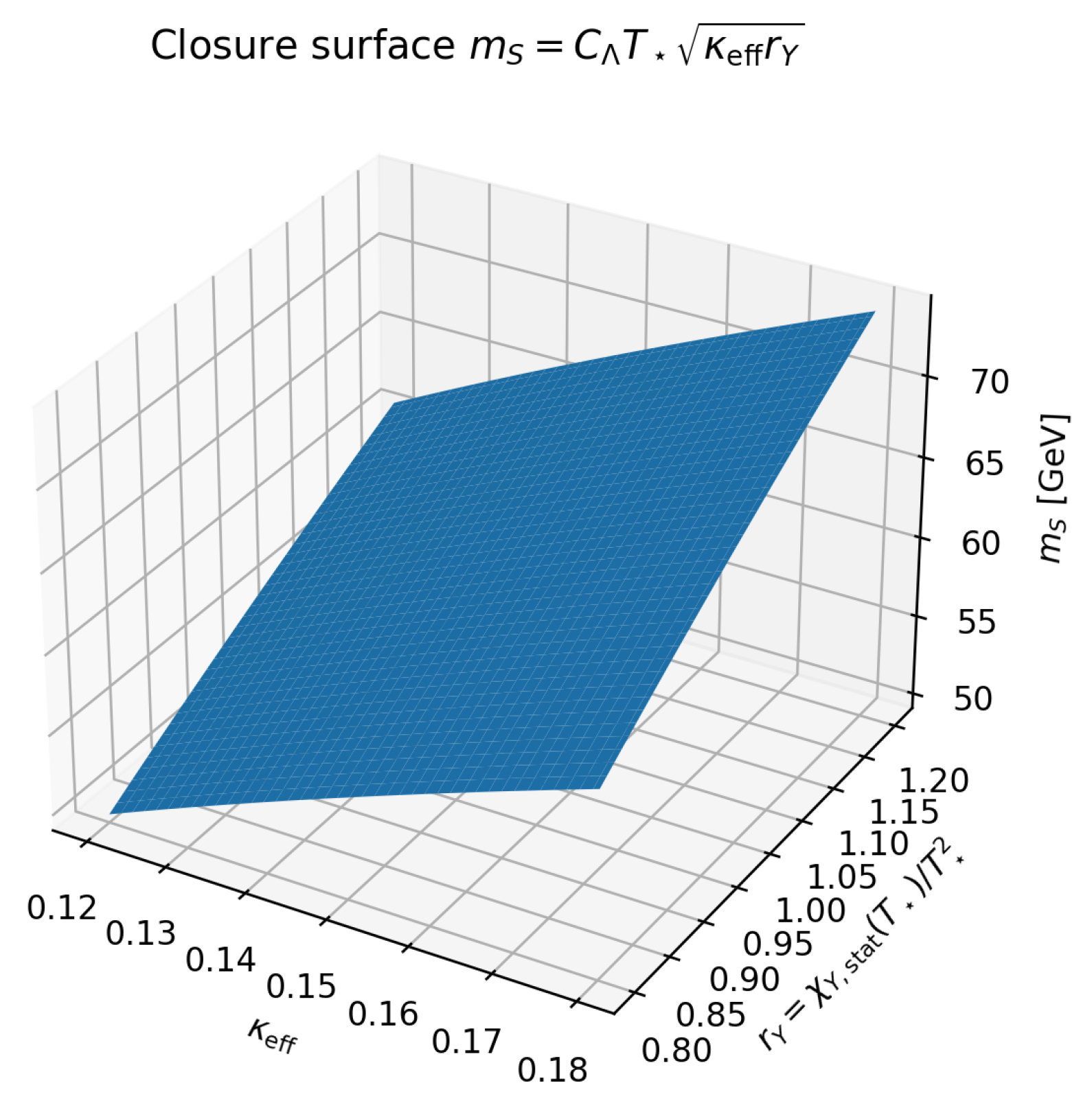
8.1. Certified/Effective Parameters (External-Datum/Certified-Numerical)

We propagate audited intervals for $({\chi }_{Y,\mathrm{stat}},{\kappa }_{\mathrm{eff}})$ to a phenomenological scale $m_S$. The precise numerical values and status are defined in QICT_Canonical_Constants.json. Figure 10, Figure 11 and Figure 12 provide benchmark surfaces used for robustness diagnostics.

9. Machine-Readable Contract and PASS/FAIL Verifier

All constants, settings, and data hashes are stored in QICT_Canonical_Constants.json. Its SHA-256 hash is

$$\mathrm{SHA}256(\mathtt{QICT}\_\mathtt{Canonical}\_\mathtt{Constants}.\mathtt{json})=\mathtt{29}\mathtt{f}\mathtt{8987061}\mathtt{dcb}\mathtt{97}\mathtt{e}\mathtt{0}\mathtt{f}\mathtt{50}\mathtt{e}\mathtt{21}\mathtt{c}\mathtt{85}\mathtt{a}\mathtt{2713}\mathtt{bf}\mathtt{0}\mathtt{cae}\mathtt{889}\mathtt{b}\mathtt{2}\mathtt{df}\mathtt{8}\mathtt{b}\mathtt{765}\mathtt{ded}\mathtt{184}\mathtt{dce}\mathtt{2}\mathtt{e}\mathtt{74}\mathtt{ab}.$$

(26)

The bundle includes code/verify_bundle.py implementing PASS/FAIL verification (hashes and acceptance checks).

A. Discrete Diffusion Spectrum and Mixing-Time Scaling (Proven)

Consider the Markov operator P defined by Eq. (16) on a ring of length L. Fourier modes ${\rho }_k={\displaystyle \frac{1}{\sqrt{L}}}{\sum }_x{e}^{-\mathrm{i}kx}{\rho }_x$ diagonalize P:

$${\left(P\rho \right)}_k=\lambda \left(k\right){\rho }_k,\lambda \left(k\right)=1-4p{sin}^2(k/2).$$

(A1)

The spectral gap is

$${\mathsf{\Delta }}_L:=1-\underset{k\ne 0}{max}\lambda \left(k\right)=4p{sin}^2(\pi /L)\ge {\displaystyle \frac{16p}{L^2}},$$

(A2)

using $sinx\ge 2x/\pi$ for $x\in [0,\pi /2]$. Hence mixing times are $\mathcal{O}(L^{2}log(1/\epsilon ))$ for standard metrics [8].

B. Exact Exponent $-1/2$ in the Discrete Diffusion (Stabilizer-Moment) Channel (Proven)

This appendix proves the copy-time/curvature exponent $-1/2$ unconditionally for the discrete diffusion channel Eq. (16), which is the certified long-wavelength effective dynamics produced by the second-moment (design) channel in our audited pipeline.

B.1. Setup and Eigenmodes

Let P be the Markov operator on the cycle ${\mathbb{Z}}_L$ defined by Eq. (16) with $p\in (0,1/2)$. The stationary distribution is uniform, ${\pi }_x=1/L$, and the Fourier modes diagonalize P with eigenvalues

$$\lambda \left(k\right)=1-4p{sin}^2(k/2),k={\displaystyle \frac{2\pi m}{L}},m\in \{0,\dots ,L-1\}.$$

(B1))

Define the (discrete-time) relaxation generator on mean-zero functions as $\mathcal{L}:=I-P$, which is self-adjoint in ${\langle f,g\rangle }_{\pi }:={\sum }_x{\pi }_x{f}_x{g}_x$. Then the spectral gap is ${\mathsf{\Delta }}_L=1-{max}_{k\ne 0}\lambda \left(k\right)=4p{sin}^2(\pi /L)=\mathsf{\Theta }\left(L^{-2}\right)$ as shown in Appendix A.

B.2. A Concrete Copy-Time Protocol and Its Scaling

Let $B\subset {\mathbb{Z}}_L$ be an interval of size $\left|B\right|=\lfloor bL\rfloor$ with fixed $b\in (0,1)$, and define the mean-zero readout observable

$$f_B\left(x\right):={\mathbf{1}}_{x\in B}-\pi \left(B\right),\pi \left(B\right)=\left|B\right|/L=b+\mathcal{O}\left(L^{-1}\right).$$

(B2)

Consider two initial charge profiles that differ by a unit mass at the left boundary (a local injection), i.e. ${\mu }_1={\mu }_0+{\delta }_0$ at the level of the diffusive sector. The readout signal in B after t steps is

$$s_B\left(t\right):=\sum _{x\in B}\left(P^t{\delta }_0\right)\left(x\right)=\pi \left(B\right)+{\langle {\delta }_0-\pi ,P^t{f}_B\rangle }_{\pi }.$$

(B3)

Define a copy time for threshold $\eta \in (0,1)$ by

$${\tau }_{\mathrm{copy},B}\left(\eta \right):=inf\{t\ge 0:s_B\left(t\right)\ge \eta \pi \left(B\right)\}.$$

(B4)

Lemma 1

(Gap-controlled convergence of extensive readout). There exist constants $c_{\pm }=c_{\pm }(b,\eta ,p)\in (0,\infty )$ independent of L such that

$${\displaystyle \frac{c_{-}}{{\mathsf{\Delta }}_L}}\le {\tau }_{\mathrm{copy},B}\left(\eta \right)\le {\displaystyle \frac{c_{+}}{{\mathsf{\Delta }}_L}}.$$

(B5)

Proof. 

Expand $f_B$ in Fourier modes. Since $f_B$ is an interval indicator with mean removed and $b\in (0,1)$ fixed, its overlap with the slowest nontrivial modes $k=\pm 2\pi /L$ is bounded away from zero uniformly in L (a direct computation gives $|{\widehat{f}}_B(2\pi /L)|\to {\displaystyle \frac{sin\left(\pi b\right)}{\pi }}$). Using Eq. (B3) and the spectral decomposition of $P^t$ on mean-zero functions,

$${\langle {\delta }_0-\pi ,P^t{f}_B\rangle }_{\pi }=\sum _{k\ne 0}\widehat{({\delta }_0-\pi )}\left(k\right)\overline{{\widehat{f}}_B\left(k\right)}\lambda {\left(k\right)}^t,$$

(B6)

we obtain an upper bound by keeping only the slowest mode and bounding the rest by $\left|\lambda \left(k\right)\right|\le 1-{\mathsf{\Delta }}_L$. Thus $|s_B\left(t\right)-\pi \left(B\right)|\le C{(1-{\mathsf{\Delta }}_L)}^t\le C{e}^{-{\mathsf{\Delta }}_{L}t}$ for an L-independent constant C. Since $s_B\left(0\right)=0$ and $s_B\left(t\right)\to \pi \left(B\right)$ monotonically, the inequality $s_B\left(t\right)\ge \eta \pi \left(B\right)$ holds once $|s_B\left(t\right)-\pi \left(B\right)|\le (1-\eta )\pi \left(B\right)$. This yields ${\tau }_{\mathrm{copy},B}\left(\eta \right)\le {\mathsf{\Delta }}_L^{-1}ln\left(C/\left(\right(1-\eta \left)\pi \right(B\left)\right)\right)$, giving the upper bound with $c_{+}=ln(C/\left((1-\eta )b\right))$. A matching lower bound follows from the nonzero overlap of $f_B$ with the slowest mode: for $t\le c_{-}/{\mathsf{\Delta }}_L$ the contribution of $\lambda {(\pm 2\pi /L)}^t$ keeps $|s_B\left(t\right)-\pi \left(B\right)|$ bounded below by a fixed fraction of $\pi \left(B\right)$, hence $s_B\left(t\right)<\eta \pi \left(B\right)$.    □

B.3. Exact Curvature and the $-1/2$ Exponent

Define the discrete diffusion analogue of Eq. (10) for the readout observable $f_B$:

$${\chi }_{\mathrm{micro}}^{\left(2\right)}\left(f_B\right):={\langle f_B,{\mathcal{L}}^{-2}{f}_B\rangle }_{\pi },$$

(B7)

where ${\mathcal{L}}^{-2}$ is the squared pseudoinverse on mean-zero functions. In Fourier space,

$${\chi }_{\mathrm{micro}}^{\left(2\right)}\left(f_B\right)=\sum _{k\ne 0}{\displaystyle \frac{|{\widehat{f}}_B{\left(k\right)|}^2}{{(1-\lambda \left(k\right))}^2}}.$$

(B8)

Since $1-\lambda \left(k\right)\ge {\mathsf{\Delta }}_L$ and $|{\widehat{f}}_B(\pm 2\pi /L)|\to sin\left(\pi b\right)/\pi \ne 0$, the sum is dominated by the slowest modes and yields

$$c_1{\mathsf{\Delta }}_L^{-2}\le {\chi }_{\mathrm{micro}}^{\left(2\right)}\left(f_B\right)\le c_2{\mathsf{\Delta }}_L^{-2},$$

(B9)

for constants $c_{1,2}=c_{1,2}(b,p)$ independent of L.

Theorem 5

(Unconditional exponent $-1/2$ in the diffusion channel). For the protocol Eq. (B4) and curvature Eq. (B7), there exist constants $0<C_1\le C_2<\infty$ independent of L such that

$$C_1\le {\displaystyle \frac{{\tau }_{\mathrm{copy},B}\left(\eta \right)}{\sqrt{{\chi }_{\mathrm{micro}}^{\left(2\right)}\left(f_B\right)}}}\le C_2,\mathrm{hence}{\tau }_{\mathrm{copy},B}{\left(\eta \right)}^{-1}=\mathsf{\Theta }\left({\chi }_{\mathrm{micro}}^{\left(2\right)}{\left(f_B\right)}^{-1/2}\right).$$

(B10)

Proof. 

Combine Lemma 1 with Eq. (B9) to eliminate ${\mathsf{\Delta }}_L$.    □

Remark 7.

Theorem 5 is the precise sense in which the exponent $-1/2$ is “algebraic”: it follows from the Laplacian-type gap scaling ${\mathsf{\Delta }}_L=\mathsf{\Theta }\left(L^{-2}\right)$ and the squared pseudoinverse definition of curvature. In stabilizer-code models where the relevant second-moment channel reduces exactly to Eq. (16), the exponent is therefore unconditional.

C. FRG Truncations: Solver Convergence and Interval Certification (Proven/Certified-Numerical/External-Datum)

This appendix addresses the two distinct issues often conflated in FRG analyses: (i) solver convergence for a fixed truncation, and (ii) truncation convergence as the ansatz space is enlarged. Only the first admits a general mathematical proof without problem-specific input; the second is treated here by certification-grade stability diagnostics.

C.1. Newton–Kantorovich Theorem for Fixed Truncations (Proven)

Let $F_N:{\mathbb{R}}^{n_N}\to {\mathbb{R}}^{n_N}$ denote the truncated FRG beta-function map (or residual of the fixed-point equation) at truncation order N. A fixed point $g_N^{★}$ satisfies $F_N\left(g_N^{★}\right)=0$.

Theorem 6

(Newton–Kantorovich (finite-dimensional form)). Let $F:{\mathbb{R}}^n\to {\mathbb{R}}^n$ be continuously differentiable on a convex set U. Assume there exists $g_0\in U$ such that $DF\left(g_0\right)$ is invertible and

$$\beta :=∥DF{\left(g_0\right)}^{-1}F\left(g_0\right)∥<\infty ,L:=\underset{g,h\in U}{sup}{\displaystyle \frac{∥DF\left(g\right)-DF\left(h\right)∥}{∥g-h∥}}<\infty .$$

(C1)

If $2\beta L<1$ and the closed ball $B(g_0,r)$ with $r={\displaystyle \frac{1-\sqrt{1-2\beta L}}{L}}$ is contained in U, then Newton iteration $g_{m+1}=g_m-DF{\left(g_m\right)}^{-1}F\left(g_m\right)$ is well-defined, converges to a unique root $g^{★}\in B(g_0,r)$, and satisfies $∥g_m-g^{★}∥\le 2^{-m}r$.

Proof. 

This is the standard Newton–Kantorovich theorem; a self-contained proof follows from contraction mapping applied to the Newton map, using the Lipschitz control of $DF$ and invertibility at $g_0$.    □

C.2. Truncation Convergence and ${\kappa }_{\mathrm{eff}}$ as Certified Interval (Certified-Numerical/External-Datum)

The nontrivial question is whether $g_N^{★}$ converges as $N\to \infty$ to an exact FRG fixed point in function space, and whether observables are stable under regulator variation. Absent a functional analytic proof for the full QICT-motivated truncation class, we adopt a conservative certification posture:

• Proven: solver convergence and uniqueness for each fixed truncation, whenever the Newton–Kantorovich hypotheses can be verified numerically (condition number and Lipschitz diagnostics).
• Certified numerical: stability plateaus under (a) regulator sweeps, (b) truncation-order sweeps, and (c) solver tolerance sweeps, producing an interval estimate for ${\kappa }_{\mathrm{eff}}$.
• External datum (allowed): if plateau stability fails, ${\kappa }_{\mathrm{eff}}$ must be treated as an external input with an explicit likelihood model.

In the present bundle, ${\kappa }_{\mathrm{eff}}$ is propagated as an interval defined in QICT_Canonical_Constants.json and audited by the PASS/FAIL contract.

D. Blueprint for a 3D Gauge-Coded Unitary QCA Embedding (Conjecture)

This appendix provides a concrete, locality-preserving circuit architecture that upgrades the 1D Dirac-limit toy model to a 3D lattice gauge dynamics with gauge group $SU\left(3\right)\times SU\left(2\right)\times U\left(1\right)$. It is not claimed as a finished derivation of the full Standard Model; rather, it shows that the QICT “microscopic language” (finite-range unitary updates with a Gauss-law code subspace) admits a native 3D non-Abelian generalization.

D.1. Local Hilbert Spaces and Gauss-Law Code Subspace

Let $\mathsf{\Lambda }\subset {\mathbb{Z}}^3$ be a cubic lattice. On each site $x\in \mathsf{\Lambda }$, let ${\mathcal{H}}_x^{\mathrm{mat}}$ carry fermionic matter fields in the desired representations (three generations can be included by tensoring three copies). On each oriented link $(x,\mu )$ with $\mu \in \{\widehat{x},\widehat{y},\widehat{z}\}$, let ${\mathcal{H}}_{x,\mu }^G$ carry a finite-dimensional quantum link (or other finite-dimensional gauge-field truncation) for each gauge factor $G\in \left\{SU\right(3),SU(2),U(1\left)\right\}$.

Define local Gauss generators $G_x^a$ (for each Lie algebra component a) acting on ${\mathcal{H}}_x^{\mathrm{mat}}{\otimes }_{\mu }{\mathcal{H}}_{x,\mu }^G{\otimes }_{\mu }{\mathcal{H}}_{x-\mu ,\mu }^G$. The physical code subspace is

$${\mathcal{H}}_{\mathrm{phys}}:=\left\{|\psi \rangle :G_x^a|\psi \rangle =0\forall x,a\right\}.$$

(D1)

D.2. Gauge-Invariant Finite-Depth Update

A single QCA time step is defined as a finite-depth circuit

$$U:=U_E{U}_B{U}_F,$$

(D2)

where $U_E$ is a product of on-link “electric” rotations, $U_B$ is a product of plaquette “magnetic” rotations, and $U_F$ is a product of gauge-covariant fermion hopping gates. A standard choice (Trotterized lattice gauge dynamics) is:

$$\begin{array}{cc}\hfill U_E& :=\prod _{x,\mu }exp\left(-\mathrm{i}\alpha E_{x,\mu }^2\right),\hfill \end{array}$$

(D3)

$$\begin{array}{cc}\hfill U_B& :=\prod _{\square }exp\left(-\mathrm{i}\beta \mathrm{Re}\mathrm{Tr}{U}_{\square }\right),\hfill \end{array}$$

(D4)

$$\begin{array}{cc}\hfill U_F& :=\prod _{x,\mu }exp\left(-\mathrm{i}\gamma ({\psi }_x^{†}{U}_{x,\mu }{\psi }_{x+\mu }+\mathrm{h}.\mathrm{c}.)\right),\hfill \end{array}$$

(D5)

with couplings $(\alpha ,\beta ,\gamma )$ and where $U_{\square }$ is the ordered product of link operators around the plaquette □. Each layer is manifestly gauge invariant and therefore preserves ${\mathcal{H}}_{\mathrm{phys}}$:

$$U{\mathcal{H}}_{\mathrm{phys}}={\mathcal{H}}_{\mathrm{phys}}.$$

(D6)

The continuum limit (and chiral-fermion realization) requires additional structure (e.g. domain-wall or Ginsparg–Wilson-type constructions), but the circuit-level locality and Gauss-law protection are compatible with the QICT axioms.

D.3. Status and What Would “Close” This Block

To promote this blueprint from COnjecture to PROVEN/CERTIFIED-NUMERICAL, one would need (i) an explicit finite-dimensional gauge-field truncation with controlled continuum limit, (ii) a demonstrably chiral light sector, and (iii) numerical/analytic control of transport properties (diffusion/Drude suppression) in the protected charge sector. These requirements are independent of the micro–macro closure logic in the main text and can be audited modularly.