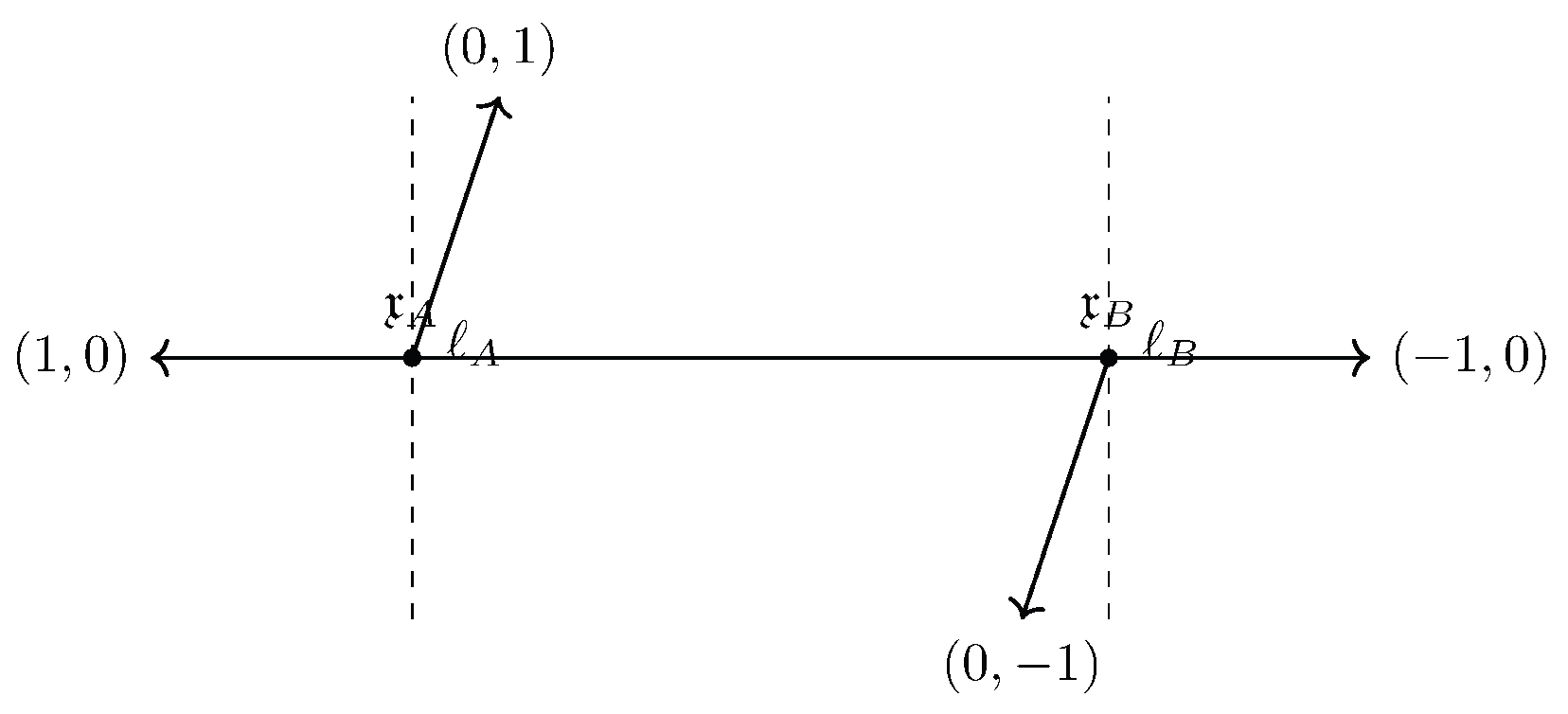(p, q)-String Junctions as Interstitial Fields on a Modal Lightcone

1. Introduction

Classical and quantum field theories have largely been developed on top of classical, bivalent logics. While there are notable exceptions (e.g. the Birkhoff–von Neumann proposal for quantum logic [3], or topos-theoretic approaches to contextuality and measurement [5]) it is still rare for modal or substructural logics to be built directly into the foundations of physical models. Nevertheless, physicists routinely use modal language informally: fields “turn on” or “turn off”, a coupling regime is “accessible” from another, a constraint “forces” or “allows” a certain vacuum, and so on. These phrases hint at an underlying logical and relational structure, but this structure is usually kept in the background as mere metaphor.

One aim of this paper is to bring that background structure to the foreground, by incorporating Kripke–Joyal-style semantics into a concrete physical setting. Very roughly, we regard a family of field configurations as a kind of Kripke frame, where worlds represent dynamical states or background geometries, and accessibility relations encode physically realizable transitions, couplings, or junctions between them. In this view, a statement such as “this field can turn on” corresponds not merely to a yes/no proposition, but to a modal claim about which neighboring configurations are dynamically reachable.

We begin with a simple schematic expression of this idea:

$$R_t:♢(\varphi )⟼\square (\varphi ),$$

(1)

in which a “possible” state for a field $\varphi$ is still “off” just before a time t, but at t is instantaneously activated. Here $R_t$ is interpreted as an accessibility relation or update operation at time t, $♢(\varphi )$ expresses the mere possibility that $\varphi$ could be turned on in some accessible configuration, while $\square (\varphi )$ expresses the stability or necessity of $\varphi$ being on throughout a suitable neighborhood (temporal, spatial, or configuration-space) of that update.

The central proposal of this work is that, when we move to the setting of $(p,q)$-string junctions, these accessibility relations can be understood as interstitial fields: additional degrees of freedom living not on a single worldsheet or brane, but “in between” them. At a junction of multiple $(p,q)$-strings, the compatibility conditions between charges, tensions, and boundary conditions can be organized into a network of possible and necessary configurations. The interstices of this network (the gaps and overlaps between individual strings and their backgrounds) carry auxiliary fields whose behavior is most naturally described in modal terms.

In more concrete terms, we will model a collection of $(p,q)$-string junctions as a structured graph or category, whose objects are local configurations and whose morphisms encode admissible deformations, splittings, and recombinations. To each such morphism we associate an accessibility relation of the form $R:♢(\varphi )\to \square (\varphi )$, and we interpret interstitial fields as those modes that control, or are controlled by, these relations. The resulting picture is that of a decorated network of junctions, in which logical modalities and physical couplings are blended into a single formalism.

This work should be read as complementary to our earlier investigation of Chan–Paton defects on open strings [6]. There we treated defects as bimodular obstructions on extended objects, generalizing Chan–Paton factors to $(A,B)$-bimodules and interpreting pseudoparticles as both physical and semantic obstructions to lifting in braided settings.1 In the present paper we focus instead on interstices in compactified ${\mathbb{M}}^{4\times 7}$ backgrounds and the associated modal field-families (FFs). Interstices are the natural higher-dimensional avatars of Chan–Paton defects; they carry the same obstruction-theoretic flavor, but are now organized by a modal lightcone, fuzzy Heyting–Kripke semantics, and internal $G_2$-sources, rather than by braids on a single open string.

2. Type IIB String Theory, Dualities, and (p, q)-Strings

In this section, we hope to encapsulate the last half-a-century-or-so worth of string history, in the fashion of a mini-primer. Naturally, many things will be left out, to prevent the length of this paper from spiralling out of control. We will first consider the origins of string theory, and make our way to our topic of interest: $(p,q)$-strings in type IIB string theory.

2.1. From Dual Resonance Models to Type IIB (A Very Short History)

String theory did not begin life as a theory of quantum gravity or unification, but as an attempt to model hadronic scattering. In the late 1960s, the S–matrix program sought amplitudes that would exhibit both Regge behavior at high energy and crossing symmetry between different channels. Veneziano’s 1968 four–point amplitude provided a remarkably simple answer: a $\beta$-function of the Mandelstam variables that produced an infinite tower of narrow resonances lying on approximately linear Regge trajectories and satisfied the desired “duality” between s– and t–channels.2 This construction was soon generalized to N–point “dual resonance models,” whose factorization properties and infinite oscillator–like spectrum suggested that some underlying extended system was being described.

Between 1969 and 1970, Nambu, Susskind, and Nielsen independently proposed that the dual resonance model could be understood as a theory of relativistic strings: one–dimensional objects whose world–sheets sweep out the surfaces underlying Veneziano’s amplitudes. In this picture, the infinite tower of resonances arises from quantized vibrational modes of an open or closed string, and the linear Regge trajectories are explained by a rotating string whose angular momentum grows linearly with its energy. The dual amplitudes acquire a geometric interpretation as correlation functions of a two–dimensional field theory on the string world–sheet, rather than as ad hoc functions engineered to fit scattering data.

2.2. Type IIB, the Axio–Dilaton, and $\mathrm{SL}(2,\mathbb{Z})$

The original bosonic string theory, however, was clearly incomplete as a fundamental theory: it lived in twenty–six dimensions, contained a tachyonic ground state, and lacked fermions. The next step was to introduce world–sheet fermions and supersymmetry (Ramond, Neveu–Schwarz), and then to impose spacetime supersymmetry in ten dimensions. This led to a family of superstring theories with vastly improved consistency properties, in particular the removal of most tachyonic instabilities and the appearance of fermionic states in the spectrum. A crucial development came in 1984, when Green and Schwarz showed that certain ten–dimensional superstrings are free of gauge and gravitational anomalies via what is now called the Green–Schwarz mechanism.3 Anomaly cancellation and other consistency conditions singled out five perturbative ten–dimensional superstring theories: Type I, Type IIA, Type IIB, heterotic $\mathrm{SO}(32)$, and heterotic $E_8\times E_8$.

Among these, Type IIB quickly emerged as the most natural arena for exploring dualities and extended objects. It is a theory of oriented closed strings with chiral $\mathcal{N}=2$ supersymmetry in ten dimensions, a self–dual five–form field strength, and a rich spectrum of D–branes on which open strings can end. Most importantly for our purposes, its low–energy supergravity description exhibits an $\mathrm{SL}(2,\mathbb{R})$ symmetry acting on the complex axio–dilaton

$$\tau ≔C_0+i{e}^{-\Phi },$$

(2)

where $C_0$ is the Ramond–Ramond scalar and $\Phi$ is the dilaton. In the full quantum theory this continuous symmetry is broken to the arithmetic group $\mathrm{SL}(2,\mathbb{Z})$, which acts as a strong–weak duality (alias: S–duality) relating different coupling regimes. Under this duality, the fundamental NS–NS string and the D1–brane transform as a doublet, and more generally one is led to consider bound states carrying a pair of integer charges $(p,q)$.

The appearance of an exact $\mathrm{SL}(2,\mathbb{Z})$ acting on $\tau$, together with a multiplet of $(p,q)$–strings and higher–dimensional branes, makes Type IIB a direct descendant of the duality ideas already implicit in the Veneziano amplitude and dual resonance models. In the remainder of this section we recall the basic structure of this $\mathrm{SL}(2,\mathbb{Z})$ symmetry and the role of $(p,q)$–strings and junctions, which will serve as the physical stage for the interstitial, modal, and probabilistic structures developed in Section 3.1 and beyond.

2.3. $(p,q)$-Strings, Junctions, and Webs as Our Arena

In Type IIB string theory the fundamental NS–NS string (usually denoted F1) and the D1–brane (D1) are not isolated species, but members of a larger multiplet of bound states. The complex axio–dilaton of equation (2) transforms under $\mathrm{SL}(2,\mathbb{Z})$ by fractional linear transformations, and the pair of integer charges $(p,q)$—measuring NS–NS and R–R string charge, respectively—transforms as a column vector in the fundamental representation. A $(p,q)$–string is, roughly speaking, a BPS bound state carrying p units of F1 charge and q units of D1 charge.4 In a fixed background $\tau$ the tension of such a state is proportional to

$$T_{(p,q)}\propto {\displaystyle \frac{|p+q\tau |}{\sqrt{\mathrm{Im}\tau }}},$$

so that the $\mathrm{SL}(2,\mathbb{Z})$ action on $(p,q)$ and on $\tau$ preserves the spectrum of BPS string tensions.

A particularly important feature of Type IIB is that these $(p,q)$–strings can meet at junctions. The simplest nontrivial case is a three–pronged junction J, in which three string segments with charges $(p_1,q_1)$, $(p_2,q_2)$, and $(p_3,q_3)$ join at a point.5 Charge conservation at the junction requires

$$p_1+p_2+p_3=0,q_1+q_2+q_3=0,$$

so that the total NS–NS and R–R charge is conserved. For a BPS configuration in flat space, the tensions of the three strings must also balance: the vectors ${\overrightarrow{T}}_i$ with magnitudes $T_{(p_i,q_i)}$ and directions along the spatial legs add up to zero. Equivalently, after fixing the complex structure in the plane of the junction, the angles between the legs are determined by the complex numbers $p_i+q_i\tau$; the three tension vectors form a closed triangle in the complex plane. This picture extends to more elaborate planar $(p,q)$–webs (as in [1,13]), in which multiple junctions and string segments are glued together to form a graph whose edges are labeled by charges and whose geometry is constrained by local charge conservation and tension balance.

Such $(p,q)$–webs play several roles in the literature: they provide a useful description of BPS states in certain supersymmetric gauge theories, a way of encoding information about 7–brane backgrounds and F–theory compactifications, and a geometric representation of the action of $\mathrm{SL}(2,\mathbb{Z})$ on charges and junctions. For our purposes, the key point is more modest; viz. a $(p,q)$–web gives a concrete geometric and kinematic scaffold on which fields can live, and along which excitations can propagate, while the duality group $\mathrm{SL}(2,\mathbb{Z})$ acts nontrivially on the discrete charge labels decorating the edges and junctions.

In subsequent sections we recast these $(p,q)$–webs in the modal and algebraic framework of Section 3.1. The individual string segments and junctions will become objects and morphisms in a category of paths and terms, and the regions “in between” them (the interstices of the web) will host auxiliary fields whose activation and propagation are naturally described in modal terms. It is in these interstitial regions, rather than on any single leg alone, that our accessibility relations and formal power series of update operations will live.

3. Modal and Algebraic Aspects

Before we can begin with the real physical panache, let’s begin with a few simple tools we will use. Having explained the relevant history, let us now turn to some simple gadgets we will use. Section 3.1 nods towards some of mine and Emmersons’ previous research, namely [6] and [7]. We will not yet fully engage with them, and inhibit ourselves enough to get out the necessary details only.

3.1. Modal Algebra at a Point on the String

Recall the schematic relation of equation (1) in which a mode $\varphi$ that is merely possible just before time t becomes necessary (or stably on) at time t. Let $\gamma$ be an open string worldline (or a spatial slice of a worldsheet), equipped with a coordinate $\sigma \in [0,1]$. We write points on $\gamma$ as $\mathfrak{x}\in \gamma$, and for each such point choose a small neighborhood

$$\mathcal{U}(\mathfrak{x})\subset \gamma .$$

A field configuration along the string will be denoted by $\varphi$, and we allow ourselves to restrict it to this neighborhood:

$$\varphi {|}_{\mathcal{U}(\mathfrak{x})}.$$

We imagine that the dynamics provides a family of time-evolution operators

$$R_t:\mathrm{Conf}(\gamma )⟶\mathrm{Conf}(\gamma ),$$

(3)

acting on the space $\mathrm{Conf}(\gamma )$ of field configurations on $\gamma$, such that $R_{t+\epsilon }$ is induced by translating by a small time-step $\epsilon >0$.6 For each integer $n\ge 0$ we write

$$R_{t+n}≔R_{t+\epsilon }^n$$

(4)

for the n-step iterate.

To connect this with the modal notation, we fix a point $\mathfrak{x}\in \gamma$ and consider the restriction of the time-evolved field to $\mathcal{U}(\mathfrak{x})$:

$$R_{t+n}\left(\varphi \right){|}_{\mathcal{U}(\mathfrak{x})}.$$

The informal statement that the mode $\varphi$ “turns on at $\mathfrak{x}$ after n time steps” can then be encoded as an accessibility relation

$$R_{t+n}\left(\varphi \right){|}_{\mathcal{U}(\mathfrak{x})}⇝{♢}_{\mathfrak{x}}^n\varphi ⤻\gamma {|}_{\mathfrak{x}},$$

(5)

where the right-hand side is read as: “after n steps, the configuration lies in a state in which $\varphi$ is accessible at the point $\mathfrak{x}$ on the string.”

Notation 1. 

We distinguish between field configurations, denoted by symbols such as ϕ and ψ, and logical propositions about those configurations, which we denote by φ and ς. The algebra $H_{\mathfrak{x}}$ (see again appendix §app:kripke-frames for more details) consists of such propositions (e.g. “ϕ is nonzero on $\mathcal{U}(\mathfrak{x})$"), and the satisfaction relation $R_{t+n}{(\Phi )|}_{\mathcal{U}(\mathfrak{x})}⊩\phi$ should be read with this in mind.

Algebraically, for each fixed $\mathfrak{x}$, this is realized by a family of local modal operators

$${♢}_{\mathfrak{x}}^n:H_{\mathfrak{x}}⟶H_{\mathfrak{x}},$$

acting on a Heyting (or Boolean) algebra $H_{\mathfrak{x}}$ of propositions about the behavior of fields in the neighborhood $\mathcal{U}(\mathfrak{x})$. The update map $R_{t+n}$ induces the modality ${♢}_{\mathfrak{x}}^n$ via restriction:

$${♢}_{\mathfrak{x}}^n(\phi )\mathrm{is}\mathrm{true}\mathrm{at}\mathrm{a}\mathrm{configuration}\Phi \iff R_{t+n}(\Phi ){|}_{\mathcal{U}(\mathfrak{x})}\vDash \phi .$$

(6)

The dual operator ${\square }_{\mathfrak{x}}^n$ encodes stability, in the sense that

$${\square }_{\mathfrak{x}}^n\phi \mathrm{holds}\mathrm{at}\Phi \iff \forall \Psi ,\left(R_{t+n}(\Phi ){|}_{\mathcal{U}(\mathfrak{x})}=R_{t+n}(\Psi ){|}_{\mathcal{U}(\mathfrak{x})}\right)\Rightarrow \Psi \vDash \phi .$$

(7)

In particular, the relation (1) can be read locally at $\mathfrak{x}$ as the statement that

$$R_t\mathrm{carries}\mathrm{a}\mathrm{configuration}\mathrm{in}\mathrm{which}{♢}_{\mathfrak{x}}\phi \mathrm{holds}\mathrm{to}\mathrm{one}\mathrm{in}\mathrm{which}{\square }_{\mathfrak{x}}\varphi \mathrm{holds}.$$

(8)

We now enrich this picture with a mild probabilistic decoration. We equip the parameter interval $[0,1]$ with a probability distribution $\mathbb{P}$, normalized so that

$${\int }_0^{1}d\mathbb{P}(\sigma )=1.$$

(9)

One can then think of an open string configuration as a pair

$$(\gamma ,\mathbb{P}),$$

(10)

and of a point $\mathfrak{x}$ together with its neighborhood as a localized probe of this weighted interval.

In the closed-string case, we identify the endpoints via $0\sim 1$, and choose a basepoint $*\in \gamma .$. The resulting decorated loop-space can be encoded schematically as

$$\widehat{\Omega }\mathfrak{x}=\left(\mathfrak{x},{\mathfrak{D}}_{\mathfrak{x}}\right),$$

(11)

where the decorator ${\mathfrak{D}}_{\mathfrak{x}}$ (as in [7]) is a (possibly infinite) product of mapping spaces

$${\mathfrak{D}}_{\mathfrak{x}}≔\prod _{j\in J}\mathrm{Maps}\left({\mathbb{p}}_j,\mathfrak{x}\right).$$

(12)

Here the family of probability marginals

$${\{{\mathbb{p}}_j\}}_{j\in J}$$

is obtained by rescaling and restricting the base distribution $\mathbb{P}$ along a poset of scales.

Remark 1. 

We will not need the full machinery of these decorated loop-spaces until we discuss junctions and interstices; for the moment, they serve only as a reminder that our local modal operators at $\mathfrak{x}$ can be organized into a richer structured space.

Returning to the open-string case, the contribution of a neighborhood of $\mathfrak{x}$ to the worldsheet action can be isolated by a bump function (alias: characteristic function)

$${\chi }_{\mathfrak{x}}:[0,1]⟶[0,1],$$

supported in $\mathcal{U}(\mathfrak{x})$ and normalized in such a way that a partition

$${\left\{{\chi }_{{\mathfrak{x}}_j}\right\}}_{j=1}^J$$

of unity along $\gamma$ satisfies

$$\sum _{j=1}^J{\chi }_{{\mathfrak{x}}_j}(\sigma )=1\mathrm{for}\mathrm{all}\sigma \in [0,1].$$

(13)

If $S(\gamma )$ denotes the full action of a field configuration along the string, we define the localized action at $\mathfrak{x}$ by

$$S(\mathfrak{x}){|}_{\varphi }≔{\int }_0^1{\chi }_{\mathfrak{x}}(\sigma )\mathcal{L}\left(\varphi (\sigma )\right)d\mathbb{P}(\sigma ),$$

(14)

so that, schematically,

$$S(\gamma )\simeq \sum _{j=1}^{J}S({\mathfrak{x}}_j){|}_{\varphi }.$$

(15)

The idea, then, is that the action $S(\mathfrak{x}){|}_{\varphi }$ becomes nonzero precisely when the modality ${♢}_{\mathfrak{x}}$ has “turned on” the corresponding mode at $\mathfrak{x}$, in the sense of (5). In this way, the collection of local modal operators

$${\left\{{♢}_{\mathfrak{x}}^n,{\square }_{\mathfrak{x}}^n\right\}}_{n\ge 0}$$

along the string, together with the time-translation monoid generated by $R_{t+\epsilon }$, encodes a “modal lightcone” of accessible and realized configurations at each point on $\gamma$.

3.2. Algebraic Aspects and Formal Power Series

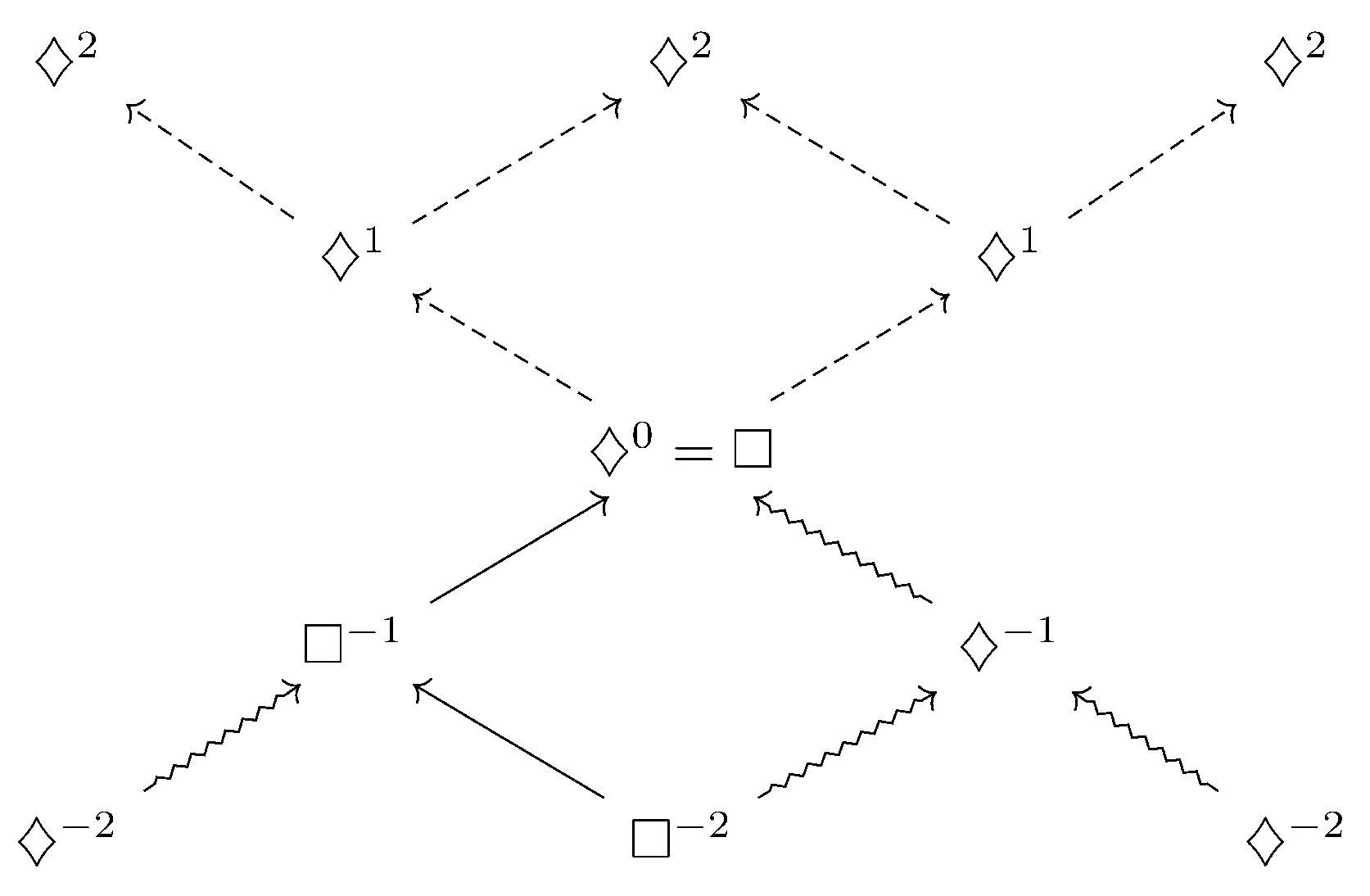
We now package the local modal dynamics at a point $\mathfrak{x}\in \gamma$ into a simple algebraic structure. The basic idea is that the iterates of the accessibility relation in (5) generate a monoid of “update operations”, and that formal power series in this monoid encode discrete histories in the modal lightcone of Figure 1.

Throughout this subsection we fix a point $\mathfrak{x}\in \gamma$ and work with the local Heyting (or Boolean) algebra $H_{\mathfrak{x}}$ and its modal operators ${\{{♢}_{\mathfrak{x}}^n,{\square }_{\mathfrak{x}}^n\}}_{n\ge 0}$ as in (5)–(7). We also fix a commutative coefficient ring

$$k≔\mathbb{C}〚\hslash 〛,$$

(16)

so that formal ℏ-expansions can later be combined with formal modal expansions using deformation quantization, if we are so-inclined.

Definition 1. 

The local update monoid at $\mathfrak{x}$ is the free monoid

$$M_{\mathfrak{x}}\cong \mathbb{N}=\{0,1,2,\dots \}$$

generated by a symbol $u_{\mathfrak{x}}$ corresponding to one forward modal update at $\mathfrak{x}$. We write $u_{\mathfrak{x}}^n$ for the word of length n, with $u_{\mathfrak{x}}^0$ the empty word.

Concretely, the generator $u_{\mathfrak{x}}$ is realized as the one-step local modality

$$u_{\mathfrak{x}}⟼{♢}_{\mathfrak{x}},$$

and the canonical representation

$${\rho }_{\mathfrak{x}}:M_{\mathfrak{x}}⟶\mathrm{End}(H_{\mathfrak{x}})$$

(17)

sends $u_{\mathfrak{x}}^n$ to the n-fold iterate ${♢}_{\mathfrak{x}}^n$. In these terms, the future layers of the modal lightcone are indexed by the elements of $M_{\mathfrak{x}}$; the nodes labeled ${♢}^1$, ${♢}^2$, ...in Figure 1 correspond to $u_{\mathfrak{x}}$, $u_{\mathfrak{x}}^2$, ...acting on the present configuration.

3.2.1. Monoid Rings and Formal Modal Power Series

The first algebraic object associated to $M_{\mathfrak{x}}$ is its monoid ring over k:

$$A_{\mathfrak{x}}≔k[M_{\mathfrak{x}}],$$

(18)

whose underlying k-module has basis ${\{u_{\mathfrak{x}}^n\}}_{n\ge 0}$ and whose multiplication extends the monoid law $u_{\mathfrak{x}}^m·u_{\mathfrak{x}}^n=u_{\mathfrak{x}}^{m+n}$. Since $M_{\mathfrak{x}}\cong \mathbb{N}$ is free on one generator, there is a natural identification

$$A_{\mathfrak{x}}\cong k[z],$$

sending $u_{\mathfrak{x}}^n$ to $z^n$ and $u_{\mathfrak{x}}$ itself to the indeterminate z.

To describe infinite modal histories we pass to the formal completion:

$${\widehat{A}}_{\mathfrak{x}}≔k〚M_{\mathfrak{x}}〛\cong k〚z〛,$$

(19)

the ring of formal power series in the generator $u_{\mathfrak{x}}$ with coefficients in $k=\mathbb{C}〚\hslash 〛$. A typical element of ${\widehat{A}}_{\mathfrak{x}}$ has the form

$$F(z)=\sum _{n\ge 0}{a}_n(\hslash )z^n,a_n(\hslash )\in \mathbb{C}〚\hslash 〛,$$

(20)

which we may symbolically rewrite as

$$F=\sum _{n\ge 0}{a}_n(\hslash )u_{\mathfrak{x}}^n\in k〚M_{\mathfrak{x}}〛.$$

Via the representation (17), any such series induces a formal modal operator on $H_{\mathfrak{x}}$:

$$F({♢}_{\mathfrak{x}})≔\sum _{n\ge 0}{a}_n(\hslash ){♢}_{\mathfrak{x}}^n.$$

(21)

Formally, (21) is a k-linear combination of endomorphisms of $H_{\mathfrak{x}}$; in situations where only finitely many iterates act nontrivially on a given proposition $\phi \in H_{\mathfrak{x}}$, the right-hand side defines an honest endomorphism of $H_{\mathfrak{x}}$. Intuitively, $F({♢}_{\mathfrak{x}})$ encodes a weighted sum over all modal futures of $\phi$, with the coefficient $a_n(\hslash )$ assigned to the n-step layer of the lightcone.

3.2.2. Modal Generating Functionals

The same formalism can be applied to the localized action (14). For a fixed field configuration $\varphi$ and point $\mathfrak{x}$, we may consider the sequence of localized actions along the iterates of the dynamics,

$$S(\mathfrak{x}){|}_{R_{t+n}(\varphi )},n\ge 0,$$

and package them into a formal “modal generating functional’’

$${\mathcal{G}}_{\mathfrak{x}}(\varphi ;z,\hslash )≔\sum _{n\ge 0}{a}_n(\hslash )S(\mathfrak{x}){|}_{R_{t+n}(\varphi )}{z}^n,$$

(22)

with coefficients $a_n(\hslash )\in \mathbb{C}〚\hslash 〛$ as in (20). While we will not commit to a specific choice of the weights $a_n(\hslash )$ here, (22) illustrates how the discrete-time evolution in (4) and the localized action in (14) can be organized into a single formal object whose combinatorics is governed by the monoid $M_{\mathfrak{x}}$ and whose coefficients live in the deformation ring k.

In this sense, the formal series ring (19) plays the role of a “modal completion’’ of the local dynamics at $\mathfrak{x}$: it encodes all finite compositions of the basic update, and their ℏ-dependent weights, without requiring any analytic convergence. This is directly analogous to the way formal power series in an operadic or PROP-based field theory keep track of all possible compositions of elementary operations or vertices, independently of analytic issues (see for example the expository discussion in [2] and the operadic frameworks developed in [14,15]).

Remark 2 

(Abstract Nonsense). At a more categorical level, one can think of the string γ as living in a product category

$$\mathbf{Paths}\times \underline{\mathbf{Terms}},$$

where $\mathrm{Paths}$ is a (2-)category of paths and homotopies between them,7 and $\underline{\mathbf{Terms}}$ encodes additional physical data such as Chan–Paton factors, background charges, or boundary conditions. A path $\tilde{\gamma }$ in $\mathbf{Paths}$, tensored with suitable term data in $\underline{\mathbf{Terms}}$, becomes a bona fide physical string configuration, and natural transformations in the bi-category $\mathbf{Paths}\times \underline{\mathbf{Terms}}$ represent symmetries or gauge invariances. The local update monoid $M_{\mathfrak{x}}$ can then be viewed as a submonoid of the endomorphisms of such an object, generated by a distinguished “one-step’’ update at $(\tilde{\gamma },\mathbf{term})$. We will not develop this categorical picture in detail here, but it provides a natural home for the monoid and power-series structures introduced above, and connects them with the broader operadic and PROP-based approaches to field theory.

3.2.3. Interaction with Probability Weights and Bump Functions

The constructions above separate two kinds of data:

• the temporal structure of updates at a fixed point $\mathfrak{x}$, encoded in the local update monoid $M_{\mathfrak{x}}$ and its formal series ring ${\widehat{A}}_{\mathfrak{x}}\cong k〚z〛$ from (19), and
• the spatial structure along the string, encoded in the probability distribution $\mathbb{P}$ and the bump function ${\chi }_{\mathfrak{x}}$ entering the localized action (14).

The monoid $M_{\mathfrak{x}}$ indexes discrete time-steps $n\ge 0$ in the evolution (4), while the measure $\mathbb{P}$ and bump ${\chi }_{\mathfrak{x}}$ determine how strongly the neighborhood $\mathcal{U}(\mathfrak{x})$ contributes to the worldsheet action at each such time-step. For each $n\ge 0$ and configuration $\varphi$, the localized action at time $t+n$ is

$$S(\mathfrak{x}){|}_{R_{t+n}(\varphi )}={\int }_0^1{\chi }_{\mathfrak{x}}(\sigma )\mathcal{L}\left(R_{t+n}(\varphi )(\sigma )\right)d\mathbb{P}(\sigma ),$$

(23)

which is just (14) evaluated on the time-evolved configuration $R_{t+n}(\varphi )$. The index n in (23) is exactly the exponent in the monoid element $u_{\mathfrak{x}}^n$ and in the iterate ${♢}_{\mathfrak{x}}^n$ appearing in the modal operator (21) and the generating functional (22).

To make the interaction between $M_{\mathfrak{x}}$ and the probabilistic data explicit, let us choose a collection of coefficients

$$w_n(\hslash )\in \mathbb{C}〚\hslash 〛,n\ge 0,$$

(24)

with the normalization condition

$$\sum _{n\ge 0}{w}_n(\hslash )=1$$

(25)

in the ring $\mathbb{C}〚\hslash 〛$. Thus the map

$$w:M_{\mathfrak{x}}⟶\mathbb{C}〚\hslash 〛,w(u_{\mathfrak{x}}^n)=w_n(\hslash ),$$

can be viewed as a formal probability distribution on the monoid of updates. Using these weights, we define a modal expectation value of the localized action at $\mathfrak{x}$ by

$${\mathbb{E}}_{\mathfrak{x}}[S\mid \varphi ]≔\sum _{n\ge 0}{w}_n(\hslash )S(\mathfrak{x}){|}_{R_{t+n}(\varphi )}.$$

(26)

Comparing (26) with the generating functional (22), we see that

$${\mathbb{E}}_{\mathfrak{x}}[S\mid \varphi ]={\mathcal{G}}_{\mathfrak{x}}(\varphi ;z,\hslash ){|}_{z=1}\mathrm{whenever}{a}_n(\hslash )=w_n(\hslash )\mathrm{for}\mathrm{all}n\ge 0.$$

(27)

Thus the same formal series that encodes the combinatorics of modal futures can, after choosing normalized coefficients, be interpreted as a formal probability distribution on the layers of the modal lightcone, and the localized action (23) weights each layer according to the bump function ${\chi }_{\mathfrak{x}}$ and the measure $\mathbb{P}$.

From this perspective, the probability distribution $\mathbb{P}$ on the string and the formal probability weights $w_n(\hslash )$ on the monoid $M_{\mathfrak{x}}$ combine into a mixed discrete–continuous structure: $\mathbb{P}$ controls the spatial sampling along $\gamma$, while w controls the temporal sampling along the modal lightcone at $\mathfrak{x}$. The partition of unity ${\{{\chi }_{{\mathfrak{x}}_j}\}}_{j=1}^J$ in (13) then yields a decomposition

$$\mathbb{E}[S\mid \varphi ]\simeq \sum _{j=1}^J{\mathbb{E}}_{{\mathfrak{x}}_j}[S\mid \varphi ],$$

(28)

in which each term ${\mathbb{E}}_{{\mathfrak{x}}_j}[S\mid \varphi ]$ is governed by its own local update monoid $M_{{\mathfrak{x}}_j}$ and formal weights $w_n(\hslash )$, but all share the same underlying worldsheet measure $\mathbb{P}$.8

In summary, the update monoid $M_{\mathfrak{x}}$ organizes the temporal structure of modal accessibility at a point on the string, while the probability distribution $\mathbb{P}$ and bump functions ${\chi }_{\mathfrak{x}}$ organize the spatial structure along the string. The formal series ring ${\widehat{A}}_{\mathfrak{x}}$ and the expectation (26) provide a convenient interface between these two pictures, which will become particularly useful when we study how local modal lightcones interact and fuse at interstices and junctions.

4. The Modal Lightcone Spacetime

We begin with the following:

Recollection 1 

(Einstein, Minkowski, and the light-cone picture). In Einstein’s 1905 formulation of special relativity, the basic ingredients were the relativity principle and the constancy of the speed of light, expressed in terms of spherical light waves in different inertial frames rather than an explicitly four-dimensional geometry. The now-familiar light-cone picture emerged a few years later, when Minkowski recast Einstein’s kinematics in terms of a four-dimensional spacetime continuum. In his 1908 Cologne lecture “Raum und Zeit” [16], he argued that space and time were henceforth to be treated as a unified “world” with a pseudo-Euclidean metric, and spacetime diagrams with null cones became the natural way to visualize causal structure and the invariant speed of light. Historical analyses such as Galison’s study of Minkowski’s spacetime program [8] emphasize how this geometric, light-cone-based viewpoint reshaped the conceptual foundations of relativity and provided the background for later developments in field theory and gravitation.

The four-dimensional spacetime then became the standard picture of relativistic physics, and arguably remains dominant to this day. The assumption most authors make, explicitly or tacitly, is that, associated to every frame of reference, there is a lightcone ${\mathbb{L}}_{\mathrm{Minkowski}}$, and that these lightcones are the leaves of a foliation spanning the complete, infinite Minkowski space $\mathbb{M}\cong {\mathbb{R}}^{3,1}$. In this paper, we make the assumption that there is one global (macroscopic) spacetime background ${\mathbb{M}}^4$ with stratification

$${\mathrm{Strat}}_{{\mathbb{M}}^4}\cong {\mathbb{L}}_{\mathrm{Minkowski}}$$

topologized by the lightcone. This is convenient, because it allows us to overlay the modal construction of Figure 1, thus giving a topology to the modal version of spacetime.

The problem many will have with this construction is that we necessarily have to fix a single, global apex. Denote the future lightcone by ${\mathbb{L}}^{+}$ and the past by ${\mathbb{L}}^{-}$, with the apex denoted by $\ell \in {\mathbb{L}}^{\pm }$.9 Then ℓ becomes a preferred coordinate in the worldline of an “eternal” photon ${\gamma }^{\infty }$. This will come across as obvious sacrilege, so allow us to re-interpret things more suitably. We do not assert the existence of ${\gamma }^{\infty }$ here, but shall remain agnostic. Instead, we begin with the observation that every photon must factor through the present moment, and thus we have, at all times and for all fields, that the localized action equation (14) gives us a number $n^{-z_j}$ for a fuzzy Heyting–Kripke proposition $\phi$.

Equivalently, evaluating a localized action at a single, infinitesimal ℓ-packet should register the value of a jet of order $z_j$. We choose $z_i$ to be a positive integer, so that the probability is normalized to the unit interval:

$$S(\mathfrak{x}){|}_{\phi }=n^{-z_j}\in [0,1],$$

(29)

and we denote this normalized value by

$$\sigma (\mathfrak{x},\phi )≔S(\mathfrak{x}){|}_{\phi }\in [0,1].$$

(30)

where $\phi$ is a fuzzy Heyting–Kripke proposition serving as a modal proxy for the underlying field configuration.

We then reinterpret the modal diagram of Figure 1 as a “lightcone” in the space of fuzzy Heyting–Kripke evaluations. The central node ${♢}^0=\square$ is identified with the ℓ-packet corresponding to the present moment, and each modal iterate ${♢}^k$ (for $k\in \mathbb{Z}$) is regarded as a “radial” step away from this apex in the space of possible string states.

For a given proposition $\phi$, the value of Equation (30) is then interpreted as a normalized “modal radius” measuring how far the localized action sits from the actual, realized history at ${♢}^0$. Large values of $\sigma$ correspond to states lying close to the realized, solid-arrow history (near the apex), while small values of $\sigma$ correspond to states pushed outward along dashed or squiggly trajectories, representing merely accessible or cancelled/unrealized configurations. In this sense, the stratification

$${\mathrm{Strat}}_{{\mathbb{M}}^4}\cong {\mathbb{L}}_{\mathrm{Minkowski}}$$

is refined by a modal layering indexed both by the discrete modal level k (the “height” in the diagram) and by the continuous fuzzy parameter $\sigma$ (the “radius” in the modal lightcone of propositions).

In this language, the “eternal photon” ${\gamma }^{\infty }$ is not taken to be a genuine physical worldline, but rather a degenerate (unphysical) modal mode. It appears when we formally attempt to push a normalized value $\sigma (\mathfrak{x},\phi )$ beyond 1 by adjoining an infinitesimal correction

$$\sigma (\mathfrak{x},\phi )⟼\sigma (\mathfrak{x},\phi )+{\epsilon }^{n_j},$$

with ${\epsilon }^{n_j+1}=0$. As soon as $\sigma (\mathfrak{x},\phi )+{\epsilon }^{n_j}>1$ in the ordinary order on $\mathbb{R}$, this cannot be encoded as a truth value in $[0,1]$. The only way to retain a “value” for such a mode is to regard $\epsilon$ as a nilpotent of order $n_j$ and work in an extended ring of fuzzy truth values

$$[0,1]\subset [0,1][\epsilon ]/({\epsilon }^{n_j+1}),$$

(31)

so that the overshoot lives entirely in the nilpotent ideal and is annihilated when we project back to the underlying interval $[0,1]$. In this sense, ${\gamma }^{\infty }$ corresponds to a purely nilpotent mode which is visible only at the level of the enriched modal semantics and is unphysical as an observable probability.

Remark 3 

(Epistemic harmony and modal healing). In the Chan–Paton defect setting of [6], a torsion-free, defect-free string is said to be epistemically harmonic : the entropy modal index vanishes, inverse-limit constructions behave well, and the domain-of-discourse-to-truth (DoD2T) maps are stable. By contrast, Chan–Paton defects generically break this harmony and force one to invoke “modal healing” procedures, such as MacNeille completions of incomplete lattices, to restore a usable logical context.

The present framework can be viewed as a lifted version of that picture. A web of $(p,q)$ strings with trivial interstices and no nilpotent ${\gamma }^{\infty }$-modes corresponds to an epistemically harmonic configuration: the $\sigma (\mathfrak{x},\phi )$ form a coherent family of truth-values across the web, and the Kripke frame has no hidden nilpotent directions in its $G_2$-sources. When interstices or nilpotent overshoots are present, one may again appeal to MacNeille-type completions on the lattice of propositions to repair broken DoD2T maps, but now the corrections are informed by the internal $G_2$ geometry and the FF structure along the web.

Modally, our truncation consists of applying the projection

$$\pi :[0,1][\epsilon ]/({\epsilon }^{n_j+1})⟶[0,1],\pi \left(\sigma (\mathfrak{x},\phi )+{\epsilon }^{n_j}\right)=\sigma (\mathfrak{x},\phi ),$$

which forgets all nilpotent corrections. At the level of the Heyting–Kripke frame, this amounts to identifying worlds whose only distinction lies in these nilpotent directions: the degenerate ${\gamma }^{\infty }$-modes are quotiented away when we pass to observable truth values. It is convenient to package these nilpotent directions into an internal “source” space attached to each spacetime point. Concretely, we assume that over ${\mathbb{M}}^4$ there is a rank-7 bundle

$$\pi :\mathcal{S}⟶{\mathbb{M}}^4,$$

whose fibers ${\mathcal{S}}_{\mathfrak{x}}$ carry a $G_2$-structure $({\phi }_{\mathfrak{x}},*{\phi }_{\mathfrak{x}})$. We refer to ${\mathcal{S}}_{\mathfrak{x}}$ as the $G_2$-source of $\mathfrak{x}$. The nilpotent corrections ${\epsilon }^{n_j}$ above are then interpreted as infinitesimal displacements inside ${\mathcal{S}}_{\mathfrak{x}}$, along directions encoding higher-order jet data of the fields at $\mathfrak{x}$.

Thus, the modal cone at $\mathfrak{x}$ is not only stratified by the discrete levels ${♢}^k$ and the fuzzy radius $\sigma (\mathfrak{x},\phi )$, but is further refined by an internal $G_2$-geometry in its source fiber ${\mathcal{S}}_{\mathfrak{x}}$. The would-be “eternal” modes live entirely in these nilpotent $G_2$-directions and are projected out when we pass back to physical truth values in $[0,1]$.

4.1. G₂-Sources and Modal Flux Superpotentials (After House–Lukas–Micu)

In standard M-theory compactifications on seven-manifolds with $G_2$-structure, one packages the internal geometry and flux into a complexified three-form

$$T_3=\phi +i{a}_3,$$

where $\phi$ is the $G_2$-structure three-form and $a_3$ is the internal component of the C-field. The effective four-dimensional $N=1$ superpotential then takes the schematic form

$$W={\displaystyle \frac{1}{8}}\int \left(d\phi +id{a}_3\right)\wedge (\phi +i{a}_3)+{\displaystyle \frac{1}{4}}\int G\wedge (\phi +i{a}_3)+\lambda ,$$

(32)

where G is the internal flux and $\lambda$ is a constant induced by dualisation, as in the constructions of House–Lukas–Micu and related work.10 The first term captures the torsion of the $G_2$-structure, the second encodes the coupling to flux, and the third is a topological constant.

In our setting, we reinterpret this pattern fiberwise over the macroscopic spacetime ${\mathbb{M}}^4$. We assume that over each spacetime point $\mathfrak{x}\in {\mathbb{M}}^4$ there is a rank-7 “source” fiber

$$\pi :\mathcal{S}⟶{\mathbb{M}}^4,{\mathcal{S}}_{\mathfrak{x}}:={\pi }^{-1}(\mathfrak{x}),$$

(33)

equipped with a $G_2$-structure $({\phi }_{\mathfrak{x}},*{\phi }_{\mathfrak{x}})$. We refer to ${\mathcal{S}}_{\mathfrak{x}}$ as the $G_2$-source of $\mathfrak{x}$. Heuristically, ${\mathcal{S}}_{\mathfrak{x}}$ collects the internal, higher-jet and charge-like degrees of freedom that are only seen indirectly in the macroscopic, Minkowski-stratified background ${\mathbb{M}}^4$.

On each fiber ${\mathcal{S}}_{\mathfrak{x}}$, we introduce a complexified “modal” three-form

$$T_{\mathrm{modal}}(\mathfrak{x})=\Phi (\mathfrak{x})+i\Psi (\mathfrak{x}),$$

where $\Phi (\mathfrak{x})$ encodes the realized field content at $\mathfrak{x}$ and $\Psi (\mathfrak{x})$ encodes the ensemble of unrealized or cancelled trajectories (those represented by squiggly arrows in Figure 1). We also introduce a fiberwise flux ${\mathcal{G}}_{\mathfrak{x}}$ and a differential D on ${\mathcal{S}}_{\mathfrak{x}}$ that plays the role of a modal exterior derivative (it reduces to d in the purely geometric limit).

By direct analogy with (32), we define a modal flux superpotential at $\mathfrak{x}$ by

$$W_{\mathrm{modal}}(\mathfrak{x})={\displaystyle \frac{1}{8}}{\int }_{{\mathcal{S}}_{\mathfrak{x}}}\left(D\Phi (\mathfrak{x})+iD\Psi (\mathfrak{x})\right)\wedge \left(\Phi (\mathfrak{x})+i\Psi (\mathfrak{x})\right)+{\displaystyle \frac{1}{4}}{\int }_{{\mathcal{S}}_{\mathfrak{x}}}{\mathcal{G}}_{\mathfrak{x}}\wedge \left(\Phi (\mathfrak{x})+i\Psi (\mathfrak{x})\right)+\lambda (\mathfrak{x}).$$

(34)

The first term measures the intrinsic “modal torsion” of the source fiber, the second its coupling to modal flux, and the last term is a local constant that can absorb topological data. The normalized fuzzy truth-value of Equation (30) for a proposition $\phi$ serving as a proxy for the underlying field configuration, is then taken to be a monotone function of the real part of this superpotential. Concretely, we may choose an integer $z_i>0$ and a base $n>1$ so that

$$\sigma (\mathfrak{x},\phi )=n^{-z_i(\mathfrak{x},\phi )},z_i(\mathfrak{x},\phi )\simeq f\left(\Re W_{\mathrm{modal}}(\mathfrak{x};\phi )\right),$$

(35)

for some suitable (dimensionless) function f. This matches our earlier convention that ${S(\mathfrak{x})|}_{\phi }=n^{-z_i}$ and provides a bridge between the local $G_2$-source geometry and the fuzzy Heyting–Kripke–Joyal semantics of $\phi$.

In the weak $G_2$ regime, the internal three-form modes relevant for four-dimensional physics are not harmonic but obey a twisted eigenvalue equation of the form

$$D\alpha =-\tau (\mathfrak{x}){*}_{\mathfrak{x}}\alpha ,$$

(36)

where $\tau (\mathfrak{x})$ is the intrinsic torsion scalar and ${*}_{\mathfrak{x}}$ is the Hodge operator determined by $({\phi }_{\mathfrak{x}},*{\phi }_{\mathfrak{x}})$ on ${\mathcal{S}}_{\mathfrak{x}}$. Following the House–Lukas–Micu picture, such eigenmodes provide the natural “light” degrees of freedom in the effective theory, with $\tau (\mathfrak{x})$ controlling their effective mass.11 In our language, we interpret (36) as a spectral constraint on admissible modal propositions at $\mathfrak{x}$: only those $\phi$ whose associated internal forms $\alpha (\mathfrak{x},\phi )$ satisfy (36) contribute nontrivially to the realized, solid-arrow history in Figure 1. The scalar $\tau (\mathfrak{x})$ thus becomes a spectral invariant of the $G_2$-source, i.e. part of the intrinsic data of the $G_2$-source of $\mathfrak{x}$.

Finally, the “eternal photon” ${\gamma }^{\infty }$ can be reinterpreted as a purely nilpotent deformation in this $G_2$-source picture. Attempting to push a normalized value $\sigma (\mathfrak{x},\phi )$ beyond 1 by adjoining a nilpotent correction

$$\sigma (\mathfrak{x},\phi )⟼\sigma (\mathfrak{x},\phi )+{\epsilon }^{n_j},{\epsilon }^{n_j+1}=0,$$

(37)

defines a degenerate mode living entirely in the nilpotent directions of the extended truth-value ring (31).

Projecting back to observable truth values via the truncation

$$\pi :[0,1][\epsilon ]/({\epsilon }^{n_j+1})⟶[0,1],\pi \left(\sigma (\mathfrak{x},\phi )+{\epsilon }^{n_j}\right)=\sigma (\mathfrak{x},\phi ),$$

(38)

annihilates these modes. In geometric terms, such ${\gamma }^{\infty }$-like configurations correspond to deformations of the $G_2$-source fiber ${\mathcal{S}}_{\mathfrak{x}}$ that are invisible once we project to the physical modal cone at $\mathfrak{x}$. They are therefore best understood as unphysical, nilpotent excitations in the internal $G_2$-geometry, rather than as literal eternal worldlines in ${\mathbb{M}}^4$.

5. Interstices and Fields on $\mathbb{M}$^4×7

By now, we have a spacetime

$${\mathbb{M}}^{4\times 7}{\mathbb{M}}^4\times G_2$$

with compact $G_2$ which agrees with the usual KK compactifications of M-theory.12 Let ${\gamma }^{\infty }{|}_N$ be the unphysical state ${\gamma }^{\infty }$ endowed with the cutoff N from Equation (A5). Then, denote the intersection of the compactified $G_2$ with ${\mathbb{M}}^4$ by:

$$⋏=G_2\cap {\mathbb{M}}^4.$$

It is clear that ⋏ is at least partially coextensive with ${\gamma }^{\infty }{|}_N$ if and only if $\sigma (\mathfrak{x},\phi )\ne 0$.

Proof. 

To prove this, assume on the contrary that $\sigma =0$. Then, $G_2\subset SO(7)$ is the null space and has zero measure in every direction; the action $SO(7)⤻{\gamma }^{\infty }{|}_N$ then does not exist, since we have already modded out the nilpotents in Equation 31.    □

5.0.1. Granularity and Contravariance

For very granular lattices, it is conceivable that ⋏ would be on the order of a single time-step. In this case, our field families (FFs) $\Phi$ and $\Psi$ admit (respectively) a continuous and co-continuous spectrum. As a “hand-wavey" analogy, consider a Chinese finger trap. It has rigid bits on its surface where the tube can fold and collapse, and in fact when both ends are pushed together, it only ever snaps to these points. However, when we pull the finger-trap apart on both ends, it progressively becomes smoother. This is like the process of letting $G_2$ admit more and more jets (essentially, higher-order derivatives13) This gives us a map

$${\mathcal{J}}^{\infty }:\underset{J\to \infty }{lim}{C}_{\mathrm{c}}^J{(\gamma )|}_{\mathcal{U}(\mathfrak{x})}$$

(39)

which acts contravariantly on the units of frequency $\omega$ of our ℓ-packet.14

Remark 4 

(On topology: Zariski vs. analytic/metric). Throughout this section we are implicitly using the usual smooth/metric topology on ${\mathbb{M}}^{4\times 7}={\mathbb{M}}^4\times G_2$: the Minkowski topology on ${\mathbb{M}}^4$ and the $C^{\infty }$ topology on the compact $G_2$ factor. This is the natural environment for talking about jets, lightcones, and the ℓ-packet picture.

From a more algebraic or “condensed” point of view, one could instead start with a (possibly truncated) algebra of observables A on ${\mathbb{M}}^{4\times 7}$ and equip $\mathrm{Spec}(A)$ with its Zariski topology. In that language, the nilpotent corrections we introduced (e.g. the ${\epsilon }^{n_j}$-modes attached to ${\gamma }^{\infty }$) live in the nilradical of A and are therefore invisible to the underlying Zariski topology: passing from A to its reduced algebra $A_{\mathrm{red}}$ does not change the open sets. In particular, loci such as

$$\{\mathfrak{x}\in {\mathbb{M}}^{4\times 7}\mid \sigma (\mathfrak{x},\phi )\ne 0\}$$

correspond, in the Zariski picture, to basic opens of the form $D(f)$ for suitable $f\in A$, and the nilpotent “eternal photon” directions do not alter this support.

Thus there is a clean separation of roles: the coarse “where is $\sigma \ne 0$?” information is compatible with a Zariski (or more generally spectral/condensed) topology, while the finer structure needed to talk about jets, frequencies, and the granular ℓ-packet dynamics genuinely depends on the analytic/metric topology of ${\mathbb{M}}^{4\times 7}$. Informally, the Zariski perspective keeps the same underlying support as our physical picture, but forgets the metric data that encodes how the Chinese-finger-trap-like lattice is allowed to stretch and fold.

5.0.2. Field Families

We now introduce the field-families (FFs) living on the three-legged junction. Let

$$\mathcal{U}≔\mathcal{U}(\mathfrak{x})\bigsqcup \mathcal{U}(\mathfrak{y})\bigsqcup \mathcal{U}(\mathfrak{z})$$

(40)

be the disjoint union of small neighborhoods around three representative points $\mathfrak{x},\mathfrak{y},\mathfrak{z}$ on the legs of a string junction. On $\mathcal{U}$ we take two S-dual field-families

$$\Phi =\{{\varphi }_1,\dots ,{\varphi }_p\},\Psi =\{{\psi }_1,\dots ,{\psi }_q\},$$

with $p,q\in \mathbb{N}$ relatively coprime. To each ${\varphi }_i$ (resp. ${\psi }_j$) we associate a fuzzy proposition ${\phi }_i$ (resp. ${\varsigma }_j$), thought of as the modal proxy for the statement “${\varphi }_i$ (resp. ${\psi }_j$) is active on $\mathcal{U}$.”

Definition 2. 

The interstice sector of $\mathcal{U}$ across the junction

$$⋏=G_2\cap {\mathbb{M}}^4$$

is defined, for each pair $(i,j)$, by

$${\mathcal{U}}_{\mathrm{int}}^{(i,j)}≔e^{i{\varphi }_i+j{\psi }_j}⋏.$$

(41)

Here $e^{i{\varphi }_i+j{\psi }_j}$ is a shorthand for the phase obtained by coupling ⋏ to the pair of fields $({\varphi }_i,{\psi }_j)$ at the junction; the indices $i,j$ will later be reinterpreted as charge labels in an $\mathrm{SL}(2,\mathbb{Z})$ doublet.

We impose that $\mathcal{U}$ carries an $\mathrm{SL}(2,\mathbb{Z})$ duality across the interstice ⋏ in the usual S-duality sense: the column vector of field-families transforms as

$$\left(\begin{array}{c}\Phi \\ \Psi \end{array}\right)⟼\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\left(\begin{array}{c}\Phi \\ \Psi \end{array}\right),\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in \mathrm{SL}(2,\mathbb{Z}),$$

so that $\Phi$ and $\Psi$ form an S-dual pair of FFs at the junction.

To distinguish primary, descendant, and auxiliary fields, we use the coprimeness of p and q. We declare ${\varphi }_1$ and ${\psi }_1$ to be the primary fields of their respective families, and we equip the combined FF with a single integer grading

$${\chi }_n,n\in \mathbb{N},$$

defined as follows:

$${\chi }_n=\left\{\begin{array}{cc}{\varphi }_{n/p}\hfill & \mathrm{if}p\mid n,\hfill \\ {\psi }_{n/q}\hfill & \mathrm{if}q\mid n,\hfill \\ \mathrm{auxiliary}\mathrm{field}\hfill & \mathrm{if}gcd(n,pq)=1.\hfill \end{array}\right.$$

(42)

Because p and q are relatively coprime, the multiples of p and the multiples of q form two interlaced arithmetic progressions, and there is a unique common multiple $pq$ in each block of length $pq$. The values of n that are multiples of p (resp. q) pick out descendant fields of the primary ${\varphi }_1$ (resp. ${\psi }_1$), while the integers n that lie strictly between these multiples and are not divisible by either p or q label auxiliary fields: they sit “between” the pure $\Phi$-descendants and the pure $\Psi$-descendants in the grading.

Remark 5. 

Heuristically, the auxiliary fields ${\chi }_n$ with $gcd(n,pq)=1$ should be thought of as genuinely mixed S-dual modes, obtained by letting the primary pair $({\varphi }_1,{\psi }_1)$ “breed” under the $\mathrm{SL}(2,\mathbb{Z})$ action across the interstice. The coprimeness of p and q ensures that each such level n corresponds to a unique combination of the two primary charge directions, so that the auxiliary spectrum does not double-count descendants of ${\varphi }_1$ or ${\psi }_1$. In particular, the pattern of indices n furnishes a discrete, number-theoretic skeleton for how the auxiliary FFs interpolate between the two primary families along the junction.

5.1. Computational Examples

5.1.1. A Numerically Explicit Model of S-Dual Field-Families

We extend the toy model of Appendix C. We make all choices explicit to illustrate how the FF machinery can be used to process data scientifically. We imagine a simple experiment in which a three-leg junction is probed repeatedly, and we record activation frequencies of an S-dual pair of field-families.

1. Fixing parameters and field-families. We take

$$p=2,q=3,n=2,$$

with p and q relatively coprime and n the base used in

$$\sigma (\mathfrak{x},\phi )=n^{-z_i}.$$

We consider the S-dual field-families

$$\Phi =\{{\varphi }_1,{\varphi }_2\},\Psi =\{{\psi }_1,{\psi }_2,{\psi }_3\},$$

living on

$$\mathcal{U}=\mathcal{U}(\mathfrak{x})\bigsqcup \mathcal{U}(\mathfrak{y})\bigsqcup \mathcal{U}(\mathfrak{z}),$$

with associated propositions

$${\varphi }_i⟷{\phi }_i,{\psi }_j⟷{\varsigma }_j.$$

As in the main text, we let the interstice

$$⋏=G_2\cap {\mathbb{M}}^4$$

and define, for example,

$${\mathcal{U}}_{\mathrm{int}}^{(1,1)}=e^{i{\varphi }_1+{\psi }_1}⋏.$$

2. Hypothetical measurement data and normalized truth-values. Assume that at a fixed spacetime point $\mathfrak{x}$ in the ℓ-packet we perform

$$N_{\mathrm{runs}}=128$$

independent runs of an experiment that tests, one at a time, whether each field in the FFs is “active” on $\mathcal{U}$. We suppose the (hypothetical) outcome counts are chosen so that the relative frequencies are exact dyadic fractions of the form $2^{-k}$:

field	counts (out of 128)	frequency
${\varphi }_1$	64	$64/128=1/2$
${\varphi }_2$	32	$32/128=1/4$
${\psi }_1$	32	$32/128=1/4$
${\psi }_2$	16	$16/128=1/8$
${\psi }_3$	8	$8/128=1/16$

We interpret these frequencies as normalized truth-values $\sigma (\mathfrak{x},·)$ for the corresponding propositions. With $n=2$, we have

$$\sigma (\mathfrak{x},{\phi }_1)={\displaystyle \frac{1}{2}}=2^{-1},\sigma (\mathfrak{x},{\phi }_2)={\displaystyle \frac{1}{4}}=2^{-2},$$

$$\sigma (\mathfrak{x},{\varsigma }_1)={\displaystyle \frac{1}{4}}=2^{-2},\sigma (\mathfrak{x},{\varsigma }_2)={\displaystyle \frac{1}{8}}=2^{-3},\sigma (\mathfrak{x},{\varsigma }_3)={\displaystyle \frac{1}{16}}=2^{-4}.$$

Thus

$$S(\mathfrak{x}){|}_{{\phi }_1}=2^{-1},S(\mathfrak{x}){|}_{{\phi }_2}=2^{-2},S(\mathfrak{x}){|}_{{\varsigma }_j}=2^{-w_j},$$

with

$$(z_1,z_2)=(1,2),(w_1,w_2,w_3)=(2,3,4),$$

consistent with our general convention ${S(\mathfrak{x})|}_{\phi }=n^{-z_i}$.

3. Grading, auxiliary fields, and a composite proposition. We equip the combined FF with the integer grading ${\chi }_n$ (cf. the main text):

$${\chi }_n=\left\{\begin{array}{cc}{\varphi }_{n/2}\hfill & \mathrm{if}2\mid n,\hfill \\ {\psi }_{n/3}\hfill & \mathrm{if}3\mid n,\hfill \\ \mathrm{auxiliary}\mathrm{field}{\chi }_n^{\mathrm{aux}}\hfill & \mathrm{if}gcd(n,6)=1.\hfill \end{array}\right.$$

For $n=1,\dots ,10$ this yields:

$$\begin{array}{ccccccccccc}n& 1& 2& 3& 4& 5& 6& 7& 8& 9& 10\\ {\chi }_n& {\chi }_1^{\mathrm{aux}}& {\varphi }_1& {\psi }_1& {\varphi }_2& {\chi }_5^{\mathrm{aux}}& (\mathrm{mixed})& {\chi }_7^{\mathrm{aux}}& {\varphi }_4(\mathrm{formally})& {\psi }_3& {\chi }_{10}^{\mathrm{aux}}\end{array}$$

In this finite toy, only ${\varphi }_1,{\varphi }_2,{\psi }_1,{\psi }_2,{\psi }_3$ are actually present, but the grading pattern still indicates which indices would correspond to pure descendants, mixed S-dual modes, or auxiliary fields in a larger FF.

Now consider the composite proposition

$${\phi }_1\wedge {\varsigma }_1,$$

i.e. “${\varphi }_1$ is active and ${\psi }_1$ is active” on $\mathcal{U}$. If we use the product t-norm for conjunction in the fuzzy Heyting–Kripke semantics, we obtain

$$\sigma (\mathfrak{x},{\phi }_1\wedge {\varsigma }_1)=\sigma (\mathfrak{x},{\phi }_1)\sigma (\mathfrak{x},{\varsigma }_1)={\displaystyle \frac{1}{2}}·{\displaystyle \frac{1}{4}}={\displaystyle \frac{1}{8}}=2^{-3}.$$

Thus the composite proposition is assigned $z_{\wedge }=3$, i.e. its normalized value lies one dyadic step further from the realized apex than ${\varphi }_1$ and at the same level as ${\psi }_2$.

4. An explicit $\mathrm{SL}(2,\mathbb{Z})$ move.

Notation 2. 

We write

$${\Phi }^{*}=\Psi ,{\Psi }_{*}=\Phi ,$$

to denote the S-dual field-families across the interstice ⋏.

Let us perform a concrete S-duality transformation on the FFs using the standard S-element

$$S=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)\in \mathrm{SL}(2,\mathbb{Z}).$$

On the doublet ${(\Phi ,\Psi )}^{\mathsf{T}}$ this acts as

$$\left(\begin{array}{c}{\Phi }^{*}\\ {\Psi }_{*}\end{array}\right)=S\left(\begin{array}{c}\Phi \\ \Psi \end{array}\right)=\left(\begin{array}{c}\Psi \\ -\Phi \end{array}\right).$$

Ignoring signs for the present toy (we treat $-\Phi$ as having the same activation statistics as $\Phi$), we effectively exchange the roles of electric-like and magnetic-like families:

$${\Phi }^{*}=\Psi ,{\Psi }_{*}=\Phi .$$

If we assume the underlying experiment is insensitive to this re-labelling, then the measured frequencies remain the same but are now interpreted as

$$\sigma (\mathfrak{x},{\phi }^{*(1)})=\sigma (\mathfrak{x},{\varsigma }_1)={\displaystyle \frac{1}{4}},\sigma (\mathfrak{x},{\varsigma }_{*}^1)=\sigma (\mathfrak{x},{\phi }_1)={\displaystyle \frac{1}{2}},$$

and similarly for the other indices. In other words, the same dataset of counts can be viewed as describing two S-dual pictures related by $S\in \mathrm{SL}(2,\mathbb{Z})$, with the FF machinery simply reorganizing how the $\sigma$-values are assigned to the graded fields.

5. A concrete nilpotent overshoot and the “eternal photon”. Finally, we illustrate the nilpotent “eternal photon” deformation with a specific numerical example. Suppose a future refinement of the experiment yields, for ${\phi }_1$, a value extremely close to 1, say

$$\sigma (\mathfrak{x},{\phi }_1)=1-2^{-10}={\displaystyle \frac{1023}{1024}}.$$

In our dyadic scheme with base $n=2$ and integer exponents, this cannot be represented exactly as $2^{-z}$ with $z\in \mathbb{N}$, so we view it as a small deformation of $\sigma =1$:

$$\sigma (\mathfrak{x},{\phi }_1)=1-\delta ,\delta =2^{-10}.$$

If we now formally push this value slightly beyond 1 by adjoining a nilpotent $\epsilon$,

$$\sigma (\mathfrak{x},{\phi }_1)⟼\sigma (\mathfrak{x},{\phi }_1)+{\epsilon }^2=1-2^{-10}+{\epsilon }^2,{\epsilon }^3=0,$$

(43)

then in the extended ring $[0,1][\epsilon ]/({\epsilon }^3)$ the overshoot

$$1-2^{-10}+{\epsilon }^2>1$$

cannot be interpreted as an ordinary truth-value. Instead, the ${\epsilon }^2$ term is understood as a purely nilpotent deformation corresponding to an unphysical, “eternal” mode ${\gamma }^{\infty }{|}_N$ living entirely in the internal $G_2$-source directions of the junction.

Projecting back to physical truth-values via

$$\pi :[0,1][\epsilon ]/({\epsilon }^3)\to [0,1],\pi \left(1-2^{-10}+{\epsilon }^2\right)=1-2^{-10},$$

kills the nilpotent and restores the observed value. Thus, even at the level of a simple dyadic counting experiment, the FF machinery shows how a concrete dataset of activation frequencies can be:

• encoded as $\sigma (\mathfrak{x},·)$ via ${S(\mathfrak{x})|}_{\phi }=2^{-z_i}$,
• combined into composite propositions using a chosen t-norm,
• reorganized under explicit $\mathrm{SL}(2,\mathbb{Z})$ duality moves, and
• extended to nilpotent, unphysical modes corresponding to ${\gamma }^{\infty }{|}_N$ in the internal $G_2$-source geometry.

In this sense, the toy model demonstrates that the interstice-and-FF formalism is not merely qualitative: it provides a concrete pipeline from discrete experimental data to modal truth-values and back.

5.1.2. A Minimal $(p,q)$ Web: Two Junctions and an Internal Edge

To see how the interstice and FF machinery behaves beyond a single junction, we now consider the simplest nontrivial $(p,q)$ web: two three-string junctions connected by an internal $(p,q)$-segment. We work again in a fixed-time slice $x^0=t_0$ of ${\mathbb{M}}^4$, in the $(x^1,x^2)$-plane.

Place two junction points at

$${\mathfrak{x}}_A=(-L/2,0),{\mathfrak{x}}_B=(L/2,0),$$

for some $L>0$. At ${\mathfrak{x}}_A$ we take charges

$$(p_1,q_1)=(1,0),(p_2,q_2)=(0,1),(p_3,q_3)=(-1,-1),$$

(44)

so that $(1,0)$ and $(0,1)$ are external legs and $(-1,-1)$ is an internal leg pointing toward ${\mathfrak{x}}_B$. At ${\mathfrak{x}}_B$ we choose

$$(p_4,q_4)=(-1,0),(p_5,q_5)=(0,-1),(p_6,q_6)=(1,1),$$

(45)

where $(-1,0)$ and $(0,-1)$ are external legs and $(1,1)$ is the internal leg arriving from ${\mathfrak{x}}_A$. Each junction satisfies charge conservation:

$$(1,0)+(0,1)+(-1,-1)=(0,0),(-1,0)+(0,-1)+(1,1)=(0,0).$$

The two internal legs are simply the same physical segment with opposite orientations. For a constant axio–dilaton $\tau \simeq i$ one can again arrange all legs at appropriate angles so that tension vectors close at each junction. A schematic planar picture is shown in Figure 2.

• Local neighborhoods and FFs on the web.

We choose small neighborhoods

$${\mathcal{U}}_A^{(1)},{\mathcal{U}}_A^{(2)},{\mathcal{U}}_A^{(3)}$$

around points on the three legs meeting at ${\mathfrak{x}}_A$, and similarly

$${\mathcal{U}}_B^{(1)},{\mathcal{U}}_B^{(2)},{\mathcal{U}}_B^{(3)}$$

around points on the three legs at ${\mathfrak{x}}_B$. The internal $(1,1)$ segment between ${\mathfrak{x}}_A$ and ${\mathfrak{x}}_B$ is covered by the pair ${\mathcal{U}}_A^{(3)}$ and ${\mathcal{U}}_B^{(3)}$, which overlap in a small open interval around the midpoint of the internal edge. We set

$${\mathcal{U}}_A={\mathcal{U}}_A^{(1)}\bigsqcup {\mathcal{U}}_A^{(2)}\bigsqcup {\mathcal{U}}_A^{(3)},{\mathcal{U}}_B={\mathcal{U}}_B^{(1)}\bigsqcup {\mathcal{U}}_B^{(2)}\bigsqcup {\mathcal{U}}_B^{(3)}.$$

Over each ${\mathcal{U}}_A$ and ${\mathcal{U}}_B$ we place the same S-dual FFs

$$\Phi =\{{\varphi }_1,{\varphi }_2\},\Psi =\{{\psi }_1,{\psi }_2,{\psi }_3\},$$

with

$${\Phi }^{*}=\Psi ,{\Psi }_{*}=\Phi ,$$

and we associate primary fields to the external legs:

$${\varphi }_1\mathrm{on}\mathrm{the}(1,0)\mathrm{and}(-1,0)\mathrm{legs},{\psi }_1\mathrm{on}\mathrm{the}(0,1)\mathrm{and}(0,-1)\mathrm{legs}.$$

The internal $(1,1)$ segment is then naturally associated to the first mixed level in the FF grading (e.g. the $n=6$ mode in the $p=2,q=3$ example), and its excitations are described by auxiliary or mixed fields in the combined ${\chi }_n$-grading.

• Gluing of modal data along the internal edge.

Let ${\varphi }_i\leftrightarrow {\phi }_i$ and ${\psi }_j\leftrightarrow {\varsigma }_j$ be the associated fuzzy propositions, as before. At each junction point ${\mathfrak{x}}_A$ and ${\mathfrak{x}}_B$ we have normalized truth-values

$$\sigma ({\mathfrak{x}}_A,{\phi }_i),\sigma ({\mathfrak{x}}_A,{\varsigma }_j),\sigma ({\mathfrak{x}}_B,{\phi }_i),\sigma ({\mathfrak{x}}_B,{\varsigma }_j)\in [0,1],$$

for instance using the dyadic values from the numerically explicit FF example:

$$\sigma ({\mathfrak{x}}_A,{\phi }_1)=\sigma ({\mathfrak{x}}_B,{\phi }_1)=\frac{1}{2},\sigma ({\mathfrak{x}}_A,{\varsigma }_1)=\sigma ({\mathfrak{x}}_B,{\varsigma }_1)=\frac{1}{4},$$

and so on for the higher descendants.

To describe propagation along the internal $(1,1)$ edge, we introduce an attenuation factor

$$0<\alpha \le 1$$

which captures the net effect of transport from ${\mathfrak{x}}_A$ to ${\mathfrak{x}}_B$ through the internal $G_2$-source and the modal lightcone. At the level of fuzzy truth-values, this is encoded by a simple gluing rule:

$$\sigma \left({\mathcal{U}}_B^{(3)},\phi \right)=\alpha \sigma \left({\mathcal{U}}_A^{(3)},\phi \right)$$

(46)

for any proposition $\phi$ that is transported along the internal leg. More refined models can replace (46) by an integral kernel or a spectral projection built from the $G_2$-source geometry; for this minimal web it suffices to keep a single scalar parameter.

As a concrete example, take $\alpha =\frac{1}{2}$ and consider the composite proposition

$${\phi }_1^{(A)}\wedge {\varsigma }_1^{(B)},$$

which states that “${\varphi }_1$ is active at the left junction and ${\psi }_1$ is active at the right junction.” Using the product t-norm for ∧, the glued truth-value is

$${\sigma }_{\mathrm{web}}\left({\phi }_1^{(A)}\wedge {\varsigma }_1^{(B)}\right)=\sigma ({\mathfrak{x}}_A,{\phi }_1)\left(\alpha \sigma ({\mathfrak{x}}_B,{\varsigma }_1)\right)={\displaystyle \frac{1}{2}}·{\displaystyle \frac{1}{2}}·{\displaystyle \frac{1}{4}}={\displaystyle \frac{1}{16}}=2^{-4}.$$

(47)

Thus the joint activation across the two-junction web sits two dyadic steps further from the realized apex than ${\varphi }_1$ alone, and one step further than the single-junction composite ${\phi }_1\wedge {\varsigma }_1$ discussed earlier. In the modal lightcone picture, this corresponds to moving one layer outward along the dashed, “merely possible” region.

• Kripke frame viewpoint.

Formally, we can regard the minimal web as a Kripke frame $(W,R)$ built from three types of worlds:

• worlds $w_A\in W_A$ localized near ${\mathfrak{x}}_A$,
• worlds $w_B\in W_B$ localized near ${\mathfrak{x}}_B$,
• worlds $w_{\mathrm{int}}\in W_{\mathrm{int}}$ along the internal $(1,1)$ segment.

The accessibility relation R contains:

$$w_{A}R{w}_{\mathrm{int}},w_{\mathrm{int}}R{w}_B,$$

reflecting causal/modal access along the internal edge. The valuation V of propositions $\phi$ is specified at $w_A$ and $w_B$ by the numbers $\sigma ({\mathfrak{x}}_A,\phi )$ and $\sigma ({\mathfrak{x}}_B,\phi )$, and extended to $w_{\mathrm{int}}$ via the gluing rule (46). The computation (47) is then simply the evaluation of a conjunction over the composite path

$$w_A⟶w_{\mathrm{int}}⟶w_B$$

in the frame.

In this way, even this minimal $(p,q)$ web realizes the full stack of structures introduced in the paper: a Minkowski lightcone apex at each junction, internal $G_2$-sources controlling attenuation and mode selection on the internal edge, S-dual FFs attached to each leg, and a Kripke/modal semantics that computes concrete, normalized truth-values for composite propositions across the web.

6. Discussion and Outlook

The inception of this paper began by considering Minkowski lightcones not merely as geometric objects, but instead decorated structures endowed with modal and fuzzy information. This ties into a general desire to fill the lacuna of non-classical logics in physics. While heterodox, the framework here is deliberately modest; propositions $\phi$ are mere proxies for field content of fields $\varphi$. We implemented a rather standard M-theoretic $G_2$-compactification, in which the relativistic information is contained in a thickened apex of a global lightcone spanning the whole of spacetime.

This gave rise to “eternal" photons ${\gamma }^{\infty }$, which are unphysical modes that required us to truncate the modal histories by fixing finite sub-lightcones containing the apex ℓ. The kinematic aspects of this neighborhood are regarded as ℓ-packets, which are a souped up version of the classical notion of wave-packets, that factor through the present moment, or in other words, the necessary frame □.

We also gave □ a dual role by implementing a map $♢\mapsto \square$ in Equation (1), which we localized in Equation (8), all while connecting to our previous work ([7] was implemented in (11) and (12), and [6] was discussed throughout), cementing the narrative within a larger research program. The implementation of the decorated loop-space (DLS) paradigm forced us to consider vibrational modes of closed strings as probabilistic phenomena, which then generalized to the open case via a similar procedure.

On top of this modal, we introduced interstices

$$⋏=G_2\cap {\mathbb{M}}^4$$

as higher-dimensional avatars of Chan–Paton defects on open strings, now sitting at $(p,q)$ junctions in a compactified ${\mathbb{M}}^{4\times 7}$ background. Each interstice carries an internal $G_2$-source fiber ${\mathcal{S}}_{\mathfrak{x}}$ and supports S-dual field-families (FFs) $\Phi$ and $\Psi$, together with a grading that separates primary, descendant, and auxiliary fields. We showed how a House–Lukas–Micu type superpotential can be reinterpreted as a modal flux superpotential, with its real part feeding into the exponents $z_i$ in $\sigma (\mathfrak{x},\phi )=n^{-z_i}$, and how nilpotent overshoots beyond $\sigma =1$ naturally realize the “eternal photon” as a degenerate, unphysical mode in the $G_2$-source directions.

The FF formalism allowed us to attach concrete S-dual data to $(p,q)$ junctions and webs. We constructed both a numerically explicit toy model of FF activation on a three-leg junction and a minimal $(p,q)$ web with two junctions connected by an internal $(1,1)$ segment. In each case, we made the $\sigma$-valuations completely explicit, used a product t-norm to evaluate composite propositions such as ${\phi }_1\wedge {\varsigma }_1$, and tracked the attenuation of truth-values along the internal edge via a simple gluing rule. Viewed as a Kripke frame, the web becomes a small network of worlds connected by an accessibility relation that respects the $(p,q)$ geometry: modal transitions along the web are the logical shadow of charge-conserving, tension-balanced configurations in Type IIB.

Several limitations of the present treatment are worth emphasizing. First, we worked with simple, static $(p,q)$ junctions and webs in a fixed-time slice of ${\mathbb{M}}^4$, with constant axio–dilaton and a highly idealized compact $G_2$ factor. The internal $G_2$-source geometry entered only through its torsion scalar and a schematic differential D, rather than via explicit solutions of the eleven-dimensional equations of motion. Second, our choice of t-norm and the scalar attenuation parameter along the internal edge were made for concreteness, not uniqueness: other fuzzy-logical choices and more structured transport operators (e.g. spectral projections built from the $G_2$ Laplacian) may be more appropriate in specific physical applications. Finally, we restricted attention to finite FFs and simple coprime gradings; richer charge lattices and higher junction multiplicities will require a more elaborate combinatorial organization.

Despite these simplifications, the formalism suggests several concrete directions for further work:

• Larger webs and networks. Extend the Kripke/FF construction to general $(p,q)$ webs and five-brane webs, analyzing how $\sigma$-valuations glue along networks with nontrivial cycles and how nilpotent modes behave under web deformations.
• Dynamical and supergravity embeddings. Embed the modal lightcone and $G_2$-source picture into explicit eleven-dimensional backgrounds, for example by solving the weak $G_2$ Killing spinor equations with flux and comparing the resulting spectrum to the FF grading and the modal flux superpotential.
• Defects and modal healing. Make precise the relationship between interstices and Chan–Paton defects, importing the entropy modal index and MacNeille-type “modal healing” procedures to repair inconsistent $\sigma$-valuations across webs with defects.
• Categorical and operadic refinements. Recast FFs and interstices in terms of higher categories or operads of junctions, so that the modal lightcone and $G_2$-sources become part of a functorial assignment of logical data to extended configurations, in line with TQFT and decorated loop-space approaches.

Taken together, these directions point toward a broader program in which spacetime lightcones, internal flux geometries, and logical modalities are treated on the same footing.