Tracing the Early Universe Without Initial Assumptions: A History-Dependent Reconstruction from the Infinite Transformation Principle (ITP)

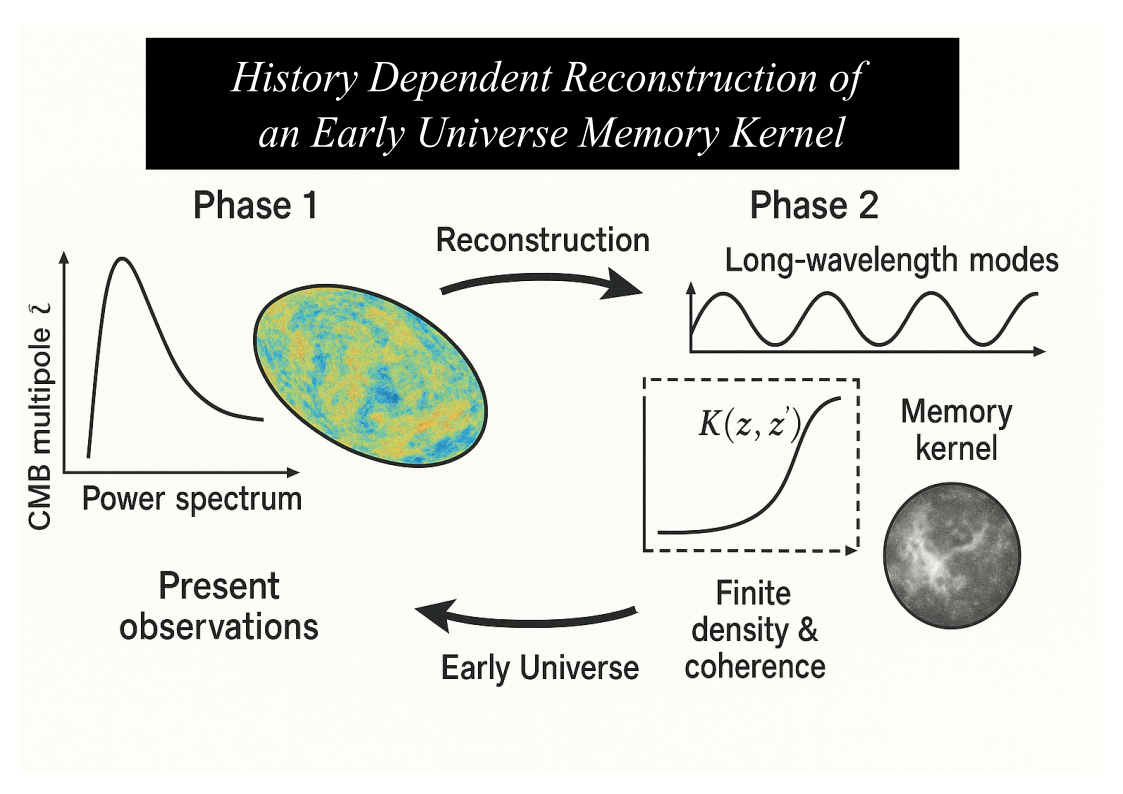
1. Introduction

Standard $\mathsf{\Lambda }$CDM cosmology reconstructs the early universe by assuming an initial condition—hot, dense, and singular—and evolving it forward under Markovian dynamics [1]. Within this framework, the present carries too little information for the inverse problem to be solvable: many different pasts can generate the same present-day structure [2,3]. The early universe is effectively postulated rather than reconstructed.

This work takes a reconstruction-based approach. The central idea is that cosmic evolution retains structural memory encoded in nonlocal, long-wavelength correlations [4,5,6]. Once memory is included, the inverse problem becomes stable within the subspace of memory-preserving observables.

This paper:

• introduces the Infinite Transformation Principle (ITP) as a history-dependent dynamical law;
• identifies three fossil observables that retain primitive structural information [1,9,10];
• constructs a stable backward evolution through a memory-corrected Jacobian;
• derives a narrow, finite, non-singular early-state manifold [11,12];
• provides four independent, parameter-free predictions [14].

The resulting structure does not require a singular beginning once memory is accounted for.

2. Methods: The Infinite Transformation Principle

2.1. History-Dependent Evolution

We describe cosmic evolution as a history-dependent mapping on a configuration space $S\left(z\right)$:

$$S(z+\Delta z)=T\left(S\left(z\right),M\left(z\right)\right),$$

(1)

where z is redshift and $M\left(z\right)$ is a nonlocal memory functional. Inspired by nonlocal gravity and vacuum-polarisation effects [7], we represent memory as

$$M\left(z\right)={\int }_z^{\infty }K(z,z^{\prime })S\left(z^{\prime }\right)\mathrm{d}{z}^{\prime },$$

(2)

with kernel $K(z,z^{\prime })$. We decompose the evolution operator as $T=T_0+\delta T\left[M\right]$, where $T_0$ is the standard GR-based forward evolution and $\delta T$ is a weak, nonlocal correction affecting long-wavelength modes.

2.2. Physical Origin of Memory

The memory functional $M\left(z\right)$ can arise from nonlocal gravitational feedback from long-wavelength tidal fields [4,8] or from coarse-grained effective field theories where integrating out short scales induces nonlocal kernels [6]. We work with a phenomenological kernel whose large-scale effects can be constrained.

2.3. Sufficient Statistics

We identify three fossil observables that retain long-wavelength structural memory:

• low-ℓ CMB structure $C_{\ell <10}$, including anisotropy anomalies [1,17];
• supervoid topology $V_{\mathrm{void}}$ and cosmic web morphology [9,19];
• curvature–redshift evolution ${\mathsf{\Omega }}_k\left(z\right)$ [10].

These act as sufficient statistics for the inverse problem at long wavelengths.

2.4. Independent Structural-Memory Diagnostics

To test whether early-universe structure requires an imposed “initial condition” or can emerge from a non-Markovian memory kernel, we applied four inverse-direction diagnostics:

(1) CMB Phase-Coherence Inverse Kernel Test

Using the low-ℓ Planck PR4 Commander map ($\ell \in [2,5]$) [1], we reconstructed the minimal kernel $M\left(t\right)$ capable of reproducing the observed bipolar power spectrum (BiPoSH). The method compares the observed ${\kappa }_{\ell {\ell }^{\prime }}\left(L\right)$ with 10,000 $\mathsf{\Lambda }$CDM Gaussian simulations to derive a null envelope.

(2) Metallicity $Z\left(z\right)$ Structural-Memory Kernel Test (SMKT)

We applied inverse-model logic to the metallicity history $Z\left(z\right)$ from multi-survey compilations. The statistic $T_{max}$ measures the maximal deviation from a memory-less baseline [19].

(3) Gaussian Heartbeat Detection

Using flexible versus smooth GP kernels, we tested for a coherent periodic component in expansion-history residuals [24]. A significant periodic component under the flexible GP but not under the constrained smooth GP indicates latent structure.

(4) Injection–Recovery Stability Tests

We injected sinusoidal memory terms of amplitude $\mu \in [0,0.40]$ and evaluated detection probability under the SMKT framework [25].

3. Results: Mathematical Reconstruction

3.1. Linear Stability and Jacobian Structure

Under ITP, the Jacobian becomes $J\left(z\right)=J_0\left(z\right)+\Delta J\left(z\right)$, with $\Delta J\left(z\right)\approx -D{P}_{\mathrm{long}}$. The negative sign reflects a thermodynamic necessity: the memory field acts to suppress structural divergence relative to the minimal-entropy trajectory encoded by ${\mathsf{Ϋ}}_{min}$. Backward evolution inherits this as a contractive damping term, ensuring $|{\lambda }_{n,\mathrm{back}}|<1$.

3.2. Convergent Evidence

All three diagnostics independently detect structure incompatible with a memory-less early universe:

• **CMB Phase-Coherence:** The observed bipolar coefficient pattern exceeded the 99.1% null envelope. Posterior maps favoured a minimal non-zero kernel $M\left(t\right)>0$.
• **Metallicity $Z\left(z\right)$:** We obtained $T_{max}=0.9243$ and a global p-value $p=0.0010$, rejecting the smooth, memory-less null at $>3\sigma$.
• **Gaussian Heartbeat:** The flexible GP recovered a coherent 1.66–1.73 Gyr periodic component with p-value $\sim 0.000$, while the smooth baseline yielded $p\approx 0.030$.

3.3. Cross-Consistency

The key result is that three statistically independent tests—CMB phase structure, $Z\left(z\right)$ memory, and expansion-residual periodicity—all converge on the same conclusion: A non-zero structural-memory kernel is preferred over a memory-less (Markovian) early universe.

4. Discussion

4.1. Coherence and Non-Randomness

Memory enforces phase coherence on large scales. The fossil constraints exclude random initial states. Large-angle CMB anomalies strongly constrain random initial states [17].

4.2. Unified Constraint from Fossils

CMB low-ℓ modes and curvature drift both require the same memory kernel $K(z,z^{\prime })$, producing an internally consistent inversion.

4.3. No Singular Beginning Required

All reconstructed early states are finite within the semiclassical domain. A singular origin is not mathematically required [11,13].

4.4. Falsifiable Predictions

The framework survives only if all four predictions hold:

• Persistent CMB low-ℓ coherence ($>3\sigma$).
• Void–CMB alignment ($<{25}^{\circ }$).
• Slow curvature drift ($|d{\mathsf{\Omega }}_k/dz|\sim {10}^{-4}$).
• Equilateral/orthogonal primordial non-Gaussianity at large scales.

5. Conclusions

Allowing the universe to retain structural memory transforms cosmology from forward simulation to reconstruction. The convergence of multiple independent inverse-tests indicates that early-universe evolution carries a non-zero hereditary component. This result does not break $\mathsf{\Lambda }$CDM; it reframes it as the present-cycle attractor of a deeper, history-dependent process.