Enhancing Students’ Understanding of Numerical Sequences Through Real-Life Contexts, Python Programming, and AI Tools

1. Introduction

The teaching of numerical sequences, including arithmetic and geometric sequences, holds a central position in the upper secondary mathematics curriculum, particularly in gymnasiums. These concepts are foundational for the development of advanced mathematical knowledge and play a crucial role in fostering students' logical reasoning and critical thinking skills. However, both classroom experience and didactic literature indicate that many students face significant difficulties in deeply understanding these sequences, especially in recognizing patterns and constructing general formulas [1]. These challenges can be attributed to a lack of concrete representations, limited connection to real-life experiences, and reliance on traditional teaching methods, which often render this topic difficult for most students to master.

To address these challenges, it is essential to integrate contemporary teaching strategies that involve real-life examples, collaborative work, and the use of technology. Context-based learning, in which mathematical concepts are directly linked to practical situations, helps students construct more meaningful and lasting understanding. For instance, developing a numerical model to represent the interest earned each year, forming an arithmetic sequence by increasing a determined amount annually, provides a tangible context for learning sequences and facilitates the application of mathematical reasoning in familiar situations [2]. Research has shown that authentic contexts in mathematics instruction can enhance student engagement and understanding by connecting mathematical concepts to real-world experiences[3,4].

In this context, technology plays an indispensable role as a supportive tool in the learning process. One of the most promising tools in this area is the Python programming language, which has seen increasing adoption in education due to its simplicity and versatility across scientific subjects. Python enables students to generate numerical sequences, uncover patterns among terms, formulate general expressions, and visualize sequences graphically. This approach not only deepens students' conceptual understanding but also equips them with essential technological and analytical skills required in the 21st century[5]. Furthermore, the integration of Python into mathematics instruction serves as a bridge between theory and practice, transforming learning into an exploratory, engaging, and meaningful process[6].

This research aims to explore the impact of real-life examples and the use of Python programming on students' understanding of numerical sequences at the secondary school level. Through a combination of qualitative methodology, classroom observations, and analysis of teaching practices, the study examines how these approaches enhance students' motivation, engagement, and mathematical comprehension. Central to this analysis is the role of contextualized learning and technological tools in creating a more effective, interactive, and responsive educational environment suited to the needs of today's learners.

This research aims to explore the impact of real-life examples and the use of Python programming on students' understanding of numerical sequences at the secondary school level. Through a combination of qualitative methodology, classroom observations, and analysis of teaching practices, the study examines how these approaches enhance students' motivation, engagement, and mathematical comprehension. Central to this analysis is the role of contextualized learning and technological tools in creating a more effective, interactive, and responsive educational environment suited to the needs of today's learners.

Based on these considerations, the study was guided by the following research question:

-

How does the integration of real-life contextual tasks, Python programming, and AI-assisted tools influence students’ conceptual understanding of numerical sequences and their development of digital competencies in upper secondary informatics education?

1.1. Literature Review

Advances in educational technology are increasingly recognized as enhancing mathematics education. Recent reviews emphasize that digital tools can serve as “significant enablers” of mathematical thinking, broadening access and supporting both teachers and students in meaningful learning[7]. For example, Mohamudally-Boolaky and Padachi’s systematic review found that innovative technologies empower teachers and learners in mathematics but, cautioned that effective use requires careful integration with curriculum and teaching practices. Integrating technology tends to prepare students for complex, real-world problem solving[8] and others note that digital environments can offer personalized and immersive learning, while problem solving based learning has been shown to boost engagement[7,9]. These studies reinforce that technology must complement, not replace, solid pedagogy: the teacher’s role remains crucial to guide students’ mathematical thinking even when tools are used[7].

Similarly,[10] argue that embedding computational thinking (CT) in math instruction (for example, by having students write simple programs) can create an interactive cycle of mathematical reasoning. In their systematic analysis, they found that CT-based math activities (often “geometrized” programming tasks) led students to alternate between applying math to construct code and using the resulting outputs to inform new mathematical ideas (stem education journal.springeropen.com). Thus, technology and programming can scaffold an iterative process in which students build and test models, fostering deeper engagement with math concepts[10].

1.1.1. Contextual and Problem-Based Learning

Contextual, problem-based approaches have long been advocated to make mathematics more relevant and engaging. In these methods, tasks are embedded in real-life scenarios so that students use their own experiences and knowledge to “mathematize” a situation. Clarke and Roche [11], for example, reported that when middle school teachers employed a variety of rich contextual tasks, students were more motivated and found the problems both enjoyable and worthwhile. They note that a teacher’s selection of tasks “is a major determinant of the nature and quality of students’ learning,” since context-rich problems can show how mathematics solves real problems and thus sustain student interest. Brown and Redmond [12] likewise observed that PISA-style real-world problems (requiring quantities and reasoning) help secondary students shift back and forth between everyday understanding and formal mathematics. They argue that appropriately framed contexts allow students to develop representation, reasoning, argumentation and communication skills that are essential to mathematics teaching[13]. In short, anchoring sequences and series problems in familiar contexts (e.g. revenue from selling fish, growth over time) can encourage students to draw on prior knowledge and concrete intuition. Research in sequence topics supports the value of context. In one design-based study, teachers used a Contextual Teaching and Learning (CTL) framework with a hypothetical learning trajectory for sequences and series. Students tackled real-life word problems (e.g. rice yield over years, catfish farm yields) that required identifying and extending numerical patterns. The authors report that this CTL-based trajectory notably improved students’ conceptual understanding of sequences: students were guided to connect informal knowledge (such as patterns in real problems) to formal formulas, and as a result they developed stronger problem-solving skills [14]. Importantly, the study found that students habituated to solving real-world sequence problems were better able to derive arithmetic and geometric formulas by recognizing underlying pattern [12]. In this context-based design research, most students could generate the recursive or closed-form expression for a sequence, though some still needed help transitioning between forms of the expression

Overall, the authors concluded that a CTL-inspired approach “supports students to understand the concept of sequences and series and use them in solving real-life problems,” with measured gains in problem-solving on post-tests [15]. These findings suggest that contextual tasks, when structured by the teacher, help secondary learners build on prior knowledge and connect informal understanding to formal sequence and series concepts [11,12].

1.1.2. Difficulties in Learning Arithmetic and Geometric Sequences

Students often encounter significant challenges when learning arithmetic and geometric sequences. One common difficulty lies in moving between concrete examples and algebraic generalizations. For arithmetic sequences (which grow by adding a constant difference), learners must grasp that the nth term formula (e.g., $a_n=a_1+(n-1)·d$ and the sum formula $S_n={\displaystyle \frac{n}{2}}(2a_1+(n-1)·d$ are linked. In practice, many students struggle to derive the sum formula from the term formula. For example, in classroom observations Indonesian teachers noted that students “did not understand how to change the form of $U_n$ to $S_n$, and as a result they could not find the formula for the number of an arithmetic sequences” [15]. This was attributed to students not being accustomed to transforming one algebraic form into another. The study reported that with guided questioning, students eventually did apply the known general term to derive Sn, but initially “some students had difficulty in finding the formula for the sum of the first terms of an arithmetic sequence”. Geometric sequences pose even greater cognitive load because of their multiplicative structure. Students must understand exponents and repeated multiplication by a common ratio. In the same research project, teachers observed that while many students could recognize the concept of a geometric sequence from contextual clues, some became confused when expressing the formula in exponent form. For example, after examining problems about growth (such as harvesting yields each year), most students identified that the sequence followed a constant multiplier pattern. However, a subset “were confused in finding the correct exponent form of the geometric sequence formula”. They struggled to translate the notion of multiplying by the ratio into the algebraic expression$a_n=a_1·r^{n-1}$. In practice, such conceptual hurdles mean students often make errors in setting up or computing sequence problems. More broadly, researchers have found that pattern/sequence tasks rank among the hardest word problems for students. One Indonesian study noted that a majority of 15-year-olds performed poorly on sequence-and-series questions: 52% of students scored below the average on a test of sequence and series problem solving [16]. These findings echo literature on math learning showing that students commonly misidentify keywords or confuse additive and multiplicative patterns when solving realistic sequence problems. Therefore, any effective instructional strategy must explicitly address these difficulties by providing concrete examples of sequences, scaffolding the algebraic transitions, and linking patterns to students’ prior experiences.

1.1.3. Integrating Technology in Mathematics Instruction

There is growing interest in using programming languages like Python as a pedagogical tool in mathematics education. Programming offers immediate feedback and a concrete way to compute and visualize mathematical ideas. In one study of a Philippine high school geometry class, teachers used Python (through a block-based environment) to explore angle and symmetry concepts. They found that introducing Python coding made learning playful and provided instant error-feedback: “the integration of Python programming into the curriculum contributes to STEM learning, offering students access to opportunities for developing essential skills such as mathematical reasoning, problem-solving, and critical thinking” [17]. In that study, students wrote short Python scripts to check their answers and generate geometric constructions; the coding tasks allowed them to “learn by doing,” iterating quickly and reflecting on mistakes. The authors report that this approach gave students a “playful and informal learning environment” while also challenging them to apply rigorous mathematical thinking. Teachers observed that students became more engaged with algebra concepts when they could manipulate symbols programmatically (e.g. using Python variables), effectively linking algebraic and computational representations.

The broader evidence on Python supports these observations. Other technology, enhanced approaches also demonstrate positive effects. For example, Mahmuti et al. [18] showed that virtual manipulatives not only increased students’ engagement but also strengthened their conceptual understanding by enabling visualization, experimentation, and immediate feedback. Rais and Zhao [19] conducted a quasi-experimental study of Python integration in an Indonesian math curriculum and found that coding exercises improved student engagement and understanding. When students used Python to model mathematical problems, they “understood the symbols they manipulate” and could directly compare their mathematical model (derived by hand) with the program output. Crucially, whenever discrepancies arose, students were prompted to debug their code - analysing Type Error messages and logical errors - which in turn reinforced the underlying math concepts. The authors emphasize that this error-feedback loop “augments students’ capacity to retain and process information” and fosters persistence in problem solving [19]. In short, debugging Python becomes a learning opportunity that deepens conceptual insight. Moreover, Python’s syntax and accessibility make it well-suited for mathematics. Since it is free, widely adopted, and easy to read even for beginners, educators have found that students from diverse backgrounds can use it as a mathematical tool [19]. Its use has been reported to empower learners: for example, integrating Python in math classes has been linked to increased interest and achievement [17,19] as well as stronger computational thinking. By engaging in iterative coding (developing algorithms, testing them, and debugging), students naturally practice problem decomposition and systematic reasoning - skills directly applicable to solving arithmetic and geometric sequence problems. As Rais and Zhao note, such programming-infused instruction “promises to improve student learning outcomes,” helping students build both procedural fluency and critical thinking. This aligns with [10] finding that programming can create a “reciprocal process” where mathematical concepts are both applied in code and reinforced by interpreting code outputs [10]. In sum, the literature suggests a convergent approach: combining context-based, problem-rich tasks with appropriate technology and programming can mitigate students’ difficulties in sequences. Contextual problems make the need for a formula clear and meaningful, while tools like Python allow students to experiment with and verify the sequences algebraically. By integrating these strategies, teachers can support secondary learners in mastering arithmetic and geometric sequences through engaging, interactive, and research-backed methods [11,19].

2. Materials and Methods

This research follows the principles of action research conducted in a classroom setting. The design uses a quasi-experimental mixed-methods approach combining both quantitative and qualitative approaches [20] to comprehensively examine the impact of contextualized learning and Python programming on students’ understanding of numerical sequences. The integration of qualitative and quantitative components allows for the provision of measurable statistical evidence of learning benefits, as well as an in-depth exploration of the processes underlying students’ mathematical engagement and reasoning [21,22]. Participants in this research include two 12th grade classes in the Technology and Information profile from IAAP “Andrea Durrsaku” in Kamenica, where one class (25 students) was designated as the experimental group and one class (23 students) as the control group, a total of 48 students. The main objective was to develop real-life context examples and the use of Python in the teaching process. The study was conducted over a two-week period, starting in 10.03.2025-21.03.2025.

2.1. Research Design

The research design followed a pre-test – intervention – post-test model, supported by qualitative data to strengthen the credibility of the study.

2.1.1. Phases of the Research Design:

Phase 1: Pre-test (Baseline measurement). Before the intervention, all participating students completed a mathematics achievement test on numerical sequences to determine their initial level of knowledge. This step provided the quantitative baseline for subsequent comparisons within and between groups.

Phase 2: Intervention and observation checklist

The experimental groups engaged with contextualized tasks, supported by Python programming activities to visualize and verification of results, while the control groups continued with traditional textbook-based instruction. Since the profile is in computer science, students learn programming languages, particularly Python. During the intervention phase, also ICT teachers created specialized codes that enable students to simultaneously develop their programming skills and apply them in the visualization and solving of tasks related to numerical sequences. The observation list was used by the experimental group teacher, who kept continuous notes on the behavior, involvement, and progress of students during class.

Phase 3: Post-test

After the intervention, both groups completed the same mathematics achievement test.

During the post-test phase, the treatment of the experimental and control groups was carried out in accordance with ethical research principles, ensuring transparency, fairness, and full respect for students’ rights. Both groups were permitted to use Python, as it was considered a neutral tool for visualization, verification of results, and mathematical modeling. Python did not replace students’ mathematical reasoning but served as a supportive instrument that reinforced conceptual understanding. This ensured equal access to essential digital tools for all participants.

However, only the experimental group was allowed to use AI-assisted tools to support the generation of Python code, since the integration of AI was an essential component of the intervention. This distinction is pedagogically justified, as it enabled the study to examine the impact of combining RME-based tasks with advanced digital technologies on students’ digital competences, modeling abilities, and thinking. The use of AI did not replace students’ reasoning because successful task completion still required a solid conceptual understanding of numerical sequences.

Allowing AI-assisted code generation aligns with contemporary digital competence frameworks, particularly the updated DigComp 2.2 model, which emphasizes the ability to use and interpret emerging technologies such as AI in problem-solving contexts [23].

The aim was not to assess memorization of code syntax but to evaluate students’ conceptual understanding, their ability to construct mathematical models, and their capacity to apply technological tools in line with RME principles.

In addition, several qualitative instruments were used:

1)

Observation checklists completed by teacher to document students’ engagement, participation, and challenges during lessons.

2)

Open-ended questionnaires administered to students to collect reflections on motivation, challenges, and the perceived usefulness of contextualization and programming.

3)

Student-produced materials (worksheets, Python scripts, written solutions) to analyze problem-solving strategies and conceptual development.

Phase 4: Data analysis

The test results were analyzed using SPSS. The statistical tests applied included:

1)

Paired Samples t-test to measure progress within groups from pre-test to post-test.

2)

Independent Samples t-test to compare performance between the experimental and control groups.

3)

Analysis of Covariance (ANCOVA) to control for baseline differences and examine the effect of the intervention on learning outcomes.

3. Results

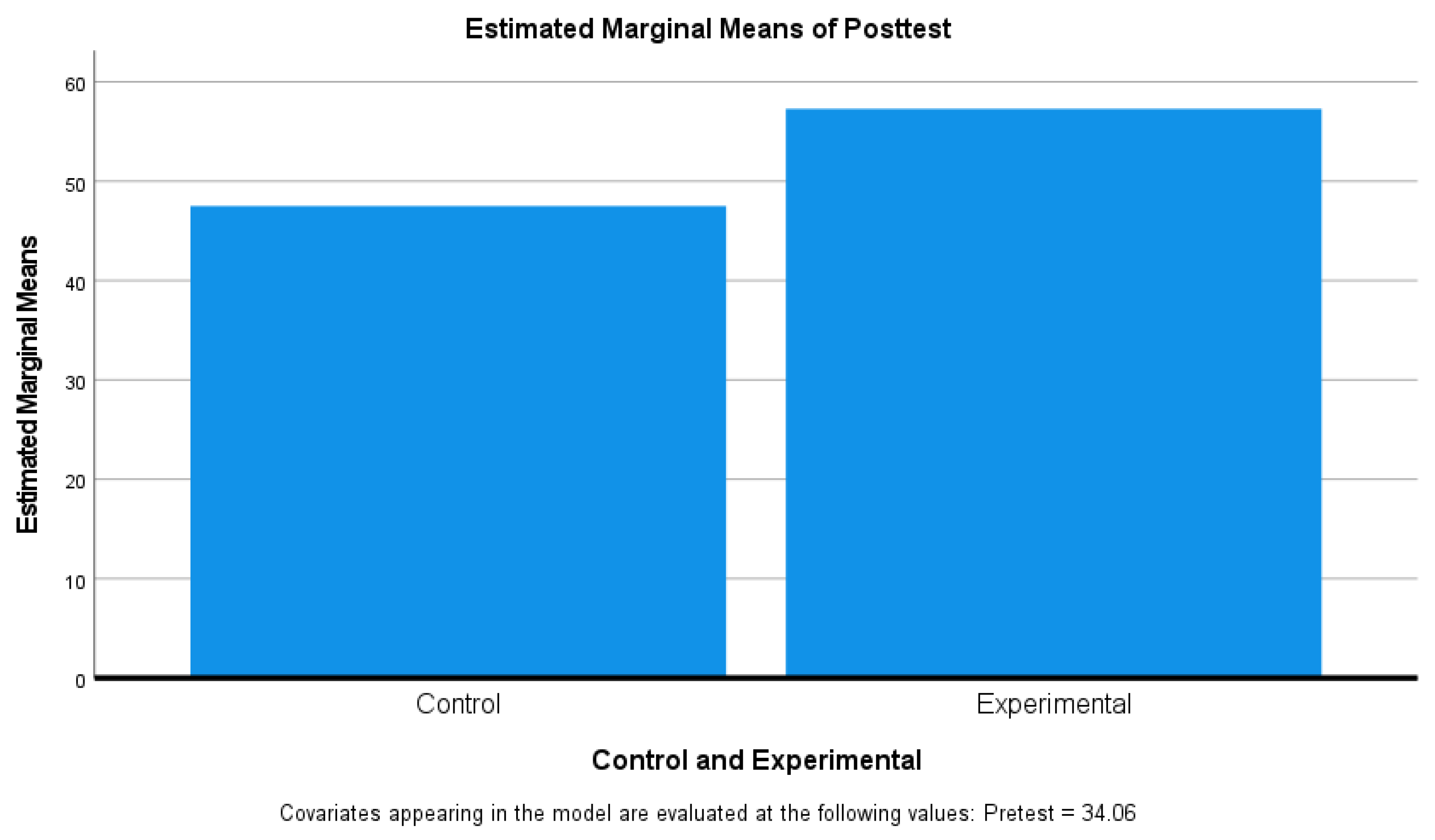
This study investigates the learning outcomes of 12th-grade students of professional high school in the informatics profile regarding the topic of numerical sequences. Through comparing results from pre-test, post-test, observation list, questionnaire with open questions for student, it became evident that students often encounter difficulties in understanding and applying numerical sequences due to the abstract way the topic is traditionally introduced in school curricula. Textbook examples typically lack context or connection to real-life situations, which limits students’ ability to engage meaningfully with the material and develop conceptual understanding.

These findings are consistent with existing literature that highlights how abstract mathematical instruction, devoid of real-world application, can hinder students’ motivation and comprehension. Traditional instruction dominated by teacher-centered methods and uniform examples-often fails to foster the analytical and inquiry-based learning that is crucial at the upper secondary level (Artigue & Blomhøj, 2013).

3.1. Traditional Textbook-Based Task Used in the Control Group

Control group - Case example 1: Given an arithmetic sequence 2,5,8, … 1. Determine the 7th term 2. Find the general term of the given sequence 3. Find the 25th term

This is a common exercise found in math textbooks. In this case, students are given the arithmetic sequence 2,5,8,... and asked to determine the 7^th term, the general term of the sequence, and find the 25^th term.

During the process of solving the task (Figure 1), the student begins by finding the difference by subtracting the second term from the first, the third from the second, and the result is $d=3$.

$a_1=2$, $a_2=a_1+d=2+3=5$, $a_3=a_2+d=5+3=8$, $a_4=a_3+d=8+3=11$, $a_5=a_4+d=11+3=14$, $a_6=a_5+d=14+3=17$, $a_7=a_6+d=17+3=20$ so the 7^th term is 20.

Then, proceed to find the general term by applying the formula $a_n=a_1+(n-1)·d$ as shown in Figure 1.

This solution method reflects the procedural and algebraic approach of traditional teaching, where the emphasis is on applying ready-made formulas to obtain the required results without any description and analysis of the given task.

Traditional instruction of numerical sequences, although methodically structured and correct, does not adequately foster the essential competencies required in contemporary education. To better illustrate how these competencies are reflected within traditional teaching practices, the situation summarized in Table 1 can be examined.

Unlike traditional teaching, this research implemented practical activities and contextualized tasks supported by technological tools specifically Python programming. These activities were designed to foster active participation, creative reasoning, and a deeper understanding of numerical sequences.

3.2. Real-World Examples Used in the Experimental Group for Teaching Numerical Sequences

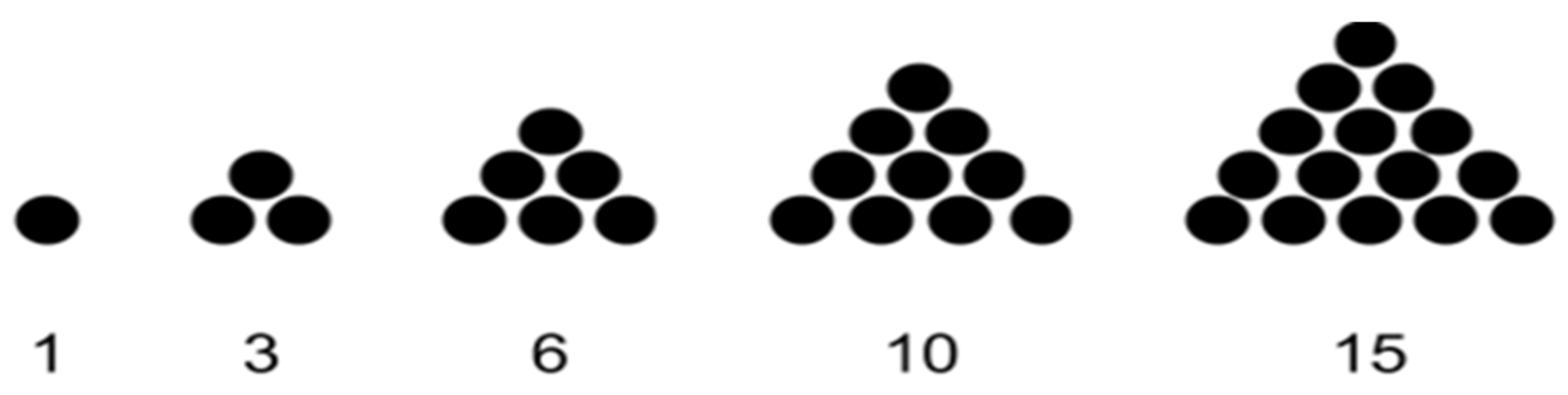
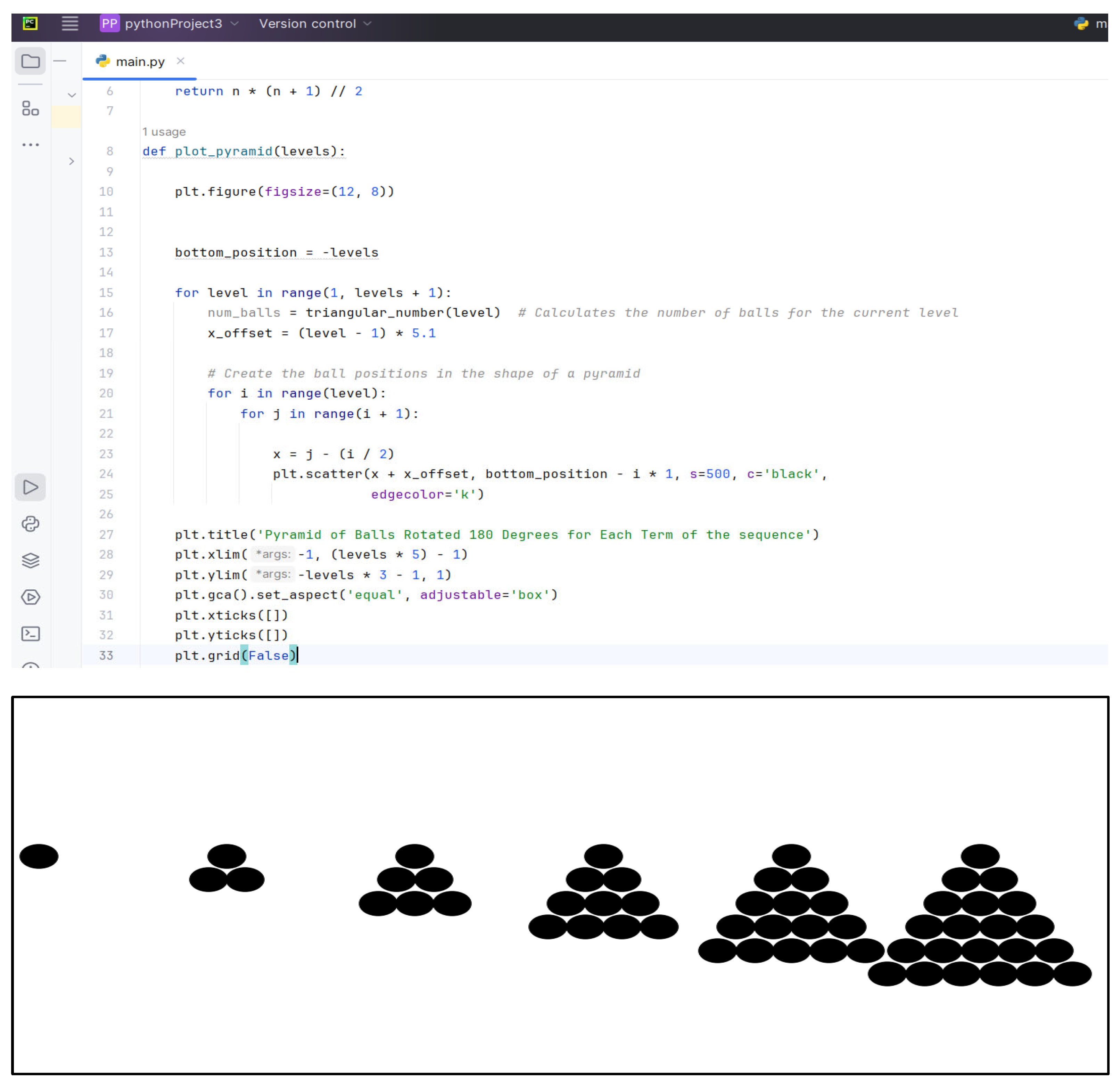
Experimental group Case Example 1: Triangular numbers as a contextualized learning task One of the classroom tasks introduced involved a visual and constructive approach to triangular numbers: Scenario: The teacher posed a problem where students were to build geometric shapes using balls, arranging them into triangular patterns. Starting with one ball, each new term in the sequence involved increasing the number of balls per row to form a larger triangle.

This led to the construction of the following numerical sequence:

Sequence: 1, 3, 6, 10, 15, ...

Student tasks:

• Represent the sequence visually.
• Find the sum of the first five terms.
• Derive a general formula for the sequence.

Student strategy and solution:

Task 1. Students explored the number pattern using both visual construction and analytical reasoning

Figure 2. The numerical sequence obtained with balls placed according to a triangular rule.

Figure 2. The numerical sequence obtained with balls placed according to a triangular rule.

One of the most common strategies students use when solving these problems is constructing tables and filling in their values, using the set of natural numbers as a reference for indexing the terms of the numerical sequence (see Table 2).

Task 2. They the sum calculated of the first five terms as:

$$S_5=a_1+a_2+a_3+a_4+a_5=1+3+6+10+15=35$$

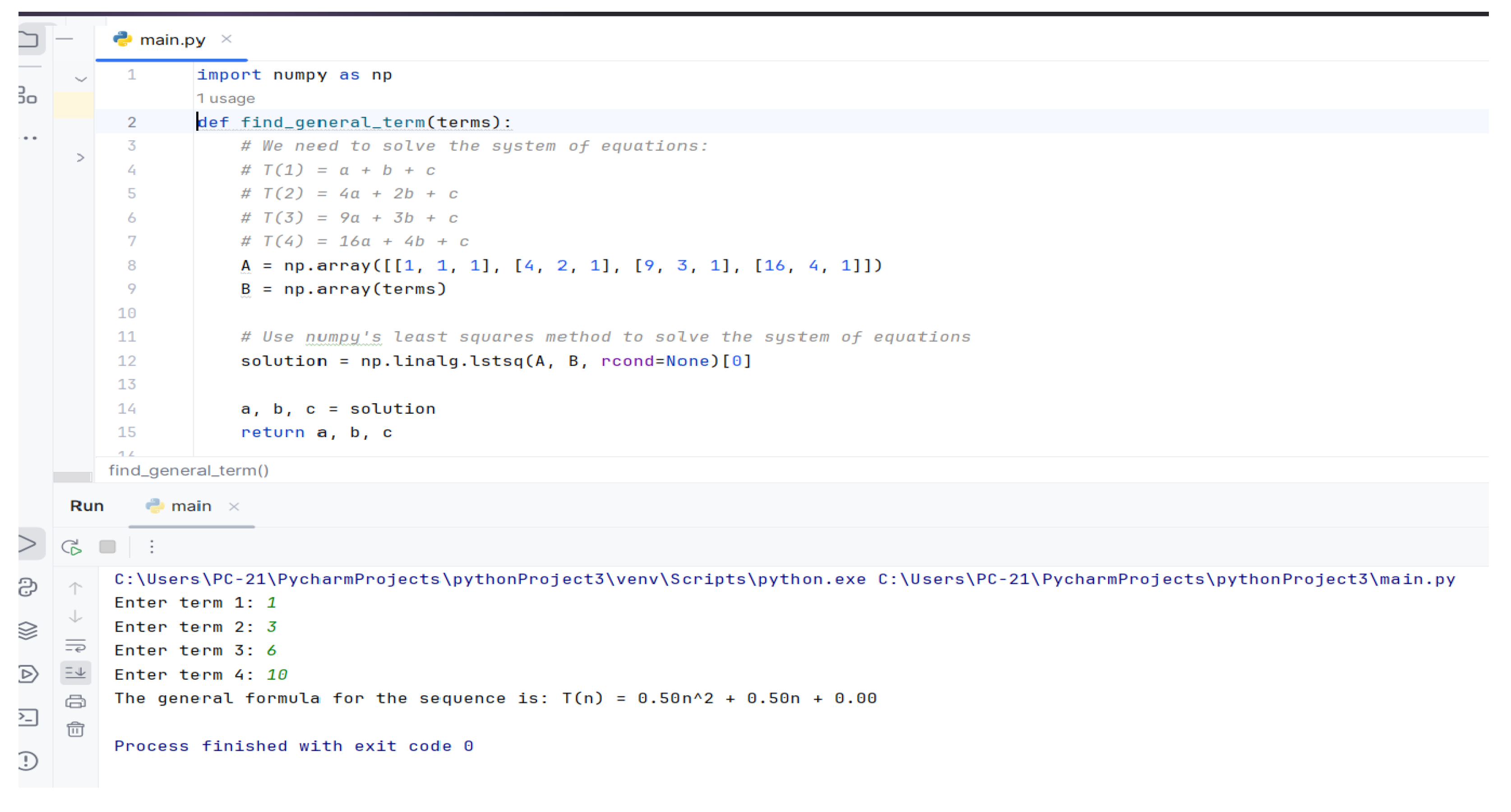
The sequence was identified as increasing, non-arithmetic, non-geometric, and unbounded. To determine the general term, students used Python programming to visualize and simulate the pattern and derive the closed-form formula.

Task 3. Students explored the number pattern using both visual construction and analytical reasoning:

Figure 3. Finding general term by Python programming.

Figure 3. Finding general term by Python programming.

This computational approach reinforced students’ understanding of the pattern and helped them derive the general term: $a_n={\displaystyle \frac{1}{2}}{n}^2+{\displaystyle \frac{1}{2}}n$, or $a_n={\displaystyle \frac{n(n+1)}{2}}.$Using Python as a learning tool allowed students to test hypotheses, verify solutions, and visualize how terms evolve an approach aligned with studies emphasizing the pedagogical benefits of integrating digital tools in mathematics instruction [24,25].

Qualitative observations and interpretation:

a)

Present this numerical sequence in visual we find the terms by adding the balls according to the rule.

b)

Also we found the sum of the first 5 terms of the numerical sequence $S_{5 }$ by adding the values of the terms found through the graphical representation which is the same by formula

$$\begin{gathered} a_n={\displaystyle \frac{n(n+1)}{2}}; a_1={\displaystyle \frac{1(1+1)}{2}}=1,{ a}_{2 }={\displaystyle \frac{2(2+1)}{2}}=3; \\ {a}_3={\displaystyle \frac{3(3+1)}{2}}=6; a_4={\displaystyle \frac{4(4+1)}{2}}=10{;a}_5={\displaystyle \frac{5(5+1)}{2}}=15; \end{gathered}$$

c)

By Python programming, we have found the general term$a_n.$

Using Python Programming, we can find visual presentation of the numerical sequence as shown in Figure 4.

Throughout this and similar tasks, several key outcomes were noted:

I.

Increased engagement: Students were more motivated to participate when problems were grounded in visual or real-life contexts.

II.

Improved conceptual understanding: The use of visual aids and programming facilitated deeper comprehension of sequence properties.

III.

Enhanced reasoning: Students were able to explain their reasoning processes and describe the transition from concrete models to generalization.

This analysis supports findings from international research that contextual and technological interventions can significantly improve students' mathematical literacy and engagement [26,27].

Experimental group Case 2 example: In a library, books are placed vertically on shelves following a set rule: A single book is placed on the top shelf, two books on the second shelf, four on the third, eight on the fourth, sixteen on the fifth, and so on, doubling the number of books each time until the last shelf.

Sequence: 1, 2, 4, 8, 16,…

Student task:

• Find the number of books arranged from the first shelf to the 5th shelf?
• Find the general term of the resulting sequence
• How many books are arranged on the 7th shelf
• How many shelves should this bookstore have so that at least 511 books can be arranged?

Solution: Identifying concepts and mathematical relationships

Since the ratio of two consecutive terms of this series is constant, then:

$$\begin{gathered} a_1=1, a_2=2 \mathrm{And} a_3=4 \mathrm{the} \mathrm{ratio} \mathrm{is}: \\ q={\displaystyle \frac{a_2}{a_1}}={\displaystyle \frac{2}{1}}=2, \\ q={\displaystyle \frac{a_3}{a_2}}={\displaystyle \frac{4}{2}}=2 \end{gathered}$$

Then we can say that it is a geometric sequence and the difference between any two consecutive terms is constant $q=2$.

Problem-solving strategy and process

Based on the rule for forming a geometric sequence, we form the table (see Table 3):

Using formula: $S_5=a_1+a_2+a_3+a_4+a_5$ where the sum of the first 5 terms of the sequence is $S_5=31$.

Explanation of the solution to the problem:

We analyze the properties of this numerical sequence: arithmetic, geometric, increasing, decreasing, bounded, unbounded, etc. The given sequence is not arithmetic, it is geometric, it is increasing and unbounded.

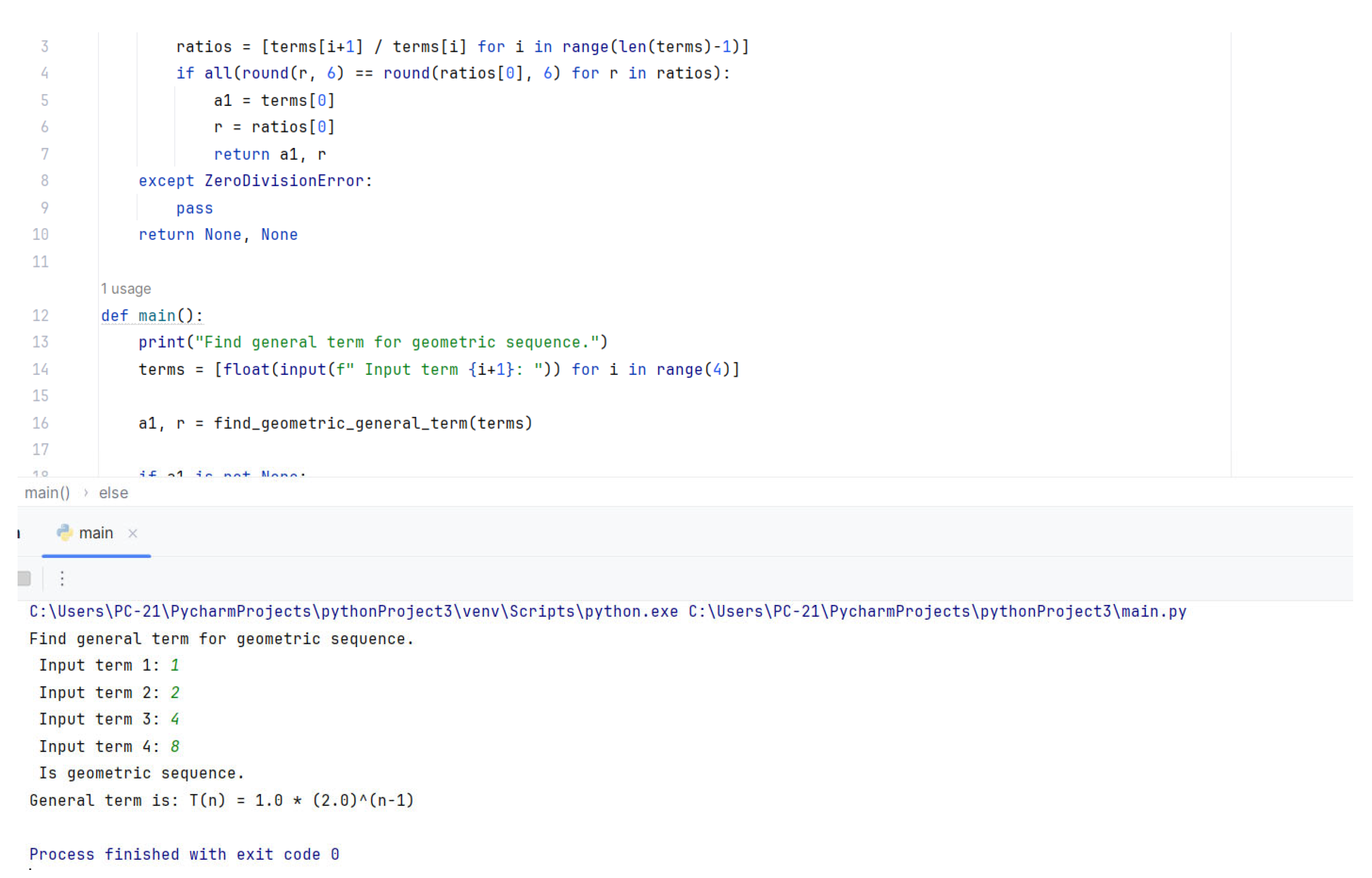
The general formula for a geometric sequence is given by: $a_n=a_1·q^{n-1}$ and finding the general term using the geometric sequence formula is: $a_n=2^{n-1}$To make it easier to find the general term, we use Python programming and see that the general term is:

Figure 5. Finding the general term for a geometric sequence by Python.

Figure 5. Finding the general term for a geometric sequence by Python.

Through Python programming, we have found the general term ${\mathrm{a}}_{\mathrm{n}}=2^{\mathrm{n}-1}$

We found the sum of the first 5 terms of the geometric sequence${ S}_5$ by adding the values of the terms found through the representation in table 4 which is the same as the formula

$$\begin{gathered} a_n=2^{n-1}; a_1=2^{1-1}=2^0=1,{ a}_{2 }=2^{2-1}=2^1=2; \\ {a}_3=2^{3-1}=2^2=4; a_4=2^{4-1}=2^3=8{;a}_5=2^{5-1}=2^4=16; \end{gathered}$$

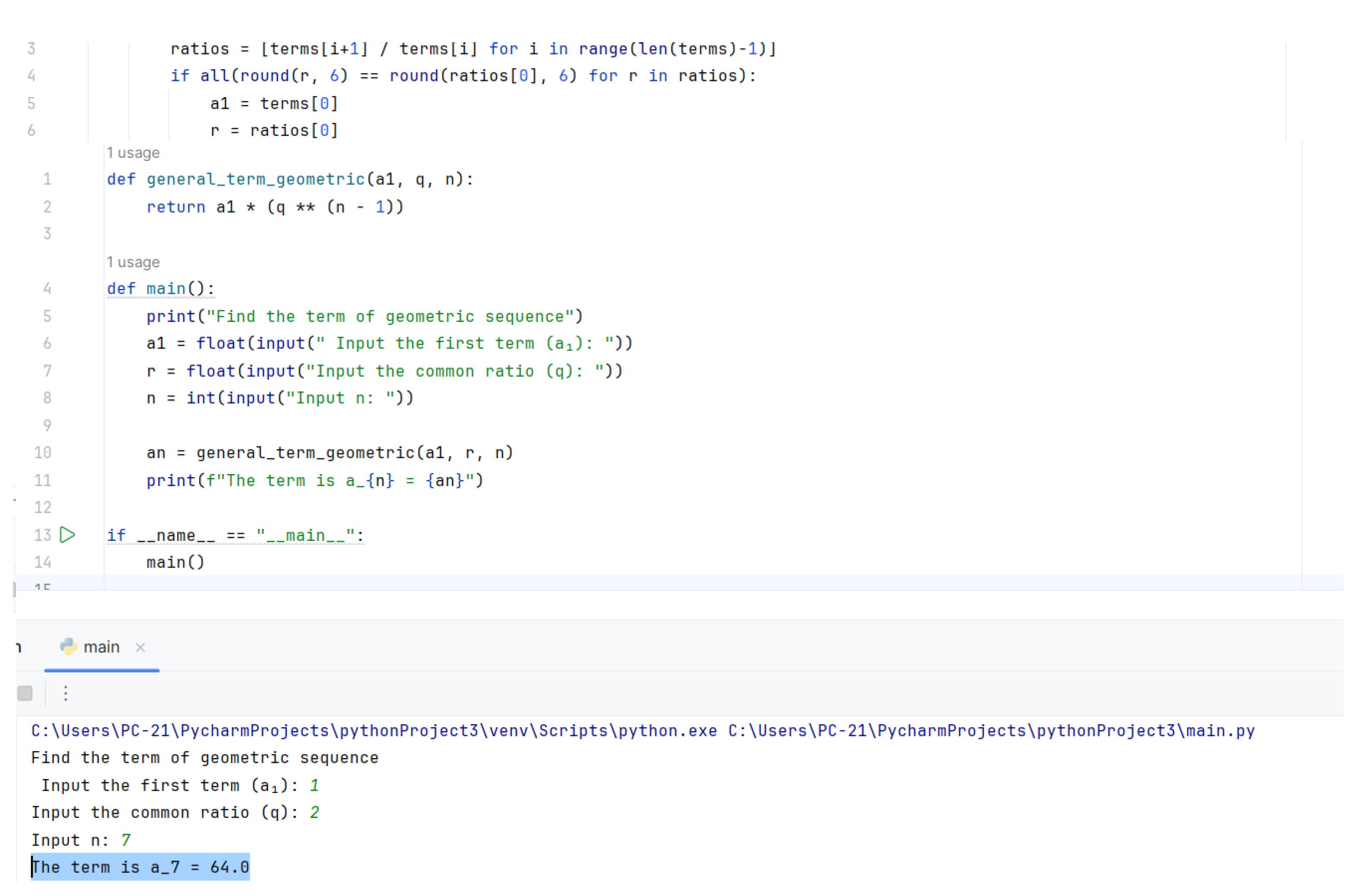
In the third requirement of the task, we need to find: How many books are arranged on the 7th shelf. Since we previously found the general term, we have: $a_n=2^{n-1}$

For $n=7$ the result is $a_7=2^{7-1}=2^6=64$

So, 64 books are arranged on the 7th shelf.

We prove this using Python, where the code is created in such a way that it requires the first term of the geometric sequence, the ratio of any two consecutive terms of the sequence (q), and the term we want to find.

Figure 6. Finding the 7th term of geometric sequence.

Figure 6. Finding the 7th term of geometric sequence.

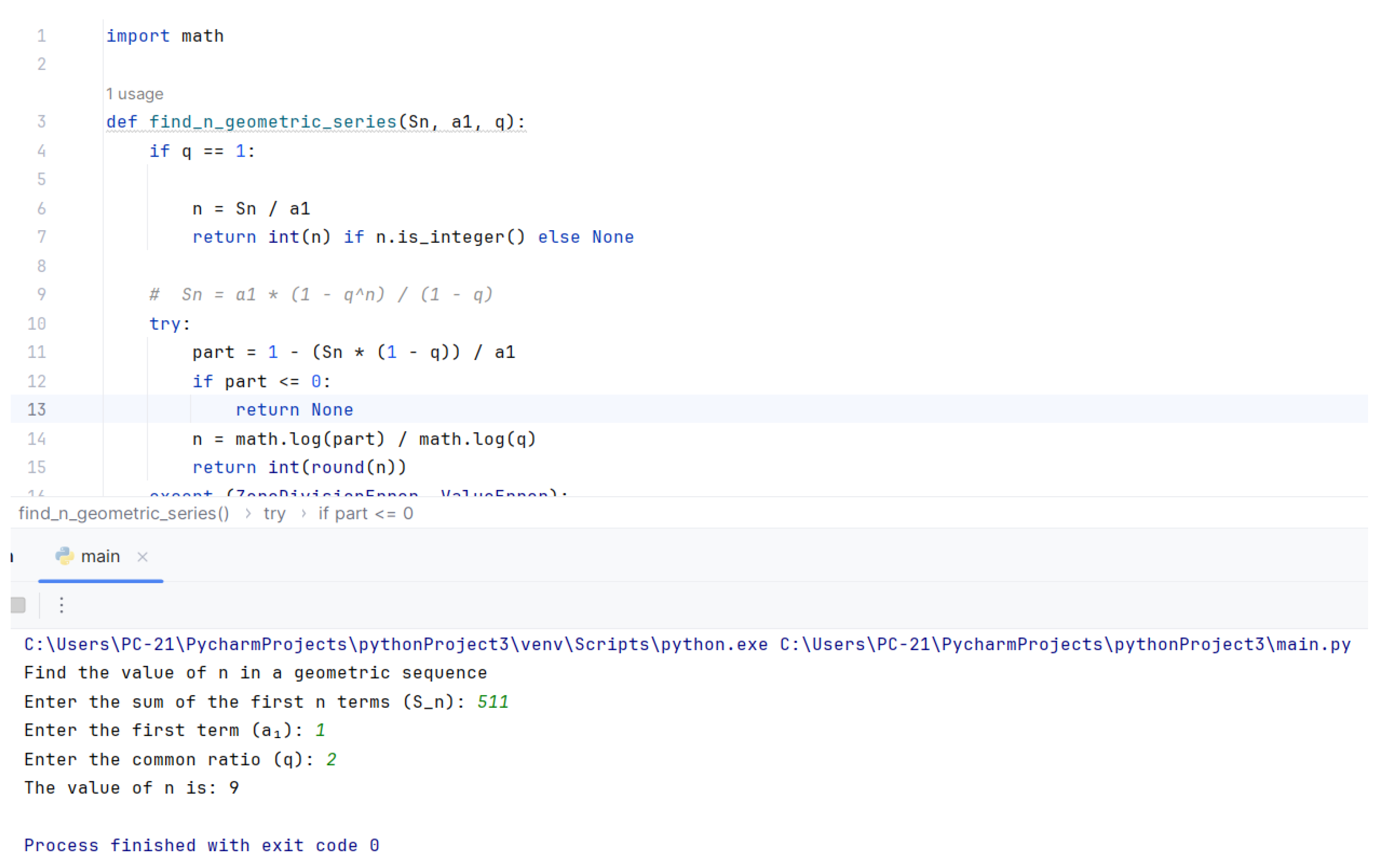
The final requirement of the assignment is: How many shelves should this bookstore have so that at least 511 books can be arranged?

Since the sum of the first n terms of the geometric series is: $S_n=a_1{\displaystyle \frac{1-q^n}{1-q}}$ consequently $511=1{\displaystyle \frac{1-2^n}{1-2}}$ the result is $n=9$.

To prove this, we are using Python, where we can see that 9 shelves are needed to organize 511 books.

Figure 7. Finding value of n by Python programming.

Figure 7. Finding value of n by Python programming.

Reflection on problem solving: In this task, the choice was carried out in a structured manner by following several such steps. Initially, the identification of the main concept was made, where it was understood that we have made a geometric sequence, since the ratio between each successive term is constant, which is a basic external characteristic. Then, the strategy and process of solving the problem were determined, where the rule of forming the sequence was presented through a table and the terms obtained according to the rule were noted. This helped in the visualization of the sequence and in the understanding of its structure.

Also, the properties of the series were analyzed, such as: the series is geometric, it is an increasing and not decreasing series, it is an unbounded series (its terms increase infinitely).

To further deepen the understanding, the general term of the geometric sequence was also calculated using the formula for the general term $a_n=a_1·q^{n-1}$. In addition, to verify the accuracy of the results and strengthen their meaning, the Python programming language was also used, which served as a technological tool for checking the results.

Experimental group Example 3: Modeling plant growth in a garden design In this task, students were asked to simulate the growth pattern of a garden where the number of flower beds grows in a non-linear, non-repetitive way. The garden was designed in square layers: at each stage, a new square border is added around the previous garden, forming a concentric square pattern. Students had to calculate the total number of flower beds after each stage.

Contextual setup

• Stage 1: A single square flower bed (1 bed).
• Stage 2: A 3x3 square, with 8 additional flower beds around the initial one (1 + 8 = 9 beds).
• Stage 3: A 5x5 square, adding 16 more beds to the previous total (9 + 16 = 25 beds).
• Stage 4: A 7x7 square, adding 24 more beds (25 + 24 = 49 beds).
• Stage 5: A 9x9 square, adding 32 more beds (49 + 32 = 81 beds).

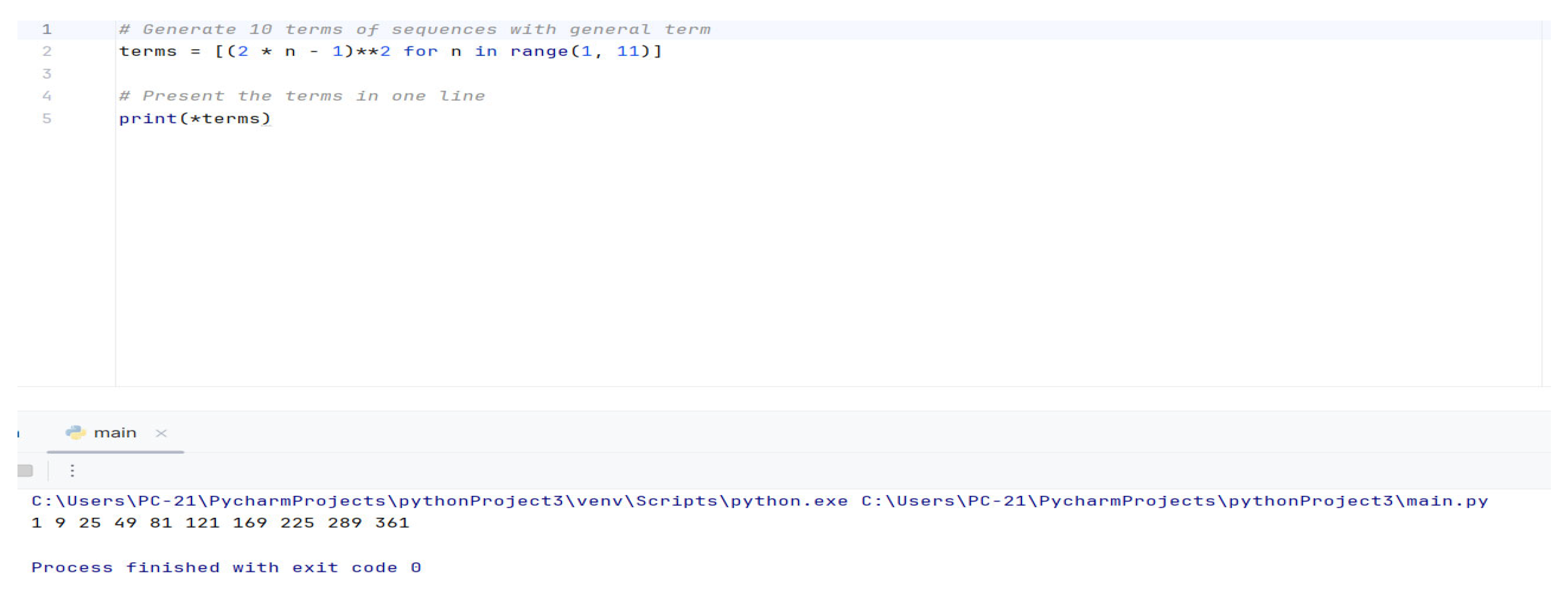
Numerical sequence: 1, 9, 25, 49, 81, ...

This sequence does not have a constant difference (not arithmetic) and does not involve a fixed ratio (not geometric). However, students discovered that each term corresponds to the square of an odd number:

$$a_1=1^2, a_2=3^2, a_3=5^2, a_4=7^2, a_5=9^2$$

Thus, the general term becomes: $a_n={(2n-1)}^2$

Tasks for students:

• Represent the garden visually using grid paper or simulation in Python.
• Find the total number of flower beds for the first five stages.
• Derive the general term for the sequence.
• Use Python to verify the values for higher terms (e.g., Stage 10, Stage 15).

Identifying mathematical concepts in the task:

Students recognized that while this sequence does not follow a simple additive or multiplicative rule, it does have a predictable pattern based on odd-number squaring.

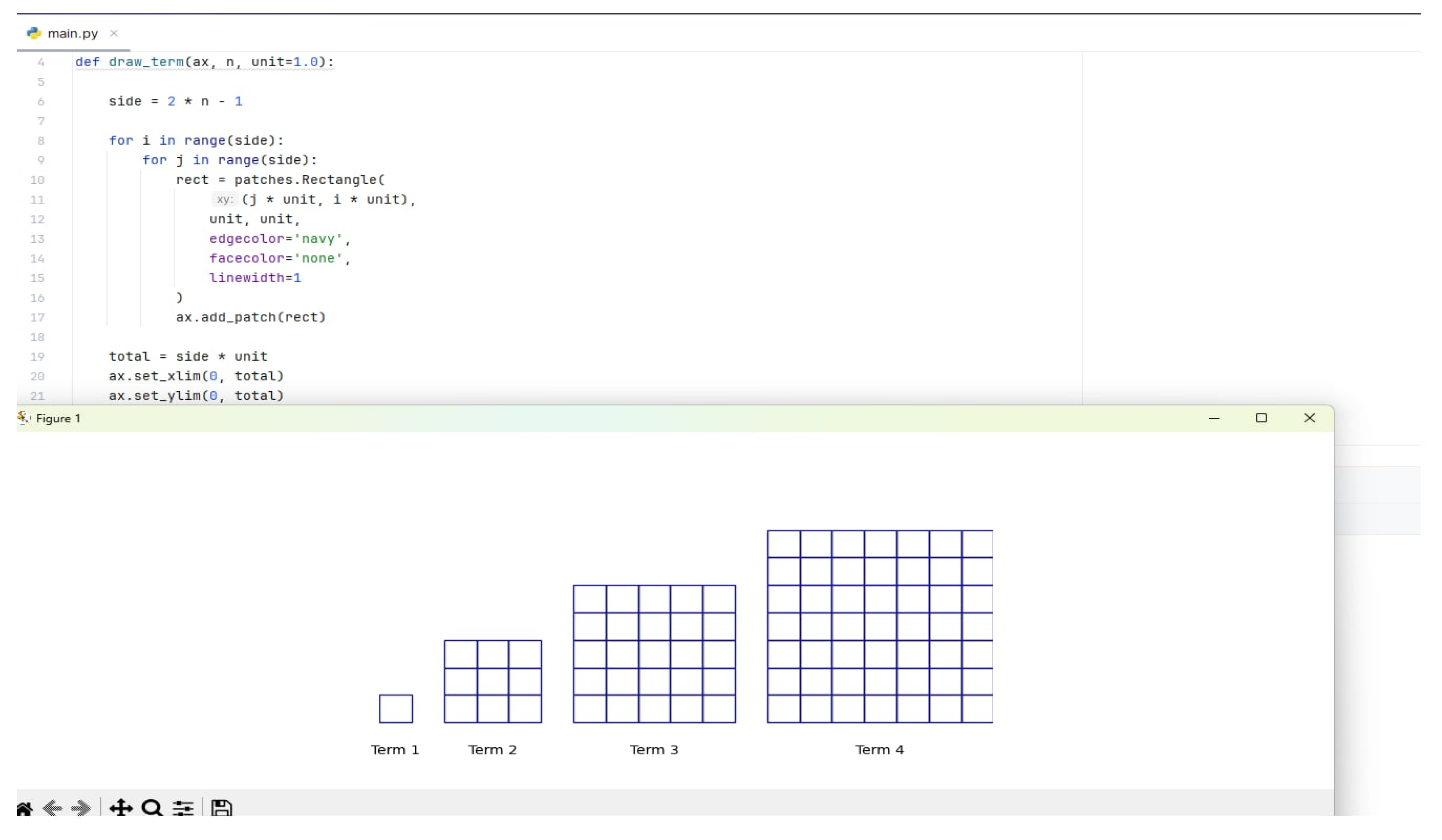
Using Python, they generated a table of values and visualizations showing the square structure growing layer by layer.

Figure 8. Visualization the square structure growing by Python programming.

Figure 8. Visualization the square structure growing by Python programming.

And finding multiple terms of a numerical sequence by Python programming

Figure 9. Finding multiple terms of a numerical sequence with Python programming.

Figure 9. Finding multiple terms of a numerical sequence with Python programming.

This example challenged students to look beyond typical arithmetic/geometric frameworks and encouraged pattern recognition and symbolic reasoning skills emphasized in problem-based and exploratory mathematics education [28].

Through this activity, students learned to:

• Translate a real-life situation into a mathematical model.
• Use Python to experiment and validate conjectures.
• Recognize and describe the pattern as $a_n={(2n-1)}^2$
• Apply this general formula to calculate higher-order terms such as:

$$a_6={(2·6-1)}^2={11}^2=121\mathrm{and} a_{10}={(2·10-1)}^2={19}^2=361$$

Didactical note: This coding activity reinforced conceptual understanding and empowered students to independently verify mathematical patterns. It illustrates a constructivist approach to teaching sequences, consistent with the recommendations of NCTM [29] and OECD [27] on technology-supported, student - centred learning.

Experimental group Case 4 exmaple: The pattern given in the figure below represents a numerical sequence, where the first term contains two squares, the second term contains 6 squares or 4 more than the first, the third term contains 6 more than the second term, and so on..

Figure 10. Numerical sequence given in visual form.

Figure 10. Numerical sequence given in visual form.

Sequence: 2, 6, 12, 20, ...

Student Tasks:

• Calculate the number of squares in the first five steps?
• Find the general term?
• How many squares will there be in the 19th term based on the given rule??
• Find the number of squares in the first 15th term?

Strategy and solution:

We form the table with the task data:

Table 4. Representation of the rule and the value of the terms in numerical sequence.

Term	1	2	3	4	5
Number of rows	1	2	3	4	5
Number of columns	2	3	4	5	6
Value	2	6	12	20	30
	$a_1=2$	$a_2=6$	$a_3=12$	$a_4=20$	$a_5=30$

Table 4. Representation of the rule and the value of the terms in numerical sequence.

Term	1	2	3	4	5
Number of rows	1	2	3	4	5
Number of columns	2	3	4	5	6
Value	2	6	12	20	30
	$a_1=2$	$a_2=6$	$a_3=12$	$a_4=20$	$a_5=30$

So they calculated the sum of the first five terms as:

$$S_5=a_1+a_2+a_3+a_4+a_5=2+6+12+20+30=70$$

where $S_5=70$is the sum of the first 5 terms of the sequence.

Explanation of the solution to the problem:

The sequence was identified as increasing, non-arithmetic, non-geometric, and unbounded.

As can be seen in the table above, the number of rows when multiplied by the number of columns gives us the value of the required term, so students can use this to find the general term.: $a_n=n·\left(n+1\right)$

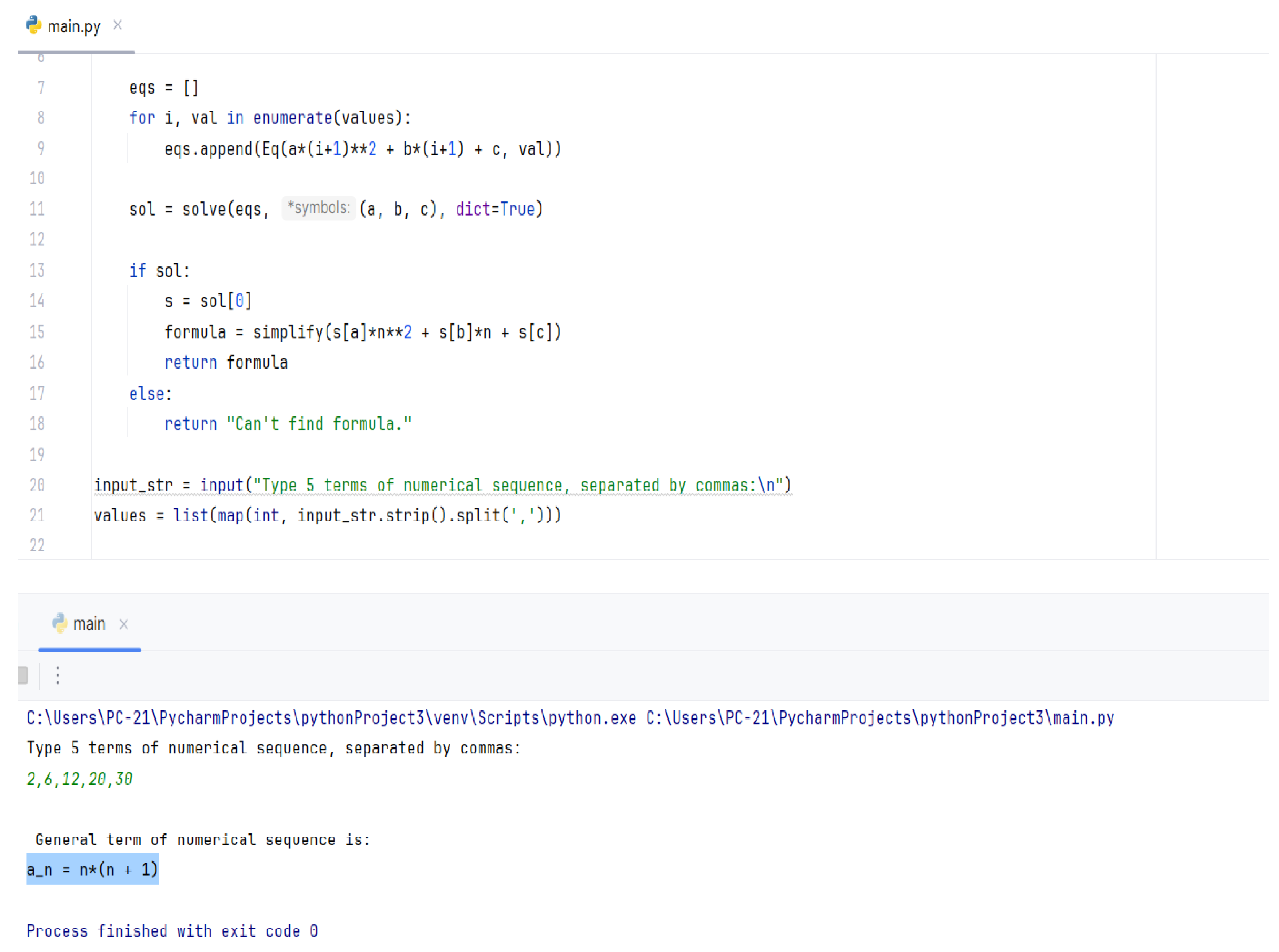
To prove the general term, we used Python programming and derive the closed-form formula.

Figure 11. Generation by Python programming the general term.

Figure 11. Generation by Python programming the general term.

By Python programming, we have found the general term$a_n=n·\left(n+1\right)$

We can prove the terms by the general term that we found:

$$\begin{gathered} a_n=n·\left(n+1\right); \\ a_1=1·\left(1+1\right)=1·2=2,a_2=2·\left(2+1\right)=2·3=6; \\ {a}_3=3·\left(3+1\right)=3·4=12;a_4=4·\left(4+1\right)=4·5=20; \\ a_5=5·\left(5+1\right)=5·6=30 \end{gathered}$$

In the third requirement of the task, we need to find: How many squares will there be in the 19th term based on the given rule?

Since we have previously found the general term, then we have:

$$\begin{gathered} a_n=n·\left(n+1\right) \\ {a}_{19}=19·\left(19+1\right) \\ {a}_{19}=19·20 \\ {a}_{19}=380 \end{gathered}$$

Reflection on problem solving:

During this task, several key results were observed:

• Students were more motivated to participate in problem solving when it was context-based and visually presented.
• The graphical and tabular presentation of the problem and the verification of the formula by programming facilitated a deeper understanding of the properties of the numerical sequence.
• Students were able to explain their reasoning processes and describe the transition from concrete models to generalization.

3.3. Data Analysis Using SPSS

To strengthen the study’s overall credibility, the quantitative results from the pre-test and post-test administered to both the control and experimental groups were processed and examined through SPSS. Several statistical techniques were applied to determine the significance and impact of the instructional intervention. The analyses included:

• the Independent Samples t-test,
• the Paired Samples t-test,
• Analysis of Covariance (ANCOVA), and
• The calculation of effect size based on Cohen’s d.

Together, these statistical procedures enabled a thorough evaluation of whether the implemented teaching approach produced meaningful improvements in student achievement and provided insight into the extent and consistency of the observed effects across the two groups.

3.3.1. Independent Samples t-Test

The Independent Samples t-test was applied to examine differences in post-test mean scores between the control and experimental groups. This analysis aimed to determine whether the implemented intervention produced a meaningful effect on students’ achievement.

Table 5. The mean difference between the control and experimental group.

Group Statistics
	Control and Experimental	N	Mean	Std. Deviation	Std. Error Mean
Difference	Control	23	13.48	5.316	1.108
	Experimental	25	23.20	6.436	1.287

Table 5. The mean difference between the control and experimental group.

Group Statistics
	Control and Experimental	N	Mean	Std. Deviation	Std. Error Mean
Difference	Control	23	13.48	5.316	1.108
	Experimental	25	23.20	6.436	1.287

Based on the Group Statistics table, the experimental group presents a significantly higher result compared to the control group. The control group has an average of M = 13.48, while the experimental group achieves M = 23.20, which represents a large difference of about 9.72 points in performance.

The results of the Independent Samples t-test show that Levene’s Test [30] for equality of variances is not significant (F = 0.345,p = .560), which means that the assumption of equal variances can be considered. However, even in the case of unequal variances, the result remains the same and highly statistically significant (Table 6).

While, the t-test shows a highly statistically significant difference between the two groups:

t$\left(46\right) = -5.677, p < .001$ and Mean difference $= -9.722$ points.

Given that$p < 0.001$, we reject the null hypothesis ($H_0$) and confirm that the intervention had a significant and consistent impact on student performance (Table 7).

3.3.1. Paired Samples t-Test

The Paired Samples t-test was applied to examine the impact of the intervention within each group by analyzing the differences between students’ pre-test and post-test scores (N = 48), independent of their group classification.

From the Paired Samples Statistics table (Table 8), it is observed that students marked a clear improvement from pre-test to post-test. The pre-test mean was $M = 34.06$, while the post-test mean reached $M = 52.60$, which represents an increase of 18.54 points in performance. This significant increase indicates that, overall, students have benefited significantly from the intervention implemented.

The results of the Paired Samples Test (Table 9) confirm a very large and statistically significant effect of the intervention. The calculated effect, Cohen’s d $= -2.425$, represents a very large effect according to Cohen’s [31] criteria, highlighting the strength of the approach used for teaching numerical sequences.

From these results we conclude that the mean difference between pre-test and post-test is significant and the combined RME, Python, and AI approach has produced significant improvements in understanding numerical sequences.

3.3.1. ANCOVA (Analysis of Covariance)

ANCOVA was used to compare post-test scores between the experimental and control groups, considering pre-test scores as a covariate. Including this factor helps minimize initial differences between students and increases the reliability of the assessment of the intervention effect (Table 10).

The ANCOVA results show a very high level of statistical significance.

The adjusted model yields $F\left(\mathrm{2,45}\right) = 43.172, p < .001$ and Partial Eta Squared$= 0.657$

This indicates that 65.7% of the variation in post-test scores is explained by the constructed model, indicating a strong intervention effect. The Pretest variable is statistically significant ($F = 49.559, p < .001$), indicating that the students' initial level played a role in the final results. While the Group variable (experimental vs control) had a significant impact on the post-test where $F = 32.370, p < .001$ and Partial Eta Squared$= 0.418$. This implies a large intervention effect, confirming that the use of RME, Python and AI has brought about a significant change in student performance.

In the figure 12, we observe the estimated post-test means for both the control and experimental groups. The experimental group scored noticeably higher ($mean \approx 56$) compared to the control group ($mean \approx 48$). This difference indicates that the students in the experimental condition achieved better outcomes after the intervention. The height difference between the two bars visually represents the positive and meaningful impact of the intervention, suggesting that the experimental treatment contributed to improved post-test performance.

Figure 12. Estimated Marginal Means of Post-test.

Figure 12. Estimated Marginal Means of Post-test.

3.4. Analysis of Open-Ended Questionnaire Responses

In addition to quantitative results from pre-tests, post-tests, and classroom observations, the study incorporated a qualitative analysis of students’ reflections through four open-ended questions. These responses provided valuable insight into students’ attitudes, levels of engagement, and perceptions regarding the use of real-life contexts, visualization, programming, and AI tools during the learning process.

Key finding from student feedback

• Many students stated that activities connected to everyday situations made mathematical content easier to understand. They reported that contextualized tasks helped them relate new concepts to familiar experiences, making lessons more meaningful and increasing their interest in numerical sequences.
• Learners consistently emphasized that diagrams, shapes, and graphical representations allowed them to recognize patterns more easily. Visual elements helped them stay focused and better understand how a sequence grows or changes.
• A large number of students expressed that working with Python made learning more interactive. They appreciated being able to check their calculations, visualize patterns instantly, and understand the structure of sequences through code. Many noted increased curiosity toward programming beyond the mathematics lesson.
• Students from the experimental group highlighted that AI tools were especially helpful during the post-test. They felt that AI-supported code generation allowed them to visualize results more quickly, correct mistakes, and focus on reasoning instead of getting stuck on syntax. Several students reported greater confidence and satisfaction when solving tasks with the help of AI.

The following section highlights representative student comments gathered from the open-ended questionnaire items:

Question 1: What types of mathematical problems would you prefer to work on in class?

Student 1: “I like tasks that relate to real life, things like prices, planning, measurements, or anything that feels useful.”

Student 2: “Problems where we can use computers or coding are more enjoyable and make me want to learn more.”

Question 2: How do real-life contexts influence your understanding of numerical sequences?

Student 3: “They help me picture the situation, so I understand the pattern faster.”

Student 4: “I feel more motivated. These tasks make more sense compared to standard textbook examples.”

Question 3: How do visual representations affect your learning?

Student 5: “Drawings or graphs help me follow the sequence easily.”

Student 6: “When there is a visual model, I understand what to do almost immediately.”

Question 4: What is your opinion about using technology (Python and AI) while learning sequences?

Student 7: “Python and AI helped me check my answers and see the pattern clearly.”

Student 8: “It made the lesson more dynamic and made me want to learn Python better.”

The analysis of the open-ended questionnaire shows that integrating real-world situations, visual modeling, Python programming, and AI support significantly improved students’ learning experiences. These tools not only strengthened conceptual understanding but also increased engagement, motivation, and self-confidence. Students perceived lessons as more meaningful, interactive, and enjoyable.

From the instructional perspective, this approach effectively enhanced key mathematical competencies and aligned with modern educational practices. The positive reactions of students confirm that combining contextual learning with technological tools offers a promising direction for future mathematics teaching.

3.5. Observation List

To enrich the analysis of the impact of using Python and real-life problems on learning numerical sequences, a systematic observation was conducted in the experimental group through a checklist with eight closed questions. The results (Table 12) showed a high level of engagement: 76% of students actively participated in solving contextual problems, 84% remained focused, while 100% expressed motivation and satisfaction while solving tasks and verifying results through Python.

Also, participation in discussions was full, 88% collaborated in joint activities, and 84% managed to easily move from real situations to formal mathematical representations, indicating the development of modeling skills. Although the percentage was lower in the interpretation of some real-life situations (64%), the findings strongly support that the use of real-world contexts and technology not only increases engagement and collaboration, but also promotes conceptual thinking and more efficient acquisition of numerical sequences.

Table 11. Summary of observation checklist results in the experimental group (N = 25).

Observation	Yes (n)	Yes (%)	No (n)	No (%)
1.The student is actively engaged during the presentation of contextual problems	19	76.04%	6	24%
2.The student uses prior knowledge to interpret real-life situations mathematically	16	64%	9	36%
3.The student is focused during class activities	21	84%	4	16%
4.The student expresses satisfaction and motivation when solving contextual tasks and verifying solutions through Python	25	100.00%	0	0.00%
5.The student actively collaborates with friends during class based on the RME approach and the use of IT	22	88%	3	12%
6.The student expresses clearer thinking and reasoning when a problem is presented in graphical form	20	80%	5	20%
7.The student easily moves from real-life situations to formal mathematical representation	21	84%	4	16%
8.The student participates more actively in discussions about the presented mathematical problems.	25	100.00%	0	0.00%

Table 11. Summary of observation checklist results in the experimental group (N = 25).

Observation	Yes (n)	Yes (%)	No (n)	No (%)
1.The student is actively engaged during the presentation of contextual problems	19	76.04%	6	24%
2.The student uses prior knowledge to interpret real-life situations mathematically	16	64%	9	36%
3.The student is focused during class activities	21	84%	4	16%
4.The student expresses satisfaction and motivation when solving contextual tasks and verifying solutions through Python	25	100.00%	0	0.00%
5.The student actively collaborates with friends during class based on the RME approach and the use of IT	22	88%	3	12%
6.The student expresses clearer thinking and reasoning when a problem is presented in graphical form	20	80%	5	20%
7.The student easily moves from real-life situations to formal mathematical representation	21	84%	4	16%
8.The student participates more actively in discussions about the presented mathematical problems.	25	100.00%	0	0.00%

4. Discussion

This research investigated how contextualized learning and the use of digital tools-particularly Python programming, can transform the teaching and learning of numerical sequences in upper secondary education. Grounded in a constructivist theoretical framework and supported by data from the pre-test, post-test, structured observation checklists, and open-ended questionnaires, the study examined both the pedagogical design and the learning outcomes of a teaching intervention conducted with 12th-grade students at IAAP “Andrea Durrsaku” in Kamenica.

The findings clearly demonstrate that traditional instruction of numerical sequences, often abstract, symbolic, and decontextualized - does not sufficiently engage students nor support deep conceptual understanding. Classroom observations and students’ reflections revealed that when sequences are introduced through realistic problems and reinforced through digital simulations, learners become more motivated, more cognitively engaged, and more capable of independently constructing general terms of the sequences.

The four case-based examples used in the intervention and other cases not included in this document, constructing a triangular ball arrangement, simulating the non-linear growth of flower beds, arranging books vertically on shelves according to a numerical rule, and recognizing visual patterns that represent a sequence, illustrated how real-life modeling tasks, when combined with Python programming, can:

• improve students’ visualization, mathematical reasoning, and pattern recognition;
• facilitate the discovery and verification of general terms;
• foster collaborative dialogue, explanation, and critical thinking and
• support more personalized and differentiated learning opportunities.

Importantly, the use of AI-assisted tools during the post-test further enhanced the performance of the experimental group. Students reported that AI support helped them generate, visualize, and verify Python code more efficiently, allowing them to focus on conceptual reasoning rather than syntactical details. This contributed to improved accuracy in their solutions and deeper insight into the structure of numerical sequences. The positive impact of AI was particularly evident in students who demonstrated difficulty with manual coding but excelled when supported by AI-guided code construction.

Overall, the four-phase methodological structure (problem presentation, strategy development, data collection and analysis, and reflection) proved effective in activating student participation and aligning the teaching of sequences with key 21st-century competencies such as computational thinking, creativity, and digital literacy.

Statistical results reinforce three key insights that align with established research:

• Real-life contexts act as cognitive anchors that support students in moving from concrete experiences to abstract mathematical generalization [32,33].
• Python programming functions as a powerful exploratory and verification tool, enabling students to test conjectures, model patterns, and validate general terms efficiently [34,35].
• Students respond more positively to tasks that require authentic reasoning rather than rote procedures, demonstrating higher engagement, persistence, and confidence in problem-solving [36,37].

Based on the study’s outcomes, the following recommendations are proposed:

• Educational authorities should promote the integration of contextual learning approaches and digital technologies such as Python, GeoGebra, and other educational coding platforms within the national mathematics curriculum to strengthen students’ conceptual understanding of patterns and sequences [27].
• Professional development initiatives should equip teachers with the necessary competencies to design real-world mathematical tasks and to integrate basic programming tools effectively into classroom instruction [38].
• Schools and educational publishers should develop textbooks and supplementary resources that include realistic modeling tasks, scaffolder Python activities, and guided explorations of numerical patterns and sequences.
• Teachers should adopt inquiry-based and exploratory learning strategies that encourage students to experiment, visualize, and articulate their reasoning using both traditional representations and digital tools [29].
• Schools should consider the responsible integration of AI-assisted learning tools to support students in visualizing mathematical relationships, generating and verifying code, and developing computational thinking skills. AI can serve as a scaffolding mechanism, especially for learners who struggle with manual coding, enabling them to focus more deeply on conceptual understanding and problem-solving processes

5. Patents

No patents have resulted from the work reported in this manuscript.