A Pedagogical Framework to Enhance Students’ Perception of Mathematics Relevance in Information Technology Education

1. Introduction

Mathematics is a crucial foundation of Information Technology (IT) and computing concepts (Kaplan & Myrzayev, 2024). Mathematical theories shape the understanding and appreciation of various fields in computing including programming, cryptography, data structures, artificial intelligence, networking, and others(Rajendrakumar Vilas Thorat, 2024). Such relevance of mathematics to computing is somewhat watered down in the classroom, where IT students regard mathematical concepts as abstract and less relevant to their industry aspirations (Kaplan & Myrzayev, 2024; Perminov & Testov, 2024; Vos et al., 2024). The effect of such perception is in two folds; firstly, learners are limited in their ability to understand key computational concepts that mathematical foundations vastly underpin (Chance et al., 2024; Mayang Nabila & Yahfizham Yahfizham, 2024). Secondly, the classroom environment is usually negatively affected as students are less enthused to engage in the teaching and learning of mathematics courses(Annisa & Darmiyati, 2024). In the long run, there is a likely decline in the efforts towards teaching, among tutors or lecturers that begin to affect teaching strategies, overall learner performance, and industry productivity (Betty & Ling Shing, 2024; Castillo et al., 2024; Mandailina, 2024). The perceived disconnect between real-world IT industry work and the mathematics concepts taught in academic settings stems from several factors like myths regarding the nature of education. These myths suggest that practical and theoretical education are mutually exclusive, that IT education focuses solely on hands-on exercises, and that mathematics lacks real-life applicability (Czaplinski et al., 2021; Kaplan & Myrzayev, 2024). The exponential growth of current computing trends such as machine learning, cybersecurity, artificial intelligence, blockchain technology, and data science, has created a greater need for understanding mathematical models as these trends are heavily reliant on them (Krishnaveni Veeranan et al., 2024; Orhan, 2024; P. Sandhya, 2024; Zahoruiko et al., 2024). Even though there is a notable insurgence in the appeal of current computing trends, and skills like programming, software development, and networking, the problem of not having a proportionate interest in learning mathematical concepts exists among IT students. This study proposes the IT Mathematics Relevance Perception Framework (ITM-RPF), a structured multi-phased pedagogical framework that seeks to reorient and reshape the perceptions of IT students on the relevance of mathematics education in their field of study. The paper’s proposed framework is comprised of four (4) key phases; the Perception Analysis and Diagnostic phase, the Contextualized Integration and Applied Learning phase, the Experiential Simulation and Performance Enhancement phase, and the Perception Shift and Continuous Learning phase. The goal of this proposed framework is specifically to boost IT students’ engagement, develop understanding, and enhance their attitudes toward mathematics education. In this research, a case study of one hundred and fifty-two (152) students at the Department of Information Technology Education, Akenten Appiah-Menka University of Skills Training and Entrepreneurial Development (AAMUSTED) is employed. In the study, an assessment of the sample population’s perceptions of mathematics is made, and the proposed framework is then integrated into their coursework for one academic semester. Afterward, the impact of the intervention on the learning experience of the students is measured. The methodology spans over 12 weeks. Generally, this study presents the following key contributions; Firstly, it proposes a novel pedagogical framework that reorients IT students and reshapes their undermining perceptions toward the relevance of mathematics, by structurally incorporating it into IT education and demonstrating its practical importance. Secondly, the research presents tangibility to supposed abstract mathematical theories by creating a direct correlation between them and real-like applications in IT or computing. Finally, provides a clear pathway on how systematic interventions can impact attitudes, understanding, and participation of IT students in mathematics education, via qualitative and quantitative analysis. The rest of the paper is organized as follows; in Section 2 we present a review of related literature. In Section 3 we explore the paper’s methodology and proposed framework. Section 4 focuses on the analysis of the results presented, and finally, Section 5 provides the Summary and Conclusion of the study.

2. Literature Review

2.1. Challenges in IT Students’ Engagement with Mathematics.

Students who study Information Technology usually perceive a disconnect between mathematics and their field of study, seeing mathematics concepts as abstract and impractical (Kaplan & Myrzayev, 2024; Perminov & Testov, 2024; Vos et al., 2024). Such negative perception affects teaching and learning processes by leading to poor academic performance, decline in interest, and apathy in mathematics-related courses (Oyaro et al., 2024; Uwitonze & Andala, 2024). Widianti et al. (2024) explained the notion that mathematics is irrelevant to IT education is caused by factors like the misalignment of curriculum with the needs of the industry. Additionally, Peña-Becerril et al. (2023) and Widianti et al.(2024) highlighted that another cause of students perceiving mathematics as irrelevant is the absence of teaching strategies that apply mathematics concepts in a practical sense. This claim was also made in the study by Febriani & Elfrianto (2023) . Furthermore, the perceived disconnect between real-world IT industry work and the mathematics concepts taught in academic settings also stems from myths regarding the nature of education. These myths suggest that practical and theoretical education are mutually exclusive, that IT education focuses solely on hands-on exercises, and that mathematics lacks real-life applicability(Czaplinski et al., 2021; Kaplan & Myrzayev, 2024). As a means of contributing to solving these problems, current studies have emphasized teaching strategies that leverage practical techniques such as context-based learning and experiential simulations (Harefa & Fatolosa Hulu, 2024; Meitei et al., 2024; Murangira et al., 2024; My Nguyen et al., 2024; Tang & Vo, 2024; Zhao, 2024). Therefore, ITM-RPF as a proposed framework aimed at enhancing the relevance of mathematics among IT students, incorporates such practical-based techniques.

2.2. Related Pedagogical Models for Enhancing Mathematics Relevance Among Students

Omosa (2024) explained that implementing pedagogical frameworks that incorporate supportive learning environments, and leverage practical tasks and technological tools, is a crucial role to boosting the relevance of mathematics in fields like IT. Such pedagogical innovation includes the Gamefied Mathematics Education (GME) presented by Toromade et al. (2024), which emphasize constructivist and reinforcement theories within the use of game mechanics, to improve IT students’ engagement and academic performance in mathematics courses. A mathematical modeling approach that aids in selecting problem types in IT education is also presented in Oichueva & Atabaev (2024). This framework aims to enhance the relevance of mathematics through the facilitation of simulations and presentation of concise information. Authors believe that by so doing, the understanding and application of mathematics will also be developed among students. In a study by Nascimento (2024), the author presents an approach that integrates the use of tools relatable to IT students, like MS Excel, Geogebra AR, and MS PowerPoint for teaching mathematics. The goal is to leverage the pre-existing interests of students to enhance their perception of mathematics relevance. Other related frameworks have also been proposed in studies by Tang & Vo (2024), Perminov & Testov (2024), Inderjeet & Bhardwaj (2024), and Matzakos et al. (2023). Most of these proposed frameworks, however, are just passive in demonstrating how mathematics theories underpin different fields of IT. Additionally, most of these frameworks are more experimental and are not fully applicable within regular classroom settings without limitations. Finally, most of the pedagogical models require intensive training of facilitators as they incorporate specialized techniques or skills that are not popular within regular IT education. In this study’s proposed ITM-RPF such gaps are addressed to enhance the perceptions of IT students regarding the study of mathematics-related courses.

3. Methodology

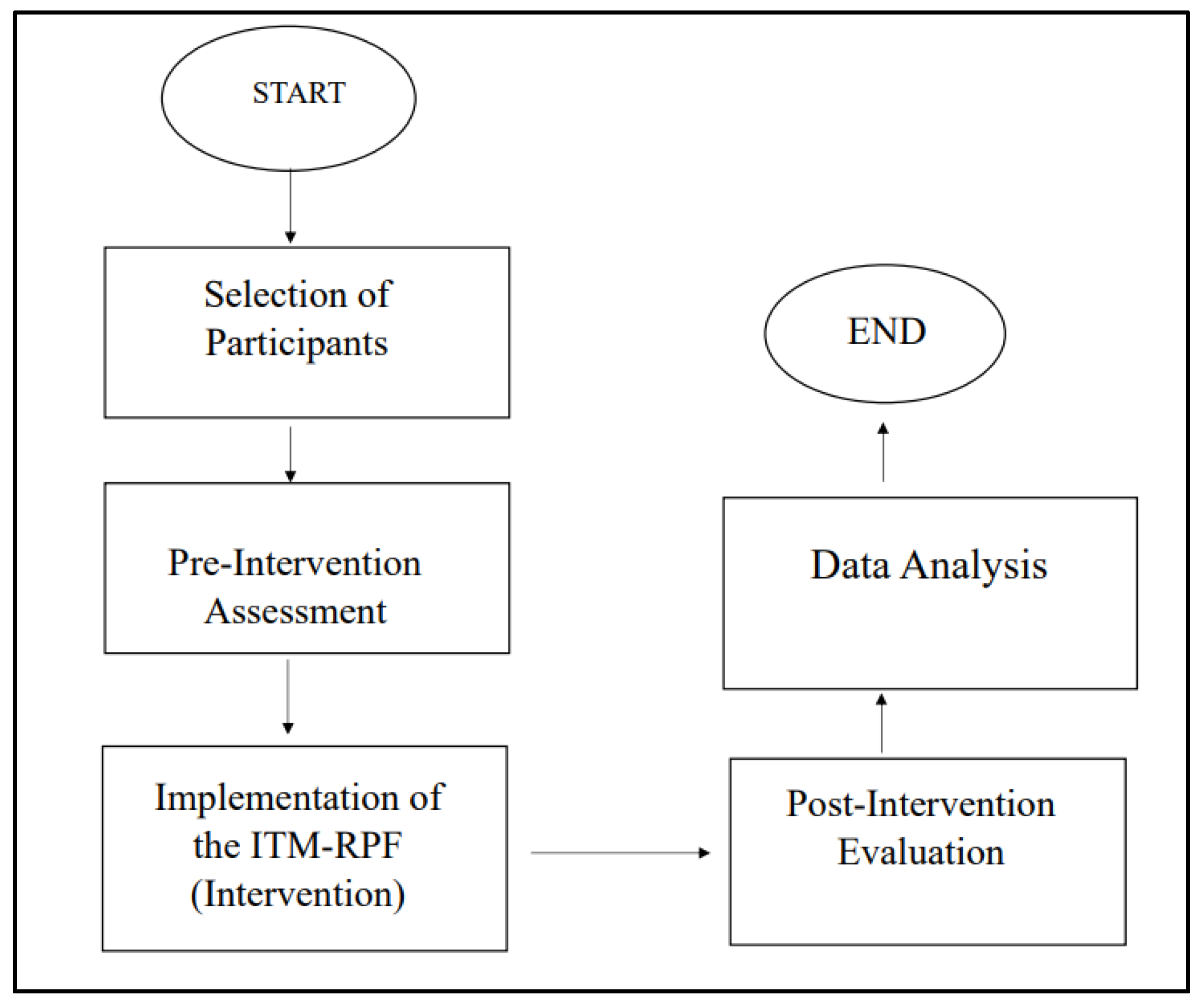
3.1. Overview of Methodology

This study adopts a quasi-experimental research design to effectively assess the weight of impact the proposed ITM-RPF has in shaping the perceptions of students for mathematics without having to randomly assign the target sample. The feasibility of this research design approach hinges on the fact that the intervention takes place in a real-world classroom setting where a fully experimental design might disrupt the organic flow of teaching and learning activities. Figure 1 presents a flowchart that illustrates the paper’s methodological overview. The flowchart highlights the key processes in the study’s methodology. The first step is the selection of the sample population. In this study, to ensure an objective assessment of the ITM-RPF’s effectiveness, a diverse representation was achieved by leveraging the stratified random sampling process. The goal of seeking diversity in the selection process was to ensure that the sample learners were fairly distributed regarding their levels of competency in mathematics. After the successful selection of participants, the step is to conduct an assessment to be informed of the baseline data of participants, before the intervention is implemented. This study conducted the pre-intervention assessment for three (3) specific reasons; Firstly, it was the general perception of participants on the relevance of studying mathematics as IT students. Secondly, it was to ensure an appropriate categorization of learners into distinct levels of competency in mathematics. Finally, the pre-intervention assessment enabled a clear evaluation of the ITM-RPF’s effectiveness after its implementation, by comparing respective variables before and after the intervention. The next step in the methodology is the actual implementation of the framework over 12 weeks. A post-intervention evaluation is then conducted to gather feedback from participants and on their perceptions and skills after going through the intervention. Finally, in the data analysis stage, methods such as paired samples t-tests, and descriptive statistical tools are used to analyze the data gathered from both pre-intervention and post-intervention assessments. The purpose of the data analysis stage is to evaluate how effective the framework was at enhancing the participants’ perceptions of mathematics in IT education.

3.2. Participants’ Selection

The study engaged one hundred and fifty-two (152) students studying a four-year BSc. Information Technology and a two-year Diploma in Information Technology at AAMUSTED, Kumasi, Ghana. Table 1 presents the demography of the selected sample population involved in the research. The table indicates a consistent pattern of participants belonging to lower academic levels having comparatively higher representation than those at higher academic levels. Such a representation pattern was adopted to ensure the possibility of tracking the proposed framework’s effectiveness over a period extended period, beyond the 12 weeks of the intervention.

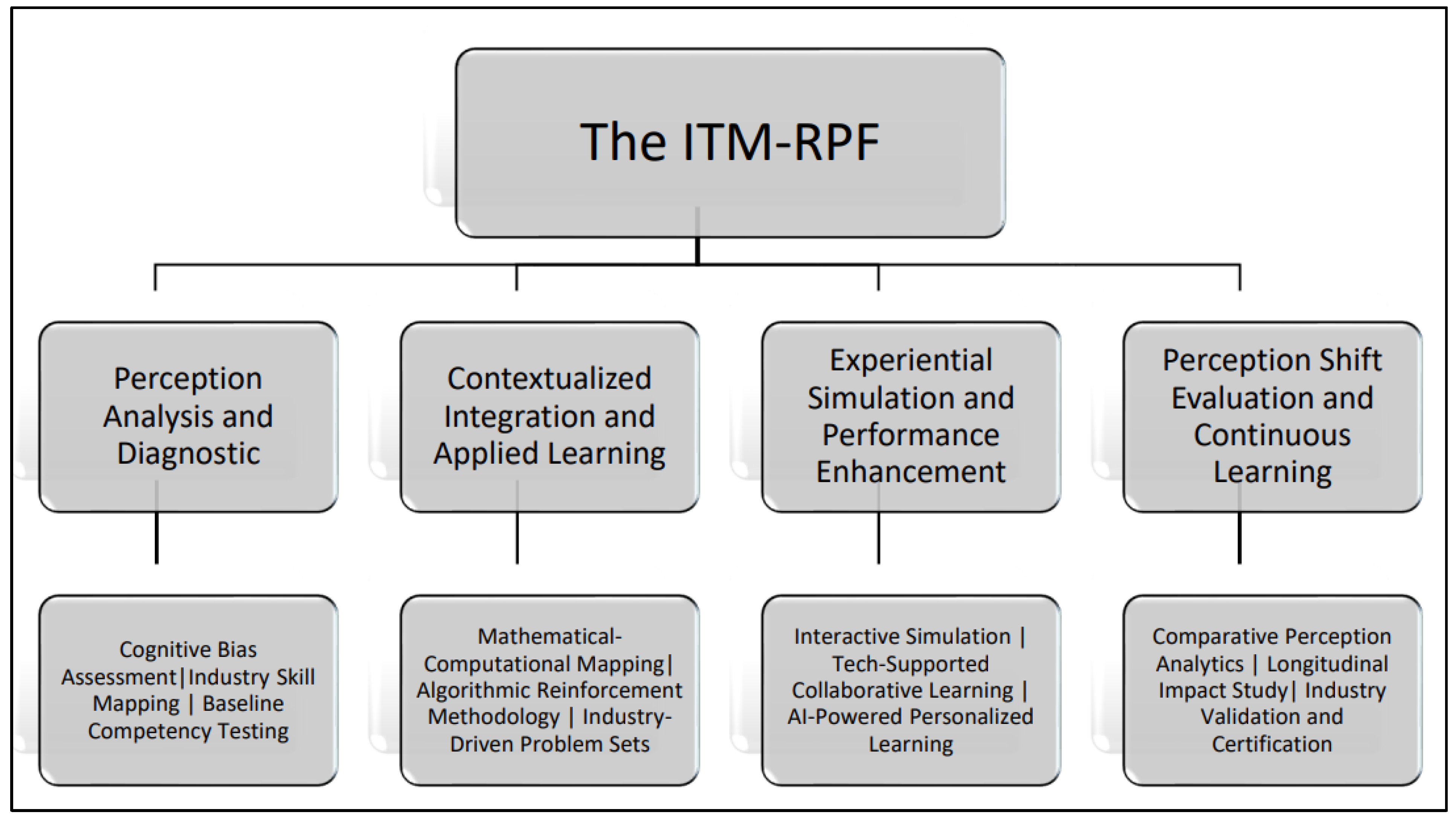
3.3. The Proposed Framework

As shown in Figure 2, the ITM-RPF comprises four (4) main phases; (i) Perception Analysis and Diagnostic (ii) Contextualized Integration and Applied Learning (iii) Experiential Simulation and Performance Enhancement (iv) Perception Shift Evaluation and Continuous Learning.

3.3.1. The Perception Analysis and Diagnostic Phase (Weeks 1-3)

The Perception Analysis and Diagnostic phase spans over the first 3 weeks. The goal is to ascertain the level of participants’ mathematical skills and perceptions and categorize them respectively using data gathered from the pre-intervention assessment, and via the cognitive bias assessment. This involved administering a survey to participants as a means of verifying their perceptions on the relevance of mathematics in IT. It then involved administering a diagnostic test scored out of 100. This test covered key mathematical areas including Algebra, Calculus, Discrete Mathematics, and Probability & Statistics, and served as the baseline for categorizing participants into three (3) groups. Figure 3 illustrates the participants’ categorization based on their scores in the diagnostic test. The figure shows that after the diagnostic test was conducted, a majority of the sample population, 52%, were categorized under weak competency in mathematics skills, while the least percentage, 13%, were classified as having strong mathematical proficiency. Additionally, in this study, as part of the perception analysis and diagnostic phase, a panel comprising academic and industry experts was set up to know the underlying opinions and misconceptions of participants on the relevance of mathematics in IT education and verify their fields of interest in computing. This also helped in determining the areas of focus in enhancing the students’ perceptions. Finally, the Perception Analysis and Diagnostic phase also involves industry skill mapping, where industry experts are invited and interviewed to provide insights on the relevance of specific mathematical fields that match specific areas in the IT industry. Table 2 details the data gathered from the industry skills mapping activity embarked on in this research. The fields in computing selected for this activity include; Machine Learning and Artificial Intelligence, Cryptography and Cybersecurity, Network and Communication Systems, Signal Processing and Multimedia Systems, Software Engineering and Development, Data Science and Big Data Analytics, and Algorithm Design and Optimization. These fields of IT were selected based on two (2) metrics; First, compatibility with the Bachelor of Science, and Diploma in Information Technology programs at AAMUSTED, and second, the most commonly preferred choices among participants. These 2 criteria ensured that while consistency with the participants’ program of study is maintained, the most common areas of interest among the sample population are also included to make the intervention highly relatable and relevant to them.

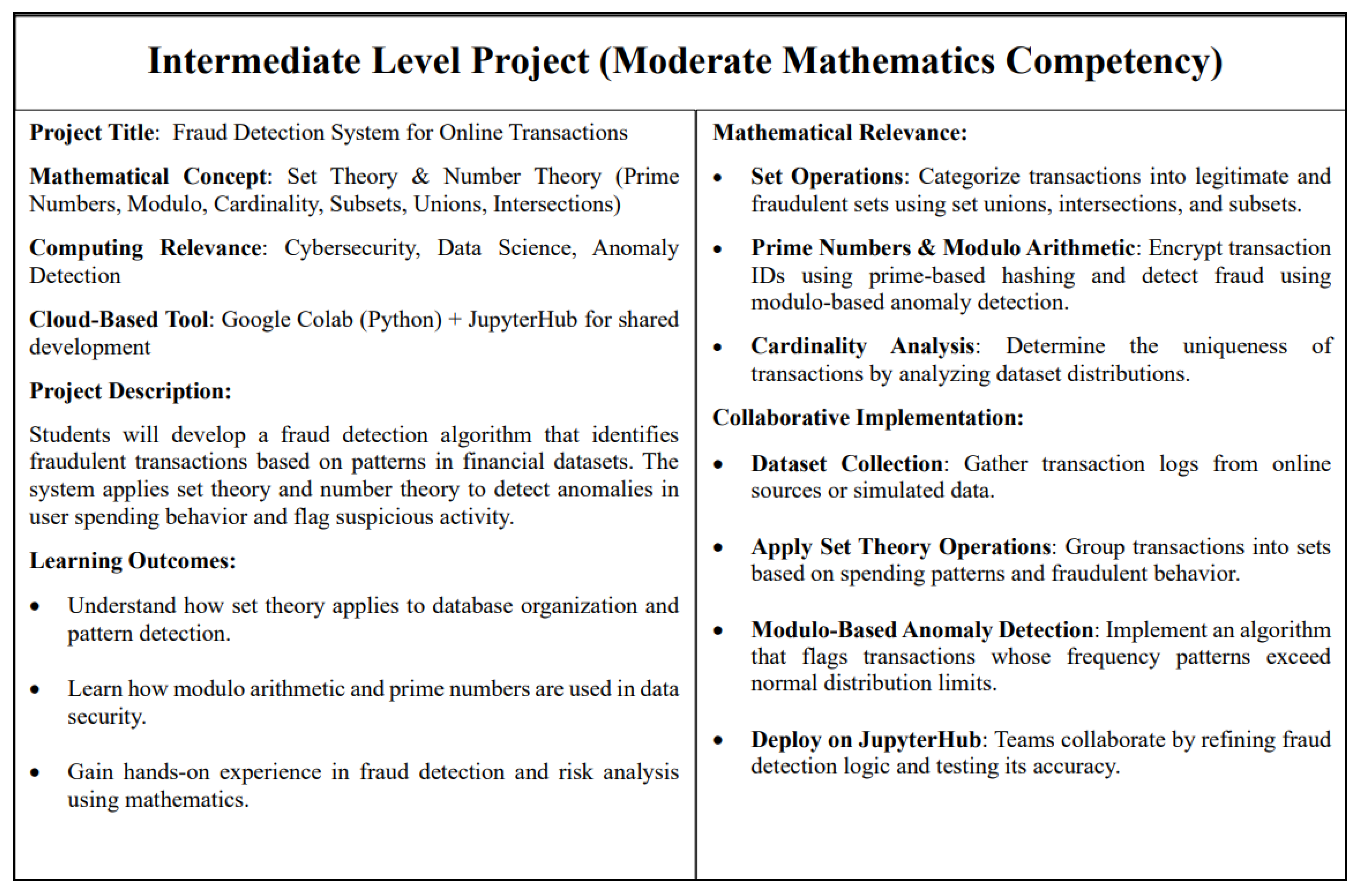
3.3.2. The Contextualized Integration and Applied Learning Phase (Weeks 4-6)

The Contextualized Integration and Applied Learning phase comprises activities that include, mathematical-computational mapping, Algorithmic reinforcement, and Industry-driven problem sets. The entire phase begins in week 4 and ends in week 6. The mathematical-computational mapping is slightly similar to the industry skill mapping activity earlier explained but differs in quite process and purpose. The mathematical-computational mappings aim to expose participants to the application of specific topics and mathematics theories and explain how they are practically used in implementations in real-world IT systems. This process provides students with a practical feel of real-world simulations and implementations that leverage mathematics concepts. Table 3 provides details on the mathematical-computational mappings activity. The next activity after the mathematical-computational mappings, is the Algorithmic reinforcement. In this sub-phase of the ITM-RPF, learners are taken through a coding-based implementation of mathematical theories. In this study, tools like Python, Java, Google Sheets App Scripts, C++, and MATLAB were leveraged to simulate various tasks using mathematical concepts such as gradients, graph theory, Shannon entropy, set theory, modular arithmetic, and logic operators. Figure 4, Figure 5, Figure 6, and Figure 7, are selected examples of code snippets used for implementing various computing tasks that leverage mathematical theories. The aim here is to validate the mathematical-computational mappings via practical demonstration or actual implementation. The final activity under the Contextualized Integration and Applied Learning phase is Industry-driven problem sets. Here, participants are guided to design or identify scenario-based IT industry problems in the real-world context. They are guided to explore possible ways through which mathematical concepts can be used to address such real-life problems.

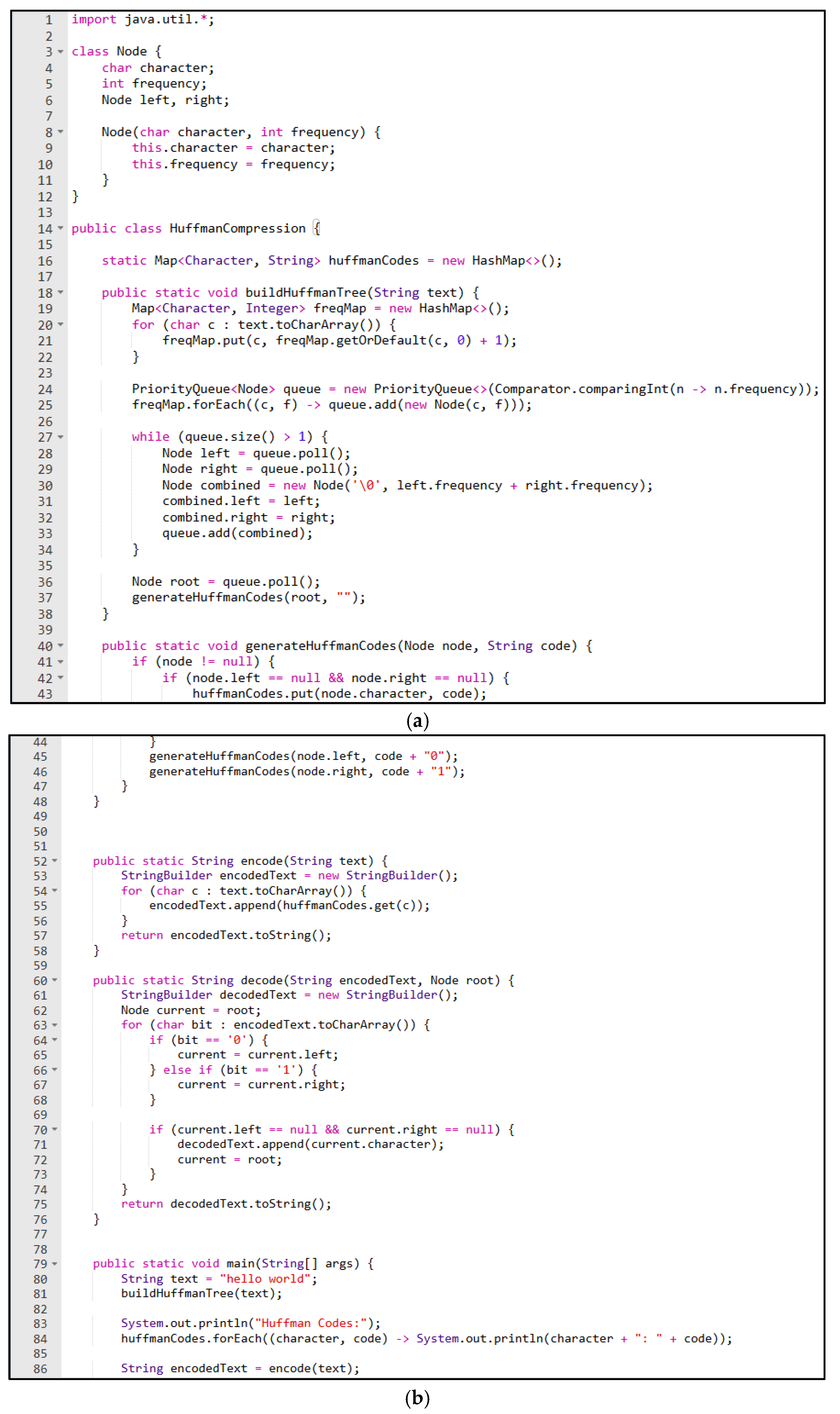
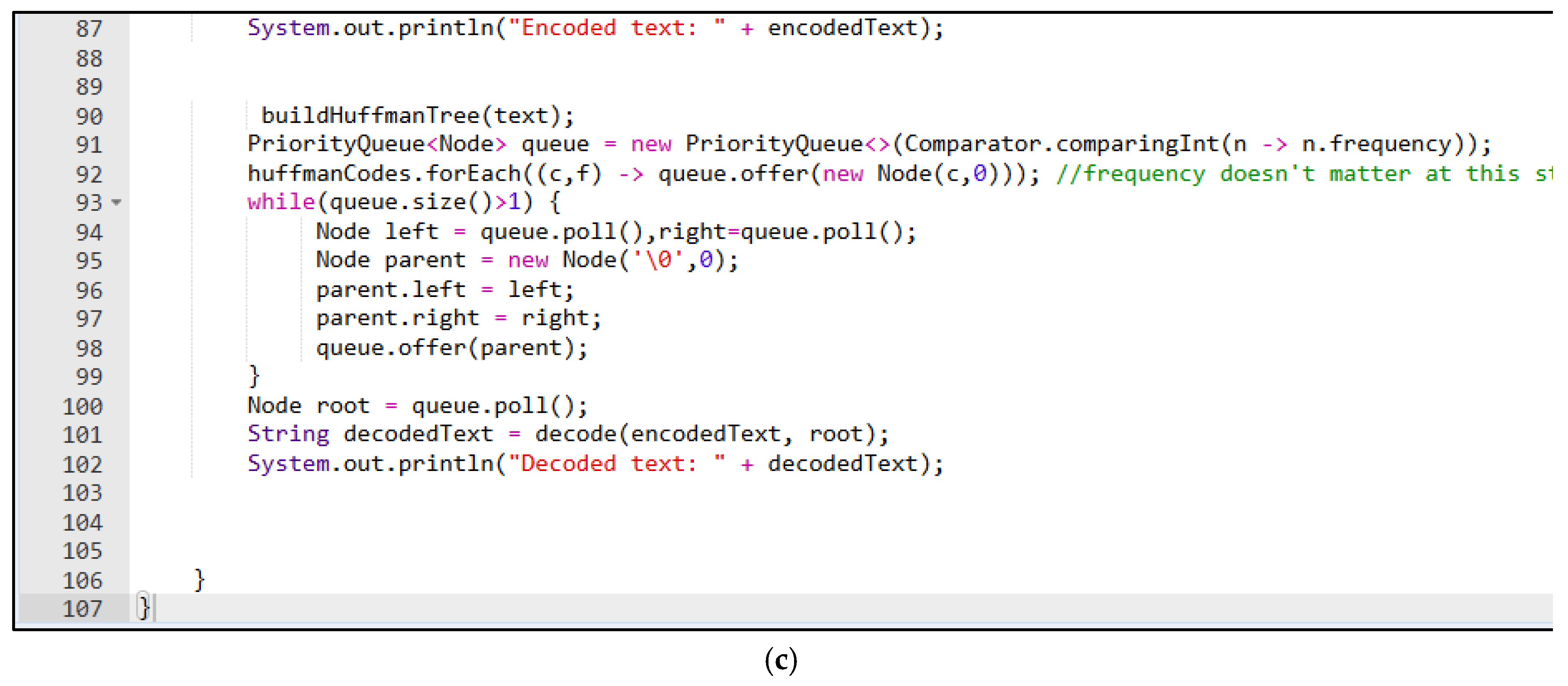
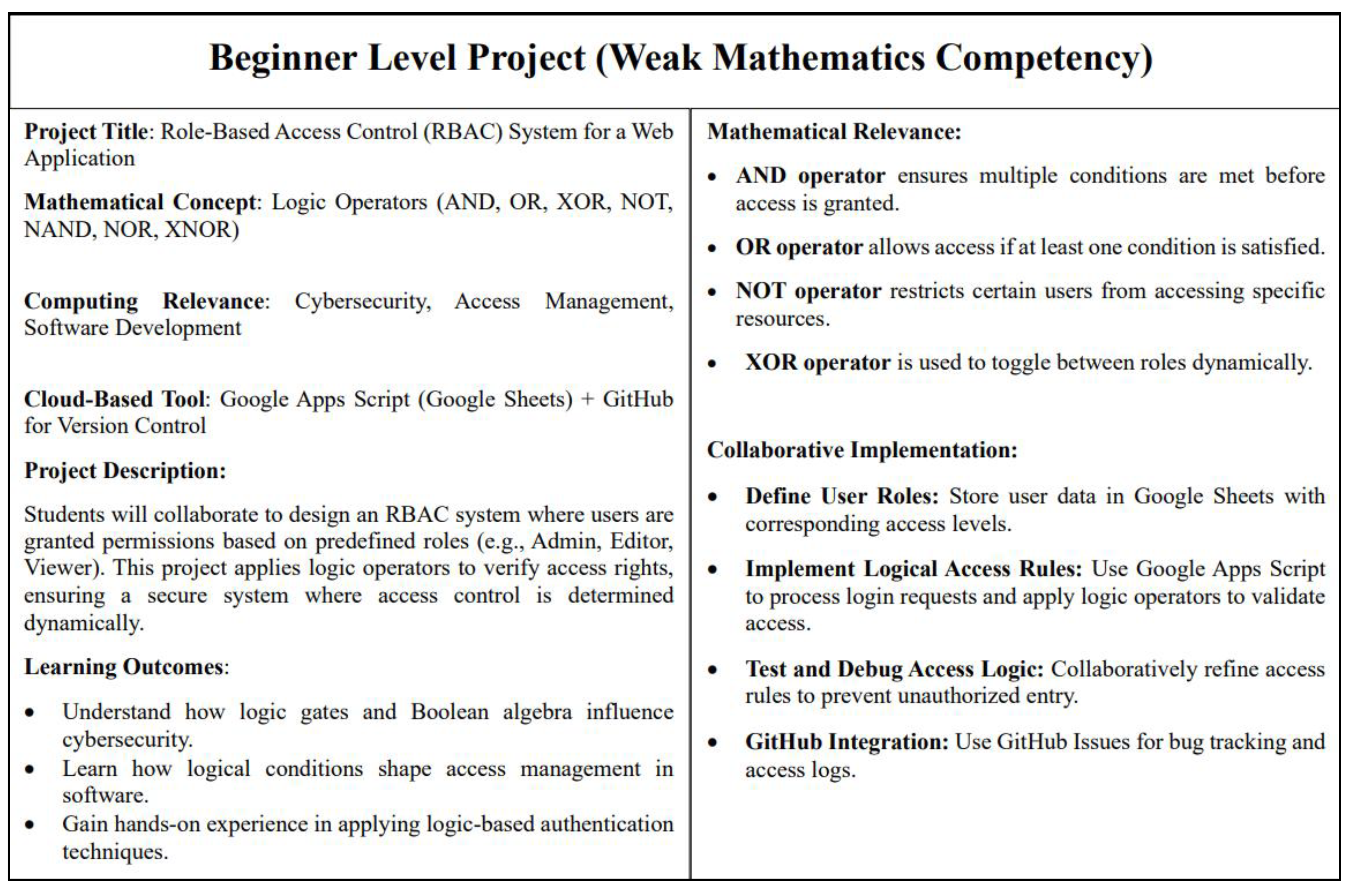
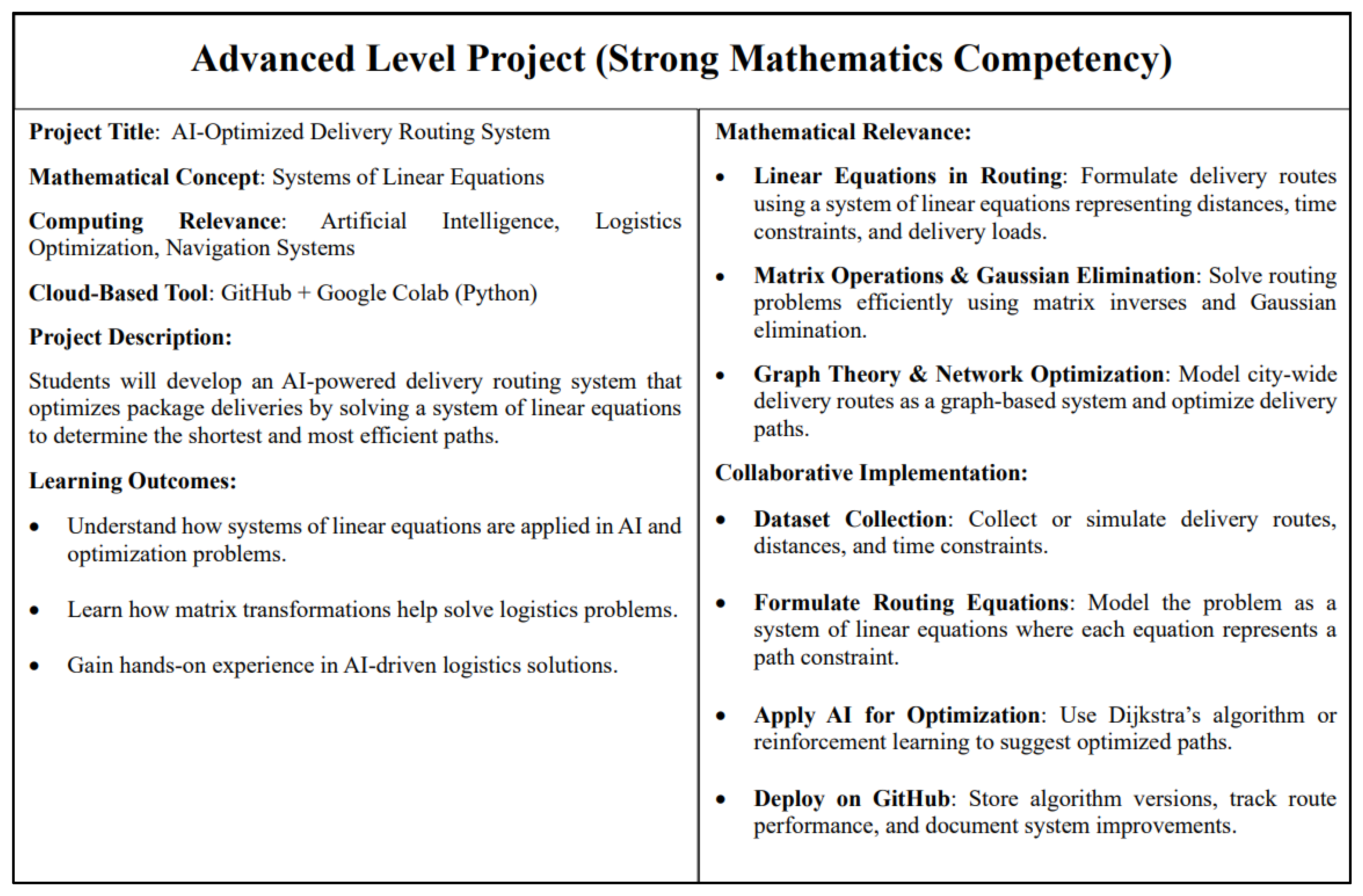
3.3.3. Experiential Simulation and Performance Enhancement Phase (Weeks 7-10)

In this last but one phase of the ITM-RPF, participants are made to actively experiment with real-world computing tasks using mathematical principles, rather than passively observe. The real-world computing tasks talked about here, are those that participants identified or designed during the industry-driven problem activity. Additionally, in the Experiential Simulation and Performance Enhancement phase participants are tasked to analyze and tweak or enhance some of the implementations presented during the Contextualized Integration and Applied Learning phase. The goal is for participants to try and explore other mathematical concepts that can be leveraged to enhance the existing simulations or suggest alternative ways via which the mathematical theories can be used. Furthermore, in this phase, participants are exposed to platforms like Google Colab and GitHub where they are made to actively engage in cloud-based collaborative projects. These projects are assigned to students based on the category of mathematics skill competence (Weak, Moderate, and Strong) they fall under. In this study, participants under each category were randomly put into groups of at most 5 people, to work on the project assigned to them. Figure 8 provides details on the project assigned to participants with weak mathematics competencies, while Figure 9 and Figure 10 represent the ones assigned to students with intermediate and strong mathematics competencies respectively. As seen in the figures the projects were aimed at guiding students to put into practice, via implementation, mathematics concepts taught in courses within their curriculum as IT undergraduates. As part of this Experiential Simulation and Performance Enhancement phase, AI-powered learning platforms are leveraged to help enhance the mathematical proficiency of participants while they work on the collaborative project. These platforms, which include Coursera and Khan Academy AI-based learning (as used in this study), help expose participants to mathematics learning paths tailored to suit their pace and level of understanding at each given point. The experience participants gain from the experiential simulation and performance enhancement phase of the proposed framework allows them to understand and practically experiment with mathematical concepts that suit their level of competence further and also aids them in growing their mathematical proficiency.

3.3.4. Perception Shift Evaluation and Continuous Learning Phase (Weeks 11-12)

The final phase in the ITM-RPF framework is the perception shift evaluation and continuous learning. It spans over the finals two weeks. This phase includes administering a summative test similar to the diagnostic test administered in the perception analysis and diagnostic phase. The summative test, which covers key mathematical areas including Algebra, Calculus, Discrete Mathematics, and Probability & Statistics, is aimed at aiding the comparative perception analytics, for post-intervention assessment. Additionally, this phase involves capstone projects and internship performance analysis. In this research, participants embarked on an individual presentation assignment where a panel of academic and industry experts verified their post-intervention understanding and perceptions of the relevance of mathematics in IT education. Furthermore, this phase generally allows experts to recommend internship opportunities tailored to the interests and competence of individual participants. The goal here is to foster continuous learning and validate the harnessed mathematical competency within IT education.

4. Results & Analysis

4.1. Pre-Intervention Results

In this section, the results of the study, before the implementation of the ITM-RFP are presented on the following; Mathematics Competency Levels of Participants, Participants’ Perceptions of the Relevance of Mathematics in IT Education, and Industry and academic experts’ Assessment of Participants’ Perceptions. These results were gathered via a diagnostic test, a survey administered to participants, and interviews by experts with individual participants.

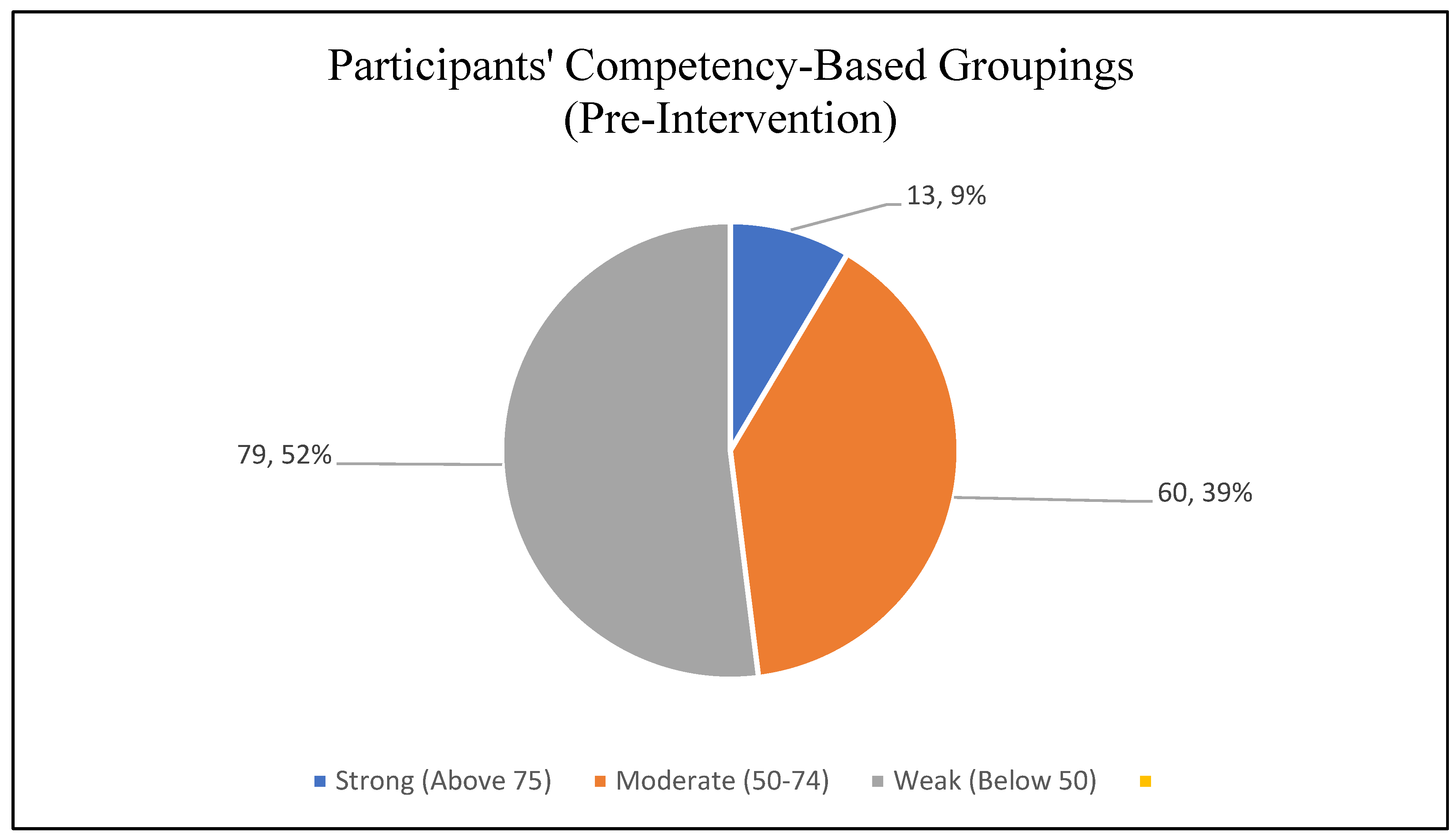
4.1.1. Mathematics Competency Levels of Participants

Table 4 is a detailed breakdown of the average score participants obtained in each section of the diagnostic test administered at the start of the interventions. Each section average is out of 100 (%). Also, the standard deviations for the scores participants obtained in test sections were calculated. From the table, participants generally performed poorly in each section of the diagnostic test indicating an overall weak mathematical proficiency within the sample population. However, the high standard deviation ranging from 10.2 to 12.5, implies that some participants performed better than as generally viewed, and hence are either moderately or strongly proficient in mathematics, as initially shown in Figure 3.

4.1.2. Participants’ Perceptions of the Relevance of Mathematics in IT Education

As part of the pre-intervention evaluation process, a survey was administered for participants to rate various responses on the relevance of Mathematics in IT education, via a Likert scale (1-5). Table 5 provides an overview of the student’s opinions on the importance of mathematics education as IT students. The table is a reflection of the baseline perceptions of participants on how important mathematics is to IT studies. Generally, with the mean scores ranging from 1.9 to 2.5, it is implied that the sample population has a low-to-moderate belief that mathematics is relevant to IT education. More specifically, it is observed that participants have very low confidence and will in the incorporation of mathematics into IT, considering that the responses “Confidence in applying Mathematics” and “Interest in using Mathematics in IT implementations” were scored 2.0 and 1.9 respectively. However, the moderate variability observed in the standard deviation column is an indication that even though most students possess negative perceptions, a few others hold positive views regarding the relevance of mathematics in their field of study (IT). This observation is consistent with the fact that some students performed relatively well in the diagnostic test and are classified as either moderately proficient or strongly proficient in mathematics.

4.1.3. Experts’ Assessments of Participant’s Perceptions on the Relevance of Mathematics in IT Education

Table 6 presents experts’ ratings on various perception categories regarding participants’ opinions on the relevance of mathematics in IT studies. The scores from experts reflect the observed disconnect between students’ perceptions and the importance of studying mathematics in IT education, with a range of 2.2 to 2.5 out of 5. The standard deviations which range from 0.7 to 0.9 suggest a strong consistency in the experts’ perspectives regarding the perceptions of students. This means that academic and industry experts have a consensus on the fact on the aggregate, participants do not have an appreciable level of understanding of mathematical applications in IT, they have low regard for the value of mathematics in IT education, they possess low confidence in applying mathematical concepts, and they are moderately willing to engage in learning mathematics. Also, from the table, it is observed that in the opinion of experts,

4.2. Post-Intervention Results

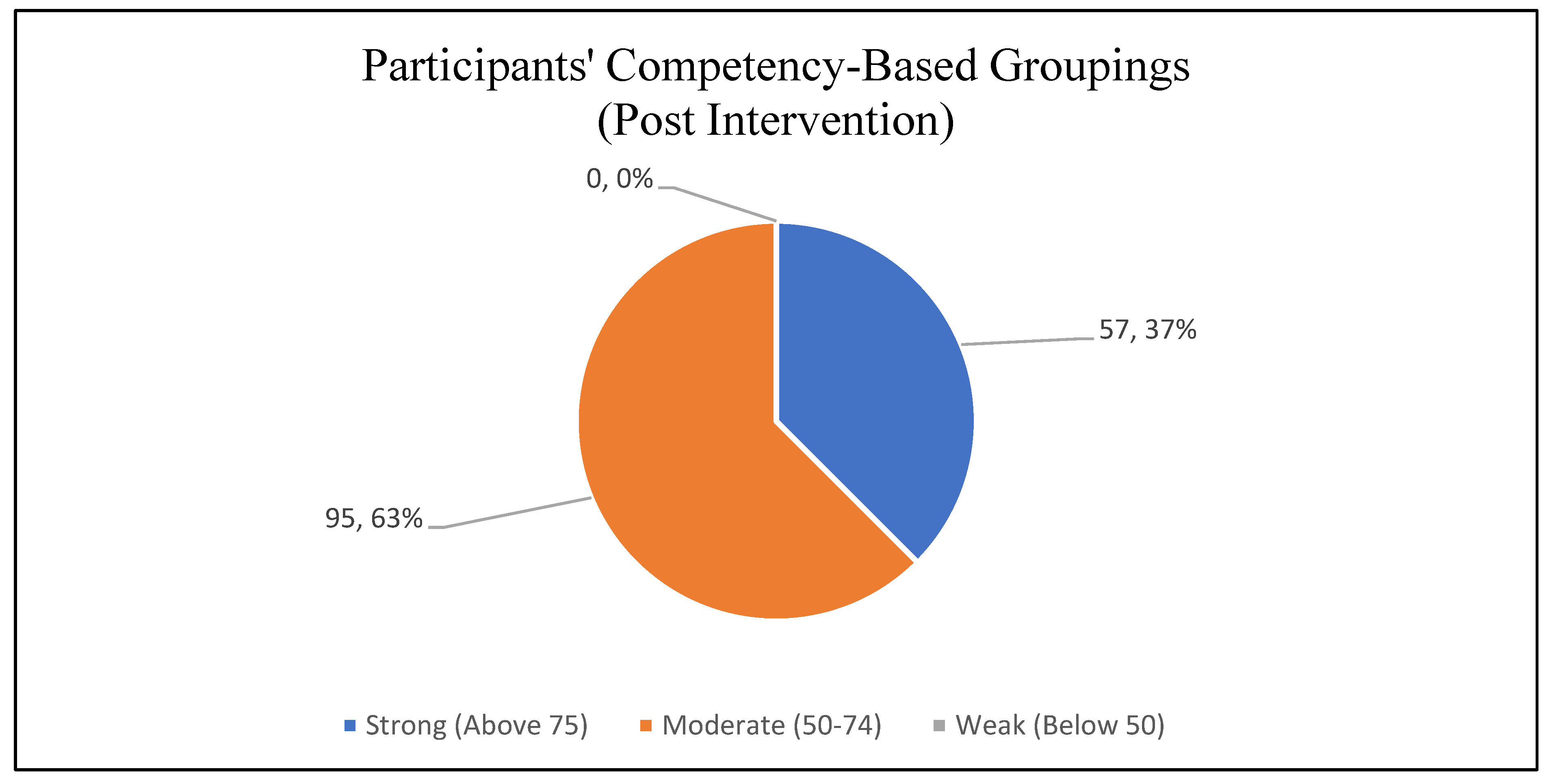
4.2.1. Mathematics Competency Levels of Participants

The average scores of participants in the respective sections of the Summative test administered at the end of the proposed intervention are shown in Table 7. From the table, the overall mathematical competency of participants is observed to be above average, with lower standard deviations indicating a lesser variation in the performance of participants. Figure 11 also illustrates the final categorization of learners as weak, moderate, or strong in mathematical competency. The figure shows that after the final test, no students were categorized as having weak mathematical proficiency., and hence a confirmation that post the intervention, all participants were considered to be above average regarding their competence in mathematical skills.

4.2.2. Participants’ Perceptions of the Relevance of Mathematics in IT Education

Table 8 provides data on the post-intervention perceptions of students on the relevance of mathematics in IT Education. The mean scores provided, which range from 3.7 to 4.1 out of 5, are indications that participants, after going through the proposed intervention, have realized how important it is for mathematics to be included in IT education. Additionally, by observing the range of standard deviation values, 0.6-0.9, it can be implied that there is little variability in the individual ratings of participants hence a strong consensus amongst them. For example, with a mean score of 4.1 and a standard deviation for the perception category stating “Mathematics is relevant to IT”, it is inferred that participants strongly agree with the claim, and such opinion is widely spread amongst the entire sample population.

4.2.3. Experts’ Assessments of Participant’s Perceptions on the Relevance of Mathematics in IT Education

Table 9 shows averages of ratings from academic and industry experts on the participants’ perceptions during their assignment presentation at the end of the ITM-RPF implementation. The mean scores ranging from 4.0 to 4.3, show that experts are in sync with the notion that participants have experienced a significant amount of shift in perceptions from negative to positive ones, regarding the need for mathematics in IT education. Also, with standard deviations ranging from 0.4 to 0.6, the ratings can be said to be consistent across all experts involved in the feedback processes.

4.3. Paired Samples T-Test Analysis

Results as shown in Table 10, Table 11, and Table 12 validate the ITM-RPF intervention to have significantly improved the mathematical competencies of students across all test sections, positively shifted their perceptions of mathematics relevance in IT education, and experts validated such progress made by the sample population. The findings that confirm the proposed framework’s effectiveness are as follows;

(i)

Means scores for all post-intervention cases are higher than their corresponding pre-intervention scores, which imply remarkable improvements in the mathematics competencies of students, enhancement of the recognition and relevance students accord mathematics concepts in IT education, and validation by experts on students’ stronger understanding, confidence, and industry alignment of mathematics principles.

(ii)

The generally lower post-intervention standard deviations in all 3 tables imply that the variability in the significantly improved results regarding students’ mathematics competence, their perceptions, and experts’ validation, decreased. In the case of mathematics competence, this indicates a higher level of uniformity in competence across learners, irrespective of their initial competency level. Again, for the participants’ self-reported perceptions, such a low standard deviation implies that there is a consensus amongst them on the positive shift of their perceptions. Finally, this also means that experts who rated these students, have a uniform agreement on the progress of the sample population.

(iii)

The t-statistics, which are large negative values in all cases of Table 10, Table 11, and Table 12, indicate that the differences between pre-intervention and post-intervention scores are highly significant, which implies the vast efficiency of the ITM-RPF.

(iv)

In paired samples t-test analysis, whenever a p-value<0.05 it implies significant change after the implementation of an intervention and hence confirms the intervention’s efficiency(Keeler & Curtis, 2023a, 2023b; Ottwell et al., 2023; Tzenios, 2023; Vejle Sørensen et al., 2023). Therefore, with p-values being 0.00 (hence, p-value<0.05) in Table 10, Table 11, and Table 12, the improvements in all post-intervention perceptions and competence of participants are not due to chance but are statistically significant.

These findings justify the adoption of structured, applied-learning pedagogical models in IT education to bridge the gap between theoretical mathematics and computing applications.

5. Summary & Conclusion

This study assessed the role mathematics plays in Information Technology (IT) education and the limitations surrounding the negative perceptions of IT students regarding its relevance. For most IT students, there is a disconnect between the real-world IT industry and the concepts they study in mathematics-related courses. Such disconnect tends to affect the performance of students in the study of mathematics courses and could create both student and tutor apathy in the classroom environment. To address this issue, this study proposed the ITM-RPF, a novel pedagogical framework that seeks to shift the perceptions of IT students regarding the relevance of mathematics education through the integration of mathematical concepts into practical IT applications. With a sample population of 152 IT undergraduate students at AAMUSTED, Ghana, the framework uses a quasi-experimental research design and was implemented over 12 weeks of intervention. Additionally, the ITM-RPF comprised of 4 structured phases; Perception Analysis and Diagnostic, Contextualized Integration and Applied Learning, Experiential Simulation and Performance Enhancement, and Perception Shift Evaluation and Continuous Learning. These phases of the proposed framework were sequentially implemented to assess students’ perceptions and competencies, match mathematics concepts to the IT industry, actively engage students in simulations that leverage mathematical principles, and conduct an evaluation to affirm a positive shift in students’ perceptions and improvement in their competencies. The study employed paired samples t-tests and descriptive statistical analysis in concluding the significant post-intervention improvements. After the implementation of the intervention, results confirmed that students had gained significant development in terms of interest, motivation, and confidence in applying mathematics concepts in IT-related tasks. Moreover, experts who engaged in both pre-test and post-test assessments validated the shift in students’ appreciation of mathematics and also noted a stronger sync between the skills of students and what the IT industry requires. The paper’s findings are a confirmation of the remarkable positive changes caused by the proposed ITM-RPF. The proposed framework effectively bridges the gap between the theories in mathematics and the practicality in IT. The ITM-RPF provides a sustainable approach to enhancing IT students’ engagement with mathematics by making it more relevant, applicable, and industry-oriented. Future research should explore long-term implementations, industry collaborations, and broader student populations to further refine and expand the framework’s effectiveness.