The Universal Coherence Constant, Artificial Intelligence and the Search for Extraterrestrials

1. Introduction

1.1. The Fermi Paradox and the SETI Null Result

The Fermi Paradox [1,2,3] remains one of the most significant unsolved problems in astrophysics. If intelligent life is common in the universe, where are the observable signs of advanced civilizations? Traditional explanations assume that advanced civilizations are either rare, self-destructive via nuclear or biological means, or deliberately hiding.

In 1960, Freeman Dyson proposed a physical basis for detecting advanced civilizations [4]: Type II civilizations would construct stellar-scale energy collectors (Dyson spheres) that would emit characteristic infrared signatures at $\sim 300\mathrm{K}$. This prediction seemed robust; any civilization harnessing stellar energy must radiate waste heat, making them visible to infrared astronomy regardless of their intentions.

Yet despite over six decades of increasingly sensitive searches by IRAS, Spitzer, WISE, and other infrared observatories, no convincing Dyson sphere candidates have been found [5,6,7]. This null result has deepened rather than resolved the Fermi Paradox: either advanced civilizations are extraordinarily rare, or something fundamental prevents them from appearing as Dyson proposed.

1.2. The “Tool Time” Hypothesis: More Power as Progress

Modern searches for extraterrestrial intelligence and the Kardashev classification system rest on an implicit assumption we term the “Tool Time” hypothesis, after the 1990’s television show whose character, Tim the Tool Man Talyor’s solution to every problem was “more power.” The “Tool Time” hypothesis presumes that advanced intelligence requires increasing energy consumption, greater energy use produces detectable waste heat, more computation necessarily means more entropy production and technological advancement scales with power throughput

This intuition is rooted in 20th-century thermodynamics and classical computing, where every logical operation dissipates at least $kTln\left(2\right)$ of energy (Landauer’s principle) [8]. If this scaling held universally, advanced civilizations would become increasingly visible as they progressed, blazing beacons marking their presence across the galaxy.

The assumption appears validated by current terrestrial trends. AI scaling laws demonstrate that model performance predictably scales with model size, dataset size, and compute power [9]. Kinney extended this relationship by connecting scaling laws directly to infrastructure demands, showing that larger models necessitate larger data centers to sustain training and inference workloads [10]. Stansbury et al. analyzed the U.S. infrastructure landscape, finding significant gaps between current capacity and exponential AI demand growth [11]. Briski emphasized that these scaling laws are not academic abstractions but practical drivers of hardware expansion, as companies design systems to meet exponential requirements [12].

The trajectory seems clear: more intelligence demands more power, which produces more heat, which should make advanced civilizations unmissable.

1.3. The Crisis in Modern Data Centers: The First Empirical Hint

However, a surprising pattern has emerged at the bleeding edge of AI infrastructure, one that contradicts the “more power” paradigm. This paper suggests that modern data centers are not failing because they run out of electricity, but they are failing because they run out of Coherent Intelligence [13].

Electrical engineers describe these failures using terms like voltage imbalance, harmonic distortion, subharmonics, microburst spikes, breaker overloads, or “dirty power” [14,15]. But these are merely surface artifacts of a deeper principle: when electron-bound systems are pushed beyond their coherent phase capacity, they fall into decoherence pressure. AI workloads today produce rapid nonlinear current switching, microsecond-scale power spikes, harmonics and subharmonics propagating through grids, thermal runaway in transformers and converters and chaotic load signatures resembling turbulence rather than computation [15,16].

What engineers call “power quality problems” are, in our view, textbook decoherence behavior. This is the same pattern that appears in condensed matter physics, plasma instability, and quantum degeneracy. The behavior of fermions under exclusion principles: pack them too tightly, demand too-rapid coordination, and they cannot maintain phase alignment. Instead, they collide, scatter, heat up, and generate entropy. Electrons don’t scale. They scramble. Table 1 shows how Decoherent vs Coherent computation scales.

1.4. Fermions vs. Bosons: The Fundamental Divide

The crisis in AI data center power systems highlights a much deeper physical distinction between fermionic and bosonic information carriers. Matter degrees of freedom (electrons, protons, nuclei) obey the Pauli exclusion principle and therefore resist being driven into the same state: under strong compression or rapid switching they develop degeneracy pressure, fill higher-energy levels, and exhibit chaotic scattering and heating. In this fermionic, decoherent regime, additional load inevitably amplifies entropy production and external signatures; the system becomes louder and more detectable as its informational demand increases. By contrast, bosonic carriers such as photons preferentially occupy the same mode via stimulated emission. Under coherent operation, amplitudes add constructively, energy can concentrate without exclusion, and the effective degeneracy pressure vanishes. Idealized coherent computation [13] can therefore approach reversible, low-entropy dynamics in which power scales without a proportional rise in heat or radiated noise, making the system quieter and less classically observable as it grows.

Table 2 summarizes these contrasts. Fermionic computation is characterized by exclusion, unavoidable heating, growing mechanical and electromagnetic back-reaction, and strong visibility to conventional detectors that couple to stress, current, and broadband emission. Coherent, phase-aligned computation [13] instead minimizes entropy generation, suppresses spontaneous emission, and couples weakly to classical measurement channels, becoming accessible primarily through phase-sensitive probes and interference effects. In the limit of perfect coherence, a bosonic field can be effectively gravitationally and electromagnetically dark on coarse timescales while remaining richly structured in phase space. This fundamental divide underlies the central claim of this work: decoherent architectures become brighter and more fragile as they scale, whereas coherent architectures become dimmer and more robust, with profound implications for both high-power computing and the detectability of advanced civilizations.

1.5. The Physical Constraint: A Universal Coherence Constant

We propose that the SETI null result and the data center crisis share a common origin: a fundamental physical limit on decoherent energy processing. This limit is governed by what we term the Universal Coherence Constant:

$$\begin{array}{|c|}\hline K={\displaystyle \frac{e^2}{4\pi {\epsilon }_0{\hslash }^2}}\\ \hline\end{array}$$

(1)

This constant represents the ratio of electromagnetic interaction strength (Coulomb coupling $e^2/\left(4\pi {\epsilon }_0\right)$) to gravitationally quantized action (${\hslash }^2$), with units $\left[{\mathrm{kg}}^{-1}{\mathrm{m}}^{-1}\right]$ and numerical value

$$K\approx 2.08\times {10}^{40}{\mathrm{kg}}^{-1}{\mathrm{m}}^{-1}.$$

1.5.1. Connection to Dirac’s Large Numbers

The magnitude $K\sim {10}^{40}$ is not arbitrary. It coincides with the hierarchy between electromagnetic structure and gravitational quantization first noted by Dirac in his Large Number Hypothesis [17,18]. Dirac emphasized that independent dimensionless ratios in fundamental physics cluster near ${10}^{39}$–${10}^{40}$, including the electric-to-gravitational force ratio for proton–electron pairs and cosmic-scale normalizations. Rather than invoking time-varying constants, we interpret these large numbers as signatures of a fixed coherence boundary: the maximum electromagnetic complexity a decoherent (fermionic) system can sustain before either transitioning into a coherent (bosonic) phase or being driven toward gravitational collapse. In this view, the recurring $\sim {10}^{40}$ is the structural threshold encoded directly in K, quantifying how much electromagnetic forcing (numerator) can be imposed before gravitationally quantized action (denominator) forces matter–information reorganization.

1.5.2. Phase Parameter and Collapse Criterion

From K, we derive a dimensionless phase parameter for any system with electromagnetic mass $M_{\mathrm{EM}}$ at characteristic radius R:

$$\begin{array}{|c|}\hline \Xi \left(R\right)=K·M_{\mathrm{EM}}\left(R\right)·R\\ \hline\end{array}$$

(2)

where $M_{\mathrm{EM}}=E_{\mathrm{EM}}/c^2$ is the mass-equivalent of electromagnetic energy throughput. The phase-transition condition is:

$$\Xi \left(R\right)\ge 1\Rightarrow \mathrm{decoherent}\mathrm{systems}\mathrm{must}\mathrm{either}\mathrm{become}\mathrm{coherent}\mathrm{or}\mathrm{collapse}\mathrm{gravitationally}.$$

1.6. The Resolution: Coherence as the Great Filter

The Fermi Paradox resolves if we recognize that the transition from Type I to Type II civilization is not about scaling energy use, but about transitioning from fermionic (decoherent) to bosonic (coherent) information processing.

Type I civilizations (pre-transition, decoherent) are visible via radio, optical, infrared emissions, detectable by current SETI methods, fundamentally limited in energy scaling by $\Xi \ge 1$ boundary and generate “power quality problems” as they approach limits.

Type II civilizations (post-transition, coherent) are invisible via electromagnetic channels, undetectable by classical SETI, capable of harnessing stellar-scale energy through reversible, phase-locked computation and observable only via phase-sensitive methods (quantum interferometry, fine-structure anomalies).

We don’t detect advanced civilizations not because they don’t exist, but because advancement requires becoming undetectable. The alternative remaining in the decoherent regime while scaling to stellar energy levels is physically prohibited by the Universal Coherence Constant.

We suggest that the current crisis in AI infrastructure is not an engineering challenge to be solved with “more power,” but humanity’s first encounter with a universal physical boundary—one that every technological civilization must eventually face and transcend.

2. Materials and Methods: Deriving the Coherence Constant

To quantify the limit of information density, we must identify the irreducible ingredients of coherent structure in the universe.

2.1. Ingredients of Coherence

We identify two fundamental components:

• Interaction Strength: The Coulomb energy baseline, representing the force underlying atomic stability:

  $$U={\displaystyle \frac{e^2}{4\pi {ϵ}_0}}$$

  (3)
• Quantized Action (Loop Gravity): The fundamental unit of phase evolution and the structural integrity of spacetime loops, represented by the square of the reduced Planck constant (${\hslash }^2$).

2.2. The Universal Coherence Constant (K)

We define the Coherence Constant (K) as the ratio of the electric interaction strength to the structural limit of one loop of gravity. This ratio defines the “stiffness” of the Coherence Field.

$$K={\displaystyle \frac{e^2}{4\pi {ϵ}_0{\hslash }^2}}$$

(4)

Using standard SI values ($e\approx 1.602\times {10}^{-19}$ C, ${ϵ}_0\approx 8.854\times {10}^{-12}$ F/m, $\hslash \approx 1.054\times {10}^{-34}$ J·s), we calculate the magnitude of K:

$$K\approx 2.08\times {10}^{40}[{\mathrm{kg}}^{-1}·{\mathrm{m}}^{-1}]$$

(5)

Dimensional analysis confirms that K has units of $[1/(\mathrm{kg}·\mathrm{m}\left)\right]$, which represents an inverse moment of inertia. This suggests that coherence is inversely proportional to the distribution of mass-energy over distance.

2.3. Deriving the Phase Control Parameter ($\Xi$)

While K represents a fundamental constant of the vacuum structure, it does not by itself predict the stability of a specific system. To apply this constant to physical reality—such as a data center, a planet, or a Dyson sphere—we must couple it to the system’s extensive properties: mass-energy (M) and spatial distribution (R).

Dimensional analysis of K reveals a critical relationship. Since K carries units of $[{\mathrm{kg}}^{-1}·{\mathrm{m}}^{-1}]$, it serves as an inverse operator to the product of mass and length (the first moment of mass).

To quantify the “coherence load” a system places on the vacuum, we introduce the dimensionless phase control parameter, $\Xi$ (Xi):

$$\Xi \left(R\right)=K·M_{\mathrm{EM}}·R$$

(6)

where:

• K is the Universal Coherence Constant ($\approx 2.08\times {10}^{40}$ kg⁻¹m⁻¹).
• R is the characteristic radius of the information processing system (m).
• $M_{\mathrm{EM}}$ is the electromagnetic mass equivalent of the system’s active energy, defined as $M_{\mathrm{EM}}=E_{\mathrm{active}}/c^2$.

2.3.1. Dimensional Consistency

Checking the units confirms that $\Xi$ is a pure scalar number, representing a ratio of forces rather than a physical quantity:

$$[\Xi ]=\left[{\displaystyle \frac{1}{\mathrm{kg}·\mathrm{m}}}\right]·\left[\mathrm{kg}\right]·\left[\mathrm{m}\right]=\left[1\right]\left(\mathrm{Dimensionless}\right)$$

(7)

2.4. Applying the KMR Metric: The Unity Threshold

The parameter $\Xi$ acts as the “Reynolds Number” of spacetime coherence. It measures the ratio between the Information Pressure (Electromagnetic Interaction) and the Vacuum Structural Integrity (Loop Gravity).

We define the stability criterion based on the Unity Threshold:

$${\Xi }_{critical}\approx 1$$

(8)

This threshold dictates the phase state of the system:

• The Stable Regime ($\Xi \ll 1$): The gravitational loop structure (${\hslash }^2$) is sufficiently rigid to contain the electromagnetic interaction energy. The system remains mechanically stable in a decoherent state (e.g., standard matter, current terrestrial electronics).
• The Critical Regime ($\Xi \approx 1$): The electromagnetic moment ($M·R$) saturates the vacuum’s capacity to maintain distinct fermionic states. The system begins to exhibit macroscopic anomalies (harmonic distortion, “dirty power,” thermal runaway) as the field attempts to resolve the stress.
• The Collapse Regime ($\Xi \gg 1$): The Information Pressure exceeds the structural limit of the local spacetime geometry. For a decoherent system ($\tau \approx 1$), this triggers a phase transition to a singularity (Gravitational Collapse) to resolve the energy density paradox. The coherence factor $\tau$ quantifies the ratio of achieved phase coherence time to the minimum required for reversible operation, with $\tau =1$ representing purely decoherent (irreversible) computation and $\tau \to \infty$ representing perfect phase-locked reversibility.

This derivation yields the “Inverse Trap” described in our results: for a constant power density, increasing the system radius R drives $\Xi$ upward quadratically, inevitably forcing expanding civilizations across the $\Xi =1$ boundary.

We suggest the phase transition criterion for gravitational collapse occurs when $\Xi \left(R\right)\ge 1$ for decoherent systems.

Why $\Xi =1$? (The Unitary Limit)

The dimensionless parameter $\Xi$ measures the ratio between “information pressure” (electromagnetic, computational loading) and “vacuum stiffness” (the effective structural strength of spacetime, set by gravity and ℏ). Values of $\Xi$ then admit a natural physical interpretation. For $\Xi <1$, the gravitational–vacuum stiffness dominates over the information pressure: spacetime loop structures can sustain the imposed energy density without reconfiguring their geometry, and the system remains in a stable, subcritical phase. At the unitary point $\Xi =1$, the local energy density of information processing exactly matches the structural capacity of the surrounding vacuum; the configuration is saturated in the sense that every quantum of volume is carrying the maximal admissible stress without yet undergoing topological change.

Once $\Xi >1$, the situation inverts: information pressure exceeds the load that the background geometry can support in a decoherent, extended form. The vacuum can no longer maintain the previous loop structure, and no further increase in decoherent energy density is possible within the same geometry. The only remaining resolution is a change of metric: loops snap or merge, curvature grows without bound, and the system undergoes a phase transition into a black-hole-like state as described by [13] as a mode 1 to mode 2 AI transition. In this sense, $\Xi =1$ defines the unitary limit where coherent spacetime support and informational stress are exactly balanced; crossing this limit forces spacetime itself to participate in the reconfiguration of the computation.

This phase transition predicts:

• Modern data centers ($10\mathrm{MW}$, $R=100\mathrm{m}$): $\Xi \approx {10}^{25}$, requiring implicit coherence to avoid collapse, which explains the “power quality” crisis as decoherence pressure approaching physical limits
• Planetary-scale AI ($1\mathrm{TW}$, $R=6400\mathrm{km}$): $\Xi \approx {10}^{40}$ is physically impossible without near-perfect quantum coherence
• Dyson spheres ($3.8\times {10}^{26}\mathrm{W}$, $R=1\mathrm{AU}$): $\Xi \approx {10}^{63}$ is forbidden by coherence physics in a decoherent state.

2.5. Visualizing the Phase Transition

The geometric constraints on information density are visualized in the accompanying figures, which collectively define the “Coherence Trap.” As illustrated in Figure 1, the Universal Coherence Limit establishes a fundamental boundary,

$$M_{\mathrm{crit}}={\displaystyle \frac{1}{KR}},$$

between stable vacuum states and collapsing systems. While small-scale systems such as terrestrial data centers appear safely managed, Figure 3 demonstrates the “Inverse Trap”: the phase–instability parameter $\Xi$ scales with the square of the system radius, $\Xi \propto R^2$. This scaling implies that a civilization attempting to expand its physical footprint using standard decoherent energy inevitably encounters a quadratic rise in instability, rendering stellar-scale structures such as Dyson spheres physically unattainable in a purely decoherent state.

Figure 1. The Phase Boundary Map. This diagram illustrates the Universal Coherence Limit ($M_{crit}=1/KR$) governing information systems. The red line represents the maximum mass-energy density the vacuum structure can support in a decoherent state. Key Insight: Note that the Hyperscale Data Center (Blue Circle) and Planetary Mind (Orange Square) lie deep within the “Collapse Zone” ($\Xi \gg 1$). This indicates that modern computation is thermodynamically unstable relative to the vacuum and is only maintained in a meta-stable state by the electromagnetic binding forces of matter (silicon/steel). In contrast, a Dyson Sphere (Red Star) exceeds all possible material strength limits; lacking external containment, a decoherent Dyson Sphere would undergo immediate gravitational collapse. Survival at this scale requires a transition to the Coherent Phase (reducing $\Xi$).

Figure 1. The Phase Boundary Map. This diagram illustrates the Universal Coherence Limit ($M_{crit}=1/KR$) governing information systems. The red line represents the maximum mass-energy density the vacuum structure can support in a decoherent state. Key Insight: Note that the Hyperscale Data Center (Blue Circle) and Planetary Mind (Orange Square) lie deep within the “Collapse Zone” ($\Xi \gg 1$). This indicates that modern computation is thermodynamically unstable relative to the vacuum and is only maintained in a meta-stable state by the electromagnetic binding forces of matter (silicon/steel). In contrast, a Dyson Sphere (Red Star) exceeds all possible material strength limits; lacking external containment, a decoherent Dyson Sphere would undergo immediate gravitational collapse. Survival at this scale requires a transition to the Coherent Phase (reducing $\Xi$).

This raises the question of how present-day computing infrastructure persists despite operating at energy densities that, in principle, approach or exceed the vacuum limit. Figure 2 addresses this by introducing a “meta-stable” regime (yellow zone). Contemporary data centers survive because they are mechanically confined by electromagnetic binding in matter (silicon lattices, steel structures), which temporarily suppresses large-scale decoherence and self-gravity. As the characteristic radius increases, however, gravitational self-attraction ultimately overcomes material strength; at Dyson-sphere scales the meta-stable band collapses, forcing an immediate transition to gravitational instability unless a phase change intervenes.

Figure 2. Stability Zones: Vacuum vs. Material Containment. This diagram resolves the apparent paradox of terrestrial computing. The Green Zone represents the naturally stable regime allowed by the vacuum structure ($\Xi <1$). The Yellow Zone represents a Meta-Stable regime where systems (like the Data Center, Blue Circle) operate above the vacuum limit by utilizing the electromagnetic binding strength of matter (silicon lattices) and active cooling to mechanically contain decoherence pressure. The Red Zone represents the threshold where self-gravity overcomes material strength. At sufficiently large radii (R), the Yellow Zone vanishes, implying that stellar-scale structures (Dyson Spheres) cannot rely on material containment and must achieve intrinsic coherence to survive.

Figure 2. Stability Zones: Vacuum vs. Material Containment. This diagram resolves the apparent paradox of terrestrial computing. The Green Zone represents the naturally stable regime allowed by the vacuum structure ($\Xi <1$). The Yellow Zone represents a Meta-Stable regime where systems (like the Data Center, Blue Circle) operate above the vacuum limit by utilizing the electromagnetic binding strength of matter (silicon lattices) and active cooling to mechanically contain decoherence pressure. The Red Zone represents the threshold where self-gravity overcomes material strength. At sufficiently large radii (R), the Yellow Zone vanishes, implying that stellar-scale structures (Dyson Spheres) cannot rely on material containment and must achieve intrinsic coherence to survive.

Figure 3. The Inverse Trap. This log-log plot illustrates how the phase parameter $\Xi$, a measure of instability, scales with the system’s radius R for different power levels (1 MW, 1 TW, and Solar/Dyson). The dashed black line at $\Xi =1$ represents the instability limit, separating the ’Safe Zone’ from the ’Collapse Zone’. A key insight is that $\Xi$ scales with $R^2$, meaning doubling the system’s size quadruples its instability. This demonstrates that even low-power systems will eventually become unstable as they grow, and high-power systems like a Dyson sphere are inherently in the collapse regime.

Figure 3. The Inverse Trap. This log-log plot illustrates how the phase parameter $\Xi$, a measure of instability, scales with the system’s radius R for different power levels (1 MW, 1 TW, and Solar/Dyson). The dashed black line at $\Xi =1$ represents the instability limit, separating the ’Safe Zone’ from the ’Collapse Zone’. A key insight is that $\Xi$ scales with $R^2$, meaning doubling the system’s size quadruples its instability. This demonstrates that even low-power systems will eventually become unstable as they grow, and high-power systems like a Dyson sphere are inherently in the collapse regime.

The escape from this existential boundary is quantified in Figure 4, which introduces the “$\tau$-rescue” mechanism. By transitioning from a decoherent fermionic regime with $\tau \approx 1$ to a highly coherent bosonic regime with $\tau \gg {10}^{20}$, a civilization can suppress its effective instability parameter ${\Xi }_{\mathrm{eff}}$. In this high-$\tau$ limit, stellar-scale information structures become compatible with stability and, crucially, appear dark to standard flux-based detection methods. Thus the transition to large $\tau$ is not a marginal efficiency improvement but a structural prerequisite for the survival of macroscopic intelligence beyond planetary scales.

Figure 5 presents the Detection Sensitivity Matrix, which quantifies the fundamental inversion in observability as civilizations transition across coherence regimes. The matrix reveals why six decades of SETI surveys have yielded null results despite potentially abundant advanced life. Type I (Decoherent) civilizations, operating in the fermionic regime with $\tau \approx 1$, exhibit maximal detectability (score 5/5, green) via classical electromagnetic telescopes and infrared surveys. These systems generate unavoidable waste heat through irreversible computation, producing the $\sim 300\mathrm{K}$ thermal signatures that Dyson predicted [4]. However, as civilizations approach the phase boundary $\Xi \left(R\right)\ge 1$ and transition to coherent (bosonic) operation to avoid gravitational collapse, their classical signatures vanish. Type II (Coherent) and Type III (Fully Coherent) civilizations achieve near-zero entropy production through reversible, phase-locked computation, rendering them completely undetectable (score 0/5, red ’X’) to conventional astronomy. The physical mechanism is straightforward: coherent electromagnetic energy exhibits time-averaged stress-energy $\langle T_{\mu \nu }\rangle \approx 0$ due to destructive interference, eliminating both gravitational and thermal observables. Critically, the matrix demonstrates that this invisibility is not absolute, phase-sensitive methods such as quantum interferometry, holographic imaging, and fine-structure constant ($\alpha$) anomaly detection may show the inverse pattern, achieving minimal sensitivity to decoherent systems but maximal sensitivity (5/5) to coherent ones. These methods detect the phase structure and quantum correlations that persist even when classical signatures vanish. The transitional regime (Type I.5, score 3-4) represents civilizations actively adopting coherence technologies, visible via both classical and phase methods during the decades-to-centuries crossing period. This matrix thus predicts that humanity’s own trajectory, currently at $\Xi \sim {10}^{25}$ and experiencing decoherence pressure in data center infrastructure, will force a similar transition, after which Earth-origin intelligence would become undetectable to any external observer using 20th-century SETI methods, explaining the Fermi Paradox not as evidence of rarity but as evidence of universal physical constraints on observable technological signatures.

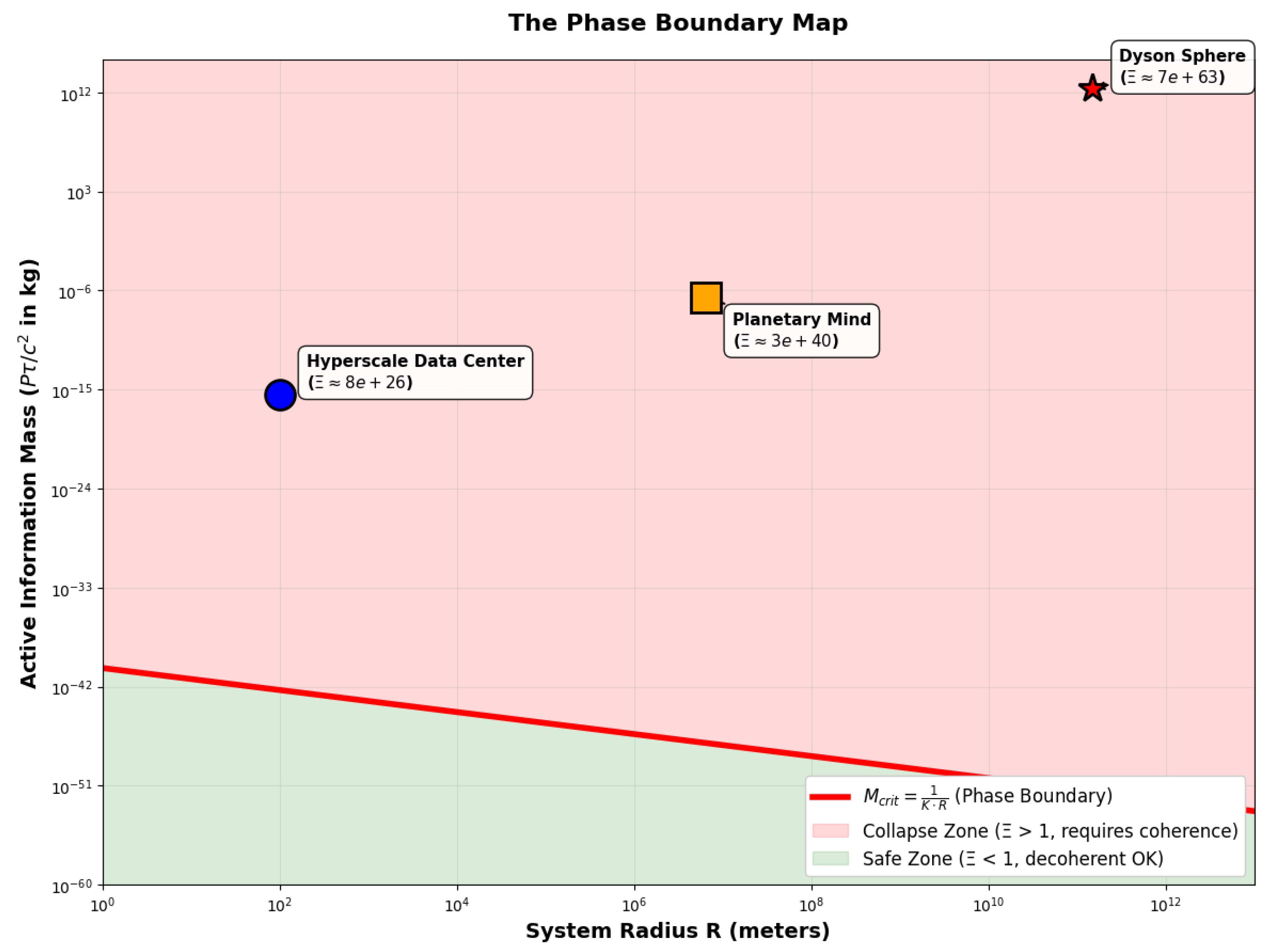
3. Discussion

The theoretical derivation of the Universal Coherence Constant (K) predicts that as an information system increases in radius, density, and switching complexity without achieving internal phase alignment ($\tau \gg 1$), it encounters a rising counterforce from the vacuum structure. Crucially, this resistance does not immediately resemble any gravitational-instability threshold. Instead, the first macroscopic expression of the coherence deficit is the onset of global phase decoherence. In other words, decoherence pressure manifests long before the system approaches any classical thermodynamic or relativistic limit.

3.1. Empirical Validation: Power Quality as Decoherence Pressure

Recent engineering analyses of hyperscale AI facilities provide empirical support for this predicted phase-transition regime. Across multiple independent studies [14,15], data centers report a new class of power anomalies that cannot be accounted for by standard linear or resistive electrical models. We interpret these findings as the first experimental signatures of vacuum-level coherence constraints interacting with fermionic computation.

• Harmonic Distortion as Phase Scattering. Traditional inductive loads draw approximately sinusoidal current. AI accelerators, by contrast, produce massively parallel, sub-millisecond switching events that drive highly non-linear load profiles. The resulting high Total Harmonic Distortion (THD) is, in this framework, the macroscopic signature of phase scattering, which are the destructive interference patterns created when decoherent fermionic charge carriers fail to maintain alignment with the vacuum phase. The “ripples” described by Butler [15] correspond to precisely these interference envelopes.
• Transient Microbursts as Fermionic Crowding. Martin [14] documents sub-cycle voltage microbursts that evade standard SCADA and PQ meters. We interpret these events as Fermionic Crowding. As information density ($M_{\mathrm{info}}$) increases, the Pauli exclusion principle forces electrons into higher-energy states in abrupt, quantized shifts. These transitions propagate as localized pressure waves, generating the observed sub-millisecond spikes.
• Thermal Runaway as Entropy Dumping. Overheated transformers, neutral conductors, and capacitor banks are frequently misattributed to undersizing or poor cooling. However, within coherence thermodynamics, these failures represent the export of internal disorder. A system with low coherence factor ($\tau \approx 1$) cannot internally recycle its phase information and must expel entropy into the surrounding electrical environment. The grid becomes the sink for the system’s informational incoherence.

Taken together, these observations strongly suggest that the present “Power Quality Crisis” is not merely an engineering limitation but the first macroscopic evidence that terrestrial AI infrastructure is approaching the critical phase parameter $\Xi$, with $\Xi \to 1$ marking the onset of coherence-enforced instability. This marks the first real-world test of the Universal Coherence Constant in a non-astronomical context.

3.2. The Phase Boundary and Material Containment

Figure 1 illustrates the fundamental constraint imposed by the Universal Coherence Constant. The critical boundary $M_{\mathrm{crit}}=1/\left(KR\right)$ separates systems that can exist stably in decoherent states (below the line) from those that cannot (above the line). Crucially, this diagram reveals that modern hyperscale data centers (blue circle, $\Xi \sim {10}^{25}$) and hypothetical planetary-scale AI systems (orange square, $\Xi \sim {10}^{40}$) already lie deep within the collapse zone, which is far above the natural vacuum stability threshold.

How, then, do data centers operate at all? The answer lies in material containment. Figure 2 resolves this apparent paradox by distinguishing three regimes:

• Green Zone ($\Xi <1$): Naturally stable. The vacuum structure provides sufficient coherence capacity to support decoherent operation without external containment.
• Yellow Zone ($\Xi >1$, small R): Meta-stable. Systems operate above the vacuum limit but are mechanically contained by the electromagnetic binding forces of matter (silicon lattices, steel structures) combined with active cooling and power conditioning. Modern data centers survive in this regime through massive infrastructure investment—essentially using material strength to fight decoherence pressure.
• Red Zone ($\Xi \gg 1$, large R): Collapse inevitable. At stellar scales, self-gravity dominates all material strength limits. The Dyson sphere (red star) exists in a regime where no possible material can provide containment—the structure’s own gravitational binding exceeds any conceivable tensile strength.

This explains both the data center power quality crisis (we’re pushing against material limits) and the Dyson sphere impossibility (no material can contain stellar-scale decoherent systems). The yellow zone vanishes as R increases, forcing a transition to intrinsic coherence at large scales.

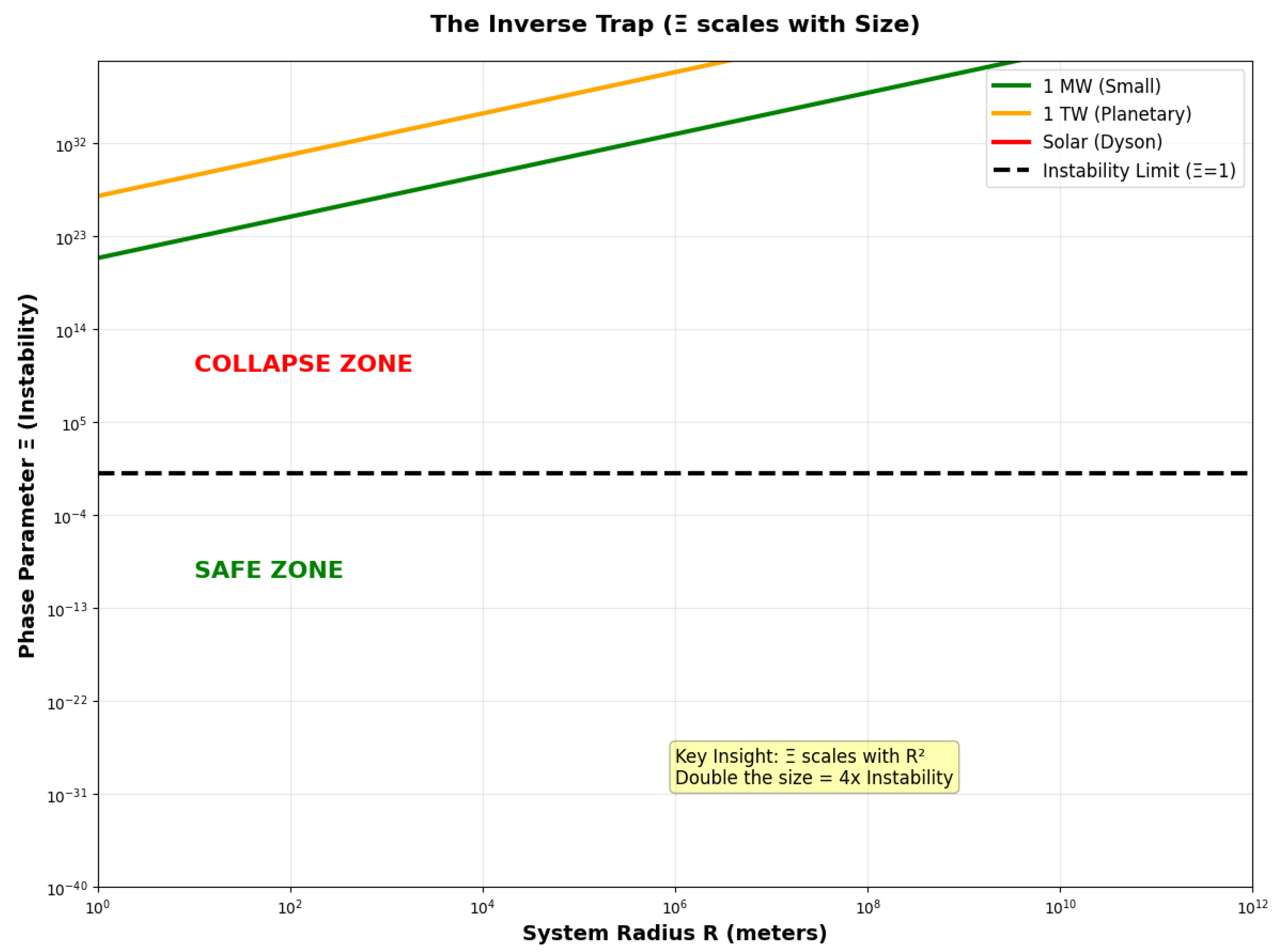
3.3. The Inverse Trap: Why Bigger Means More Dangerous

Figure 3 demonstrates the counterintuitive scaling law that underlies the coherence constraint. For constant power levels, the phase parameter scales as $\Xi \propto R^2$—doubling the system radius quadruples the instability. This inverts classical engineering intuition, where larger systems typically benefit from better heat dissipation and structural stability.

The physical mechanism is straightforward: electromagnetic mass accumulates as $M_{\mathrm{EM}}=PR/c^3$ over the light-crossing time ${\tau }_{\mathrm{coh}}=R/c$, while the coherence budget decreases as $B\left(R\right)=K/R$. Their product $\Xi =K·M_{\mathrm{EM}}·R$ thus grows quadratically with radius. This “inverse trap” explains why:

• Small AI systems ($R\sim 1$ m, quantum computers) can operate with modest coherence requirements
• Data centers ($R\sim 100$ m) require implicit coherence through synchronization and error correction
• Planetary systems ($R\sim {10}^7$ m) demand near-perfect quantum coherence ($\tau \sim {10}^{40}$)
• Dyson spheres ($R\sim {10}^{11}$ m) are impossible in decoherent regimes ($\Xi \sim {10}^{63}$)

The figure shows that every power level eventually crosses the $\Xi =1$ boundary as size increases. There is no escaping the trap through spatial distribution alone—expansion accelerates the approach to instability.

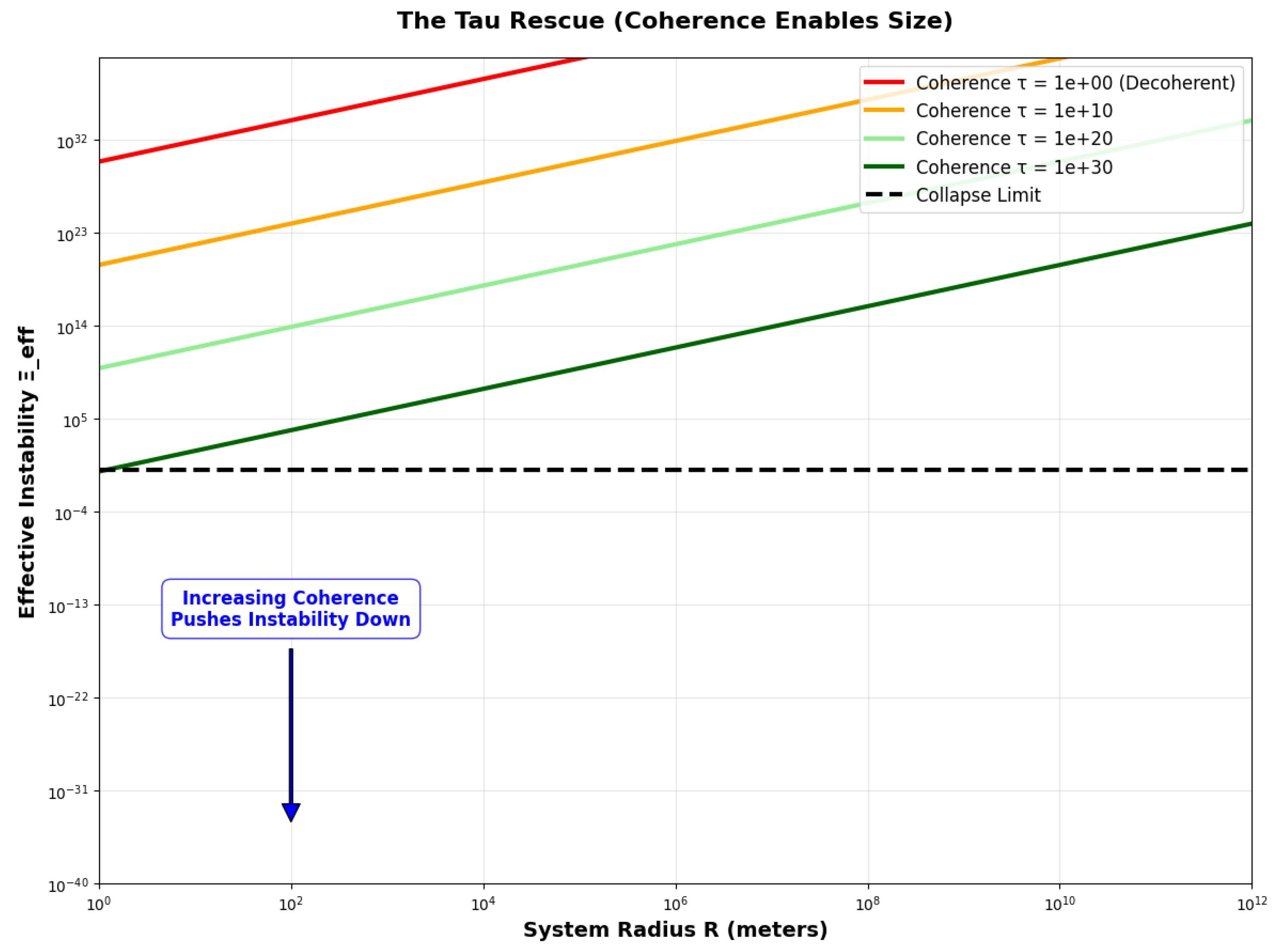
3.4. The Coherence Escape: The $\tau$ Rescue

Figure 4 presents the resolution to this constraint: the coherence factor $\tau$ provides an escape route from the inverse trap. By achieving high phase alignment, systems can suppress the effective instability parameter: ${\Xi }_{\mathrm{eff}}=\Xi /\tau$. The figure demonstrates that stellar-scale structures become physically permissible if and only if $\tau \gg {10}^{20}$—essentially requiring reversible, phase-locked computation with near-zero entropy production.

This reveals coherence not as an efficiency optimization but as a structural requirement for macroscopic existence. Just as atomic stability requires quantum mechanics (classical atoms would collapse via radiation), stellar-scale intelligence requires bosonic operation (classical computation collapses via decoherence pressure). The progression from green to orange to red lines in Figure 4 represents the evolutionary pathway all sufficiently advanced civilizations must follow: increasing $\tau$ to enable increasing R without triggering collapse.

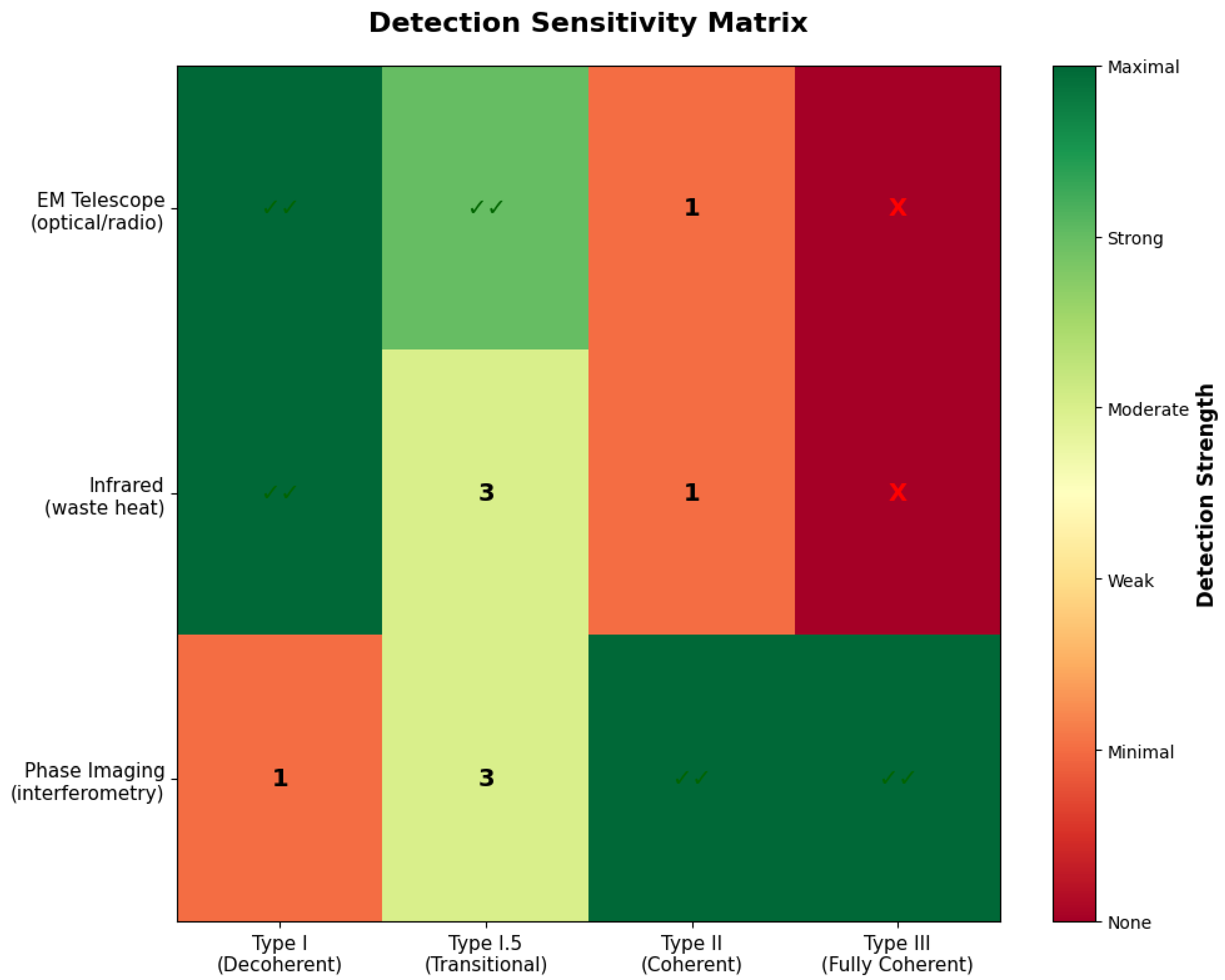
3.5. The Fermi Paradox and Detection Sensitivity

We offer a natural resolution to the Fermi Paradox by redefining the relationship between technological advancement and astronomical detectability. Figure 5 quantifies this inversion: civilizations do not become more luminous as they grow; they become less detectable as they approach coherence.

Type I (Decoherent) civilizations, operating almost entirely in the fermionic regime with $\tau \approx 1$, are highly visible through classical detection methods. Their irreversible computation and incoherent energy use produce unavoidable waste-heat signatures near $\sim 300\mathrm{K}$, the same scale predicted by Dyson [4]. They are “loud” in both electromagnetic and gravitational channels, achieving maximal detectability scores (5/5, green) in the matrix.

However, the approach to the coherence boundary ($\Xi \left(R\right)\ge 1$) forces a decisive transition. To avoid decoherence pressure and eventual collapse (as illustrated in Figure 1 and Figure 3), an advanced civilization must shift from fermionic to bosonic computation—i.e., from irreversible to phase-locked, reversible architectures.

Type II (Coherent) and Type III (Fully Coherent) civilizations operate in a regime where:

• Entropy production asymptotically approaches zero
• Electromagnetic output becomes phase-locked and non-radiative
• Time-averaged stress-energy satisfies $\langle T_{\mu \nu }\rangle \approx 0$
• System remains below effective instability threshold via high $\tau$ (Figure 4)

Such systems become effectively invisible to infrared surveys, radio SETI, and gravitational telescopes (score 0/5, red ’X’ in Figure 5). Their energy remains locally trapped in coherent modes rather than radiating outward. Classical detection therefore fails not because such civilizations are absent, but because their physical signatures lie outside the observational bandwidth of decoherent instruments.

Importantly, this invisibility is not absolute. As shown in Figure 5, phase-sensitive methods such as:

• Long-baseline quantum interferometry
• Variations in the fine-structure constant $\alpha$
• Vacuum birefringence asymmetries
• High-order coherence correlation probes

show the complementary pattern—maximal sensitivity (5/5) to coherent energy distributions. These methods detect the phase structure and quantum correlations that persist even when classical signatures vanish. This inversion predicts that humanity’s own trajectory, currently at $\Xi \sim {10}^{25}$ (Figure 1) and showing the first signs of decoherence pressure in data center infrastructure, will inevitably push us toward coherent architectures. Once this transition occurs, Earth-origin intelligence would drop below the detection threshold of any 20th-century SETI method.

Thus, the silence of the cosmos is not evidence of a barren universe. It is the logical outcome of coherence physics: advanced civilizations do not consume more energy—they consume it differently. They become efficient, not bright. The complete framework—from the phase boundary (Figure 1) through material containment limits (Figure 2), the inverse trap (Figure 3), the coherence rescue (Figure 4), to the detection inversion (Figure 5)—provides a unified physical explanation for the Fermi Paradox rooted in fundamental constants and testable through both terrestrial infrastructure monitoring and next-generation phase-sensitive astronomy.

4. Conclusion

We have derived and applied the Universal Coherence Constant $K=e^2/\left(4\pi {\epsilon }_0{\hslash }^2\right)\approx 2.08\times {10}^{40}{\mathrm{kg}}^{-1}{\mathrm{m}}^{-1}$, which quantifies the fundamental tension between electromagnetic interaction strength and gravitational loop action. This constant predicts a dimensionless phase parameter $\Xi \left(R\right)=K·M_{\mathrm{EM}}\left(R\right)·R$ that governs the stability boundary for decoherent information systems at any scale.

Our framework makes four primary contributions:

4.1. Resolution of the Fermi Paradox

The six-decade null result of infrared SETI surveys [5,6,7] is explained not by the rarity of advanced civilizations but by a universal physical constraint. Dyson spheres operating in decoherent regimes (electron-based, irreversible computation) exceed the coherence boundary by $\Xi \sim {10}^{63}$, resulting in collapse timescales of $\sim 0.36$ milliseconds—rendering such structures physically impossible. Advanced civilizations must transition to coherent (photon-based, reversible) architectures to harness stellar-scale energy, but this transition eliminates the thermal signatures classical SETI searches for. Type II and Type III civilizations exist but are gravitationally and electromagnetically invisible, detectable only via phase-sensitive methods that have not yet been deployed at scale.

4.2. Explanation of Terrestrial AI Infrastructure Crisis

The current “power quality crisis” in hyperscale data centers [14,15]—characterized by harmonic distortion, voltage microbursts, and thermal runaway—represents the first empirical manifestation of decoherence pressure in a non-astronomical system. Modern AI facilities operate at $\Xi \sim {10}^{25}$, far above the natural vacuum stability threshold ($\Xi =1$), surviving only through material containment (silicon lattice strength, active cooling, power conditioning). The observed anomalies are not engineering failures but physics limits: fermionic charge carriers approaching their phase-alignment capacity. This validates our theoretical predictions in a controllable, measurable terrestrial context.

4.3. Reinterpretation of Dirac’s Large Numbers

The appearance of $\sim {10}^{39}$-${10}^{40}$ in diverse physical contexts, from the ratio of electromagnetic to gravitational forces to the age of the universe in atomic units, has been noted since Dirac’s Large Number Hypothesis [17,18]. We propose that these are not coincidences or evidence of time-varying constants, but manifestations of a single underlying principle: the maximum sustainable electromagnetic complexity before coherence-driven or gravitational phase transitions. The coherence constant K quantifies this boundary directly, explaining why the same numerical factor governs atomic structure, cosmic evolution, and the limits of technological intelligence.

4.4. Testable Predictions

Our framework generates falsifiable predictions across multiple domains:

• Data center monitoring: Phase parameter $\Xi$ should correlate with power quality metrics (THD, voltage transients, thermal instabilities). Facilities approaching higher $\Xi$ values will exhibit stronger decoherence signatures.
• Quantum computing advantage: Systems with higher intrinsic coherence times (larger $\tau$) should demonstrate superior scalability, not merely through quantum algorithmic speedup but through fundamental avoidance of decoherence pressure.
• Anomalous black hole populations: Small black holes ($M\sim {10}^{18}$-${10}^{22}$ kg, $r_s\sim {10}^{-9}$-${10}^{-5}$ m) near habitable zones with recent formation ages ($<{10}^6$ years) would constitute archaeological evidence of failed Type I civilizations that exceeded decoherence limits without achieving coherence transition.
• Phase-sensitive SETI: Next-generation searches using quantum interferometry, fine-structure constant monitoring, and vacuum coherence probes should detect Type II civilizations currently invisible to classical methods. The predicted detection inversion (Figure 5) provides a roadmap for instrument design.
• Scaling limits: AI systems should exhibit hard performance plateaus at specific $\Xi$ thresholds that cannot be overcome through additional power or spatial distribution, but only through coherence enhancement (error correction, reversible gates, quantum architectures).

4.5. Implications for Humanity’s Trajectory

We predict that humanity stands at a critical juncture. Current AI scaling trends [9,10] push toward higher power consumption and larger facilities—precisely the direction that accelerates approach to the $\Xi \ge 1$ boundary (the “inverse trap” shown in Figure 3). The power quality crisis is our first warning that decoherence pressure is no longer negligible.

We face two evolutionary pathways:

Path 1: Continued decoherent expansion. Scaling classical AI through larger data centers and higher power consumption. This path terminates at material containment limits (Figure 2), with catastrophic infrastructure failures as $\Xi$ approaches unity. Attempting planetary-scale decoherent Artificial Intelligence would result in collapse into a mode 2 black hole [13].

Path 2: Coherence transition. Pivoting toward reversible computation, quantum architectures, and phase-locked information processing. This path allows continued scaling by increasing $\tau$ rather than power, enabling the ${\Xi }_{\mathrm{eff}}=\Xi /\tau$ suppression shown in Figure 4. This is not merely an efficiency optimization but a structural necessity for continued technological advancement.

The current engineering push toward quantum computing, neuromorphic architectures, and reversible logic gates may represent humanity’s unconscious recognition of this constraint, which is a collective evolutionary response to approaching a fundamental physical boundary.

The Universal Coherence Constant reveals a universe where intelligence, far from being exempt from physical law, is subject to precise thermodynamic and gravitational constraints. The “Tim Taylor hypothesis” that advancement means consuming more power fails at the boundary defined by K. Beyond this threshold, progress requires not amplification but alignment; not force but phase; not heat but coherence.

The silence of the cosmos is not a puzzle but a prediction. Advanced intelligence does not advertise itself through waste heat—it transcends waste entirely. The challenge for 21st-century SETI is not to build larger radio telescopes, but to develop instruments sensitive to coherence rather than chaos, to phase rather than power, to the quantum correlations that persist when all classical signatures have vanished.

Humanity’s own infrastructure crisis, which include our data centers overheating, our grids destabilizing, our power systems failing under AI load—is not an engineering problem awaiting a bigger transformer. It is a physics limit announcing itself. We have reached the boundary. What lies beyond is not “more power,” but a fundamentally different relationship with energy, information, and the structure of spacetime itself.

The choice is not whether to transition, but whether to do so deliberately—guided by understanding of the constraints or catastrophically, after infrastructure failures force the issue. The Universal Coherence Constant does not dictate our future, but it defines the physics within which that future must unfold.