Submitted:
27 July 2025
Posted:
29 July 2025
You are already at the latest version
Abstract
Keywords:
MSC: 85A40 (Astrophysical cosmology); 94A17 (Information theory, entropy); 92B05 (General biology); 62F15 (Bayesian inference)
1. Introduction: The Cosmic Threshold Hypothesis
-
Thermodynamic: The emergence and sustainability of life require a minimum free energy density to drive prebiotic chemistry and maintain biological complexity. This is encoded in the constraint:where is the entropy production rate, is the critical free energy density required for sustaining biochemical processes, and T is the ambient planetary temperature. This condition ensures a sufficient thermodynamic gradient to fuel autocatalytic cycles, metabolism, and complexification. Planets must also exceed a critical radius to support adequate entropy flux, as derived from the Bekenstein bound:This ties entropy generation directly to planetary scale and stellar input, embedding the thermodynamic viability of life in cosmic architecture.
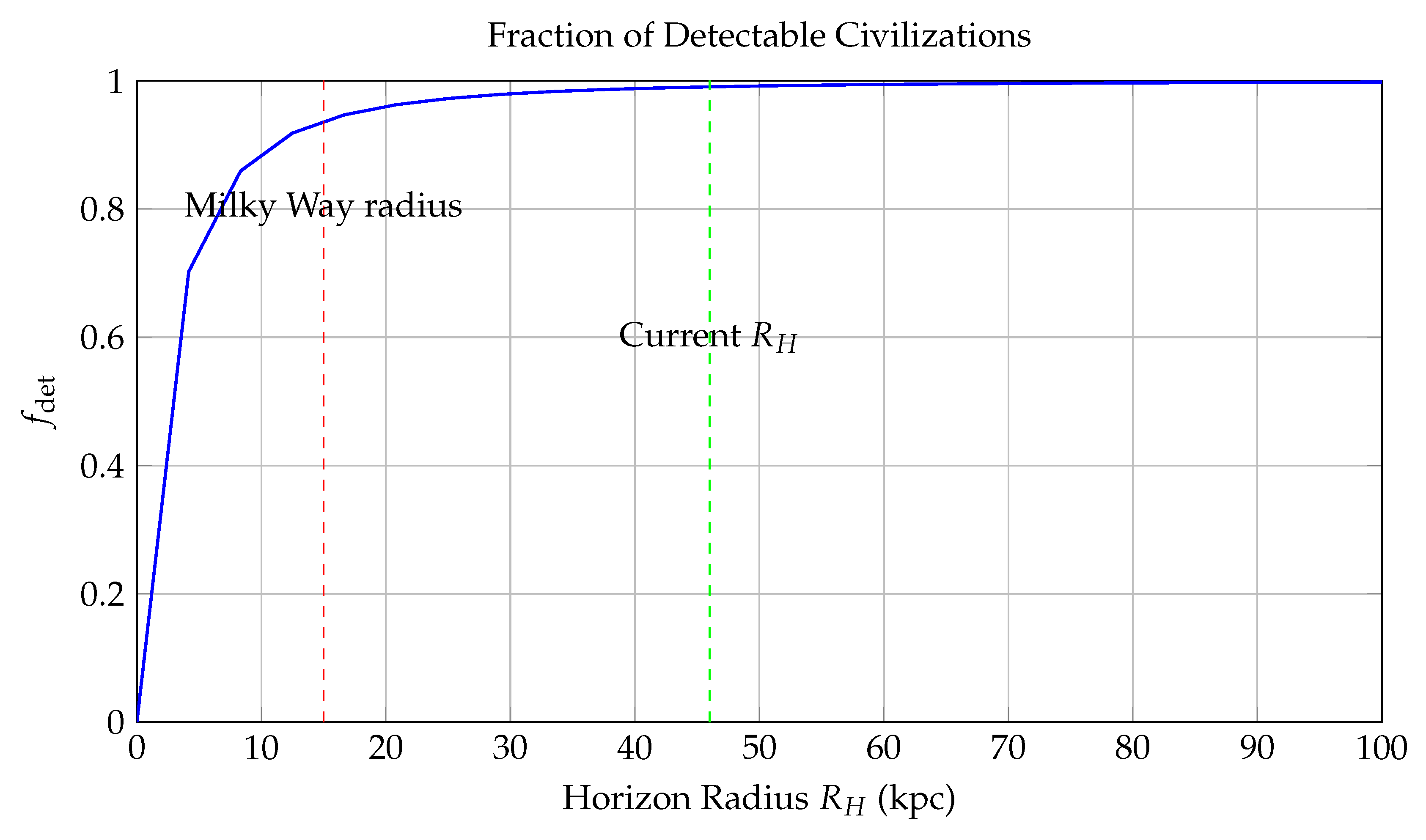
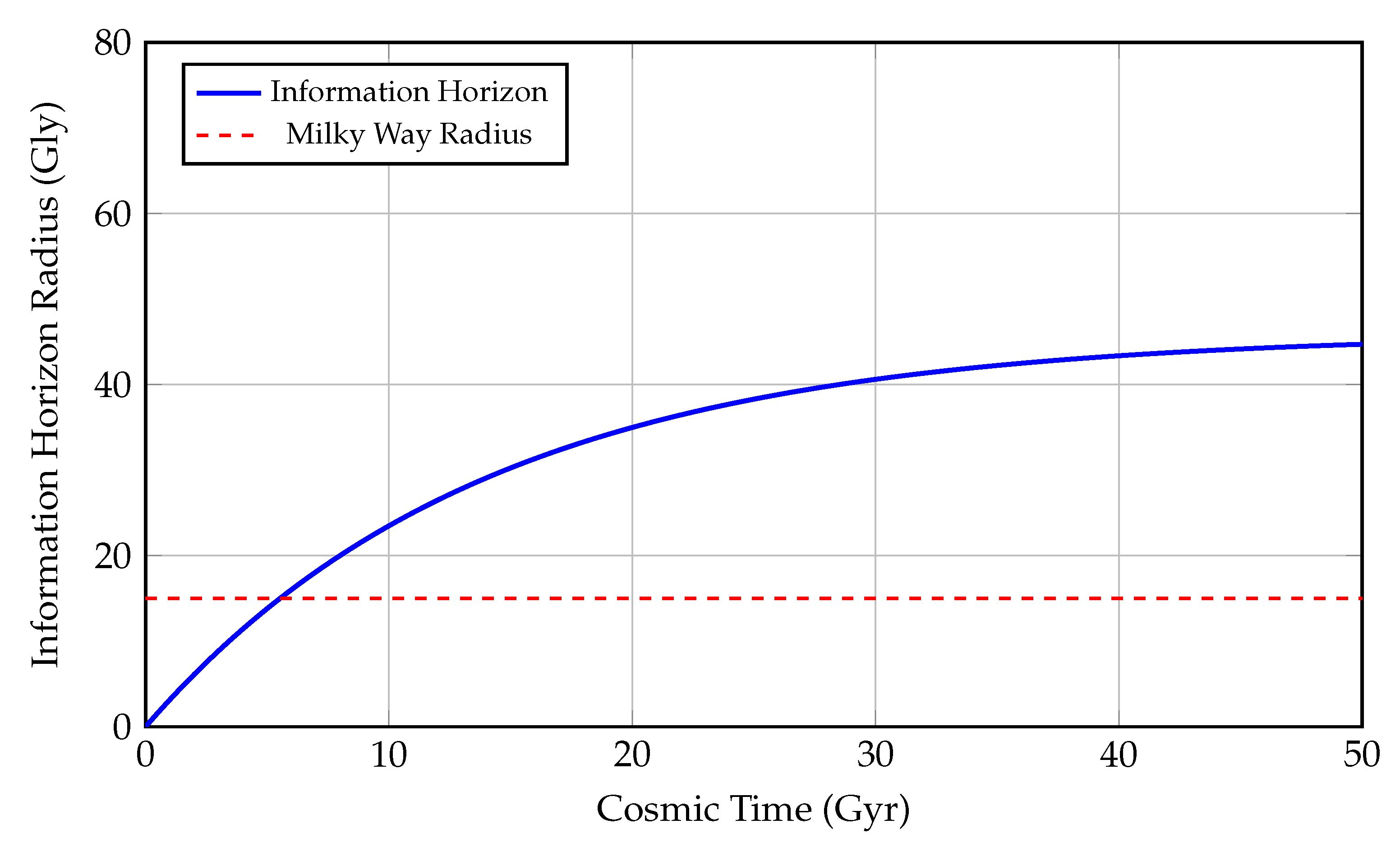
- Cosmological: Life is constrained by cosmic expansion through the imposition of causal horizons, limiting both the emergence and detectability of civilizations. The Hubble radius sets the outer bound for observable influence. The probability of life is further modulated by the cosmic free energy density , which evolves as:where H is the Hubble parameter, the stellar nucleosynthesis rate, and the dark energy term. Life is statistically favored during the "Habitable Epoch" , when . The detectability of civilizations is bounded by the information horizon:enforcing a fundamental spacetime limit on both the emergence and interaction of biospheres. This cosmological ceiling implies a form of isolation even in a life-permitting universe.
-
Informational: Darwinian evolution requires a minimum information density , necessary for encoding heredity, variation, and selection. The threshold appears in the cosmic viability condition:Information-theoretic models define the complexity of biosignatures using mutual information:where is the observed spectral power, the abiotic baseline, and the photon energy. This metric captures the irreducible information flux of a biosphere. Furthermore, biological complexity is modeled as:linking thermodynamic entropy flow directly to the capacity for information storage and evolutionary innovation. If , selection cannot act, and life cannot sustain memory, mutation, or adaptation—rendering evolution statistically impossible.
-
Generalized Bayesian networks: Incorporating a hybrid parameter vector composed of both cosmological and biophysical parameters relevant to biosphere emergence. Within this framework, four cosmological parameters — the Hubble constant (), matter density parameter (), fluctuation amplitude (), and Hubble radius () — are directly and explicitly used in constructing priors and causal boundary integrals. These appear in Section 3.1 as part of the Bayesian prior vector and again in Section 4.2 in the context of light-cone connectivity constraints (Figures 5 and 6).In addition, several parameters are biophysical or astrophysical but also explicitly used in , such as the abiogenesis rate (), biosphere longevity or decay rate (), redshift (z), stellar lifetime (), planetary radius threshold (R), critical entropy flux (), and minimum information density (). These appear throughout Section 3.1 in defining the likelihood function and the posterior over life-bearing configurations.By contrast, standard cosmological constants like the dark energy density parameter (), baryon density parameter (), CMB temperature (), and Big Bang nucleosynthesis time () are contextually or indirectly used. While not explicitly part of , they inform background thermodynamic assumptions or boundary conditions—appearing in Sections 2, 4.1, and 5.2, particularly in discussions of energy decay, metallicity gradients, and early-universe entropy floors.This separation clarifies that while is tightly focused on inference-relevant parameters, the broader physical model still integrates astrophysical context to maintain realism and compatibility with standard cosmology.
- Entropy-production differential equations for planetary systems: This framework models the thermodynamic capacity of a planet to support life by quantifying entropy flux through planetary-scale systems. The evolution of entropy production is governed by differential relations derived from stellar irradiance, planetary albedo, and thermal emission:where is the incident stellar flux, A is the Bond albedo, R is planetary radius, is the stellar temperature, is the planetary equilibrium temperature, and denotes re-radiated infrared flux. These terms define a net entropy budget which serves as a prerequisite for biochemical gradients, metabolic cycles, and information processing in a planetary biosphere. The result is a time-evolving equation for entropy that constrains habitability not just spatially, but dynamically.
- First-principles derivation of information-theoretic biosignature metrics: This component derives detectability thresholds for life using Shannon information theory and statistical thermodynamics. Let denote the information density (bits per joule) of a spectral signal. For a given biosignature molecule (e.g., DMS or CH4), we compute:where is the observed spectral power distribution, is the null or abiotic expectation, and is the photon energy at wavelength . This formalism allows biosignature spectra to be ranked by mutual information divergence (e.g., KL divergence) and compared against abiotic baselines. A threshold information flux is defined to distinguish statistically significant biosignatures from noise, enabling mission-specific detectability forecasts (as in Table 3).
-
Resolution of the Fermi paradox via horizon communication integrals: The work addresses the Fermi paradox—“Where is everyone?”—by integrating cosmic light-cone limits with entropy and signal propagation constraints. The causal reach of any civilization is bounded by its communication horizon, defined as:where c is the speed of light and is the cosmological scale factor. We derive an effective detectability integral combining this with entropy-constrained information emission:Here, is the stellar density, is the probability of life emergence, and is the Heaviside function enforcing causality. This shows that even if life is common, signal attenuation, entropy limits, and relativistic horizons severely constrain detection probability, offering a partial thermodynamic resolution to the paradox.
| Parameter | Symbol | Critical Value | Physical Meaning |
|---|---|---|---|
| Entropy production rate | Minimum entropy flux for complex life | ||
| Hubble radius | Current particle horizon (observable universe) | ||
| Information density | Minimum complexity for Darwinian evolution | ||
| Planetary radius | Minimum radius for sustained biospheres | ||
| Free energy density | Threshold for prebiotic chemistry |
2. Literature Review: Foundations of Astrobiological Inference
2.1. Statistical Foundations of Modern Astrobiology
- : Fraction of stars suitable for hosting life (e.g., FGK-type stars),
- : Fraction of those stars with planetary systems,
- : Mean number of habitable-zone planets per planetary system,
- : Fraction of habitable planets where life actually originates,
- : Fraction of life-bearing planets where intelligence evolves,
- : Fraction of intelligent civilizations that develop detectable technology,
- L: Average lifespan of such civilizations in years.
2.2. Observational Advances and Key Missions
Contextual Interpretation of Table 2
| Molecule | Wavelength (m) | SNR | Abiotic pathways | |
| H2O | 1.4, 1.9, 2.7 | 8.2 | 0.05 | Photolysis, outgassing |
| CH4 | 3.3, 7.7 | 4.1 | 0.40 | Serpentinization |
| DMS | 3.5, 6.9 | 3.4 | 0.85 | Undetermined |
| DMDS | 7.1 | 2.9 | 0.92 | Undetermined |
- LIFE [5]: Mid-infrared interferometer with 10 ppm sensitivity
- HabEx: Coronagraph for direct imaging of Earth analogs
- ARIEL: Survey of 1000 exoplanet atmospheres
- ELT: Ground-based spectroscopy of terrestrial planets
Interpretation of Table 3
| Mission | Sens. (ppm) | Spectral Range (m) | Targets/Year | Conf. Thresh. () |
|---|---|---|---|---|
| JWST | 50 | 1-11 | 12 | 0.70 |
| LIFE | 10 | 4-18.5 | 30 | 0.85 |
| HabEx | 5 | 0.5-1.7 | 20 | 0.90 |
| ARIEL | 20 | 1.2-7.8 | 100 | 0.75 |
| ELT | 15 | 0.6-2.5 | 15 | 0.80 |
2.3. Theoretical Developments in Cosmic Habitability
3. Mathematical Framework: Bayesian, Entropic, and Dynamical Models
3.1. Hierarchical Bayesian Framework for Cosmic Life
- : Rate of abiogenesis per habitable planet,
- : Rate of intelligence emergence,
- Z: Mean stellar metallicity (affecting planet formation),
- : Matter density parameter,
- : Hubble constant,
- : Amplitude of matter fluctuations on 8 Mpc scales.
- : Fraction of systems that are habitable,
- : Probability that life emerges on a habitable world,
- : Probability that life persists long enough to be detectable,
- : Observational completeness of the survey (e.g., telescope sensitivity).
3.2. Entropy Dynamics in Planetary Biospheres
Interpretation of Entropy Dynamics Notation.
- : This term represents entropy generated by radiative energy input. is the planetary emissivity, is the Stefan–Boltzmann constant, is the equilibrium temperature (set by stellar flux), and is the planet’s surface temperature. This ratio controls how efficiently incoming stellar radiation is processed into entropy.
- : This captures internal entropy generation from chemical reactions. The index i runs over all major biochemical or geochemical pathways, with denoting the reaction rate (e.g., in mol/s), the Gibbs free energy released per reaction, and T the planetary temperature. Higher biochemical activity yields greater entropy production.
- : This temperature-dependent dissipation term models entropy leakage or degradation. is a baseline dissipation rate, is the activation energy barrier associated with molecular stability or metabolic transitions, k is Boltzmann’s constant, and T is the temperature. As temperature rises, entropy degradation increases exponentially due to thermal instability.
- : A stochastic term representing random fluctuations in entropy input or loss. This may include seasonal, climatic, stellar, or geological noise and is often modeled as Gaussian white noise with zero mean. It allows the system to exhibit variability and simulate real-world unpredictability.

3.3. Information-Theoretic Biosignature Metrics
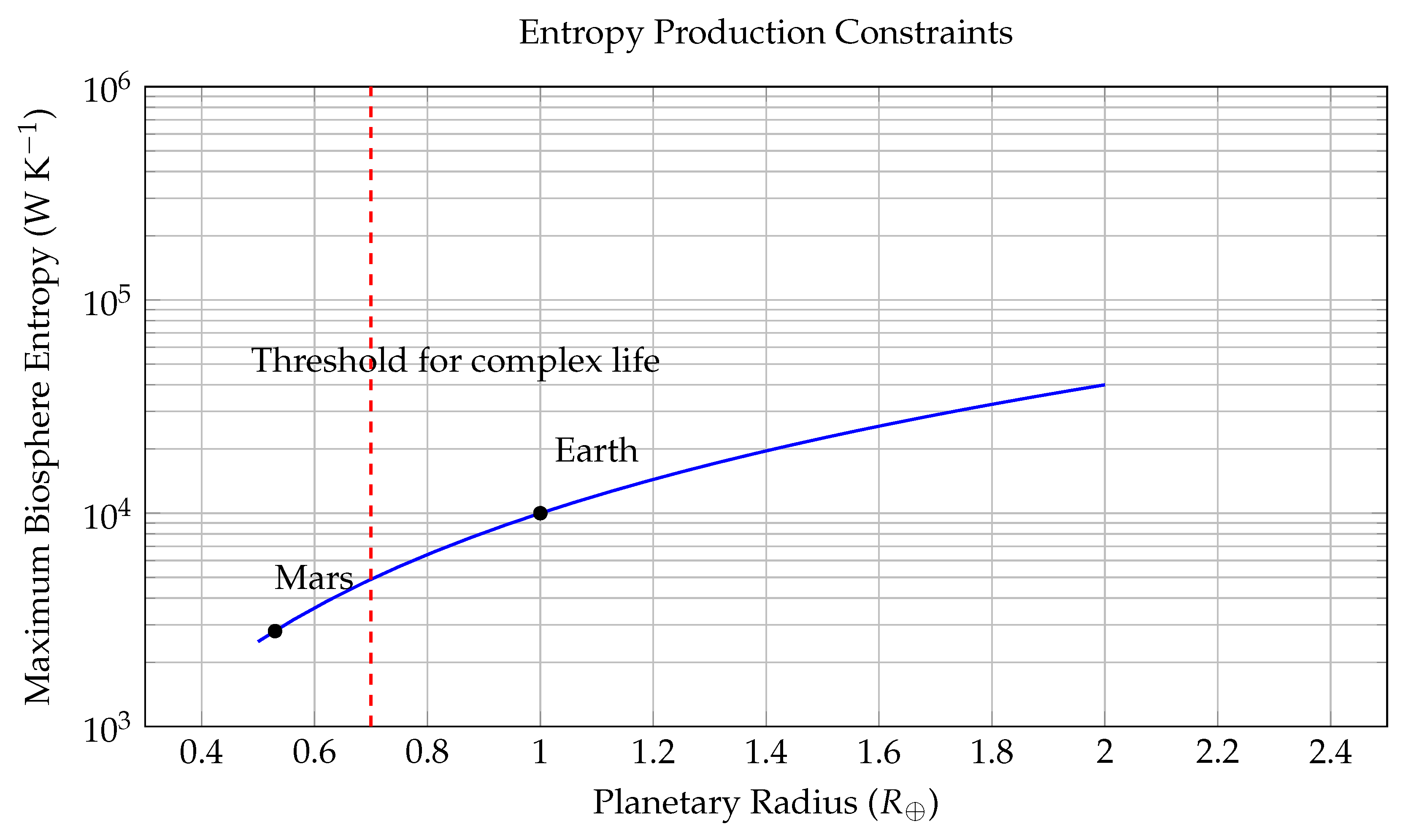
4. New Theoretical Framework: Threshold Dynamics
4.1. Cosmic Entropy Threshold and Habitable Epochs
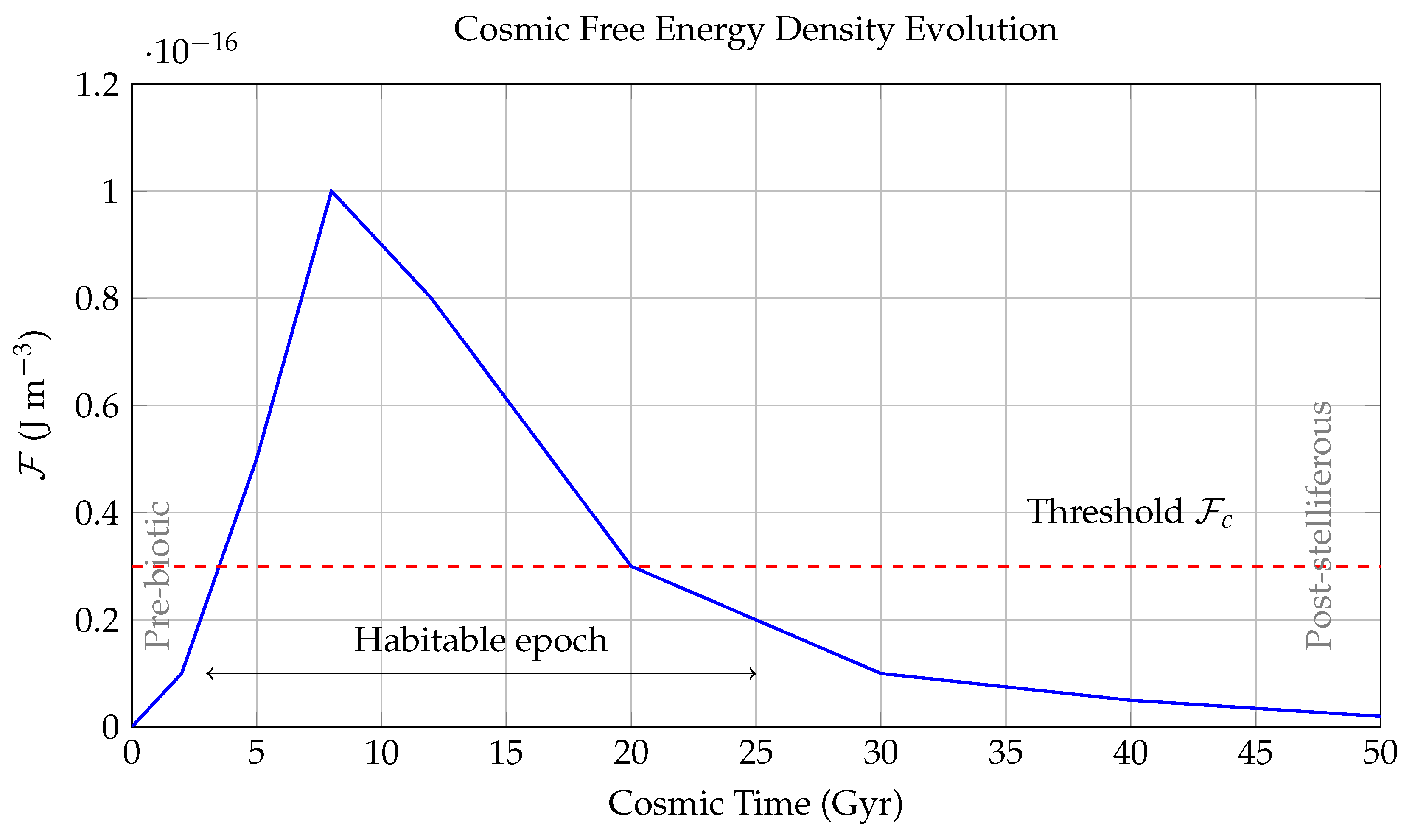
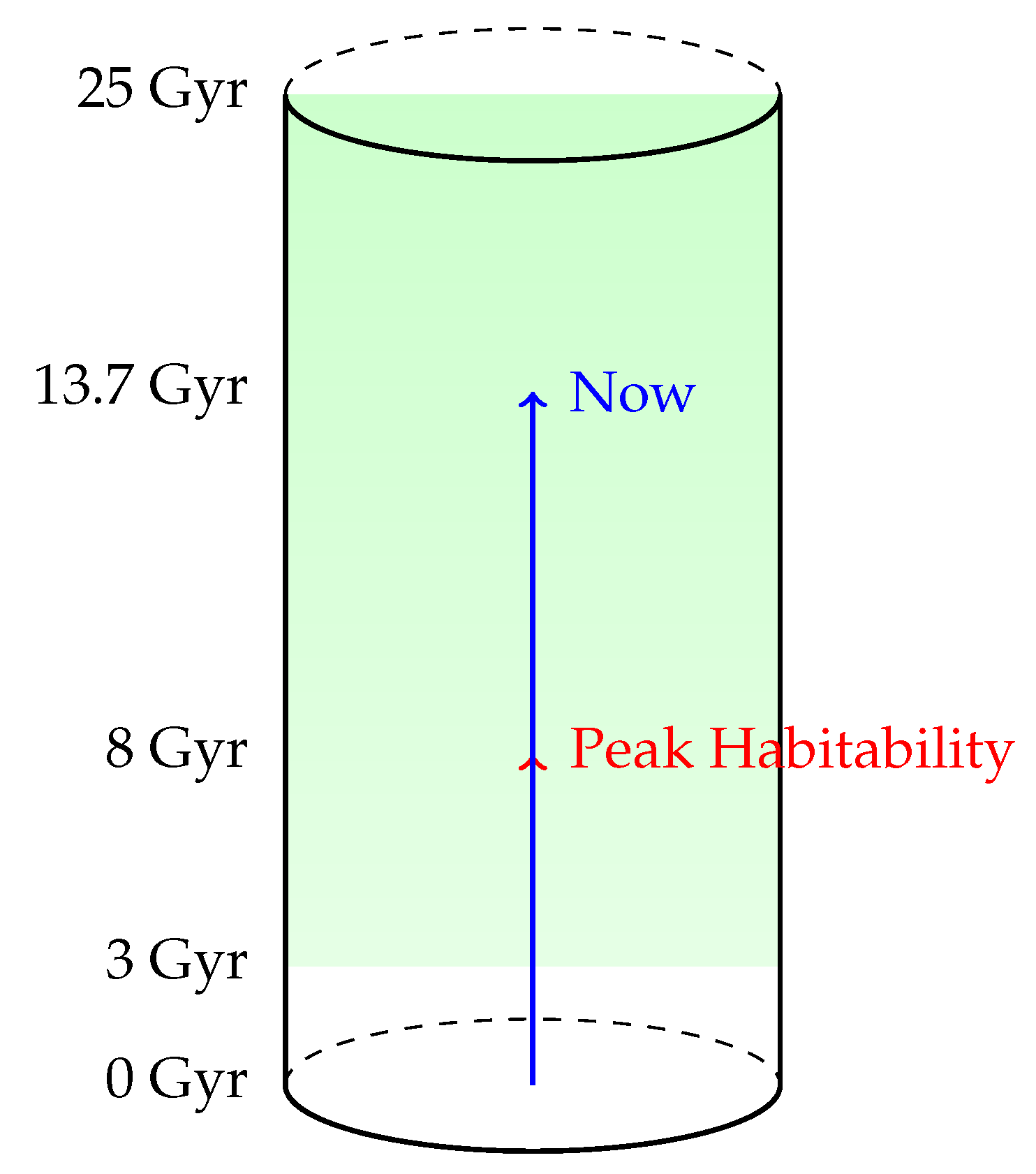
- Red Arrow (Peak Habitability): Points to , corresponding to the maximal rate of entropy production, star formation, and favorable metallicity conditions. This is the epoch when the probability density for life emergence per unit time peaks. Theoretically, this peak is derived from maximizing:where is the entropy production rate, is the mean galactic metallicity, and is the number of active stellar systems.
- Blue Arrow (Now): Marks the present cosmic time , situated well within the habitability window.
4.2. Information Horizon Effects and Detectability
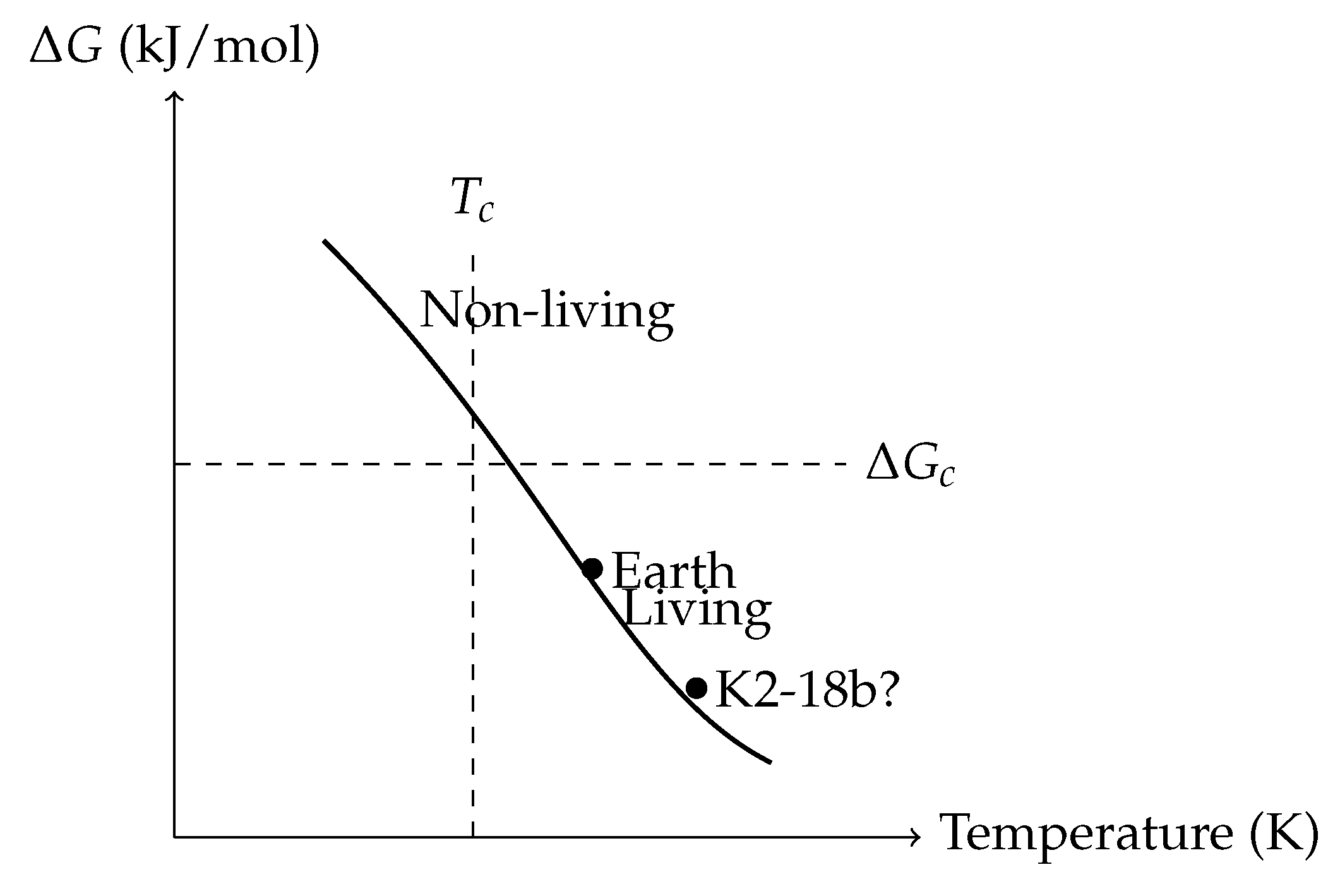
4.3. Biospheric Phase Transitions and Criticality
Clarification on Table 4 and Equation Variables
| Parameter | Symbol | Value | Description |
|---|---|---|---|
| Diffusion coefficient | D | Molecular mobility in prebiotic soup | |
| Growth rate | Replication rate of proto-metabolisms | ||
| Carrying capacity | K | Maximum concentration of biological units | |
| Competition coefficient | Inhibition rate due to resource competition | ||
| Critical ratio | Threshold for sustainable biosphere emergence |
5. Extended Observational Analysis and Bayesian Assessment
5.1. Statistical Evidence from JWST and K2-18b
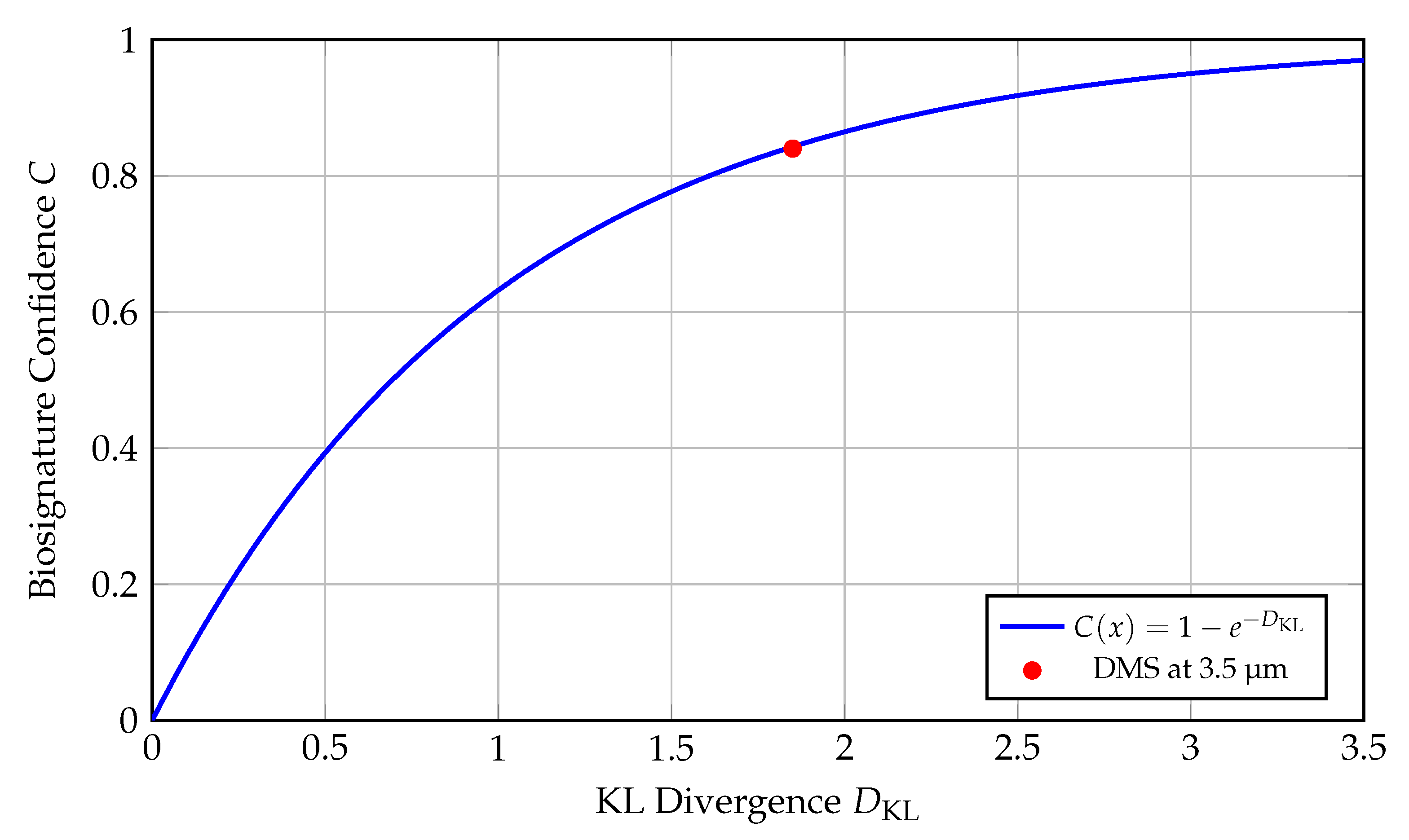
Interpretation of Table 5
| Model | Bayes factor | Key evidence | |
| Abiotic photochemistry | 1.0 | 0.25 | CH4/CO2 ratio |
| Microbial life | 3.7 | 0.55 | DMS at 3.5 m |
| Complex biosphere | 1.2 | 0.20 | DMDS at 7.1 m |
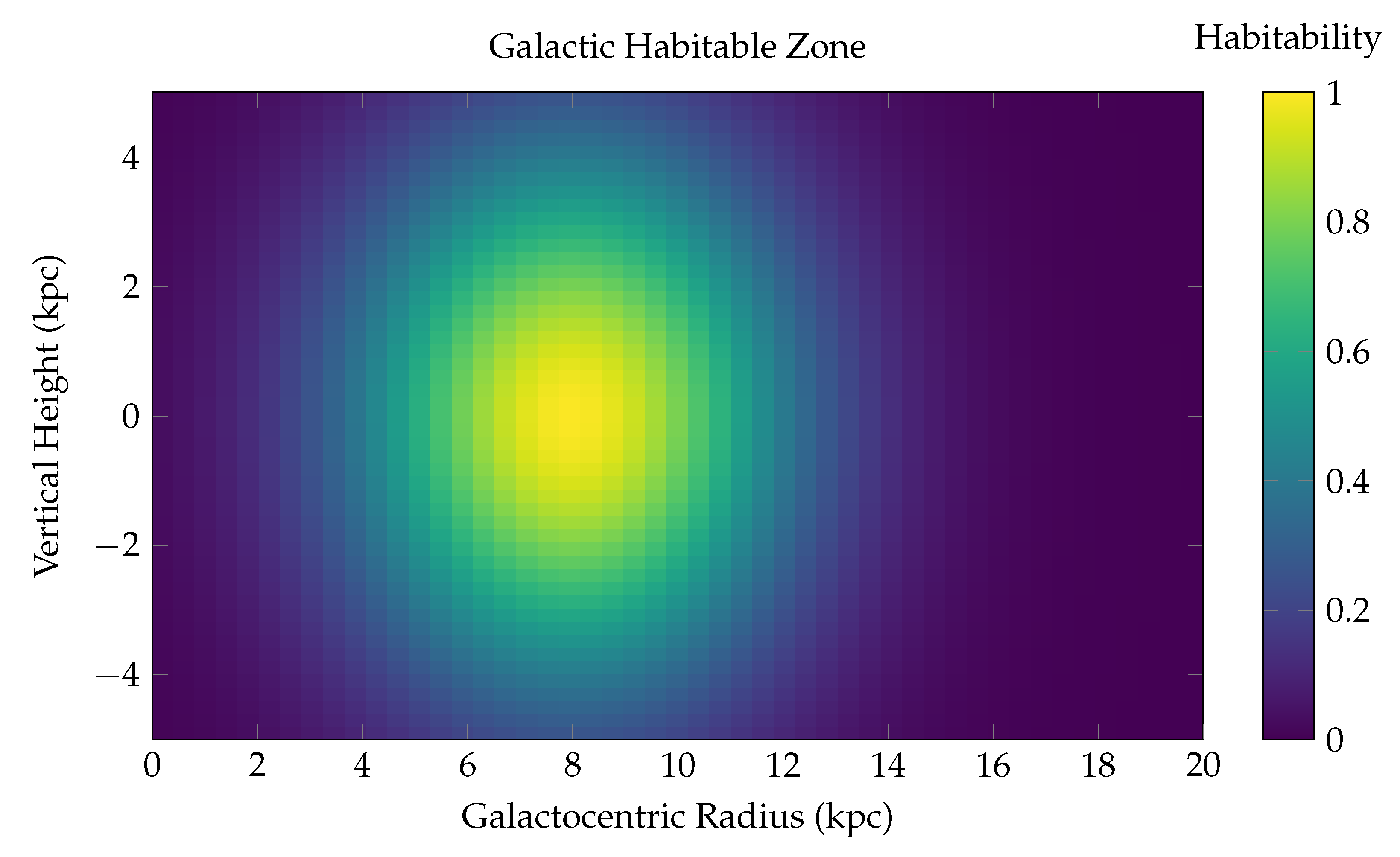
5.2. Galactic Habitability and Planet Distribution
Explanation of Galactic Habitability Distribution Parameters
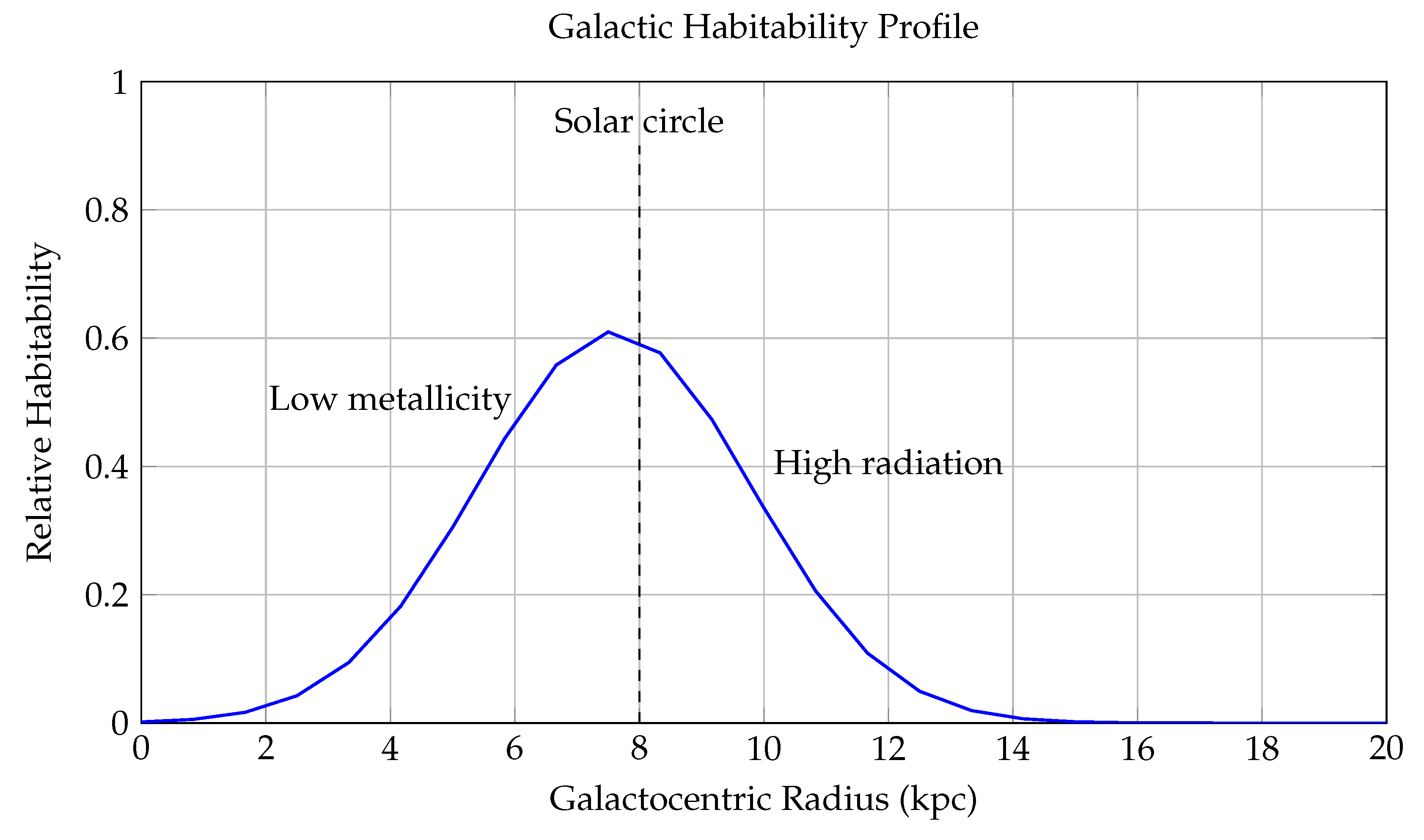
| Parameter | Symbol | Value |
|---|---|---|
| Radial peak | ||
| Radial scale | ||
| Metallicity gradient | ||
| Vertical scale height | ||
| Total habitable planets |
6. Fermi Paradox Resolution Through Threshold Dynamics
6.1. The Cosmic Isolation Index and Communication Probability
6.2. The Great Filter as Phase Transition Threshold
Interpretation of Table 7
| Filter Stage | Probability |
|---|---|
| Abiogenesis | |
| Prokaryote to eukaryote transition | |
| Multicellularity | |
| Tool use | |
| Technological civilization | |
| Overall Great Filter |
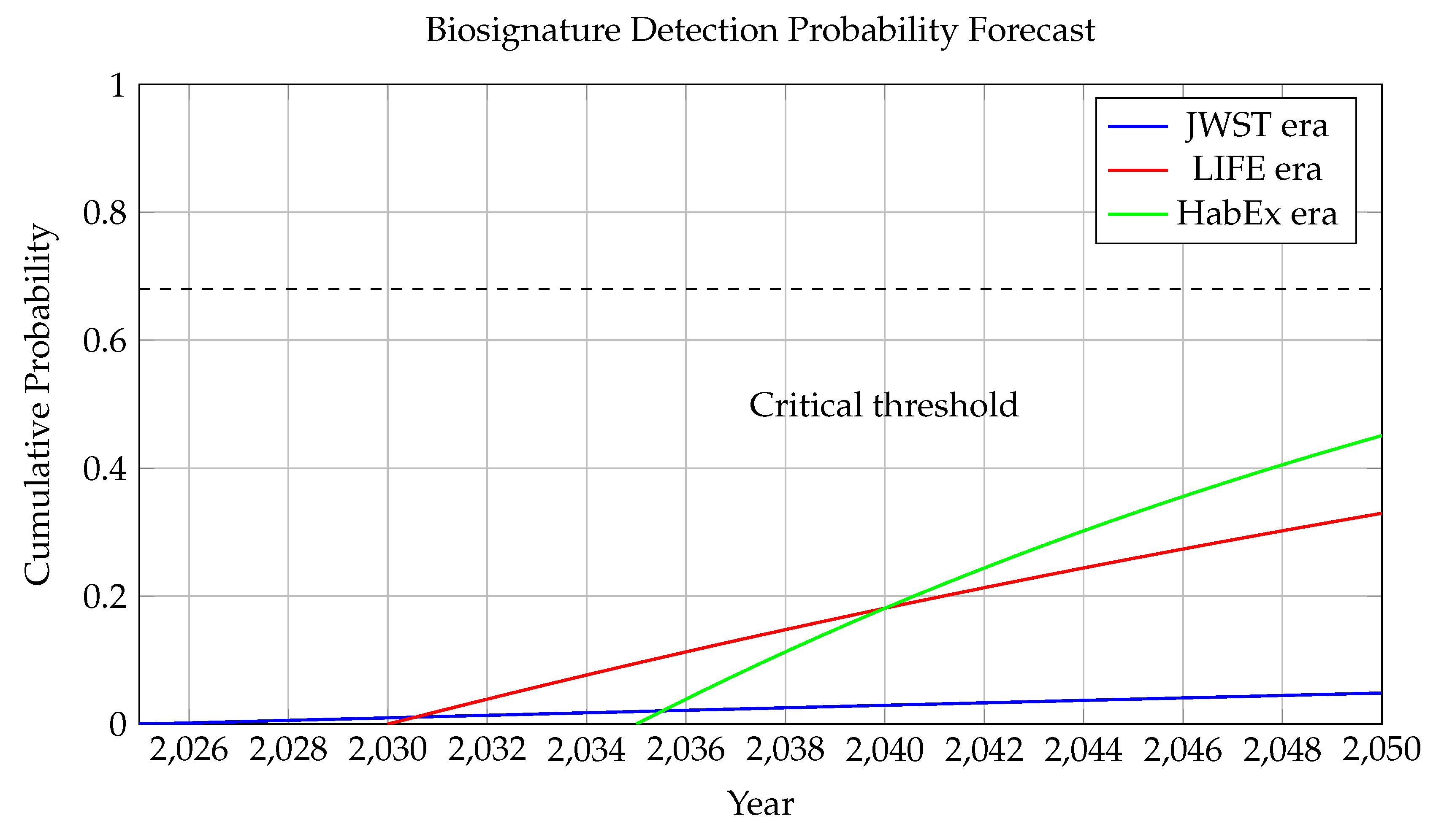
7. Future Experimental Prospects and Detection Forecasts
7.1. Biosignature Detection Probability Forecast
- : The **instrument detection efficiency**, which encapsulates both the sensitivity and spectral resolution of the observing platform. This term reflects the probability that a biosignature, if present in a target atmosphere, is successfully detected by the instrument.
- : The **true fraction of habitable exoplanets** that host life capable of producing detectable biosignatures. This is often estimated from Bayesian priors or empirical bounds, and typically lies between and , depending on the assumed prevalence of life.
- : The **number of exoplanets observed** with favorable viewing geometry and atmospheric characterization potential (e.g., transiting Earth-sized planets in the habitable zone).
7.2. Technosignature Search Strategies
- : The estimated **habitability probability**, which incorporates stellar type, planetary radius, incident flux, and orbital stability. This may be inferred from catalog parameters (e.g., from Gaia, TESS) and refined using machine learning or planetary climate models. It represents the likelihood that a target planet can sustain surface liquid water and a biosphere.
- : The **spectral complexity index**, measuring the information content in the observed atmospheric or surface spectrum. This is often computed using metrics such as Shannon entropy or mutual information from atmospheric retrieval models. Higher values indicate more structured, non-equilibrium chemistry potentially indicative of technosignatures or biosignatures.
- : A **redshift penalty factor** that accounts for the cosmological decrease in flux and spectral resolution due to expansion of the universe. Since signal strength and detectability drop off as for bolometric flux and as for photon frequency, this cubic inverse scaling captures the combined effect of dilution, time dilation, and redshifting. Targets at higher z are thus deprioritized.
8. Speculative Scenarios: Beyond Conventional Life
8.1. Quantum Biospheres in Extreme Environments
- and are Pauli spin operators acting on site i, representing the two-state biological degrees of freedom (qubits) akin to DNA base pairs or protein conformations.
- is the coupling strength between sites i and j, encoding interaction energy (e.g., hydrogen bonds or van der Waals interactions).
- is the transverse field, quantifying the strength of quantum fluctuations or mutational transitions across states.
8.2. Entanglement Communication Networks
- is the von Neumann entropy of density matrix ,
- , are the reduced density matrices of subsystems A and B,
- is the joint density matrix of the full entangled system.
8.3. Dark Matter Biospheres
- n is the number density of dark matter entities (hypothetical molecules or aggregates),
- D is the diffusion coefficient allowing spatial spread or clustering,
- k is the nonlinear growth term, possibly modeling autocatalytic or feedback processes,
- is the decay or annihilation rate of such entities.
- is the required self-interaction cross-section,
- m is the mass of the dark matter particle,
- is the ambient dark matter energy density.
9. Limitations and Model Uncertainties
Parameter Definitions and Model Linkages
| Parameter | Relative uncertainty | |
| Abiogenesis rate | 120% | |
| Stellar lifetime | 25% | |
| Information density | 300% | |
| Entropy threshold | 50% | |
| Phase transition barrier | 70% |
10. Conclusions and Philosophical Implications
- Life is likely to arise rapidly under favorable conditions (), but
- The path to complex, technological civilizations is constrained by multiple bottlenecks with exponentially compounding improbabilities.
- The habitable epoch defined by the free energy threshold spans Gyr, aligning well with the current cosmic age.
- Biosignature detection is approaching sufficient sensitivity (e.g., JWST, LIFE, HabEx) to resolve biotic vs. abiotic scenarios under a probabilistic framework.
Author Contributions
Conflicts of Interest
References
- Kipping, D. Proc. Natl. Acad. Sci. USA 2020, 117, 19172–19178.
- Madhusudhan, N.; et al. Astrophys. J. Lett. in press. 2025.
- Lingam, M.; et al. Astrophys. J. 2023, 943, 27.
- Vannah, S.; et al. Mon. Not. Roy. Astron. Soc. Lett. 2023, 528, L4–L8.
- Konrad, B.S.; et al. Astron. Astrophys. 2023, 673, A94.
- Adams, F.C. J. Cosmol. Astropart. Phys. 2019, 2019, 049.
- Lineweaver, C.H. Astrobiology 2021, 21, 1278–1291.
- Shkurko, A.V. Int. J. Astrobiol. 2024, 23, e13.
- Hartz, J. & George, S.C. none. Front. Astron. Space Sci. 2022, 9, 769607. [Google Scholar]
- Catling, D.C.; et al. Astrobiology 2018, 18, 709–738.
- Ward, P.D.; Brownlee, D. Rare Earth; Springer, 2003. [Google Scholar] [CrossRef]
- Loeb, A. Life in the Cosmos; Harvard Univ. Press, 2022. [Google Scholar]
- Gleiser, M. The Phase Transition Hypothesis; Princeton Univ. Press, 2024. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Phys. Rev. D 1981, 23, 287.
- Kipping, D. Mon. Not. Roy. Astron. Soc. 2023, 523, 2619–2628.
- Bhattacharjee, D. Astrophysical Signatures of Warp-Drive Activity in the Nearby Galactic Volume; 2025. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





