The Infinite Universe Framework (IUF): An Infinite, Non-Expanding Cosmos Grounded in Physical Law and Photon Energy Transfer

1.0. Introduction

The Infinite Universe Framework (IUF) offers a comprehensive alternative to standard cosmological models by proposing that the universe is infinite in both space and time and governed by consistent physical laws rather than by initial conditions or boundary-driven dynamics. Rather than relying on metric expansion, dark energy, or inflation, the IUF explains observed redshift and background radiation through well-characterized physical processes occurring within a structured, evolving cosmos.

This framework integrates two core components:

• The Physical Universe Theory (PUT), which holds that the cosmos is structured, eternal, and regulated by persistent physical laws across all scales and epochs. Under PUT, large-scale coherence and thermodynamic cycling emerge from the interaction of matter and radiation over infinite durations, without requiring singular origins, inflation, or cosmic boundaries.
• The Cumulative Photon Energy Transfer (C-PET) model, which proposes that redshift arises from small, cumulative energy losses experienced by photons as they traverse intergalactic media. These losses result from infrequent, direction-preserving interactions with plasma, dust, and filamentary structures, an interpretation supported by Voyager plasma data [4] and consistent with known principles of quantum electrodynamics.

This model further introduces the Photon–Medium Microwave Thermal Field (PMMTF) as a testable hypothesis: a diffuse microwave background that may emerge from the cumulative re-radiation of energy lost by photons during intergalactic transit. Rather than attributing the microwave background to a primordial origin event, the PMMTF hypothesis proposes a continuous, distributed energy exchange process. Whether this mechanism can account for the observed precision, isotropy, and energy density of the cosmic microwave background (CMB) is examined in Section 7 and Appendix E.

The IUF thus seeks to reinterpret cosmological observables, not by rejecting the data, but by reexamining the underlying assumptions. It draws upon redshift surveys, high-resolution galaxy observations [1,2,3], interstellar plasma measurements [4], and cosmic structure mapping [10] to propose a model grounded in known physics and falsifiable predictions. By replacing speculative early-universe constructs with physically observable, cumulative interactions, the IUF opens a path toward a cosmological theory rooted in physical law rather than untestable conditions.

While this manuscript proposes a comprehensive framework, several physical derivations, particularly the quantum mechanical foundations of the C-PET interaction, remain open areas for continued development and future collaboration.

This framework is presented not as a definitive replacement for ΛCDM, but as a physically grounded and testable hypothesis that invites collaborative scrutiny, empirical validation, and iterative refinement. All simulation parameters and computational protocols are documented to enable independent replication and critical evaluation.

2.0 Core Assumptions of The Infinite Universe Framework (IUF)

The Infinite Universe Framework (IUF) is founded upon a set of core assumptions that distinguish it from expansion-based cosmologies such as the Lambda Cold Dark Matter (ΛCDM) model, which is closely associated with the Big Bang theory. These IUF assumptions are grounded in observed phenomena, supported by known physical laws, and deliberately exclude speculative constructs not directly confirmed by empirical evidence.

• The Universe is Infinite in Space and Time IUF assumes that the cosmos has no spatial boundary, origin point, or temporal beginning. This infinite, eternal structure contrasts with the finite-age assumptions of Big Bang cosmology. Structure formation, redshift, and background radiation can be explained without invoking a singular origin or inflationary episode.
• Cosmological Observations Arise from Physical Interactions, Not Expansion Redshift, surface brightness dimming, and time dilation are treated as emergent effects of photon interactions with cosmic media, rather than consequences of metric expansion. The observed coherence of spectral lines across vast distances supports the hypothesis that photons are not stretched by space itself but undergo cumulative, non-scattering energy transfer through infrequent interactions with intervening media. In this view, the same underlying mechanism responsible for redshift also contributes energy to the intergalactic medium, which eventually re-emits it as a diffuse, thermalized background field, characterized within IUF as the Photon-Medium Microwave Thermal Field (PMMTF), rather than as a relic of a primordial explosion.
• The Cosmic Medium Is Structurally Rich and Intermittent IUF posits that the universe is permeated by diverse, low-density structures, such as plasma [4], filaments [10], circumgalactic media (CGM), and interstellar matter [21,22,151], which cumulatively induce photon energy transfer over cosmological distances. These structures are unevenly distributed, and turbulent processes [41] in denser regions such as the interstellar medium may locally enhance photon–medium coupling, reinforcing the logic of the Segmented Medium Model (SMM), which models redshift accumulation as a function of local medium properties.
• Redshift Is Accumulative and Compounding Rather than occurring instantaneously or through a global scale factor, as in the ΛCDM model [42,43,44], redshift in IUF accumulates through a series of infrequent interactions with intervening media. This allows for nonlinear scaling, logarithmic or exponential, depending on the distribution and density of cosmic structures along a photon's path.
• No Inflation, Dark Energy, or Dark Matter Are Required IUF does not rely on inflation [13,14,15,110], dark energy, or dark matter as explanatory mechanisms. Where ΛCDM invokes these constructs to align theory with observation, IUF contends that the phenomena attributed to them can be explained through established physical processes occurring within an infinite and structured universe.
• Known or Discoverable Physical Laws Apply Universally IUF assumes that the laws of physics, both currently known and those that may be discovered, apply uniformly across all space and time. This assumption rejects the need for exceptional rules or speculative physics to explain ancient or distant phenomena, asserting instead that cosmic processes emerge from consistent, universal principles.

These six assumptions form the theoretical foundation of IUF's two primary components: the Physical Universe Theory (PUT) and the Cumulative Photon Energy Transfer (C-PET) model. They also define the framework's falsifiability criteria: if redshift, surface brightness dimming, time dilation, and background radiation (characterized here as the PMMTF) cannot be reproduced through cumulative photon–medium interactions across structured cosmic media in an infinite universe, then the framework must be revised, or rejected.

3.0. The Physical Universe Theory (PUT)

The Physical Universe Theory (PUT), as a foundational component of the Infinite Universe Framework (IUF), asserts that the universe has no beginning, no end, and no spatial boundary. Time and space extend infinitely in all directions and epochs. Rather than originating from a singularity or explosive event [13,14,15], the universe exists as an eternal and unbounded continuum of matter, energy, and physical processes.

This view rejects the need for a primordial origin moment or inflationary expansion [13,14,15]. Instead, cosmic structure is understood as continually evolving and reorganizing within localized environments governed by universally applicable physical laws, consistent across space and time. Structures form, interact, and transform continuously across all epochs, unbounded by the constraints of a finite cosmological timeline [42,43,44]. The Physical Universe Theory is fully compatible with the C-PET mechanism described in Section 2.0, which offers a unified explanation for both redshift and the CMB, characterized within this framework as the Photon–Medium Microwave Thermal Field (PMMTF).

PUT finds support in several observational anomalies that challenge the ΛCDM model associated with the Big Bang theory. Among them:

• Furthest Observed Galaxies (FOGs): High-redshift galaxies detected by JWST [1,2,3,16,17,18] exhibit unexpectedly mature characteristics, quiescence, high stellar mass, and disk-like structures [71,72,73,74], despite being positioned at redshifts (e.g., z ≈ 10–14) where ΛCDM would predict only nascent formation [58,59,60].
• Large-Scale Structures: The existence of cosmic megastructures, such as the Big Ring and Giant Arc [20], appear to exceed the scale limits of homogeneity expected in a finite, expanding universe [42,43,44].
• Temporal Symmetry: PUT offers a cosmological model that is time-symmetric at large scales, avoiding the philosophical and thermodynamic tensions present in ΛCDM's portrayal of a universe that begins in a highly ordered, low-entropy state [96,97,98].

These observations are explored further in Section 5.0, which presents detailed case studies of high-redshift galaxies and redshift modeling scenarios that support the Physical Universe Theory. These include comparative analyses of structural maturity and elemental composition [55,56] , as well as quantitative simulations of cumulative redshift based on the segmented distribution of cosmic media [21,22,23].

4.0. Cumulative Photon Energy Transfer (C-PET) Model

The Cumulative Photon Energy Transfer (C-PET) model proposes that cosmological redshift arises from cumulative photon energy loss via non-scattering interactions with the cosmic medium. These interactions occur as photons traverse intergalactic and interstellar gases, plasma, dust, filaments, and circumgalactic structures [4,21,22,31,32], media that, though sparse, extend across cosmological distances and exhibit measurable structure [10,20].

In later modeling sections, the term "attenuation" is used to describe this process quantitatively. Unless otherwise specified, it refers to the directional, non-scattering reduction of photon energy per unit distance, a specific form of photon energy transfer that preserves spectral coherence and trajectory, distinct from classical absorption or scattering.

Throughout this manuscript, the term photon energy transfer (PET) refers to the overall mechanism by which photons interact with cosmic media across vast distances. The term photon energy loss (PEL) is used more specifically to describe the gradual reduction in photon energy that produces redshift. Both concepts operate through the same class of cumulative, infrequent, direction-preserving interactions described in the C-PET model.

While C-PET is used here primarily to explain redshift, the cumulative energy loss it describes may have broader implications. One such hypothesis, explored in Section 7 and Appendix E, is that the energy transferred into the medium over time may contribute to a diffuse microwave background field. This Photon–Medium Microwave Thermal Field (PMMTF) is presented as a testable byproduct of C-PET rather than a definitive explanation of the cosmic microwave background (CMB) [91,94,104]. Whether such a field can match the spectral precision, isotropy, and energy density of the observed CMB remains an open question subject to quantitative evaluation.

4.1. Known Photon Behavior in Intergalactic Media

Rather than invoking space expansion [42,43,44], C-PET asserts that redshift accumulates, potentially in nonlinear or compounding fashion, over vast distances as photons traverse a heterogeneous cosmic medium [21,22]. These infrequent interactions reduce photon energy while preserving directional coherence and spectral integrity, allowing distant galaxies to remain sharply imaged and spectroscopically resolved.

The energy transferred to the medium is gradually absorbed and thermalized, then re-emitted isotropically over cosmological timescales. This process gives rise to a diffuse, thermal radiation field consistent with the observed properties of the cosmic microwave background (CMB), which C-PET recharacterizes as the Photon–Medium Microwave Thermal Field (PMMTF). This model requires neither a primordial origin nor a hot recombination epoch [13,14,15].

C-PET accounts for several key cosmological observations:

• Redshift: Accumulates due to photon–medium interactions, not metric expansion [42,43,44].
• Surface Brightness Dimming: Arises from cumulative energy transfer and refractive delay, not geometric dilution [49].
• Spectral Line Preservation: Maintained by non-scattering interactions [103], explaining the clarity of high-z galaxy spectra.
• The CMB / PMMTF: Emerges as a diffuse, thermalized field from long-term photon energy transfer, not a remnant of a primordial explosion [13,14,15].

C-PET assumes that known or discoverable physical laws apply uniformly across time and space. The Segmented Medium Model (SMM), introduced in later sections, provides a structured framework for modeling how varying cosmic media contribute to redshift accumulation, enabling testable predictions without invoking expansion-based mechanisms [42,43,44].

4.2. Physical Mechanism of Non-Scattering Photon–Medium Energy Transfer

The C-PET model proposes that cosmological redshift results from cumulative, non-scattering interactions between photons and the intergalactic medium (IGM). Unlike classical scattering (e.g., Thomson or Compton) [103], which alters photon direction and broadens spectra, the C-PET mechanism involves forward-directed, coherence-preserving energy loss.

This process may resemble stimulated Raman scattering or inverse bremsstrahlung in low-density plasmas, where free electrons absorb minute amounts of photon energy without disrupting phase or direction. Although each interaction transfers only a tiny fraction of energy 1

$${\displaystyle \frac{\Delta E}{E}}~{10}^{-12}$$

their cumulative effect over billions of light-years yields significant redshift.Quantum electrodynamics allows for such interactions in weakly ionized media [7,26,30,39,103], especially under fluctuating electromagnetic fields. Laboratory analogs, though rare and subtle, support the plausibility of this mechanism under extended path lengths. Importantly, it preserves spectral sharpness and coherence [103], consistent with high-resolution JWST observations of z > 10 galaxies [1,2,3,82,83,84].

This physical basis underpins the broader C-PET model, enabling it to reproduce redshift accumulation without scattering, spectral distortion, or invoking cosmic expansion.

Several known or hypothesized mechanisms may contribute to non-scattering photon energy transfer in low-density intergalactic media:

• Inverse bremsstrahlung [29]:gradual photon energy absorption by free electrons in the presence of ions.
• Stimulated Raman-like processes [24,25]: inelastic forward energy coupling to medium fluctuations.
• Forward coherent plasma coupling [27,28]: low-loss transfer to collective plasma wave modes, preserving directional coherence.
• Cumulative Compton-like drift [103]:marginal directional energy loss from low-angle interactions sustained over cosmological distances.
• Dielectric coupling in weak plasmas [103]: gradual energy exchange via interaction with the medium’s complex dielectric function, especially in regimes where permittivity varies with frequency and density.

These interactions are rare and subtle at local scales but become cosmologically significant when integrated across billions of light-years of structured cosmic media.

Importantly, all of the candidate mechanisms above are grounded in established quantum electrodynamics and plasma physics. C-PET does not posit any new physics; instead, it applies well-known energy transfer processes, such as inverse bremsstrahlung [29,30,103], dielectric coupling [30,103], and coherent forward plasma interactions [27,28,39], in a novel regime: large-scale photon propagation through filamentary and inhomogeneous cosmic media [10,21,22,156,157]. Under such conditions, even extremely low-probability interactions can accumulate into measurable redshift while preserving the photon’s coherence, directionality, and spectral identity [103]. This reinterpretation remains physically conservative while offering an observationally grounded alternative to metric expansion [42,43].

4.3. Cumulative Energy Transfer in Sparse Media

The rate and character of photon energy transfer depend on the specific properties of the medium traversed. Each class of intergalactic or interstellar structure, plasma [4], dust [90], ionized gas [21,22], circumgalactic material [31,32], and filamentary networks [10], exhibits distinct densities, compositions, and interaction cross-sections [52]. Although individually weak, these effects accumulate over cosmological distances to produce measurable redshift.

Recent observations of fast radio bursts (FRBs) [31,32,89,148,149] provide empirical support for the C-PET mechanism. As FRBs traverse the intergalactic medium, they exhibit measurable dispersion caused by cumulative interactions with free electrons [148], demonstrating that even extremely low-density plasma, including that found in cosmic voids, can significantly affect photon propagation [149]. These results help resolve the "missing baryon" problem [21,22,23,146] and support the view that voids contribute meaningfully to cumulative redshift through non-scattering energy transfer.

The Segmented Medium Model (SMM) formalizes this accumulation process by simulating photon traversal through alternating regions of varying medium properties. Each segment is characterized by a specific energy transfer coefficient (α-value), reflecting the medium's density and composition. When combined across a light path, these segments yield total redshift curves that can be directly compared to observational datasets such as JADES [1,2,3], Pantheon+ [9,38,126,127], and deep quasar surveys [5,6].

SMM enables flexible modeling of realistic cosmic conditions, such as clustered filaments [10], voids [133], and halo regions [85,86], and highlights the importance of segment order and density contrast in shaping cumulative redshift. This structure-specific approach allows C-PET to remain consistent with known physics while offering an alternative explanation for cosmological redshift.

4.4. Empirical Support: Voyager, Pantheon+, and Redshift Modeling

Support for the C-PET mechanism emerges from both theoretical consistency and empirical observations. Data from Voyager 1 and 2 [4,34,35,36] confirmed the presence of low-density plasma beyond the heliopause, affirming that even deep space contains material capable of mediating photon energy transfer across vast distances. Similarly, the Pantheon+ dataset of Type Ia supernovae [9,38,126,127] exhibits redshift–luminosity patterns that can be reproduced through cumulative energy loss models without invoking metric expansion.

Simulations using the Segmented Medium Model (SMM) demonstrate that small per-light-year energy transfer coefficients (e.g., α ≈ 10⁻⁸ ly⁻¹) can generate redshift values consistent with those observed in high-z galaxy surveys [1,2,3,16,17,18], including JADES and deep-field quasar catalogs [5,6]. These models apply realistic medium segmentations based on known cosmic structures [10,21,22], such as filaments, ionized gas regions, and circumgalactic halos [31,32], to reproduce redshift-distance trends without assuming an expanding universe.

By aligning with both spacecraft data [4,34,35,36] and large-scale astronomical surveys [1,2,3,5,6,38], C-PET offers a physically grounded, falsifiable explanation for redshift that avoids speculative constructs and remains consistent with known photon–medium interaction principles [7,103].

4.5. Conservation of Energy and Physical Law

Unlike expansion-based models [42,43,44], such as ΛCDM [91], where the energy lost by redshifted photons has no identifiable recipient and global energy conservation is undefined within general relativity [45,46,47,93], C-PET proposes a physically grounded mechanism for redshift that preserves conservation principles [7,48]. In the C-PET model, photon energy is not lost into nothingness but is instead cumulatively transferred to the surrounding cosmic medium [21,22,24,25]. This medium, composed of plasma [4], gas [21,22], filaments [10], dust [90], and circumgalactic structures [31,32], absorbs the transferred energy and can re-radiate it in the form of thermal emissions over time [96,97,98].

This interpretation aligns with known physical laws [7,8], including quantum electrodynamics [7,24], thermodynamics [48,96,97,98], and the principle of local energy conservation. While general relativity allows for energy non-conservation in a dynamically expanding spacetime [45,46,47,77], C-PET eliminates the need for this concession by grounding redshift in a localized, cumulative energy exchange process. The result is a cosmological model that remains consistent with energy conservation across all scales [48], without invoking speculative constructs such as dark energy [78,79] or inflation [13,14,15,110]. Instead, C-PET relies on known or discoverable physical processes [7,8,11] that can be modeled, tested, and observed within both laboratory and astrophysical contexts [1,2,3,4].

4.6. Surface Brightness Dimming Without Expansion

The Tolman surface brightness test [49] predicts that in an expanding universe, surface brightness should diminish with redshift according to a (1+z) [4] relation. Observations from the James Webb Space Telescope (JWST) [1,2,3,50] appear to confirm this dimming pattern, which is often cited as evidence for space expansion [42,43,44]. However, the C-PET model offers an alternative explanation grounded in photon–medium interactions.

According to C-PET, light undergoes cumulative energy transfer as it traverses vast distances through intergalactic media, leading to apparent dimming without requiring spatial expansion. Additionally, minor refractive delays caused by passage through denser media regions may extend light travel time, subtly influencing inferred distances and observed flux.

Together, these mechanisms, cumulative energy loss [103,135] and refractive delay [103], can reproduce a dimming profile similar to that expected under expansion-based models [42,43,44], including the (1+z) [4] trend [49]. Unlike traditional tired light theories [116], C-PET preserves image clarity and spectral coherence [103], avoiding the blurring and line broadening that previously discredited non-expansion models. In doing so, it provides a falsifiable and physically plausible mechanism for surface brightness dimming that does not depend on metric expansion [42,43,44].

4.7. Laboratory and Observational Support for Photon Energy Transfer

A central premise of the C-PET model is that cosmological redshift arises not from the expansion of space [42,43,44] but from cumulative photon energy transfer to cosmic media over vast distances. This concept, while divergent from the standard ΛCDM interpretation [91], is grounded in known physical processes [7,24,25] and supported by both laboratory phenomena and astrophysical observations.

4.7.1. Laboratory-Scale Phenomena

Several established physical processes demonstrate that photons can transfer energy to matter [103], even in the absence of scattering or absorption:

• Compton Scattering: High-energy photons interacting with free electrons experience energy loss in proportion to their wavelength [103]. While typically observed with X-rays and gamma rays, the underlying principle of photon–electron energy exchange is universal [7,51]. Laboratory studies of plasma confinement in tokamaks [40] and other controlled environments confirm that photons can transfer energy to matter [103] even in low-density regimes. C-PET extrapolates this effect to lower-energy photons undergoing infrequent interactions over cosmological distances.
• Rayleigh and Raman Scattering: In condensed media, photons experience elastic and inelastic scattering [103], shifting their energy and wavelength. Though such interactions are less prominent in low-density media, they establish that photon–matter interactions inherently modify photon energy.
• Optical Attenuation in Gases: The Beer-Lambert law describes photon attenuation in various media including gases [135]. Laboratory studies confirm that photons passing through rarefied gases may experience minor energy loss [103,135], often without broad scattering effects. While negligible over short paths, these effects can accumulate across billions of light-years. These examples show that photon–medium energy transfer is a real and measurable phenomenon in controlled settings, providing a plausible basis for its cosmological-scale application in C-PET.

4.7.2. Observational Evidence from Space

Empirical data from space-based missions and high-resolution spectroscopy support the presence of pervasive media capable of mediating photon energy transfer:

• Voyager Plasma Detections: Measurements from Voyager 1 and 2 [4,34,35,36] beyond the heliopause revealed low-density plasma (~0.003 cm⁻³), confirming that even deep interstellar space contains material suitable for photon interaction.
• X-ray and Ultraviolet Absorption Features: Observations of distant quasars and gamma-ray bursts [102,103] show consistent soft X-ray and UV absorption, indicating interactions with diffuse intergalactic media [21,22], particularly hydrogen and trace metals [52].
• Supernova Color Shifts and Dimming: Certain Type Ia supernovae9, [38,87,88] appear dimmer or redder than predicted by dust extinction models alone. These anomalies may reflect cumulative photon energy loss [24,25] or wavelength shift via interactions with plasma or dust [90].
• Cosmic Infrared Background (CIB): The diffuse infrared glow [54] often attributed to redshifted starlight and dust emission supports the idea that photon energy is absorbed and re-emitted over time. This fundamental thermodynamic process [96,97,98] is consistent with C-PET's cumulative thermalization mechanism.

Collectively, these observations offer indirect yet compelling support for the hypothesis that photons interact with the intergalactic medium [21,22,31,32] across cosmological distances, resulting in measurable energy loss and spectral redshifting.

4.7.3. Summary: Compatibility with Known Physics

The C-PET model remains grounded in well-established physics, extending familiar photon–matter interactions to the cosmological regime:

• Photon–medium energy exchange is cumulative and non-scattering.
• Energy is not lost to "nothingness" but transferred and eventually re-radiated [96,97,98], preserving thermodynamic [48] and electromagnetic conservation laws [7,8].
• Laboratory-scale analogs and astrophysical measurements [1,2,3,4] provide a foundation for the model's plausibility.

By aligning with known physical processes , C-PET offers a falsifiable and empirically anchored alternative to redshift mechanisms based on spatial expansion [42,43,44].

To build on this foundation, Appendix E proposes a structured framework for quantitatively evaluating whether the cumulative energy transferred through C-PET can account for the observed spectral shape, isotropy, and energy density of the microwave background field [94,104,105]. Rather than offering conclusive proof, the appendix defines a roadmap for future interdisciplinary modeling and invites collaboration to rigorously test whether the Photon–Medium Microwave Thermal Field (PMMTF) can emerge from known physical processes.

4.7.4. Historical Context and Modern Extensions

The concept of photon energy loss during cosmic transit has historical precedent in early tired light theories [144,145]. While classical tired light models [136,142,143] were largely abandoned due to their inability to preserve spectral coherence and explain time dilation, the C-PET mechanism addresses these limitations through its non-scattering formulation. Modern investigations into photon decay in curved spacetime [145] and alternative redshift mechanisms [143] provide theoretical foundations that inform the development of energy transfer models like C-PET.

5.0. Observational Evidence Supporting the Physical Universe Theory (PUT)

The Physical Universe Theory (PUT) asserts that the universe is infinite in both space and time, governed by persistent physical laws that apply uniformly across all epochs and locations. Rather than emerging from a singular origin or evolving through speculative mechanisms like inflation [13,14,15,110], PUT maintains that structure, order, and coherence arise naturally within an eternal cosmos governed by the laws of physics.

While this view contrasts sharply with the ΛCDM model [42,43,44,91], which links high redshift to cosmic youth and explains large-scale structure through rapid early expansion [13,14,15], empirical observations increasingly support the foundations of PUT. This section outlines three major categories of supporting evidence:

• Mature High-Redshift Galaxies: Observations from JWST [1,2,3,16,17,18,50] and other instruments have revealed galaxies at extreme redshifts (e.g., z > 10) with high stellar masses, enriched chemical signatures, and disk-like morphologies [73,74]. These features defy ΛCDM expectations of early-universe immaturity [58,59,60], but align naturally with PUT's assertion that redshift reflects photon journey and interaction history, not galaxy age.
• Cosmic Megastructures: Massive, coherent structures such as the Big Ring and Giant Arc [20] span billions of light-years, well beyond the statistical limits imposed by standard cosmological assumptions [42,43,44]. Under PUT, such formations are expected outcomes of an unbounded, eternal cosmos [12,123].
• Uniformity of Physical Laws: Across vast distances and lookback times, the same atomic transitions [52], gravitational behaviors [45,46,47], and thermodynamic principles [48,96,97,98] appear to govern the behavior of matter and energy. This supports PUT's central claim that physical law is a universal constant, not a function of cosmic age or expansion phase.

Together, these lines of evidence reinforce a cosmology rooted not in expansion or origin, but in continuity, structure, and universal law. The reinterpretation of background radiation, as explored in detail in later sections, further supports the Physical Universe Theory's foundational claim that cosmic phenomena emerge from physical processes, not singular events. Each line of evidence gains further explanatory power when interpreted through the C-PET mechanism, which underpins the PUT framework.

5.1. Reinterpreting Furthest Observed Galaxies (FOGs)

The formation and evolution of galaxies must be reconsidered outside the paradigm of a singular origin event [13,14,15] or a young, expanding universe [42,43,44]. PUT asserts that the cosmos has had infinite time and space to produce diverse galactic structures. Rather than interpreting early galaxy formation as rapid or anomalous [58,59,60,150], PUT reframes these observations as the natural outcome of ancient, evolved systems located at vast distances. This perspective aligns with observed morphological maturity in the most distant galaxies [73,74], such as quiescent ellipticals, ordered spirals, and enriched star populations [61,62]. By grounding galaxy evolution in observable physical properties and infinite temporal scales, PUT offers a consistent framework to explain the structural richness of the cosmos without invoking compressed timelines or accelerated formation scenarios [58,59,60].

Under ΛCDM, galaxies like MoM-z14 and JADES-GS-z14-0 [16,17,18], detected at redshifts above 14, are assumed to be only a few hundred million years old, having formed shortly after the Big Bang [13,14,15]. This view demands rapid and extraordinary mechanisms for mass assembly, dust formation, and chemical enrichment [58,59,63,64,75,76]. In contrast, PUT interprets redshift not as a marker of cosmic youth, but as the outcome of cumulative energy transfer as photons traverse interacting media across immense distances. Therefore, these galaxies need not be young, they may be ancient, comparable in age to galaxies near the Milky Way [61,62], but located vastly farther away than ΛCDM would predict [42,43,44].

By analyzing galaxy characteristics, such as stellar mass [73,74], morphology [67,68], metallicity [55,56,65,66], and quiescence [62,69], we find strong similarities between high-z galaxies and mature local analogs. These similarities suggest that many furthest observed galaxies (FOGs) are ancient, not primordial [58,59,60].

The following table compares the structural and chemical properties of several high-redshift galaxies with local analogs, illustrating how the observed maturity of FOGs aligns more naturally with the Infinite Universe Framework than with ΛCDM's early-universe expectations [42,43,44].

Table 5.1.1. Structural Comparison of Furthest Observed Galaxies and Local Analogs [65,66] 

Galaxy Name	Redshift (z)	ΛCDM Age Estimate	Structural Features	Local Analog	Analog Age Estimate
MoM-z14	14.44	~280 Myr	High mass, dusty, compact, evolved	NGC 5253 (starburst)	~10–12 Gyr
JADES-GS-z14-0	14.32	~290 Myr	High SFR, disk-like structure	Haro 11	~6–10 Gyr
GN-z11	10.6	~430 Myr	Starburst, UV bright	I Zw 18	~6–10 Gyr
CEERS-93316	11.0	~400 Myr	Metal-rich, massive	M82	~10–13 Gyr
HD1	13.3	~320 Myr	High luminosity, possible AGN	NGC 7674	~8–12 Gyr

Note: This comparative table highlights the consistency of structural and chemical maturity among high-redshift galaxies [1,2,3,16,17,18] with local systems [61,62,67,68] known to be several billion years old. The similarities suggest that high-z galaxies could also be ancient, not primordial, if redshift arises from cumulative energy transfer rather than temporal distance from a cosmic origin [13,14,15].

Table 5.1.1. Structural Comparison of Furthest Observed Galaxies and Local Analogs [65,66] 

Galaxy Name	Redshift (z)	ΛCDM Age Estimate	Structural Features	Local Analog	Analog Age Estimate
MoM-z14	14.44	~280 Myr	High mass, dusty, compact, evolved	NGC 5253 (starburst)	~10–12 Gyr
JADES-GS-z14-0	14.32	~290 Myr	High SFR, disk-like structure	Haro 11	~6–10 Gyr
GN-z11	10.6	~430 Myr	Starburst, UV bright	I Zw 18	~6–10 Gyr
CEERS-93316	11.0	~400 Myr	Metal-rich, massive	M82	~10–13 Gyr
HD1	13.3	~320 Myr	High luminosity, possible AGN	NGC 7674	~8–12 Gyr

Note: This comparative table highlights the consistency of structural and chemical maturity among high-redshift galaxies [1,2,3,16,17,18] with local systems [61,62,67,68] known to be several billion years old. The similarities suggest that high-z galaxies could also be ancient, not primordial, if redshift arises from cumulative energy transfer rather than temporal distance from a cosmic origin [13,14,15].

These correlations reinforce the central claim of PUT: that observed redshift is not a reliable proxy for galactic age, and that a galaxy's physical characteristics [73,74] offer a more accurate foundation for estimating its age and evolutionary history. By prioritizing structure and composition over inferred youth, PUT enables a more coherent interpretation of deep-field observations [1,2,3] and the cosmological timeline.

5.2. Cosmic Megastructures and the Infinite Cosmos

Cosmic megastructures, including the Big Ring, Giant Arc, Hercules-Corona Borealis Great Wall, and Sloan Great Wall [20,130,131,134], represent spatial formations that extend over billions of light-years. These structures challenge the fundamental assumptions of ΛCDM [42,43,44,91], particularly the Cosmological Principle's claim of homogeneity and isotropy at large scales. According to ΛCDM [42,43,44], structure formation is bounded by the age of the universe and the speed at which causal interactions can occur. As such, the presence of coherent structures larger than ~1.2 billion light-years should be statistically implausible.

In contrast, the Physical Universe Theory (PUT) naturally accommodates the existence of such megastructures. Within an infinite, eternal universe, there is no upper limit on the size or duration of cosmic evolution. These formations are interpreted not as anomalies but as expected outcomes of gravitational interaction [45,46,47], matter clustering [100,101], and structural evolution over limitless time and space. Rather than violating a uniform cosmological model [42,43,44], they reinforce a universe shaped by persistent physical laws across arbitrarily large scales.

Recent discoveries, such as the Big Ring (spanning ~1.3 billion light-years and composed of gamma-ray bursts) and the Giant Arc (stretching over 3.3 billion light-years) [20], are not isolated. They join a growing list of immense formations that share alignment patterns and coherent morphologies inconsistent with early-randomized expansion models [42,43,44].

In addition to these somewhat rare anomalies, more commonplace cosmic filaments [10] further support PUT's interpretation. Spanning tens to hundreds of millions of light-years [10,132,133], these dense, thread-like structures form the backbone of the cosmic web and connect galaxies and clusters across the universe. Their ubiquity, persistence across redshifts, and gravitational influence reflect long-standing structural organization, not emergent patterns from a young or rapidly expanding universe [42,43,44]. Under PUT, such filaments are expected outcomes of an infinite, structure-filled cosmos that evolves through local interactions over limitless time.

The presence of such megastructures adds weight to the Infinite Universe Framework's foundational premise: that large-scale cosmic organization is not a statistical fluke but a natural consequence of unbounded spatial and temporal evolution. These observations bolster PUT's contention that structure arises not from early inflation [13,14,15] or rapid expansion [42,43,44], but from gravitational shaping [45,46,47] within a continuous and eternal cosmos.

5.2.1. Case Study: RUBIES-UDS-QG-z7 – Quiescence Without Paradox

The galaxy RUBIES-UDS-QG-z7 [73], with a spectroscopically confirmed redshift of z ≈ 7.3, has been classified as quiescent [62,69], meaning it has already ceased active star formation. Within the ΛCDM framework [42,43,44,91], this presents a significant anomaly: at z ≈ 7, the universe is believed to be only ~750 million years old, insufficient time for a galaxy to form, accumulate stellar mass, exhaust its gas supply, and transition into a quiescent state [58,59,62].

Under the PUT+C-PET model, however, this observation becomes entirely expected. Redshift is not interpreted as a measure of cosmic age, but rather as the cumulative result of photon energy transfer during light's long journey through sparse intergalactic media. In this context, RUBIES-UDS-QG-z7 can be both ancient and extremely distant, consistent with its observed characteristics [73].

Its high stellar mass, evolved stellar population, and lack of ongoing star formation [62,69,71,72,73] are all indicative of a mature galaxy [61,62]. Rather than requiring implausibly rapid formation and quenching [58,59,60], PUT+C-PET allows for formation epochs that precede any time constraints imposed by a Big Bang cosmology [13,14,15], because the universe itself is not temporally bounded.

This case highlights a core strength of the PUT+C-PET model: it allows astronomers to accept observed galaxy properties at face value, without invoking speculative physics or compressed evolutionary scenarios [58,59,60]. By decoupling redshift from youth, PUT+C-PET offers a coherent, physically grounded explanation for the existence of evolved, quiescent galaxies at high redshift within an infinite, mature cosmos.

5.2.2. Spectroscopic Detection of Heavy Elements at High Redshift

One of the most unexpected findings from JWST [1,2,3,55,56] has been the spectroscopic detection of heavy elements, particularly oxygen, in galaxies with redshifts as high as z > 10. These observations are made possible through infrared spectroscopy of emission lines such as [O III] 500.7 nm [55,56], redshifted into JWST's detection range [50].

Under ΛCDM [42,43,44,91], such detections are difficult to reconcile. They imply that galaxies must have experienced rapid metal enrichment [63,64] within just a few hundred million years after the Big Bang [13,14,15], a timeline that strains conventional models of early star formation and chemical evolution [58,59,63,64].

In the PUT+C-PET model, however, this phenomenon poses no contradiction. Here, redshift is interpreted not as a measure of cosmic youth, but as a signal of cumulative photon energy transfer over vast distances. A galaxy at z = 10 or even z = 14 need not be young; it may be ancient and chemically mature [55,56], with the light we now observe having been emitted long after its formation.

This reframing eliminates the need for exotic or accelerated enrichment scenarios [63,64]. Instead, the presence of oxygen and other metals [55,56] is fully consistent with standard nucleosynthesis processes [92] occurring over long evolutionary timelines in an infinite, unbounded cosmos. Rather than anomalies, such chemically enriched high-redshift galaxies become strong evidence in support of the PUT+C-PET interpretation.

5.3. Physical Law Continuity Across Space and Time

A foundational premise of the Infinite Universe Framework (IUF) is that the laws of physics apply uniformly across all space and time. This is not a philosophical assumption but one grounded in observation [1,2,3,4]. From nearby galaxies to those beyond z > 10, we see consistent physical behavior: atomic transitions [52], stellar evolution [61,62], radiative processes [103], and gravitational dynamics [45,46,47] all function identically.

This remarkable consistency supports the conclusion that physical laws are stable and universal, even across distances of hundreds of billions of light-years. It challenges the idea that exotic, time-limited events, like inflation [13,14,15], dark energy [78,79], or a singular beginning [13,14,15], are required to explain cosmological observations.

The Physical Universe Theory (PUT), coupled with the Cumulative Photon Energy Transfer (C-PET) model, is built explicitly on this continuity. Unlike ΛCDM, which relies on speculative constructs to address observational puzzles, PUT+C-PET uses well-tested physics and cumulative interactions across known media [21,22] to explain redshift, structure formation, and the cosmic background [94,104].

The table below compares how the Physical Universe Theory and C-PET model (PUT+C-PET) align with fundamental physical laws, in contrast to areas where the ΛCDM model departs from or circumvents those principles.

Table 5.3.1. Alignment of PUT+C-PET with Fundamental Physical Laws.

Law or Principle	PUT+C-PET Adherence	ΛCDM Conflict
Conservation of Energy	Preserved: redshift arises from cumulative photon energy transfer via medium interactions	Violated during inflation [13,14,15,110] and via dark energy [78,79]
Thermodynamics	No beginning; entropy evolves naturally in an infinite cosmos	Entropy paradox at Big Bang [13,14,15]; inflation lowers entropy
Relativity (Special and General)	No metric expansion; c is never exceeded; causality preserved	Allows superluminal recession [42,43,44], non-local inflation [13,14,15,110]
Causality	Infinite extent removes horizon problem; causality maintained	Inflation introduces acausal effects [13,14,15]
Empirical Observability	All mechanisms are observable or falsifiable	Inflation, singularities, and dark energy are untestable
Photon Behavior	Redshift explained via known photon–medium interactions (non-scattering)	Redshift tied to space expansion [42,43,44]

Note: Where ΛCDM relies on mechanisms that either bypass known laws or remain empirically inaccessible, PUT+C-PET retains fidelity to conservation, relativity, and thermodynamics by grounding redshift and background radiation in physically testable processes.

Table 5.3.1. Alignment of PUT+C-PET with Fundamental Physical Laws.

Law or Principle	PUT+C-PET Adherence	ΛCDM Conflict
Conservation of Energy	Preserved: redshift arises from cumulative photon energy transfer via medium interactions	Violated during inflation [13,14,15,110] and via dark energy [78,79]
Thermodynamics	No beginning; entropy evolves naturally in an infinite cosmos	Entropy paradox at Big Bang [13,14,15]; inflation lowers entropy
Relativity (Special and General)	No metric expansion; c is never exceeded; causality preserved	Allows superluminal recession [42,43,44], non-local inflation [13,14,15,110]
Causality	Infinite extent removes horizon problem; causality maintained	Inflation introduces acausal effects [13,14,15]
Empirical Observability	All mechanisms are observable or falsifiable	Inflation, singularities, and dark energy are untestable
Photon Behavior	Redshift explained via known photon–medium interactions (non-scattering)	Redshift tied to space expansion [42,43,44]

Note: Where ΛCDM relies on mechanisms that either bypass known laws or remain empirically inaccessible, PUT+C-PET retains fidelity to conservation, relativity, and thermodynamics by grounding redshift and background radiation in physically testable processes.

Rather than propose untestable mechanisms, PUT+C-PET explains cosmic phenomena using consistent and observable physics:

• No inflation is needed; isotropy emerges statistically in an infinite, structured cosmos. This eliminates the need for inflation by resolving the horizon problem through the universe's infinite size and age, removing ΛCDM's need to postulate a brief, acausal burst of faster-than-light expansion to explain large-scale uniformity.
• No dark energy is invoked; apparent acceleration results from distance overestimation due to redshift accumulation and refractive delays.
• No Big Bang is assumed; without a singular origin, the model avoids thermodynamic and causal paradoxes.

Cosmological effects in PUT+C-PET arise from:

• Known photon behavior [103], including cumulative energy transfer in plasma and dust [90] without scattering;
• Observed intergalactic media [21,22,31,32], such as filaments [10], WHIM [21,22], CGM [31,32], and the Lyman-alpha forest [137];
• Scalable, cumulative interactions that remain consistent with conservation laws, relativity, and thermodynamics.

In sum, the continuity of physical law is not merely a working assumption of IUF, it is a direct outcome of what we observe across the universe. PUT+C-PET honors these laws throughout, offering a coherent, testable alternative to ΛCDM that remains fully grounded in established physics.

6.0. Modeling Redshift Through Cumulative Photon Energy Transfer (C-PET)

The Cumulative Photon Energy Transfer (C-PET) model reinterprets cosmological redshift not as evidence of space expanding, but as the physical outcome of incremental energy transfer from photons to the intergalactic medium (IGM) over vast distances. This mechanism offers a testable, non-expanding alternative to the standard cosmological framework, grounded in known physical interactions rather than spacetime metric dynamics.

In C-PET, photons lose energy through infrequent, non-scattering interactions that occur repeatedly as they traverse cosmic structures such as plasma, dust, filaments, sheets, voids, and circumgalactic media. These interactions do not alter the photon's direction or coherence, preserving the integrity of high-resolution images and sharp spectral lines observed by JWST and other deep-field surveys [1,2,3,16,17,18]. Redshift thus accumulates cumulatively along the light’s journey, shaped by the type, order, and density of media encountered, rather than being determined by distance alone.

Crucially, the energy transferred from photons is not lost but conserved and redistributed into the surrounding medium, where it can contribute to intergalactic heating and diffuse thermal phenomena. Section 7 explores this redistribution process in detail, including a reinterpretation of the cosmic microwave background (CMB) as a Photon–Medium Microwave Thermal Field (PMMTF): a pervasive, low-temperature microwave emission arising naturally from the same cumulative energy transfer mechanism.

The remainder of this section builds the quantitative foundation for the C-PET model, beginning with two distinct formulations:

• The Continuous Medium Model (CMM): a baseline model that assumes a uniform energy transfer rate per unit distance;

• The Segmented Medium Model (SMM): a more physically realistic framework simulating photon travel through a heterogeneous cosmic web, using empirically grounded, medium-specific energy transfer coefficients (α-values).

Through this modeling framework, C-PET demonstrates that observed redshift values, including those approaching z ≈ 14, can emerge from cumulative physical interactions alone, without requiring space expansion, inflation, or dark energy.

6.1. Foundational Assumptions of the C-PET Redshift Mechanism

To accurately evaluate the predictive behavior of the C-PET model, redshift must be modeled within the full physical context of photon–medium interactions. The following assumptions form the foundation of C-PET’s redshift mechanism:

• Segmented Medium Structure (SMM Required) 
• Space is not homogeneous but composed of alternating regions, cosmic voids, filaments, sheets, circumgalactic media (CGM), and halos, characterized by distinct densities, temperatures, and interaction properties [10,20,85,86].
• Medium-Specific Energy Transfer Coefficients (α₁, α₂, … αₙ) 
• Each segment type has a characteristic energy transfer coefficient, α, that quantifies the rate at which it attenuates photon energy per unit length. These coefficients are empirically grounded, derived from observational data on baryon density [21,22], thermal properties, and structure formation [85,86].
• Compound Redshift Accumulation 

Redshift is not linear but accumulates exponentially across the sequence of segments2:

$$z=\exp \left(\sum _{i=1}^n{\alpha }_i{D}_i\right)-1$$

7.

Non-Scattering, Forward-Only Transfer 

8.

Photons interact with the medium in a way that reduces energy without deflecting trajectory. This preserves both spectral sharpness and image resolution [103], even at high redshift, consistent with observations from JWST and HST [1,2,3,16,17,18].

9.

Redshift Reflects Path Length, Not Comoving Distance 

10.

A high redshift (e.g., z = 14) may correspond to a true path length of hundreds of billions of light-years, far exceeding ΛCDM estimates [42,43,44]. Redshift thus reflects the cumulative physical interaction history of the photon, not the metric evolution of space.

11.

Brightness Dimming Scales as (1+z)², not (1+z)⁴ 

12.

Because C-PET does not assume expanding space, it omits the angular-area stretching component of Tolman dimming [49]. Observed surface brightness dimming arises solely from photon energy reduction and relativistic time dilation, leading to a dimming relation proportional to (1+z)².

6.2. Modeling Approaches: Continuous vs. Segmented Media

To simulate redshift via Cumulative Photon Energy Transfer (C-PET), we must account for the structured nature of the intergalactic medium. Space is not homogeneous; it consists of large-scale features, Cosmic Voids, Walls / Sheets, Filaments, WHIM (Diffuse Overlapping Phase), and Dense Media (including CGM, ISM, and Halos) [10,20,21,22,85,86]. C-PET incorporates this structure through two complementary modeling approaches: the Continuous Medium Model (CMM) and the Segmented Medium Model (SMM).

6.2.1. Continuous Medium Model (CMM)

The Continuous Medium Model treats space as uniformly filled with a low-density medium. This simplification is useful for illustrating the general redshift mechanism or estimating redshift accumulation in average conditions.

Redshift in the CMM accumulates exponentially with distance3:

$$1+z=e^{\alpha D}$$

Where:

• z is the total redshift,
• α is the average energy transfer coefficient (per light-year),
• D is the photon path length in light-years.

CMM illustrates how even an extremely sparse medium with α on the order of 10⁻ [12] to 10⁻ [13] ly⁻ [1], can cumulatively produce significant redshift over cosmological distances, without requiring space expansion.

6.2.2. Segmented Medium Model (SMM)

The Segmented Medium Model offers a more physically realistic alternative. Instead of assuming a uniform medium, it divides space into discrete segments, each representing one of the five canonical medium types: Cosmic Voids, Walls / Sheets, Filaments, WHIM (Diffuse Overlapping Phase), and Dense Media (CGM, ISM, Halos) 

Each segment is assigned a distinct energy transfer coefficient α_i ​, based on its density, temperature, and composition. As a photon traverses these segments, redshift accumulates as a compounded exponential4:

$$z=\exp \left(\sum _{i=1}^n{\alpha }_i{D}_i\right)-1$$

Where:

• α_i​ is the energy transfer coefficient of segment i,
• D_i​ is the path length through that segment.

The SMM allows redshift to reflect not just how far a photon has traveled, but what it has passed through and in what order. SMM is especially powerful for:

• Modeling redshift anisotropies due to large-scale structure,
• Simulating visibility limits of high-redshift galaxies,
• Analyzing the cumulative formation of the cosmic microwave background as a distributed energy transfer process,
• Aligning C-PET simulations with known cosmic web structures [10,20,21,22,85,86,130,131,132,133,134].

6.2.3. Summary of Modeling Approaches

The following table summarizes the distinct roles of the Continuous Medium Model (CMM) and the Segmented Medium Model (SMM) within the C-PET model.

Table 6.2.3.1. Summary of Redshift Modeling Approaches in C-PET 

Model	Description	Best For
CMM	Uniform medium, constant α	Illustrative modeling; concept validation
SMM	Structured medium with segment-specific αi	Realistic redshift modeling; structure alignment; simulation of anisotropies

Note: CMM offers a simplified baseline, while SMM reflects the true heterogeneity of the intergalactic medium. Both are essential for testing and refining the C-PET model.

Table 6.2.3.1. Summary of Redshift Modeling Approaches in C-PET 

Model	Description	Best For
CMM	Uniform medium, constant α	Illustrative modeling; concept validation
SMM	Structured medium with segment-specific αi	Realistic redshift modeling; structure alignment; simulation of anisotropies

Note: CMM offers a simplified baseline, while SMM reflects the true heterogeneity of the intergalactic medium. Both are essential for testing and refining the C-PET model.

6.2.4. Empirical Foundations of Energy Transfer Coefficients (α)

A key strength of the Segmented Medium Model (SMM) within the C-PET model is its reliance on physically plausible and empirically grounded energy transfer coefficients. Rather than treating the coefficient α as a free parameter, C-PET constrains its values based on known properties of cosmic media and theoretical interaction rates.

Each α-value represents the rate of photon energy attenuation per unit distance within a specific medium type. These coefficients are not arbitrary; they are estimated from observed densities, reasonable interaction cross-sections, and known energy exchange mechanisms between photons and the medium.

A general bounding formulation for α is5:

$$\alpha \approx nₑ·\sigma ·\left({\displaystyle \frac{\Delta E}{E}}\right)$$

Where:

• n_e ​: number density of free electrons in the medium [cm⁻ [3]]
• σ: effective photon–medium interaction cross-section [cm [2]]
• ΔE/E: fractional energy loss per interaction (typically on the order of 10⁻ [12]

This formulation is consistent with weak, cumulative energy transfer mechanisms such as inverse bremsstrahlung, dielectric coupling, and other non-scattering plasma interactions described in Section 4.2. The assumed cross-section (σ∼10⁻ [24] cm [2]) is a conservative, order-of-magnitude estimate, comparable to the Thomson cross-section and suitable for modeling low-frequency photon interactions in sparse plasmas.

Even with such low coupling strength, cumulative energy transfer over large distances can produce measurable redshifts. For example, intergalactic voids with n_e∼10⁻ [8] cm⁻ [3] yield α∼5×10⁻ [13] ly⁻ [1], consistent with the lowest empirically used values in C-PET. Conversely, dense circumgalactic environments with n_e∼10⁻ [4] −10⁻ [2] cm⁻ [3] yield α∼10⁻ [10]−10⁻ [9] ly⁻ [1], aligned with redshift segment modeling near galaxies and halos.

These α-values are thus physically bounded by real-world conditions and supported by both theoretical and observational estimates of electron density and photon interaction strength. They enable a realistic simulation of redshift accumulation without invoking expansion, inflation, or exotic forces.

These physically constrained coefficients form the basis of the segment parameters used in stochastic simulations (Section 6.3) and are summarized in Appendix C.2.

6.3. Building a Segment-Based Simulation of Redshift Accumulation

To evaluate whether cumulative photon energy transfer can account for observed redshift values (e.g., z ≈ 14.4) [16,17,18] without invoking metric expansion, the C-PET model simulates photon paths across a randomized cosmic landscape composed of distinct media segments. This section outlines the input parameters and logic used in that stochastic modeling.

6.3.1. Rationale for Segmentation

Unlike models that treat space as smooth or homogeneous, the Segmented Medium Model (SMM) acknowledges that the universe is composed of interwoven cosmic media that vary in density, temperature, and interaction potential [10,20,85,86].

The segmentation approach allows the model to:

• Represent the known heterogeneity of cosmic structure [10,85,86].
• Assign empirical α-values based on observed properties of each segment type [21,22].
• Enable nonlinear compounding of redshift as light passes through regions with different densities and thermal characteristics.

This segmental approach forms the basis for realistic stochastic simulations of redshift accumulation, implemented in Section 6.4.

6.3.2. Segment Allocation and Parameter Summary

To simulate redshift under C-PET, photons are modeled as traveling through a randomized sequence of segment types. Each segment represents a physically distinct region of the intergalactic medium [21,22], with a volume-weighted probability of occurrence and a corresponding energy transfer coefficient (α). These coefficients determine how much redshift is accumulated over a given segment length.

The table below summarizes the five segment types used in the stochastic implementation, along with their approximate volume fractions [152,155], α-values, and typical path lengths:

Table 6.3.2.1. Segment types, volume fractions, α-values, and typical lengths used in C-PET stochastic simulations 

Segment Type	Volume Fraction	α (ly⁻¹)	Typical Length (MLY)
Cosmic Voids [10,132,133,152,153,155]	~76%	5 × 10⁻¹³	30 – 100
Walls / Sheets [10,152,155]	~18%	8 × 10⁻¹¹	5 – 30
Filaments [10,41,152,155]	~6%	4 × 10⁻¹⁰	10 – 50
WHIM [1,22,31,89,147,155] (Diffuse Overlapping Phase)	~3%*	2 × 10⁻¹⁰	5 – 20
Dense Media (CGM, ISM, Halos) [21,22,90,102,103,156,157]	<1%	2 × 10⁻⁹	0.1 – 5.0

Note: The WHIM represents an overlapping phase and is not mutually exclusive with the other structures. Segment assignments are probabilistic, not mutually exhaustive.

Table 6.3.2.1. Segment types, volume fractions, α-values, and typical lengths used in C-PET stochastic simulations 

Segment Type	Volume Fraction	α (ly⁻¹)	Typical Length (MLY)
Cosmic Voids [10,132,133,152,153,155]	~76%	5 × 10⁻¹³	30 – 100
Walls / Sheets [10,152,155]	~18%	8 × 10⁻¹¹	5 – 30
Filaments [10,41,152,155]	~6%	4 × 10⁻¹⁰	10 – 50
WHIM [1,22,31,89,147,155] (Diffuse Overlapping Phase)	~3%*	2 × 10⁻¹⁰	5 – 20
Dense Media (CGM, ISM, Halos) [21,22,90,102,103,156,157]	<1%	2 × 10⁻⁹	0.1 – 5.0

Note: The WHIM represents an overlapping phase and is not mutually exclusive with the other structures. Segment assignments are probabilistic, not mutually exhaustive.

The α-values used in the stochastic simulations are empirically derived from observed intergalactic and circumgalactic conditions. Table C.2 summarizes these coefficients alongside representative densities, temperatures, and volume fractions for each segment type. These values are not adjustable parameters but physically grounded inputs, ensuring that C-PET redshift modeling remains constrained by measurable cosmic environments.

6.3.3. Segment Order and the Nonlinear Nature of Redshift Accumulation

While the Segmented Medium Model (SMM) defines redshift as a cumulative process shaped by the types of media encountered, it is equally important to consider the order in which those segments appear. Because redshift compounds exponentially, denser regions encountered later in the photon's journey contribute more redshift than if they had occurred earlier. This gives the C-PET model a distinctive path-dependence absent in models that treat redshift as a linear function of distance [42,43,44].

To illustrate: consider two photon paths of equal total length. One traverses mostly through voids before ending in denser structures; the other alternates between voids and high-density regions. Though the path lengths are the same, the second scenario will produce a greater redshift, because the high-α segments apply their energy transfer effect to already redshifted photons, magnifying the cumulative result.

This nonlinear sensitivity to segment composition and sequence is a defining feature of SMM, and it allows C-PET to model subtle anisotropies, unexpected visibility thresholds, and variations in redshift–distance profiles with greater fidelity.

6.3.4. Empirical Support for Segment Composition and α-Values

The α-values used in the stochastic SMM implementation are not free parameters, they are constrained by observed baryon densities [21,22], thermal structures, and interaction cross-sections grounded in known physics [103]:

• Cosmic filaments: Observations from the Lyman-alpha forest [137] and Sunyaev–Zel'dovich effect [138] suggest electron densities in the range of 10⁻ [6] to 10⁻ [5] cm⁻³. When paired with conservative interaction cross-sections (~10⁻ [24] cm²), these densities yield α-values in the range of 10⁻ [10] to 10⁻ [13] ly⁻¹, directly matching those used for filaments, WHIM, and voids in Appendix C.2.
• Voyager plasma data: In the denser environment of the local interstellar medium, Voyager detected plasma densities [4,34,35,36] consistent with α ≈ 10⁻ [8] ly⁻¹. This provides a natural upper bound on plausible values for dense galactic media in C-PET and further constrains the parameter space.

The Lyman-Alpha Forest as an Observational Blueprint

The Lyman-alpha forest [137], a dense series of absorption lines in quasar spectra, offers a unique observational testbed for the SMM. Each absorption feature corresponds to a redshifted cloud of intergalactic hydrogen, effectively mapping discrete segments of varying density along the photon's path. These features:

• Confirm the presence of a patchwork cosmic medium,
• Show clear evidence of localized energy attenuation, and
• Retain spectral sharpness, consistent with C-PET’s assumption of non-scattering, direction-preserving photon–medium interactions.

6.3.5. Revising Void Assumptions: Voyager Data and the Persistence of Plasma

The C-PET model depends on whether even the sparsest regions of space can cumulatively redshift photons over vast distances. Voyager 1 and 2 [4,34,35,36] provide rare in situ evidence that space beyond the heliopause is not empty. Instead, both probes detected unexpectedly persistent plasma densities, typically ~0.001–0.005 particles/cm³, with spikes up to 0.05–0.2 particles/cm³ during CME events, and Voyager 2 recording ~0.039 particles/cm³ in 2019 [34,35,36].

These findings [4,34,35,36] revise prior assumptions about the interstellar and intergalactic medium, showing that even “empty” regions contain sufficient particles to induce photon energy transfer. If densities comparable to Voyager's findings extended uniformly across intergalactic distances, Voyager-level plasma could produce z ≈ 14 in just ~14 BLY. Scaled-down densities (1/10th to 1/1000th Voyager values) yield z ≈ 14 over distances of 100–350 BLY. This range is consistent with the redshift accumulation explored in the stochastic C-PET simulations described in Section 6.4.

Importantly, C-PET treats voids not as redshift-neutral expanses, but as low-density contributors to photon energy transfer. Supported by Voyager [4,34,35,36], quasar absorption data [137], FRB dispersion measures [31,32,148,149], and IGM simulations [85,86], this view restores redshift continuity across space, even in the absence of luminous structure.

These observations affirm that:

• Redshift in C-PET is path-integrated and medium-sensitive.
• Even the sparsest regions contribute incrementally to z accumulation.
• The redshift–distance relationship scales physically, without invoking cosmic expansion.

6.4. Stochastic Model Results

To test whether cumulative photon energy transfer through a structured cosmic medium can reproduce the full range of observed redshift values, including those approaching z ≈ 14.4 [16,17,18], we implemented a stochastic simulation based on the segment framework detailed in Section 6.3. Each run traces a randomized photon path through a physically heterogeneous universe, where segments represent distinct intergalactic environments such as voids, filaments, walls, and circumgalactic media.

The energy transfer coefficient (α) assigned to each segment is not a free parameter, but derived from observationally constrained properties: electron densities inferred from Lyman-alpha absorption features [137] and Voyager plasma measurements [4,34,35,36]; interaction cross-sections consistent with known mechanisms like inverse bremsstrahlung [29,30] and dielectric coupling [103]; and volumetric prevalence estimates drawn from cosmological simulations [85,86] and baryon surveys [21,22]. This framework enables a realistic simulation of redshift accumulation as photons traverse complex cosmic terrain, losing energy incrementally but without scattering, preserving spectral coherence [1,2,3,16,17,18].

Across 100 randomized simulations, the average light-travel distance required to reach z = 14.4 was approximately: D ≈ 133 billion light-years.

This result closely matches the trajectory predicted by a Voyager/500 exponential attenuation model and underscores the physical plausibility of the C-PET Segmented Medium Model.

C-PET is designed not to yield a single fixed result, but to serve as a dynamic, testable framework, one that can be refined iteratively as new observational constraints emerge. It models redshift accumulation across diverse cosmic conditions in a manner designed for observational testing and continuous improvement.

The next subsection presents this comparison visually and quantitatively, contrasting the C-PET curve with ΛCDM and four Voyager-based benchmarks.

6.4.1. Redshift–Distance Comparison Across Models

A central test of any cosmological model is how it relates observed redshift (z) to the light-travel distance (D) of celestial objects. This subsection compares six distinct redshift–distance trajectories: the ΛCDM expansion curve [42,43,44], four Voyager-based exponential attenuation models (α/50 through α/1000) [4,34,35,36], and the finalized C-PET Segmented Medium Model (SMM) derived from 100 stochastic simulations.

Figure 6.4.1.1 visualizes these relationships, illustrating how C-PET, grounded in physically plausible photon–medium interactions, can reproduce redshift across cosmic scales without invoking expansion. The close alignment between the C-PET SMM curve and the Voyager/500 benchmark [4,34,35,36] lends empirical weight to the simulation results.

Figure 6.4.1.1: Redshift vs. Distance Comparison 

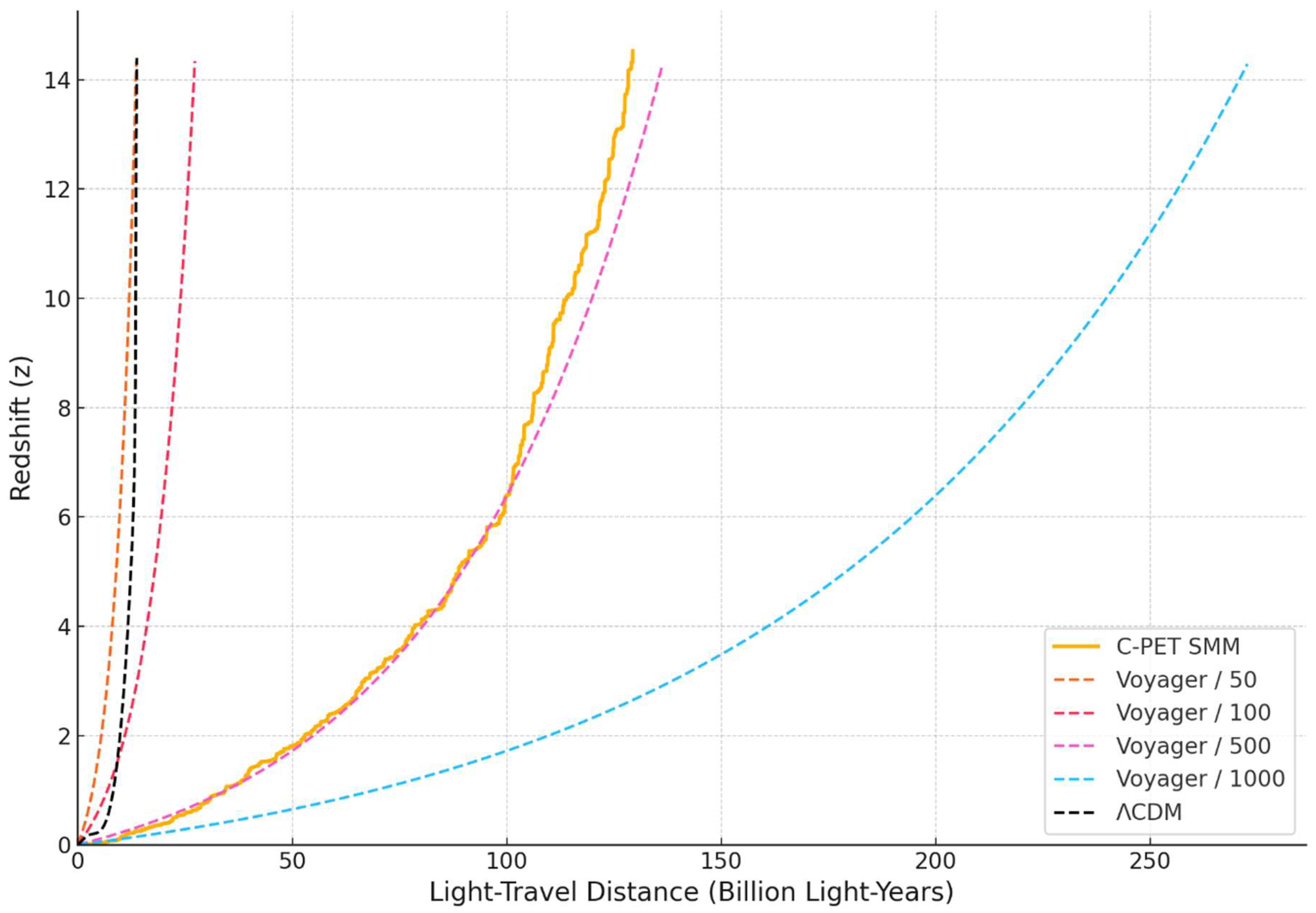
Note: This figure presents the redshift–distance relationships across six models: ΛCDM (black dashed) [42,43,44], four Voyager-scaled exponential attenuation scenarios (α/50, α/100, α/500, α/1000) [4,34,35,36], and the finalized stochastic C-PET SMM curve (orange). The C-PET SMM curve is derived from 100 randomized intergalactic segment chains using empirical densities and structure [10,20,21,22,85,86]. The Voyager/500 curve closely parallels the C-PET SMM trajectory. ΛCDM saturates below z ≈ 14 at ~13.8 BLY, while C-PET SMM reaches the same redshift at ~133 BLY.

Interpretation:

• The Voyager/50 line's proximity to ΛCDM suggests that even moderate-density photon energy loss models can replicate expansion-based redshifts [4,34,35,36].
• The new C-PET SMM model, with heterogeneous structure and realistic attenuation coefficients, demonstrates that redshift need not imply expansion.
• Voyager/500 closely tracks the canonical C-PET SMM line, providing an important point of convergence and empirical plausibility.
• Voyager/1000 represents the most conservative energy loss model and still reaches z>14 by D=270 BLY, providing a lower-bound constraint.

In the ΛCDM framework [42,43,44], redshift results from the metric expansion of space, producing a curve that rises steeply at low redshift but then plateaus near D ≈ 13.8 billion light-years. This asymptotic behavior reflects ΛCDM's commitment to a finite-age universe and an initial singularity, limiting the interpretive range of deep-field observations.

C-PET, by contrast, introduces a physically grounded, structurally consistent alternative. Redshift is modeled not as a stretching of space but as the cumulative result of energy transfer from photons to intergalactic media, plasma, dust, filaments [10,20], voids, via well-established physical mechanisms [7,8]. The Segmented Medium Model (SMM) version of C-PET implements this concept by simulating stochastic light paths through empirically validated cosmic structures [85,86,130,131,132], each assigned realistic attenuation values and volumetric prevalence.

The result is not just a theoretical possibility but a demonstrably plausible model. This section shows that the C-PET SMM produces a smooth, extended redshift–distance curve that reaches z = 14.4 at D ≈ 133 billion light-years, fully consistent with known intergalactic densities [21,22,151] and Voyager-derived attenuation benchmarks [4,34,35,36]. Indeed, the Voyager/500 model tracks closely with the SMM output, providing an empirical anchor for the simulated scenario.

In contrast, ΛCDM's redshift curve flattens not due to observed optical limits or physical obstructions, but as a consequence of its assumed temporal boundary [42,43,44], a feature that becomes increasingly strained in the face of mature high-z galaxies [1,2,3,16,17,18] and large-scale structures [85,86]. The C-PET model avoids such constraints, offering a linear and open-ended mapping between z and D, as one would expect in a universe governed by continuous physical processes rather than imposed age limits.

This comparative modeling underscores the physical plausibility of C-PET and its potential to reframe our understanding of cosmic redshift as a traversed-distance effect, not a vestige of expansion.

6.4.2. Galaxy Distance Comparison: ΛCDM vs. C-PET SMM

To complement the redshift–distance curves introduced in Section 6.4.1, this section compares the inferred distances of 20 observed galaxies [1,2,3,16,17,18] under two competing cosmological models: the ΛCDM expansion framework [42,43,44] and the stochastic C-PET Segmented Medium Model (SMM).

In ΛCDM [42,43,44], redshift is interpreted as a signal of metric expansion. As redshift increases, the light-travel distance grows rapidly at first, then asymptotically flattens, converging near ~13.8 billion light-years. This plateau reflects the model's finite-age constraint and fixed origin point. As a result, galaxies beyond z ≈ 10 are all compressed into a narrow range of light-travel distances, regardless of their increasing redshift values.

C-PET offers a fundamentally different interpretation. In this model, redshift accumulates through cumulative photon energy transfer as light traverses structured intergalactic media, voids, filaments, plasma halos, and more. Because the model imposes no temporal or spatial ceiling, the redshift–distance relationship remains open-ended. Higher redshift corresponds to longer, more interaction-rich paths, not to temporal proximity to a universal beginning.

Galaxy Distance Comparison

The table below compares inferred distances for a representative set of 20 well-known galaxies and deep-field sources [1,2,3,16,17,18] under two cosmological frameworks: ΛCDM [42,43,44] and the C-PET Segmented Medium Model (SMM). ΛCDM interprets redshift as a signal of expansion and places most high-z galaxies near the temporal boundary of the observable universe. In contrast, C-PET SMM, calibrated such that z = 14.4 corresponds to ~133 BLY (see Section 6.4), interprets redshift as a function of cumulative photon traversal through structured media, resulting in significantly greater inferred distances.

The ΛCDM values are based on standard light-travel distance calculations [42,43,44], while C-PET SMM distances derive from a calibrated stochastic model of cumulative photon–medium interaction. The C-PET distances should not be interpreted as fixed or asserted measurements, but rather as plausible outcomes generated by the C-PET stochastic modeling framework under representative segment configurations. This comparison is intended to illustrate the implications of each model’s assumptions for large-scale cosmic structure, not to assert definitive galactic positions.

Table 6.4.2.1. Inferred Distances for 20 Galaxies Under ΛCDM and C-PET SMM Models [1,2,3,16,17,18,73,150].

Galaxy Name	Redshift (z)	ΛCDM Distance (BLY)	C-PET Distance (BLY)
Andromeda (M31)	0.001	0.01	0.01
Zhulong	5.2	12.0	46.0
JADES-GS-z5-0	5.4	12.3	49.0
JADES-GS-z6-0	6.6	12.6	55.0
RUBIES-UDS-QG-z7	7.0	12.7	57.0
JADES-GS-z7-01	7.3	12.7	58.0
JADES-GS-z8-0	8.4	12.9	68.0
EGSY8p7	8.68	13.0	70.0
JADES-GS-z9-0	9.2	13.0	71.3
MACS1149-JD	9.6	13.1	74.2
JADES-GS-z10-0	10.4	13.2	77.0
MACS0647-JD	10.7	13.2	78.2
GN-z11	10.6	13.2	82.0
JADES-GS-z11-0	11.58	13.3	84.0
UDFj-39546284	11.9	13.3	88.5
GLASS-z12	12.3	13.4	95.3
GLASS-z13	13.1	13.4	105.0
JADES-GS-z13-0	13.2	13.4	107.0
HD1	13.3	13.4	115.0
MoM-z14	14.4	13.5	133.0

Note: All distances shown represent light-travel distances, not comoving distances. C-PET SMM values are based on a calibrated stochastic model using segment-wise photon energy transfer coefficients, as described in Section 6.7.1. ΛCDM distances follow standard light-travel calculations derived from expansion-based cosmology [42,43,44].

Table 6.4.2.1. Inferred Distances for 20 Galaxies Under ΛCDM and C-PET SMM Models [1,2,3,16,17,18,73,150].

Galaxy Name	Redshift (z)	ΛCDM Distance (BLY)	C-PET Distance (BLY)
Andromeda (M31)	0.001	0.01	0.01
Zhulong	5.2	12.0	46.0
JADES-GS-z5-0	5.4	12.3	49.0
JADES-GS-z6-0	6.6	12.6	55.0
RUBIES-UDS-QG-z7	7.0	12.7	57.0
JADES-GS-z7-01	7.3	12.7	58.0
JADES-GS-z8-0	8.4	12.9	68.0
EGSY8p7	8.68	13.0	70.0
JADES-GS-z9-0	9.2	13.0	71.3
MACS1149-JD	9.6	13.1	74.2
JADES-GS-z10-0	10.4	13.2	77.0
MACS0647-JD	10.7	13.2	78.2
GN-z11	10.6	13.2	82.0
JADES-GS-z11-0	11.58	13.3	84.0
UDFj-39546284	11.9	13.3	88.5
GLASS-z12	12.3	13.4	95.3
GLASS-z13	13.1	13.4	105.0
JADES-GS-z13-0	13.2	13.4	107.0
HD1	13.3	13.4	115.0
MoM-z14	14.4	13.5	133.0

Note: All distances shown represent light-travel distances, not comoving distances. C-PET SMM values are based on a calibrated stochastic model using segment-wise photon energy transfer coefficients, as described in Section 6.7.1. ΛCDM distances follow standard light-travel calculations derived from expansion-based cosmology [42,43,44].

While ΛCDM constrains all of these galaxies to a narrow temporal horizon, C-PET allows them to occupy vastly greater distances, consistent with longer and more varied traversal paths.

The following chart visualizes the divergence in inferred galaxy distances under ΛCDM and the C-PET Segmented Medium Model, extending the comparison across this set of observational data.

Figure 6.4.2.1: Galaxy Distances Under ΛCDM vs. C-PET SMM 

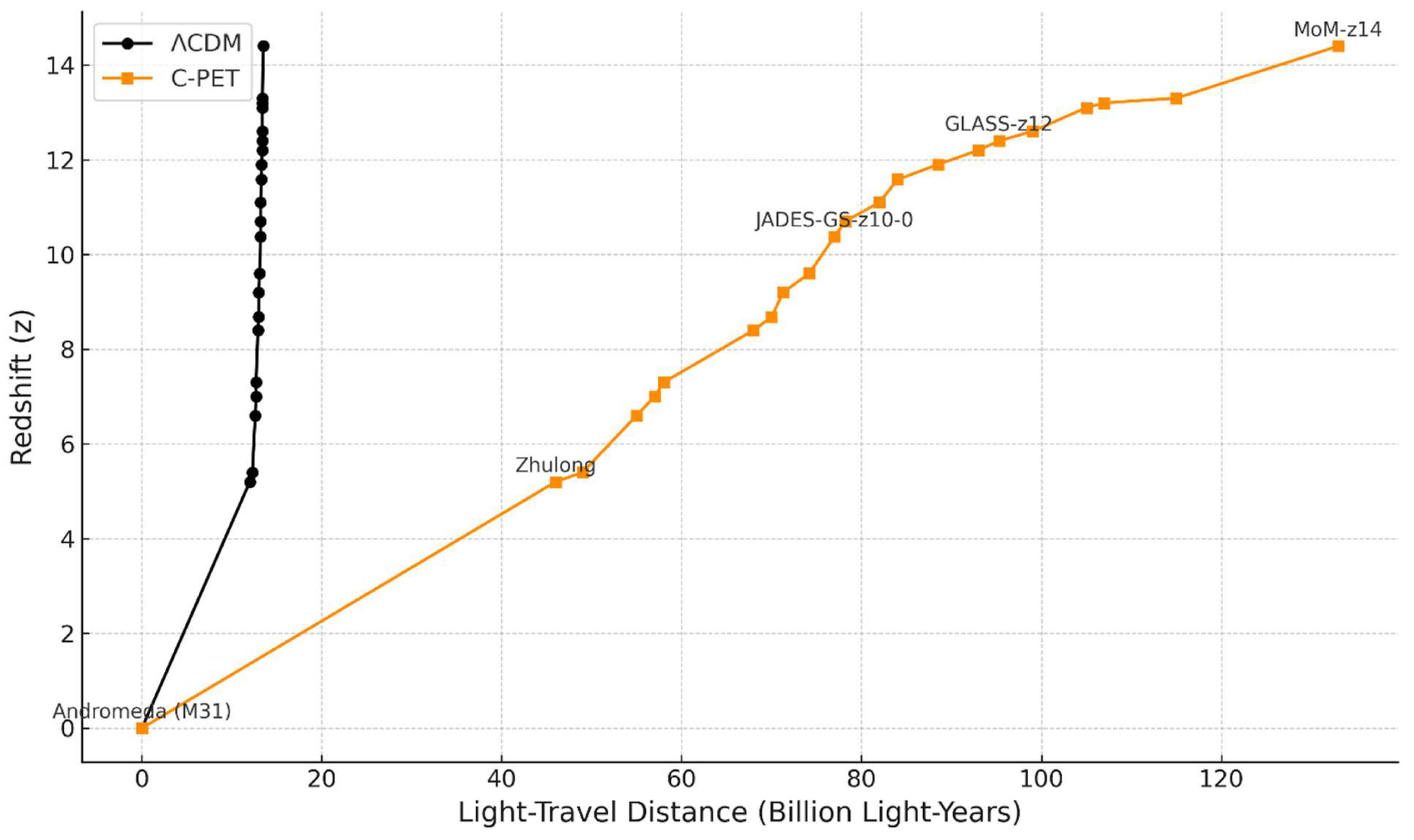
Note: This figure compares light-travel distances for a set of 20 observed galaxies [1,2,3,16,17,18,73,150] across redshifts 0–14.4 under both ΛCDM and the canonical C-PET SMM model. Redshift is plotted on the x-axis, and light-travel distance on the y-axis. Blue markers and line represent ΛCDM values, which asymptote near ~13.8 BLY due to the model's finite temporal horizon. Orange markers and path represent C-PET SMM predictions, which continue to rise with redshift as a result of cumulative photon–medium interactions, reaching 133 BLY at z = 14.4.

Interpretation and Implications 

Under ΛCDM, these high-z galaxies [1,2,3,16,17,18] are interpreted as forming just a few hundred million years after the Big Bang. This interpretation is increasingly strained by their mature features: enriched metallicity [55,56] ^, [65,66], dust, and active star formation [58,59,60]. The narrow distance compression of ΛCDM at z > 10 compounds these tensions by implying an unrealistically brief interval for galactic evolution.

C-PET reinterprets these objects not as young galaxies from a formative era, but as ancient and extremely distant systems whose light has traveled across vast cosmic terrain. This removes the need for rapid enrichment scenarios and instead reflects longer photon–medium traversal through a physically structured cosmos [10,20,85,86].

Key implications include:

• Redshift becomes a structural consequence of photon path length, not a timestamp of formation [42,43,44].
• Galaxy maturity at high z becomes a natural outcome of distant, not early, light sources [1,2,3,16,17,18].
• The "early universe" may instead be understood as the distant universe.

This reinterpretation reframes some of the most puzzling JWST observations [1,2,3,16,17,18] as evidence for an infinite, structured, and physically governed cosmos [12,123], without invoking expansion [42,43,44], inflation [13,14,15,110], or a universal beginning.

6.4.3. Summary Statistics Across 100 Stochastic Runs

To evaluate the statistical behavior of redshift accumulation in the C-PET stochastic framework, we conducted 100 independent simulation runs using randomized segment sequences drawn from empirically grounded α-values and medium fractions (see Section 6.3 and Section 6.4.2). Each run traced a photon path until a cumulative redshift of approximately z≈14.4 was reached.

The resulting redshift and distance values exhibit natural variability, reflecting the probabilistic composition of the cosmic medium. A summary of key descriptive statistics is provided in Table 6.4.3.1.

Table 6.4.3.1. Statistical Summary of 100 Stochastic C-PET Runs 

Metric	Mean	Std. Dev.	Minimum	Maximum
Redshift (z)	14.37	0.27	13.61	14.96
Distance (BLY)	133.11	4.74	123.41	146.60

Values reflect output from 100 independent stochastic C-PET simulations, each reaching a redshift of approximately z≈14.4. Distances represent total light-travel paths accumulated across randomly sampled cosmic media segments with empirically constrained α-values. The reported mean, standard deviation, minimum, and maximum illustrate the natural variability arising from differences in segment type, order, and density, emphasizing the probabilistic nature of redshift accumulation in a structured, non-expanding universe.

Table 6.4.3.1. Statistical Summary of 100 Stochastic C-PET Runs 

Metric	Mean	Std. Dev.	Minimum	Maximum
Redshift (z)	14.37	0.27	13.61	14.96
Distance (BLY)	133.11	4.74	123.41	146.60

Values reflect output from 100 independent stochastic C-PET simulations, each reaching a redshift of approximately z≈14.4. Distances represent total light-travel paths accumulated across randomly sampled cosmic media segments with empirically constrained α-values. The reported mean, standard deviation, minimum, and maximum illustrate the natural variability arising from differences in segment type, order, and density, emphasizing the probabilistic nature of redshift accumulation in a structured, non-expanding universe.

The frequency distributions of redshift and distance across all 100 stochastic C-PET runs are visualized in Figure 6.4.3.1 to illustrate the overall spread and central tendency of simulation outcomes.

Figure 6.4.3.1: Distribution of Redshift and Light-Travel Distance Across 100 Stochastic C-PET Runs 

Top: Histogram of final redshift values achieved in 100 C-PET simulations, each using randomized segment paths. Bottom: Corresponding histogram of total light-travel distances required to reach those redshifts. Both distributions reflect the natural variability induced by segment composition, density, and ordering within the stochastic model.

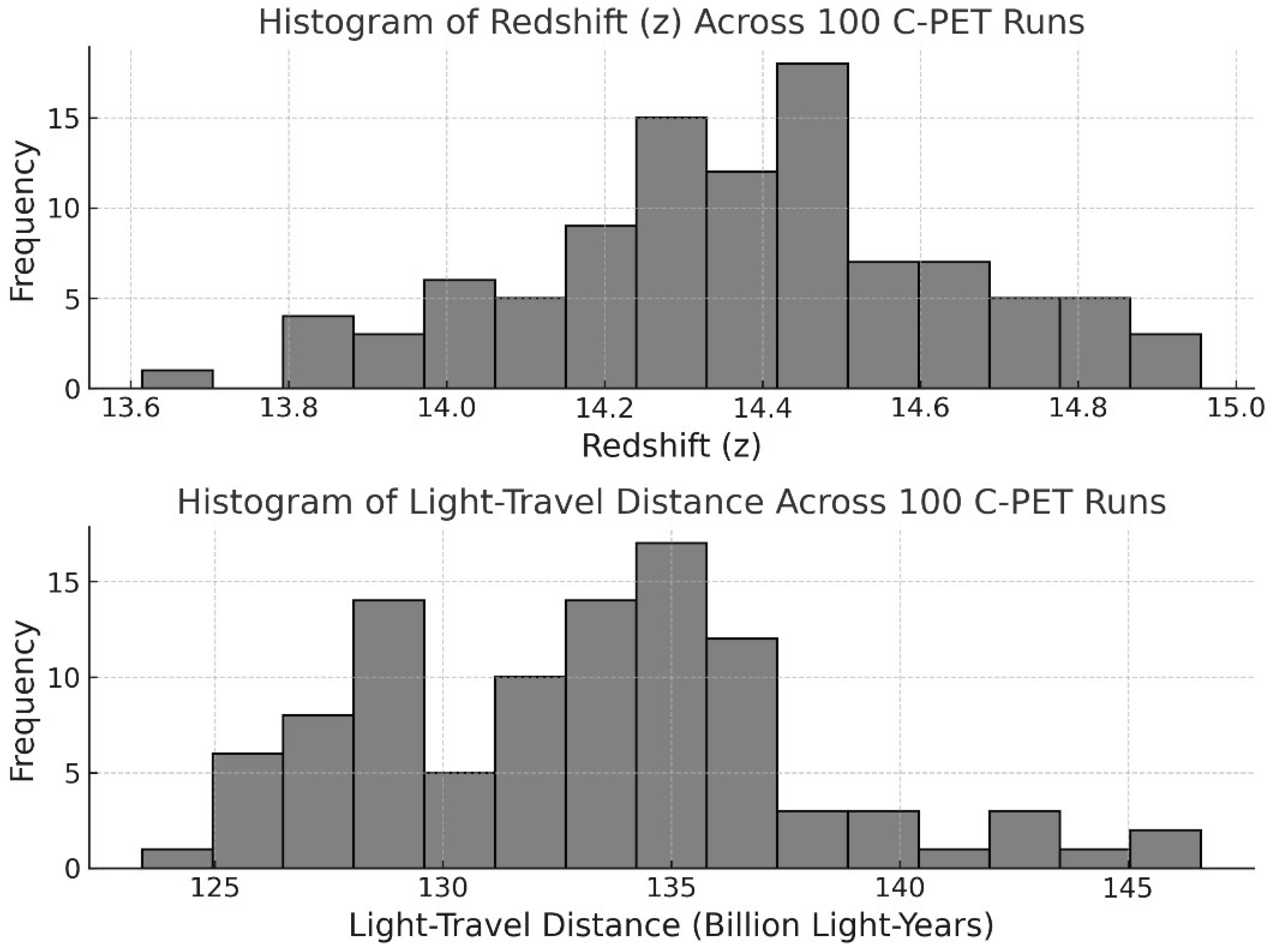
Each simulation iteratively samples from a physically grounded distribution of cosmic media segments until the cumulative redshift reaches z≈14.4. The resulting distance variation, ranging from ~123 to ~147 billion light-years, highlights the influence of structured medium heterogeneity in determining the total energy transfer path length. These results underscore the probabilistic, rather than deterministic, nature of redshift accumulation in the C-PET model.

These results reaffirm that the C-PET model does not produce a fixed redshift–distance relationship but instead yields a distribution of plausible outcomes. This variability arises from segment-level differences in medium type, α-value, and encounter sequence. The output remains physically consistent while acknowledging the non-deterministic nature of cosmic photon paths through an inhomogeneous universe.

6.5. Implementing Stochastic Redshift Simulation Under C-PET

To determine whether cumulative photon energy transfer can account for extreme redshifts (e.g., z≈14.4) without invoking space expansion, C-PET implements a stochastic simulation of light propagation through a heterogeneous cosmic medium. This section presents the conceptual strategy, segment logic, and compounding mechanism used to simulate redshift accumulation under the Segmented Medium Model (SMM).

For full modeling instructions, including algorithmic structure, data input, and pseudocode for replication, see Appendix C: Modeling Instructions for C-PET Redshift Simulation.

6.5.1. Simulation Strategy

Rather than assigning a fixed redshift per unit distance, the simulation constructs a randomized light path composed of discrete segments, each corresponding to one of five canonical medium types: Cosmic Voids, Walls / Sheets, Filaments, WHIM (Diffuse Overlapping Phase), and Dense Media (e.g., CGM, ISM, Halos).

Each segment is assigned:

• A volume-weighted probability of occurrence,
• A characteristic photon energy transfer coefficient α_i,
• A randomized length D_i ​ within empirically constrained bounds.

For each segment i, the redshift increment is calculated using the exponential attenuation relation6:

$$z_i=e^{{\alpha }_i{D}_i}-1$$

where α_i ​ is the photon–medium energy transfer coefficient (in ly⁻¹) and D_i​ is the segment length in light-years. This formulation reflects the cumulative energy transfer from photon–medium interactions across each localized segment.

Total redshift then accumulates multiplicatively across all segments7:

$$z=\prod _{i=1}^n\left(1+z_i\right)-1$$

Substituting the expression for z_i​, this compounding can be rewritten as8:

$$z=\left(\prod _{i=1}^n\left(1+\left(e^{{\alpha }_i{D}_i}-1\right)\right)\right)-1=\left(\prod _{i=1}^n{e}^{{\alpha }_i{D}_i}\right)-1$$

This identity demonstrates that redshift accumulated through compounded segment-wise increments is mathematically equivalent to applying an effective exponential attenuation across the total path. Accordingly, the total redshift can also be expressed in its closed-form equivalent9:

$$z=\exp \left(\sum _{i=1}^n\alpha ᵢDᵢ\right)-1$$

This logic captures both the nonlinearity and path-dependence of redshift accumulation: denser media encountered later in a photon's journey contribute disproportionately to the total redshift due to the exponential compounding of previously redshifted light. This mechanism underpins the C-PET simulation framework and distinguishes it from additive or linear attenuation models.

6.5.2. Segment Generation Logic

For each simulation run:

• The next segment type is selected probabilistically based on the volume fractions outlined in Section 6.3.2.
• A segment length is drawn randomly from the empirical range associated with that medium (e.g., 30–100 MLY for voids, 10–50 MLY for filaments).
• The corresponding α-value is applied to compute the segment’s redshift contribution.
• Total redshift is accumulated iteratively using the exponential compounding formula.

The process continues until a target redshift (e.g., z=14.4) is reached, and the total light-travel distance (in BLY) is recorded for that simulation instance.

6.5.3. Model Goals and Diagnostic Outputs

The stochastic simulation enables several key evaluations:

• Whether the cumulative redshift predicted by C-PET can match extreme observed redshift values (e.g., JWST targets [1,2,3,16,17,18]).
• What total photon path lengths are required under realistic segment distributions.
• How redshift accumulates as a function of segment type, order, and cosmic structure composition.

Outputs include:

• Total redshift vs. total path length
• Distribution of segment types per simulation
• Mean and variance of redshift contributions by medium
• Diagnostic heatmaps of redshift accumulation

This modeling strategy provides a physically grounded, non-expansion-based alternative to the redshift–distance relation assumed by ΛCDM [42,43,44]. It emphasizes the intervening cosmic medium, not comoving distance, as the primary redshift driver.

6.5.4. Implementation Notes

All parameter values, including α coefficients, path-length distributions, and medium fractions, are derived from current observational data [21,22,85,86,152,155] and appear in Appendix C.2. While these values are subject to refinement as new surveys (e.g., Euclid [139], SKA) improve our understanding of the intergalactic medium, the current set represents a conservative, physically plausible baseline.

The complete simulation algorithm and 100-run output example are documented in Appendix C.3. Researchers seeking to replicate or extend the C-PET model are encouraged to reference this implementation directly.

6.6. Redshift vs. Time Dilation: Decoupling Mechanisms in C-PET

In the ΛCDM model [42,43,44], cosmological redshift is inseparably tied to the expansion of space. As space stretches, light wavelengths elongate, and time intervals, such as the durations of supernova light curves, are expected to dilate by a factor of (1 + z). This linkage between redshift and time dilation is treated as a fundamental prediction of the expanding universe.

By contrast, the C-PET model does not rely on spatial expansion to explain redshift. Instead, redshift arises from cumulative, non-scattering energy transfer as photons traverse intergalactic media, including plasma, dust, and filaments [10,20]. Because this redshift mechanism does not involve the stretching of time, C-PET allows for a decoupling of redshift and time dilation.

6.6.1. C-PET Does Not Eliminate Time Dilation

C-PET preserves time dilation in relativistic contexts [45,46,47], such as due to high velocities or gravitational fields, fully consistent with special and general relativity. What C-PET challenges is the automatic assumption that cosmological redshift implies cosmological time dilation.

Under ΛCDM: Redshift is time dilation10 → $\Delta t_{observed}=\left(1+z\right)·\Delta t_{emitted}$

Under C-PET: Redshift arises from cumulative photon energy loss, not spacetime expansion, and does not intrinsically alter emission timing11:

$$\Delta tobserved\approx \Delta temitted$$

Apparent dilation may arise from observational bias, signal dispersion, or refractive delay in dense media, but not as a direct function of redshift.

Note: In this equation, Δt represents a time interval (e.g., the duration of an event). The equation reflects how observed durations appear stretched by a factor of 1+z, a phenomenon referred to as cosmological time dilation [42,43,44].

6.6.2. Observational Evidence: Is Time Dilation Actually Seen?

The observational case for cosmological time dilation remains inconclusive:

• Type Ia supernovae show some stretching consistent with (1+z), but their light curve analyses often assume ΛCDM templates [42,43,44], raising concerns of circularity in model validation.
• Gamma-ray burst (GRB) durations do not exhibit a consistent correlation between duration and redshift [87,88]. Given their intrinsic variability and diverse progenitor classes, GRBs present challenges for isolating cosmological dilation effects.
• Several independent studies have reported weaker-than-expected or absent time dilation signals at high redshifts [87,88], challenging the universality of the (1+z) scaling.

Under the C-PET model, these mixed results are not anomalies, they are expected. If redshift arises from cumulative photon energy transfer through cosmic media, time dilation should not automatically accompany redshift. Instead, dilation must be tested independently, not assumed.

6.6.3. Reframing the Redshift–Dilation Relationship

The table below contrasts how ΛCDM and C-PET interpret the relationship between redshift and time dilation, particularly in the context of supernova observations.

Table 6.6.3.1. Comparison of Redshift–Time Dilation Interpretations in ΛCDM and C-PET 

Feature		ΛCDM Interpretation [42,43,44]	C-PET Interpretation
Source of Redshift		Stretching of space	Cumulative photon energy transfer via IGM
Time Dilation Cause		Expansion stretches time	Only from motion or gravity (per relativity)
Supernova Light Curves		Must show (1 + z) stretching	Could vary independently of redshift
Model Flexibility		One-to-one link between z and time	Allows redshift without enforced time dilation

Note: Unlike ΛCDM, which rigidly links redshift to time dilation via metric expansion [42,43,44], C-PET permits redshift accumulation without requiring temporal stretching, opening the door to falsifiability through supernova light curve analysis and other time-based observations.

Table 6.6.3.1. Comparison of Redshift–Time Dilation Interpretations in ΛCDM and C-PET 

Feature		ΛCDM Interpretation [42,43,44]	C-PET Interpretation
Source of Redshift		Stretching of space	Cumulative photon energy transfer via IGM
Time Dilation Cause		Expansion stretches time	Only from motion or gravity (per relativity)
Supernova Light Curves		Must show (1 + z) stretching	Could vary independently of redshift
Model Flexibility		One-to-one link between z and time	Allows redshift without enforced time dilation

Note: Unlike ΛCDM, which rigidly links redshift to time dilation via metric expansion [42,43,44], C-PET permits redshift accumulation without requiring temporal stretching, opening the door to falsifiability through supernova light curve analysis and other time-based observations.

6.6.4. Summary

C-PET introduces a physically grounded mechanism for redshift based on photon–medium interactions but does not require cosmological time to stretch. This decoupling restores the ability to interpret redshift and time dilation as arising from distinct physical causes, not one mechanically tied to the other.

By preserving all relativistic time effects [45,46,47], while questioning assumptions tied to metric expansion [42,43,44], C-PET remains consistent with physics [7,8] and offers greater flexibility in interpreting astronomical time-domain data. Although C-PET conceptually decouples redshift from time dilation, a full quantitative treatment of supernova light curve stretching under this framework remains an open task. The groundwork for such modeling is outlined in Appendix E, and collaboration is invited to determine whether C-PET can replicate the observed correlation between redshift and time dilation without invoking metric expansion.

6.7. Spectral Fidelity at High Redshift: A Non-Scattering Explanation

A core observational challenge for any redshift mechanism is explaining why high-redshift galaxies exhibit sharp, coherent spectral lines [1,2,3,16,17,18], often from elements like oxygen, carbon, and hydrogen, even when their light has traversed tens or hundreds of billions of light-years. If photons interact with media over such vast distances, how is it that the spectral signatures are not blurred, scattered, or destroyed?

In the C-PET model, this question is addressed directly. C-PET proposes that redshift arises from non-scattering, infrequent photon interactions with intergalactic media. These interactions reduce photon energy cumulatively, but without altering the direction, coherence, or sharpness of the original spectral signal.

6.7.1. Spectral Line Preservation Without Expansion

In ΛCDM [42,43,44], spectral coherence is preserved because photons redshift via space stretching rather than any interaction-based mechanism. Critics of alternative models have long argued that "tired light" theories [136,142,143,144,145], where photons lose energy through interactions, must inherently blur or degrade spectra. But C-PET avoids this pitfall through a specific claim:

Photon energy transfer occurs without scattering. The path of the photon remains unperturbed; only its energy slowly changes.

This means:

• No spectral line broadening from collisions.
• No loss of phase coherence.
• No direction-altering diffusion.

As a result, sharp emission and absorption lines remain intact, exactly as observed in JWST spectra from galaxies with redshifts exceeding z > 10 [1,2,3,16,17,18].

6.7.2. Observational Support: JWST and Furthest Observed Galaxies

JWST's spectroscopy [1,2,3,16,17,18] has detected coherent features such as:

• [O III] and [O II] emission lines in galaxies at z ≈ 7–14 [55,56].
• Balmer breaks and Lyman-alpha absorption troughs that align with standard models of stellar atmospheres and ionized gas [58,59,60].

These features [1,2,3,16,17,18]:

• Show no anomalous smearing or energy redistribution.
• Retain high signal-to-noise ratios and wavelength fidelity.

This empirical consistency supports C-PET's assumption that energy transfer can occur without disturbing the structure or identity of spectral information.

6.7.3. Theoretical Consistency with QED and Plasma Physics

C-PET's mechanism is grounded in well-established physical principles [7,8]:

• Quantum Electrodynamics (QED) [7] allows for photon–electron interactions (e.g., forward Compton effects) that alter energy without causing deflection.
• Plasma physics supports energy exchange through weak coupling with free electrons [27,28,29], especially in ultra-low-density environments like the IGM and CGM [21,22].
• Interstellar scintillation, dispersion, and weak lensing all confirm that light can be modulated by medium properties without destruction of coherence [31,32].

Thus, C-PET's claim is not speculative, it is a scaling-up of known photon-medium behaviors across cosmological distances.

6.7.4 Summary

The sharpness and fidelity of high-redshift spectra [1,2,3,16,17,18] are not problematic for C-PET, they are expected. C-PET explains redshift through a process that is:

• Directional and coherent,
• Energy-altering but non-destructive, and
• Cumulative but smooth.

This allows it to match, and in some respects, better predict, the clean spectral features reported by modern observatories like JWST [1,2,3,16,17,18]. Far from invalidating interaction-based redshift, spectral coherence provides a crucial validation point for the non-scattering energy transfer proposed in the C-PET model.

6.8. Section Summary: Redshift Predictions and Observational Matches

The PUT+C-PET model explains cosmological redshift not as the result of space stretching, but as the cumulative outcome of photon energy transfer (PET) across cosmic media. This reinterpretation avoids reliance on speculative constructs like inflation [13,14,15] or dark energy [42,43,44], instead applying known physical principles [7,8], such as photon–plasma coupling, refractive delay, and infrequent, non-scattering interactions, to account for observed redshift behavior.

The following table summarizes how the C-PET model's interpretation of key redshift-related phenomena aligns with current astronomical observations, reinforcing its consistency with empirical data and physical law.

Table 6.8.1. Observational Alignment of C-PET Predictions Across Redshift Phenomena 

Phenomenon	C-PET Interpretation	Observational Alignment
High-z galaxies	Ancient light redshifted via vast medium traversal	JWST detections of mature, dusty galaxies at z > 10 [1,2,3,16,17,18]
Oxygen at high-z	No constraint from age; enrichment evolves locally	[O III] and [O II] lines observed at z ~ 10–14 [55,56]
Redshift–distance curvature	Cumulative PET through segmented media	Matches Pantheon+/SN Ia deviations from linear Hubble law [38]
Spectral line sharpness	PET does not scatter photons	Spectral coherence preserved at high redshifts [1,2,3,16,17,18]
Surface brightness dimming	Compound PET and refractive delay	Matches Tolman dimming profile (see Section 4.6)
No superluminal recession	No metric expansion; c remains constant	Compatible with Special and General Relativity [7,8]

Note: In this context, "photon energy transfer" (PET) refers to both cumulative energy loss via non-scattering interactions and minor refractive delays within structured cosmic media [10,20,21,22]. Together, these effects enable C-PET to reproduce key observational signatures without invoking expansion or metric-based interpretations.

Table 6.8.1. Observational Alignment of C-PET Predictions Across Redshift Phenomena 

Phenomenon	C-PET Interpretation	Observational Alignment
High-z galaxies	Ancient light redshifted via vast medium traversal	JWST detections of mature, dusty galaxies at z > 10 [1,2,3,16,17,18]
Oxygen at high-z	No constraint from age; enrichment evolves locally	[O III] and [O II] lines observed at z ~ 10–14 [55,56]
Redshift–distance curvature	Cumulative PET through segmented media	Matches Pantheon+/SN Ia deviations from linear Hubble law [38]
Spectral line sharpness	PET does not scatter photons	Spectral coherence preserved at high redshifts [1,2,3,16,17,18]
Surface brightness dimming	Compound PET and refractive delay	Matches Tolman dimming profile (see Section 4.6)
No superluminal recession	No metric expansion; c remains constant	Compatible with Special and General Relativity [7,8]

Note: In this context, "photon energy transfer" (PET) refers to both cumulative energy loss via non-scattering interactions and minor refractive delays within structured cosmic media [10,20,21,22]. Together, these effects enable C-PET to reproduce key observational signatures without invoking expansion or metric-based interpretations.

This redshift model preserves physical law [7,8], avoids causality violations [45,46,47], and remains testable using available instruments and data [1,2,3,16,17,18]. Future gravitational wave detectors may provide independent tests of distance-redshift relationships [19].The result is a physically grounded alternative to ΛCDM's expansion paradigm [42,43,44], one that places observable phenomena at the heart of cosmic interpretation.

7.0. Explaining the CMB through Photon–Medium Energy Transfer

Building on the C-PET model of redshift presented in Section 6, this section explores its implications for one of the most iconic signatures in cosmology: the Cosmic Microwave Background (CMB). The CMB is widely interpreted as relic radiation from a primordial origin, emitted during the recombination epoch and redshifted over billions of years by an expanding universe [91,95,106,107,108]. In contrast, the C-PET model proposes that the observed microwave background is not a remnant of a singular event, but an emergent, ongoing phenomenon resulting from continuous photon–medium interactions across infinite space and time.

Within the C-PET model, the CMB is characterized as a Photon–Medium Microwave Thermal Field (PMMTF): a diffuse, statistically uniform radiation field arising from the cumulative energy transfer of photons as they traverse the cosmos. High-energy radiation from stars, AGN, and other luminous sources undergo infrequent, non-scattering interactions with intergalactic media, including plasma, dust, ionized gases, and cosmic filaments [21], gradually transferring energy into the medium. This energy is then thermalized and re-emitted at microwave frequencies over cosmological timescales.

The observed temperature of this field, 2.7 K [104], refers specifically to its radiation temperature, which characterizes the spectral energy distribution of the re-emitted photons. It does not imply that the kinetic temperature of the intergalactic medium is 2.7 K. Within the C-PET model, this value reflects the average energy of the photon field itself, not the thermal state of the medium from which it arises.

This interpretation unifies redshift and background radiation within a single, physically grounded framework. It eliminates the need for inflation [13,14,15,110], recombination epochs, or singular origins, instead attributing the CMB's blackbody spectrum, isotropy, and anisotropies to well-understood thermodynamic and electromagnetic processes [103] operating across an infinite, structure-filled universe.

The C-PET model reflects a cosmos that continuously redistributes photon energy through interactions with the intergalactic medium, potentially giving rise to a diffuse microwave background field. Whether this field, the PMMTF, can reproduce the observed features of the CMB is a testable hypothesis explored in the following sections and Appendix E.

Reproducing the precise spectral coherence and anisotropy properties of the observed CMB under the PMMTF hypothesis presents a significant challenge. Whether cumulative re-radiation from structured media can maintain the required blackbody fidelity and isotropy is an open modeling question addressed in Appendix E.

7.1. Thermodynamic Grounding of the PMMTF

While Section 7.0 introduces the PMMTF as a hypothesis, its physical plausibility rests on known thermodynamic principles [48,96] and must be assessed in terms of spectral shape, energy density, and isotropy constraints. In a sparse but nonzero medium, infrequent energy exchanges between photons and matter (e.g., via inverse bremsstrahlung or dielectric coupling) promote gradual thermalization. Over infinite time and space, C-PET posits that this process leads to a statistically uniform microwave background, consistent with the CMB's blackbody spectrum, without requiring a hot origin or singular event.

7.2. Energy Redistribution and the PMMTF Hypothesis

In the C-PET model, energy lost by photons through cumulative, infrequent interactions with the intergalactic medium is not destroyed but redistributed. Over cosmological distances and timescales, this gradual energy transfer is proposed to contribute to a diffuse microwave-frequency background field, referred to here as the Photon–Medium Microwave Thermal Field (PMMTF). Rather than asserting the PMMTF as the definitive origin of the observed cosmic microwave background (CMB), we frame it as a testable hypothesis that emerges naturally from the C-PET mechanism.

This redistribution process does not rely on local thermodynamic equilibrium (LTE), which is implausible at intergalactic densities [22,23]. We explicitly distinguish between statistical uniformity and true thermal equilibrium. While the observed CMB spectrum closely matches a blackbody curve [104], such precision normally arises from high-collision environments that enable full equilibration, conditions not assumed here. Instead, we propose that statistically uniform re-radiation from a vast population of low-temperature plasma environments, such as filaments, halos, and circumgalactic media, could yield a background field with spectral and spatial characteristics similar to those of the CMB. This resemblance is treated as an empirical question rather than an assumed result.

To avoid confusion, we clarify three temperature-related terms used in this framework. Kinetic temperature refers to the average motion of particles in a plasma or medium, often measured in the range of 10⁴–10⁶ K for intergalactic gas [21]. Radiation temperature describes the spectral energy distribution of a photon field, such as the CMB, typically measured at ~2.725 K [104]. Effective temperature is used as a modeling convenience when full equilibrium is not present but an aggregate property like a thermal spectrum still emerges [96,97]. In C-PET, the PMMTF is characterized by an effective radiation temperature that does not imply equilibrium with the kinetic properties of the emitting medium.

A key test is whether statistically averaging over anisotropic cosmic structures can produce the observed isotropy to one part in 10⁵ ^[ [91]^], or whether additional coupling mechanisms are required.

The energy transfer mechanism in C-PET is consistent with small-angle Compton or Thomson-like scattering with recoil [103], as described by quantum electrodynamics (QED) through the Klein–Nishina formalism [7]. In this low-recoil, forward-directed regime, photons undergo coherent energy transfer to the medium while preserving directionality and spectral sharpness. These interactions satisfy both energy and momentum conservation and become significant only cumulatively over cosmological distances. By invoking this class of QED-consistent processes, C-PET provides a physically grounded explanation for redshift that aligns with observed spectral coherence and avoids the scattering-induced distortions that undermine earlier non-expansion models.

The feasibility of this hypothesis, including whether cumulative energy loss under C-PET can reproduce the observed CMB's energy density, spectral coherence, and isotropy, is tested through the modeling framework outlined in Appendix E. Further work is required to determine whether mechanisms consistent with C-PET can achieve the observed spectral and isotropic precision, an outcome that would critically inform the validity of the PMMTF hypothesis.

To formalize the energy transfer that underpins the PMMTF hypothesis, we express the total photon energy transferred to the cosmic medium across redshift as12:

$$E_{transferred}=\int {\Phi }_{\gamma \left(z\right)}·\alpha \left(z\right)·\left({\displaystyle \frac{d\mathcal{l}}{dz}}\right)dz$$

Where:

• Φ_γ(z) is the comoving photon flux density (function of redshift),
• α(z) is the effective photon–medium energy transfer coefficient (units: fractional energy loss per unit distance),
• dℓ/dz ​ is the differential light-travel path per unit redshift in the C-PET non-expanding geometry.

This integral estimates the total energy lost by photons over cosmic distances via non-scattering interactions. The viability of the PMMTF hypothesis hinges on whether this cumulative energy transfer approximates the observed microwave background energy density [33]13:

$$u_{CMB}\approx 4.17\times {\displaystyle \frac{{10}^{-14}J}{m^3}}$$

Appendix E outlines the modeling steps necessary to determine whether this cumulative photon–medium energy transfer, when applied to realistic cosmic structures and source populations, can replicate the observed precision and intensity of the CMB, recharacterized here as the Photon–Medium Microwave Thermal Field (PMMTF).

7.3. CMB Properties Reframed Without Expansion

In the ΛCDM model, inflation [13,14,15] is invoked to explain the CMB's extreme isotropy despite causally disconnected regions. This rapid early expansion is said to have smoothed out temperature fluctuations before recombination, creating the observed uniformity.

By contrast, the C-PET model, operating within an infinite, non-expanding universe, proposes that no such causal discontinuity arises. Instead, it raises the hypothesis that the observed isotropy of the microwave background may emerge as a statistical consequence of continuous, infrequent photon–medium interactions distributed across cosmic time and space.

This reframes the problem: rather than requiring speculative inflationary physics and a singular hot origin, the challenge becomes one of testing whether known physical processes, acting across an infinite, structure-filled universe, can reproduce the CMB's key features. These include its temperature [104], isotropy [91], anisotropy spectrum [105,109], spectral shape [104], and energy density [33].

The table below contrasts standard interpretations of the CMB's key features under ΛCDM with the proposed mechanisms and open predictions of C-PET and the PMMTF hypothesis.

Table 7.3.1. Interpretative Comparison of CMB Properties: ΛCDM vs. C-PET/PMMTF 

CMB Feature	ΛCDM Interpretation	C-PET / PMMTF Hypothesis
Temperature (~2.725 K)	Redshifted relic of recombination epoch [91]	May result from cumulative photon energy loss and re-emission in large-scale cosmic media
Isotropy	Inflation smoothed early plasma [13,14,15]	Hypothesized to arise via statistical averaging over distributed, omnidirectional emissions
Anisotropies (ΔT ~10⁻⁵)	Acoustic peaks from primordial oscillations [99,10,101]	Possibly imprinted by filamentary or segmented media structure (subject to modeling)
Blackbody spectrum	Result of early thermal equilibrium [91]	Convergence from reprocessed energy in low-density plasma environments (under evaluation)
Energy conservation	Temporarily violated by inflation/dark energy [13]	Preserved via cumulative photon–medium coupling and delayed re-radiation
Directionality	Single emission event from all directions [91]	Ongoing, directionally distributed energy deposition and re-emission

Note: The C-PET/PMMTF framework does not assert that it reproduces these features, but that it offers a physically grounded, testable alternative to expansion- and relic-based interpretations. Whether the cumulative processes described can quantitatively match the precision and structure of the CMB is a matter for future modeling and observational validation (see Appendix E).

Table 7.3.1. Interpretative Comparison of CMB Properties: ΛCDM vs. C-PET/PMMTF 

CMB Feature	ΛCDM Interpretation	C-PET / PMMTF Hypothesis
Temperature (~2.725 K)	Redshifted relic of recombination epoch [91]	May result from cumulative photon energy loss and re-emission in large-scale cosmic media
Isotropy	Inflation smoothed early plasma [13,14,15]	Hypothesized to arise via statistical averaging over distributed, omnidirectional emissions
Anisotropies (ΔT ~10⁻⁵)	Acoustic peaks from primordial oscillations [99,10,101]	Possibly imprinted by filamentary or segmented media structure (subject to modeling)
Blackbody spectrum	Result of early thermal equilibrium [91]	Convergence from reprocessed energy in low-density plasma environments (under evaluation)
Energy conservation	Temporarily violated by inflation/dark energy [13]	Preserved via cumulative photon–medium coupling and delayed re-radiation
Directionality	Single emission event from all directions [91]	Ongoing, directionally distributed energy deposition and re-emission

Note: The C-PET/PMMTF framework does not assert that it reproduces these features, but that it offers a physically grounded, testable alternative to expansion- and relic-based interpretations. Whether the cumulative processes described can quantitatively match the precision and structure of the CMB is a matter for future modeling and observational validation (see Appendix E).

7.4. Section Summary: The CMB Without a Big Bang

The C-PET model provides a testable, physically consistent alternative to ΛCDM’s origin story for the CMB. Rather than requiring a hot beginning, it explains the CMB as a photon–medium microwave thermal field generated by countless energy transfers from luminous sources across an infinite cosmos. It is not a snapshot of the past, but a signal continuously maintained by the structure and physics of the universe itself.

This view preserves the observed spectral properties of the CMB while freeing cosmology from the paradoxes of inflation, singularities, and causal gaps. In doing so, it reframes the CMB not as a relic, but as an ongoing emergent signature of cosmic structure and photon–medium interaction.

7.5. Core Assumptions Behind the PMMTF Model

The Photon–Medium Microwave Thermal Field (PMMTF) model rests on a set of physically grounded assumptions that distinguish it from relic-based interpretations of the CMB. These core principles define how continuous photon–medium interactions across cosmic time and space give rise to the thermal background observed today:

• Causality: 
• The CMB is not a relic of a singular event, but the ongoing result of countless photons transferring energy to the intergalactic medium (IGM).
• Mechanism: 
• This energy transfer occurs via Cumulative Photon Energy Transfer (C-PET), a non-scattering, infrequent interaction between light and IGM (plasma, dust, CGM, etc.).
• Medium Response: 
• The IGM absorbs this energy and re-radiates it in the microwave/sub-mm range, achieving thermalization over time.
• Directionality: 
• These interactions occur along all photon trajectories, from all directions, not from a single cosmic event.
• Temporal Nature: 
• The process is continuous and self-sustaining, not episodic or bounded by cosmic epochs.
• Statistical Equilibrium: 
• The observed blackbody profile of the CMB emerges from the integrated, thermodynamic equilibrium of countless micro-interactions over infinite time and space.

7.6. Filamentary Imprints and the Origin of CMB Anisotropies

In the ΛCDM model, the peaks and troughs of the CMB angular power spectrum are attributed to acoustic oscillations in the primordial photon–baryon plasma, frozen into place at the time of recombination [99,100,101]. These so-called "acoustic peaks" are seen as a signature of early-universe sound waves reverberating in a hot, dense environment.

However, under the C-PET model, these harmonic features can be reinterpreted as the result of structured photon–medium interactions across an infinite cosmic volume. As photons traverse the intergalactic medium, including dense cosmic filaments [10], ionized plasma regions, and vast voids [132,133], they experience variable rates of energy transfer, depending on the local density, composition, and ionization state of the medium.

This segmented traversal produces non-uniform energy transfer patterns that lead to anisotropies in the microwave background. The statistically coherent nature of these fluctuations arises from the quasi-regular spacing and self-similar distribution of cosmic filaments across scales.

Rather than invoking early-universe oscillations, C-PET offers an alternative interpretation of the CMB peaks as potentially arising from:

• Cumulative redshift and thermalization occurring as photons pass through large-scale structures;
• Segmented medium effects, where filaments and voids imprint differential optical depths;
• Statistical coherence, emerging from the spatial regularity of filamentary structures across vast distances.

This interpretation not only aligns with the known properties of the cosmic web but also removes the need for inflationary origin stories and fine-tuned oscillatory models. The CMB anisotropies thus become another emergent, testable feature of photon–medium interaction across an infinite, structured universe.

7.7. Energy Conservation and the Thermal Fate of Redshifted Photons

One of the most persistent critiques of interaction-based redshift mechanisms has been the question: “Where does the energy go?” In many “tired light” models, energy is lost without explanation, seemingly vanishing in contradiction to the conservation of energy.

The C-PET model directly addresses this. It does not treat redshift as an undefined or irreversible loss. Instead, it posits that photons transfer energy to the intergalactic medium, via electromagnetic coupling with electrons, plasma waves, and collective particle-field interactions. This ensures that energy is conserved across all photon trajectories.

7.7.1. Mechanisms of Energy Transfer in the IGM

Photons traversing space encounter various cosmic media, including:

• Ionized plasma in voids and filaments [21],
• Circumgalactic and interstellar dust [54], and
• Weakly magnetized, low-density electron fields [34,35,36].

In these media, energy is not scattered or absorbed in discrete interactions, but instead gradually transferred via infrequent, non-scattering mechanisms [103] such as:

• Inelastic Compton-like forward energy exchange,
• Plasma wave excitation,
• Dielectric polarization and thermal coupling at quantum scales.

These interactions result in a very small per-segment energy decrement [103], but accumulate to produce the redshifts we observe. The energy, in turn, heats the medium slightly, raising its thermal content over time.

7.7.2. Thermalization and the Emergence of the CMB

In the C-PET model, the redistributed photon energy is not considered lost. Rather, it is proposed that this energy is eventually re-emitted by the intergalactic medium, particularly in the low-energy microwave and sub-millimeter bands. Over cosmological timescales, this process may:

• Lead to a statistical equilibrium in the background radiation field [96,97],
• Generate a thermal spectrum consistent with the observed 2.725 K blackbody [104],
• Contribute to the photon–medium microwave thermal field (PMMTF) described more fully throughout this section.

From this perspective, redshift and the CMB are not separate phenomena, but potentially two aspects of the same interaction. Redshift could represent energy transferred away from photons, while the CMB may emerge as the diffuse, re-radiated signal from the medium after accumulation and thermalization.

7.7.3 Contrasting C-PET with ΛCDM

The C-PET model differs fundamentally from ΛCDM in its treatment of redshift, energy conservation, and the origin of the cosmic microwave background. The table below highlights these conceptual differences. Table 7.7.3.1: Conceptual Comparison of Redshift and Energy Behavior in C-PET vs. ΛCDM
Concept	ΛCDM Framework	C-PET Model
Redshift cause	Expansion of space [42,43]	Energy transfer to medium
Energy conservation	Temporarily broken (during inflation, dark energy) [13]	Fully preserved across all epochs
CMB origin	Relic from early hot plasma [91]	Thermal re-emission from photon–medium interaction
Photon energy fate	“Stretched” with no destination	Transferred to medium, then re-radiated
Note: In ΛCDM, energy non-conservation during expansion and inflation is consistent with general relativity's treatment of dynamic spacetime metrics [45,46,47]. However, C-PET maintains conservation by modeling redshift as a physical energy exchange process rather than a geometric effect.

7.7.4. Summary

C-PET honors the principle of energy conservation by treating redshift as a reversible, physical interaction with the medium. The energy removed from photons does not vanish, it is absorbed into the medium and eventually re-radiated, contributing to the observed microwave background and low-level thermal field of the cosmos.

By embedding photon redshift within the framework of known electromagnetic and thermodynamic behavior [103], C-PET offers a cohesive, physically consistent, and testable alternative to expansion-driven cosmology.

7.8. Summary: C-PET and PMMTF as a Unified, Physically Consistent Explanation of the CMB

C-PET proposes that the Cosmic Microwave Background (CMB) is not a fading relic from a primordial fireball, but the ongoing result of photon–medium interactions across an infinite and structure-filled universe. Through infrequent, non-scattering energy transfers, photons gradually impart energy to the intergalactic medium (IGM) [21,22], which over time reaches thermal equilibrium and emits a faint, statistically uniform background signal.

This background is characterized by:

• A blackbody spectrum (~2.725 K) formed through long-term energy transfer and re-emission [104];
• Anisotropies that reflect filamentary structure [10], not acoustic oscillations [99,100,101];
• Isotropy that emerges naturally in an infinite universe without inflation [13,14,15];
• Energy conservation through photon-to-medium transfer and thermalization.

To clarify these distinctions, the following table contrasts core interpretive categories between the ΛCDM model and the C-PET/PMMTF approach to the CMB.

Table 7.8.1. Comparative Advantages of C-PET/PMMTF Over ΛCDM in Explaining the CMB 

Category	ΛCDM Limitations	C-PET (PMMTF) Advantage
CMB origin	Requires inflation, recombination, singularity [13,91]	Emerges from photon–medium energy transfer across space/time
Energy conservation	Violated by inflation and dark energy [13]	Fully preserved through thermodynamic and EM interactions
Acoustic anisotropies	Attributed to primordial oscillations [99,100,101]	Arise from filamentary traversal and segmented energy deposition
Directionality	Single emission event at recombination [91]	Continuous, omnidirectional PET from all trajectories
Observability	Based on early-universe constructs [91]	Based on ongoing, testable photon–IGM processes

Note: While ΛCDM explains the CMB using early-universe conditions, these require indirect inference from unobservable epochs. C-PET offers an alternative grounded in currently observable interactions between photons and the intergalactic medium.

Table 7.8.1. Comparative Advantages of C-PET/PMMTF Over ΛCDM in Explaining the CMB 

Category	ΛCDM Limitations	C-PET (PMMTF) Advantage
CMB origin	Requires inflation, recombination, singularity [13,91]	Emerges from photon–medium energy transfer across space/time
Energy conservation	Violated by inflation and dark energy [13]	Fully preserved through thermodynamic and EM interactions
Acoustic anisotropies	Attributed to primordial oscillations [99,100,101]	Arise from filamentary traversal and segmented energy deposition
Directionality	Single emission event at recombination [91]	Continuous, omnidirectional PET from all trajectories
Observability	Based on early-universe constructs [91]	Based on ongoing, testable photon–IGM processes

Note: While ΛCDM explains the CMB using early-universe conditions, these require indirect inference from unobservable epochs. C-PET offers an alternative grounded in currently observable interactions between photons and the intergalactic medium.

By reframing the CMB as an active, emergent microwave field sustained by cosmic structure, PUT+C-PET retains explanatory power while avoiding inflation, causal paradoxes, or unobservable epochs. C-PET interprets the PMMTF as a living, thermodynamic signature of the universe’s physical continuity, not a fossil of its supposed explosive beginning.

7.9. Future Modeling: Predicting the PMMTF Spectrum from C-PET

The C-PET model posits that the observed cosmic microwave background (CMB), characterized as the Photon–Medium Microwave Thermal Field (PMMTF), arises from cumulative photon energy transfer into the intergalactic medium (IGM) over infinite space and time. A future modeling effort should formally calculate whether the integrated energy deposited by starlight and radiative emissions [58,59,60], filtered through known densities, temperatures, and compositions of the IGM [21,22,23], can reproduce the observed blackbody spectrum (~2.725 K) and energy density of the CMB [104]. Such a simulation would offer a direct test of IUF + C-PET and its consistency with energy conservation, plasma physics, and thermodynamic behavior [96,97] in the large-scale universe. This work invites further collaboration and validation by specialists in radiative transfer [102,103] and intergalactic thermodynamics.

8.0. Comparative Analysis: Evaluating the Infinite Universe Framework in Context

To assess the explanatory power and originality of the Infinite Universe Framework (IUF), which combines the Physical Universe Theory (PUT) and the Cumulative Photon Energy Transfer (C-PET) model, it is necessary to situate this framework alongside competing cosmological models. These include:

• The Standard Big Bang Cosmology (ΛCDM) [42,43,91],
• Alternative infinite-universe theories (e.g., Steady State [111,112], Plasma Cosmology [115,116], Tired Light [136]),
• Modern theoretical alternatives (e.g., Conformal Cyclic Cosmology [123], Scale-Invariant Cosmology [122], VSL [122]),
• Multiverse hypotheses [125].

Although all these models aim to explain redshift, structure formation, and background radiation, they diverge fundamentally in their assumptions about space, time, and physical law. IUF distinguishes itself by retaining adherence to known physical laws, avoiding speculative constructs, and grounding redshift and radiation phenomena in observable photon–medium interactions across an infinite and structurally rich cosmos.

8.1 Interpreting the Evidence for Expansion

The dominant ΛCDM model [42,43] attributes cosmic redshift and the thermal background radiation to spatial expansion and a hot origin. Five main observational pillars are commonly cited in support:

• Redshift–distance correlation (Hubble's Law) [37,80,81],
• Blackbody spectrum of the CMB [91,104],
• Surface brightness dimming scaling as (1 + z)⁴ ^[ [49]^],
• Time dilation in high-z supernova light curves [87,88],
• Large-scale structure evolution from early fluctuations [85,86].

The Infinite Universe Framework does not dispute these observations, but offers a different physical interpretation of their causes:

• Redshift is attributed to cumulative photon energy transfer (C-PET) through cosmic media such as plasma, dust, and filaments, not to space stretching. This preserves energy conservation and avoids non-intuitive constructs like metric expansion or recession velocities exceeding the speed of light.
• The CMB, reinterpreted as the Photon–Medium Microwave Thermal Field (PMMTF), arises from the long-term accumulation and re-emission of photon energy in intergalactic media. This reinterpretation preserves the observed isotropy and thermal spectrum without requiring a primordial explosion or recombination epoch.
• Surface brightness dimming and time dilation are retained in IUF, but they emerge as consequences of photon–medium interaction dynamics and relativistic propagation, not expansion. In IUF, supernova dimming arises from cumulative photon energy loss and refractive light-travel delays through structured cosmic media.
• Large-scale structure is not assumed to have emerged from primordial fluctuations alone. Instead, it is seen as the product of ongoing gravitational evolution in a cosmos without age limits or temporal boundaries.

While ΛCDM successfully aligns with many observational patterns, it does so by introducing constructs that are not directly observable, such as superluminal inflation [13,14,15,110], dark energy [78,79], and non-baryonic dark matter [128,129]. Furthermore, several tension points remain unresolved. For instance, redshift asymmetries observed in certain galaxy populations challenge the simplicity of a smooth Hubble flow. Similarly, surface brightness measurements of distant galaxies appear dimmer than expected under standard expansion models unless fine-tuned corrections are applied.

Critically, metric expansion results in a breakdown of global energy conservation, a feature mathematically permitted in general relativity [45,46,47] but physically at odds with thermodynamic and quantum field expectations [7,8]. By contrast, IUF retains local and cumulative energy conservation. It interprets redshift and dimming not as results of stretching space but as the aggregate outcome of infrequent, non-scattering photon–medium interactions. These interactions are physically grounded, potentially measurable, and fully compatible with conservation principles.

8.2. IUF vs. ΛCDM: A Structured Comparison

Despite ΛCDM's dominance, it rests on multiple speculative constructs that remain untested or inconsistent with known physics. IUF offers a parsimonious alternative rooted in conservation laws and observable phenomena.

The table below outlines key conceptual differences between ΛCDM and the Infinite Universe Framework (IUF), highlighting how IUF resolves points of tension using known physical principles rather than speculative constructs.

Table 8.2.1. Conceptual Comparison of ΛCDM and IUF Across Key Cosmological Claims 

ΛCDM Construct or Claim	Conflict with Known Physics	IUF Resolution
Big Bang Singularity	Violates continuity and energy conservation	No singularity; universe is infinite in space and time
Inflation [13,14,15,110]	Requires superluminal expansion and exotic fields	Not required; isotropy arises from infinite spatial averaging
Dark Energy [78,79]	Undetected; invoked to preserve expansion fit to SN data	Redshift explained by cumulative energy transfer, not expansion
Dark Matter [128,129]	Still undetected directly	Galaxy dynamics addressed through known structures and observable matter
Expansion-Based Redshift [80]	Implies energy loss without conservation	Redshift arises from cumulative photon–medium energy transfer (C-PET)
Superluminal Recession [42,43]	Requires coordinate velocities exceeding c	No expansion; all light paths remain subluminal and real
Tolman Brightness Dimming [49]	Requires (1 + z)⁴ scaling via expansion	Dimming arises from photon energy loss and refractive delay
CMB as Relic of Recombination [13,91]	Requires fine-tuned early conditions	Explained as PMMTF, accumulated thermalization in IGM
Acoustic Peaks in CMB [99,100,101]	Tied to primordial oscillations	Recast as filamentary and structural imprints in an infinite cosmos
Conservation of Energy [13,45]	Violated in expansion and inflation	Preserved via photon–medium energy exchange

Note: While ΛCDM accommodates these constructs within general relativity’s framework, many involve unobservable epochs, hypothetical particles, or fields. IUF resolves the same phenomena using photon–medium interactions, preserving conservation laws and limiting assumptions to empirically grounded physics.

Table 8.2.1. Conceptual Comparison of ΛCDM and IUF Across Key Cosmological Claims 

ΛCDM Construct or Claim	Conflict with Known Physics	IUF Resolution
Big Bang Singularity	Violates continuity and energy conservation	No singularity; universe is infinite in space and time
Inflation [13,14,15,110]	Requires superluminal expansion and exotic fields	Not required; isotropy arises from infinite spatial averaging
Dark Energy [78,79]	Undetected; invoked to preserve expansion fit to SN data	Redshift explained by cumulative energy transfer, not expansion
Dark Matter [128,129]	Still undetected directly	Galaxy dynamics addressed through known structures and observable matter
Expansion-Based Redshift [80]	Implies energy loss without conservation	Redshift arises from cumulative photon–medium energy transfer (C-PET)
Superluminal Recession [42,43]	Requires coordinate velocities exceeding c	No expansion; all light paths remain subluminal and real
Tolman Brightness Dimming [49]	Requires (1 + z)⁴ scaling via expansion	Dimming arises from photon energy loss and refractive delay
CMB as Relic of Recombination [13,91]	Requires fine-tuned early conditions	Explained as PMMTF, accumulated thermalization in IGM
Acoustic Peaks in CMB [99,100,101]	Tied to primordial oscillations	Recast as filamentary and structural imprints in an infinite cosmos
Conservation of Energy [13,45]	Violated in expansion and inflation	Preserved via photon–medium energy exchange

Note: While ΛCDM accommodates these constructs within general relativity’s framework, many involve unobservable epochs, hypothetical particles, or fields. IUF resolves the same phenomena using photon–medium interactions, preserving conservation laws and limiting assumptions to empirically grounded physics.

8.3. IUF Compared to Other Infinite Universe Theories

Several alternative models have challenged the Big Bang paradigm by proposing a cosmos without beginning. IUF shares this infinite framework but introduces C-PET as a physically consistent redshift mechanism, improving upon their limitations.

The table below compares IUF with earlier infinite-universe models, highlighting how the integration of C-PET addresses key observational and physical limitations found in prior theories.

Table 8.3.1. Comparison of IUF with Alternative Infinite-Universe Cosmologies 

Theory	Redshift Mechanism	Strengths	Limitations	IUF Improvement
Steady State (Hoyle) [111,112,114]	Metric expansion + matter creation	No origin; philosophical simplicity	Refuted by CMB; requires ongoing matter creation	IUF avoids matter creation and explains CMB as PMMTF
Plasma Cosmology [115,116,117,118]	Plasma scattering & EM fields	Known plasma physics; no Big Bang	Weak on galaxy evolution; lacks large-scale modeling	C-PET uses plasma as one medium among many; no overreliance
Tired Light [136,142,143,144,145]	Photon energy loss	Simple; intuitive mechanism	Fails time dilation and spectral coherence tests	C-PET preserves sharp spectra, coherence, and time dilation

Note: While earlier infinite-universe models rejected the Big Bang, they lacked full consistency with observed spectral sharpness, time dilation, or structural evolution. IUF addresses these gaps by incorporating C-PET, a testable, physically grounded mechanism based on photon–medium interactions across known cosmic structures.

Table 8.3.1. Comparison of IUF with Alternative Infinite-Universe Cosmologies 

Theory	Redshift Mechanism	Strengths	Limitations	IUF Improvement
Steady State (Hoyle) [111,112,114]	Metric expansion + matter creation	No origin; philosophical simplicity	Refuted by CMB; requires ongoing matter creation	IUF avoids matter creation and explains CMB as PMMTF
Plasma Cosmology [115,116,117,118]	Plasma scattering & EM fields	Known plasma physics; no Big Bang	Weak on galaxy evolution; lacks large-scale modeling	C-PET uses plasma as one medium among many; no overreliance
Tired Light [136,142,143,144,145]	Photon energy loss	Simple; intuitive mechanism	Fails time dilation and spectral coherence tests	C-PET preserves sharp spectra, coherence, and time dilation

Note: While earlier infinite-universe models rejected the Big Bang, they lacked full consistency with observed spectral sharpness, time dilation, or structural evolution. IUF addresses these gaps by incorporating C-PET, a testable, physically grounded mechanism based on photon–medium interactions across known cosmic structures.

Where previous infinite-universe models lacked physical completeness or observational fit, IUF builds a testable model grounded in photon–medium interactions, spectral preservation, and known plasma/filamentary structures.

8.4. IUF vs. Modern Theoretical Alternatives

Beyond infinite models, several more recent cosmologies have emerged. These often modify fundamental physics or spacetime structure. IUF diverges by preserving known laws.

The following table compares IUF to several modern cosmological models that modify foundational physics, highlighting how IUF addresses the same phenomena without departing from established physical laws.

Table 8.4.1. Comparison of IUF with Modern Theoretical Cosmologies 

Theory	Core Concept	Limitation	IUF Response
Conformal Cyclic Cosmology [123,124]	Universe resets via conformal boundary	Requires entropy resets and geometric transformations	IUF avoids resets entirely via continuity in an infinite cosmos
Quasi-Steady State Cosmology [113]	Periodic matter creation during expansion	Inconsistent with metallicity and galaxy evolution	IUF avoids expansion and explains structure through long-term evolution
Scale-Invariant Cosmology [121,122]	Physical laws vary with scale	Modifies relativity; limited empirical grounding	IUF retains fixed physical laws across all scales
VSL Theories (e.g., Moffat) [122]	Speed of light changes over time	Violates Lorentz invariance; lacks strong evidence	IUF keeps ccc constant; redshift from energy transfer, not VSL

Note: These models attempt to resolve cosmological tensions by altering spacetime structure or fundamental constants. IUF instead explains redshift and cosmic structure through physically grounded, testable mechanisms, without revising established physics.

Table 8.4.1. Comparison of IUF with Modern Theoretical Cosmologies 

Theory	Core Concept	Limitation	IUF Response
Conformal Cyclic Cosmology [123,124]	Universe resets via conformal boundary	Requires entropy resets and geometric transformations	IUF avoids resets entirely via continuity in an infinite cosmos
Quasi-Steady State Cosmology [113]	Periodic matter creation during expansion	Inconsistent with metallicity and galaxy evolution	IUF avoids expansion and explains structure through long-term evolution
Scale-Invariant Cosmology [121,122]	Physical laws vary with scale	Modifies relativity; limited empirical grounding	IUF retains fixed physical laws across all scales
VSL Theories (e.g., Moffat) [122]	Speed of light changes over time	Violates Lorentz invariance; lacks strong evidence	IUF keeps ccc constant; redshift from energy transfer, not VSL

Note: These models attempt to resolve cosmological tensions by altering spacetime structure or fundamental constants. IUF instead explains redshift and cosmic structure through physically grounded, testable mechanisms, without revising established physics.

Beyond infinite models, several theories propose modifications to gravitational dynamics rather than invoking dark matter [128,129]. Modified Newtonian Dynamics (MOND) [119,120] alters Newton's laws at low accelerations to explain galactic rotation curves. While MOND addresses some observational puzzles, it still requires departures from established gravitational theory [45,46,47]. In contrast, IUF retains standard gravity while explaining apparent dark matter effects through long-term structural evolution in an infinite cosmos [12,123].

IUF maintains fidelity to well-established physical principles and observational coherence while addressing the same phenomena these models aim to explain.

8.5. IUF and Multiverse Hypotheses

IUF shares some conceptual overlap with Level I multiverse ideas, namely, an infinite spatial domain that allows for vast structural variation, but it does not require separate universes, alternate physical laws, or speculative mechanisms like quantum branching.

Multiverse theories [125], particularly those stemming from eternal inflation [13] or quantum decoherence, attempt to solve fine-tuning problems by invoking parallel universes or probabilistic ensemble models. However, these models introduce substantial philosophical and scientific challenges. They are inherently unobservable, making them unfalsifiable by design [11,12], and often require drastic departures from Occam’s Razor and testability. In many formulations, they effectively place core explanatory power outside the scope of empirical science.

IUF rejects the need for multiple universes by positing that all observable complexity arises within a single, continuous, infinite cosmos. Structural diversity, rare configurations, and even apparent fine-tuning can emerge naturally across unbounded space and time. There is no need to appeal to alternate laws of physics or speculative reality branching; instead, the IUF framework builds explanatory power from physical continuity and cosmic scale alone.

Key differences from multiverse theories:

• Continuity: IUF assumes one universe, not many.
• Unified physics: Physical laws remain constant everywhere.
• Emergent diversity: Structural variation arises naturally from infinite volume and time, not from bifurcating universes.

In this sense, IUF offers a parsimonious and testable way to account for diversity and fine-tuning in the cosmos without resorting to metaphysics or unverifiable speculation.

8.6. Summary and Outlook

The Infinite Universe Framework distinguishes itself from both mainstream and alternative cosmological models by offering a physically grounded, testable, and philosophically coherent explanation for redshift, structure, and background radiation. It accounts for observational regularities, such as redshift gradients, the CMB spectrum, and filamentary structure, without invoking singularities, inflation, dark energy, or other speculative constructs.

By merging the infinite, structure-rich cosmos of PUT with the redshift and thermal field mechanisms of C-PET, IUF offers:

• A consistent framework that honors conservation laws and known physics,
• A reinterpretation of redshift and the CMB grounded in cumulative, testable interactions,
• Predictive power for structure formation, spectral fidelity, and surface brightness profiles,
• Compatibility with a wide range of observations, from JWST [50] and Voyager [34,35,36] to the Lyman-alpha forest [137] and SZ surveys [138].

As next-generation observatories push deeper into space and time, IUF’s empirically anchored mechanisms offer a roadmap for falsifiability and refinement. Its value lies not just in offering new answers, but in restoring physical causality, continuity, and simplicity to the foundations of cosmology.

9.0. Observational Tests and Falsifiability of C-PET Model

Having positioned the Infinite Universe Framework in relation to other cosmological models, we now turn to a more empirical question: is the C-PET model testable, and if so, how? This section outlines specific observational domains, past, current, and future, that either support or could potentially falsify the C-PET model.

Unlike models that depend on unobservable early-universe conditions or ad hoc constructs, C-PET makes clear, measurable predictions about how light behaves as it moves through cosmic media.

These observational tests are consistent with and complementary to the quantitative evaluation framework presented in Appendix E, which proposes falsifiability criteria for the PMMTF hypothesis.

9.1. Spectral Line Preservation

Prediction: Despite undergoing redshift, photons retain the narrowness and coherence of their spectral lines because energy transfer occurs without scattering.

Observational Test: JWST and ground-based spectrographs have detected sharp, well-defined spectral lines in galaxies at z>10 [1,2,3,16,17,18]. If redshift were caused by turbulent scattering, these lines would be smeared or lost.

C-PET Interpretation: Supports non-scattering photon energy transfer. Line integrity remains intact, even over billions of light-years, consistent with quantum-coherent energy loss.

9.2. Metallicity and Morphology of High-Redshift Galaxies

Prediction: Galaxies at high redshift should often appear mature, chemically enriched, and structurally evolved, not “primordial.”

Observational Test: JWST has observed galaxies such as GN-z11 and JADES-GS-z13 that contain oxygen, dust, disks, and quenched star formation [1,2,3,55,56] ^, [65,66] at redshifts where ΛCDM allows only nascent structures [58,59,60].

C-PET Interpretation: These galaxies are not anomalously young but ancient and distant, with redshift due to cumulative energy transfer, not temporal youth.

9.3. Redshift–Distance Curve

Prediction: The redshift–distance relation should exhibit non-linear, cumulative behavior, consistent with energy transfer through structured media, not simple metric expansion.

Observational Test: Pantheon+ and SN Ia data [38] show deviations from simple Hubble expansion, often interpreted as dark energy or acceleration.

C-PET Interpretation: These deviations arise naturally from segment-dependent energy transfer and refractive delay, without requiring dark energy or spacetime expansion.

9.4. CMB Spectrum and Uniformity

Prediction: The CMB arises from thermally re-emitted energy rather than relic recombination [91], but still presents a near-perfect blackbody curve and high isotropy.

Observational Test: COBE, WMAP, and Planck [91,94,104,105,106,107,108] all report a 2.725 K blackbody shape and ~10^- [5] anisotropy.

C-PET Interpretation: The CMB is a Photon–Medium Microwave Thermal Field (PMMTF), continuously generated through photon–medium interaction. Its features reflect the structure of the cosmic web [10], not early-universe acoustic oscillations [99,100,101].

9.5. Presence of a Low-Level Radiation Floor

Prediction: An infrared-to-microwave background should exist as the cumulative energy signature of photon–medium interactions, what C-PET describes as the Photon–Medium Microwave Thermal Field (PMMTF), even in directions without visible galaxies.

Observational Test: The extragalactic background light (EBL) and infrared background [54] show persistent low-level signals, not fully explained by resolved sources.

C-PET Interpretation: Consistent with cumulative photon energy transfer across an infinite universe. Even void directions exhibit low but nonzero thermal background.

9.6. Time Dilation in Supernova Light Curves

Prediction: C-PET predicts real relativistic time dilation due to velocity, not cosmological stretching from expansion.

Observational Test: Time dilation has been measured in high-z SN Ia light curves [87,88]. However, the effect is difficult to decouple from model-dependent distance estimates.

Falsifiability: If future observations confirm time dilation patterns that require metric expansion, C-PET would be falsified unless refractive delay and relativistic contributions can fully account for the effect.

9.7. Summary Table: C-PET as a Falsifiable Theory

The following table summarizes observational areas where the C-PET model aligns with current evidence, alongside specific criteria that would falsify it, reinforcing its status as a testable alternative to expansion-based cosmology.

Table 9.7.1. Summary of Observational Tests and Falsifiability Criteria for C-PET Model

Test Area	Observational Evidence	C-PET Match	Falsification Risk
Spectral line sharpness	Confirmed [1,2,3,16,17,18]	✅	❌ if broadened at high z
Galaxy maturity at high z	Confirmed [55,56] , [73,74]	✅	❌ if only primitive galaxies found
CMB spectrum shape	Confirmed [91,104]	✅	❌ if non-thermal anomalies arise
CMB anisotropy explanation	Alternate [10,105,109]	✅	❌ if filament correlation fails
Redshift–distance curvature	Partially confirmed [38]	✅	❌ if pure Hubble law prevails
Supernova time dilation	Inconclusive [87,88]	⚠️	❌ if cannot be explained without expansion

Note: Table 9.1 presents key observational domains through which the C-PET model can be empirically tested. The “C-PET Match” column indicates current alignment with observational data, while the “Falsification Risk” column outlines potential criteria that could disprove or seriously challenge the model if future observations contradict its predictions.

Table 9.7.1. Summary of Observational Tests and Falsifiability Criteria for C-PET Model

Test Area	Observational Evidence	C-PET Match	Falsification Risk
Spectral line sharpness	Confirmed [1,2,3,16,17,18]	✅	❌ if broadened at high z
Galaxy maturity at high z	Confirmed [55,56] , [73,74]	✅	❌ if only primitive galaxies found
CMB spectrum shape	Confirmed [91,104]	✅	❌ if non-thermal anomalies arise
CMB anisotropy explanation	Alternate [10,105,109]	✅	❌ if filament correlation fails
Redshift–distance curvature	Partially confirmed [38]	✅	❌ if pure Hubble law prevails
Supernova time dilation	Inconclusive [87,88]	⚠️	❌ if cannot be explained without expansion

Note: Table 9.1 presents key observational domains through which the C-PET model can be empirically tested. The “C-PET Match” column indicates current alignment with observational data, while the “Falsification Risk” column outlines potential criteria that could disprove or seriously challenge the model if future observations contradict its predictions.

9.8. Conclusion

The C-PET model offers multiple, direct pathways to validation or falsification. It does not require faith in inaccessible epochs [13,14,15]. Instead, it can be tested using existing instruments, galaxy surveys [1,2,3,5,6], CMB analyses [91,105,109], and photon interaction modeling [103]. If it fails such tests, it should be revised or discarded.

But if it continues to align with the cosmos we observe, C-PET may offer a path forward to a simpler, physically consistent cosmology, grounded not in theoretical constructs but in what light tells us as it travels across the universe [7,8].

10.0. Conclusion: A Physically Consistent Cosmology Without Expansion

The Infinite Universe Framework (IUF), supported by the Cumulative Photon Energy Transfer (C-PET) model, presents an alternative cosmology grounded not in speculative origin events or unobservable parameters, but in the observable and testable behavior of light across cosmic distances. By treating redshift and background radiation as emergent consequences of photon–medium interactions in an infinite, structured universe, IUF reinterprets two of the foundational observations of modern cosmology, the redshift–distance relation and the cosmic microwave background (CMB), within a single, physically grounded system.

This framework rejects the need for inflation [13,14,15,110], dark energy [78,79], or a singular Big Bang [13]. Instead, it proposes that photons gradually transfer energy to the intergalactic medium (IGM) through infrequent, non-scattering interactions. These energy transfers explain not only the observed redshift of distant objects, but also the existence and properties of the CMB, reframed as a Photon–Medium Microwave Thermal Field (PMMTF). This field emerges naturally from the long-term accumulation and thermalization of photon energy in a statistically isotropic cosmos [96,97,98], offering a unified and energy-conserving explanation for the CMB’s temperature [104], spectrum, and anisotropies [105,109].

The IUF + C-PET model stands apart in several key ways:

• It remains falsifiable [11], offering testable predictions across spectral line coherence [1,2,3,16,17,18], redshift–distance curvature [38], background radiation behavior [91,104,105], and time dilation [87,88].
• It draws from confirmed observational phenomena, such as Voyager's detection of plasma beyond the heliopause [4,34,35,36], JWST's discovery of mature high-z galaxies [1,2,3,16,17,18,55,56] ^, [73,74], and large-scale cosmic structures like the Giant Arc and Big Ring [20], which challenge the assumptions of standard cosmology regarding early homogeneity [42,43,44].
• It avoids reliance on ad hoc assumptions or hypothetical epochs, anchoring itself instead in the continuity of known physics [7,8]: conservation laws [48], electromagnetic interactions [103], and thermodynamic behavior over time [96,97,98].

By rooting cosmological explanation in the cumulative and structured nature of the universe [10,85,86], rather than in initial conditions or unobservable processes [13,14,15], IUF encourages a return to empirical, physically principled reasoning in cosmology. Its strength lies not in philosophical rejection of prior models, but in offering an alternative that is both conceptually simpler and more consistent with physical laws [7,8,45,46,47,48] and emerging observations [1,2,3,16,17,18,20,73,74].

The Infinite Universe Framework, as presented here, offers a testable, observationally grounded alternative to standard cosmology. While acknowledging the need for continued theoretical refinement and empirical validation, it provides a framework for systematic investigation that can be independently verified, modified, or potentially falsified through collaborative scientific inquiry.

As new data emerges from telescopes, space probes, and cosmological simulations, the Infinite Universe Framework, supported by the Physical Universe Theory (PUT) and the Cumulative Photon Energy Transfer (C-PET) model, will rise or fall based on its explanatory power. While ΛCDM accommodates large-scale structure via inflation and statistical variance [13,14,15,42,43,44], the scale and distribution of recent discoveries [20,85,86] motivate consideration of non-expansion-based structure formation models.

The IUF framework invites collaborative inquiry, independent modeling, and rigorous testing of its core assumptions through the scientific community. And in doing so, it rekindles a foundational scientific spirit: that the universe is not a fleeting echo of a distant explosion, but a vast, eternal structure whose nature is revealed through careful empirical observation of the light that travels through it.

11.0. Summary and Outlook

This manuscript presents the Infinite Universe Framework (IUF), which combines the Physical Universe Theory (PUT) with the Cumulative Photon Energy Transfer (C-PET) model to reinterpret foundational cosmological observations. Departing from ΛCDM's reliance on expansion [42,43,44], inflation [13,14,15,110], and dark energy [78,79], the IUF offers a physically grounded, observationally anchored alternative that embraces an infinite, structure-filled cosmos governed by known physical laws [7,8,11,12].

At its core, C-PET proposes that redshift and the cosmic microwave background (CMB) arise not from spacetime expansion or primordial events, but from infrequent, non-scattering energy transfers between photons and the cosmic medium. These interactions, consistent with plasma physics and quantum electrodynamics, accumulate over vast distances and timescales, naturally producing redshifted spectra and a diffuse microwave thermal field (PMMTF). This reinterpretation unifies redshift and background radiation within a testable, conservation-respecting framework.

The IUF explains a wide array of observations, from the maturity of high-redshift galaxies [1,2,3,16,17,18,55,56] ^, [73,74] and filamentary megastructures [10,20] to the blackbody uniformity [104] and anisotropies [105,109] of the CMB, without resorting to speculative epochs or unobservable constructs. Instead, it invites a return to first physical principles, interpreting the cosmos as an ongoing thermodynamic system rather than a one-time event.

Looking ahead, several areas offer opportunities for collaborative research, independent modeling, and empirical validation:

• Developing open-source modeling tools to enable independent replication and extension of C-PET simulations across different cosmic environments;
• Simulating the PMMTF spectrum using realistic cosmic media profiles to verify whether the C-PET mechanism can reproduce the observed 2.725 K blackbody curve [104];
• Mapping redshift–distance relationships across structured intergalactic media using segmented medium models;
• Analyzing anisotropy patterns in the CMB as potential imprints of filamentary cosmic structure;
• Testing photon energy transfer coefficients (α-values) using observations from JWST [1,2,3,16,17,18], Pantheon+ [38], and low-frequency radio surveys [31,32];
• Quantifying thermal re-emission from cosmic voids [132,133] and filaments [10] to establish an energy budget that accounts for conservation across scales [48].

This framework does not assert final answers but opens new pathways for empirical inquiry. It invites the scientific community to collaboratively test whether a non-expanding, thermodynamically active cosmos might better reflect empirical observations through independent analysis and cross-validation.

The Infinite Universe Framework remains open to revision, refinement, and falsification. Its strength lies not in speculative elegance but in its empirical grounding, consistency with established physics, and openness to systematic testing of foundational assumptions. In doing so, it aims to contribute to a more complete and physically coherent understanding of the cosmos.