1. Introduction
Energy is the main driving force when it comes to the progress of humanity. The transition from muscle power to fire, then to coal, from fossil to electricity in the industrial age were the biggest turning points in human history [
1,
2,
3,
4,
5]. Through energy, societies industrialize, living standards improve and technology expands. However, the dependence on non-renewable sources of energy has caused numerous economical and environmental consequences. Air pollution, greenhouse gas emissions, and global warming have been the direct results of prolonged reliance on these sources [
6,
7,
8]. Additionally, the finite nature of the fossil fuel reserves has raised concerns about long-term energy security and the sustainability of global development. Wind energy is one of the many ways we can extract clean energy from our surroundings. It is the process in which the kinetic energy in the wind particles flowing over a turbine is converted into mechanical energy by rotating the turbine blades, thus rotating the generator connected to it and producing electrical energy [
1,
9,
10]. The generation of wind energy is primarily achieved through wind turbines, which are broadly categorized into Horizontal Axis Wind Turbines (HAWTs) and Vertical Axis Wind Turbines (VAWTs) as shown in
Figure 1.
Horizontal Axis Wind Turbines (HAWTs) are the most common type and are deployed in large-scale wind farms. Their blades rotate around a horizontal axis and must be aligned with the wind direction to function [
11,
12,
13,
14]. Although efficient at large-scale projects, they require tall towers, complex yaw systems, and considerable land area. Their main disadvantages are sensitivity to fore casted conditions, noise generated by the blades, and visual and ecological impact (especially on birds) [
1,
15,
16]. This issue, however, can be mitigated by decentralizing the production of wind power by using VAWTs. Vertical Axis Wind Turbines (VAWTs) have blades arranged around a vertical axis. They capture wind from any direction without the need for orientation mechanisms. Their design allows installation in urban areas and smaller spaces, often closer to where energy is consumed. Their ability to function effectively in turbulent winds and operate at lower heights makes the VAWTs a practical solution for decentralized energy production [
17,
18,
19,
20], allowing households, communities, and small enterprises to meet a portion of their energy needs sustainably.
Building upon these advantages of VAWTs, this design is proposed to maximize their performance and adaptability. This concept is the “Wind Wall,” which utilizes an array of vertical axis turbines arranged in a compact frame to optimize energy capture. Unlike traditional standalone turbines, this configuration allows multiple VAWTs to work collectively, enhancing efficiency while minimizing land usage [
17,
21,
22]. The following section outlines the structural and functional aspects of this design.
The Wind Wall is a combination of vertical axis wind turbines (VAWTs) arranged in a frame that resembles a wall as shown in
Figure 2 . It is designed to extract the kinetic energy from the wind and convert it into electrical energy. For this Wind Wall, the blade has a profile of the Ugrinsky type with a helical twist to allow operation at low wind speeds and relative independence from wind direction [
23,
24,
25]. The Ugrinsky type of wind turbine falls under the group of drag-type turbines. These turbines operate by using the difference of drag on the two sides of the blade; one side of the turbine experiences less drag while the other experiences more, creating an uneven force along the axis of the turbine. This force spins the blades, which in turn rotates the generator to produce power. By grouping the VAWTs in a frame, efficiency and power generation are increased, while the overall usage of available space is reduced.
Symmetry plays an important role in the aerodynamic behavior of the Wind Wall. The Ugrinsky blade profile used in this study is geometrically symmetrical, ensuring that drag forces are distributed evenly along the rotating surface. Likewise, the turbines are arranged in a symmetric pattern inside the frame, allowing uniform flow acceleration and balanced torque production among the neighboring turbines. This combination of blade symmetry and spatial symmetry contributes to much smoother rotation, reduced vibration, and improved energy extraction compared to non-symmetric turbine arrays.
A vertical axis wind turbine (VAWT) without a helical twist in its blades tends to experience torque fluctuations. For example, in a Savonius-type turbine with two or more blades, one blade may face the incoming wind while the other faces the opposite direction. This configuration produces alternating torque peaks, leading to a ripple-like variation in rotational motion, which prevents smooth operation. By introducing a helical twist to the turbine blades, the torque is distributed more evenly along the turbine height. The opposing aerodynamic forces acting on different sections of the blade are no longer directly in opposition, thereby producing a more constant torque and smoother rotation with fewer vibrations [
23,
26]. Increasing the helical twist improves torque uniformity; however, beyond a certain angle, the effective torque decreases because the wind tends to deflect past the blades rather than applying useful momentum, thus reducing energy capture efficiency.
Figure 3.
Ugrinsky Blade.
Figure 3.
Ugrinsky Blade.
Figure 4.
Top View of the Ugrinsky blade profile.
Figure 4.
Top View of the Ugrinsky blade profile.
The blade profile used in this research is the Ugrinsky type, developed in the Soviet Union by Professor Ugrinsky and his team. This turbine design offers a balance between efficiency and starting capability, with reported power coefficients in the range of 0.25–0.35 [
24,
25]. The efficiency is greater than that of a pure Savonius-type turbine and is comparable to certain Darrieus-type turbines. The Ugrinsky turbine therefore combines the self-starting ability of drag-based designs with the improved efficiency typically observed in lift-based turbines.
Figure 5.
Turbines with helix angles, from left to right the angles are: 0°,10°,20°,30°,40°,50°,60°.
Figure 5.
Turbines with helix angles, from left to right the angles are: 0°,10°,20°,30°,40°,50°,60°.
In this study, the optimum helical twist (helix angle) is determined through Computational Fluid Dynamics (CFD) simulations by analyzing the torque generated at different twist angles under constant wind speed. Once the optimum twist is identified, the ideal spacing between adjacent turbines in the wind wall is calculated. When turbines are positioned close together, the airflow between them accelerates due to the Venturi-like effect, as the same volume of air is forced through a narrower spacing. This acceleration is consistent with Bernoulli’s principle and results in higher effective wind speeds acting on the turbines [
27,
28,
29,
30]. By examining this effect, a correlation between the effective velocity (the wind passing between turbines) and the spacing of the turbines is established.
2. Problem Statement
The efficiency of Vertical Axis Wind Turbines (VAWTs) can be significantly influenced by blade geometry and the aerodynamic interference between adjacent units. Therefore, optimizing the helix angle and turbine spacing is crucial for improving energy capture and ensuring stable operation in compact wind wall arrays. The primary objective of this research is given below:
To determine the optimum helix angle of a single vertical axis wind turbine (VAWT) [
11,
31].
To identify the optimum spacing between turbines arranged within the wind wall frame [
17,
32].
To establish a correlation between the effective velocity of airflow through adjacent turbines and the spacing between them. This correlation is explained through the venturi-like effect, in which airflow accelerates between narrow spacing according to Bernoulli’s principle [
33].
The helical twist of the turbine blades plays a central role in this investigation. As previously discussed, the introduction of a twist reduces torque fluctuations and produces smoother rotation [
34]. Identifying the most effective helix angle is therefore critical, as it directly affects turbine efficiency and the consistency of power generation [
35].
The computational study was conducted using Computational Fluid Dynamics (CFD) simulations [
36]. A single turbine with a height of 1 m and a diameter of 0.17 m was modeled. The performance was evaluated at a constant wind speed of 8 m/s for helix angles of 0°, 10°, 20°, 30°, 40°, 50°, and 60°. Once the optimum helix angle was identified, a multi-turbine configuration was simulated to analyze the effect of spacing [
37]. The spacing between turbines were varied as 0 cm, 0.5 cm, 1.66 cm, 4 cm, 7 cm, 11 cm, and 16 cm. These values were selected to cover both closely spaced and widely separated configurations, allowing the effect of turbine interaction to be captured effectively.
3. Numerical Methodology
3.1. Mathematical Formulations
This computational analysis was carried out using the Reynolds-Averaged Navier–Stokes (RANS) equations in combination with the standard
k–
turbulence model. This approach is widely adopted for simulating incompressible and mildly compressible turbulent flows due to its balance between accuracy and computational efficiency [
38,
39]. Together, these equations establish the mathematical framework required to capture the mean flow characteristics and turbulence behavior in the computational domain.
Here,
is the velocity vector,
is the eddy viscosity,
is the fluid density , and
is the turbulence production term. The standard model constants used are
,
,
, and
[
38,
39]. In the standard
k–
model, the eddy viscosity is calculated as
with
.
3.2. Simulation Details for Finding the Optimal Blade Twist
The computational simulations were performed in a wind tunnel domain. A total of two materials were used in the setup: air for the flow medium and ABS plastic for the turbine. The solver was configured with 100 time steps, a reference temperature of 33 °C, and the standard
k–
turbulence model was employed [
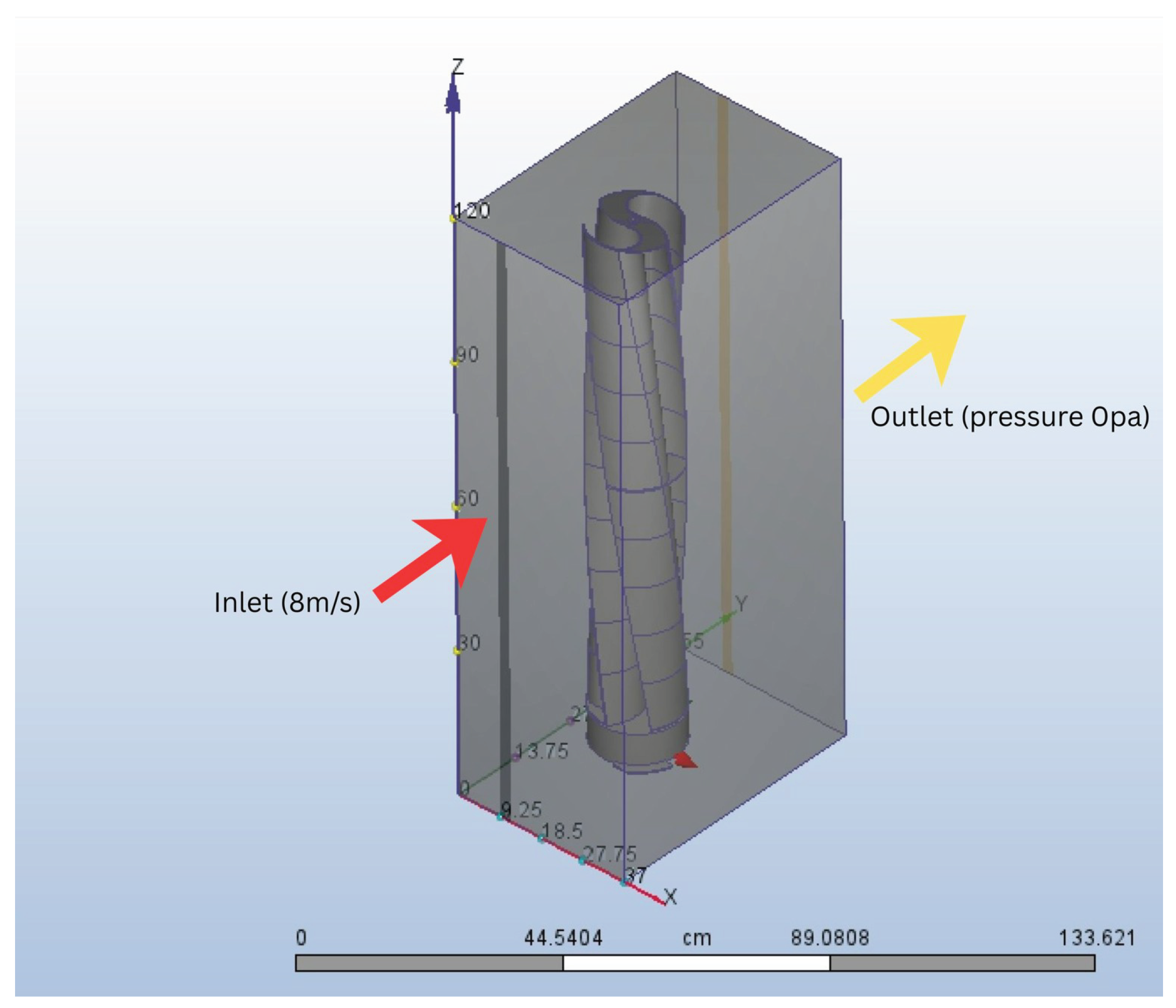
38]. The flow was defined as turbulent and compressible. Boundary conditions were specified with one velocity inlet of 8 m/s and one pressure outlet (0 Pa gauge pressure) positioned directly opposite to the inlet face.
Figures of the computational domain and wind tunnel geometry are provided for clarity in
Figure 6. The tunnel walls perpendicular to the inlet and outlet faces—namely, the top, bottom, and side boundaries—were modeled as slip surfaces. This assumption allowed air to pass without boundary layer formation on these walls, thereby avoiding artificial wall effects that could distort the velocity distribution around the turbine. The inlet and outlet walls, in contrast, were maintained as velocity and pressure boundaries respectively.
To evaluate turbine performance, the torque coefficient (
) was used as a key parameter. The torque coefficient is defined as [
11,
33]:
where:
T = torque acting on the turbine (Nm)
= density of air (kg/m³)
A = frontal area of the turbine (m²)
R = radius of the turbine (m)
V= incoming velocity of air (m/s)
The torque coefficient provides a dimensionless representation of turbine performance, allowing results to be normalized and compared across varying conditions. Torque (T) is directly related to through the above relation, meaning that higher torque values correspond to higher torque coefficients for given flow conditions.
3.3. Simulation Details of Finding the Optimal Distance Between the Blades of the VAWTs
The simulations were again carried out in a three-dimensional wind tunnel domain. Two materials were employed in the model: air as the working fluid and (ABS) plastic as the solid part for the turbine blades. The turbine geometry used in all spacing cases corresponded to the single-turbine geometry previously described (height H=1.00 m, diameter D=0.17 m). All boundary conditions were prescribed (0 unknowns). The following solver and boundary settings were used:
Flow regime: Turbulent, compressible flow (compressible solver option was enabled).
Turbulence model: Standard k-epsilon.
Inlet: One velocity inlet with free-stream velocity V=8 m/s.
Outlet: One pressure outlet located on the wall opposite the inlet with gauge pressure set to 0 Pa.
Room temperature: 33 °C.
Solver time-marching: 100 steps; each step was run with 1 iteration
Although compressibility was enabled in the solver, the flow remained in the low-Mach regime (Mach << 0.3), making compressibility effects negligible; however, solver settings were kept consistent across all cases. The global mesh statistics for the model were: total nodes = 994,196 and total elements = 3,966,264. The spacing cases were selected to span a wide range from closely coupled to weakly interacting configurations, with inter-turbine edge-to-edge spacings of 0 cm, 0.5 cm, 1.66 cm, 4 cm, 7 cm, 11 cm, and 16 cm. Corresponding non-dimensional spacings, normalized using the rotor diameter (D = 17), were s/D=[0,0.029,0.094,0.23,0.41,0.64,0.94]. Presenting spacing non-dimensionally allows the results to be generalized across different rotor sizes.
Figure 7.
image showing the inlet and outlet of the simulation domain.
Figure 7.
image showing the inlet and outlet of the simulation domain.
All lateral tunnel walls that were perpendicular to the inlet–outlet direction (top, bottom, and side walls) were modeled as slip surfaces so that boundary layer formation on those walls was suppressed and artificial wall effects were minimized. The front (inlet) and back (outlet) faces of the tunnel were prescribed as velocity inlet and pressure outlet, respectively. The rotor surfaces were treated as no-slip ABS solid surfaces with the appropriate material properties assigned for force/torque extraction.
A typical mesh used for the 3 blade VAWT configuration is shown in
Figure 8.
5. Results and Discussions
Comprehensive simulations were performed using the software ‘Autodesk CFD’ (version 2024) to thoroughly investigate the impact of varying the helix angle and the spacing ratio on the aerodynamic efficiency of the proposed blade design. The input values for these parameters used are shown in
Table 1. The evaluation of the blade’s capabilities was conducted using specific performance metrics, namely the torque generation and the moment coefficient associated with the blade, to provide a detailed understanding of its performance characteristics. The subsequent sections provide an in-depth examination and discussion of these various aspects.
5.1. Effect of Helix Angle on the Torque and Moment Coefficient
Table 2 presents the variation of torque and moment coefficient (Cm) with helix angle. Each case corresponds to a specific twist angle of the turbine blade, with the resulting torque (in Nm) and corresponding Cm values listed. It can be observed that torque and Cm increase significantly from (0°) by 471% at just 20° of helical twist, reaching peak values at 50°–60°(around 831%), (both with reference to 0°). In contrast, the untwisted case (0°) shows minimal performance, highlighting the importance of blade twist in enhancing turbine efficiency by a great amount.
Figure 10.
Variation of Coefficient of Moment with change in Helix Angle.
Figure 10.
Variation of Coefficient of Moment with change in Helix Angle.
From the simulations, it was observed that the introduction of a slight helical twist (approximately 10°, and below 20°) increased the torque produced by the turbine to nearly twice that of a turbine without any twist [
34,
41]. Further increases in the twist angle (beyond 20°) resulted in torque values up to five times higher than those of the untwisted configuration [
31]. Between 20° and 40°, the increase in torque became less pronounced, with values stabilizing around a near-optimum range [
42]. At approximately 50°, a further rise in torque was noted, although subsequent increases in twist produced only marginal improvements. The simulations were limited to a maximum twist of 60° due to the increasing complexity associated with modeling and manufacturing highly twisted blades. In practice, fabricating a turbine with an
Ugrinsky profile and high helical twist presents significant design and cost challenges [
11].
The results can also be expressed in terms of the coefficient of moment (Cm). A similar trend was observed, where Cm increased sharply at lower twist angles, nearly doubling at 10° (from 0.035 to 0.053), and reaching up to five times the untwisted value between 20° and 30° (from 0.035 to 0.2) [
34,
41]. Beyond this range, the growth of Cm began to plateau, showing only incremental improvements until approximately 50° [
31]. At this point, a secondary increase was observed (from 0.2 to 0.32), after which further twisting produced negligible gains. This curve indicates that the aerodynamic performance of the turbine is highly sensitive to small twists at low angles but becomes less responsive at higher twists, as the blades begin to shed or deflect airflow rather than capturing it efficiently [
42].
The analysis indicates that an optimum helix angle for the Wind Wall lies within the range of 20°–30° [
34,
41]. At this range, the torque output and coefficient of moment are significantly improved compared to the 0 degree helix case, while the structural design and manufacturing process remain manageable. Although higher angles (50°–60°) demonstrated higher torque coefficients, the added benefit is offset by the greater complexity and expense of blade fabrication [
11]. From a practical perspective, an increase in coefficient of moment alone does not justify the higher production costs, as the primary goal is to maximize net energy output while maintaining economic feasibility.
Therefore, the optimum helix angle is defined not only by aerodynamic performance but by a balance between torque enhancement, coefficient of moment behavior, manufacturability, and cost-effectiveness [
31,
34,
41]. This trade-off ensures that the Wind Wall remains both technically efficient and economically feasible, thus fulfilling its purpose of delivering reliable electricity generation in a scalable and practical form.
5.2. Effect of Spacing Between the Blades on the Torque and Moment Coefficient
The spacing between turbine blades plays a crucial role in the aerodynamic performance of the blade. This section delves into a detailed analysis of how variations in blade spacing influence both the torque and the coefficient of moment (Cm) across a range of helix angles associated with the blades. By examining these dynamics, the study aims to elucidate the complex interplay between blade arrangement and overall turbine performance, thus providing deeper insights into the aerodynamic optimization of turbine systems.
-
optimal spacing for 0 degrees helix turbines:
The results for the 0 degree helix configuration show a clear dependence of the coefficient of moment (Cm) on the spacing between adjacent turbines. At zero spacing, the torque and Cm values are relatively low (T=0.052 Nm, Cm=0.092) due to strong wake interference. As the spacing increases slightly to 0.5–1.6 cm, both torque and Cm increase significantly, reaching Cm=0.158. The maximum performance is observed at a spacing of 4 cm (Cm=0.22), where constructive flow acceleration through the narrowed passage appears to enhance the effective velocity on the turbine. Beyond this optimum spacing, a rapid decline in performance is observed, with Cm dropping back to near baseline levels at 7 cm (0.096) and further diminishing to very low values at 11–16 cm (0.027).
Figure 11.
Variation of Coefficient of Moment with change in distance between the Turbines ().
Figure 11.
Variation of Coefficient of Moment with change in distance between the Turbines ().
Table 3.
Variation of Torque and coefficient of moment (Cm) for different spacings at helix angle .
Table 3.
Variation of Torque and coefficient of moment (Cm) for different spacings at helix angle .
| Case |
Spacing (cm) |
Torque (N·m) |
Cm |
| 1 |
0.0 |
0.052 |
0.092 |
| 2 |
0.5 |
0.083 |
0.142 |
| 3 |
1.6 |
0.088 |
0.158 |
| 4 |
4.0 |
0.125 |
0.220 |
| 5 |
7.0 |
0.0538 |
0.096 |
| 6 |
11.0 |
0.020 |
0.045 |
| 7 |
16.0 |
0.010 |
0.027 |
-
Optimal spacing for 10 degrees helix turbines:
Table 4.
Variation of Torque and coefficient of moment (Cm) for different distances at helix angle .
Table 4.
Variation of Torque and coefficient of moment (Cm) for different distances at helix angle .
| Case |
spacing (cm) |
Torque (N·m) |
Cm |
| 1 |
0 |
0.060 |
0.107 |
| 2 |
0.5 |
0.067 |
0.119 |
| 3 |
1.6 |
0.120 |
0.217 |
| 4 |
4 |
0.045 |
0.080 |
| 5 |
7 |
0.0438 |
0.078 |
| 6 |
11 |
0.031 |
0.055 |
| 7 |
16 |
0.020 |
0.036 |
Figure 12.
Variation of Coefficient of Moment with change in Distance between the Turbines ().
Figure 12.
Variation of Coefficient of Moment with change in Distance between the Turbines ().
For the 10 degree helix configuration, the variation of torque and coefficient of moment (Cm) with turbine spacing demonstrates a distinct performance profile. At zero spacing, the initial Cm is slightly higher than the 0° case (Cm=0.107), reflecting the stabilizing effect of the helical twist in reducing destructive interference. A gradual increase is observed at a spacing of 0.5 cm (Cm=0.119), followed by a sharp rise to the peak value of Cm=0.217 at 1.6 cm. This indicates that the helical twist enables stronger constructive aerodynamic interactions at relatively closer spacings than in the untwisted configuration, likely due to smoother flow redirection and reduced pulsations in the torque.
-
Optimal spacing for 20 degrees helix turbines:
Table 5.
Variation of Torque and coefficient of moment (Cm) for different distances at helix angle .
Table 5.
Variation of Torque and coefficient of moment (Cm) for different distances at helix angle .
| Case |
spacing (cm) |
Torque (N·m) |
Cm |
| 1 |
0 |
0.052 |
0.092 |
| 2 |
0.5 |
0.179 |
0.319 |
| 3 |
1.6 |
0.196 |
0.350 |
| 4 |
4 |
0.098 |
0.175 |
| 5 |
7 |
0.075 |
0.133 |
| 6 |
11 |
0.060 |
0.100 |
| 7 |
16 |
0.078 |
0.138 |
Figure 13.
Variation of Coefficient of Moment with change in Distance between the Turbines(()).
Figure 13.
Variation of Coefficient of Moment with change in Distance between the Turbines(()).
This results shows us that the turbine interaction is highly spacing-dependent, with maximum aerodynamic benefit occurring at smaller separations. Starting from a baseline Cm=0.092 at zero spacing, performance rises sharply to a peak of Cm=0.35(torque 0.196 Nm) at 1.6 cm, nearly quadrupling the baseline due to strong constructive flow interactions and a venturi-like effect that boosts effective velocity. Beyond this optimum range (0.5–1.6 cm), the moment coefficient declines rapidly, dropping to 0.1 by 11 cm, though a minor recovery to 0.138 at 16 cm suggests residual flow re-alignment. Overall, the findings highlight that close turbine spacing strongly enhances aerodynamic performance, while larger spacing diminish interactions and cause the turbines to behave more independently.
-
Optimal spacing for 30 degrees helix turbines:
Table 6.
Variation of Torque and coefficient of moment (Cm) for different distances at helix angle .
Table 6.
Variation of Torque and coefficient of moment (Cm) for different distances at helix angle .
| Case |
spacing (cm) |
Torque (N·m) |
Cm |
| 1 |
0 |
0.084 |
0.151 |
| 2 |
0.5 |
0.087 |
0.156 |
| 3 |
1.6 |
0.099 |
0.177 |
| 4 |
4 |
0.113 |
0.200 |
| 5 |
7 |
0.115 |
0.215 |
| 6 |
11 |
0.103 |
0.180 |
| 7 |
16 |
0.097 |
0.170 |
Figure 14.
Variation of Coefficient of Moment with change in Distance between the Turbines ()
Figure 14.
Variation of Coefficient of Moment with change in Distance between the Turbines ()
In this one, the turbine performance shows a more gradual and sustained enhancement compared to the previous case. Starting from a baseline of Cm=0.151 at zero spacing, the coefficient increases steadily with separation, peaking at Cm=0.215 (torque 0.115 Nm) at 7 cm. Unlike the sharp optimum observed earlier, this setup exhibits a broader effective range, with relatively high values maintained between 4–7 cm before declining moderately at larger spacing (Cm=0.18 at 11 cm and 0.17 at 16 cm). This trend suggests that the aerodynamic interaction is less dependent on very close spacing and instead benefits from a wider spacing window, where flow stabilization and smoother energy exchange between turbines sustain improved performance due to the change in the helix angle.
-
Optimal spacing for 40 degrees helix turbines:
Table 7.
Variation of Torque and coefficient of moment (Cm) for different distances at helix angle .
Table 7.
Variation of Torque and coefficient of moment (Cm) for different distances at helix angle .
| Case |
spacing (cm) |
Torque (N·m) |
Cm |
| 1 |
0 |
0.110 |
0.197 |
| 2 |
0.5 |
0.122 |
0.218 |
| 3 |
1.6 |
0.080 |
0.144 |
| 4 |
4 |
0.096 |
0.171 |
| 5 |
7 |
0.096 |
0.171 |
| 6 |
11 |
0.094 |
0.172 |
| 7 |
16 |
0.078 |
0.140 |
Figure 15.
Variation of Coefficient of Moment with change in Distance between the Turbines()
Figure 15.
Variation of Coefficient of Moment with change in Distance between the Turbines()
In this case, turbine interaction peaks at very small spacing before rapidly diminishing. The baseline performance at zero spacing is already strong (Cm=0.197), rising slightly to its maximum of Cm=0.218 (torque 0.122 Nm) at 0.5 cm. However, unlike previous configurations, the performance drops sharply at 1.6 cm (Cm=0.144) and only partially recovers at 4–11 cm, where values stabilize around Cm=0.171–0.172. At the largest spacing of 16 cm, the coefficient decreases further to 0.14. Furthermore for this helix angle, there is a plateauing effect of the Cm from distance coefficient 0.2 - 0.638 and then decreases further.
-
Optimal spacing for 50 degrees helix turbines:
Table 8.
Variation of Torque and coefficient of moment (Cm) for different distances at helix angle .
Table 8.
Variation of Torque and coefficient of moment (Cm) for different distances at helix angle .
| Case |
spacing (cm) |
Torque (N·m) |
Cm |
| 1 |
0 |
0.144 |
0.257 |
| 2 |
0.5 |
0.140 |
0.250 |
| 3 |
1.6 |
0.118 |
0.210 |
| 4 |
4 |
0.135 |
0.242 |
| 5 |
7 |
0.111 |
0.190 |
| 6 |
11 |
0.126 |
0.220 |
| 7 |
16 |
0.020 |
0.358 |
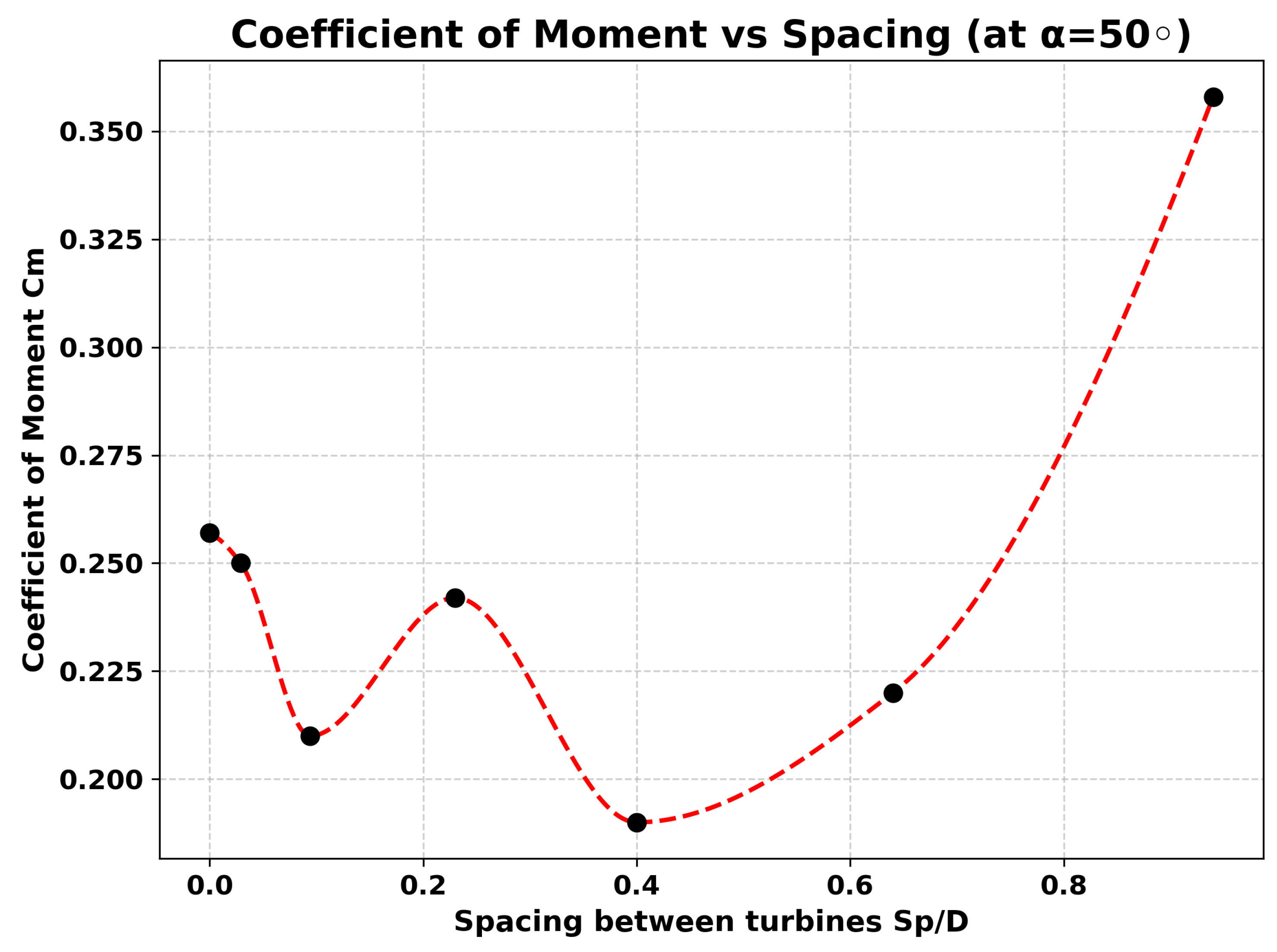
At 50 degrees, it displays a distinctive interaction pattern with both strong initial performance and an unusual late surge. At zero spacing, the turbines already achieve a high Cm=0.257, which remains nearly unchanged at 0.5 cm before gradually declining to 0.21 at 1.6 cm. A partial recovery occurs at 4 cm (Cm=0.242), followed by another dip at 7 cm. Interestingly, performance rises again at 11 cm (Cm=0.22) and then shows an anomalously high spike at 16 cm, where Cm jumps to 0.358 despite a very low torque value (0.02 Nm). This suggests that while the turbines maintain relatively strong interactions across small to moderate spacing, the unexpected efficiency spike at large separation may indicate unique flow reorganization or measurement sensitivity at extreme spacing.
Figure 16.
Variation of Coefficient of Moment with change in Distance between the Turbines().
Figure 16.
Variation of Coefficient of Moment with change in Distance between the Turbines().
Optimal spacing for 60 degrees helix turbines:
At 60 degrees, the turbines show relatively stable and moderate spacing-sensitivity: the baseline at zero spacing is Cm=0.206 (torque 0.115 Nm) and values fluctuate only mildly with separation, rising slightly to a local peak of Cm=0.216 (torque 0.121 Nm) at 4 cm and reaching the overall maximum Cm=0.239(torque 0.134 Nm) at 11 cm. Intermediate spacings (0.5 -7 cm) produce nearly constant performance around Cm 0.20 - 0.213, while the largest spacing (16 cm) shows a modest drop to Cm=0.189. Overall this configuration suggests more robust, less spacing-sensitive aerodynamic coupling compared with earlier cases, with a clear mid-to-large spacing optimum near 11 cm.
Figure 17.
Variation of Coefficient of Moment with change in Distance between the Turbines().
Figure 17.
Variation of Coefficient of Moment with change in Distance between the Turbines().
Table 9.
Variation of Torque and coefficient of moment (Cm) for different distances at helix angle .
Table 9.
Variation of Torque and coefficient of moment (Cm) for different distances at helix angle .
| Case |
spacing (cm) |
Torque (N·m) |
Cm |
| 1 |
0 |
0.115 |
0.206 |
| 2 |
0.5 |
0.114 |
0.200 |
| 3 |
1.6 |
0.116 |
0.208 |
| 4 |
4 |
0.121 |
0.216 |
| 5 |
7 |
0.119 |
0.213 |
| 6 |
11 |
0.134 |
0.239 |
| 7 |
16 |
0.105 |
0.189 |
5.2.1. Analysis of Result
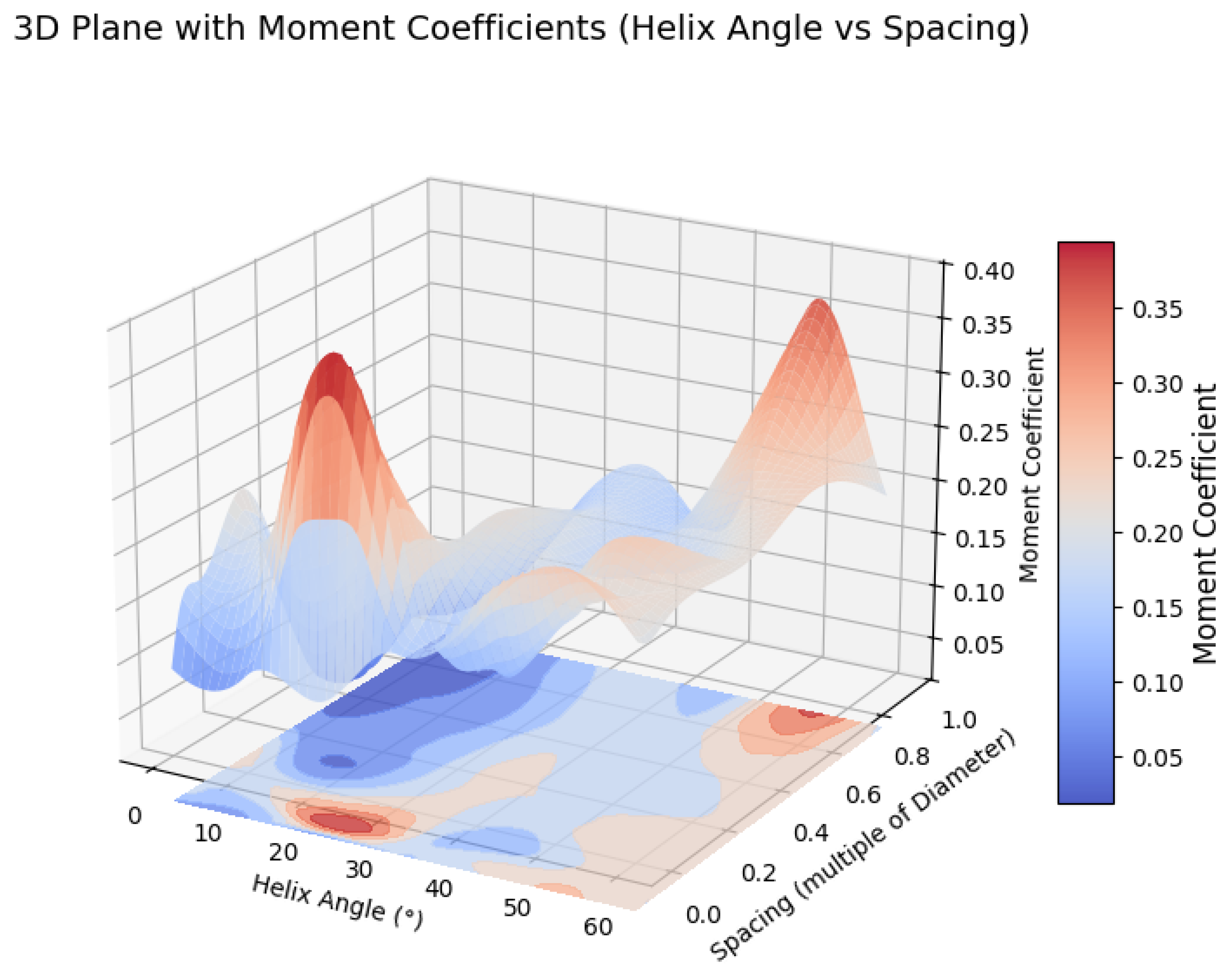
The experimental results demonstrate that inter-turbine spacing and helix angle jointly govern aerodynamic coupling between adjacent VAWT units. Normalizing spacing by rotor diameter (s=spacing/D) reveals that some helix angles produce strong, narrow peaks in moment coefficient at small s (e.g. 10 degree and 20 degree at s=0.094), while other angles (30 degree and 60 degree) show broader mid-spacing optima (s=0.412 - 0.647). We can interpret sharp small-spacing maxima as the result of local flow acceleration through a constricted passage combined with constructive phase alignment of shed vortical structures that augment blade loading. In contrast, larger helix angles introduce axial flow components and smoother temporal loading, giving more performance over a wider spacing window. It is seen that at higher helix angles, the maxima of Cm is reached at larger spacing between the turbines. Taken together, the results indicate a trade-off between peak achievable moment coefficient and spacing tolerance: angles that produce very large peaks are highly sensitive to spacing, whereas angles with modest maxima but broad plateaus (30 degree - 60 degree) are preferable for practical, mass-produced wind-wall installations if the complexity of manufacturing a highly twisted blade can be reduced.
Figure 18.
3d plot showing various moment coefficient for different helix angle at different spacing.
Figure 18.
3d plot showing various moment coefficient for different helix angle at different spacing.
5.3. Corelation Between the Effective Velocity and Distance Coefficient
In a Wind Wall configuration, the Vertical Axis Wind Turbines (VAWTs) are positioned in series, which causes the incoming wind to undergo a
venturi effect due to the presence of adjacent turbines. This aerodynamic phenomenon accelerates the airflow between the turbines, thereby increasing the
effective velocity (Ve) experienced by each turbine [
17,
26,
27]. As a result, the torque generated on the turbine blades rises significantly.
The torque (T) on a turbine can be expressed as [
11,
33]:
where
is the air density,
A is the swept area of the turbine,
is the effective velocity, and
is the coefficient of moment. It is evident from this relation that the torque is directly influenced by the square of the effective velocity and the aerodynamic efficiency of the blade profile captured in
.
The determination of
can be approached using fluid dynamic principles. According to Bernoulli’s principle, the effective velocity is inversely proportional to the spacing (
) between adjacent turbines [
27,
43,
44]. In other words, as the spacing decreases, the constriction of the flow intensifies, which enhances the venturi effect and increases
. Additionally, the turbine diameter (
D) plays a key role, since a larger diameter captures more wind and intensifies the velocity variation between turbines. These dependencies can be represented as:
Here,
V is the free-stream incoming velocity, and
is a dimensionless parameter that characterizes the intensity of aerodynamic interactions [
17,
26]. The value of
depends on several factors, including wake interactions, turbulence levels, and the degree of flow redirection introduced by helical twisting of the blades. This parameter is not easily defined analytically and must typically be obtained through computational fluid dynamics (CFD) simulations.
To simplify the expression further, the ratio of spacing to turbine diameter can be introduced as the
coefficient of distance (
S), defined as:
Rewriting the correlation in terms of
S:
This formulation makes it easier to evaluate turbine performance, as the spacing effect is normalized by turbine size. The coefficient of distance also allows the spacing between turbines in a Wind Wall to be estimated once the desired effective velocity and the parameter are known.
From a CFD perspective, the effective velocity can be measured by defining the rotor plane — the plane coinciding with the rotation axis of the VAWT. In the Wind Wall configuration, if the wind approaches directly from the front, all turbines share a common rotor plane facing the incoming flow. By averaging the velocity across this plane, the effective velocity can be computed, which in turn can be used to estimate torque output using the torque equation.
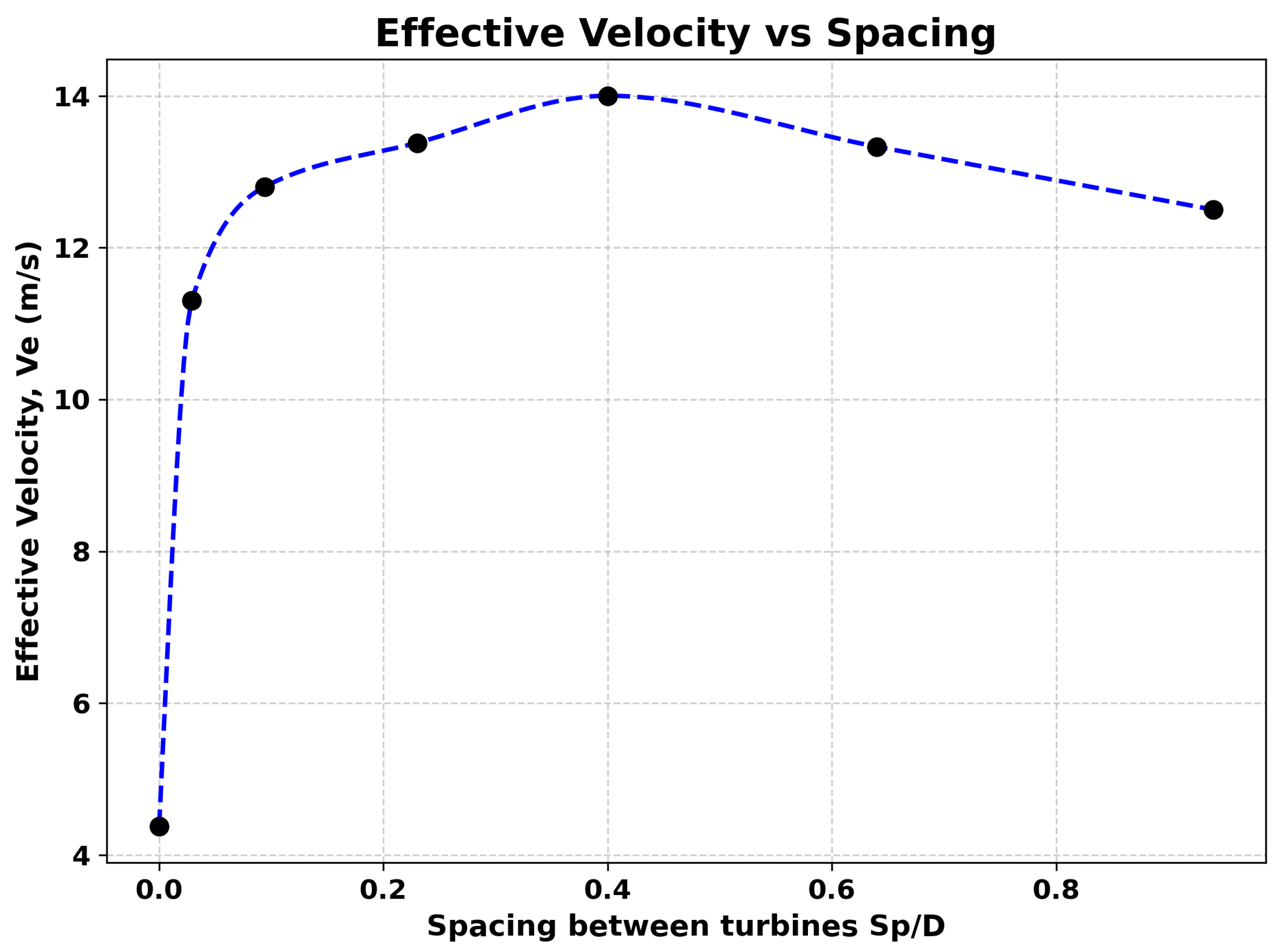
For the present study, the incoming wind speed (V) is fixed at 8 m/s. Using the above correlations and CFD-derived parameters, the optimal turbine spacing can be determined to maximize the effective velocity and, consequently, the torque generation of the Wind Wall system.
the relation between Ve and S is shown in the graph below:
Figure 19.
Graph showing the effective velocity(Ve) for different turbine spacing.
Figure 19.
Graph showing the effective velocity(Ve) for different turbine spacing.
6. Conclusions
The computational fluid dynamics tool is used to study the vertical axis wind turbine. A symmetrical Ugrinsky profile blade has been employed for this analysis. The governing equations are solved using the package Autodesk CFD. The objectives of this study are:
first, to determine the optimal helix angle for different spacings of the blades, and
second, to identify the best inter-blade spacing corresponding to each angle.
The performance of the turbine is evaluated using the torque coefficient and the moment coefficients. Furthermore, a correlation has been proposed between the effective velocity and the blade-spacing using this dataset, which will be useful in the future design of wind wall systems.
This study of the “Wind Wall” design, which integrates Vertical Axis Wind Turbines (VAWTs) with helical twists, highlights its considerable potential for enhancing torque generation and improving overall energy efficiency [
23,
24,
26]. The computational simulations and analyses conducted have provided meaningful insights into the influence of helix angle, blade spacing, and aerodynamic interactions on turbine performance [
17,
27]. The results indicate that the introduction of a moderate helix angle plays a pivotal role in improving torque characteristics [
25,
26]. Specifically, a slight twist in the range of 10–30 degrees was found to substantially enhance torque uniformity and mitigate pulsations when compared to a straight-blade configuration. Among these, a helix angle of approximately 20 degrees emerged as the most practical choice, offering an effective balance between aerodynamic efficiency and manufacturability. While higher twists can yield further improvements in torque, they introduce complexities in fabrication that may outweigh the performance gains [
23,
45,
46,
47]. Blade spacing was also identified as a critical parameter in determining aerodynamic efficiency [
17,
27]. The interaction between turbines generates a venturi effect, influencing the effective velocity of the incoming wind and, consequently, the torque output. The correlation established between effective velocity and spacing provides a predictive framework that can simplify the design of Wind Walls without relying exclusively on trial-and-error methods. By applying this relationship, turbine arrays can be configured to maximize performance in constrained environments [
11]. Incorporating Ugrinsky-profile blades and helical twists into the design not only improves energy capture at low wind speeds but also makes the system more adaptable to variable wind directions [
23,
24]. These design considerations strengthen the viability of Wind Walls for deployment in urban or limited spaces, where conventional large-scale wind turbines may not be feasible. This configuration as a wind wall can be useful in places like beach boardwalks, airport fences, tops of buildings, or between buildings where the wind is guided like a funnel, across seawall promenades, etc. [
17].
Looking ahead, further research is recommended to explore the effects of larger helix angles and to conduct dynamic simulations under variable wind conditions [
25,
26]. Such investigations would provide a more comprehensive understanding of the long-term performance and robustness of the system. Expanding the scope of study will also aid in evaluating the Wind Wall concept as a scalable and reliable renewable energy solution [
1,
6].
Author Contributions
Conceptualization, Poireinganba L. and Ajith Kumar S.; methodology, Poireinganba L. and Ajith Kumar S.; software, Poireinganba L.; validation, Poireinganba L. and Ajith Kumar S.; formal analysis, Poireinganba L. ; investigation, Poireinganba L., Swathy M. and Ajith Kumar S.; resources, Poireinganba L. and Ajith Kumar S.; data curation, Poireinganba L.; writing—original draft preparation, Poireinganba L.; writing—review and editing, Poireinganba L., Swathy M. and Ajith Kumar S.; visualization, Poireinganba L.; supervision, Swathy M. and Ajith Kumar S.; project administration, Swathy M. and Ajith Kumar S.; funding acquisition, Swathy M. and Ajith Kumar S. All authors have read and agreed to the published version of the manuscript.
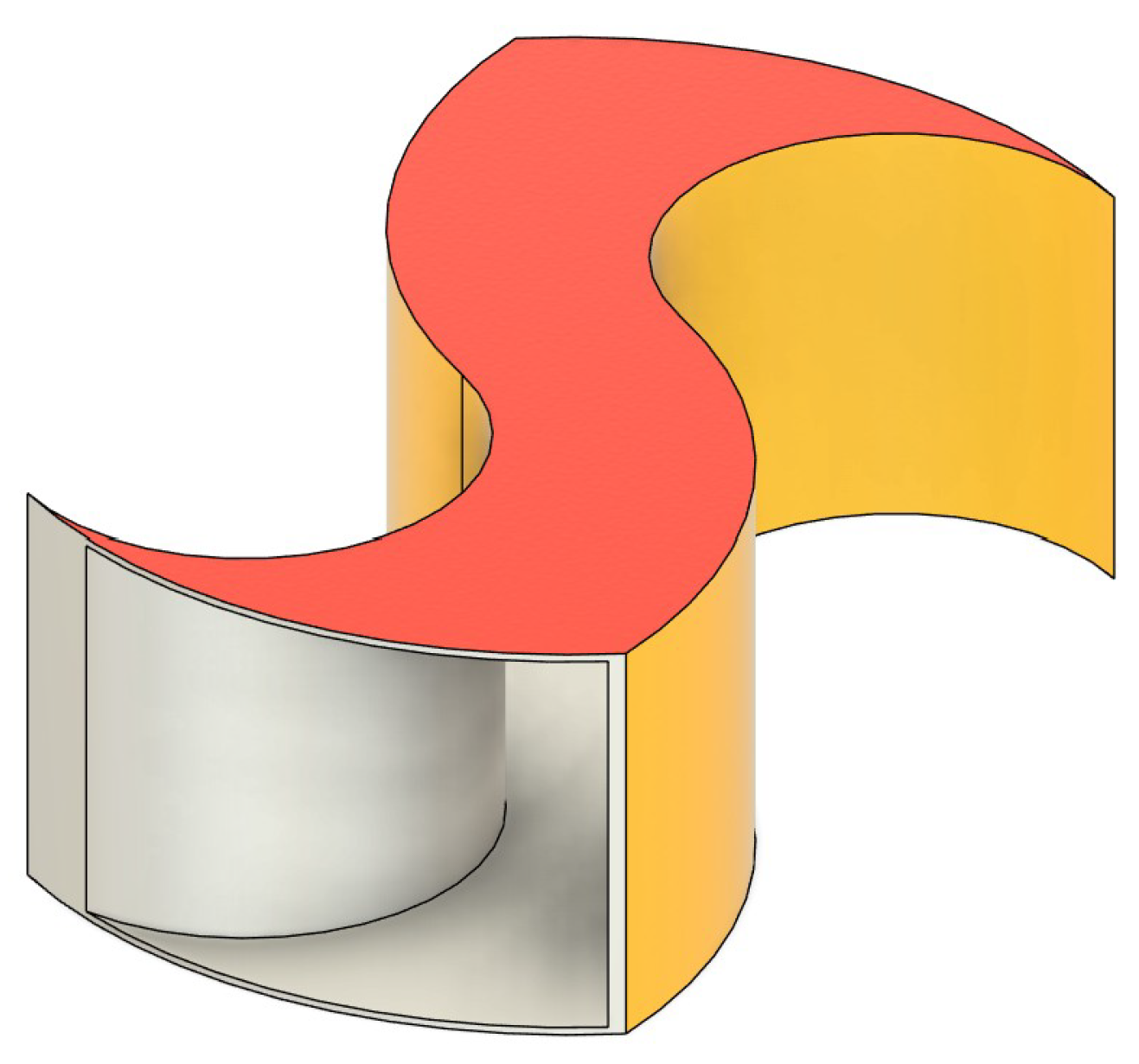

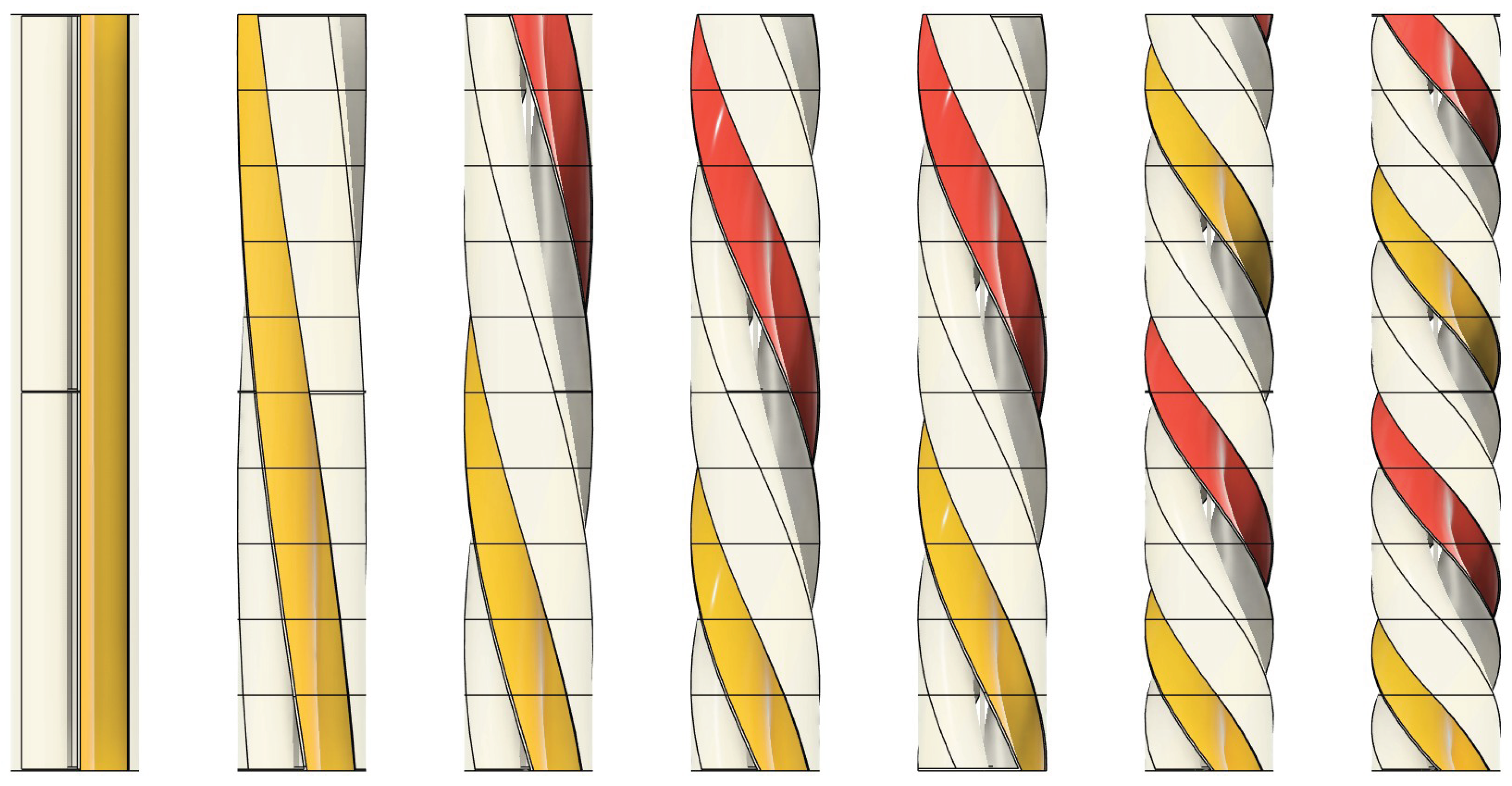
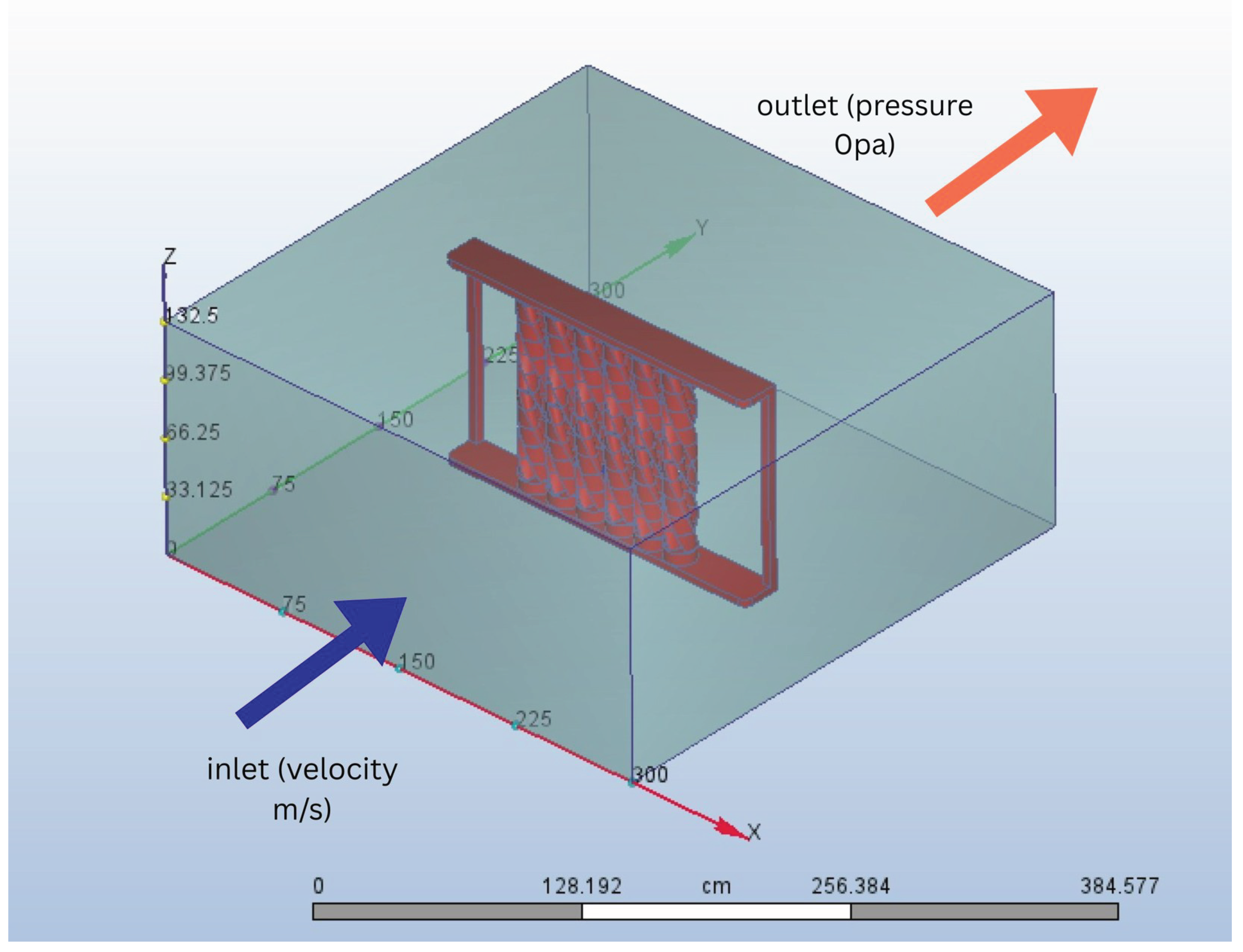
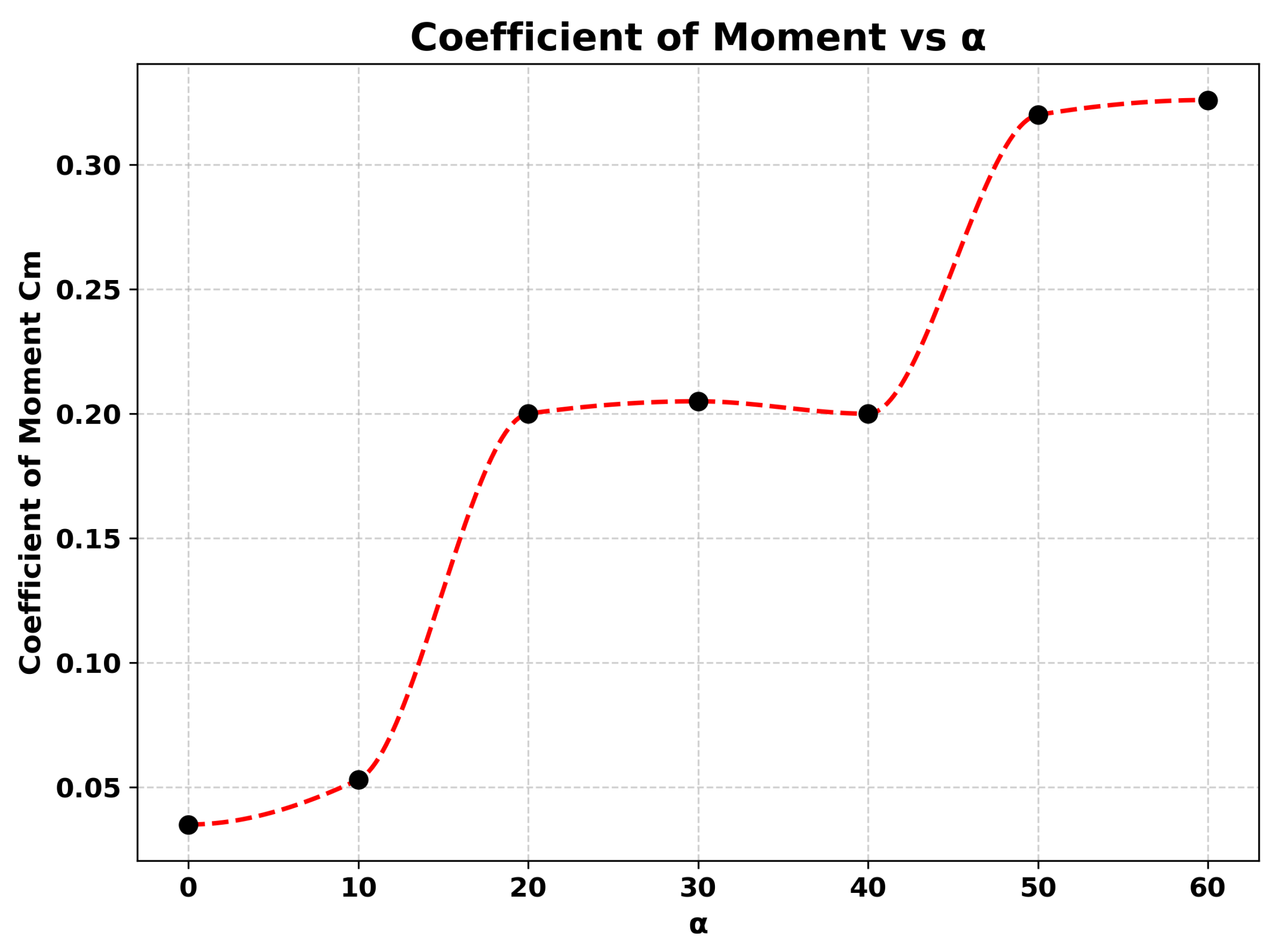
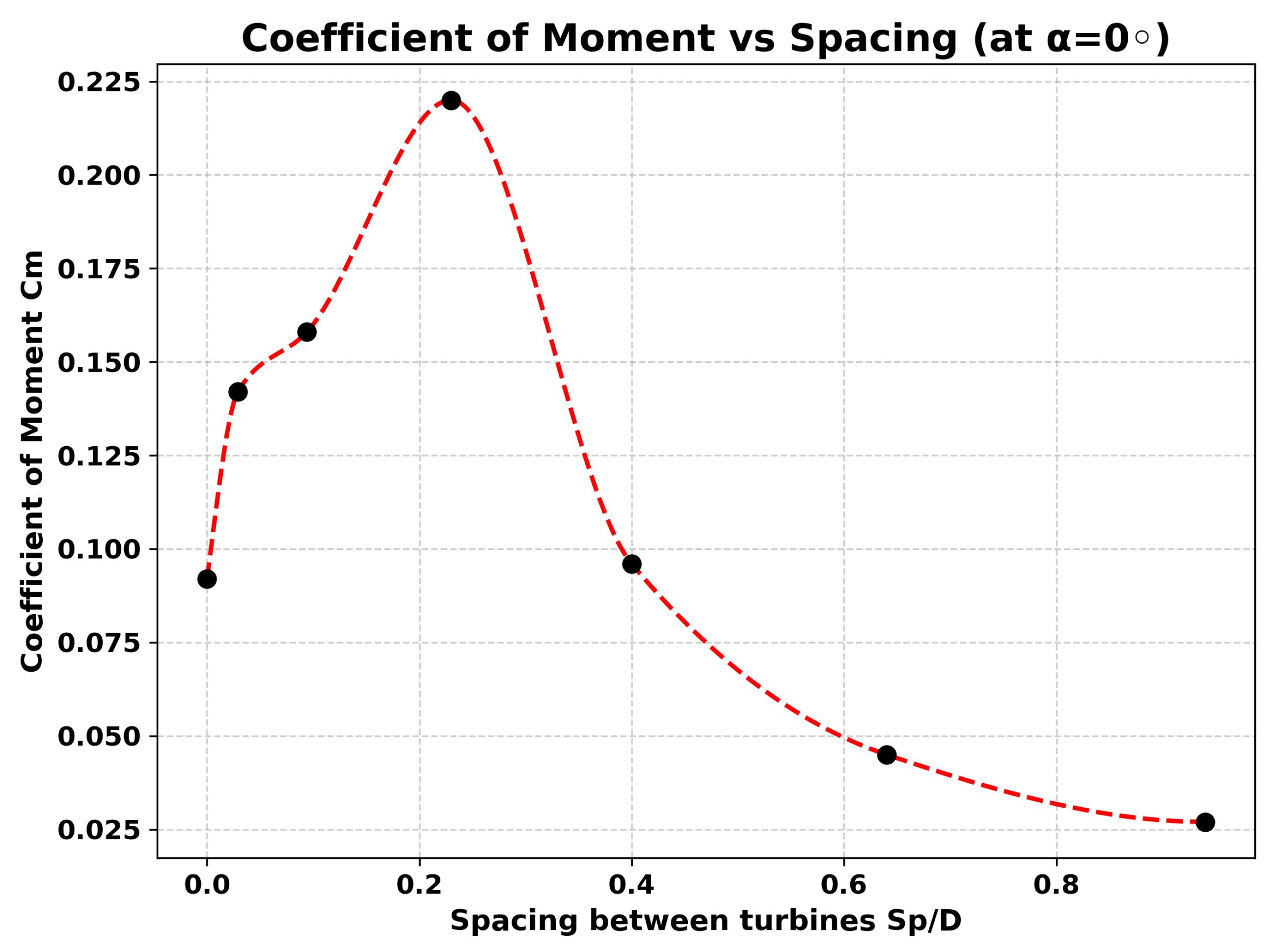 Table 3. Variation of Torque and coefficient of moment (Cm) for different spacings at helix angle .
Table 3. Variation of Torque and coefficient of moment (Cm) for different spacings at helix angle .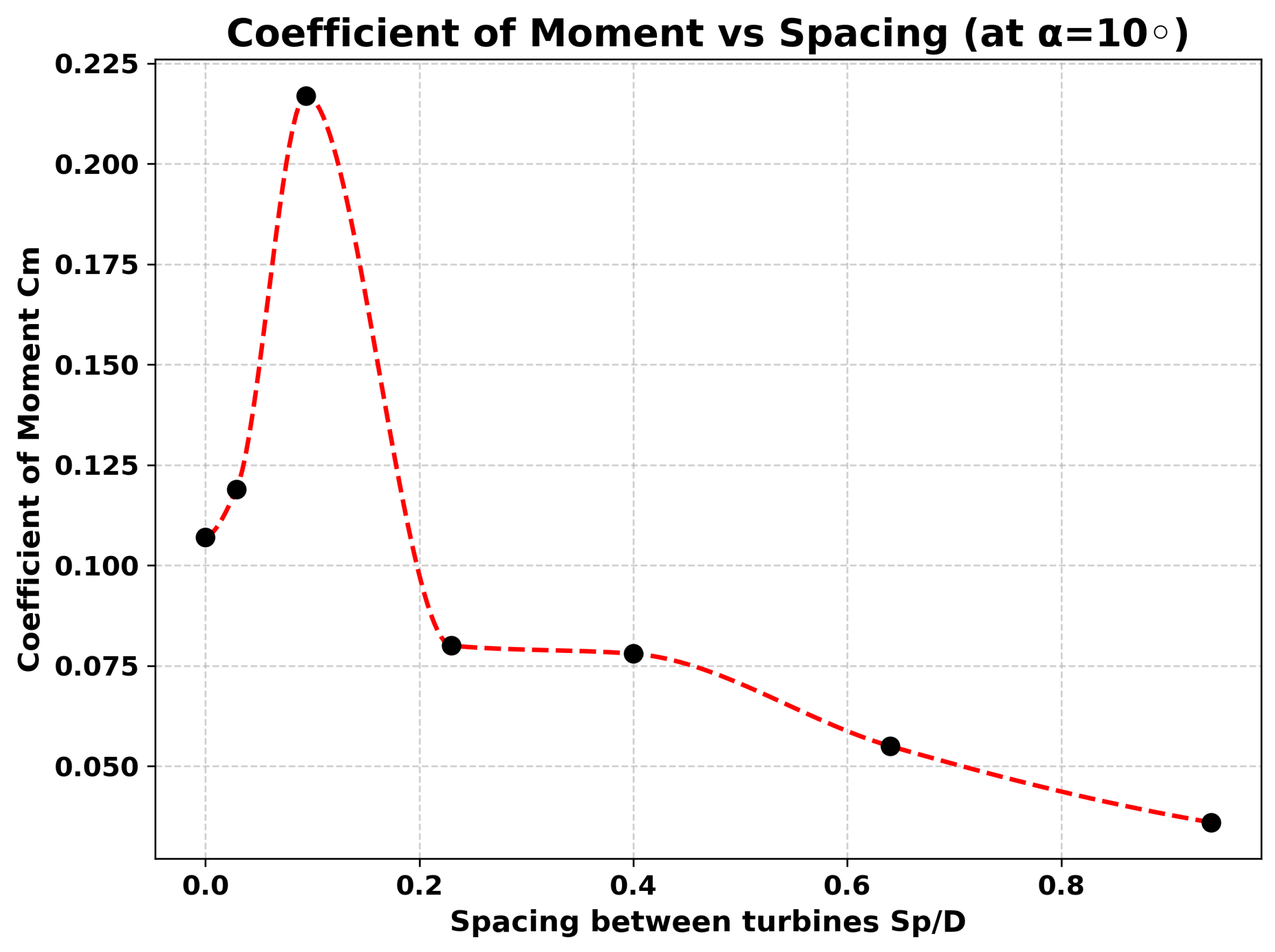 For the 10 degree helix configuration, the variation of torque and coefficient of moment (Cm) with turbine spacing demonstrates a distinct performance profile. At zero spacing, the initial Cm is slightly higher than the 0° case (Cm=0.107), reflecting the stabilizing effect of the helical twist in reducing destructive interference. A gradual increase is observed at a spacing of 0.5 cm (Cm=0.119), followed by a sharp rise to the peak value of Cm=0.217 at 1.6 cm. This indicates that the helical twist enables stronger constructive aerodynamic interactions at relatively closer spacings than in the untwisted configuration, likely due to smoother flow redirection and reduced pulsations in the torque.
For the 10 degree helix configuration, the variation of torque and coefficient of moment (Cm) with turbine spacing demonstrates a distinct performance profile. At zero spacing, the initial Cm is slightly higher than the 0° case (Cm=0.107), reflecting the stabilizing effect of the helical twist in reducing destructive interference. A gradual increase is observed at a spacing of 0.5 cm (Cm=0.119), followed by a sharp rise to the peak value of Cm=0.217 at 1.6 cm. This indicates that the helical twist enables stronger constructive aerodynamic interactions at relatively closer spacings than in the untwisted configuration, likely due to smoother flow redirection and reduced pulsations in the torque. This results shows us that the turbine interaction is highly spacing-dependent, with maximum aerodynamic benefit occurring at smaller separations. Starting from a baseline Cm=0.092 at zero spacing, performance rises sharply to a peak of Cm=0.35(torque 0.196 Nm) at 1.6 cm, nearly quadrupling the baseline due to strong constructive flow interactions and a venturi-like effect that boosts effective velocity. Beyond this optimum range (0.5–1.6 cm), the moment coefficient declines rapidly, dropping to 0.1 by 11 cm, though a minor recovery to 0.138 at 16 cm suggests residual flow re-alignment. Overall, the findings highlight that close turbine spacing strongly enhances aerodynamic performance, while larger spacing diminish interactions and cause the turbines to behave more independently.
This results shows us that the turbine interaction is highly spacing-dependent, with maximum aerodynamic benefit occurring at smaller separations. Starting from a baseline Cm=0.092 at zero spacing, performance rises sharply to a peak of Cm=0.35(torque 0.196 Nm) at 1.6 cm, nearly quadrupling the baseline due to strong constructive flow interactions and a venturi-like effect that boosts effective velocity. Beyond this optimum range (0.5–1.6 cm), the moment coefficient declines rapidly, dropping to 0.1 by 11 cm, though a minor recovery to 0.138 at 16 cm suggests residual flow re-alignment. Overall, the findings highlight that close turbine spacing strongly enhances aerodynamic performance, while larger spacing diminish interactions and cause the turbines to behave more independently.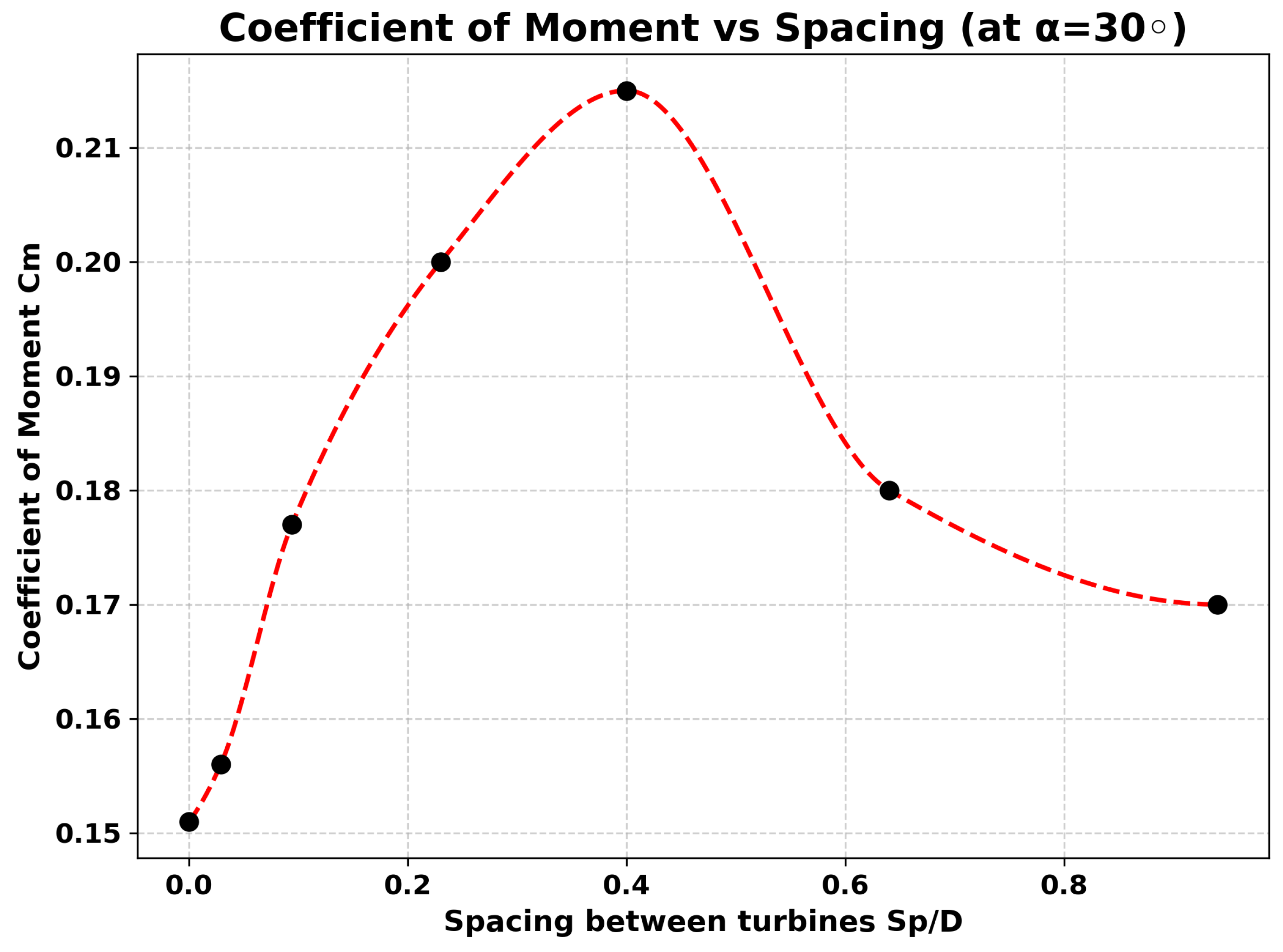 In this one, the turbine performance shows a more gradual and sustained enhancement compared to the previous case. Starting from a baseline of Cm=0.151 at zero spacing, the coefficient increases steadily with separation, peaking at Cm=0.215 (torque 0.115 Nm) at 7 cm. Unlike the sharp optimum observed earlier, this setup exhibits a broader effective range, with relatively high values maintained between 4–7 cm before declining moderately at larger spacing (Cm=0.18 at 11 cm and 0.17 at 16 cm). This trend suggests that the aerodynamic interaction is less dependent on very close spacing and instead benefits from a wider spacing window, where flow stabilization and smoother energy exchange between turbines sustain improved performance due to the change in the helix angle.
In this one, the turbine performance shows a more gradual and sustained enhancement compared to the previous case. Starting from a baseline of Cm=0.151 at zero spacing, the coefficient increases steadily with separation, peaking at Cm=0.215 (torque 0.115 Nm) at 7 cm. Unlike the sharp optimum observed earlier, this setup exhibits a broader effective range, with relatively high values maintained between 4–7 cm before declining moderately at larger spacing (Cm=0.18 at 11 cm and 0.17 at 16 cm). This trend suggests that the aerodynamic interaction is less dependent on very close spacing and instead benefits from a wider spacing window, where flow stabilization and smoother energy exchange between turbines sustain improved performance due to the change in the helix angle.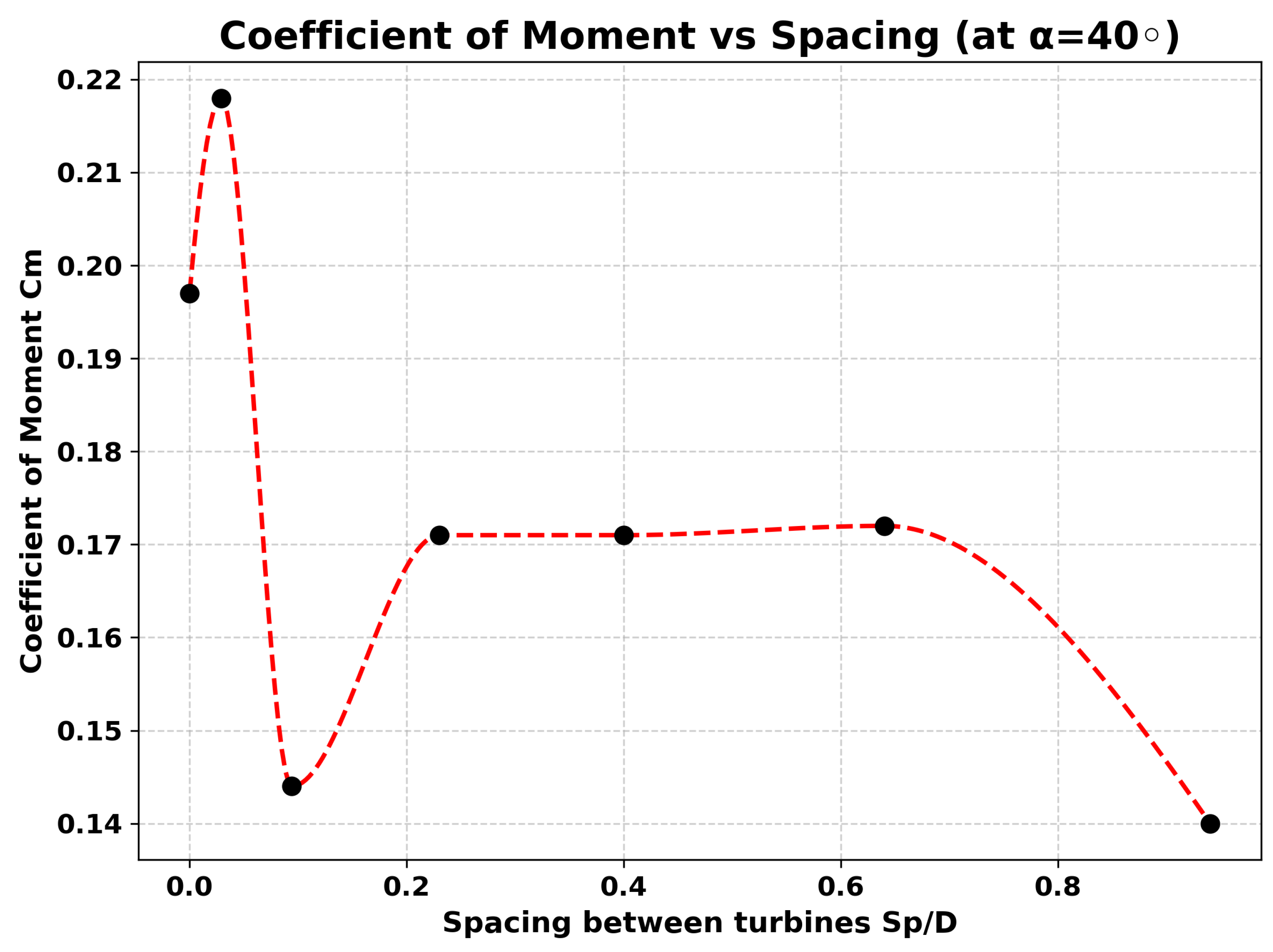 In this case, turbine interaction peaks at very small spacing before rapidly diminishing. The baseline performance at zero spacing is already strong (Cm=0.197), rising slightly to its maximum of Cm=0.218 (torque 0.122 Nm) at 0.5 cm. However, unlike previous configurations, the performance drops sharply at 1.6 cm (Cm=0.144) and only partially recovers at 4–11 cm, where values stabilize around Cm=0.171–0.172. At the largest spacing of 16 cm, the coefficient decreases further to 0.14. Furthermore for this helix angle, there is a plateauing effect of the Cm from distance coefficient 0.2 - 0.638 and then decreases further.
In this case, turbine interaction peaks at very small spacing before rapidly diminishing. The baseline performance at zero spacing is already strong (Cm=0.197), rising slightly to its maximum of Cm=0.218 (torque 0.122 Nm) at 0.5 cm. However, unlike previous configurations, the performance drops sharply at 1.6 cm (Cm=0.144) and only partially recovers at 4–11 cm, where values stabilize around Cm=0.171–0.172. At the largest spacing of 16 cm, the coefficient decreases further to 0.14. Furthermore for this helix angle, there is a plateauing effect of the Cm from distance coefficient 0.2 - 0.638 and then decreases further.