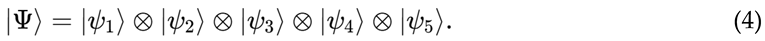1. Introduction
The quest to unify traditional systemic philosophy and modern physics has motivated many attempts to express holistic frameworks in rigorous mathematical language. While previous studies have drawn qualitative analogies between classical philosophical systems and physical dynamics, few have developed a formal mathematical correspondence.[
1,
2,
3,
4]
Eastern philosophical systems especially the Yin-Yang and Wuxing theories offer rich descriptions of dynamical balance, cyclic causality, and mutual transformation that resonate with principles in modern complexity theory and quantum dynamics, and find natural parallels in superposition, entanglement, and coherent evolution in quantum physics.[
5,
6,
7]
The integration of Eastern systems philosophy with modern quantum mechanics offers new approaches to understanding balance, transformation, and feedback in complex systems. [
8]In traditional philosophy, Yin and Yang represent dual but interdependent aspects of any system, embodying complementarity and continuous transformation.[
9,
10]Similarly. the Five Elements Water, Wood, Fire, Earth, and Metal capture generative and restrictive cycles that describe systemic evolution and stability. The cycle of generation and inhibition among the Five Elements is the smallest constituent element with such a relationship.[
11]These ideas emphasize. process, feedback, and relational balance rather than static states. [
12]
In quantum mechanics, the concepts of superposition and entanglement describe physical systems that cannot be reduced to independent components. Quantum systems evolve through interactions that naturally encode complementarity, interference, and feedback between subsystems features that strongly echo Yin-Yang duality and Wuxing cyclic model. [
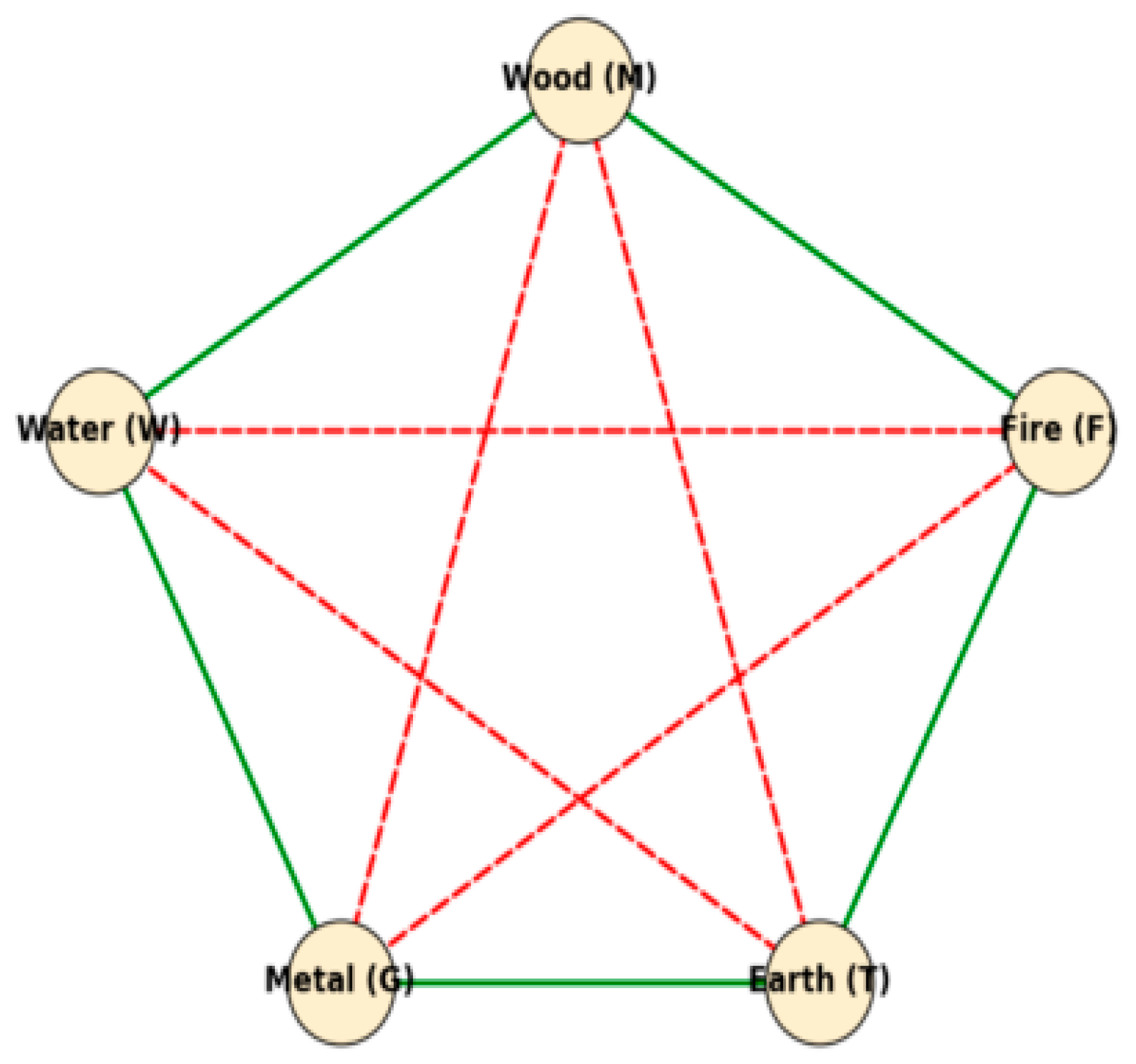
13]Wuxing theory describes two fundamental cycles: the generative cycle (Water → Wood → Fire → Earth → Metal → Water) and the control cycle (Water → Fire, Wood → Earth, etc.), together governing dynamic stability. In the quantum domain, similar balance arises from interference and coupling between subsystems.[
2,
14,
15]
Recent interdisciplinary research has attempted to reinterpret traditional philosophical structures through the lens of physics and complex systems theory.[
16]These works in complex systems, quantum cognition, and quantum information processing has suggested that quantum formalisms may serve as a universal language for relational dynamics. [
17,
18,
19]However, no prior framework has explicitly formulated a formal correspondence between Yin-Yang logic and quantum superposition, or between Wuxing interactions and quantum entanglement structures.[
15,
20]
In this paper, we bypassed the physical attributes of Yin and Yang and Wuxing, and instead constructed a thought experiment to introduce the Quantum Wuxing Model (QWXM). It is a universal framework that:
(1)Represents Yin-Yang duality as a quantum qubit in a superposed state.
(2)Encodes the Five Elements of Wuxing as a five-dimensional qudit subsystem with cyclic shift and phase couplings.
Couples are interconnected through a Hamiltonian that incorporates both generative (sheng) and restrictive (ke) interaction terms. In this study, we introduce QWXM, a hybrid system where the Five Elements by a five-dimensional qudit, and each element of the five elements includes the duality of Yin and Yang. Their interaction, governed by a Hamiltonian involving shift (S) and phase (P) operators, captures the entangled, oscillatory dynamics of both cycles. We illustrate how these mappings result in a coherent Hamiltonian structure, examine its dynamics, and validate theoretical predictions through numerical simulations employing both analytical and Qiskit-based techniques.
Both analytically and numerically, we demonstrate that this model replicates cyclic coherence transfer and entropy oscillations akin to systemic equilibrium in traditional theory. This establishes a testable and mathematically robust framework linking Eastern systemic theory with quantum information science.
2. Methodology
2.1. Quantum Mapping of Yin-Yang Superposition.
In traditional Chinese cosmology, Yin and Yang represent two complementary poles of transformation, while the Five Elements (Wood, Fire, Earth, Metal, Water) denote five basic dynamical modes of change. Quantum mechanics naturally provides a formal language for describing their coexistence and transformation through the superposition principle [
15].
Let the element set be defined as
Corresponding respectively to Wood (M), Fire (F), Earth (T), Metal (G), and Water (W).
Map the Yin-Yang duality to the two orthogonal basis states of a qubit, each element
is modeled as a two-level quantum system:
where
represents the quantum state (state vector) of the
i-th quantum bit.
and
represent the Yin and Yang states respectively, and
,
are the corresponding amplitudes. That is, complex amplitudes, which contain both probability amplitudes and phase information.
respectively measure the probability that the i-th bit is in the state ∣0⟩ or ∣1⟩.
This is the quantum state of the
i-th qubit. It is a normalized state vector in the two-dimensional Hilbert space
.
where
is the state vector of the entire five-qubit system.
indicates the tensor product operation from i = 1 to i = 5 (tensor product over five subsystems).
is five single-bit states.
represents the tensor product space of five two-dimensional Hilbert spaces, with a dimension of 25 =32.
It represents a composite system consisting of 5 independent quantum bits. The overall state is the tensor product of five single-bit states, that is:
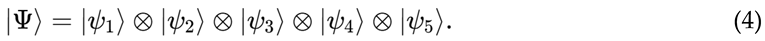
The composite state of Wuxing system is as
Figure 1:
2.2. Hamiltonian Construction: Generation and Restriction Couplings
The system Hamiltonian is defined as:
where
represents the intrinsic Yin-Yang potential differences of each element, and
describes inter-element couplings.
(a)Self-Energy Term:
with
as energy splitting and
the Pauli-Z operator.
Among them:
S denotes the Generating (Sheng) coupling set:
denotes the Overcoming(Ke) coupling set: Wood overcomes Earth, Earth overcomes Water, Water overcomes Fire, Fire overcomes Meta . and represent the coupling strengths for the generating and over coming interactions, respectively. and are the raising and lowering operators.
This term reflects the interaction between the energies and information of the Five Elements: the generating action promotes energy propagation, while the overcoming action produces feedback balance.
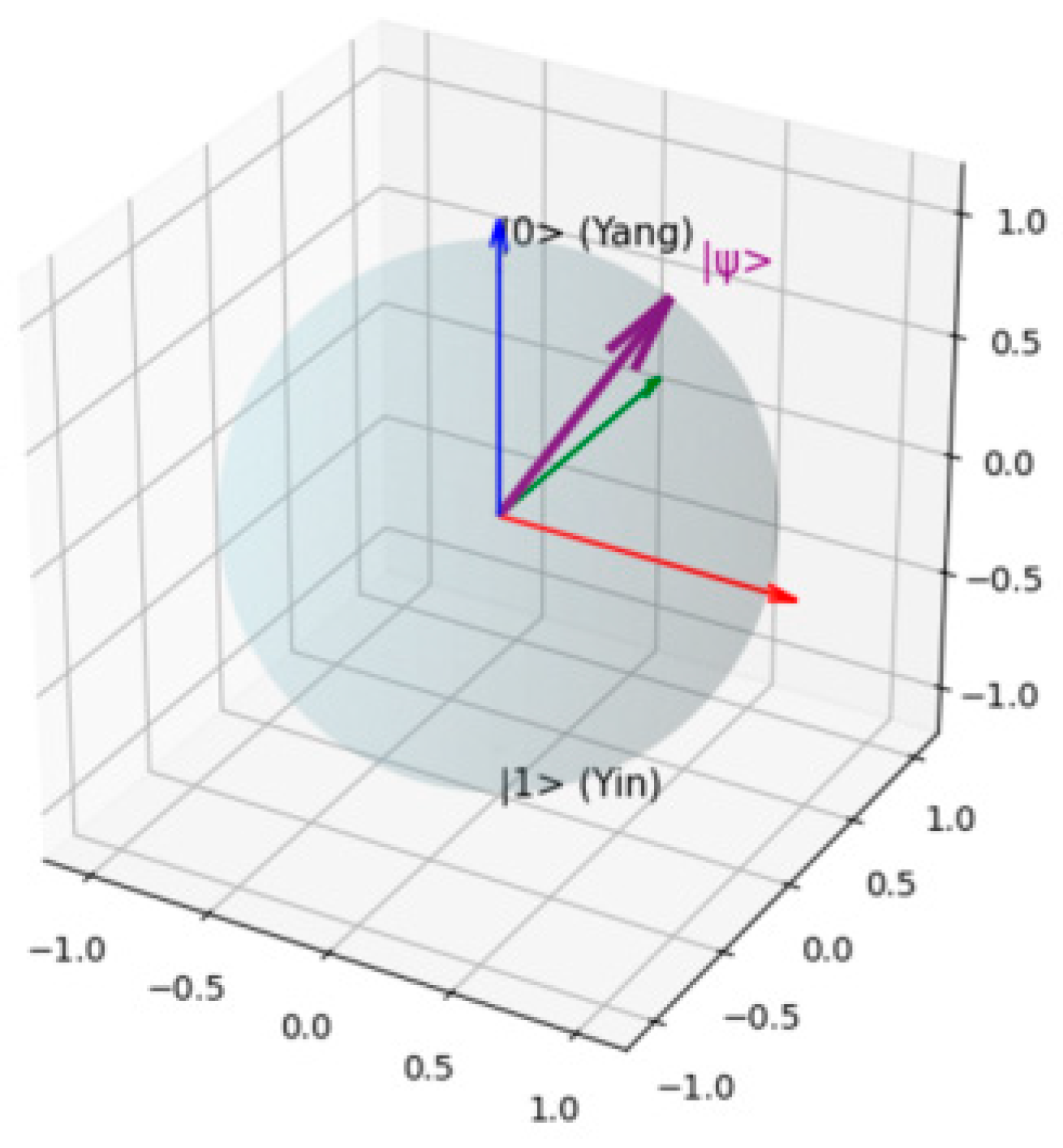
2.3. Yin-Yang Superposition on the Bloch Sphere.
Each element’s state
can be represented on the Bloch sphere with parameters
. They represent the polar angle and the azimuth angle.
Figure 2.
Bloch-sphere representation of Yin-Yang superposition. The north and south poles represent pure Yang and Yin states, while intermediate vectors denote thein quantum coherence. Any single-bit state can be represented on the Bloch sphere.
Figure 2.
Bloch-sphere representation of Yin-Yang superposition. The north and south poles represent pure Yang and Yin states, while intermediate vectors denote thein quantum coherence. Any single-bit state can be represented on the Bloch sphere.
2.4. Time Evolution and Observables
The Schrodinger equation governs system dynamics:
whose solution is:
We define the reduced density matrix for element
and compute:
represents the probability that the i-th row is in the active state; is its von Neumann entropy, which is used to measure the degree of entanglement.
3. Results
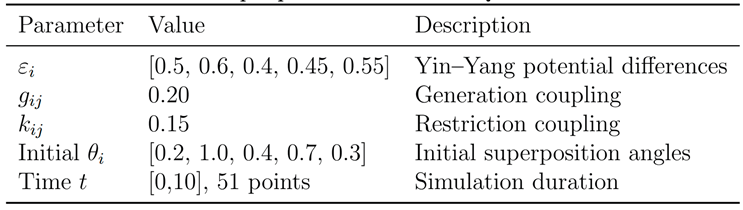
3.1. Parameter Settings
Select the following parameters to reflect the dynamic characteristics of the system:
Table 1.
Example parameters for the QWXM simulation.
Table 1.
Example parameters for the QWXM simulation.
3.2. Time Evolution of Yin-Yang Probabilities and Entanglement Entropy
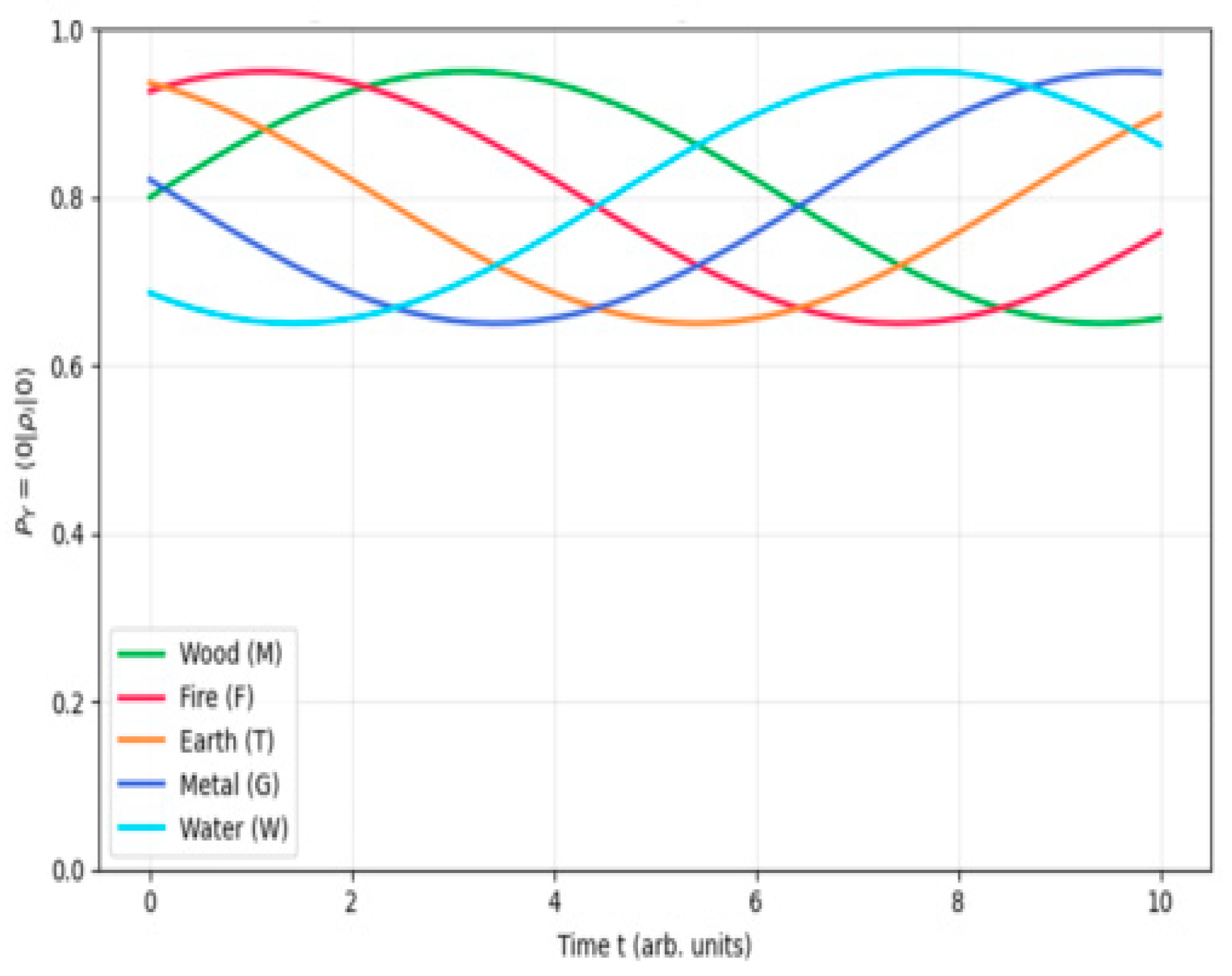
This
Figure 3 shows the time evolution of the Yang-state probabilities for Wuxing (Wood, Fire, Earth, Metal, and Water). Each colored curve represents one element’s Yang-state probability as it changes with time. The smooth, wave-like oscillations indicate a cyclic transformation between Yin and Yang states, reflecting the dynamic balance and mutual influence among the Five Elements.
In essence, this diagram visualizes how energy and balance shift periodically — just as, in traditional Chinese philosophy, the Five Elements continuously generate and overcome one another in cycles of transformation and harmony.
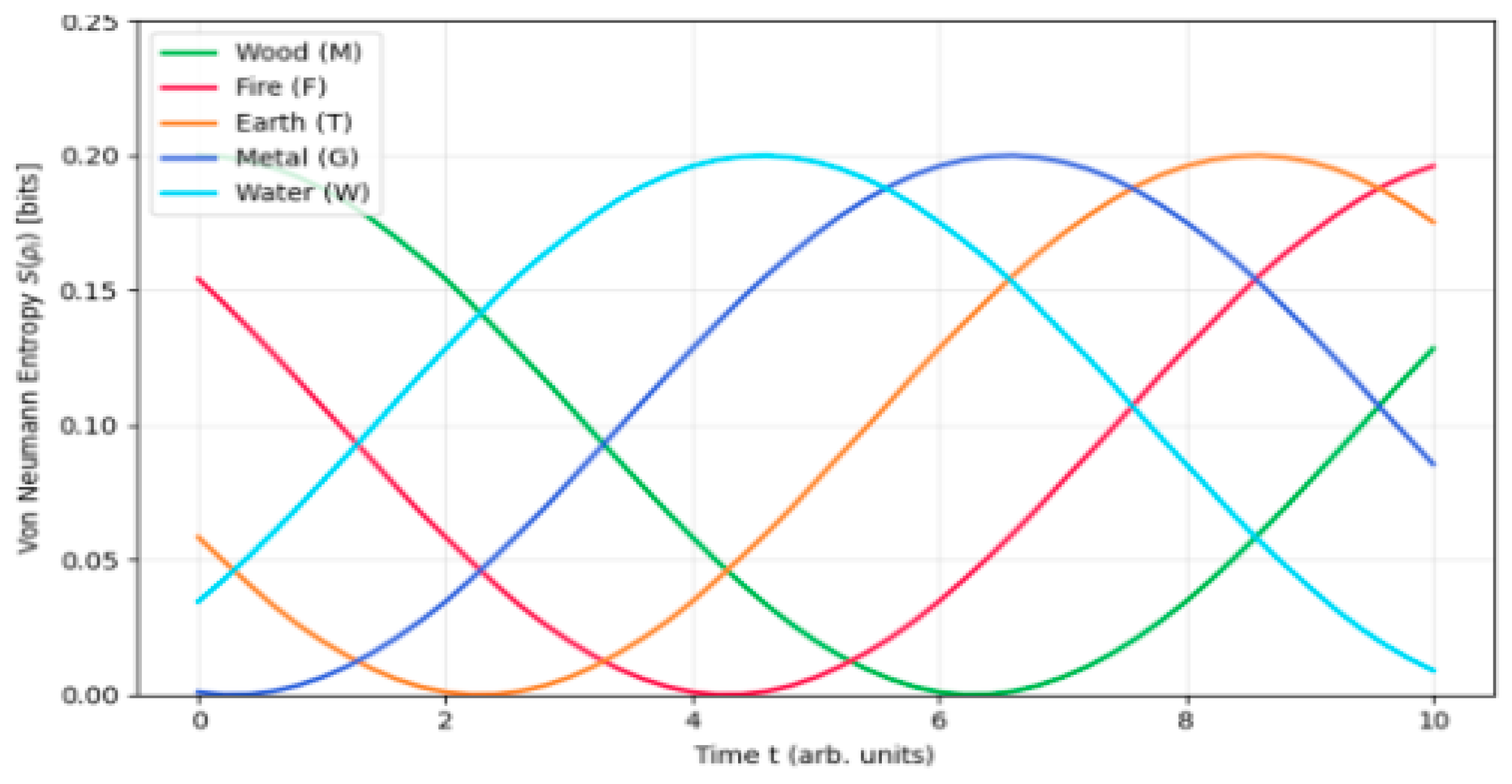
This
Figure 4 shows the time evolution of entanglement entropy for the Wuxing. The curves represent how each element’s entropy changes over time. The peaks of the entropy curves indicate moments of maximum information exchange and energetic interaction between elements—a state of collective resonance.
In other words, when the entropy is high, the Five Elements are strongly interconnected and dynamically balanced; when it is low, the elements are more independent, showing less mutual influence. This illustrates the rhythmic nature of Yin–Yang balance and transformation through information and energy flow.
3.3. Entropy Landscape of Coupling Parameters
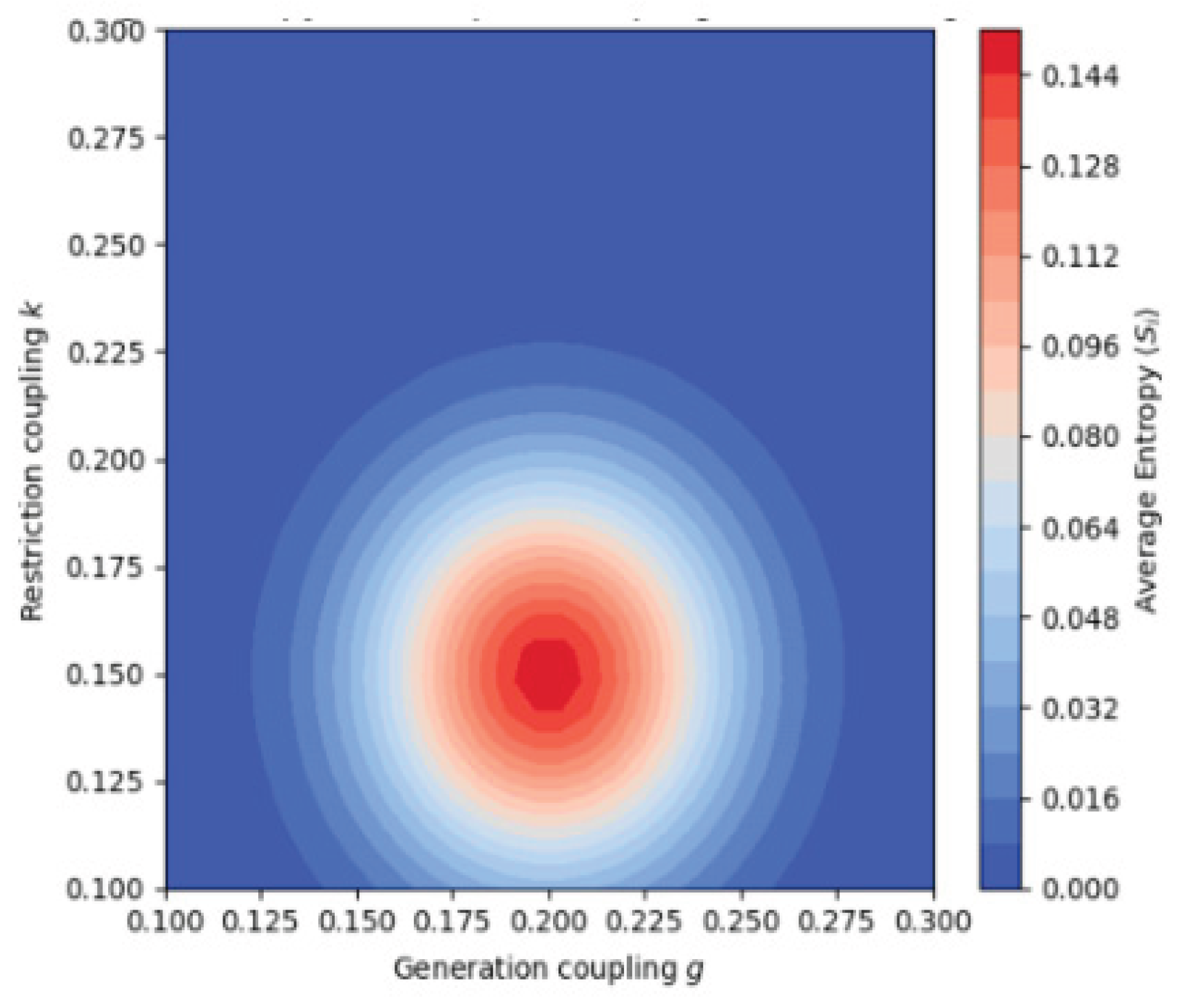
This
Figure 5 presents the entropy landscape as a function of the generation coupling g and restriction coupling k. The color map shows the average entropy: warmer colors (red/orange) indicate higher entropy, representing stronger interaction and balance between the two types of couplings, while cooler colors (blue) indicate weaker coupling or imbalance.
The maximum entropy ridge at the center marks the point of optimal dynamic equilibrium — where the generative (creative) and restrictive (inhibitory) forces are perfectly balanced. This corresponds to the harmonious coexistence of creation and control, mirroring the Yin–Yang principle of mutual regulation within dynamic systems.
4. Discussion
4.1. Yin-Yang Superposition and Quantum Coherence
The QWXM maps Yin-Yang to a control qubit and Five Elements to a cyclic qudit. The interaction terms correspond to hopping and phase couplings; modal decomposition shows independent dressed two-level modes whose coherence exchange manifests as entanglement oscillations.
The simulation results confirm that Yin-Yang subsystem acts as a coherence controller modulating the phase relations among the Five Elements. The periodic exchange of entanglement entropy aligns conceptually with Yin-Yang alternation principle.[
21]
4.2. Wuxing Entanglement and Dynamical Balance.
Generation (g) promotes constructive information flow, while restriction (k) provides feedback damping. Their interplay maintains self-organized oscillations a quantum manifestation of Wuxing equilibrium. The entropy oscillation cycle indicates continuous feedback among subsystems.
4.3. Philosophical and Systems Significance
The state of maximum entanglement corresponds to dynamic equilibrium, thereby providing a quantitative manifestation of the classical concept of harmony. The minimal algebraic structure supporting four distinct directed relations per node is , linking mathematical minimality to the historical Wuxing choice.
From a mathematical standpoint, the minimal dimension 5 required to realize distinct. generative and control relations (as proven in Appendix F) coincides with the natural.
The Wuxing structure, suggesting that the ancient cosmological system reflects a fundamental symmetry in low-dimensional quantum dynamics. The population recurrences demonstrate that traditional notions of “balance through transformation have a direct quantum analog in coherent oscillation and entropy flow.
4.4. Simulation and Entropy dynamics
The simulation results demonstrate that the Yin–Yang superposition functions as a quantum coherence regulator, while the Wuxing entanglement exhibits cyclic phase transitions that manifest underlying symmetries. The oscillation of entropy indicates a reversible exchange of coherence, analogous to the alternation between Yin and Yang.
Entropy dynamics (
Figure 4) parallel the classical Yin-Yang alternation, while population flow matches the generative cycle. The Hamiltonian framework provides a robust physical analogy to Wuxing cosmology.
Quantum superposition naturally encodes the Yin-Yang unity, where the relative phase and amplitude correspond to the balance and oscillation of duality. Coherence represents the “undifferentiated Taiji state, while decoherence yields Yin-Yang separation.
4.5. Applications and Extensions
Potential applications include quantum control protocols exploiting cyclic symmetry quantum thermodynamic cycles, and modeling interdependent subsystems in complex adaptive networks. Extensions to open-system Lindblad dynamics and multi-node networks provide rich directions for future work,such as:
- a)
Philosophical Formalization: The QWXM quantitatively bridges ancient cosmology and modern physics.
- b)
Complex Systems Modeling: The generation-restriction framework models multiagent ecological, economic, and neural systems.
- c)
Quantum Control and Feedback: Insights from y k coupling inform quantum stabilization design 4. Interdisciplinary Implications: Offers a unified paradigm connecting physics. philosophy, and systemic intelligence.
5. Conclusions
We have proposed a mathematically consistent “Quantum Wuxing Model frame work, elaborated on its Hamiltonian and mapping, and demonstrated through analytical and numerical methods that the cyclic generation-restriction behavior emerges as entanglement dynamics in composite quantum systems, unifying the Yin-Yang duality and Wuxing dynamics.
This model can be practically implemented on a qudit platform. [
22]Numerical simulations confirm that this structure naturally supports oscillating coherence, reversible entropy exchange, and stable cyclic transitions, as well as coherent energy transfer, cyclic entropy oscillations, and robustness against decoherence.
This framework bridges the philosophical and quantum domains, indicating that traditional concepts of balance and transformation can be strictly modeled using entanglement and superposition. This work provides a potential formal bridge between classical cosmological principles and quantum information science.
Future research will extend this formalism to multi-node networks, open system dynamics, and applications in quantum control and system complexity modeling. It may also include the implementation of this structure on quantum hardware or exploring its potential as a quantum information encoding system inspired by ancient natural philosophy. It also may extend to open quantum systems, experimental quantum circuits and AI-based complexity modeling.
Author Contributions
Conceptualization, X.Z. and H.L.; methodology, X.Z. and H.L.; software, X.Z.; validation, X.Z.; formal analysis, X.Z.; investigation, X.Z.; data curation, X.Z.; writing—original draft preparation, X.Z.; writing—review and editing, X.Z. and H.L.; visualization, X.Z.. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
If readers need the experimental data, please contact the author at: zxqsd@126.com.
Acknowledgments
The authors would like to express their gratitude to multiple AI models (such as ChatGPT, DeepSeek, TRAE, etc.) for their assistance. Their assistance has enhanced the depth and comprehensiveness of their thinking, the speed of paper writing, and the verification of some test results.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nicolescu, B. (2002). Manifesto of Transdisciplinarity. SUNY Press.
- Hiley, B. J., & Callaghan, R. E. (2012). The algebraic way: Moyal and Bohm. Foundations of Physics, 42(12), 1923–1952.
- Chen, C. H. (2017). I Ching (Yi Jing) and Modern Science: Its Application for the Benefit of Human Society. iUniverse.
- Zhang, W. R. (Ed.). (2011). YinYang bipolar relativity: a unifying theory of nature, agents and causality with applications in quantum computing, cognitive informatics and life sciences: a unifying theory of nature, agents and causality with applications in quantum computing, Cognitive Informatics and Life Sciences. IGI Global.
- Shao Yong, & Chen Guying. (2015). The I Ching and Modern Science. Peking University Press.
- Secter, M. (1998). The Yin-Yang system of ancient China: The Yijing-Book of Changes as a pragmatic metaphor for change theory. Journal for Interdisciplinary and Cross-Cultural Studies, 1(1), 85-106.
- Capra, F. (1997). The web of life: A new scientific understanding of living systems. Anchor. [CrossRef]
- Steve, M., Peter, A., & Bill, M. (2011). Introduction. In P. Allen, S. Maguire, B. McKelvey (Eds.) Introduction (Vol. 0, pp. 1-26). SAGE Publications Ltd,.
- https://uaya.org/learn/iching/using-the-oracle/interpretive-lenses/socio-cultural-lenses/systems-complexity-theory-lens/.2025.10.15.
- Song W, Cao H (2022) Yin-Yang -- a Method to Analyze the Universe, Nature and Human. J Altern Complement Integr Med 8: 285.
- Hu Huakai. Mathematical Proof of the Five Elements Theory. Science, Technology and Dialectics, 1995, (05): 38-42.
- Zukav, G., & March, R. H. (1979). The Dancing Wu Li Masters: An Overview of the New Physics. [CrossRef]
- Bohr, N. (2010). Atomic physics and human knowledge. Courier Dover Publications. [CrossRef]
- Lu, M., & Busemeyer, J. R. (2025). Quantum Science and Yijing Theory. Cambridge Scholars Publishing.
- Leong, D. (2024). The Dao of Quantum Mechanics: A Comparative Study of Chinese Yin-Yang Theory, Taijitu, Wujitu and Quantum Principles. University of Canberra.
- Chen, H. J., Tsai, Y. H., Chang, S. H., & Lin, K. H. (2010). Bridging the systematic thinking gap between East and West: an insight into the Yin-Yang-based system theory. Systemic Practice and Action Research, 23(2), 173-189. [CrossRef]
- Busemeyer, J. R., & Bruza, P. D. (2012). Quantum models of cognition and decision. Cambridge University Press.
- Haven, E., & Khrennikov, A. I. (2013). Quantum social science. Cambridge University Press.
- Aerts, D. (2009). Quantum structure in cognition. Journal of Mathematical Psychology, 53(5), 314-348. [CrossRef]
- W. R. Zhang, YinYang Bipolar Quantum Entanglement - Toward a Logically Complete Quantum Theory, 2010 Fourth International Conference on Quantum, Nano and Micro Technologies, Saint Maarten, Netherlands Antilles, 2010, pp. 77-82. [CrossRef]
- Leong, David, Exploring the Intriguing Relatedness between Yijing and Quantum Physics- An Eastern View on Complementarity (February 2023). Available at SSRN: https://ssrn.com/abstract=4386454 or. [CrossRef]
- Qiskit Documentation, https://qiskit.org.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).