Estimation for Longitudinal Varying Coefficient Partially Nonlinear Models Based on QR Decomposition

1. Introduction

In recent years, longitudinal data have attracted much attention due to their wide applications in fields such as biomedicine, economics and social sciences. This type of data is obtained through repeated observations of the same subject at different time points. As a result, multiple measurement results of the same subject exhibit temporal or spatial dependence, which makes the traditional independent and identically distributed assumption no longer applicable. To address this issue, the varying coefficient partially nonlinear model has become one of the research hotspots, as it combines the interpretability of parametric models and the flexibility of nonparametric models. Li and Mei [1] put forward a profile nonlinear least squares estimation approach to estimate the parameter vector and coefficient function vector of the varying coefficient partially nonlinear model, and further derived the asymptotic characteristics of the obtained estimators.

Important progress has been made in model estimation in existing studies. Yu and Zhu et al. [2] constructed robust estimators for the partially linear additive model under functional data. Yan and Tan et al. [3] explored the empirical likelihood inference targeting the partially linear errors-in-variables model under longitudinal data. Varying coefficient partially nonlinear model based on mode regression, a robust two-stage method for estimation and variable selection was proposed by Xiao and Liang [4]. Zhao and Zhou et al. [5] put forward a new orthogonality-based empirical likelihood inference method through orthogonal estimation techniques and empirical likelihood inference methods, which is used to estimate the parametric and nonparametric components in a class of varying coefficient partially linear instrumental variable models for longitudinal data. Liang and Zeger [6] applied the generalized estimating equation to longitudinal data analysis, which effectively handles the correlation issue of longitudinal data. For the varying coefficient partially nonlinear quantile regression model under randomly left-censored data, Xu and Fan et al. [7] introduced a three-stage estimation weighting method.

However, significant challenges still exist in the existing methods for estimating the varying coefficient partially nonlinear model. For instance, the estimation of nonlinear parameters is easily disturbed by nonparametric components and longitudinal correlation structures, leading to reduced estimation efficiency; when there is multicollinearity among explanatory variables, the ill-posed nature of the design matrix will further decrease the stability of estimation. Such issues severely limit the performance and practicality of the model in practical applications.

To address the above issues, existing studies have proposed a variety of improved methods. For example, Qu and Lindsay et al. [8] used the quadratic inference function to improve the estimating equation, and this method maintains optimal performance even when the working correlation structure is misspecified. Bai and Fung et al. [9] applied the quadratic inference function to handle longitudinal data, and the results demonstrate that the proposed estimation method exhibits excellent asymptotic properties. Schumaker [10] used B-spline basis functions to approximate the varying coefficient part, which improves the computational efficiency. Wei and Wang et al. [11] proposed a model averaging method for linear models with randomly missing response variables. Jiang and Ji et al. [12] proposed an estimation method for the varying coefficient partially nonlinear model based on the exponential squared loss function. Xiao and Chen [13] proposed a procedure for local bias-corrected cross-sectional nonlinear least squares estimation. For left-censored data, Xu and Fan et al. [14] established a quantile regression estimation and variable selection method for the varying coefficient partially nonlinear model. Based on the varying coefficient partially nonlinear model where the nonparametric part has measurement errors, Qian and Huang [15] discussed a modified profile least squares estimation method. Wang and Zhao et al. [16] proposed an inverse probability weighted cross-sectional least squares method to estimate unknown parameters and nonparametric functions for the varying coefficient partially nonlinear model.

This paper proposes an orthogonal estimation framework that integrates QR decomposition and the QIF. QR decomposition can effectively eliminates the ill-posed nature of the design matrix and improves numerical stability. The QIF method avoids the limitations of traditional generalized estimating equations by adaptively weighting the intra-group correlation structure, significantly enhancing estimation efficiency. This study not only provides a new theoretical tool for longitudinal data analysis but also offers a feasible solution to complex modeling problems in practical applications.

The structure of this paper is arranged as follows: Section 2 introduces the model specification and estimation method, including the specific implementation of QR decomposition and QIF; Section 3 discusses the asymptotic properties of the estimators; Section 4 verifies the superiority of the proposed method through simulation experiments; The proof process of the main conclusions is provided in the Appendix.

2. Models and Methods

Consider the varying coefficient partially nonlinear model introduced by Li and Mei [1]:

$$Y=X^T\alpha \left(U\right)+g\left(Z,\beta \right)+\epsilon ,$$

(1)

where, $Y\in R$ is the response variable, $X\in R^p$, $U\in R$, and $Z\in R^r$ are covariates, $\alpha \left(U\right)={\left({\alpha }_1\left(U\right),{\alpha }_2\left(U\right),\dots ,{\alpha }_p\left(U\right)\right)}^T$ and ${\alpha }_k\left(U\right),k=1,2,\dots ,p$ are unknown smooth functions, $g(·,·)$ is a nonlinear function with a known form, $\beta ={\left({\beta }_1,{\beta }_2,\dots ,{\beta }_q\right)}^T$ denotes a q-dimensional unknown parameter vector, and $\epsilon$ is the model error with mean zero and variance ${\sigma }^2$.

2.1. Estimation of Parameter Vector

Considering the model (1) under longitudinal data, suppose the j-th observation of the i-th individual satisfies:

$$\begin{array}{c}{Y}_{ij}=X_{ij}^T\alpha \left(U_{ij}\right)+g\left(Z_{ij},\beta \right)+{\epsilon }_{ij},i=1,2,\dots ,n,j=1,2,\dots ,n_i,\end{array}$$

(2)

among them,${\epsilon }_{ij}$ has a mean of zero, and $X_{ij}\in R^p,Z_{ij}\in R^r,U_{ij}$ are covariates.

Based on the idea of Schumaker [10], the unknown function ${\alpha }_k\left(·\right),k=1,2,\dots ,p$ can be approximated using basis functions. The B-spline basis functions are denoted by the vector $B\left(u\right)={\left(B_1\left(u\right),B_2\left(u\right),\dots ,B_L\left(u\right)\right)}^T$. The dimension L is defined as $L=K+M$, where K and M represent the number of interior knots and the order of the spline, respectively. Then ${\alpha }_k\left(u\right)$ can be approximately expressed as

$$\begin{array}{c}{\alpha }_k\left(u\right)\approx B{\left(u\right)}^T{\gamma }_k,k=1,2,\dots ,p,\end{array}$$

(3)

here ${\gamma }_k={\left({\gamma }_{k1},{\gamma }_{k2},\dots ,{\gamma }_{kL}\right)}^T$ are the coefficient vector for the B-spline basis functions. model (2) can be expressed as

$$Y_{ij}\approx W_{ij}^T\gamma +g\left(Z_{ij},\beta \right)+{\epsilon }_{ij},i=1,2,\dots ,n,j=1,2,\dots ,n_i,$$

(4)

define $W_{ij}=I_p\otimes B\left(U_{ij}\right)·X_{ij}$, where ⊗ is the Kronecker product, and let $\gamma ={\left({\gamma }_1^T,{\gamma }_2^T,\dots ,{\gamma }_p^T\right)}^T$, $Y_i={\left(Y_{i1},Y_{i2},\dots ,Y_{i{n}_i}\right)}^T$, $W_i={\left(W_{i1},W_{i2},\dots ,W_{i{n}_i}\right)}^T$, $g(Z_i,\beta )=\left(g(Z_{i1},\beta ),g(Z_{i2},\beta ),\dots ,\right.$ ${\left.g(Z_{i{n}_i},\beta )\right)}^T$, ${\epsilon }_i={\left({\epsilon }_{i1},{\epsilon }_{i2},\dots ,{\epsilon }_{i{n}_i}\right)}^T$. Then model (4) can be expressed as

$$Y_i\approx W_i\gamma +g\left(Z_i,\beta \right)+{\epsilon }_i,i=1,2,\dots ,n.$$

(5)

Suppose that for all $i=1,2,\dots ,n$, the matrices $W_i$ have full column rank, their QR decomposition can be expressed as:

$$\begin{array}{c}{W}_i=Q_i\left(\begin{array}{c}{R}_i\\ \mathbf{0}\end{array}\right),\end{array}i=1,2,\dots ,n,$$

(6)

where $Q_i$ is an $n_i\times n_i$ orthogonal matrix, $R_i$ is a $pL\times pL$ triangular matrix, and $\mathbf{0}$ denotes a $\left(n_i-pL\right)\times pL$ zero matrix. The matrix $Q_i$ can be divided into two parts as $Q_i=\left(Q_{i1},Q_{i2}\right)$, where $Q_{i1}$ is a $n_i\times pL$ matrix and $Q_{i2}$ is a $n_i\times \left(n_i-pL\right)$ matrix. Substitute the decomposition of $Q_i$ into (6) to obtain $W_i=Q_{i1}{R}_i$, from the properties of orthogonal matrices, $Q_{i2}^T{Q}_{i1}=0$ can be derived, and then $Q_{i2}^T{W}_i=Q_{i2}^T{Q}_{i1}{R}_i=0$ is obtained. Multiplying both sides of Equation (5) by $Q_{i2}^T$, and we get:

$$Q_{i2}^T{Y}_i\approx Q_{i2}^{T}g\left(Z_i,\beta \right)+Q_{i2}^T{\epsilon }_i,i=1,2,\dots ,n.$$

(7)

It is easy to see that model (7) is a regression model containing only unknown parameters. Following Liang [6], the generalized estimating equation for $\beta$ can be defined as:

$$\sum _{i=1}^n{g}^{\left(1\right)}{(Z_i,\beta )}^T{Q}_{i2}{V}_i^{-1}{Q}_{i2}^T(Y_i-g(Z_i,\beta ))=0,$$

(8)

among them, $g^{\left(1\right)}(Z_i,\beta )={(g^{\left(1\right)}(Z_{i1},\beta ),\dots ,g^{\left(1\right)}(Z_{i{n}_i},\beta ))}^T$, $V_i=Q_{i2}^T{\Sigma }_i{Q}_{i2}$, ${\Sigma }_i$ is the covariance matrices of $Y_i$, and the structure of $V_i$ can also be expressed as $V_i=A_i^{{\displaystyle \frac{1}{2}}}R\left(\rho \right)A_i^{{\displaystyle \frac{1}{2}}}$ according to the method of Liang [6], where $A_i$ is a diagonal matrix, $R\left(\rho \right)$ is a working correlation matrix, and $\rho$ is a correlation parameter. Since a consistent estimator of $\rho$ is not always available in practice, we adopt the QIF method to approximate the working correlation matrix $R^{-1}\left(\rho \right)$ through a set of basis matrices, thereby avoiding direct specification of the correlation structure. Let $M_1,M_2,\dots ,M_s$ be a set of basis matrices and $a_1,a_2,\dots ,a_s$ be coefficients satisfying:

$$R^{-1}\left(\rho \right)\approx a_1{M}_1+a_2{M}_2+\dots +a_s{M}_s.$$

(9)

Substituting (9) into (8), we obtain:

$$\sum _{i=1}^n{g}^{\left(1\right)}{(Z_i,\beta )}^T{Q}_{i2}{A}_i^{-\frac{1}{2}}(a_1{M}_1+\dots +a_s{M}_s)A_i^{-\frac{1}{2}}{Q}_{i2}^T(Y_i-g(Z_i,\beta ))=0.$$

(10)

Define the extended score function as follows:

$$G_n\left(\beta \right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\eta }_i\left(\beta \right)\triangleq {\displaystyle \frac{1}{n}}\sum _{i=1}^n\left(\begin{array}{c}{g}^{\left(1\right)}{(Z_i,\beta )}^T{Q}_{i2}{A}_i^{-\frac{1}{2}}{M}_1{A}_i^{-\frac{1}{2}}{Q}_{i2}^T(Y_i-g(Z_i,\beta ))\\ g^{\left(1\right)}{(Z_i,\beta )}^T{Q}_{i2}{A}_i^{-\frac{1}{2}}{M}_2{A}_i^{-\frac{1}{2}}{Q}_{i2}^T(Y_i-g(Z_i,\beta ))\\ ⋮\\ g^{\left(1\right)}{(Z_i,\beta )}^T{Q}_{i2}{A}_i^{-\frac{1}{2}}{M}_s{A}_i^{-\frac{1}{2}}{Q}_{i2}^T(Y_i-g(Z_i,\beta ))\end{array}\right).$$

(11)

Thus, the QIF for $\beta$ can be defined as:

$$M_n\left(\beta \right)=G_n^T\left(\beta \right){\Phi }_n^{-1}\left(\beta \right)G_n\left(\beta \right),$$

(12)

where ${\Phi }_n\left(\beta \right)={\displaystyle \frac{1}{n}}\underset{i=1}{\sum ^n}{\eta }_i\left(\beta \right){\eta }_i^T\left(\beta \right)$, in this case, the estimator $\widehat{\beta }$ of $\beta$ is obtained by minimizing the objective function $M_n\left(\beta \right)$:

$$\widehat{\beta }=arg\underset{\beta }{min}{M}_n\left(\beta \right).$$

(13)

2.2. Estimation of the Coefficient Functions

The QIF effectively handles the correlation in longitudinal data and improves estimation efficiency by constructing a set of estimating equations. Therefore, after obtaining the initial estimates of the parameters $\beta$, we also use the QIF method to estimate the coefficient functions ${\alpha }_k\left(u\right),k=1,2,\dots ,p.$

Substitute the estimator of into Equation (5), resulting in:

$${\tilde{Y}}_i\approx W_i\gamma +{\epsilon }_i,i=1,2,\dots ,n,$$

(14)

where ${\tilde{Y}}_i=Y_i-g_i\left(Z_i,\widehat{\beta }\right)$, assuming that the covariance matrix of ${\tilde{Y}}_i$ is ${\mathsf{\Psi }}_i$, and its structure is expressed following Liang [6] as ${\mathsf{\Psi }}_i=A_i^{{\displaystyle \frac{1}{2}}}R\left(\rho \right)A_i^{{\displaystyle \frac{1}{2}}}$, where $A_i$ is a diagonal matrix, $R\left(\rho \right)$ is a working correlation matrix, and $\rho$ is a correlation parameter. Assuming $V_i$ is known, construct the following estimating equation:

$$\underset{i=1}{\sum ^n}{W}_i^T{\mathsf{\Psi }}_i^{-1}\left({\tilde{Y}}_i-W_i\gamma \right)=0.$$

(15)

In practical applications, $V_i$ is usually unknown. Based on this, we still adopt the QIF method and use $M_1,M_2,\dots ,M_s$ to approximate $R_i^{-1}$, then we have:

$$\underset{i=1}{\sum ^n}{W}_i^T{A}_i^{-{\displaystyle \frac{1}{2}}}\left(a_1{M}_1+a_2{M}_2+\dots +a_s{M}_s\right)A_i^{-{\displaystyle \frac{1}{2}}}\left(Y_i-W_i\gamma \right)=0.$$

(16)

Define the extended score function as follows:

$$G_n\left(\gamma \right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\phi }_i\left(\gamma \right)\triangleq {\displaystyle \frac{1}{n}}\sum _{i=1}^n\left(\begin{array}{c}{W}_i^T{A}_i^{-{\displaystyle \frac{1}{2}}}{M}_1{A}_i^{-{\displaystyle \frac{1}{2}}}\left(Y_i-W_i\gamma \right)\\ W_i^T{A}_i^{-{\displaystyle \frac{1}{2}}}{M}_2{A}_i^{-{\displaystyle \frac{1}{2}}}\left(Y_i-W_i\gamma \right)\\ ⋮\\ W_i^T{A}_i^{-{\displaystyle \frac{1}{2}}}{M}_s{A}_i^{-{\displaystyle \frac{1}{2}}}\left(Y_i-W_i\gamma \right)\end{array}\right).$$

(17)

Thus, the QIF for $\gamma$ can be defined as:

$$Q_n\left(\gamma \right)=G_n^T\left(\gamma \right)C_n^{-1}\left(\gamma \right)G_n\left(\gamma \right),$$

(18)

where $C_n\left(\gamma \right)={\displaystyle \frac{1}{n}}\underset{i=1}{\sum ^n}{\phi }_i\left(\gamma \right){\phi }_i^T\left(\gamma \right)$. In this case, the estimate $\widehat{\gamma }$ of $\gamma$ can be obtained by minimizing the objective function $Q_n\left(\gamma \right)$:

$$\widehat{\gamma }=argmin{Q}_n\left(\gamma \right).$$

(19)

Thus, the estimate of the coefficient function ${\alpha }_k\left(u\right)$ can be expressed as:

$${\widehat{\alpha }}_k\left(u\right)\approx B{\left(u\right)}^T{\widehat{\gamma }}_k,k=1,2,\dots ,p.$$

(20)

where ${\widehat{\gamma }}_k$ is the component corresponding to the k-th coefficient function in $\widehat{\gamma }$.

3. Main Conclusions

This section studies the asymptotic properties of the estimators $\widehat{\beta }$ and ${\widehat{\alpha }}_k\left(u\right),k=1,2,\dots ,p$, assuming that ${\beta }_0$ and ${\alpha }_0(·)$ are the true values of $\beta$ and $\alpha (·)$ respectively, ${\gamma }_0$ is the true value of $\gamma$, and ${\alpha }_{k0}(·)$ and ${\gamma }_{k0}$ are the k-th components of ${\alpha }_0(·)$ and $\gamma$ respectively. First, we present some common regularity conditions in longitudinal data analysis:

(C1) The random variable U has a bounded support $\Omega$, and its probability density function $f_u\left(·\right)$ is positive and has continuous second-order derivatives.

(C2) The varying coefficient function ${\alpha }_1\left(u\right),\dots ,{\alpha }_p\left(u\right)$ is continuously differentiable of order r on $\left[0,1\right]$, where $r>2$.

(C3) For any Z, $g\left(Z,\beta \right)$ is continuous with respect to $\beta$, and $g\left(Z,\beta \right)$ has continuous partial derivatives of order r.

(C4) ${sup}_i∥E\left({\epsilon }_i{\epsilon }_i^T\right)∥<\infty$ holds, and there exists some $\delta >0$ satisfying $E\left({∥{\epsilon }_i∥}^{2+\delta }\right)<\infty$.

(C5) The covariates $X_{ij}$ and $Z_{ij}$ are assumed to satisfy the following conditions: $\underset{ij}{sup}E\left\{{∥X_{ij}∥}^4\right\}<\infty$, $\underset{ij}{sup}E\left\{{∥Z_{ij}∥}^4\right\}<\infty$, $i=1,2,\dots n,j=1,2,\dots ,n_i.$

(C6) Let $t_1,\dots ,t_k$ be interior nodes on $\left[0,1\right]$. Furthermore, let $t_0=0,t_{k+1}=1,{\xi }_i=t_i-t_{i-1},$ then there exists a constant $C_0$ such that:${\displaystyle \frac{max\left\{{\xi }_i\right\}}{min\left\{{\xi }_i\right\}}}\le C_0,max\left\{\left|{\xi }_{i+1}-{\xi }_i\right|\right\}=o\left(K^{-1}\right)$

(C7) Define $P_{ik}=Q_{i2}{A}_i^{-\frac{1}{2}}{M}_k{A}_i^{-\frac{1}{2}}{Q}_{i2}^T$, then we have:

$${\displaystyle \frac{1}{n}}\sum _{i=1}^{n}E\left\{g^{\left(1\right)}{(Z_i,\beta )}^T{P}_{ik}{g}^{\left(1\right)}(Z_i,\beta )\right\}\stackrel{P}{\to }{D}_k,k=1,2,\dots ,s.$$

$${\displaystyle \frac{1}{n}}\sum _{i=1}^{n}E\left\{g^{\left(1\right)}{(Z_i,\beta )}^T{P}_{il}^T{V}_i{P}_{il}{g}^{\left(1\right)}(Z_i,\beta )\right\}\stackrel{P}{\to }{\Omega }_{lk},l,k=1,2,\dots ,s.$$

Among them, $D_k$ and ${\Omega }_{lk}$ are constant matrices, and $\stackrel{P}{\to }$ denotes convergence in probability. Define ${\Omega }_0={\left({\Omega }_{lk}\right)}_{ps\times ps}$ and ${\mathsf{\Gamma }}_0={(D_1^T,\dots ,D_s^T)}^T$, additionally, assume that ${\Omega }_0$ and ${\mathsf{\Gamma }}_0^T{\Omega }_0^{-1}{\mathsf{\Gamma }}_0$ are both invertible.

It is noted that, conditions (C1) to (C5) are common conditions in varying coefficient partially nonlinear models components, Condition (C6) indicates that $t_0,\dots ,t_{k+1}$ is a uniform partition sequence over the interval $\left[0,1\right]$, and Condition (C7) is used for subsequent proofs.

Theorem 1. 

Under conditions (C1) to (C7), and when $n\to \infty$, it follows that:

$$\sqrt{n}(\widehat{\beta }-{\beta }_0)\stackrel{L}{\to }N(0,\sum ),$$

where the matrix $\sum ={\left({\mathsf{\Gamma }}_0^T{\Omega }_0^{-1}{\mathsf{\Gamma }}_0\right)}^{-1}$, $\stackrel{L}{\to }$ denotes convergence in distribution.

Theorem 2. 

Under conditions (C1) to (C7), the number of nodes $K=O\left(n^{\frac{1}{2r+1}}\right)$, and when $n\to \infty$, it follows that:

$$∥{\widehat{\alpha }}_k\left(·\right)-{\alpha }_{k0}\left(·\right)∥=O_p\left(n^{-\frac{r}{2r+1}}\right),k=1,2,\dots ,p.$$

where $∥·∥$ denotes the $L_2$ norm of the function.

4. Simulation Study

This section evaluates the finite-sample performance of the proposed orthogonality estimation method based on QR decomposition and quadratic inference functions in varying coefficient partially nonlinear models through a Monte Carlo simulation study. Consider the following model:

$$Y=X^T\alpha \left(U\right)+g\left(Z,\beta \right)+\epsilon ,$$

among them, the covariates $X,Z={(Z_1,Z_2)}^T$ both follow normal distributions, the nonlinear function $g(Z,\beta )$ is defined as $g(Z,\beta )={\beta }_1{Z}_1+{\beta }_{2}exp\left(Z_2\right)$, with the parameter vector $\beta ={({\beta }_1,{\beta }_2)}^T={(0.8,-0.5)}^T$. Additionally, $U\sim U(0,1)$, the coefficient function $\alpha \left(U\right)=sin\left(2\pi U\right)$, the error term $\epsilon$ follows an AR(1) process, and its structure is: ${\epsilon }_{i,j}=0.5{\epsilon }_{i,j-1}+v_{i,j}$, where $v_{i,j}\sim N(0,0.5\sqrt{1-{0.5}^2})$ to ensure the error variance is 0.5.

The sample size is set to $n=100,150,200$, for the i-th subject, the number of repeated measurements is $m_i\equiv 8$, and 1000 simulation runs are conducted for each case. The method combining QR decomposition and QIF proposed in this paper (OQIF) is compared with the profile nonlinear least squares method (PNLS) proposed by Li and Mei [1]. After sorting out, the following Table 1 and Table 2 are obtained.

It can be seen from the results in Table 1 that as the sample size increases, the bias and standard deviation of both methods decrease. However, the bias and standard deviation of the OQIF method are smaller, indicating more accurate estimation. Although a larger sample size improves the estimation accuracy of both methods, the OQIF method performs better in bias control.

The results in Table 2 show that the average length of the confidence interval of the OQIF method is significantly shorter than that of the PNLS method, demonstrating higher estimation efficiency, the coverage rate of the OQIF method is closer to the ideal 95%, while although the coverage rate of the PNLS method has improved, it is still below 95%.

In conclusion, when the sample size increases from 100 to 200, the OQIF method demonstrates higher estimation accuracy and stronger robustness across all evaluation indicators. These trend analyses further confirm the theoretical advantages and practical application value of the OQIF method in handling nonlinear longitudinal data.

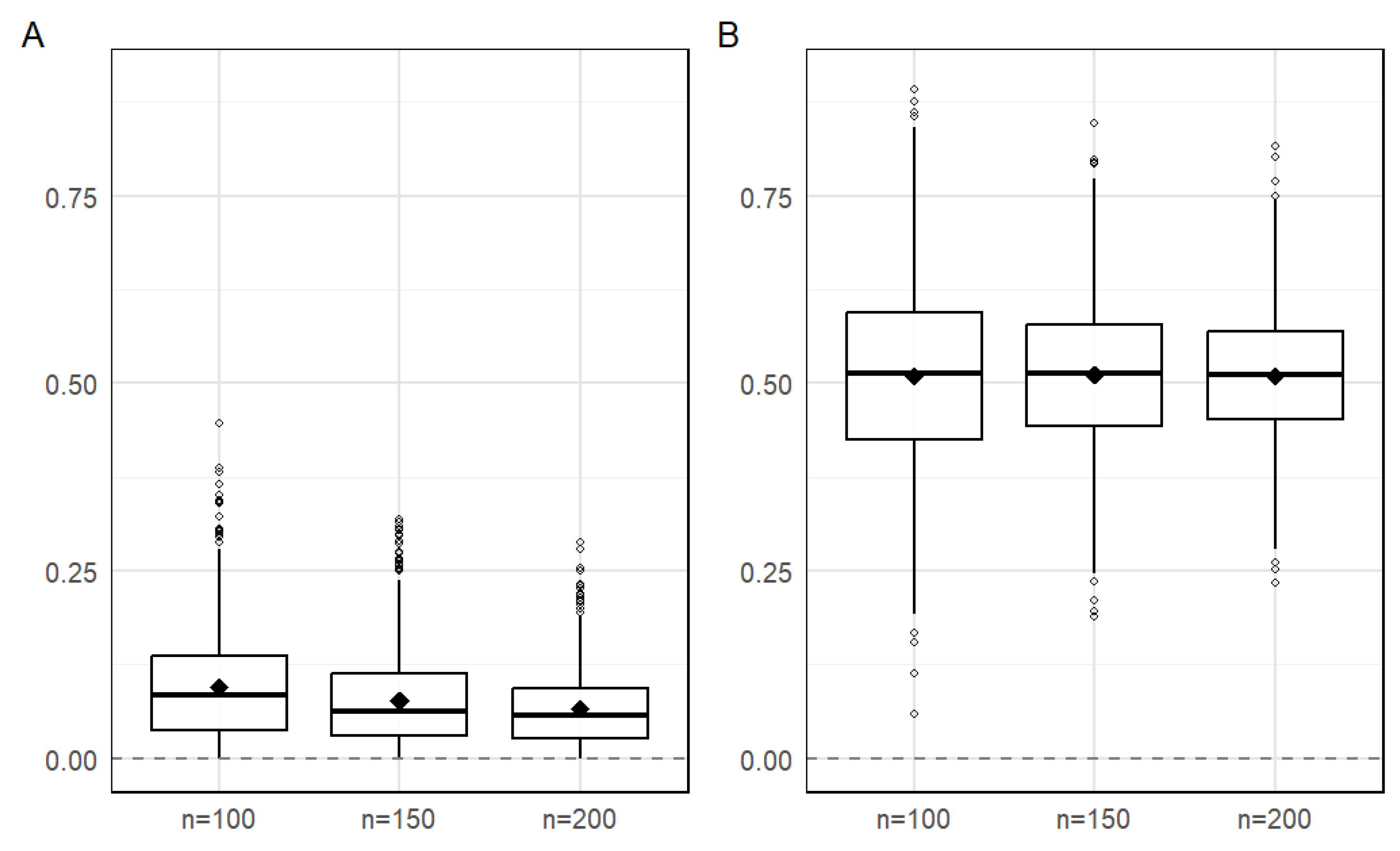
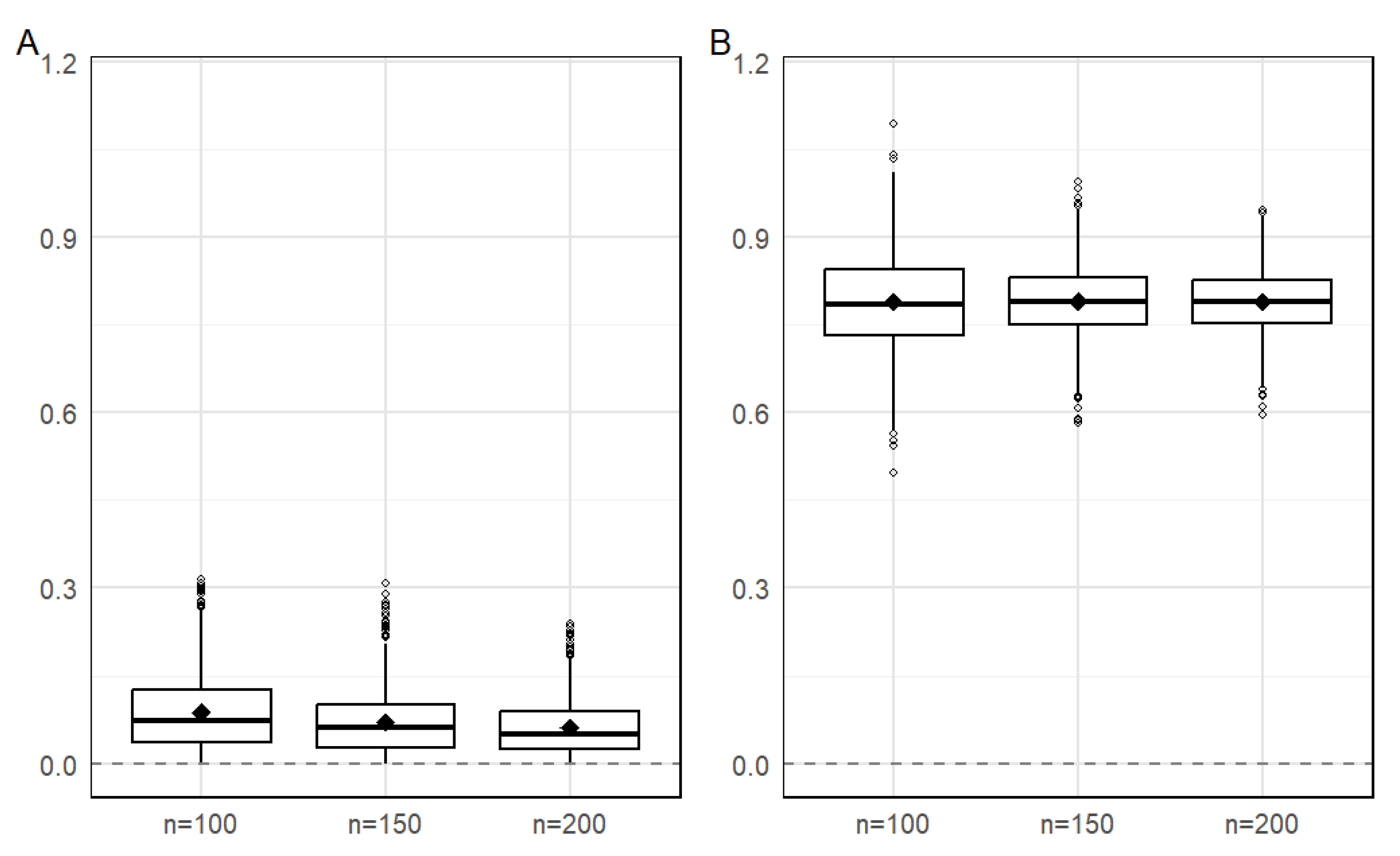
We further conducted 1000 simulations and plotted boxplots of the 1000 RMSE values for parameters ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_2$, as shown in Figure 1 and Figure 2. From the figures, we can observe the following: the RMSE values of ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_2$ for both methods decrease as the sample size increases, however, the OQIF method already exhibits good performance with a small sample size (n=100), while the PNLS method requires a larger sample size to achieve similar accuracy. The boxplots of the OQIF method are more symmetric and compact, indicating that the distribution of its estimators is closer to the normal distribution and has better statistical properties. Additionally, the OQIF method has significantly fewer outliers than the PNLS method, demonstrating stronger robustness against abnormal data. This suggests that the overall performance of the OQIF method in parameter estimation is superior to that of the PNLS method, with more pronounced advantages especially in cases of finite samples.

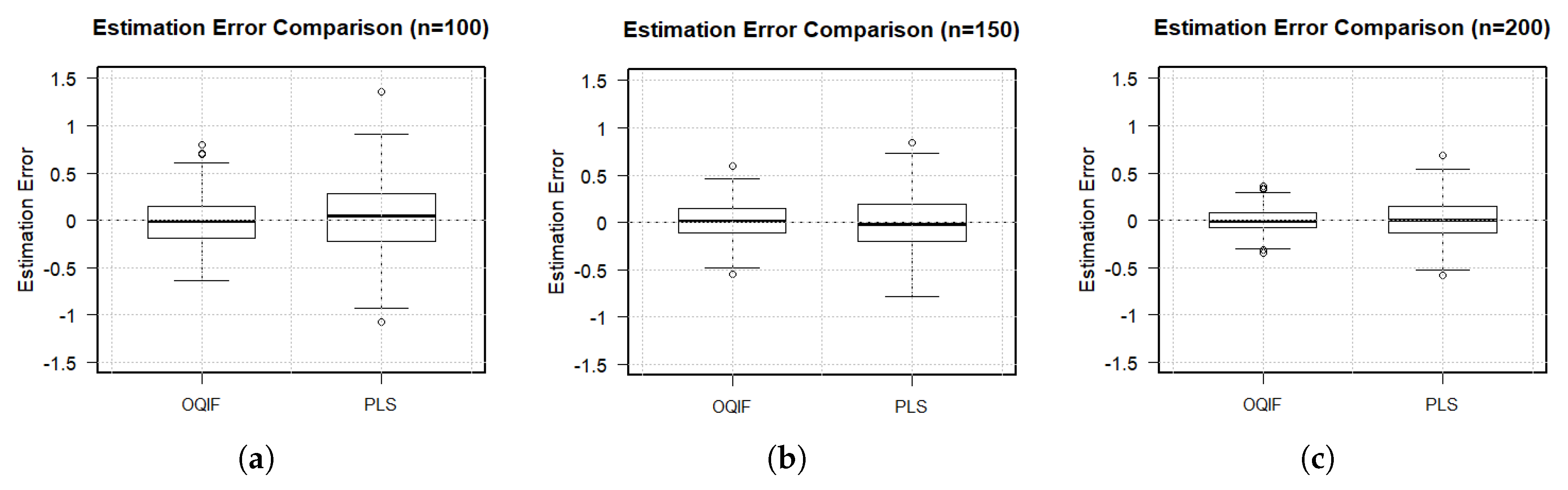
Next, we estimate the coefficient function $\widehat{\alpha }\left(U\right)$, simulate 1000 times and draw the box plot of the RMSE of $\widehat{\alpha }\left(U\right)$ under different samples, resulting in Figure 3 below.

As can be seen from the above boxplots: with the increase in sample size, the error distributions of both the OQIF method and the PNLS method become more concentrated, but the error of the OQIF method is significantly smaller than that of the PNLS method. This further verifies the superiority of the OQIF method in the varying coefficient partially nonlinear model.