Submitted:
02 July 2024
Posted:
03 July 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Basic Definitions and Methods
1.2. Related Works
1.3. Main Contributions
- First, the regressions between independent variables including time and dependent variable is estimated on each time series data, and the parameters are estimated by curve_fit. Experts should guess the distribution functions between independent variables and the dependent variable based on professional theory and experience. The functions can be linear, which can be thought of as specially nonlinear, or they can be nonlinear. Users follow curve_fit to verify the matching degree of the functions until satisfied, otherwise adjust the functions. Similarly, the coeffect of the whole panel data is also initially estimated.
- Second, the distance between regressions is defined, and then the coeffect function between the series regressions is obtained on the initial co-effect with curve_fit. Series regressions may be affected by coeffect in panel data, which reflects the commonality of these functions in distributions. To find coeffect functions that minimizes the sum of the squares of the average distance from each series sub-function as the common function. Thus, curve_fitting method is improved for the co-effect finding.
- Third, the time-effects and individual fixed-effects for each series data in the panel data are estimated on the differences of series regressions and coeffect function. However, coeffect may be affected by time or other independent variables, which may cause bias in the analysis. Thus, We divide each regression into two sub-functions according to time and other independent variables. By eliminating the coeffect in series regressions, new individual fixed-effect and time-effect are obtained to better reflect the heterogeneity.
- Additionally, the effectiveness of the proposed method is varified on the synthetic data. The method of verifying the validity of the classical model is usually based on expert knowledge and lacks objective metrics. This paper generates synthetic data based on the theory of fixed-effects, and determines the validity of model estimation by comparing the similarity between the expected fixed-effects and the estimated fixed-effects.
- (1)
- First of all, the nonlinear relationships which generally exist in the real world are reflected by nonlinear functions, so that the fixed-effects model can be effectively extended at the application level.
- (2)
- Secondly, the prior knowledge of experts is fully utilized in the proposed fixed-effects analysis through the estimation function to prevent the separation of theory and empirical research, so that the model has better interpretability and is easier to be understood.
- (3)
- Thirdly, the proposed time-effects eliminate the coeffect of time in panel data, which can more effectively reflect the heterogeneity of time series datas in time distribution. Finally, individual fixed-effects can be either correlated or uncorrelated with independent variables, avoiding the distinction between fixed-effects and random effects.
- (4)
- In addition, based on synthetic data, a method to verify the validity of the fixed-effects model is proposed.
2. Proposed Method
2.1. Redefinition
2.2. Solutions
2.2.1. Curve Fitting
2.2.2. Detailed Steps
2.3. Algorithms


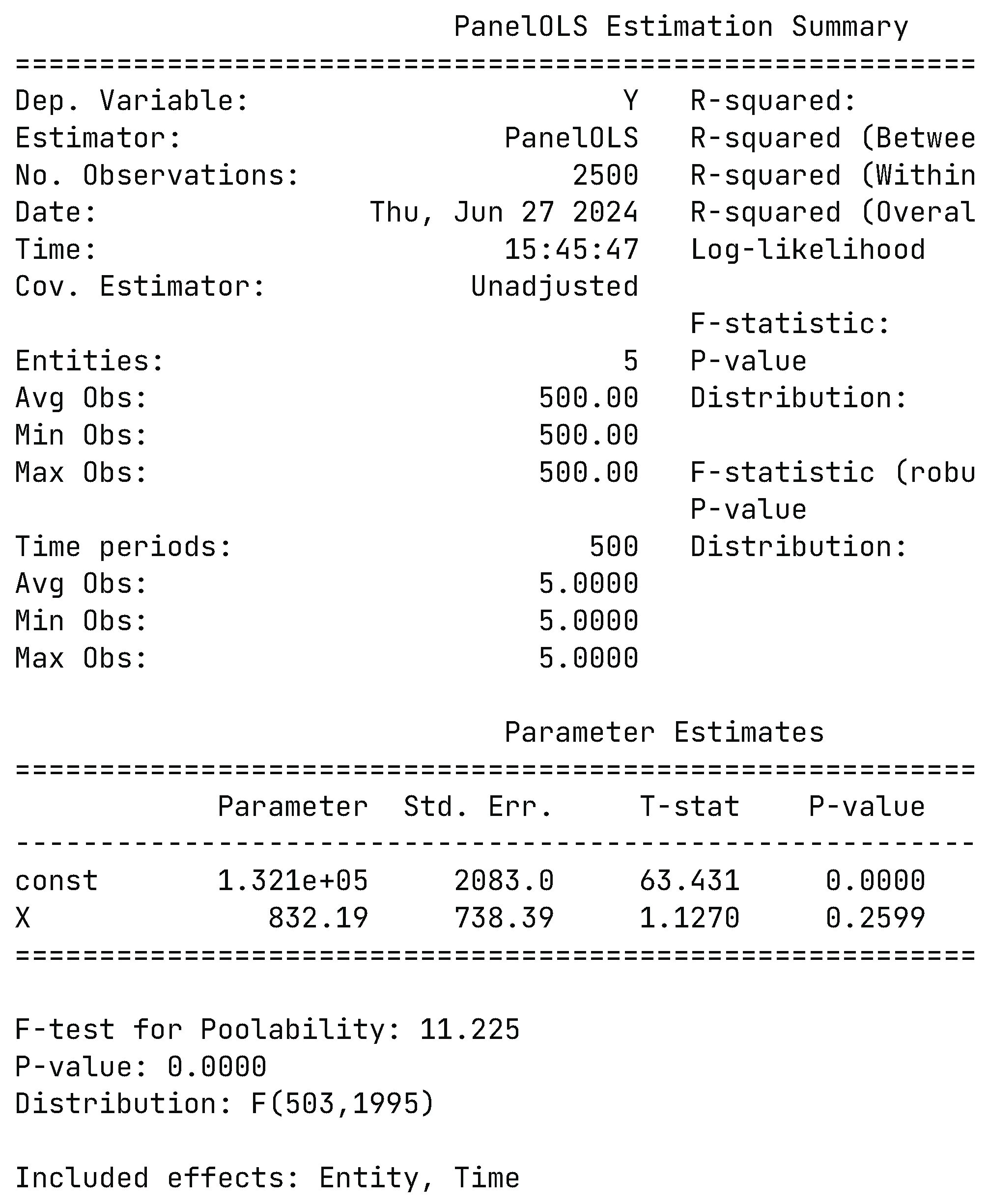
3. Experimental Results
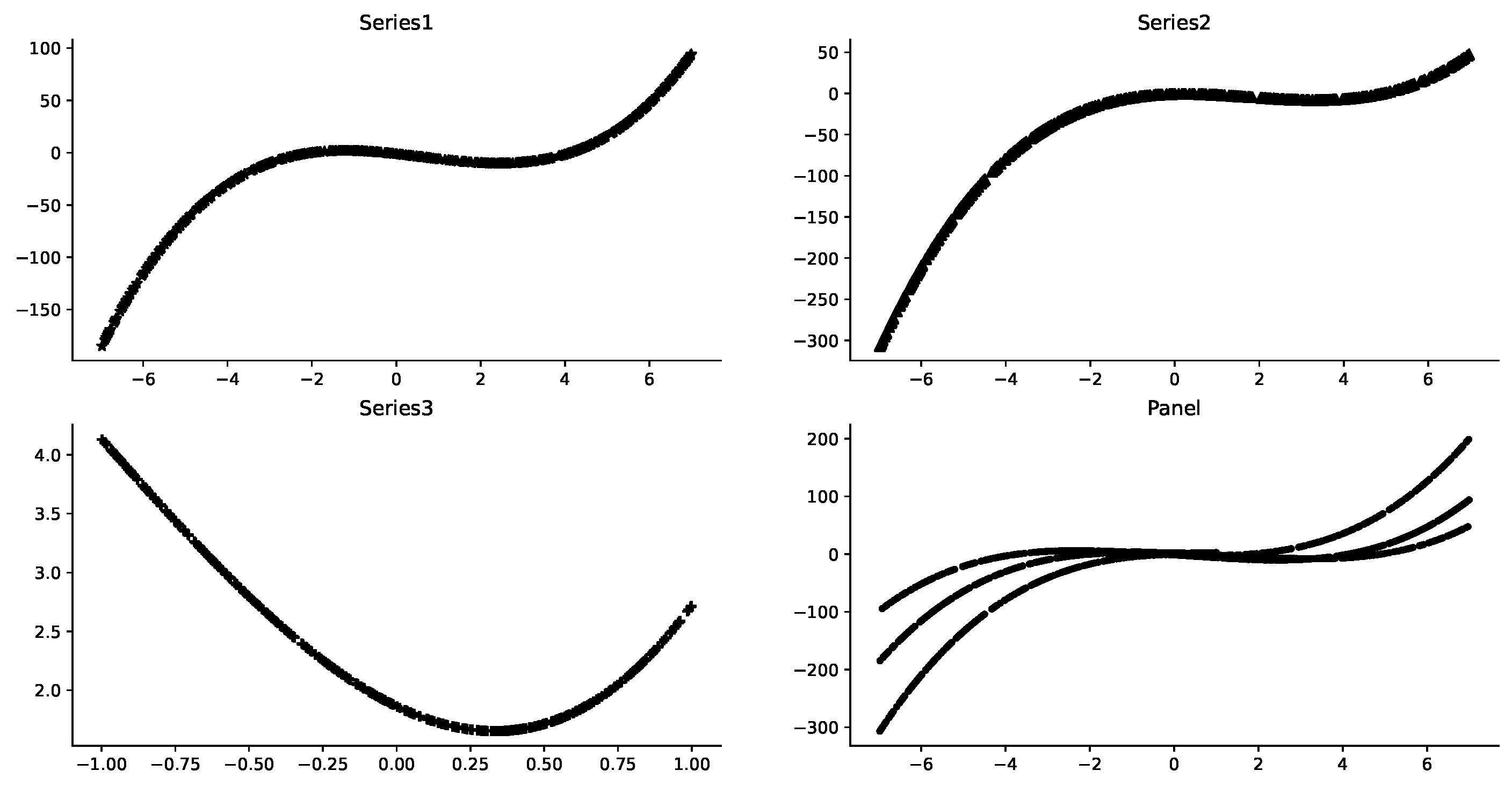
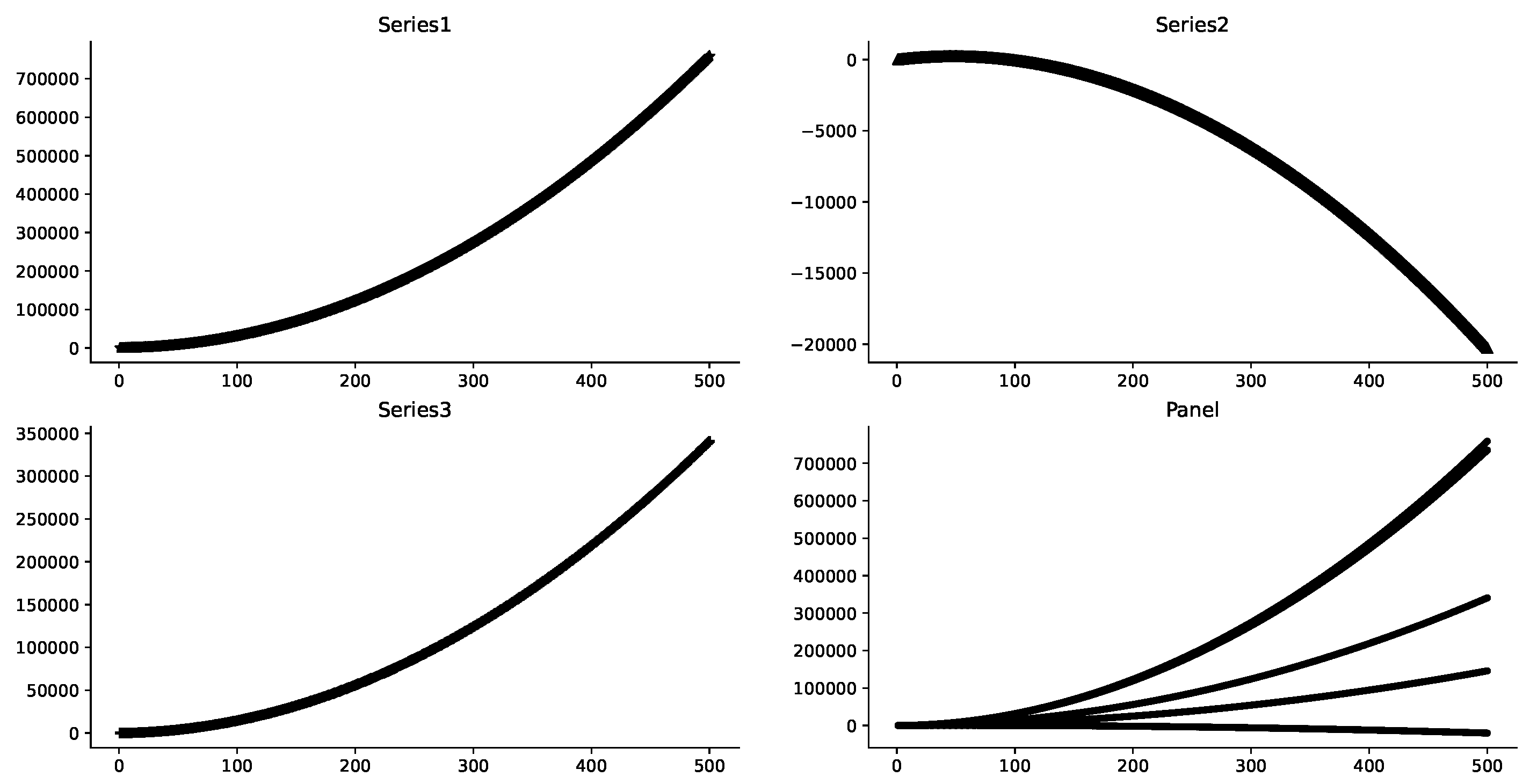
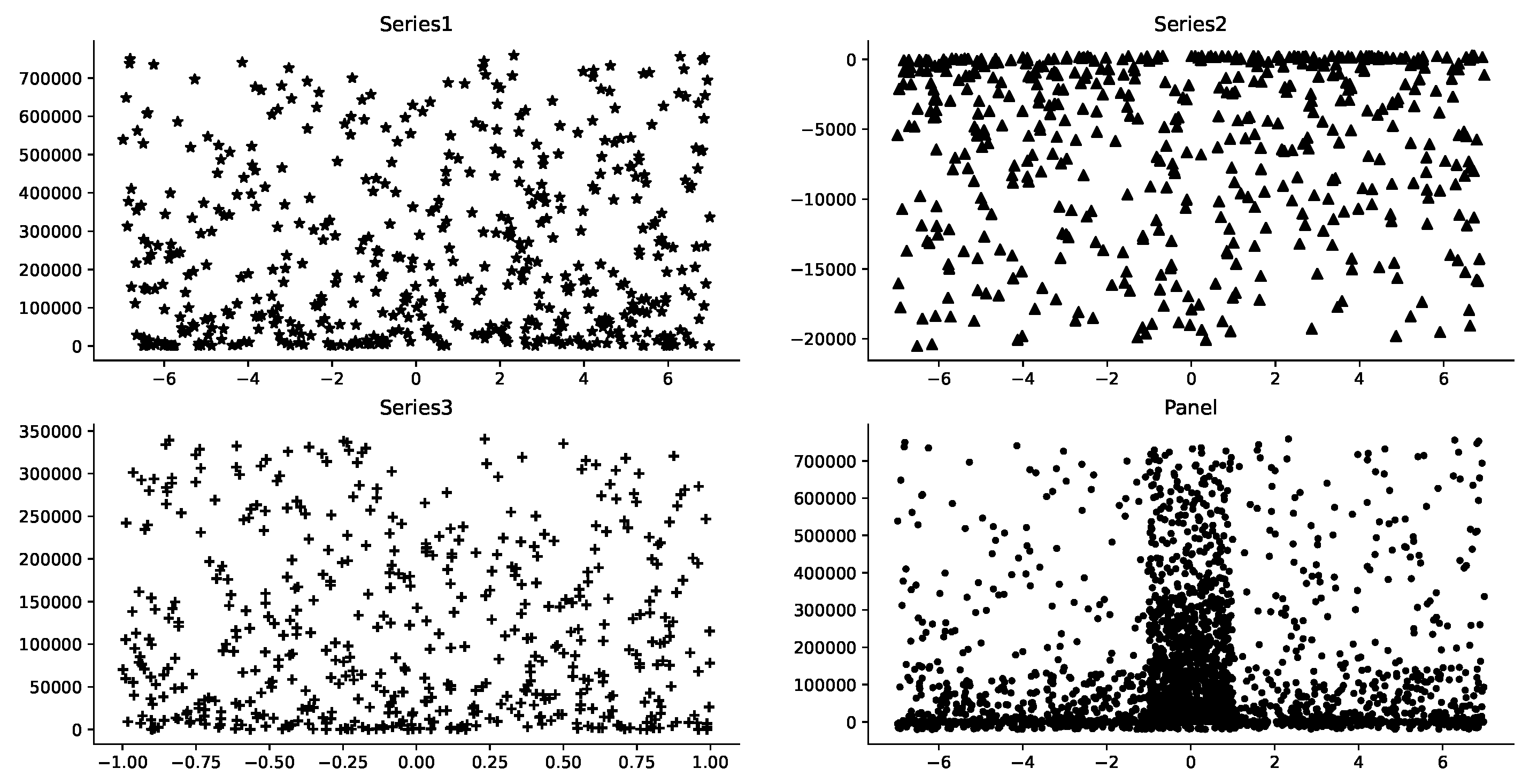
3.1. Data Synthesis
3.2. Data Distribution Observation
3.3. Estimate Results
4. Discussion and Conclusions
4.1. Discussion
4.2. Conclusions
4.3. Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Balázsi, L.; Mátyás, L.; Wansbeek, T. , L., Ed.; Springer International Publishing: Cham, 2024; pp. 1–37. https://doi.org/10.1007/978-3-031-49849-7_1.Models. In The Econometrics of Multi-dimensional Panels: Theory and Applications; Matyas, L., Ed.; Springer International Publishing: Cham, 2024; Springer International Publishing: Cham, 2024; pp. 1–37. [Google Scholar] [CrossRef]
- Hill, T.D.; Davis, A.P.; Roos, J.M.; French, M.T. Limitations of Fixed-Effects Models for Panel Data. Sociological Perspectives 2020, 63, 357–369. [Google Scholar] [CrossRef]
- Broström, G.; Holmberg, H. Generalized linear models with clustered data: Fixed and random effects models. Computational Statistics and Data Analysis 2011, 55, 3123–3134. [Google Scholar] [CrossRef]
- Allison, P.D. Fixed effects regression models; SAGE publications, 2009.
- Lee, L.; Yu, J. Estimation of Spatial Panels; Foundations and trends in econometrics, Now, 2011.
- Craven, B.; Islam, S.M. Ordinary least-squares regression. The SAGE dictionary of quantitative management research.
- Correia, S.; Guimarães, P.; Zylkin, T. Fast Poisson estimation with high-dimensional fixed effects. The Stata Journal 2020, 20, 95–115. [Google Scholar] [CrossRef]
- Hui, F.; Nghiem, L. Sufficient dimension reduction for clustered data via finite mixture modelling. Australian & New Zealand Journal of Statistics 2022, 64, 133–157. [Google Scholar]
- Serghiou, S.; Goodman, S.N. Random-effects meta-analysis: summarizing evidence with caveats. Jama 2019, 321, 301–302. [Google Scholar] [CrossRef]
- Fernández-Val, I.; Weidner, M. Fixed effects estimation of large-T panel data models. Annual Review of Economics 2018, 10, 109–138. [Google Scholar] [CrossRef]
- Hsiao, C.; Pesaran, M.H.; Tahmiscioglu, A.K. Maximum likelihood estimation of fixed effects dynamic panel data models covering short time periods. Journal of econometrics 2002, 109, 107–150. [Google Scholar] [CrossRef]
- Oneal, J.R.; Russett, B. Clear and clean: The fixed effects of the liberal peace. International Organization 2001, 55, 469–485. [Google Scholar] [CrossRef]
- Gunasekara, F.I.; Richardson, K.; Carter, K.; Blakely, T. Fixed effects analysis of repeated measures data. International Journal of Epidemiology 2013, 43, 264–269. [Google Scholar] [CrossRef] [PubMed]
- Bai, J. Fixed-effects dynamic panel models, a factor analytical method. Econometrica 2013, 81, 285–314. [Google Scholar]
- Moon, H.R.; Weidner, M. Dynamic linear panel regression models with interactive fixed effects. Econometric Theory 2017, 33, 158–195. [Google Scholar] [CrossRef]
- Su, L.; Ju, G. Identifying latent grouped patterns in panel data models with interactive fixed effects. Journal of Econometrics 2018, 206, 554–573. [Google Scholar] [CrossRef]
- Berger, M.; Tutz, G. Tree-structured clustering in fixed effects models. Journal of computational and graphical statistics 2018, 27, 380–392. [Google Scholar] [CrossRef]
- Simchoni, G.; Rosset, S. Integrating random effects in deep neural networks. Journal of Machine Learning Research 2023, 24, 1–57. [Google Scholar]
- Golenvaux, N.; Alvarez, P.G.; Kiossou, H.S.; Schaus, P. An lstm approach to forecast migration using google trends. arXiv preprint arXiv:2005.09902, arXiv:2005.09902 2020.
- Marquart, L.; Haynes, M. Misspecification of multimodal random-effect distributions in logistic mixed models for panel survey data. Journal of the Royal Statistical Society Series A: Statistics in Society 2019, 182, 305–321. [Google Scholar] [CrossRef]
- Sadeghirad, B.; Foroutan, F.; Zoratti, M.J.; Busse, J.W.; Brignardello-Petersen, R.; Guyatt, G.; Thabane, L. Theory and practice of Bayesian and frequentist frameworks for network meta-analysis. BMJ Evidence-Based Medicine 2023, 28, 204–209. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.; Gu, Q.; Li, S.; Sun, Y. A knowledge transfer-based adaptive differential evolution for solving nonlinear equation systems. Knowledge-Based Systems 2023, 261, 110214. [Google Scholar] [CrossRef]
- Greene, W.H. The behavior of the fixed effects estimator in nonlinear models 2002. pp. 1–48.
- Charbonneau, K. Multiple fixed effects in nonlinear panel data models. Unpublished manuscript 2012. [Google Scholar]
- Botosaru, I.; Muris, C. Identification of time-varying counterfactual parameters in nonlinear panel models. Journal of Econometrics, 1056. [Google Scholar] [CrossRef]
- Xu, R. Measuring explained variation in linear mixed effects models. Statistics in medicine 2003, 22, 3527–3541. [Google Scholar] [CrossRef]
- Bell, A.; Jones, K. Explaining fixed effects: Random effects modeling of time-series cross-sectional and panel data. Political Science Research and Methods 2015, 3, 133–153. [Google Scholar] [CrossRef]
- Wu, Q.; Ying, Y.; Zhou, D.X. Learning Rates of Least-Square Regularized Regression. Foundations of Computational Mathematics 2006, 6, 171–192. [Google Scholar] [CrossRef]
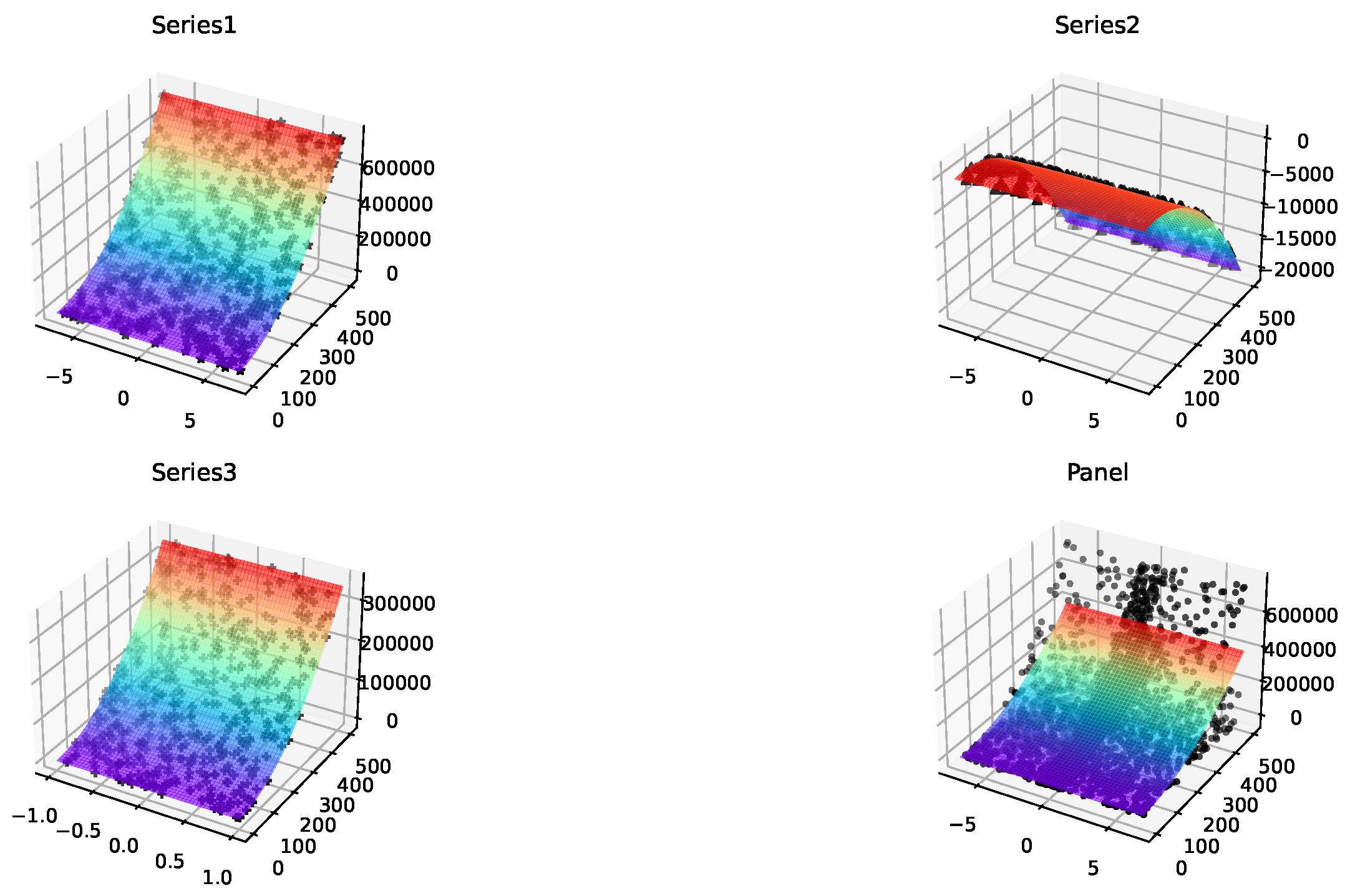
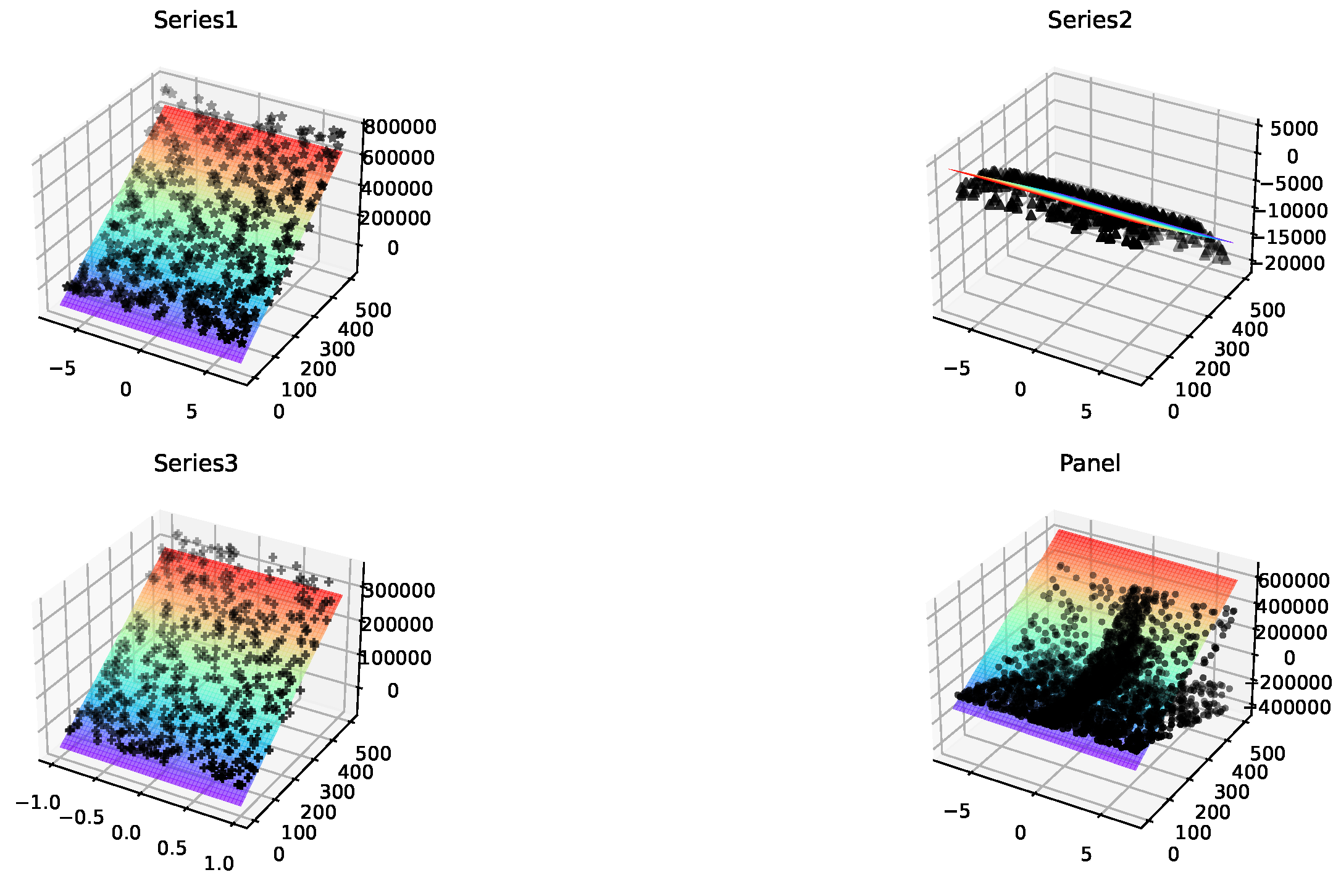
| Fixed-effects | Series data 1 | Series data 2 | Series data 3 | Panel data(Coeffect) |
|---|---|---|---|---|
| ]3*Time-effects | ||||
| * | * | * | * | |
| ** | ** | ** | ** | |
| ]3*Individual fixed-effect | ||||
| * | * | * | * | |
| ** | ** | ** | ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




