Equilibrium Shape for 2D Asymmetric Cylindrical Droplet on Heterogeneous Surface

1. Introduction

The wetting behavior of droplets on solid surfaces governs diverse phenomena ranging from microfluidic manipulation [1] and digital microfluidics [2] to spray coating [3], self-cleaning surfaces [4], and biological interfaces [5]. Classical wetting theory describes droplet equilibrium on homogeneous surfaces through the Young-Laplace equation, which balances capillary pressure with gravitational and external forces. However, real-world applications increasingly involve heterogeneous substrates with spatially varying wettability, where chemical patterning or material discontinuities create regions with distinct contact angles. Understanding droplet equilibrium configurations and dynamics on such surfaces is crucial for designing functional materials with controlled liquid transport and droplet manipulation capabilities [6,7].

Heterogeneous wetting has been extensively studied through experimental [8,9] and numerical approaches [10,11]. Brochard [12] theoretically analyzed droplet motion induced by chemical or thermal gradients, predicting spontaneous migration toward regions of lower surface energy. Joanny and de Gennes [13] developed models for contact angle hysteresis on chemically heterogeneous surfaces, revealing the role of surface energy variations in pinning and depinning transitions. More recently, Devic et al. [14] investigated equilibrium shapes of droplets on tilted substrates with chemical steps using Surface Evolver, identifying critical volumes beyond which stable equilibrium becomes inaccessible. Numerical simulations based on phase-field methods [15] and volume-of-fluid techniques [16] have also provided insights into dynamic wetting on complex surfaces.

Recent advances have highlighted the importance of chemical steps—elementary patterns in chemically heterogeneous substrates featuring two regions of different wettability separated by a sharp border [17]. Long and Gao [17] systematically investigated droplet motion driven by chemical steps within the framework of lubrication theory, identifying two distinct stages: a migration stage where the droplet traverses both regions, and an asymmetric spreading stage where the droplet spreads on the hydrophilic region while being constrained by the border. Their matched asymptotic analysis for 2D droplets revealed that steady translational motion with constant speed can occur during migration, while a boundary layer exists near pinned contact lines during asymmetric spreading. For 3D droplets, their numerical simulations demonstrated that lateral flow significantly affects evolution, leading to non-monotonic variations in droplet length and width. These findings provide fundamental insights into droplet behavior on stepped wettability patterns, which are ubiquitous in applications ranging from digital microfluidics to water harvesting systems.

The control of droplet motion through wettability modulation has emerged as a critical capability for numerous technologies. Tenjimbayashi and Manabe [6] provided a comprehensive review categorizing droplet manipulation strategies into three main approaches: (i) application of driving force to droplets on non-sticking surfaces (utilizing superhydrophobic surfaces, liquid-infused surfaces, or liquid marbles), (ii) formation of gradient surface chemistry or structure (inspired by natural systems such as spider silk [18], cactus spines [19], and Namib beetle bumps [20]), and (iii) formation of anisotropic surface chemistry or structure (exemplified by directional wetting patterns and ratchet structures). These strategies have enabled diverse applications including printing [21], microreactors [22], cargo transport [23], bioanalysis [24], electricity generation [25], heat transfer [26], water harvesting [27], desalination [28], self-cleaning [29], and anti-fogging [30]. Understanding the fundamental principles underlying these strategies is essential for rational design of functional surfaces with tailored droplet manipulation capabilities.

Despite these advances, analytical frameworks for predicting equilibrium configurations on heterogeneous surfaces remain limited, particularly for asymmetric systems where the droplet straddles a wetting boundary. The challenge lies in simultaneously satisfying the Young-Laplace equation governing interface curvature, Young’s law at each contact line, and the global volume constraint, while determining the unknown equilibrium position relative to the heterogeneous boundary. Most existing approaches rely on full numerical optimization of the coupled differential-algebraic system, which can be computationally expensive and sensitive to initial conditions. Furthermore, the interplay between static equilibrium configurations and dynamic migration processes on chemical steps requires careful consideration of contact line dynamics, including pinning phenomena and contact angle hysteresis [31,32].

In this work, we present a systematic numerical framework for computing asymmetric droplet shapes on heterogeneous surfaces with a wetting boundary separating two regions of distinct contact angles. Our approach combines rigorous energy minimization principles with efficient parametric numerical methods to achieve accurate solutions across diverse contact angle configurations and gravitational regimes characterized by the Bond number. The key innovation is a two-stage computational strategy: first, we compute a reference droplet shape by solving the parametric Young-Laplace equations using Newton-Raphson iteration; second, we apply an algebraic spreading condition derived from energy minimization to determine the equilibrium position through simple translation. This decoupling dramatically reduces computational cost compared to fully coupled approaches while maintaining high accuracy.

We derive the spreading condition from first principles through Lagrange multiplier analysis of the constrained Gibbs free energy functional. The resulting equilibrium criterion relates the contact line position ratio to the spreading function ratio $L_2/|L_1|=S\left({\theta }_1\right)/S\left({\theta }_2\right)$, where $S\left(\theta \right)=sin\theta tan\theta$ encodes the unbalanced Young stress at each contact line. Under appropriate approximations valid for small to moderate Bond numbers, this condition reduces to an explicit algebraic relation that eliminates the need for iterative root-finding. The parametric formulation using tangent angle as the independent variable naturally handles vertical tangent singularities near contact lines, ensuring robust numerical integration.

We validate the framework through systematic parameter studies examining contact angle asymmetry in both hydrophilic and hydrophobic regimes, and Bond number variations spanning capillary-dominated to gravity-influenced regimes. The results reveal fundamental behaviors including the counterintuitive spreading of hydrophobic droplets toward regions with larger contact angles, the invariance of horizontal partitioning under gravitational effects, and the strong nonlinear sensitivity of asymmetry to contact angles near $\pi /2$. These findings advance our understanding of wetting on heterogeneous surfaces and provide quantitative design criteria for applications in microfluidics, surface patterning, and droplet-based technologies, complementing recent advances in dynamic droplet manipulation [6,17].

The remainder of this paper is organized as follows. Section 2 formulates the problem, derives the governing Young-Laplace equation, and develops the spreading condition from energy minimization principles. Section 3 presents the two-stage numerical method including parametric ODE formulation, Newton-Raphson iteration, and algebraic spreading condition satisfaction. Section 4 presents comprehensive results across parameter space, and Section 5 concludes with implications and future directions.

2. Problem Formulation

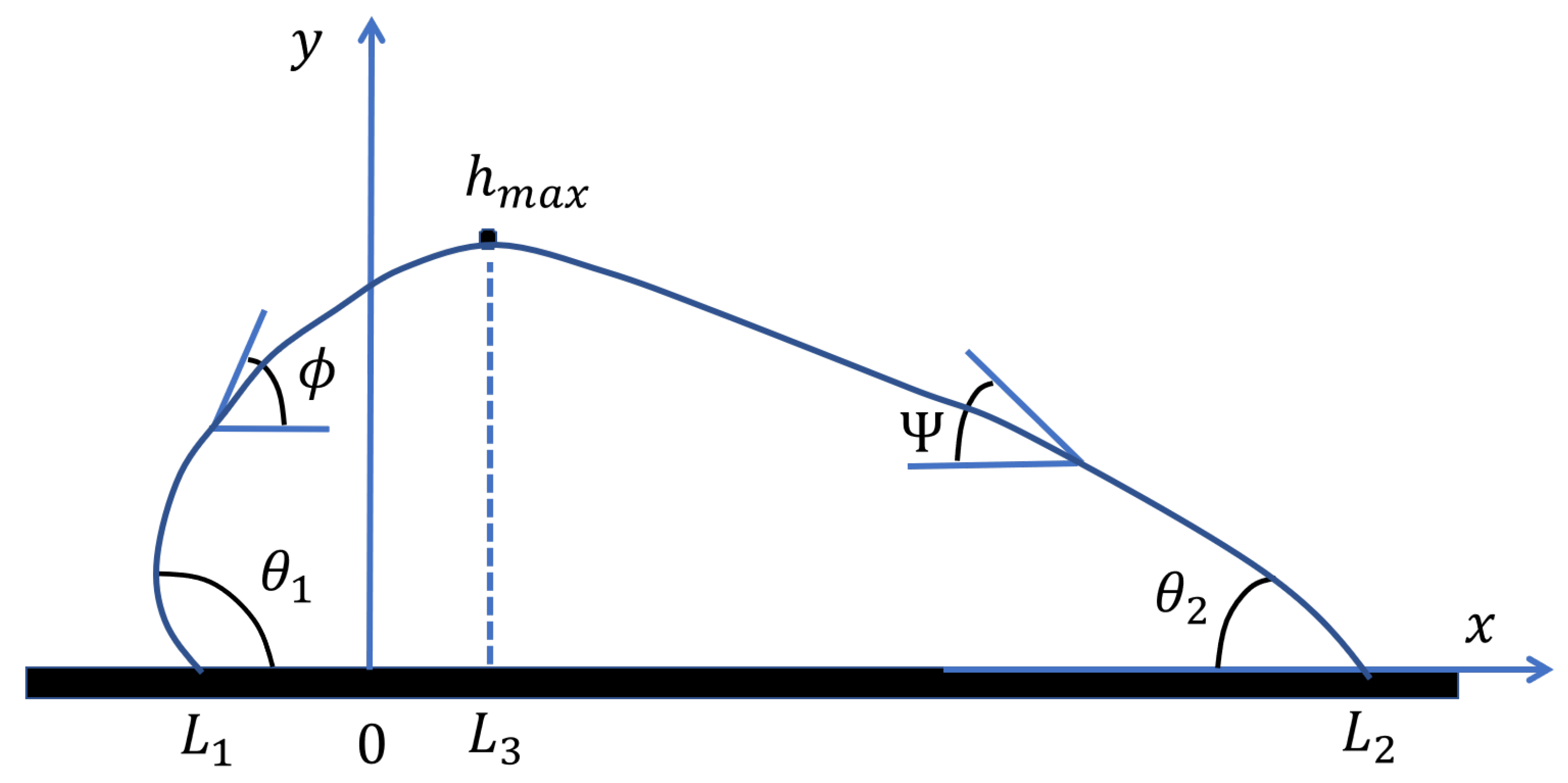
We consider a two-dimensional cylindrical droplet resting on a horizontal plane with a heterogeneous wetting boundary located at $x=0$. The surface exhibits different equilibrium contact angles on either side of this boundary, with ${\theta }_1$ on the left side where $x<0$ and ${\theta }_2$ on the right side where $x>0$. The droplet makes contact with the surface at position $L_1<0$ on the left and $L_2>0$ on the right, with a fixed total volume (area in 2D) denoted as $V_0$, as shown in Figure 1.

The droplet shape is governed by the Young-Laplace equation, which relates the curvature of the liquid-gas interface to the pressure difference across the interface. The fundamental statement of the Young-Laplace equation expresses the pressure jump across a curved interface as

$$\Delta P=\gamma \kappa$$

(1)

where $\gamma$ is the surface tension and $\kappa$ is the mean curvature of the interface. For a two-dimensional surface described by $y=h\left(x\right)$, the curvature is given by

$$\kappa ={\displaystyle \frac{h^{″}\left(x\right)}{{(1+h^{\prime 2})}^{3/2}}}$$

(2)

where the prime denotes differentiation with respect to x.

At the free surface of the droplet, the pressure balance requires that the atmospheric pressure minus the liquid pressure equals the capillary pressure. Inside the liquid at height $h\left(x\right)$, the pressure is given by hydrostatic considerations as $P_{\mathrm{liquid}}=P_0-\rho gh$ where $P_0$ is a reference pressure at $y=0$ and $\rho gh$ accounts for the gravitational pressure variation. The pressure balance at the interface thus becomes

$$P_{\mathrm{atm}}-(P_0-\rho gh)=\gamma \kappa$$

which can be rearranged as

$$\gamma \kappa =(P_{\mathrm{atm}}-P_0)+\rho gh=C+\rho gh$$

where $C=P_{\mathrm{atm}}-P_0$ is a constant throughout the domain that must be determined from boundary conditions. Substituting the expression for curvature, we obtain the dimensional Young-Laplace equation

$$\gamma {\displaystyle \frac{h^{″}}{{(1+h^{\prime 2})}^{3/2}}}=C+\rho gh$$

(3)

To express this equation in dimensionless form, we introduce a characteristic length scale R based on the initial droplet area. Assuming the initial droplet area $S_0$ corresponds to a circular configuration with radius R, we have $S_0=\pi R^2$, which gives $R=\sqrt{S_0/\pi }$. We define dimensionless variables as $\overline{x}=x/R$, $\overline{h}=h/R$, and a dimensionless pressure constant $\overline{C}=CR/\gamma$. The derivatives transform according to $h^{\prime }=d\overline{h}/d\overline{x}$ and $h^{″}=(1/R)d^2\overline{h}/d{\overline{x}}^2$. Substituting these into the dimensional equation and multiplying through by R yields

$${\displaystyle \frac{d^2\overline{h}}{d{\overline{x}}^2}}{\left(1+{\left({\displaystyle \frac{d\overline{h}}{d\overline{x}}}\right)}^2\right)}^{-3/2}={\displaystyle \frac{CR}{\gamma }}+{\displaystyle \frac{\rho g{R}^2}{\gamma }}\overline{h}$$

(4)

The dimensionless group $Bo=\rho g{R}^2/\gamma$ is the Bond number, which represents the ratio of gravitational forces to surface tension forces. This can also be expressed as $Bo=R^2/{\ell }_c^2$ where ${\ell }_c=\sqrt{\gamma /\left(\rho g\right)}$ is the capillary length. Droplets with $R\ll {\ell }_c$ (equivalently $Bo\ll 1$) are in the capillary-dominated regime where surface tension dominates gravity, while droplets with $R\gg {\ell }_c$ (equivalently $Bo\gg 1$) are gravity-dominated. The dimensionless Young-Laplace equation becomes

$${\displaystyle \frac{h^{″}}{{(1+h^{\prime 2})}^{3/2}}}=C+Bo·h$$

(5)

where we have dropped the overbars for notational convenience. This equation must be solved subject to appropriate boundary conditions at the contact lines and the constraint that the total dimensionless area equals $\pi$.

A critical feature of droplets on heterogeneous surfaces is that the pressure constant must be allowed to differ on each side of the wetting boundary. We denote the left-side pressure constant as $C_L$ and the right-side constant as $C_R$. This difference arises from the surface energy discontinuity at $x=L_3$ and is essential for capturing the curvature discontinuity that develops at the heterogeneous boundary. When the contact angles differ (${\theta }_1\ne {\theta }_2$), the maximum height of the droplet shifts away from the heterogeneity boundary to some position $x=L_3$ where $L_1<L_3<L_2$.

The droplet profile exhibits a maximum height at position $x=L_3$ where the slope vanishes. We split the domain into left and right regions relative to this maximum point. For the left side where $L_1\le x\le L_3$, the governing equation becomes

$${\displaystyle \frac{h^{″}}{{(1+h^{\prime 2})}^{3/2}}}=C_L+Bo·h$$

(6)

with the boundary conditions $h\left(L_1\right)=0$ and $h^{\prime }\left(L_1\right)=tan{\theta }_1$. For the right side where $L_3\le x\le L_2$, we have

$${\displaystyle \frac{h^{″}}{{(1+h^{\prime 2})}^{3/2}}}=C_R+Bo·h$$

(7)

with the boundary conditions $h\left(L_2\right)=0$ and $h^{\prime }\left(L_2\right)=-tan{\theta }_2$. At the maximum height location $x=L_3$, both sides must satisfy $h^{\prime }\left(L_3\right)=0$ and the height must be continuous, though the curvature may be discontinuous with a jump of magnitude $\Delta \kappa =C_L-C_R$.

3. Variational Analysis for Spreading Condition

The equilibrium configuration must satisfy the spreading condition derived from energy minimization. We derive this condition through systematic variational analysis starting from the Gibbs free energy functional with volume constraint.

At each contact line, the equilibrium condition is governed by Young’s equation. At the left and right contact points, we have

$$cos{\theta }_1={\displaystyle \frac{{\gamma }_{SG,1}-{\gamma }_{SL,1}}{{\gamma }_{LG}}}\mathrm{and}cos{\theta }_2={\displaystyle \frac{{\gamma }_{SG,2}-{\gamma }_{SL,2}}{{\gamma }_{LG}}}.$$

The total Gibbs free energy change from a reference state, where the entire surface is a solid-gas interface, consists of four contributions. The first contribution comes from the liquid-gas interface energy

$$E_{LG}={\gamma }_{LG}{\int }_{L_1}^{L_2}\sqrt{1+{\left({\displaystyle \frac{dh}{dx}}\right)}^2}dx={\gamma }_{LG}{A}_{LG}$$

where $A_{LG}$ represents the arc length of the liquid-gas interface. The second contribution arises from the solid-liquid interface on the left side

$$E_{SL,\mathrm{left}}=({\gamma }_{SL,1}-{\gamma }_{SG,1})|L_1|=-{\gamma }_{LG}cos{\theta }_1·|L_1|$$

The third contribution comes from the right contact area

$$E_{SL,\mathrm{right}}=({\gamma }_{SL,2}-{\gamma }_{SG,2})L_2=-{\gamma }_{LG}cos{\theta }_2·L_2$$

The fourth contribution is the gravitational potential energy

$$E_{\mathrm{gravity}}=\rho g{\int }_{L_1}^{L_2}{\int }_0^{h\left(x\right)}zdzdx={\displaystyle \frac{\rho g}{2}}{\int }_{L_1}^{L_2}{h}^2\left(x\right)dx$$

Combining all four components and introducing dimensionless variables using a characteristic length scale R and the Bond number $Bo=\rho g{R}^2/{\gamma }_{LG}$, the dimensionless energy functional becomes

$$\Delta G=A_{LG}-cos{\theta }_1|L_1|-cos{\theta }_2{L}_2+{\displaystyle \frac{Bo}{2}}{\int }_{L_1}^{L_2}{h}^{2}dx$$

(8)

subject to the volume constraint

$$V={\int }_{L_1}^{L_2}h\left(x\right)dx=V_0.$$

(9)

We decompose the total volume at the heterogeneity boundary $x=0$ into left and right contributions

$$V_L={\int }_{L_1}^{0}h\left(x\right)dx\mathrm{and}{V}_R={\int }_0^{L_2}h\left(x\right)dx$$

(10)

with the constraint $V=V_L+V_R=V_0$.

We now examine how the energy changes with respect to variations in the contact positions. At the contact point $L_1$, the arc length element satisfies $ds=\sqrt{1+h^{\prime 2}\left(L_1\right)}|dx|=sec{\theta }_1|dx|$ where we have used the contact angle condition $h^{\prime }\left(L_1\right)=tan{\theta }_1$. When $L_1$ changes, the arc length contribution gives

$${\displaystyle \frac{\partial A_{LG}}{\partial L_1}}=-sec{\theta }_1$$

The surface energy contribution varies as

$${\displaystyle \frac{\partial }{\partial L_1}}(-cos{\theta }_1|L_1|)=cos{\theta }_1$$

where we have used $\partial |L_1|/\partial L_1=-1$ for $L_1<0$. The gravitational contribution requires more careful analysis. When $L_1$ changes, both the integration limits and the shape $h(x;L_1,L_2)$ change. The total derivative is

$${\displaystyle \frac{d}{d{L}_1}}\left[{\displaystyle \frac{Bo}{2}}{\int }_{L_1}^{L_2}{h}^2(x;L_1,L_2)dx\right]=-{\displaystyle \frac{Bo}{2}}{h}^2\left(L_1\right)+Bo{\int }_{L_1}^{L_2}h{\displaystyle \frac{\partial h}{\partial L_1}}dx$$

(11)

The first term represents the direct boundary contribution, which vanishes since $h\left(L_1\right)=0$. However, the second term represents the shape variation and does not vanish. Combining all three contributions, the total energy derivatives for the left and right contact position are

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d\Delta G}{d{L}_1}}=-sin{\theta }_{1}tan{\theta }_1+Bo{\int }_{L_1}^{L_2}h{\displaystyle \frac{\partial h}{\partial L_1}}dx\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d\Delta G}{d{L}_2}}=sin{\theta }_{2}tan{\theta }_2+Bo{\int }_{L_1}^{L_2}h{\displaystyle \frac{\partial h}{\partial L_2}}dx\hfill \end{array}$$

(13)

To find the equilibrium configuration, we employ the method of Lagrange multipliers to enforce the volume constraint

$$\mathcal{L}=\Delta G-\lambda (V-V_0)$$

(14)

where $\lambda$ is the Lagrange multiplier. The equilibrium conditions require

$${\displaystyle \frac{d\mathcal{L}}{d{L}_1}}={\displaystyle \frac{d\Delta G}{d{L}_1}}-\lambda {\displaystyle \frac{dV}{d{L}_1}}=0\mathrm{and}{\displaystyle \frac{d\mathcal{L}}{d{L}_2}}={\displaystyle \frac{d\Delta G}{d{L}_2}}-\lambda {\displaystyle \frac{dV}{d{L}_2}}=0$$

(15)

Substituting the expressions for energy and volume derivatives, we obtain the equilibrium conditions

$$-sin{\theta }_{1}tan{\theta }_1+Bo{\int }_{L_1}^{L_2}h{\displaystyle \frac{\partial h}{\partial L_1}}dx=\lambda {\displaystyle \frac{dV}{d{L}_1}}$$

(16)

and

$$sin{\theta }_{2}tan{\theta }_2+Bo{\int }_{L_1}^{L_2}h{\displaystyle \frac{\partial h}{\partial L_2}}dx=\lambda {\displaystyle \frac{dV}{d{L}_2}}.$$

(17)

To eliminate the Lagrange multiplier $\lambda$, we divide Eq.(16) by Eq.(17)

$${\displaystyle \frac{-sin{\theta }_{1}tan{\theta }_1+Bo{\int }_{L_1}^{L_2}h\frac{\partial h}{\partial L_1}dx}{sin{\theta }_{2}tan{\theta }_2+Bo{\int }_{L_1}^{L_2}h\frac{\partial h}{\partial L_2}dx}}={\displaystyle \frac{dV/d{L}_1}{dV/d{L}_2}}.$$

(18)

Since $V(L_1,L_2)=V_0$ is constant, the total differential must vanish

$$dV={\displaystyle \frac{dV}{d{L}_1}}d{L}_1+{\displaystyle \frac{dV}{d{L}_2}}d{L}_2=0.$$

(19)

This immediately gives the fundamental relationship between contact line motions

$${\displaystyle \frac{d{L}_2}{d{L}_1}}{|}_{V=V_0}=-{\displaystyle \frac{dV/d{L}_1}{dV/d{L}_2}}.$$

(20)

Substituting Eq.(20) into Eq.(18), we obtain the general spreading condition

$${\displaystyle \frac{-sin{\theta }_{1}tan{\theta }_1+Bo{\int }_{L_1}^{L_2}h\frac{\partial h}{\partial L_1}dx}{sin{\theta }_{2}tan{\theta }_2+Bo{\int }_{L_1}^{L_2}h\frac{\partial h}{\partial L_2}dx}}=-{\displaystyle \frac{d{L}_2}{d{L}_1}}{|}_{V=V_0}.$$

(21)

Note that at equilibrium, the ratio of total forces (capillary plus gravitational) equals the negative of the constrained contact line motion ratio. This form is valid for arbitrary Bond numbers.

The general spreading condition (21) can be reformulated into a more compact form by applying the chain rule to relate the partial derivatives. Under the volume constraint $V(L_1,L_2)=V_0$, the total differential of $h(x;L_1,L_2)$ with respect to $L_1$ while maintaining constant volume is

$${\displaystyle \frac{dh}{d{L}_1}}{|}_{V=V_0}={\displaystyle \frac{\partial h}{\partial L_1}}+{\displaystyle \frac{\partial h}{\partial L_2}}{\displaystyle \frac{d{L}_2}{d{L}_1}}{|}_{V=V_0}.$$

We can be rewritten as

$${\displaystyle \frac{\partial h}{\partial L_1}}={\displaystyle \frac{dh}{d{L}_1}}{|}_{V=V_0}-{\displaystyle \frac{\partial h}{\partial L_2}}{\displaystyle \frac{d{L}_2}{d{L}_1}}{|}_{V=V_0}.$$

(22)

Substituting this back into Eq.(21) and cancelling the term involving $Bo{\int }_{L_1}^{L_2}h{\displaystyle \frac{\partial h}{\partial L_2}}dx$, the general spreading condition can be simplified as

$$Bo{\int }_{L_1}^{L_2}h\left(x\right){\displaystyle \frac{dh}{d{L}_1}}{|}_{V=V_0}dx=sin{\theta }_{1}tan{\theta }_1-{\displaystyle \frac{d{L}_2}{d{L}_1}}{|}_{V=V_0}sin{\theta }_{2}tan{\theta }_2.$$

(23)

This elegant result expresses the equilibrium condition using a single integral term. The left-hand side represents the gravitational contribution under constrained contact line motion (total derivative with volume constraint), while the right-hand side combines the capillary forces from both contact lines weighted by their geometric ratio. The general spreading condition establishes that at equilibrium, the gravitational shape variation contribution exactly balances the difference in capillary spreading forces from both contact lines, weighted by the constrained contact line motion ratio. This represents a fundamental force balance that determines the equilibrium configuration for arbitrary Bond numbers.

For the case of horizontal translation of a fixed droplet shape (which is appropriate when the droplet shape has already been determined independently), the shape does not change with the translation, so $dh/d{L}_1{|}_{V=V_0}=0$ throughout the domain. This causes the integral term in Eq.(23) to vanish, simplifying the spreading condition to

$${\displaystyle \frac{d{L}_2}{d{L}_1}}{|}_{V=V_0}={\displaystyle \frac{sin{\theta }_{1}tan{\theta }_1}{sin{\theta }_{2}tan{\theta }_2}}={\displaystyle \frac{S\left({\theta }_1\right)}{S\left({\theta }_2\right)}}$$

(24)

where $S\left(\theta \right)=sin\theta tan\theta$ is the spreading function. This function represents the effective spreading force at each contact line arising from the unbalanced Young stress. This function vanishes at $\theta =0$ (complete wetting) and $\theta =90°$ (neutral wetting), and increases for larger contact angles.

Under the geometric self-similarity assumption, which is valid for small to moderate Bond numbers when the droplet shape in each region scales proportionally with domain size, we have the additional relation

$${\displaystyle \frac{d{L}_2}{d{L}_1}}{|}_{V=V_0}={\displaystyle \frac{L_2}{|L_1|}}$$

(25)

Combining Eq.(24) and Eq.(25) yields the simplifed spreading condition

$${\displaystyle \frac{L_2}{|L_1|}}={\displaystyle \frac{S\left({\theta }_1\right)}{S\left({\theta }_2\right)}}$$

(26)

Together with the constraint on total droplet width

$$|L_1|+L_2=L_{\mathrm{total}}$$

(27)

where $L_{\mathrm{total}}$ is the width of the reference droplet, we obtain a closed algebraic system that can be solved explicitly for the equilibrium contact positions. The simplified spreading condition Eq.(26) states that at equilibrium, the ratio of contact positions equals the ratio of spreading functions. This can be interpreted as a balance of spreading intensities: the tendency to spread at the left contact line exactly balances the tendency to spread at the right contact line, with the contact positions adjusting to maintain this balance.

4. Numerical Implementation

The numerical solution strategy consists of two stages. In the first stage, we compute a reference droplet shape with the maximum height positioned at an arbitrary location (we choose $L_3=0$ without loss of generality). This yields a droplet shape characterized by three unknown parameters: $h_{max}$, $C_L$, and $C_R$. In the second stage, we apply the spreading condition to determine the correct heterogeneity boundary position through algebraic calculation, effectively translating the reference shape horizontally to satisfy equilibrium.

To solve the Young-Laplace equation numerically, we employ a parametric formulation that uses the tangent angle as the independent variable rather than the horizontal coordinate x. This approach naturally handles the vertical tangent singularities that occur near the contact lines and provides a robust computational framework. For the left side, we introduce the angle variable $\Phi \in [0,{\theta }_1]$ defined such that $h^{\prime }=tan\Phi$. For the right side, we use $\Psi \in [0,{\theta }_2]$ with $h^{\prime }=-tan\Psi$. At the maximum height where $L_3=0$, both angles vanish since the slope is zero.

Starting from the relation $h^{\prime }=tan\Phi$ for the left side, we obtain $h^{″}={sec}^2\Phi ·d\Phi /dx$. Using the trigonometric identity $1+{tan}^2\Phi ={sec}^2\Phi$, we find ${(1+h^{\prime 2})}^{3/2}={sec}^3\Phi$. Substituting these into the Young-Laplace equation and rearranging yields the parametric ordinary differential equations

$${\displaystyle \frac{dx}{d\Phi }}={\displaystyle \frac{cos\Phi }{C_L+Bo·h}},{\displaystyle \frac{dh}{d\Phi }}={\displaystyle \frac{sin\Phi }{C_L+Bo·h}}$$

(28)

which we integrate from $\Phi =0$ at the maximum to $\Phi ={\theta }_1$ at the left contact point with initial conditions $x\left(0\right)=0$ and $h\left(0\right)=h_{max}$.

Similarly, for the right side starting from $h^{\prime }=-tan\Psi$, we obtain

$${\displaystyle \frac{dx}{d\Psi }}=-{\displaystyle \frac{cos\Psi }{C_R+Bo·h}},{\displaystyle \frac{dh}{d\Psi }}={\displaystyle \frac{sin\Psi }{C_R+Bo·h}}$$

(29)

which we integrate from $\Psi =0$ to $\Psi ={\theta }_2$ with the same initial conditions at the maximum height.

The problem now reduces to finding three unknown variables that satisfy three constraint equations. The unknowns are the maximum height $h_{max}$, the left pressure constant $C_L$, and the right pressure constant $C_R$. These parameters completely characterize the reference droplet shape positioned at $L_3=0$.

The three constraint equations ensure that the solution satisfies all physical requirements. The first constraint requires that the left side profile reaches zero height at the left contact angle, which gives $F_1=h_L\left({\theta }_1\right)=0$ where $h_L$ denotes the height computed by integrating the left-side ODEs. The second constraint requires that the right side profile reaches zero height at the right contact angle, giving $F_2=h_R\left({\theta }_2\right)=0$. The third constraint enforces the volume condition $F_3=V_L+V_R-V_0=0$, where the regional volumes are computed by integrating

$$V_L={\int }_0^{{\theta }_1}h{\displaystyle \frac{dx}{d\Phi }}d\Phi ,V_R={\int }_0^{{\theta }_2}h{\displaystyle \frac{dx}{d\Psi }}d\Psi$$

(30)

along with the parametric ODEs during the integration process.

We solve this system of nonlinear equations using the Newton-Raphson method. At each iteration k, we update the solution vector according to

$${\left[\begin{array}{c}{h}_{max}\\ C_L\\ C_R\end{array}\right]}^{(k+1)}={\left[\begin{array}{c}{h}_{max}\\ C_L\\ C_R\end{array}\right]}^{\left(k\right)}-{\mathbf{J}}^{-1}\left[\begin{array}{c}{F}_1\\ F_2\\ F_3\end{array}\right]$$

(31)

where $\mathbf{J}$ is the $3\times 3$ Jacobian matrix containing the partial derivatives of the constraint functions with respect to the unknown variables. The Jacobian matrix elements are computed using finite difference approximations with perturbation parameters $\delta h$ and $\delta C$ typically set to ${10}^{-4}$.

The initial guess for the iterative procedure must be chosen carefully to ensure convergence. For a typical case with moderate Bond numbers and asymmetric contact angles, reasonable initial values can be estimated from simplified analytical solutions or from solutions at nearby parameter values. The iteration continues until the constraint functions are sufficiently small, typically when $max(|F_1|,|F_2|,|F_3|)<ϵ$ where $ϵ={10}^{-6}$ is a prescribed tolerance. Convergence is usually achieved within 5-10 iterations for well-chosen initial guesses.

Once converged, the reference solution provides the complete droplet profile $h\left(x\right)$ positioned at $L_3=0$, along with the contact positions $L_1^{\mathrm{ref}}=x_L\left({\theta }_1\right)<0$ and $L_2^{\mathrm{ref}}=x_R\left({\theta }_2\right)>0$ for this reference configuration. The total droplet width is $L_{\mathrm{total}}=|L_1^{\mathrm{ref}}|+L_2^{\mathrm{ref}}$, which will be preserved under horizontal translation.

The reference droplet shape computed in the first stage satisfies the Young-Laplace equation, the contact angle conditions, and the volume constraint. However, the contact line positions $L_1^{\mathrm{ref}}$ and $L_2^{\mathrm{ref}}$ generally do not satisfy the spreading condition Eq.(26). To find the equilibrium configuration, we must determine the correct contact positions $L_1$ and $L_2$ that satisfy the spreading condition. The key insight is that horizontal translation of the droplet along the substrate preserves the droplet shape $h\left(x\right)$, the total volume $V_0$, and the total width $L_{\mathrm{total}}$. The translation only changes the positions of the contact lines relative to the heterogeneity boundary at $x=0$. Therefore, we seek new contact positions $L_1$ and $L_2$ satisfying two conditions of Eq.(26) and Eq.(27). These are a simple algebraic system of two equations in two unknowns for $|L_1|$ and $L_2$. Therefore, the explicit solutions are

$$|L_1|={\displaystyle \frac{L_{\mathrm{total}}}{1+\alpha }},L_2={\displaystyle \frac{L_{\mathrm{total}}·\alpha }{1+\alpha }}.$$

(32)

where $\alpha =S\left({\theta }_1\right)/S\left({\theta }_2\right)$ is the ratio of spreading functions.

The horizontal shift required to move from the reference configuration to the equilibrium configuration is

$$\Delta x=L_1^{\mathrm{ref}}-L_1$$

(33)

Finally, the equilibrium droplet profile is then obtained by applying this horizontal translation

$$x_{\mathrm{eq}}\left(s\right)=x_{\mathrm{ref}}\left(s\right)-\Delta x$$

(34)

where s parameterizes points along the droplet surface. The maximum height position in the equilibrium configuration is located at $L_3=-\Delta x$, and the heterogeneity boundary is at $x=0$. The horizontal translation approximation assumes that the droplet shape does not change as it translates along the substrate, so $dh/d{L}_1{|}_{V=V_0}=0$. This is exactly satisfied when we first compute the reference shape independently and then translate it horizontally.

This algebraic approach is computationally trivial compared to iterative root-finding methods. Once the reference shape is computed in the first stage, the equilibrium configuration is determined by simple arithmetic operations. The volumes $V_L$ and $V_R$ on each side of the heterogeneity boundary can be computed by numerical integration (e.g., trapezoidal rule) of the translated profile, providing verification that the spreading condition is satisfied.

The two-stage solution strategy offers several computational advantages. By decoupling the shape computation from the spreading condition satisfaction, we reduce the dimensionality of the nonlinear system in the first stage from potentially four or five unknowns to only three, making the Newton-Raphson iteration more robust and faster to converge. In the second stage, the problem reduces to explicit algebraic formulas, eliminating the need for iterative root-finding entirely.

The parametric ODE formulation in the first stage requires careful numerical integration. We typically employ the MATLAB ode45 function (based on the Dormand-Prince method). The integration proceeds from the maximum height at $\Phi =0$ (or $\Psi =0$) where the denominator $C_L+Bo·h_{max}$ (or $C_R+Bo·h_{max}$) is well-behaved, avoiding potential singularities near the contact lines.

5. Results

We now present numerical solutions demonstrating droplet equilibrium configurations on heterogeneous surfaces across a wide parameter space. The results are organized to systematically examine the influence of contact angle asymmetry and gravitational effects: we first analyze the asymmetry parameter $\alpha$ in contact angle space (Figure 2), then explore droplet shapes for hydrophilic surfaces (Figure 3), hydrophobic surfaces (Figure 4), and finally investigate Bond number variations (Figure 5).

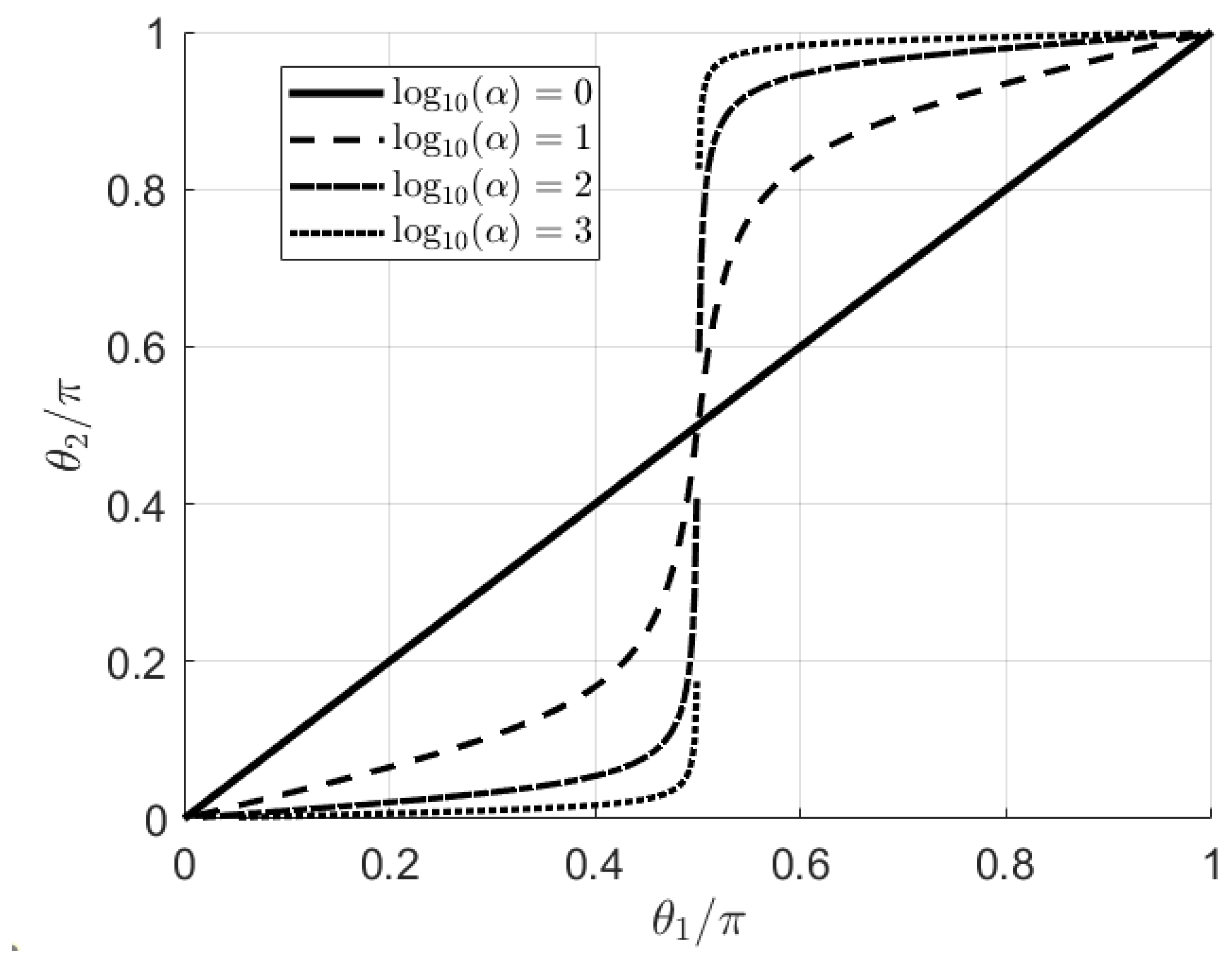
Figure 2 presents contour lines of ${log}_{10}\left(\alpha \right)$ as a function of normalized contact angles ${\theta }_1/\pi$ and ${\theta }_2/\pi$, where $\alpha$ is defined as:

$$\alpha ={\displaystyle \frac{sin\left({\theta }_1\right)tan\left({\theta }_1\right)}{sin\left({\theta }_2\right)tan\left({\theta }_2\right)}}$$

The parameter $\alpha$ characterizes the asymmetry in droplet geometry on heterogeneous surfaces, with ${\theta }_1$ and ${\theta }_2$ representing the contact angles at opposite sides of the droplet. The diagonal line (solid line) represents ${log}_{10}\left(\alpha \right)=0$, corresponding to $\alpha =1$, which occurs when ${\theta }_1={\theta }_2$. This represents a symmetric droplet configuration on a homogeneous surface. Above this diagonal (${\theta }_1>{\theta }_2$), $\alpha >1$ indicates physically realizable asymmetric droplet shapes. The dashed, dash-dot, and dotted lines represent ${log}_{10}\left(\alpha \right)=1,2$, and 3, corresponding to $\alpha =10,100$, and 1000, respectively. These contours show increasing levels of asymmetry as ${\theta }_1$ becomes significantly larger than ${\theta }_2$. The contours cluster near ${\theta }_1\approx \pi /2$, indicating that the asymmetry parameter $\alpha$ becomes extremely sensitive to changes in contact angle in this region due to the singularity of $tan\left(\theta \right)$ at $\pi /2$. The region below the diagonal (${\theta }_1<{\theta }_2$) corresponds to $\alpha <1$, or equivalently, ${log}_{10}\left(\alpha \right)<0$. While mathematically valid, these negative logarithm values represent less asymmetric droplet configurations where ${\theta }_2>{\theta }_1$. Since the definition of $\alpha$ is not symmetric with respect to interchange of ${\theta }_1$ and ${\theta }_2$, the region with ${log}_{10}\left(\alpha \right)<0$ is simply the mirror image of the $\alpha >1$ region, and thus is not shown in this plot.

Importantly, the condition where one contact angle is greater than $\pi /2$ (hydrophobic) while the other is less than $\pi /2$ (hydrophilic) leads to $\alpha <0$, which is physically meaningless. In such extreme wettability gradient conditions, a static equilibrium droplet configuration cannot exist. The droplet would spontaneously migrate toward the more hydrophilic region due to the imbalance in interfacial forces. Therefore, only the region where both contact angles are on the same side of $\pi /2$ (both less than or both greater than $\pi /2$) represents physically realizable droplet states. This contour map is particularly useful for predicting droplet behavior on surfaces with controlled wettability gradients, which has applications in microfluidics, self-cleaning surfaces, and droplet manipulation technologies.

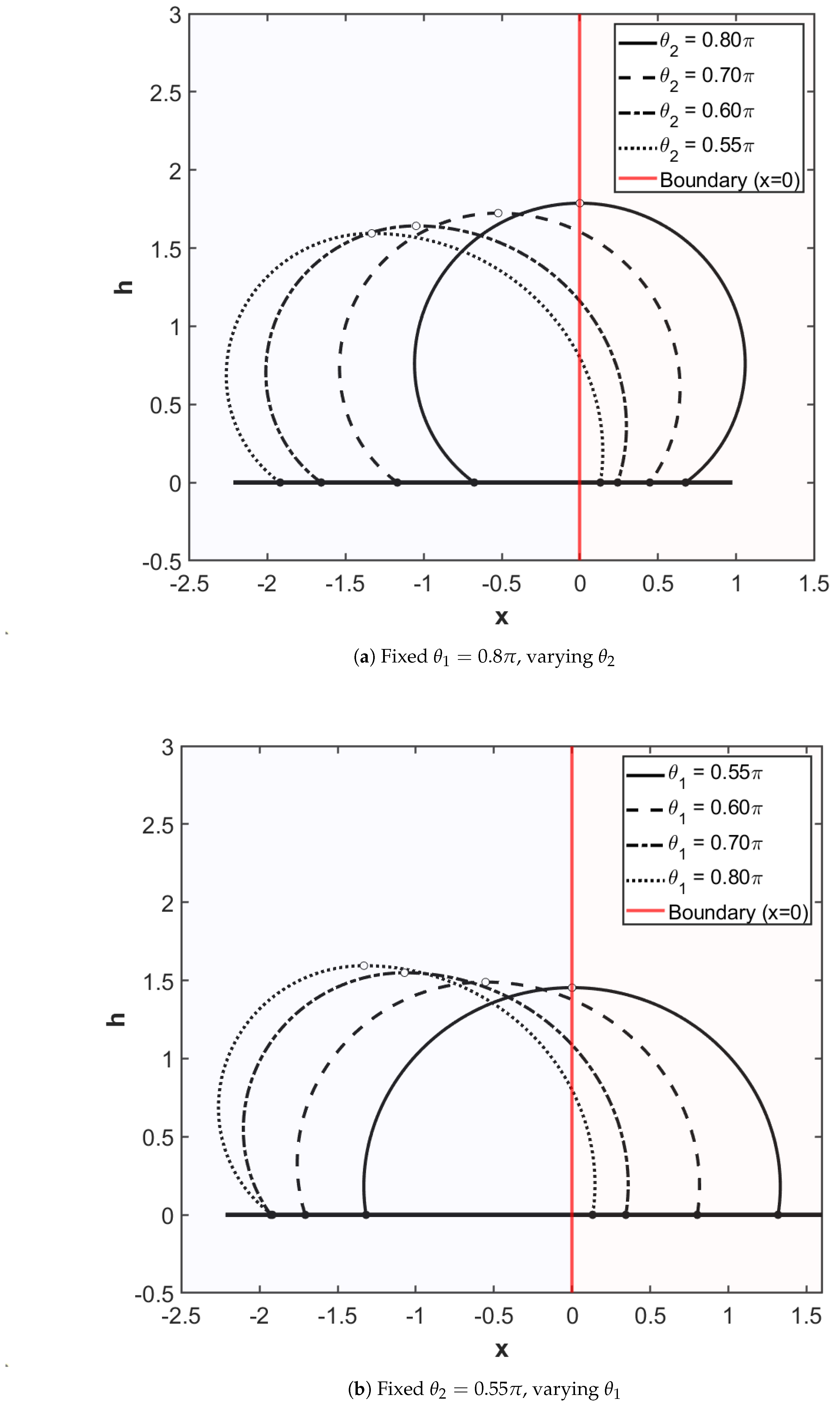
Figure 3 illustrates the variation of droplet shapes at Bond number $Bo=0.1$ for different contact angle configurations, with corresponding data provided in Table 1. The vertical line in (a) and (b) indicates the heterogeneous wetting boundary at $x=0$.

Figure 3(a) examines the case where the left contact angle is fixed at ${\theta }_1=0.45\pi$ while the right contact angle ${\theta }_2$ decreases from $0.45\pi$ to $0.2\pi$. As ${\theta }_2$ decreases, the droplet progressively shifts toward the right side (the region with smaller contact angle) in accordance with the spreading condition. This asymmetric configuration demonstrates the fundamental principle that droplets tend to spread preferentially toward regions with better wettability. When both contact angles are equal (${\theta }_1={\theta }_2=0.45\pi$), the droplet exhibits a symmetric shape with zero curvature difference ($C_R-C_L=0$) and a balanced length ratio ($L_2/|L_1|=1$). As the contact angle difference increases, several key trends emerge from the data: the curvature difference $C_R-C_L$ increases significantly from 0 to 0.66591, the length ratio $L_2/|L_1|$ increases dramatically from 1 to 14.60252 (reflected in the asymmetry parameter $\alpha$), and the maximum height $h_{max}$ decreases from 1.29742 to 0.97999. These changes indicate that greater wettability contrast leads to more pronounced asymmetry and flattening of the droplet profile.

Figure 3(b) presents the complementary scenario where the right contact angle is fixed at ${\theta }_2=0.2\pi$ while the left contact angle ${\theta }_1$ decreases from $0.45\pi$ toward $0.2\pi$. As ${\theta }_1$ approaches ${\theta }_2$, the droplet transitions from an asymmetric to a symmetric configuration. The curvature difference $C_R-C_L$ decreases progressively as the contact angles converge, and the length ratio $L_2/|L_1|$ approaches unity, indicating restoration of geometric symmetry. Notably, the maximum height $h_{max}$ in the symmetric case (${\theta }_1={\theta }_2=0.2\pi$) is substantially lower at 0.83096 compared to 1.29742 when both angles equal $0.45\pi$. This demonstrates that droplets with smaller equilibrium contact angles (more hydrophilic surfaces) naturally adopt flatter profiles due to enhanced spreading.

Together, these two panels comprehensively demonstrate how the spreading condition governs the equilibrium position and shape of droplets on heterogeneous surfaces, highlighting the interplay between contact angle asymmetry, curvature distribution, geometric proportions, and overall droplet morphology.

Figure 4 demonstrates droplet behavior on hydrophobic heterogeneous surfaces at $Bo=0.1$, where both contact angles exceed $\pi /2$. The numerical data for this configuration are tabulated in Table 2. The heterogeneous boundary at $x=0$ is marked by the vertical line in both panels. Unlike hydrophilic surfaces where droplets spread extensively, hydrophobic surfaces resist wetting, resulting in characteristically tall and compact droplet profiles.

In Figure 4(a), we investigate droplets with ${\theta }_1=0.8\pi$ on the left side while systematically varying ${\theta }_2$ from $0.8\pi$ down to $0.55\pi$ on the right. The physical behavior contrasts markedly with hydrophilic cases: as ${\theta }_2$ becomes smaller (less hydrophobic), the droplet redistributes its volume preferentially to the left side where the contact angle remains large. Table 2 reveals a striking asymmetry evolution: starting from the symmetric baseline (${\theta }_2=0.8\pi$) where $L_2/|L_1|=1.0$ and $C_R-C_L=0$, the length ratio plummets to $L_2/|L_1|=0.06848$ when ${\theta }_2=0.55\pi$, while the curvature difference rises to $C_R-C_L=0.40934$. This nearly fifteenfold reduction in the length ratio (equivalently, $\alpha =0.0685$) indicates extreme geometric asymmetry where the droplet base extends far more on the hydrophobic left side. The maximum height decreases modestly from $h_{max}=1.78734$ to $h_{max}=1.59422$, suggesting that while the droplet becomes more asymmetric, it maintains relatively tall profiles characteristic of hydrophobic wetting.

Figure 4(b) explores the inverse scenario: fixing ${\theta }_2=0.55\pi$ on the right while increasing ${\theta }_1$ from $0.55\pi$ to $0.8\pi$. Beginning from a symmetric configuration at ${\theta }_1={\theta }_2=0.55\pi$ where $h_{max}=1.45374$, the droplet responds to increasing left-side hydrophobicity by developing pronounced asymmetry toward the left. The data show that $h_{max}$ rises to $1.59422$ as ${\theta }_1$ reaches $0.8\pi$, reflecting the tendency of larger contact angles to elevate droplet height by restricting lateral spreading. The length ratio decreases systematically, and the curvature difference $C_R-C_L$ grows from zero to $0.30449$. Comparing the two symmetric limits reveals an important scaling: $h_{max}=1.78734$ at ${\theta }_1={\theta }_2=0.8\pi$ versus $h_{max}=1.45374$ at ${\theta }_1={\theta }_2=0.55\pi$, demonstrating that droplet height scales strongly with the degree of hydrophobicity.

The key physical insight from Figure 4 is the reversal of spreading directionality on hydrophobic surfaces: droplets preferentially occupy regions with larger contact angles (greater hydrophobicity) rather than smaller ones. This counterintuitive behavior arises because on hydrophobic surfaces, the spreading function $S\left(\theta \right)=sin\theta tan\theta$ dictates that equilibrium requires the droplet to extend more on the side where wetting is most unfavorable. The resulting droplet morphologies are tall, compact, and strongly asymmetric, with curvature discontinuities at the heterogeneous boundary that become more pronounced as contact angle disparity increases.

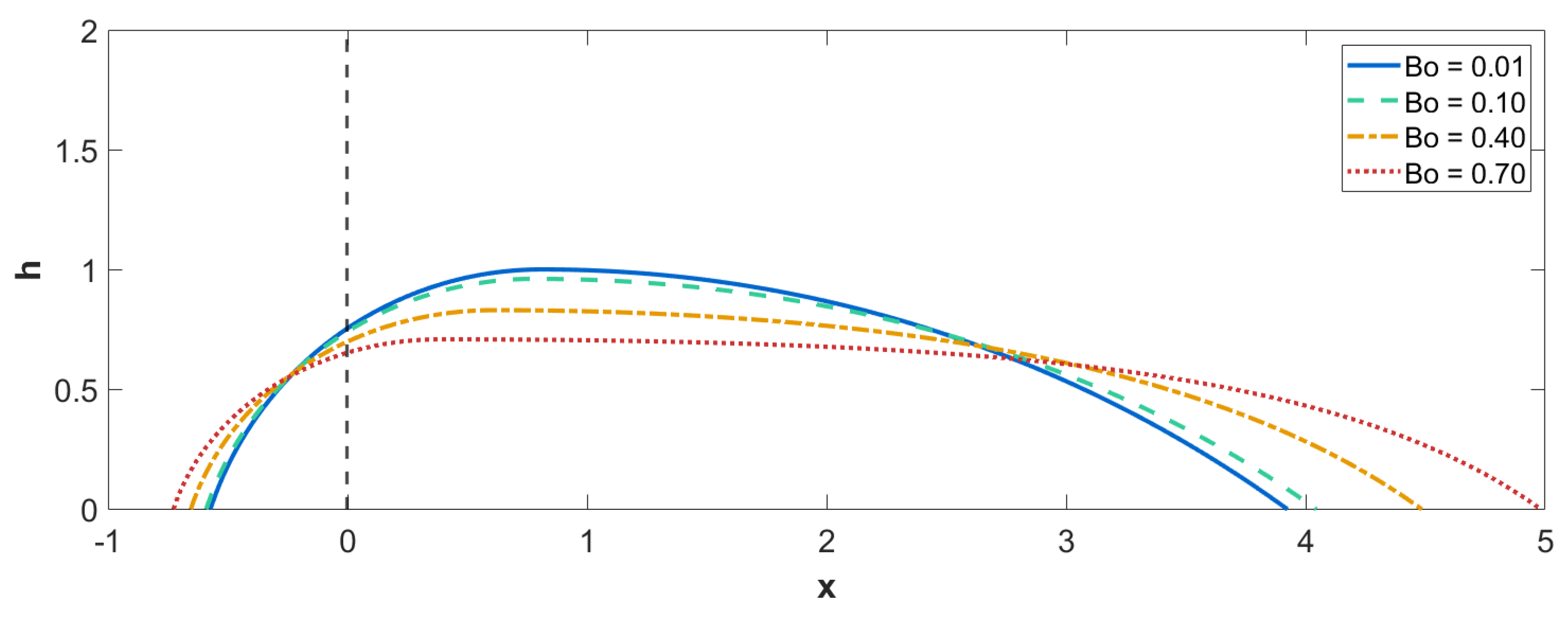
Figure 5 examines the influence of Bond number on asymmetric droplet morphology while maintaining fixed contact angles at ${\theta }_1=0.4\pi$ and ${\theta }_2=0.2\pi$. The Bond number varies from $Bo=0.01$ (capillary-dominated regime) to $Bo=0.7$ (significant gravitational influence), with quantitative data summarized in Table 3. The vertical dashed line at $x=0$ marks the heterogeneous boundary position in this coordinate system.

The figure clearly demonstrates the progressive flattening of droplet profiles as gravitational effects become increasingly important. At the smallest Bond number $Bo=0.01$, surface tension dominates the force balance, producing a tall, nearly spherical cap with maximum height $h_{max}=1.001877$. This configuration closely resembles the capillary-length-limited ideal where gravity plays a negligible role. As the Bond number increases to $Bo=0.1$, gravitational deformation becomes noticeable, reducing the maximum height to $h_{max}=0.962521$. The droplet begins to deviate from the spherical profile, with the apex slightly depressed and the base correspondingly widened. Further increasing the Bond number to $Bo=0.4$ and $Bo=0.7$ amplifies this trend dramatically: the maximum heights decrease to $h_{max}=0.831647$ and $h_{max}=0.709894$, respectively. The droplet progressively adopts a puddle-like geometry where lateral extent dominates over vertical height, characteristic of gravity-dominated sessile drops.

A crucial observation from Table 3 is that the curvature difference $C_R-C_L$ increases systematically with Bond number, rising from $0.499063$ at $Bo=0.01$ to $0.704331$ at $Bo=0.7$. This reflects the fact that gravitational effects modify the pressure distribution within the droplet, leading to enhanced curvature asymmetry across the heterogeneous boundary. The pressure constants $C_L$ and $C_R$ become increasingly negative as Bond number grows, indicating that the reference pressure adjustment required to satisfy boundary conditions becomes more substantial when gravity competes with surface tension.

Despite these morphological changes, a fundamental geometric invariant persists: the asymmetry parameter $\alpha =sin{\theta }_{1}tan{\theta }_1/sin{\theta }_{2}tan{\theta }_2\sim 6.854$ remains constant for all Bond numbers since the contact angles are fixed. Consequently, the length ratio $L_2/|L_1|$ maintains the same value of $\alpha$ across all cases shown, as dictated by the spreading condition equation. This demonstrates that while the Bond number profoundly affects the vertical extent and curvature distribution of the droplet, it does not alter the horizontal partitioning of the droplet base as determined by the contact angle ratio. The spreading condition, which governs the equilibrium position relative to the heterogeneous boundary, is independent of gravitational effects and depends solely on the contact angle configuration.

The transition from $Bo=0.01$ to $Bo=0.7$ thus represents a crossover from capillary-dominated to gravity-influenced droplet shapes, where the competition between surface tension and gravitational body forces reshapes the interface while preserving the fundamental asymmetry encoded in the contact angle boundary conditions. This behavior is critical for understanding droplet dynamics across different length scales, from microscale droplets in microfluidic devices (small $Bo$) to millimeter-scale drops on patterned surfaces (moderate to large $Bo$).

The comprehensive results presented in Figure 2, Figure 3, Figure 4 and Figure 5 validate the theoretical framework and demonstrate the robustness of the two-stage numerical method across a wide parameter space. The asymmetry parameter $\alpha =sin{\theta }_{1}tan{\theta }_1/sin{\theta }_{2}tan{\theta }_2$ emerges as the fundamental quantity governing droplet geometry on heterogeneous surfaces, capturing the competition between spreading forces at opposite contact lines. Figure 2 reveals that $\alpha$ exhibits strong nonlinear sensitivity to contact angle variations, particularly near $\theta \approx \pi /2$ where the tangent function diverges, creating regions of extreme asymmetry. Physically realizable equilibrium configurations exist only when both contact angles lie on the same side of $\pi /2$; mixed hydrophilic-hydrophobic boundaries (${\theta }_1<\pi /2<{\theta }_2$ or vice versa) yield negative spreading functions that violate equilibrium conditions, driving spontaneous droplet migration.

Figure 3 and Figure 4 systematically explore the contact angle parameter space for fixed Bond number $Bo=0.1$, revealing fundamentally different behaviors in hydrophilic versus hydrophobic regimes. For hydrophilic surfaces (Figure 3), droplets preferentially spread toward regions with smaller contact angles (better wettability), producing asymmetric shapes where the maximum height shifts away from the heterogeneous boundary. The length ratio $L_2/|L_1|$ can exceed 14 when contact angle disparity is large (${\theta }_1=0.45\pi$, ${\theta }_2=0.2\pi$), while maximum heights decrease as spreading becomes more favorable. Conversely, hydrophobic surfaces (Figure 4) exhibit counterintuitive behavior: droplets occupy greater area on the side with larger contact angles (poorer wettability), reflecting the dominance of capillary pressure gradients that favor extension into regions resisting wetting. These droplets maintain substantially greater heights ($h_{max}\approx 1.5$–$1.8$) compared to hydrophilic counterparts, adopting compact, nearly spherical geometries that minimize contact area. The curvature difference $C_R-C_L$ serves as a diagnostic for asymmetry strength, increasing monotonically with contact angle disparity in both regimes.

Figure 5 isolates the effect of gravitational deformation by varying Bond number from $Bo=0.01$ (capillary-dominated) to $Bo=0.7$ (gravity-influenced) while holding contact angles fixed at ${\theta }_1=0.4\pi$ and ${\theta }_2=0.2\pi$. The results demonstrate systematic gravitational flattening: maximum height decreases from $h_{max}=1.002$ to $h_{max}=0.710$ as droplet weight increasingly distorts the interface from its capillary-determined shape. Remarkably, the length ratio $L_2/|L_1|\approx 6.854$ remains constant across all Bond numbers, confirming that horizontal partitioning is determined exclusively by the spreading function ratio $S\left({\theta }_1\right)/S\left({\theta }_2\right)$ and is independent of gravitational effects. The curvature difference $C_R-C_L$ increases with Bond number, reflecting enhanced hydrostatic pressure contributions that amplify asymmetry in the normal stress balance. This invariance of the spreading condition under gravitational variation validates the theoretical prediction that contact line equilibrium positions are determined by interfacial energy considerations rather than body forces.

Collectively, these results establish that the spreading condition $L_2/|L_1|=S\left({\theta }_1\right)/S\left({\theta }_2\right)$ constitutes a universal equilibrium criterion for droplets on heterogeneous surfaces, valid across diverse wettability contrasts and gravitational regimes. The two-stage computational strategy—computing a reference shape via parametric Young-Laplace integration followed by algebraic translation to satisfy spreading equilibrium—proves both accurate and efficient, converging within seconds for typical parameter values. The physical insights gained illuminate fundamental mechanisms in wetting phenomena: the spreading function encodes the unbalanced Young stress driving contact line motion, while the Bond number controls morphological transitions from spherical caps to puddle-like geometries without affecting lateral asymmetry ratios. These findings provide quantitative predictions for droplet manipulation on chemically patterned substrates, with implications for microfluidic transport, surface coating technologies, and self-assembly processes where controlled wettability gradients guide fluid motion.

6. Conclusion

This study presents a comprehensive theoretical and numerical framework for analyzing asymmetric droplet configurations on heterogeneous surfaces with discontinuous wettability. By combining rigorous energy minimization principles with efficient parametric numerical methods, we have developed a two-stage computational strategy that accurately predicts equilibrium droplet shapes across diverse contact angle configurations and gravitational regimes.

The central theoretical contribution is the derivation of the general spreading condition from first principles through Lagrange multiplier analysis of the constrained energy functional. This condition, expressed as the ratio of capillary spreading functions $S\left({\theta }_1\right)/S\left({\theta }_2\right)=sin{\theta }_{1}tan{\theta }_1/sin{\theta }_{2}tan{\theta }_2$, governs the horizontal partitioning of droplet volume across the heterogeneous boundary and remains valid for arbitrary Bond numbers. The simplified algebraic form, applicable under geometric self-similarity assumptions, enables explicit calculation of equilibrium contact line positions through the relation $L_2/|L_1|=S\left({\theta }_1\right)/S\left({\theta }_2\right)$, eliminating the need for iterative root-finding procedures. This analytical insight transforms what would traditionally require coupled nonlinear optimization into a straightforward two-stage process: first computing a reference droplet shape via parametric Young-Laplace integration, then applying algebraic translation to satisfy equilibrium.

The numerical results validate the theoretical framework and reveal rich physical behaviors across parameter space. The asymmetry parameter $\alpha$ exhibits strong nonlinear sensitivity near $\theta \approx \pi /2$, creating regions where modest contact angle variations produce dramatic geometric asymmetries with length ratios exceeding 14:1. Critically, physically realizable equilibrium configurations require both contact angles to lie on the same side of $\pi /2$; mixed hydrophilic-hydrophobic boundaries violate equilibrium conditions and drive spontaneous migration. Hydrophilic surfaces ($\theta <\pi /2$) exhibit intuitive spreading toward regions with better wettability, producing flattened profiles with heights $h_{max}\approx 0.8$–$1.3$. In contrast, hydrophobic surfaces ($\theta >\pi /2$) display counterintuitive behavior where droplets preferentially occupy regions with larger contact angles, maintaining tall, compact geometries with $h_{max}\approx 1.5$–$1.8$ that minimize interfacial area.

Bond number variations reveal the decoupling of vertical and horizontal equilibrium mechanisms: gravitational deformation systematically reduces droplet height from $h_{max}=1.002$ at $Bo=0.01$ to $h_{max}=0.710$ at $Bo=0.7$, reflecting the transition from capillary-dominated spherical caps to gravity-flattened puddles. However, the length ratio $L_2/|L_1|$ remains invariant across Bond numbers, confirming that horizontal partitioning depends exclusively on interfacial energy ratios encoded in the spreading function. This independence validates the theoretical prediction that contact line equilibrium is determined by Young stress imbalances rather than gravitational body forces. The curvature difference $C_R-C_L$ increases with both contact angle disparity and Bond number, serving as a quantitative measure of asymmetry strength that reflects both wetting heterogeneity and hydrostatic pressure contributions.

The computational methodology demonstrates exceptional efficiency and robustness. The parametric formulation using tangent angle as the independent variable naturally handles vertical tangent singularities near contact lines, while the Newton-Raphson iteration for the reference shape converges within 5–10 iterations with machine precision accuracy. The algebraic nature of the spreading condition satisfaction eliminates iterative overhead in the second stage, yielding total solution times under one second for typical parameter values on modern hardware. This efficiency makes the method particularly well-suited for parametric studies and inverse design problems where numerous configurations must be evaluated.

The physical insights developed here have significant implications for applications involving controlled wettability patterns. In microfluidic devices, chemically patterned substrates with engineered contact angle gradients can guide droplet positioning and transport without external forcing, enabling passive self-assembly and mixing operations. Self-cleaning surfaces exploit wettability heterogeneities to direct contaminated droplets toward drainage regions. Digital microfluidic platforms manipulate discrete droplets on electrode arrays where localized electrowetting creates dynamic wettability patterns. Our framework provides quantitative design criteria for these technologies, predicting droplet response to specified wettability contrasts and enabling optimization of pattern geometries to achieve desired droplet configurations.

Several extensions of this work merit future investigation. The current analysis assumes static equilibrium with pinned contact lines at prescribed contact angles; relaxing this constraint to incorporate contact angle hysteresis and contact line mobility would capture dynamic wetting transitions and metastable states. Three-dimensional droplets on surfaces with two-dimensional wettability patterns present considerably greater geometric complexity but are essential for realistic device geometries. Incorporating evaporation, thermal effects, or surfactant transport would extend applicability to non-isothermal systems and complex fluids. Finally, experimental validation through high-resolution imaging of droplets on fabricated heterogeneous substrates would provide critical verification of the theoretical predictions and reveal potential physics beyond the continuum Young-Laplace framework, such as line tension effects or molecular-scale interactions near the wetting boundary.

In conclusion, this work establishes a rigorous theoretical foundation and efficient computational methodology for asymmetric droplet wetting on heterogeneous surfaces. The spreading condition emerges as a universal equilibrium criterion, independent of gravitational effects and valid across diverse wettability contrasts. The parametric numerical approach combines accuracy with computational efficiency, making it a practical tool for both fundamental studies and engineering applications. By elucidating the interplay between interfacial energy, contact angle asymmetry, and gravitational deformation, these results advance our understanding of wetting phenomena and provide predictive capabilities for designing surfaces with tailored droplet manipulation properties.