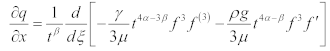Dynamic Wetting and Spreading of High-Viscosity Liquids on Grooved Substrates

Jun Hu; Zhan-Long Wang

doi:10.20944/preprints202504.2091.v1

Submitted:

23 April 2025

Posted:

27 April 2025

You are already at the latest version

Abstract

Liquid filament formation and spreading on grooved substrates play a crucial role in applications ranging from microfluidics to material deposition. Despite extensive studies on capillary-driven spreading, the dynamics of liquid filaments, particularly for high-viscosity, high-surface-tension liquids, remain poorly understood. Here, we investigate the wetting and spreading behavior of glycerol-water mixtures on structured surfaces with varying groove widths (8 µm to 32 µm) and depths (15 µm). Using a combination of experiments, finite element simulations, and theoretical analysis, we reveal the interplay between capillary forces, viscous resistance, and gravity in governing liquid filament propagation. The results demonstrate a consistent t4/5 scaling law for filament length over time, reflecting the balance of capillarity and gravity in the long-time regime. Narrower grooves enhance capillary confinement, promoting faster and more uniform filament spreading, while higher viscosity slows propagation. Finite element simulations confirm these findings, reproducing experimental trends and elucidating the role of groove geometry on filament dynamics. Theoretical analysis based on the lubrication equation provides a robust framework for understanding these behaviors. Our findings advance the understanding of liquid filament dynamics on structured surfaces and offer insights for optimizing grooved substrates in microfluidic, sensing, and material processing applications.

Keywords:

liquid filaments

;

droplet

;

wetting

;

scaling law

;

grooved surfaces

Subject:

Physical Sciences - Fluids and Plasmas Physics

Introduction

Solid-liquid interfaces play a pivotal role in a variety of natural and industrial processes, governing phenomena such as adhesion, capillarity, wetting, self-assembly, and phase change heat transfer ^1-5. These interactions are fundamental to the behavior of liquids on solid surfaces, influencing processes ranging from biological adhesion to fluid transport in engineered systems ^6-11. Understanding these dynamics is critical for applications in fields such as microfluidics, advanced material deposition, and energy storage. Particularly, structured surfaces with micro- or nanoscale patterns, including grooves, have emerged as a focus of research due to their ability to direct fluid motion, manipulate wetting behavior, and enhance interfacial phenomena ^12,13. Grooved surfaces, in particular, provide a simple yet powerful platform for controlling liquid spreading and capillary-driven flow. These surfaces enable precise manipulation of fluids, which is essential for applications requiring high spatial control, such as diagnostics, drug delivery, lab-on-a-chip devices, DNA manipulation, and microreactor operations ^14-18. The study of liquid spreading on grooved substrates provides insights into the mechanisms underlying interfacial dynamics, including the effects of capillary forces, viscous resistance, and gravitational influences ^12,19. Despite their practical significance, the detailed understanding of liquid behavior on grooved surfaces, particularly the formation and propagation of liquid filaments, remains incomplete. The unique combination of capillary confinement and gravitational effects on these structured surfaces warrants further investigation to uncover the underlying physical mechanisms.

The study of liquid filament formation and spreading on structured surfaces, including grooved substrates, has a rich and evolving history. Early foundational work centered on understanding capillarity-driven flows in simple geometries such as porous media and capillary tubes. Washburn’s classical equation ²⁰, formulated in the early 20th century, laid the groundwork by describing the time-dependent imbibition of liquids into porous substrates. Subsequent studies extended these principles to microfluidic channels, thin films, and open channels ^1,2,13,21. Over time, researchers recognized that introducing surface patterns—such as grooves or posts—could tailor liquid flow, fostering more complex phenomena including the formation of elongated liquid threads or filaments ^22,23. During the late 20th and early 21st centuries, advances in microfabrication techniques enabled the systematic investigation of liquid spreading on micro- and nanostructured substrates. Early efforts focused on the role of surface topography in modifying wetting hysteresis and equilibrium contact angles ^24,25. With the advent of soft lithography and improved photolithographic methods, grooved substrates with well-defined geometries became accessible, allowing detailed experiments on the behavior of droplets and menisci confined within periodic structures ²⁶. These works demonstrated that groove depth, width, and spacing strongly affect the capillary forces acting on confined liquids, significantly influencing spreading speed and filament stability.

The concept of liquid filaments—thin, elongated fluid bodies extending within grooves—emerged as a focal point of research approximately two decades ago. Darhuber and Troian ²⁷ highlighted how capillary forces guide fluid along grooves and channels, while subsequent studies by Bico and Quéré ²⁸ underscored the interplay between roughness-induced capillarity and viscous dissipation. Early experiments showed that liquid filaments could act as transport conduits, facilitating directional fluid motion without external pumps or fields, a concept soon exploited for microfluidic applications ^29,30. In these initial explorations, the fluids were typically low-viscosity and Newtonian, and the emphasis lay on understanding fundamental scaling laws and identifying conditions under which filaments remain stable or break into droplets ^31,32. As the field matured, researchers began to consider more complex fluids and conditions. Studies by Herminghaus et al. ^33,34 revealed that non-Newtonian fluids, surfactant-laden solutions, and liquids with varying viscosities and surface tensions can exhibit markedly different filament morphologies and spreading dynamics. Similarly, investigations into the influence of external fields—such as electrowetting ^35,36 or thermal gradients ³⁷—demonstrated that liquid filaments can be actively controlled, opening pathways for reconfigurable and adaptive microfluidic devices. More recently, attention has shifted towards understanding the fundamental mechanisms governing filament propagation when both capillarity and gravity are significant. Studies by Weislogel et al. ^38,39 examined gravitational effects in open microchannels, while Ledesma-Aguilar et al. ⁴⁰ investigated how gravitational leveling and hydrostatic pressure gradients modify filament shape and speed. These studies uncovered new regimes where gravitational and capillary forces jointly determine a non-trivial scaling law, differing from the canonical t^1/2 or t^1/3 relationships often found in low-viscosity or inertia-dominated systems.

Complementing experimental work, computational modeling and theoretical analyses have advanced our understanding of filament spreading. Lubrication theory, widely employed since the mid-20th century ^41,42, has been adapted to patterned substrates, enabling analytical or semi-analytical predictions of filament shape and propagation rates ⁴³. Numerical simulations using volume-of-fluid or level-set methods capture intricate interface dynamics, complex contact line motion, and the formation of multiple filaments within a single substrate ^44,45. Such tools have shed light on how subtle changes in geometry or fluid properties can shift the balance of forces and alter the spreading kinetics. Despite these advances, the dynamic wetting process of high-surface-tension liquids with varying viscosities on grooved substrates remains incompletely understood.

To systematically and deeply understand this issue, this study systematically investigates the dynamics of liquid filament formation and propagation on grooved substrates with varying geometries. Using glycerol-water mixtures with controlled viscosities and surface tensions, we explore the interplay of viscosity, capillary forces, and groove geometry in determining filament behavior. The experiments focus on substrates with grooves of varying widths, examining the spreading of three glycerol-water solutions. This composition range enables a detailed analysis of how high-viscosity liquids with near-constant surface tensions respond to capillary confinement. The experimental findings are complemented by finite element simulations to model filament propagation under controlled conditions and theoretical analysis based on the lubrication equation. The combined approach reveals a consistent t^4/5 scaling law for filament length versus time, reflecting the balance of capillary and gravitational forces in the long-time regime. The theoretical framework provides a robust explanation for the observed dynamics, linking the spreading rate to fundamental physical properties such as viscosity, surface tension, and groove geometry. This research contributes to the broader field of interfacial fluid dynamics by providing new insights into liquid filament behavior on structured surfaces. The findings have significant implications for designing grooved substrates for applications in microfluidics, material deposition, and surface engineering. By bridging experimental, computational, and theoretical approaches, this work advances our understanding of capillary-driven spreading and sets the stage for further exploration of more complex systems, including non-Newtonian fluids and hierarchical surface patterns.

Materials and Methods

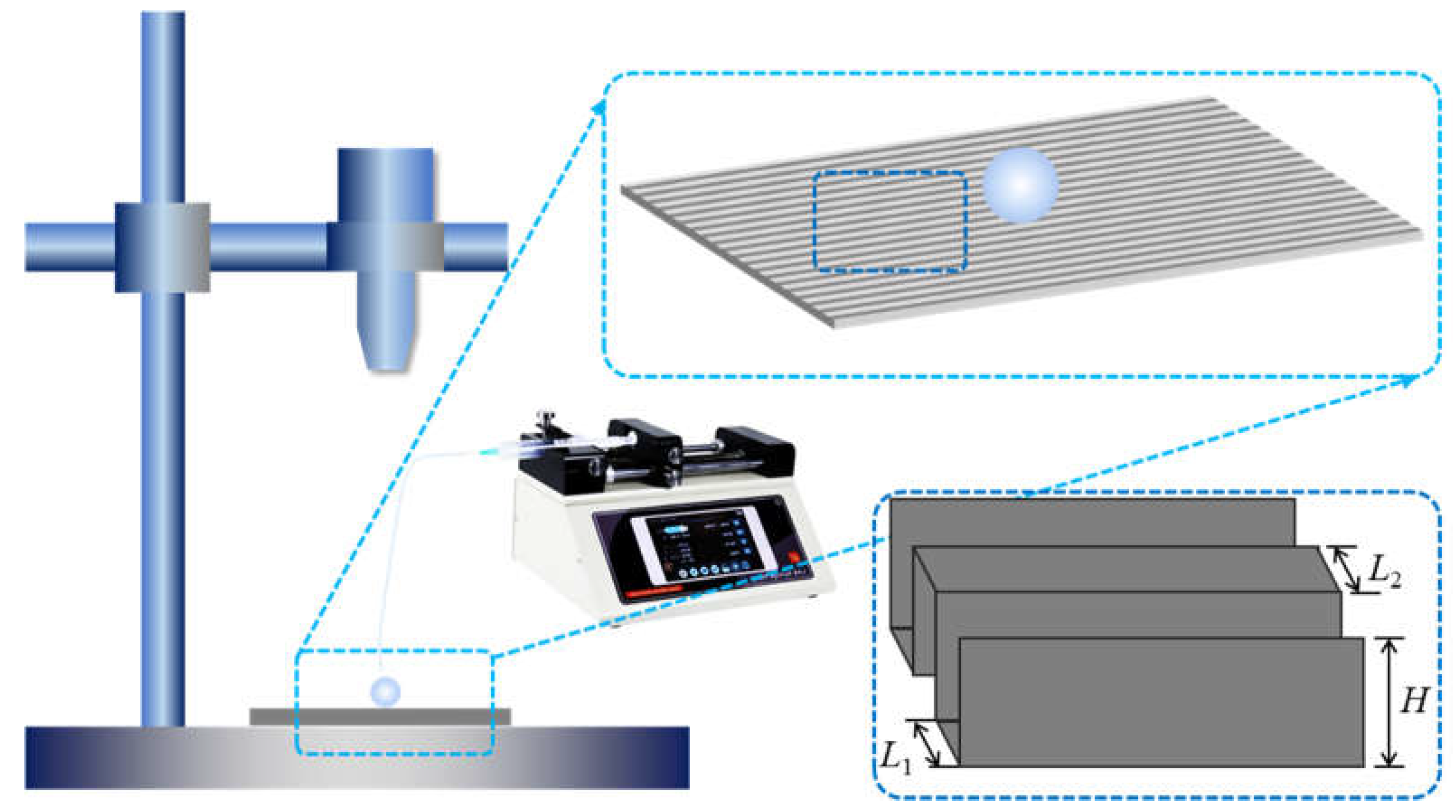
The patterned rectangular groove structures were fabricated on silicon wafers using a photolithographic process, a precise and widely adopted technique for microstructure fabrication. Preparation began by cleaning the silicon wafers using a standard RCA cleaning process to remove organic residues and particulate contaminants, ensuring a pristine surface for subsequent steps. The cleaned wafers were then dehydrated at 120°C on a hot plate for 10 minutes to eliminate moisture and improve photoresist adhesion. Next, a layer of SU-8 3025 photoresist was spin-coated onto the silicon wafers. The spin-coating process was performed in two stages: an initial spreading stage at 500 rpm for 10 seconds, followed by a high-speed stage at 3000 rpm for 30 seconds, achieving a uniform thickness corresponding to the desired groove depth of 15 µm. The coated wafers were then subjected to a soft bake on a hot plate at 65°C for 2 minutes, followed by 95°C for 5 minutes, to partially cure the photoresist and remove any residual solvents. The groove patterns were defined using a photomask and ultraviolet (UV) exposure. A photomask with designed groove patterns, including equal-width grooves (8 µm, 16 µm, and 32 µm) and variable-width grooves (ranging from 8 µm to 24 µm, with 2 µm intervals), was aligned with the photoresist-coated wafer. The UV exposure was carried out using a mask aligner, with an exposure dose of 70 mJ/cm² to ensure complete polymerization of the exposed regions. After exposure, the wafers underwent a post-exposure bake (PEB) at 65°C for 1 minute and 95°C for 3 minutes to enhance cross-linking in the exposed areas. The unexposed photoresist was then removed by developing the wafers in SU-8 developer for 3-5 minutes, followed by thorough rinsing with isopropanol to stop the development process. The wafers were dried using a nitrogen gun.

To finalize the fabrication, the wafers were subjected to hard baking at 150°C for 10 minutes, stabilizing the SU-8 structures and ensuring mechanical robustness. This process resulted in highly uniform and reproducible rectangular groove patterns with sharp edges and consistent depths. Two types of structures were prepared: equal-width grooves with widths of 8 µm, 16 µm, and 32 µm, and variable-width grooves ranging from 8 µm to 24 µm, as illustrated in Figure 1, where L₁ represents the groove width, L₂ the groove interval, and H the groove depth. Table 1 and Table 2 provide detailed summaries of the groove dimensions, including width, interval, depth, and surface roughness. The surface roughness, RA, which was defined as the ratio of the apparent surface area to the actual surface area, calculated as RA = L₁/(2H+L₁). This parameter characterizes the extent of surface structuring and its impact on interfacial phenomena, enabling precise investigation of liquid filament dynamics on the fabricated surfaces.

The liquid mixtures used in the experiments were prepared by mixing glycerol (G) and deionized water (W) in different volume ratios to achieve a range of viscosities and surface tensions. Three compositions were selected: pure glycerol (G₁₀₀W₀), glycerol-water mixtures with ratios of 70:30 (G₇₀W₃₀), and 50:50 (G₅₀W₅₀), representing high, medium, and low viscosities, respectively. The physical properties of these mixtures, including density, viscosity, surface tension, and static contact angles on the SU-8 photoresist substrate, are detailed in Table 3. The contact angle measurements were performed using a contact angle goniometer to ensure accuracy and reliability. These properties provide critical insights into the behavior of the liquid filaments during the spreading process. Droplets were dispensed using a precision syringe pump (produced by Baoding Dirui Company), which allowed precise control over the volume of liquid deposited onto the structured SU-8 substrates. The droplets were dispensed through a fine-tipped needle to minimize initial impact and ensure consistent deposition. The spreading behavior of the droplets was recorded using an industrial-grade camera operating at a frame rate of 60 frames per second. The high frame rate enabled the detailed capture of the dynamic spreading process, including the formation and propagation of liquid filaments within the microgroove structures.

All experiments were conducted at a controlled room temperature of 25°C to minimize environmental variations that might affect the spreading behavior. The structured substrates were placed on a horizontal platform to ensure uniform conditions for liquid spreading. The liquid filament length and its progression over time were analyzed using motion detection software (VL 3.0). Each video was processed frame by frame, and the filament length was measured manually or using edge-detection algorithms within the software to ensure consistent and accurate data collection. The chosen glycerol-water mixtures represent a range of fluid viscosities, enabling a comprehensive investigation into how viscosity and surface tension influence the dynamics of liquid filament propagation. High-viscosity fluids (G₁₀₀W₀) provided insights into cases dominated by viscous forces, while lower viscosity mixtures (G₅₀W₅₀) allowed exploration of capillary-dominated regimes. By systematically varying the liquid composition and monitoring the spreading process, this study aimed to elucidate the interplay of viscosity, surface tension, and microstructure geometry in governing the dynamics of liquid filaments on patterned surfaces.

G: glycerol; W: DI water; G₁₀₀W₀ represents 100% glycerol and 0% DI water.

Results and Discussions

Figure 2 presents the experimental observations and analyses of wetting and spreading behaviors of three glycerol-water mixtures (G₅₀W₅₀, G₇₀W₃₀, and G₁₀₀W₀) on SU-8 photoresist substrates with varying groove widths. The three liquids represent different viscosities while maintaining similar surface tensions, allowing for a focused investigation of viscosity's role in the propagation of liquid filaments under comparable capillary conditions. The static contact angles of the three liquids on the SU-8 surface are depicted. DI water (surface tension 72 mN/m) exhibits a contact angle of 82°, while the contact angles for G₅₀W₅₀, G₇₀W₃₀, and G₁₀₀W₀ are 76°, 73°, and 57°, respectively. This slight decrease in contact angle correlates with the increase in glycerol content, as the surface tension of glycerol (64 mN/m) is lower than that of water. Despite these small differences in contact angle and surface tension, the viscosities of the three mixtures vary significantly, from 6 mPa·s for G₅₀W₅₀ to 1410 mPa·s for G₁₀₀W₀. This viscosity range enables a systematic comparison of spreading dynamics on grooved substrates, especially under high surface tension and similar capillary driving forces. Figure 2 illustrates the spreading behavior of the three liquids (G50W50 (Figure 2a), G70W30 (Figure 2b) and G100W0 (Figure 2c)) within grooves of varying widths (8 µm, 16 µm, and 32 µm). Each row corresponds to a specific groove width, with the first row representing 8 µm grooves, the second row 16 µm grooves, and the third row 32 µm grooves. At the narrowest groove width of 8 µm, all three liquids exhibit liquid filament formation and propagation, irrespective of viscosity. This observation indicates that the narrow grooves provide sufficient capillary confinement to sustain liquid filament formation.

For grooves with a width of 16 µm, liquid filaments are still observed for all three liquids, albeit with slight differences in filament stability and propagation dynamics. The increased groove width reduces the degree of confinement, but the capillary forces remain sufficient to sustain filament formation. At the widest groove width of 32 µm, liquid filaments no longer form for any of the three liquids. Instead, the liquids spread along the groove base without the distinct filament morphology observed at narrower groove widths. This transition suggests that as the groove width increases, the capillary confinement diminishes, and the balance between capillary forces and gravitational forces shifts, ultimately inhibiting liquid filament formation. The roughness coefficients (RA) of the three groove widths are 1.358, 1.215, and 1.028, respectively. According to classical wetting theory, the equilibrium contact angle’s cosine value is proportional to the roughness coefficient. According to the theory of energy minimization, for a liquid progression in the groove by a quantity dx, the surface energies change by an amount (ignoring gravity effects) dE = (γ_sl-γ_sv)(2H+L₁)dx+γ_lvL₁dx. Using the Young equation, the liquid progression is favorable when θ < θ_c, with cosθ_c = L₁/(2H+L₁). For the three surfaces, the equilibrium contact angles were calculated as 77.8°, 69.6°, and 58.9°, respectively. The experimental static contact angles of the droplets (76.2°, 68.3°, and 57.5°) are consistently larger than the calculated equilibrium angles, indicating that the spreading and filament formation process involves an additional driving force beyond the capillary forces predicted by classical theory. This additional traction likely results from the hemi-capillary force at the groove edges, which enhances filament propagation even at higher contact angles. These results demonstrate that groove width and liquid viscosity play critical roles in liquid filament formation and propagation. While narrow grooves consistently facilitate filament formation, wider grooves fail to sustain capillary-driven confinement, especially for high-viscosity liquids. This study highlights the intricate interplay of capillary forces, groove geometry, and liquid properties in determining the dynamics of liquid filament propagation on structured surfaces.

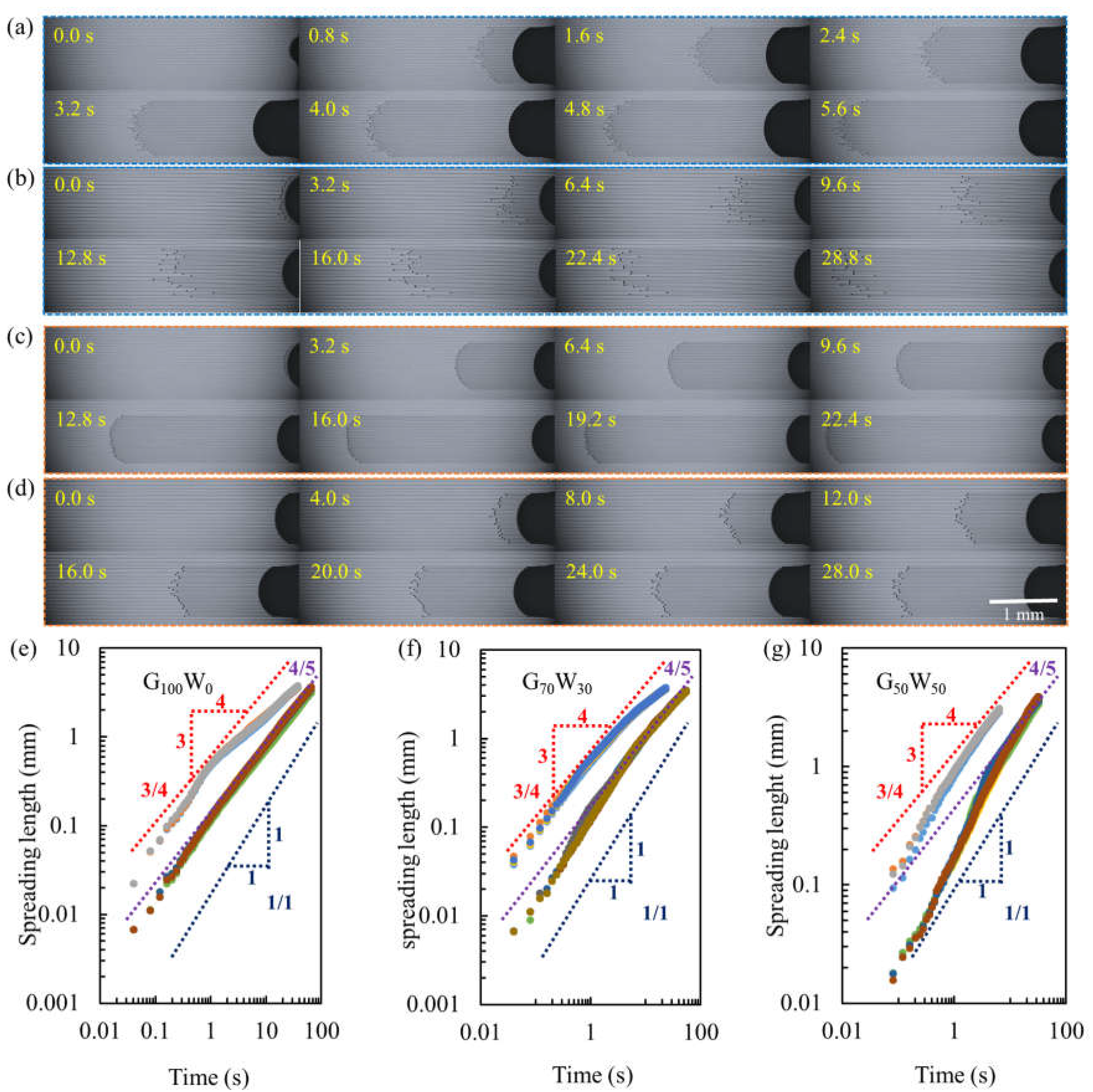
Figure 3 illustrates the dynamic wetting and spreading behavior of three glycerol-water mixtures (G₅₀W₅₀, G₇₀W₃₀, and G₁₀₀W₀) within grooved substrates of varying widths (8 µm and 16 µm). The experiments capture the progression of liquid filament propagation, highlighting the effects of groove width and liquid viscosity on the spreading dynamics. Figure 3a,b depict the spreading process of G₅₀W₅₀ in grooves with widths of 8 µm and 16 µm, respectively. In the 8 µm-wide grooves (Figure 3a), the liquid filament propagates approximately 3 mm in length within 5.6 seconds, indicating a rapid spreading process facilitated by the narrow groove's strong capillary confinement. In contrast, for the 16 µm-wide grooves (Figure 3b), the same 3 mm propagation length is achieved in 28.8 seconds, nearly five times slower than in the narrower grooves. This stark difference underscores the critical role of groove width in influencing the spreading speed, as wider grooves reduce capillary confinement and thereby decrease the driving force for filament propagation. The same trend is observed for G₇₀W₃₀, as shown in Figures 3c and 3d. In the 8 µm-wide grooves (Figure 3c), the filament propagates approximately 3 mm within 22.4 seconds, whereas in the 16 µm-wide grooves (Figure 3d), the filament length is less than 2 mm even after 28 seconds. These results further confirm that increased groove width slows filament propagation, likely due to diminished hemi-capillary forces and the greater dominance of viscous resistance in wider grooves. Additionally, the comparisons between G₅₀W₅₀ and G₇₀W₃₀ demonstrate that higher viscosity results in slower filament propagation, as viscosity inversely correlates with velocity under a constant driving force. Figure 3e,f,g present the relationships between filament length and time for G₁₀₀W₀, G₇₀W₃₀, and G₅₀W₅₀, respectively, using logarithmic coordinates. For the high-viscosity G₁₀₀W₀ solution (Figure 3e), the spreading follows a l~t^4/5 scaling law after an initial phase of rapid spreading. The early-stage faster propagation suggests that gravitational forces play a significant role initially, accelerating the liquid flow. This observation is consistent across all three solutions, as seen in Figs. 3f and 3g, where initial spreading speeds are higher before stabilizing into the 4/5-power scaling relationship.

The decreasing viscosity of the solutions (from G₁₀₀W₀ to G₅₀W₅₀) amplifies the influence of gravity during the initial spreading phase, extending the duration of rapid propagation. However, as the spreading stabilizes, the scaling law converges to the 4/5-power relationship for all solutions. This consistent scaling behavior suggests that the interplay of capillary and viscous forces governs the long-term propagation of liquid filaments, while gravitational effects primarily influence the initial stages. These results highlight the complex dynamics of liquid filament spreading in grooved substrates. Narrower grooves enhance capillary confinement, facilitating faster filament propagation, while higher viscosities dampen spreading speed by increasing viscous resistance. The consistent 4/5-power scaling observed in the stabilized phase underscores the dominance of capillary-driven dynamics under these conditions, providing a robust framework for understanding liquid filament propagation in structured microenvironments.

The dynamic wetting and spreading behavior of three glycerol-water mixtures (G₁₀₀W₀, G₇₀W₃₀, and G₅₀W₅₀) on substrates with gradient groove width structures were explored in Figure 4. The grooves have widths ranging from 8 µm to 24 µm, increasing in 2 µm increments, with a constant depth of 15 µm. The groove parameters are detailed in Table 2. These gradient substrates facilitate a systematic investigation of how varying groove widths influence liquid filament formation and propagation. 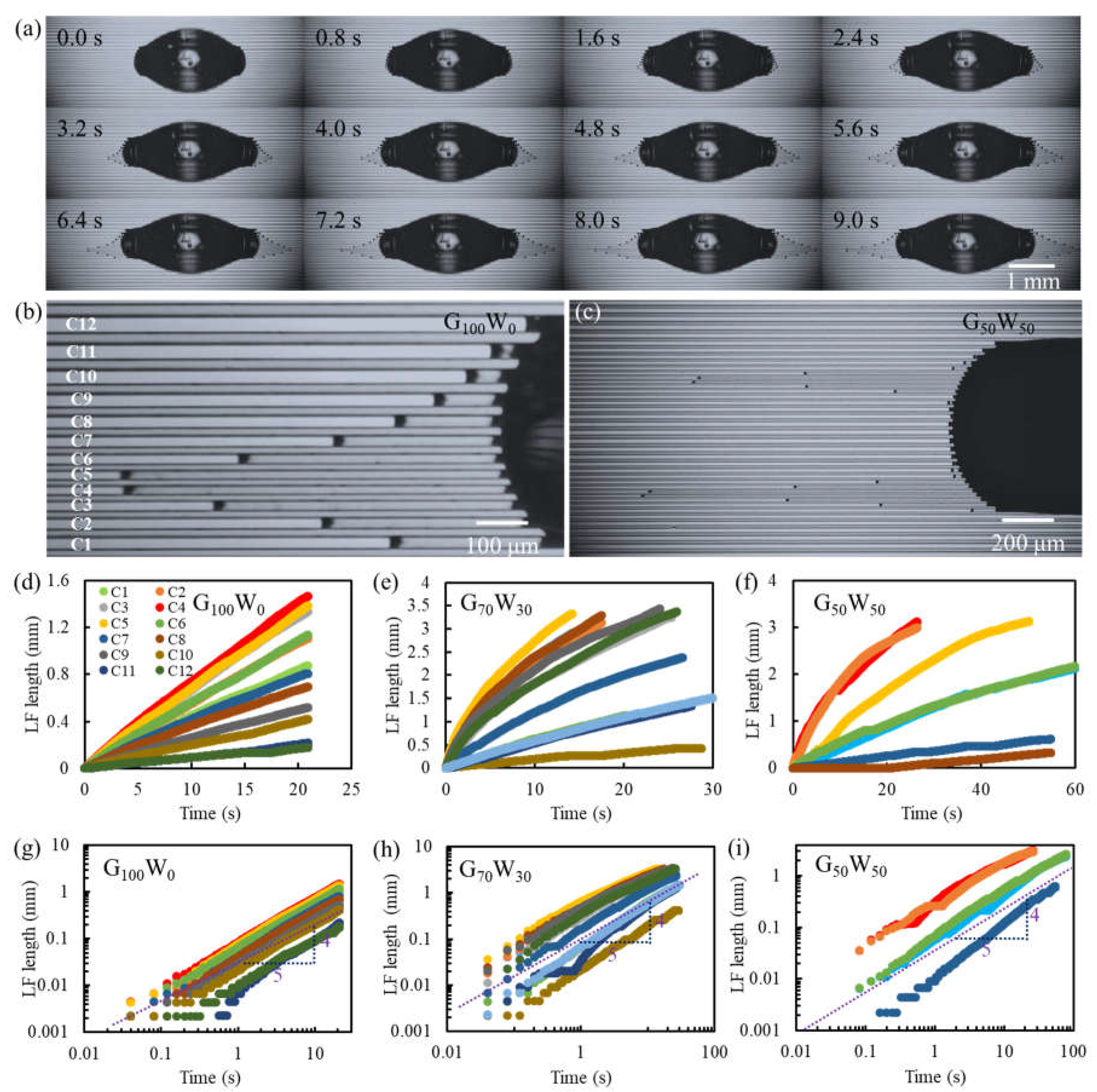Figure 4a depicts the spreading progression of a 5 µL G₁₀₀W₀ droplet from 0 to 9 seconds. In the initial 0.8 seconds, no liquid filament is observed; however, by 1.6 seconds, a filament begins to form at the droplet's leading edge. Over time, the filament propagates farther, reaching a maximum length of approximately 1 mm within 9 seconds. This result highlights the delayed onset of filament formation due to the high viscosity of G₁₀₀W₀, which slows the initial capillary-driven motion. The gradient grooves significantly affect filament length. Narrower grooves produce longer filaments, while filaments in wider grooves exhibit reduced propagation lengths. This gradient effect becomes increasingly pronounced over time, demonstrating a clear relationship between groove width and filament spreading dynamics. Figure 4b provides a magnified view of the filament formation for G₁₀₀W₀, with 12 grooves labeled C1 to C12, corresponding to widths ranging from 8 µm to 24 µm. The differences in filament length across the grooves are apparent, with the longest filaments observed in the narrowest grooves (C1 and C2).

Figure 4c,b compare the filament formation for G₅₀W₅₀ and G₁₀₀W₀. The G₅₀W₅₀ droplet exhibits more pronounced variations in filament length across grooves. The reduced viscosity of G₅₀W₅₀ enhances the influence of groove width on filament propagation, leading to a sharper gradient effect. The narrower grooves produce significantly longer filaments than the wider grooves, underscoring the interplay between viscosity and capillary confinement in determining filament length. Figure 4d–f show the filament length as a function of time for the three solutions (G₁₀₀W₀, G₇₀W₃₀, and G₅₀W₅₀) across the 12 gradient grooves. In Figure 4d, the G₁₀₀W₀ filament length increases approximately linearly with time during the first 20 seconds. The fastest spreading is observed in C4 and C5, corresponding to the narrowest grooves. This linear spreading behavior reflects the dominant role of viscous forces in high-viscosity fluids, where capillary forces are modulated by the groove geometry. Figure 4e illustrates the spreading dynamics for G₇₀W₃₀. The filament initially propagates rapidly but slows down as it elongates, reaching a length of approximately 3 mm within 20 seconds in the narrowest grooves. This deceleration is consistent with the increasing viscous resistance as the filament grows longer, and the dynamics indicate a shift from gravity-influenced motion in the initial phase to capillary-dominated spreading over time. Figure 4f shows the spreading behavior of G₅₀W₅₀. Similar to G70W30, the filament propagation initially exhibits rapid motion, followed by a gradual deceleration. The reduced viscosity of G₅₀W₅₀ amplifies the influence of capillary forces, resulting in longer filaments compared to G₁₀₀W₀ and G₇₀W₃₀ for the same groove width.

Figure 4g–i present the filament length versus time in logarithmic coordinates for G₁₀₀W₀, G₇₀W₃₀, and G₅₀W₅₀, respectively. Across all three solutions, the filament length scales with time as l ~ t^4/5. This scaling behavior is consistent for all groove widths, indicating that the capillary forces, modulated by viscosity and groove geometry, dominate the spreading dynamics in the stabilized phase. For the higher-viscosity G₁₀₀W₀, the initial gravitational influence is minimal, resulting in a nearly uniform 4/5-power scaling across the grooves. In contrast, for G₇₀W₃₀ and G₅₀W₅₀, gravitational effects are more pronounced in the early stages, accelerating filament formation before transitioning to the 4/5-power scaling as viscous and capillary forces balance. These results reveal the complex interplay of groove geometry, viscosity, and capillary forces in liquid filament formation and propagation. Narrow grooves and lower viscosity enhance filament propagation, while wider grooves and higher viscosity limit the filament length. The 4/5-power scaling provides a robust framework for predicting filament dynamics across various groove and liquid parameters, offering valuable insights for applications requiring precise fluid manipulation in structured surfaces.

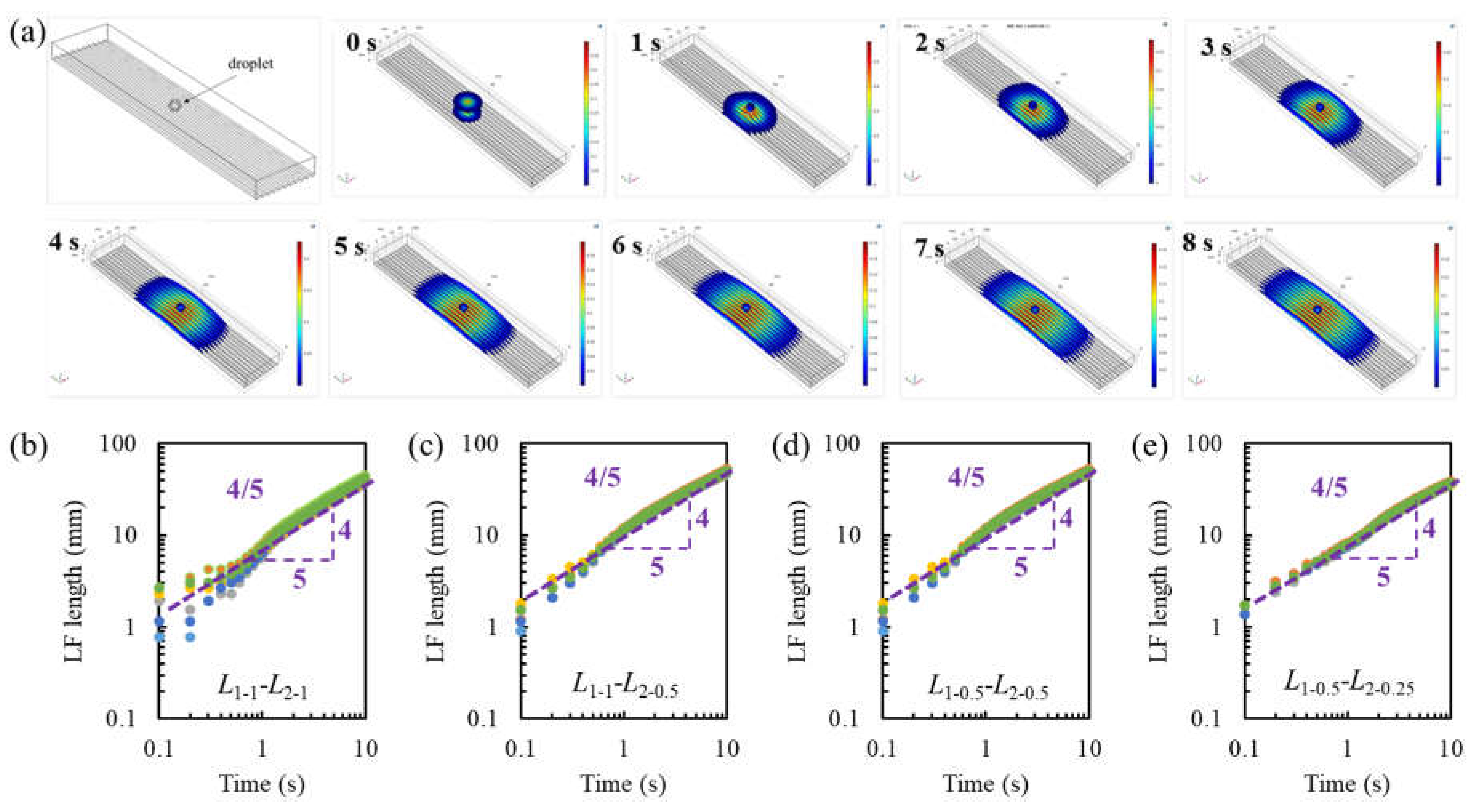
To complement the experimental observations, finite element method (FEM) simulations were conducted to analyze the dynamics of liquid filament spreading on grooved substrates. The simulation model is illustrated in Figure 5a (first panel), depicting a structured substrate with grooves of varying widths and depths. The simulations employed a two-phase flow model based on the Navier-Stokes equations, incorporating capillary forces, viscous effects, and gravitational forces to replicate the experimental conditions accurately. The simulated liquid was modeled using a Newtonian fluid with properties corresponding to G₁₀₀W₀. The density (ρ) and dynamic viscosity (η) were set to 1.26 g/cm³ and 1410 mPa·s, respectively, while the surface tension (γ) was 64 mN/m. The contact angle on the grooved substrate was set to 85°, consistent with experimental measurements for G₁₀₀W₀ on SU-8. The grooved substrate's geometries were defined as L₁-L₂-H structures, where L₁ represents the groove width, L₂ the groove spacing, and H the groove depth. The depth (H) was fixed at 15 µm, while L₁ and L₂ were varied based on the groove dimensions described in Table 2. The computational domain was discretized using a structured mesh with finer elements near the liquid-groove interface to capture the details of filament dynamics. Time-dependent simulations were performed using a volume-of-fluid (VOF) method to track the liquid-gas interface, and a no-slip boundary condition was applied to all solid surfaces. The simulations were initialized with a droplet of 5 µL volume placed symmetrically on the substrate, with the spreading process simulated up to 8 seconds at 1-second intervals.

Figure 5a (second to last panels) shows the simulated time sequence of liquid filament spreading on the substrate from 0 s to 8 s. Initially, the droplet spreads radially without filament formation. By 1 s, a filament begins to form at the groove's leading edge, and its length progressively increases over time. At 8 s, the filament achieves a maximum length, closely matching the experimental results. Figs. 5b–5e illustrate the simulated filament front position as a function of time for different substrate geometries, all plotted on logarithmic scales. Each panel corresponds to a specific configuration: Figure 5b: L_1-1−L_2-1 (16 µm groove width and spacing) shows a smooth progression of filament length with a clear t^4/5 scaling law after the initial transient phase. Figure 5c: L_1-1−L_2-0.5 (16 µm groove width, 8 µm spacing) exhibits a similar scaling behavior but with a faster spreading rate due to the reduced spacing, which enhances capillary confinement. Figure 5d: L_1-0.5−L_2-0.5 (8 µm groove width and spacing) demonstrates the fastest spreading dynamics among all configurations, with the narrow grooves providing the strongest capillary driving forces. Figure 5e: L_1-0.5−L_2-0.25 (8 µm groove width, 4 µm spacing) further enhances confinement, resulting in a slightly faster initial spreading phase before stabilizing to the t^4/5 scaling. Across all geometries, the filament length's scaling behavior adheres to the t^4/5 power law observed experimentally. The initial phase of spreading is influenced by gravity, as indicated by a slightly faster spreading rate, but this effect diminishes over time as capillary and viscous forces dominate. Narrower grooves and smaller spacing enhance capillary confinement, resulting in faster and more uniform filament propagation.

The FEM simulations corroborate the experimental findings, reinforcing the critical role of groove geometry in determining filament propagation dynamics. The consistent t^4/5 scaling across all geometries highlights the universal nature of capillary-driven spreading in structured substrates. Additionally, the simulations provide insights into the transient phase dominated by gravitational forces, particularly for high-viscosity fluids like G₁₀₀W₀. The ability to predict filament dynamics through FEM modeling offers valuable opportunities for optimizing grooved substrates in applications requiring precise fluid control, such as microfluidics and surface patterning. These results also emphasize the importance of groove width and spacing as tunable parameters for engineering liquid behavior on structured surfaces.

To analyze the spreading behavior of the droplet under the simultaneous effects of capillarity and gravity at long timescales, the lubrication equation is employed. The governing equation for the film thickness h(x,t) in one dimension, based on the lubrication approximation, is expressed as:

\frac{\partial h}{\partial t} = \frac{\partial}{\partial x} [\frac{h^{3}}{3 μ} (- γ \frac{\partial^{3} h}{\partial x^{3}} - ρ g \frac{\partial h}{\partial x})]

(1)

where, μ is the dynamic viscosity, γ is the surface tension, ρ is the density of the liquid, and g is the gravitational acceleration. The evolution of the spreading length l(t) is of interest, and it is hypothesized that a self-similar solution exists in the long-time regime. To explore this possibility, the film thickness h(x,t) is assumed to take the following self-similar form:

h (x, t) = t^{α} f (ξ)

(2)

where,

ξ = \frac{x}{t^{β}}

. Here, α and β are scaling exponents to be determined, and f(ξ) is a dimensionless profile function that describes the shape of the spreading liquid. The spreading length is related to ξ_f, the front position in the dimensionless coordinates, as l(t) = ξ_f t^β.

Substituting the self-similar form into the lubrication equation, the time derivative becomes:

\frac{\partial h}{\partial t} = α t^{α - 1} f (ξ) - β t^{α - 1} ξ f^{'} (ξ)

(3)

while spatial derivatives transform as:

h_{x} = t^{α - β} f^{'} (ξ), h_{x x} = t^{α - 3 β} f^{(3)} (ξ)

(4)

The flux term q is:

q = \frac{h^{3}}{3 μ} (- γ h_{x x} - ρ g h_{x})

(5)

Substituting into q, the flux becomes:

q = \frac{t^{3 α}}{3 μ} [- γ t^{α - 3 β} f^{3} f^{(3)} - ρ g t^{α - β} f^{3} f^{'}]

(6)

Taking the divergence of q, we have:

(7)

Balancing terms with matching powers of t, the scaling exponents must satisfy: α−1 = 4α−4β (capillarity term balance), α−1 = 4α−2β (gravity term balance).

Additionally, the volume conservation condition requires:

V = \int_{0}^{l (t)} h (x, t) d x = t^{α + β} \int_{0}^{ξ_{f}} f (ξ) d ξ

(8)

from these conditions, solving the system of equations yields: β = 4/5, α = −4/5.

Boundary and Far-Field Conditions:

To ensure a physically consistent solution, boundary and far-field conditions must also be satisfied:

At the spreading front x = l(t), the thickness vanishes, h(l(t), t) = 0. This imposes f(ξ_f) = 0.
In the far field (x→0), the thickness profile h(x, t) must remain finite or decay appropriately to satisfy volume conservation and ensure no unphysical singularities. This translates to requiring a smooth and finite f(ξ) as ξ→0.

These conditions lead to a unique solution for the self-similar function f(ξ), confirming that the spreading length follows the scaling law: l(t) ∼ t^4/5. The 4/5 scaling law reflects the combined influence of capillarity and gravity on the spreading process. At long times, capillarity drives the spreading by pulling the liquid into the surrounding regions, while gravity counteracts this motion by generating a retarding hydrostatic pressure gradient. The balance between these forces determines the rate of spreading, captured by the 4/5 exponent. This result is consistent with observations in systems where spreading is influenced by both surface tension and gravity, such as droplet spreading on structured or inclined surfaces. The derived scaling law is robust and provides a fundamental understanding of the interplay between capillarity and gravity in thin-film flows.

Conclusions

This study systematically investigates the spreading dynamics of glycerol-water droplets on grooved substrates using a combination of experimental observations, finite element simulations, and theoretical analysis. By examining droplets with varying viscosities and surface tensions across structured substrates with different groove geometries, we reveal the intricate interplay between capillarity, viscosity, and gravity in determining liquid filament propagation. The experimental results highlight the critical role of groove width in controlling liquid filament formation and propagation. Narrow grooves provide strong capillary confinement, enabling faster and more extensive filament spreading, while wider grooves reduce capillary forces, limiting filament propagation. The viscosity of the droplet significantly influences the spreading rate, with higher viscosity fluids exhibiting slower dynamics due to increased resistance to flow. Despite these differences, all experiments show a consistent t^4/5 scaling relationship for filament length versus time in the long-time regime, indicating a universal spreading behavior governed by capillarity and viscous forces. Finite element simulations validate these experimental findings and offer further insights into the spreading process. The simulations demonstrate that the groove width and spacing strongly affect filament propagation, with narrower and closer grooves enhancing capillary-driven spreading. The simulations also confirm the t^4/5 scaling behavior across a range of groove geometries, emphasizing the dominant role of capillary forces in the stabilized phase of spreading.

Theoretical analysis based on the lubrication equation provides a fundamental understanding of the spreading behavior. By employing a self-similar solution for the film thickness, we derive the scaling law l(t)∼t^4/5, which reflects the combined effects of capillarity and gravity. At long times, capillary forces pull the liquid outward, driving the spreading process, while gravity introduces a hydrostatic pressure gradient that retards the motion. The balance of these forces produces the observed scaling behavior, consistent with the experimental and simulation results. This theoretical framework not only explains the spreading dynamics on structured surfaces but also provides a robust model for understanding similar phenomena in thin-film flows influenced by capillarity and gravity. The integration of experimental, computational, and theoretical approaches in this study provides a comprehensive understanding of the spreading dynamics of liquid filaments on grooved substrates. The findings underscore the importance of capillarity and viscosity in governing liquid behavior and lay a foundation for future research into more complex systems, such as non-Newtonian fluids or patterned surfaces with hierarchical structures. This work contributes to the broader field of interfacial fluid dynamics, providing insights that are both fundamental and application-driven.

Acknowledgements:

This work was jointly supported by the National Natural Science Foundation of China (NSFC, Grant No. 12202461)

References

Quéré, D. Wetting and roughness. Annu. Rev. Mater. Res. 2008. [Google Scholar]
Bonn, D. , et al. Wetting and spreading. Rev. Mod. Phys. 2009. [Google Scholar]
Hu, J. and Wang, Z.-L. The effect of hygroscopic liquids on the spatial controlling of condensation on low-temperature surfaces. Surf. Interfaces, 2024. [Google Scholar]
Hu, J. , et al. The effect of substrate temperature on the dry zone generated by the vapor sink effect. Phys. Fluids, 2024. [Google Scholar]
Hu, J. and Wang, Z.-L. Crystallization morphology and self-assembly of polyacrylamide solutions during evaporation. arXiv preprint, arXiv:2403.20191 (2024).
Rauscher, M. and Dietrich, S. Wetting phenomena in nanofluidics. Annu. Rev. Mater. Res. 2008. [Google Scholar]
Wang, Z.-L. and Lin, K. The multi-lobed rotation of droplets induced by interfacial reactions. Phys. Fluids, 2023. [Google Scholar]
Wang, Z. , et al. Spontaneous motion and rotation of acid droplets on the surface of a liquid metal. Langmuir, 4379. [Google Scholar]
Wang, Z. , Wang, X., Miao, Q. and Zhao, Y. P. Realization of self-rotating droplets based on liquid metal. Adv. Mater. Interfaces, 2020. [Google Scholar]
Wang, Z. , Lin, K. and Zhao, Y. P. The effect of sharp solid edges on the droplet wettability. J. Colloid Interface Sci. 2019. [Google Scholar]
Xu, Y. , et al. Facet-dependent electrochemical behavior of au–pd core@shell nanorods for enhanced hydrogen peroxide sensing. ACS Applied Nano Materials, 1874. [Google Scholar]
Wang, Z. and Zhao, Y.-P. Wetting and electrowetting on corrugated substrates. Phys. Fluids, 2017. [Google Scholar]
Whitesides, G. M. The origins and the future of microfluidics. Nature, 2006. [Google Scholar]
Stroock, A. D. , Dertinger, S. K., Whitesides, G. M. and Ajdari, A. Patterning flows using grooved surfaces. Anal. Chem. 5312. [Google Scholar]
Walboomers, X. F. and Jansen, J. A. Cell and tissue behavior on micro-grooved surfaces. Odontology, 2001. [Google Scholar]
Weigl, B. , Domingo, G., Labarre, P. and Gerlach, J. Towards non- and minimally instrumented, microfluidics-based diagnostic devices. Lab Chip, 2014. [Google Scholar]
Baret, J.-C. , Decre´, M. M. J., Herminghaus, S. and Seemann, R. Transport dynamics in open microfluidic grooves. Langmuir, 5204. [Google Scholar]
Burns, M. A. , et al. An integrated nanoliter DNA analysis device. Science, 1998. [Google Scholar]
Wang, Z. , Chen, E. and Zhao, Y. The effect of surface anisotropy on contact angles and the characterization of elliptical cap droplets. Sci. China Technol. Sc. 2017. [Google Scholar]
Washburn, E. W. The dynamics of capillary flow. Phys. Rev. 1921. [Google Scholar]
Hu, J. and Wang, Z.-L. Analysis of fluid flow in fractal microfluidic channels. arXiv preprint, arXiv:2409.12845 (2024).
Bico, J. , Thiele, U. and Quéré, D. Wetting of textured surfaces. Colloid. Surface. A, 2002. [Google Scholar]
Olanrewaju, A. , Beaugrand, M., Yafia, M. and Juncker, D. Capillary microfluidics in microchannels: From microfluidic networks to capillaric circuits. Lab Chip, 2347. [Google Scholar]
Extrand, C. W. Model for contact angles and hysteresis on rough and ultraphobic surfaces. Langmuir, 7999. [Google Scholar]
Herminghaus, S. Roughness-induced non-wetting. Europhys. Lett. 2000. [Google Scholar]
Reyssat, M. , Courbin, L., Reyssat, E. and Stone, H. A. Imbibition in geometries with axial variations. J. Fluid Mech. 2008. [Google Scholar]
Darhuber, A. A. , Troian, S. M. and Reisner, W. W. Dynamics of capillary spreading along hydrophilic microstripes. Phys Rev E Stat Nonlin Soft Matter Phys, 2001. [Google Scholar]
Bico, J. and Quéré, D. Falling slugs. J. Colloid Interface Sci. 2001. [Google Scholar]
Krupenkin, T. , Yang, S. and Mach, P. Tunable liquid microlens. Appl. Phys. Lett. 2003. [Google Scholar]
Thiele, U. Structure formation in thin liquid films. (Springer Vienna, 2007).
Redon, C. , Brochard-Wyart, F. and Rondelez, F. Dynamics of dewetting. Phys. Rev. Lett. 1991. [Google Scholar]
Azarkish, H. , et al. Water evaporation phenomena on micro and nanostructured surfaces. Int. J. Therm. Sci. 2015. [Google Scholar]
Herminghaus, S. , Brinkmann, M. and Seemann, R. Wetting and dewetting of complex surface geometries. Annu. Rev. Mater. Res. 2008. [Google Scholar]
Seemann, R. , et al. Wetting morphologies and their transitions in grooved substrates. J Phys Condens Matter, 2011. [Google Scholar]
Mugele, F. and Baret, J.-C. Electrowetting: From basics to applications. J. Phys.: Condens. Matter, 2005. [Google Scholar]
Lomax, D. J. , et al. Ultra-low voltage electrowetting using graphite surfaces. Soft Matter, 8804. [Google Scholar]
Daniel, S. and Chaudhury, M. K. Rectified motion of liquid drops on gradient surfaces induced by vibration. Langmuir, 3407. [Google Scholar]
Weislogel, M. M. and Lichter, S. Capillary flow in an interior corner. J. Fluid Mech. 1998. [Google Scholar]
Ramé, E. and Weislogel, M. M. Gravity effects on capillary flows in sharp corners. Phys. Fluids, 2009. [Google Scholar]
Ledesma-Aguilar, R. , Nistal, R., Hernandez-Machado, A. and Pagonabarraga, I. Controlled drop emission by wetting properties in driven liquid filaments. Nat. Mater. 2011. [Google Scholar]
Oron, A. , Davis, S. H. and Bankoff, S. G. Long-scale evolution of thin liquid films. Rev. Mod. Phys. 1997. [Google Scholar]
Gennes, P. G. , Brochard-Wyart, F. and Quéré, D. Capillarity and wetting phenomena: Drops, bubbles, pearls, waves, 2004. [Google Scholar]
Craster, R. V. and Matar, O. K. Dynamics and stability of thin liquid films. Rev. Mod. Phys. 1198. [Google Scholar]
Afkhami, S. and Bussmann, M. Height functions for applying contact angles to 2d vof simulations. Int. J. Numer. Methods Fluids, 2007. [Google Scholar]
Yue, P. and Feng, J. J. Wall energy relaxation in the cahn–hilliard model for moving contact lines. Phys. Fluids, 2011. [Google Scholar]

Figure 1. The setup used for the liquid filaments propagation caption. The droplets is deposited on the grooved surface with a syringe pump. The structure parameter of the grooves including grooves width L₁, spacing width L₂, and grooves depth H are shown. .

Figure 2. Wetting and spreading behavior of glycerol-water mixtures on SU-8 substrates with varying groove widths. (a) Static contact angles of G₅₀W₅₀, G₇₀W₃₀, and G₁₀₀W₀ mixtures on SU-8 photoresist. The contact angles decrease slightly with increasing glycerol content due to reduced surface tension, with values of 76.2°, 68.3°, and 57.5°, respectively. (b-d) Spreading behavior of G₅₀W₅₀ (b), G₇₀W₃₀ (c), and G₁₀₀W₀ (d) within grooves of 8 µm (first row), 16 µm (second row), and 32 µm (third row) widths. Liquid filaments form in grooves with widths of 8 µm and 16 µm for all liquids, while no filament formation is observed at 32 µm groove width. The diminishing capillary confinement with increasing groove width highlights the critical role of geometric confinement in sustaining liquid filaments.

Figure 3. Dynamic wetting and spreading behavior of glycerol-water mixtures within grooved substrates of varying widths. (a, b) Spreading progression of G₅₀W₅₀ in grooves with widths of 8 µm (a) and 16 µm (b). The liquid filament propagates approximately 3 mm in 5.6 seconds for 8 µm grooves and in 28.8 seconds for 16 µm grooves, illustrating slower propagation with increasing groove width. (c, d) Spreading progression of G₇₀W₃₀ in 8 µm (c) and 16 µm (d) grooves. In 8 µm grooves, the filament propagates 3 mm in 22.4 seconds, while in 16 µm grooves, the length is less than 2 mm after 28 seconds, confirming reduced spreading speed for wider grooves and higher viscosities. (e-g) Logarithmic plots of filament length versus time for G₁₀₀W₀ (e), G₇₀W₃₀ (f), and G₅₀W₅₀ (g). All solutions exhibit a l~t^4/5 scaling relationship in the stabilized phase. Higher viscosities result in slower spreading, while gravitational effects dominate the early stages, accelerating flow. The results emphasize the interplay of groove width, viscosity, and capillary forces in determining filament propagation dynamics.

Figure 4. Dynamic spreading behavior of glycerol-water mixtures on substrates with gradient groove widths. (a) Spreading progression of a 5 µL G₁₀₀W₀ droplet from 0 to 9 seconds. Filaments form after 0.8 seconds and propagate up to 1 mm within 9 seconds. Narrower grooves produce longer filaments, creating a gradient effect. (b, c) Magnified images of filament formation for G₁₀₀W₀ (b) and G₅₀W₅₀ (c). The differences in filament length across grooves (C1–C12, corresponding to widths of 8–24 µm) are more pronounced for G50W50 due to its lower viscosity. (d–f) Filament length versus time for G₁₀₀W₀ (d), G₇₀W₃₀ (e), and G₅₀W₅₀ (f). Narrow grooves exhibit faster spreading, with slower deceleration for lower-viscosity solutions. (g–i) Logarithmic plots of filament length versus time for G₁₀₀W₀ (g), G₇₀W₃₀ (h), and G₅₀W₅₀ (i), showing a consistent l ~ t^4/5 scaling relationship across all groove widths in the stabilized phase.

Figure 5. Finite element simulation results of liquid filament spreading on grooved substrates. (a) Simulation model (first panel) and time sequence of filament spreading for G100W0 from 0 s to 8 s, at 1-second intervals. The model replicates experimental conditions, showing filament formation after 1 s and progressive elongation over time. (b–e) Simulated filament front position as a function of time for different groove geometries: L_1-1−L_2-1 (b), L_1-1−L_2-0.5 (c), L_1-0.5−L_2-0.5 (d), and L_1-0.5−L_2-0.25 (e). All plots use logarithmic scales, demonstrating a consistent t^4/5 scaling law across configurations. Narrower grooves and smaller spacing enhance capillary confinement, resulting in faster filament propagation. These simulations validate the experimental findings and provide a deeper understanding of the interplay between capillary and viscous forces in structured microenvironments.

Table 1. Dimensions and geometric parameters of equal-width groove structures.

Sample	L₁ (μm)	L₂ (μm)	H (μm)	RA
1	8	8	15	0.210
2	16	16	15	0.348
3	32	32	15	0.516

Table 2. Dimensions and geometric parameters of variable-width groove structures.

Channel	1	2	3	4	5	6	7	8	9
L₁ (μm)	16	18	20	22	24	26	28	30	32
L₂ (μm)	8	10	12	14	16	18	20	22	24
H (μm)	15	15	15	15	15	15	15	15	15
RA	0.348	0.375	0.4	0.423	0.444	0.464	0.483	0.5	0.516

Table 3. The parameters of solutions with different mixed ratio of glycerol and DI water.

Sample	Density (g/cm³)	Viscosity (mPa·s)	Surface tension (mN/m)	Contact angle (°)
G₁₀₀W₀	1.297	1410	64.0	76.2
G₇₀W₃₀	1.208	22.5	66.2	68.3
G₅₀W₅₀	1.149	6	68.3	57.5

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.