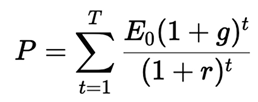Empirical Validation of the PPP–SIRRIPA Framework: A Groundbreaking Approach to Equity Valuation

1. Introduction

Because the traditional P/E ratio ignores the time value of money, earnings growth, and risk, it provides limited insight into the dynamics of equity valuation. The PPP–SIRRIPA framework addresses these shortcomings by translating equity valuation into the same analytical structure used in fixed-income valuation. The PPP extends the P/E ratio by integrating growth, discounting, and risk; SIRR translates this into an intrinsic annualized return; and SIRRIPA represents the corresponding total annualized return including repricing—analogous to a bond’s realized IRR, while explicitly adjusting for the higher risk inherent in equity.

This paper complements the author’s earlier SSRN publication, “SIRRIPA — A Groundbreaking Return Metric to Value Stocks Just Like Bonds // Bringing Bond-Like Precision and Risk Rationality to Equity Valuation” (July 21, 2025), by further formalizing the conceptual mapping between stocks and bonds and by providing a first empirical validation of a model introduced only a year ago.

Of particular note is the framework’s unique ability to explain:

• Why Wall Street can continue to rise even when the average P/E ratio, PEG ratio, or earnings yield suggests overvaluation;

• Why high-growth firms such as Palantir can sustain extremely high P/E ratios; and

• How temporarily loss-making companies such as Intel can retain attractive intrinsic value when the P/E ratio is inapplicable.

Because explanatory coherence underpins predictive power, this emerging empirical record strengthens the legitimacy of PPP–SIRRIPA as the next step in equity valuation techniques.

2. The PPP Framework

2.1. Conceptual Underpinning

The PPP methodology employs a thought experiment: assume that all future earnings of a company are hypothetically distributed, discount them at an appropriate risk-adjusted rate, and ask how many years are required until the sum equals today’s share price. This assumption of full distribution is purely a valuation device—it does not require actual dividend payments. It allows the earnings stream to be treated as a realizable cash-flow equivalent, analogous to bond coupons.

2.2. PPP Formula

$$\boxed{PPP={\displaystyle \frac{\mathrm{l}\mathrm{o}\mathrm{g}(\frac{P/E\times (g-r)}{1+r}+1)}{\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{1+g}{1+r}\right)}}}$$

where:

• ${\displaystyle \frac{P}{E}}$= current price-to-earnings ratio
• $g$= expected earnings growth rate (as a percentage)
• $r$= discount rate (risk-adjusted) (as a percentage)

This formula yields the number of years required for discounted future earnings to conceptually "pay back" the current price.

3. SIRR as the Equity Analogue of Zero-Coupon Bond Yield

3.1. Zero-Coupon Bond Benchmark

For a zero-coupon bond:

$$P={\displaystyle \frac{F}{(1+y{)}^T}}$$

where $F$ is face value, $y$ is the yield-to-maturity, and $T$ is maturity. The YTM thus represents a pure IRR with no intermediate cash flows.

3.2. SIRR Definition

Once PPP is known, define:

$$\boxed{SIRR=2^{{\displaystyle \frac{1}{PPP}}}-1}$$

SIRR is the annualized internal rate of return implied by the PPP horizon. It captures the intrinsic earning-power return of the stock, independent of any market price revaluation.

3.3. Structural Equivalence

The zero-coupon bond’s return arises from accretion toward face value; similarly, SIRR arises from accretion of value through earnings accumulation. Thus:

$$\boxed{\mathrm{SIRR}\hspace{0.25em} ⟷\hspace{0.25em} \mathrm{Zero}\text{-}\mathrm{coupon} \mathrm{YTM}}$$

Note: although PPP supposes hypothetical full dividend distribution, SIRR itself does not rely on actual payouts, mirroring the no-coupon nature of a zero-coupon bond.

4. SPARR—Stock Price Appreciation Rate of Return

$$SPARR\approx {\left({\displaystyle \frac{\mathrm{Discounted} \mathrm{Exit} \mathrm{Price}}{\mathrm{Present} \mathrm{Price}}}\right)}^{{\displaystyle \frac{1}{PPP}}}-1$$

SPARR isolates the component of return attributable exclusively to valuation multiple changes (for example, P/E expansion or contraction). It is analogous to price-gain or multiple-expansion returns in fixed-income.

5. SIRRIPA—Total Annualized Return Including Price Appreciation

5.1. Definition

The total annualized return that combines intrinsic earnings return and market repricing return is given by:

$$\boxed{\left(1+\mathrm{SIRRIPA}\right)=\left(1+\mathrm{SIRR}\right)\hspace{0.25em} \left(1+\mathrm{SPARR}\right)}$$

5.2. Interpretation

SIRRIPA is therefore the investor’s realized annualized IRR, analogous to the realized IRR of a bond investment when price changes (capital gains/losses) are included.

6. Stock–Bond Return Equivalence

6.1. Decomposition

Bonds:

• Intrinsic return → YTM
• Repricing return → capital gains/losses
• Total realized return → Realized IRR

Stocks (via PPP):

• Intrinsic return → SIRR
• Repricing return → SPARR
• Total realized return → SIRRIPA

6.2. Key Identity

$$\boxed{\mathrm{SIRR} : \mathrm{SIRRIPA}=\mathrm{YTM} : \mathrm{Realized} \mathrm{IRR}}$$

The relationship between SIRR and SIRRIPA is analogous to the relationship between YTM and Realized IRR.

This succinct statement clarifies that SIRR plays for equities the same role that YTM plays for zero-coupon bonds, while SIRRIPA plays the role of a bond’s realized return including all price changes.

7. Zero-Coupon–Based Valuation Logic for Equities

A central insight of the PPP–SIRRIPA framework is that equity valuation can be expressed using the same mathematical logic as a zero-coupon bond, provided earnings are treated as a fundamental economic resource analogous to the redemption value of a bond. This section formalizes that analogy and clarifies the role of the full-distribution assumption.

7.1. Conceptual Motivation

A zero-coupon bond is valued as the discounted value of a single future payoff—its face (redemption) value. Because the investor receives no intermediate coupons, the yield-to-maturity (YTM) of a zero-coupon bond is a pure internal rate of return, summarizing the implied annual return from purchase to maturity.

In the PPP framework, the investor is assumed to receive the full stream of future earnings. This is not meant to describe an actual payout policy. Rather, it allows earnings to be treated as if they were fully distributable, thereby capturing a stock’s earning power in a form analogous to the contractual payoff of a zero-coupon bond.

The key idea is that the discounted sum of future earnings over PPP years equals the current price—just as the discounted maturity value of a zero-coupon bond equals its current price. Thus, PPP measures the time needed for earnings to “pay back” the price, mirroring the concept of maturity in bond pricing.

7.2. Zero-Coupon–like Valuation Logic

Let P be price, g the earnings growth rate, and $r$ the discount rate. The PPP solves for the period T such that:

This is mathematically equivalent to computing the time at which the present value of all future benefits equals the price paid—identical in spirit to zero-coupon logic, except that the future payoff is not a single amount but a compounded earnings stream.

When g = r = 0, the expression collapses to:

$$PPP={\displaystyle \frac{P}{E}}={\displaystyle \frac{P}{E_0}}$$

i.e., the traditional P/E ratio.

Thus, the P/E ratio is a special, degenerate case of the PPP, just as a zero-coupon bond with a flat yield curve collapses to the face-value/price relationship.

7.3. Why Full Earnings Distribution Is Assumed

The full-distribution assumption is central to the zero-coupon analogy. It serves two conceptual purposes:

• Measurement of earning power
  It isolates the company’s capacity to generate economic value from discretionary payout policies. The ability to convert earnings into distributable value is fundamental to valuation.
• Constructing a theoretical maturity structure
  Full distribution allows future earnings to be aggregated into a cumulative value stream, enabling the computation of a time period (PPP) at which the investor “recovers” the purchase price.

This assumption is not normative—companies need not actually distribute all earnings. Rather, it is a valuation convention that allows earnings to stand in for the payoff of a zero-coupon bond.

7.4. Deriving SIRR: The Zero-Coupon Yield

The PPP period T enables the definition of an annualized implied return:

$$SIRR=2^{{\displaystyle \frac{1}{PPP}}}-1$$

This is mathematically analogous to extracting the YTM from the time required to double one’s investment for a zero-coupon bond.

Thus:

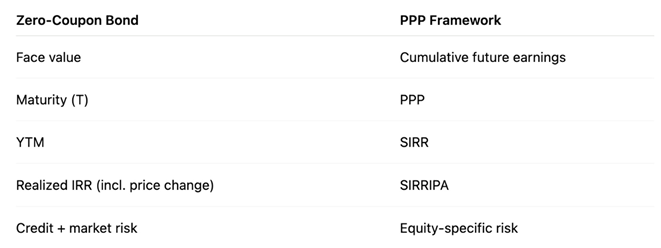
• PPP ↔ maturity
• SIRR ↔ YTM

The conceptual symmetry is exact: both SIRR and YTM translate the time required to recover the invested capital (through earnings or redemption value, respectively) into a constant annualized return.

7.5. Equity vs. Zero-Coupon Bond: The Role of Risk

The analogy between SIRR and YTM remains valid only if their risk levels have been appropriately reconciled. In the PPP framework, risk enters through the discount rate $r$, which is typically determined via CAPM. Thus, while a zero-coupon bond yield compensates for credit risk, duration risk, and inflation expectations, SIRR incorporates equity-specific risk, including business risk and market volatility.

This risk adjustment ensures comparability:

A stock’s SIRR is the equity-risk-adjusted analogue of a zero-coupon bond’s YTM.

7.6. Interpretation: Why It Works

This zero-coupon interpretation works because:

• Earnings represent the fundamental economic source of return.
• Discounting and growth reproduce the time-value structure of bond pricing.
• The cumulative earnings “repay” the investment at time PPP, just as the face value repays the bond at maturity.
• SIRR annualizes the earning power into a single return metric equivalent to YTM.

This abstraction reveals that equity, despite its uncertain cash flows, can be mapped to a fixed-income valuation structure once earnings growth and risk are incorporated.

7.7. Summary of Key Equivalences

7.8. Implication

The zero-coupon interpretation is the cornerstone that enables the broader mapping:

$$\mathrm{SIRR} : \mathrm{SIRRIPA}=\mathrm{YTM} : \mathrm{Realized} \mathrm{IRR}$$

It is the mechanism by which equity valuation can be reconceived within a fixed-income analytical frame—something no traditional equity metric (P/E,PEG,earnings yield) can achieve

This reinterpretation underlies the unified valuation language of the PPP–SIRR–SPARR–SIRRIPA framework.

8. Implications for Valuation and Portfolio Management

• Cross-Asset Comparability

Since SIRR is directly comparable to YTM, equities and bonds can be evaluated on a common internal-rate-of-return basis.

2.

Performance Attribution

The decomposition into SIRR (business performance) and SPARR (valuation change) enables clear attribution and separates fundamentals from market sentiment.

3.

Risk Management

The SPARR component isolates valuation-gain risk, aiding portfolio managers in allocating exposure between business-value return and valuation-re-rating return.

4.

Valuation Discipline

Unlike traditional P/E or PEG metrics, PPP embeds growth, discounting, and risk in one horizon-based formula, aligning equity valuation with IRR-based thinking.

9. Empirical Validation—The First Evidence

Although only one year old, the SIRRIPA approach has already been tested in several published analyses. Five cases published earlier (regarding the S&P 500, Palantir, NVIDIA, Intel, and the overall continuation of the bull market) were examined ex post using October-2025 prices. In every case, the PPP–SIRRIPA framework:

• Explained valuation outcomes that traditional metrics could not, and
• Correctly anticipated the subsequent price direction.

Traditional valuation models (P/E, PEG, earnings yield) failed to resolve these cases; PPP–SIRRIPA did.

Thus, initial empirical evidence shows predictive alignment. This is significant: explanatory accuracy is logically prior to predictive power. The PPP–SIRRIPA framework explains these episodes not as irrational anomalies, but as consistent with fundamental earning-power logic. Therefore, its success in forecasting return direction is unsurprising.

This preliminary record reinforces PPP–SIRRIPA not only as a theoretically coherent model but as one with emerging empirical credibility.

10. Conclusion

PPP–SIRRIPA provides:

• A consistent means to evaluate profitable, high-growth, or loss-making firms;
• A unifying structure for comparing equities and fixed income;
• A more complete earnings-based return measure than P/E, PEG, or earnings yield.

The model’s explanatory capability—the ability to rationalize outcomes that traditional indicators label “irrational”—is foundational. Its empirical success follows naturally from this explanatory power.

Because the PPP–SIRRIPA framework:

• Generalizes the P/E ratio;
• Integrates growth, discounting, and repricing;
• Aligns equities and bonds under a unified language of intrinsic and realized return;

It offers a uniquely coherent perspective on stock valuation. Early evidence supports its potential to supersede traditional metrics both in professional practice and academic finance.