Pedigree-Based Assessment of Inbreeding Effects on Conformation and Performance Traits in the Peruvian Paso Horse: Implications for Sustainable Genetic Improvement

Jorge Vilela; Paola Quintana; Maria Lourdes Velarde; José Dextre

doi:10.20944/preprints202510.2411.v1

Submitted:

30 October 2025

Posted:

30 October 2025

You are already at the latest version

Abstract

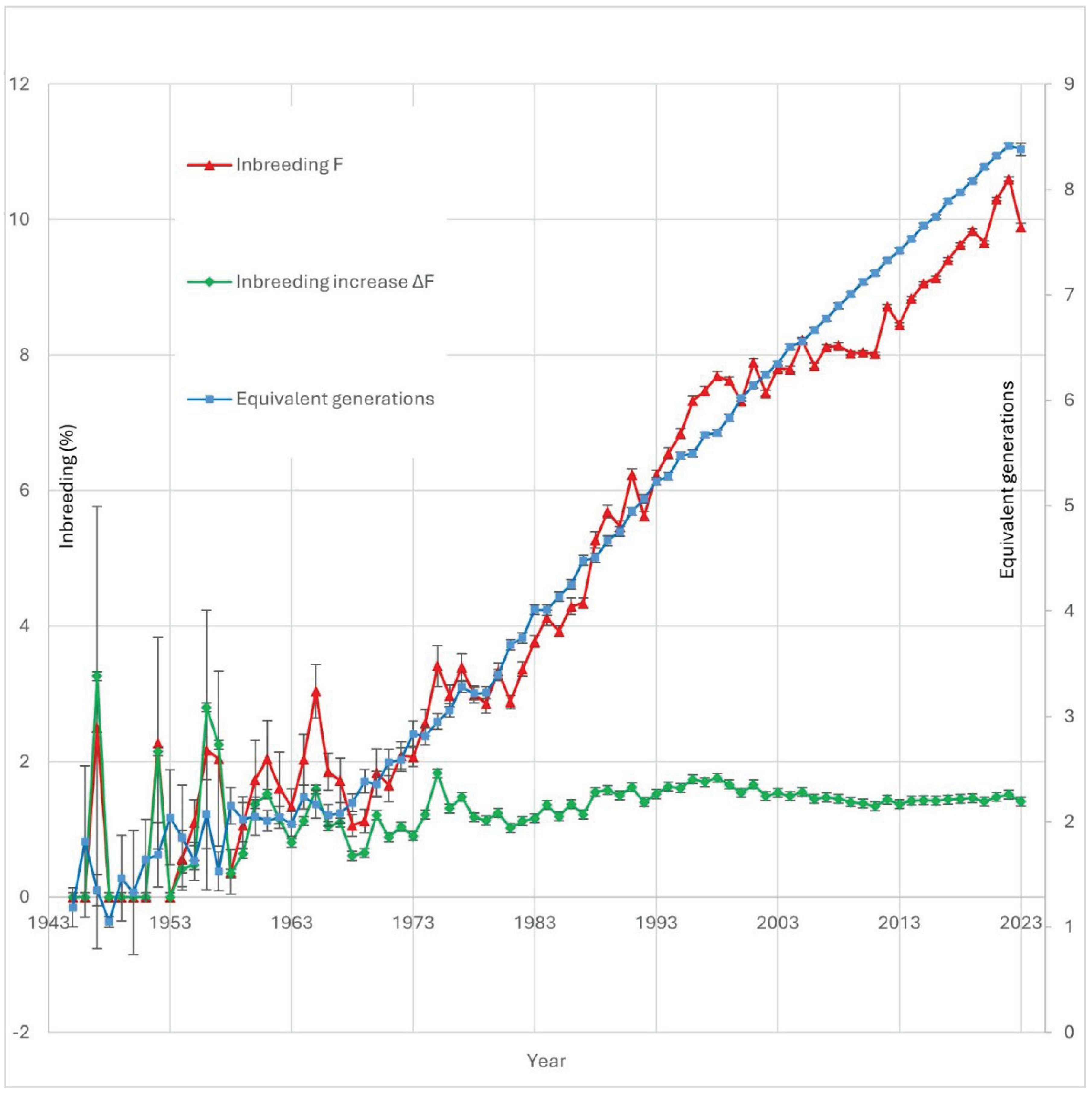
Objective: The aim of this study was to analyze inbreeding depression in the Peruvian paso horse (PPH), with a focus on its effects on morphometric, physiological, and functional traits. Methods: A total of 35 traits were evaluated in 148 animals, using pedigree records up to 2023 provided by the National Association of Breeders and Owners of the PPH. Multivariate animal models were employed to estimate heritability, and a Best Linear Unbiased Prediction (BLUP) model was applied to calculate estimated breeding values (EBVs), accounting for fixed effects including sex, stud farm, gait speed, and age. Results: The findings indicate that both the inbreeding coefficient (F) and its rate of change (ΔF) have significant effects on multiple traits. Pedigree analyses revealed that both parents recorded for over 94% of animals, indicating good pedigree depth. Certain historical periods were identified as having reduced ancestral diversity, highlighting the importance of monitoring genetic diversity to prevent population bottlenecks. The number of equivalent complete generations ranged from 2.355 to 8.417 between 1970 and 2023. Inbreeding exerted a negative impact on key traits such as withers height and scapulo-humeral angle. Furthermore, ΔF demonstrated a more immediate and pronounced effect on specific traits. Notably, differential impacts were observed between F and ΔF. Correlations between EBVs calculated with and without inclusion of inbreeding as a covariate were significantly below 0.99 for certain traits, suggesting that inbreeding introduces estimation bias, likely due to the expression of recessive deleterious alleles. Conclusions: Our results demonstrate that inbreeding affects not only linear body measurements but also anatomical angles, potentially reflecting the influence of pleiotropic genes affecting multiple morphological traits. Moreover, functional and physiological traits were found to be particularly sensitive to inbreeding effects, underscoring the need for strategic genetic management in this breed.

Keywords:

peruvian horse

;

inbreeding depression

;

genetic diversity

;

breeding value

Subject:

Biology and Life Sciences - Animal Science, Veterinary Science and Zoology

Introduction

The Peruvian paso horse (PPH) is a breed distinguished by its unique four-beat lateral gait, originating from horses brought to Peru during the Spanish conquest beginning in 1532. Today, this breed holds considerable international relevance, with active breed associations established in countries such as Argentina, Panama, other Central American nations, Ecuador, Canada, and the United States [1,2]. However, it faces significant genetic challenges related to declining genetic diversity and inbreeding depression, which may substantially affect conformation and performance traits.

Inbreeding depression refers to the reduction in biological fitness and phenotypic performance resulting from mating between related individuals, leading to increased homozygosity and the expression of recessive deleterious alleles [3,4]. Although inbreeding has historically been employed to fix desirable traits, it is now critically important to monitor its levels to preserve genetic variability and ensure the sustainable genetic improvement of the breed [2].

There remains a notable gap in understanding the specific impact of inbreeding depression in the PPH. While studies exist in other breeds, such as the Old Kladruber, Purebred Spanish Horse, and Campolina, their findings are not directly transferable due to genetic and selection differences [5,6,7]. In Ecuadorian PPH populations, Larrea et al. [2] reported average inbreeding coefficients as high as 8.11% and effective population sizes below 50 and Montenegro et al. [8] found values of 5.44%. These figures suggest a loss of genetic variability attributable to historical bottlenecks and genetic drift. Nevertheless, the quantitative effect of inbreeding on productive or functional traits in the PPH has not yet been assessed. This study aimed to address this gap in knowledge by analyzing the impact of inbreeding on genetic variability and morphometric, physiological, and functional traits.

Mitigating inbreeding depression is essential for the sustainable development of the PPH. Linear regression models, widely used in quantitative genetics, relate inbreeding coefficients to phenotypic traits while incorporating environmental covariates, thereby improving estimation accuracy by isolating genetic effects [9,10]. The rate of inbreeding (ΔF) is preferably employed over the absolute inbreeding coefficient (F), as it provides a more dynamic and precise indicator for managing genetic diversity [11,12]. The impact of inbreeding can also be evaluated through its effect on estimated breeding values (EBVs), which reflect the genetic merit of an individual and its relatives [13]. Comparing EBVs calculated with and without adjustment for inbreeding enables quantification of its negative effect on performance [14,15]. Incorporating correlations between adjusted and unadjusted EBVs into genetic models enhances understanding of inbreeding depression and informs mitigation strategies within breeding programs.

By evaluating levels of inbreeding and their phenotypic consequences through advanced genetic modeling, this study will provide critical insights for breeders and geneticists. It will facilitate the development of strategies to preserve genetic diversity, enhance performance, and maintain the quality of the PPH, while also serving as a model for the conservation and improvement of other equine breeds. Therefore, the objectives of this research are: 1) To analyze the rate of inbreeding accumulation in registered PPH individuals; 2) To evaluate its effect on morphometric, functional, and physiological traits; and 3) To determine the correlation between EBVs estimated with and without adjustment for inbreeding.

Material and Methods

Animals and Pedigree

All the data and measurements for each animal were collected between October 2021 and March 2023. All animal handling and procedures were conducted in strict accordance with animal welfare principles, ensuring no harm was caused, and were approved by the Institutional Ethics Committee for Animal and Biodiversity Research at the Universidad Científica del Sur (Approval Code: 029-2022-PRO99). Written informed consent was obtained from all owners prior to data collection.

This study compiled genealogical records of all registered PPH up to the year 2023, provided by the Asociación Nacional de Criadores y Propietarios del Caballo Peruano de Paso (ANCPCPP). A systematic and thorough review of the database was performed using a custom-designed template in .xlsx format. Individual records, including those of each animal, its sire and dam, were extracted and compiled into a pedigree file for subsequent analysis to estimate individual inbreeding coefficients (F) and individual rates of inbreeding accumulation (ΔF).

Animals whose parents were recorded with duplicate names, lacked registration numbers, or presented identification errors were excluded from the final dataset. A total of 40,993 animals were included in the final pedigree file. A total of 151 animals were phenotyped for this study.

ENDOG v4.8 software was used to calculate individual F and individual ΔF [16]. The annual increase in the rate of inbreeding was estimated as the mean and standard deviation, alongside the average number of equivalent complete generations per year. The mean age of phenotyped animals was 8.02 ± 2.56 years.

Traits

A total of 35 traits were evaluated in this study. A full description of all the traits is provided in Supplementary Material. Animals for which certain traits could not be measured were excluded from the corresponding regression models; consequently, the sample size varied across individual regression analyses.

Measurements

Withers height, croup height, sub-pectoral height, and mid-dorsal height were measured using an aluminum hippometer with a leveling device (NC Equine, UK). Thoracic girth, metacarpal circumference, metatarsal circumference, forelimb pastern perimeter, and hindlimb pastern perimeter were recorded using a flexible measuring tape (SUMVIBE model, Tape 3M-3Y, USA). Angular measurements, including back inclination angle, hock angle, coxofemoral angle, scapulohumeral angle, femorotibial angle, and brachial angle, were obtained using a digital goniometer (GemRed Model 82305, USA). All angular measurements were taken three times per animal, and the arithmetic mean was used for subsequent analyses. Linear measurements, including upper arm length, chest width, femur length, metacarpal length, metatarsal length, croup length, croup width, neck length, body length, and head length, were recorded using a 5-meter retractable tape measure (Stanley Black & Decker, USA). Forelimb and hindlimb pastern lengths were measured using a digital electronic caliper (Ubermann, Germany).

Functional traits, overreach, extension, term, acuteness and vertical acceleration, were obtained via video recording of each animal performing the paso llano gait, led by a handler over a distance of 50-meters at speeds between 2.5 and 4.0 m/s. Recordings were made using a smartphone camera (Motorola Edge 30 Fusion, USA) with a resolution of 1920 × 1080 pixels at 60 frames per second. The camera was mounted on a professional tripod (Benro T980, USA) positioned 1.3 m above ground level, spatially aligned along the X, Y, and Z axes, and placed perpendicular to the animal’s direction of motion at a distance of approximately 12 m. Lateral motion was recorded for all traits except term, for which frontal recording was used.

Reference anatomical landmarks were marked with 4 × 4 cm adhesive tape to facilitate motion tracking. All videos were stored in MP4 format and processed using Kinovea software, version 0.9.5 (Free Software Foundation, Inc., Boston, MA, USA; http://www.kinovea.org/). Overreach, extension, acuteness and term were measured 3 to 5 times (once per stride), and the arithmetic mean was used for correlation analyses with other recorded traits. For correlations among functional traits themselves, all the repetitions observed were included.

Vertical acceleration was recorded continuously throughout the lateral displacement of each animal, with measurements captured every 15 ms. A 10-cm adhesive tape strip, placed parallel to the ground on the ribcage side facing the camera, served as the spatial calibration reference. All frames recorded during the paso llano gait were processed through a two-pass Butterworth filter to reduce image noise. Vertical acceleration values (m/s²) were averaged using the root mean square (RMS) formula:

R M S = \sqrt{\sum \frac{a_{i}^{2}}{n}}

, where a_i = individual vertical acceleration value, and n = number of observations during the gait cycle.

Gluteal temperature difference and maximum gluteal temperature difference were measured using an infrared thermal camera HTI-19, resolution: 320 × 240 pixels, 300k px, emissivity coefficient: 0.95 (Dongguan Xintai Instrument Co., Ltd., China), positioned 20 cm from the animal’s surface, in accordance with the manufacturer’s guidelines. Temperatures (°C) were recorded before and after performance of the paso llano gait, under identical environmental and solar positioning conditions. The final temperature difference was used for statistical analysis.

Genetic and Statistical Analysis

For the estimation of heritability values for the traits, two models were considered, following the approach described by Vilela et al. [1]. A multivariate repeated measures animal model was applied to the functional traits of overreach, extension, term and acuteness (Model A). For all other traits, a standard multivariate animal model was used (Model B). Model A is expressed as follows:

Y_{i j k} = μ + {{S e x}_{i} + A n i m a l}_{j} + {{H o r s e}_{k} + e}_{i j k}

, where

Y_{i j}

is the phenotypical value of each trait, µ mean of population,

{S e x}_{i}

effect fixed of sex (2 levels);

{A n i m a l}_{j}

the random effect of the animal

~ N D (0, A σ_{a}^{2}), A

represent the matrix numerator of relationship between animals and

σ_{a}^{2}

the additive variance;

{H o r s e}_{k}

is the random effect of the k^th measurement of the animal (3 to 5 levels)

~ N D (0, I σ_{p e}^{2}),

where I is the identity matrix,

σ_{p e}^{2}

is the permanent environment variance, and

e_{i j k}

residual random effect

~ N D (0, I σ_{e}^{2})

. Model B is identical to Model A, except that the random effect of

{H o r s e}_{k}

is not considered.

To assess the effect of inbreeding on animal performance, 151 stallions and mares were phenotyped across 35 morphometric, functional, and physiological traits. Records from animals with questionable data or missing measurements were excluded from the analyses on a trait-by-trait basis. Of these, between 88 and 148 animals (depending on trait completeness) were analyzed using a linear regression model, with specific model structures applied according to trait type.

For morphometric traits, the following model was applied:

Y_{i j k l m n} = a + E_{i} b_{1} + S_{j} b_{2} + A_{k} b_{3} + C_{l} b_{4} + F_{m} b_{5} + e_{i j k l m n}

For functional traits, the following model was applied:

Y_{i j k l m n o} = a + E_{i} b_{1} + S_{j} b_{2} + A_{k} b_{3} + C_{l} b_{4} + F_{m} b_{5} + {V_{o} b_{6} + e}_{i j k l m n o}

Where Y_jklmno, represents the measured trait, E_i = age, S_j = sex, A_k = year of birth, C_l = stud farm, F_m inbreeding coefficient or rate of inbreeding (ΔF), V_o = covariate of gait speed and e_jklmno = residual effect. The b coefficients represent the covariability coefficients for each trait.

For the estimation of the EBVs of each animal, the Best Linear Unbiased Prediction (BLUP) model was applied. EBV estimation was carried out using six different models. Models 1, 2, and 3 were applied to morphometric traits, while models 4, 5, and 6 were applied to physiological and functional traits. The general animal model is as follows:

y = X β + Z u + e

, where y is the vector of observations, X is the design matrix for random effects, β is the vector of fixed effects, Z is the design matrix for random effects, , u is the vector of additive genetic effects (u ~ N (0, Aσ²ₐ)), and e is the vector of residual errors (e ~ N (0, Iσ²ₑ)). The BLUP equations are derived by maximizing the likelihood under the mixed model framework. Solutions for

\hat{β}

(fixed effects) and

\hat{u}

(EBV) are obtained by solving:

[\binom{X' X}{Z' X} \binom{X' Z}{Z^{'} Z + A^{- 1} λ}] [\binom{\hat{β}}{\hat{μ}}] = [\binom{X' y}{Z' y}]

Where: λ = σ²ₑ / σ²ₐ: Variance ratio (residual to additive genetic) and A⁻¹: Inverse of the genetic relationship matrix A. The models are specified below:

Model 1: y_ijk=μ+Sex_i+Breeder_j+b₁⋅Age_k+u_k+e_ijk

Model 2: y_ijk=μ+Sex_i+Breeder_j+b₁⋅Age_k+b₂⋅F_k+u_k+e_ijk

Model 3: y_ijk=μ+Sex_i+Breeder_j+b₁⋅Age_k+b₃⋅ΔF_k+u_k+e_ijk

Model 4: y_ijk=μ+Sex_i+Breeder_j+b₄⋅Speed_k+b₁⋅Age_k+u_k+e_ijk

Model 5: y_ijk=μ+Sex_i+Breeder_j+b₄⋅Speed_k+b₁⋅Age_k+b₂⋅F_k+u_k+e_ijk

Model 6: y_ijk=μ+Sex_i+Breeder_j+b₄⋅Speed_k+b₁⋅Age_k+b₃⋅ΔF_k+u_k+e_ijk

Where μ: Overall mean, Sex_i: Fixed effect of sex, Breeder_j: Fixed effect of the breeding farm (or breeder), b₁⋅Age_k: Fixed effect of age as a continuous covariate, where b₁ is the regression coefficient and Age_k is the age of animal k, b₂⋅F_k: Fixed effect of inbreeding coefficient F as a continuous covariate, where b₂ is the regression coefficient and F_k is the inbreeding coefficient of animal k, b₃⋅ΔF_k: Fixed effect of individual inbreeding increase ΔF as a continuous covariate, where b₃ is the regression coefficient and ΔF_k is the inbreeding increase of animal k, b₄⋅Speed_k: Fixed effect of speed as a continuous covariate, where b₄ is the regression coefficient and Speed_k is the speed value for animal k, u_k: Random additive effect of animal k where u∼N(0, A

σ_{a}^{2}

), e_ijk: Residual error, where e∼N(0,I

σ_{e}^{2}

).

To assess the association between EBVs with and without inclusion of the inbreeding effect, Pearson and Spearman correlation analyses were performed. The significance of differences between correlation coefficients was determined using Fisher’s z statistic, comparing against a reference value corresponding to 99% correlation in all cases. Genetic parameter estimation was carried out using the software Wombat (Wombat, Armidale, Australia), and linear regression analyses were conducted using JASP (JASP 0.19, Amsterdam, Netherlands). A significance level of 0.05 was used for all analyses.

Results

Descriptive Analysis of Morphometric, Physiological, and Functional Traits

Thirty-five traits were analyzed in the PPHs studied (148 valid records; 3 discarded), including measurements of angles, body lengths, and perimeters. Table 1 summarizes the descriptive statistics and normality (Anderson-Darling test): most traits were normally distributed (p > 0.05), with a few exceptions (p < 0.001). Heritability estimates (h²) and their standard errors were also obtained using animal models.

Pedigree Structure and Population Genetic Parameters

The total population in the pedigree (40,993 animals) comprised 39.2% males and 60.8% females; in the phenotyped subpopulation (151 individuals), 22.5% were males and 77.5% females (Table 2). In the total population, both parents recorded in more than 94% of animals; in the phenotyped group, this figure was 100%, indicating higher pedigree accuracy in this subset. Average inbreeding was 6.74% (total population) and 9.02% (phenotyped group), with a similar annual increase (~1.4%). The average relatedness coefficient indicates a high level of genetic relationship. The total population spans 5.75 generations, whereas the phenotyped group spans 7.70 generations. A total of 1,758 and 310 founders were identified, respectively; however, only 27 and 17 founders effectively contributed (f_e), and even fewer as the effective number of ancestors (fa: 18 and 11), revealing a strong dependence on a small number of individuals in the genetic base.

Wright’s fixation indices indicate a genetically homogeneous structure: the Fixation Index within subpopulations (FIS) was 0.025 for the total population and 0.0265 for the phenotyped population, reflecting a slight excess of homozygosity within subpopulations. The Fixation Index among subpopulations (FST) was nearly zero (<0.002), revealing that almost all genetic variation was due to individual differences, with high gene flow. The Fixation Index for the total population (FIT) (0.0266) confirmed that overall inbreeding is primarily driven by FIS and not by differentiation among subpopulations. The average age at which individuals first become parents (A_p) was 9.30 years (total population) and 5.28 years (phenotyped). Regression of A_p on F shows negative coefficients: β = -5.20 (total) y β = -38.48 (phenotyped), suggesting that higher inbreeding is associated with earlier reproduction, particularly in the phenotyped subpopulation. However, given the magnitude of these estimates, a nonlinear model or the inclusion of additional covariates may be necessary to better capture this relationship.

Analysis of Inbreeding, Temporal Trends, and Genetic Impact

Average inbreeding showed significant fluctuations throughout the period evaluated. Values ranged from 0% to 10.2%, with notable peaks in specific years. Figure 1 displays the annual trends for the inbreeding coefficient F, ΔF and Equivalent Generations (EG) per year. EG reflects the average number of generations separating current individuals from their common ancestors, reaching its highest value in 2022 (8.417). The observed inbreeding peaks suggest periods of intensified mating among related individuals, possibly due to demographic bottlenecks or constraints in population size.

Linear Regression Analysis with Respect to Inbreeding

The effects of F (inbreeding coefficient) and ΔF (individual rate of inbreeding) on 35 PPH traits were evaluated (Table 3). F significantly affected 6 traits (p < 0.05; regression coefficients b ranging from –0.308 to 0.369), showing a moderate negative association. ΔF significantly influenced only 4 traits, with larger standard errors, indicating greater variability. Standardized regression coefficients were included to enable comparison of effects across variables measured in different units. These standardized coefficients revealed that although unstandardized coefficients suggest a stronger impact of inbreeding on the trait of brachial angle (BA) compared to withers height (WH), the standardized coefficients indicate similar or even greater sensitivity in WH, highlighting the importance of using standardized measures to correctly interpret the magnitude of inbreeding effects.

For example, when comparing WH and BA, the unstandardized regression coefficient suggests that F affects BA nearly 1.6 times more than WH, and ΔF affects BA 1.9 times more than WH. However, because these traits are measured in different units, such a direct comparison does not allow for accurate interpretation. In contrast, when comparing standardized coefficients, it becomes evident that both traits are affected by F and ΔF almost equally, or, in some cases, WH may even be affected by F up to 1.2 times more than BA.

Effect of Inbreeding on EBVs

Table 4 shows the correlations (Pearson/Spearman: 0.606–1.00) between EBVs estimated with and without the inclusion of inbreeding. Values close to 1 indicate little influence of F or ΔF; however, several traits showed correlations <0.99 (in blue), demonstrating a significant impact. When analyzing extreme values, correlations were lower among the 20 animals with the lowest EBVs, suggesting that inbreeding has a greater effect on individuals with lower genetic merit.

Discussion

Pedigree Structure

The pedigree presents high connectivity: 95% of sires and dams are known in the total population and 100% in the phenotyped subset, a critical factor for unbiased estimation of genetic parameters [3]. Pedigree depth (maximum average of 11.58 and 16.00 generations, respectively) is consistent with findings in domestic species, in which greater depth improves the accuracy of genetic diversity assessments [17]. Inbreeding levels (6.74% in the total population and 9.02% in the phenotyped group) indicate moderate inbreeding, falling within the range observed in species under intense selection [18]. The higher homogeneity in the phenotyped group suggests selective mating practices or demographic bottlenecks. The high average relatedness (8.37% and 11.98%) reflects strong genetic interconnectivity, which, according to Sørensen et al. [19], increases the risk of inbreeding depression without proper management of genetic diversity. The generation interval (8.90 years in the total population and 9.04 years in the phenotyped group) is long compared to other species, likely linked to extended reproductive lifespan and management practices. Although this slows the accumulation of inbreeding, it also limits the population’s capacity to adapt to environmental or economic changes [20].

Analysis of Inbreeding, Temporal Trends, and Genetic Impact

Since 1970, inbreeding (F and ∆F) has increased markedly, following minimal levels observed between 1945 and 1950, when the genetic base was broad and artificial selection was less intense [17]. This rise is associated with intensive breeding practices and the repeated use of a limited number of breeding animals, which reduces genetic diversity [3]. The current annual ∆F, which ranges between 1% and 1.5%, exceeds the recommended threshold of 1% [21], thereby compromising the long-term maintenance of genetic viability. EG have risen from 1.19 (1945) to 8.42 (2023), reflecting improved pedigree recording and greater accuracy in inbreeding calculations. However, the concurrent increase in both F and ∆F indicates a genuine loss of genetic diversity, posing a risk to the future health and performance of the breed [22].

Wright’s fixation indices (FIS, FST, FIT) assess genetic structure. The FIS was 0.025 (total population) and 0.0265 (phenotyped subset), indicating a slight excess of homozygosity, a pattern commonly observed in horse breeds under selection [3,18]. In the PPH, this may be attributed to selection for specific traits (morphological or functional), which reduces genetic variability within subpopulations [23,24]. The FST was very low (0.0016 in the total population; 0.000082 in the phenotyped group), indicating minimal genetic differentiation, typical of horse populations with consistent gene flow [17]. Similar results have been reported in Croatian horse breeds, with an FST of 0.0260 [25], and, in Pantaneiro horses, in which the FST ranged from 0.008 to 0.056 [26]. In the context of inbreeding depression, this low genetic differentiation suggests that inbreeding-related risks affect the entire population, underscoring the need to implement comprehensive, population-wide strategies to manage genetic diversity.

The observed FIT is consistent with previous studies in horses [20], in which moderate inbreeding allows for effective management of inbreeding without compromising population viability. The values of the FIS, FST, and FIT align with those reported for breeds such as Andalusians [27] and Arabians [28]. Although genetic variability is still present, the current inbreeding levels (6.74% in the total population; 9.02% in the phenotyped subset) necessitate proactive strategies, such as breeding animal rotation or the introduction of new lineages, to preserve genetic diversity.

Effect of Inbreeding on Traits

Inbreeding reduces genetic variability, negatively affecting morphological traits such as WH in the PPH [2], consistent with findings in other species [3,5,18]. However, WH was not affected in Mangalarga Marchador horses, [29], indicating that the impact of inbreeding varies across breeds or populations. The trait of scapulohumeral angle (SHA) also showed a significant association with both F and ΔF. Studies on morphological traits and their response to inbreeding depression suggest that SHA may exhibit similar susceptibility to inbreeding-related changes [30,31]. Traits such as SHA may be particularly sensitive to inbreeding due to their dependence on complex genetic interactions [17]. Brachial angle (BA) and metacarpal length (MCL) also showed associations with F and ΔF, indicating that inbreeding affects not only linear measurements but also angles, thereby altering key proportions relevant to performance [28]. Although there are no direct studies on MCL, in Spanish Purebred horses, cannon circumference was affected by inbreeding [30], suggesting a potentially similar impact on MCL.

The functional/physiological traits acuteness (ACS) and gluteal temperature difference (GTD) were associated with ΔF; notably, ACS was also associated with F. Interestingly, F had a positive effect on ACS, contrary to expectations, suggesting that inbreeding might have fixed favorable alleles through intentional selection [31]. However, this finding contrasts with other studies demonstrating that inbreeding can impair functional traits related to physical performance in horses [32]. The authors emphasize that a greater elevation angle (ACS) does not necessarily imply improved functionality or health, as an excessive increase in ACS could raise energy expenditure or biomechanical stress, potentially compromising the horse’s overall functionality in contexts other than PPH competitions [33].

GTD showed negative regression coefficients with both F and ΔF, indicating that higher inbreeding reduces thermoregulatory capacity, possibly due to genetic load affecting metabolism or key physiological functions involved in thermoregulation [34,35]. Similar results have been observed in cattle under heat stress [19]. Although some traits exhibited significant associations with both F and ΔF, the magnitudes of their regression coefficients differed markedly. This can be explained by the fact that F reflects accumulated homozygosity (exerting a gradual effect on heritable traits), whereas ΔF captures recent inbreeding, which can have a more immediate and severe impact due to the rapid accumulation of deleterious alleles [20]. Therefore, ΔF is a critical parameter for assessing inbreeding depression in horses and other species.

Effect of Inbreeding on EBVs

This study demonstrates that inbreeding significantly affects EBV estimation in PPH, particularly for functional and physiological traits such as ACS (rp = 0.847) and GTD (rp = 0.862), consistent with findings in other horse breeds and species [18,30,32]. Correlations below 0.99 confirm that both F and ΔF alter predicted genetic merit. This effect is especially pronounced for functional and physiological traits, such as ACS and GTD, which appear to be particularly sensitive to inbreeding.

The comparison between the effects of F and ΔF reveals interesting differences in their impact on EBVs. F and ΔF influence EBVs differently: F moderately affects traits like WH (rp = 0.805), whereas ΔF has a stronger effect on others, such as GTD (rp= 0.767), likely due to the recent accumulation of deleterious alleles [20]. Including both F and ΔF in genetic models can enhance the accuracy and reliability of EBVs; conversely, ignoring them may lead to underestimation or overestimation of true EBVs, particularly in populations with high levels of inbreeding [36,37,38].

Conclusions

This study underscores the importance of monitoring and managing inbreeding in PPH populations to ensure their long-term viability. The data presented reveal an increasing trend in inbreeding, highlighting the need for proactive measures to preserve genetic diversity and safeguard the integrity of this emblematic breed. Regarding Wright’s fixation indices, the findings emphasize the necessity of developing genetic improvement programs that balance the selection of desirable traits with the conservation of genetic diversity. Furthermore, future studies should incorporate molecular analyses to complement pedigree-based data and provide a more accurate assessment of genetic diversity within this population.

Concerning the effect of inbreeding on PPH traits, evidence indicates that inbreeding significantly impacts certain morphometric, functional, and physiological characteristics, particularly those with high heritability or genetic sensitivity. Genetic models should prioritize ΔF over F to improve accuracy and avoid biases related to pedigree depth. Moreover, these models must be tailored to each species to optimize the estimation of genetic value and support effective diversity conservation.

These results align with previous studies in horses and other domestic species, reinforcing the critical importance of monitoring and managing inbreeding in genetic improvement programs. Future research should focus on integrating molecular tools to complement pedigree information and deliver a more precise evaluation of genetic diversity.

Funding

The authors are grateful for the support by “Fondo Semilla Docente 2021-1” by Directorial Resolution 004-DGIDI-CIENTIFICA-2021 of the Universidad Científica del Sur.

Supplementary Material

List of trait names, abbreviations, and operational definitions

Authors’ Contributions

Conceptualization: Vilela J, Quintana P, Dextre J. Data curation: Vilela J. Formal analysis: Vilela J, Quintana P, Velarde M, Dextre J. Methodology: Vilela J, Quintana P, Velarde M. Software: Vilela J. Validation: Quintana P, Velarde M, Dextre J. Investigation: Vilela J, Quintana P. Writing – original draft: Vilela J. Writing – review & editing: Vilela J, Quintana P, Velarde M, Dextre J.

Acknowlegments

The authors would like to thank the breeders who provided the animals and facilities for this research. We would also like to thank Dr. Molly Nicodemus (PhD) for her reviews and recommendations.

Data Availability

The data is not published due to privacy restrictions.

Ethics Approval

The study was approved by the Institutional Committee of Ethics in Research with Animals and Biodiversity of the Universidad Cientifica del Sur (N° 078-CIEI-AB-CIENTÍFICA-2022).

Declaration of Genertive AI and AI-Assisted Technologies in the Writing Process

During the preparation of this work the authors used “Qwen” in order to improve readability and language of this paper, particularly by assisting with word reduction in accordance with Animal Bioscience guidelines and translating phrases from Spanish into English. Subsequently, the authors engaged the services of a professional translator. After using this tool and service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.

Conflict of Interest

The authors state that records of eight animals owned by José Dextre were used. It is also stated that José Dextre was Chairman of the Board of the Universidad Científica del Sur during the development of the methodological phase of this research.

References

Vilela JL, Quintana PG, Velarde ML, Vargas T, Gonzales RG, Dextre J. Preliminary analysis of the development of a breeding program of the Peruvian Paso horse in field conditions. Revista Mexicana De Ciencias Pecuarias 2025; 16(1): 194–207. [CrossRef]
Larrea Izurieta COL, Carpio MG, Landi V, Hurtado EA, Andrade JIM, Loor LEV, Rivadeneira EL, Macas LFC. Evaluation of inbreeding and genetic variability of the Peruvian Paso Horse registered in Ecuador. Revista de Investigaciones Veterinarias Del Peru 2022; 33(5). [CrossRef]
Leroy G. Inbreeding depression in livestock species: Review and meta-analysis. Animal Genetics 2014; 45(5): 618–628. [CrossRef]
Keller LF, Waller DM. Inbreeding effects in wild populations. Trends in Ecology and Evolution 2002; 17(5): 230–241. [CrossRef]
Bussiman FO, Perez BC, Ventura RV, Peixoto MGCD, Curi RA, Balieiro JC. Pedigree analysis and inbreeding effects over morphological traits in Campolina horse population. Animal 2018; 12(11): 2246–2255. [CrossRef]
Gutiérrez JP, Cervantes I, Molina A, Valera M, Goyache F. Individual increase in inbreeding allows estimating effective sizes from pedigrees. Genetics Selection Evolution 2008; 40(4): 359–378. [CrossRef]
Vostry L, Vostra-Vydrova H, Citek J, Gorjanc G, Curik I. Association of inbreeding and regional equine leucocyte antigen homozygosity with the prevalence of insect bite hypersensitivity in Old Kladruber horse. Animal Genetics 2021; 52(4): 422–430. [CrossRef]
Montenegro V, Vilela JL, Wurzinger M. Assessment of generation interval and inbreeding in Peruvian Paso Horse. Proc XI World Congress on Genetics Applied to Livestock Production. Auckland, New Zealand, 2018. https://www.researchgate.net/publication/340875981_Assessment_of_Generation_Interval_and_Inbreeding_in_Peruvian_Paso_Horse.
Cortes O, Cañon J, Andrino S, Fernanadez M, Carleos C. Inbreeding depression and runs of homozygosity islands in Asturiana de los Valles cattle breed after 30 years of selection. Journal of Animal Breeding and Genetics 2024; 141(4): 440–452. [CrossRef]
Chaves LJ, Vencovsky R, Silva RSM, de Campos Telles MP, Zucchi MI, Coelho ASG. Estimating inbreeding depression in natural plant populations using quantitative and molecular data. Conservation Genetics 2011; 12(2): 569–576. [CrossRef]
Caballero A, Villanueva B, Druet T. On the estimation of inbreeding depression using different measures of inbreeding from molecular markers. Evolutionary Applications 2021; 14(2): 416–428. [CrossRef]
Gómez-Raya L, Rodríguez C, Barragán C, Silió L. Genomic inbreeding coefficients based on the distribution of the length of runs of homozygosity in a closed line of Iberian pigs. Genetics Selection Evolution 2015; 47(1), art. no. 81. [CrossRef]
Lowman B. Estimated breeding values for beef cattle. In Practice 2004; 26(4): 206–211. [CrossRef]
Becker PJJ, Hegelbach J, Keller LF, Postma E. Phenotype-associated inbreeding biases estimates of inbreeding depression in a wild bird population. Journal of Evolutionary Biology 2016; 29(1): 35–46. [CrossRef]
Townsend SM, Jamieson IG. Molecular and pedigree measures of relatedness provide similar estimates of inbreeding depression in a bottlenecked population. Journal of Evolutionary Biology 2013; 26(4): 889–899. [CrossRef]
Gutiérrez JP, Goyache F. A note on ENDOG: a computer program for analysing pedigree information. Journal of Animal Breeding and Genetics 2005; 122: 172–176.
Goyache F, Gutiérrez JP, Fernández I, Alvarez I, Royo LJ. Using pedigree information to monitor genetic variability of endangered populations: The Xalda sheep breed of Asturias as an example. Journal of Animal Breeding and Genetics 2003; 120(2): 95–105. [CrossRef]
Curik I, Ferenčaković M, Sölkner J. Inbreeding and runs of homozygosity: A possible solution to an old problem. Livestock Science 2014; 166: 26–34. [CrossRef]
Sørensen AC, Sørensen MK, Berg P. Inbreeding in Danish dairy cattle breeds. Journal of Dairy Science 2005; 89(5): 1865–1872. [CrossRef]
McParland S, Kearney JF, Rath M, Berry DP. Inbreeding trends and pedigree analysis of Irish dairy and beef cattle populations. Journal of Animal Science 2007; 85(2): 322–331. [CrossRef]
Food and Agriculture Organization of the United Nations (FAO). Molecular genetic characterization of animal genetic resources. FAO Animal Production and Health Guidelines No. 9. 2011. http://www.fao.org/3/i2413e/i2413e.pdf.
Boichard D, Maignel L, Verrier E. The value of using probabilities of gene origin to measure genetic variability in a population. Genetics Selection Evolution 1997; 29(1): 5–23. [CrossRef]
Li Z, Ran Z, Zhang Y, Xiao X, An M. Genetic Diversity and Structure of Geodorum eulophioides, a Plant Species with Extremely Small Populations in China. Diversity 2023; 15(9). [CrossRef]
Frigo MJ, Mangolin CA, Oliveira Jr RS, Machado MDFPS. Esterase polymorphism for analysis of genetic diversity and structure of wild poinsettia (Euphorbia heterophylla) populations. Weed Science 2009; 57(1): 54–60. [CrossRef]
Ivanković A, Ramljak J, Dovč P, Kelava N, Konjačić M. Genetic structure of three Croatian horse breeds: Implications for their conservation strategy. Italian Journal of Animal Science 2009; 8(4): 677–689. [CrossRef]
Nogueira MB, McManus C, de Faria DA, Santos SAO, Ianella P, Paiva SR. Fine-scale genetic diversity of the Brazilian Pantaneiro horse breed adapted to flooded regions. Tropical Animal Health and Production 2021; 53(6). [CrossRef]
Valera M, Molina A, Gutiérrez JP, Gómez J, Goyache F. Pedigree analysis in the Andalusian horse: population structure, genetic variability and influence of the Carthusian strain. Livestock Production Science 2005; 95(1–2): 57–66. [CrossRef]
Cervantes I, Molina A, Goyache F, Gutiérrez JP, Valera M. Population history and genetic variability in the Spanish Arab Horse assessed via pedigree analysis. Livestock Science 2008; 113(1): 24–33. [CrossRef]
Gonçalves RW, Costa MD, Rezende ASC, Rocha Júnior VR, Leite JRA. Effect of inbreeding on morphometric traits in Mangalarga Marchador horses. Arquivo Brasileiro de Medicina Veterinaria e Zootecnia 2012; 64(2): 419–426. [CrossRef]
Gómez MD, Valera M, Molina A, Gutiérrez JP, Goyache F. Assessment of inbreeding depression for body measurements in Spanish Purebred (Andalusian) horses. Livestock Science 2009; 122(2–3): 149–155. [CrossRef]
Poyato-Bonilla J, Perdomo-González DI, Sánchez-Guerrero MJ, Varona L, Molina A, Casellas J, Valera M. Genetic inbreeding depression load for morphological traits and defects in the Pura Raza Española horse. Genetics Selection Evolution 2020; 52(1). [CrossRef]
Leroy G, Mary-Huard T, Verrier E, Danvy S, Charvolin E, Danchin-Burge C. Methods to estimate effective population size using pedigree data: Examples in dog, sheep, cattle and horse. Genetics Selection Evolution 2013; 45(1): 1–12. [CrossRef]
Bartolomé E, Perdomo-González DI, Sánchez-Guerrero MJ, Valera M. Genetic Parameters of Effort and Recovery in Sport Horses Assessed with Infrared Thermography. Animals 2021; 11: 832. [CrossRef]
Oh SH. Evaluation of optimum genetic contribution theory to control inbreeding while maximizing genetic response. Asian-Australasian Journal of Animal Sciences 2012; 25(3): 299–303. [CrossRef]
Jensen P, Overgaard J, Loeschcke V, Schou MF, Malte H, Kristensen TN. Inbreeding effects on standard metabolic rate investigated at cold, benign and hot temperatures in Drosophila melanogaster. Journal of Insect Physiology 2014; 62(1): 11–20. [CrossRef]
Aguilar I, Fernandez EN, Blasco A, Ravagnolo O, Legarra A. Effects of ignoring inbreeding in model-based accuracy for BLUP and SSGBLUP. Journal of Animal Breeding and Genetics 2020; 137(4): 356–364. [CrossRef]
Gorjanc G, Bijma P, Hickey JM. Reliability of pedigree-based and genomic evaluations in selected populations. Genetics Selection Evolution 2015; 47(1). [CrossRef]
Santana ML, Oliveira PS, Eler JP, Gutierrez JP, Ferraz JB. Pedigree analysis and inbreeding depression on growth traits in Brazilian Marchigiana and Bonsmara breeds. Journal of Animal Science 2012; 90(1): 99–108. [CrossRef]

Figure 1. Average inbreeding, average annual inbreeding increase and equivalent generations per year. Error bars indicate the standard error of the mean.

Table 1. Descriptive statistical analysis and heritability estimates (h²) with their standard errors (SE).

Trait¹⁾	Observations	Mean	Standard deviation	Minimum	Maximum	Coefficient of variation (%)	p-value Anderson-Darling	h²	SE
WH	148	145.08	2.98	137.00	153.00	2.05	0.273	0.625	0.343
CRH	148	146.05	3.59	132.00	155.00	2.46	0.089	0.715	0.328
SH	148	75.04	6.57	67.00	148.50	8.76	0.175	0.704	0.362
MDH	148	137.59	3.62	128.90	149.00	2.63	0.348	0.644	0.316
CHW	148	34.02	2.31	29.00	39.00	6.78	0.252	0.784	0.339
TG	148	176.93	7.27	155.00	198.00	4.11	0.378	0.693	0.346
BL	148	153.58	5.65	140.00	168.00	3.68	0.800	0.643	0.367
MC	148	17.53	0.85	15.00	20.00	4.85	<0.001	0.601	0.348
MT	148	18.68	0.86	17.00	21.00	4.63	<0.001	0.426	0.339
BIA	148	63.15	4.30	49.33	77.00	6.82	0.087	0.776	0.232
HA	148	139.12	3.92	129.67	154.67	2.82	0.097	0.723	0.290
SHA	148	91.66	3.06	81.33	103.33	3.34	<0.001	0.776	0.352
FTA	148	124.25	5.07	116.67	139.33	4.08	<0.001	0.734	0.313
BA	148	123.06	5.55	110.67	158.83	4.51	<0.001	0.599	0.312
CFA	148	91.66	2.86	85.00	104.33	3.12	<0.001	0.734	0.334
FPL	148	11.27	1.37	7.96	23.00	12.19	<0.001	0.663	0.352
HPL	148	11.26	1.24	7.81	21.00	11.04	<0.001	0.604	0.400
NL	148	60.57	3.83	48.00	69.00	6.32	0.517	0.738	0.251
UL	148	34.83	2.48	29.00	53.00	7.11	0.021	0.630	0.254
FL	148	35.91	2.51	29.00	44.00	7.00	0.229	0.756	0.287
FPP	148	16.70	0.90	14.00	21.00	5.40	<0.001	0.569	0.308
HPP	148	17.58	0.82	15.50	21.00	4.67	<0.001	0.501	0.350
CW	148	34.96	4.41	25.00	56.00	12.62	0.050	0.762	0.323
CL	148	49.18	3.78	32.00	58.00	7.68	0.062	0.756	0.286
HW	148	22.40	1.26	20.00	31.00	5.61	<0.001	0.588	0.399
HL	148	61.47	2.28	56.00	68.00	3.70	0.187	0.765	0.347
MCL	148	26.57	1.75	22.00	30.00	6.58	0.017	0.701	0.263
MTL	148	30.54	1.72	26.00	35.00	5.64	0.061	0.736	0.304
EXT	134	42.23	4.60	22.07	55.33	10.89	0.361	0.250	0.217
OVR	136	27.95	20.99	-14.04	72.44	75.09	0.780	0.427	0.203
TER	137	25.30	5.97	8.93	43.47	23.60	0.858	0.471	0.198
ACS	134	71.55	6.68	52.03	87.37	9.33	0.938	0.415	0.226
GTD	88	1.60	2.02	-3.40	9.40	125.98	0.425	0.684	0.466
GTDX	88	1.05	2.99	-6.60	13.10	286.35	0.066	0.770	0.518
RMS	135	2.63	0.93	0.85	5.36	35.33	0.888	0.582	0.368
¹⁾ WH: Withers height; CRH: Croup height; SH: Sub-pectoral height; MDH: Mid-dorsal height; CHW: Chest width; TG: Thoracic girth; BL: Body length; MC: Metacarpal circumference; MT: Metatarsal circumference; BIA: Back inclination angle; HA: Hock angle; SHA: Scapulohumeral angle; FTA: Femorotibial angle; BA: Brachial angle; CFA: Coxofemoral angle; FPL: Forelimb pastern length; HPL: Hindlimb pastern length; NL: Neck length; UL: Upper arm length; FL: Femur length; FPP: Forelimb pastern perimeter; HPP: Hindlimb pastern perimeter; CW: Croup width; CL: Croup length; HW: Head width; HL: Head length ; MCL: Metacarpal length; MTL: Metatarsal length ; EXT: Extension; OVR: Overreach; TER: Term; ACS: Acuteness; GTD: Gluteal temperature difference; GTDX: Maximum gluteal temperature difference; RMS: Vertical acceleration.

Table 2. Pedigree structure and genetic parameters for the total and phenotyped populations.

Parameter		Total population	Phenotyped population
Animals		40993	151
	Males	16061	34
	Females	24932	117
Animals with known parents
	With known father	95.25	100.00
	With known mother	94.90	100.00
Inbreeding
	Mean F (%)	6.74	9.02
	Mean ΔF (%)	1.38	1.41
Average relatedness coefficient (%)		8.37	11.98
Average maximum generations		11.58	16.00
Average complete generations		3.62	4.85
Average equivalent generations		5.75	7.70
Effective population size per equivalent generation		37.46	40.66
Founders		1758	310
Equivalent founders		1661	291
Ancestors contributing to the population		1592	140
Effective number of founders (f_e)		27	17
Effective number of ancestors (f_a)		18	11
Wright’s fixation indices
	FIS	0.0250	0.0265
	FST	0.0016	0.000082
	FIT	0.0266	0.0266
Generation interval ± ES		8.90 ± 0.03	9.04 ± 0.30
Age at first reproductionz(A_p)		9.30	5.28
Regression coefficient (β) of A_p on F ± SE		-5.20 ± 0.62	-38.48 ± 12.57
Regression coefficient (β) of A_p on ΔF ± SE		6.54 ± 2.08	-189.73 ± 103.56

Table 3. Standardized and unstandardized regression coefficients (b) including the independent variables: individual inbreeding coefficient (F) and individual inbreeding rate (ΔF). SE: Standard error of the coefficients.

	F				ΔF
Trait ¹⁾	b unstandardized	b standardized	SE	p-value	b unstandardized	b standardized	SE	p-value
WH	-0.193	-0.240	0.081	0.018	-1.052	-0.210	0.493	0.035
CRH	-0.132	-0.134	0.094	0.177	-0.613	-0.100	0.573	0.287
SH	-0.111	-0.164	0.064	0.086	-0.546	-0.129	0.394	0.168
MDH	-0.189	-0.193	0.100	0.062	-0.945	-0.155	0.614	0.126
CHW	-0.022	-0.035	0.058	0.706	-0.151	-0.039	0.354	0.670
TG	-0.160	-0.081	0.163	0.327	-0.852	-0.069	0.994	0.393
BL	-0.096	0.150	0.063	0.522	-0.392	-0.041	0.916	0.669
MC	-0.003	-0.011	0.021	0.906	-0.006	-0.004	0.130	0.966
MT	-0.022	-0.096	0.024	0.353	-0.132	-0.090	0.146	0.370
BIA	0.106	0.092	0.107	0.322	0.685	0.095	0.651	0.295
HA	0.074	0.070	0.096	0.443	0.366	0.560	0.587	0.534
SHA	-0.236	-0.298	0.074	0.002	-1.459	-0.296	0.452	0.002
FTA	0.048	0.035	0.122	0.698	0.216	0.025	0.745	0.773
BA	-0.308	-0.207	0.149	0.041	-2.017	-0.218	0.906	0.028
CFA	-0.047	-0.064	0.075	0.537	-0.246	-0.054	0.458	0.593
FPL	0.042	0.112	0.035	0.228	0.278	0.119	0.211	0.192
HPL	0.002	0.006	0.031	0.947	-0.012	-0.005	0.188	0.951
NL	0.172	0.165	0.090	0.060	0.948	0.146	0.552	0.089
UL	-0.029	-0.043	0.058	0.623	-0.111	-0.027	0.355	0.756
FL	-0.016	-0.024	0.054	0.766	-0.172	-0.041	0.329	0.603
FPP	0.003	0.013	0.021	0.885	0.035	0.023	0.131	0.791
HPP	0.012	0.055	0.021	0.563	0.130	0.094	0.129	0.315
CW	-0.105	-0.087	0.106	0.323	-0.495	-0.066	0.647	0.446
CL	0.075	0.074	0.076	0.321	0.613	0.096	0.459	0.185
HW	-0.061	-0.178	0.033	0.069	-0.138	-0.150	0.203	0.120
HL	-0.003	-0.005	0.056	0.955	0.061	0.016	0.339	0.858
MCL	-0.091	-0.193	0.036	0.013	-0.441	-0.150	0.224	0.051
MTL	-0.034	-0.075	0.041	0.400	-0.103	-0.036	0.248	0.680
EXT	0.200	0.087	1.067	0.502	1.201	0.154	0.805	0.139
OVR	-0.190	-0.037	0.422	0.653	-1.575	-0.049	2.561	0.540
TER	0.116	0.073	0.162	0.475	0.679	0.069	0.986	0.492
ACS	0.369	0.203	0.183	0.047	2.090	0.186	1.118	0.065
GTD	-0.138	-0.240	0.063	0.034	-0.825	-0.241	0.368	0.030
GTDX	-0.107	-0.145	0.100	0.293	-0.582	-0.133	0.583	0.324
RMS	0.008	0.035	0.022	0.695	0.040	0.027	0.131	0.758
¹⁾ WH: Withers height; CRH: Croup height; SH: Sub-pectoral height; MDH: Mid-dorsal height; CHW: Chest width; TG: Thoracic girth; BL: Body length; MC: Metacarpal circumference; MT: Metatarsal circumference; BIA: Back inclination angle; HA: Hock angle; SHA: Scapulohumeral angle; FTA: Femorotibial angle; BA: Brachial angle; CFA: Coxofemoral angle; FPL: Forelimb pastern length; HPL: Hindlimb pastern length; NL: Neck length; UL: Upper arm length; FL: Femur length; FPP: Forelimb pastern perimeter; HPP: Hindlimb pastern perimeter; CW: Croup width; CL: Croup length; HW: Head width; HL: Head length ; MCL: Metacarpal length; MTL: Metatarsal length ; EXT: Extension; OVR: Overreach; TER: Term; ACS: Acuteness; GTD: Gluteal temperature difference; GTDX: Maximum gluteal temperature difference; RMS: Vertical acceleration

Table 4. Correlations¹⁾ between estimated breeding values (EBVs) for the top 20 and bottom 20 animals, considering the inbreeding coefficient (F) and the individual rate of inbreeding (ΔF), compared to EBVs estimated without accounting for inbreeding.

	Top 20				Bottom 20
Trait²⁾	F		ΔF		F		ΔF
Trait²⁾	rp	rs	rp	rs	rp	rs	rp	rs
WH	0.808	0.710	0.830	0.723	0.805	0.826	0.827	0.838
CRH	0.976	0.920	0.981	0.923	0.962	0.898	0.976	0.946
SH	0.939	0.832	0.957	0.901	0.968	0.904	0.981	0.935
MDH	0.974	0.955	0.979	0.958	0.917	0.759	0.946	0.854
CHW	0.994	0.989	0.990	0.980	0.998	0.985	0.997	0.980
TG	0.989	0.974	0.986	0.970	0.949	0.967	0.955	0.964
BL	0.984	0.934	0.991	0.959	0.961	0.946	0.983	0.968
MC	1.000	0.998	1.000	1.000	1.000	0.998	1.000	1.000
MT	0.981	0.962	0.984	0.962	0.935	0.913	0.937	0.916
BIA	0.964	0.812	0.951	0.704	0.994	0.964	0.993	0.973
HA	0.999	0.988	1.000	0.994	0.994	0.971	0.998	0.991
SHA	0.902	0.785	0.895	0.761	0.762	0.654	0.749	0.606
FTA	0.928	0.899	0.930	0.899	0.826	0.814	0.821	0.794
BA	0.991	0.854	0.990	0.851	0.880	0.827	0.861	0.821
CFA	0.991	0.961	0.992	0.968	0.940	0.907	0.947	0.920
FPL	0.998	0.795	0.997	0.788	0.919	0.836	0.893	0.818
HPL	1.000	0.985	1.000	0.977	0.998	0.995	0.995	0.989
NL	0.948	0.940	0.960	0.931	0.943	0.868	0.947	0.886
UL	0.997	0.910	0.998	0.937	0.993	0.929	0.996	0.967
FL	0.997	0.970	0.996	0.959	0.980	0.961	0.959	0.917
FPP	0.999	0.997	1.000	1.000	0.993	0.979	0.999	0.992
HPP	1.000	1.000	0.994	0.980	0.999	0.994	0.981	0.977
CW	0.998	0.931	0.999	0.959	0.982	0.911	0.991	0.917
CL	0.986	0.937	0.978	0.926	0.973	0.928	0.949	0.923
HW	0.992	0.898	0.994	0.911	0.927	0.798	0.937	0.853
HL	0.999	0.995	1.000	0.998	0.999	0.997	1.000	0.998
MCL	0.822	0.795	0.868	0.841	0.888	0.758	0.934	0.827
MTL	0.987	1.000	0.995	0.979	0.982	0.970	0.994	0.982
EXT	0.893	0.820	0.889	0.818	0.960	0.797	0.961	0.797
OVR	0.993	0.959	0.991	0.932	0.948	0.928	0.932	0.913
TER	0.994	0.979	0.993	0.979	0.989	0.944	0.987	0.935
ACS	0.892	0.815	0.904	0.823	0.847	0.612	0.850	0.623
GTD	0.948	0.920	0.946	0.934	0.862	0.767	0.869	0.755
GTDX	0.978	0.956	0.982	0.965	0.978	0.962	0.980	0.962
RMS	0.994	0.980	0.997	0.986	0.985	0.977	0.992	0.991
¹⁾ rp: Pearson correlation; rs: Spearman correlation. F: Inbreeding coefficient; ΔF: Individual rate of inbreeding. All correlations were statistically significant at p < 0.001, except for traits ACS (0.612 and 0.623) and SHA (0.654 and 0.606), which had p-values < 0.01. Values in blue are statistically different from 0.99, as determined by Fisher’s Z-test.
²⁾ WH: Withers height; CRH: Croup height; SH: Sub-pectoral height; MDH: Mid-dorsal height; CHW: Chest width; TG: Thoracic girth; BL: Body length; MC: Metacarpal circumference; MT: Metatarsal circumference; BIA: Back inclination angle; HA: Hock angle; SHA: Scapulohumeral angle; FTA: Femorotibial angle; BA: Brachial angle; CFA: Coxofemoral angle; FPL: Forelimb pastern length; HPL: Hindlimb pastern length; NL: Neck length; UL: Upper arm length; FL: Femur length; FPP: Forelimb pastern perimeter; HPP: Hindlimb pastern perimeter; CW: Croup width; CL: Croup length; HW: Head width; HL: Head length ; MCL: Metacarpal length; MTL: Metatarsal length ; EXT: Extension; OVR: Overreach; TER: Term; ACS: Acuteness; GTD: Gluteal temperature difference; GTDX: Maximum gluteal temperature difference; RMS: Vertical acceleration

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Pedigree-Based Assessment of Inbreeding Effects on Conformation and Performance Traits in the Peruvian Paso Horse: Implications for Sustainable Genetic Improvement

Abstract

Keywords:

Subject:

Introduction

Material and Methods

Animals and Pedigree

Traits

Measurements

Genetic and Statistical Analysis

Results

Descriptive Analysis of Morphometric, Physiological, and Functional Traits

Pedigree Structure and Population Genetic Parameters

Analysis of Inbreeding, Temporal Trends, and Genetic Impact

Linear Regression Analysis with Respect to Inbreeding

Effect of Inbreeding on EBVs

Discussion

Pedigree Structure

Analysis of Inbreeding, Temporal Trends, and Genetic Impact

Effect of Inbreeding on Traits

Effect of Inbreeding on EBVs

Conclusions

Funding

Supplementary Material

Authors’ Contributions

Acknowlegments

Data Availability

Ethics Approval

Declaration of Genertive AI and AI-Assisted Technologies in the Writing Process

Conflict of Interest

References

MDPI Initiatives

Important Links

Subscribe