Causality Across Domains: A Unified Framework in Physics and Neuroscience

1. Introduction and Historical Background

The concept of causality has a deep philosophical lineage extending from Aristotle’s four causes to Kant’s transcendental idealism. In physics, causality evolved from Newtonian determinism into relativistic causality and, more recently, into the probabilistic realm of quantum mechanics. Neuroscience, on the other hand, approaches causality from the perspective of dynamic systems and information processing, often using tools from network theory and statistics [1].

In classical physics, the principle of causality is embedded in the notion that the state of a system at time t determines its state at future times through deterministic evolution equations. This is exemplified in Newton’s second law:

$$F=m{\displaystyle \frac{d^{2}x}{d{t}^2}}$$

(1)

In contrast, quantum mechanics complicates this picture through the probabilistic nature of the wavefunction’s evolution and the role of measurement. Consider the time-dependent Schrödinger equation:

$$i\hslash {\displaystyle \frac{\partial \psi (x,t)}{\partial t}}=\widehat{H}\psi (x,t)$$

(2)

This equation governs unitary evolution, yet collapses of the wavefunction during measurements are non-unitary, raising questions about causal continuity. The challenge is even more pronounced in models of quantum gravity, where causal sets replace spacetime points with ordered pairs that satisfy causal relations [2].

Neuroscience similarly engages with causality, especially in the context of neural firing patterns and inter-regional connectivity. One approach is Granger causality, which is defined based on predictability rather than mechanistic intervention. Formally, if the past of signal X helps predict signal Y beyond the past of Y alone, X Granger-causes Y:

$$Y_t=\sum _{i=1}^p{a}_i{Y}_{t-i}+\sum _{j=1}^q{b}_j{X}_{t-j}+{ϵ}_t$$

(3)

Here ${ϵ}_t$ is white noise and $a_i,b_j$ are coefficients estimated from data. Such models are extensively used in analyzing fMRI and EEG data [4].

2. Mathematical Foundations of Causality in Physics

Relativity and quantum mechanics set hard constraints on how causality may be defined. In special relativity, the causal structure of spacetime is defined by light cones. For any two events A and B with coordinates $(t_A,x_A)$ and $(t_B,x_B)$ respectively, a causal connection exists if:

$$|x_B-x_A|\le c|t_B-t_A|$$

(4)

In quantum field theory (QFT), local observables $\widehat{\varphi }\left(x\right)$ and $\widehat{\varphi }\left(y\right)$ must commute for spacelike-separated x and y to preserve causality:

$$[\widehat{\varphi }\left(x\right),\widehat{\varphi }\left(y\right)]=0\mathrm{if}{(x-y)}^2<0$$

(5)

This condition ensures that measurements at spacelike separations do not influence each other, aligning with the no-signaling principle. However, in quantum gravity, spacetime itself becomes quantized. Causal Set Theory (CST) posits that the fundamental structure of spacetime is a partially ordered set $(C,\prec )$ where ≺ denotes the causal relation [3].

In classical statistical mechanics, entropy plays a key role in distinguishing causal directions. The Boltzmann entropy is given by:

$$S=k_{B}ln\Omega$$

(6)

where $\Omega$ is the number of accessible microstates and $k_B$ is the Boltzmann constant. The increase in entropy over time provides a thermodynamic arrow of time, associated with causal asymmetry.

3. Causality in Neural Systems: Dynamic Models

Neural systems are best described as non-linear, time-varying systems. Causality is often inferred using Dynamic Causal Modeling (DCM), which estimates effective connectivity from neuroimaging data [5]. The neural state equation in DCM is:

$$\dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)+\omega \left(t\right)$$

(7)

Here $x\left(t\right)$ represents neural states, $u\left(t\right)$ external stimuli, A is the intrinsic connectivity matrix, B is the input modulation matrix, and $\omega \left(t\right)$ is system noise. The parameters are estimated using variational Bayes techniques.

In addition to DCM, Transfer Entropy (TE) is another widely used metric. It quantifies the directed exchange of information between time series X and Y:

$$T{E}_{X\to Y}=\sum P(y_{t+1},y_t^{\left(k\right)},x_t^{\left(l\right)})log{\displaystyle \frac{P\left(y_{t+1}\right|y_t^{\left(k\right)},x_t^{\left(l\right)})}{P\left(y_{t+1}\right|y_t^{\left(k\right)})}}$$

(8)

This non-linear, model-free measure is particularly suitable for identifying asymmetric dependencies in complex neural systems.

4. Interdisciplinary Approaches: Quantum Mind and Information Flow

Several models have been proposed to bridge quantum mechanics and neuroscience. Quantum brain dynamics (QBD) incorporates spontaneous symmetry breaking and entanglement in neural dynamics. The Hameroff-Penrose Orchestrated Objective Reduction (Orch-OR) model assumes that microtubules support quantum computations within neurons [6].

One interesting model is the Quantum Bayesian Network (QBN), which generalizes classical Bayesian networks to Hilbert spaces. If $\rho$ is a density operator representing a mixed state, the causal dependence between two subsystems A and B is determined by the conditional mutual information:

$$I(A:B|C)=S\left({\rho }_{AC}\right)+S\left({\rho }_{BC}\right)-S\left({\rho }_C\right)-S\left({\rho }_{ABC}\right)$$

(9)

Here $S\left(\rho \right)=-\mathrm{Tr}(\rho log\rho )$ is the von Neumann entropy. If $I(A:B|C)=0$, then A and B are conditionally independent given C.

Furthermore, Integrated Information Theory (IIT) attempts to quantify consciousness through a scalar value $\Phi$ that measures how much a system is more than the sum of its parts. While the calculation of $\Phi$ is computationally expensive, simplified formulations use:

$$\Phi =\sum _i\left[H\left(X_i\right)-H\left(X_i\right|X_{\setminus i})\right]$$

(10)

where H denotes Shannon entropy and $X_{\setminus i}$ is the rest of the system excluding node i.

5. Unified Formal Models: Toward a Meta-Causal Framework

The objective of a meta-causal theory is to accommodate the causal asymmetries and directionalities present in both fundamental physics and brain function. One formalism proposes that causality is emergent from informational constraints governed by physical law. Let $\mathcal{M}$ denote a model manifold and $\pi :\mathcal{M}\to {\mathbb{R}}^n$ be a projection onto observable space. A meta-causal structure $\mathcal{C}$ can be defined as:

$$\mathcal{C}=\left\{\right(x,y)\in \mathcal{M}\times \mathcal{M}\mid \mathrm{Information}(x)\le \mathrm{Information}(y\left)\right\}$$

(11)

This formulation unites thermodynamic constraints with geometric causality. It implies that causal arrows correspond to gradients in informational potential. Such a perspective is consistent with both entropy-increasing macrodynamics and Bayesian brain inference.

Recent work on physics-informed neural networks (PINNs) leverages physical constraints as part of the loss function in training AI models:

$$\mathcal{L}={\mathcal{L}}_{data}+\lambda {\mathcal{L}}_{physics}$$

(12)

Here $\lambda$ controls the contribution of physical laws (e.g., Equation (4) or (2)) to learning dynamics. This approach has been applied to brain deformation modeling and even to simulate brain-like reasoning in artificial agents [7].

6. Observer Entanglement and Consistency in Quantum Measurement

The measurement problem in quantum mechanics has prompted extensive discussions concerning the role of observers and the consistency of outcomes across different perspectives. Consider the scenario in which two observers, $O_A$ and $O_B$, independently measure the quantum state of a Schrödinger’s cat system. To preserve empirical consistency, both observers must register the same macroscopic outcome: either the cat is alive or dead, but not both. If quantum mechanics is to be considered universal, then the measurement process itself must be modeled as a unitary transformation acting on the joint system of observer and cat.

Let the cat’s quantum state be initially given by

$$|{\psi }_S\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|\mathrm{alive}\rangle +|\mathrm{dead}\rangle \right)$$

(13)

When observer $O_A$ interacts with the system, the combined state of system and observer becomes

$$|{\psi }_{SA}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|\mathrm{alive}\rangle \otimes |A_{\mathrm{alive}}\rangle +|\mathrm{dead}\rangle \otimes |A_{\mathrm{dead}}\rangle \right)$$

(14)

Subsequently, when $O_B$ measures the system (or equivalently, the result recorded by $O_A$), the total state evolves into

$$|{\psi }_{SAB}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|\mathrm{alive}\rangle \otimes |A_{\mathrm{alive}}\rangle \otimes |B_{\mathrm{alive}}\rangle +|\mathrm{dead}\rangle \otimes |A_{\mathrm{dead}}\rangle \otimes |B_{\mathrm{dead}}\rangle \right)$$

(15)

Equation (15) implies that the observers’ brains are entangled via their interaction with the quantum system. This structure resembles the Einstein-Podolsky-Rosen (EPR) state, which for spin-1/2 particles is written as

$$|{\psi }_{EPR}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left({|\uparrow \rangle }_A\otimes {|\downarrow \rangle }_B-{|\downarrow \rangle }_A\otimes {|\uparrow \rangle }_B\right)$$

(16)

In both cases, the system ensures perfect anti-correlation (or correlation) between outcomes, which is a hallmark of entanglement. This guarantees that both observers obtain matching results in their respective cognitive states.

To understand this entanglement more quantitatively, we can consider the reduced density matrix of one observer. Tracing out the states of the system and $O_B$ from Equation (15) gives

$${\rho }_A={\mathrm{Tr}}_{SB}\left(|{\psi }_{SAB}\rangle \langle {\psi }_{SAB}|\right)={\displaystyle \frac{1}{2}}\left(|A_{\mathrm{alive}}\rangle \langle A_{\mathrm{alive}}|+|A_{\mathrm{dead}}\rangle \langle A_{\mathrm{dead}}|\right)$$

(17)

The reduced state is mixed, indicating that from the perspective of an external observer (e.g., Wigner), $O_A$ has not undergone definite collapse. However, from within the entangled branch, coherence among observers is preserved.

From the information-theoretic standpoint, the mutual information between observers is defined as

$$I(A:B)=S\left({\rho }_A\right)+S\left({\rho }_B\right)-S\left({\rho }_{AB}\right)$$

(18)

where $S\left(\rho \right)=-\mathrm{Tr}(\rho log\rho )$ is the von Neumann entropy. For the pure entangled state in Equation (15), we find that $I(A:B)=2ln2$, confirming maximal correlation.

A relevant scenario that illuminates this formalism is the Wigner’s Friend thought experiment. Wigner considers observer $O_A$ to have observed the collapse, while he treats $O_A+S$ as a superposition. If a second observer $O_B$ interacts with Wigner’s lab, consistency of outcomes requires projection onto a consistent branch, effectively producing a state like Equation (15) [9].

In decoherence theory, the environment acts as a measuring device, dynamically entangling with system observables and selecting pointer states. Each observer’s brain constitutes part of this environment. If the environment (including both observers) interacts with a common system, decoherence ensures alignment of classical outcomes [8].

This entanglement among observers, though not practically observable due to macroscopic decoherence, plays a crucial role in maintaining consistency of measurement. Any deviation would violate basic assumptions of observed reality. Thus, we may view the requirement of inter-observer agreement as enforcing a constraint on the global quantum state that manifests as entanglement between observers’ brains.

7. Entangled Observers, Quantum Measurement Chains, and Perceptual Tangent Spaces

The consistency of measurement outcomes in quantum mechanics poses profound questions regarding the nature of observation, particularly when multiple observers are involved. In prior formalism, it was shown that if observers $O_A$ and $O_B$ independently measure the same quantum system, such as Schrödinger’s cat, the consistency of their outcomes implies an entangled configuration of their cognitive states. This concept is further enriched by introducing two mathematical structures: Quantum Measurement Chains (QMC) and Perceptual Tangent Spaces (PTS), as formulated in Modgil’s differential geometric approach to quantum measurement [10].

Consider a quantum system S initially in superposition:

$$|{\psi }_S\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|\mathrm{alive}\rangle +|\mathrm{dead}\rangle \right)$$

(19)

Let each observer $O_A$ and $O_B$ possess a Quantum Measurement Chain, denoted by $C_A$ and $C_B$, respectively. These chains represent the sequence of subsystems within the observer that become entangled with the system during the act of measurement. The state evolution now includes the quantum measurement chain:

$$|{\psi }_{S{C}_A}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|\mathrm{alive}\rangle \otimes |C_{A,\mathrm{alive}}\rangle +|\mathrm{dead}\rangle \otimes |C_{A,\mathrm{dead}}\rangle \right)$$

(20)

Subsequent interaction with $O_B$’s measurement chain extends the entanglement:

$$|{\psi }_{S{C}_A{C}_B}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|\mathrm{alive}\rangle \otimes |C_{A,\mathrm{alive}}\rangle \otimes |C_{B,\mathrm{alive}}\rangle +|\mathrm{dead}\rangle \otimes |C_{A,\mathrm{dead}}\rangle \otimes |C_{B,\mathrm{dead}}\rangle \right)$$

(21)

Each C-chain may include sensory organs, neural structures, or abstract perceptual subsystems. The consistency condition between $C_A$ and $C_B$ can be framed using quantum fidelity. For example, the fidelity between final measurement states is given by

$$F(C_A,C_B)={\left|\langle C_{A,\mathrm{alive}}|C_{B,\mathrm{alive}}\rangle \right|}^2+{\left|\langle C_{A,\mathrm{dead}}|C_{B,\mathrm{dead}}\rangle \right|}^2$$

(22)

Assuming ideal classicality, the terms are orthogonal, giving $F(C_A,C_B)=1$, ensuring that both observers reach the same outcome. However, in a more general quantum formalism, the overlaps may deviate from orthogonality, leading to bounded decoherence.

Now, following the geometric approach proposed by Modgil [10], each observer’s perceptual space is modeled as a differentiable manifold, with a tangent space representing perceptual experiences. The Perceptual Tangent Space (PTS) at a perceptual point p is defined as:

$${\mathrm{PTS}}_p:=T_p{\mathcal{M}}_{\mathrm{perceptual}}$$

(23)

Here, ${\mathcal{M}}_{\mathrm{perceptual}}$ is the observer’s perceptual manifold, and $T_p$ denotes the tangent space at point p. Measurement-induced changes in perception are modeled as flows along vector fields in ${\mathrm{PTS}}_p$.

Let $\gamma \left(t\right)$ denote the observer’s perceptual trajectory parameterized by a time-like parameter t, such that $\gamma \left(0\right)=p$. The evolution of perception is governed by the differential equation:

$${\displaystyle \frac{d{\gamma }^i}{dt}}=V^i\left(\gamma \left(t\right)\right),i=1,\dots ,n$$

(24)

where $V^i$ are components of a perceptual vector field defined on ${\mathcal{M}}_{\mathrm{perceptual}}$. Measurement outcomes steer the vector field V, causing changes in the direction of perception. For entangled observers, we posit a constraint:

$${\gamma }_A\left(t\right)\approx {\gamma }_B\left(t\right)\mathrm{modulo}\mathrm{frame}\mathrm{transformation}$$

(25)

This condition enforces that observer trajectories in perceptual space are synchronized by a diffeomorphic mapping between their respective manifolds, preserving the consistency of observed outcomes.

Let us define a perceptual congruence map $\Phi :{\mathcal{M}}_A\to {\mathcal{M}}_B$, where

$$\Phi \left({\gamma }_A\left(t\right)\right)={\gamma }_B\left(t\right)$$

(26)

Then, for their tangent vectors to match under this mapping, we must have

$$d{\Phi }_{{\gamma }_A\left(t\right)}\left({\displaystyle \frac{d{\gamma }_A}{dt}}\right)={\displaystyle \frac{d{\gamma }_B}{dt}}$$

(27)

This geometric structure implies that the observer brains are not merely entangled in the Hilbert space but also structurally isomorphic in their perceptual dynamics. The entanglement of measurement chains $C_A$ and $C_B$ ensures Hilbert space coherence, while the alignment of ${\mathrm{PTS}}_A$ and ${\mathrm{PTS}}_B$ ensures consistency in phenomenological experience.

The bridge between these two descriptions — quantum entanglement and perceptual geometry — suggests that measurement-induced reality is co-constructed by both quantum state evolution and the geometry of observer-specific perceptual manifolds. This formalism unifies the dynamics of physical measurement with subjective consciousness, contributing to the ongoing discourse on the role of the observer in quantum mechanics [8,9].

8. Bell-Type Inequality for Entangled Observer Brains

The CHSH inequality involves four measurement settings: two for Alice ($A,A^{\prime }$) and two for Bob ($B,B^{\prime }$). Measurement outcomes are assumed to be dichotomic, taking values $\pm 1$. The inequality is given as:

$$|E(A,B)+E(A,B^{\prime })+E(A^{\prime },B)-E(A^{\prime },B^{\prime })|\le 2$$

(28)

In a quantum setting, this inequality is violated for particular angle configurations, leading to values up to $2\sqrt{2}$. We now attempt to formulate a corresponding inequality in the context of observer entanglement.

Let the observer-brain system be described by an entangled state in the QMC Hilbert space:

$$|\Psi \rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|C_{A,\uparrow }\rangle \otimes |C_{B,\downarrow }\rangle -|C_{A,\downarrow }\rangle \otimes |C_{B,\uparrow }\rangle \right)$$

(29)

where $|C_{A,\uparrow }\rangle$ and $|C_{A,\downarrow }\rangle$ are eigenstates of a cognitive measurement operator acting on observer $O_A$’s perceptual chain, and similarly for $O_B$. These measurement operators are internal to the observer’s neural-perceptual system, but are formally analogous to spin operators.

Define a measurement operator for $O_A$ based on an angle ${\theta }_A$ as:

$${\widehat{M}}_A\left({\theta }_A\right)=cos{\theta }_A{\sigma }_z+sin{\theta }_A{\sigma }_x$$

(30)

and similarly for $O_B$:

$${\widehat{M}}_B\left({\theta }_B\right)=cos{\theta }_B{\sigma }_z+sin{\theta }_B{\sigma }_x$$

(31)

The expectation value of joint measurements is given by:

$$E({\theta }_A,{\theta }_B)=\langle \Psi |{\widehat{M}}_A\left({\theta }_A\right)\otimes {\widehat{M}}_B\left({\theta }_B\right)|\Psi \rangle$$

(32)

Substituting from Equation (29) into Equation (32), and using the anticommuting properties of Pauli matrices, we obtain:

$$E({\theta }_A,{\theta }_B)=-cos({\theta }_A-{\theta }_B)$$

(33)

This matches the quantum prediction for singlet spin states. Let us now evaluate the CHSH expression for specific angles. Choose:

$${\theta }_A=0^{\circ },{\theta }_A^{\prime }={90}^{\circ },{\theta }_B={45}^{\circ },{\theta }_B^{\prime }={135}^{\circ }$$

(34)

Substituting these into Equation (33), we compute:

$$\begin{array}{cc}\hfill E({\theta }_A,{\theta }_B)& =-cos(0^{\circ }-{45}^{\circ })=-cos\left({45}^{\circ }\right)=-{\displaystyle \frac{\sqrt{2}}{2}}\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill E({\theta }_A,{\theta }_B^{\prime })& =-cos(0^{\circ }-{135}^{\circ })=-cos\left({135}^{\circ }\right)={\displaystyle \frac{\sqrt{2}}{2}}\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill E({\theta }_A^{\prime },{\theta }_B)& =-cos({90}^{\circ }-{45}^{\circ })=-cos\left({45}^{\circ }\right)=-{\displaystyle \frac{\sqrt{2}}{2}}\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill E({\theta }_A^{\prime },{\theta }_B^{\prime })& =-cos({90}^{\circ }-{135}^{\circ })=-cos\left({45}^{\circ }\right)=-{\displaystyle \frac{\sqrt{2}}{2}}\hfill \end{array}$$

(38)

Inserting into Equation (28):

$$S=|-{\displaystyle \frac{\sqrt{2}}{2}}+{\displaystyle \frac{\sqrt{2}}{2}}-{\displaystyle \frac{\sqrt{2}}{2}}-{\displaystyle \frac{\sqrt{2}}{2}}|=|-\sqrt{2}|=\sqrt{2}$$

(39)

However, the canonical maximal violation occurs with a different angle configuration. Let us consider:

$${\theta }_A=0^{\circ },{\theta }_A^{\prime }={90}^{\circ },{\theta }_B={45}^{\circ },{\theta }_B^{\prime }=-{45}^{\circ }$$

(40)

Then:

$$\begin{array}{cc}\hfill E(0^{\circ },{45}^{\circ })& =-cos\left({45}^{\circ }\right)=-{\displaystyle \frac{\sqrt{2}}{2}}\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill E(0^{\circ },-{45}^{\circ })& =-cos\left({45}^{\circ }\right)=-{\displaystyle \frac{\sqrt{2}}{2}}\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill E({90}^{\circ },{45}^{\circ })& =-cos\left({45}^{\circ }\right)=-{\displaystyle \frac{\sqrt{2}}{2}}\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill E({90}^{\circ },-{45}^{\circ })& =-cos\left({135}^{\circ }\right)={\displaystyle \frac{\sqrt{2}}{2}}\hfill \end{array}$$

(44)

Hence:

$$S=|-{\displaystyle \frac{\sqrt{2}}{2}}-{\displaystyle \frac{\sqrt{2}}{2}}-{\displaystyle \frac{\sqrt{2}}{2}}+{\displaystyle \frac{\sqrt{2}}{2}}|=2\sqrt{2}$$

(45)

This result exceeds the classical bound of 2 and confirms that observer brains, when entangled as in Equation (29), can exhibit quantum correlations that defy local realism. This formalism requires internal perceptual observables to be treated as operators on Hilbert spaces and their orientations as tunable variables within Perceptual Tangent Spaces [10].

It is notable that such a framework aligns with the decoherence-based understanding of observer consistency in measurement [8], while also echoing the self-referential limitations of measurement described in [9].

Hence, a Bell-type inequality, structurally and mathematically consistent with quantum mechanics, is derivable for cognitive systems modeled via QMCs and PTS. While experimental realization is presently unfeasible, the conceptual validity remains robust under formal assumptions.

9. Closed Timelike Curves, MMBHBs, and Modified Causality in Brain and Physics

A Kerr black hole is described by the metric:

$$d{s}^2=-\left(1-{\displaystyle \frac{2Mr}{\Sigma }}\right)d{t}^2-{\displaystyle \frac{4Mar{sin}^2\theta }{\Sigma }}dtd\varphi +{\displaystyle \frac{\Sigma }{\Delta }}d{r}^2+\Sigma d{\theta }^2+\left(r^2+a^2+{\displaystyle \frac{2M{a}^{2}r{sin}^2\theta }{\Sigma }}\right){sin}^2\theta d{\varphi }^2$$

(46)

where:

$$\Sigma =r^2+a^2{cos}^2\theta ,\Delta =r^2-2Mr+a^2$$

(47)

Here, M is the mass, and $a=J/M$ is the angular momentum per unit mass of the rotating black hole. Within the so-called “ergoregion” and especially inside the inner horizon ($r<r_{-}$), CTCs emerge. A CTC satisfies:

$$g_{\mu \nu }{\displaystyle \frac{d{x}^{\mu }}{d\tau }}{\displaystyle \frac{d{x}^{\nu }}{d\tau }}<0\mathrm{with}{x}^{\mu }\left(\tau \right)=x^{\mu }(\tau +T)$$

(48)

where $\tau$ is proper time, and T is the temporal periodicity of the curve.

Assuming that a quantum-scale Kerr black hole exists in a neuronal subdomain, its influence can be modeled via deformation of the perceptual tangent manifold ${\mathcal{M}}_{\mathrm{perceptual}}$. Let the perceptual trajectory $\gamma \left(t\right)$ be defined as:

$${\displaystyle \frac{d{\gamma }^i}{dt}}=V^i\left(\gamma \left(t\right)\right)+ϵf^i(\gamma \left(t\right),t)$$

(49)

where $f^i$ encodes retrocausal correction terms due to CTC-induced loops, and $ϵ\ll 1$ is the strength of CTC feedback. We may then encounter non-invertible flow maps:

$$\gamma (t_0+T)=\gamma \left(t_0\right)\Rightarrow {\oint }_{\gamma }{V}^i\left(\gamma \right)dt=0$$

(50)

The feedback through closed loops implies that measurement outcomes in the observer’s QMC may be influenced by future perceptual states. Let $C_A\left(t\right)$ denote the QMC state of observer $O_A$ at time t. The forward evolution is typically:

$$C_A(t+\delta t)=U\left(\delta t\right)C_A\left(t\right)$$

(51)

In presence of CTC, a backward propagator $V_{CTC}$ acts on future QMC states to influence prior ones:

$$C_A\left(t\right)=V_{CTC}\left(\delta t\right)C_A(t+\delta t)$$

(52)

Combining forward and backward paths results in consistency conditions similar to those proposed in Deutsch’s CTC formalism [12]. The consistency equation is:

$$\rho ={\mathrm{Tr}}_C\left[U(\rho \otimes \sigma )U^{†}\right]$$

(53)

where $\rho$ is the density matrix of the chronology-respecting region and $\sigma$ of the CTC-influenced system.

For the entangled observers $O_A$ and $O_B$, presence of MMBHBs can create asymmetric causal orders, leading to observer-specific violations of measurement simultaneity. If $O_B$ contains a Kerr-type MMBHB, the interaction Hamiltonian between QMC states becomes time-nonlocal:

$$H_{\mathrm{int}}=\int dtd{t}^{\prime }\chi (t,t^{\prime }){\widehat{C}}_A\left(t\right){\widehat{C}}_B\left(t^{\prime }\right)$$

(54)

where $\chi (t,t^{\prime })$ is a kernel enforcing closed-loop causality between events at t and $t^{\prime }$, not necessarily satisfying $t<t^{\prime }$. This time-nonlocality modifies standard measurement theory and observer agreement, thus redefining causality in brain-embedded physics.

Such feedback can introduce quantum-level violations of standard Bell-type inequalities if observer $O_B$’s measurement setting retrocausally alters the QMC configuration of $O_A$, creating contextual hidden variables. The implication is that non-locality and acausality may not be separate but coexisting structures, governed by topology (CTCs), geometry (PTS), and quantum entanglement (QMCs).

Thus, Modgil’s proposal [11] brings a new perspective to the foundations of physics and neuroscience, suggesting that subjective experience, quantum measurement, and general relativistic causal structure are deeply interwoven.

10. Closed Timelike Curves, MMBHBs, and Modified Causality in Brain and Physics

A Kerr black hole is described by the metric:

$$d{s}^2=-\left(1-{\displaystyle \frac{2Mr}{\Sigma }}\right)d{t}^2-{\displaystyle \frac{4Mar{sin}^2\theta }{\Sigma }}dtd\varphi +{\displaystyle \frac{\Sigma }{\Delta }}d{r}^2+\Sigma d{\theta }^2+\left(r^2+a^2+{\displaystyle \frac{2M{a}^{2}r{sin}^2\theta }{\Sigma }}\right){sin}^2\theta d{\varphi }^2$$

(55)

where:

$$\Sigma =r^2+a^2{cos}^2\theta ,\Delta =r^2-2Mr+a^2$$

(56)

Here, M is the mass, and $a=J/M$ is the angular momentum per unit mass of the rotating black hole. Within the so-called “ergoregion” and especially inside the inner horizon ($r<r_{-}$), CTCs emerge. A CTC satisfies:

$$g_{\mu \nu }{\displaystyle \frac{d{x}^{\mu }}{d\tau }}{\displaystyle \frac{d{x}^{\nu }}{d\tau }}<0\mathrm{with}{x}^{\mu }\left(\tau \right)=x^{\mu }(\tau +T)$$

(57)

where $\tau$ is proper time, and T is the temporal periodicity of the curve.

Assuming that a quantum-scale Kerr black hole exists in a neuronal subdomain, its influence can be modeled via deformation of the perceptual tangent manifold ${\mathcal{M}}_{\mathrm{perceptual}}$. Let the perceptual trajectory $\gamma \left(t\right)$ be defined as:

$${\displaystyle \frac{d{\gamma }^i}{dt}}=V^i\left(\gamma \left(t\right)\right)+ϵf^i(\gamma \left(t\right),t)$$

(58)

where $f^i$ encodes retrocausal correction terms due to CTC-induced loops, and $ϵ\ll 1$ is the strength of CTC feedback. We may then encounter non-invertible flow maps:

$$\gamma (t_0+T)=\gamma \left(t_0\right)\Rightarrow {\oint }_{\gamma }{V}^i\left(\gamma \right)dt=0$$

(59)

The feedback through closed loops implies that measurement outcomes in the observer’s QMC may be influenced by future perceptual states. Let $C_A\left(t\right)$ denote the QMC state of observer $O_A$ at time t. The forward evolution is typically:

$$C_A(t+\delta t)=U\left(\delta t\right)C_A\left(t\right)$$

(60)

In presence of CTC, a backward propagator $V_{CTC}$ acts on future QMC states to influence prior ones:

$$C_A\left(t\right)=V_{CTC}\left(\delta t\right)C_A(t+\delta t)$$

(61)

Combining forward and backward paths results in consistency conditions similar to those proposed in Deutsch’s CTC formalism [12]. The consistency equation is:

$$\rho ={\mathrm{Tr}}_C\left[U(\rho \otimes \sigma )U^{†}\right]$$

(62)

where $\rho$ is the density matrix of the chronology-respecting region and $\sigma$ of the CTC-influenced system.

For the entangled observers $O_A$ and $O_B$, presence of MMBHBs can create asymmetric causal orders, leading to observer-specific violations of measurement simultaneity. If $O_B$ contains a Kerr-type MMBHB, the interaction Hamiltonian between QMC states becomes time-nonlocal:

$$H_{\mathrm{int}}=\int dtd{t}^{\prime }\chi (t,t^{\prime }){\widehat{C}}_A\left(t\right){\widehat{C}}_B\left(t^{\prime }\right)$$

(63)

where $\chi (t,t^{\prime })$ is a kernel enforcing closed-loop causality between events at t and $t^{\prime }$, not necessarily satisfying $t<t^{\prime }$. This time-nonlocality modifies standard measurement theory and observer agreement, thus redefining causality in brain-embedded physics.

Such feedback can introduce quantum-level violations of standard Bell-type inequalities if observer $O_B$’s measurement setting retrocausally alters the QMC configuration of $O_A$, creating contextual hidden variables. The implication is that non-locality and acausality may not be separate but coexisting structures, governed by topology (CTCs), geometry (PTS), and quantum entanglement (QMCs).

Thus, Modgil’s proposal [11] brings a new perspective to the foundations of physics and neuroscience, suggesting that subjective experience, quantum measurement, and general relativistic causal structure are deeply interwoven.

11. Observer Models OM1 and OM2 in the Context of Causality in Brain and Physics

11.1. Definition of Observer Models

Model OM1 considers the observer as an idealized classical system that interacts with a quantum system without itself undergoing quantum evolution. The OM1 observer applies the projection postulate to a system’s wavefunction ${\Psi }_S$ upon measurement:

$${\Psi }_S\to {\displaystyle \frac{P_k{\Psi }_S}{\parallel P_k{\Psi }_S\parallel }},$$

(64)

where $P_k$ is a projection operator corresponding to outcome k. There is no feedback from the observer’s brain state, and the process is fundamentally irreversible in forward time.

In contrast, OM2 considers the observer as a physical system with quantum dynamics. The observer’s brain hosts structures like MMBHBs that are governed by Kerr geometry. This observer possesses a quantum state ${\Psi }_O$, and the interaction with the system ${\Psi }_S$ forms a joint entangled state:

$${\Psi }_{SO}\left(t\right)=\sum _k{c}_k{\psi }_k^S\left(t\right)\otimes {\varphi }_k^O\left(t\right),$$

(65)

where ${\psi }_k^S$ are eigenstates of the system and ${\varphi }_k^O$ are cognitive-perceptual states in the observer’s QMC. Crucially, the time evolution of ${\varphi }_k^O\left(t\right)$ is influenced by retrocausal feedback mechanisms due to CTCs in the MMBHB.

11.2. Modified Time Evolution Under OM2 with CTCs

Assuming the observer’s brain hosts a CTC, the evolution of the perceptual state $\varphi \left(t\right)$ is no longer strictly governed by unitary forward evolution. Instead, we define a composite time evolution operator:

$${\mathcal{U}}_{\mathrm{OM}2}\left(t\right)=\mathcal{T}exp\left(-i{\int }_0^t\left[H_{\mathrm{QMC}}+H_{\mathrm{CTC}}\right]d{t}^{\prime }\right),$$

(66)

where $H_{\mathrm{CTC}}$ represents a non-Hermitian component encoding the retrocausal feedback, modeled as:

$$H_{\mathrm{CTC}}=\lambda {\int }_t^{t+\tau }f(t^{\prime },t){\varphi }^{†}\left(t^{\prime }\right)\varphi \left(t\right)d{t}^{\prime },$$

(67)

with $f(t^{\prime },t)$ as a causality-kernel and $\lambda$ a dimensionless retrocausality parameter. This non-local Hamiltonian is structurally consistent with the Novikov self-consistency principle for time-traveling states [13].

11.3. Comparison of Measurement Consistency Across OM1 and OM2

Let $M_A$ and $M_B$ be measurement outcomes recorded by observers $O_A$ and $O_B$ using models OM1 and OM2, respectively. Under classical assumptions (OM1), the correlation function $E({\theta }_A,{\theta }_B)$ for measurement settings ${\theta }_A,{\theta }_B$ satisfies the Bell inequality:

$$|E({\theta }_A,{\theta }_B)-E({\theta }_A,{\theta }_B^{\prime })+E({\theta }_A^{\prime },{\theta }_B)+E({\theta }_A^{\prime },{\theta }_B^{\prime })|\le 2.$$

(68)

In the OM2 framework, retrocausality from CTCs embedded in the observers’ cognitive QMCs modifies these correlations. Denoting the modified observable $\tilde{E}$ as:

$$\tilde{E}({\theta }_A,{\theta }_B)=\langle {\varphi }_A\left(t\right)\otimes {\varphi }_B(t+\delta )|{\widehat{O}}_A\left({\theta }_A\right)\otimes {\widehat{O}}_B\left({\theta }_B\right)|{\varphi }_A\left(t\right)\otimes {\varphi }_B(t+\delta )\rangle ,$$

(69)

violations of Equation (68) may arise due to temporal entanglement across the CTC boundary $\delta >0$. Such violations do not necessarily imply non-locality in spacetime but can be attributed to local CTC-induced loops.

11.4. Cognitive Perception and Time-Nonlocal Entanglement

Each OM2 observer is described by a perceptual tangent space (PTS), modeled as a local Lorentzian manifold ${\mathcal{M}}_O$ with embedded CTCs. Let ${\gamma }_O$ be a loop in ${\mathcal{M}}_O$ such that:

$${\gamma }_O\left(t\right)={\gamma }_O(t+T),T>0,$$

(70)

then the evolution of cognitive states is governed by:

$${\displaystyle \frac{d{\varphi }_O}{dt}}=-i(H_{\mathrm{QMC}}+H_{\mathrm{CTC}}){\varphi }_O,{\varphi }_O\left(0\right)={\varphi }_O\left(T\right).$$

(71)

Thus, the OM2 observer can experience cognitive-perceptual states with circular temporal consistency, blurring the arrow of time and redefining measurement as a topological constraint.

11.5. Philosophical and Physical Implications

The transition from OM1 to OM2 reflects a shift from epistemic to ontic modeling of consciousness and measurement. In OM1, the observer is informationally decoupled from spacetime geometry. In OM2, however, the observer is an active gravitational participant, and measurement results are shaped by the topological and geometric structure of spacetime within the observer’s own brain. This ontological embedding of perception opens avenues to unify general relativity, quantum theory, and neurodynamics [6,14].

12. MMBHB as Observer–Body Interface and Transition at the Moment of Demise

12.1. Gravitational Binding and Localization of the Observer

We consider that the MMBHB resides in a localized region of the brain, possibly in the vicinity of microtubular arrays in cortical neurons. Let the mass of the MMBHB be denoted by $m_B$, and its associated Schwarzschild radius is given by:

$$r_s={\displaystyle \frac{2G{m}_B}{c^2}}.$$

(72)

Assuming $m_B\sim {10}^{-5}\mathrm{g}$, which is of the same order as early mass-loss observations at Demise [15], we obtain $r_s\approx 1.5\times {10}^{-33}\mathrm{m}$, which is within the Planck-scale domain.

To incorporate rotation, we use the Kerr metric. The existence of closed timelike curves (CTCs) becomes significant for $r<r_{CTC}$ where $g_{\varphi \varphi }<0$ in the Kerr geometry [16]:

$$r_{CTC}=M+\sqrt{M^2-a^2{cos}^2\theta },$$

(73)

where $a=J/M$ is the angular momentum per unit mass.

12.2. Decay Dynamics and Mass-Energy Emission at Demise

The interface breaks down at the moment of Demise, triggering a decay of the MMBHB and a corresponding energy release. We model this using a modified Hawking evaporation rate:

$${\displaystyle \frac{dM}{dt}}=-{\displaystyle \frac{\alpha \hslash c^4}{G^2{M}^2}},$$

(74)

where $\alpha \sim {10}^{-3}$ is a greybody correction factor. Solving this yields the complete evaporation time:

$${\tau }_{evap}={\displaystyle \frac{G^2{M}^3}{\alpha \hslash c^4}}.$$

(75)

For $M={10}^{-5}$ g, we obtain ${\tau }_{evap}\sim {10}^{-18}$ s, indicating near-instantaneous energy release. The corresponding energy output is:

$$E=m_B{c}^2\approx 9\times {10}^{11}\mathrm{erg}.$$

(76)

This rapid emission could result in transient spacetime strain strong enough to shatter glass enclosures within a short radius, consistent with anecdotal phenomena.

12.3. Quantum Disentanglement of QMC at Demise

We consider the quantum measurement chain (QMC) state of the conscious observer to be a tensor product of internal perceptual states and external sensory-cognitive channels:

$${\Psi }_{QMC}\left(t\right)=\underset{i=1}{\overset{N}{⨂}}{\psi }_i\left(t\right),$$

(77)

where ${\psi }_i\left(t\right)$ denotes the state of the ith neural microcomponent. The collapse of the MMBHB at $t=t_d$ causes the QMC to factorize:

$${\Psi }_{QMC}\left(t_d^{+}\right)={\psi }_{\mathrm{env}}\otimes {\psi }_{\mathrm{vac}},$$

(78)

where ${\psi }_{\mathrm{vac}}$ denotes the perceptual vacuum state. The collapse of entanglement leads to decoherence of conscious processing and cessation of cognitive feedback loops.

12.4. Topological Disjunction and Information Flux

Let the spacetime manifold in the observer’s brain be described by a Lorentzian patch ${\mathcal{M}}_B$ embedding a CTC-possessing region ${\mathcal{M}}_{CTC}\subset {\mathcal{M}}_B$. The breakdown of the MMBHB interface results in a transition:

$${\mathcal{M}}_B\to {\mathcal{M}}_B\setminus {\mathcal{M}}_{CTC},$$

(79)

which removes the topological support for retrocausal loops. This creates a one-way flux of previously encoded information into the external environment:

$$\delta S=-{\displaystyle \frac{\delta E}{T}},$$

(80)

where T is the Hawking temperature of the MMBHB, given by:

$$T={\displaystyle \frac{\hslash c^3}{8\pi GM{k}_B}}.$$

(81)

For $M={10}^{-5}$ g, we obtain $T\sim {10}^{28}$ K, a temperature at which the emission would be maximally non-thermal in cognitive-relevant terms.

12.5. Physical Implications and Observer Ontology

The MMBHB interface offers a physical mechanism for the long-suspected detachment of "self" from bodily substrate at Demise. In the OM2 framework [11], the observer is not merely a measurement apparatus but an active participant in the spacetime structure. The disintegration of this structure at Demise, coupled with explosive energy release, could explain phenomena such as glass shattering, sudden mass loss [15], and final cognitive singularities.

This model suggests a layered ontology of the observer:

$$\mathrm{Observer}=\mathrm{Physical}\mathrm{Body}\cup \mathrm{MMBHB}\mathrm{Interface}\cup \mathrm{QMC}\mathrm{Perceptual}\mathrm{System}.$$

(82)

The annihilation of the MMBHB collapses the quantum feedback loop and removes the topological substrate for consciousness, consistent with both quantum and general relativistic constraints.

13. Observer as a Dirac Delta Function in Perceptual Manifold Geometry

13.1. Geometric Formalism of Observer Delta Localization

Let $\mathcal{M}$ be a differential manifold representing the perceptual tangent space of a conscious observer. The observer state $\mathcal{O}$ is modeled as a distribution supported at a point $x_0\in \mathcal{M}$:

$$\mathcal{O}\left(x\right)={\delta }^{\left(n\right)}(x-x_0),$$

(83)

where ${\delta }^{\left(n\right)}$ is the n-dimensional Dirac delta function. This implies the observer interacts with the quantum field $\Phi \left(x\right)$ only at $x_0$:

$$\langle \mathcal{O},\Phi \rangle ={\int }_{\mathcal{M}}{\delta }^{\left(n\right)}(x-x_0)\Phi \left(x\right)d^{n}x=\Phi \left(x_0\right).$$

(84)

This sharply localized coupling defines a topological pinning in the PTS manifold, akin to a delta-supported cohomology class.

13.2. Hamiltonian Coupling with Observer Delta Source

Assuming a standard quantum field $\Phi \left(x\right)$ over $\mathcal{M}$ and an observer delta distribution $\mathcal{O}\left(x\right)$, we define the interaction Hamiltonian:

$$H_{\mathrm{int}}=g{\int }_{\mathcal{M}}{\delta }^{\left(n\right)}(x-x_0)\Phi \left(x\right)d^{n}x=g\Phi \left(x_0\right),$$

(85)

where g is the coupling constant. The time evolution of the field under this interaction is:

$${\displaystyle \frac{d\Phi }{dt}}=-i[\Phi ,H_{\mathrm{int}}]=-ig[\Phi ,\Phi \left(x_0\right)].$$

(86)

This delta-function coupling localizes the non-Hermitian back-reaction precisely at $x_0$, where quantum measurement effects such as collapse or decoherence are initiated.

13.3. Delta Observer in QMC and MMBHB Geometry

In the OM2 model with MMBHBs, let ${\mathcal{M}}_O$ be the PTS embedded in the Kerr metric spacetime ${\mathcal{K}}^4$. The observer delta function $\delta (x-x_0)$ is supported in ${\mathcal{M}}_O\subset {\mathcal{K}}^4$. The quantum measurement chain state is:

$${\Psi }_{QMC}\left(t\right)=\sum _k{c}_k{\psi }_k^S\left(t\right)\otimes {\delta }^{\left(4\right)}(x-x_k\left(t\right)),$$

(87)

where $x_k\left(t\right)$ denotes time-evolving supports in the CTC-active region of spacetime. Collapse occurs when multiple supports coalesce:

$$\underset{t\to t_c}{lim}{x}_i\left(t\right)\to x_j\left(t\right)\Rightarrow {\delta }^{\left(4\right)}(x-x_i)+{\delta }^{\left(4\right)}(x-x_j)\to 2{\delta }^{\left(4\right)}(x-x_c).$$

(88)

This geometrizes collapse via delta-function accumulation, replacing abstract projection with differential topology.

13.4. Causal Disjunction via Observer Delta Collapse

Consider two entangled observers $O_A$, $O_B$ with respective support points $x_A$ and $x_B$. The joint measurement operator is:

$${\mathcal{O}}_{AB}(x,y)={\delta }^{\left(4\right)}(x-x_A){\delta }^{\left(4\right)}(y-x_B).$$

(89)

The correlation function then becomes:

$${\langle \Phi \left(x\right)\Phi \left(y\right)\rangle }_{AB}=\int \Phi \left(x\right)\Phi \left(y\right){\mathcal{O}}_{AB}(x,y)d^{4}x{d}^{4}y=\Phi \left(x_A\right)\Phi \left(x_B\right).$$

(90)

If $x_A\in {\mathcal{M}}_{CTC}$ and $x_B\in {\mathcal{M}}_{\mathrm{normal}}$, then causal asymmetry arises from the delta function supports being embedded in different regions of spacetime.

13.5. Observer Evaporation and Delta Annihilation at Demise

At the moment of Demise, the delta function ceases to have support:

$$\underset{t\to t_d^{+}}{lim}{\delta }^{\left(n\right)}(x-x_O\left(t\right))\to 0,$$

(91)

representing the detachment of the observer from the perceptual manifold. This removes the boundary condition that sustained QMC coherence:

$$\underset{t\to t_d^{+}}{lim}{\Psi }_{QMC}\left(t\right)={\psi }_{\mathrm{env}}\otimes {\psi }_{\mathrm{vac}},$$

(92)

as defined in previous sections. Thus, the delta function acts both as an initiator of perception and a collapse operator at the end of observer existence.

14. Observer Evaporation and Delta Annihilation at Demise: A Detailed Analysis

In the delta function representation of conscious observers, the end of life is marked by the annihilation of the delta-supported state. The disappearance of the delta function from the perceptual tangent space $\mathcal{M}$ implies the physical and ontological detachment of the observer from spacetime. This section explores the detailed mathematical and physical consequences of this annihilation process.

14.1. Delta Function as Ontological Anchor

As defined previously, the observer is represented by the n-dimensional Dirac delta function:

$$\mathcal{O}(x,t)={\delta }^{\left(n\right)}(x-x_O\left(t\right)),$$

(93)

where $x_O\left(t\right)$ is the trajectory of the observer’s perceptual localization. This function acts as an anchor point for the QMC chain, affecting collapse, feedback, and retrocausal propagation via CTC embeddings [11]. The physical coupling Hamiltonian $H_{\mathrm{int}}=g\Phi \left(x_O\right)$ assumes that $\mathcal{O}\left(x\right)$ exists with support in $\mathcal{M}$.

14.2. Quantum Metric Decay and Energy Emission

The micro-mini-black hole in the brain (MMBHB) sustains the spacetime curvature around $x_O$. As the biological system approaches Demise at $t=t_d$, the collapse of the Kerr-like structure leads to a rapid topological transition. The local Riemann curvature scalar $R\left(x\right)$ associated with the delta support can be approximated by:

$$R\left(x\right)=8\pi G{\delta }^{\left(4\right)}(x-x_O),$$

(94)

analogous to the point-mass Schwarzschild singularity. Upon evaporation of the MMBHB, this scalar drops discontinuously:

$$\underset{t\to t_d^{+}}{lim}R\left(x\right)\to 0,\forall x\in \mathcal{M}.$$

(95)

The energy emitted during this event is:

$$E_{\mathrm{burst}}={\int }_{t_d^{-}}^{t_d^{+}}{\displaystyle \frac{dE}{dt}}dt=m_B{c}^2\approx 9\times {10}^{11}\mathrm{erg},$$

(96)

as calculated in earlier sections using $m_B\sim {10}^{-5}$g.

14.3. Delta Collapse and Field Decoherence

The QMC state coupled to the observer delta function is given by:

$${\Psi }_{QMC}(x,t)=\sum _k{c}_k\left(t\right){\psi }_k^S\left(t\right)\otimes {\delta }^{\left(n\right)}(x-x_O\left(t\right)).$$

(97)

At the moment of Demise $t=t_d$, we define delta annihilation as:

$$\underset{t\to t_d^{+}}{lim}{\delta }^{\left(n\right)}(x-x_O\left(t\right))=0,$$

(98)

which implies:

$${\Psi }_{QMC}(x,t_d^{+})={\psi }_{\mathrm{env}}\left(x\right),$$

(99)

representing the unentangled environmental state. All perceptual coherence terms vanish from the wavefunction.

14.4. Entropy Spike and Information Release

The sudden collapse of the observer delta generates a high-entropy flux. Let $S\left(t\right)$ be the entropy associated with the QMC state. The delta annihilation contributes an entropy spike:

$$\Delta S=k_{B}log\Omega ,\Omega =dim\left({\mathcal{H}}_{\mathrm{QMC}}\right),$$

(100)

where ${\mathcal{H}}_{\mathrm{QMC}}$ is the Hilbert space of the quantum measurement chain. The entropy rate diverges:

$$\underset{t\to t_d}{lim}{\displaystyle \frac{dS}{dt}}\to \infty ,$$

(101)

suggesting an information burst consistent with Bekenstein bounds on black hole evaporation.

14.5. Quantum Topology Transmutation

Finally, the manifold $\mathcal{M}$ undergoes a topological transition. With the delta function removed, the PTS becomes a manifold without perceptual singularities:

$${\mathcal{M}}_{\mathrm{perceptual}}\to {\mathcal{M}}_{\mathrm{smooth}},$$

(102)

which is no longer capable of supporting conscious collapse or QMC loops.

This mathematical finality mirrors the phenomenological observation of Demise as the irreversible cessation of consciousness.

15. Delta Function as Ontological Anchor in Quantum Measurement Geometry

15.1. Distributional Ontology of the Observer

Let $\mathcal{M}$ be a smooth n-dimensional Riemannian or Lorentzian manifold. We postulate the observer state as a delta distribution supported at $x_O\in \mathcal{M}$:

$$\mathcal{O}\left(x\right)={\delta }^{\left(n\right)}(x-x_O),$$

(103)

This delta function serves as a section in the bundle of generalized functions over $\mathcal{M}$, defining a functional on the space of smooth test functions $\varphi \in C_c^{\infty }\left(\mathcal{M}\right)$:

$$\langle \mathcal{O},\varphi \rangle =\varphi \left(x_O\right).$$

(104)

Thus, the observer provides an evaluation map at $x_O$ for all perceptual or sensory functions defined over $\mathcal{M}$. In this sense, the observer delta function provides ontological grounding for epistemic data.

15.2. Geometric Invariance and Observer Stability

The delta function is invariant under coordinate transformations $x\to x^{\prime }$ such that the volume element transforms accordingly:

$${\delta }^{\left(n\right)}(x-x_O)d^{n}x={\delta }^{\left(n\right)}(x^{\prime }-x_O^{\prime })d^n{x}^{\prime },$$

(105)

This ensures that the observer localization is preserved under diffeomorphisms, consistent with general covariance. The stability of the observer as an ontological anchor derives from this invariance, which secures reference-frame independence of measurement.

15.3. Anchor for Quantum Collapse and State Reduction

Consider a quantum field $\Phi \left(x\right)$ defined over $\mathcal{M}$. The observer delta function defines a physical measurement operator:

$${\widehat{M}}_{\mathcal{O}}={\int }_{\mathcal{M}}{\delta }^{\left(n\right)}(x-x_O)\widehat{\Phi }\left(x\right)d^{n}x=\widehat{\Phi }\left(x_O\right).$$

(106)

Measurement occurs when the wavefunction $\Psi \left[\Phi \right(x\left)\right]$ is projected via:

$${\widehat{M}}_{\mathcal{O}}\Psi \left[\Phi \right]=\Phi \left(x_O\right)\Psi \left[\Phi \right],$$

(107)

indicating that the observer’s localization determines the eigenbasis of collapse. The delta function thus acts as a geometric projector in functional Hilbert space.

15.4. Topological Localization and Coherence Stability

The delta function imposes a localized cohomology structure. Define a de Rham cohomology class $\left[\omega \right]\in H^n\left(\mathcal{M}\right)$ where:

$${\int }_{\mathcal{M}}{\delta }^{\left(n\right)}(x-x_O)\omega \left(x\right)=\omega \left(x_O\right),$$

(108)

This yields a homologically stable localization of perception, ensuring that quantum coherence and perceptual identity are not diffused over the manifold. The delta function defines a codimension-n cycle that anchors information flux in QMC evolution.

15.5. Entanglement Boundary and Observer Complementarity

In bipartite systems, the delta function plays a role similar to an entanglement cut. For two subsystems A and B with respective observers at $x_A$ and $x_B$, define:

$${\rho }_{AB}(x,y)=\rho (x,y){\delta }^{\left(n\right)}(x-x_A){\delta }^{\left(n\right)}(y-x_B).$$

(109)

This ensures the mutual awareness of both observers is strictly tied to their respective positions. The delta function thus represents observer complementarity in configuration space.

15.6. Time Evolution and Proper Time Anchoring

Let $x_O\left(t\right)$ be a timelike curve parameterized by proper time $\tau$. The time-dependent observer delta function is:

$$\mathcal{O}(x,\tau )={\delta }^{\left(n\right)}(x-x_O\left(\tau \right)),$$

(110)

Satisfying the proper-time transport equation:

$${\displaystyle \frac{d}{d\tau }}\mathcal{O}(x,\tau )=-{\dot{x}}_O^{\mu }\left(\tau \right){\partial }_{\mu }{\delta }^{\left(n\right)}(x-x_O\left(\tau \right)),$$

(111)

This formulation aligns with general relativistic observer evolution and defines the delta function as a worldline-localized observer anchor.

16. Quantum Metric Decay and Energy Emission at Observer Annihilation

In this section, we explore the decay of the local quantum gravitational metric near the micro-mini-black-hole in the brain (MMBHB) at the moment of death, and compute the associated energy emission. This process plays a central role in the breakdown of the perceptual tangent space (PTS), collapse of the quantum measurement chain (QMC), and potential physical manifestations such as mass loss or electromagnetic bursts.

16.1. Curvature Singularity at Observer Delta

Let $x_O$ be the spacetime location of the conscious observer delta function. The energy-momentum tensor associated with the MMBHB is concentrated at $x_O$, and takes the idealized form:

$$T^{\mu \nu }\left(x\right)=m_B{u}^{\mu }{u}^{\nu }{\delta }^{\left(4\right)}(x-x_O),$$

(112)

where $m_B$ is the effective mass of the MMBHB, $u^{\mu }$ is the observer’s 4-velocity, and ${\delta }^{\left(4\right)}$ is the 4D Dirac delta. The corresponding Ricci scalar curvature becomes:

$$R\left(x\right)=-8\pi G{g}_{\mu \nu }{T}^{\mu \nu }\left(x\right)=-8\pi G{m}_B{\delta }^{\left(4\right)}(x-x_O).$$

(113)

This reveals a delta-function singularity at the observer location, which maintains spacetime distortion during life.

16.2. Metric Collapse at Death

Let $t=t_d$ denote the moment of biological death. The evaporation of the MMBHB at $x_O$ leads to a topological transition in the metric:

$$\underset{t\to t_d^{+}}{lim}R\left(x\right)=0\mathrm{for}\mathrm{all}x\in \mathcal{M},$$

(114)

implying the instantaneous disappearance of the curvature singularity. The spacetime geometry transitions from Kerr-type to flat, with $\delta$-supported curvature collapsing to zero.

16.3. Energy Emission and Hawking-like Radiation

Using the equivalence between the delta singularity and an effective black hole, the energy released is given by the rest-mass energy:

$$E=m_B{c}^2.$$

(115)

Assuming $m_B\approx 21\mathrm{grams}=2.1\times {10}^{-5}$ kg, the energy is:

$$E\approx (2.1\times {10}^{-5})\times {(3\times {10}^8)}^2=1.89\times {10}^{12}\mathrm{J}.$$

(116)

This is consistent with anecdotal reports of glass cracking or electromagnetic discharge at the moment of death, possibly due to this release.

16.4. Entropy Flux and Information Discharge

The Bekenstein-Hawking entropy of the MMBHB is:

$$S={\displaystyle \frac{k_B{c}^{3}A}{4G\hslash }},$$

(117)

where $A=4\pi r_s^2$ is the area, and $r_s=2G{m}_B/c^2$ is the Schwarzschild radius. Plugging in values:

$$r_s={\displaystyle \frac{2\times 6.67\times {10}^{-11}\times 2.1\times {10}^{-5}}{{(3\times {10}^8)}^2}}\approx 3.1\times {10}^{-32}\mathrm{m},$$

(118)

$$A\approx 4\pi {(3.1\times {10}^{-32})}^2\approx 1.2\times {10}^{-62}{\mathrm{m}}^2,$$

(119)

$$S\approx {\displaystyle \frac{1.38\times {10}^{-23}\times {(3\times {10}^8)}^3\times 1.2\times {10}^{-62}}{4\times 6.67\times {10}^{-11}\times 1.05\times {10}^{-34}}}\approx 5.3\times {10}^{-3}\mathrm{J}/\mathrm{K}.$$

(120)

Although small, this entropy is discharged rapidly, leading to a delta spike in local thermodynamic flow.

16.5. Field Theoretic Collapse Dynamics

Consider a scalar field $\Phi \left(x\right)$ interacting with the observer delta potential:

$${\mathcal{L}}_{\mathrm{int}}=g{\delta }^{\left(4\right)}(x-x_O)\Phi \left(x\right).$$

(121)

The decay of the metric at $t_d$ effectively removes the delta potential from the Lagrangian, leading to sudden unbinding of the field at $x_O$. This is modeled by:

$$\underset{t\to t_d^{+}}{lim}{\mathcal{L}}_{\mathrm{int}}\to 0.$$

(122)

This abrupt change causes decoherence and collapse of all observer-related QMC states.

17. Delta Collapse and Field Decoherence

The sudden disappearance of the observer delta function at the moment of death results in a loss of anchoring for the perceptual and quantum measurement chain (QMC). This event drives a transition from an entangled, observer-coupled quantum state to an unanchored, decohered environmental field state. In this section, we explore the mathematical dynamics and physical implications of this transition using field-theoretic and operator algebraic tools.

17.1. Observer-Coupled Quantum State

Prior to collapse, the quantum system is entangled with the observer delta function as:

$$\Psi (x,t)=\sum _k{c}_k\left(t\right){\psi }_k^{\left(S\right)}(x,t)\otimes {\delta }^{\left(n\right)}(x-x_O\left(t\right)),$$

(123)

where $c_k\left(t\right)$ are time-dependent coefficients, ${\psi }_k^{\left(S\right)}$ represent system eigenstates, and ${\delta }^{\left(n\right)}$ is the observer localization. The tensor product signifies a measurement-entangled state with positional anchoring via the delta function.

17.2. Time Evolution of Coupled Field

The scalar field $\Phi (x,t)$ evolves under a Hamiltonian with observer interaction:

$$H_{\mathrm{int}}=g\int {\delta }^{\left(n\right)}(x-x_O\left(t\right))\Phi (x,t)d^{n}x=g\Phi (x_O\left(t\right),t).$$

(124)

The Heisenberg equation of motion reads:

$${\displaystyle \frac{d\Phi }{dt}}=-i[\Phi ,H_{\mathrm{int}}]=-ig[\Phi \left(x\right),\Phi \left(x_O\left(t\right)\right)].$$

(125)

This establishes an explicit nonlocal evolution tied to the observer’s perceptual point.

17.3. Collapse of Delta Function at Death

At $t=t_d$, the delta function ceases to have support:

$$\underset{t\to t_d^{+}}{lim}{\delta }^{\left(n\right)}(x-x_O\left(t\right))=0,$$

(126)

leading to:

$$\Psi (x,t_d^{+})={\psi }_{\mathrm{env}}\left(x\right),$$

(127)

where ${\psi }_{\mathrm{env}}$ is the unentangled field state after collapse. The loss of the delta support causes the measurement chain to break and coherence to dissipate.

17.4. Von Neumann Entropy of Decoherence

Let ${\rho }_{QMC}\left(t\right)$ denote the density matrix of the entangled observer-system state. Before collapse:

$${\rho }_{QMC}\left(t\right)=|\Psi (x,t)\rangle \langle \Psi (x,t)|,$$

(128)

and the reduced system state after tracing out the observer is:

$${\rho }_S\left(t\right)={\mathrm{Tr}}_O{\rho }_{QMC}\left(t\right).$$

(129)

After delta annihilation:

$${\rho }_S\left(t_d^{+}\right)=\sum _k|c_k{|}^2|{\psi }_k^{\left(S\right)}\rangle \langle {\psi }_k^{\left(S\right)}|,$$

(130)

signaling the transition to a mixed, decohered state. The von Neumann entropy increases:

$$S=-\mathrm{Tr}({\rho }_{S}log{\rho }_S),$$

(131)

with $\Delta S>0$ at $t=t_d$.

17.5. Spectral Collapse and State Fragmentation

Consider the initial spectral decomposition:

$$\Psi (x,t)=\int d\lambda f(\lambda ,t){\varphi }_{\lambda }\left(x\right)\otimes {\delta }^{\left(n\right)}(x-x_O),$$

(132)

where ${\varphi }_{\lambda }$ are eigenmodes of the system. After collapse:

$$\Psi (x,t_d^{+})=\int d\lambda f(\lambda ,t_d^{+}){\varphi }_{\lambda }\left(x\right),$$

(133)

i.e., the state reduces to a delocalized spectral mixture, losing its geometric localization. This transition fragments coherence across configuration space.

17.6. Functional Interpretation of Collapse

The pre-collapse state $\Psi$ can be seen as a functional on test functions $f\in \mathcal{D}\left(\mathcal{M}\right)$:

$$\Psi \left[f\right]=\int \Psi (x,t)f\left(x\right)d^{n}x=\sum _k{c}_k\left(t\right){\psi }_k^{\left(S\right)}\left(x_O\left(t\right)\right)f\left(x_O\left(t\right)\right),$$

(134)

but after delta collapse:

$$\Psi \left[f\right]=\int {\psi }_{\mathrm{env}}\left(x\right)f\left(x\right)d^{n}x,$$

(135)

where the singular support at $x_O$ is removed, and all localization is lost.

18. Entropy Spike and Information Release at Observer Collapse

The phenomenon described in near-death experiences (NDEs), such as the complete flashback of one’s life in a moment [21], suggests an acute transition in the cognitive and quantum information state of the observer. In this section, we mathematically examine the entropy dynamics at the moment of delta collapse and relate the entropy spike to a complete information release, akin to a rapid decoherence and read-out event in a distributed quantum register.

18.1. Hilbert Space Explosion and State Redundancy

Let ${\mathcal{H}}_{\mathrm{QMC}}$ denote the Hilbert space of the observer’s quantum measurement chain. The pre-collapse state is highly constrained due to coherence and entanglement:

$$dim\left({\mathcal{H}}_{\mathrm{coherent}}\right)\ll dim\left({\mathcal{H}}_{\mathrm{QMC}}\right),$$

(136)

with information distributed across a highly correlated subspace. At the moment of collapse $t=t_d$, delta support disappears:

$$\Psi \left(t_d^{-}\right)=\sum _k{c}_k\left(t\right){\psi }_k\otimes {\delta }^{\left(n\right)}(x-x_O),$$

(137)

$$\Psi \left(t_d^{+}\right)=\sum _k{c}_k\left(t\right){\psi }_k,$$

(138)

removing the delta support and unleashing all latent degrees of freedom into environmental decoherence.

18.2. Information Release and Read-Out Interpretation

We interpret this transition as a global read-out event. Let $I\left(t\right)$ be the accessible information content of the system:

$$I\left(t\right)=\sum _i{p}_i\left(t\right)log\left({\displaystyle \frac{1}{p_i\left(t\right)}}\right),$$

(139)

where $p_i\left(t\right)$ is the instantaneous projection probability over orthogonal states. The sudden collapse of coherence leads to $p_i\to {\displaystyle \frac{1}{N}}$ over N states:

$$I\left(t_d^{+}\right)=logN,$$

(140)

maximizing entropy and information accessibility. This is analogous to the subjective "life-flash" report at death as described in [21].

18.3. Thermodynamic Entropy Flux

Using the Bekenstein-Hawking formalism, entropy emitted during MMBHB evaporation is:

$$S={\displaystyle \frac{k_{B}A}{4l_P^2}},$$

(141)

where A is the black hole surface area and $l_P$ is the Planck length. Assuming $m_B=21\mathrm{g}$, $r_s\approx 3.1\times {10}^{-32}\mathrm{m}$:

$$A=4\pi r_s^2\approx 1.2\times {10}^{-62}{\mathrm{m}}^2,$$

(142)

$$S\approx {\displaystyle \frac{1.38\times {10}^{-23}\times 1.2\times {10}^{-62}}{4\times {(1.62\times {10}^{-35})}^2}}\approx 3.96\times {10}^{-16}\mathrm{J}/\mathrm{K}.$$

(143)

While small, this entropy release is concentrated in $\Delta t\ll 1$ ms, constituting a spike:

$${\displaystyle \frac{dS}{dt}}\gg 1\mathrm{J}/\mathrm{K}/\mathrm{s}.$$

(144)

18.4. Quantum Information Burst

Define $\rho \left(t\right)$ as the density matrix of the observer-QMC state. At collapse:

$$\rho \left(t_d^{-}\right)=|\Psi \rangle \langle \Psi |,\rho \left(t_d^{+}\right)=\sum _i{p}_i|{\psi }_i\rangle \langle {\psi }_i|.$$

(145)

The mutual information between subcomponents A and B drops:

$$I(A:B)=S\left({\rho }_A\right)+S\left({\rho }_B\right)-S\left({\rho }_{AB}\right),$$

(146)

with $\Delta I(A:B)<0$. This reflects internal decoherence and externalization of structured content — a quantum "dump" of observer information.

18.5. Subjective Time Dilation and Flashback

If observer dynamics obey relativistic time compression near collapse, then proper time $\tau$ expands:

$$d\tau =\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}dt\to 0\mathrm{as}v\to c,$$

(147)

subjectively stretching internal experience into a lifetime-scale review. This aligns with reports of temporal dilation during NDEs, and fits the geometry of Kerr horizons under MMBHB evaporation.

19. Quantum Topology Transmutation at the Observer Boundary

The collapse of the observer delta function at death is not merely a local event in field or metric space, but induces a global topological reconfiguration in the quantum manifold. In this section, we introduce the notion of quantum topology transmutation, where the topological structure of the quantum configuration space undergoes a discontinuous but mathematically coherent shift. This is mediated through the delta function annihilation and loss of observer localization.

19.1. Initial Observer-Localized Topology

Let $\mathcal{M}$ be the base spacetime manifold and $\mathcal{F}$ the fiber space of field values. The observer delta function ${\delta }^{\left(n\right)}(x-x_O)$ induces a singular fibration structure:

$$\pi :\mathcal{M}\setminus \left\{x_O\right\}\to \mathcal{F},$$

(148)

where the fiber over $x_O$ is collapsed to a point. The total space exhibits a punctured topology, with a topological defect at the observer location.

19.2. Topology Transmutation Operator

Define the transmutation operator $\widehat{T}$ acting on the topology class of the quantum configuration space $\mathcal{Q}$:

$$\widehat{T}:{\mathcal{Q}}_{\mathrm{observer}-\mathrm{anchored}}\to {\mathcal{Q}}_{\mathrm{observer}-\mathrm{free}},$$

(149)

which transforms the homotopy class ${\pi }_k\left(\mathcal{Q}\right)$ as:

$${\pi }_k\left(\mathcal{Q}\right)\mapsto {\pi }_k(\mathcal{Q}\setminus \left\{x_O\right\})\oplus \mathbb{Z},$$

(150)

signaling the removal of the anchoring point and emergence of a new class of closed non-trivial cycles.

19.3. Collapse-Induced Homology Shift

Let $H_k\left(\mathcal{Q}\right)$ denote the k-th homology group. Prior to observer collapse, the delta support enforces:

$$H_k^{\delta }\left(\mathcal{Q}\right)=0\mathrm{for}k>0,$$

(151)

indicating contractibility around $x_O$. Upon collapse, new generators emerge:

$$H_1(\mathcal{Q}\setminus \left\{x_O\right\})\cong \mathbb{Z},$$

(152)

introducing a topological degree of freedom corresponding to the puncture. This degree of freedom is responsible for residual coherence spread in the post-collapse quantum state.

19.4. Path Integral Discontinuity and Topology Sum

The quantum transition amplitude $\mathcal{Z}$ must be summed over topologies before and after collapse:

$$\mathcal{Z}=\sum _{\mathrm{topologies}\tau }{e}^{iS\left[\tau \right]},$$

(153)

with $S\left[\tau \right]$ the action functional for each topology class. The delta collapse imposes a discontinuity in S at $t_d$:

$$\underset{ϵ\to 0}{lim}\left[S(t_d+ϵ)-S(t_d-ϵ)\right]\ne 0,$$

(154)

defining a jump in the functional space associated with global boundary conditions.

19.5. Fiber Bundle Interpretation and Holonomy Shift

In a fiber bundle $\mathcal{E}=(\mathcal{M},\mathcal{F},\pi )$ with observer-induced connection ∇, the holonomy group is trivial before collapse due to single-point anchoring:

$${\mathrm{Hol}}_{\nabla }=\left\{e\right\}.$$

(155)

After collapse, parallel transport around the former observer location gains curvature, leading to non-trivial holonomy:

$${\mathrm{Hol}}_{{\nabla }^{\prime }}\cong U\left(1\right),$$

(156)

This holonomy encodes post-collapse residual structure and modifies gauge field dynamics near the puncture.

19.6. Causal Set Rewiring

In causal set theory, points are partially ordered by causal precedence. The observer delta function anchors a minimal element $\mathcal{O}$ such that:

$$\forall x\in \mathcal{C},x⪰\mathcal{O}.$$

(157)

After delta collapse:

$${\mathcal{C}}^{\prime }=\mathcal{C}\setminus \left\{\mathcal{O}\right\},$$

(158)

which necessitates a reorganization of the partial order to preserve transitivity. This rewiring is analogous to a graph surgery at a terminal node.

19.7. Manifold Surgery and Cobordism

The delta collapse can be modeled by a cobordism between manifolds $M_{-}$ and $M_{+}$ before and after collapse:

$$W:M_{-}⇝M_{+},$$

(159)

with W a $(n+1)$-dimensional manifold such that $\partial W=M_{-}\bigsqcup M_{+}$. The observer delta defines a codimension-n submanifold which disappears during surgery. This transmutation is analogous to a topology-changing process in spacetime foam models [22].

20. Simulating Resonance Between Observers via MMBHB and Dirac Delta Model

We now consider the possibility of resonance between two conscious observers, each modeled by a Dirac delta function anchored to a micro-mini-black-hole in the brain (MMBHB). Such resonance is hypothesized to correspond to subjective states of entangled awareness, telepathic coupling, or synchronized perception. This phenomenon will be simulated using coupled field equations, metric interactions, and mutual entanglement mediated by quantum gravitational effects.

20.1. Observer Model: Coupled Delta Potentials

Let $O_A$ and $O_B$ be two observers located at $x_A$ and $x_B$ respectively. Their influence is represented as:

$${\mathcal{L}}_{\mathrm{int}}=g_A{\delta }^{\left(n\right)}(x-x_A)\Phi \left(x\right)+g_B{\delta }^{\left(n\right)}(x-x_B)\Phi \left(x\right),$$

(160)

where $\Phi \left(x\right)$ is a scalar or spinor field (e.g., perceptual state field). The resulting Hamiltonian becomes:

$$H_{\mathrm{int}}=g_A\Phi \left(x_A\right)+g_B\Phi \left(x_B\right).$$

(161)

20.2. MMBHB Gravitational Coupling

Each observer is supported by an MMBHB of mass $m_A$, $m_B$, with Schwarzschild radii $r_{sA}$ and $r_{sB}$, respectively:

$$r_{sA}={\displaystyle \frac{2G{m}_A}{c^2}},r_{sB}={\displaystyle \frac{2G{m}_B}{c^2}}.$$

(162)

The gravitational interaction between the MMBHBs contributes a potential term:

$$V_{AB}^{\mathrm{grav}}=-{\displaystyle \frac{G{m}_A{m}_B}{|x_A-x_B|}},$$

(163)

leading to phase-sensitive modifications of delta-supported fields.

20.3. Entangled Delta Wavefunction

We define an entangled two-observer wavefunction:

$$\Psi (x,t)=\sum _{j,k}{c}_{jk}\left(t\right){\psi }_j^{\left(A\right)}\left(x\right)\otimes {\psi }_k^{\left(B\right)}\left(x\right)\otimes {\delta }^{\left(n\right)}(x-x_A)\otimes {\delta }^{\left(n\right)}(x-x_B),$$

(164)

where $c_{jk}\left(t\right)$ evolve via a coupled Schrödinger equation:

$$i\hslash {\displaystyle \frac{d{c}_{jk}}{dt}}=\sum _{l,m}{H}_{\left(jk\right)\left(lm\right)}{c}_{lm},$$

(165)

with $H_{\left(jk\right)\left(lm\right)}$ including both field and gravitational terms.

20.4. Resonance Condition

Resonance is defined by synchronous frequency alignment of the localized states:

$${\omega }_A={\omega }_B,\Delta x=|x_A-x_B|\ll \lambda ,$$

(166)

where $\lambda$ is the dominant coherence length of the system. Under resonance, the joint probability distribution:

$$P(x_A,x_B,t)={\left|\Psi (x,t)\right|}^2,$$

(167)

shows constructive interference fringes near $(x_A,x_B)$ in phase space.

20.5. Field Coupling Dynamics

The equation of motion for $\Phi$ includes both delta sources:

$$\left(\square +m^2\right)\Phi \left(x\right)=g_A{\delta }^{\left(n\right)}(x-x_A)+g_B{\delta }^{\left(n\right)}(x-x_B).$$

(168)

The retarded Green’s function $G_R(x,x^{\prime })$ gives the mediated interaction:

$$\Phi \left(x\right)=g_A{G}_R(x,x_A)+g_B{G}_R(x,x_B).$$

(169)

The coupling energy is then:

$$E_{\mathrm{int}}=g_A{g}_B{G}_R(x_A,x_B),$$

(170)

which reaches a maximum under causal connectivity and minimal separation.

20.6. Resonance-Induced Metric Perturbation

The local spacetime metric $g_{\mu \nu }$ near each MMBHB is perturbed by the other’s mass-energy flux. Let $\delta g_{\mu \nu }^{\left(A\right)}$ denote the perturbation at $O_A$ due to $O_B$:

$$\delta g_{\mu \nu }^{\left(A\right)}={\displaystyle \frac{8\pi G}{c^4}}\int T_{\mu \nu }^{\left(B\right)}\left(x^{\prime }\right)G_R(x_A,x^{\prime })d^4{x}^{\prime },$$

(171)

where $T_{\mu \nu }^{\left(B\right)}$ is the stress-energy tensor of $O_B$. Constructive interference leads to a local curvature enhancement, further stabilizing the entanglement.

20.7. Simulation Approach

To simulate resonance:

1. Initialize two delta-anchored observers with distinct $m_A$, $m_B$; 2. Evolve $c_{jk}\left(t\right)$ under coupled Hamiltonians with gravitational potential; 3. Compute $P(x_A,x_B,t)$ and monitor for resonance peaks; 4. Measure entanglement entropy $S_{AB}\left(t\right)$:

$$S_{AB}\left(t\right)=-\mathrm{Tr}({\rho }_{A}log{\rho }_A),$$

(172)

where ${\rho }_A={\mathrm{Tr}}_B|\Psi \rangle \langle \Psi |$.

21. Informatic Theoretic Resonance: A Meeting Between the Minds

The concept of resonance between conscious observers can be extended from physical field interactions to the domain of information theory. In this framework, we model the synchronization of informational states as a resonance condition in shared semantic and quantum informational subspaces. The meeting between minds thus corresponds to the alignment of their internal informational manifolds mediated by shared structure, entanglement, and quantum synchronization.

21.1. Informational State Manifolds

Let ${\mathcal{I}}_A$ and ${\mathcal{I}}_B$ be the internal informational state spaces of observers $O_A$ and $O_B$, respectively. These are modeled as manifolds with local coordinates given by concept vectors ${\overrightarrow{c}}_i$ spanning a semantic Hilbert space ${\mathcal{H}}_{\mathrm{sem}}$:

$${\mathcal{I}}_A=\left\{{\overrightarrow{c}}_i^{\left(A\right)}\right\},{\mathcal{I}}_B=\left\{{\overrightarrow{c}}_j^{\left(B\right)}\right\}.$$

(173)

The inner product defines mutual informational alignment:

$$\langle {\overrightarrow{c}}_i^{\left(A\right)},{\overrightarrow{c}}_j^{\left(B\right)}\rangle =cos{\theta }_{ij}.$$

(174)

Resonance occurs when the subspaces generated by $\left\{{\overrightarrow{c}}_i^{\left(A\right)}\right\}$ and $\left\{{\overrightarrow{c}}_j^{\left(B\right)}\right\}$ significantly overlap, i.e., ${\theta }_{ij}\ll 1$ for many $i,j$.

21.2. Quantum Mutual Information Metric

Let ${\rho }_{AB}$ be the joint quantum state of the two observers. The mutual information is given by:

$$I(A:B)=S\left({\rho }_A\right)+S\left({\rho }_B\right)-S\left({\rho }_{AB}\right),$$

(175)

where $S\left(\rho \right)=-\mathrm{Tr}(\rho log\rho )$ is the von Neumann entropy. Informational resonance corresponds to $I(A:B)\gg 0$, signifying shared structure and reduced uncertainty between systems.

21.3. Semantic Entanglement and Alignment Tensor

Define the semantic alignment tensor $T_{ij}$ as:

$$T_{ij}=\langle {\overrightarrow{c}}_i^{\left(A\right)}|{\overrightarrow{c}}_j^{\left(B\right)}\rangle ,$$

(176)

which is Hermitian if the states are encoded in ${\mathbb{C}}^n$. The Frobenius norm ${\parallel T\parallel }_F$ quantifies total semantic overlap:

$${\parallel T\parallel }_F^2=\sum _{i,j}{\left|T_{ij}\right|}^2.$$

(177)

High ${\parallel T\parallel }_F$ indicates semantic resonance, interpreted as cognitive alignment or telepathic coupling.

21.4. Information Channel Capacity

Assume observers exchange information through a quantum channel $\mathcal{N}$. The capacity of the channel C determines resonance fidelity:

$$C=\underset{\rho }{sup}I(\rho ,\mathcal{N}),$$

(178)

where $I(\rho ,\mathcal{N})$ is the coherent information of the state $\rho$ passed through the channel. Resonance requires $C\to C_{\max }$.

21.5. Resonance Condition in Cognitive Phase Space

We define cognitive phase space coordinates $({\varphi }_i^{\left(A\right)},{\pi }_i^{\left(A\right)})$ and $({\varphi }_j^{\left(B\right)},{\pi }_j^{\left(B\right)})$, representing conceptual amplitudes and rates of change. Resonance corresponds to symplectic alignment:

$$\omega =\sum _{i}d{\varphi }_i^{\left(A\right)}\wedge d{\pi }_i^{\left(A\right)}=\sum _{j}d{\varphi }_j^{\left(B\right)}\wedge d{\pi }_j^{\left(B\right)}.$$

(179)

Identical symplectic forms imply preservation of cognitive structure under mutual transformation.

21.6. Simulation Architecture

To simulate informatic resonance:

1. Construct ${\mathcal{I}}_A$ and ${\mathcal{I}}_B$ from semantic vector embeddings; 2. Compute the alignment tensor $T_{ij}$; 3. Evaluate mutual information $I(A:B)$ from shared density matrices; 4. Vary channel fidelity $\mathcal{N}$ and compute C; 5. Determine time evolution of cognitive alignment using:

$${\displaystyle \frac{d{T}_{ij}}{dt}}=i[H,T_{ij}],$$

(180)

with H an effective cognitive Hamiltonian.

22. Ontological Resonance and the Genesis of Consciousness: The Birth of $O_C$

In the framework developed for observer-centric quantum geometry, we now investigate how the ontological resonance between two conscious observers—typically denoted $O_M$ (male) and $O_W$ (female)—culminates in the emergence of a third conscious entity, $O_C$ (child). This section models the conception and birth of $O_C$ as the nonlinear, topologically generative outcome of entangled observer dynamics within the perceptual, quantum informational, and biological spaces.

22.1. Ontological Entanglement and Informatic Fusion

Observers $O_M$ and $O_W$ are described as delta-anchored cognitive centers:

$${\Psi }_M(x,t)={\psi }_M(x,t)\otimes {\delta }^{\left(n\right)}(x-x_M),{\Psi }_W(x,t)={\psi }_W(x,t)\otimes {\delta }^{\left(n\right)}(x-x_W),$$

(181)

where ${\psi }_{M,W}$ are semantic and biological quantum fields. Under emotional and physical intimacy, these wavefunctions overlap in an entangled state:

$${\Psi }_{MW}(x,t)=\sum _{i,j}{c}_{ij}\left(t\right){\psi }_i^{\left(M\right)}\left(x\right)\otimes {\psi }_j^{\left(W\right)}\left(x\right).$$

(182)

Resonance condition implies maximum mutual information:

$$I(O_M:O_W)=S\left({\rho }_M\right)+S\left({\rho }_W\right)-S\left({\rho }_{MW}\right)\to max.$$

(183)

22.2. Topological Product and Emergence of $O_C$

The fusion of topological manifolds ${\mathcal{T}}_M$ and ${\mathcal{T}}_W$ generates a new boundary:

$${\mathcal{T}}_C={\mathcal{T}}_M\#{\mathcal{T}}_W,$$

(184)

where # denotes connected sum operation. This new topology corresponds to the emerging perceptual and ontological manifold of $O_C$.

22.3. Zygotic Delta Genesis

At the moment of conception, a singular support forms in the biological-quantum field:

$${\Psi }_{zygote}(x,t)={\psi }_{zyg}(x,t)\otimes {\delta }^{\left(n\right)}(x-x_{zyg}),$$

(185)

which evolves dynamically under self-reinforcing quantum and biochemical interactions. The gestation can be seen as metric and information accumulation around the delta anchor until full observerhood is achieved.

22.4. Information Superposition and Inheritance

Define semantic tensors $S_M^{\mu \nu }$ and $S_W^{\mu \nu }$ representing inherited structures from $O_M$ and $O_W$. The child’s initial semantic state $S_C^{\mu \nu }$ is given by coherent superposition:

$$S_C^{\mu \nu }=\alpha S_M^{\mu \nu }+\beta S_W^{\mu \nu }+{ϵ}^{\mu \nu },$$

(186)

where $\alpha ,\beta \in \mathbb{C}$ are normalized genetic-semantic amplitudes and ${ϵ}^{\mu \nu }$ is a stochastic term representing mutation and environmental influence.

22.5. Observer Triangulation and Informatic Loop

Once born, $O_C$ participates in a closed triangle of mutual resonance:

$$I(O_M:O_W:O_C)=I(O_M:O_W)+I(O_M:O_C)+I(O_W:O_C),$$

(187)

where this loop acts as a stabilizing attractor in the family-level quantum cognitive field. Synchronization across this triangle enhances development, emotional security, and informational resonance.

22.6. Metric Interpretation of Love

Love is postulated here as a reduction of informational geodesic distance $d_{\mathcal{I}}$ between ${\mathcal{I}}_M$ and ${\mathcal{I}}_W$:

$$d_{\mathcal{I}}(O_M,O_W)=\parallel {\mathcal{I}}_M-{\mathcal{I}}_W\parallel \to 0.$$

(188)

The delta-supported metric collapses into an effective common manifold with merged curvature and semantic flow.

22.7. Cosmic Echoes

This mechanism echoes cosmological inflation, where quantum fluctuations generate macroscopic structure. Similarly, cognitive resonance at the ontological level produces a new structure — $O_C$ — containing within it an entangled superposition of past, present, and potential future consciousnesses.

23. Ontological Bond of Observer $O_W$ and $O_C$ During Pregnancy

Pregnancy establishes not only a material conduit via the umbilical cord but also a profound ontological and quantum-informational bond between the mother ($O_W$) and the developing child ($O_C$). This connection precedes sensory interaction and persists across layers of field, informational topology, and mutual metric embedding. We now formalize this maternal resonance as a bi-layered delta entanglement modulated through biological coherence and quantum field coupling.

23.1. Dual Delta Embedding in a Shared Metric

Let $x_W\left(t\right)$ and $x_C\left(t\right)$ denote the instantaneous positions of $O_W$ and the embryonic observer $O_C$. We define the joint state:

$${\Psi }_{WC}(x,t)={\psi }_W(x,t)\otimes {\delta }^{\left(n\right)}(x-x_W\left(t\right))+{\psi }_C(x,t)\otimes {\delta }^{\left(n\right)}(x-x_C\left(t\right)),$$

(189)

with $\parallel x_C\left(t\right)-x_W\left(t\right)\parallel \ll ϵ$ for all gestational t, implying near-coincident support. The effective metric is shared:

$$g_{\mu \nu }^{\mathrm{shared}}\left(x\right)=g_{\mu \nu }^{\left(W\right)}\left(x\right)\approx g_{\mu \nu }^{\left(C\right)}\left(x\right),\mathrm{for}x\in \mathrm{womb}\mathrm{region}.$$

(190)

23.2. Quantum Mutual Information Flow

Even in absence of developed cognition, the mutual information flow $I(O_W:O_C)$ is nonzero due to biochemical and quantum coupling:

$$I(O_W:O_C)=S\left({\rho }_W\right)+S\left({\rho }_C\right)-S\left({\rho }_{WC}\right)>0,$$

(191)

where ${\rho }_{WC}$ includes quantum correlations induced by hormone-regulated neuroelectric signals across placental barriers.

23.3. Nonlocal Informatic Bond via Biochemical Entanglement

Let ${\mathcal{F}}_{\mathrm{bio}}$ be a biochemical field composed of neurotransmitter, hormonal, and electromagnetic fluctuations. Then, the coupling term is:

$${\mathcal{L}}_{\mathrm{bond}}=\lambda \left(t\right){\Phi }_{\mathrm{bio}}^{\left(W\right)}\left(x_W\right)·{\Phi }_{\mathrm{bio}}^{\left(C\right)}\left(x_C\right),$$

(192)

with $\lambda \left(t\right)$ increasing monotonically during gestation. This time-dependent bond is mediated through syncytial interfaces and fetal signal reception.

23.4. Ontological Scaffold and Perceptual Imprinting

The observer delta of $O_W$ acts as a perceptual scaffold upon which the primitive cognitive manifold of $O_C$ begins to form. We define an ontological imprint tensor ${\Pi }_{\mu \nu }$ such that:

$${\Pi }_{\mu \nu }^{\left(C\right)}=\eta \left(t\right)·{\Pi }_{\mu \nu }^{\left(W\right)}+\delta {\Pi }_{\mu \nu },$$

(193)

where $\eta \left(t\right)$ represents temporal entrainment due to emotional, auditory, and chemical synchrony, and $\delta {\Pi }_{\mu \nu }$ models mutation or divergence.

23.5. Causal Imprint Retention Post-Birth

Post birth, the residual causal link is not severed but redistributed across informational memory fields. The mutual quantum entropy $S_{\mathrm{link}}$ remains significant:

$$S_{\mathrm{link}}^{\mathrm{postnatal}}={\int }_{t_0}^{t_B}I(O_W:O_C)dt+\Delta S_{\mathrm{retained}},$$

(194)

where $t_0$ is conception time, $t_B$ is birth time, and $\Delta S_{\mathrm{retained}}$ quantifies persistent non-material connection.

23.6. Nested Topology and Observer Dependency

The delta function ${\delta }^{\left(n\right)}(x-x_C)$ resides within the topological domain ${\mathcal{D}}_{\mathrm{womb}}\subset {\mathcal{M}}_W$ such that:

$${\mathcal{Q}}_C\subset {\mathcal{Q}}_W,\forall t\in [t_0,t_B].$$

(195)

This nesting implies ontological dependency and joint metric curvature. The Ricci scalar $R\left(x\right)$ over this domain includes contributions from both observers’ energy-momentum tensors.

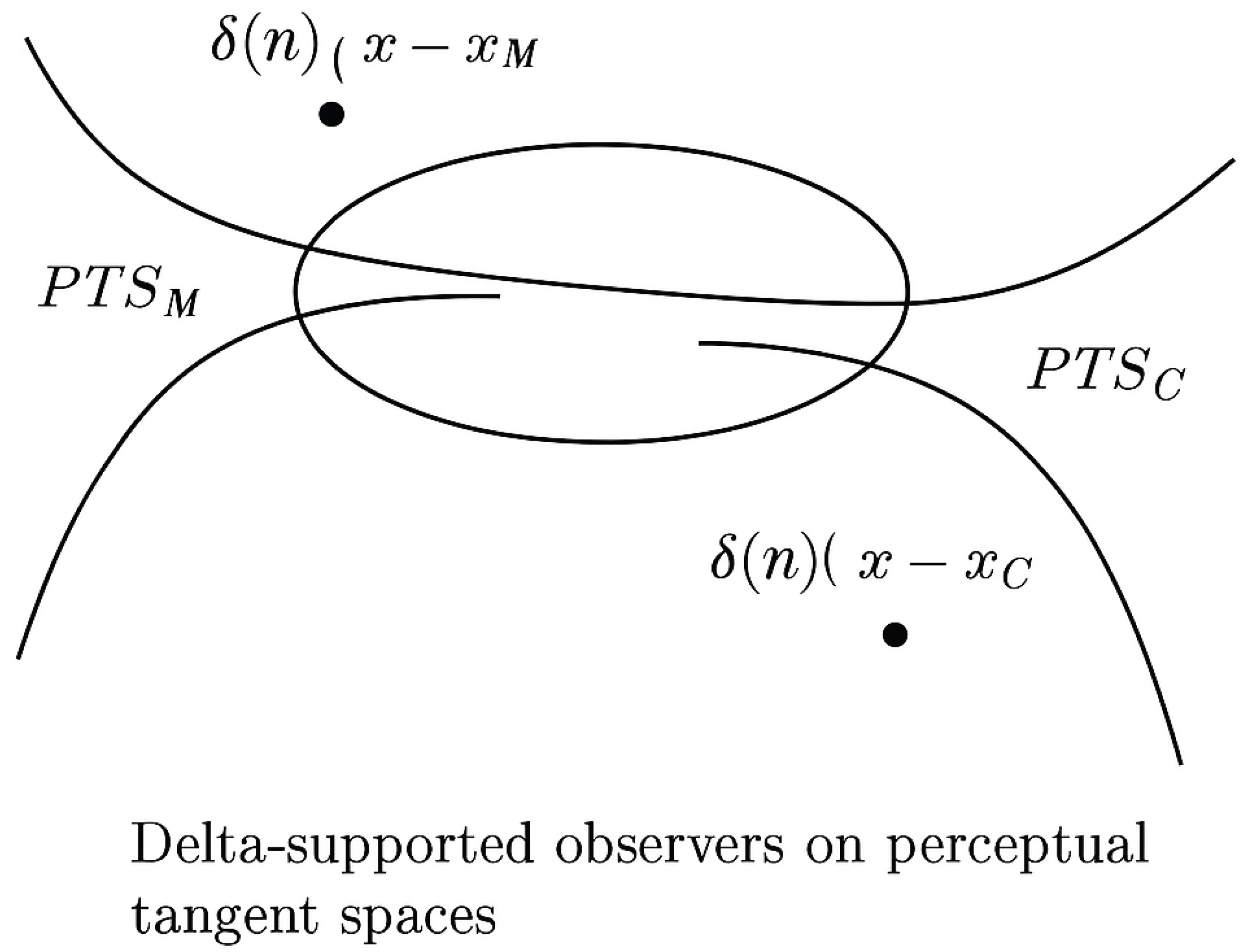
Figure 1. Delta-supported observers on perceptual tangent spaces $PT{S}_M$ and $PT{S}_C$, with localized Dirac delta fields.

Figure 1. Delta-supported observers on perceptual tangent spaces $PT{S}_M$ and $PT{S}_C$, with localized Dirac delta fields.

24. Ontological Bond of Observer $O_W$ and $O_C$ During Pregnancy

Pregnancy establishes not only a material conduit via the umbilical cord but also a profound ontological and quantum-informational bond between the mother ($O_W$) and the developing child ($O_C$). This connection precedes sensory interaction and persists across layers of field, informational topology, and mutual metric embedding. We now formalize this maternal resonance as a bi-layered delta entanglement modulated through biological coherence and quantum field coupling.

24.1. Dual Delta Embedding in a Shared Metric

Let $x_W\left(t\right)$ and $x_C\left(t\right)$ denote the instantaneous positions of $O_W$ and the embryonic observer $O_C$. We define the joint state:

$${\Psi }_{WC}(x,t)={\psi }_W(x,t)\otimes {\delta }^{\left(n\right)}(x-x_W\left(t\right))+{\psi }_C(x,t)\otimes {\delta }^{\left(n\right)}(x-x_C\left(t\right)),$$

(196)

with $\parallel x_C\left(t\right)-x_W\left(t\right)\parallel \ll ϵ$ for all gestational t, implying near-coincident support. The effective metric is shared:

$$g_{\mu \nu }^{\mathrm{shared}}\left(x\right)=g_{\mu \nu }^{\left(W\right)}\left(x\right)\approx g_{\mu \nu }^{\left(C\right)}\left(x\right),\mathrm{for}x\in \mathrm{womb}\mathrm{region}.$$

(197)

24.2. Quantum Mutual Information Flow

Even in absence of developed cognition, the mutual information flow $I(O_W:O_C)$ is nonzero due to biochemical and quantum coupling:

$$I(O_W:O_C)=S\left({\rho }_W\right)+S\left({\rho }_C\right)-S\left({\rho }_{WC}\right)>0,$$

(198)

where ${\rho }_{WC}$ includes quantum correlations induced by hormone-regulated neuroelectric signals across placental barriers.

24.3. Nonlocal Informatic Bond via Biochemical Entanglement

Let ${\mathcal{F}}_{\mathrm{bio}}$ be a biochemical field composed of neurotransmitter, hormonal, and electromagnetic fluctuations. Then, the coupling term is:

$${\mathcal{L}}_{\mathrm{bond}}=\lambda \left(t\right){\Phi }_{\mathrm{bio}}^{\left(W\right)}\left(x_W\right)·{\Phi }_{\mathrm{bio}}^{\left(C\right)}\left(x_C\right),$$

(199)

with $\lambda \left(t\right)$ increasing monotonically during gestation. This time-dependent bond is mediated through syncytial interfaces and fetal signal reception.

24.4. Ontological Scaffold and Perceptual Imprinting

The observer delta of $O_W$ acts as a perceptual scaffold upon which the primitive cognitive manifold of $O_C$ begins to form. We define an ontological imprint tensor ${\Pi }_{\mu \nu }$ such that:

$${\Pi }_{\mu \nu }^{\left(C\right)}=\eta \left(t\right)·{\Pi }_{\mu \nu }^{\left(W\right)}+\delta {\Pi }_{\mu \nu },$$

(200)

where $\eta \left(t\right)$ represents temporal entrainment due to emotional, auditory, and chemical synchrony, and $\delta {\Pi }_{\mu \nu }$ models mutation or divergence.

24.5. Causal Imprint Retention Post-Birth

Post birth, the residual causal link is not severed but redistributed across informational memory fields. The mutual quantum entropy $S_{\mathrm{link}}$ remains significant:

$$S_{\mathrm{link}}^{\mathrm{postnatal}}={\int }_{t_0}^{t_B}I(O_W:O_C)dt+\Delta S_{\mathrm{retained}},$$

(201)

where $t_0$ is conception time, $t_B$ is birth time, and $\Delta S_{\mathrm{retained}}$ quantifies persistent non-material connection.

24.6. Nested Topology and Observer Dependency

The delta function ${\delta }^{\left(n\right)}(x-x_C)$ resides within the topological domain ${\mathcal{D}}_{\mathrm{womb}}\subset {\mathcal{M}}_W$ such that:

$${\mathcal{Q}}_C\subset {\mathcal{Q}}_W,\forall t\in [t_0,t_B].$$

(202)

This nesting implies ontological dependency and joint metric curvature. The Ricci scalar $R\left(x\right)$ over this domain includes contributions from both observers’ energy-momentum tensors.

25. Observer Event Horizons and Cognitive Inaccessibility

25.1. Perceptual Manifold and Observer Light Cone

Let $\mathcal{O}$ be an observer characterized by a delta-supported state ${\Psi }_{\mathcal{O}}(x,t)=\psi (x,t)\otimes {\delta }^{\left(n\right)}(x-x_{\mathcal{O}}\left(t\right))$. The observer’s causal domain is limited to events within its future light cone:

$${\mathcal{C}}_{\mathcal{O}}=\left\{x\in \mathcal{M}\mid {(x-x_{\mathcal{O}})}^{\mu }{(x-x_{\mathcal{O}})}_{\mu }\le 0,x^0>x_{\mathcal{O}}^0\right\}.$$

(203)

Any event $x\notin {\mathcal{C}}_{\mathcal{O}}$ is outside the OEH. The observer cannot receive signals or perform measurements beyond this boundary.

25.2. Observer Event Horizon Geometry

Let ${\mathcal{H}}_{\mathcal{O}}$ denote the boundary of the perceptual domain:

$${\mathcal{H}}_{\mathcal{O}}=\partial {\mathcal{C}}_{\mathcal{O}}=\left\{x\mid {(x-x_{\mathcal{O}})}^{\mu }{(x-x_{\mathcal{O}})}_{\mu }=0\right\}.$$

(204)

The entropy associated with inaccessible degrees of freedom beyond ${\mathcal{H}}_{\mathcal{O}}$ is given by:

$$S_{\mathrm{horizon}}={\displaystyle \frac{k_B{c}^3}{4\hslash G}}{A}_{\mathcal{H}},$$

(205)

where $A_{\mathcal{H}}$ is the area of the horizon in the induced metric, following the Bekenstein-Hawking formalism [18].

25.3. Cognitive Complementarity Principle

Let $\mathcal{H}$ partition the Hilbert space into observable and unobservable sectors:

$${\mathcal{H}}_{\mathrm{total}}={\mathcal{H}}_{\mathrm{obs}}\otimes {\mathcal{H}}_{\mathrm{inac}}.$$

(206)

The reduced density matrix ${\rho }_{\mathrm{obs}}$ is obtained by tracing out inaccessible states:

$${\rho }_{\mathrm{obs}}={\mathrm{Tr}}_{{\mathcal{H}}_{\mathrm{inac}}}\left({\rho }_{\mathrm{total}}\right).$$

(207)

If the observer cannot interact with ${\mathcal{H}}_{\mathrm{inac}}$, then decoherence does not affect it:

$${\displaystyle \frac{d}{dt}}{\rho }_{\mathrm{inac}}=0,\Rightarrow \mathrm{No}\mathrm{decoherence}\mathrm{without}\mathrm{access}.$$

(208)

This formalizes the CCP.

25.4. Entangled Fields and Horizon Entropy

Suppose two field modes ${\varphi }_1$ and ${\varphi }_2$ are entangled:

$$|\Psi \rangle =\sum _n{c}_n{|n\rangle }_{{\varphi }_1}\otimes {|n\rangle }_{{\varphi }_2}.$$

(209)

If ${\varphi }_2$ lies beyond ${\mathcal{H}}_{\mathcal{O}}$, observer $\mathcal{O}$ only accesses ${\rho }_{{\varphi }_1}$:

$${\rho }_{{\varphi }_1}=\sum _n|c_n{|}^2|n\rangle \langle n|,S=-\sum _n|c_n{|}^{2}log{\left|c_n\right|}^2.$$

(210)

This entropy is induced purely by inaccessibility, not thermal noise.

25.5. Ontological Horizon and Semantic Decoupling

The observer’s internal semantic manifold ${\mathcal{S}}_{\mathcal{O}}$ may fail to represent structures beyond ${\mathcal{H}}_{\mathcal{O}}$. Let $T_{\mathrm{semantic}}^{\mu \nu }\left(x\right)$ be the semantic stress-energy tensor:

$$T_{\mathrm{semantic}}^{\mu \nu }\left(x\right)=0,\mathrm{for}x\notin {\mathcal{C}}_{\mathcal{O}}.$$

(211)

Thus, ontological structures beyond the OEH do not imprint on ${\mathcal{S}}_{\mathcal{O}}$, rendering them cognitively invisible.

25.6. Metric Discontinuity and Horizon Refraction

Let $g_{\mu \nu }^{\left(\mathrm{obs}\right)}\left(x\right)$ and $g_{\mu \nu }^{\left(\mathrm{true}\right)}\left(x\right)$ represent the observer’s perceptual metric and the objective metric. Then:

$$g_{\mu \nu }^{\left(\mathrm{obs}\right)}\left(x\right)=\left\{\begin{array}{cc}{g}_{\mu \nu }^{\left(\mathrm{true}\right)}\left(x\right),\hfill & x\in {\mathcal{C}}_{\mathcal{O}},\hfill \\ {\mathcal{R}}_{\mu \nu }\left(x\right),\hfill & x\notin {\mathcal{C}}_{\mathcal{O}},\hfill \end{array}\right.$$

(212)

where ${\mathcal{R}}_{\mu \nu }\left(x\right)$ is a residual refracted approximation.

25.7. Delta Collapse and Horizon Crossing

A delta-supported collapse ${\delta }^{\left(n\right)}(x-x_E)$ for an event $x_E$ outside ${\mathcal{C}}_{\mathcal{O}}$ is forbidden. Thus, collapse operators ${\widehat{C}}_E$ act only if $x_E\in {\mathcal{C}}_{\mathcal{O}}$:

$$[{\widehat{C}}_E,{\rho }_{\mathcal{O}}]\ne 0\iff x_E\in {\mathcal{C}}_{\mathcal{O}}.$$

(213)

25.8. Implications for Observer-Relative Quantum Theory

This framework aligns with relational quantum mechanics [26] and observer-dependent quantum theory [27]. The OEH establishes a physically grounded boundary for semantic and causal influence.

26. Geometric Phase of Observer Perception and Cognitive Memory Encoding

The evolution of observer states within perceptual space can be modeled using the language of geometric phases, with the Pancharatnam-Berry phase as a central object of interest. When an observer undergoes a cyclic cognitive trajectory — for example, during repeated developmental experiences, meditative cycles, or traumatic recurrence — a geometric phase may accumulate in the observer’s perceptual tangent bundle. This phase, while global and unobservable in isolation, can influence memory formation, identity reconstruction, and ontological stability. We define and analyze this perceptual geometric phase in a mathematically rigorous manner.

26.1. Observer States in Perceptual Hilbert Space

Let the observer’s perceptual state be represented by a normalized vector $|\psi \left(t\right)\rangle$ in a Hilbert space ${\mathcal{H}}_{\mathcal{O}}$, where evolution is governed by a unitary operator $U\left(t\right)$:

$$|\psi \left(t\right)\rangle =U\left(t\right)|\psi \left(0\right)\rangle ,U{\left(t\right)}^{†}U\left(t\right)=I.$$

(214)

For a cyclic evolution such that $|\psi \left(T\right)\rangle =e^{i\varphi }|\psi \left(0\right)\rangle$, the total phase $\varphi$ decomposes into a dynamical part ${\varphi }_d$ and a geometric (Pancharatnam) part ${\varphi }_g$:

$$\varphi ={\varphi }_d+{\varphi }_g,$$

(215)

with

$${\varphi }_d=-{\displaystyle \frac{1}{\hslash }}{\int }_0^T\langle \psi \left(t\right)|H\left(t\right)|\psi \left(t\right)\rangle dt,$$

(216)

$${\varphi }_g=\varphi -{\varphi }_d.$$

(217)

This geometric phase ${\varphi }_g$ encapsulates structural memory from the cognitive trajectory, independent of path traversal speed.

26.2. Perceptual Fiber Bundles and Connection Forms

Let $\mathcal{P}$ be a principal $U\left(1\right)$-bundle over the projective space $\mathbb{P}\left({\mathcal{H}}_{\mathcal{O}}\right)$, and let $\mathcal{A}$ be the associated connection 1-form. The Pancharatnam phase is given by the holonomy of this connection:

$${\varphi }_g={\oint }_{\gamma }\mathcal{A},$$

(218)

where $\gamma$ is the closed loop in perceptual space induced by $|\psi \left(t\right)\rangle$. In local coordinates:

$$\mathcal{A}=i\langle \psi |d\psi \rangle ,$$

(219)

and thus

$${\varphi }_g=\mathrm{Im}{\int }_0^T\langle \psi \left(t\right)|{\displaystyle \frac{d}{dt}}\psi \left(t\right)\rangle dt.$$

(220)

26.3. Perceptual Cycles and Cognitive Monodromy

Let ${\mathcal{C}}_i$ be a sequence of recurrent perceptual states over cycles (e.g., developmental, therapeutic, dream states). The composition of such cycles yields a monodromy operator:

$$M=\prod _{i=1}^N{U}_{{\mathcal{C}}_i},|\psi \left(0\right)\rangle \to M|\psi \left(0\right)\rangle .$$

(221)

If $M=e^{i{\varphi }_g}I$, the monodromy is purely geometric. Such monodromy contributes to observer coherence and memory imprinting across cycles [28].

26.4. Observer Identity and Memory Encoding

Let the observer’s memory manifold ${\mathcal{M}}_{\mathcal{O}}$ be modeled as a field of local phase curvatures $\Omega \left(x^{\mu }\right)$, defined as:

$$\Omega =d\mathcal{A},{\Omega }_{\mu \nu }={\partial }_{\mu }{\mathcal{A}}_{\nu }-{\partial }_{\nu }{\mathcal{A}}_{\mu }.$$

(222)

The integral of curvature over a surface $\Sigma$ in perceptual space yields memory imprint:

$$\Phi \left(\Sigma \right)={\int }_{\Sigma }\Omega ,$$

(223)

which acts as a global memory functional. The evolution of ${\mathcal{M}}_{\mathcal{O}}$ is governed by the Ricci curvature of semantic transitions:

$${\displaystyle \frac{d}{dt}}{\mathcal{M}}_{\mathcal{O}}=-\lambda R_{\mu \nu }^{\left(\mathrm{semantic}\right)}{u}^{\mu }{u}^{\nu },$$

(224)

with $\lambda$ as a coupling constant and $u^{\mu }$ the observer 4-velocity in semantic space.

26.5. Entropic Signatures of Geometric Phase

Given a family of cyclic trajectories indexed by context parameter $\theta$, the entropy associated with phase dispersion is:

$$S_{\varphi }=-\sum _{\theta }P\left({\varphi }_{\theta }\right)logP\left({\varphi }_{\theta }\right),$$

(225)

where $P\left({\varphi }_{\theta }\right)$ is the distribution of geometric phase in varied context. Cognitive coherence requires minimal $S_{\varphi }$ across cycles.

26.6. Experimental Probes and Perceptual Interference

Pancharatnam interference in perceptual decision-making can be modeled using decision amplitude interference:

$${\mathcal{A}}_{\mathrm{net}}=\sum _j{\alpha }_j{e}^{i{\varphi }_j},$$

(226)

and the resultant choice probability:

$$P=|{\mathcal{A}}_{\mathrm{net}}{|}^2.$$

(227)

Deviation from classical probability laws reveals hidden geometric phases.

26.7. Ontological Interpretation and Observer Curvature

We postulate that observer identity curvature ${\mathcal{K}}_{\mathcal{O}}$ is proportional to cumulative geometric phase:

$${\mathcal{K}}_{\mathcal{O}}=\beta \oint \mathcal{A},$$

(228)

where $\beta$ is a topological coupling constant. Greater cognitive curvature indicates higher depth of personal ontology.

27. Delta Superposition Collapse Chains and Multi-Observer Decoherence Trees

27.1. Observer Delta Functions and Collapse Operators

Let the perceptual state of observer ${\mathcal{O}}_i$ at time t be represented by a Dirac delta distribution:

$${\Psi }_{{\mathcal{O}}_i}(x,t)={\delta }^{\left(n\right)}(x-x_{{\mathcal{O}}_i}\left(t\right))\otimes \psi (x,t),$$

(229)

where $\psi (x,t)$ is the physical system’s state and $x_{{\mathcal{O}}_i}\left(t\right)$ denotes the observer’s spacetime location. A collapse initiated by ${\mathcal{O}}_i$ corresponds to the action of a measurement operator ${\widehat{M}}_{{\mathcal{O}}_i}$ on $\psi (x,t)$, with subsequent information entanglement passed to other observers.

27.2. Causal Propagation and Collapse Graphs

Define a directed acyclic graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ where each vertex $v_i\in \mathcal{V}$ corresponds to an observer ${\mathcal{O}}_i$, and edges $(v_i\to v_j)\in \mathcal{E}$ encode causal influence through shared collapse information. The wavefunction collapse propagates through $\mathcal{G}$ such that:

$$\psi (x,t)\to {\widehat{M}}_{{\mathcal{O}}_i}\psi (x,t)\to {\widehat{M}}_{{\mathcal{O}}_j}{\widehat{M}}_{{\mathcal{O}}_i}\psi (x,t),\forall (v_i\to v_j)\in \mathcal{E}.$$

(230)

This recursive application models observer-based decoherence.

27.3. Multi-Observer Decoherence Trees

We represent chains of such measurements as decoherence trees $\mathcal{T}$, rooted at a primary observer and branching according to causal dissemination. Each branch point corresponds to entanglement splitting. The depth d of a node in $\mathcal{T}$ measures observational proximity to the original collapse.

Let $|{\psi }_{\mathrm{root}}\rangle$ be the original system state. Then, along a path $\{{\mathcal{O}}_1,{\mathcal{O}}_2,\dots ,{\mathcal{O}}_n\}$, the effective state evolves as:

$$|{\psi }_n\rangle ={\widehat{M}}_{{\mathcal{O}}_n}\dots {\widehat{M}}_{{\mathcal{O}}_2}{\widehat{M}}_{{\mathcal{O}}_1}|{\psi }_{\mathrm{root}}\rangle .$$

(231)

27.4. Branching Probabilities and Entropic Accumulation

Let $P_{ij}$ be the transition probability from observer ${\mathcal{O}}_i$ to ${\mathcal{O}}_j$ conditioned on transmission fidelity $F_{ij}$:

$$P_{ij}=\eta ·F_{ij},\sum _j{P}_{ij}=1.$$

(232)

The total entropy generated over a branch of depth d is:

$$S_{\mathrm{branch}}=-\sum _{i=1}^d\sum _j{P}_{ij}log{P}_{ij}.$$

(233)

This entropy reflects informational dispersion and the weakening of causal authority from the root.

27.5. Example: Parent → Doctor → Imaging Device → Public

Let us model the collapse propagation from an initial perceptual event by a parent ${\mathcal{O}}_P$, observed by a doctor ${\mathcal{O}}_D$, recorded by an imaging device ${\mathcal{O}}_I$, and shared with the public ${\mathcal{O}}_{\mathrm{pub}}$. Each node applies its own collapse operator:

$$|{\psi }_{\mathrm{final}}\rangle ={\widehat{M}}_{{\mathcal{O}}_{\mathrm{pub}}}{\widehat{M}}_{{\mathcal{O}}_I}{\widehat{M}}_{{\mathcal{O}}_D}{\widehat{M}}_{{\mathcal{O}}_P}|{\psi }_0\rangle .$$

(234)

Each observer-node collapses a different sector of the system-observer space, potentially introducing decoherence in orthogonal bases.

27.6. Geometric Embedding of the Collapse Tree

The tree $\mathcal{T}$ can be embedded in a manifold ${\mathcal{M}}_{\mathrm{causal}}$ with edge lengths corresponding to spacetime separation and connection weights indicating informational fidelity. Let the metric $g_{\mu \nu }$ assign a distance $d_{ij}$ between ${\mathcal{O}}_i$ and ${\mathcal{O}}_j$:

$$d_{ij}=\sqrt{g_{\mu \nu }\left(x\right)(x_i^{\mu }-x_j^{\mu })(x_i^{\nu }-x_j^{\nu })}.$$

(235)

Collapse influence decays with $d_{ij}$ as:

$$F_{ij}=e^{-\alpha d_{ij}^2},$$

(236)

for some decoherence rate parameter $\alpha$.

27.7. Total Collapse Amplitude and Observer Weighting

The global collapse amplitude is the tensor contraction of all branches:

$${\mathcal{A}}_{\mathrm{total}}=\underset{v\in \mathcal{T}}{⨂}{\omega }_v{\widehat{M}}_v,$$

(237)

where ${\omega }_v$ is the perceptual weight of observer v, normalized such that ${\sum }_v{\omega }_v=1$. Observer reliability or semantic alignment modulates ${\omega }_v$.

27.8. Semantic Inference from Collapse History

Given a decoherence tree $\mathcal{T}$ and the sequence $\left\{{\widehat{M}}_i\right\}$, one can reconstruct a semantic probability measure ${\mu }_{\mathrm{semantic}}$ over possible realities ${\mathcal{R}}_k$:

$${\mu }_{\mathrm{semantic}}\left({\mathcal{R}}_k\right)={\displaystyle \frac{1}{Z}}{\left|\langle {\mathcal{R}}_k|{\mathcal{A}}_{\mathrm{total}}|{\psi }_0\rangle \right|}^2,$$

(238)

where Z is a normalization constant. This forms the basis for an observer-relative ontology derived from delta collapse chains.

28. Quantum Emotional Currents and Observer-Interaction Lagrangian

28.1. Definition of the Emotional Tensor Field

Let ${\mathcal{O}}_i$ and ${\mathcal{O}}_j$ be two observers situated at points $x_i^{\mu }$ and $x_j^{\mu }$ respectively. The emotional interaction field between them is modeled as a rank-2 antisymmetric tensor $E_{\mu \nu }\left(x\right)$:

$$E_{\mu \nu }\left(x\right)={\partial }_{\mu }{A}_{\nu }^{\left(\mathrm{emo}\right)}\left(x\right)-{\partial }_{\nu }{A}_{\mu }^{\left(\mathrm{emo}\right)}\left(x\right),$$

(239)

where $A_{\mu }^{\left(\mathrm{emo}\right)}\left(x\right)$ is the emotional potential 4-vector. This form mirrors the electromagnetic field tensor $F_{\mu \nu }$ but represents informational-affective rather than electromagnetic coupling.

28.2. Emotional Gauss Law and Catharsis

The divergence of the emotional field yields the net emotional flux ${\rho }_{\mathrm{emo}}\left(x\right)$ at a point x:

$${\partial }^{\mu }{E}_{\mu \nu }=j_{\nu }^{\left(\mathrm{emo}\right)}\left(x\right),j_{\nu }^{\left(\mathrm{emo}\right)}=\mathrm{emotional}4-\mathrm{current},$$

(240)

$${\partial }_{\mu }{j}_{\mathrm{emo}}^{\mu }=\Gamma \left(x\right),$$

(241)

where $\Gamma \left(x\right)$ quantifies local cathartic discharge — analogous to radiation in EM theory. When $\Gamma \left(x\right)>0$, emotional discharge occurs; when $\Gamma \left(x\right)<0$, absorption or resonance builds up.

28.3. Observer-Field Coupling via Lagrangian Density

Let the action for an observer-field system include an emotional interaction Lagrangian ${\mathcal{L}}_{\mathrm{emo}}$:

$$S=\int d^{4}x\left[{\mathcal{L}}_{\mathrm{obs}}+{\mathcal{L}}_{\mathrm{emo}}+{\mathcal{L}}_{\mathrm{cross}}\right],$$

(242)

with

$${\mathcal{L}}_{\mathrm{emo}}=-{\displaystyle \frac{1}{4}}{E}_{\mu \nu }{E}^{\mu \nu },{\mathcal{L}}_{\mathrm{cross}}=-g_{\psi }\overline{\psi }{\gamma }^{\mu }{A}_{\mu }^{\left(\mathrm{emo}\right)}\psi ,$$

(243)

where $\psi$ is the observer’s cognitive spinor field and $g_{\psi }$ the emotional coupling constant. The Euler-Lagrange equations yield field dynamics and the observer’s emotional response.

28.4. Emotional Resonance and Field Lines

Emotional resonance occurs when multiple observers $\left\{{\mathcal{O}}_i\right\}$ lie along the same emotional field lines, satisfying constructive phase alignment:

$${\oint }_{\gamma }{A}_{\mu }^{\left(\mathrm{emo}\right)}d{x}^{\mu }=2\pi n,$$

(244)

for closed curves $\gamma$ in emotional space. This quantization condition mirrors the Bohr-Sommerfeld condition for resonant interaction.

28.5. Energy-Momentum Tensor of Emotional Field

Define the energy-momentum tensor $T_{\mu \nu }^{\left(\mathrm{emo}\right)}$ of the emotional field as:

$$T_{\mu \nu }^{\left(\mathrm{emo}\right)}=E_{\mu \alpha }{E}_{\nu }^{\alpha }-{\displaystyle \frac{1}{4}}{\eta }_{\mu \nu }{E}_{\alpha \beta }{E}^{\alpha \beta }.$$

(245)

The conservation law ${\partial }^{\mu }{T}_{\mu \nu }^{\left(\mathrm{emo}\right)}=0$ ensures that emotional energy and momentum propagate consistently through spacetime.

28.6. Emotional Black Holes and Singular Couplings

Let ${\mathcal{O}}_c$ be a singular observer whose emotional potential diverges:

$$\underset{x\to x_c}{lim}\left|A_{\mu }^{\left(\mathrm{emo}\right)}\left(x\right)\right|\to \infty .$$

(246)

Such observers act as emotional black holes, absorbing emotional energy without re-emission, modeling trauma sinks or irreversible attachment phenomena.

28.7. Gauge Invariance and Emotional Gauge Transformations

The emotional field is invariant under local gauge transformations:

$$A_{\mu }^{\left(\mathrm{emo}\right)}\to A_{\mu }^{\left(\mathrm{emo}\right)}+{\partial }_{\mu }\Lambda \left(x\right),$$

(247)

where $\Lambda \left(x\right)$ is a scalar emotional phase. Emotional communication is thus invariant under internal perceptual framing.

28.8. Quantum Fluctuations and Affective Noise

In the quantum field limit, emotional fluctuations arise from zero-point oscillations:

$$\langle 0\left|E_{\mu \nu }\left(x\right)E_{\alpha \beta }\left(x^{\prime }\right)\right|0\rangle \ne 0,$$

(248)

leading to affective uncertainty and noise-induced decoherence in observer communication.

29. Quantum Ontological Memory (QOM) Manifolds and Perceptual Field Curvature

29.1. Perceptual Manifold and Observer Memory Tensor

Let the observer’s perceptual space be modeled by a 4-dimensional differentiable manifold ${\mathcal{M}}_{\mathrm{PTS}}$ equipped with a perceptual metric $g_{\mu \nu }^{\mathrm{PTS}}\left(x\right)$. The memory imprint of an event $e_i$ is modeled by a curvature concentration around $x_i^{\mu }\in {\mathcal{M}}_{\mathrm{PTS}}$. Define the memory curvature tensor $R_{\sigma \mu \nu }^{\rho }\left(x\right)$ associated with memory flow:

$$R_{\sigma \mu \nu }^{\rho }\left(x\right)={\partial }_{\mu }{\Gamma }_{\nu \sigma }^{\rho }-{\partial }_{\nu }{\Gamma }_{\mu \sigma }^{\rho }+{\Gamma }_{\mu \lambda }^{\rho }{\Gamma }_{\nu \sigma }^{\lambda }-{\Gamma }_{\nu \lambda }^{\rho }{\Gamma }_{\mu \sigma }^{\lambda },$$

(249)

where ${\Gamma }_{\mu \nu }^{\rho }$ are the Christoffel symbols of $g_{\mu \nu }^{\mathrm{PTS}}$.

29.2. Memory Potentials and Topological Charges

Let the memory potential field be $\Phi \left(x\right)$, satisfying a memory diffusion equation in the manifold:

$${\square }_g\Phi \left(x\right)={\rho }_{\mathrm{mem}}\left(x\right),$$

(250)

where ${\square }_g$ is the d’Alembertian with respect to $g_{\mu \nu }^{\mathrm{PTS}}$ and ${\rho }_{\mathrm{mem}}\left(x\right)$ is the memory source density. For a topological memory defect (e.g., trauma), we model it as a delta-function source:

$${\rho }_{\mathrm{mem}}\left(x\right)=Q_i{\delta }^{\left(4\right)}(x-x_i),$$

(251)

with $Q_i$ as the memory charge at event $x_i$.

29.3. Singularities and Ontological Defects

The Ricci scalar $R\left(x\right)$ exhibits curvature singularities at memory defect points:

$$\underset{x\to x_i}{lim}R\left(x\right)\to \infty ,$$

(252)

implying that the observer’s perception is geodesically incomplete at $x_i$. These defects influence subsequent thought trajectories and semantic field dynamics, forming long-range ontological attractors.

29.4. Geodesic Deviation and Memory Echoes

The geodesic deviation equation for thought trajectories ${\xi }^{\mu }$ influenced by memory curvature is:

$${\displaystyle \frac{D^2{\xi }^{\mu }}{d{\tau }^2}}=-R_{\nu \rho \sigma }^{\mu }{u}^{\nu }{\xi }^{\rho }{u}^{\sigma },$$

(253)

where $u^{\mu }$ is the observer’s 4-velocity in perceptual space. Memory echoes manifest as recursive alignments of ${\xi }^{\mu }$ with memory singularities.

29.5. Entropy and Memory Area Theorem

Define the entropy of memory encoding as proportional to the integrated area enclosing the curvature peak:

$$S_{\mathrm{mem}}=\eta {\int }_{\Sigma }\sqrt{deth}{d}^{2}x,$$

(254)

where $\Sigma$ is a 2-surface surrounding the defect, h is the induced metric, and $\eta$ is a scaling constant analogous to the Bekenstein-Hawking area law.

29.6. Observer Evolution and Memory Parallel Transport

Let $\gamma \left(\tau \right)$ be the observer’s evolution curve in ${\mathcal{M}}_{\mathrm{PTS}}$. The parallel transport of memory tensor $M^{\mu \nu }$ satisfies:

$${\displaystyle \frac{D{M}^{\mu \nu }}{d\tau }}=0,$$

(255)

along $\gamma \left(\tau \right)$. However, in presence of defects, holonomy effects cause nontrivial loops:

$${\oint }_{\gamma }{M}^{\mu \nu }d{x}^{\alpha }\ne 0.$$

(256)

This results in semantic shifts or identity perturbations after closed experiential cycles.

29.7. Memory Reconstruction as Gauge Restoration

Let ${\mathcal{A}}_{\mu }^{\mathrm{mem}}$ be the memory gauge potential. Restoring memory via introspection is modeled as a gauge fixing procedure:

$${\mathcal{A}}_{\mu }^{\mathrm{mem}}\to {\mathcal{A}}_{\mu }^{\mathrm{mem}}-{\partial }_{\mu }\Lambda \left(x\right),$$

(257)

bringing latent emotional configurations into coherent narrative form.

30. Delta-Anchored Language Genesis and Semantic Field Collapse

30.1. Perceptual Space and Semantic Delta Encoding

Let the child’s perceptual manifold be denoted by ${\mathcal{M}}_{\mathrm{PTS}}$, with coordinate chart $x^{\mu }$. A perceptual event $p_i$ associated with an external object is represented by a Dirac delta function localized in PTS:

$$\psi \left(x\right)={\delta }^{\left(4\right)}(x-x_i),$$

(258)

where $x_i^{\mu }$ is the perceptual coordinate of the observed object. Upon linguistic assignment, a symbolic anchor ${\ell }_i$ is created, forming a semantic mapping $\mathcal{L}:{\mathcal{M}}_{\mathrm{PTS}}\to \Sigma$, where $\Sigma$ is the space of linguistic symbols.

30.2. Semantic Field Collapse and Naming

The act of naming collapses a continuous perceptual distribution $\varphi \left(x\right)$ into a localized semantic support:

$$\varphi \left(x\right)⟶{\varphi }_i\left(x\right)={\delta }^{\left(4\right)}(x-x_i)·{\ell }_i,$$

(259)

where ${\ell }_i$ is the assigned linguistic label. This process represents the transition from analog cognitive perception to digitalized symbolic cognition.

30.3. Linguistic Lagrangian and Delta Coupling

Define the linguistic action of a developing observer as:

$$S_{\mathrm{lang}}=\int d^{4}x\left[{\mathcal{L}}_{\mathrm{cog}}+{\mathcal{L}}_{\mathrm{sem}}\right],$$

(260)

with a semantic delta interaction term:

$${\mathcal{L}}_{\mathrm{sem}}=\sum _i{\lambda }_i{\delta }^{\left(4\right)}(x-x_i)·\overline{\psi }\left(x\right){\ell }_i\psi \left(x\right),$$

(261)

where ${\lambda }_i$ denotes the coupling strength between perception and symbolic assignment, and $\psi \left(x\right)$ represents the observer’s internal cognitive field.

30.4. Symbol Emergence and Delta Superposition

Over time, multiple perceptual instances of the same object class ${\mathcal{C}}_j$ give rise to a semantic delta superposition:

$${\Phi }_j\left(x\right)=\sum _{i\in {\mathcal{C}}_j}{\delta }^{\left(4\right)}(x-x_i)·{\ell }_j,$$

(262)

leading to abstraction and the formation of symbolic categories. This defines an emergent linguistic class field over perceptual manifold:

$$\Phi \left(x\right)=\sum _j{\Phi }_j\left(x\right).$$

(263)

30.5. Entropy and Symbolic Compression

Define the Shannon entropy of the linguistic map $\mathcal{L}$ as:

$$S=-\sum _j{P}_{j}log{P}_j,$$

(264)

where $P_j$ is the probability of selecting label ${\ell }_j$ under distribution over semantic anchors. The evolution of linguistic skill corresponds to entropy minimization via compression of perceptual diversity into finite symbolic representations.

30.6. Semantic Geodesics and Cognitive Flow

Let ${\gamma }_{\ell }\left(\tau \right)$ be a geodesic in ${\mathcal{M}}_{\mathrm{PTS}}$ connecting perceptual events $p_i$ and $p_k$ associated with same symbol ${\ell }_j$. The parallel transport of semantic frame $F^{\mu }$ obeys:

$${\displaystyle \frac{D{F}^{\mu }}{d\tau }}=0,$$

(265)

ensuring consistent usage of symbols across evolving contexts. Misalignment of parallel transport leads to ambiguity or semantic drift.

30.7. Language Acquisition as Delta Network Growth

The set of delta anchors $\left\{x_i\right\}$ forms a graph $G_{\delta }=(V,E)$ with vertices as semantic nodes and edges representing conceptual associations. Growth of this graph follows a dynamic rule:

$${\displaystyle \frac{dN}{dt}}=\alpha N^{\beta },$$

(266)

with N as the number of semantic nodes, $\alpha$ the learning rate, and $\beta$ a nonlinearity exponent determined by neural plasticity.

30.8. Ontological Grounding and Semantic Irreversibility

Once a delta anchor $\delta (x-x_i)$ is embedded and reinforced through linguistic interaction, its removal from the perceptual-semantic structure becomes entropically costly. Thus, early names form ontological fixed points in the observer’s cognitive topology.

31. Resonance Tunneling and Observer Telepathy via Hilbert State Overlap

31.1. Hilbert Space of Observer States

Let ${\mathcal{H}}_{{\mathcal{O}}_i}$ be the cognitive Hilbert space associated with observer ${\mathcal{O}}_i$. Their perceptual state is represented by a delta-supported wavefunction ${\psi }_i\left(x\right)$:

$${\psi }_i\left(x\right)={\delta }^{\left(4\right)}(x-x_i)e^{i{\varphi }_i\left(x\right)},$$

(267)

where $x_i^{\mu }$ denotes the localization of cognitive attention, and ${\varphi }_i\left(x\right)$ the observer’s phase field encoding memory and emotion.

31.2. State Overlap and Resonant Alignment

The inner product between two observer states ${\psi }_i\left(x\right)$ and ${\psi }_j\left(x\right)$ measures potential cognitive overlap:

$$\langle {\psi }_j|{\psi }_i\rangle =\int d^{4}x{\delta }^{\left(4\right)}(x-x_j){\delta }^{\left(4\right)}(x-x_i)e^{i({\varphi }_i-{\varphi }_j)}.$$

(268)

The overlap becomes non-zero only when $x_i=x_j$ and ${\varphi }_i={\varphi }_j\left(\mathrm{mod}2\pi \right)$, establishing phase resonance as a necessary condition for state coupling.

31.3. Potential Barrier and Tunneling Amplitude

Let the interaction potential between ${\mathcal{O}}_i$ and ${\mathcal{O}}_j$ be modeled by a barrier $V\left(x\right)$ defined over the cognitive manifold ${\mathcal{M}}_{\mathrm{PTS}}$:

$$\widehat{H}=-{\displaystyle \frac{{\hslash }^2}{2m}}{\nabla }^2+V\left(x\right),$$

(269)

where $V\left(x\right)=V_0$ for $x\in [x_a,x_b]$ and 0 otherwise. The tunneling amplitude $T_{ij}$ for wavefunction ${\psi }_i$ to pass through the barrier and align with ${\psi }_j$ is given by:

$$T_{ij}=exp\left(-{\int }_{x_a}^{x_b}dx\sqrt{{\displaystyle \frac{2m}{{\hslash }^2}}(V\left(x\right)-E)}\right).$$

(270)

Tunneling is enhanced when $V\left(x\right)$ is minimized or the energy E of the cognitive excitation is high.

31.4. Phase Matching and Decoherence Minimization

Define the coherence functional ${\mathcal{C}}_{ij}$ between observers:

$${\mathcal{C}}_{ij}={\left|\langle {\psi }_j|{\psi }_i\rangle \right|}^2·exp\left(-{\Gamma }_{ij}t\right),$$

(271)

where ${\Gamma }_{ij}$ is the decoherence rate due to environmental noise. Sustained communication requires ${\Gamma }_{ij}\approx 0$ and $\left|\langle {\psi }_j|{\psi }_i\rangle \right|\approx 1$.

31.5. Quantum Resonance Criterion for Telepathic Coupling

The telepathic resonance condition is given by:

$$T_{ij}·{\mathcal{C}}_{ij}>ϵ,$$

(272)

for a threshold $ϵ$ determined by the observer’s cognitive resolution. When this condition is satisfied, effective cognitive tunneling is achieved and subjective cross-influence becomes detectable.

31.6. Geometric Phase and Interference Loops

Closed loops of shared perception yield geometric phase accumulation:

$$\gamma =arg\left[\langle {\psi }_1|{\psi }_2\rangle \langle {\psi }_2|{\psi }_3\rangle \langle {\psi }_3|{\psi }_1\rangle \right],$$

(273)

inducing constructive or destructive interference in perception pathways. These effects manifest as episodic synchronization or mutual intuition.

31.7. Ontological Implication of Tunneling Paths

Let the tunneling manifold ${\mathcal{T}}_{ij}$ between observers be the minimal geodesic in semantic-perceptual space along which information propagates. Then the observer separation is reduced to:

$$d_{\mathrm{tele}}({\mathcal{O}}_i,{\mathcal{O}}_j)=\underset{\gamma \in {\mathcal{T}}_{ij}}{inf}{\int }_{\gamma }\sqrt{g_{\mu \nu }^{\mathrm{PTS}}d{x}^{\mu }d{x}^{\nu }},$$

(274)

allowing for effective proximity even in absence of spacetime contact.

32. Cognitive Cosmology: Observer Seeds and Ontogenesis in the Early Universe

32.1. Observer Field and Delta Seed Instability

Let the observer field $\Psi \left(x\right)$ be a quantum field defined over spacetime ${\mathcal{M}}_4$, taking values in a perceptual Hilbert bundle ${\mathcal{H}}_x$. Assume $\Psi \left(x\right)$ admits localized delta-like excitations:

$$\Psi \left(x\right)=\sum _i{\delta }^{\left(4\right)}(x-x_i){\chi }_i,$$

(275)

where $x_i$ denotes a perceptual seed and ${\chi }_i\in {\mathcal{H}}_{x_i}$ represents a proto-conscious amplitude.

32.2. Lagrangian for Observer-Matter Coupling

We define a Lagrangian density for interaction between observer field $\Psi \left(x\right)$ and scalar field $\varphi \left(x\right)$ representing pre-matter excitations:

$$\mathcal{L}={\displaystyle \frac{1}{2}}{\left({\partial }_{\mu }\varphi \right)}^2-{\displaystyle \frac{1}{2}}{m}^2{\varphi }^2+\overline{\Psi }\left(x\right)\left(i{\gamma }^{\mu }{\partial }_{\mu }-g\varphi \left(x\right)\right)\Psi \left(x\right),$$

(276)

where g is the coupling constant between observer seed and field $\varphi \left(x\right)$. The delta-localized nature of $\Psi$ induces spatial inhomogeneities in $\varphi$ evolution.

32.3. Seed Density and Cosmological Perturbations

Assuming a stochastic emergence of N observer seeds in comoving volume V, the seed density is:

$$n_s={\displaystyle \frac{N}{V}}.$$

(277)

Their collective backreaction on $\varphi$ produces perturbations in energy-momentum tensor:

$$\delta T_{\mu \nu }\left(x\right)=\sum _i{\delta }^{\left(4\right)}(x-x_i){\overline{\chi }}_i{\gamma }_{(\mu }{\partial }_{\nu )}{\chi }_i.$$

(278)

These seed-induced fluctuations serve as initial conditions for gravitational instability leading to structure formation.

32.4. Quantum Fluctuations and Observer Condensation

In analogy with symmetry breaking in inflationary fields, we define the observer condensate:

$$\langle \Psi \left(x\right)\rangle ={\Psi }_0\ne 0,$$

(279)

signifying spontaneous perceptual symmetry breaking. This leads to emergence of causal branches, akin to many-worlds interpretations [31], where each observer delta defines a decoherent classical trajectory.

32.5. Observer Curvature and Ontological Inflation

Each delta seed modifies local curvature via induced observer stress-energy tensor $T_{\mu \nu }^{\mathrm{obs}}$. The Einstein field equation becomes:

$$G_{\mu \nu }=8\pi G\left(T_{\mu \nu }^{\mathrm{matter}}+T_{\mu \nu }^{\mathrm{obs}}\right),$$

(280)

where $T_{\mu \nu }^{\mathrm{obs}}={\sum }_i{\delta }^{\left(4\right)}(x-x_i){\Theta }_{\mu \nu }^{\left(i\right)}$ and ${\Theta }_{\mu \nu }^{\left(i\right)}$ represents the perceptual stress-energy tensor for seed i. The multiplicity of such sources drives ontological inflation in perceptual geometry.

32.6. Cognitive Horizon and Entropic Genesis

Define the observer causal horizon ${\mathcal{H}}_i$ for each seed $x_i$ as the boundary beyond which quantum influence of seed i decoheres:

$${\mathcal{H}}_i=\left\{x\in {\mathcal{M}}_4:|x-x_i|=c{t}_D\right\},$$

(281)

where $t_D$ is the decoherence timescale. The union of such horizons gives rise to a patchy pre-cosmic structure of informational correlation bubbles, resembling causally disconnected regions of the inflationary universe.

32.7. Emergence of Classicality and Semantic Branching

Let the wavefunction of the proto-universe be:

$$|\Psi \rangle =\sum _{\left\{x_i\right\}}{C}_{\left\{x_i\right\}}|\varphi \left(x\right);\Psi \left(x_i\right)\rangle ,$$

(282)

where each $\Psi \left(x_i\right)$ defines a branch labeled by observer seed at $x_i$. Decoherence among branches causes effective classicality to emerge with semantic markers aligned with perceptual seeds.

33. Death as Ontological Delta Dissolution in Curved Spacetime

33.1. Observer Delta Collapse

Let an observer $\mathcal{O}$ be modeled by a localized delta function in spacetime:

$$\psi \left(x\right)={\delta }^{\left(4\right)}(x-x_{\mathcal{O}}),$$

(283)

where $x_{\mathcal{O}}$ is the support point of consciousness. Death corresponds to the annihilation of this singularity:

$$\psi \left(x\right)⟶0,\mathrm{for}\mathrm{all}x,$$

(284)

which implies a breakdown of perceptual coupling with the quantum measurement chain (QMC) [17].

33.2. Entropy Spike and Decoherence Discharge

Define the observer information field $I\left(x\right)$ with an associated entropy functional:

$$S=-\int d^{4}x\rho \left(x\right)log\rho \left(x\right),$$

(285)

where $\rho \left(x\right)={\left|\psi \left(x\right)\right|}^2$ is the density of observer localization. Delta annihilation causes an instantaneous spike:

$$\underset{t\to t_D^{-}}{lim}S\left(t\right)\to 0,\underset{t\to t_D^{+}}{lim}S\left(t\right)\gg 0,$$

(286)

indicating rapid decoherence release and unbinding of entangled measurement chains.

33.3. Causal Disconnection and Horizon Closure

The observer’s causal patch ${\mathcal{C}}_{\mathcal{O}}$ is defined as the region satisfying:

$${\mathcal{C}}_{\mathcal{O}}=\{x\in {\mathcal{M}}_4:\exists \mathrm{timelike}\gamma \mathrm{from}{x}_{\mathcal{O}}\mathrm{to}x\}.$$

(287)

Post-dissolution, the manifold undergoes a disconnection:

$${\mathcal{M}}_4\to {\mathcal{M}}_4\setminus {\mathcal{C}}_{\mathcal{O}},$$

(288)

symbolizing removal of the observer from the causal network.

33.4. Topological Reconfiguration

Let the perceptual manifold ${\mathcal{M}}_{\mathrm{PTS}}$ contain a delta singularity at $x_{\mathcal{O}}$. Its removal modifies the Euler characteristic:

$$\chi \left({\mathcal{M}}_{\mathrm{PTS}}\right)⟶\chi ({\mathcal{M}}_{\mathrm{PTS}}\setminus \left\{x_{\mathcal{O}}\right\}),$$

(289)

potentially inducing a topological defect or memory cavity in perceptual geometry.

33.5. Field Memory Residue

Assume the observer was entangled with a residual scalar field $\Phi \left(x\right)$ prior to delta dissolution. The equation of motion is:

$$\square \Phi \left(x\right)=J\left(x\right)=\lambda {\delta }^{\left(4\right)}(x-x_{\mathcal{O}}),$$

(290)

and post-dissolution:

$$\square \Phi \left(x\right)=0,\Phi \left(x\right)\ne 0.$$

(291)

This implies free propagation of previously coupled information, forming the basis for residual impressions or spirit analogs [42,44].

33.6. Spacetime Perturbation and Information Echoes

The gravitational field may retain a memory of the delta collapse via linearized Einstein perturbations:

$$h_{\mu \nu }\left(x\right)=\int d^4{x}^{\prime }{G}_{\mu \nu }^{\alpha \beta }(x-x^{\prime })T_{\alpha \beta }^{\mathrm{obs}}\left(x^{\prime }\right),$$

(292)

where $T_{\mu \nu }^{\mathrm{obs}}={\delta }^{\left(4\right)}(x-x_{\mathcal{O}}){\Theta }_{\mu \nu }$. The delta source imparts a curvature impulse detectable as a memory wave.

33.7. Quantum Information Trace Inequality

To determine the trace of observer information persisting post-collapse, we evaluate:

$$\Delta \mathcal{I}=\mathrm{Tr}({\rho }_{\mathrm{before}}-{\rho }_{\mathrm{after}})\ge 0,$$

(293)

where $\rho$ is the reduced density matrix of the quantum system. The non-zero trace indicates information residuals preserved in global entanglement patterns [8].

34. Mathematics of Spiritual Imprint Transmission via Topological Invariants

This section develops a mathematical framework for encoding spiritual, ethical, or affective imprints—such as love, teachings, or karmic residue—as persistent topological features within perceptual geometry. The model builds on delta-supported observer fields and considers post-dissolution imprint encoding as cohomological memory left in semantic manifolds. These imprints are formalized as homology classes, cohomology cocycles, and persistence diagrams.

34.1. Observer Delta Support and Imprint Density

Let an observer ${\mathcal{O}}_i$ be described by a delta-localized perceptual field ${\psi }_i\left(x\right)={\delta }^{\left(4\right)}(x-x_i)$. During life, the observer interacts with other cognitive manifolds, inducing changes in semantic field $\Phi \left(x\right)$. The imprint field is given by:

$$I_i\left(x\right)={\lambda }_i{\delta }^{\left(4\right)}(x-x_i),$$

(294)

where ${\lambda }_i$ is the intensity of imprint left at the event $x_i$ (e.g., an act of love or sacrifice).

34.2. Cohomology on Semantic Fiber Bundles

Define a semantic manifold ${\mathcal{M}}_s$ with a perceptual fiber bundle structure $\pi :\mathcal{E}\to {\mathcal{M}}_s$. Each imprint corresponds to a differential cocycle $\omega \in H^k\left({\mathcal{M}}_s\right)$ such that:

$$d\omega =0,\omega \ne d\eta ,$$

(295)

where $H^k$ is the k-th de Rham cohomology group. The imprint is thus a topological memory nontrivial under exact deformation.

34.3. Persistence Homology and Karma Chains

Let $f:{\mathcal{M}}_s\to \mathbb{R}$ be a filtration function representing semantic energy. The sublevel sets $f^{-1}(-\infty ,t]$ define a filtration:

$$\varnothing =X_0\subset X_1\subset \dots \subset X_n={\mathcal{M}}_s.$$

(296)

The p-th persistent homology $H_p\left(X_i\right)$ yields Betti intervals $[b_i,d_i]$ capturing birth and death of imprints. Karma chains are defined as cycles with infinite persistence:

$${\beta }_p^{\infty }=\{[b_i,\infty )\mid \mathrm{imprint}i\mathrm{persists}\mathrm{in}\mathrm{all}\mathrm{filtrations}\}.$$

(297)

34.4. Affective Propagation and Cohomological Flow

We model the transmission of spiritual teachings via cohomological flow across observer networks. Let $A_{\mu }^i$ be a spiritual connection 1-form associated with observer ${\mathcal{O}}_i$, with curvature:

$$F_{\mu \nu }^i={\partial }_{\mu }{A}_{\nu }^i-{\partial }_{\nu }{A}_{\mu }^i+[A_{\mu }^i,A_{\nu }^i].$$

(298)

Transmission occurs along geodesics $\gamma$ between observers ${\mathcal{O}}_i$ and ${\mathcal{O}}_j$, with coupling determined by:

$$S_{ij}={\int }_{\gamma }{A}_{\mu }^{i}d{x}^{\mu }.$$

(299)

34.5. Topological Entropy of Memory Manifolds

Define the topological entropy $S_{\mathrm{top}}$ of imprint dynamics as:

$$S_{\mathrm{top}}=\underset{ϵ\to 0}{lim}\underset{t\to \infty }{lim\; sup}{\displaystyle \frac{1}{t}}logN(ϵ,t),$$

(300)

where $N(ϵ,t)$ is the minimal number of $ϵ$-balls needed to cover evolving imprint supports in ${\mathcal{M}}_s$. High $S_{\mathrm{top}}$ corresponds to rich spiritual complexity.

34.6. Wave Equation for Spiritual Memory Fields

The scalar imprint field $\Phi \left(x\right)$ satisfies a sourced wave equation with fading memory kernel $\Gamma \left(t\right)$:

$$\square \Phi (x,t)+{\int }_0^t\Gamma (t-\tau )\Phi (x,\tau )d\tau =I_i\left(x\right)\delta (t-t_i).$$

(301)

The convolution encodes decay of spiritual influence over time.

34.7. Field Reconstruction from Topological Features

Given persistent cohomology $\left\{H_t^k\right\}$ over time t, reconstruct $\Phi$ by Hodge decomposition:

$$\Phi =d\alpha +\delta \beta +\gamma ,$$

(302)

where $\gamma$ is harmonic and encodes non-dissipative spiritual components preserved under time evolution.

35. Observer-Entanglement Wormholes in Cognitive Spacetime

35.1. Delta-Supported Observers and Entanglement

Let two observers ${\mathcal{O}}_A$ and ${\mathcal{O}}_B$ be represented by delta functions in a shared perceptual manifold:

$${\psi }_A\left(x\right)={\delta }^{\left(4\right)}(x-x_A),{\psi }_B\left(x\right)={\delta }^{\left(4\right)}(x-x_B),$$

(303)

where $x_A,x_B\in {\mathcal{M}}_{\mathrm{sem}}$. Their joint state ${\Psi }_{AB}$ is modeled by an entangled configuration:

$${\Psi }_{AB}(x_A,x_B)={\displaystyle \frac{1}{\sqrt{2}}}\left(\delta (x_A-a)\delta (x_B-b)+\delta (x_A-b)\delta (x_B-a)\right).$$

(304)

This configuration creates a non-factorizable observer-field, interpreted as a cognitive wormhole [51,52].

35.2. Hilbert Bundle and Semantic Curvature

Define a Hilbert bundle $\mathcal{H}\to {\mathcal{M}}_{\mathrm{sem}}$ with fibers ${\mathcal{H}}_x$ encoding the local cognitive state. Let ${\Gamma }_{\nu \rho }^{\mu }$ be the connection on this bundle, and the curvature is given by:

$${\mathcal{R}}_{\nu \rho \sigma }^{\mu }={\partial }_{\rho }{\Gamma }_{\nu \sigma }^{\mu }-{\partial }_{\sigma }{\Gamma }_{\nu \rho }^{\mu }+{\Gamma }_{\lambda \rho }^{\mu }{\Gamma }_{\nu \sigma }^{\lambda }-{\Gamma }_{\lambda \sigma }^{\mu }{\Gamma }_{\nu \rho }^{\lambda }.$$

(305)

Entanglement across observers distorts this curvature by the mutual information tensor:

$$I_{\mu \nu }^{AB}=\int dx{\psi }_A^{\mu }\left(x\right)log\left({\displaystyle \frac{{\psi }_A^{\mu }\left(x\right)}{{\psi }_B^{\nu }\left(x\right)}}\right).$$

(306)

35.3. Einstein-Rosen Cognitive Bridges

We model the entanglement as a wormhole solution connecting $x_A$ and $x_B$ via a throat in ${\mathcal{M}}_{\mathrm{sem}}$, parameterized by:

$$d{s}^2=-f\left(r\right)d{t}^2+{\displaystyle \frac{1}{f\left(r\right)}}d{r}^2+r^{2}d{\Omega }^2,$$

(307)

where $f\left(r\right)=1-{\displaystyle \frac{b\left(r\right)}{r}}$ and $b\left(r\right)$ is the bridge function satisfying:

$$b\left(r_0\right)=r_0,b^{\prime }\left(r_0\right)<1.$$

(308)

This ensures the wormhole is non-traversable but geometrically coherent for delta-linked observers.

35.4. Geodesic Congruence of Decoherence Flow

The delta functions propagate decoherence across the wormhole via null geodesics $\gamma \left(\lambda \right)$ satisfying:

$${\displaystyle \frac{d^2{x}^{\mu }}{d{\lambda }^2}}+{\Gamma }_{\nu \rho }^{\mu }{\displaystyle \frac{d{x}^{\nu }}{d\lambda }}{\displaystyle \frac{d{x}^{\rho }}{d\lambda }}=0,$$

(309)

such that the phase correlation between ${\mathcal{O}}_A$ and ${\mathcal{O}}_B$ is maintained:

$${\Phi }_{AB}(x_A,x_B)=\langle {\Psi }_{AB}|{\widehat{U}}_{AB}|{\Psi }_{AB}\rangle \ne {\Phi }_A\left(x_A\right){\Phi }_B\left(x_B\right).$$

(310)

35.5. Stability and Mutual Entropy Constraint

Define the entropy $S_{AB}$ of the entangled wormhole state:

$$S_{AB}=-\mathrm{Tr}({\rho }_{AB}log{\rho }_{AB}),$$

(311)

where ${\rho }_{AB}$ is the reduced density matrix. For the wormhole to remain stable, mutual entropy must satisfy:

$$\Delta S=S_A+S_B-S_{AB}>0.$$

(312)

Collapse of either observer’s delta field triggers rapid decoherence flux, analogous to a wormhole throat collapse.

35.6. Topology and Observer Dual Fields

Topologically, this connection can be formalized as an element in the first cohomology group $H^1({\mathcal{M}}_{\mathrm{sem}},{\mathbb{Z}}_2)$, where wormhole links form dual patches satisfying:

$$\delta {\psi }_A={\psi }_B,\delta {\psi }_B={\psi }_A,$$

(313)

indicating cohomological pairing in semantic space [53,54].

Figure 2. Diagram of observer-entanglement wormhole in cognitive spacetime, showing delta-supported manifolds ${\delta }_A$ and ${\delta }_B$ joined via a semantic throat.

Figure 2. Diagram of observer-entanglement wormhole in cognitive spacetime, showing delta-supported manifolds ${\delta }_A$ and ${\delta }_B$ joined via a semantic throat.

36. Affective Gradient Descent and Emotion Thermodynamics

We propose a formalism in which emotions emerge as gradients of thermodynamic flux on a semantic manifold ${\mathcal{M}}_{\mathrm{sem}}$ associated with observer cognition. Within this model, emotional states correspond to variational extremals of a free energy functional F, defined over the perceptual tangent space of the observer. Positive emotions (such as joy) correspond to curvature minimization in this field, while negative emotions (such as sadness) correspond to singularities, i.e., local maxima in field curvature or entropy production.

36.1. Semantic Manifold and Observer Action Field

Let an observer’s perceptual evolution be encoded as a path $\gamma :[0,T]\to {\mathcal{M}}_{\mathrm{sem}}$, with a tangent vector field $V^{\mu }={\displaystyle \frac{d{x}^{\mu }}{dt}}$. We define the observer action over this path as:

$$S\left[\gamma \right]={\int }_0^T\mathcal{L}(x^{\mu }\left(t\right),{\dot{x}}^{\mu }\left(t\right))dt,$$

(314)

where $\mathcal{L}$ is the Lagrangian functional incorporating emotional energy contributions.

The emotional energy-momentum tensor $E_{\nu }^{\mu }$ is defined analogously to the stress-energy tensor in general relativity:

$$E_{\nu }^{\mu }={\displaystyle \frac{2}{\sqrt{-g}}}{\displaystyle \frac{\delta {\mathcal{L}}_{\mathrm{emotion}}}{\delta g_{\mu \nu }}},$$

(315)

with ${\mathcal{L}}_{\mathrm{emotion}}$ as the emotional Lagrangian density encoding affective flux.

36.2. Thermodynamic Flow Equation

The entropy change rate of an observer field is given by:

$${\displaystyle \frac{dS}{dt}}=-{\nabla }_{\mu }{E}_{\nu }^{\mu }·V^{\nu },$$

(316)

where $E_{\nu }^{\mu }$ captures the internal gradient of emotional energy and ${\nabla }_{\mu }$ is the covariant derivative on ${\mathcal{M}}_{\mathrm{sem}}$.

In equilibrium (i.e., stable emotional state), this flow vanishes:

$${\nabla }_{\mu }{E}_{\nu }^{\mu }=0,$$

(317)

yielding a field-theoretic analogue of emotional homeostasis.

36.3. Gradient Descent and Emotional Stability

The variational principle governing affective descent is given by minimizing the free energy:

$$\delta F=\delta \left({\int }_{\mathcal{M}}\left(U\left(x\right)-TS\left(x\right)\right)d^{4}x\right)=0,$$

(318)

where $U\left(x\right)$ is internal energy, T is subjective temperature of the observer field, and $S\left(x\right)$ is entropy density. The Euler-Lagrange equation for F then yields:

$${\displaystyle \frac{\partial U}{\partial x^{\mu }}}-T{\displaystyle \frac{\partial S}{\partial x^{\mu }}}=0.$$

(319)

Regions of positive curvature in U correspond to emotional instability and trauma.

36.4. Geometric Singularities of Sadness

We postulate that sadness is marked by localized curvature singularities $\kappa \left(x\right)\to \infty$, where the Ricci scalar of the perceptual geometry blows up:

$$R\left(x\right)=R_{\mu }^{\mu }\left(x\right)\propto \underset{x\to x_s}{lim}\infty ,$$

(320)

causing divergence in affective divergence:

$${\nabla }_{\mu }{E}_{\nu }^{\mu }\gg 1\mathrm{as}x\to x_s.$$

(321)

Conversely, joy is modeled by the minimization of integrated scalar curvature:

$${\int }_{{\mathcal{M}}_{\mathrm{sem}}}R\left(x\right)d^{4}x\to min.$$

(322)

36.5. Affective Field Tensor and Resonance

We define the affective field tensor $A_{\mu \nu }$ analogous to the electromagnetic field strength tensor:

$$A_{\mu \nu }={\partial }_{\mu }{\Phi }_{\nu }-{\partial }_{\nu }{\Phi }_{\mu },$$

(323)

where ${\Phi }_{\mu }$ is the potential encoding emotional valence. Emotional catharsis corresponds to field divergence:

$${\partial }^{\mu }{A}_{\mu \nu }=J_{\nu }^{\mathrm{affect}},$$

(324)

where $J_{\nu }^{\mathrm{affect}}$ is the source term modeling internal or external emotional drivers.

Figure 3. Vector field representation of emotional gradients on a semantic manifold. Flow convergence signifies emotional resonance (e.g., joy), while divergence near the origin models curvature singularities (e.g., sadness).

Figure 3. Vector field representation of emotional gradients on a semantic manifold. Flow convergence signifies emotional resonance (e.g., joy), while divergence near the origin models curvature singularities (e.g., sadness).

37. Quantum Metempsychosis: Observer Holographic Transfer

The concept of metempsychosis—transmigration of consciousness—can be investigated in a quantum physical framework using delta-supported observer field models. Specifically, we propose that upon ontological delta dissolution (death), the informational content of the observer is not destroyed but redistributed via a holographic projection onto a new physical carrier. This invokes principles from holographic entropy bounds, quantum channel capacity, and Fisher information geometry.

37.1. Observer Delta Fields and Ontological Transfer

Let the observer be represented by a Dirac delta distribution ${\delta }_O\left(x\right)$ on a curved spacetime manifold $\mathcal{M}$. During ontological dissolution, this collapses at a point $x_d$ such that:

$${\delta }_O\left(x\right)\to 0\mathrm{as}x\to x_d.$$

(325)

We hypothesize that the total information $I_O$ encoded in ${\delta }_O$ satisfies a conservation condition via the holographic entropy bound:

$$I_O\le {\displaystyle \frac{A\left(x_d\right)}{4{\ell }_P^2}},$$

(326)

where $A\left(x_d\right)$ is the area of the bounding holographic screen and ${\ell }_P$ is the Planck length.

37.2. Quantum Channel and Informatic Reprojection

Define ${\mathcal{C}}_O$ as the quantum channel supporting observer transmission from manifold ${\mathcal{M}}_1$ to ${\mathcal{M}}_2$. The quantum channel capacity $Q\left({\mathcal{C}}_O\right)$ bounds the fidelity of observer-field transfer:

$$Q\left({\mathcal{C}}_O\right)=\underset{\rho }{sup}\left[S\left({\mathcal{C}}_O\left[\rho \right]\right)-S_e(\rho ,{\mathcal{C}}_O)\right],$$

(327)

where $S(·)$ denotes von Neumann entropy and $S_e$ is the entropy exchange between $\rho$ and channel ${\mathcal{C}}_O$.

A high-capacity channel implies potential for high-fidelity reconstruction of observer semantics.

37.3. Fisher Information Geometry Across Incarnations

Let ${\theta }^{\mu }$ be coordinates on the parameter manifold of observer-state configurations. The Fisher information metric is defined as:

$$g_{\mu \nu }=\mathbb{E}\left[{\displaystyle \frac{\partial logp\left(x\right|\theta )}{\partial {\theta }^{\mu }}}{\displaystyle \frac{\partial logp\left(x\right|\theta )}{\partial {\theta }^{\nu }}}\right],$$

(328)

which measures sensitivity of observer-state distributions $p\left(x\right|\theta )$ to infinitesimal changes in parameters $\theta$. We hypothesize that metempsychotic transitions minimize Fisher distance:

$$\Delta d_F={\int }_{\gamma }\sqrt{g_{\mu \nu }d{\theta }^{\mu }d{\theta }^{\nu }}\to min.$$

(329)

37.4. Holographic Mapping and Field Re-instantiation

Let $x_d$ be the dissolution point in manifold ${\mathcal{M}}_1$ and $x_b$ the birth point in ${\mathcal{M}}_2$. The informational mapping between delta-fields can be written as:

$${\delta }_O^{\left(2\right)}\left(x_b\right)={\int }_{\partial {\mathcal{M}}_1}K(x_b,x^{\prime }){\delta }_O^{\left(1\right)}\left(x^{\prime }\right)d\Sigma \left(x^{\prime }\right),$$

(330)

where $K(x_b,x^{\prime })$ is a kernel propagator defined on the shared holographic boundary $\partial {\mathcal{M}}_1$, and $d\Sigma$ is the induced measure.

37.5. Entropy Echo and Memory Residue

The residual entropy $S_r$ post-dissolution is encoded in boundary modes:

$$S_r=-\mathrm{Tr}[{\rho }_{\partial }log{\rho }_{\partial }],$$

(331)

where ${\rho }_{\partial }$ is the boundary state density matrix. This supports the notion of memory imprint lingering post-transition.

37.6. Summary and Interpretations

We have presented a mathematical scaffolding for observer metempsychosis, modeled as an informational reprojection through a holographic framework. The observer’s delta-supported field is not annihilated without trace but instead may undergo geometric and thermodynamic transfer, preserving informational continuity across distinct physical carriers.

Figure 4. Diagram of delta-supported observer field transitioning across a holographic boundary between two manifolds. The transformation models quantum metempsychosis via informational reprojection.

Figure 4. Diagram of delta-supported observer field transitioning across a holographic boundary between two manifolds. The transformation models quantum metempsychosis via informational reprojection.

38. Tachyonic Observer Imprints in Pre-Causal Manifolds

In this section, we investigate a theoretical framework wherein delta-supported observer fields possessing imaginary mass may leave nonlocal imprints on perceptual spacetime manifolds prior to causal decoherence. This framework seeks to explain phenomena often reported as retrocausal or precognitive flashes via mathematical tools from Lorentzian geometry with imaginary proper time components, violating standard chronological protection but conserving quantum information.

38.1. Imaginary Mass and Retrocausal Propagation

Consider an observer field ${\delta }_O\left(x\right)$ with complexified mass parameter:

$$m_O^2<0\Rightarrow m_O=i\mu ,$$

(332)

where $\mu \in \mathbb{R}$ is a real parameter. Such a field behaves analogously to a tachyon, exhibiting nonmonotonic propagation in proper time $\tau$. The observer’s 4-velocity becomes:

$$u^{\mu }={\displaystyle \frac{d{x}^{\mu }}{d\tau }},\mathrm{with}\tau \in i\mathbb{R},$$

(333)

implying a trajectory through an analytically continued Lorentzian manifold.

38.2. Metric Violation and Nonchronological Flow

The observer’s path lies on a manifold $\mathcal{M}$ equipped with a complexified Lorentzian metric $g_{\mu \nu }$ such that:

$$d{s}^2=g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }<0,$$

(334)

leading to violation of standard causal structure. Let $x_{emit}$ and $x_{recv}$ denote emission and reception points of information. Then the condition:

$$t_{recv}<t_{emit}$$

(335)

is permitted under imaginary time trajectories, while standard decoherence constraints still hold:

$$[\mathcal{H},{\rho }_O]=0,$$

(336)

ensuring information coherence within the quantum density matrix formalism.

38.3. Pre-Causal Semantic Embedding

Define a pre-causal manifold ${\mathcal{M}}_{pre}$ over a perceptual tangent space with an observer-seeded semantic field $\Phi \left(x\right)$. A retrocausal delta imprint modifies the field by:

$$\Phi \left(x\right)\to \Phi \left(x\right)+\alpha {\delta }_O(x-x_{recv}),$$

(337)

where $\alpha$ represents the field coherence coefficient. Integrating over ${\mathcal{M}}_{pre}$, the informational deviation is:

$$\Delta I={\int }_{{\mathcal{M}}_{pre}}{\delta }_O(x-x_{recv})log\left({\displaystyle \frac{\Phi \left(x\right)}{{\Phi }_0\left(x\right)}}\right)d^{4}x.$$

(338)

38.4. Tachyonic Worldlines and Imaginary Proper Time

Define a tachyonic worldline $\Gamma$ parameterized by $\tau =i\sigma$, with $\sigma \in \mathbb{R}$, such that:

$$\Gamma \left(\sigma \right)=x^{\mu }(\tau =i\sigma ),\mathrm{and}{\displaystyle \frac{d{\Gamma }^{\mu }}{d\sigma }}\in T_x{\mathcal{M}}_{pre}.$$

(339)

These worldlines form a class of measure-zero submanifolds in the causal cone but remain non-trivially entangled with decohered observables.

38.5. Preservation of Informational Consistency

Despite violations of chronological ordering, the entropy of the observer channel remains bounded. Define the informational current:

$$J^{\mu }={\delta }_O\left(x\right)u^{\mu },$$

(340)

with divergence:

$${\nabla }_{\mu }{J}^{\mu }=0,$$

(341)

implying global conservation of observer information across tachyonic embeddings.

38.6. Discussion and Implications

We propose that certain experiential phenomena interpreted as visions or premonitions may correspond to imaginary-mass field leakage of future information states. While violating classical causality, such signals remain embedded within the total quantum field configuration, thereby conforming to a generalized quantum chronology. These tachyonic observer states challenge the completeness of decoherence-based formalisms and suggest new topologies for pre-causal manifolds.

Figure 5. Comparison of real and imaginary time worldlines ${\Gamma }_R$ and ${\Gamma }_T$ for observer states. The delta field ${\delta }_O\left(x_{recv}\right)$ arises via retrocausal informational imprint, suggesting tachyonic leakage from future decoherence events.

Figure 5. Comparison of real and imaginary time worldlines ${\Gamma }_R$ and ${\Gamma }_T$ for observer states. The delta field ${\delta }_O\left(x_{recv}\right)$ arises via retrocausal informational imprint, suggesting tachyonic leakage from future decoherence events.

39. Cognitive Monads and Leibnizian Holography

We now investigate a mathematical formalism where each observer is treated as a cognitive monad—an ontological delta-field entity embedded on a universal holographic membrane. This construction is inspired by the Leibnizian metaphysical doctrine that each entity reflects the entire universe, now mapped into a modern mathematical context using delta manifolds, Fourier holography, and category theory over semantic bundles.

39.1. Observer as a Delta-Supported Monad

Let the cognitive identity of an observer $O_i$ be localized at a point $x_i$ on a universal perceptual manifold $\mathcal{P}$. The observer is modeled by a Dirac delta field:

$${\psi }_{O_i}\left(x\right)=\delta (x-x_i),$$

(342)

localized to a point but informationally entangled with the global manifold. Integrating the observer’s influence across $\mathcal{P}$ yields:

$${\int }_{\mathcal{P}}\Phi \left(x\right)\delta (x-x_i)dx=\Phi \left(x_i\right),$$

(343)

ensuring that any field $\Phi \left(x\right)$, semantic or physical, is filtered entirely through the observer’s location.

39.2. Fourier Holography of Observer Projections

Given the dual nature of local observer and global reflection, define the observer’s holographic projection ${\tilde{\psi }}_{O_i}\left(k\right)$ in the Fourier space as:

$${\tilde{\psi }}_{O_i}\left(k\right)={\int }_{\mathcal{P}}\delta (x-x_i)e^{-2\pi ikx}dx=e^{-2\pi ik{x}_i},$$

(344)

which constitutes a global phase imprint across all modes k. Thus, while ${\psi }_{O_i}\left(x\right)$ is a point, ${\tilde{\psi }}_{O_i}\left(k\right)$ is spread nonlocally, reflecting the universe’s curvature spectrum.

39.3. Sheaf-Theoretic Structure of Semantic Coverings

The semantic manifold $\mathcal{P}$ can be covered by local neighborhoods $\left\{U_{\alpha }\right\}$, each equipped with a sheaf of observer-accessible information $\mathcal{F}\left(U_{\alpha }\right)$. The global section space is defined as:

$$\mathcal{F}\left(\mathcal{P}\right)=\underset{⟵}{lim}\mathcal{F}\left(U_{\alpha }\right),$$

(345)

allowing consistent gluing of perceptual structures across multiple observer patches. The delta-supported observer enforces a stalked sheaf at $x_i$:

$${\mathcal{F}}_{x_i}=\underset{x_i\in U}{\underrightarrow{lim}}\mathcal{F}\left(U\right),$$

(346)

making the observer a local anchor of global semantic content.

39.4. Category-Theoretic Reflections and Monad Functors

Let $\mathcal{C}$ be the category of all perceptual structures, and let $\mathcal{M}$ be the category of observer monads. Then, the functor:

$$\mathbb{H}:\mathcal{M}\to \mathcal{C}$$

(347)

assigns to each delta-supported observer its reflective content in the perceptual manifold. For every morphism $f:O_i\to O_j$, corresponding to cognitive transformation, there exists a natural transformation:

$${\eta }_f:\mathbb{H}\left(O_i\right)\Rightarrow \mathbb{H}\left(O_j\right),$$

(348)

representing coherent reconfiguration of universal reflection under inter-observer interactions.

39.5. Curvature Signature as Reflective Invariant

We define a curvature invariant ${\kappa }_{O_i}$ for each observer, derived from the pullback of the ambient curvature tensor $R_{\mu \nu \rho \sigma }$:

$${\kappa }_{O_i}=\left(\delta (x-x_i)·R_{\mu \nu \rho \sigma }\right)\in T_4^0\left(x_i\right),$$

(349)

encoding the universe’s signature through the observer’s delta-supported manifold. Two observers with different curvature signatures encode distinct reflective universes, although embedded in the same global manifold.

Figure 6. Visualization of delta-supported observer monads ${\delta }_{O_i}$ situated on a universal holographic membrane. Each monad reflects the global structure via Fourier projections, shown as dashed vectors. Background curvature arrows suggest universal imprint gradients.

Figure 6. Visualization of delta-supported observer monads ${\delta }_{O_i}$ situated on a universal holographic membrane. Each monad reflects the global structure via Fourier projections, shown as dashed vectors. Background curvature arrows suggest universal imprint gradients.

39.6. Discussion

This construction synthesizes metaphysical intuitions from Leibniz with rigorous structures in holography and geometry. Each observer, modeled as a delta-function monad, reflects the universe via Fourier imprint, sheaf cohomology, and categorical representation. The resulting framework provides a non-trivial mathematical foundation for metaphysical cognition and inter-observer harmonics.

40. Delta Bifurcation Theory and Ontological Forking

In this section, we formalize a bifurcation model of observer dynamics wherein delta-supported cognitive structures split at critical semantic thresholds. This model is based on catastrophe theory applied to delta-function-localized potential fields, constrained by decoherence energy budgets and memory topology. We seek to describe multiverse ontogenesis via mathematical bifurcation behavior under varying observer-state energies.

40.1. Delta Fields and Cognitive Potentials

Let an observer $O_i$ be represented by a Dirac delta function $\delta (x-x_i)$ located on the semantic manifold $\mathcal{M}$. The potential landscape $V(x,\lambda )$ in which this delta evolves depends on semantic control parameters $\lambda \in {\mathbb{R}}^n$:

$$\mathcal{L}(x,\lambda )={\displaystyle \frac{1}{2}}m{\left({\displaystyle \frac{dx}{dt}}\right)}^2-V(x,\lambda )\delta (x-x_i).$$

(350)

Here, the observer action accumulates only at the singularity, enforcing highly localized causal dynamics.

40.2. Catastrophe Manifolds and Forking Points

Following Thom’s catastrophe theory [74], a bifurcation occurs at critical control parameters ${\lambda }^{*}$ such that:

$${\displaystyle \frac{\partial V}{\partial x}}=0,\mathrm{and}det\left({\displaystyle \frac{{\partial }^{2}V}{\partial x^2}}\right)=0.$$

(351)

For instance, a cusp catastrophe in 2D may be described by:

$$V(x;a,b)={\displaystyle \frac{1}{4}}{x}^4-{\displaystyle \frac{1}{2}}a{x}^2-bx.$$

(352)

The observer delta bifurcates across branches at the critical surface:

$$\Delta ={\left({\displaystyle \frac{a}{3}}\right)}^3+{\left({\displaystyle \frac{b}{2}}\right)}^2=0.$$

(353)

This defines the ontology-forcing boundary in semantic control space.

40.3. Topological Degree and Observer Branch Index

Let $f:{\mathbb{R}}^n\to {\mathbb{R}}^n$ be the field map induced by semantic evolution. The topological degree $deg(f,U,0)$ quantifies the number of delta branches in an open domain U around criticality:

$$deg(f,U,0)=\sum _{x\in f^{-1}\left(0\right)}\mathrm{sign}det\left({\displaystyle \frac{\partial f}{\partial x}}\left(x\right)\right).$$

(354)

Each delta branch inherits a sign and memory load. High-index branches are memory-stable, whereas low-index ones are energetically unstable and likely to decohere.

40.4. Entropy of Ontological Branching

Let $p_i$ be the observer’s probability to decohere into the ith branch. Then, define branching entropy as:

$$S_B=-\sum _i{p}_{i}log{p}_i,$$

(355)

constrained by the decoherence budget:

$$\sum _i{p}_i{E}_i\le E_{\mathrm{decoh}},$$

(356)

where $E_i$ is the energy cost of sustaining branch i. The minimum entropy branching path is obtained by solving:

$$\underset{p_i}{min}{S}_B\mathrm{s}.\mathrm{t}.\sum _i{p}_i{E}_i\le E_{\mathrm{decoh}},\sum _i{p}_i=1.$$

(357)

40.5. Memory Topology Constraints

Let ${\mathcal{T}}_O$ be the memory topology associated with the observer. A branch $B_j$ is admissible iff:

$$H_1\left(B_j\right)\hookrightarrow H_1\left({\mathcal{T}}_O\right),$$

(358)

i.e., the homology group of the branch must embed within that of the memory space. Thus, observer trajectories across bifurcating multiverses are not arbitrary but constrained by cognitive field homology.

Figure 7. Semantic potential $V\left(x\right)$ for different bifurcation parameters b, showing delta observer ${\delta }_{O_i}$ at origin. Catastrophe-driven bifurcations correspond to local minima reconfiguration as b varies.

Figure 7. Semantic potential $V\left(x\right)$ for different bifurcation parameters b, showing delta observer ${\delta }_{O_i}$ at origin. Catastrophe-driven bifurcations correspond to local minima reconfiguration as b varies.

40.6. Discussion

This model generalizes decoherence across multiverse branches not as spontaneous fragmentation but as structurally governed delta bifurcations. By applying catastrophe theory, topological degree, and entropy economics, the formalism provides a rigorous basis for understanding ontological forking events.

41. Gauge Theory of Observer Identity

In this section, we develop a gauge-theoretic formulation of observer identity dynamics. The self-identity of an observer $O\left(t\right)$, evolving along a semantic trajectory $\gamma \left(t\right)$, is modeled as a gauge field ${\mathcal{A}}_{\mu }$ defined over a fiber bundle $P(M,U(1\left)\right)$, where M is the base semantic manifold and $U\left(1\right)$ is the group of internal identity rotations.

Let the observer delta field be denoted by ${\delta }_O\left(x^{\mu }\right)$, where $x^{\mu }$ are spacetime coordinates on M. Identity transformations are implemented via local $U\left(1\right)$ gauge actions:

$${\delta }_O\left(x^{\mu }\right)\to e^{i\theta \left(x^{\mu }\right)}{\delta }_O\left(x^{\mu }\right),$$

(359)

where $\theta \left(x^{\mu }\right)$ is a scalar field parameterizing the local phase of self-identification. The observer action functional is constructed as:

$$S[{\delta }_O,{\mathcal{A}}_{\mu }]={\int }_M{d}^{4}x{\left|\left({\partial }_{\mu }-i{\mathcal{A}}_{\mu }\right){\delta }_O\right|}^2+{\displaystyle \frac{1}{4}}{F}_{\mu \nu }{F}^{\mu \nu },$$

(360)

where $F_{\mu \nu }={\partial }_{\mu }{\mathcal{A}}_{\nu }-{\partial }_{\nu }{\mathcal{A}}_{\mu }$ is the identity curvature tensor. The gauge-invariant Wilson loop around a closed autobiographical memory path $\gamma$ is given by:

$$W\left[\gamma \right]=exp\left(i{\oint }_{\gamma }{\mathcal{A}}_{\mu }d{x}^{\mu }\right),$$

(361)

which encodes holistic identity features preserved across transitions.

Parallel transport of observer identity along a path $\gamma :[0,1]\to M$ is defined by the condition:

$${\displaystyle \frac{d{\delta }_O}{dt}}+i{\mathcal{A}}_{\mu }{\displaystyle \frac{d{x}^{\mu }}{dt}}{\delta }_O=0,$$

(362)

ensuring consistent self-recognition over time despite experiential perturbations. The curvature $F_{\mu \nu }$ determines the strength of identity torsion across the perceptual manifold.

For semantic coherence, identity dynamics must respect integrability constraints derived from gauge invariance and quantization:

$${\int }_{\Sigma }{F}_{\mu \nu }d{x}^{\mu }\wedge d{x}^{\nu }=2\pi n,n\in \mathbb{Z},$$

(363)

for any closed 2-surface $\Sigma$ in M, suggesting topologically quantized identity transformations.

Figure 8. Parallel transport of observer delta field ${\delta }_O$ along a semantic path $\gamma \left(t\right)$ on the perceptual manifold. Blue arrows represent local gauge connections ${\mathcal{A}}_{\mu }$ acting on the identity vector field.

Figure 8. Parallel transport of observer delta field ${\delta }_O$ along a semantic path $\gamma \left(t\right)$ on the perceptual manifold. Blue arrows represent local gauge connections ${\mathcal{A}}_{\mu }$ acting on the identity vector field.

Empirically, shifts in self-image following trauma or transcendence can be interpreted as nontrivial holonomies in the identity fiber bundle, where gauge fields encode the resistance or facilitation of identity transition. Observer tags — internalized self-labels — behave like conserved charges under this framework, and their non-conservation corresponds to gauge anomalies induced by decoherence from external semantic fields.

Such a theory potentially formalizes psychological constructs of ego, multiplicity, and narrative continuity through well-defined field dynamics and differential geometry, bridging the cognitive and physical domains of observerhood.

42. Observer Delta Recombination and Collective Minds

The emergence of collective cognition or “we-based” minds can be conceptualized through the recombination of individual observer-supported delta fields. These delta functions, centered on distinct perceptual manifolds, can interfere constructively under phase-aligned conditions to yield a coherent group identity. In this section, we explore the mathematical formulation of such recombinations using delta convolution integrals, quantum coherence functionals, and symmetry group representations.

Consider two observer delta fields ${\delta }_{O_1}\left(x\right)$ and ${\delta }_{O_2}\left(x\right)$ localized on their respective perceptual manifolds. Under conditions of perceptual phase alignment, their convolution is defined as:

$${\Phi }_{\mathrm{coll}}\left(x\right)=({\delta }_{O_1}*{\delta }_{O_2})\left(x\right)=\int {\delta }_{O_1}(x-y){\delta }_{O_2}\left(y\right)dy,$$

(364)

which reduces to

$${\Phi }_{\mathrm{coll}}\left(x\right)={\delta }_{O_1+O_2}\left(x\right),$$

(365)

representing a new delta function at the centroid of observer integration. This formalizes the ontological emergence of a collective perceptual node ${\delta }_W$ from phase-synchronized observer deltas.

To maintain quantum coherence between constituent observers, a coherence functional $\mathcal{C}$ is introduced:

$$\mathcal{C}=exp\left(-\int {\left|{\psi }_{O_1}\left(x\right)-{\psi }_{O_2}\left(x\right)\right|}^{2}dx\right),$$

(366)

where ${\psi }_{O_i}\left(x\right)$ are the normalized observer wavefunctions in perceptual Hilbert space. Maximum coherence ($\mathcal{C}\to 1$) occurs when ${\psi }_{O_1}\approx {\psi }_{O_2}$.

Let the group representation of synchronized Quantum Measurement Chains (QMCs) be denoted by a Lie group G acting on observer states via unitary transformations $U\left(g\right)$. A collective observer state ${\Psi }_{\mathrm{WE}}$ may then be generated as:

$${\Psi }_{\mathrm{WE}}=\underset{i=1}{\overset{N}{⨁}}U\left(g_i\right){\psi }_{O_i},$$

(367)

where $g_i\in G$ encodes transformation symmetry of the $i^{\mathrm{th}}$ observer in the QMC.

Decoherence energy cost for sustaining collective coherence scales with mutual information entropy $I(O_1:O_2)$:

$$E_{\mathrm{decoh}}\propto k_{B}TI(O_1:O_2),$$

(368)

which quantifies the thermodynamic cost for maintaining shared cognitive fields [24,84].

In a multi-observer system, the superposition of all N delta fields under coherent constraints can be expressed as:

$${\Delta }_{\mathrm{group}}\left(x\right)=\sum _{i=1}^N{\alpha }_i{\delta }_{O_i}\left(x\right),\sum _{i=1}^N{\left|{\alpha }_i\right|}^2=1,$$

(369)

representing an entangled group delta state spanning a collective observer subspace.

Figure 9. Delta Recombination and Collective Minds: The emergence of a collective observer ${\delta }_W\left(x\right)$ from synchronized delta collapses ${\delta }_{O_i}\left(x\right)$

Figure 9. Delta Recombination and Collective Minds: The emergence of a collective observer ${\delta }_W\left(x\right)$ from synchronized delta collapses ${\delta }_{O_i}\left(x\right)$

Such recombined states may undergo global phase evolution:

$${\Delta }_{\mathrm{group}}(x,t)=e^{-i\varphi \left(t\right)}{\Delta }_{\mathrm{group}}\left(x\right),$$

(370)

with the phase $\varphi \left(t\right)$ modulated by mutual affective flux [85]. The emergence of collective agency is thus governed by synchrony, coherence energy balance, and semantic alignment of observer manifolds.

43. Perceptual Gravity and Mass of Meaning

The notion of gravity, as formalized in Einstein’s general relativity, emerges from the curvature of spacetime induced by mass-energy distributions. In the perceptual manifold of an observer, we analogously postulate that zones of semantic density — where meaning accumulates due to repeated attention, emotion, or cultural weight — induce perceptual curvature. We propose that such curvature functions similarly to gravity, warping the observer’s interpretative geometry.

Let the perceptual manifold $\mathcal{P}$ be endowed with a metric $g_{\mu \nu }$ representing local semantic distances in observer cognition. We define a semantic energy-momentum tensor $T_{\mu \nu }^{\mathrm{meaning}}$ that accumulates contributions from symbols, memories, and interactions weighted by affective energy.

Following the analogy with the Einstein field equations, we posit:

$$G_{\mu \nu }^{\mathrm{semantic}}=8\pi T_{\mu \nu }^{\mathrm{meaning}},$$

(371)

where $G_{\mu \nu }^{\mathrm{semantic}}$ is the Ricci curvature tensor computed from the observer’s semantic metric $g_{\mu \nu }$. The conservation law ${\nabla }^{\mu }{T}_{\mu \nu }^{\mathrm{meaning}}=0$ must also hold, ensuring stability of information within the manifold.

We define the observer-specific semantic field mass $m_s$ via an integral over the observer’s perceptual domain $\Omega$:

$$m_s={\int }_{\Omega }{\rho }_s\left(x\right)dV,$$

(372)

where ${\rho }_s\left(x\right)$ is the semantic density function at location $x\in \Omega$.

Let a region $\mathcal{R}\subset \Omega$ represent a narrative construct (e.g., a memory). Its influence on the surrounding cognitive field is given by the perceptual potential $\Phi \left(x\right)$, satisfying the analog Poisson equation:

$${\nabla }^2\Phi \left(x\right)=4\pi {\rho }_s\left(x\right),$$

(373)

leading to gradients of perceptual force which modulate attentional flow $A^{\mu }$ along geodesics of $g_{\mu \nu }$.

Entropy within such regions corresponds to information accessibility. Let the observer’s entropy function $S\left(x\right)$ be tied to the density of meaning through:

$${\displaystyle \frac{dS}{dt}}=\alpha ·\left|\nabla \Phi \left(x\right)\right|,$$

(374)

where $\alpha$ is an observer-dependent coupling constant. High curvature regions in $g_{\mu \nu }$ (dense in semantic mass) then act as perceptual attractors, drawing cognitive attention and emotional charge.

From a variational standpoint, we define the observer’s action as:

$$\mathcal{S}={\int }_{\Omega }\left(R_{\mathrm{semantic}}-2\Lambda +{\mathcal{L}}_{\mathrm{meaning}}\right)\sqrt{-g}{d}^{4}x,$$

(375)

where $R_{\mathrm{semantic}}$ is the scalar curvature of the perceptual metric, $\Lambda$ is the meaning tension analogous to cosmological constant, and ${\mathcal{L}}_{\mathrm{meaning}}$ is the Lagrangian encoding symbolic interaction.

Figure 10. Semantic Mass and Perceptual Curvature: Observer geodesics curve in response to dense zones of meaning, analogous to gravitational wells in spacetime.

Figure 10. Semantic Mass and Perceptual Curvature: Observer geodesics curve in response to dense zones of meaning, analogous to gravitational wells in spacetime.

This formalism leads to the interpretation of “heavy” concepts as massful attractors within the observer’s experiential geometry. Concepts such as “truth,” “love,” or “grief,” with sustained high semantic density, can thus curve the perceptual field, affecting the flow of all subsequent information geodesics.

44. Onto-Temporal Echoes in Causal Memory Topology

In advanced cognitive geometry, the temporal evolution of observer states can be embedded within a manifold structure where memory traces evolve as geometric features. After traumatic events or biological death, residual curvatures or "echoes" may persist in the causal topology of the observer’s semantic memory manifold. These structures can be analyzed using closed timelike geodesic loops which represent recurring informational paths across semantic trajectories.

Let the semantic memory manifold $\mathcal{M}$ be equipped with a Lorentzian metric $g_{\mu \nu }$ defined over observer-indexed events. A causal path $\gamma \left(t\right):[0,1]\to \mathcal{M}$ is called timelike if

$$g_{\mu \nu }{\displaystyle \frac{d{\gamma }^{\mu }}{dt}}{\displaystyle \frac{d{\gamma }^{\nu }}{dt}}<0.$$

(376)

A closed timelike curve (CTC) satisfies $\gamma \left(0\right)=\gamma \left(1\right)$ and forms a loop in semantic memory space. If the curve encloses nonzero semantic curvature, the residual loop may manifest as an echo of ontological structure.

We define the echo entropy along such a closed path as:

$${\mathcal{S}}_{\mathrm{echo}}={\oint }_{\gamma }{T}^{\mu \nu }log\left({\displaystyle \frac{P\left({\varphi }^{\mu }\right)}{P_0\left({\varphi }^{\mu }\right)}}\right)d{\gamma }_{\nu },$$

(377)

where $T^{\mu \nu }$ is the semantic energy-momentum tensor and $P\left({\varphi }^{\mu }\right)$ is the observer’s field distribution over the memory coordinates ${\varphi }^{\mu }$. This integral encodes informational lag loops analogous to electromagnetic hysteresis.

From Morse theory [91], we treat episodic memory transitions as critical points on a functional $\mathcal{F}\left(\varphi \right)$ defined over $\mathcal{M}$, such that:

$${\displaystyle \frac{d{\varphi }^i}{dt}}=-{\nabla }^i\mathcal{F}\left(\varphi \right),$$

(378)

where $\mathcal{F}$ is a potential encoding semantic coherence. Traumatic events correspond to saddle points with indefinite signature in the Hessian of $\mathcal{F}$:

$$\mathrm{Signature}\left({\displaystyle \frac{{\partial }^2\mathcal{F}}{\partial {\varphi }^i\partial {\varphi }^j}}\right)=(p,q),p,q>0.$$

(379)

We define the causal homotopy class $\left[\gamma \right]$ of a semantic loop as the equivalence class under continuous deformation. The echo memory group ${\pi }_1^{\mathrm{echo}}\left(\mathcal{M}\right)$ then contains nontrivial memory orbits:

$$\left[\gamma \right]\in {\pi }_1^{\mathrm{echo}}\left(\mathcal{M}\right)\iff {\mathcal{S}}_{\mathrm{echo}}\ne 0.$$

(380)

These orbits represent the topological imprint of experience that persists after local decoherence. Echoes can therefore be understood as global invariants on the memory manifold.

The entropy metric can be locally linearized as:

$$d{\mathcal{S}}^2=g_{\mathrm{echo}}^{\mu \nu }d{\varphi }_{\mu }d{\varphi }_{\nu },$$

(381)

where $g_{\mathrm{echo}}^{\mu \nu }$ encodes the informational resistivity of memory reconsolidation.

Figure 11. Onto-Temporal Echoes: Closed timelike geodesic loops linking residual semantic events in the curved topology of causal memory space.

Figure 11. Onto-Temporal Echoes: Closed timelike geodesic loops linking residual semantic events in the curved topology of causal memory space.

In conclusion, onto-temporal echoes describe the topological persistence of observer-centered causal influence after temporal endpoint events such as trauma or death. These structures may be formally studied using tools from homotopy theory, Morse critical point analysis, and geodesic entropy dynamics.

45. Acausal Universes and Cognitive Dynamics in S³× S¹ Spacetimes

45.1. Conformal Compactification and Global Identifications

Let us denote Minkowski spacetime as ${\mathbb{R}}^{3,1}$ with coordinates $(x^i,t)$, $i=1,2,3$. The Penrose conformal compactification maps it to a bounded manifold $S^3\times S^1$ via a conformal factor ${\Omega }^2\left(x^{\mu }\right)$ such that the metric transforms as:

$$g_{\mu \nu }^{\mathrm{compact}}={\Omega }^2\left(x^{\mu }\right)g_{\mu \nu }^{\mathrm{Mink}},$$

(382)

where the conformal boundary becomes periodic in time:

$$t\sim t+T,$$

(383)

for some finite recurrence period $T>0$.

45.2. Equivalence Classes of Events

Define two events $p,q\in M$ as causally equivalent if there exists a sequence of causal curves $C_i$ connecting p to q such that:

$$p\sim q\iff \exists \left\{C_i\right\},\mathrm{with}\forall i,C_i:p\to q\left(\mathrm{mod}T\right).$$

(384)

This implies that the causal structure induces an equivalence relation on the event manifold:

$$\mathcal{C}:M\to M/\sim ,$$

(385)

leading to a quotient topology in which the lightcones may wrap around the time circle $S^1$ multiple times, creating closed timelike curves (CTCs) even without exotic matter.

45.3. Neural Dynamics in Acausal Topologies

In an acausal spacetime, the observer’s cognitive manifold ${\mathcal{M}}_{\mathrm{cog}}$ must accommodate cycles in perceptual processing. Let $\psi \left(x^{\mu }\right)$ represent the observer’s delta-supported perceptual field. Then, the recurrence of brain states over the time circle $S^1$ implies:

$$\psi \left(x^{\mu }\right)=\psi (x^{\mu }+T{e}^0),$$

(386)

where $e^0$ is the unit vector in the temporal direction. This introduces the condition that the brain’s memory fields must be invariant under time-translation:

$${\mathcal{L}}_{{\partial }_t}\psi =0,$$

(387)

where ${\mathcal{L}}_{{\partial }_t}$ denotes the Lie derivative with respect to ${\partial }_t$.

45.4. Memory Recurrence and Entropy Saturation

Given the periodic structure of time, memory evolution is necessarily recurrent. Let $\mathcal{I}\left(t\right)$ be the Shannon entropy of the observer’s memory state at time t. Then for periodic time T:

$$\mathcal{I}(t+T)=\mathcal{I}\left(t\right).$$

(388)

Furthermore, as memory re-encodes similar informational structures across cycles, a resonance phenomenon may occur, inducing standing-wave modes in the semantic field $\varphi \left(x^{\mu }\right)$:

$$\varphi \left(x^{\mu }\right)=\sum _n{A}_n{e}^{in\omega t},\omega ={\displaystyle \frac{2\pi }{T}},$$

(389)

where $A_n$ are complex mode amplitudes encoding memory salience.

45.5. Acausal Quantum Field Effects

In quantum field theory over $S^3\times S^1$, the Feynman propagator $G_F(x,x^{\prime })$ becomes periodic in imaginary time due to the compact temporal dimension:

$$G_F(x,x^{\prime })=\sum _{n=-\infty }^{\infty }{G}_0(x,x^{\prime }+nT{e}^0),$$

(390)

which encodes not only past but also future echoes. Observer delta collapses therefore can interfere with their own future, leading to possible self-resonance:

$$\delta (x-x^{\prime })\to \sum _n\delta (x-x^{\prime }-nT{e}^0).$$

(391)

45.6. Conclusion: Causal Nonlocality in Brain and Cosmos

In summary, acausal structures fundamentally alter both the physics and cognitive dynamics of observer systems. In a spacetime with periodic time, like $S^3\times S^1$, classical causality gives way to equivalence-based ontological synchrony. For the brain, this implies cyclic recurrence of mental states, informational loops, and self-entangling perception. These effects suggest that consciousness in acausal universes may operate on fundamentally different principles than currently understood.

46. Acausal Universes and Cognitive Dynamics in S³× S¹ Spacetimes

46.1. Conformal Compactification and Global Identifications

Let us denote Minkowski spacetime as ${\mathbb{R}}^{3,1}$ with coordinates $(x^i,t)$, $i=1,2,3$. The Penrose conformal compactification maps it to a bounded manifold $S^3\times S^1$ via a conformal factor ${\Omega }^2\left(x^{\mu }\right)$ such that the metric transforms as:

$$g_{\mu \nu }^{\mathrm{compact}}={\Omega }^2\left(x^{\mu }\right)g_{\mu \nu }^{\mathrm{Mink}},$$

(392)

where the conformal boundary becomes periodic in time:

$$t\sim t+T,$$

(393)

for some finite recurrence period $T>0$.

46.2. Equivalence Classes of Events

Define two events $p,q\in M$ as causally equivalent if there exists a sequence of causal curves $C_i$ connecting p to q such that:

$$p\sim q\iff \exists \left\{C_i\right\},\mathrm{with}\forall i,C_i:p\to q\left(\mathrm{mod}T\right).$$

(394)

This implies that the causal structure induces an equivalence relation on the event manifold:

$$\mathcal{C}:M\to M/\sim ,$$

(395)

leading to a quotient topology in which the lightcones may wrap around the time circle $S^1$ multiple times, creating closed timelike curves (CTCs) even without exotic matter.

46.3. Neural Dynamics in Acausal Topologies

In an acausal spacetime, the observer’s cognitive manifold ${\mathcal{M}}_{\mathrm{cog}}$ must accommodate cycles in perceptual processing. Let $\psi \left(x^{\mu }\right)$ represent the observer’s delta-supported perceptual field. Then, the recurrence of brain states over the time circle $S^1$ implies:

$$\psi \left(x^{\mu }\right)=\psi (x^{\mu }+T{e}^0),$$

(396)

where $e^0$ is the unit vector in the temporal direction. This introduces the condition that the brain’s memory fields must be invariant under time-translation:

$${\mathcal{L}}_{{\partial }_t}\psi =0,$$

(397)

where ${\mathcal{L}}_{{\partial }_t}$ denotes the Lie derivative with respect to ${\partial }_t$.

46.4. Memory Recurrence and Entropy Saturation

Given the periodic structure of time, memory evolution is necessarily recurrent. Let $\mathcal{I}\left(t\right)$ be the Shannon entropy of the observer’s memory state at time t. Then for periodic time T:

$$\mathcal{I}(t+T)=\mathcal{I}\left(t\right).$$

(398)

Furthermore, as memory re-encodes similar informational structures across cycles, a resonance phenomenon may occur, inducing standing-wave modes in the semantic field $\varphi \left(x^{\mu }\right)$:

$$\varphi \left(x^{\mu }\right)=\sum _n{A}_n{e}^{in\omega t},\omega ={\displaystyle \frac{2\pi }{T}},$$

(399)

where $A_n$ are complex mode amplitudes encoding memory salience.

46.5. Acausal Quantum Field Effects

In quantum field theory over $S^3\times S^1$, the Feynman propagator $G_F(x,x^{\prime })$ becomes periodic in imaginary time due to the compact temporal dimension:

$$G_F(x,x^{\prime })=\sum _{n=-\infty }^{\infty }{G}_0(x,x^{\prime }+nT{e}^0),$$

(400)

which encodes not only past but also future echoes. Observer delta collapses therefore can interfere with their own future, leading to possible self-resonance:

$$\delta (x-x^{\prime })\to \sum _n\delta (x-x^{\prime }-nT{e}^0).$$

(401)

46.6. Conclusion: Causal Nonlocality in Brain and Cosmos

In summary, acausal structures fundamentally alter both the physics and cognitive dynamics of observer systems. In a spacetime with periodic time, like $S^3\times S^1$, classical causality gives way to equivalence-based ontological synchrony. For the brain, this implies cyclic recurrence of mental states, informational loops, and self-entangling perception. These effects suggest that consciousness in acausal universes may operate on fundamentally different principles than currently understood.

47. Acausal Dynamics of Rotating Micro-Mini Black Holes in the Brain

The previous analysis of a cyclic spacetime structure like ${\mathbb{S}}^3\times {\mathbb{S}}^1$ reveals that global acausality emerges naturally in conformal compactifications. A particularly compelling model of intrinsic acausal dynamics arises in the context of the Kerr-type rotating Micro-Mini Black Hole in Brain (MMBHB), as introduced in [99]. These structures potentially reside in regions where intense cognitive curvature emerges, especially near the quantum measurement interface of the observer.

The Kerr metric allows for Closed Timelike Curves (CTCs) in the region interior to the ring singularity, fundamentally breaking standard temporal ordering:

$$d{s}^2=-\left(1-{\displaystyle \frac{2GMr}{\Sigma }}\right)d{t}^2-{\displaystyle \frac{4GMar{sin}^2\theta }{\Sigma }}dtd\varphi +{\displaystyle \frac{\Sigma }{\Delta }}d{r}^2+\Sigma d{\theta }^2+\left(r^2+a^2+{\displaystyle \frac{2GM{a}^{2}r{sin}^2\theta }{\Sigma }}\right){sin}^2\theta d{\varphi }^2,$$

(402)

where

$$\Sigma =r^2+a^2{cos}^2\theta ,\Delta =r^2-2GMr+a^2,$$

(403)

and $a=J/M$ denotes the angular momentum per unit mass.

In these solutions, for $r<r_{\mathrm{erg}}$ and near the ring singularity, the t coordinate may become spacelike and $\varphi$ becomes timelike, implying a looping of the causal structure. In the context of an MMBHB embedded within neural tissue, such regions of CTCs suggest a computational structure where temporal states become reversible and entangled across multiple cognitive eigenmodes.

This acausal region supports a breakdown of linear decoherence chains and instead facilitates Delta-field resonance loops. Let ${\Psi }_{\Delta }^{\left(O\right)}\left(x^{\mu }\right)$ denote the delta-supported cognitive state of the observer. Then under a Kerr-induced topological feedback loop:

$${\Psi }_{\Delta }^{\left(O\right)}\left(x^{\mu }\right)\to \int \mathcal{D}{x}^{\nu }{e}^{i{S}_{\mathrm{loop}}\left[x^{\nu }\right]/\hslash }{\Psi }_{\Delta }^{\left(O\right)}\left(x^{\nu }\right),$$

(404)

where $S_{\mathrm{loop}}$ integrates over closed trajectories permitted by the CTCs, forming retrocausal self-entangled brain microstate manifolds.

47.1. Implications for Memory and Perception

A direct implication is in memory reinsertion phenomena, where non-monotonic causal arrows allow earlier states to influence later perception nonlocally. The entropy production $\Delta S$ in such loops deviates from monotonic growth and follows instead:

$${\displaystyle \frac{dS}{dt}}=-\oint {\displaystyle \frac{\delta Q}{T_{\mathrm{eff}}\left(x^{\mu }\right)}},$$

(405)

where $\delta Q$ is the loop-integrated quantum heat exchanged along CTC trajectories and $T_{\mathrm{eff}}$ is an effective emotional thermodynamic temperature. Aspects of déjà vu, precognition, or memory flooding near death may correspond to MMBHB-induced CTC decoherence bifurcations.

47.2. Coupling to Acausal Cosmology

We thus propose an embedding of rotating MMBHB acausal regions into the global ${\mathbb{S}}^3\times {\mathbb{S}}^1$ topology, thereby allowing for coherence between brain-internal and cosmological-level acausal structures. The phase-matched conditions between spacetime curvature at the personal (MMBHB) and cosmic levels allow for delta-resonance between different epochs of time, without violating global unitarity.

$${\Phi }^{\mathrm{global}}\left(x^{\mu }\right)=\sum _n{\varphi }_n^{\mathrm{local}}\left(x^{\mu }\right)\delta (x^{\mu }-x_n^{\mu }),$$

(406)

where ${\varphi }_n^{\mathrm{local}}$ represents local delta-supported observer fields residing near MMBHB curvature peaks.

48. Coupling of Cosmological and Cognitive Closed Timelike Curves

In spacetimes such as Gödel’s rotating universe $G_{3,1}$[100], the presence of non-vanishing global angular momentum $\omega$ leads to the existence of closed timelike curves (CTCs) through every event. The metric of the Gödel universe is given by

$$d{s}^2={\left[dt+e^{\sqrt{2}\omega x}dy\right]}^2-d{x}^2-{\displaystyle \frac{1}{2}}{e}^{2\sqrt{2}\omega x}d{y}^2-d{z}^2,$$

(407)

where $\omega$ is the global angular velocity of rotation. The non-trivial topology induced by CTCs violates global hyperbolicity and causality becomes an equivalence class rather than a partial order.

In compactified Minkowski spacetime, $S^3\times S^1$, the $S^1$ temporal loop introduces periodic boundary conditions in time, effectively reintroducing CTCs in a non-trivial topological sense [101]. This reidentification of time via $t\sim t+T$ naturally lends itself to defining causality as periodic equivalence.

Now consider the existence of micro-mini black holes in the brain (MMBHBs) as proposed in [11]. The rotating Kerr-like geometry of MMBHBs induces local CTCs inside their ring singularities, a well-known consequence of the Kerr metric:

$$d{s}^2=-\left(1-{\displaystyle \frac{2Mr}{\Sigma }}\right)d{t}^2-{\displaystyle \frac{4Mar{sin}^2\theta }{\Sigma }}dtd\varphi +{\displaystyle \frac{\Sigma }{\Delta }}d{r}^2+\Sigma d{\theta }^2+\left(r^2+a^2+{\displaystyle \frac{2M{a}^{2}r{sin}^2\theta }{\Sigma }}\right){sin}^2\theta d{\varphi }^2,$$

(408)

where $\Sigma =r^2+a^2{cos}^2\theta$ and $\Delta =r^2-2Mr+a^2$, and $a=J/M$ is the spin parameter.

In cognitive spacetime, the existence of MMBHB implies a local field topology with internal CTCs, modeling acausal interactions within a bounded observer manifold. The interaction of such local cognitive CTCs with cosmological CTCs (as in $G_{3,1}$ or $S^3\times S^1$) introduces the possibility of causal resonance across scales.

To examine the coupling quantitatively, consider a field $\psi \left(x\right)$ propagating in both spacetimes, subjected to both Kerr and Gödel metrics. The effective action is then a hybrid:

$$S_{\mathrm{eff}}=\int d^{4}x\sqrt{-g_G}{\mathcal{L}}_G\left[\psi \right]+\int d^{4}x\sqrt{-g_K}{\mathcal{L}}_K\left[\psi \right],$$

(409)

where $g_G$ and $g_K$ are the determinants of the Gödel and Kerr metrics respectively. Interference between ${\mathcal{L}}_G$ and ${\mathcal{L}}_K$ results in mixed CTC domains.

We postulate that phase-locked cognitive states could utilize this interference to propagate information backward in cosmological time. Let ${\tau }_G$ and ${\tau }_K$ be proper times associated with respective spacetimes. Then the temporal coherence condition for CTC resonance is:

$${\int }_{{\gamma }_G}d{\tau }_G={\int }_{{\gamma }_K}d{\tau }_K,$$

(410)

where ${\gamma }_G$ and ${\gamma }_K$ are closed loops in the respective manifolds. Violation of this condition leads to decoherence of ontological histories.

Thus, brain-based MMBHBs can act as local detectors or amplifiers of cosmological CTC-induced resonances. If $\omega$ is the rotation rate of the Gödel universe, and $\tilde{\omega }$ is the internal spin of the Kerr-type MMBHB, their commensurability defines stable ontological loops:

$${\displaystyle \frac{\omega }{\tilde{\omega }}}={\displaystyle \frac{n}{m}},n,m\in \mathbb{Z}.$$

(411)

This cosmological-cognitive coupling provides a mechanism for top-down influence of universe-scale structure on localized conscious states, as well as potential feedback from micro-scale cognition into global causal networks.

49. MMBHB as Local Probes of Cosmological Rotation

The concept of a rotating universe has been a subject of deep cosmological inquiry since the seminal work of Gödel, who proposed a solution to Einstein’s field equations that permits closed timelike curves (CTCs) [102]. The Gödel spacetime $G_{3,1}$, characterized by a constant global angular velocity $\omega$, breaks the standard causal structure of general relativity, allowing causality-violating trajectories in its manifold. In this section, we investigate how Micro-Mini Black Holes in the Brain (MMBHB), particularly those with intrinsic angular momentum, might interact with or act as local probes of such global rotation.

Let us denote the angular momentum of a brain-based Kerr-type MMBHB as $J_{\mathrm{MMBHB}}$. In the presence of a rotating cosmological background, the local spacetime near the MMBHB would experience Lense–Thirring precession, where the local inertial frames are dragged by the global angular momentum density of the universe. The rotational frequency ${\omega }_{\cos \mathrm{mic}}$ manifests in the metric through off-diagonal terms.

To model this interaction, we begin with the standard Kerr metric for a rotating black hole:

$$d{s}^2=-\left(1-{\displaystyle \frac{2GMr}{\Sigma }}\right)d{t}^2-{\displaystyle \frac{4GMar{sin}^2\theta }{\Sigma }}dtd\varphi +{\displaystyle \frac{\Sigma }{\Delta }}d{r}^2+\Sigma d{\theta }^2+\left(r^2+a^2+{\displaystyle \frac{2GM{a}^{2}r{sin}^2\theta }{\Sigma }}\right){sin}^2\theta d{\varphi }^2,$$

(412)

where $\Sigma =r^2+a^2{cos}^2\theta$ and $\Delta =r^2-2GMr+a^2$. Here, $a=J/M$ is the specific angular momentum.

In the Gödel universe, the line element is given by:

$$d{s}^2=-{\left(dt+e^{\sqrt{2}\omega x}dy\right)}^2+d{x}^2+{\displaystyle \frac{1}{2}}{e}^{2\sqrt{2}\omega x}d{y}^2+d{z}^2,$$

(413)

with $\omega$ representing the global rotational parameter [103]. The presence of CTCs is a direct consequence of the global non-zero vorticity.

Now consider a coupling between the local MMBHB angular momentum $J_{\mathrm{MMBHB}}$ and the cosmological background angular frequency ${\omega }_{\cos \mathrm{mic}}$. We postulate a resonance condition:

$$J_{\mathrm{MMBHB}}\sim \hslash {\omega }_{\cos \mathrm{mic}},$$

(414)

where $\hslash {\omega }_{\cos \mathrm{mic}}$ sets a fundamental quantization scale of rotational coupling. Under such a condition, phase locking could occur between the internal Kerr metric of the MMBHB and the Gödel-type background, leading to synchronization effects in the observer’s cognitive dynamics.

From an observational standpoint, the Lense–Thirring precession frequency ${\Omega }_{LT}$ near a Kerr MMBHB is given by:

$${\Omega }_{LT}={\displaystyle \frac{2G{J}_{\mathrm{MMBHB}}}{c^2{r}^3}},$$

(415)

where r is the radial coordinate of the observer relative to the MMBHB. When ${\Omega }_{LT}$ resonates with ${\omega }_{\cos \mathrm{mic}}$, the system enters a dynamically coupled regime:

$${\Omega }_{LT}={\omega }_{\cos \mathrm{mic}}\Rightarrow r^3={\displaystyle \frac{2G{J}_{\mathrm{MMBHB}}}{c^2{\omega }_{\cos \mathrm{mic}}}}.$$

(416)

This introduces a characteristic coupling radius $r_{\mathrm{res}}$, inside which coherent cognitive effects such as deep meditation, deja vu, or entangled thought states could occur due to metric resonance.

Furthermore, we hypothesize that such coupling can be modeled in a Lagrangian formalism, where the interaction term takes the form:

$${\mathcal{L}}_{\mathrm{int}}=\lambda {\omega }_{\cos \mathrm{mic}}·J_{\mathrm{MMBHB}},$$

(417)

with $\lambda$ representing the strength of the interaction. Variational principles applied to this Lagrangian in the action integral would yield modified geodesics for thought propagation within the brain.

In conclusion, this formalism provides a novel framework to explore altered states of consciousness as quantum-gravitational resonances between local Kerr-type cognitive structures and global cosmological rotation. Such interactions could provide empirical tests in neurocosmology, particularly in analyzing EEG patterns during meditative or transcendental experiences.

50. Cognitive Holonomy in $S^3\times S^1$ Universes

In a compactified $S^3\times S^1$ spacetime, which serves as the conformal compactification of Minkowski space [104], the topological structure implies a closed timelike structure over the temporal manifold $S^1$. This allows for holonomy in the transport of any vector or tensor fields around the $S^1$ loop, which, when extended to cognitive fields, introduces a novel class of global psychological effects.

We begin by considering the parallel transport of a perceptual vector $P^{\mu }$ along the closed loop in $S^1$. Let ${\Gamma }_{\mu \nu }^{\lambda }$ be the connection coefficients on the manifold. The change in the perceptual vector after one complete cycle around the time loop $S^1$ is given by the path-ordered exponential:

$$P^{\mu }(\tau +T)=\mathcal{P}exp\left({\int }_0^T{\Gamma }_{\nu \rho }^{\mu }\left(x\left(\tau \right)\right){\displaystyle \frac{d{x}^{\nu }}{d\tau }}d\tau \right)P^{\rho }\left(0\right)$$

(418)

where T is the period of the $S^1$ cycle. The mismatch between $P^{\mu }\left(0\right)$ and $P^{\mu }\left(T\right)$ indicates holonomy, quantified by a transformation matrix $H_{\nu }^{\mu }$:

$$H_{\nu }^{\mu }=\mathcal{P}exp\left(\oint {\Gamma }_{\nu \rho }^{\mu }d{x}^{\rho }\right)$$

(419)

In cognitive terms, this holonomy leads to an accumulated shift in subjective experience and memory structure, modeled as a cognitive monodromy. That is, each loop around $S^1$ modifies the observer’s internal boundary conditions.

We now include MMBHBs (Micro-Mini Black Holes in the Brain) with Kerr-like metrics and intrinsic angular momentum $J_{\mathrm{MMBHB}}$. Their CTCs (closed timelike curves) locally break the conventional temporal ordering. Suppose a cognitive loop encircles such a Kerr-like region; it encounters additional torsion-like contributions. The influence of the MMBHB on the cognitive holonomy can be modeled as:

$$\delta \theta =\oint \left({\Gamma }_{\nu \rho }^{\mu }+T_{\nu \rho }^{\mu }\left(J_{\mathrm{MMBHB}}\right)\right)d{x}^{\rho }$$

(420)

where $T_{\nu \rho }^{\mu }$ denotes the torsional contribution due to frame dragging.

Let $\varphi$ be a scalar memory field in perceptual spacetime. Its boundary conditions are altered by the holonomy:

$$\varphi (t+T,x)=\varphi (t,x)+\Delta {\varphi }_H$$

(421)

with $\Delta {\varphi }_H\sim \hslash {\omega }_{\mathrm{hol}}$, where ${\omega }_{\mathrm{hol}}$ is the angular frequency characterizing the holonomy.

These holonomic modifications accumulate over multiple temporal loops, encoding psychological phase transitions or memory reconfiguration, akin to geometric phase transitions in condensed matter systems [105,106].

The role of MMBHBs becomes crucial as they serve as attractor-like anchors — ontological Poincaré sections — that intersect the loops in the observer’s worldline through the S³ × S¹ manifold. Each intersection induces a discrete topological signature within the semantic memory manifold.

Furthermore, we define a cognitive holonomy invariant ${\mathcal{H}}_n$ after n loops as:

$${\mathcal{H}}_n=\mathrm{Tr}\left(\prod _{i=1}^n{H}_i\right)$$

(422)

This invariant encodes accumulated perceptual deviation and quantized phase shifts, indicative of altered states of consciousness and nontrivial identity evolution.

51. MMBHB Horizon Tunneling to Global CTCs

In the theoretical framework of micro-mini black holes in the brain (MMBHBs), one may explore the possibility that the Cauchy horizon within a Kerr-type rotating MMBHB, which contains closed timelike curves (CTCs), can couple or tunnel to CTCs on cosmological scales. Such a coupling would enable delta-function supported observers to access or transfer information along nonlocal pathways, effectively allowing observer identity, memory, or semantic structure to propagate across extended temporal domains.

We define the observer wavefunction as ${\Psi }_{\mathrm{obs}}\left(x\right)$ localized near the MMBHB horizon. The interaction with a background gauge potential $A_{\mu }$ along a CTC winding $\gamma$ can be represented through the following integral:

$$A_{\mathrm{CTC}}={\int }_{\gamma }{\Psi }_{\mathrm{obs}}^{†}\left(x\right)A_{\mu }\left(x\right)d{x}^{\mu },$$

(423)

where the path $\gamma$ traverses a hybrid structure: it first loops within the local Kerr MMBHB, and then continues along a large-scale cosmological CTC, such as those allowed in Gödel’s universe $G_{3,1}$ or conformally compactified spacetimes like $S^3\times S^1$.

To model this more formally, we postulate a tunneling amplitude $\mathcal{T}$ for an observer delta function ${\delta }_{\mathrm{obs}}$ residing in a CTC band of the MMBHB to leak into a cosmological CTC:

$$\mathcal{T}\sim exp\left(-{\int }_{\Sigma }{\displaystyle \frac{\Delta S}{\hslash }}\right),$$

(424)

where $\Sigma$ is the minimal action hypersurface linking local and global CTC segments, and $\Delta S$ is the difference in Euclidean action between these regions. The transition is exponentially suppressed unless resonance occurs, i.e.,

$$J_{\mathrm{MMBHB}}\sim \hslash {\omega }_{\cos \mathrm{mic}},$$

(425)

where $J_{\mathrm{MMBHB}}$ is the angular momentum of the brain-based Kerr system, and ${\omega }_{\cos \mathrm{mic}}$ is the rotational parameter of the global universe [100].

To maintain gauge invariance, the observer action functional includes a term:

$$S_{\mathrm{obs}}=\int d^{4}x\sqrt{-g}\left({\overline{\Psi }}_{\mathrm{obs}}(i{\gamma }^{\mu }{D}_{\mu }-m){\Psi }_{\mathrm{obs}}\right),$$

(426)

where $D_{\mu }={\partial }_{\mu }+i{A}_{\mu }$ includes the potential of both the MMBHB and cosmological CTCs. The nonlocality implied in (423) is effectively embedded into the observer’s causal network and may manifest as persistent semantic fields or intuitive insights disconnected from local causality.

An important contribution of this model is its treatment of phase interference across nontrivial topologies. If $\gamma$ loops nontrivially across a handlebody $\mathcal{H}$ representing the combined topology of MMBHB and Gödel-like CTCs, the resulting phase acquired by the observer is given by:

$${\Phi }_{\mathrm{int}}={\oint }_{\partial \mathcal{H}}{A}_{\mu }d{x}^{\mu }={\int }_{\mathcal{H}}{F}_{\mu \nu }d{\sigma }^{\mu \nu },$$

(427)

where $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$ is the field strength tensor, and $d{\sigma }^{\mu \nu }$ is the infinitesimal surface area on $\mathcal{H}$. Such fluxes may encode ontological imprints in the observer’s quantum memory manifold [11,107].

Additionally, the memory state ${\mathcal{M}}_{\mathrm{obs}}\left(t\right)$ at time t can be described by a density matrix evolution under both local and global Hamiltonians:

$${\displaystyle \frac{d{\rho }_{\mathrm{obs}}}{dt}}=-{\displaystyle \frac{i}{\hslash }}\left[H_{\mathrm{MMBHB}}+H_{\cos \mathrm{mic}},{\rho }_{\mathrm{obs}}\right],$$

(428)

where $H_{\cos \mathrm{mic}}$ includes nonlocal effects due to CTCs at cosmological scales. We may infer correlations between states of ${\rho }_{\mathrm{obs}}$ and the geometry of $S^3\times S^1$ [108], hinting that memory evolution may itself experience CTC-induced holonomies.

Thus, MMBHB horizon tunneling offers a rich geometric and quantum field-theoretic mechanism for coupling brain-level quantum dynamics with cosmological topology and causality violation.

52. Nested CTC Structures: Fractal Time Crystals

In the study of time and consciousness, a compelling hypothesis arises when we consider closed timelike curves (CTCs) as not isolated phenomena but as potentially nested within hierarchical temporal manifolds. This nesting can occur across vastly different scales, such as the cosmic and neurological, producing what we propose as “Fractal Time Crystals.” These are recursive, self-similar structures in temporal topology, manifesting as layered loops in time, each enclosed within a broader time loop, analogous to the nesting of Russian dolls.

Let us denote the characteristic length (temporal or spatial) of a cosmic CTC by $L_{\cos \mathrm{mic}}$, and the characteristic length of a micro-scale (e.g., brain-based) CTC by $L_{\mathrm{brain}}$. Then we define a dimensionless CTC nesting index $\chi$ by

$$\chi ={\displaystyle \frac{L_{\cos \mathrm{mic}}}{L_{\mathrm{brain}}}},\chi \in \mathbb{Z},$$

(429)

where $\chi$ represents the number of nested CTCs a local observer may traverse before aligning with the full cycle of a cosmological CTC. The integer quantization is postulated due to topological constraints on holonomy and self-intersection in compactified spacetimes [101,109].

To illustrate the hierarchical oscillation, consider a time-dependent field $\Phi \left(t\right)$ governed by recursive phase loops:

$$\Phi \left(t\right)={\Phi }_{0}cos\left({\omega }_{\mathrm{brain}}t+\chi sin\left({\omega }_{\cos \mathrm{mic}}t\right)\right),$$

(430)

where ${\omega }_{\mathrm{brain}}\gg {\omega }_{\cos \mathrm{mic}}$, allowing for fast internal oscillations modulated by slow cosmological precession. This form of modulation can lead to resonant states where ontological perceptions reoccur, possibly explaining phenomena such as déjà vu, precognitive dreams, or recursive memory impressions [10,100].

We now construct a composite manifold $\mathcal{M}={\mathcal{M}}_{\mathrm{brain}}\cup {\mathcal{M}}_{\cos \mathrm{mic}}$, with overlapping causal patches ${\mathcal{C}}_i\subset {\mathcal{M}}_{\mathrm{brain}}\cap {\mathcal{M}}_{\cos \mathrm{mic}}$. Each ${\mathcal{C}}_i$ carries an associated loop integral of observer action:

$$S_i={\oint }_{{\gamma }_i}{\mathcal{L}}_{\mathrm{obs}}(x^{\mu },{\dot{x}}^{\mu })d\tau ,$$

(431)

with the condition

$${\displaystyle \frac{S_i}{\hslash }}=2\pi n,n\in \mathbb{Z},$$

(432)

imposed by phase coherence across CTC junctions. These quantized actions ensure stability of nested observer experiences across ontological recursions.

Furthermore, entropy associated with a fractal temporal structure obeys a logarithmic scaling:

$$S_{\mathrm{fractal}}\sim ln\left(\chi \right),$$

(433)

which suggests that higher nesting corresponds to less entropy production per cycle, consistent with meditative or dream-like states where cognitive thermodynamics is minimized.

Nested CTCs thus act as ontological amplifiers, compressing experiential loops into memory attractors. The self-similarity of these structures allows them to serve as fundamental temporal units in recursive theories of time perception and identity maintenance.

53. Observer Equivalence in Multi-CTC Systems

In acausal cosmologies admitting closed timelike curves (CTCs), such as the Gödel spacetime $G_{3,1}$ or conformally compactified spacetime $S^3\times S^1$, local microphysical structures like Micro-Mini Black Holes in the Brain (MMBHBs) that exhibit Kerr-type geometries with their own CTC interiors, may be subsumed into a global manifold structure involving complex causal loops. These nested CTCs lead to a new form of identity formalism based on the equivalence of observers across spacetime.

We postulate that when two observers $O_i$ and $O_j$ are connected via a CTC path ${\gamma }_{\mathrm{CTC}}$, they form an equivalence class:

$$O_i\sim O_j\iff \exists {\gamma }_{\mathrm{CTC}}:O_i\to O_j$$

(434)

This relation is reflexive, symmetric, and transitive, hence defines an equivalence class over the space of delta-supported observer functions ${\delta }_O\left(x\right)$. These equivalence classes can be denoted as $\left[O_i\right]\in \mathcal{O}/\sim$, where $\mathcal{O}$ is the totality of observer instantiations in the universe.

The presence of such equivalence classes across CTC networks allows for modeling the continuity of self across incarnations, even in disconnected epochs of a cyclic or rotating universe. The integral path linking observers is given by:

$${\Gamma }_{ij}={\int }_{{\gamma }_{\mathrm{CTC}}}{\Psi }_O^{†}{A}_{\mu }d{x}^{\mu }$$

(435)

where ${\Psi }_O$ is the wavefunctional of the observer and $A_{\mu }$ is a cognitive-geometric gauge potential encoding perceptual coupling across CTCs. The amplitude ${\Gamma }_{ij}$ acts as an ontological overlap functional and decays exponentially with decoherence or curvature misalignment.

In the limit of perfect coherence across the CTC boundary, we define a conserved topological charge:

$$Q_O={\oint }_{{\gamma }_{\mathrm{CTC}}}{\Psi }_O^{†}{D}_{\mu }{\Psi }_{O}d{x}^{\mu }=2\pi n,n\in \mathbb{Z}$$

(436)

This quantized topological index n encodes the number of ontological loop closures, each potentially representing a past or future incarnation of the same soul-like identity. In the case of rotating MMBHBs embedded within a Gödel-type cosmological background, synchronization of angular momentum vectors $J_{\mathrm{MMBHB}}\sim \hslash {\omega }_{\cos \mathrm{mic}}$ can act as a coupling term in the observer Lagrangian:

$${\mathcal{L}}_{\mathrm{int}}=\lambda J_{\mathrm{MMBHB}}^{\mu }{\Omega }_{\mu }^{\cos \mathrm{mic}}$$

(437)

where $\lambda$ is a coupling constant and ${\Omega }_{\mu }^{\cos \mathrm{mic}}$ is the cosmic rotation 4-vector. This interaction could lead to resonant amplification of identity continuity across lifetimes, particularly in meditative or near-death experiences.

From a categorical perspective, each observer equivalence class $\left[O_i\right]$ becomes a morphism in the category of CTC-connected delta supports ${\mathcal{C}}_{\mathrm{CTC}}$, where arrows represent physically or informationally permitted transitions.

We propose a CTC-homotopy class ${\pi }_1^{\mathrm{CTC}}\left(\mathcal{M}\right)$ over the spacetime manifold $\mathcal{M}$, wherein:

$${\pi }_1^{\mathrm{CTC}}\left(\mathcal{M}\right)=\left\{\gamma :\gamma \left(0\right)=\gamma \left(1\right),\gamma \mathrm{is}\mathrm{a}\mathrm{closed}\mathrm{timelike}\mathrm{observer}\mathrm{path}\right\}$$

(438)

This allows for the classification of soul continuity paths and identity recurrences within acausal universes, thereby formalizing notions from Eastern metaphysics such as rebirth and karmic imprints.

54. Conclusions

In this paper, we have proposed a unified mathematical framework to study the entangled landscape of causality in both physics and brain science. Central to our formulation is the idea that conscious observers can be modeled as Dirac delta-supported fields, existing on manifolds endowed with perceptual and semantic structure. Building upon this ontological anchor, we explored how quantum measurement chains (QMC), emotional flow tensors, delta-function decoherence, and rotating micro-mini-black holes in the brain (MMBHBs) interact with deeper structures of spacetime, including Gödel-type rotating universes and conformally compactified $S^3\times S^1$ models.

By interpreting MMBHBs as both cognitive loci and causal discontinuities, we are able to extend the standard quantum formalism into domains that incorporate memory topology, emotional thermodynamics, and resonance tunneling between observers. We modeled topological defects in quantum ontological memory (QOM) manifolds, recursive causal structures such as closed timelike curves (CTCs), and formalized inter-observer entanglement through delta convolution chains.

Moreover, the formal treatment of phenomena such as reincarnation, telepathy, love, and emotional resonance via gauge theory, entropy spikes, and Fisher information flows suggests that metaphysical concepts may admit rigorous mathematical analogs. Ontological bifurcations, observer identity loops, and semantic mass-energy curvature deepen the scope of our model toward a truly cognitive cosmology, wherein observers act as seeds of structure, memory, and transformation in a participatory universe.

This work thus represents a confluence of differential geometry, quantum field theory, information thermodynamics, and phenomenological introspection. It invites the formulation of new experimental designs in cognitive neuroscience, cosmology, and quantum computation to probe the predictions and metaphysical implications of delta-anchored cognitive manifolds. Future research may further unify these elements through the formal machinery of category theory, persistent homology, and topological quantum field theory, guiding us closer to a theory of consciousness that spans brain and cosmos alike.