Submitted:
16 October 2025
Posted:
17 October 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Theoretical Methods
3. Results and Discussions
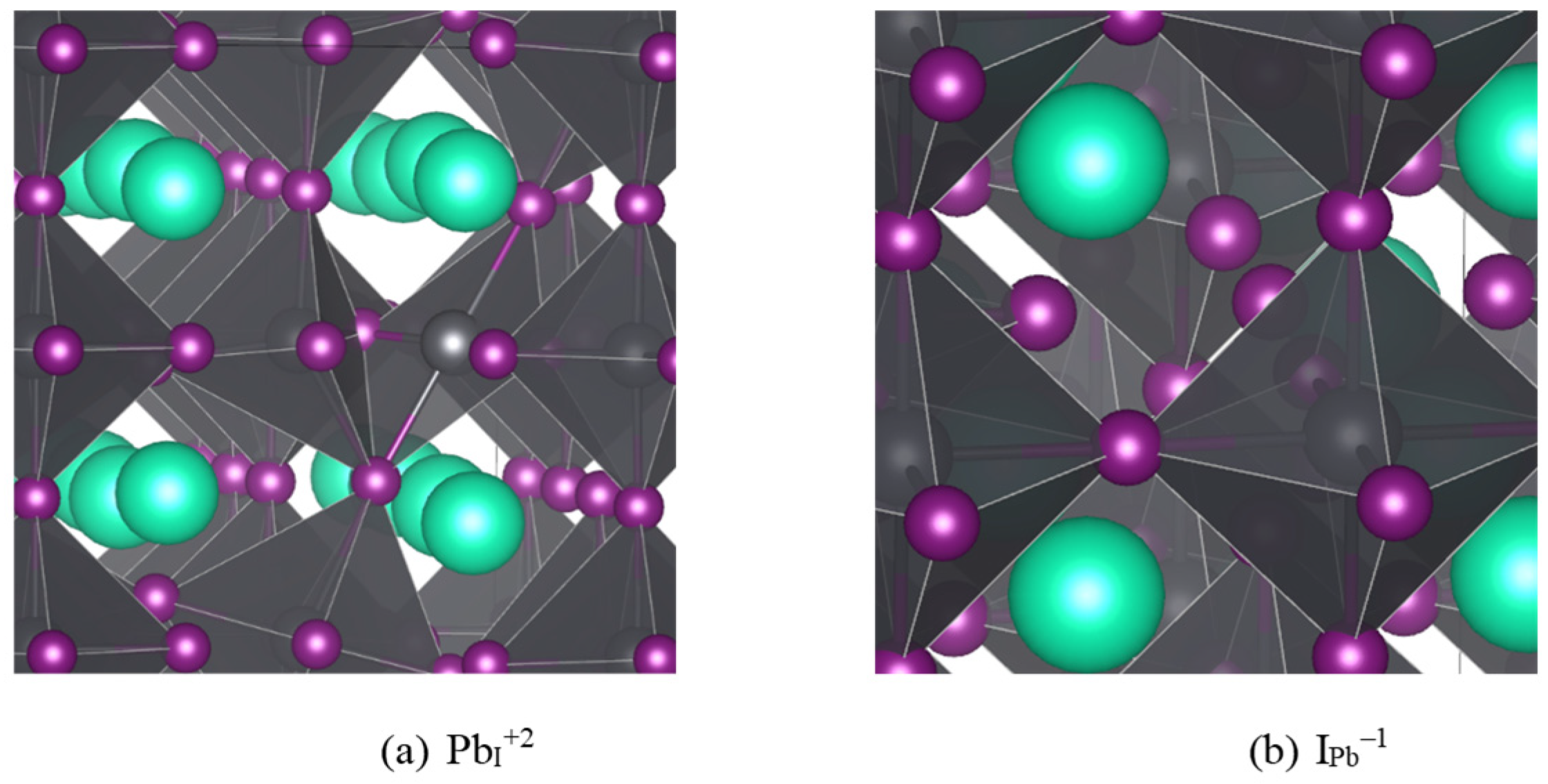
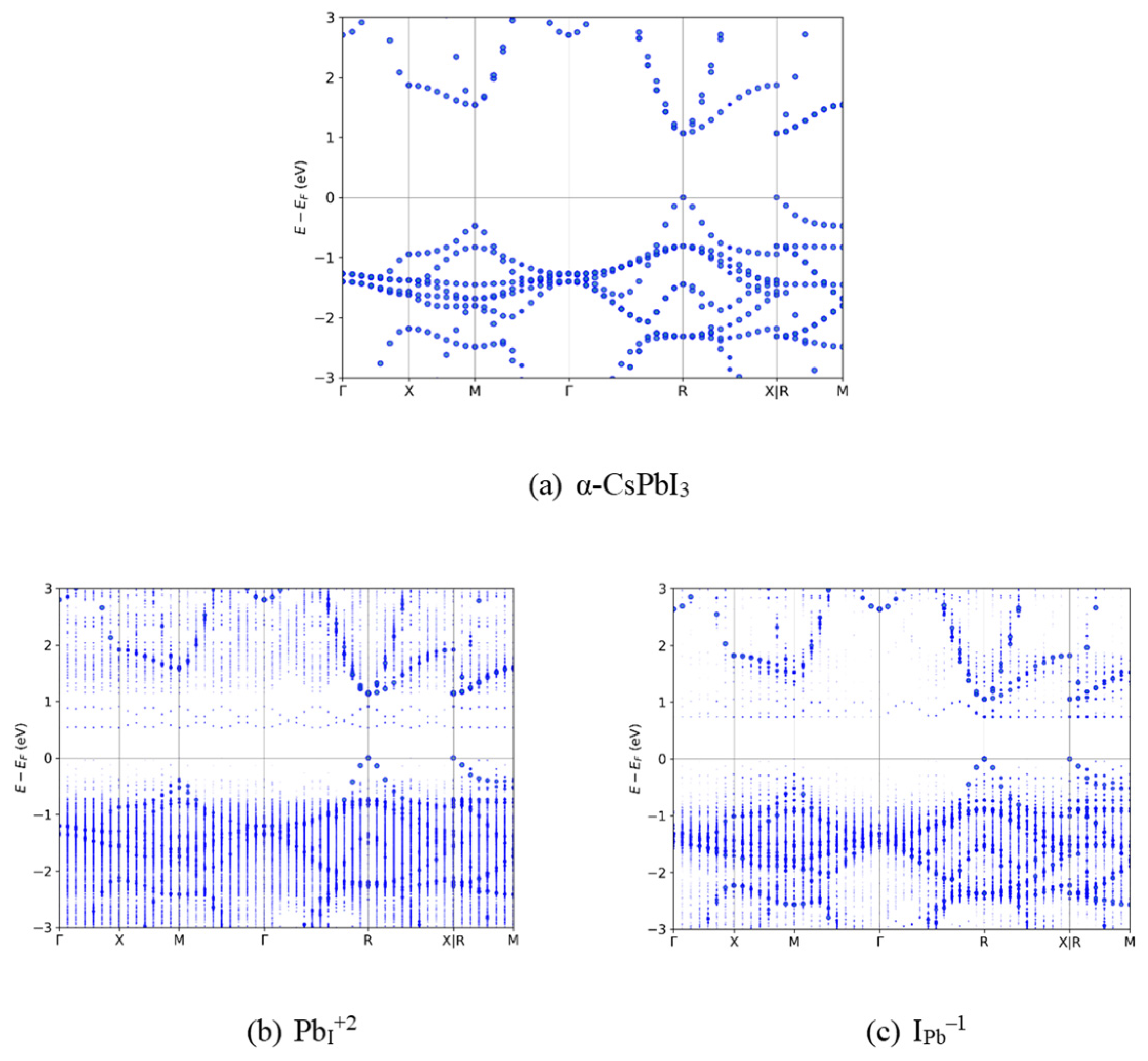
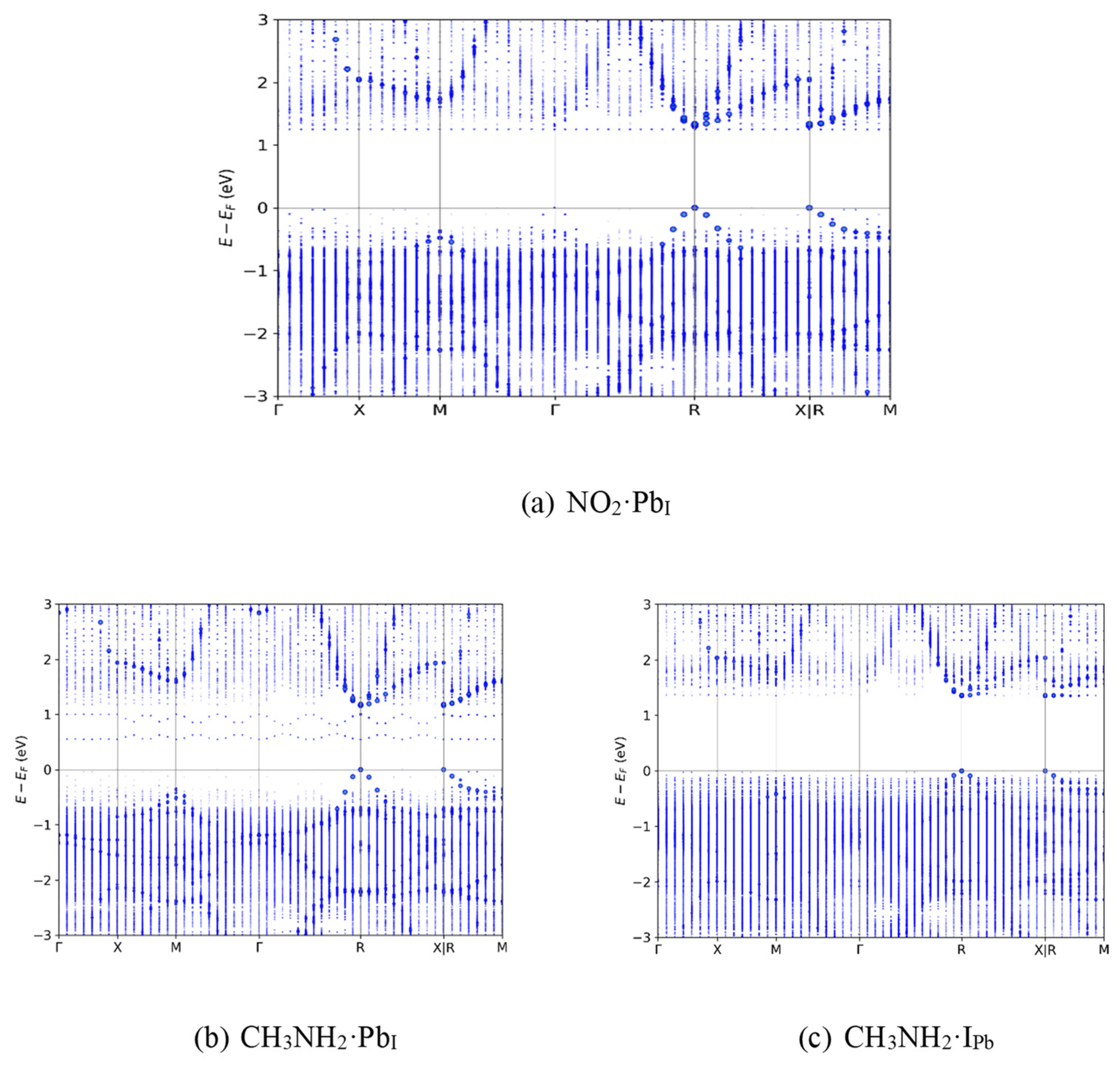
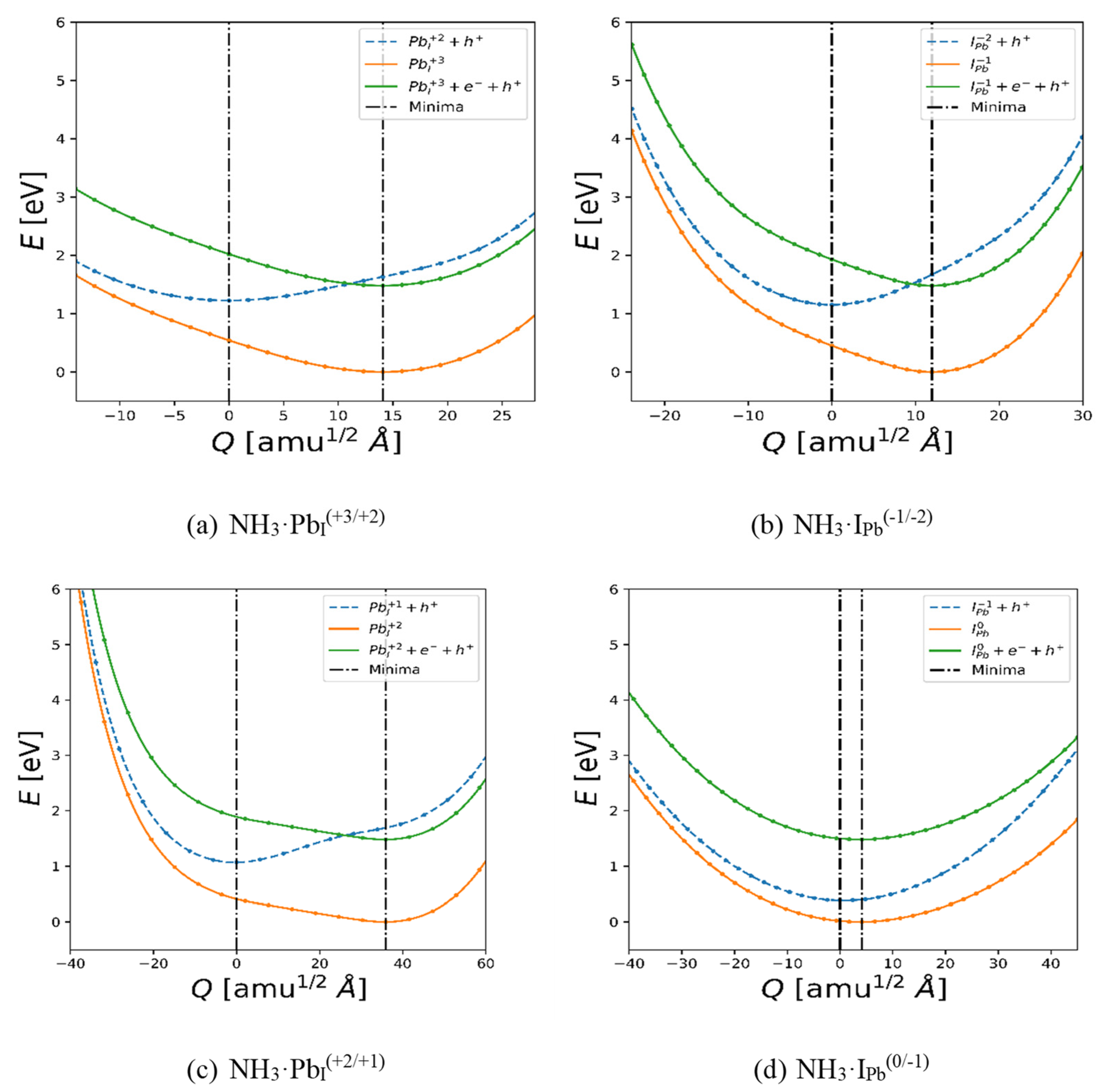
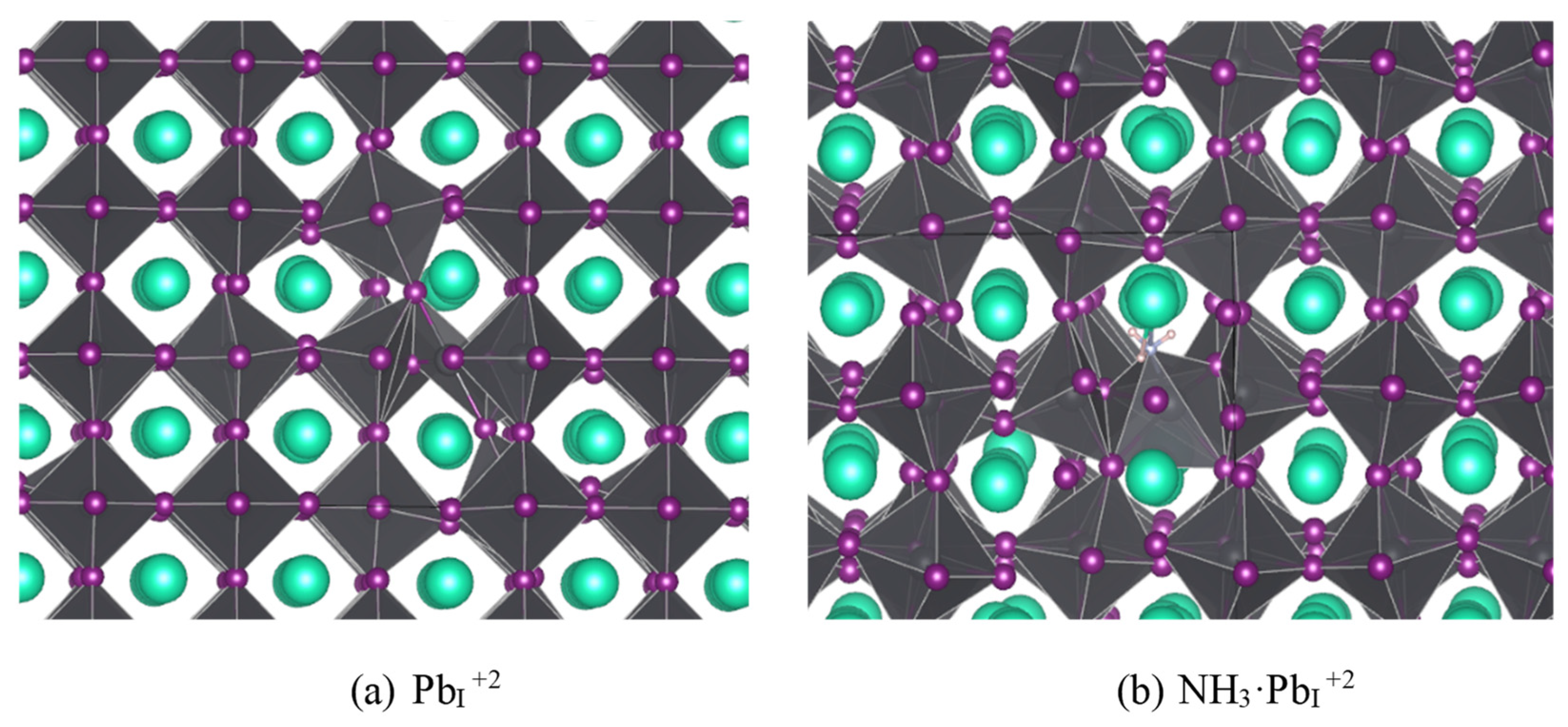
3.1. Defect Characterization and Band Structure Analysis
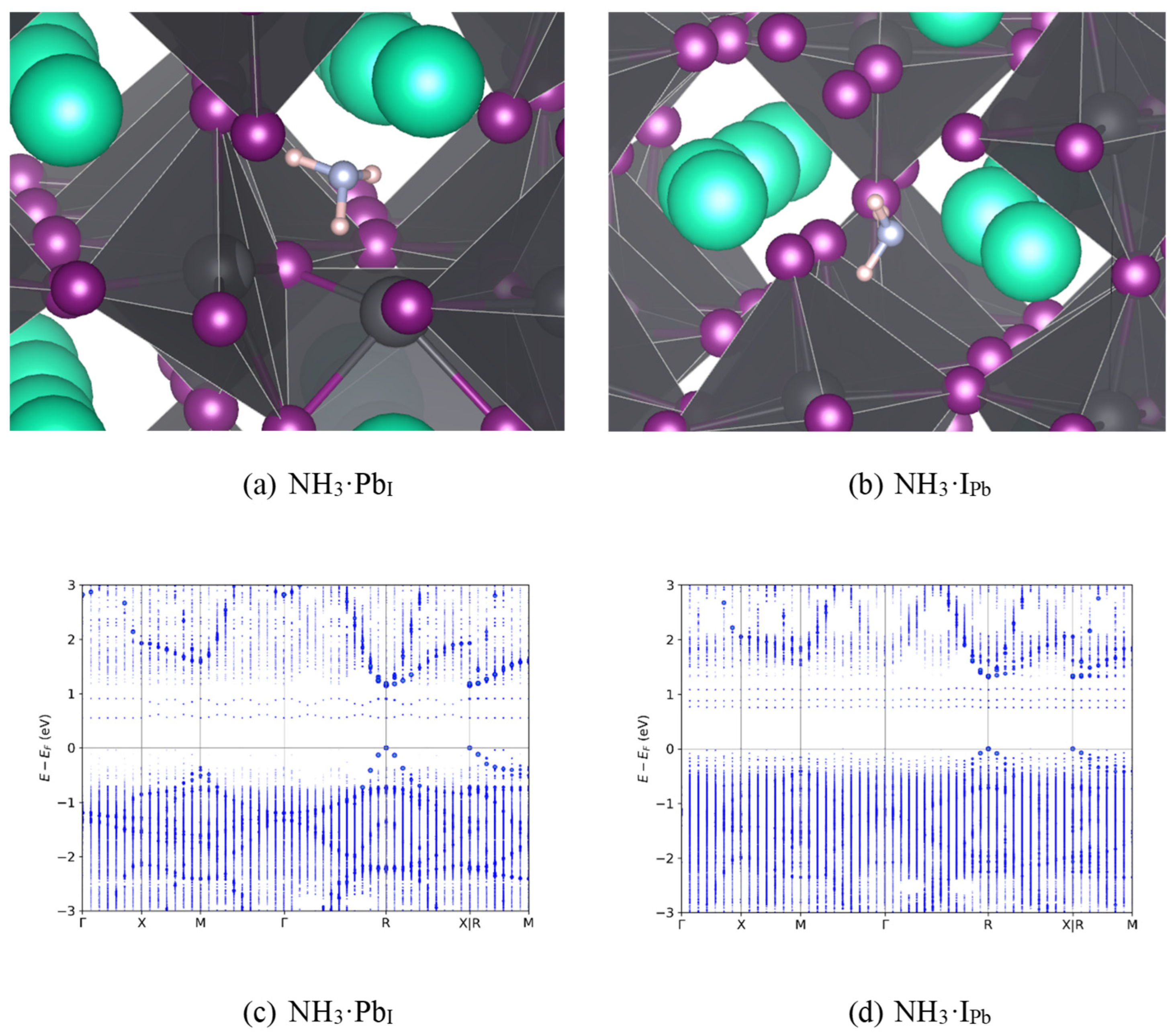
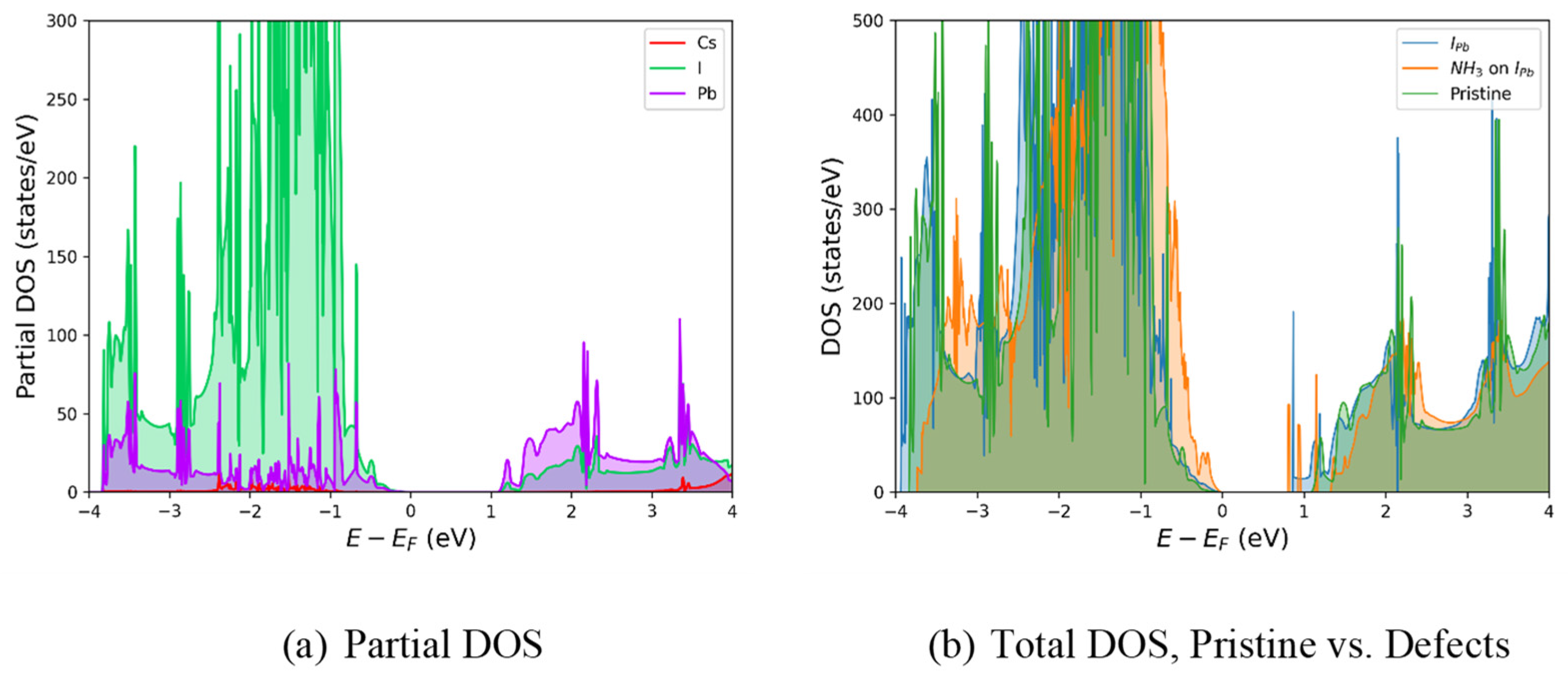
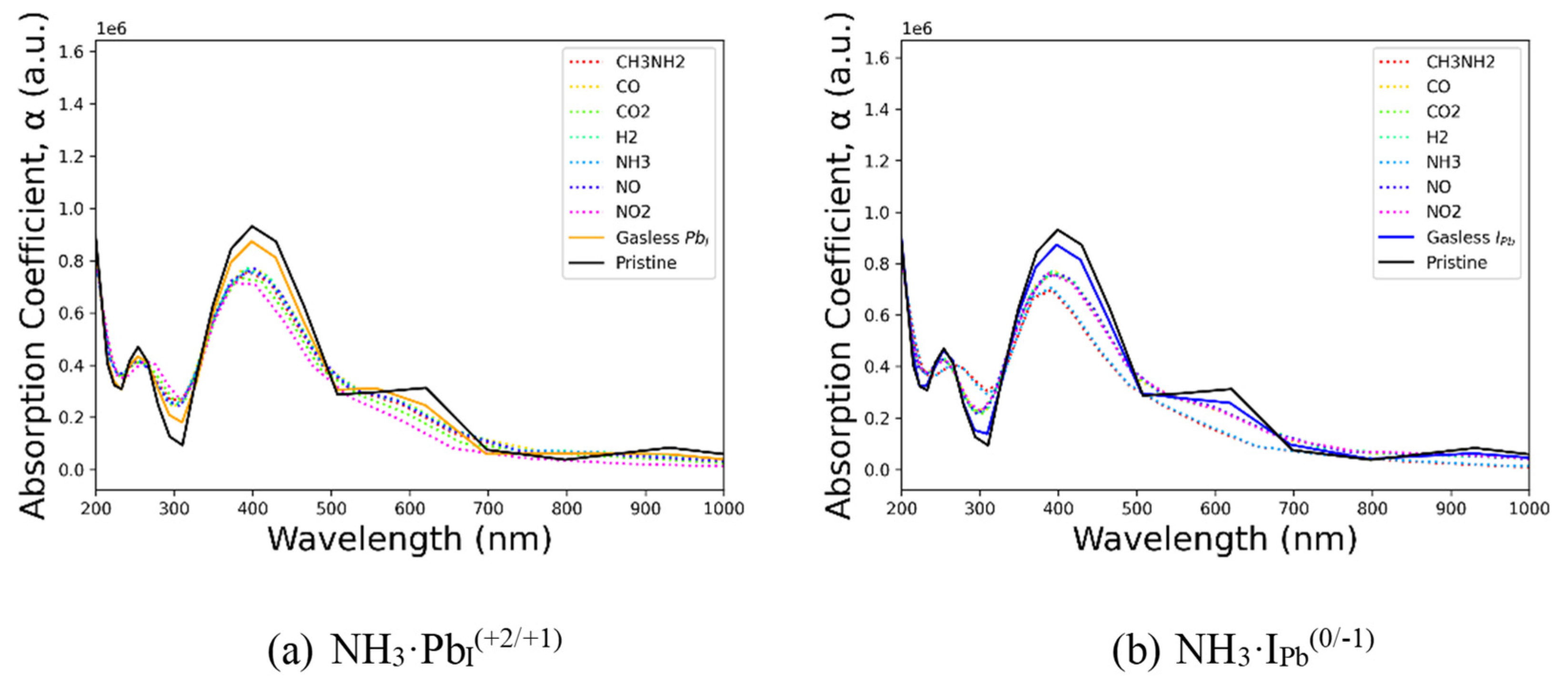
3.2. Gas Absorption Effects
3.3. Recombination Times via Nonadiabatic Molecular Dynamics
| System | Transition | Eg (eV) | NACs (meV) | Dephasing Time (ps) | Τ (ns) |
| Pristine | VBM-CBM | 1.68±0.04 | 0.77 | 16.49 | 797 |
| NH3·Pristine | VBM-CBM | 1.64±0.06 | 0.52 | 11.08 | 492 |
| IPb | VBM-D3 | 1.74±0.04 | 21.27 | 24.29 | 23 |
| D2-D3 | 0.49 | 2.65 | |||
| D2-D1 | 63.62 | 2.66 | |||
| D1-CBM | 42.81 | 42.66 | |||
| NH3·IPb | VBM-D2 | 1.70±0.04 | 30.60 | 27.71 | 30 |
| D2-D1 | 0.28 | 3.12 | |||
| D1-CBM | 82.06 | 3.17 | |||
| PbI | VBM-D3 | 2.23±0.08 | 1.43 | 5.57 | 1 |
| D2-D3 | 2.40 | 6.98 | |||
| D2-D1 | 40.24 | 17.43 | |||
| D1-CBM | 44.38 | 81.69 | |||
| NH3·PbI | VBM-D2 | 2.24±0.09 | 4.09 | 5.29 | 0 |
| D2-D1 | 4.29 | 6.55 | |||
| D1-CBM | 57.00 | 54.11 |
| System | Transition | Eg (eV) | NACs (meV) | Dephasing Time (ps) | Τ (ns) |
| Pristine | VBM-CBM | 1.68±0.04 | 0.77 | 16.49 | 797 |
| NH3·Pristine | VBM-CBM | 1.64±0.06 | 0.52 | 11.08 | 492 |
| IPb | VBM-D3 | 1.74±0.04 | 21.27 | 24.29 | 23 |
| D2-D3 | 0.49 | 2.65 | |||
| D2-D1 | 63.62 | 2.66 | |||
| D1-CBM | 42.81 | 42.66 | |||
| NH3·IPb | VBM-D2 | 1.70±0.04 | 30.60 | 27.71 | 30 |
| D2-D1 | 0.28 | 3.12 | |||
| D1-CBM | 82.06 | 3.17 | |||
| PbI | VBM-D3 | 2.23±0.08 | 1.43 | 5.57 | 1 |
| D2-D3 | 2.40 | 6.98 | |||
| D2-D1 | 40.24 | 17.43 | |||
| D1-CBM | 44.38 | 81.69 | |||
| NH3·PbI | VBM-D2 | 2.24±0.09 | 4.09 | 5.29 | 0 |
| D2-D1 | 4.29 | 6.55 | |||
| D1-CBM | 57.00 | 54.11 |
3.4. Ammonia-Driven Phase Change and Photoluminescent Detection Pathways
4. Conclusions
Supplementary Materials
Author Contributions
Data Availability Statement
Acknowledgements
Conflicts of Interest
References
- Ni, Z.; Jiao, H.; Fei, C.; Gu, H.; Xu, S.; Yu, Z.; Yang, G.; Deng, Y.; Jiang, Q.; Liu, Y.; Yan, Y.; Huang, J. Evolution of Defects during the Degradation of Metal Halide Perovskite Solar Cells under Reverse Bias and Illumination. Nat Energy 2022, 7 (1), 65–73. [CrossRef]
- Zhu, H.; Teale, S.; Lintangpradipto, M. N.; Mahesh, S.; Chen, B.; McGehee, M. D.; Sargent, E. H.; Bakr, O. M. Long-Term Operating Stability in Perovskite Photovoltaics. Nat Rev Mater 2023, 8 (9), 569–586. [CrossRef]
- Khan, M. R.; Schwenzer, J. A.; Lehr, J.; Paetzold, U. W.; Lemmer, U. Emergence of Deep Traps in Long-Term Thermally Stressed CH3NH3PbI3 Perovskite Revealed by Thermally Stimulated Currents. Journal of Physical Chemistry Letters 2022, 13 (2), 552–558. [CrossRef]
- Bera, S.; Saha, A.; Mondal, S.; Biswas, A.; Mallick, S.; Chatterjee, R.; Roy, S. Review of Defect Engineering in Perovskites for Photovoltaic Application. Mater. Adv. 2022, 3 (13), 5234–5247. [CrossRef]
- Zhuang, J.; Wang, J.; Yan, F. Review on Chemical Stability of Lead Halide Perovskite Solar Cells. Nano-Micro Lett. 2023, 15 (1), 84. [CrossRef]
- Wang, R.; Mujahid, M.; Duan, Y.; Wang, Z.-K.; Xue, J.; Yang, Y. A Review of Perovskites Solar Cell Stability. Advanced Functional Materials 2019, 29 (47), 1808843. [CrossRef]
- Best Research-Cell Efficiency Chart | Photovoltaic Research | NREL. https://www.nrel.gov/pv/cell-efficiency.html (accessed 2023-11-13).
- Parfenov, A. A.; Yamilova, O. R.; Gutsev, L. G.; Sagdullina, D. K.; Novikov, A. V.; Ramachandran, B. R.; Stevenson, K. J.; Aldoshin, S. M.; Troshin, P. A. Highly Sensitive and Selective Ammonia Gas Sensor Based on FAPbCl3 Lead Halide Perovskites. Journal of Materials Chemistry C 2021, 9 (7), 2561–2568. [CrossRef]
- Nations, S.; Gutsev, L.; Bala Ramachandran, ab; Aldoshin, S.; Duan, Y.; Wang, S. First-Principles Study of the Defect-Activity and Optical Properties of FAPbCl3. Materials Advances 2022, 2022, 3897. [CrossRef]
- Shockley, W.; Read, W. T. Statistics of the Recombinations of Holes and Electrons. Physical Review 1952, 87 (5), 835–842. [CrossRef]
- Alkauskas, A.; Dreyer, C. E.; Lyons, J. L.; Van de Walle, C. G. Role of Excited States in Shockley-Read-Hall Recombination in Wide-Band-Gap Semiconductors. Phys. Rev. B 2016, 93 (20), 201304. [CrossRef]
- Yamada, Y.; Kanemitsu, Y. Electron-Phonon Interactions in Halide Perovskites. NPG Asia Mater 2022, 14 (1), 1–15. [CrossRef]
- Wu, Y. N.; Saidi, W. A.; Wuenschell, J. K.; Tadano, T.; Ohodnicki, P.; Chorpening, B.; Duan, Y. Anharmonicity Explains Temperature Renormalization Effects of the Band Gap in SrTiO3. Journal of Physical Chemistry Letters 2020, 11 (7), 2518–2523. [CrossRef]
- Duan, Y.; Ohodnicki, P.; Chorpening, B.; Hackett, G. Electronic Structural, Optical and Phonon Lattice Dynamical Properties of Pure- and La-Doped SrTiO3: An Ab Initio Thermodynamics Study. Journal of Solid State Chemistry 2017, 256 (August), 239–251. [CrossRef]
- Jia, T.; Zeng, Z.; Lin, H. Q.; Duan, Y.; Ohodnicki, P. First-Principles Study on the Electronic, Optical and Thermodynamic Properties of ABO3 (A = La,Sr, B = Fe,Co) Perovskites. RSC Advances 2017, 7 (62), 38798–38804. [CrossRef]
- Qi, H.; Lee, Y. L.; Yang, T.; Li, W.; Li, W.; Ma, L.; Hu, S.; Duan, Y.; Hackett, G. A.; Liu, X. Positive Effects of H2O on the Hydrogen Oxidation Reaction on Sr2Fe1.5Mo0.5O6-δ-Based Perovskite Anodes for Solid Oxide Fuel Cells. ACS Catalysis 2020, 10 (10), 5567–5578. [CrossRef]
- Jia, T.; Zeng, Z.; Zhang, X.; Ohodnicki, P.; Chorpening, B.; Hackett, G.; Lekse, J.; Duan, Y. The Influence of Oxygen Vacancy on the Electronic and Optical Properties of ABO3-: δ (A = La, Sr, B = Fe, Co) Perovskites. Physical Chemistry Chemical Physics 2019, 21 (36), 20454–20462. [CrossRef]
- Jia, T.; Ohodnicki, P.; Chorpening, B.; Lekse, J.; Hackett, G.; Duan, Y. Theoretical Study of the Optical and Thermodynamic Properties of La: XSr1- xCo1- yFeyO3- δ (x / y = 0.25, 0.5, 0.75) Perovskites. Physical Chemistry Chemical Physics 2019, 21 (47), 26117–26122. [CrossRef]
- Fan, Z.; Sun, K.; Wang, J. Perovskites for Photovoltaics: A Combined Review of Organic-Inorganic Halide Perovskites and Ferroelectric Oxide Perovskites. Journal of Materials Chemistry A 2015, 3 (37), 18809–18828. [CrossRef]
- Ouedraogo, N. A. N.; Chen, Y.; Xiao, Y. Y.; Meng, Q.; Han, C. B.; Yan, H.; Zhang, Y. Stability of All-Inorganic Perovskite Solar Cells. Nano Energy 2020, 67, 104249. [CrossRef]
- Wang, B.; Novendra, N.; Navrotsky, A. Energetics, Structures, and Phase Transitions of Cubic and Orthorhombic Cesium Lead Iodide (CsPbI3) Polymorphs. Journal of the American Chemical Society 2019, 141 (37), 14501–14504. [CrossRef]
- Boldyreva, A. G.; Frolova, L. A.; Zhidkov, I. S.; Gutsev, L. G.; Kurmaev, E. Z.; Ramachandran, B. R.; Petrov, V. G.; Stevenson, K. J.; Aldoshin, S. M.; Troshin, P. A. Unravelling the Material Composition Effects on the Gamma Ray Stability of Lead Halide Perovskite Solar Cells: MAPbI3 Breaks the Records. Journal of Physical Chemistry Letters 2020, 11 (7), 2630–2636. [CrossRef]
- Wang, Q.; Zheng, X.; Deng, Y.; Zhao, J.; Chen, Z.; Huang, J. Stabilizing the α-Phase of CsPbI3 Perovskite by Sulfobetaine Zwitterions in One-Step Spin-Coating Films. Joule 2017, 1 (2), 371–382. [CrossRef]
- Masi, S.; Gualdrón-Reyes, A. F.; Mora-Seró, I. Stabilization of Black Perovskite Phase in FAPbI3and CsPbI3. ACS Energy Letters 2020, 5 (6), 1974–1985. [CrossRef]
- Jena, A. K.; Kulkarni, A.; Sanehira, Y.; Ikegami, M.; Miyasaka, T. Stabilization of α-CsPbI3 in Ambient Room Temperature Conditions by Incorporating Eu into CsPbI3. Chemistry of Materials 2018, 30 (19), 6668–6674. [CrossRef]
- Dastidar, S.; Egger, D. A.; Tan, L. Z.; Cromer, S. B.; Dillon, A. D.; Liu, S.; Kronik, L.; Rappe, A. M.; Fafarman, A. T. High Chloride Doping Levels Stabilize the Perovskite Phase of Cesium Lead Iodide. Nano Lett. 2016, 16 (6), 3563–3570. [CrossRef]
- Sutton, R. J.; Eperon, G. E.; Miranda, L.; Parrott, E. S.; Kamino, B. A.; Patel, J. B.; Hörantner, M. T.; Johnston, M. B.; Haghighirad, A. A.; Moore, D. T.; Snaith, H. J. Bandgap-Tunable Cesium Lead Halide Perovskites with High Thermal Stability for Efficient Solar Cells. Advanced Energy Materials 2016, 6 (8), 1502458. [CrossRef]
- Liu, L.; Lu, J.; Wang, H.; Cui, Z.; Giorgi, G.; Bai, Y.; Chen, Q. A-Site Phase Segregation in Mixed Cation Perovskite. Materials Reports: Energy 2021, 1 (4), 100064. [CrossRef]
- DuBose, J. T.; Kamat, P. V. Hole Trapping in Halide Perovskites Induces Phase Segregation. Acc. Mater. Res. 2022, 3 (7), 761–771. [CrossRef]
- Motti, S. G.; Patel, J. B.; Oliver, R. D. J.; Snaith, H. J.; Johnston, M. B.; Herz, L. M. Phase Segregation in Mixed-Halide Perovskites Affects Charge-Carrier Dynamics While Preserving Mobility. Nat Commun 2021, 12 (1), 6955. [CrossRef]
- Kröger, F. A.; Vink, H. J. Relations between the Concentrations of Imperfections in Crystalline Solids. Solid State Physics - Advances in Research and Applications 1956, 3 (C), 307–435. [CrossRef]
- Chen, B.; Rudd, P. N.; Yang, S.; Yuan, Y.; Huang, J. Imperfections and Their Passivation in Halide Perovskite Solar Cells. Chem. Soc. Rev. 2019, 48 (14), 3842–3867. [CrossRef]
- Wang, R.; Xue, J.; Wang, K.-L.; Wang, Z.-K.; Luo, Y.; Fenning, D.; Xu, G.; Nuryyeva, S.; Huang, T.; Zhao, Y.; Yang, J. L.; Zhu, J.; Wang, M.; Tan, S.; Yavuz, I.; Houk, K. N.; Yang, Y. Constructive Molecular Configurations for Surface-Defect Passivation of Perovskite Photovoltaics. Science 2019, 366 (6472), 1509–1513. [CrossRef]
- Frolova, L. A.; Luchkin, S. Y.; Lekina, Y.; Gutsev, L. G.; Tsarev, S. A.; Zhidkov, I. S.; Kurmaev, E. Z.; Shen, Z. X.; Stevenson, K. J.; Aldoshin, S. M.; Troshin, P. A. Reversible Pb2+/Pb0 and I−/I3− Redox Chemistry Drives the Light-Induced Phase Segregation in All-Inorganic Mixed Halide Perovskites. Advanced Energy Materials 2021, 11 (12), 2002934.
- Xue, H.; Vicent-Luna, J. M.; Tao, S.; Brocks, G. Compound Defects in Halide Perovskites: A First-Principles Study of CsPbI3. J. Phys. Chem. C 2023, 127 (2), 1189–1197. [CrossRef]
- Yang, Z.-L.; Zhang, Z.-Y.; Fan, W.-L.; Hu, C.; Zhang, L.; Qi, J.-J. High-Performance g-C3N4 Added Carbon-Based Perovskite Solar Cells Insulated by Al2O3 Layer. Solar Energy 2019, 193, 859–865. [CrossRef]
- Freysoldt, C.; Grabowski, B.; Hickel, T.; Neugebauer, J.; Kresse, G.; Janotti, A.; Van De Walle, C. G. First-Principles Calculations for Point Defects in Solids. Reviews of Modern Physics 2014, 86 (1), 253–305. [CrossRef]
- Perdew, J. P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Physical Review Letters 1996, 77 (18), 3865–3868. [CrossRef]
- Joubert, D.; Kresse, G. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Physical Review B - Condensed Matter and Materials Physics 1999, 59 (3), 1758–1775. [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. Journal of Chemical Physics 2010, 132 (15), 24103. [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Physical Review Letters 2015, 115 (3), 036402. [CrossRef]
- Sun, J.; Remsing, R. C.; Zhang, Y.; Sun, Z.; Ruzsinszky, A.; Peng, H.; Yang, Z.; Paul, A.; Waghmare, U.; Wu, X.; Klein, M. L.; Perdew, J. P. Accurate First-Principles Structures and Energies of Diversely Bonded Systems from an Efficient Density Functional. Nature Chemistry 2016, 8 (9), 831–836. [CrossRef]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code. Computer Physics Communications 2021, 267, 108033. [CrossRef]
- Ku, W.; Berlijn, T.; Lee, C. C. Unfolding First-Principles Band Structures. Physical Review Letters 2010, 104 (21), 216401. [CrossRef]
- Makov, G.; Payne, M. C. Periodic Boundary Conditions in Ab Initio Calculations. Phys. Rev. B 1995, 51 (7), 4014–4022. [CrossRef]
- Alkauskas, A.; Yan, Q.; Van De Walle, C. G. First-Principles Theory of Nonradiative Carrier Capture via Multiphonon Emission. Physical Review B 2014, 90 (7), 075202. [CrossRef]
- Turiansky, M. E.; Alkauskas, A.; Engel, M.; Kresse, G.; Wickramaratne, D.; Shen, J.-X.; Dreyer, C. E.; Van de Walle, C. G. Nonrad: Computing Nonradiative Capture Coefficients from First Principles. Computer Physics Communications 2021, 267, 108056. [CrossRef]
- Alkauskas, A.; Yan, Q.; Van De Walle, C. G. First-Principles Theory of Nonradiative Carrier Capture via Multiphonon Emission. Physical Review B - Condensed Matter and Materials Physics 2014, 90 (7). [CrossRef]
- Wang, H.; Li, B.; Liu, F.; Zhan, W.; Feng, M.; Guo, J.; Wang, S.; Liang, Y.; Fan, Y.; Chen, Y.; Miao, Y.; Zhao, Y. 2D Capping Layer Passivation toward Inorganic CsPbI3 Perovskite Minimodule. Advanced Functional Materials 2025, 35 (35), 2423397. [CrossRef]
- Chu, W.; Prezhdo, O. V. Concentric Approximation for Fast and Accurate Numerical Evaluation of Nonadiabatic Coupling with Projector Augmented-Wave Pseudopotentials. J. Phys. Chem. Lett. 2021, 12 (12), 3082–3089. [CrossRef]
- Jaeger, H. M.; Fischer, S.; Prezhdo, O. V. Decoherence-Induced Surface Hopping. The Journal of Chemical Physics 2012, 137 (22), 22A545. [CrossRef]
- Liu, D.; Wang, B.; Vasenko, A. S.; Prezhdo, O. V. Decoherence Ensures Convergence of Non-Adiabatic Molecular Dynamics with Number of States. The Journal of Chemical Physics 2024, 161 (6), 064104. [CrossRef]
- Jaeger, H. M.; Fischer, S.; Prezhdo, O. V. Decoherence-Induced Surface Hopping. The Journal of Chemical Physics 2012, 137 (22), 22A545. [CrossRef]
- Zheng, Q.; Chu, W.; Zhao, C.; Zhang, L.; Guo, H.; Wang, Y.; Jiang, X.; Zhao, J. Ab Initio Nonadiabatic Molecular Dynamics Investigations on the Excited Carriers in Condensed Matter Systems. WIREs Computational Molecular Science 2019, 9 (6), e1411. [CrossRef]
- Gajdoš, M.; Hummer, K.; Kresse, G.; Furthmüller, J.; Bechstedt, F. Linear Optical Properties in the Projector-Augmented Wave Methodology. Physical Review B - Condensed Matter and Materials Physics 2006, 73 (4), 045112. [CrossRef]
- Nations, S.; Jia, T.; Wang, S.; Duan, Y. Electronic and Optical Properties of Orthorhombic (CH3NH3)BX3(B = Sn, Pb; X = F, Cl, Br, I) Perovskites: A First-Principles Investigation. RSC Advances 2021, 11 (36), 22264–22272. [CrossRef]
- Svensson, P. H.; Kloo, L. Synthesis, Structure, and Bonding in Polyiodide and Metal Iodide−Iodine Systems. Chem. Rev. 2003, 103 (5), 1649–1684. [CrossRef]
- Liu, Z.; Liu, F.; Wu, Y.-S. Exotic Electronic States in the World of Flat Bands: From Theory to Material. Chinese Phys. B 2014, 23 (7), 077308. [CrossRef]
- Pokryshkin, N. S.; Mantsevich, V. N.; Timoshenko, V. Y. Anti-Stokes Photoluminescence in Halide Perovskite Nanocrystals: From Understanding the Mechanism towards Application in Fully Solid-State Optical Cooling. Nanomaterials 2023, 13 (12), 1833. [CrossRef]
- Zhang, X.; Turiansky, M. E.; Van de Walle, C. G. Correctly Assessing Defect Tolerance in Halide Perovskites. The Journal of Physical Chemistry C 2020, 124 (11), 6022–6027. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





