Quantization of the Cosmic Critical Density

1. Introduction

The cosmic critical density is a key parameter determining the geometric curvature of the universe. The primary motivation for its quantization study stems from two major conflicts: the vacuum energy catastrophe and the coincidence problem [3,4,5,6,7,8,9]. Vacuum energy contributions from quantum fluctuations require renormalization, yet face fundamental contradictions [10,11]. Within the framework of loop quantum cosmology, the critical density becomes intricately linked to the discrete structure of spacetime [12]. The string landscape hypothesis leads to a random distribution of cosmic critical density among ${10}^{500}$ vacuum solutions, with the anthropic principle selecting habitable values, albeit lacking a dynamical mechanism [13]. Shen. J proposed a spin connection gauge theory where the local Lorentz group acts as the gauge group, preventing vacuum energy from contributing to the field equations and thus avoiding the fine-tuning problem of cosmic critical density, though resulting in third-order differential gravitational field equations [14]. The holographic principle also offers an explanatory path via the multiverse; meanwhile, dynamical field models and precision experiments (e.g., cold atoms, cosmological observations) [17,18] are gradually building bridges for empirical verification.

The structure of this paper is as follows. In Sec. 2, we derive the quantized formula for the cosmic critical density. In Sec. 3, we prove the second and third parts of this formula. In Sec. 4, we compare the three components of the formula through function graphs. We conclude in Sec. 5.

2. Quantization of Cosmic Critical Density

This section applies a generalized relational expression to derive the quantized formula for the cosmic critical density.

Let’s review a generalized relational expression. The basic relationship is

$${\mathrm{A}~\mathrm{A}}_{\mathrm{P}}={\left[{\mathrm{ħ}}^{\left(\delta +\epsilon +\zeta +\eta \right)}{\mathrm{G}}^{\left(\delta -\epsilon +\zeta -\eta \right)}{\mathrm{c}}^{-\left(3\delta -\epsilon +5\zeta -5\eta \right)}{\mathsf{\kappa }}^{-2\eta }{\mathrm{e}}^{2\lambda }\right]}^{1/2}$$

(1)

Where A is any physical quantity, [A] = ${\left[\mathrm{L}\right]}^{\delta }{\left[\mathrm{M}\right]}^{\epsilon }{\left[\mathrm{T}\right]}^{\zeta }{\left[\mathsf{\Theta }\right]}^{\eta }{\left[\mathrm{Q}\right]}^{\lambda }$ its dimensions, L, M, T, Θ and Q are the dimensions of length, mass, time, temperature and electric charge separately (here we use the LMTΘQ units), ${\mathrm{A}}_{\mathrm{P}}$ the corresponding Planck scale of A, $\delta$, $\epsilon$, $\zeta$, $\eta$ and $\lambda$ the real number, ħ, G, c, κ and e the reduced Planck constant, gravitational constant, speed of light in vacuum, Boltzmann constant and elementary charge separately.

The Generalized Relational Expression is

$${\prod }_{\mathrm{i}=1}^{\mathrm{n}}{A}_{\mathrm{i}}^{a_{\mathrm{i}}}\text{～}{\prod }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{A}}_{\mathrm{i}\mathrm{P}}^{a_{\mathrm{i}}};i=1,2,3\dots n$$

(2)

where $A_{\mathrm{i}}$ is the physical quantity, ${\alpha }_{\mathrm{i}}$ the real number, and $A_{\mathrm{i}\mathrm{P}}$ the corresponding Planck scale.

So assuming the cosmic critical density $\rho$ depends solely on the Hubble constant H, we obtain

$$\rho H^{\alpha }{~\mathsf{\rho }}_P{\mathrm{H}}_P^{\alpha }={\mathrm{ħ}}^{-(2+\alpha )/2}{\mathrm{G}}^{-(4+\alpha )/2}{\mathrm{c}}^{5(2+\alpha )/2}$$

(3)

where ${\mathsf{\rho }}_P$=$c^5/\mathrm{ħ}{\mathrm{G}}^2$ is the Planck mass density, ${\mathrm{H}}_P$=$\sqrt{c^5/\mathrm{ħ}\mathrm{G}}$ the Planck Hubble constant.

Setting 2+$\alpha$=0, → $\alpha$= ─ 2，we give

$$\rho ~H^2/\mathrm{G}$$

which is ${\rho }_c$=$3H_0^2/8\mathsf{\pi }\mathrm{G}$ [1], where $H_0$ is today Hubble constant.

Ordering 4+$\alpha$=0, → $\alpha$= ─ 4，obtain

$$\rho ~{\mathrm{ħ}H}^4/c^5$$

(4)

it represents the quantization of the cosmic critical density.

Taking $\alpha$= ─ 6，find

$$\rho {{~\mathrm{ħ}}^2\mathrm{G}H}^6/c^{10}$$

(5)

which represents the gravitational quantization of the cosmic critical density. Thus

$$\rho {~H}^2/\mathrm{G}{+\mathrm{ħ}H}^4/c^5{{+\mathrm{ħ}}^2\mathrm{G}H}^6/c^{10}{~\rho }_{\mathrm{I}}{+\rho }_{\mathrm{I}\mathrm{I}}{+\rho }_{\mathrm{I}\mathrm{I}\mathrm{I}}$$

(6)

This is the quantized formula for the cosmic critical density. As ħ → 0, $\rho$～$H^2/\mathrm{G}$, consistent with the result from general relativity.

3. Proof of ${\mathit{\rho }}_{\mathbf{I}\mathbf{I}}$ and ${\mathit{\rho }}_{\mathbf{I}\mathbf{I}\mathbf{I}}$

This section proves the quantized formula (6) for the cosmic critical density.

3.1. Proof of ${\mathit{\rho }}_{\mathbf{I}\mathbf{I}}$

In quantum field theory, the vacuum energy density for a free scalar field is

$$\rho =0.5{\int }_0^{k_{max}}{\displaystyle \frac{d^{3}k}{{\left(2\pi \right)}^3}}\mathrm{ħ}{\mathsf{\omega }}_k$$

where $E=\mathrm{ħ}{\mathsf{\omega }}_k/2$ is the zero-point energy [20], ${\mathsf{\omega }}_k$ the frequency, and $k$ the wavenumber. For a massless scalar field, ${\mathsf{\omega }}_k$=$\mathrm{c}k$. In three-dimensional momentum space, $d^{3}k$=4$\pi k^{2}dk$, substituting them into the above equation, we obtain

$$\rho =\mathrm{ħ}\mathrm{c}{k}_{max}^4/16{\pi }^2$$

If the cutoff wavenumber $k_{max}$ is chosen as the Hubble radius $R_H$=$\mathrm{c}/H$, then the minimum wavelength ${\lambda }_{min}$=$R_H$=$\mathrm{c}/H$, and the maximum wavenumber is $k_{max}$=2π${/\lambda }_{min}$=2π$H/\mathrm{c}$. Substituting into the above formula, we get

$${\rho }_{\mathrm{I}\mathrm{I}}={{\pi }^2\mathrm{ħ}H}^4/c^5$$

(7)

Proof completes.

3.2. Proof of ${\mathit{\rho }}_{\mathbf{I}\mathbf{I}\mathbf{I}}$

Similarly, assuming

$\rho$=2$\pi {\int }_0^{k_{max}}{\displaystyle \frac{d^{3}k}{{\left(2\pi \right)}^3}}{\displaystyle \frac{{\mathrm{ħ}}^2\mathrm{G}{\omega }_k^3}{c^5}}$

where $E=2\pi {\mathrm{ħ}}^2\mathrm{G}{\omega }_k^3/c^5$ [21]. Substituting ${\mathsf{\omega }}_k$=$\mathrm{c}k$,$d^{3}k$=4$\pi k^{2}dk$，and $k_{max}$=2π${/\lambda }_{min}$=2πH/c into above equation, we find

$${\rho }_{\mathrm{I}\mathrm{I}\mathrm{I}}=8{\pi }^5{\mathrm{ħ}}^2{\mathrm{G}H}^6/3c^{10}$$

(8)

Thus, we obtain

$$\rho {=3H}^2/8\mathsf{\pi }\mathrm{G}+{{\pi }^2\mathrm{ħ}H}^4/c^5+8{\pi }^5{\mathrm{ħ}}^2{\mathrm{G}H}^6/3c^{10}$$

(9)

As ħ → 0, $\rho$=${3H}^2/8\mathsf{\pi }\mathrm{G}$.

4. Comparison of ${\mathit{\rho }}_{\mathbf{I}}$, ${\mathit{\rho }}_{\mathbf{I}\mathbf{I}}$ and ${\mathit{\rho }}_{\mathbf{I}\mathbf{I}\mathbf{I}}$

This section compares the three terms in Eq. (9) via $\mathrm{l}\mathrm{g}\rho -\mathrm{l}\mathrm{g}t$ function graphs.

As the universe expands, H gradually decreases. However, since Eq. (9) involves powers 2, 4, and 6 of H, a direct comparison is inconvenient. Therefore, we substitute $H=1/t$, where $t$ is the age of the universe, yielding

$$\mathrm{l}\mathrm{g}\rho =\mathrm{l}\mathrm{g}(3/8\mathsf{\pi }\mathrm{G}{t}^2{+{\pi }^2\mathrm{ħ}/c^{5}t}^4+8{\pi }^5{\mathrm{ħ}}^2{\mathrm{G}/3c^{10}t}^6)=\mathrm{l}\mathrm{g}({\rho }_{\mathrm{I}}+{\rho }_{\mathrm{I}\mathrm{I}}+{\rho }_{\mathrm{I}\mathrm{I}\mathrm{I}})$$

(10)

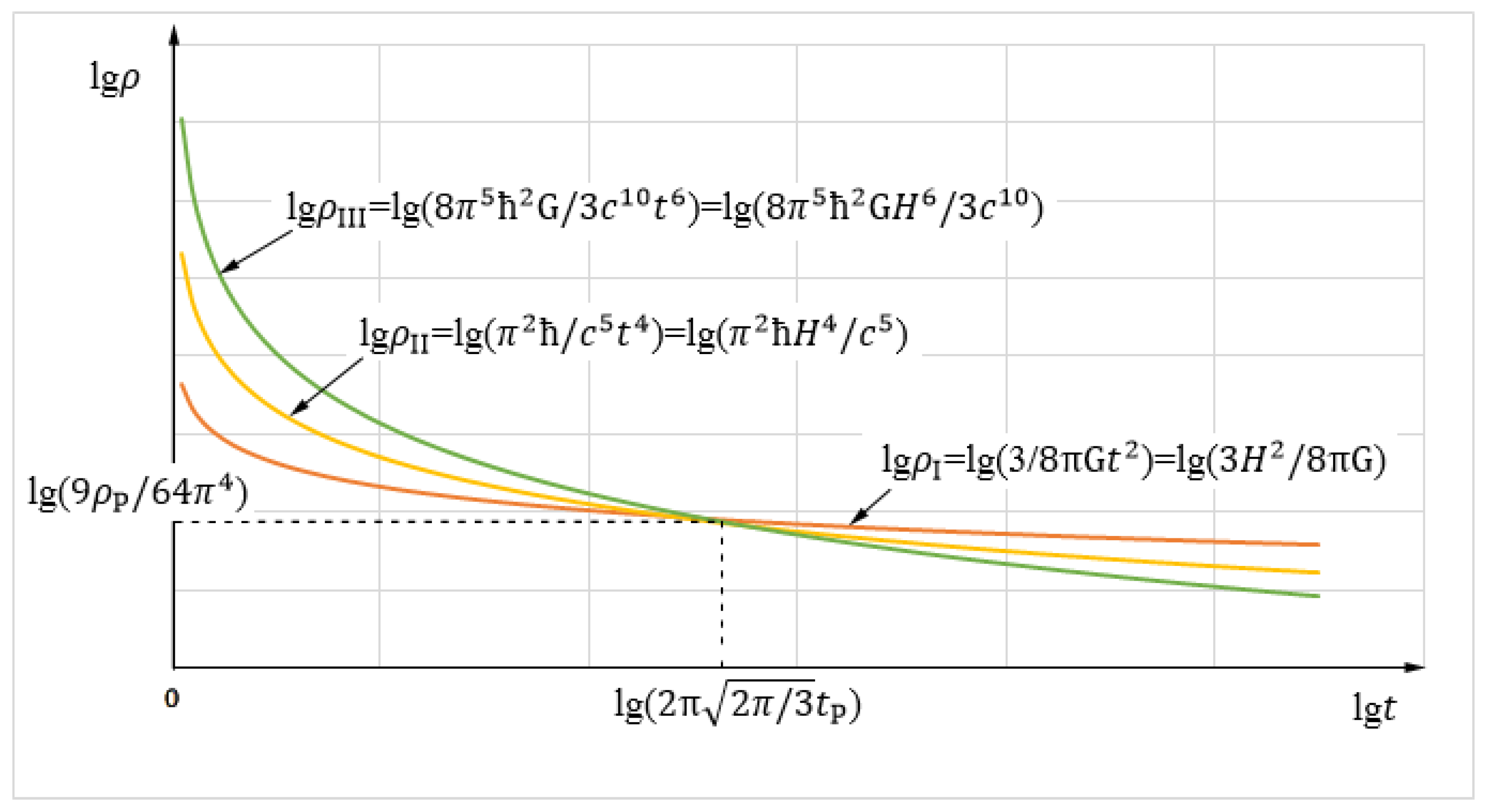
Plotting the $\mathrm{l}\mathrm{g}\rho -\mathrm{l}\mathrm{g}t$ function graph gives

Figure 1. Schematic diagram showing the evolution of ${\rho }_{\mathrm{I}},{\rho }_{\mathrm{I}\mathrm{I}},\mathrm{and}{\rho }_{\mathrm{I}\mathrm{I}\mathrm{I}}$ with cosmic time $t$. ${\rho }_{\mathrm{I}}$ (~1/$t^2$) dominates at late times, ${\rho }_{\mathrm{I}\mathrm{I}}$ (~1/$t^4$) is significant at intermediate times, and ${\rho }_{\mathrm{I}\mathrm{I}\mathrm{I}}$ (~1/$t^6$) dominates at very early times near $t_{\mathrm{P}}$.

Figure 1. Schematic diagram showing the evolution of ${\rho }_{\mathrm{I}},{\rho }_{\mathrm{I}\mathrm{I}},\mathrm{and}{\rho }_{\mathrm{I}\mathrm{I}\mathrm{I}}$ with cosmic time $t$. ${\rho }_{\mathrm{I}}$ (~1/$t^2$) dominates at late times, ${\rho }_{\mathrm{I}\mathrm{I}}$ (~1/$t^4$) is significant at intermediate times, and ${\rho }_{\mathrm{I}\mathrm{I}\mathrm{I}}$ (~1/$t^6$) dominates at very early times near $t_{\mathrm{P}}$.

Clearly, when $t$=${2\mathsf{\pi }\sqrt{2\pi /3}t}_{\mathrm{P}}$ (i.e., $H=H_{\mathrm{P}}\sqrt{3/2\pi }/2\mathsf{\pi }$), ${\rho }_{\mathrm{I}}$=${\rho }_{\mathrm{I}\mathrm{I}}$=${\rho }_{\mathrm{I}\mathrm{I}\mathrm{I}}$=$9{\rho }_{\mathrm{P}}/64{\pi }^4$, where $H_{\mathrm{P}}$=$1/t_{\mathrm{P}}$ and $t_{\mathrm{P}}$=$\sqrt{\mathrm{ħ}\mathrm{G}/c^5}$ is the Planck time.

When $t>{20\mathsf{\pi }\sqrt{2\pi /3}t}_{\mathrm{P}}$, ${\rho }_{\mathrm{I}\mathrm{I}}/{\rho }_{\mathrm{I}}<$0.01，${\rho }_{\mathrm{I}\mathrm{I}\mathrm{I}}/{\rho }_{\mathrm{I}\mathrm{I}}<$0.01, allowing ${\rho }_{\mathrm{I}\mathrm{I}}$ and ${\rho }_{\mathrm{I}\mathrm{I}\mathrm{I}}$ to be neglected, we obtain $\rho$=${3H}^2/8\mathsf{\pi }\mathrm{G}$.

When $0<t<{0.2\mathsf{\pi }\sqrt{2\pi /3}t}_{\mathrm{P}}$, ${\rho }_{\mathrm{I}}/{\rho }_{\mathrm{I}\mathrm{I}}<$0.01，${\rho }_{\mathrm{I}\mathrm{I}}/{\rho }_{\mathrm{I}\mathrm{I}\mathrm{I}}<$0.01, allowing ${\rho }_{\mathrm{I}}$ and ${\rho }_{\mathrm{I}\mathrm{I}}$ to be neglected, give $\rho$=$8{\pi }^5{\mathrm{ħ}}^2{\mathrm{G}H}^6/3c^{10}$.

This indicates that the gravitational quantization term dominates from the very beginning of the universe until approximately 0.91 times the Planck time, suggesting that this may be a result of a complete theory of quantum gravity. Therefore, the cosmic critical density today differs from that during the very early universe and near the Planck time.

5. Conclusion

In this paper we have studied the quantization of the cosmic critical density. Applying a generalized relational expression [1], we derived a quantized formula. This formula includes the result from general relativity, a quantization term, and a gravitational quantization term. It reduces to the general relativity result when quantum effects are neglected. Then we prove the latter two terms. We compared the three components via $\mathrm{l}\mathrm{g}\rho -\mathrm{l}\mathrm{g}t$ graphs, it showed that the gravitational quantization term dominates during the very early universe until approximately 0.91times the Planck time, suggesting it is a consequence of a complete theory of quantum gravity. Our discussion is intriguing and provides heuristic inspiration for developing a complete theory of quantum gravity.