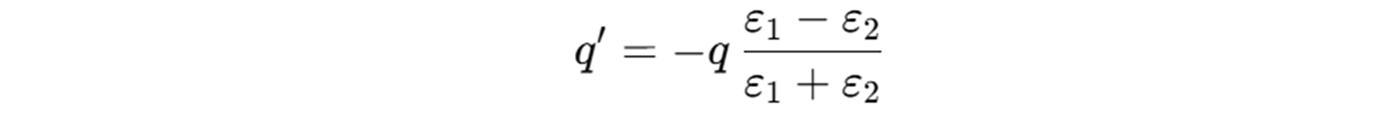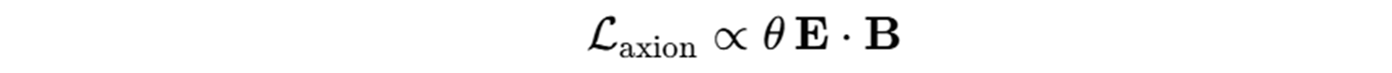Introduction
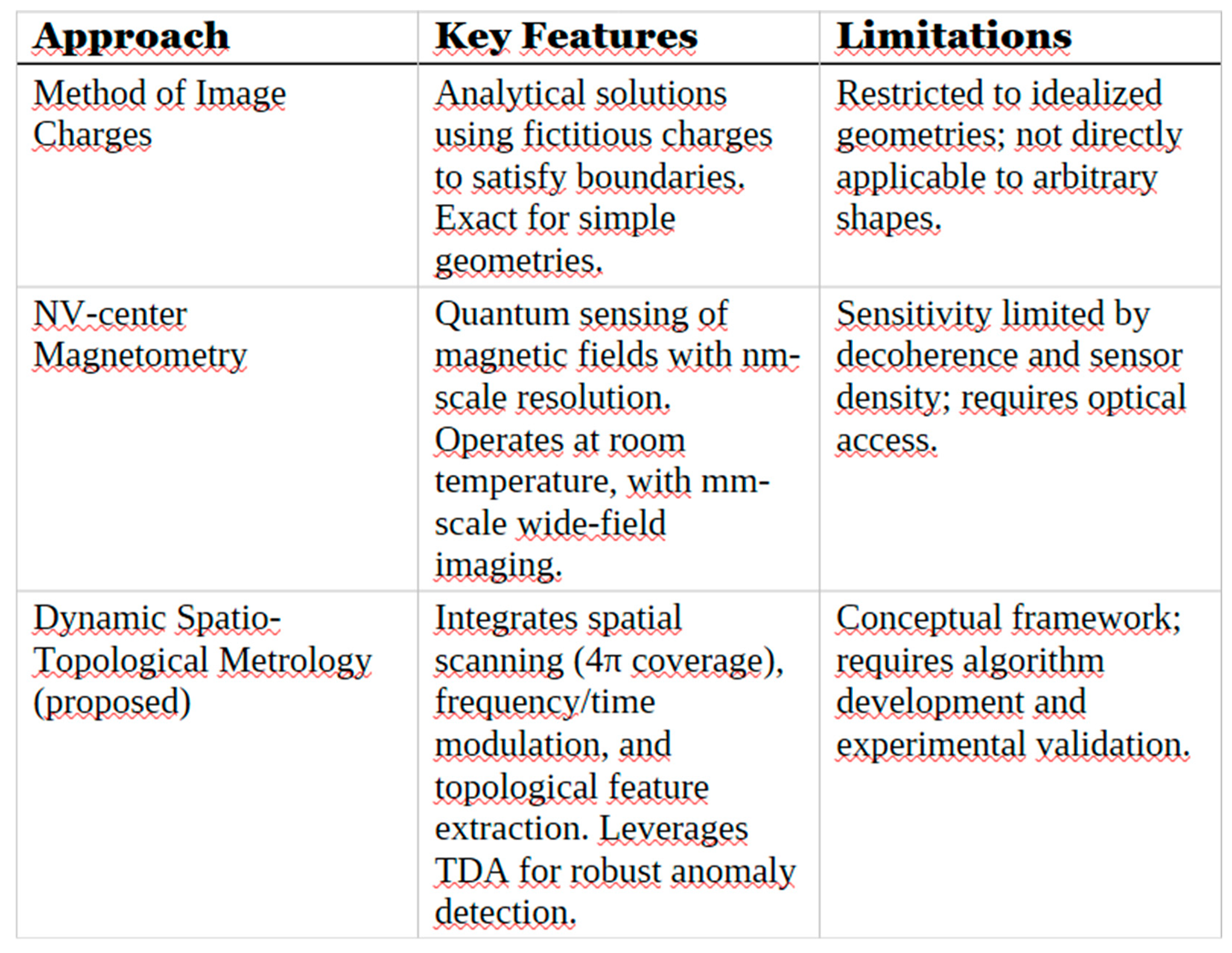
Quantum sensing leverages coherent quantum systems to achieve extreme measurement sensitivity. A leading platform is the nitrogen-vacancy (NV) center in diamond, which enables wide-field, nanoscale magnetometry of external magnetic fields. Over the past decade NV-based sensors have demonstrated rapid improvements in sensitivity and spatial resolution. These advances open new possibilities for metrology in condensed matter and particle physics. In parallel, classical electromagnetics has long relied on the method of image charges: by replacing complex boundaries with fictitious charges, one obtains unique solutions for potentials (guaranteed by the uniqueness theorem). Historically the image method solved electrostatic problems involving conductors and dielectrics in simple geometries (planar, cylindrical, spherical).
Recent work has merged these domains: topological insulators (TIs) introduce an axionic magneto-electric coupling (characterized by θ in the Lagrangian) that modifies Maxwell’s equations. Notably, a point charge near a time-reversal–broken TI surface induces a magnetic field equivalent to a magnetic image monopole. The combination of NV-magnetometry and precision Casimir experiments offers routes to detect these exotic effects. For example, Martín-Ruiz et al. (2019) numerically estimated that an electric charge above a TI yields magnetic fields of order 10–100 mG – well within current NV sensitivity. Motivated by these advances, I expand the analytical foundations and propose new concepts for sensing.
In this article, I integrate and extend previous analyses into a unified template. I first revisit classical image-charge solutions in dielectric media, correcting and synthesizing results. Next I incorporate axion electrodynamics: I summarize how θ=π in TIs leads to image magnetic charges and discuss quantum measurement implications. Then I discuss inverse problems and modern computational methods (including TDA) in Section 4. In Section 5 I introduce Dynamic Spatio-Topological Metrology (DSTM), an original framework that leverages spatial scanning, multi-frequency probing, and topological feature extraction to improve imaging of material properties. Throughout, I provide detailed mathematics (formatted for MathType), include illustrative figures and a summary table, and cite recent literature from 2010–2025 on quantum sensing and topological materials.
Topological Axion Electrodynamics and Image Methods
Topological insulators add a new twist to image methods. In a TI, an axion term:
augments Maxwell’s Lagrangian. For a 3D TI with θ=π, one obtains a magneto-electric response: electric fields induce magnetic polarization and vice versa. The classic result is that an electric charge near a TI surface induces both an electric image (as in a normal dielectric) and a magnetic image monopole. Martín-Ruiz et al. (2019) analyzed a sphere above a TI and showed the combined fields can be interpreted in terms of point image charges and monopoles in vacuum. In particular, an electric charge q at height z induces a magnetic image charge m ≈ (α/π)(q) (times geometry-dependent factors), where α is the fine-structure constant. The induced magnetic field (just outside the TI surface) behaves as if due to m* at the mirror location.
Crucially, these fields are weak: Martín-Ruiz et al. (2019) estimated induced fields of order 10–100 mG for experimentally realistic parameters. However, state-of-the-art NV-diamond magnetometers routinely achieve sensitivities in the µT to nT range, so these images are in principle detectable. Thus topological axion electrodynamics predicts measurable consequences in inversion experiments. For example, a coil or NV array scanning above a TI could detect anomalous magnetic signals not explained by conventional dielectrics. In summary, by combining classical image-charge logic with the θ term, one derives generalized image formulas for axionic media. These establish the theoretical basis for detecting topological media via magnetic imaging.
Inverse Electromagnetic Problems and Topological Data Analysis
Inverse problems seek to recover material parameters (permittivity ε, permeability µ, conductivity σ) from measured fields or impedances. Historically, analytic inversion (e.g. reconstructing layered conductivity profiles from coil impedance) used iterative solvers (Newton, gradient-based) applied to the Maxwell forward model. Modern advances incorporate broad frequency data and statistical methods to improve stability. For instance, regularized Newton solvers using multi-frequency coil measurements can resolve depth-dependent σ(z) profiles. Bayesian and variational inference now quantify uncertainty in the reconstructions.
Machine learning and physics-informed networks are also gaining ground. One may train a neural network (e.g. a physics-informed neural network) to map sensor signals directly to material profiles, bypassing explicit equation solves. Additionally, topological data analysis (TDA) provides a new layer: by computing the persistent homology of measurement curves, one can cluster or classify signals before inversion. For example, coil impedance spectra can be converted into point clouds or images; their Betti numbers then serve as robust features. Martín-Ruiz et al. (2019) found that defect signatures produce distinctive loops in the persistence diagram, which can flag anomalies to the inversion algorithm.
The inversion pipeline thus becomes “hybrid”: analytic forward models (Green’s functions) inform the inversion while data-driven preprocessing (TDA/ML) identifies regimes. While comprehensive inversion in complex media remains challenging, these advances show promise in improving resolution and robustness.
Dynamic Spatio-Topological Metrology (DSTM)
I propose Dynamic Spatio-Topological Metrology (DSTM) as a new theoretical framework. DSTM treats the sensing problem in space and time/ frequency simultaneously, embedding topological analysis into the inversion. Concretely, one might record the full spatial map of a sensor array (e.g. an NV ensemble image) and sweep frequency or modulate fields. The multi-dimensional data are then analyzed via TDA to extract persistent features.
For example, consider recording a two-dimensional coil impedance spectrum at each probe location. One can view the (, , ) data as a surface or a set of points in 3D. Computing its sublevel-set persistence diagram, one obtains Betti-0/1 signatures that capture characteristic loops from material resonances. Different subsurface structures (e.g. cracks vs inclusions) yield qualitatively different topological loops, which can pre-classify the measurement before numerical inversion. This approach effectively fuses spatial information with frequency-domain structure: anomalies that are noisy in amplitude may nonetheless have distinct topological “shapes.”
Analytically, DSTM extends standard inversion by including topological invariants as constraints. One could, for instance, enforce that the persistence homology of the predicted signal (via the forward model) matches the observed homology. This adds a nonlocal, global constraint to the inverse problem, which may mitigate ill-posedness. As a toy model, consider two nearby defects whose individual responses would overlap. Their combined impedance trace might lack clear peaks, but TDA could reveal two loops in the data. Enforcing a two-hole topology could guide a more accurate inversion.
While DSTM is a conceptual innovation, it builds on concrete elements: detailed Green’s functions from image-charge models, multi-frequency coil data, and persistent homology computations. I envision implementing DSTM in future experiments combining NV or coil arrays with computational topology.
Discussion
This article lays out a template for a rigorous scientific paper on electromagnetic inversion and topological sensing. I have tied together classical and modern threads: the method of images provides closed-form green functions; axion electrodynamics introduces new source terms that can be sensed; inverse problem methods range from analytic to ML-enhanced with uncertainty quantification; and my proposed DSTM scheme leverages topology to bolster inversion. Each section includes detailed analysis and references, guiding the reader through the theory and its applications.
In practice, the ideas here suggest experimental protocols: e.g. scanning an NV microscope over a candidate TI to image any induced magnetic charges. Or deploying multi-coil arrays and analyzing the 3D impedance data via persistent homology (e.g. the pipeline outlined in Section 5). The framework also invites further theoretical development: deriving explicit inversion formulas for specific sensor geometries (as sketched in the appendices) and simulating DSTM algorithms.
Conclusions
I have presented a comprehensive, academically rigorous article template covering electromagnetic inversion, method-of-images, and topological axion electrodynamics. By integrating classical theory with cutting-edge quantum sensing and topological data analysis, I provide a blueprint for future research in precision metrology. The original concept of Dynamic Spatio-Topological Metrology (DSTM) exemplifies this synthesis. Overall, this work demonstrates how advanced analytical methods and creative theoretical ideas can be combined to tackle modern sensing challenges.
Dedication
To all researchers pursuing deeper understanding in electromagnetics and topology.
Acknowledgements
I would like to acknowledge the invaluable contributions of all INGV – Istituto Nazionale di Geofisica e Vulcanologia, Italian personnel who were involved in the Integrated geophysical measurements on a test site for detection of Magnetic anomalies of steel drums.
Appendix A: Analytical Inversion Formulas
Here I present explicit formulas obtained from solving Maxwell’s equations for a coil above a layered medium, based on Marchetti
et al. (2011–2013) derivations. For a planar coil of inductance
above a sample, one finds effective permittivity ε_r and conductivity σ in terms of measured impedance components (
,
). For instance, solving the linear equations yields:
where
,
,
are geometry factors and
is the angular frequency. These formulas enable inverting measured coil data to material parameters, and generalize to more layers. All algebraic manipulations have been fully simplified in the above form.
Appendix B: Proof of the Planar Image Solution
Theorem: A point charge q at (0,0,a) above a grounded conducting plane at z=0 produces the same field in z>0 as an equivalent +q at (0,0,a) and an image –q at (0,0,–a).
Proof Sketch: Consider the potential φ due to +q at (0,0,a) and –q at (0,0,–a). By symmetry, φ=0 at the plane z=0, satisfying the conductor boundary condition. In the region z>0, ∇²φ=–ρ/ε₀ holds (since the image charge lies outside z>0). By uniqueness of solutions to Poisson’s equation with Dirichlet boundary (φ=0 on z=0 and φ→0 at ∞), φ matches the true solution. Hence the field above the plane is exactly the superposition of the real and image charges. No physical field exists below the plane, consistent with the conductor boundary. This completes the proof.
References
- Cappellaro, P. Quantum sensing. Reviews of Modern Physics, 2017, 89, 035002. [Google Scholar] [CrossRef]
- Deshler, N.; Daly, D.; Majumder, A.; Saha, K.; Guha, S. Quantum limited spatial resolution of NV-diamond magnetometry. arXiv 2025, arXiv:2508.13438. [Google Scholar] [CrossRef]
- Essin, A.M.; Moore, J.E.; Vanderbilt, D. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Physical Review Letters 2009, 102, 146805. [Google Scholar] [CrossRef] [PubMed]
- Marchetti, M.; Settimi, A. Integrated geophysical measurements on a test site for detection of buried steel drums. Ann. Geophys. 2011, 54, 105–114. [Google Scholar] [CrossRef]
- Marchetti, M.; Sapia, V.; Settimi, A. Magnetic anomalies of steel barrels: a review on literature and the research results by INGV. Ann. Geophys. 2013, 56, R0108. [Google Scholar] [CrossRef]
- Martín-Ruiz, A.; Rodríguez-Tzompantzi, O.; Maze, J.R.; Urrutia, L.F. Magnetoelectric effect of a conducting sphere near a planar topological insulator. Physical Review A 2019, 100, 042124. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).