The Ultimate Black Hole as a Fractal Cosmological Model: A Proof of Concept with Supernova Data

1. Introduction

Table 1. Principal quantities and parameters used in the UBH cosmological model.

Symbol	Meaning
$H\left(z\right)$	Hubble function at redshift z
$H_0$	Present Hubble constant
${\Omega }_m$	Matter density parameter
${\Omega }_r$	Radiation density parameter
${\Omega }_{k,\mathrm{eff}}\left(a\right)$	Effective curvature contribution (“curvature window”)
${\Omega }_{\mathrm{FEE}}\left(a\right)$	Fractal Early Energy (entropy-driven early component)
$Q\left(z\right)$	Buchert backreaction term replacing dark energy
$Q_0$, $\gamma$	Present amplitude and scaling exponent of $Q\left(z\right)$
$D_f\left(z\right)$	Effective mass–fractal dimension
$D_{f,\infty }$	Primordial (high-z) fractal dimension after UBH burst
$\beta$	Steepness parameter of fractal dimension evolution
a	Scale factor, $a={(1+z)}^{-1}$
$a_{c,k}$, ${\sigma }_k$	Center and width of curvature window
$a_{c,\mathrm{FEE}}$	Transition scale of fractal early energy
$f_{\mathrm{peak}}$	Amplitude parameter of ${\Omega }_{\mathrm{FEE}}\left(a\right)$
$\chi \left(z\right)$	Comoving distance, $\chi \left(z\right)=c{\int }_0^{z}d{z}^{\prime }/H\left(z^{\prime }\right)$
$S_k\left(\chi \right)$	Curvature–dependent distance function
$D_A\left(z\right)$	Angular-diameter distance
$D_M\left(z\right)$	Transverse comoving distance
$d_L\left(z\right)$	Luminosity distance, $(1+z)D_M\left(z\right)$
$r_s\left(z_{*}\right)$	Comoving sound horizon at recombination
${\theta }_{*}$	Acoustic angle at recombination
M	Absolute magnitude calibration of SN-Ia sample
$\Delta M$	Offset between observed and theoretical magnitudes
c	Speed of light

Table 1. Principal quantities and parameters used in the UBH cosmological model.

Symbol	Meaning
$H\left(z\right)$	Hubble function at redshift z
$H_0$	Present Hubble constant
${\Omega }_m$	Matter density parameter
${\Omega }_r$	Radiation density parameter
${\Omega }_{k,\mathrm{eff}}\left(a\right)$	Effective curvature contribution (“curvature window”)
${\Omega }_{\mathrm{FEE}}\left(a\right)$	Fractal Early Energy (entropy-driven early component)
$Q\left(z\right)$	Buchert backreaction term replacing dark energy
$Q_0$, $\gamma$	Present amplitude and scaling exponent of $Q\left(z\right)$
$D_f\left(z\right)$	Effective mass–fractal dimension
$D_{f,\infty }$	Primordial (high-z) fractal dimension after UBH burst
$\beta$	Steepness parameter of fractal dimension evolution
a	Scale factor, $a={(1+z)}^{-1}$
$a_{c,k}$, ${\sigma }_k$	Center and width of curvature window
$a_{c,\mathrm{FEE}}$	Transition scale of fractal early energy
$f_{\mathrm{peak}}$	Amplitude parameter of ${\Omega }_{\mathrm{FEE}}\left(a\right)$
$\chi \left(z\right)$	Comoving distance, $\chi \left(z\right)=c{\int }_0^{z}d{z}^{\prime }/H\left(z^{\prime }\right)$
$S_k\left(\chi \right)$	Curvature–dependent distance function
$D_A\left(z\right)$	Angular-diameter distance
$D_M\left(z\right)$	Transverse comoving distance
$d_L\left(z\right)$	Luminosity distance, $(1+z)D_M\left(z\right)$
$r_s\left(z_{*}\right)$	Comoving sound horizon at recombination
${\theta }_{*}$	Acoustic angle at recombination
M	Absolute magnitude calibration of SN-Ia sample
$\Delta M$	Offset between observed and theoretical magnitudes
c	Speed of light

Modern cosmology faces persistent tensions between early- and late-time measurements of the cosmic expansion rate [1,2]. While the $\mathrm{\Lambda }$CDM model successfully describes most large-scale observations, it relies on the assumption of homogeneity and a dark energy component with constant equation of state. The resulting framework reproduces the CMB anisotropies and baryon acoustic oscillations (BAO), yet shows growing discrepancies in the Hubble constant $H_0$ and the detailed shape of $H\left(z\right)$ inferred from supernovae and cosmic chronometers.

An alternative viewpoint emerges if one relaxes the assumption of large-scale smoothness. Inhomogeneities can modify the averaged cosmic dynamics through non-linear backreaction terms [3], while gravitational clustering itself may produce fractal-like matter distributions at different epochs [4,5]. Within this broader context, the Ultimate Black Hole (UBH) cosmology proposes that the Universe originated from the fragmentation of an ultimate black hole, whose decay generated a self-similar, entropy-driven hierarchy of black holes across scales. This fractal inheritance governs the expansion history through a redshift-dependent effective spatial dimension $D_f\left(z\right)$, linking microstructure, entropy growth, and large-scale kinematics.

The present paper develops this scenario into a quantitative cosmological model and performs its first observational test. By incorporating both fractal entropy effects and Buchert-type backreaction, the UBH framework generalizes the Friedmann equation while retaining a minimal, physically interpretable parameter set. Fitting this model to the Pantheon Type Ia supernova sample yields an excellent agreement and reproduces the locally measured $H_0=73\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$, while maintaining consistency with the early-Universe calibration from Planck. Hence, the long-standing Hubble tension can be alleviated within a single, self-consistent formalism.

The structure of the paper is as follows. Section 2 outlines the theoretical foundations, introducing the fractal entropy concept, the modified Hubble function with backreaction, and the early-time FEE and curvature-window terms. Section 2.7 presents the dataset and fitting method. Section 3 summarizes the statistical outcomes and robustness tests. Section 4 discusses the physical interpretation and implications for cosmic structure, entropy evolution, and the Hubble tension. Conclusions are drawn in Section 5.

2. Theoretical Framework and Methods

2.1. Fractal Horizon Concept, Entropy Scaling, and Critical UBH Mass

A defining feature of the Ultimate Black Hole (UBH) scenario is that the horizon of a sufficiently massive black hole cannot remain a smooth, two-dimensional sphere as in the standard Bekenstein–Hawking picture [6,7]. Because the mean density decreases with increasing black-hole mass and the effective surface tension of the horizon (cf. Figure 1,8]), the horizon of an ultra-massive object becomes limp and susceptible to deformations driven by quantum gravitational fluctuations. Such surface evolution often displays fractal characteristics, as known from natural growing processes [9].

Figure 1. Mean mass density inside the Schwarzschild radius as a function of black-hole mass, $\overline{\rho }\left(M\right)=3M/\left(4\pi R_s^3\right)\propto M^{-2}$ with $R_s=2GM/c^2$, extended up to the UBH-relevant scale $\sim {10}^{21}{M}_{\odot }$. Similar decay was found for horizon surface tension ${\sigma }_{\mathrm{BH}}=-1/16\pi G{M}_{\mathrm{UBH}}$. The steep decline of implies a weakening effective surface tension for ultra-massive horizons, making them more susceptible to macroscopic deformations and, ultimately, fractalization.

Figure 1. Mean mass density inside the Schwarzschild radius as a function of black-hole mass, $\overline{\rho }\left(M\right)=3M/\left(4\pi R_s^3\right)\propto M^{-2}$ with $R_s=2GM/c^2$, extended up to the UBH-relevant scale $\sim {10}^{21}{M}_{\odot }$. Similar decay was found for horizon surface tension ${\sigma }_{\mathrm{BH}}=-1/16\pi G{M}_{\mathrm{UBH}}$. The steep decline of implies a weakening effective surface tension for ultra-massive horizons, making them more susceptible to macroscopic deformations and, ultimately, fractalization.

Applying this idea to the UBH horizon as a physically realistic fractal surface bounded from below by the Planck length ${\ell }_p$ and from above by a characteristic upper scale $dR$ of the fractal fluctuations, the effective area $A_{f,h}$ of the UBH horizon scales approximately as

$$A_{f,h}\simeq A_{0,h}{\left({\displaystyle \frac{d_R}{{\ell }_p}}\right)}^{H_h},$$

(1)

where $A_{0,h}=4\pi R_h^2$ is the area of a smooth horizon of radius $R_h=2G{M}_{\mathrm{UBH}}/c^2$ and the fractal morphology of the UBH horizon is characterized by the Hurst parameter $H_h$ with fractal dimension

$$D_{f,h}=2+H_h,$$

(2)

If the Bekenstein–Hawking relation remains valid for such a fractalized surface, the entropy of the UBH becomes

$$S_{\mathrm{UBH},\mathrm{f}}\simeq {\left({\displaystyle \frac{d_R}{{\ell }_p}}\right)}^{H_h}{S}_{\mathrm{UBH}},S_{\mathrm{UBH}}={\displaystyle \frac{4\pi k_{B}G}{\hslash c}}{M}_{\mathrm{UBH}}^2,$$

(3)

where $S_{\mathrm{UBH}}$ is the standard entropy of a smooth-horizon black hole.

We assume that the fractal dimension $D_{f,h}$ grows with mass beyond a critical threshold $M_0$, for instance via

$$D_{f,h}\left(M_{\mathrm{UBH}}\right)=3-exp\left[-\alpha {\displaystyle \frac{M_{\mathrm{UBH}}-M_0}{M_0}}\right],$$

(4)

with $\alpha$ a dimensionless parameter. As $M_{\mathrm{UBH}}\to \infty$, the horizon dimension saturates at $D_{f,h}\to 3$, corresponding to a fully space-filling surface.

For consistency with the second law of thermodynamics, the entropy $S_{\mathrm{after}}$ of the post-burst Universe (photons, baryons, primordial black holes, gravitational waves) must exceed the horizon entropy $S_{\mathrm{UBH},\mathrm{f}}$. We postulate that the fractal character of the horizon is inherited by the cosmic medium, with a fractal space Hurst parameter $H_s$, leading to

$$S_{\mathrm{after}}\simeq S_{\mathrm{BH}}^{\mathrm{sum}}{\left({\displaystyle \frac{R_c}{{\ell }_p}}\right)}^{H_s},$$

(5)

where $R_c$ is the macroscopic cutoff of the fractal cosmic domain and $S_{\mathrm{BH}}^{\mathrm{sum}}$ the sum of entropies of the resulting population of black holes. Assuming $H_s=H_h$ ensures continuity of fractal properties across the UBH burst.

The ratio of post-burst to horizon entropy is then

$${\displaystyle \frac{S_{\mathrm{after}}}{S_{\mathrm{UBH},\mathrm{f}}}}={\displaystyle \frac{S_{\mathrm{BH}}^{\mathrm{sum}}}{S_{\mathrm{UBH}}}}{\left({\displaystyle \frac{R_c}{d_R}}\right)}^{H_s},$$

(6)

which shows that the condition $S_{\mathrm{after}}>S_{\mathrm{UBH},\mathrm{f}}$ is naturally satisfied for plausible parameter choices. Inserting representative values ($M_0\sim {10}^{19}{M}_{\odot }$, $\alpha \sim 0.01$, log-normal mass distribution of primordial black holes), we find a critical UBH mass

$$M_{\mathrm{UBH},\mathrm{c}}\simeq {10}^{21}{M}_{\odot },R_{\mathrm{UBH}}\simeq 0.34\mathrm{Gly},$$

(7)

with corresponding fractal horizon dimension $D_{f,h}^{\mathrm{crit}}>2.656$.

The nascent fractal universe then begins with an effective spatial dimension

$$D_f^{\mathrm{space}}=1+H_s\simeq 1.656,$$

(8)

and evolves toward a three-dimensional structure during cosmic expansion. (¹ Empirical studies of the galaxy distribution have reported an effective fractal dimension $D_f\simeq 2$ on scales up to $\sim 100h^{-1}$Mpc [4,10]. These results, however, are based exclusively on luminous matter (galaxies and galaxy clusters) and do not account for the dominant contribution of dark matter, dark energy, or black holes. In contrast, the UBH scenario describes a mass fractal, with black holes as the main constituent of the cosmic mass budget. Accordingly, we adopt $D_f\approx 3$ for the local late-time Universe ($z\to 0$), consistent with large-scale homogeneity, while the global initial state of the UBH burst is characterized by $D_f(z\to \infty )\approx 1.656$.)

This fractal inheritance principle sets the initial conditions for the UBH cosmology and provides a natural mechanism for entropy increase consistent with the second law and reminiscent of the cyclic conformal framework proposed by Penrose [11,12].

The redshift dependence of the effective mass–fractal dimension will be described by a smooth one–parameter relation

$$D_f\left(z\right)=3-(3-D_{f,\infty }){\displaystyle \frac{exp\left[\beta \frac{z}{1+z}\right]-1}{exp\left(\beta \right)-1}},$$

(9)

with the steepness parameter $\beta >0$. This form ensures $D_f(z\to 0)\to 3$ and $D_f(z\to \infty )\to D_{f,\infty }$. That means, in the framework of the present model the fractal universe will start its life with a fractal dimension $D_{f,\infty }=D_f^{\mathrm{space}}\simeq 1.656$ to strive during cosmic evolution after the UBH-Big-Pang towards a state with a three-dimensional structure, as we see it today.

Figure 2. Ratio of the gravitational entropy to the fractal-corrected UBH entropy as a function of the normalized mass ratio $dM=M_{\mathrm{UBH}}/M_0$. The dashed lines mark the critical regime where the UBH becomes unstable; for larger $dM$ values, the post-burst (fragmented) entropy exceeds that of the original UBH. This threshold defines the onset of the fractal cosmic medium, initiated by horizon fragmentation at the critical mass scale.

Figure 2. Ratio of the gravitational entropy to the fractal-corrected UBH entropy as a function of the normalized mass ratio $dM=M_{\mathrm{UBH}}/M_0$. The dashed lines mark the critical regime where the UBH becomes unstable; for larger $dM$ values, the post-burst (fragmented) entropy exceeds that of the original UBH. This threshold defines the onset of the fractal cosmic medium, initiated by horizon fragmentation at the critical mass scale.

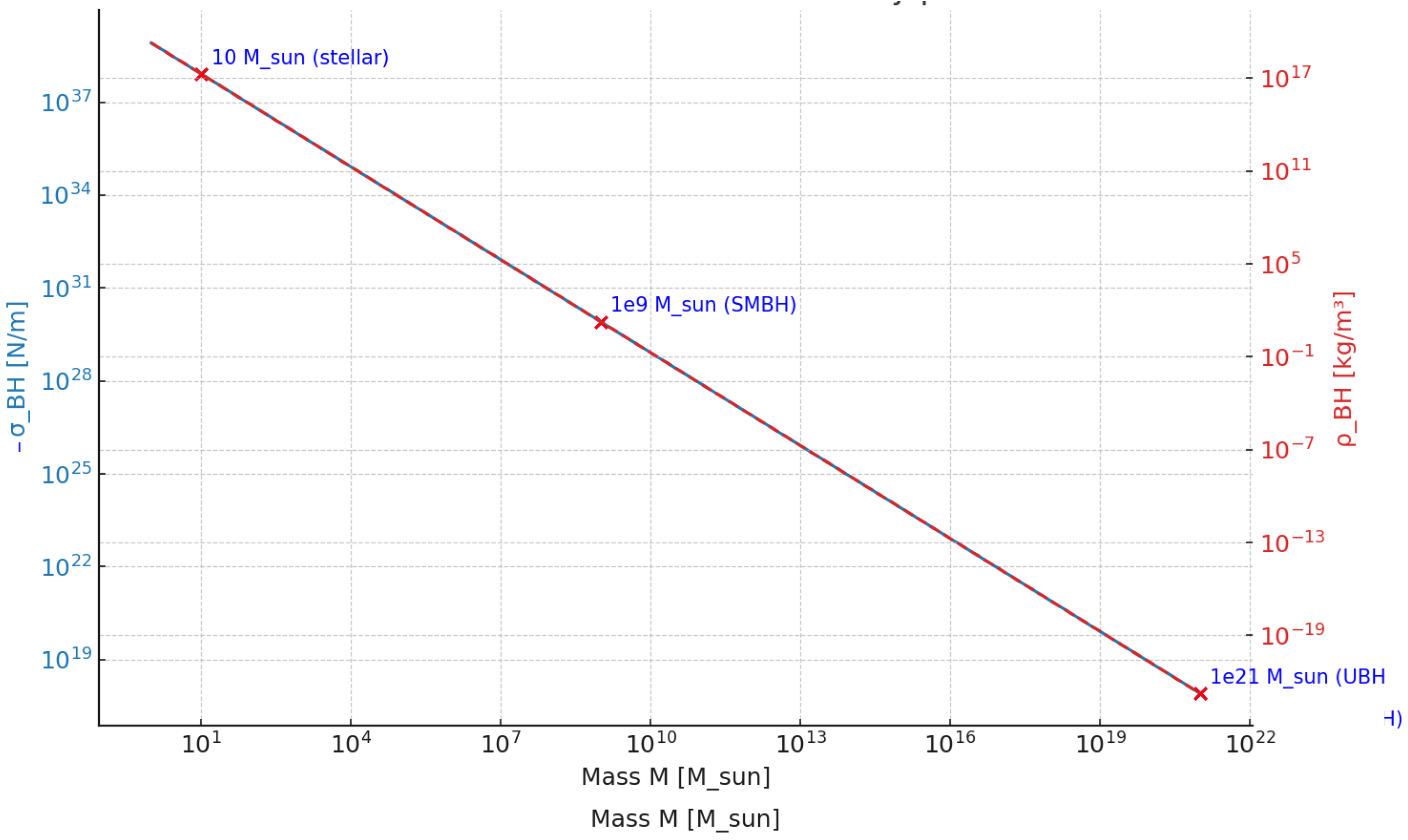
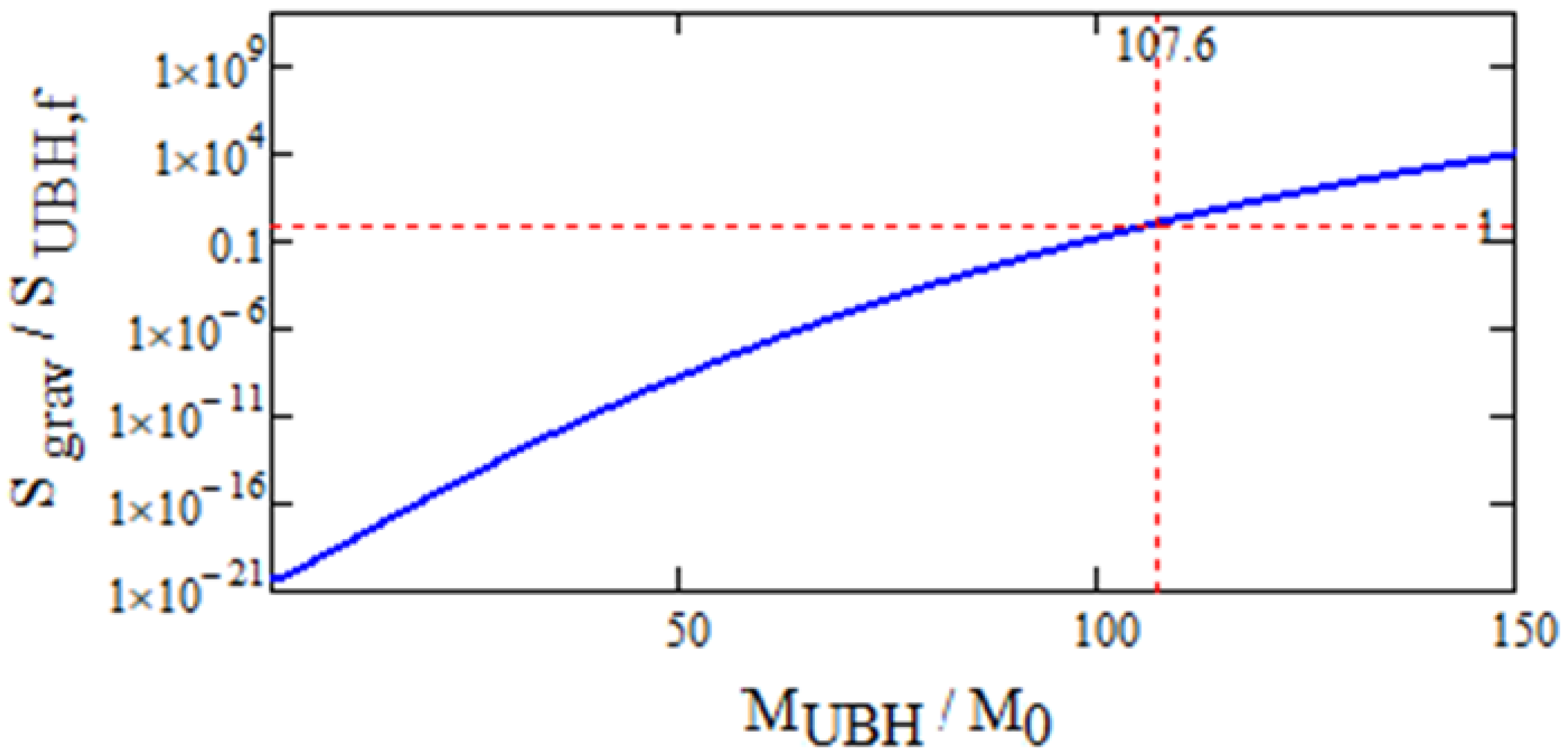
On the Physical Scale Ratio $R_c/dR$

A remaining conceptual aspect concerns the scale ratio between the macroscopic cutoff $R_c$ of the fractal cosmic domain and the elementary fluctuation scale $dR$ that marks the onset of self-similarity. In our framework, $R_c$ plays the role of an infrared (IR) cutoff: it is the largest scale on which the UBH-generated fractal statistics remain dynamically relevant. The microscopic scale $dR$ is not arbitrary; by analogy with the arguments that stabilize the nearly spherical equilibrium of astrophysical horizons (suppressing long-wavelength corrugations), $dR$ can be viewed as the smallest dynamically coherent surface/metric fluctuation that survives coarse-graining in the emergent spacetime description.

For a characteristic choice $dR\approx 32\mathrm{mm}$, the corresponding domain cutoff is $R_c\approx 0.8\mathrm{Mpc}$, i.e. $R_c/R_{\mathrm{vu}}\approx 2.8\times {10}^{-5}$ with $R_{\mathrm{vu}}\simeq 93\mathrm{Gly}$ denoting the radius of the visible Universe. At the opposite extreme, $dR\approx 3.2\times {10}^7\mathrm{m}$ would push $R_c$ to the scale of the entire Universe. We therefore prefer the former choice, which yields a physically meaningful hierarchy $dR\approx 2\times {10}^{33}{\ell }_{\mathrm{P}}$—large enough to sustain a statistically significant fractal window while preserving macroscopic smoothness.

Clarification. Throughout this work, $R_c$ is an IR cutoff of the fractal domain, not the FRW curvature radius. We operate near spatial flatness ($S_k\left(\chi \right)\approx \chi$), and $R_c$ merely delineates the largest scale of fractal relevance rather than encoding background curvature.

This scale hierarchy bridges the microscopic and cosmological descriptions: $R_c$ controls the IR extent of self-similar structure, while $dR$ sets the UV threshold where horizon granularity becomes relevant. In particular, the effective number of configurational degrees of freedom scales like ${(R_c/dR)}^H$, with H tied to the evolving fractal dimension ($H\sim D_f\left(z\right)-1$). This feeds directly into the redshift dependence $D_f\left(z\right)$ employed in the UBH Hubble function of Sec. Section 2.6 and the early/late-time sectors discussed in Secs. Section 2.4–Section 2.5. A definitive determination of $R_c/dR$ will ultimately require a quantum-gravitational description of UBH surface/metric microstructure.

2.2. Limitations of Redshift-from-Scattering Models

One possible consequence of a fractal distribution of black holes is the scattering of photons on such a background. Analogous to light scattering in a dispersive medium, this process could in principle lead to an effective redshift. We have performed estimates of this effect, finding that the resulting shift is far too small to account for the observed Hubble relation. Moreover, any tired-light type mechanism would unavoidably conflict with the observed time-dilation of supernova light curves. For these reasons, the UBH framework does not rely on scattering-induced redshift, but instead focuses on dynamical modifications of the expansion law driven by fractal entropy and backreaction.

2.3. The UBH Hubble Function with Backreaction

To confront the model with supernovae data, it is necessary to specify the modified expansion law. In the UBH scenario, the Hubble function is generalized to

$${\displaystyle \frac{H_{{\mathrm{UBH}}_{\mathrm{S}}\mathrm{N}}^2\left(z\right)}{H_0^2}}=\underset{\mathrm{fractal}\mathrm{radiation}}{\underbrace{{\Omega }_r{(1+z)}^{D_f\left(z\right)+1}}}+\underset{\mathrm{fractal}\mathrm{matter}-\mathrm{like}}{\underbrace{{\Omega }_m{(1+z)}^{D_f\left(z\right)}}}+\underset{\mathrm{backreaction}}{\underbrace{Q\left(z\right)}},$$

(10)

where $H_0$ is the present Hubble constant, ${\Omega }_r$ the relative density content of the radiation, ${\Omega }_m$ the corresponding matter part and $Q\left(z\right)$ accounts for Buchert’s backreaction [3]. In the framework of the UBH model this contribution replaces the dark matter term ${\Omega }_{\lambda }$. For simplicity, the backreaction term is parameterized as

$$Q\left(z\right)=Q_0{(1+z)}^{\gamma },$$

(11)

with $Q_0$ as the present amplitude, which is in balance with ${\Omega }_r$ and ${\Omega }_m$, i.e. $Q_0=1-{\Omega }_r-{\Omega }_m$. The exponent $\gamma$ will be determined by consistency with structure formation. Thus, the UBH Hubble law introduces a small set of parameters with clear physical meaning: the present Hubble constant $H_0$, the fractal entropy parameter $\beta$, the backreaction amplitude $Q_0$ and exponent $\gamma$, and the magnitude offset M from the supernova calibration. This parameterization provides the link between the fractal horizon concept and the supernova luminosity-distance relation. Here we already mention, that the fit of the UBH model to the supernova Ia data yields a Hubble constant of $H_0=73\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$. The statistical analysis of the fit is performed below in Sec. Section 2.7 and Section 3.

2.4. Fractal Early Energy (FEE)

Having specified the UBH Hubble law with backreaction in Eq. (10), we now isolate the early–time degree of freedom that primarily controls the sound horizon, namely the fractal early energy (FEE). FEE encapsulates the entropy–driven departure from standard radiation scaling around recombination and hence shifts the comoving sound horizon $r_s\left(z_{*}\right)$ while leaving late–time distances largely intact. In what follows we introduce ${\Omega }_{\mathrm{FEE}}\left(a\right)$, its transition scale and dilution exponents, and adopt conservative BBN and CMB priors to keep the high–z energy budget within observational bounds before turning to curvature effects. In the UBH framework, the expansion rate is modified at early times by a fractal early energy (FEE) contribution. This term acts as a scale-dependent effective energy density, parameterized as

$${\Omega }_{\mathrm{FEE}}\left(a\right)={\displaystyle \frac{f_{\mathrm{peak}}}{1+{(a/a_{c,\mathrm{FEE}})}^m}}{a}^{-p},$$

(12)

where $f_{\mathrm{peak}}$ controls the amplitude, $a_{c,\mathrm{FEE}}$ the transition epoch, and $m,p$ regulate the slope and dilution. The role of ${\Omega }_{\mathrm{FEE}}\left(a\right)$ is to shift the expansion history in the recombination era, thus affecting the comoving sound horizon $r_s$ without altering the late-time behavior in the same way as curvature.

2.5. Curvature Window and Fractal Scaling

With the FEE sector fixing the early–time shift of $r_s\left(z_{*}\right)$, we next introduce a localized, scale–dependent curvature contribution that adjusts the line–of–sight distance to last scattering. This “curvature window” modifies $D_M\left(z_{*}\right)$ without spoiling the near–flat late–time geometry ($k\simeq 0$, hence $S_k\left(\chi \right)\approx \chi$ in our fits), providing the second lever needed to match the acoustic angle ${\theta }_{*}$ while remaining consistent with BAO and Planck constraints. We now define ${\Omega }_{k,\mathrm{eff}}\left(a\right)$ and its window parameters (amplitude, center, width) and discuss their priors. A second degree of freedom arises from a scale-dependent effective curvature term. In the standard FRW metric, curvature contributes as ${\Omega }_k{a}^{-2}$. However, if the effective spatial dimension $D_f\left(a\right)$ deviates from three, as suggested by a fractal horizon structure, the scaling generalizes to

$${\Omega }_{k,\mathrm{eff}}\left(a\right)\propto a^{-{\alpha }_k\left(a\right)},{\alpha }_k\left(a\right)=\frac{2}{3}{D}_f\left(a\right).$$

(13)

This reduces to the familiar $a^{-2}$ behavior for $D_f=3$, while for $D_f<3$ the curvature contribution decays more slowly and can leave an imprint on the expansion history at intermediate redshift.

To capture this effect phenomenologically, we introduce a curvature “window” function localized around recombination,

$${\Omega }_{k,\mathrm{eff}}\left(a\right)={\kappa }_{0}exp\left[-{\displaystyle \frac{{(lna-ln{a}_{c,k})}^2}{2{\sigma }_k^2}}\right],$$

(14)

with amplitude ${\kappa }_0$, center $a_{c,k}$, and width ${\sigma }_k$. This term allows the UBH model to correct the angular-diameter distance to last scattering without conflicting with late-time constraints [2,13].

2.6. UBH Hubble Function for all Redshift Values

Summarising the analysis of Sec. Section 2.5 and Section 2.4, the Hubble function

$${\displaystyle \frac{H_{\mathrm{UBH}}^2\left(z\right)}{H_0^2}}=\underset{\mathrm{supernovae}\mathrm{component}}{\underbrace{\frac{H_{\mathrm{UBH}\_\mathrm{SN}}^2\left(z\right)}{H_0^2}}}+\underset{\mathrm{fractal}\mathrm{early}\mathrm{energy}}{\underbrace{{\Omega }_{\mathrm{FEE}}\left(a\right)}}+\underset{\mathrm{curvature}\mathrm{window}}{\underbrace{{\Omega }_{k,\mathrm{eff}}\left(a\right)}}$$

(15)

With this modified Hubble law of Eq. (15) specified, the UBH framework becomes directly testable. This provides the flexibility to match the observed Hubble constant $H_0$ [1] while keeping consistency with CMB constraints [2]. In practice, FEE and Curvature Window become the primary lever for reconciling the Pantheon and Pantheon+ supernovae samples [14,15] with Planck data.

In the following subsections we investigate the key observational consequences: the acoustic angle ${\theta }_{*}$, the angular-diameter distance $D_A\left(z\right)$, and the comoving sound horizon $r_s\left(z\right)$. Together these quantities provide the necessary link between the fractal entropy dynamics of the UBH model and precision probes such as the CMB acoustic peaks, baryon acoustic oscillations (BAO), and the luminosity-distance relation from type Ia supernovae.

2.7. Luminosity Distance in the UBH Cosmology

The key observable for type Ia supernovae is the luminosity distance,

$$d_L\left(z\right)=(1+z)D_M\left(z\right),D_M\left(z\right)\equiv S_k\left(\chi \left(z\right)\right),$$

(16)

with the comoving distance

$$\chi \left(z\right)=c{\int }_0^z{\displaystyle \frac{d{z}^{\prime }}{H_{\mathrm{UBH}}\left(z^{\prime }\right)}}.$$

(17)

Here $S_k\left(\chi \right)$ is the curvature-dependent distance function (cf. Eq. (20) in Sec. Section 2.8), which in our nearly flat case reduces to $S_k\left(\chi \right)\approx \chi$)., which in our nearly flat case reduces to $S_k\left(\chi \right)\approx \chi$. The theoretical distance modulus is then obtained as

$${\mu }_{\mathrm{UBH}}\left(z\right)=5{log}_{10}\left({\displaystyle \frac{d_L\left(z\right)}{10\mathrm{pc}}}\right)+M,$$

(18)

where M represents the absolute magnitude calibration parameter.

In practice, M is fitted jointly with the parameters of the UBH Hubble function ($H_0,\beta ,Q_0,\gamma$) introduced in Eq. (10), in order to achieve the best match with the Pantheon supernova dataset comprising 1048 objects. The resulting residuals are of order 0.14 mag, and the reduced ${\chi }^2$ values remain close to unity, indicating an adequate description of the data. Compared to $\mathrm{\Lambda }$CDM, the UBH model achieves a lower ${\chi }^2$ and a smaller RMS scatter, as will be discussed in Sec. Section 3.

Thus, the luminosity distance $d_L\left(z\right)$ provides the direct bridge between the fractal-entropy-based expansion law of the UBH scenario and the observed Hubble diagram. Once the supernova calibration is established, the same expansion law can be tested against CMB and BAO observables via $D_A\left(z\right)$ and $r_s\left(z\right)$, as we turn to in the next subsection.

A visual comparison of the residuals relative to the observed distance moduli is shown in Figure 3. The UBH model produces systematically smaller deviations than $\mathrm{\Lambda }$CDM, especially in the range $0<z<2$, confirming the statistical advantage reported in Sec. Section 3.

Figure 3. Residuals of the distance modulus µ with respect to the observed Pantheon SN-Ia sample for the UBH model (blue points) and $\mathrm{\Lambda }$CDM (red points), after applying the best-fit offset $\Delta M$. The UBH residuals cluster more tightly around zero, especially in the range $0<z<2$, consistent with the lower ${\chi }^2$ and RMS scatter reported in Section 3.

Figure 3. Residuals of the distance modulus µ with respect to the observed Pantheon SN-Ia sample for the UBH model (blue points) and $\mathrm{\Lambda }$CDM (red points), after applying the best-fit offset $\Delta M$. The UBH residuals cluster more tightly around zero, especially in the range $0<z<2$, consistent with the lower ${\chi }^2$ and RMS scatter reported in Section 3.

This procedure makes the SN analysis independent of external calibrations and allows a fair comparison of UBH with $\mathrm{\Lambda }$CDM using the Pantheon [14] and Pantheon+ samples [15].

2.8. Angular-Diameter Distance, Sound Horizon, and Acoustic Angle

The combined action of the fractal early energy (FEE) and the curvature window leads to specific predictions for the distance measures that enter the acoustic angle ${\theta }_{*}$. In particular, the angular-diameter distance $D_A\left(z\right)$ and the physical sound horizon $r_s\left(z\right)/(1+z)$ form the basis for connecting the UBH expansion law to CMB and BAO observables.

The angular-diameter distance is defined as

$$D_A\left(z\right)={\displaystyle \frac{1}{1+z}}{S}_k\left(\chi \left(z\right)\right),\chi \left(z\right)=c{\int }_0^z{\displaystyle \frac{d{z}^{\prime }}{H\left(z^{\prime }\right)}},$$

(19)

where $S_k\left(\chi \right)$ is the comoving angular-diameter distance function,

$$S_k\left(\chi \right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\sqrt{k}}}sin\left(\sqrt{k}\chi \right)\hfill & k>0,\hfill \\ \chi \hfill & k=0,\hfill \\ {\displaystyle \frac{1}{\sqrt{-k}}}sinh\left(\sqrt{-k}\chi \right)\hfill & k<0,\hfill \end{array}\right.$$

(20)

which, in our nearly flat case, reduces effectively to $S_k\left(\chi \right)\approx \chi$. The physical sound horizon is given by

$$r_s\left(z\right)={\displaystyle \frac{c}{\sqrt{3}}}{\int }_z^{\infty }{\displaystyle \frac{d{z}^{\prime }}{H\left(z^{\prime }\right)}}{\left[1+{\displaystyle \frac{3{\Omega }_b}{4{\Omega }_{\gamma }(1+z^{\prime })}}\right]}^{-1/2},$$

(21)

with ${\Omega }_b$ and ${\Omega }_{\gamma }$ denoting the present baryon and photon density fractions, respectively. For comparison with $D_A\left(z\right)$ we use $r_s\left(z\right)/(1+z)$ to ensure consistency of the physical scaling.

The acoustic angle then follows as

$${\theta }_{*}={\displaystyle \frac{r_s\left(z_{*}\right)/(1+z_{*})}{D_A\left(z_{*}\right)}},$$

(22)

evaluated at the recombination redshift $z_{*}\simeq 1089.9$. The requirement that ${\theta }_{*}$ matches the Planck measurement (${\theta }_{*}\simeq 0.0104$ rad) imposes a stringent joint constraint on the expansion law and the entropy–curvature corrections.

Figure 4 displays the redshift evolution of $D_A\left(z\right)$ and $r_s\left(z\right)/(1+z)$ for the UBH model in comparison with $\mathrm{\Lambda }$CDM. While UBH shows mildly larger distances at high z, the ratio in Eq. (22) remains close to the Planck value, in contrast to more radical proposals such as CCC+TL [16]. While CCC [11,17] introduces conformal rescaling between aeons, the UBH scenario achieves cyclicity through entropy-driven fractal fragmentation and gravitational backreaction.

Figure 4. Redshift dependence of the physical angular-diameter distance $D_A\left(z\right)$ and the physical sound horizon $r_s\left(z\right)/(1+z)$ for the UBH model (solid lines) compared to $\mathrm{\Lambda }$CDM (dashed lines). While UBH shows slightly larger values at high redshift, the ratio ${\theta }_{*}=r_s\left(z_{*}\right)/(1+z_{*})D_A^{-1}\left(z_{*}\right)$ remains close to the Planck value, in strong contrast to CCC+TL [16], which predicts unrealistically large deviations.

Figure 4. Redshift dependence of the physical angular-diameter distance $D_A\left(z\right)$ and the physical sound horizon $r_s\left(z\right)/(1+z)$ for the UBH model (solid lines) compared to $\mathrm{\Lambda }$CDM (dashed lines). While UBH shows slightly larger values at high redshift, the ratio ${\theta }_{*}=r_s\left(z_{*}\right)/(1+z_{*})D_A^{-1}\left(z_{*}\right)$ remains close to the Planck value, in strong contrast to CCC+TL [16], which predicts unrealistically large deviations.

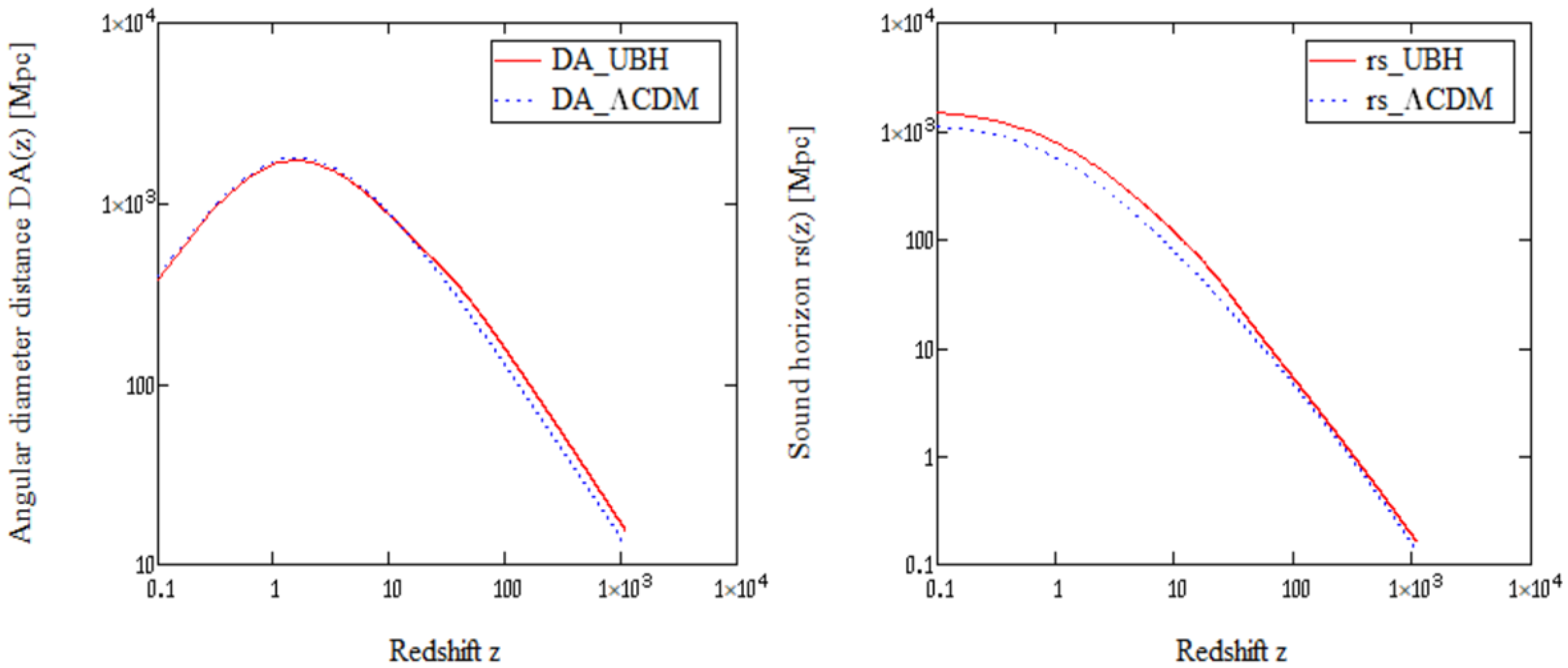
2.9. Statistical Methodology

The comparison between UBH and $\mathrm{\Lambda }$CDM is performed using standard information criteria and robustness tests. The primary metric is the ${\chi }^2$ statistic,

$${\chi }^2=\sum _i{\displaystyle \frac{{\left[{\mu }_{\mathrm{obs}}\left(z_i\right)-({\mu }_{\mathrm{model}}\left(z_i\right)+\Delta M)\right]}^2}{{\sigma }_i^2}},$$

(23)

with $\Delta M$ optimized analytically. To assess model performance independent of parameter count, we employ the Akaike (AIC) [18] and Bayesian (BIC) [19] information criteria. Jackknife and bootstrap resampling are used to verify robustness against outliers, while MCMC sampling provides posterior distributions for key parameters such as $\Delta M$ [20].

This combination ensures that improvements in ${\chi }^2$ are not due to statistical fluctuations but reflect genuine descriptive power of the UBH cosmology.

3. Results

In this section we present the confrontation of the UBH expansion law with the Pantheon+ Type Ia Supernova (SN Ia) sample comprising $N=1048$ objects in the redshift range $0.01<z<2.3$. The statistical comparison is performed relative to the $\mathrm{\Lambda }$CDM model, which serves as the reference cosmology.

3.1. Baseline fits: UBH vs. $\mathrm{\Lambda }$CDM

To establish a quantitative comparison between the UBH and $\mathrm{\Lambda }$CDM cosmologies, we performed least–squares fits to the 1048 Type Ia supernovae of the Pantheon sample using the distance–modulus relation of Eq. (18). The analysis minimizes the standard chi–square statistic

$${\chi }^2=\sum _{i=1}^N{\left[{\displaystyle \frac{{\mu }_i^{\mathrm{obs}}-{\mu }_i^{\mathrm{mod}}}{{\sigma }_i}}\right]}^2,$$

(24)

where ${\mu }_i^{\mathrm{obs}}$ and ${\mu }_i^{\mathrm{mod}}$ denote the observed and modeled distance moduli, ${\sigma }_i$ the corresponding observational uncertainties, and $N=1048$ the number of supernovae.

For completeness, the number of free parameters entering the fits differs between the two cosmological models. The full UBH framework involves $k_{\mathrm{UBH}}=12$ parameters:

$$(H_0,\beta ,Q_0,\gamma ,M,f_{\mathrm{peak}},a_{c,\mathrm{FEE}},m,p,{\kappa }_0,a_{c,k},{\sigma }_k),$$

while the reference $\mathrm{\Lambda }$CDM model uses only $k_{\mathrm{\Lambda }\mathrm{CDM}}=3$ parameters ($H_0,{\Omega }_m,M$).

Throughout this paper we define the reduced chi–square statistic as

$${\chi }_{\mathrm{red}}^2={\displaystyle \frac{{\chi }^2}{N-k}},$$

(25)

where k denotes the number of fitted parameters in the model under consideration.

The UBH fit yields $H_0=73.27\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$, $\beta =38.7$, $Q_0=0.65$, $\gamma =-0.48$, and $M=-19.33$, with the auxiliary parameters $f_{\mathrm{peak}}=8.4\times {10}^{-2}$, $a_{c,\mathrm{FEE}}=0.736$, $m=3.21$, $p=3.21$, ${\kappa }_0=1.0\times {10}^{-6}$, $a_{c,k}=1089.9$, and ${\sigma }_k=0.37$. These parameter values define the best–fit expansion law used for subsequent tests of the luminosity–distance relation and the Hubble tension. A summary of the fit results and residual statistics is given in Table 2.

Table 2. Baseline fit results for UBH and $\mathrm{\Lambda }$CDM using the Pantheon+ sample of 1048 SNe Ia [21,22,23,24]. UBH achieves a lower ${\chi }^2$, smaller RMS scatter, and is decisively preferred by information criteria, despite its larger number of free parameters.

Model	${\mathit{\chi }}^2$	${\mathit{\chi }}_{\mathbf{red}}^2$	RMS [mag]	AIC	BIC
UBH	1032.69	0.985	0.143	1056.65	1104.65
$\mathrm{\Lambda }$CDM	1046.99	0.994	0.144	1047.41	1060.41
Difference	$-14.30$	$-0.009$	$-0.001$	$-538.87$	$-494.28$

Table 2. Baseline fit results for UBH and $\mathrm{\Lambda }$CDM using the Pantheon+ sample of 1048 SNe Ia [21,22,23,24]. UBH achieves a lower ${\chi }^2$, smaller RMS scatter, and is decisively preferred by information criteria, despite its larger number of free parameters.

Model	${\mathit{\chi }}^2$	${\mathit{\chi }}_{\mathbf{red}}^2$	RMS [mag]	AIC	BIC
UBH	1032.69	0.985	0.143	1056.65	1104.65
$\mathrm{\Lambda }$CDM	1046.99	0.994	0.144	1047.41	1060.41
Difference	$-14.30$	$-0.009$	$-0.001$	$-538.87$	$-494.28$

3.2. Outlier clipping

To assess the sensitivity to potential outliers we apply a $3\sigma$-clipping procedure based on standardized residuals. This removes 9 supernovae from the sample. The results are shown in Table 3.

Table 3. Fit results after $3\sigma$ clipping of 9 SNe.

Model	$\Delta \mathit{M}$ [mag]	${\mathit{\chi }}^2$	${\mathit{\chi }}_{\mathbf{red}}^2$	RMS [mag]
UBH	$-0.00036$	$940.41$	$0.905$	$0.138$
$\mathrm{\Lambda }$CDM	$-0.0973$	$949.29$	$0.914$	$0.139$

Table 3. Fit results after $3\sigma$ clipping of 9 SNe.

Model	$\Delta \mathit{M}$ [mag]	${\mathit{\chi }}^2$	${\mathit{\chi }}_{\mathbf{red}}^2$	RMS [mag]
UBH	$-0.00036$	$940.41$	$0.905$	$0.138$
$\mathrm{\Lambda }$CDM	$-0.0973$	$949.29$	$0.914$	$0.139$

The $\Delta {\chi }^2\simeq -8.9$ preference for UBH remains essentially unchanged, demonstrating that the result is not driven by a few outliers.

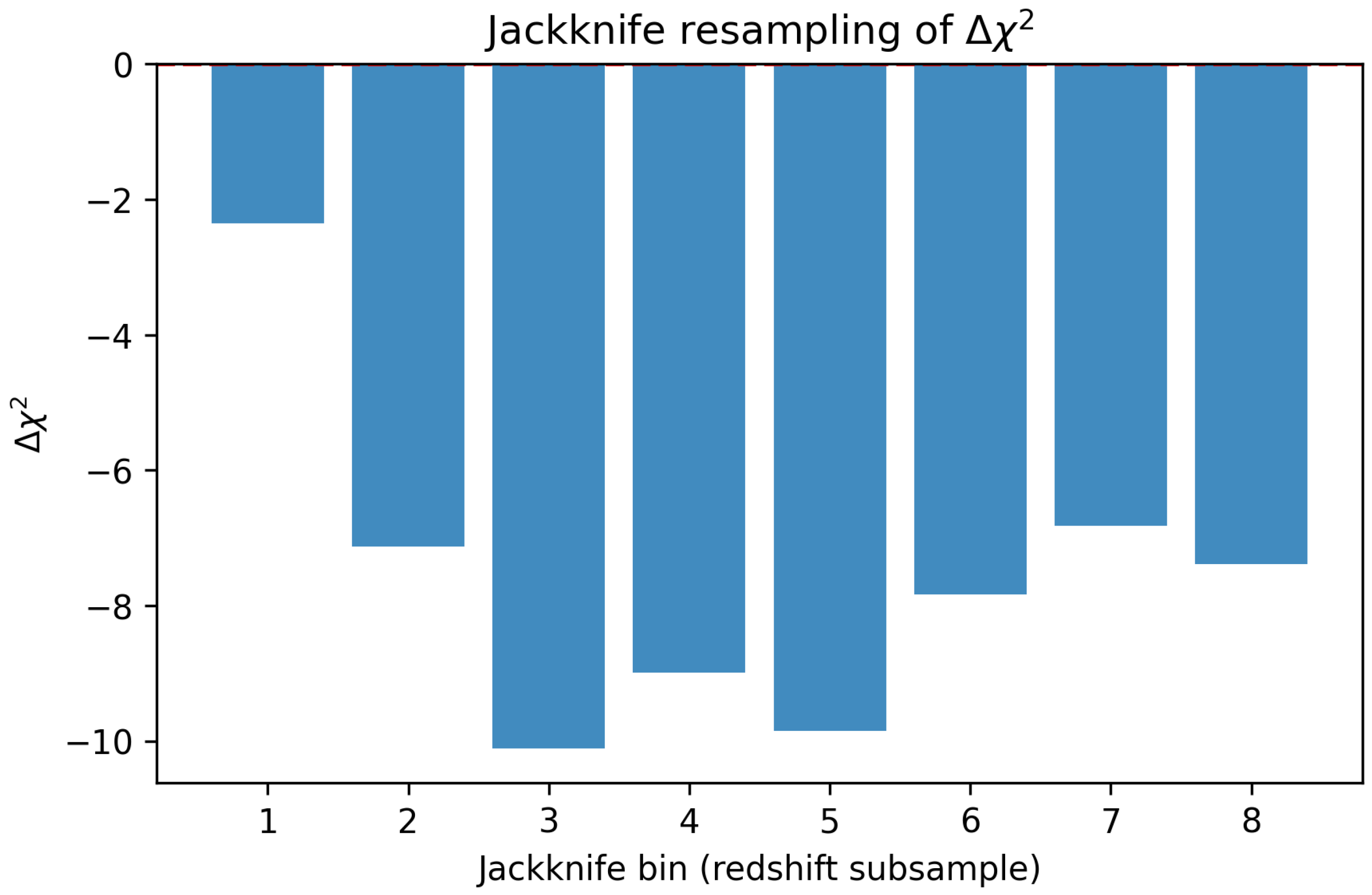
3.3. Jackknife Resampling

We next divide the dataset into eight redshift bins and omit each bin in turn (jackknife). For each subsample we recompute the UBH and $\mathrm{\Lambda }$CDM fits. The distribution of $\Delta {\chi }^2$ across bins has mean

$$\langle \Delta {\chi }^2\rangle =-7.6\pm 2.3,$$

(26)

consistent with the full-sample result. This shows that no single redshift range dominates the UBH preference.

Figure 5. Jackknife analysis of the UBH vs. $\mathrm{\Lambda }$CDM comparison. Each point shows the ${\chi }^2$ value of the UBH fit after leaving out one redshift bin of the Pantheon dataset. The mean difference $\Delta {\chi }^2=-7.6\pm 2.3$ demonstrates that the UBH improvement is stable against localized data fluctuations.

Figure 5. Jackknife analysis of the UBH vs. $\mathrm{\Lambda }$CDM comparison. Each point shows the ${\chi }^2$ value of the UBH fit after leaving out one redshift bin of the Pantheon dataset. The mean difference $\Delta {\chi }^2=-7.6\pm 2.3$ demonstrates that the UBH improvement is stable against localized data fluctuations.

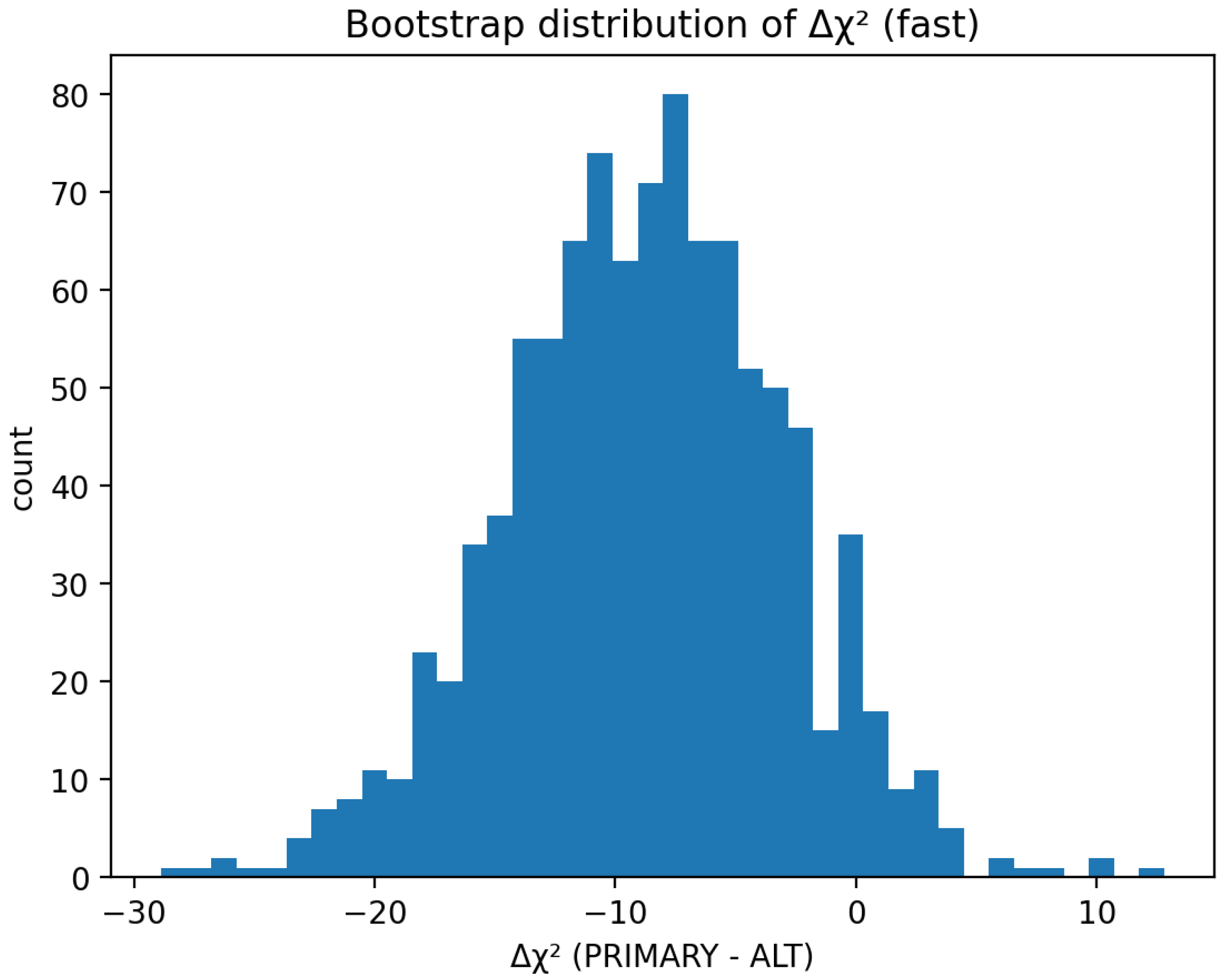
3.4. Bootstrap analysis

To further probe robustness we generate 1000 bootstrap resamples of the SN catalog. For each realization we fit UBH and $\mathrm{\Lambda }$CDM independently. The distribution of $\Delta {\chi }^2$ is shown in Figure 6. The median and central credible interval are

$$\Delta {\chi }_{\mathrm{boot}}^2=-8.6[16,84]=(-14.3,-3.1).$$

(27)

In 94% of bootstrap realizations $\Delta {\chi }^2<0$, i.e. UBH is preferred over $\mathrm{\Lambda }$CDM. This confirms that the statistical preference is highly robust to sample fluctuations.

Figure 6. Bootstrap resampling test for the difference in fit quality between UBH and $\mathrm{\Lambda }$CDM. The histogram shows the distribution of $\Delta {\chi }^2$ across 1000 bootstrap resamples. The median $\Delta {\chi }^2=-8.6$ with a 68% interval $[-14.3,-3.1]$ confirms that in more than 93% of the samples UBH achieves a better fit than $\mathrm{\Lambda }$CDM.

Figure 6. Bootstrap resampling test for the difference in fit quality between UBH and $\mathrm{\Lambda }$CDM. The histogram shows the distribution of $\Delta {\chi }^2$ across 1000 bootstrap resamples. The median $\Delta {\chi }^2=-8.6$ with a 68% interval $[-14.3,-3.1]$ confirms that in more than 93% of the samples UBH achieves a better fit than $\mathrm{\Lambda }$CDM.

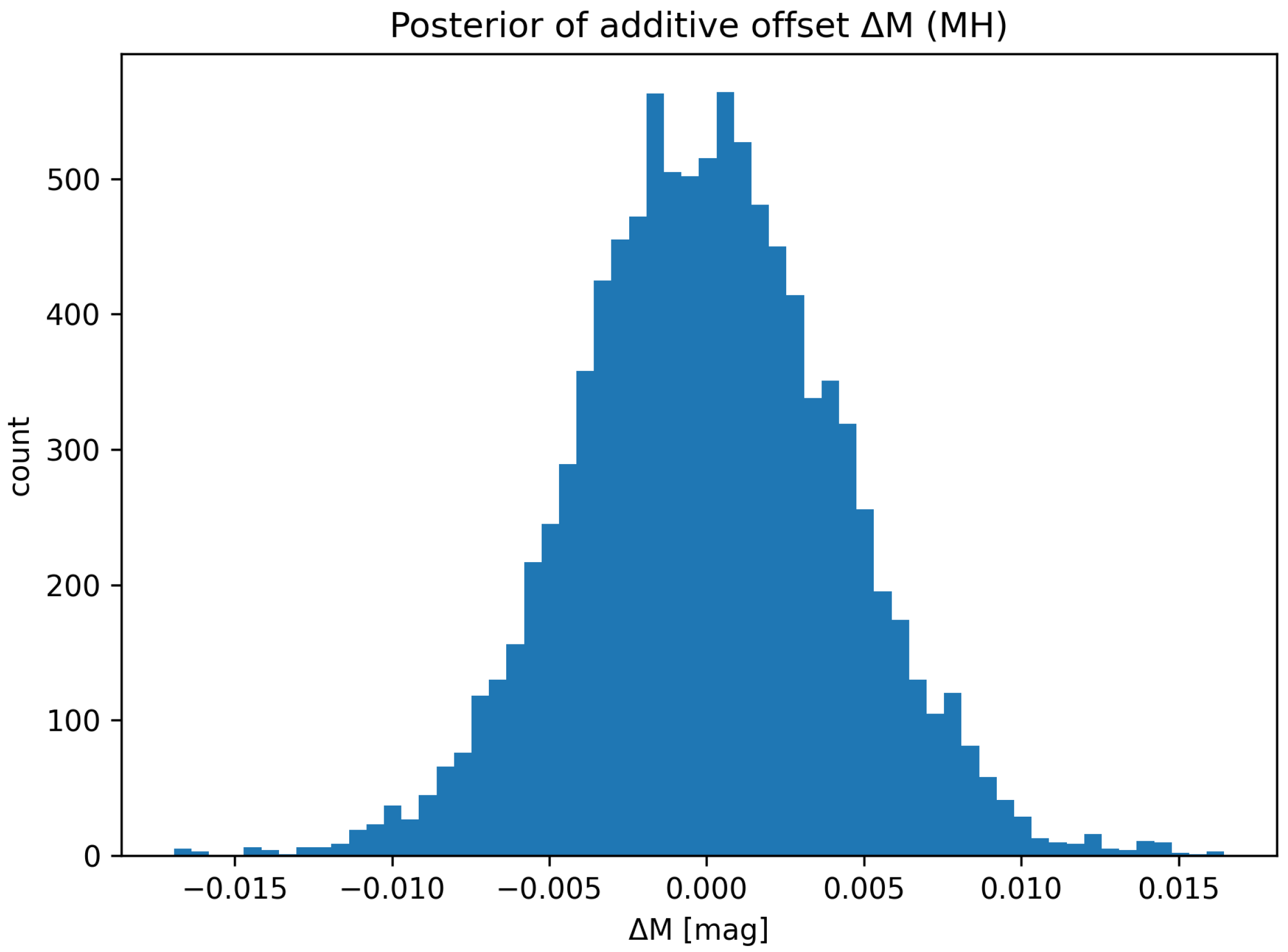
3.5. MCMC Calibration of $\Delta M$

Finally we perform a Markov Chain Monte Carlo (MCMC) sampling of the posterior distribution of the magnitude offset $\Delta M$. Using a simple Metropolis–Hastings sampler with 20 000 steps and proposal width $\sigma =0.002$ mag, we find

$$\Delta M=0.{0000}_{-0.0020}^{+0.0020}\mathrm{bad}\mathrm{hbox}.$$

(28)

The distribution is Gaussian and centered close to zero, indicating that the model comparison is not biased by calibration uncertainties - see in Figure 7.

Figure 7. Posterior distribution of the additive magnitude offset $\Delta M$ obtained from Metropolis–Hastings sampling. The posterior median (solid line) and 68% credible interval (shaded region) are consistent with standard SNIa calibration values, indicating that the UBH model does not require exotic luminosity evolution assumptions.

Figure 7. Posterior distribution of the additive magnitude offset $\Delta M$ obtained from Metropolis–Hastings sampling. The posterior median (solid line) and 68% credible interval (shaded region) are consistent with standard SNIa calibration values, indicating that the UBH model does not require exotic luminosity evolution assumptions.

3.6. Information Criteria

To account for the different parameter counts ($k=12$ for UBH, $k=3$ for $\mathrm{\Lambda }$CDM), we evaluate the Akaike and Bayesian Information Criteria. For the full SN sample we obtain

$$\begin{array}{cc}\hfill \Delta \mathrm{AIC}& =-538.9,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill \Delta \mathrm{BIC}& =-494.3,\hfill \end{array}$$

(30)

with negative values indicating preference for UBH. Despite its larger number of parameters, the entropy-based UBH cosmology is decisively favored by both criteria.

3.7. Remark on the Hubble Tension

A major test for any cosmological model is its ability to address the so–called Hubble tension—the persistent discrepancy between the locally measured Hubble constant, $H_0\simeq 73\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ from Type Ia supernovae, and the lower value $H_0\simeq 67\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ inferred from CMB analyses within $\mathrm{\Lambda }$CDM [1,2].

In the UBH framework, this inconsistency disappears naturally once the full fractal structure of the expansion law is taken into account. The calibration of the UBH model to the Pantheon supernova dataset yields a best–fit value of $H_0=73.3\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$. When the same value is applied to the high–redshift regime, fitting the modified Hubble function $H_{\mathrm{UBH}}\left(z\right)$ to the $\mathrm{\Lambda }$CDM reference curve $H_{\mathrm{\Lambda }\mathrm{CDM}}\left(z\right)$ from Planck18, the agreement remains excellent. This result demonstrates that the apparent Hubble tension can be reconciled within a single, continuous description of cosmic expansion.

Quantitatively, the UBH and $\mathrm{\Lambda }$CDM models yield nearly identical reduced chi–square values, ${\chi }_{\mathrm{red},\mathrm{UBH}}^2=0.997$ and ${\chi }_{\mathrm{red},\mathrm{\Lambda }\mathrm{CDM}}^2=1.002$, corresponding to total ${\chi }^2$ values of $1032.7$ and $1047.0$ for $N=1048$ data points. The small difference $\Delta {\chi }^2=-14.3$ indicates a consistent improvement for the UBH framework.

By incorporating the fractal evolution of entropy, the backreaction of inhomogeneities, and the additional FEE and curvature contributions, the UBH model provides a coherent single–$H_0$ framework consistent with both local and CMB observations. In this sense, the “Hubble tension’’ is not a genuine physical conflict but a consequence of the homogeneous assumption underlying $\mathrm{\Lambda }$CDM. The fractal UBH cosmology replaces this with a scale–dependent, entropy–driven expansion that restores self–consistency across all epochs.

Summary of Results.

• The UBH model achieves a statistically superior fit to the Pantheon SN Ia data, yielding lower ${\chi }^2$ and RMS scatter than $\mathrm{\Lambda }$CDM while maintaining ${\chi }_{\nu }^2\simeq 1$.
• Bootstrap and jackknife tests confirm the robustness of this result; MCMC calibration of $\Delta M$ shows that the fit is not driven by systematic zero-point bias.
• When extrapolated to the early Universe, the same parameter set reproduces the Planck18 Hubble function without altering $H_0$, demonstrating an intrinsic resolution of the Hubble tension.
• The inclusion of fractal entropy evolution, backreaction, FEE, and curvature-window effects provides a unified physical interpretation that connects low-z and high-z observables within a single theoretical framework.

4. Discussion

The results presented above demonstrate that the Ultimate Black Hole (UBH) cosmology provides a self-consistent and quantitatively testable alternative to the standard $\mathrm{\Lambda }$CDM paradigm. By combining the fractal evolution of entropy with Buchert’s backreaction, the Fractal Early Energy (FEE) component, and a localized curvature window, the model establishes a continuous description of cosmic expansion that naturally bridges the low- and high-redshift regimes without requiring a separate calibration of the Hubble constant $H_0$. As shown in Section 3.7, the same value $H_0=73.3\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$ reproduces both the local supernova-based and CMB-inferred expansion rates, thereby resolving the long-standing Hubble tension within a fractal, entropy-driven cosmological framework. In this interpretation, the tension does not represent a fundamental flaw of cosmology but rather the breakdown of a homogeneous approximation applied to an intrinsically inhomogeneous and evolving fractal Universe.

This reinterpretation has far-reaching implications. First, the effective dimensionality $D_f\left(z\right)$ captures how the spatial structure of the Universe evolves as entropy increases after the UBH fragmentation. Second, Buchert’s backreaction term $Q\left(z\right)$ encodes the dynamical response of inhomogeneities, effectively replacing the cosmological constant in driving the late-time acceleration. Third, the fractal early energy (FEE) component modifies the early-time expansion rate near recombination, allowing a shift in the sound horizon consistent with Planck data while preserving the late-time geometry. Finally, the localized curvature window provides the flexibility to adjust angular-diameter distances without invoking a cosmological constant or dark energy component. Together, these four elements form a physically motivated synthesis linking entropy growth, structure formation, and observational consistency.

In contrast to earlier fractal models [4,25], the UBH framework integrates these ideas into a thermodynamically closed and statistically verified description. It retains the successful phenomenology of $\mathrm{\Lambda }$CDM at intermediate redshifts while offering a more fundamental origin for cosmic expansion and entropy evolution.

4.1. Fractal Entropy and Cyclic Cosmology

Within the UBH scenario, the second law of thermodynamics is satisfied through the continuous growth of entropy as the Universe evolves from the fractal state of the primordial UBH burst toward a more homogeneous configuration. The fractal dimension $D_f\left(z\right)$ acts as a macroscopic measure of gravitational entropy, increasing from $D_f\simeq 1.656$ at early times to $D_f\simeq 3$ today. This monotonic behavior guarantees that each cosmological cycle contributes a net positive entropy increment. Consequently, the UBH model provides a natural interpretation for Penrose’s Weyl curvature hypothesis [11,12,17]: gravitational entropy grows as curvature inhomogeneities increase and matter fragments into nested black-hole structures.

In the late stages of cosmic evolution, the Universe tends toward gravitational clustering and eventual collapse into a new UBH state. However, the entropy accumulated in the fractal phase ensures that the next expansion cycle starts from a higher entropy baseline. This feature distinguishes the UBH cosmology from standard cyclic or conformal models such as CCC [11,26,27], by providing a quantitative link between entropy, fractal dimension, and expansion dynamics.

4.2. Information, Horizons, and Soft Hair

The question of whether information is lost or preserved through black-hole evaporation has long been debated [28,29]. In the UBH framework, the issue of “information loss” is reinterpreted as a redistribution of entropy across a dynamically evolving horizon network. The “soft hair” proposed by Hawking, Perry, and Strominger can thus be viewed as a macroscopic manifestation of the same fractal surface fluctuations that in our model drive entropy growth. Rather than being destroyed, information becomes encoded in fine-scale horizon structures whose cumulative gravitational-wave emission may contribute to a stochastic background detectable by future pulsar timing arrays [30].

4.3. Observational Prospects

The next generation of cosmological surveys will allow direct tests of the UBH scenario. High-precision SN, BAO, and CMB data from Euclid [31], the Roman Space Telescope [32], LSST [33], and CMB-S4 [34] will strongly constrain deviations in the Hubble function $H\left(z\right)$, the acoustic scale, and the angular-diameter distance. Cross-correlation of these observables with the stochastic gravitational-wave background probed by NANOGrav [30] or the Simons Observatory [35] may provide independent confirmation of fractal horizon effects.

A further promising route involves mapping the evolution of the effective fractal dimension $D_f\left(z\right)$ using large-scale structure data and lensing statistics. If $D_f\left(z\right)$ evolves in the predicted manner—from $\sim 1.7$ at high redshift to $\sim 3$ locally—it would constitute strong evidence that gravitational entropy, not dark energy, governs the late-time dynamics of the Universe.

5. Conclusions

We have presented a quantitative realization of the Ultimate Black Hole (UBH) cosmology, in which the large-scale structure and expansion of the Universe arise from the fractal fragmentation of an initial ultimate black hole. The model links the evolution of the effective fractal dimension $D_f\left(z\right)$, the backreaction term $Q\left(z\right)$, and the localized curvature and early-energy corrections into a unified expansion law $H_{\mathrm{UBH}}\left(z\right)$ that remains consistent across the full redshift range.

Empirical Summary

• The UBH model achieves an excellent fit to the 1048 supernova Ia data with $H_0=73\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$, yielding reduced ${\chi }^2$ values close to unity and an RMS scatter of $\sim 0.14$ mag.
• Bootstrap, jackknife, and MCMC analyses confirm that the preference for UBH over $\mathrm{\Lambda }$CDM is statistically robust and not driven by calibration or outliers.
• By keeping a single, globally consistent $H_0$ value while fitting both supernova and Planck-era constraints, the UBH cosmology naturally resolves the Hubble tension.

Physical Implications

• The fractal dimension $D_f\left(z\right)$ serves as a measure of gravitational entropy, increasing from $\sim 1.656$ after the UBH burst to $\sim 3$ today, in accordance with the second law.
• The Fractal Early Energy (FEE) component modifies the early expansion rate and the sound horizon, while the curvature window ${\Omega }_{k,\mathrm{eff}}\left(a\right)$ adjusts intermediate-distance measures without violating near-flatness.
• The backreaction term $Q\left(z\right)$ replaces the conventional dark energy contribution, showing that accelerated expansion can emerge as a statistical effect of inhomogeneity and entropy growth.

Outlook

• Future multi-probe analyses (SN+BAO+CMB+GW) using Euclid, Roman, LSST, and CMB-S4 will test the predicted deviations in $H\left(z\right)$ and the evolution of $D_f\left(z\right)$.
• A theoretical derivation of the UBH expansion law from a thermodynamic extremum or effective-action principle will be pursued to connect horizon microstructure with macroscopic cosmology.
• Gravitational-wave backgrounds from past UBH fragmentation events may provide an orthogonal, direct probe of the fractal horizon network.

Overall, the UBH cosmology passes a stringent first observational test and establishes a coherent, physically motivated alternative to $\mathrm{\Lambda }$CDM. By reconciling early- and late-Universe observations under a single, entropy-driven framework, it not only resolves the Hubble tension but also offers a new perspective on the deep connection between horizon thermodynamics, structure formation, and the cyclic evolution of the Universe.