1. Background
A central question in contemporary theoretical physics is whether the geometry of spacetime is a fundamental construct or an emergent phenomenon arising from a deeper pre-geometric substrate. This question lies at the heart of quantum gravity research and has motivated a wide range of approaches that seek to reconstruct spacetime from more primitive, often relational, degrees of freedom. Despite their formal and conceptual differences, these frameworks converge on the idea that spacetime may not be an input to the theory but a derived structure.
One prominent approach is holographic duality, most notably realized in the AdS/CFT correspondence [
1], wherein a theory of quantum gravity in a bulk anti-de Sitter spacetime is dual to a lower-dimensional conformal field theory defined on its boundary. Within this framework, geometric notions such as distance and connectivity are believed to emerge from quantum entanglement patterns in the boundary theory [
26,
27]. More specifically, the Ryu–Takayanagi formula makes this connection precise by relating entanglement entropy to the area of minimal surfaces in the bulk [
2]. Subsequent developments have provided further evidence that bulk spacetime is encoded in entanglement structure, rather than prescribed independently [
3,
4,
5].
Parallel insights have arisen from the study of scattering amplitudes in quantum field theory. It has been shown that certain classes of amplitudes admit simple representations in terms of combinatorial and geometric objects such as the amplituhedron, associahedron, and cosmological polytopes [
6,
7,
8,
9]. What is remarkable is that these geometric constructions generate amplitudes without relying on the usual formulation involving particles moving through space and time. Instead, key physical principles such as locality and unitarity emerge from the internal structure of the geometry itself. This suggests that the underlying rules governing interactions may be more fundamentally tied to geometric and combinatorial principles than to traditional spacetime-based dynamics.
A contrasting line of research is causal set theory (CST), which proposes that spacetime is not continuous but fundamentally discrete, consisting of elementary events organized into a partially ordered set where the order encodes causal relations [
10]. In this framework, the familiar continuum of spacetime geometry is not fundamental but emerges in an appropriate coarse-grained limit of the discrete structure. The causal order captures the light-cone structure of spacetime, while volume is encoded by counting elements—that is, the number of events corresponds to the spacetime volume in Planck units [
11,
20]. This approach is motivated by the insight that causality and discreteness together might form a minimal substrate from which geometry can emerge, without invoking background manifolds or coordinate systems. CST has developed tools to reconstruct manifold-like behavior from the order-theoretic data alone, including approximate dimension estimators [
22], methods to recover curvature [
23], and phenomenological models of cosmic expansion and entropy bounds [
13,
24]. Overall, CST exemplifies a fundamentally discrete approach in which spacetime is built from the bottom up—from individual events and their causal links—offering a radical departure from continuum-based field theories and aligning with the broader emergentist paradigm.
A related paradigm, motivated by the computational universe hypothesis, considers that physical law might arise from the evolution of symbolic systems governed by local rewriting rules. In this view, space, time, and causality are emergent constructs resulting from the iterative application of minimal substitution operations on discrete combinatorial structures. Recent work in hypergraph models and computational frameworks has proposed that such processes may underlie both quantum mechanics and gravity [
18,
21].
This is just a sampling of the approaches that exemplify a shift away from treating spacetime as a fundamental arena and toward viewing it as a manifestation of deeper, often discrete and relational, organizational principles (e.g., [
31,
34,
35,
36,
37,
38]). The convergence of insights from holography, positive geometry, causal order, and symbolic computation suggests that it may be possible to formulate a unified framework in which spacetime and its attendant structures arise from compatibility conditions among more basic informational elements.
2. Introduction
In this work, we propose a new framework within the paradigm of non-spatiotemporal foundations, grounded in the idea that physical structure originates from relational compatibility among primitive informational elements. We stress that the program presented herein does not seek to supplant existing paradigms. Our goal is to identify a unifying principle that may underlie their apparent successes.
Our central hypothesis is that space, time, and topology are not fundamental constructs, but rather stabilized expressions of a dynamic balance between the promotion of local informational diversity and the preservation of global coherence. We argue that this principle—formulated as a competition between relational variety and order—can give rise to rich structural and dynamical behavior without the assumption of a background spacetime.
At a foundational level, we propose that geometric and temporal structure emerge as the result of deeper patterns of intrinsic relations between discrete, label-bearing informational elements. As such, physical order—such as the appearance of spatial locality or causal flow—emerges from an interplay between diversity and coherence within a relational substrate. Under certain conditions, local regions of high compatibility organize into stable structures, which then act as seeds for further structural development. This process gives rise to an evolving network of relational configurations that encodes both the architecture and temporal unfolding of emergent space. Therefore, geometry and time are not imposed externally, but emerge through internal transitions within the relational system. As coherent structures accumulate, a directional pattern of ancestry develops, yielding a natural notion of temporal order. Spatial organization, meanwhile, appears through a reinterpretation of internal relational degrees of freedom, effectively projecting a geometric scaffold from patterns of informational agreement.
This framework can be seen as a synthesis of core insights from the approaches to quantum gravity described is Sec.
Section 1. More specifically, like holographic duality, it suggests that geometry is deeply connected to entanglement. It also incorporates the causal primacy emphasized in CST, yet derives causal order dynamically from relational ancestry rather than postulating it axiomatically. The emphasis on emergent locality and combinatorial structure was motivated by the developments in positive geometry, such as associahedra and cosmohedra. Finally, the use of discrete, rule-governed informational updates resonates with symbolic and computational models, while grounding the emergence of structure in optimization principles rather than rewriting rules. In this sense, our proposal aims to offer a unifying perspective that retains the strengths of each approach while advancing a new organizing principle: the emergence of space and time from the interplay between informational diversity and relational coherence.
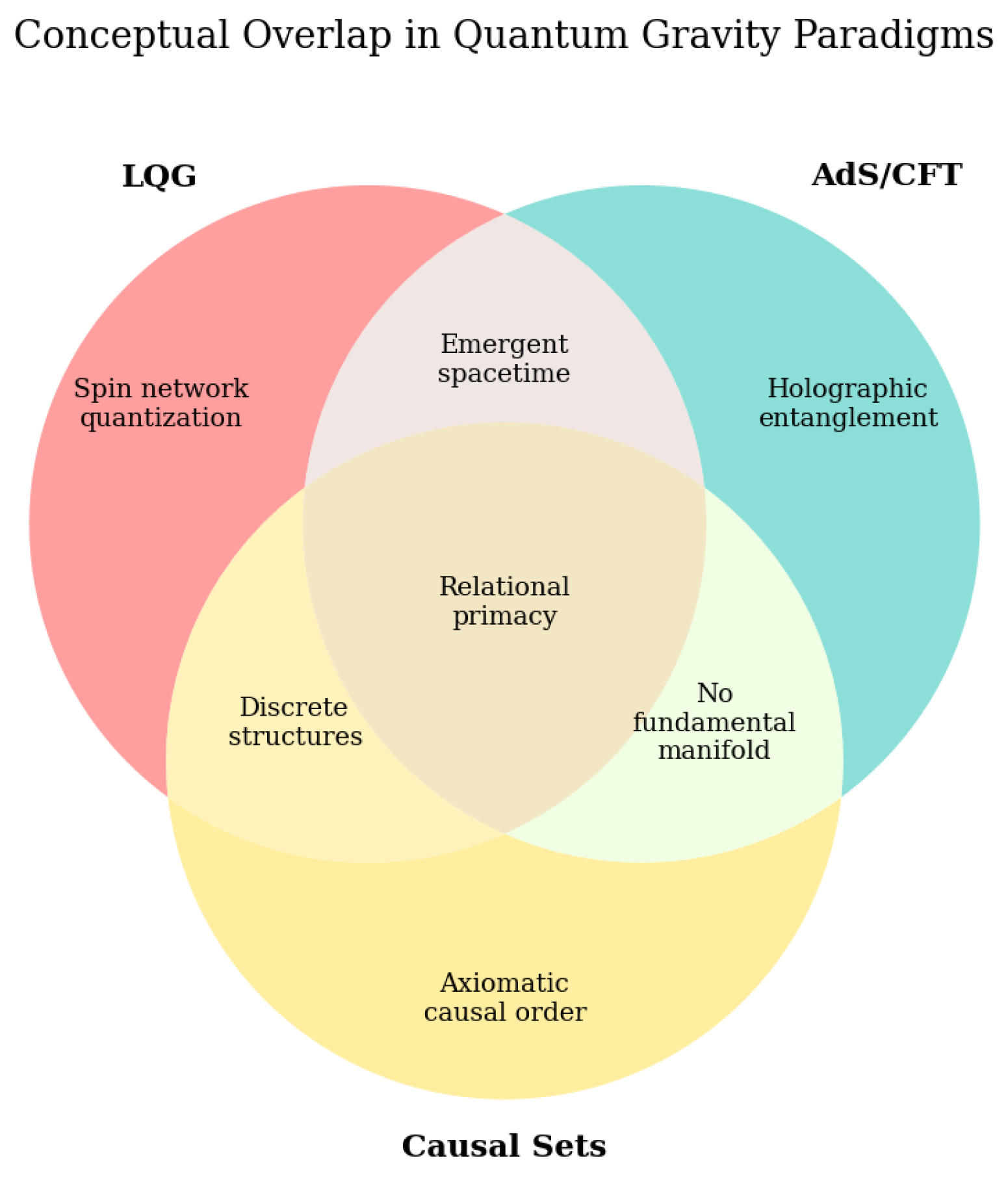
With respect to Fig.
Figure 1, we compare three of the major paradigms within the contemporary landscape of quantum gravity: the AdS/CFT correspondence, CST, and loop quantum gravity (LQG). Each of these frameworks offers a distinct approach to the emergence of spacetime. Despite their differences, these approaches exhibit key areas of conceptual overlap. Both AdS/CFT and LQG treat spacetime as an emergent phenomenon rather than a primitive manifold. Causal set theory and LQG both rest on discrete structures and reject the continuum as fundamental. AdS/CFT and causal sets, though coming from different angles, each deny the primacy of a smooth manifold—either replacing it with a lower-dimensional quantum theory or with a discrete causal order.
At the heart of all three is a commitment to relational primacy: none rely on absolute background structures, fixed coordinates, or pre-defined geometry. Instead, they seek to reconstruct spacetime from patterns of relation—whether in the form of entanglement (AdS/CFT), causal structure (causal sets), or spin network connectivity (LQG).
The relational framework proposed in this work builds on these shared commitments while introducing a fundamental synthesizing principle – Variety-Coherence Optimization (VCO). It draws from the informational and structural insights of these three (and other) paradigms, but grounds emergence in a distinct mechanism: the saturation of coherence among relational primitives. In this picture, geometric structure arises not from assumed symmetries or topological scaffolds, but from the collective phase dynamics that drive the formation of irreducible, saturated patches. These patches encode both adjacency and directed ancestry, providing the foundation for an emergent spacetime architecture. The Venn diagram highlights this synthesis by showing how our model integrates and extends foundational features of each of the three established approaches. This framework does not seek to replace existing quantum gravity approaches, but rather to identify common structural principles across disparate models.
The remainder of this paper is organized as follows. In Sec.
Section 3, we define our ontology as a space of relational primitives and develop the suppression kernel based on variety-coherence optimization. Sec.
Section 4 introduces the concept of coherence patches and details the criteria for saturation. In Sec.
Section 5, we formalize the structure of relational faces and describe the propagation rules that lead to a directed architecture in Sec.
Section 6.1. The geometric interpretation via a Foruier duality is developed in Sec.
Section 7.
Notation
: label domain k (Polish metric space) with metric and Borel measure .
: product label space with product measure .
: weights with ; relational divergence .
: max-entropy kernel (row-stochastic); : partition function; : inverse temperature.
: phase field; : mean resultant; : variance-like saturation.
P: coherence patch; : complex of saturated patches; : directed acyclic hypergraph of patch formation.
3. Relational Space and the Structure of Informational Compatibility
The foundational entity in this framework is not a particle, spacetime point, or embedded field, but an irreducible relational primitive (or coherence unit). What defines them—and allows structure to eventually emerge—is a set of intrinsic labels. We denote the space of all relational primitives by
, whose elements
constitute the non-reducible objects of the theory (see, e.g., [
28]). Each
is ontologically fundamental: it has no internal structure, spatial interpretation, or temporal evolution. It is simply a bare informational unit—a point in the space of relational possibility, each carrying an internal label space that defines how it may participate in coherent structures.
Table 1.
Conceptual analogs for relational primitives. While similar in function to known constructs, their role in this model is distinctly relational.
Table 1.
Conceptual analogs for relational primitives. While similar in function to known constructs, their role in this model is distinctly relational.
| Analog |
Similarity |
Difference |
| Qubits |
Internal phase , irreducibility, relational coherence |
No Hilbert space, no unitarity, no defined observable |
| Spin networks (LQG) |
Discrete, combinatorial, labeled |
Labels are relational and not embedded in spacetime |
| Causal set elements |
Fundamental events, assembled into a poset |
Causality is emergent from coherence, not postulated axiomatically |
| Wolfram tokens |
Symbolic, rule-based, adjacency-driven |
Dynamics arise from entropy–coherence balance, not substitution logic |
| Topos atoms |
Exist only via contextual structure |
No logical framework, but similar ontological minimalism |
To each relational primitive
, we associate an internal label
that encodes its intrinsic relational structure. The labels do not represent positions, coordinates, or dynamical variables in spacetime. Rather, they define the internal degrees of freedom by which relational primitives can be relationally compared, akin to the role of quantum reference frames in relational quantum mechanics [
28,
29].
We define the label function
which assigns to each relational primitive
a label
. To make the internal structure of the label space explicit, we write each label as a tuple:
where each component
takes values in a fixed domain
appropriate to the informational context. The label space
is therefore a product space,
with each
furnishing a distinct informational dimension for comparison across primitives. These domains may be discrete (e.g.,
), continuous (e.g.,
), or drawn from combinatorial and topological structures.
This decomposition plays a critical operational role: it enables component-wise evaluation of relational divergence, ensuring that informational differences are meaningfully and consistently assessed. The tuple thus defines the primitive’s relational profile—a structured specification of its intrinsic features relative to others in the system.
No specific structure is imposed on the form of , but typical components may include: discrete class identifiers (e.g., representation sectors, symbolic types), algebraic invariants (e.g., parity, charge, spin), and logical or topological indices (e.g., graph coloring, homotopy class). The formulation is intended to be general at this stage, enabling the model to support a broad range of physical and computational interpretations.
The divergence between two primitives
and
is defined as
where each
is a domain-appropriate measure of dissimilarity. For numeric or algebraic components,
may be the absolute difference
; for modular types, a cyclic distance; and for symbolic or categorical components, a binary mismatch. The total divergence is a scalar quantity that vanishes when all label components match and increases with informational disparity. It is symmetric and non-negative, but does not satisfy the triangle inequality—hence,
is not a metric, but a purely relational comparator.
The divergence function plays a central role as a coherence discriminator. Low divergence indicates high compatibility and the potential to participate in a common coherent patch; high divergence suggests incompatibility, which suppresses joint stabilization.
A central postulate of the framework is that coherence is not auxiliary—it defines existence. A relational primitive has no physical meaning in isolation. It becomes ontologically viable only when it participates in a mutually coherent configuration of other primitives. Structure emerges not from imposed geometry, but from the spontaneous coherence of internally compatible informational elements.
The Suppression Kernel from Variety-Coherence Optimization
When considering how evolution might occur in this relational space, we follow the simple observation that relational systems seek to have the maximize diversity of possible coherent interactions (entropy), while preserving local compatibility (suppression of incoherence).
We define a kernel
, which quantifies the potential for coherence between informational states
and
. Specifically, we define the relational variety by the Shannon entropy of the kernel weights:
where,
. We constrain the
local coherence by
where
is a fixed scalar threshold that regulates the expected relational divergence. The expectation constraint on divergence means that structure can only emerge when relational coherence is preserved. Without this restriction, maximizing entropy would favor fully delocalized distributions, thereby destroying any meaningful structural alignment. Fixing the expected divergence ensures that the system explores diversity within a relationally meaningful band, preventing incoherent scattering. This mimics the same structural role as a fixed energy budget in thermodynamic ensembles. Just as a thermal system maximizes entropy under a fixed energy constraint—preventing it from heating into incoherent noise—this framework maximizes relational entropy under a fixed divergence constraint, preserving internal coherence across the informational structure.
where
and
are Lagrange multipliers and
is the target expected divergence.
The suppression kernel
is well-defined if the partition function
converges for all relational configurations
. This convergence follows from two intrinsic properties of the relational divergence function
. First, for any fixed configuration
, the set of configurations whose divergence from
is less than a given threshold
, namely
is finite in the discrete case, or effectively finite in practice in the continuous case due to the rapid decay of the exponential suppression factor
. Thus, although the total label space
may be infinite or continuous, the number of significantly coherent configurations remains bounded in effect, ensuring that coherence remains concentrated rather than delocalized.
Convergence
For continuous or unbounded label spaces, convergence of
follows under a mild growth condition on the volume of divergence balls: there exist constants
such that
Then for all . Absent such a bound, we regard convergence as holding under appropriate regularity assumptions on the label-space measure.
In addition, the exponential decay
suppresses the contribution of highly divergent configurations so sharply that distant relational states contribute negligibly to the partition function. Together, these two features ensure that the sum (or integral) defining
converges for all
, without the need for any external cutoff or regularization. The coherence scale
thus functions as a natural, intrinsic cutoff arising from the relational structure itself. This affirms a core principle of the VCO framework: the universe tends to explore relational variety, but only to the extent that local compatibility is maintained.
4. Coherence Patches and the Onset of Structure
To understand how structure emerges from a fundamentally background-free relational space, we consider what it means for a group of informational configurations to exhibit internal consistency. To do this, we define a coherence patch as a subset of in which . This condition ensures that no member of the patch is entirely incompatible with another. The patch is an emergent object: a minimal expression of internal coherence provided by the suppression kernel within the otherwise unstructured relational space.
These coherence patches grow through the inclusion of additional primitives, but their internal alignment becomes increasingly difficult to sustain. The suppression kernel decays exponentially with relational divergence, and large patches tend to accumulate internal tension. To that end, we define a phase field as a mechanism that regulates and ultimately limits the growth of patches.
We clarify that the
phase field in our model is not a conventional dynamical field defined over spacetime, but rather a relational construct defined over coherence-compatible pairs of informational primitives. Specifically, it is a
-valued function
that encodes internal phase alignment within coherence patches. This relational phase structure is defined over a non-spatiotemporal domain, which we term a
relational phase space—a configuration space of pairwise informational agreement. More precisely, the phase field is a function of the form:
where
I denotes the set of irreducible relational primitives, and
assigns a phase value in the unit circle group
to each pair of primitives
. Upon reaching a critical coherence threshold (
), the accumulated phase structure is projected via Fourier duality into emergent spatial geometry. The use of
phase field and
phase space in this context is thus operational and structural, rather than geometric or canonical.
More specifically, for a given patch
P, we define the mean pairwise phase deviation as
where
is the number of distinct pairs in the patch.
We define the phase dispersion as
and say that a patch saturates when
for a fixed threshold
.
which captures the average phase spread across the patch. This quantity plays a central role in coherence dynamics: as more primitives are added, the patch becomes less tightly aligned in relational phase space, and increases. Small, highly compatible patches exhibit low phase deviation and can grow by incorporating additional elements with similar relational characteristics. However, this growth is self-limiting.
Once the internal phase spread reaches a critical value, the structure can no longer sustain coherence across all its members. As described above, a limit is reached beyond which the coherence of a patch cannot be preserved. This defines a saturation point: a transition where the patch can no longer grow without violating the mutual coherence that enabled its formation. The mechanism governing this transition is rooted in the patch’s internal phase structure. Once the dispersion exceeds a fixed threshold , destructive interference overwhelms constructive alignment and the patch stabilizes into an irreducible structure.
In this way, coherence patches mark the earliest emergence of form from pure informational compatibility. They are not externally imposed or statically defined, but rather assemble dynamically through local accumulation of mutual coherence. Their growth is regulated by the coherence field and the relational divergence, and they terminate naturally when internal agreement can no longer be maintained. Saturation thus signals not failure, but completion: the coherent configuration has reached the limit of its internal consistency.
5. Saturation and the Stabilization of Structure
As described in Sec.
Section 4, coherence within a patch is quantified by the resultant
and its dispersion
. As additional primitives are incorporated, alignment decreases and dispersion grows. When
exceeds a fixed threshold
, the patch can no longer sustain global coherence and saturates into an irreducible unit.
This criticality is not imposed externally but follows from the compact nature of the phase space: once dispersion becomes too large, destructive interference overwhelms constructive alignment. Saturation therefore marks the boundary between viable relational growth and collapse. Coherence does not fade gradually—it halts abruptly when the dispersion threshold is crossed. The resulting saturated unit cannot admit further elements without breaking internal consistency.
6. The Relational Polytope
In recent developments across high-energy theory, positive geometries have emerged as powerful tools for encoding physical constraints in a purely combinatorial and geometric language [
6,
7,
8,
9]. These structures reveal that many aspects of quantum field theory and cosmology can be captured through the intrinsic geometry of admissible configurations. In a similar spirit, we introduce a
relational polytope,
, to describe the coherent organization of relational primitives—not in an ambient space, but as a combinatorial object encoding adjacency, ancestry, and saturation relationships among irreducible patches. Unlike conventional polytopes embedded in
, the relational polytope arises from internal informational constraints, and its faces represent saturated coherence patches rather than spatial simplices. This approach provides a geometric scaffold for coherence propagation, entanglement lineage, and emergent causal structure within a background-free framework.
The result is a combinatorial structure whose `faces’ are coherent patches and whose adjacency structure is induced by shared ancestry and saturation rules. Each relational face, or R-face, represents a coherence-saturated region, and R-faces are adjacent if they share informational ancestry or mutually coherent boundaries. Because saturated patches emerge through local, adjacency-preserving updates, and no patch may overlap or subsume another, the collection of all patches defines a tiling of relational space.
As coherence propagates, new patches are seeded by existing faces, producing a directed network of R-faces. This network forms the backbone of the polytope’s growth, and encodes both causal order and relational structure. In later sections, this polytope will serve as the domain from which geometry, tiling, and entanglement arise.
We represent a finite subset of such labeled states as a set of vertices , where each corresponds to a relational primitive , and carries its label . This shift does not endow the elements with any new geometric status. The representation as vertices is introduced solely to support the construction of coherent subsets whose internal structure can be analyzed. That is, a patch is coherent if for all , we have .
The stabilized subset is what we identify as an R-face. It is not merely a coherent patch—it is a structure that has crystallized, reaching the irreducible limit of relational compatibility. Beyond this point, it can neither grow nor dissolve without violating the coherence dynamics that brought it into existence. Its informational agreement is complete, and its structure is defined.
To characterize an R-face more precisely, we now formalize the criteria that distinguish such a structure. Let be a finite subset of labeled vertices. Then F qualifies as a relational face if it satisfies the following conditions, taken together and not in isolation.
First, all members of F must exhibit nonzero mutual coherence. The suppression kernel must be finite and strictly positive for every pair of distinct elements in F. This ensures that no configuration in the face is incoherent with any other. Second, the face must exhibit a consistent internal relational structure, characterized by a well-defined representative phase, a dominant or invariant symmetry class, and a coherent set of conserved quantities. These attributes must be unambiguous and consistent across the patch, ensuring compatibility with the mutual coherence condition. Third, the face must be non-degenerate. Its internal structure must not be contradictory, and must not admit multiple or ill-defined phase representatives, parity labels, or invariant components. Finally, the face must be irreducible: no proper subset of F may satisfy the same structural criteria. The coherence and internal consistency of the face cannot be attributed to any smaller grouping of its members.
An R-face, then, is a minimal, saturated unit of structure. It is the endpoint of relational accumulation, and the seed of higher-order combinatorial form. In the sections that follow, we will show how these saturated faces interconnect and propagate coherence forward into the relational space. Their interrelation defines a new layer of emergent structure: a directed architecture of stable coherence that encodes not only compatibility, but the irreversible passage of time.
6.1. Coherence Propagation and the Emergence of the Directed Architecture
In the fully emergent formulation of the framework, no combinatorial structure is assumed in advance. Each R-face arises through local coherence accumulation among relationally labeled configurations. The propagation of coherence from one face to another is likewise governed by internal relations alone. There is no global topology, no coordinate system, and no external time parameter. Structure grows from coherence, one saturated patch at a time.
After a patch
P has crystallized into an R-face
, each vertex
defines a local neighborhood in relational space, consisting of configurations that remain compatible under the suppression kernel. We define the forward coherence neighborhood of
v as
This neighborhood represents the set of relationally accessible configurations that may participate in new coherence patches seeded from v. It is determined entirely by the suppression kernel T, which is a function of the intrinsic labels alone.
New coherence patches are then dynamically assembled via the suppression kernel `testing’ subsets of , along with the seeding vertex v, for mutual compatibility and eventual saturation. If the accumulated relational phase among such a subset reaches the critical value , and if the patch satisfies irreducibility, a new R-face is formed. This crystallization event is a direct descendant of the seed face , and we denote this relation as a directed link .
This process iterates locally. From every vertex in a saturated R-face, new neighborhoods are scanned and new patches may form. Each successful saturation event extends the structure outward, preserving local coherence but introducing global order. The resulting architecture is a
directed acyclic hypergraph (DAH), built from relational ancestry rather than imposed connections. Each node corresponds to a saturated R-face and each directed edge reflects a coherence propagation path through relational space. This ordering was strongly motivated by results in causal set theory (CST), as introduced by Bombelli, Lee, Meyer, and Sorkin [
10], which modeled spacetime as a discrete partially ordered set where causal structure is fundamental. In our framework, this similar causal architecture emerges from the propagation of coherence through saturated patches. This process yields the DAH structure akin to a causal set, but grounded in informational compatibility. As such, it invites reinterpretation of results from CST and causal entropy bounds [
13,
20] in terms of relational saturation and coherence dynamics.
The DAH encodes both the structure and the history of emergence. It is directed, because saturation is irreversible: once coherence collapses, the structure is fixed. It is acyclic, because no face can form from another without breaking the coherence hierarchy established by prior saturation events. And it is hypergraphic, because each R-face may seed multiple subsequent faces, and each new face may draw coherence from more than one ancestor. Crucially, a coherence history is fixed per R-face, but the primitive might still participate in new, orthogonal coherence contexts.
This relational growth mechanism defines a unique kind of locality, where each R-face arises only through coherence inherited from an existing face. No face can crystallize spontaneously or at random and coherence must be transmitted through compatible kernel values from previously saturated configurations. This guarantees that all growth proceeds from existing structure, and that the relational space expands in a coherence-preserving, causally ordered sequence.
In this way, the DAH provides not only the structural skeleton of the emergent system, but also a holds the `memory’ of its temporal unfolding. Causal direction, irreversibility, and relational locality all emerge naturally from the propagation rules encoded in the suppression kernel and the saturation condition. The model constructs its own dynamical history—without invoking a background time, metric, or spacetime manifold.
7. Geometry from Phase: Spectral Projection and Spatial Tiling
At this stage, no geometric content has yet been invoked and the structure remains entirely relational. However, a critical transition occurs once an R-face saturates. Prior to saturation, the coherence field governs the internal alignment of the patch, acting as a dynamical register of relational compatibility. These phase values accumulate over paths of coherence propagation, and their spread determines the stability of the structure.
When the average pairwise phase deviation reaches the critical value
we define
and declare saturation when
for a fixed
. At this point, coherence collapses. As established in
Section 5, this is not merely a numerical threshold but an analytic boundary encoded in Euler’s identity,
. Beyond this point, destructive interference dominates, and no further elements can be added without destabilizing the configuration. At this juncture, a saturated R-face has reached a condition of internal irreducibility: its growth halts, and its coherence becomes structurally fixed.
To continue representation beyond this coherence collapse, the model undergoes a transformation—a
Fourier projection. The internal relational structure of a saturated patch is captured by a phase coherence distribution
which encodes the aggregate interference structure over the patch. This distribution is compactly supported on
and reflects the full phase content of the R-face.
We define the emergent spatial wavefunction via Fourier transform:
where
is interpreted as an emergent spatial coordinate. This map reinterprets phase interference as spatial localization: what had previously been oscillatory coherence in relational phase space becomes separation in emergent space. The transformation is not imposed, but necessitated by the collapse of coherence. Saturation demands a new representation. Geometry arises as the dual image of coherence. In this way, space is necessary to accommodate increasing variety.
This duality also imposes a relational uncertainty principle. Since the phase coherence distribution
is compactly supported on
, its Fourier transform
must obey the standard uncertainty relation:
where
characterizes the width of coherence in phase space and
its spatial localization. At the saturation boundary
, phase uncertainty reaches its maximal allowable spread, and
becomes correspondingly localized. This lower bound defines the smallest resolvable spatial tile, linking the Planck scale to the collapse of coherence.
This projection acts on a coherence field prior to geometry. It preserves background independence and inherits its structure entirely from internal phase dynamics. Saturated R-faces thus tile emergent space not by physical embedding, but by spectral distinction. Adjacency in this space corresponds to overlap in phase ancestry: if two R-faces share a coherence lineage, their spatial wavefunctions exhibit correlated localization.
This structure defines a relational tiling: each R-face corresponds to a discrete spatial tile, and their connectivity reflects coherence ancestry through the directed acyclic hypergraph. Even when multiple faces crystallize from a shared boundary, their spatial identities are inherited from phase structure and remain entangled through spectral adjacency. Geometry arises from coherence propagation rather than distance.
The emergent space defined by this process is discrete, spectral, and causally scaffolded. The Fourier transform acts as the boundary map between pre-geometric coherence and post-saturation structure. The DAH becomes a geometric scaffold: a tiling of saturated, relationally locked structures, joined by their shared causal and informational past. In this framework, what appears as spatial adjacency is the spectral shadow of relational coherence.
7.1. Justification of the Fourier Projection
The analytic transition from relational phase to emergent spatial structure is governed by spectral projection. When a coherence patch saturates at
, its internal dynamics cease to evolve. The accumulated interference has reached a fixed point, and no further growth is possible within the phase representation. At this stage, the Fourier transform emerges as the unique and necessary continuation
1. This necessity is grounded in three key features of the model:
(i) Collapse at Criticality: At , the coherence field becomes maximally disordered. The phase contributions across the patch destructively interfere, and the suppression kernel degenerates. This collapse is not numerical but structural: the relational representation no longer supports further differentiation. The Fourier transform resolves this by re-representing the saturated configuration as a localized amplitude distribution in a conjugate domain. The interference kernel is mapped to , which defines a projective geometry free of phase singularities.
(ii) Spectral Irreducibility: Saturated patches cannot be refined by further phase analysis. The only remaining operation is spectral decomposition. The Fourier transform is the unique linear map that (a) preserves total informational content, (b) projects from a compact domain to an extended one, and (c) diagonalizes translation-invariant convolution operators such as the suppression kernel. No other continuation satisfies these constraints while preserving background independence and informational closure.
(iii) Structural Continuity: The coherence kernel prior to saturation is governed by phase-based suppression:
. After saturation, the spatial coherence kernel becomes its spectral dual.
Translation-invariant kernels
on
are diagonal in the Fourier series basis with eigenvalues given by Eq. (
20). This expression is not imposed; it is inherited. The coherence decay scale
remains unchanged, reflecting the critical bandwidth of the saturated phase distribution. The Fourier transform transmits this structure into geometry without introducing new parameters.
Proposition (Uniqueness of Fourier-like Emergence)
Let be a real-valued coherence distribution defined on the compact phase space , with structure defined by modular interference. Any linear, invertible, and information-preserving map into a non-compact space that diagonalizes translation-invariant relational kernels must be (up to unitary equivalence) the Fourier transform.
Proof sketch
Let
, with inner product:
We assume a linear map
that satisfies:
Unitarity: ,
Translation compatibility: convolution with a phase-invariant kernel maps to multiplication in the dual space: ,
Minimal spectral support: compact phase corresponds to unbounded localization (dual decay).
These are exactly the defining properties of the Fourier transform as the unitary operator that diagonalizes circulant kernels on . By the spectral theorem, no other linear transform on preserves these properties and maps into an extended domain while retaining inner product structure.
Therefore, the Fourier transform is the unique (modulo basis choice) structure-preserving continuation of compact phase dynamics into non-compact geometric localization. □
Thus, the Fourier projection is not an optional maneuver. It is the canonical map that preserves internal relational symmetry, resolves phase degeneracy, and reveals the latent spatial structure encoded in coherence. It does not assume geometry—it derives it. This transition from interference to localization defines the boundary between relational dynamics and spatial representation, and marks the moment when informational agreement becomes geometric form
2.
7.2. Geometric Signature from Phase
The projection of saturated relational coherence into geometry produces two distinct structural layers: spatial tiling and causal order. This projection is a Fourier dualization of coherence information—transforming internal interference into external localization. Once a coherence patch saturates, the accumulated phase structure becomes analytically closed and must be re-expressed in its conjugate representation. The Fourier transform performs this task, translating relational alignment into spatial localization and coherence ancestry into temporal structure.
Euclidean Spatial Tiling
The internal phase distribution
of a saturated R-face defines its coherence structure. Its Fourier dual
localizes this structure in an emergent spatial coordinate
, giving rise to a discrete Euclidean geometry. Since phase spread is bounded by
, the associated spatial support is finite. The suppression kernel becomes a real exponential (Eqn.
20, inducing spatial adjacency and forming a tiling in the dual space. This tiling is not metric-imposed but coherence-derived: spatial separation encodes the degree of spectral orthogonality between saturated patches.
Lorentzian Causal Order
The directed acyclic hypergraph (DAH) defines a relational ancestry structure between R-faces. Let
denote the set of all saturated R-faces. Define a binary relation ≺ such that
if
was seeded by one or more coherence-preserving vertices from
. This relation is asymmetric, transitive, and irreflexive, forming a partial order. The DAH therefore defines a causal structure not through spacetime metrics, but through coherence propagation. Temporal separation is defined by path length in the DAH:
where a finite constant
plays the role of a maximal coherence propagation speed.
Resolution: Layered Emergence
There is no conflict between spatial tiling and temporal order. The coherence projection yields a layered structure:
where
is the relational polytope of coherence-saturated R-faces, and the right-hand side expresses its two emergent facets:
: a spatial domain formed by the Fourier duals of saturated phase distributions,
: a causal order over saturated patches, defined by coherence ancestry in the DAH.
This projection reveals that what appears as spatial adjacency is in fact spectral proximity, and what appears as temporal succession is the record of stabilization. The poset encodes an irreversible informational topology: each R-face is fixed by a past coherence event, and coherence can only propagate outward. Time, in this model, is not a dimension—it is the structure of relational ancestry.
Table 2.
Emergent spacetime layers
Table 2.
Emergent spacetime layers
| Component |
Origin |
Signature |
| Spatial coordinates |
Fourier projection of phase |
Euclidean |
| Temporal order |
DAH edge direction
|
Lorentzian |
| Lightcone structure |
a finite constant constraint |
Causal |
Three consequences follow. First, the projection from relational phase into geometry is not an imposed analytic continuation but a spectral emergence map. Second, causal structure arises independently through coherence ancestry and path dependence in the DAH, avoiding any tension with Euclidean tiling. Third, the coherence threshold
acts as an entropic bound, matching holographic scaling relations [
2] without invoking Lorentzian metric structure.
In this way, the apparent dichotomy between space and time is dissolved. Both emerge from coherence, but in different modalities: space through spectral decomposition, time through irreversible ancestry. The DAH becomes a scaffold for both: tiling space through coherence duals, and ordering time through stabilization memory. Spacetime, in this model, is not a manifold—it is the layered record of relational saturation.
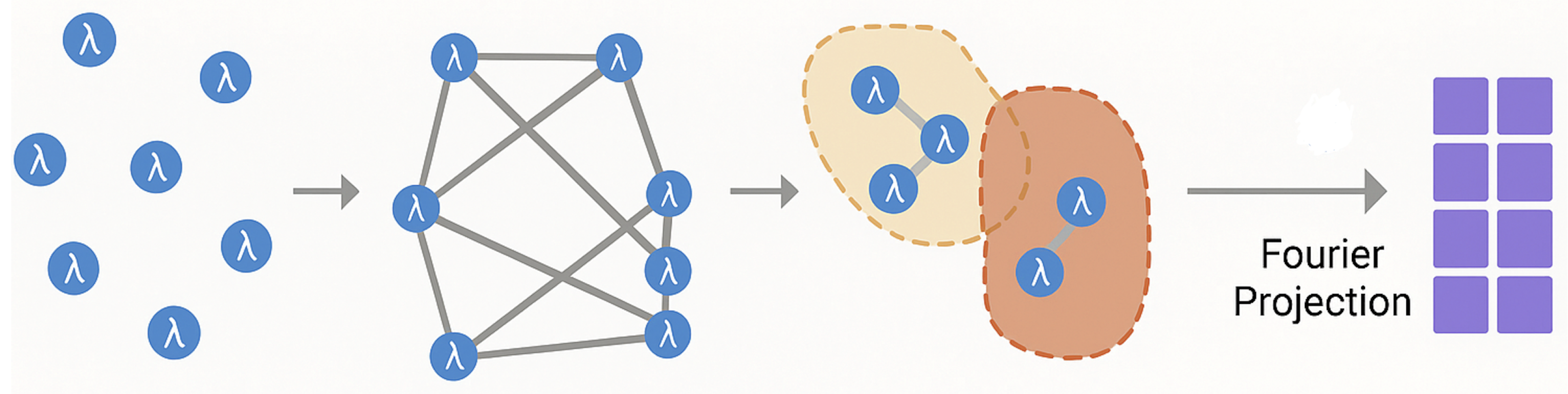
Figure 2 schematically illustrates the sequential emergence of spacetime from background-independent informational primitives: initially unstructured relational elements become linked by mutual compatibility, forming a coherence kernel that organizes into saturated coherence patches. When internal phase deviations reach the critical threshold
, these patches crystallize into irreducible units (R-faces). The projection of their internal relational phase structure via Fourier transform then yields emergent spatial localization and geometry, with spectral proximity encoding adjacency and relational ancestry defining causal order.
8. Shared Features with Quantum Gravity Paradigms
The framework presented in this paper offers a novel approach to quantum gravity, grounded in informational coherence and relational saturation. This perspective resonates with broader efforts to reconstruct spacetime from non-geometric principles. A closely related formal precedent is the AdS/CFT correspondence [
1,
19], wherein gravitational geometry in anti-de Sitter space emerges from a lower-dimensional conformal field theory. In that context, bulk geometry is encoded in patterns of entanglement across the boundary, with the Ryu–Takayanagi formula relating entanglement entropy to minimal surfaces in the bulk [
2,
12]. The present framework draws from this spirit, though it proceeds without invoking conformal symmetry or a prescribed holographic duality. Here, the effective boundary arises from the causal ancestry structure within the relational polytope, and overlapping paths in the adjacency graph fulfill the role of minimal surfaces. Entanglement arises from shared relational origin rather than computation within a dual field theory.
This conceptual alignment extends further. The exponential decay of the suppression kernel,
, ensures that coherent correlations remain intrinsically localized. This behavior reflects the holographic principle’s assertion that physical information is encoded on boundaries. The saturation threshold at
further enforces localization by truncating long-range phase coherence. This parallels how tensor networks realize area-law entanglement scaling through limited entanglement propagation [
4,
16]. In addition, the irreversible crystallization of R-faces functions analogously to a decoding process: unstable phase fluctuations, conceptualized as errors, transform into stable spatial tiles representing logical states. The directed acyclic hypergraph (DAH) records a fault-tolerant history, with each saturation event projecting noisy relational data into geometrically robust structures. These connections suggest that the model intrinsically incorporates non-local redundancy and entropy scaling, features central to both AdS/CFT and quantum computing-inspired approaches to quantum gravity.
Causal set theory (CST) provides another relevant precedent. In the foundational work of Bombelli, Lee, Meyer, and Sorkin [
10], spacetime is modeled as a discrete partially ordered set, with causal structure captured by the order relation. In the present framework, causal order arises dynamically through the directed architecture of saturated coherence patches, which naturally form a causal set generated through coherence propagation. This opens avenues for reinterpreting results from causal set cosmology and entropy bounds [
13,
20] in terms of relational saturation and coherence dynamics, potentially yielding new insights into constraints on causal patch growth.
Loop quantum gravity (LQG) and spin foam models similarly regard spacetime as a combinatorial structure built from quantum excitations [
14,
15]. The emphasis on discrete area elements and fundamental quanta of geometry resonates with the interpretation of saturated R-faces in this framework. Here, discreteness arises from relational phase coherence and informational thresholds, providing an emergent origin for quantization rather than one rooted in Hilbert space structures or operator dynamics.
Recent models developed by Wolfram and collaborators [
18,
21] propose that space and time emerge from the evolution of hypergraphs governed by local rewriting rules. These approaches share a focus on causal structure and discrete evolution with the present model. However, here the dynamics are governed by internal compatibility and coherence propagation. The DAH arises through relational criticality, without reliance on externally imposed update procedures.
Finally, the study of combinatorial and geometric structures in scattering amplitudes, particularly through the amplituhedron and positive geometries [
6,
7,
9], has demonstrated the power of emergent structures in encoding physical laws. Though developed in a distinct context, this work exemplifies a broader principle echoed here: the emergence of geometric form from deeper combinatorial and relational structure. In this light, the relational polytope introduced in this framework may offer an analogous object, a geometry projected from relational coherence rather than embedded within spacetime.
9. Conclusions
This work presents a relational, information-theoretic framework in which spacetime emerges from the interplay of informational diversity and coherence. The central organizing principle, Variety–Coherence Optimization, balances local variation with global compatibility and serves as a structural foundation that cuts across multiple approaches to quantum gravity.
We have shown how coherent relational configurations stabilize into irreducible units, termed R-faces, once a critical phase threshold is reached. These structures propagate coherence through a directed acyclic hypergraph (DAH), generating an emergent causal order grounded in relational ancestry. A Fourier duality then maps the saturated phase structure into discrete spatial geometry, producing a tiling that encodes adjacency through coherence lineage.
This paper should be understood as a conceptual and operational proof of concept for emergent spacetime, rather than a fully realized physical model. Extending this framework to incorporate matter, recover known gravitational dynamics, and connect more directly to observational phenomena remains an open and promising direction for future work.
References
- Maldacena, J.M. The large-N limit of superconformal field theories and supergravity. [Adv. Theor. Math. Phys. 2, 231 (1998)]. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef]
- S. Ryu and T. Takayanagi. Holographic derivation of entanglement entropy from AdS/CFT. Phys. Rev. Lett. 2006, 96, 181602. [Google Scholar] [CrossRef]
- M. Van Raamsdonk. Building up spacetime with quantum entanglement. Gen. Rel. Grav. 2010, 42, 2323–2329. [Google Scholar] [CrossRef]
- B. Swingle. Entanglement renormalization and holography. Phys. Rev. D 2012, 86, 065007. [Google Scholar] [CrossRef]
- A. Almheiri, X. Dong and D. Harlow. Bulk locality and quantum error correction in AdS/CFT. JHEP 2015, 04, 163. [Google Scholar]
- N. Arkani-Hamed and J. Trnka. The amplituhedron. JHEP 2014, 10, 30. [Google Scholar]
- N. Arkani-Hamed, Y. Bai and T. Lam. Positive geometries and canonical forms. JHEP 2018, 11, 039. [Google Scholar]
- Y. Bai, S. He and G. Yan. Scattering amplitudes as canonical forms on positive geometries. Phys. Rep. 2022, 969, 1–59. [Google Scholar]
- N. Arkani-Hamed, T. Lam and J. Trnka. The Cosmological Bootstrap: Inflationary Correlators from Geometry. JHEP 2023, 06, 107. [Google Scholar]
- L. Bombelli, J. Lee, D. Meyer and R. D. Sorkin. Space-time as a causal set. Phys. Rev. Lett. 1987, 59, 521–524. [Google Scholar] [CrossRef]
- R. D. Sorkin, “Causal sets: Discrete gravity,” in Lectures on Quantum Gravity, edited by A. Gomberoff and D. Marolf (Springer, Boston, 2005).
- V. E. Hubeny, M. Rangamani and T. Takayanagi. A covariant holographic entanglement entropy proposal. JHEP 2007, arXiv:0705.0016 [hep-th]]07. [Google Scholar]
- F. Dowker. Introduction to causal sets and their phenomenology. Gen. Rel. Grav. 2013, arXiv:1211.5085 [gr-qc]45, 1651–1667. [Google Scholar] [CrossRef]
- C. Rovelli, Quantum Gravity (Cambridge University Press, 2004).
- A., Perez. The spin foam approach to quantum gravity. Living Rev. Relativ. 2013, 16, 3. [Google Scholar] [CrossRef] [PubMed]
- F. Pastawski, B. Yoshida, D. Harlow and J. Preskill. Holographic quantum error-correcting codes: Toy models for the bulk/boundary correspondence. JHEP 2015, arXiv:1503.06237 [hep-th]06, 149. [Google Scholar]
- P. Hayden, S. Nezami, X.-L. Qi, N. Thomas, M. Walter and Z. Yang. Holographic duality from random tensor networks. JHEP 2016, arXiv:1601.01694 [hep-th]]11, 009. [Google Scholar]
- J. Gorard. Some relativistic and gravitational properties of the Wolfram model. Complex Systems 2020, arXiv:2004.14810 [gr-qc]]29, 599–654. [Google Scholar] [CrossRef]
- E. Witten. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, arXiv:hep-th/98021502, 253–291. [Google Scholar] [CrossRef]
- R. D. Sorkin, “Causal sets: Discrete gravity,” in Lectures on Quantum Gravity, edited by A. Gomberoff and D. Marolf (Springer, Boston, 2005), arXiv:gr-qc/0309009.
- S. Wolfram, “A Class of Models with the Potential to Represent Fundamental Physics,” Wolfram Physics Project Technical Introduction (2020),https://www.wolframphysics.org/technical-documentation/.
- D. A. Meyer, The Dimension of Causal Sets, Ph.D. thesis, Massachusetts Institute of Technology (1988).
- D. M. T. Benincasa and F. Dowker. The Scalar Curvature of a Causal Set. Phys. Rev. Lett. 2010, 104, 181301. [Google Scholar] [CrossRef]
- D. Rideout and R. D. Sorkin. Classical sequential growth dynamics for causal sets. Phys. Rev. 1999, D 61, 024002. [Google Scholar]
- S. Johnston, Quantum Fields on Causal Sets, Ph.D. thesis, Imperial College London (2008).
- T. Jacobson. Thermodynamics of spacetime: The Einstein equation of state. Phys. Rev. Lett. 1995, 75, 1260. [Google Scholar] [CrossRef]
- J. Maldacena and L. Susskind. Cool horizons for entangled black holes. Fortschr. Phys. 2013, 61, 781–811. [Google Scholar] [CrossRef]
- C. Rovelli. Relational quantum mechanics. Int. J. Theor. Phys. 1996, 35, 1637–1678. [Google Scholar] [CrossRef]
- F. Giacomini, E. Castro-Ruiz, and Č. Brukner. Quantum mechanics and the covariance of physical laws in quantum reference frames. Nat. Commun. 2019, 10, 494. [Google Scholar] [CrossRef]
- J. B. Hartle and S. W. Hawking. Wave function of the universe. Phys. Rev. D 1983, 28, 2960–2975. [Google Scholar] [CrossRef]
- J. Ambjørn, J. Jurkiewicz, and R. Loll. Nonperturbative quantum gravity. Phys. Rep. 2012, 519, 127–210. [Google Scholar] [CrossRef]
- S. Hossenfelder. Minimal length scale scenarios for quantum gravity. Living Rev. Rel. 2013, 16, 2. [Google Scholar] [CrossRef] [PubMed]
- T. Padmanabhan. Thermodynamical aspects of gravity: New insights. Rep. Prog. Phys. 2010, 73, 046901. [Google Scholar] [CrossRef]
- E. Verlinde. On the origin of gravity and the laws of Newton. JHEP 2011, 04, 029. [Google Scholar]
- M. B. Green, J. H. Schwarz, and E. Witten, Superstring Theory, Cambridge University Press, 1987.
- M. Reuter. Nonperturbative Evolution Equation for Quantum Gravity. Phys. Rev. D 1998, arXiv:hep-th/960503057, 971. [Google Scholar] [CrossRef]
- D. Oriti. The microscopic dynamics of quantum space as a group field theory. In Foundations of Space and Time; Cambridge University Press, 2012. [Google Scholar]
- A. Connes. Gravity Coupled with Matter and the Foundations of Noncommutative Geometry. Commun. Math. Phys. 1996, arXiv:hep-th/9603053182, 155. [Google Scholar] [CrossRef]
- Planck Collaboration, Planck 2018 results. VI. Cosmological parameters, Astron. Astrophys. 641, A6 (2020).
- J. Maldacena. Non-Gaussian features of primordial fluctuations in single field inflationary models. JHEP 2003, 05, 013. [Google Scholar]
- A. G. Riess et al. A Comprehensive Measurement of the Local Value of the Hubble Constant. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar]
- DES Collaboration. Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2022, 105, 023520. [Google Scholar] [CrossRef]
- J. Fullwood and V. Vedral. Geometry from Quantum Temporal Correlations. Phys. Rev. A 2025, arXiv:2502.13293 [quant-ph]111, 052438. [Google Scholar] [CrossRef]
| 1 |
We emphasize that the Fourier projection is not claimed to be the only possible route to emergent spatial structure in this framework. It is, however, the natural linear continuation of the phase coherence field given the U(1) structure and the translation-invariant suppression kernel. Other embedding schemes, such as those based on correlation functions (see [ 43]) or nonlinear mappings of relational ancestry, could also be explored. |
| 2 |
We note that while the present treatment focuses on the U(1) phase structure, a natural extension involves considering higher symmetry groups such as SU(2), particularly if relational primitives possess spin-like or multi-component degrees of freedom. We defer exploration of SU(2)-based Fourier duality and its implications for emergent geometry to future work. |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).