1. Introduction
Skewed and heavy-tailed data are prevalent in various applied domains, including econometrics, environmental science, and risk analysis. Income distributions, housing prices, and insurance claims often display asymmetry and excess kurtosis; the tail behavior encodes meaningful extremes, such as financial losses or contaminant spikes, that should not be dismissed as outliers; see, for example, [
1,
2,
3] and Ahmad et al. [
4].
A natural starting point for modeling asymmetry is the skew-normal distribution introduced by Azzalini [
5] (see also [
6]). By augmenting the normal distribution with a skewness parameter, the skew-normal preserves analytical tractability while allowing controlled departures from symmetry. However, because the skew-normal remains light-tailed, it is ill-suited to settings where leptokurtosis is intrinsic to the data-generating process.
To address heavy tails alongside asymmetry, the Skew-
t family extends the
t distribution by introducing a skewness parameter. An influential approach views Skew-
t laws as scale mixtures of skew-normal variables [
5,
7], a perspective adopted and elaborated by several authors, including Hasan et al. [
8]. Related extensions, such as extended skew
t (EST) and alternative parameterizations, further enhance the modeling flexibility (see, for example, [
9]). Empirically, Skew-
t models have seen broad application, from financial time series and risk assessment to environmental monitoring and robust analysis under truncation or censoring [
10,
11]. Noncentral variants expand the toolkit and have been studied in detail, with their properties and use cases documented in Hasan et al. [
8], Hasan [
12].
Despite this progress, the assessment of the Skew-t model remains essential. In practice, misspecification of tail weight or asymmetry can distort inference on extremes, dependence, and risk. This motivates rigorous goodness-of-fit (GoF) procedures tailored to Skew-t families—methods that can diagnostically test statistical adequacy against alternatives that differ in tail behavior, asymmetry, or both.
In this paper, we develop an energy-based goodness of fit test for Azzalini’s standard Skew-
distribution proposed in [
6] and defined as a random variable with probability density function (pdf) that takes the following form:
where
g and
G are the regular probability density function (PDF) and the cumulative distribution function (CDF) of the Student’s
t distribution. Parameters
and
are referred to as skewness and degrees of freedom, respectively. We will denote this density by
. The special case for
reduces to the standard Student’s
t distribution with
degrees of freedom. The corresponding CDF of the skew
t distribution is given by:
which does not have a closed form. Its first moment is given as
where
,
. It should be noted that the PDF given in equation (
Section 1) is referred to as the standard Azzalini’s Skew-
t distribution. In the literature, a scale-location extension has been proposed. The reader is referred to [
6,
13] for more details.
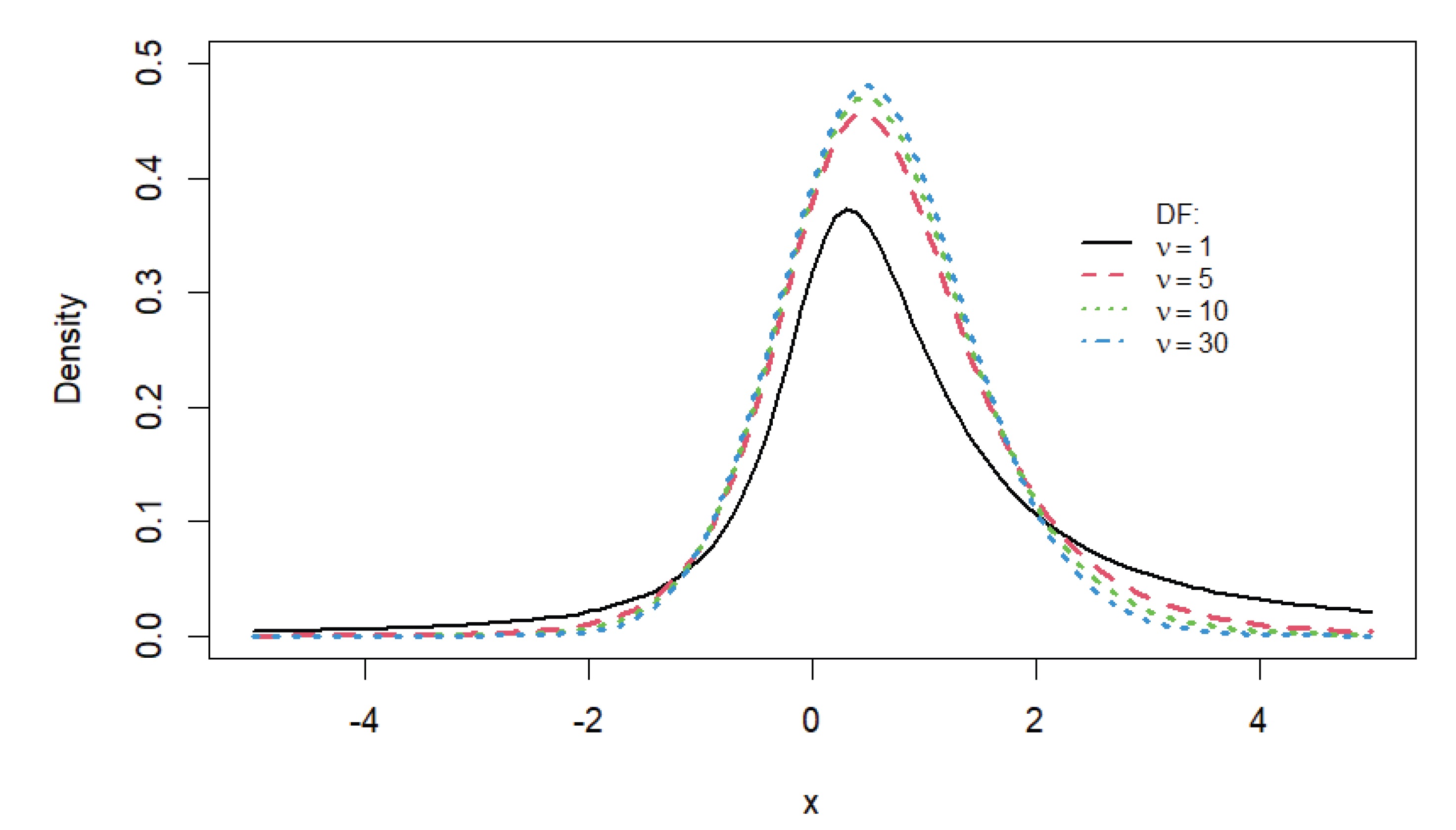
Figure 1 provides density estimates of the Skew-
t distribution for varying degrees of freedom (
) when the skewness parameter
is held constant.
There is limited research on the goodness-of-fit test for Azzalini’s Skew-
t distributions except those based on empirical distribution functions (EDFs) such as Kolmogorov-Sminorv, Cramer-von-Mises, etc., discussed and modified in [
14,
15]. Recently, [
16] proposed a goodness-of-fit test for Azzalini’s Skew-
t distribution based on the correlation coefficient (
r). Most studies related to Skew-
t distributions focus on properties, extensions, generalizations, change point analysis, and applications; see for example, [
12,
17,
18], and [
19], among many others. We therefore develop the goodness-of-fit test for the Skew-
t distribution using these well-established properties to achieve desirable powers for any given sample size and the chosen parameters
and
.
In this article, we propose a new one-sample (univariate) energy goodness-of-fit test based on energy statistics proposed by [
20] and [
21]. In the most recent work, Opperman and Ning [
22,
23], and [
24] proposed goodness-of-fit tests based energy statistics for the Skew-normal, Inverse Gaussian, and Lindley distributions, respectively. For a given sequence of independent random variables of size
n and with a cdf
G, the test statistic based on energy statistics will reject the null hypothesis that
for large values of the test statistic. If the null distribution,
F, and the given data come from the same underlying distribution
G, then the values of the test statistic are expected to be smaller. Furthermore, there have been numerous studies involving energy statistics such as testing for multivariate normality ([
25,
26]), testing for equality of distributions ([
27,
28]), one-sample goodness-of-fit tests ([
22,
24,
29,
30]), change point analysis ([
31,
32,
33,
34]), among many others.
The energy distance is defined as a statistical distance between the distributions of random vectors which characterizes equality of distributions, see for example [
29,
35] and [
21]. The concept of energy statistics described by Sźekely [
21] is based on the notion of Newton’s gravitational potential energy, which is a function of the distance between two bodies. The idea of energy statistics, therefore, is to consider statistical observations as heavenly bodies governed by a statistical potential energy, which is zero if and only if an underlying statistical null hypothesis is true, see for example [
29,
36].
Definition 1.
Sźekely and Rizzo [35] defined the energy distance between distributions of two independent and univariate random samples X and Y with finite expectations as follows
, and equality holds if and only if X and Y are identically distributed.
1.1. Contribution and Novelty
In this work, we propose a procedure that is more superior for goodness-of-fit test for the Skew-
t distribution based on energy distance statistics [
35] and [
13] definition of the Skew-
t distribution. Unlike the proposed method based on energy statistics, many existing methods depend on the distribution function of random variables. Energy statistic-based tests have been shown to be typically more powerful against general alternatives than corresponding tests based on classical statistics (non-energy type) such as Kormogorov-Smirnov, Correlation, Anderson Darling, and Cramer-Von-Mises. In addition, energy statistic-based tests have an invariance property with respect to any distance-preserving transformation of the data set, see for example [
29,
33,
36]. This makes it possible to extend studies involving energy statistics to multivariate and high dimensional settings.
In
Section 2, we propose a test procedure based on energy statistics for the goodness-of-fit of Azzalini’s Skew-
t distribution and discuss its theoretical properties. We perform various simulations in
Section 3 to compare the approach with other existing methods. In
Section 4, we apply our method to two real-life datasets. The conclusion is provided in
Section 5.
2. Proposed Energy-based Goodness of Fit Test
We propose a one-sample univariate goodness-of-fit test based on the energy statistics proposed by [
26,
35] for the Skew-
t distribution. The null hypothesis is that the data
X follow the null distribution
which is a Skew-
t distribution, against the alternative that the Skew-
t distribution is a poor fit for the data.
Definition 2.
Let be a random sample from a univariate population with distribution F and let be the observed values of the random variables in the sample. Then, the one-sample energy statistic goodness-of-fit test for testing the hypothesis vs is defined as follows.
where X and are independent and identically distributed variables with distribution , and the expectations are taken with respect to the null distribution .
The null hypothesis,
is rejected for large values of the test statistic
. Under the null hypothesis, the limiting distribution of
is a quadratic quantity of the form
such that
are i.i.d. standard normal random variables and
are nonnegative constants that depend on the null distribution. Thus, the goodness-of-fit test can be implemented by finding the constants
. In practice, this could be difficult, and we therefore resort to the use of empirical critical values of
so that
This fact is guaranteed since the test based on
is a consistent goodness-of-fit test, see for example, [
26] and [
25].
The goodness of fit test statistic based on energy statistics is dependent on the derivation of the expected values of and where X and are independent and identically distributed random variables from the null distribution
Proposition 1.
Let where is defined in Eq. (2). Then, for any fixed
where is the CDF of the Skew-t distribution.
Proof (Proof of Proposition 1). Let
. Then, for every fixed real number
x we have
where the integral term can be numerically evaluated in R using the command
dst() available in Azzalini
sn package. □
Sometimes the derivation of the second term in Eq. (
5) may not be analytically feasible and, therefore, we can use the following approximation as suggested in [
22].
Proposition 2.(Quantile-based Approximation) Let X and be independent and identically distributed random variables with a well-defined cumulative distribution function, . Given that the quantile or inverse CDF function of X exists, we have the following.
where m is the number of equally sized sub-intervals of and is chosen from the sub-interval. It is worth noting that the Proposition 2 applies for all distribution functions.
Proof. This proof is provided by Opperman and Ning [
22]. □
3. Simulations and Results
This section presents a simulation-based assessment of the proposed goodness-of-fit (GoF) test for Azzalini’s Skew-t distribution, built upon the energy distance framework. We evaluate the test’s performance across varying values of the skewness parameter () and degrees of freedom (). Simulations are conducted under both the null hypothesis and multiple alternative distributions, and Type I error and empirical power are computed.
In this simulation study, we calculate two key quantities. The size of the test (type I error) and the empirical power (1-type II error). We used R (R version 4.4.2) and the
sn package
https://cran.r-project.org/web/packages/sn/refman/sn.html to carry out the simulations. Due to the complexity of repeatedly evaluating the Skew-
t CDF and performing numerical integration, all simulations were parallelized using the
foreach and
doParallel R packages. Simulations were distributed across available cores, significantly accelerating the evaluation of the test under various scenarios.
3.1. The Univariate Energy Test Statistic
The univariate energy test statistic is derived from the expected pairwise distances between observations and a reference Skew-
t distribution. Let
be the cumulative distribution function (CDF) of Azzalini’s Skew-
t distribution with parameter vector
. The test statistic for a sample
is:
This expression is approximated using the following.
- (1)
A term involving the integral of up to each data point.
- (2)
A quantile-based approximation for the inter-distributional expectation .
- (3)
A linear-order statistic approximation for the within-sample expectation .
According to Rizzo [
20], the last term of the test statistic
in Eq. (
5) can be linearized in order to reduce the computational complexity of the test from
to
which is useful during extensive simulations and applications. Let
be the ordered sample of the random sample
. Then the linearization of the double sum of the test
is given as
3.2. Critical Value Simulation Under Varying and
In this section, we conduct a simulation study to estimate the critical values for the energy-based goodness-of-fit test under Azzalini’s skew
t distribution. The critical value simulations are summarized in
Table 1. We selected degrees of freedom
to account for different levels of heavy tail behavior and skewness coefficient
to cover the three possible scenarios of right skew, symmetry, and left skew. We used 5,000 replicates in this study, with sample sizes
.
Table 2 presents the results of Type I error simulations, illustrating that the empirical values are very close to the theoretical value of 0.05, regardless of the sample size and the parameter values chosen for each sample.
3.3. Type I Error Control
To explore the sensitivity of the test, we vary the skewness parameter and degrees of freedom . For each combination of , we:
- (1)
Generate samples of size from the Skew-t distribution with parameters .
- (2)
Estimate the parameters using the maximum penalized likelihood method available in the sn package.
- (3)
Standardize the data to standard Skew-
t random variables and compute the energy goodness-of-fit statistic using the formula in equation (
8).
- (4)
Determine the empirical percentile critical value under the null hypothesis.
The empirical Type I error is then evaluated across different parameter settings to confirm robustness
Table 2 shows that the proposed energy-based test maintained the nominal significance level in all examined configurations. For
, the empirical Type I error was close to 0.05, although slightly conservative in extreme skewness or low degrees of freedom. As the sample size increased, the test stabilized and consistently aligned with the theoretical level.
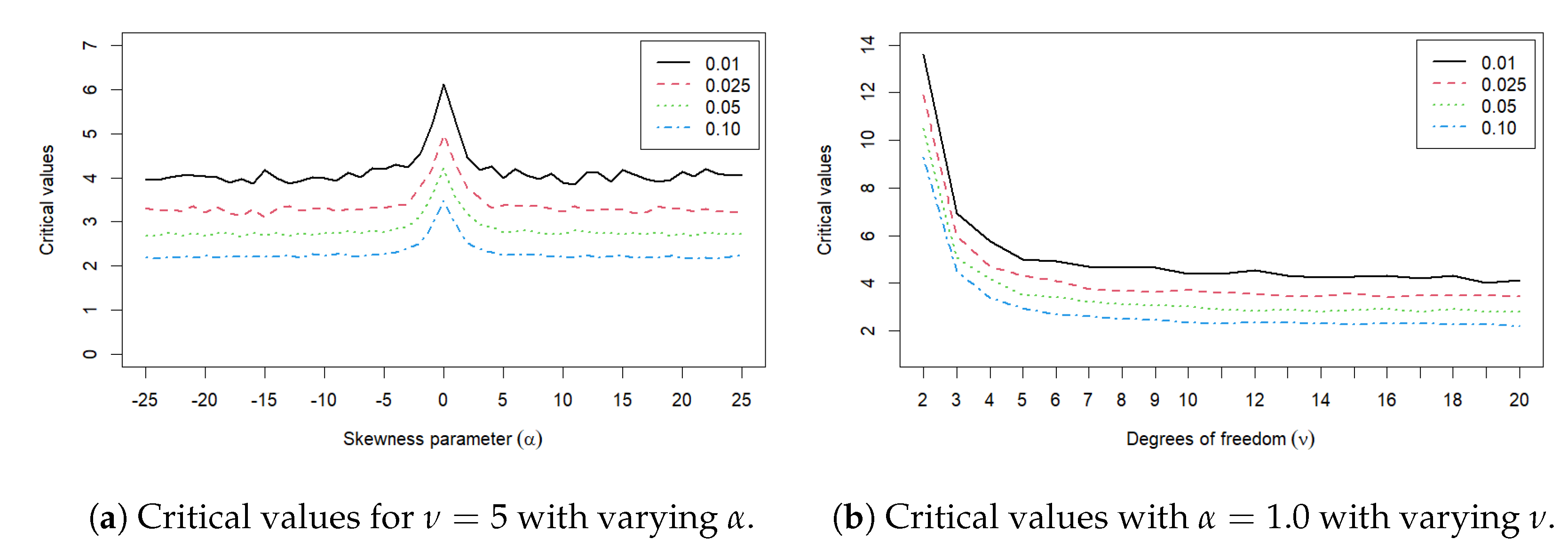
Figure 2 shows critical values with varying
for
and sample size
. For each selected level of significance (
), the critical values seem to stabilize as the skewness parameter
progresses further from 0. At
, we see a dramatic increase in the simulated critical value. Note that Azzalini’s skew
t distribution reduces to the classic Student
t distribution when
. In this special case, Azzalini’s skewness
t might be an overfitting model for the data because the skewness parameter is no longer needed, and Student’s
t distribution is a better fit for the data. If
, the critical value stabilizes. This implies that for a fixed predetermined confidence level, the actual value of the skewness parameter
has little to no effect on the critical value as long as
; in other words, the data exhibit noticeable skewness.
Figure 2 shows critical values with varying
for
and sample size
. When the degrees of freedom
, Azzalini’s skew
t distribution reduces to Cauchy’s distribution, and this is why we see higher critical values for the goodness-of-fit test. As the degrees of freedom increase
, critical values for a predetermined significance level stabilize as depicted by the nearly horizontal lines in
Figure 2.
3.4. Power Analysis under Various Alternatives
The simulation findings demonstrate the superior statistical power of the proposed energy-based goodness-of-fit,, test statistic compared to several established goodness-of-fit tests, including Anderson-Darling (A-D), Cramér-von Mises (CvM), Watson, Kolmogorov-Smirnov (K-S), and Kuiper tests. The analysis was conducted across various alternative distributions with sample sizes (n) of 50, 100, 150, and 200.
For power studies, samples are drawn from alternative distributions that deviate from Azzalini’s Skew-t distribution family. These include:
Chi-square: asymmetric, heavy-tailed.
Standard Gusset’s t: symmetric, heavy-tailed.
Exponential: lighter tail, positive skew.
SHASH: The SHASH (Sinh-Arcsinh) distribution that was discussed in [
37] is a highly flexible statistical distribution defined by four parameters that separately control the location, scale, skewness, and kurtosis of a variable.
Generalized t (GT): to assess sensitivity to misspecification.
Log-normal: asymmetric, heavy-tailed.
For each setting, the test statistic is calculated and compared to the critical value obtained under the corresponding null distribution with (
,
). Empirical power is computed as the proportion of times the null is rejected across
repetitions.
Table 3 summarizes the results of the power comparison simulations. For each case, the bold font indicates the highest power achieved at the combination of sample size and alternative distribution displayed in the row heading, and for each of the tests shown in the column heading.
3.5. Superior Performance of the Test
As illustrated in
Table 3, across
all scenarios, the energy-based test exhibited the highest power. This dominance is particularly evident in cases of heavy-tailed and skewed distributions.
For the Log-Normal () distribution, the test achieved a power of 0.9701 at a sample size of just 50, far exceeding the next best test, Watson test, which had a power of 0.3988.
Against the GT() distribution, the test reached a power of 1.0000 for sample sizes of 150 and 200, indicating perfect detection in the simulation.
For the Exponential (Exp(1)) distribution, the power of ranged from 0.8413 to 0.9848, consistently outperforming all other competitors.
The K−S and A−D tests underperformed in almost all scenarios, especially for skewed and heavy-tailed data. The correlation-based test was competitive but slightly less sensitive to departures in kurtosis. The energy test consistently ranked among the top-performing methods in all conditions.
3.6. Effect of Sample Size and Parameters
As anticipated, the power for all tests increased with the sample size. For instance, in the case of the SHASH distribution, the power of the test rose from 0.5734 for to 0.6749 for . It should be noted that for the standard distribution, which is a special case of Azzalini’s t distribution when the skewness coefficient , all tests showed very low power. The highest power achieved was only 0.2790 by the test at . This suggests that all tests face difficulties in distinguishing the two distributions, although the test still holds a relative advantage. The proposed energy-based test achieved the highest power under conditions of high skewness () and low degrees of freedom (). As increased, the power decreased slightly. This decrease in power is likely because the Skew t distribution converges to the Skew-normal family as the degrees of freedom, , making it harder to distinguish Skew-normal from Skew-t distribution as the degrees of freedom increase.
3.7. Summary
In summary, the simulation results provide strong evidence that the energy-based, , statistic is a more powerful goodness-of-fit test than the other methods considered in the study, especially for non-normal distributions with skewness or heavy tails. Overall, the energy-based GoF test for the Skew-t distribution demonstrates:
Robust control of Type I error
Superior power in a wide range of alternatives
Flexibility for skewed, heavy-tailed, and multi-modal data
Its simplicity and effectiveness make it a promising tool for model validation in applied settings. Although the proposed method relies on a Monte Carlo approximation for expectation terms, the computational cost is manageable and can be parallelized. Use of linearized summation and pre-simulated reference distributions further improves efficiency.
4. Real Data Application
To evaluate the practical utility of the proposed test, we applied it to two real-world datasets. These two datasets are: body mass index (BMI) for 102 male Australian athletes (Cook and Weisberg [
38]) and the daily rate of returns for Apple stock Macrotrends [
39], which provides the historical price of the stock.
Since the underlying distributions of these datasets are not exactly known in advance, we use the bootstrap algorithm to determine whether or not they come from Azzalini’s Skew-t distribution. The bootstrap procedure is performed to approximate the associated p-value of the proposed test as given below.
- (1)
Fit the real data
with an Azzalini’s Skew-
t distribution in Eq. (
Section 1), and obtain the maximum likelihood estimates (MLEs) of
and
from the Azzalini’s
sn package available in R.
- (2)
Use the formula in Eq. (
8) to calculate the energy goodness-of-fit statistic of the real data and denote it
.
- (3)
Simulate , a random sample of size from the Azzalini Skew-t distribution with parameters specified as and that were obtained in step 1.
- (4)
Standardize the data to standard Skew-
t distribution and compute the energy goodness-of-fit statistic for the simulated data using the formula in Eq. (
8) and denote this value as
.
- (5)
Repeat this process for B times and obtain B energy goodness-of-fit statistics and denote them by .
- (6)
The bootstrap p-value is therefore approximated as
where
is an indicator function that takes the value of one when
and zero otherwise.
In the application, the first dataset represents the body mass index (BMI) of male Australian athletes recorded in
Table A1 and is available in the
dr package in R, see for example [
38]. This dataset was previously analyzed by Maghami and Bahrami [
16] with the correlation coefficient as the measure of goodness-of-fit. The dataset exhibits moderate skewness and potential heavy tails, making it an ideal candidate for Skew-
t modeling. The second dataset consists of the closing prices of Apple Inc. stock. This data was used as part of [
19] analysis for detecting structural changes in the distribution via the MIC-based method. The dataset is obtained from [
39], which provides historical stock price information. We limited the data to the range from
January 31, 2019, to January 24, 2020 to avoid the heterogeneity introduced by change points. The stock price shows a general upward trend with some noticeable fluctuations. Given that stock prices exhibit time dependence, we transform the raw closing prices,
, into daily returns, defined as
This transformation allows us to analyze relative price changes rather than absolute levels. The resulting data consist of 248 daily return observations, which we suspect follow a Skew-
t distribution. The complete transformed data is available in
Table A2 in the Appendix.
4.1. Model Fitting
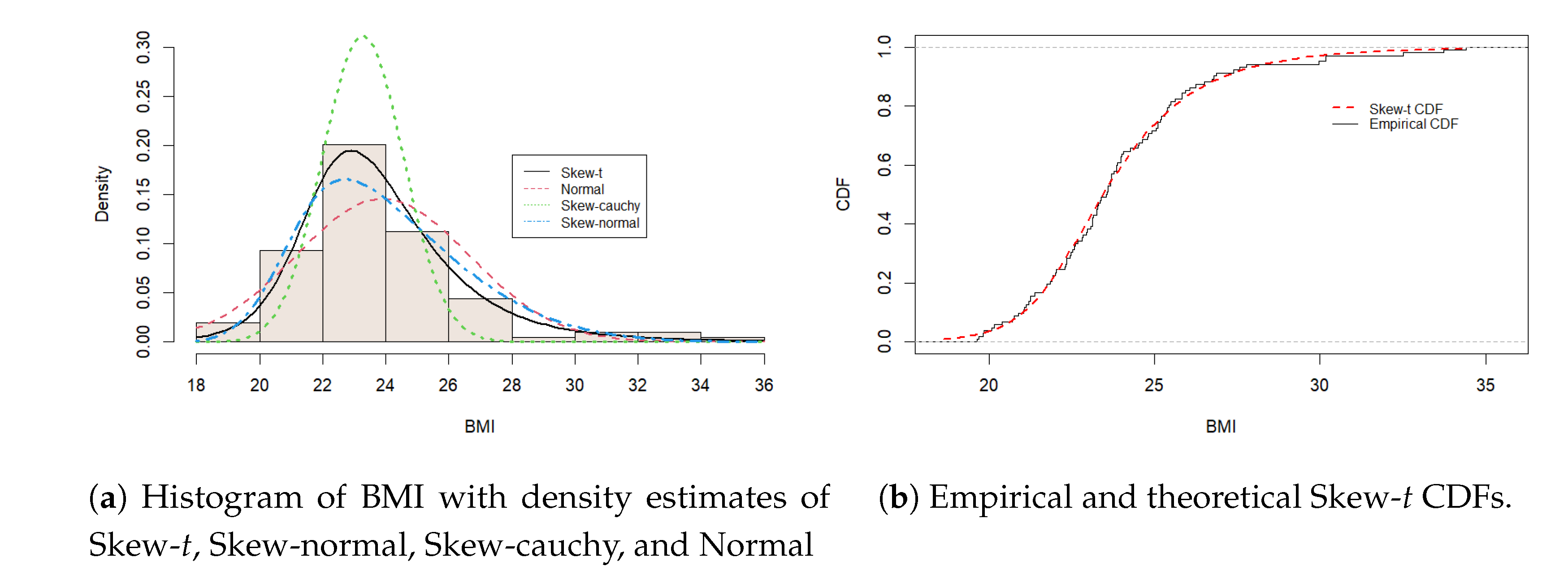
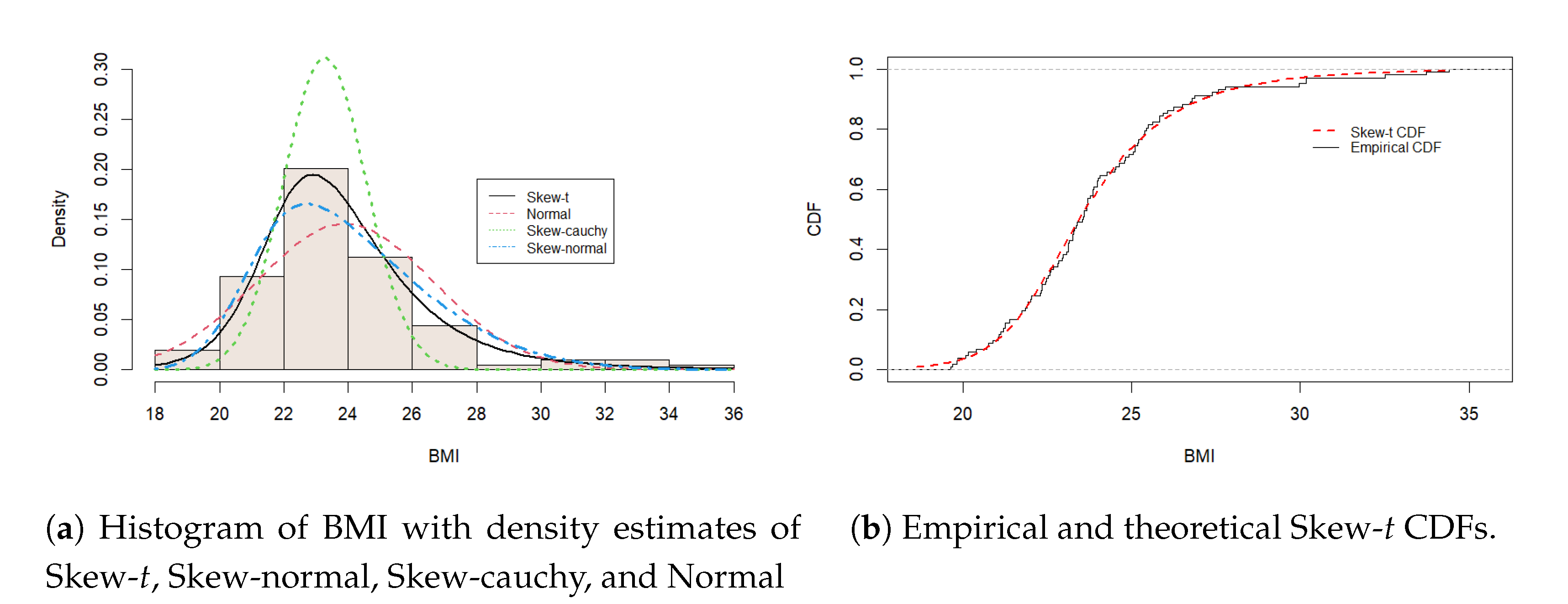
The histograms of the data in
Figure 3 and
Figure 4 reveal skewness; thus, distributions such as the Skew-
t, Skew-normal, Skew-Cauchy, and Normal distributions can be good candidates for modeling these datasets. Parameter estimation is conducted using the maximum likelihood method. The results of the penalized maximum likelihood estimates (PMLE), log-likelihood (LogL), Akaike information criterion (AIC), and Schwarz information criterion (SIC) are reported in
Table 4 and
Table 5. In both datasets, the Skew-
t distribution yielded the lowest AIC values, suggesting a better fit overall. Surprisingly, the skew-normal distribution gave a lower SIC value for the body mass index (BMI) dataset.
In the first dataset (BMI), our proposed test statistic is 1.7109, and its corresponding p-value is 0.5840, supporting the assertion that the BMI data follow the Skew-
t distribution. Other tests considered in the study also supported the null hypothesis that body mass index (BMI) data can be modeled using the Skew-
t distribution (
Table 6). In the second data, the test statistic of the proposed procedure is 3.9635, and the corresponding p-value is given as 0.5473. These results support the fact that the data follow the Azzalini’s Skew-
t distribution. Similar results are observed for the empirical distribution function (EDF) tests, as they suggest that the data can be modeled with the Skew-
t distribution. These results are summarized in
Table 6 and
Table 7. Furthermore, density estimates and empirical cumulative functions suggest that the Azzalini Skew-
t distribution fits the datasets adequately, as shown in
Figure 3 and
Figure 3 for the BMI dataset and in
Figure 4 and
Figure 4 for the Apple stock prices dataset, respectively.
4.2. Discussion
In both applications, the Skew-
t distribution fits the data adequately and has the minimum AIC value compared to other distributions. This assertion is also well confirmed by the density and empirical CDF estimates as shown in
Figure 3 and
Figure 4. Through simulations, 2000 bootstrap samples are drawn from the Skew-
t distribution with the specified parameter estimates in
Table 4 and
Table 5 and the approximate p-values of the proposed test for BMI and Apple stock daily return datasets are obtained as 0.5840 and 0.5473, respectively. We thus fail to reject the null hypothesis and conclude that both data can be modeled with the Skew-
t distribution.
This case study highlights the test’s ability to validate Skew-t modeling in real data scenarios, particularly where skewness and heavy tails are present. It further illustrates the utility of energy distance-based approaches in detecting misfit across a range of candidate models.
Figure 1.
Azzalini’s Standard Skew-t Density Curves when The Skewness Parameter , and the Different Degrees of Freedom, , varies over .
Figure 1.
Azzalini’s Standard Skew-t Density Curves when The Skewness Parameter , and the Different Degrees of Freedom, , varies over .
Figure 2.
Critical values for various parameter values. at sample size at levels of significance
Figure 2.
Critical values for various parameter values. at sample size at levels of significance
Figure 3.
Histogram, density curves, and CDFs of The body mass index (BMI) of 102 male Australian Athletes.
Figure 3.
Histogram, density curves, and CDFs of The body mass index (BMI) of 102 male Australian Athletes.
Figure 4.
Histogram, density curves, and CDFs of Apple’s daily returns with 248 observations.
Figure 4.
Histogram, density curves, and CDFs of Apple’s daily returns with 248 observations.
Table 1.
Simulated Critical Values for Energy Statistic of Skew- Distribution
Table 1.
Simulated Critical Values for Energy Statistic of Skew- Distribution
| |
|
| n |
(1,5) |
(0,5) |
(-1,5) |
(1,10) |
(0,10) |
(-1,10) |
(1,30) |
(0,30) |
(-1,30) |
|
| 50 |
3.7856 |
3.8663 |
4.0781 |
2.0441 |
1.9596 |
1.9143 |
1.3624 |
1.3332 |
1.3421 |
| 100 |
4.5742 |
4.6635 |
4.6401 |
2.3416 |
2.3314 |
2.3443 |
1.6584 |
1.5815 |
1.6448 |
| 150 |
5.3913 |
5.6910 |
5.3485 |
2.8291 |
2.8642 |
2.8279 |
2.0239 |
2.0291 |
2.0270 |
| 200 |
6.3893 |
6.6986 |
6.3946 |
3.3414 |
3.4878 |
3.3710 |
2.4003 |
2.4172 |
2.3981 |
Table 2.
Simulated size of the test for Skew- Distribution
Table 2.
Simulated size of the test for Skew- Distribution
| |
|
| n |
(1,5) |
(0,5) |
(-1,5) |
(1,10) |
(0,10) |
(-1,10) |
(1,30) |
(0,30) |
(-1,30) |
|
| 50 |
0.0508 |
0.0532 |
0.0513 |
0.0476 |
0.0508 |
0.0513 |
0.0510 |
0.0484 |
0.0540 |
| 100 |
0.0484 |
0.0476 |
0.0492 |
0.0511 |
0.0487 |
0.0503 |
0.0501 |
0.0558 |
0.0488 |
| 150 |
0.0496 |
0.0506 |
0.0524 |
0.0513 |
0.0509 |
0.0491 |
0.0478 |
0.0492 |
0.0508 |
| 200 |
0.0503 |
0.0494 |
0.0506 |
0.0505 |
0.0498 |
0.0501 |
0.0497 |
0.0496 |
0.0499 |
Table 3.
Power Comparison with
Table 3.
Power Comparison with
| Distribution |
Sample size n
|
|
|
|
|
|
|
|
50 |
0.8369 |
0.2248 |
0.2134 |
0.2809 |
0.2460 |
0.3878 |
| |
100 |
0.8933 |
0.2924 |
0.2832 |
0.3850 |
0.3298 |
0.5061 |
| |
150 |
0.9559 |
0.4018 |
0.3638 |
0.5103 |
0.4288 |
0.6223 |
| |
200 |
0.9715 |
0.4973 |
0.4418 |
0.6184 |
0.5069 |
0.7270 |
|
50 |
0.1066 |
0.0342 |
0.0396 |
0.0332 |
0.0382 |
0.0372 |
| |
100 |
0.1736 |
0.0356 |
0.0418 |
0.0392 |
0.0380 |
0.0384 |
| |
150 |
0.2268 |
0.0360 |
0.0398 |
0.0334 |
0.0382 |
0.0378 |
| |
200 |
0.2790 |
0.0387 |
0.0410 |
0.0413 |
0.0393 |
0.0397 |
|
50 |
0.8413 |
0.2640 |
0.2491 |
0.3069 |
0.2692 |
0.4092 |
| |
100 |
0.9152 |
0.5090 |
0.4924 |
0.5538 |
0.5140 |
0.6128 |
| |
150 |
0.9655 |
0.6496 |
0.6224 |
0.7012 |
0.6486 |
0.7702 |
| |
200 |
0.9848 |
0.7439 |
0.7169 |
0.8012 |
0.7421 |
0.8601 |
|
50 |
0.5734 |
0.1145 |
0.1292 |
0.1345 |
0.1302 |
0.1545 |
| |
100 |
0.6045 |
0.2131 |
0.2154 |
0.2546 |
0.2328 |
0.261 |
| |
150 |
0.6401 |
0.3032 |
0.3072 |
0.3844 |
0.3498 |
0.3958 |
| |
200 |
0.6749 |
0.4166 |
0.4196 |
0.5184 |
0.4742 |
0.5261 |
|
50 |
0.9596 |
0.1128 |
0.1166 |
0.1306 |
0.1188 |
0.3350 |
| |
100 |
0.9916 |
0.1562 |
0.1860 |
0.2004 |
0.1966 |
0.4480 |
| |
150 |
1.0000 |
0.2306 |
0.2756 |
0.3228 |
0.3232 |
0.5816 |
| |
200 |
1.0000 |
0.3030 |
0.3798 |
0.4278 |
0.4292 |
0.6720 |
|
50 |
0.9701 |
0.3331 |
0.1950 |
0.3988 |
0.2304 |
0.4611 |
| |
100 |
0.9931 |
0.33691 |
0.2092 |
0.3974 |
0.2441 |
0.4644 |
| |
150 |
0.9995 |
0.3449 |
0.2179 |
0.4102 |
0.2586 |
0.4775 |
| |
200 |
0.9998 |
0.3639 |
0.2409 |
0.4429 |
0.2818 |
0.5155 |
Table 4.
MLE, LogL, AIC and SIC values for BMI dataset
Table 4.
MLE, LogL, AIC and SIC values for BMI dataset
|
Skew-t
|
Normal |
Skew-cauchy |
Skew-normal |
|
21.6490 |
23.9036 |
22.7889 |
20.8765 |
|
2.6570 |
2.7403 |
1.3762 |
4.0610 |
|
1.6421 |
- |
0.5126 |
3.2992 |
|
4.5503 |
- |
- |
- |
| LogL |
-236.0511 |
-248.0613 |
-247.5519 |
-237.9670 |
| AIC |
480.1022 |
500.1227 |
501.1037 |
481.9341 |
| SIC |
490.6020 |
505.3726 |
508.9787 |
489.8090 |
Table 5.
MLE, LogL, AIC and SIC values for Apple stock daily return dataset
Table 5.
MLE, LogL, AIC and SIC values for Apple stock daily return dataset
|
Skew-t
|
Normal |
Skew-cauchy |
Skew-normal |
|
0.5254 |
0.2749 |
0.1798 |
1.3519 |
|
1.1514 |
1.4259 |
0.7655 |
1.7858 |
|
-0.2285 |
- |
0.1191 |
-1.1688 |
|
5.3556 |
- |
- |
- |
| LogL |
-431.3161 |
-440.3975 |
-461.9316 |
-438.1367 |
| AIC |
870.6321 |
884.795 |
929.8633 |
882.2733 |
| SIC |
884.6858 |
891.8219 |
940.4036 |
892.8136 |
Table 6.
Summary of test statistics and corresponding p-values of BMI data
Table 6.
Summary of test statistics and corresponding p-values of BMI data
| Test |
|
|
|
|
|
|
| Statistic value |
1.7109 |
0.0454 |
0.8731 |
0.0295 |
0.0290 |
0.2321 |
| P-value |
0.5840 |
0.9847 |
0.9847 |
0.9827 |
0.9840 |
0.9807 |
Table 7.
Summary of test statistics and p-values of Apple daily return data
Table 7.
Summary of test statistics and p-values of Apple daily return data
| Test |
|
|
|
|
|
|
| Statistic value |
3.9635 |
0.0357 |
1.0576 |
0.0291 |
0.0290 |
0.1737 |
| P-value |
0.5473 |
0.8260 |
0.8167 |
0.9381 |
0.9380 |
0.9913 |