Submitted:
16 October 2025
Posted:
16 October 2025
You are already at the latest version
Abstract
Keywords:
Introduction
Section One: Proposed Parametric Quantile Regression Model
1.1. Logit Link Function
1.1.1. Estimation Using Log-Likelihood Function
1.2. Log-Log Median Link Function
1.3. Complementary Log-Log Link Function
Section Two
2.1. Goodness of Fit Measures
2.2. Model Selection Criteria
Section Three: Real Data Analysis, Results and Discussion
3.1. Descriptive Analysis
3.2. The Model: Regressing Water Quality on Air Pollution
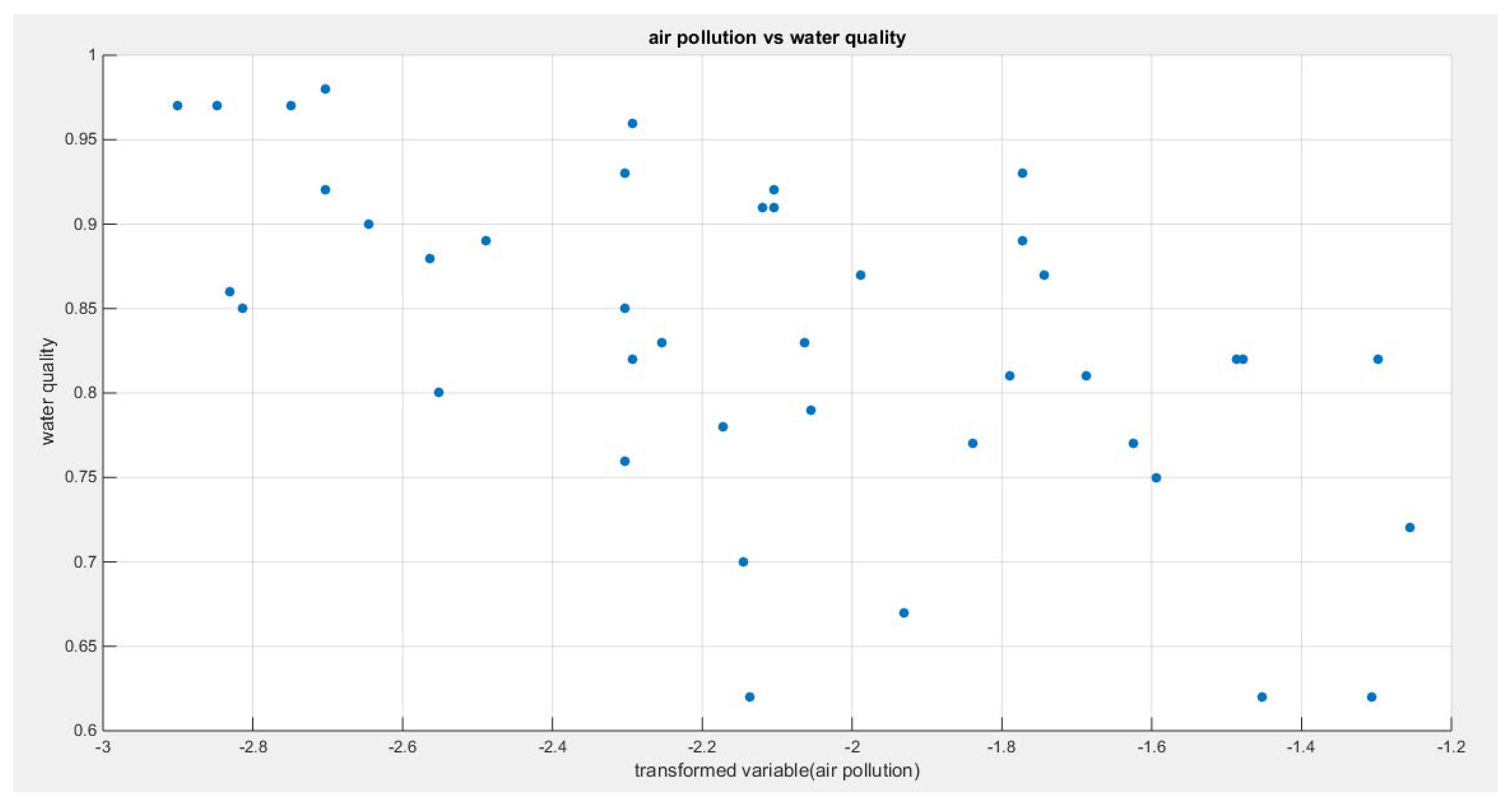
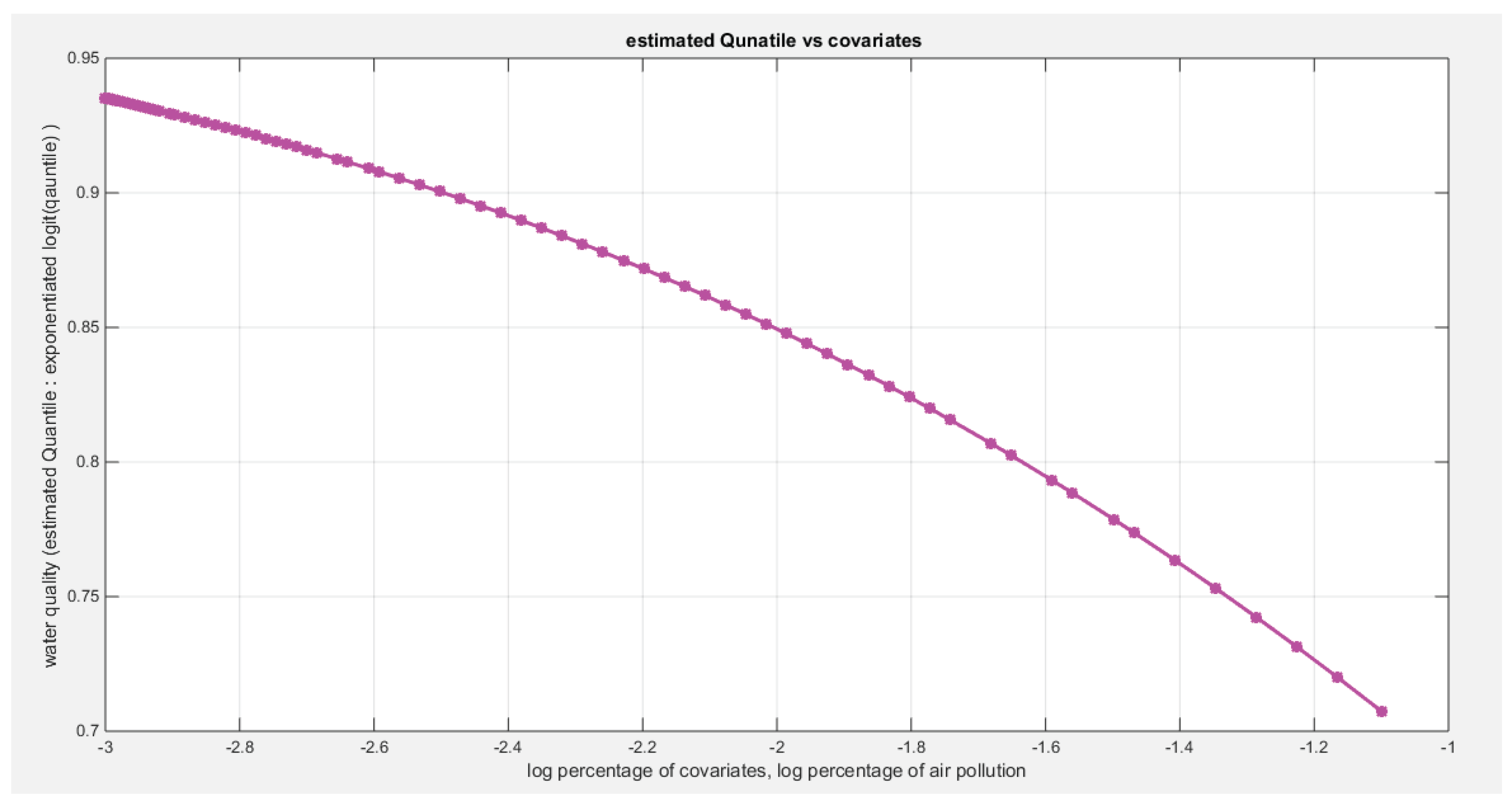
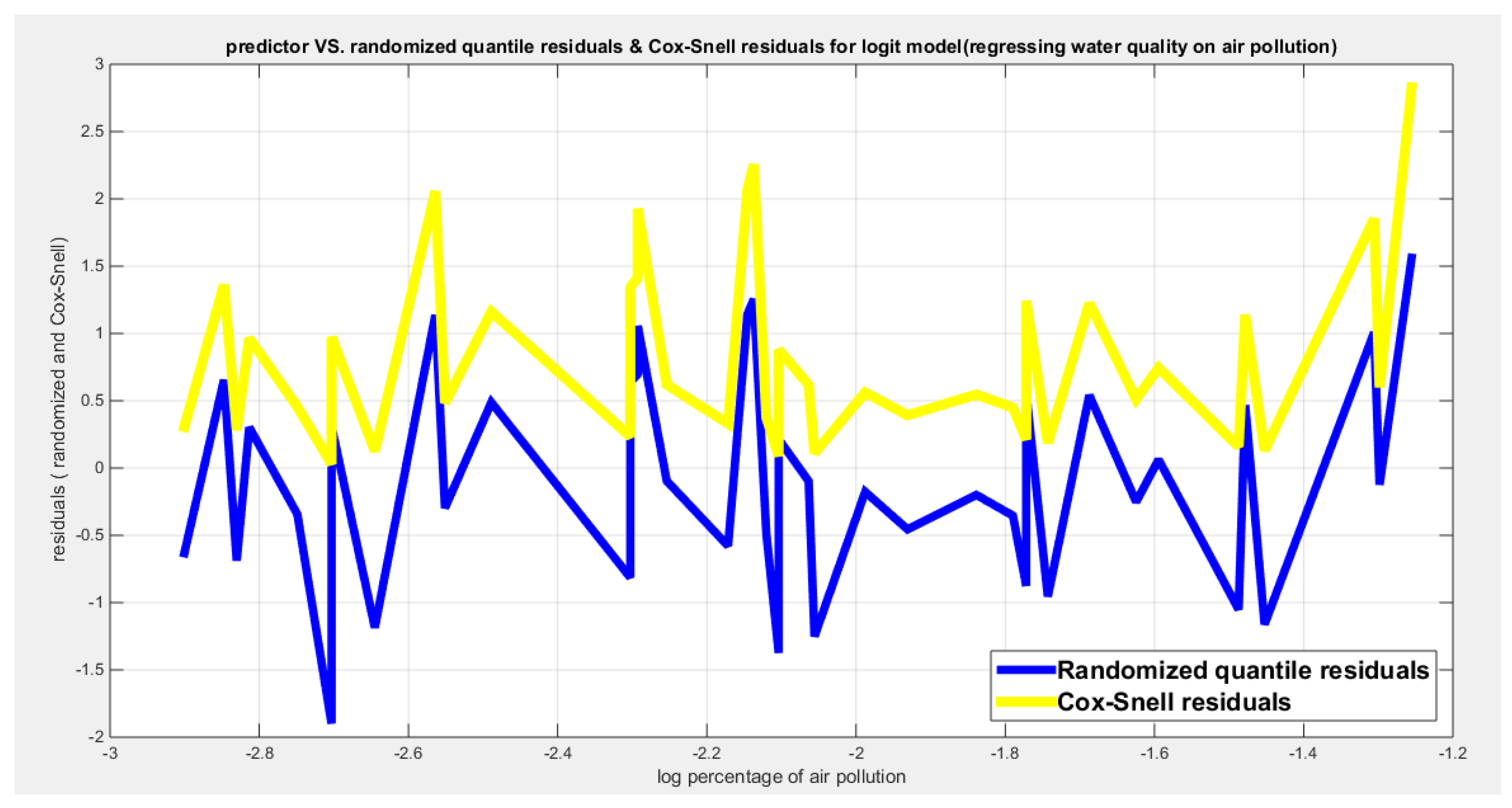
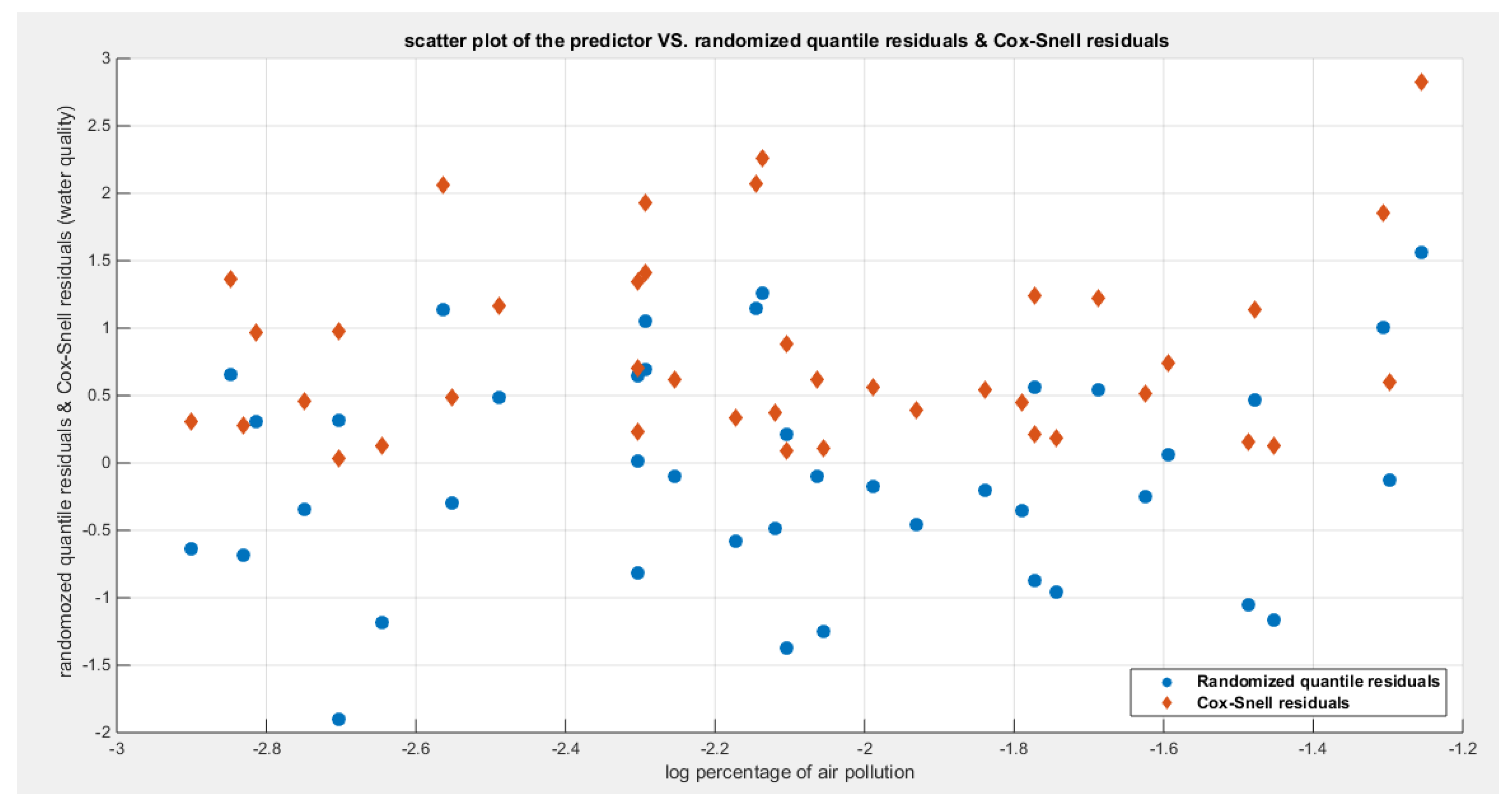
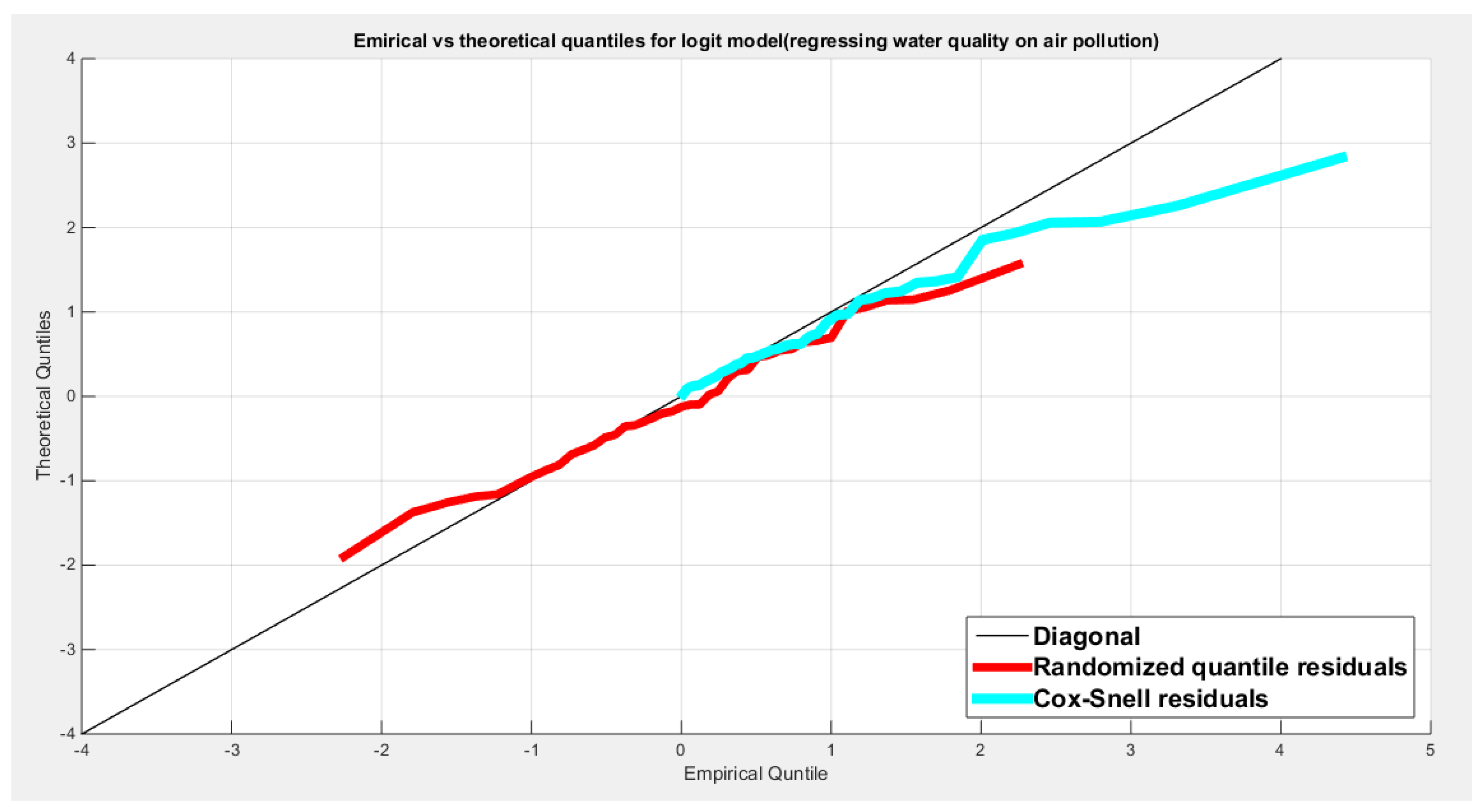
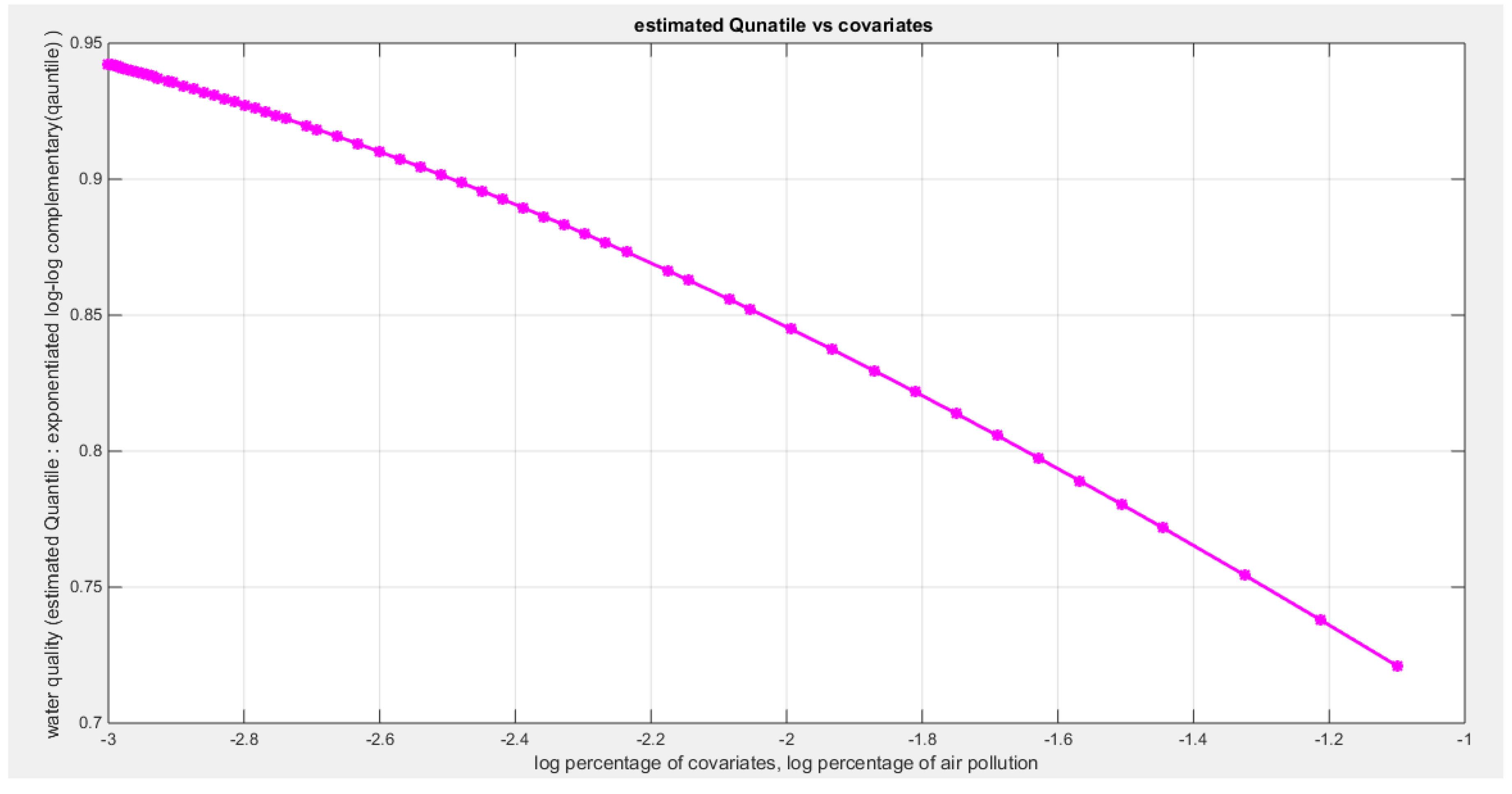
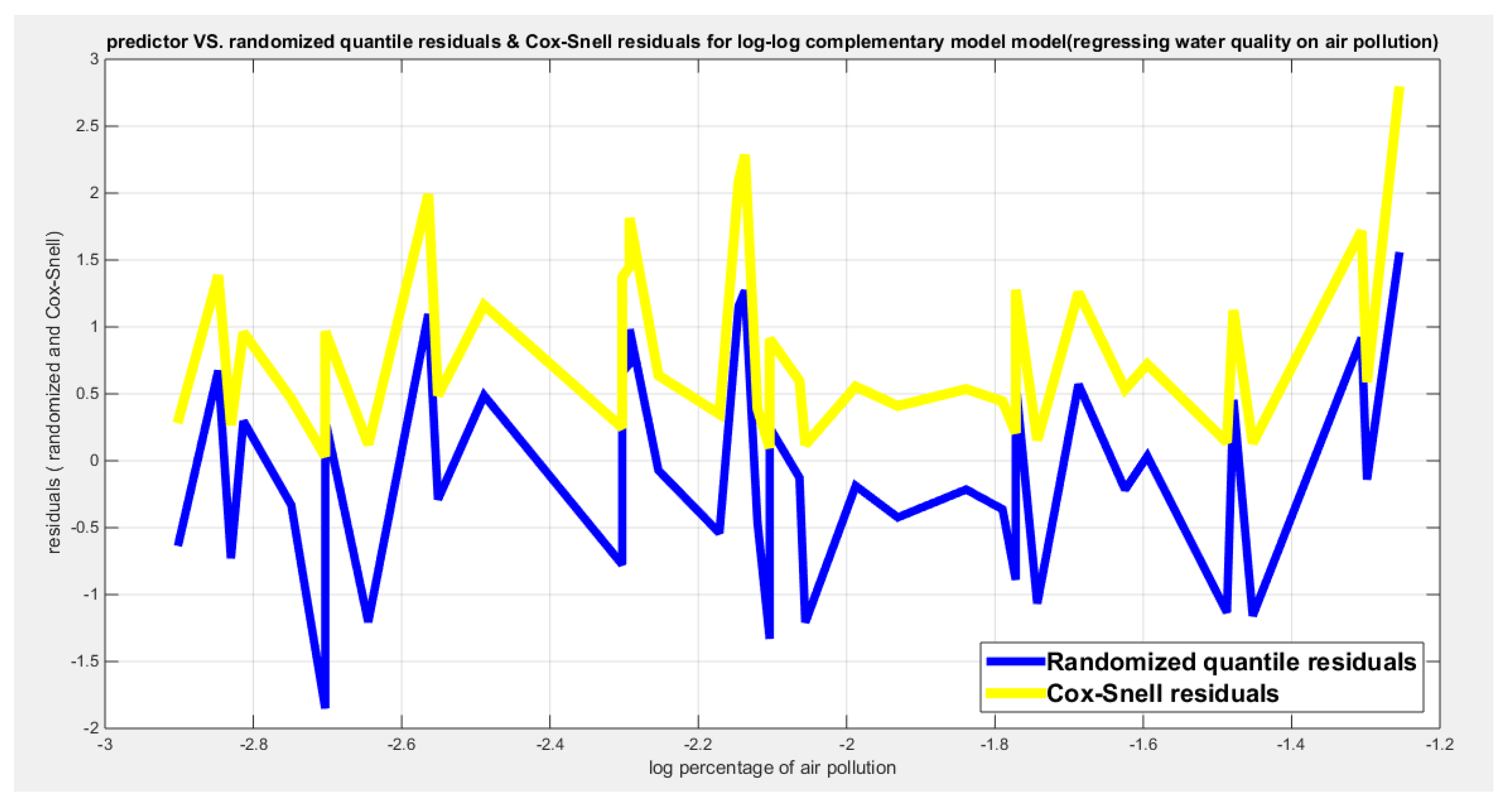
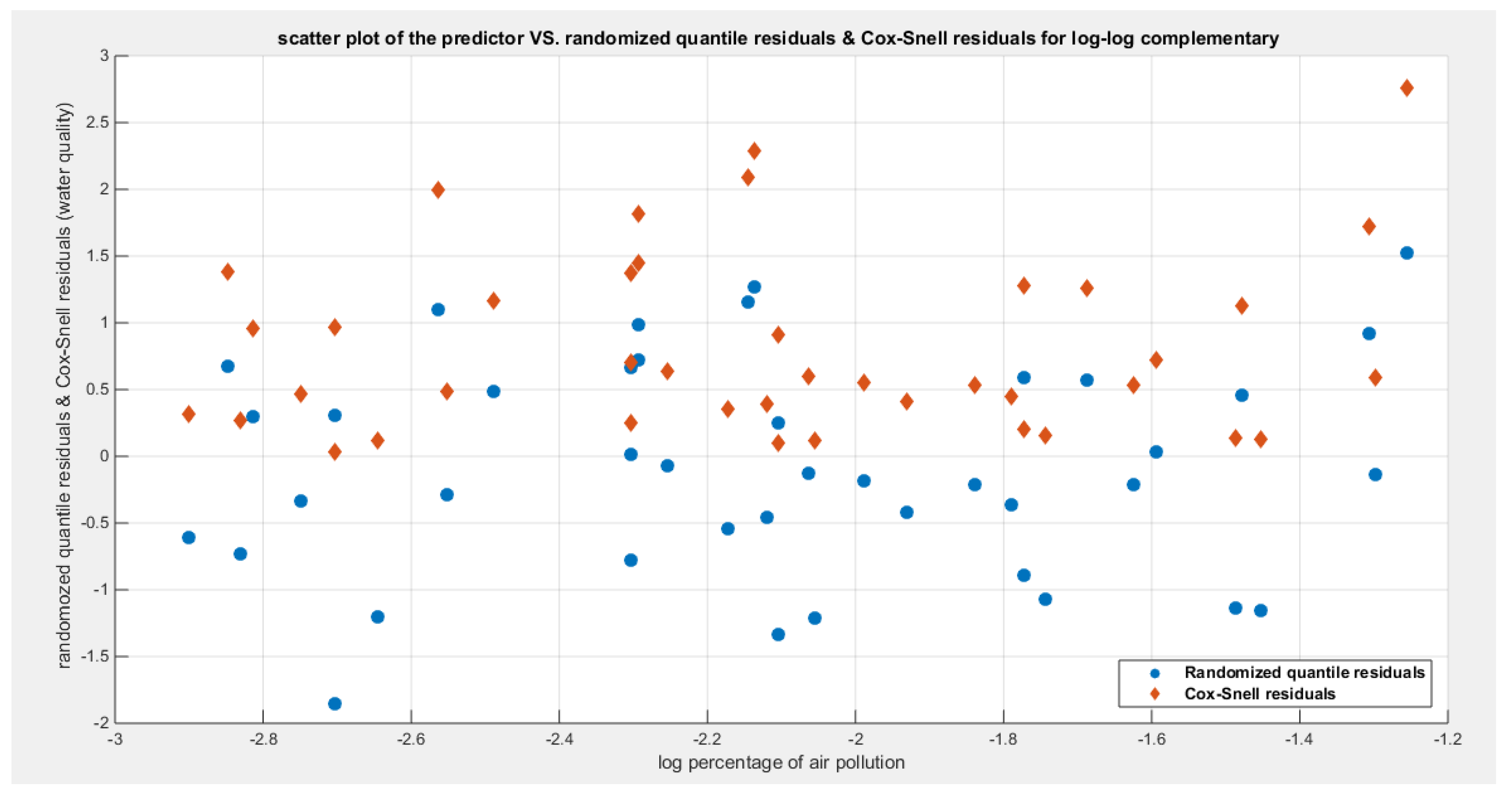
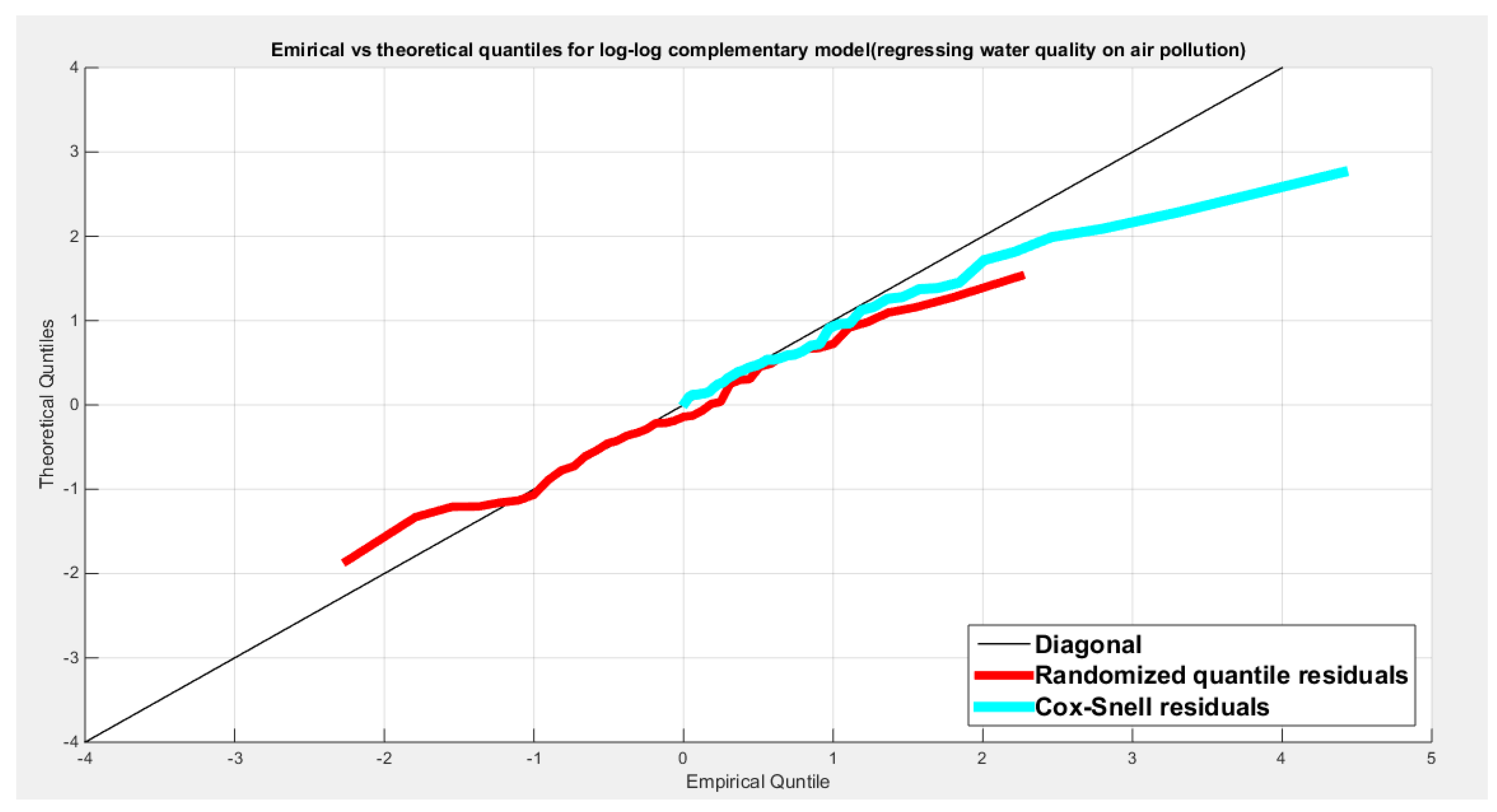
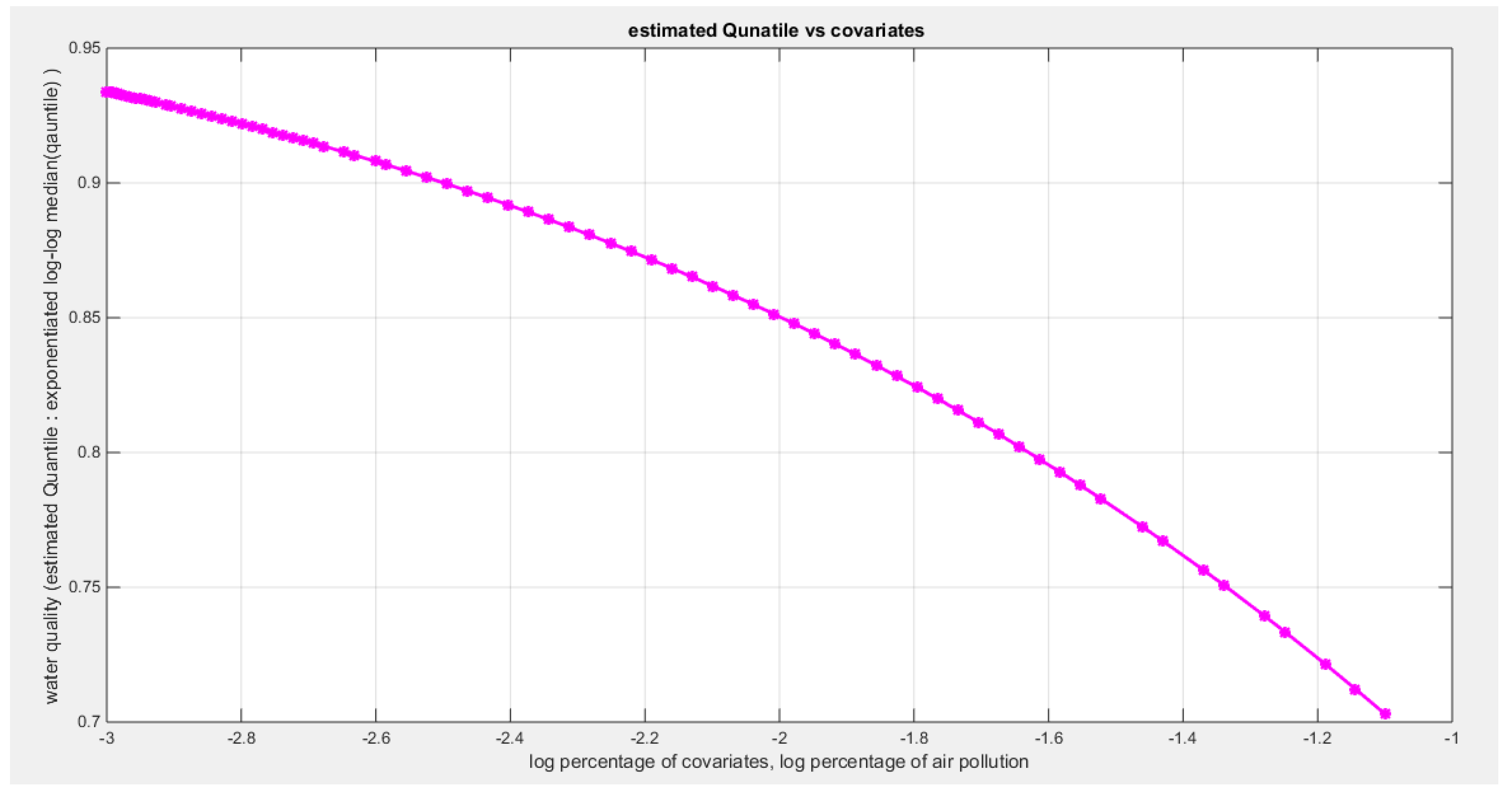
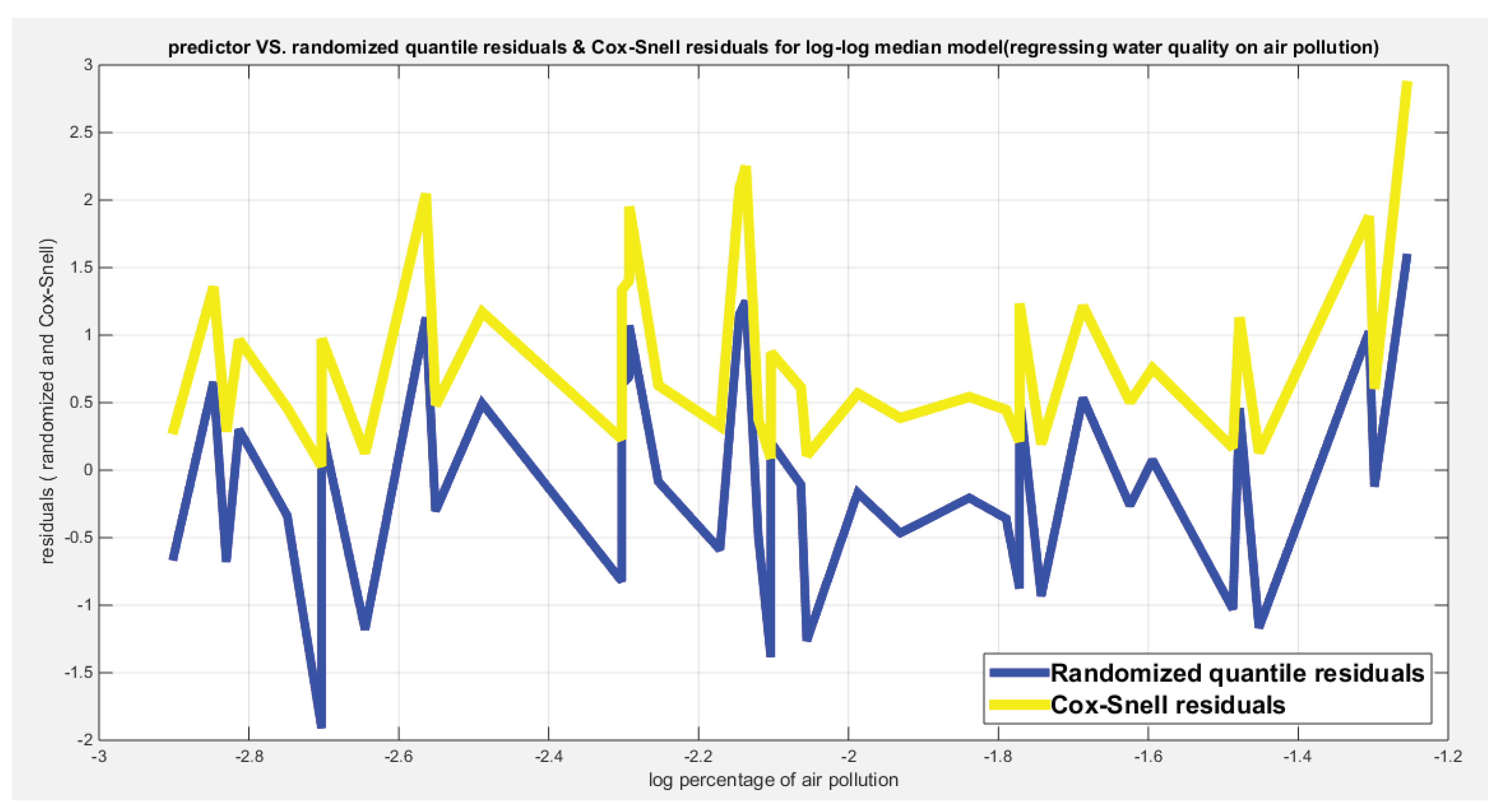
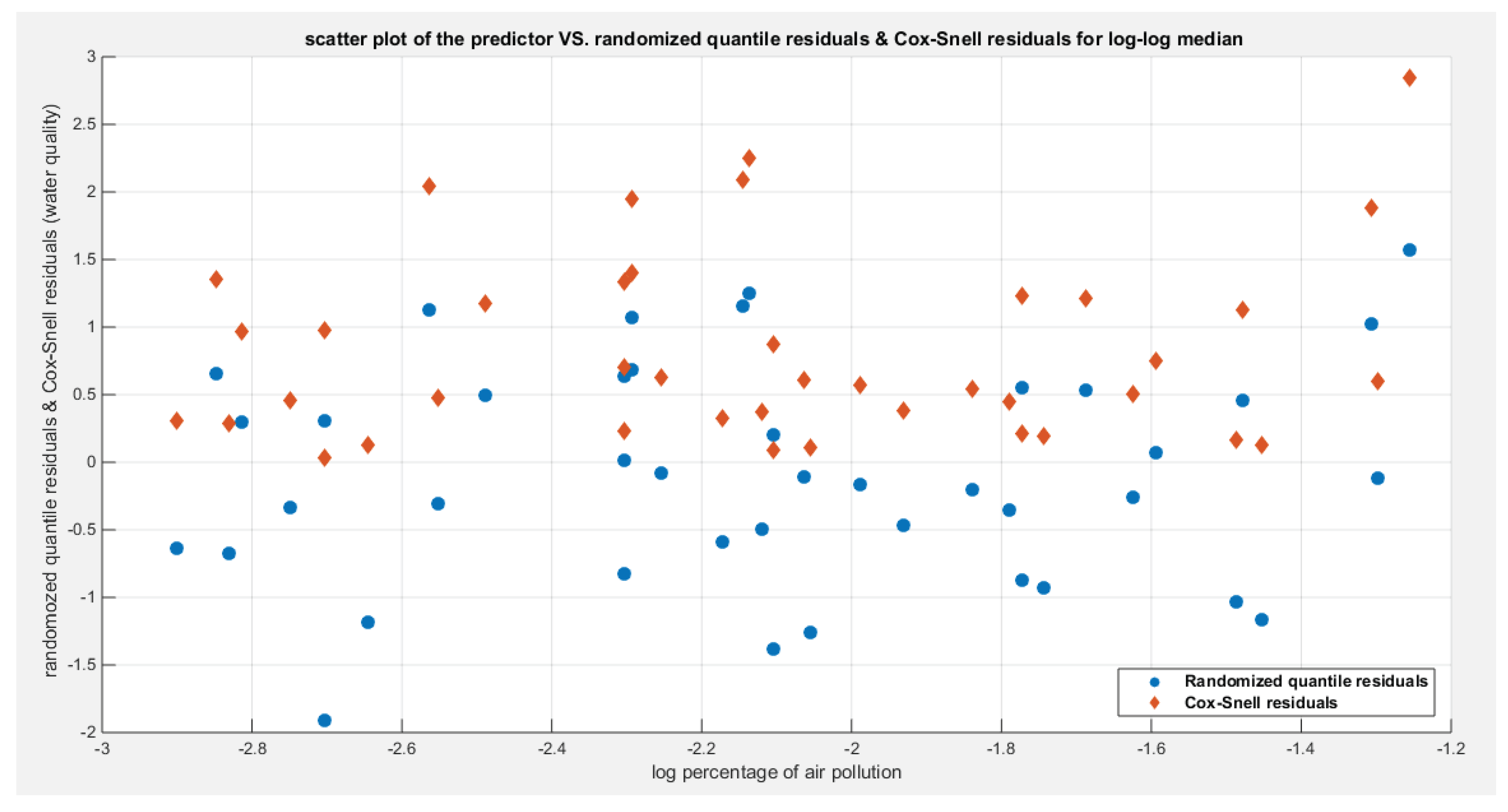
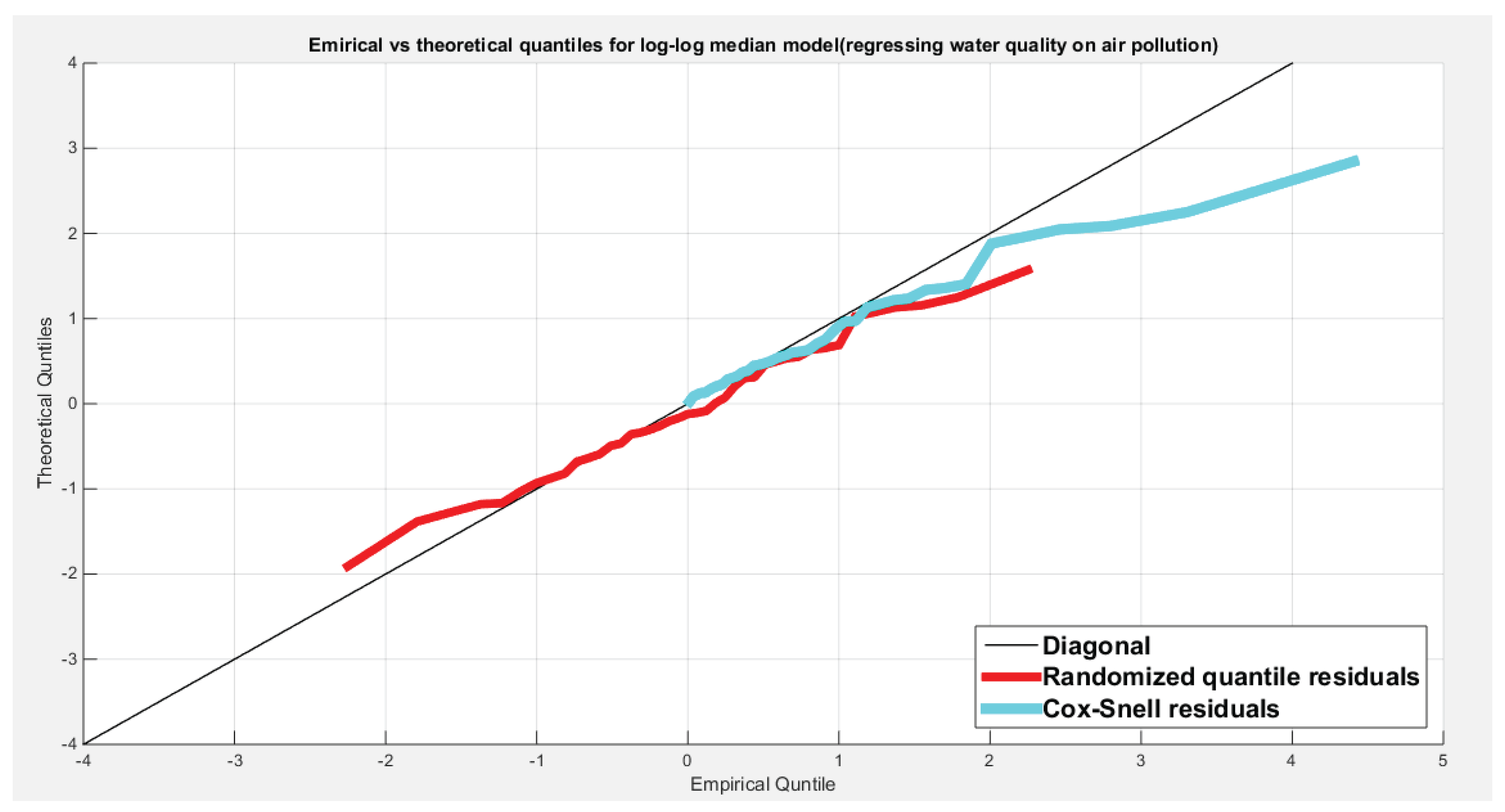
Section Four: Conclusion
Future Work
Authors’ Contribution
Ethics Approval and Consent to Participate
Consent for Publication
Availability of Data and Material
Competing Interests
Funding
Acknowledgement
References
- Attia, I. (2024). A Novel Unit Distribution Named as Median Based Unit Rayleigh (MBUR): Properties and Estimations. [CrossRef]
- Garcia-Papani, F.; Leiva, V.; Uribe-Opazo, M.A.; Aykroyd, R.G. Birnbaum-Saunders spatial regression models: Diagnostics and application to chemical data. Chemometrics and Intelligent Laboratory Systems 2018, 177, 114–128. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç.; Chesneau, C. On the unit Burr-XII distribution with the quantile regression modeling and applications. Computational and Applied Mathematics 2021, 40, 29. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç.; Chesneau, C.; Korkmaz, Z.S. On the Arcsecant Hyperbolic Normal Distribution. Properties, Quantile Regression Modeling and Applications. Symmetry 2021, 13, 117. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç.; Chesneau, C.; Korkmaz, Z.S. A new alternative quantile regression model for the bounded response with educational measurements applications of OECD countries. Journal of Applied Statistics 2023, 50, 131–154. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.; Dey, S.; Ormoz, E.; MirMostafaee, S.M.T.K. Inference for the unit-Gompertz model based on record values and inter-record times with an application. Rendiconti Del Circolo Matematico Di Palermo Series 2 2020, 69, 1295–1319. [Google Scholar] [CrossRef]
- Leão, J.; Leiva, V.; Saulo, H.; Tomazella, V. Incorporation of frailties into a cure rate regression model and its diagnostics and application to melanoma data. Statistics in Medicine 2018, 37, 4421–4440. [Google Scholar] [CrossRef] [PubMed]
- Leiva, V. (Ed.). (2016). The Birnbaum-Saunders distribution. Elsevier.
- Leiva, V.; Santos, R.A.D.; Saulo, H.; Marchant, C.; Lio, Y. Bootstrap control charts for quantiles based on log-symmetric distributions with applications to the monitoring of reliability data. Quality and Reliability Engineering International 2023, 39, 1–24. [Google Scholar] [CrossRef]
- Marchant, C.; Leiva, V.; Cysneiros, F.J.A. A Multivariate Log-Linear Model for Birnbaum-Saunders Distributions. IEEE Transactions on Reliability 2016, 65, 816–827. [Google Scholar] [CrossRef]
- Mazucheli, J.; Alves, B.; Korkmaz, M.Ç. The Unit-Gompertz Quantile Regression Model for the Bounded Responses. Mathematica Slovaca 2023, 73, 1039–1054. [Google Scholar] [CrossRef]
- Mazucheli, J.; Alves, B.; Korkmaz, M.Ç.; Leiva, V. Vasicek Quantile and Mean Regression Models for Bounded Data: New Formulation, Mathematical Derivations, and Numerical Applications. Mathematics 2022, 10, 1389. [Google Scholar] [CrossRef]
- Mazucheli, J.; Leiva, V.; Alves, B.; Menezes, A.F.B. A New Quantile Regression for Modeling Bounded Data under a Unit Birnbaum–Saunders Distribution with Applications in Medicine and Politics. Symmetry 2021, 13, 682. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.B.; Chakraborty, S. On the one parameter unit-Lindley distribution and its associated regression model for proportion data. Journal of Applied Statistics 2019, 46, 700–714. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.B.; Fernandes, L.B.; De Oliveira, R.P.; Ghitany, M.E. The unit-Weibull distribution as an alternative to the Kumaraswamy distribution for the modeling of quantiles conditional on covariates. Journal of Applied Statistics 2020, 47, 954–974. [Google Scholar] [CrossRef] [PubMed]
- Noufaily, A.; Jones, M.C. Parametric Quantile Regression Based on the Generalized Gamma Distribution. Journal of the Royal Statistical Society Series C: Applied Statistics 2013, 62, 723–740. [Google Scholar] [CrossRef]
- Sánchez, L.; Leiva, V.; Galea, M.; Saulo, H. Birnbaum-Saunders Quantile Regression Models with Application to Spatial Data. Mathematics 2020, 8, 1000. [Google Scholar] [CrossRef]
- Sánchez, L.; Leiva, V.; Galea, M.; Saulo, H. Birnbaum-Saunders quantile regression and its diagnostics with application to economic data. Applied Stochastic Models in Business and Industry 2021, 37, 53–73. [Google Scholar] [CrossRef]
- Sánchez, L.; Leiva, V.; Saulo, H.; Marchant, C.; Sarabia, J.M. A New Quantile Regression Model and Its Diagnostic Analytics for a Weibull Distributed Response with Applications. Mathematics 2021, 9, 2768. [Google Scholar] [CrossRef]
- R packages:, R. Koenker, quantreg: quantile regression, 2021, https://CRAN.R- project.org/package=quantreg. R package version 5.86.
- J. Mazucheli, B. J. Mazucheli, B. Alves, Ugomquantreg: quantile regression modeling for unit-Gompertz responses, 2021a, R package version 1.0.0.
- J. Mazucheli, A.F.B. J. Mazucheli, A.F.B. Menezes, unitBSQuantReg: unit-Birnbaum-Saunders quantile regression, 2020, https://github.com/AndrMenezes/unitBSQuantReg. R package version 0.1.0.
- A.F.B. Menezes, Uwquantreg: unit-Weibull quantile regression, 2020, https://github.com/AndrMenezes/uwquantreg. R package version 0.1.0.
- R Core Team, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, 2020. Available online: https://www.R-project.org/.
| Logit link function | Log-log complementary | Log-log median | ||||
|---|---|---|---|---|---|---|
| b0 | -0.1521 | -0.2213 | -0.0937 | |||
| b1 | -0.9411 | -0.4233 | 0.8630 | |||
| LL | 46.2983 | 46.5111 | 46.2508 | |||
| Wald stat. of b0 | -0.2498 (p > 0.025) | -0.7878 (p > 0.025) | -0.1704 (p > 0.025) | |||
| Wald stat. of b1 | -3.3696 (p < 0.025) | -3.4562 (p < 0.025) | 3.3798 (p < 0.025) | |||
| AIC | -88.5967 | -89.0223 | -88.5016 | |||
| CAIC | -88.2809 | -88.7065 | -88.1858 | |||
| BIC | -85.1695 | -85.5951 | -85.0745 | |||
| HQIC | -87.3487 | -87.7743 | -87.2537 | |||
| LRT | 11.6015(p-val.=0.0007) | 12.0271(p-val=0.00052) | 11.5064(0.0007) | |||
| R-squared | 0.2465 | 0.2442 | 0.2447 | |||
| P-value for randomized quantile residuals | 0.7791 | 0.8083 | 0.778 | |||
| p-value for Cox-snell residuals | 0.7791 | 0.8083 | 0.778 | |||
| Variance-covariance matrix | 0.3706 | 0.1666 | 0.0789 | 0.0339 | 0.3024 | 0.1375 |
| 0.1666 | 0.0780 | 0.0339 | 0.015 | 0.1375 | 0.0652 | |
| QR vs. predictor(t,p) | 0.0159,0.8927 | 0.0159,0.8927 | 0.0159,0.8927 | |||
| CS vs. predictor(t,p) | 0.0159,0.8927 | 0.0159,0.8927 | 0.0159,0.8927 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





