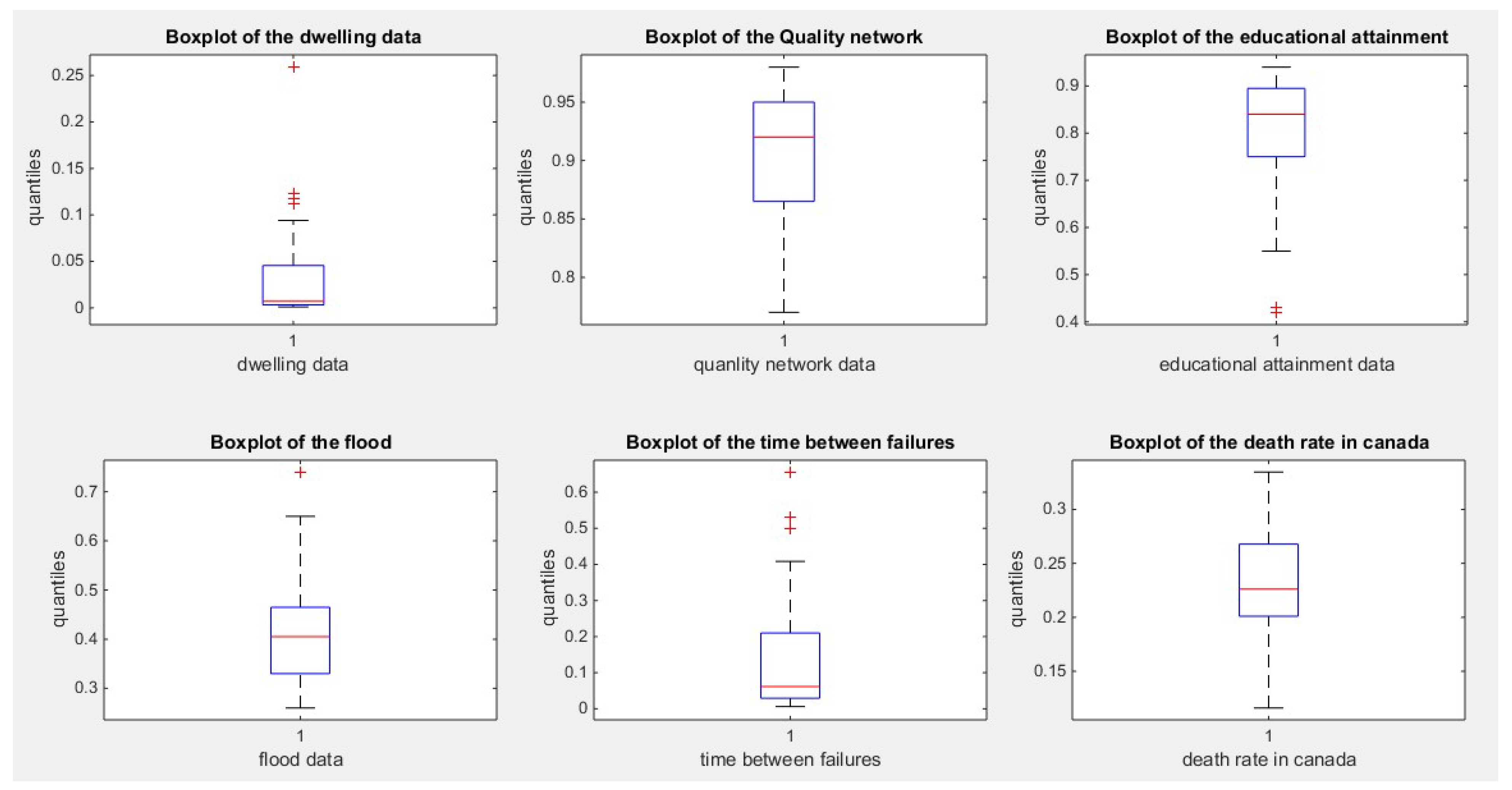
Figure 1.
illustrates the boxplot of the first 6 datasets.
Figure 1.
illustrates the boxplot of the first 6 datasets.
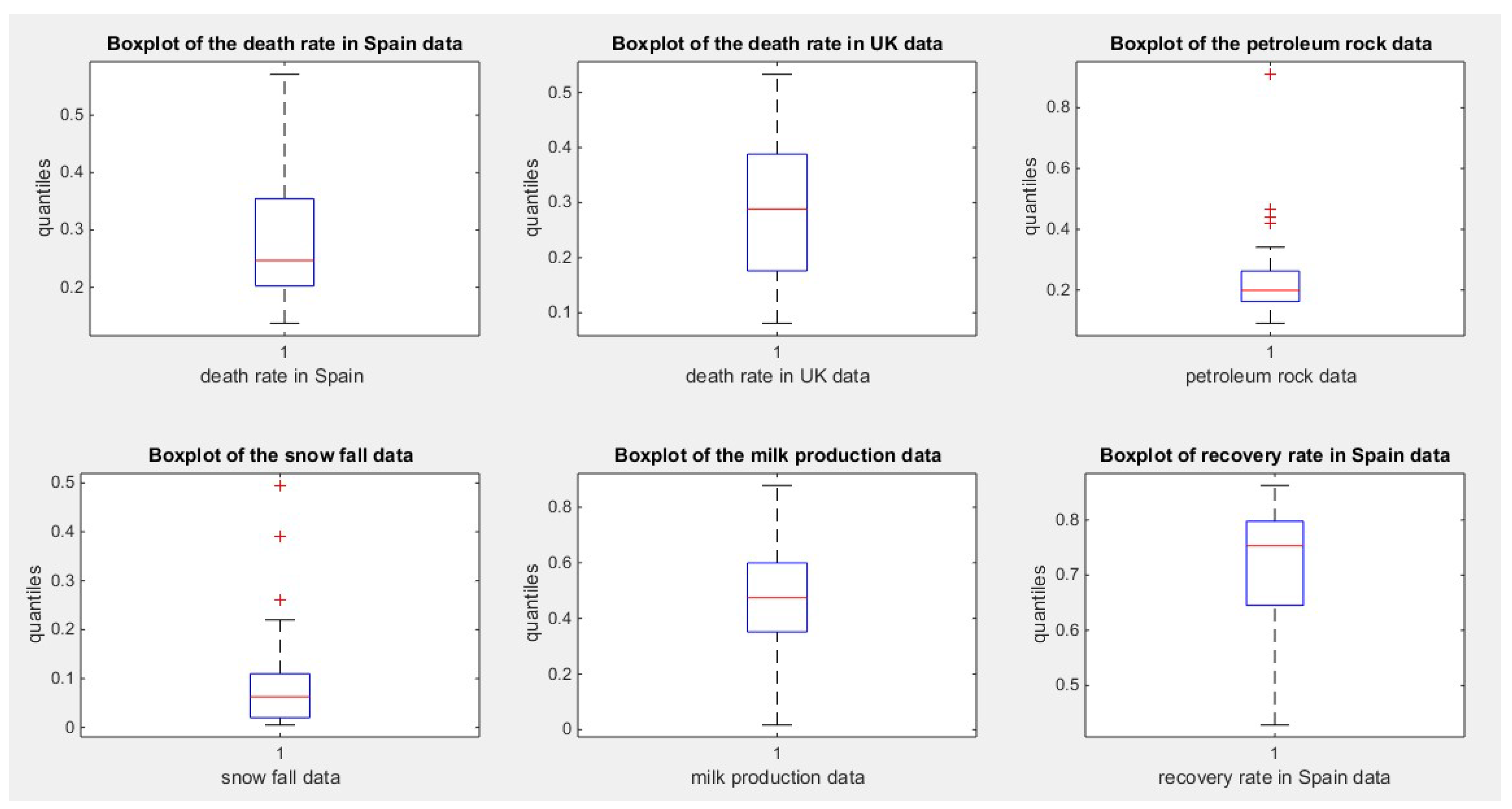
Figure 2.
illustrates the boxplot of the second 6 datasets.
Figure 2.
illustrates the boxplot of the second 6 datasets.
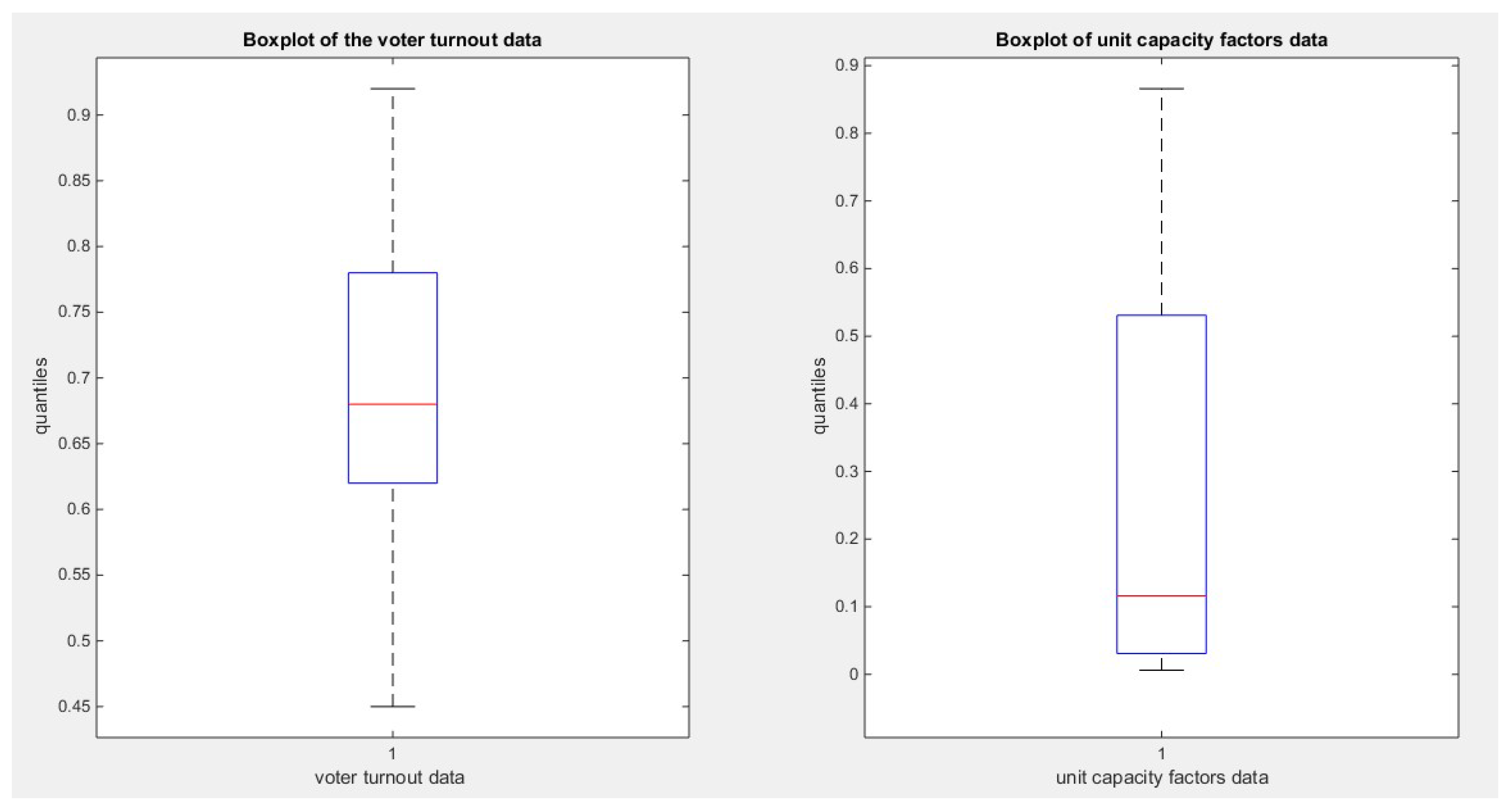
Figure 3.
illustrates the boxplot of the last 2 datasets.
Figure 3.
illustrates the boxplot of the last 2 datasets.
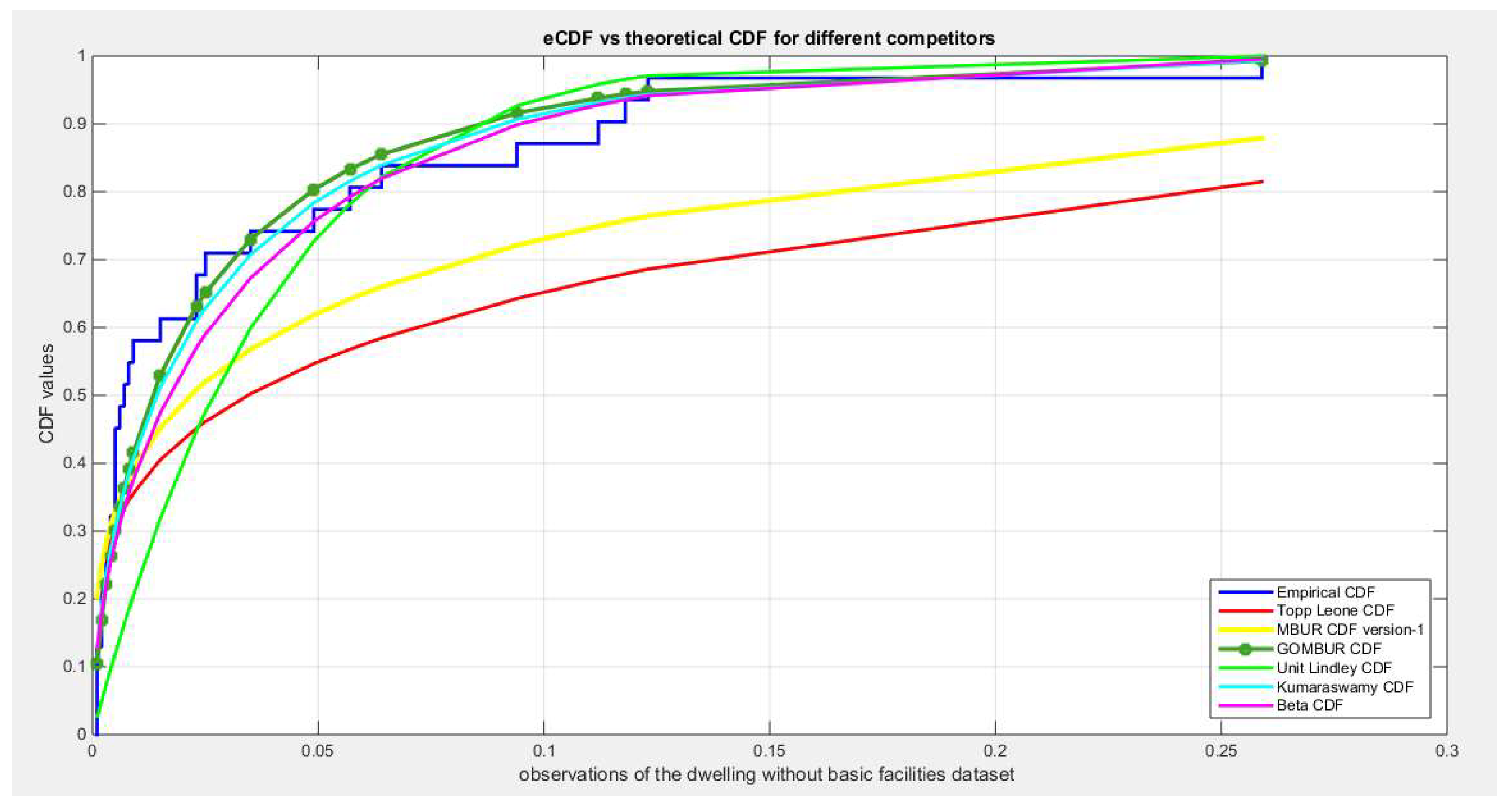
Figure 1.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of dwelling data.
Figure 1.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of dwelling data.
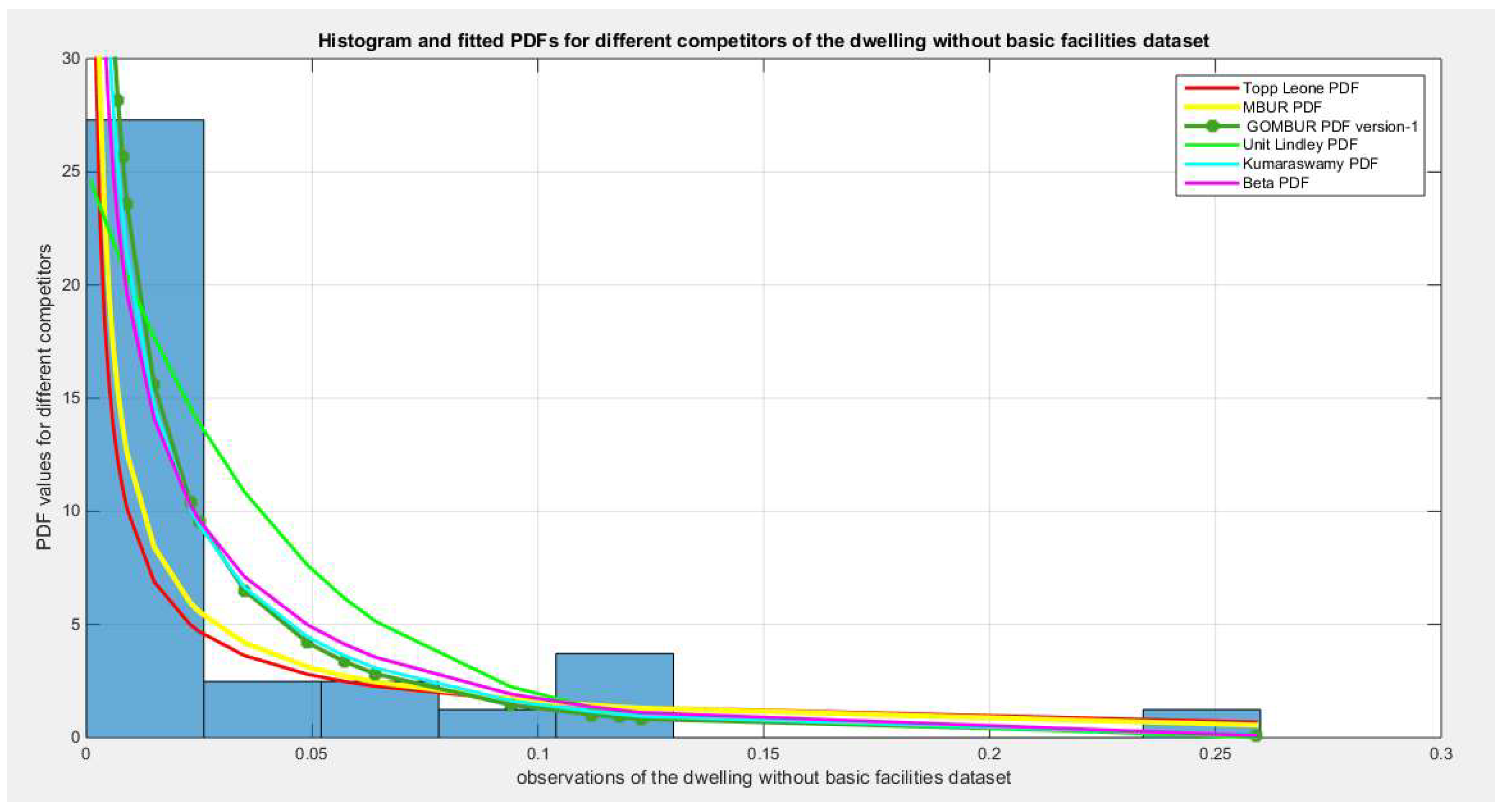
Figure 2.
shows the histogram of the dwelling data and the theoretical PDFs for the fitted distributions.
Figure 2.
shows the histogram of the dwelling data and the theoretical PDFs for the fitted distributions.
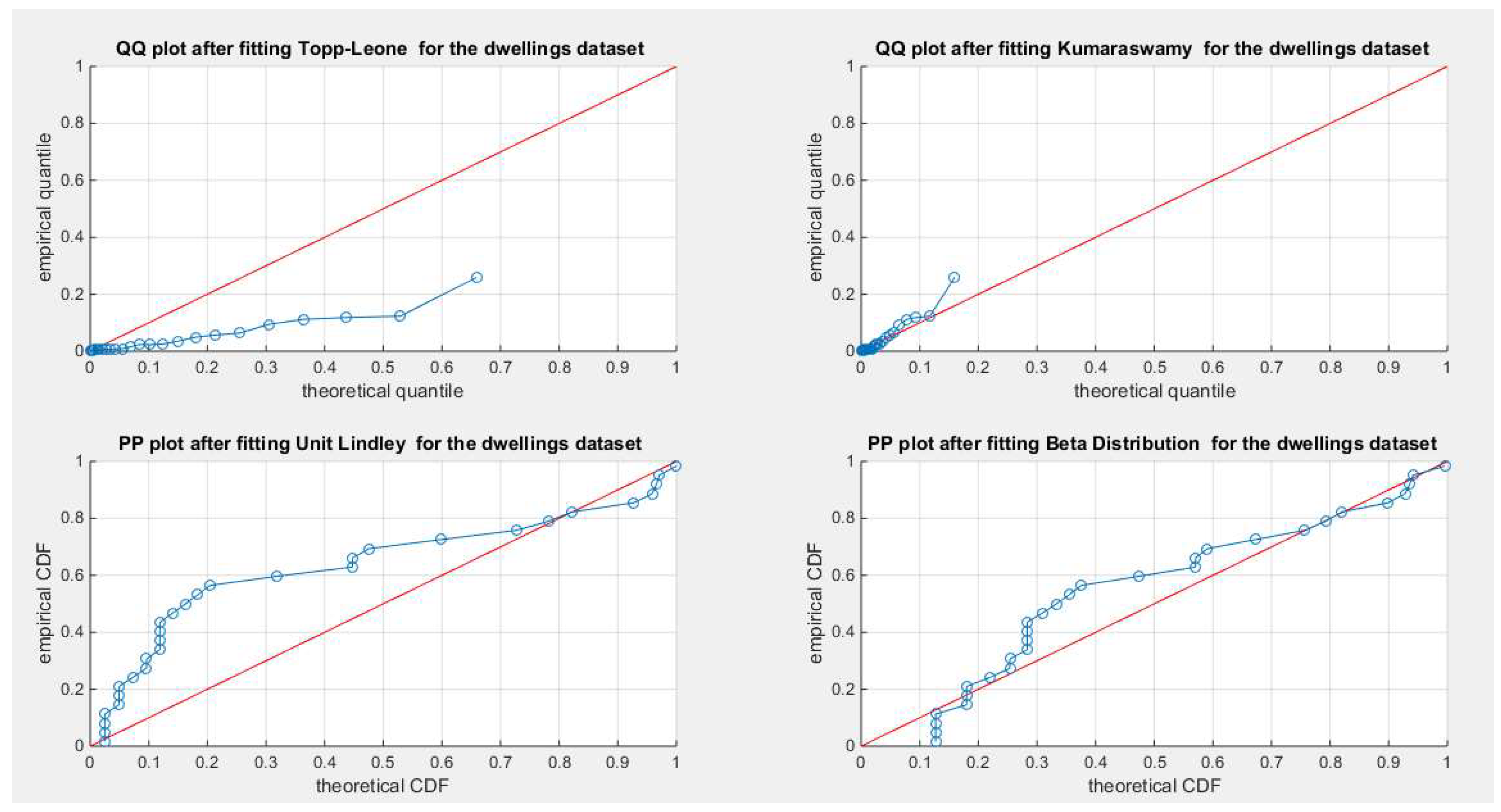
Figure 3.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution as regards dwelling dataset.
Figure 3.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution as regards dwelling dataset.
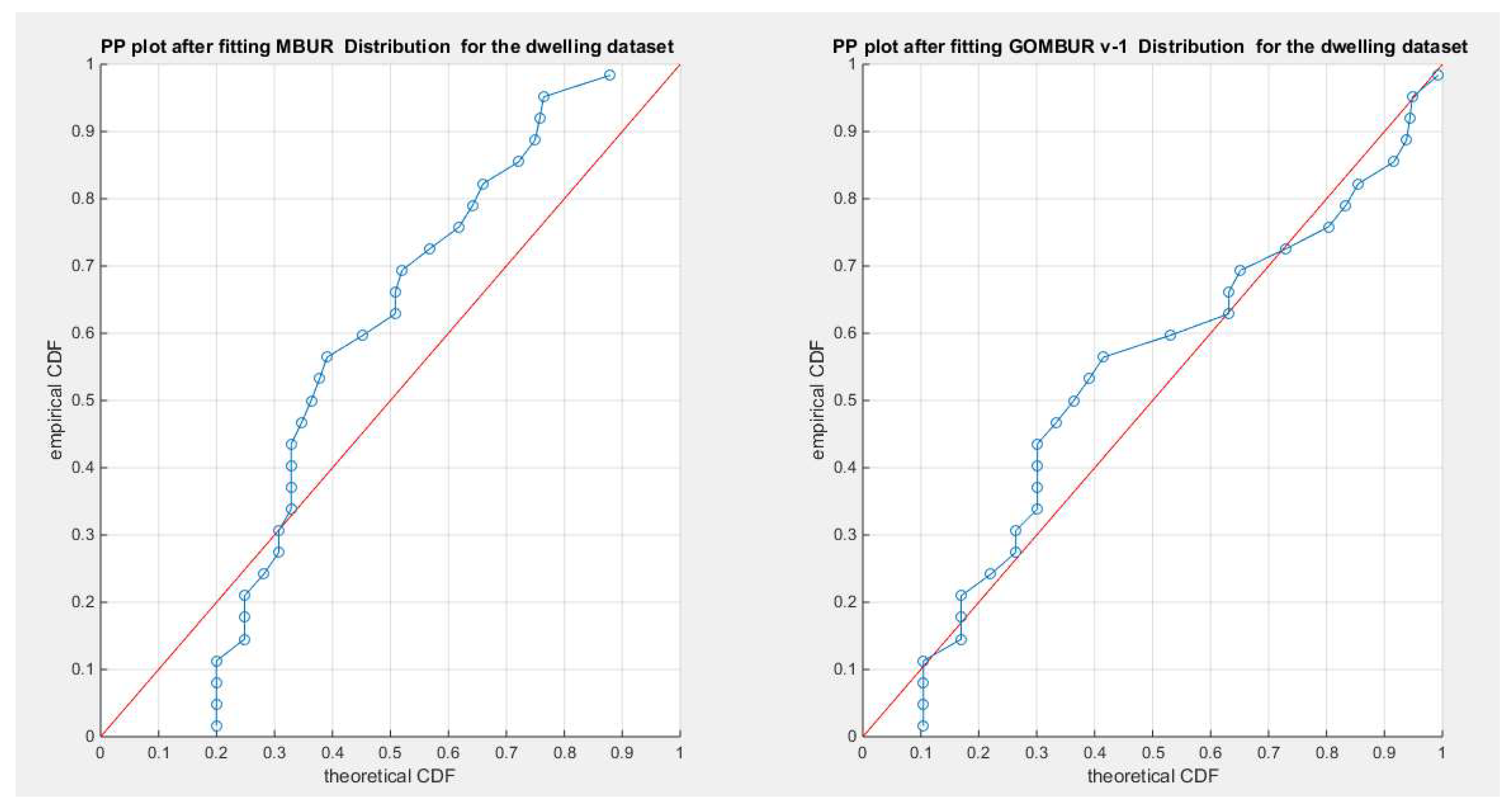
Figure 4.
shows the PP plot for the fitted MBUR & GOMBUR-1 as regards dwelling dataset. GOMBUR-1 on the right side are better aligned with the diagonal especially at the upper and lower tails than the center, in comparison with the MBUR distribution on the left subplot. This is attributed to the better fit of the generalized version than the fit of the MBUR distribution.
Figure 4.
shows the PP plot for the fitted MBUR & GOMBUR-1 as regards dwelling dataset. GOMBUR-1 on the right side are better aligned with the diagonal especially at the upper and lower tails than the center, in comparison with the MBUR distribution on the left subplot. This is attributed to the better fit of the generalized version than the fit of the MBUR distribution.
Figure 5.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 as regards dwelling dataset. They are identical.
Figure 5.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 as regards dwelling dataset. They are identical.
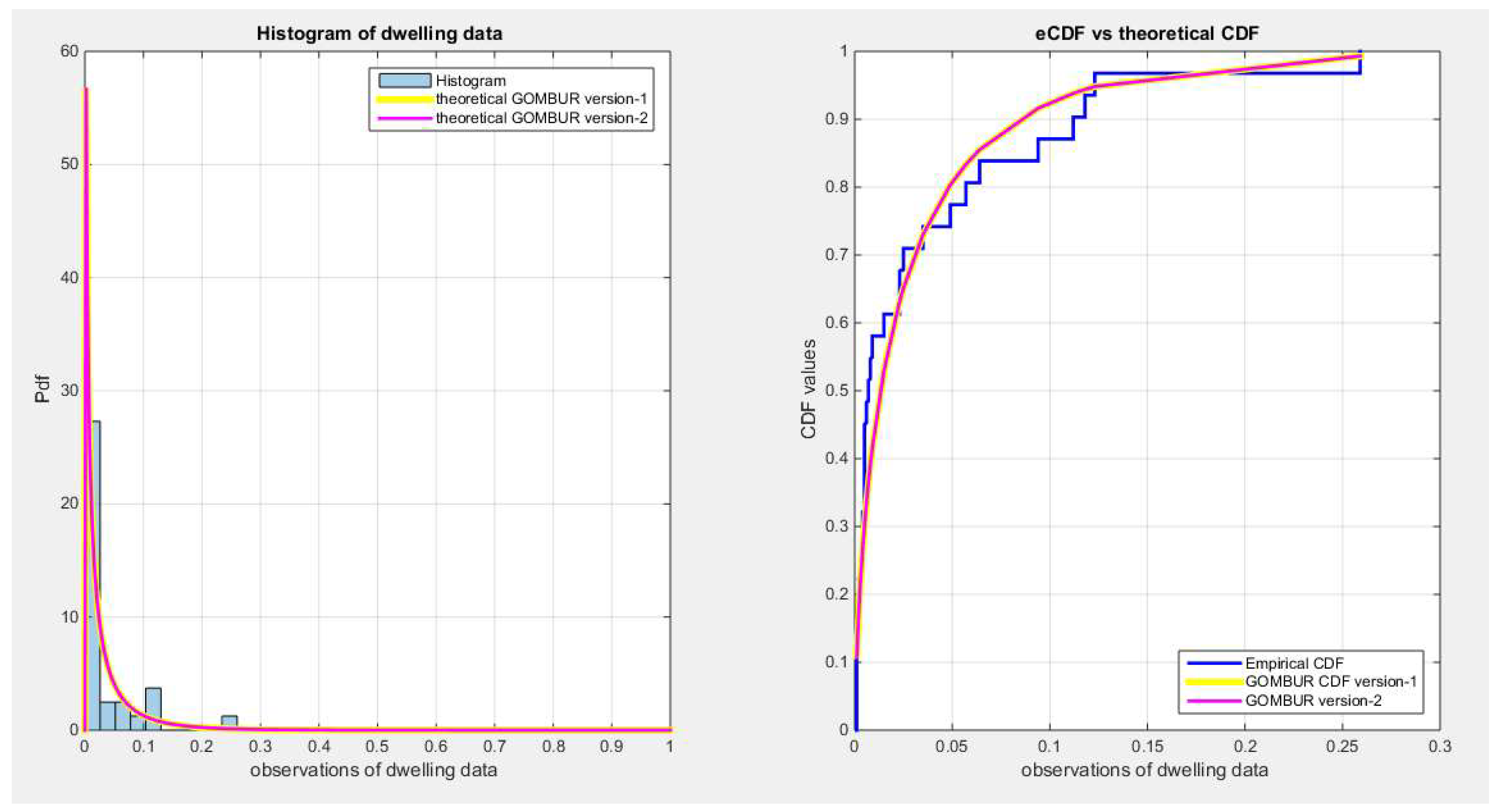
Figure 6.
shows on the left subplot the histogram of the dwelling data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Figure 6.
shows on the left subplot the histogram of the dwelling data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
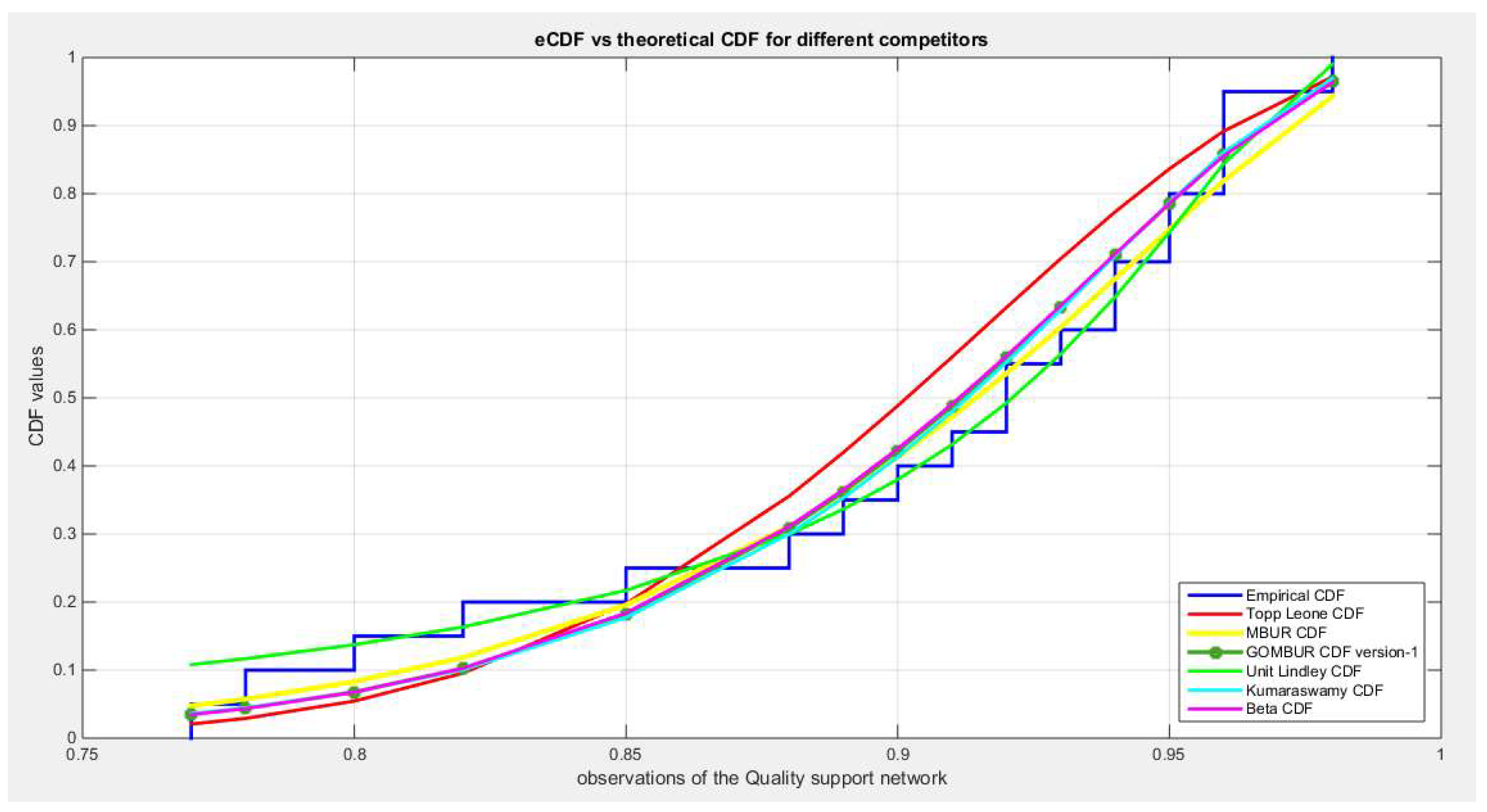
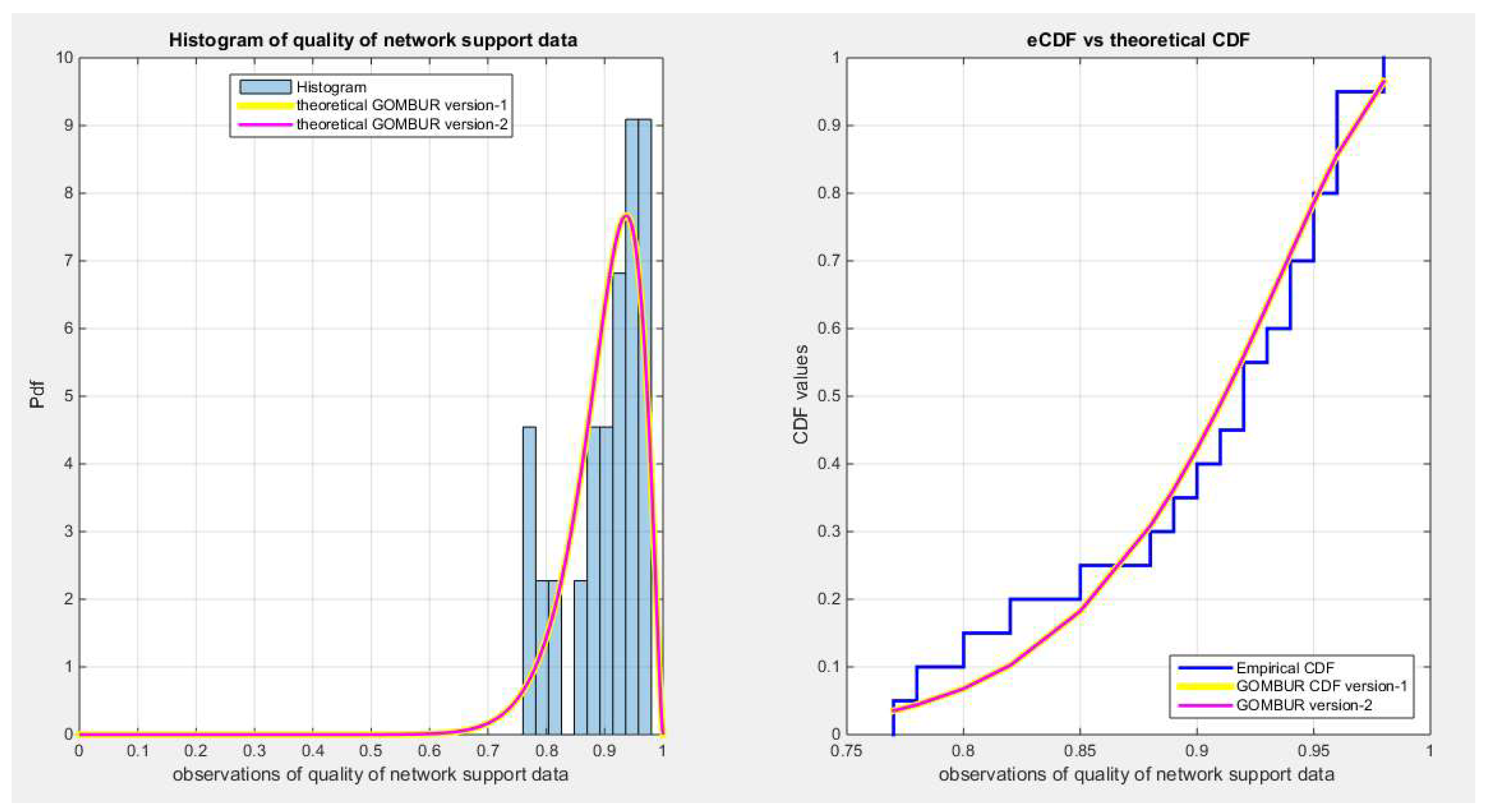
Figure 7.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of quality data.
Figure 7.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of quality data.
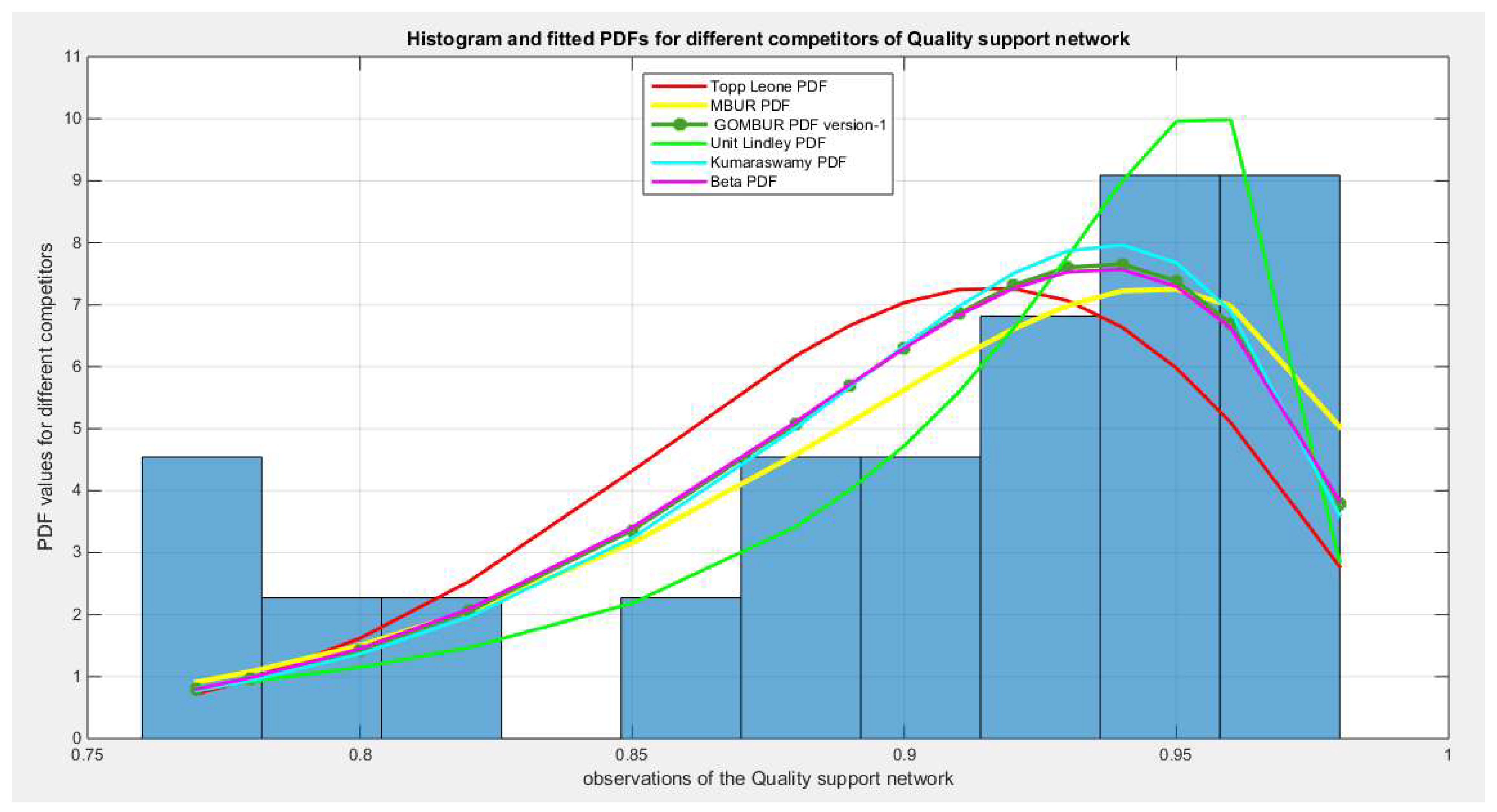
Figure 8.
shows the histogram of the quality data and the theoretical PDFs for the fitted distributions.
Figure 8.
shows the histogram of the quality data and the theoretical PDFs for the fitted distributions.
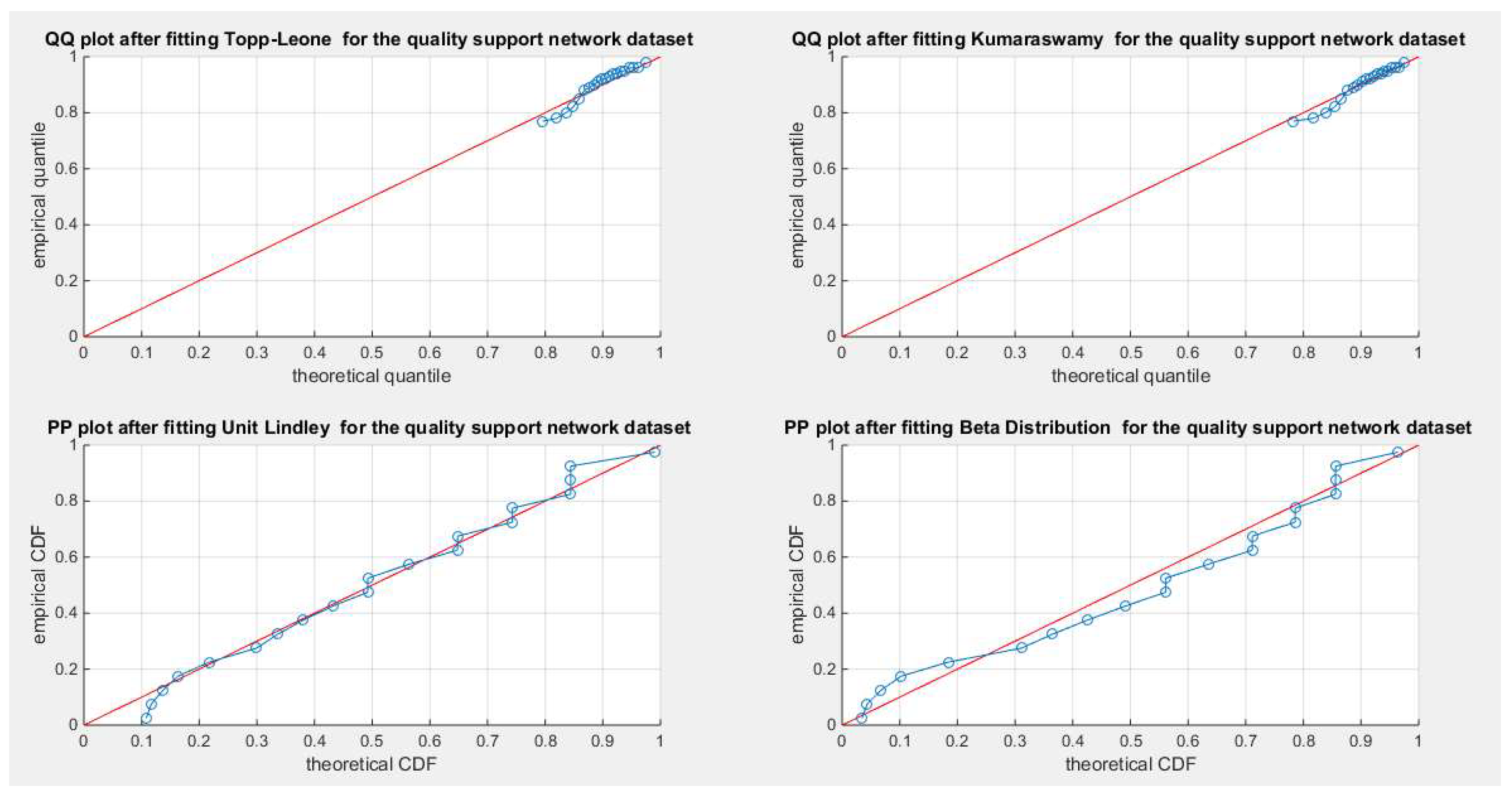
Figure 9.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution as regards quality dataset.
Figure 9.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution as regards quality dataset.
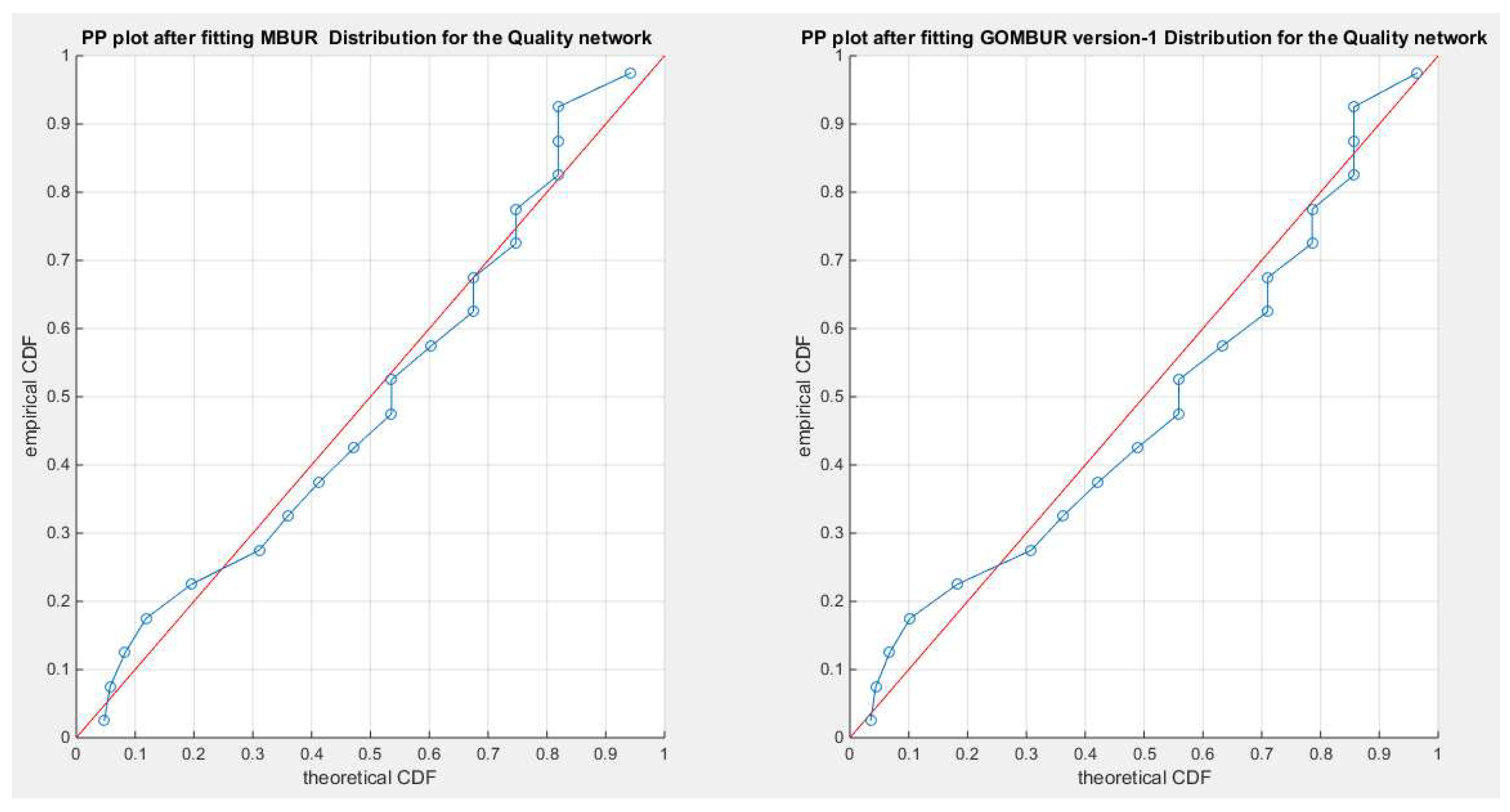
Figure 10.
shows the PP plot for the fitted MBUR & GOMBUR-1 as regards quality dataset.
Figure 10.
shows the PP plot for the fitted MBUR & GOMBUR-1 as regards quality dataset.
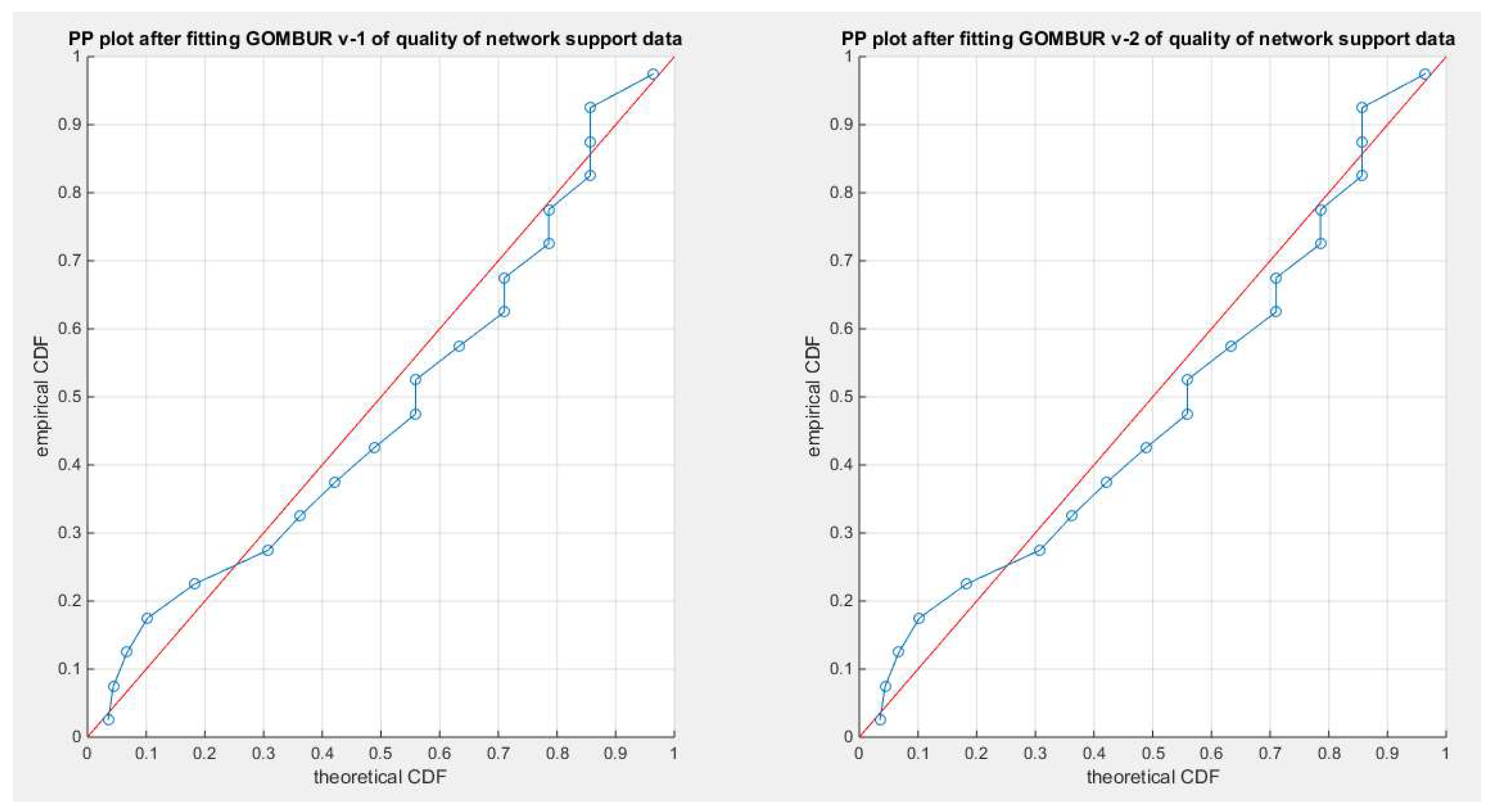
Figure 11.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 as regards quality dataset. They are identical.
Figure 11.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 as regards quality dataset. They are identical.
Figure 12.
shows on the left subplot the histogram of the quality data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Figure 12.
shows on the left subplot the histogram of the quality data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
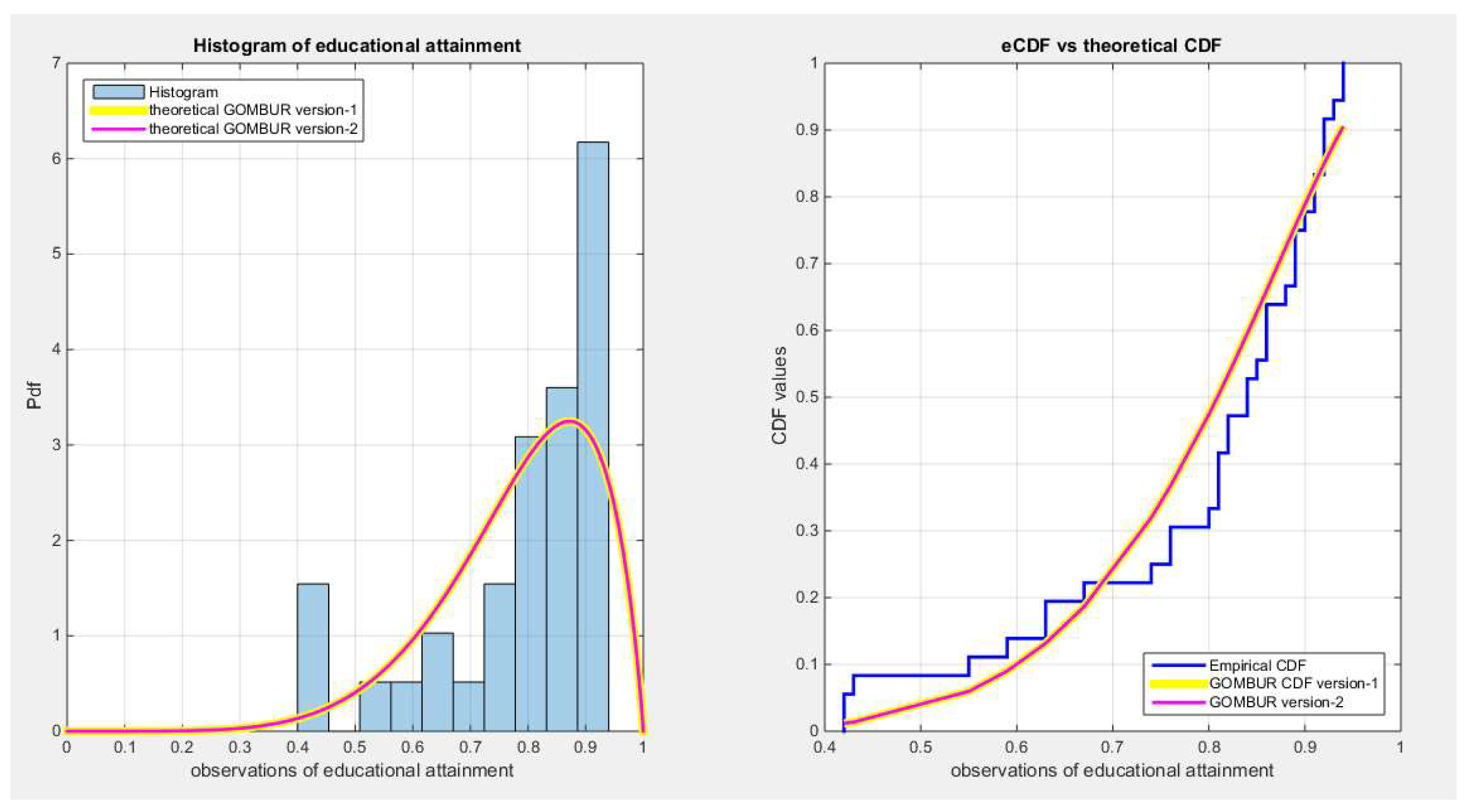
Figure 13.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of educational attainment data.
Figure 13.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of educational attainment data.
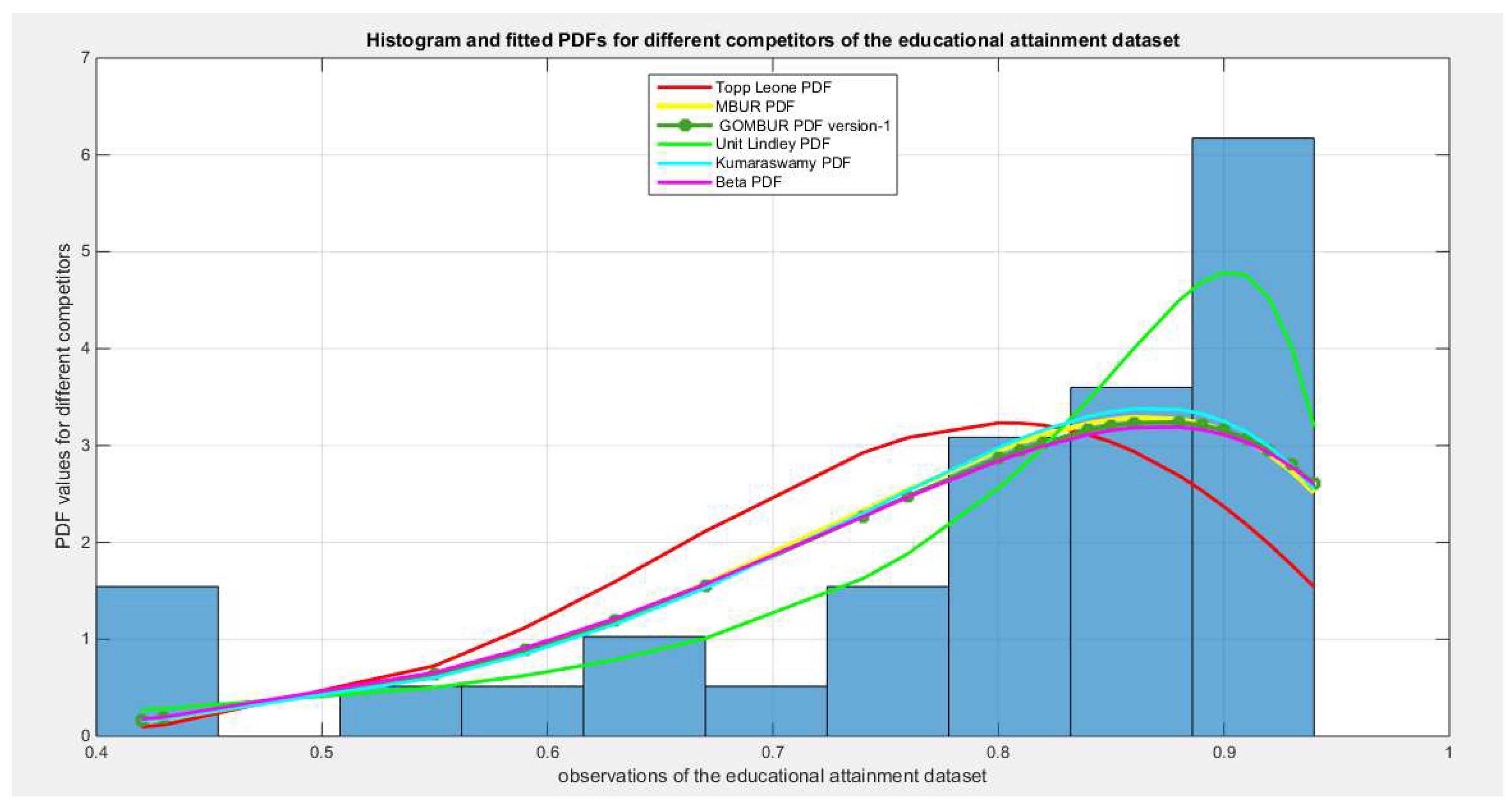
Figure 14.
shows the histogram of the educational attainment data and the theoretical PDFs for the fitted distributions.
Figure 14.
shows the histogram of the educational attainment data and the theoretical PDFs for the fitted distributions.
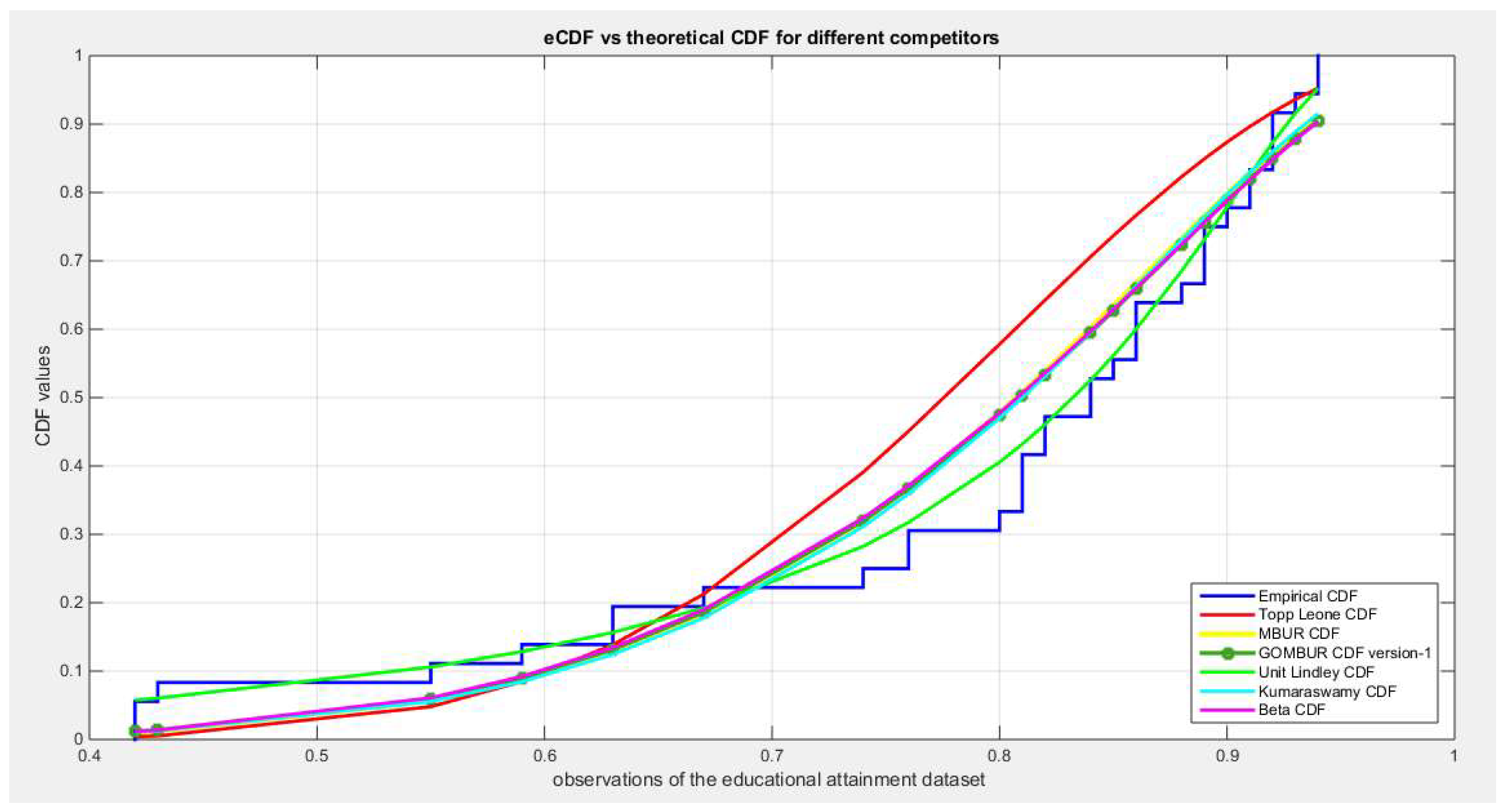
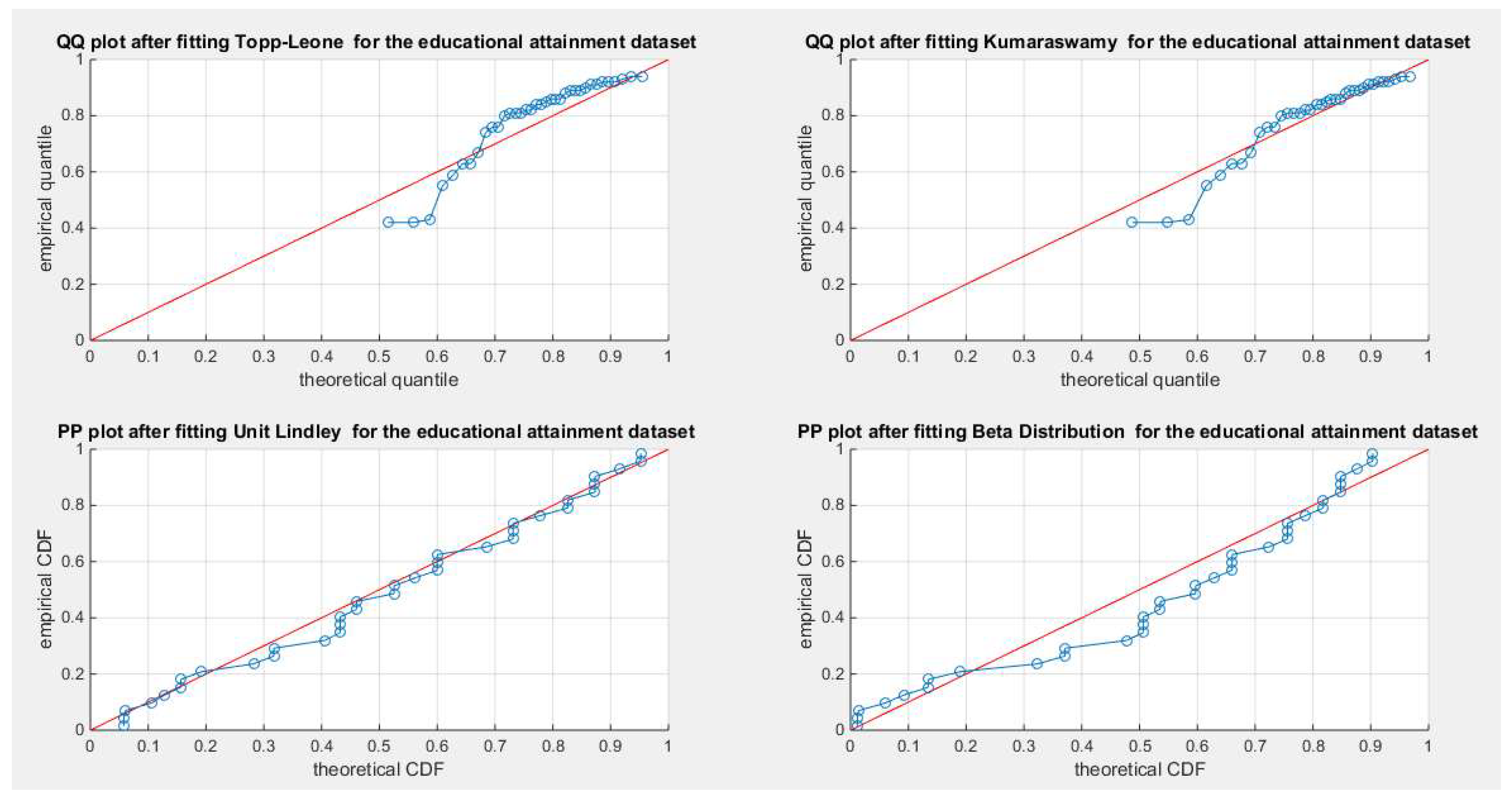
Figure 15.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution as regards educational attainment dataset.
Figure 15.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution as regards educational attainment dataset.
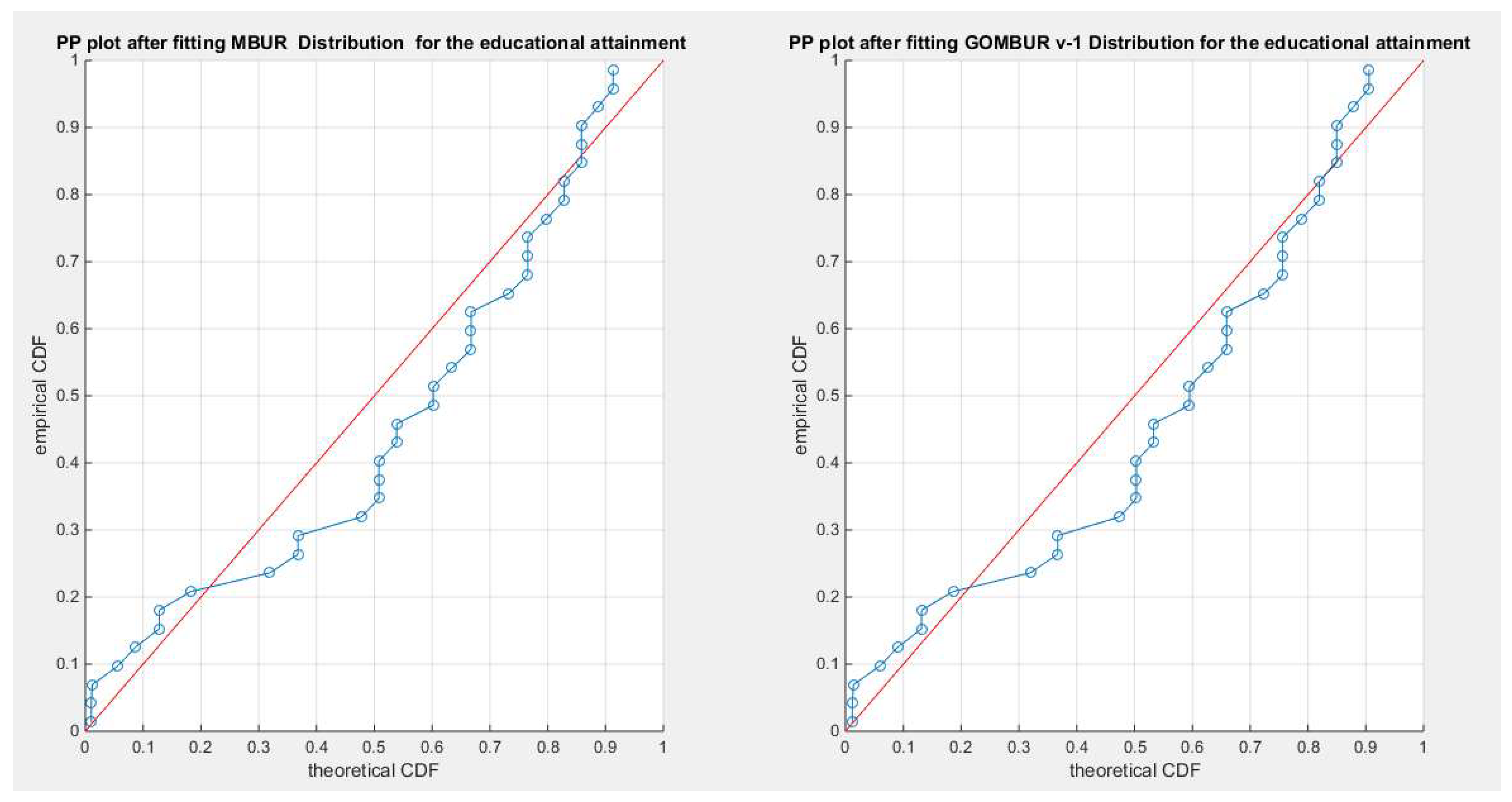
Figure 16.
shows the PP plot for the fitted MBUR & GOMBUR-1 as regards educational attainment dataset. The alignments with the diagonal are nearly identical all through the course.
Figure 16.
shows the PP plot for the fitted MBUR & GOMBUR-1 as regards educational attainment dataset. The alignments with the diagonal are nearly identical all through the course.
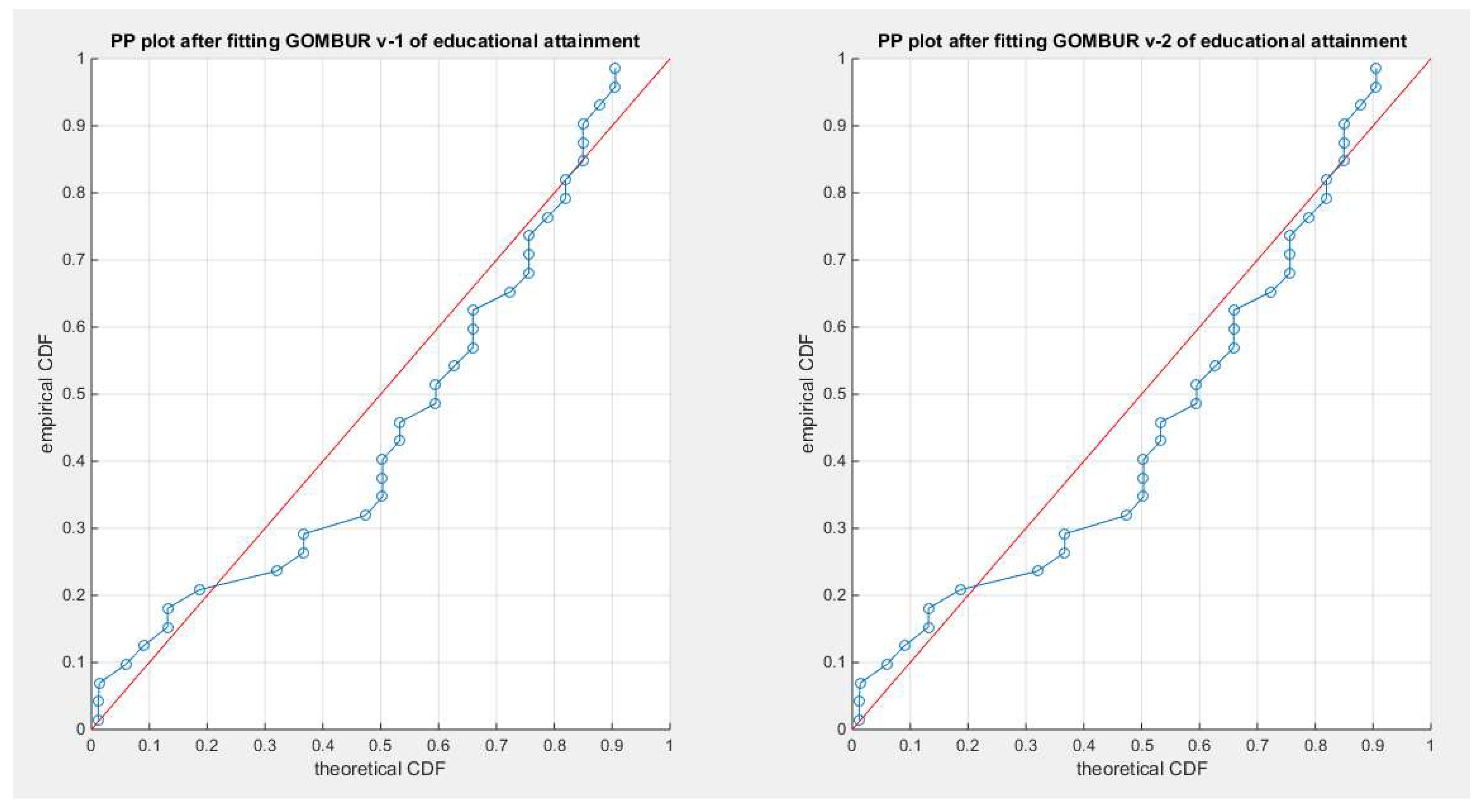
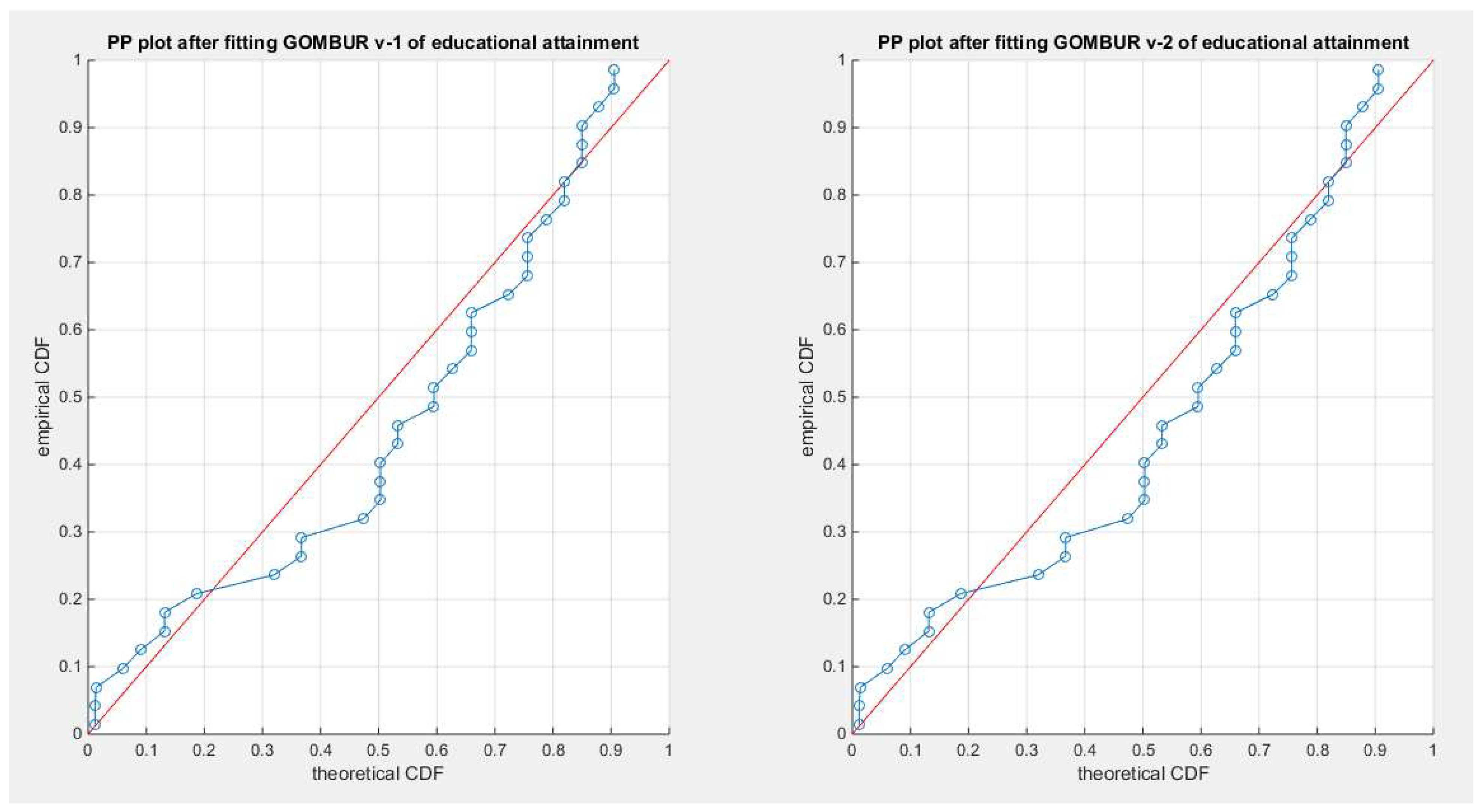
Figure 17.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for educational attainment dataset. They are identical.
Figure 17.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for educational attainment dataset. They are identical.
Figure 18.
shows on the left subplot the histogram of the educational attainment data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Figure 18.
shows on the left subplot the histogram of the educational attainment data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Figure 19.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of flood data.
Figure 19.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of flood data.
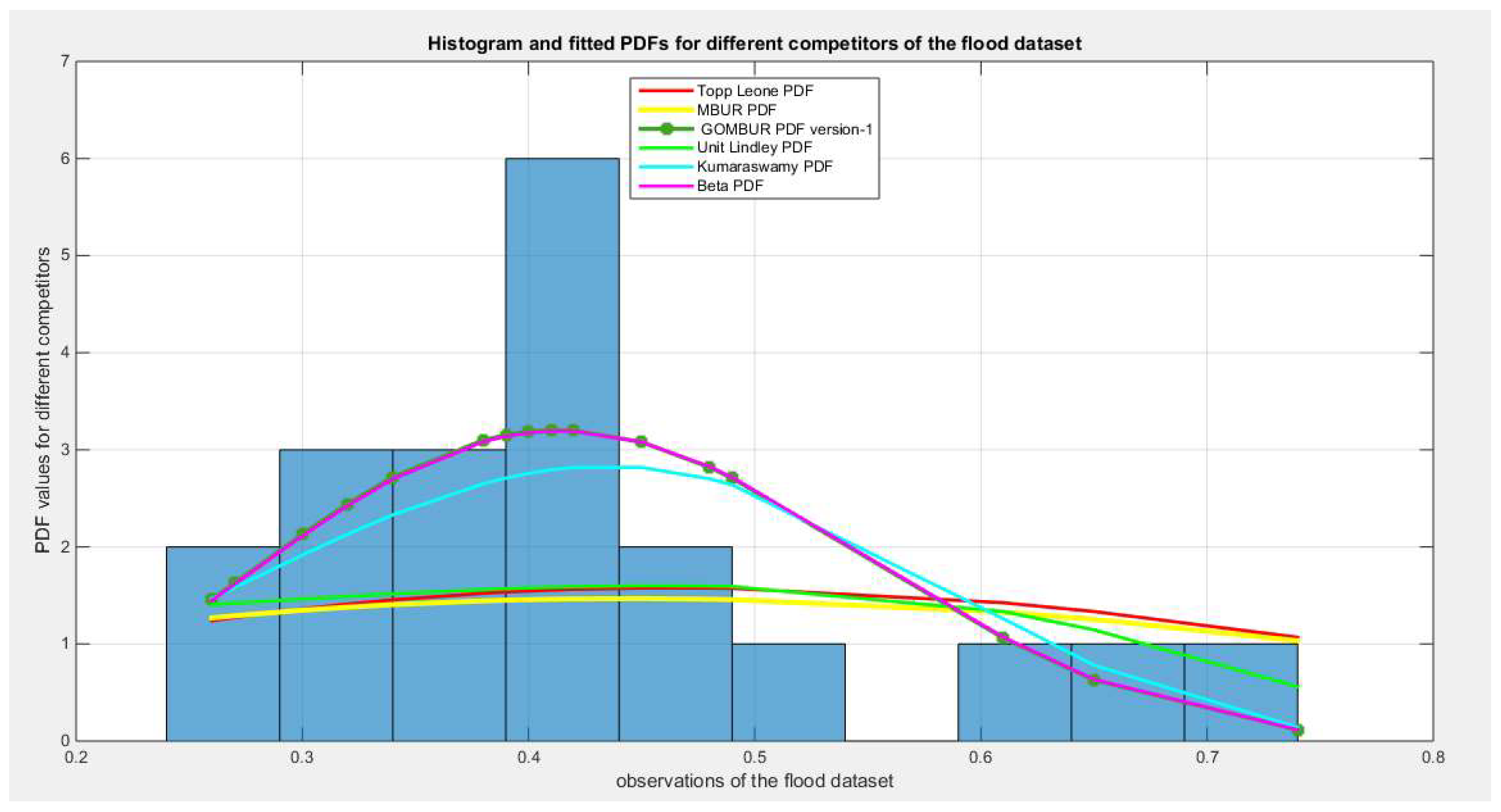
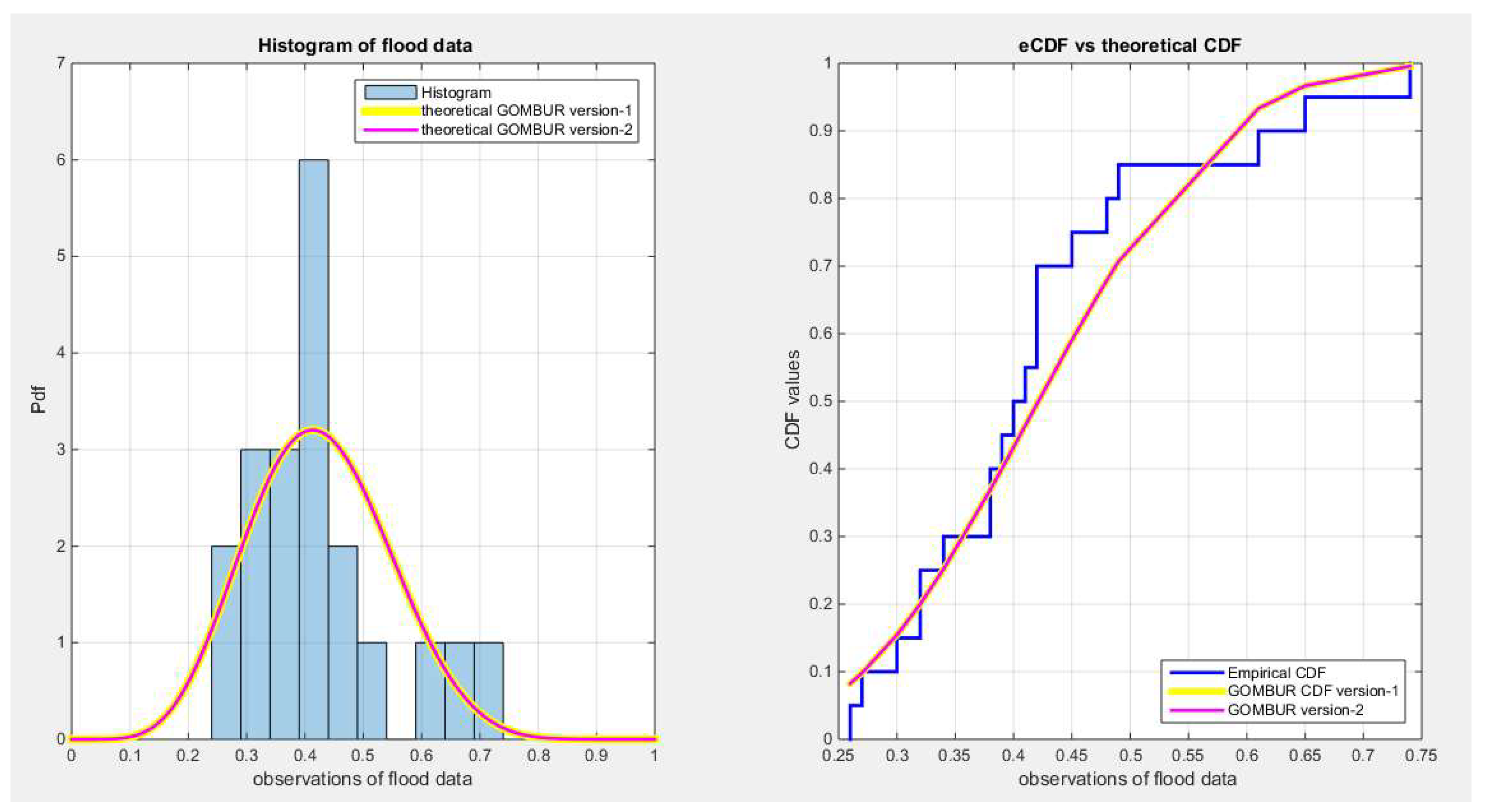
Figure 20.
shows the histogram of the flood data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 perfectly aligns with the Beta distribution.
Figure 20.
shows the histogram of the flood data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 perfectly aligns with the Beta distribution.
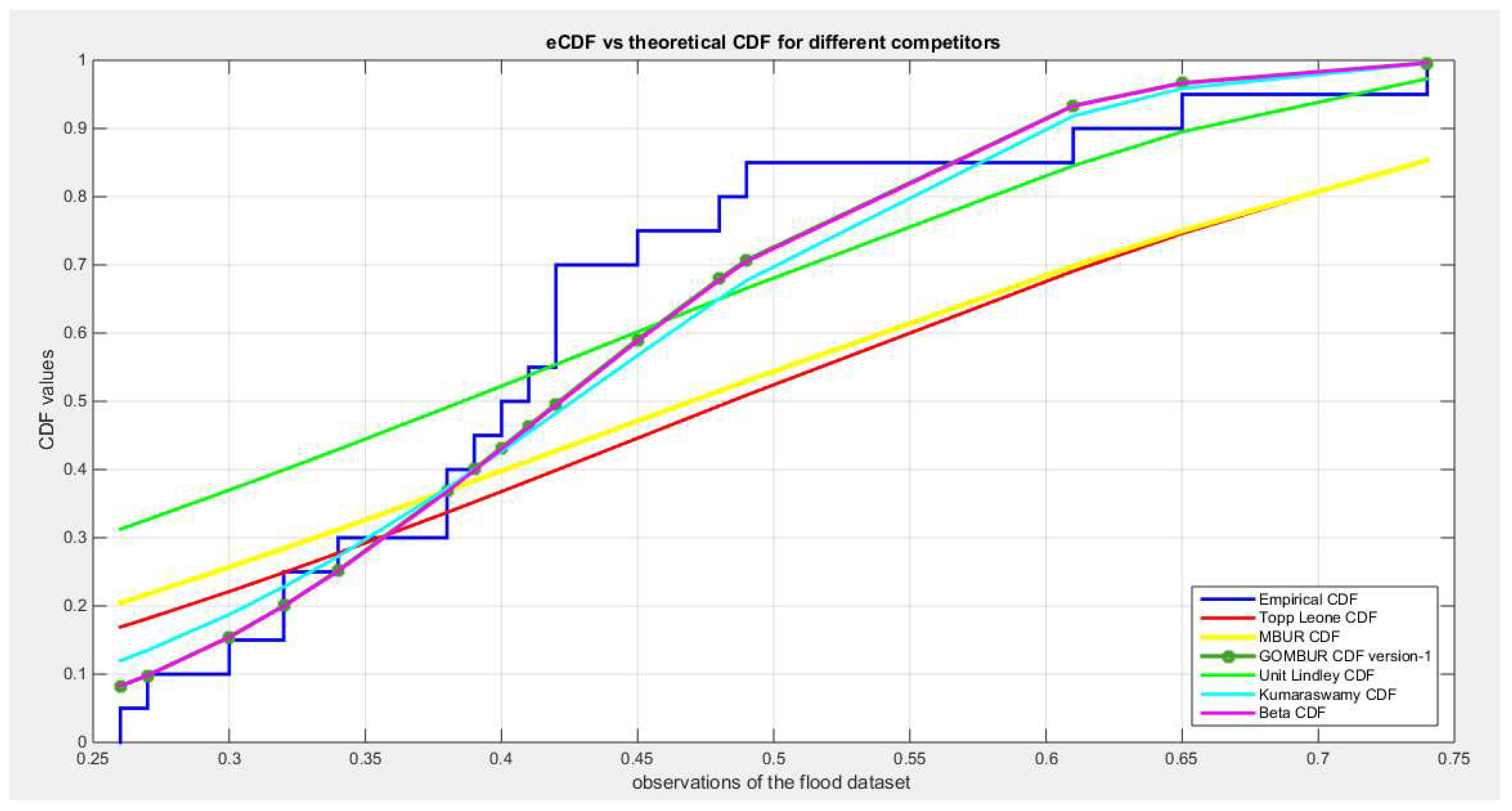
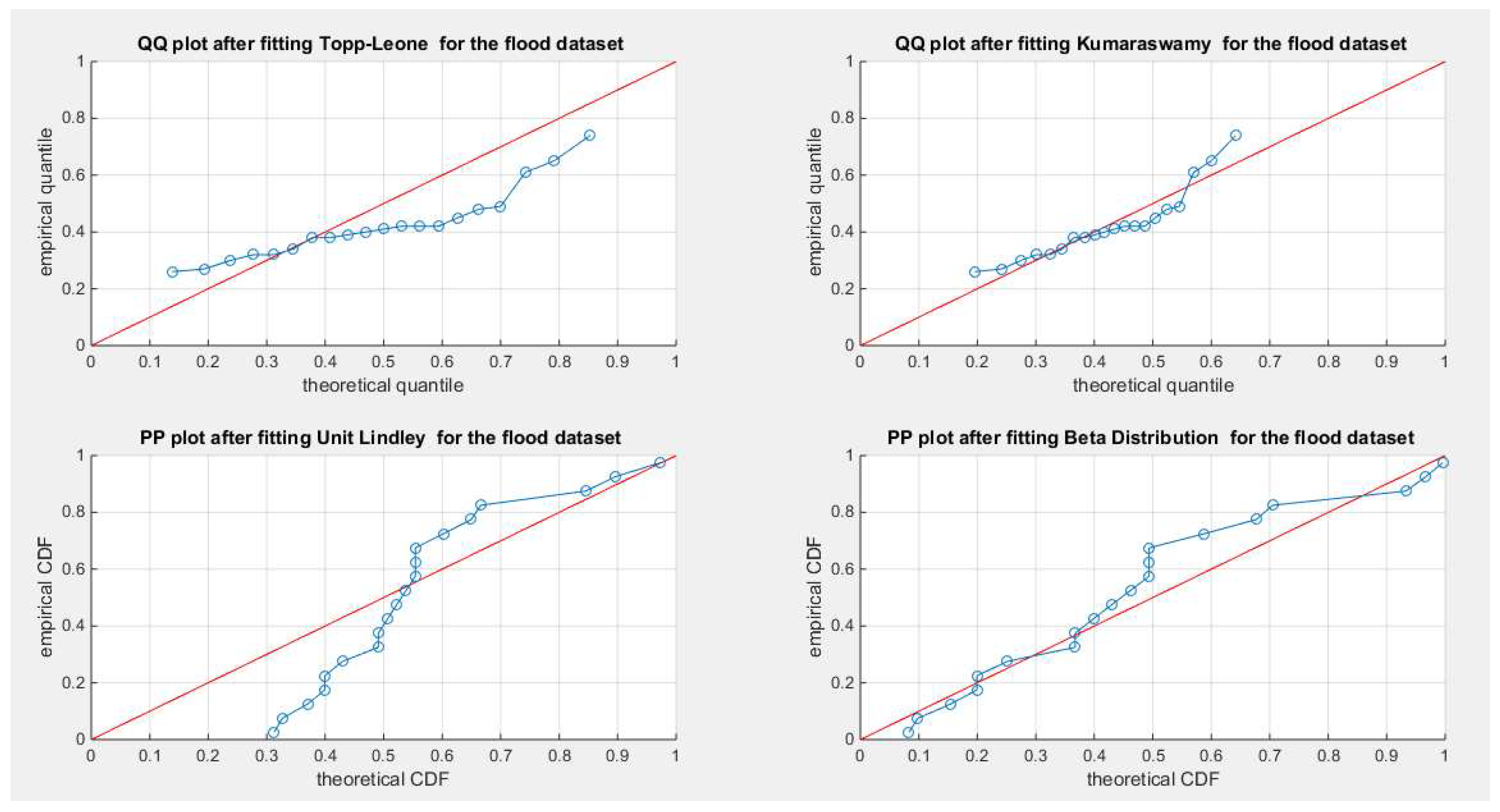
Figure 21.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the flood dataset.
Figure 21.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the flood dataset.
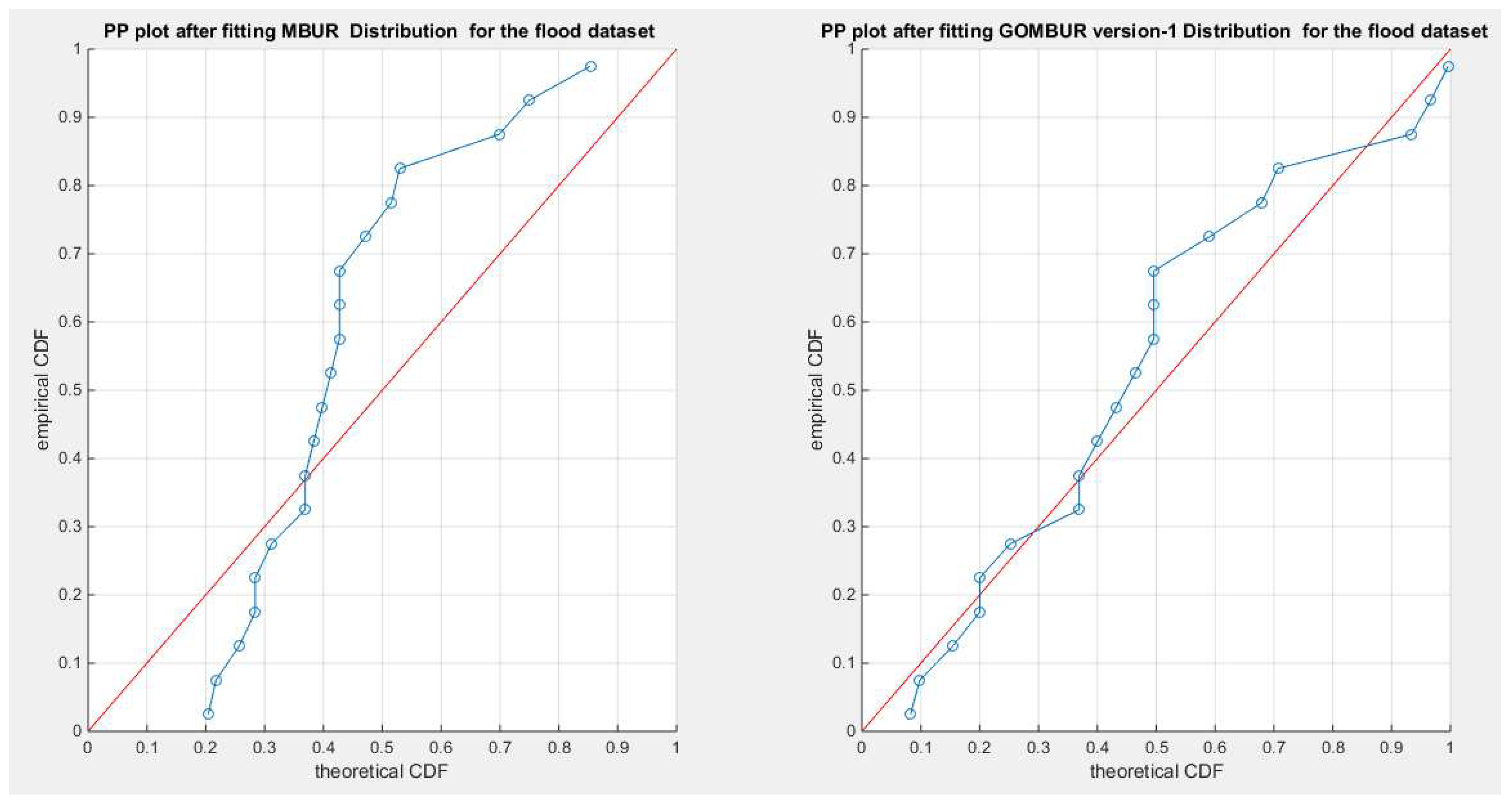
Figure 22.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the flood dataset. The alignments with the diagonal shows marked improvement after fitting the GOMBUR-1 than the alignment with MBUR especially at the lower and upper tails.
Figure 22.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the flood dataset. The alignments with the diagonal shows marked improvement after fitting the GOMBUR-1 than the alignment with MBUR especially at the lower and upper tails.
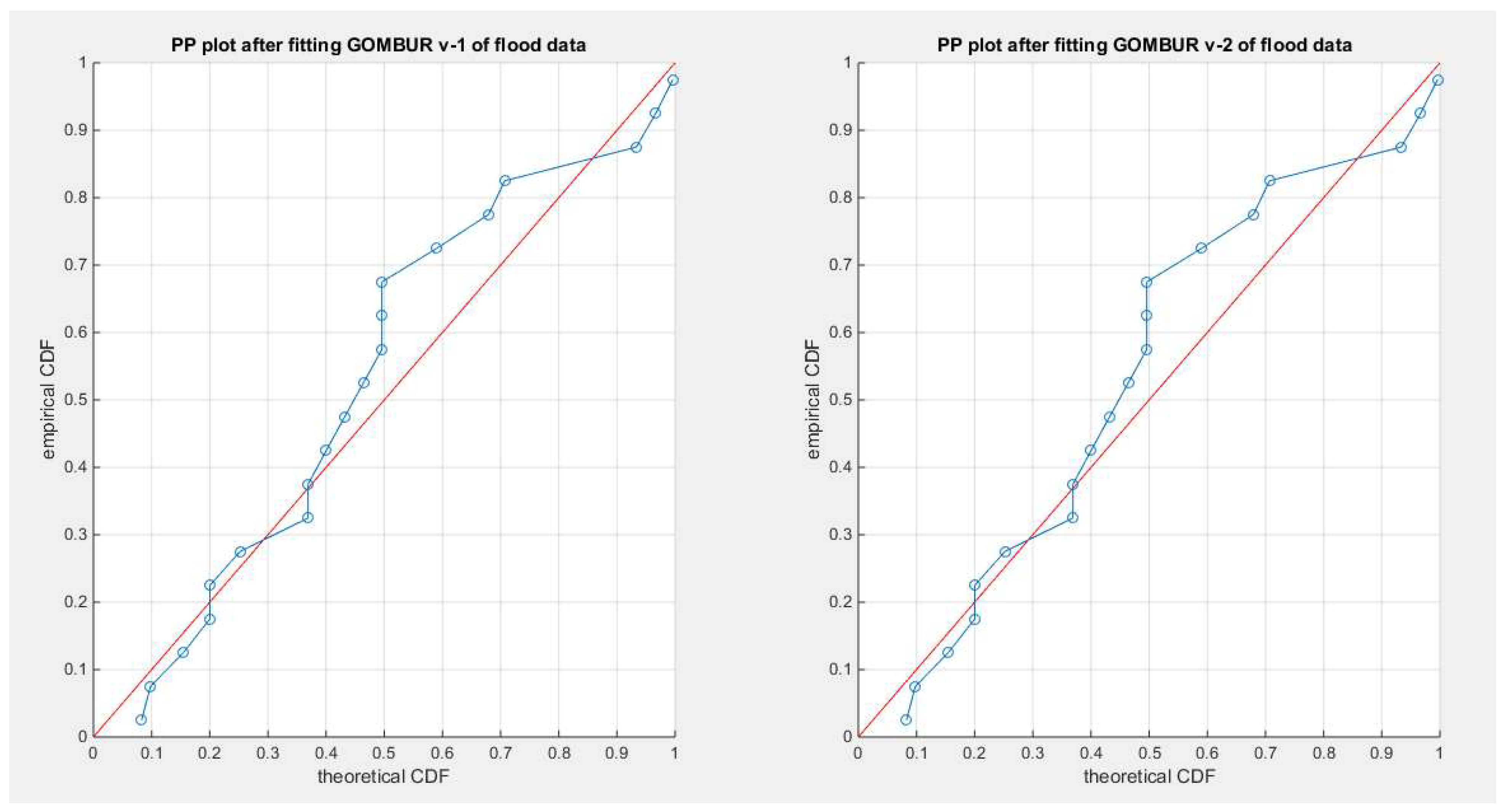
Figure 23.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for flood dataset. They are identical.
Figure 23.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for flood dataset. They are identical.
Figure 24.
shows on the left subplot the histogram of the flood data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Figure 24.
shows on the left subplot the histogram of the flood data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Figure 25.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of time between failures data.
Figure 25.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of time between failures data.
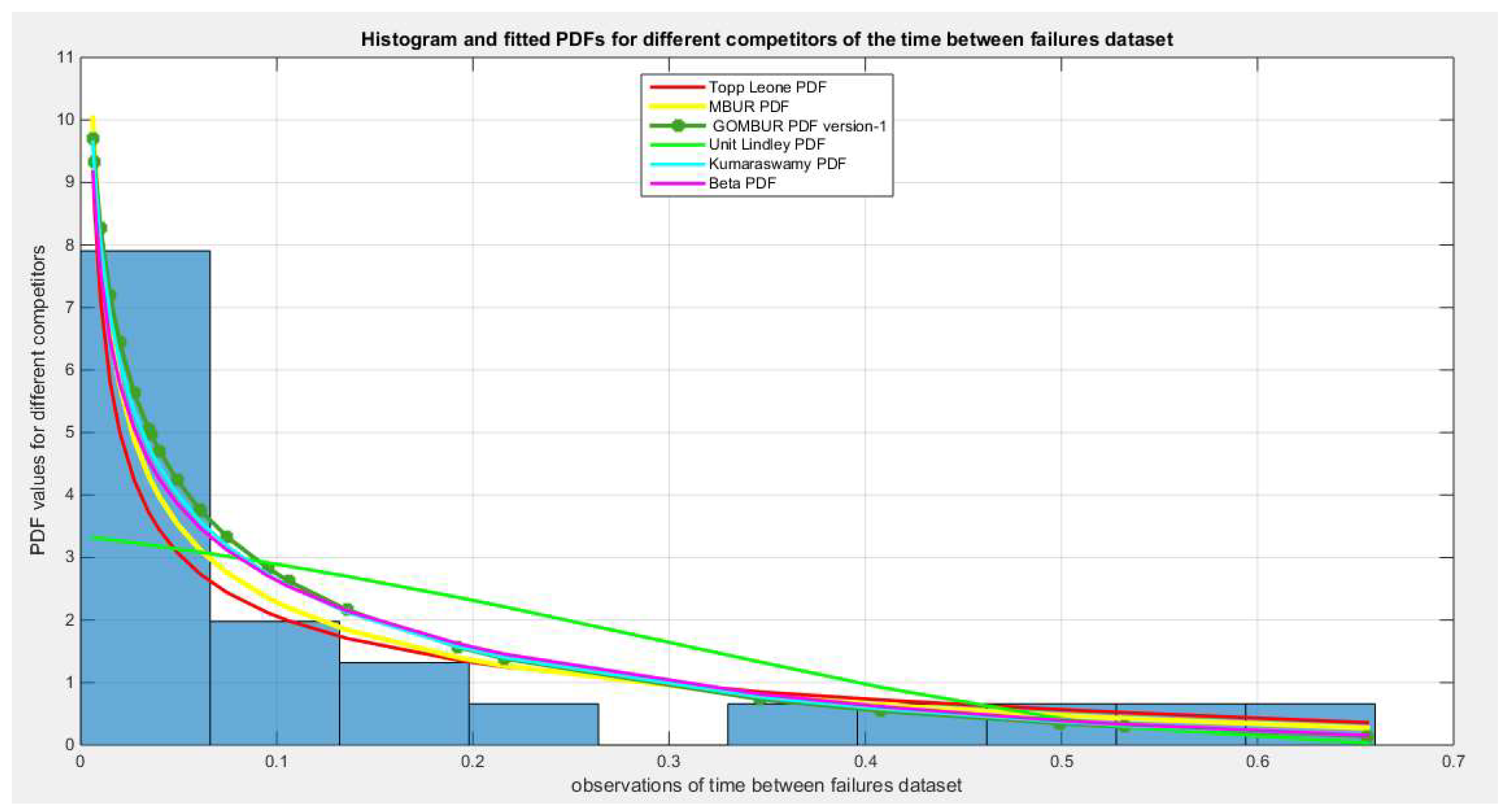
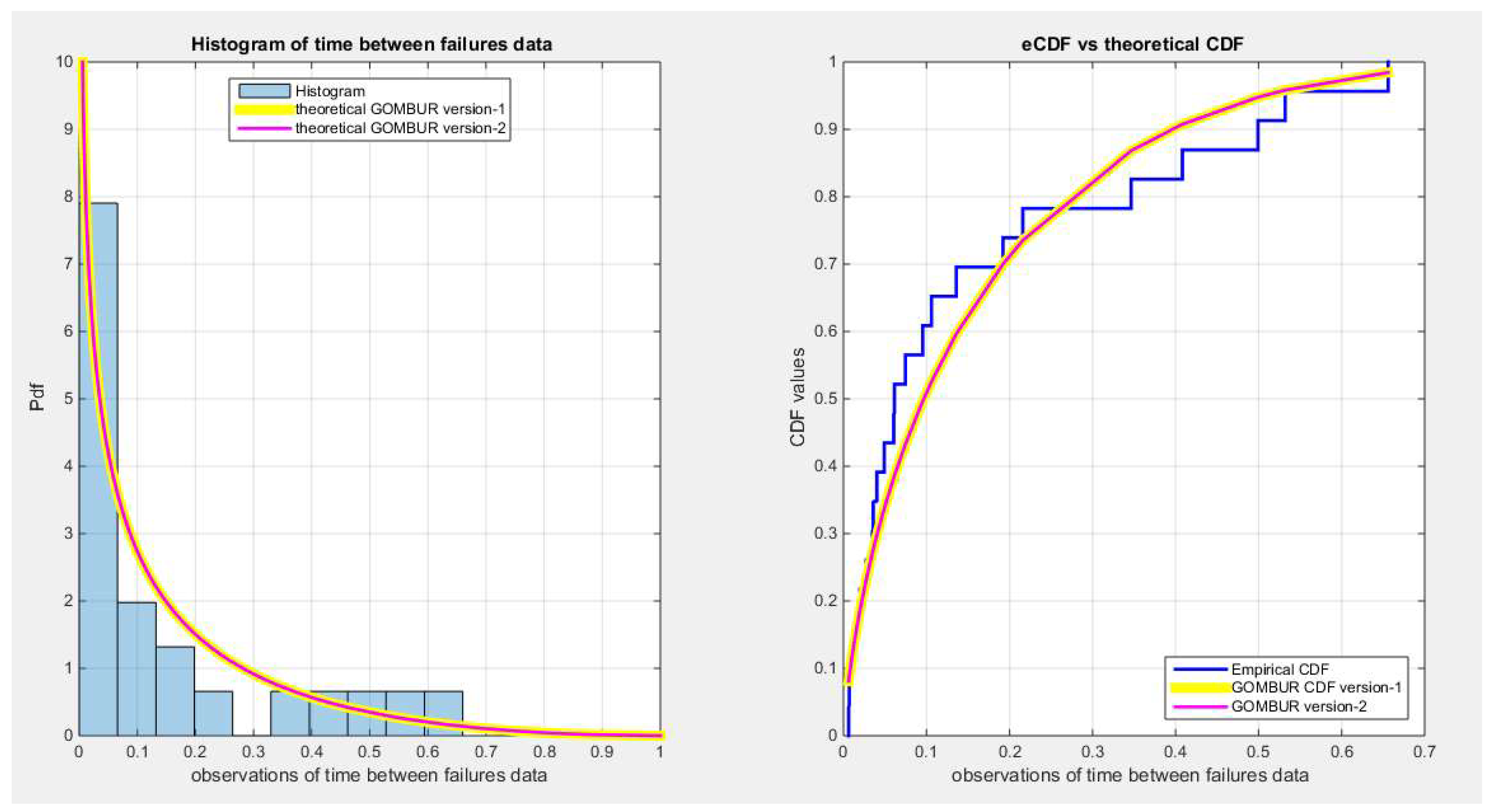
Figure 26.
shows the histogram of the time between failures data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 shows near perfect alignments with all distributions at the boundaries except with Unit Lindley which does not fit the data.
Figure 26.
shows the histogram of the time between failures data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 shows near perfect alignments with all distributions at the boundaries except with Unit Lindley which does not fit the data.
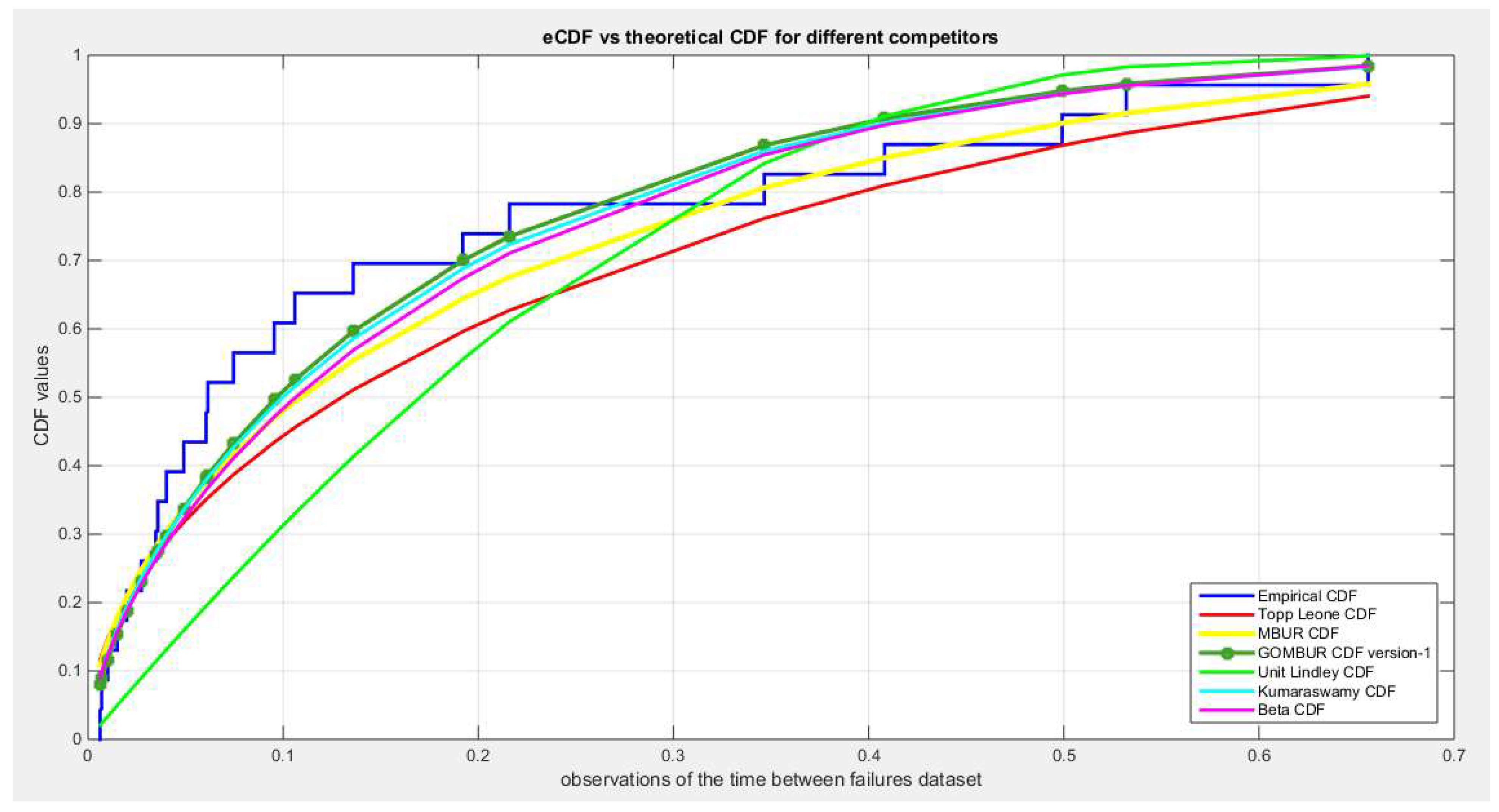
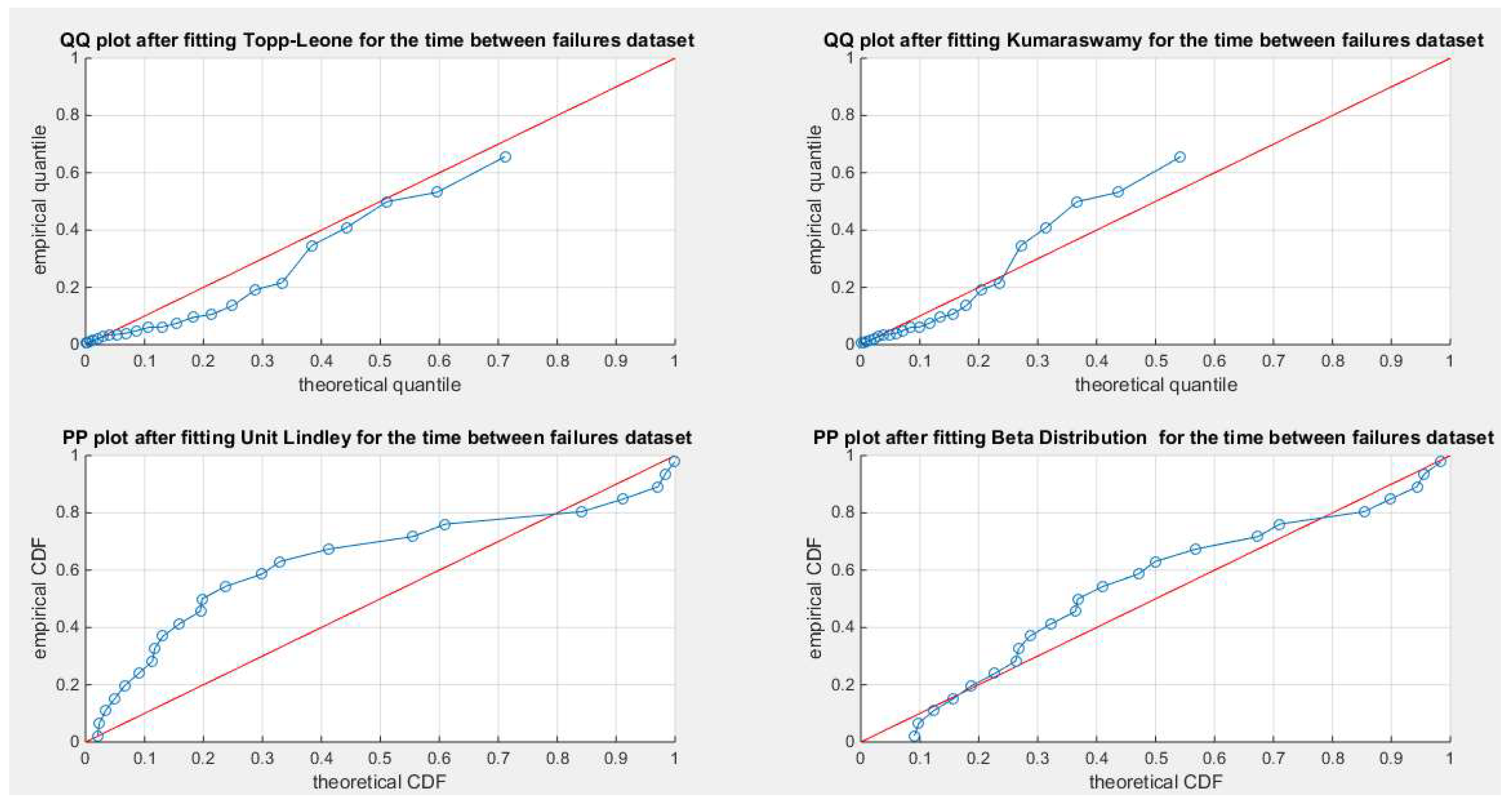
Figure 27.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the time between failures dataset.
Figure 27.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the time between failures dataset.
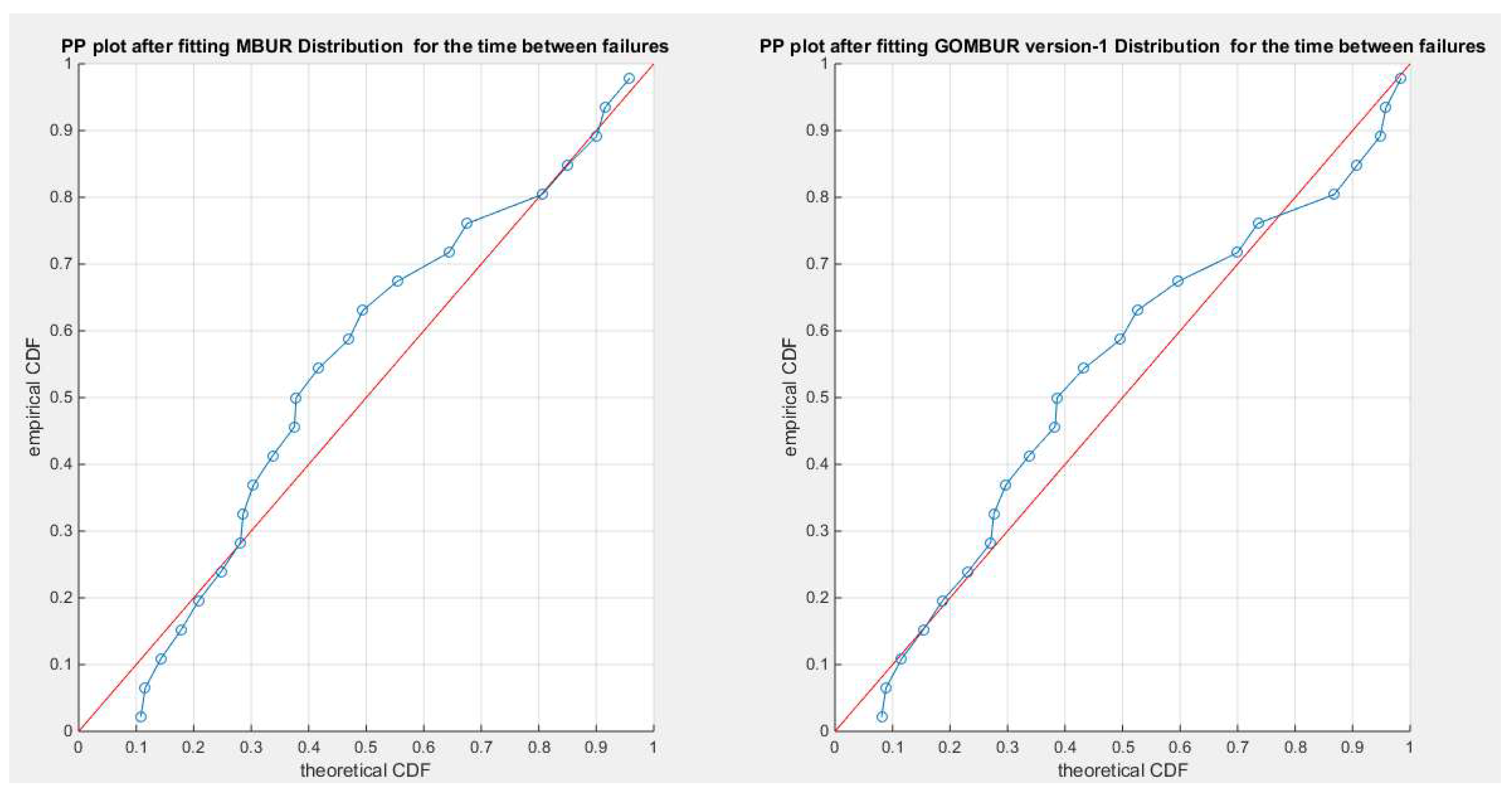
Figure 28.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the time between failures dataset. The alignment with the diagonal shows improvement after fitting the GOMBUR-1 than the alignment with MBUR especially at the lower tail.
Figure 28.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the time between failures dataset. The alignment with the diagonal shows improvement after fitting the GOMBUR-1 than the alignment with MBUR especially at the lower tail.
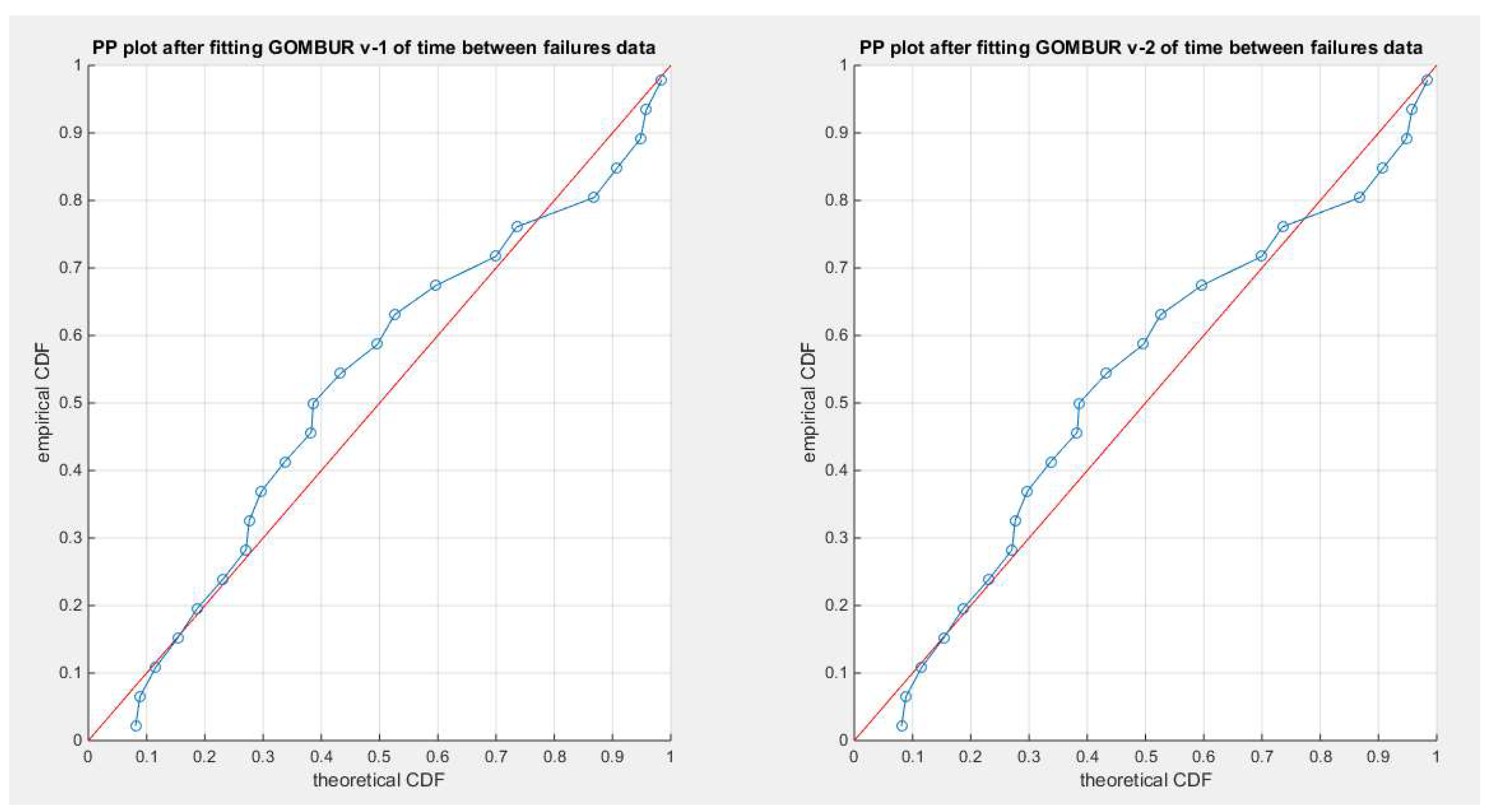
Figure 29.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for time between failure dataset. They are identical.
Figure 29.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for time between failure dataset. They are identical.
Figure 30.
shows on the left subplot the histogram of the time between failures data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Figure 30.
shows on the left subplot the histogram of the time between failures data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
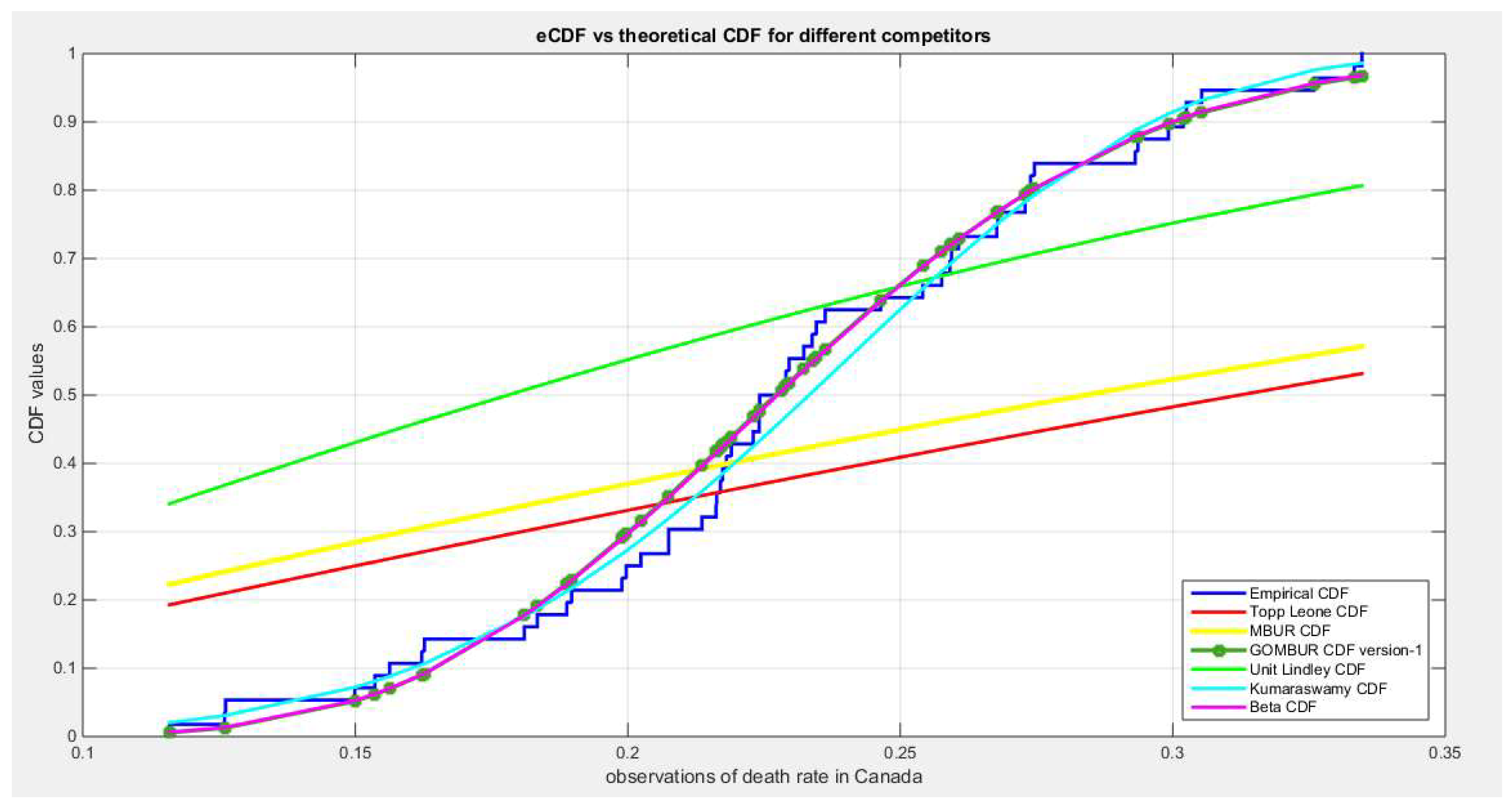
Figure 31.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of death rate in Canada data.
Figure 31.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of death rate in Canada data.
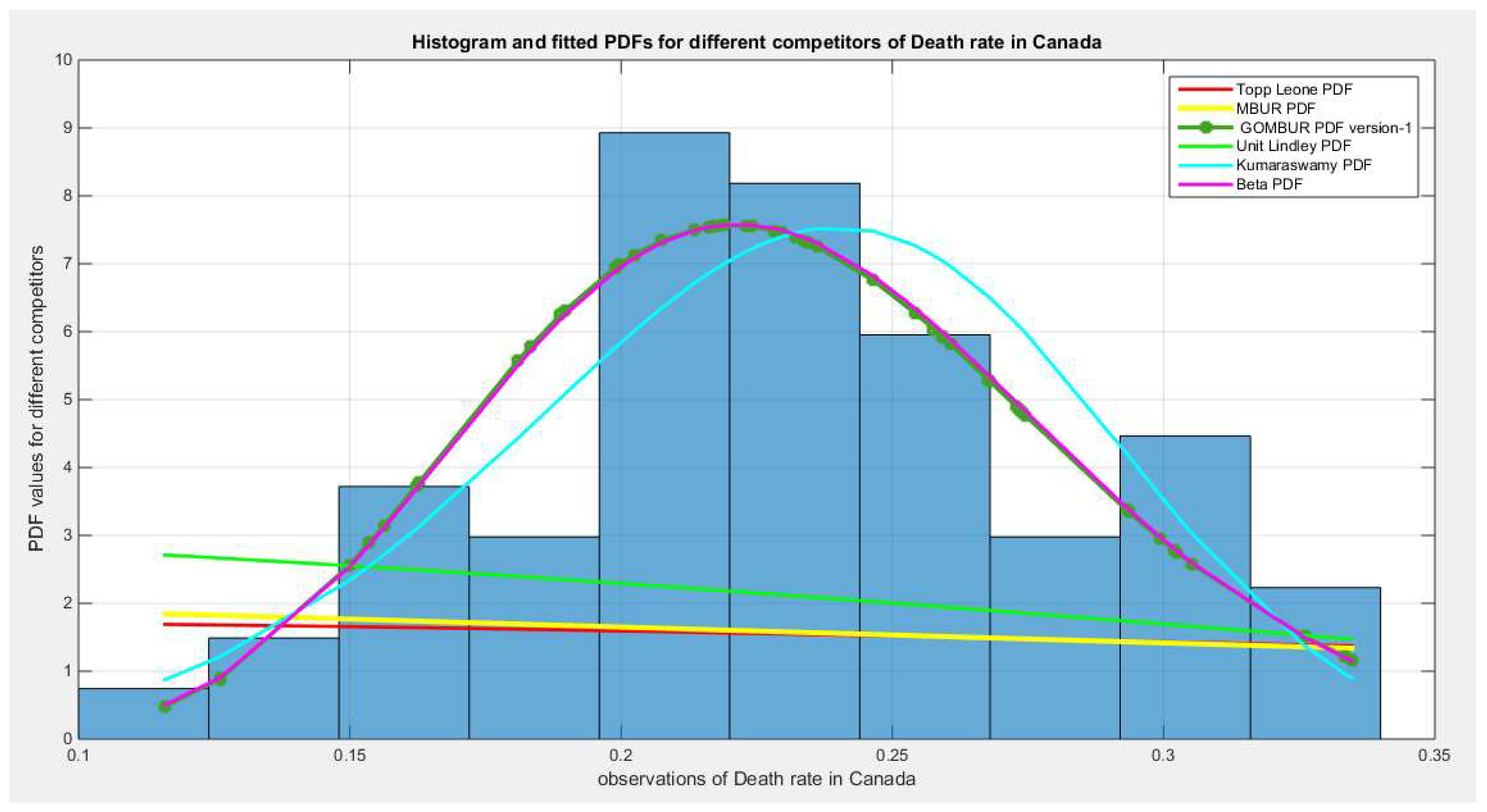
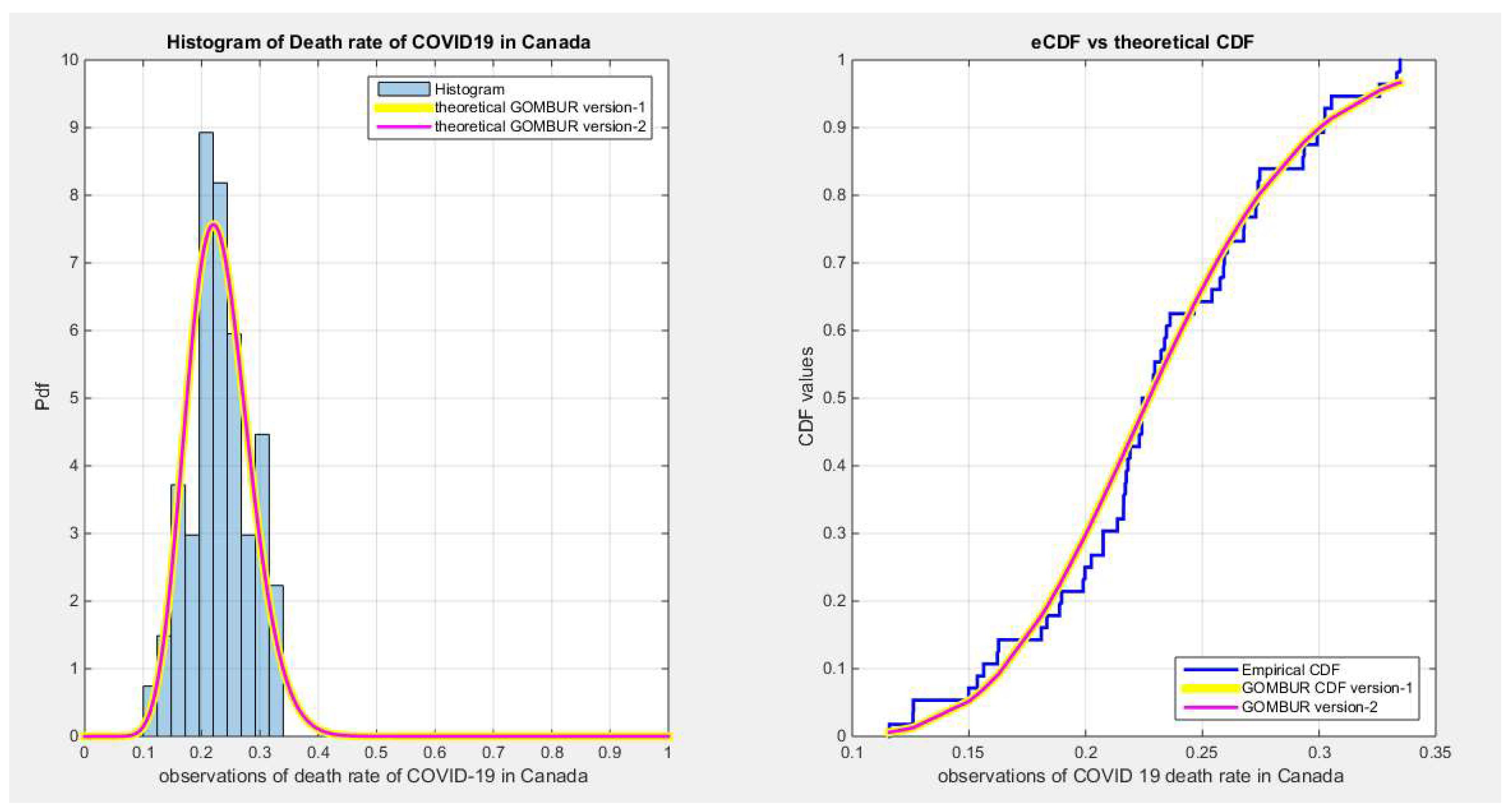
Figure 32.
shows the histogram of the COVID-19 death rate in Canada data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 shows near perfect alignments with Beta distribution. Kumaraswamy distribution fits the data. BMUR , Topp Leone, Unit Lindley distributions do not fit the data. .
Figure 32.
shows the histogram of the COVID-19 death rate in Canada data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 shows near perfect alignments with Beta distribution. Kumaraswamy distribution fits the data. BMUR , Topp Leone, Unit Lindley distributions do not fit the data. .
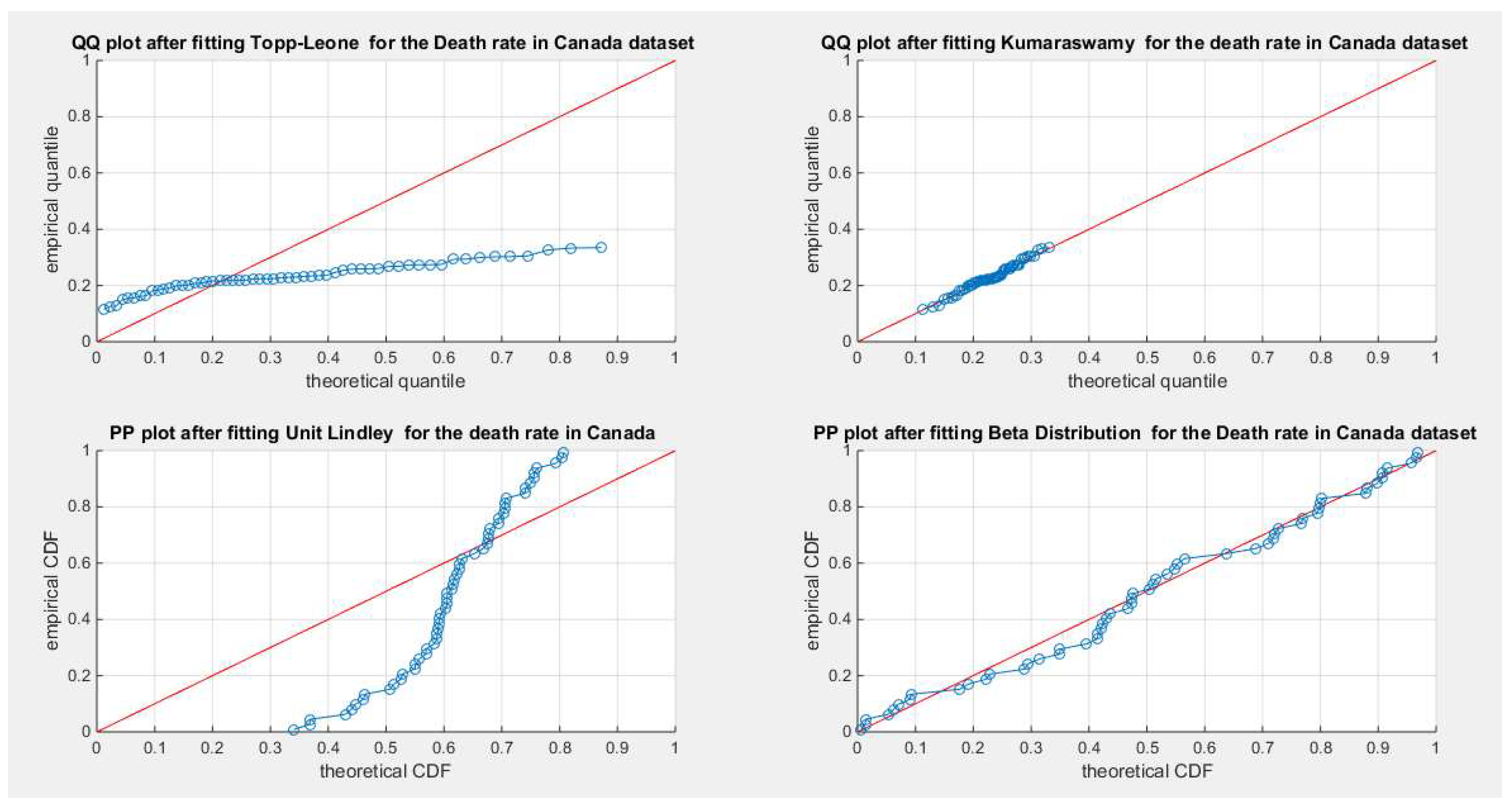
Figure 33.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the death rate in Canada dataset.
Figure 33.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the death rate in Canada dataset.
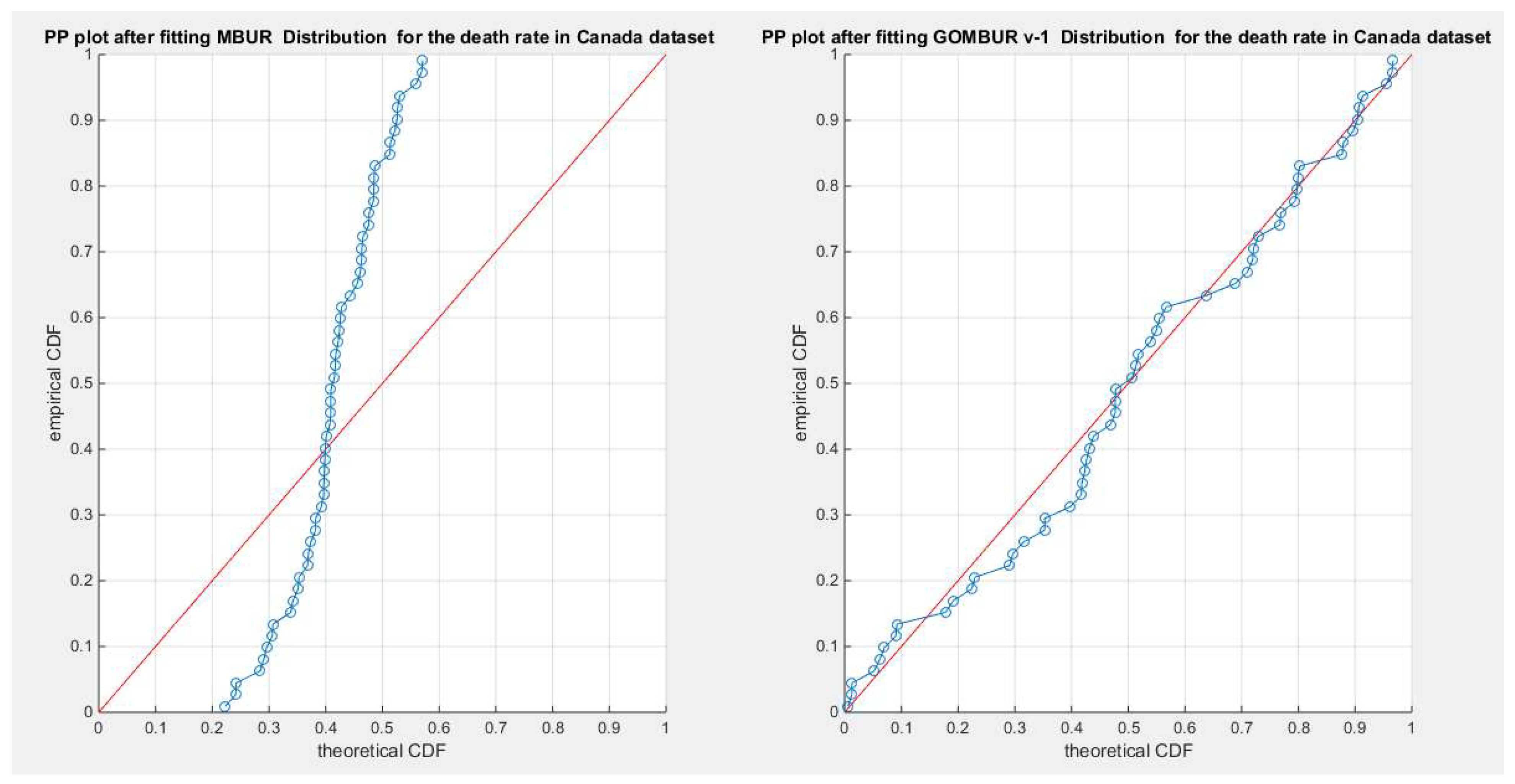
Figure 34.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the death rate in Canada dataset. The Generalization of MBUR enhances the diagonal alignment of GOMBUR-1 along both ends and along the center of the distribution.
Figure 34.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the death rate in Canada dataset. The Generalization of MBUR enhances the diagonal alignment of GOMBUR-1 along both ends and along the center of the distribution.
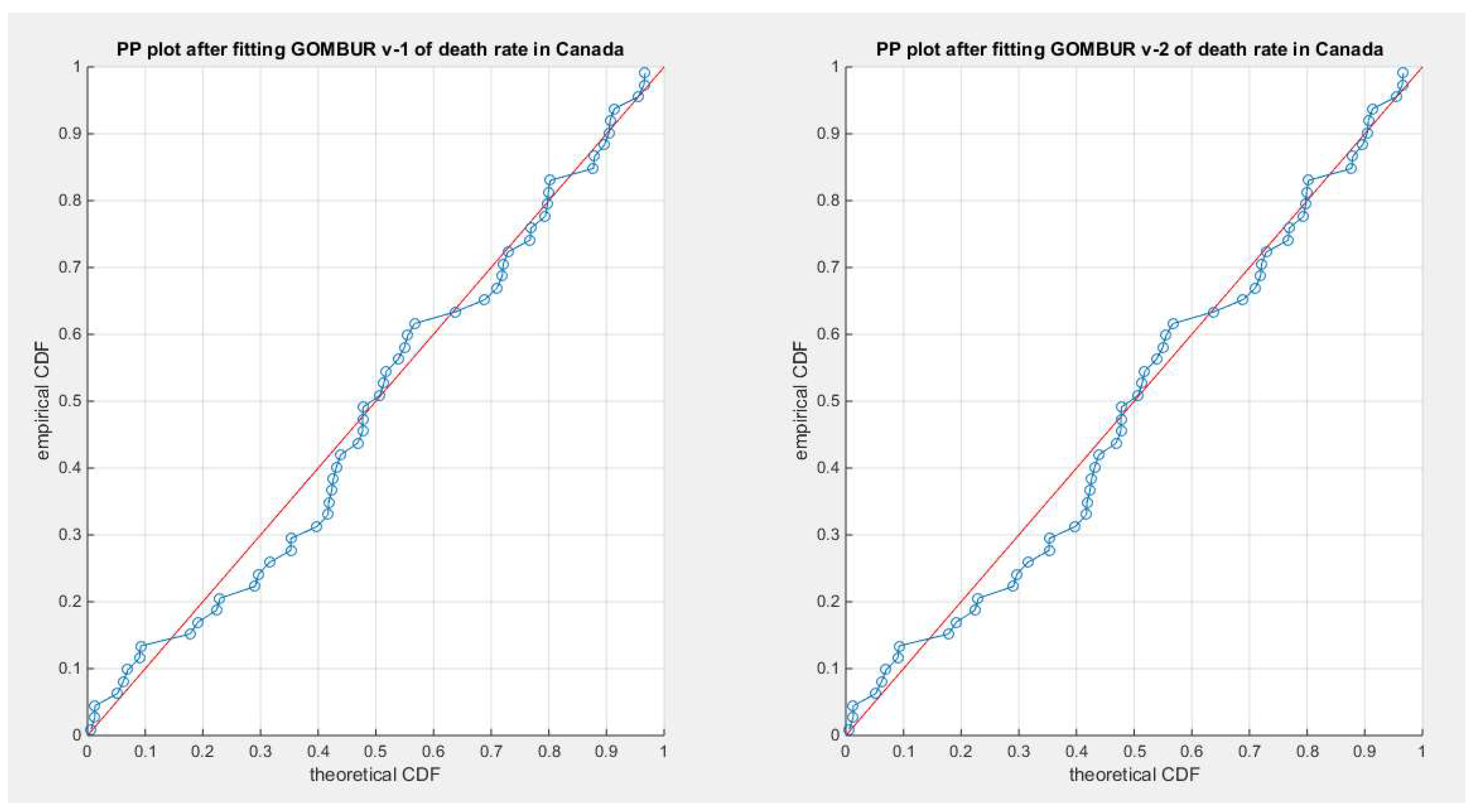
Figure 35.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for death rate in Canada dataset. They are identical.
Figure 35.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for death rate in Canada dataset. They are identical.
Figure 36.
shows on the left subplot the histogram of the death rate in Canada data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Figure 36.
shows on the left subplot the histogram of the death rate in Canada data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
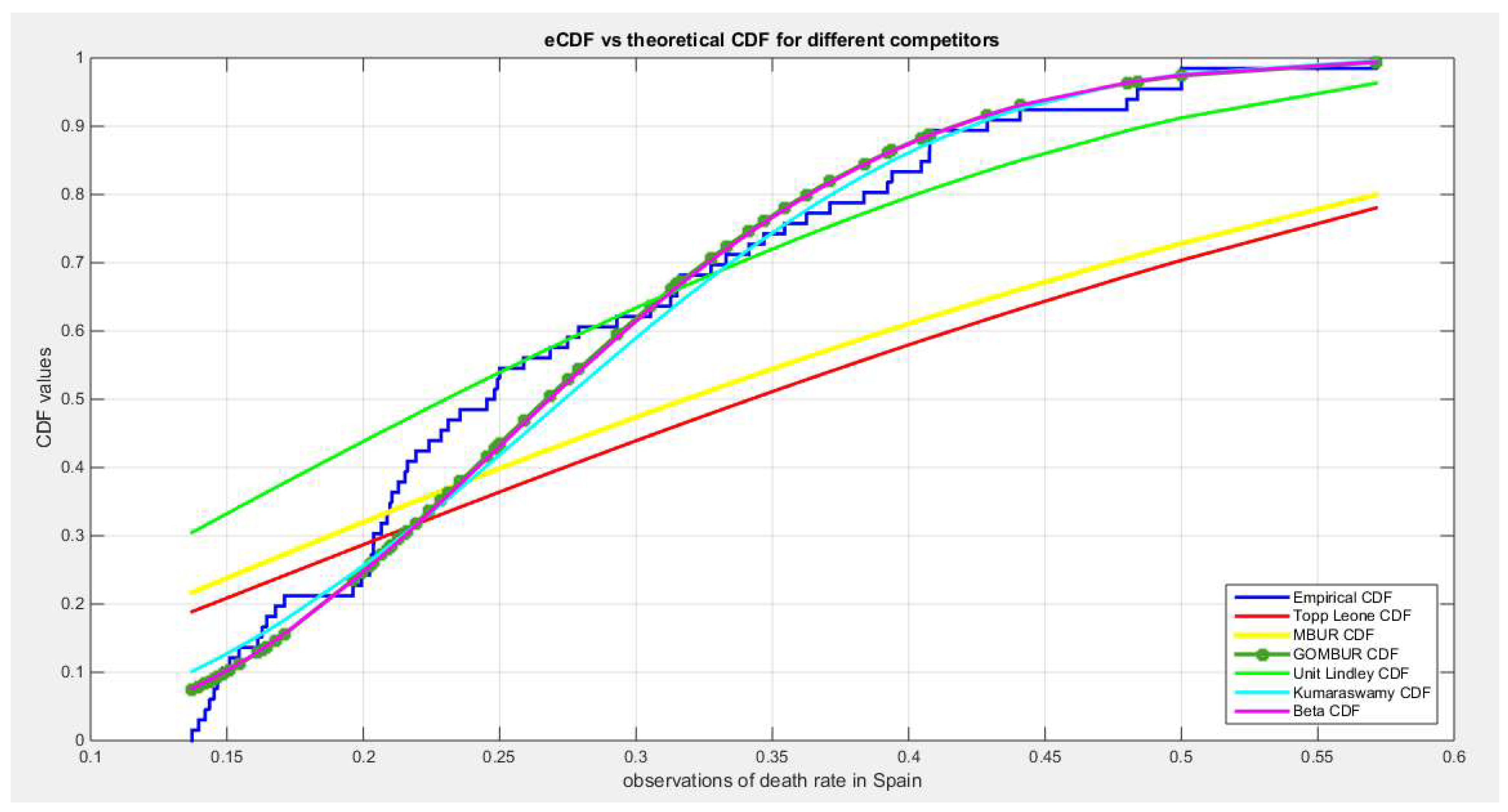
Figure 37.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of death rate in Spain data.
Figure 37.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of death rate in Spain data.
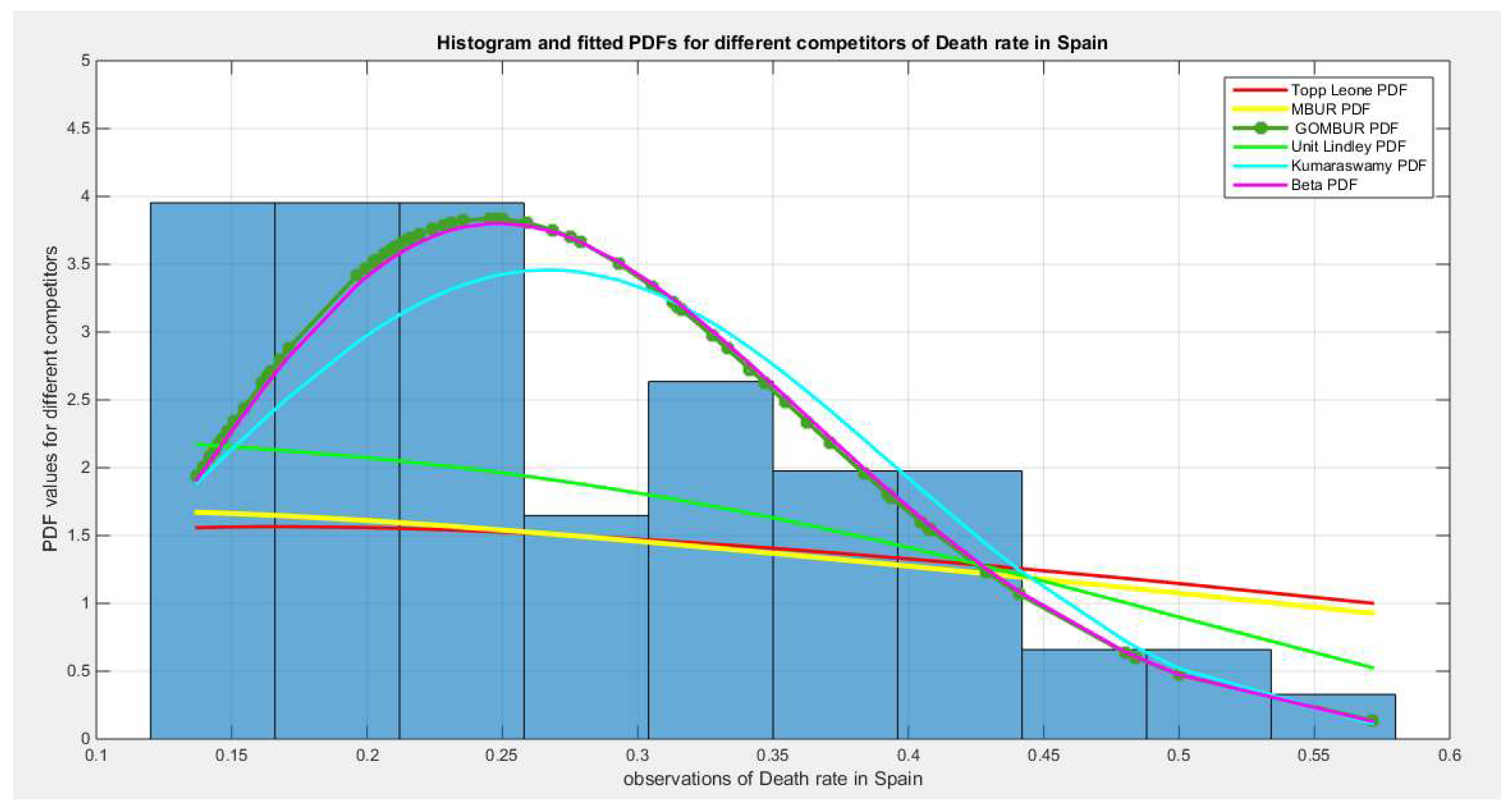
Figure 38.
shows the histogram of the COVID-19 death rate in Spain data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 shows near perfect alignments with Beta distribution. Kumaraswamy distribution fits the data. BMUR , Topp Leone, Unit Lindley distributions do not fit the data. .
Figure 38.
shows the histogram of the COVID-19 death rate in Spain data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 shows near perfect alignments with Beta distribution. Kumaraswamy distribution fits the data. BMUR , Topp Leone, Unit Lindley distributions do not fit the data. .
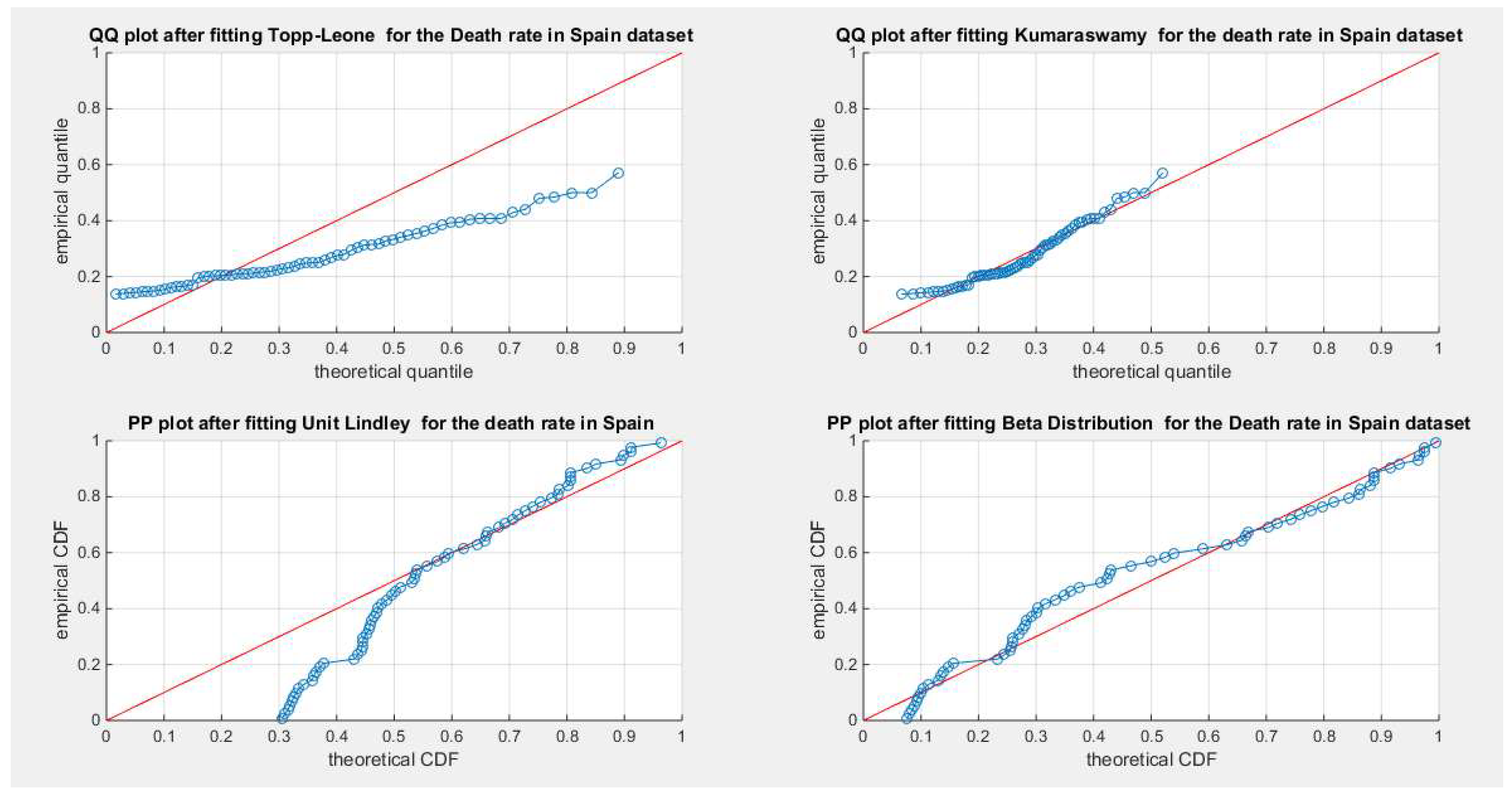
Figure 39.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the death rate in Spain dataset.
Figure 39.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the death rate in Spain dataset.
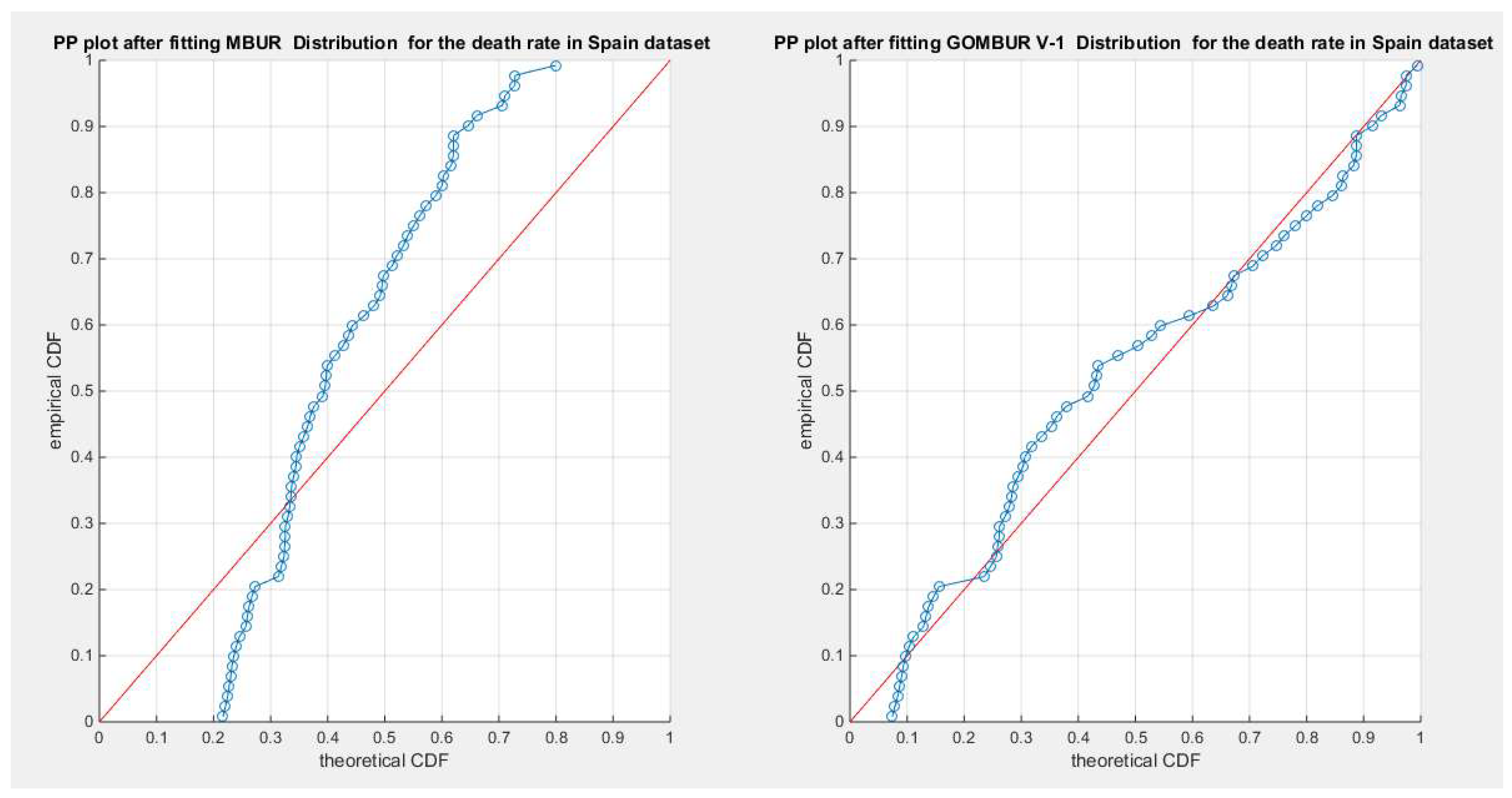
Figure 40.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the death rate in Spain dataset. The Generalization of MBUR enhances the diagonal alignment of GOMBUR-1 along both ends and along the center of the distribution.
Figure 40.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the death rate in Spain dataset. The Generalization of MBUR enhances the diagonal alignment of GOMBUR-1 along both ends and along the center of the distribution.
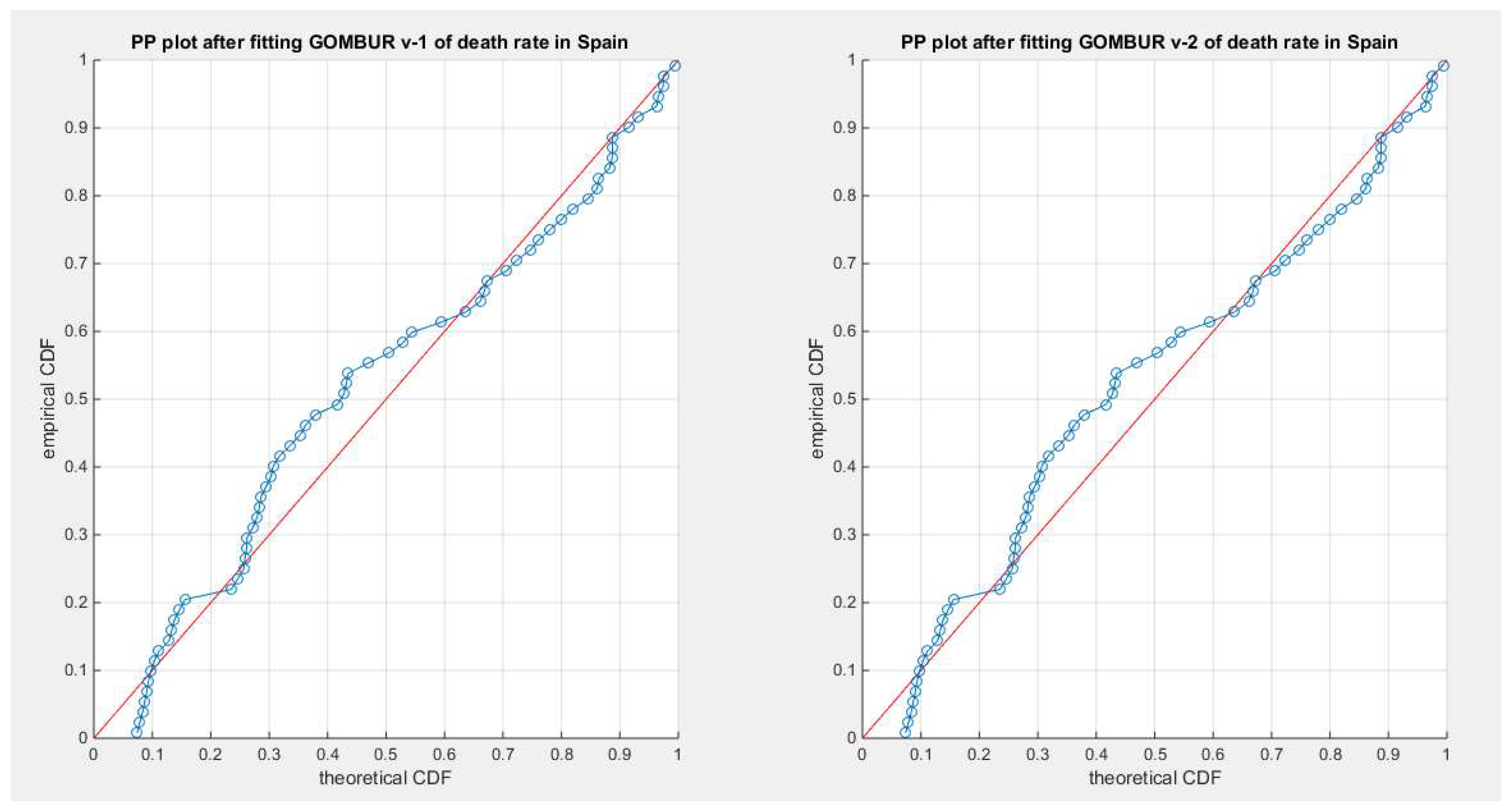
Figure 41.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for death rate in Spain dataset. They are identical.
Figure 41.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for death rate in Spain dataset. They are identical.
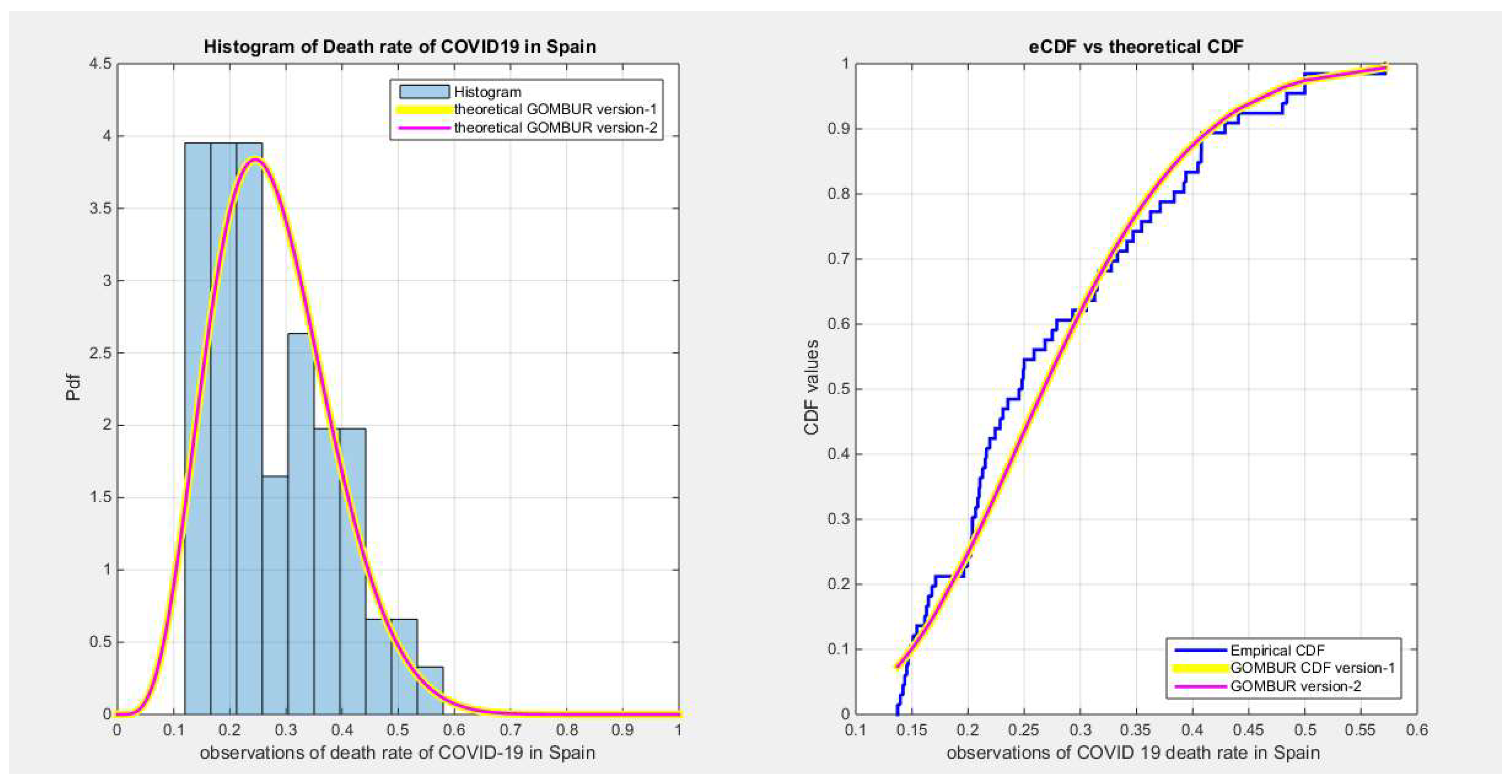
Figure 42.
shows on the left subplot the histogram of the death rate in Spain data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical. The PDF curve is slightly right skewed.
Figure 42.
shows on the left subplot the histogram of the death rate in Spain data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical. The PDF curve is slightly right skewed.
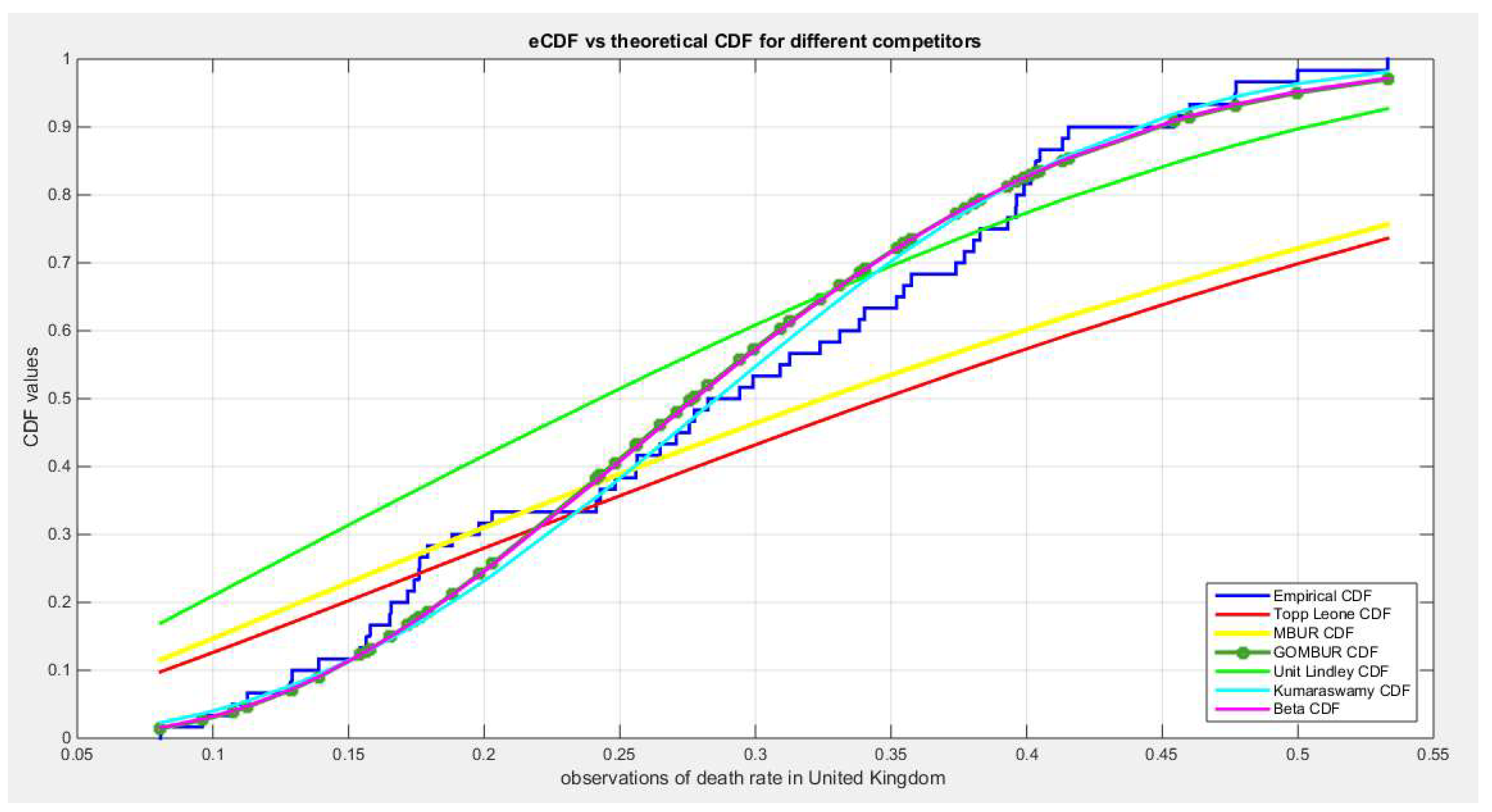
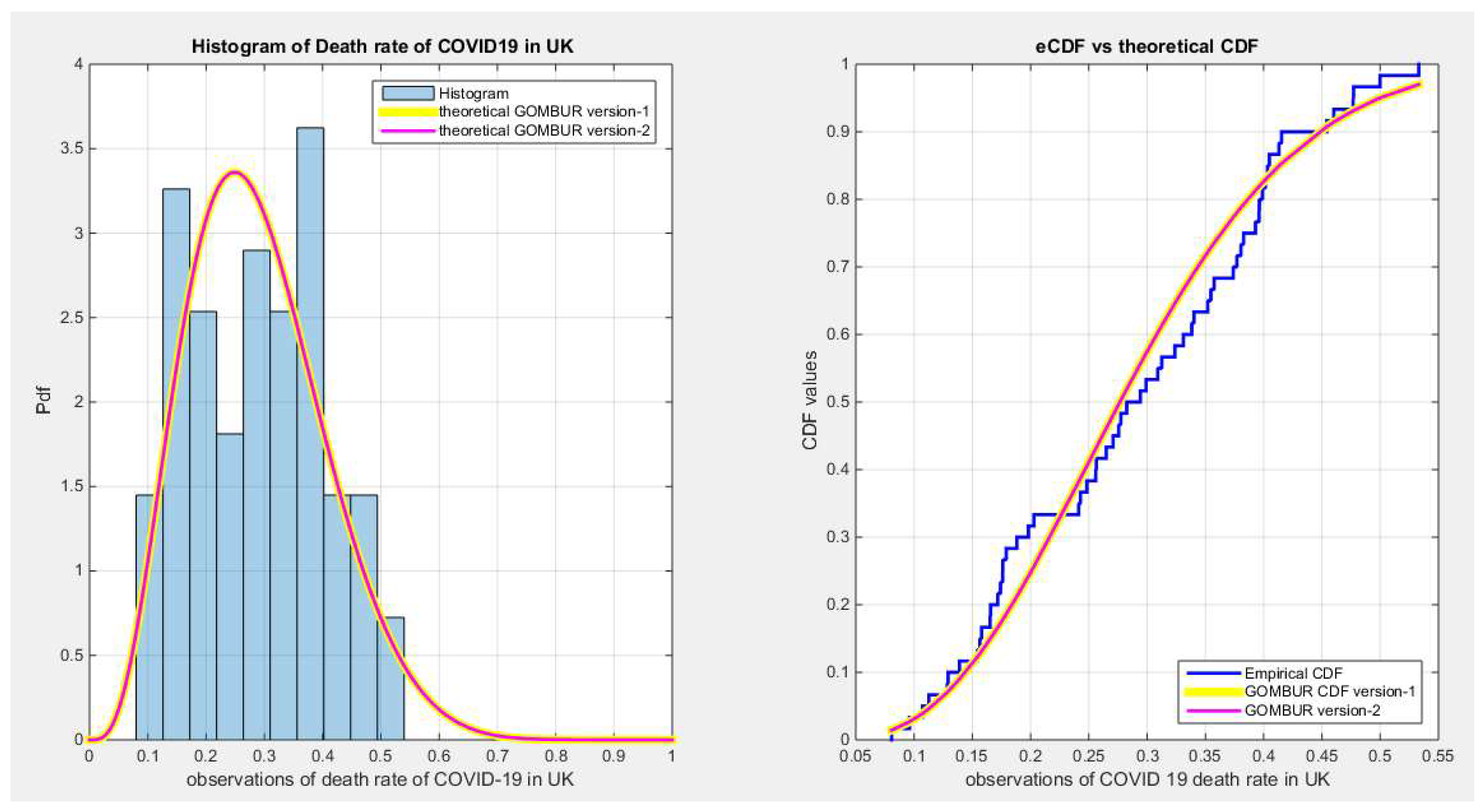
Figure 43.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of death rate in UK data.
Figure 43.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of death rate in UK data.
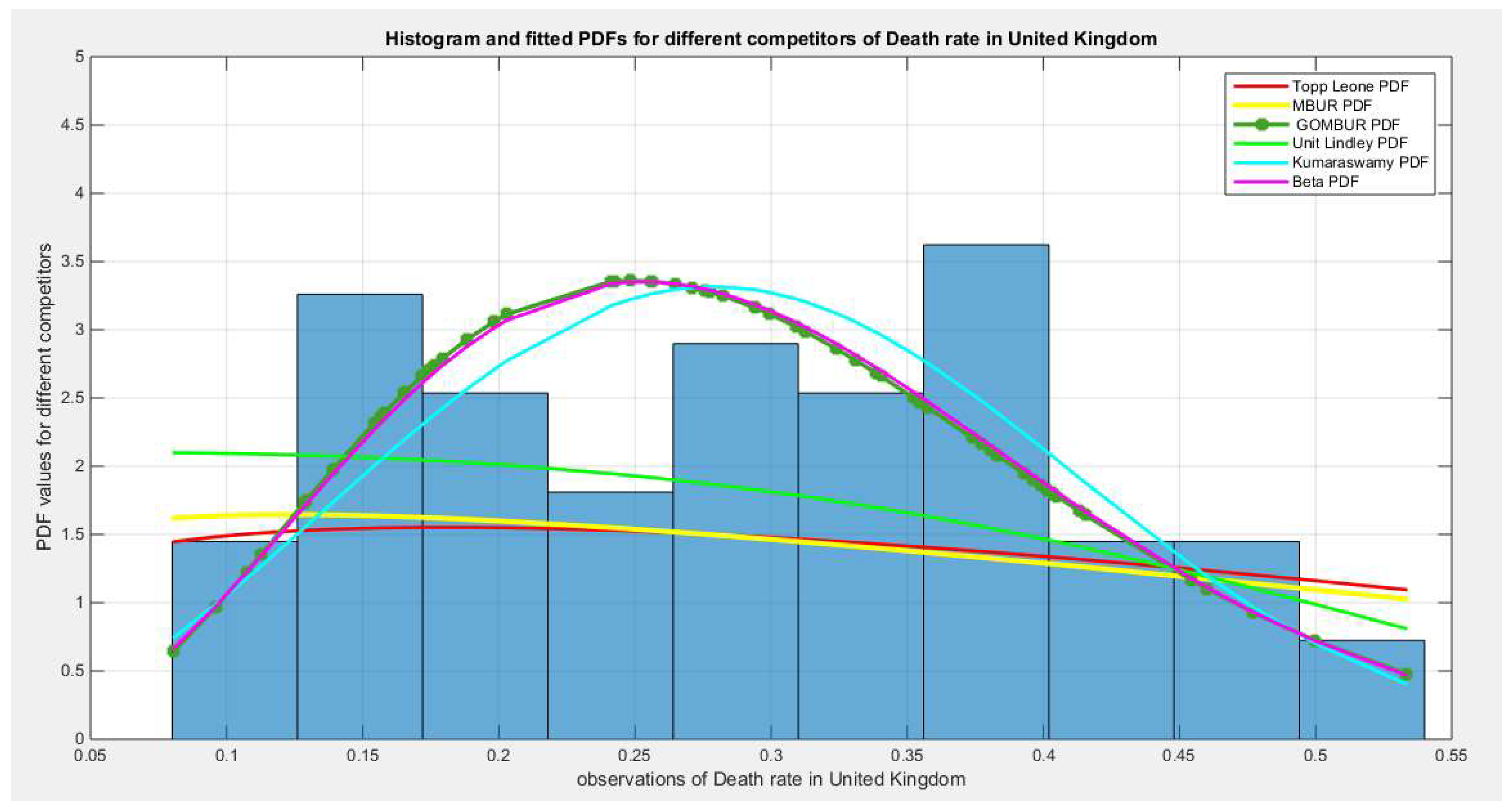
Figure 44.
shows the histogram of the COVID-19 death rate in UK data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 shows near perfect alignments with Beta distribution. Kumaraswamy distribution fits the data. BMUR , Topp Leone, Unit Lindley distributions did not fit the data. .
Figure 44.
shows the histogram of the COVID-19 death rate in UK data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 shows near perfect alignments with Beta distribution. Kumaraswamy distribution fits the data. BMUR , Topp Leone, Unit Lindley distributions did not fit the data. .
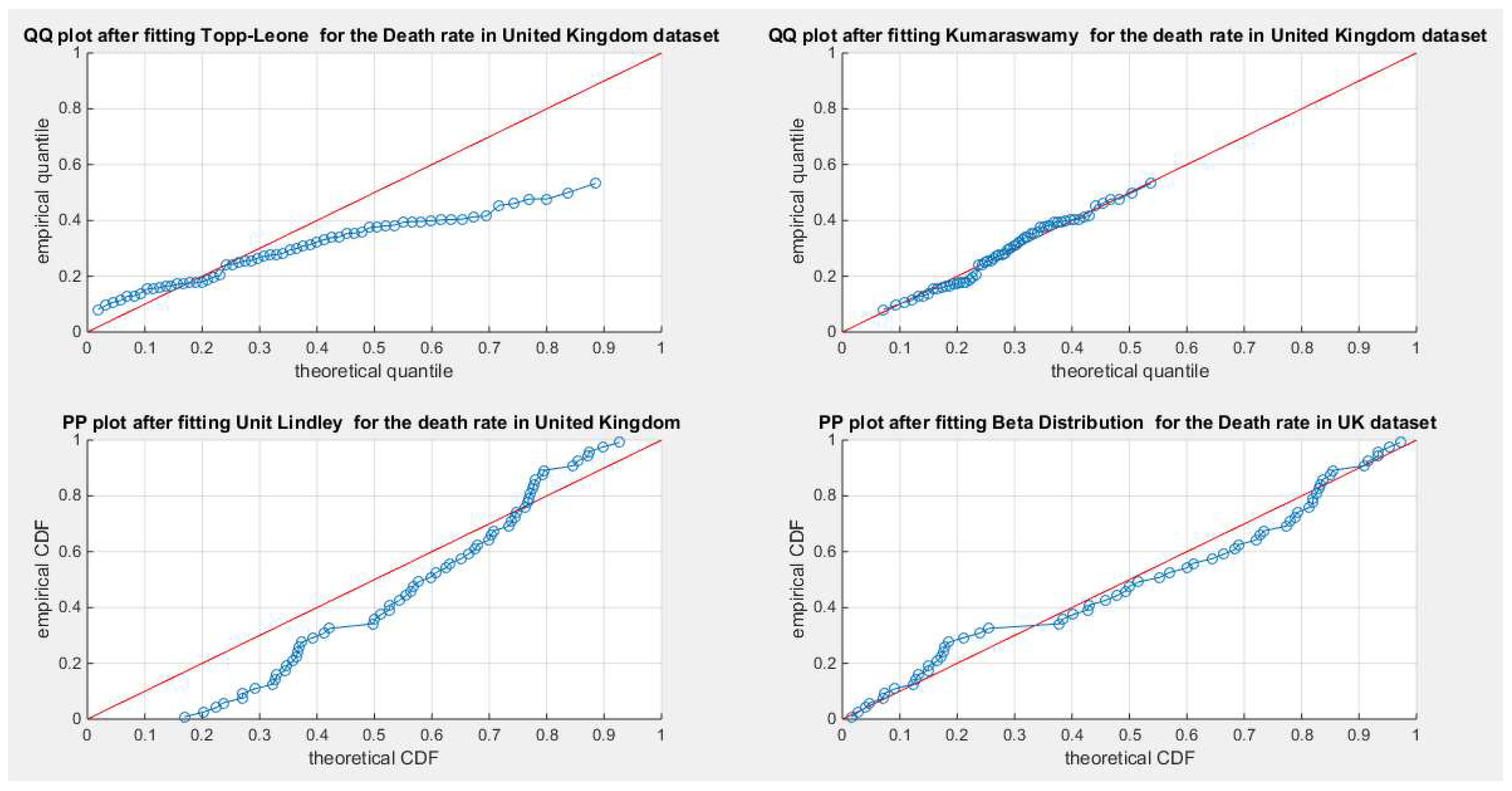
Figure 45.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the death rate in UK dataset.
Figure 45.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the death rate in UK dataset.
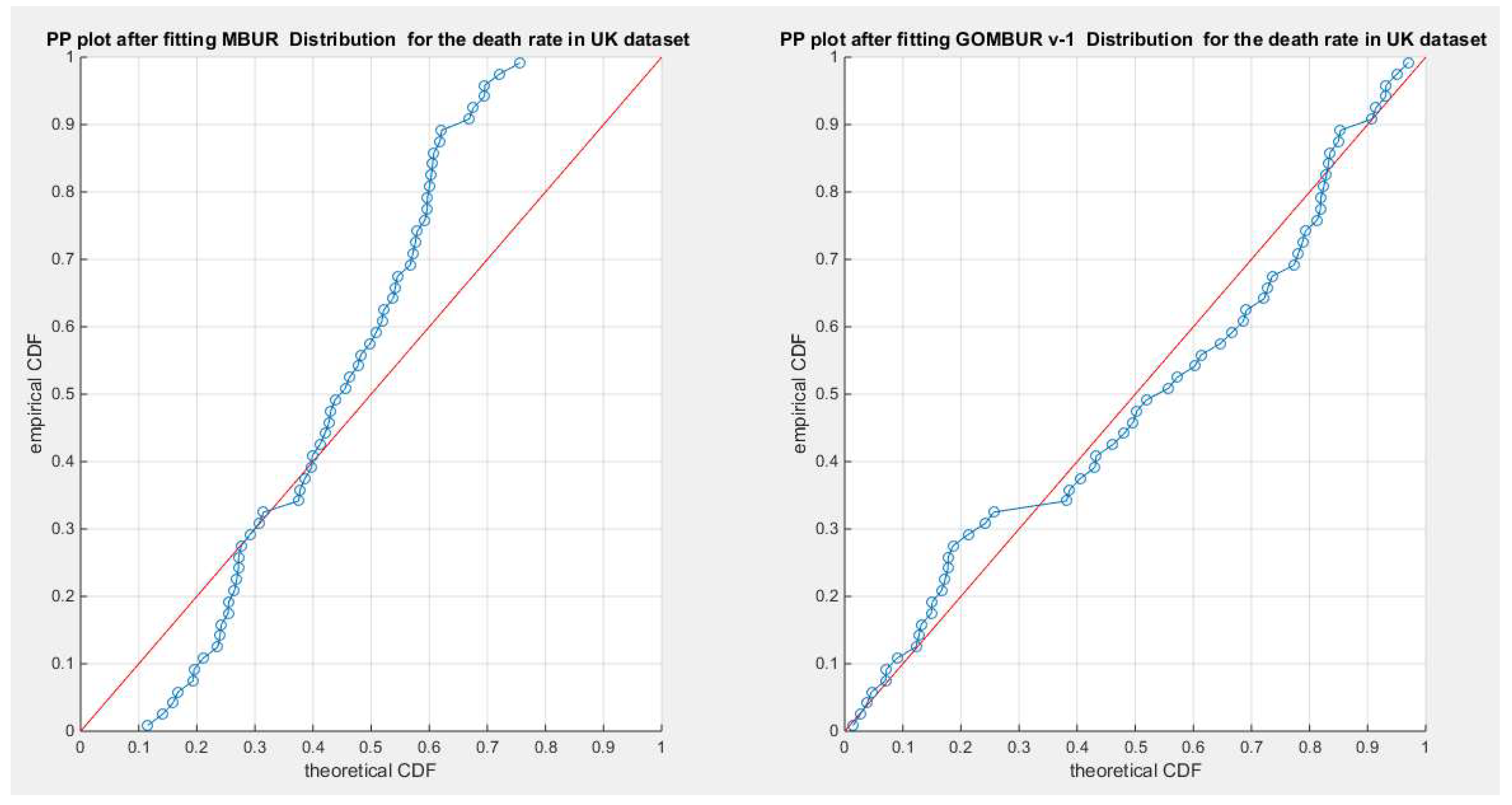
Figure 46.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the death rate in UK dataset. The Generalization of MBUR enhances the diagonal alignment of GOMBUR-1 along both ends and along the center of the distribution.
Figure 46.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the death rate in UK dataset. The Generalization of MBUR enhances the diagonal alignment of GOMBUR-1 along both ends and along the center of the distribution.
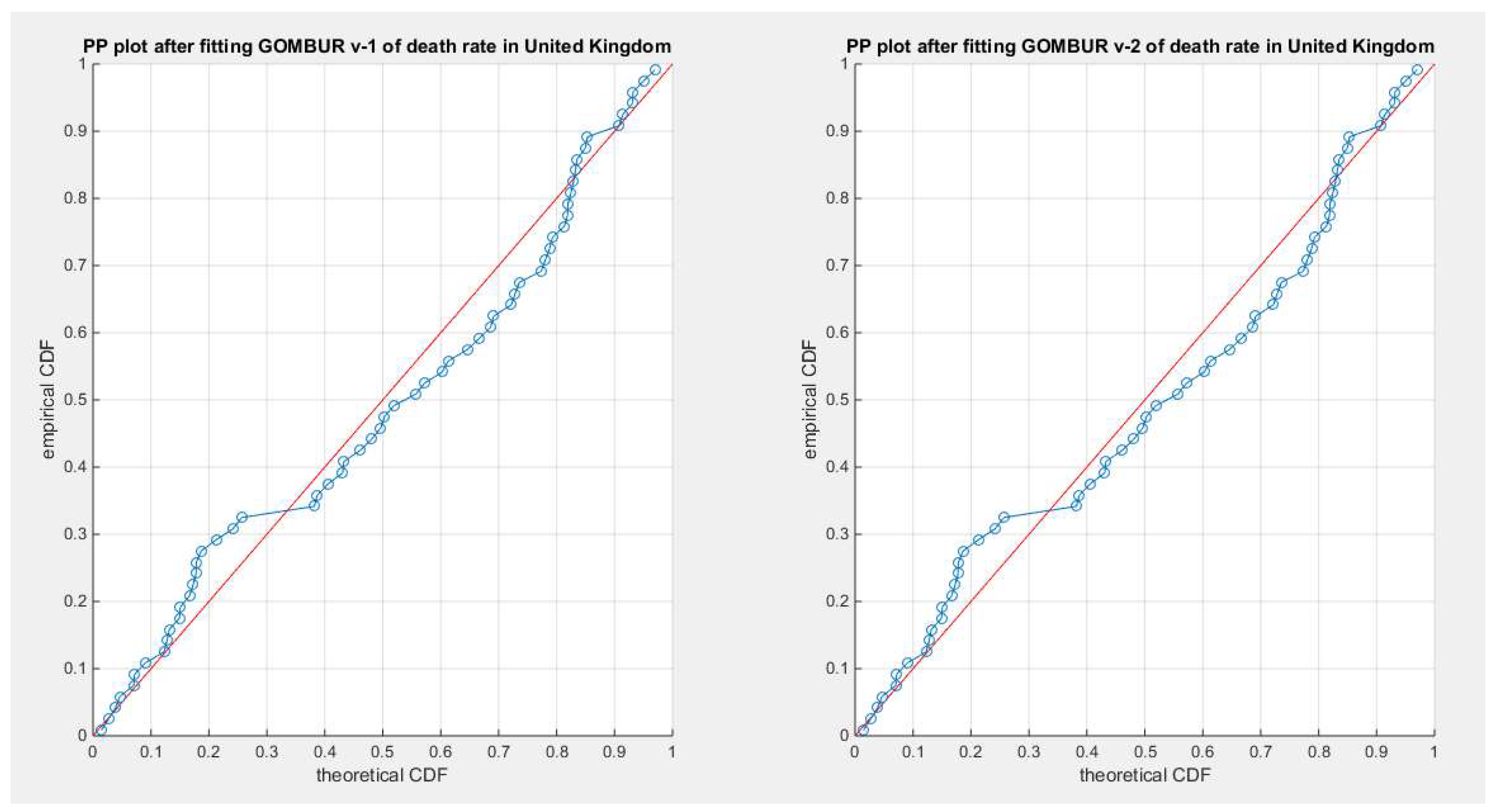
Figure 47.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for death rate in UK dataset. They are identical.
Figure 47.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for death rate in UK dataset. They are identical.
Figure 48.
shows on the left subplot the histogram of the death rate in UK data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical. The PDF curve is slightly right skewed.
Figure 48.
shows on the left subplot the histogram of the death rate in UK data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical. The PDF curve is slightly right skewed.
Figure 49.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of petroleum rock data.
Figure 49.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of petroleum rock data.
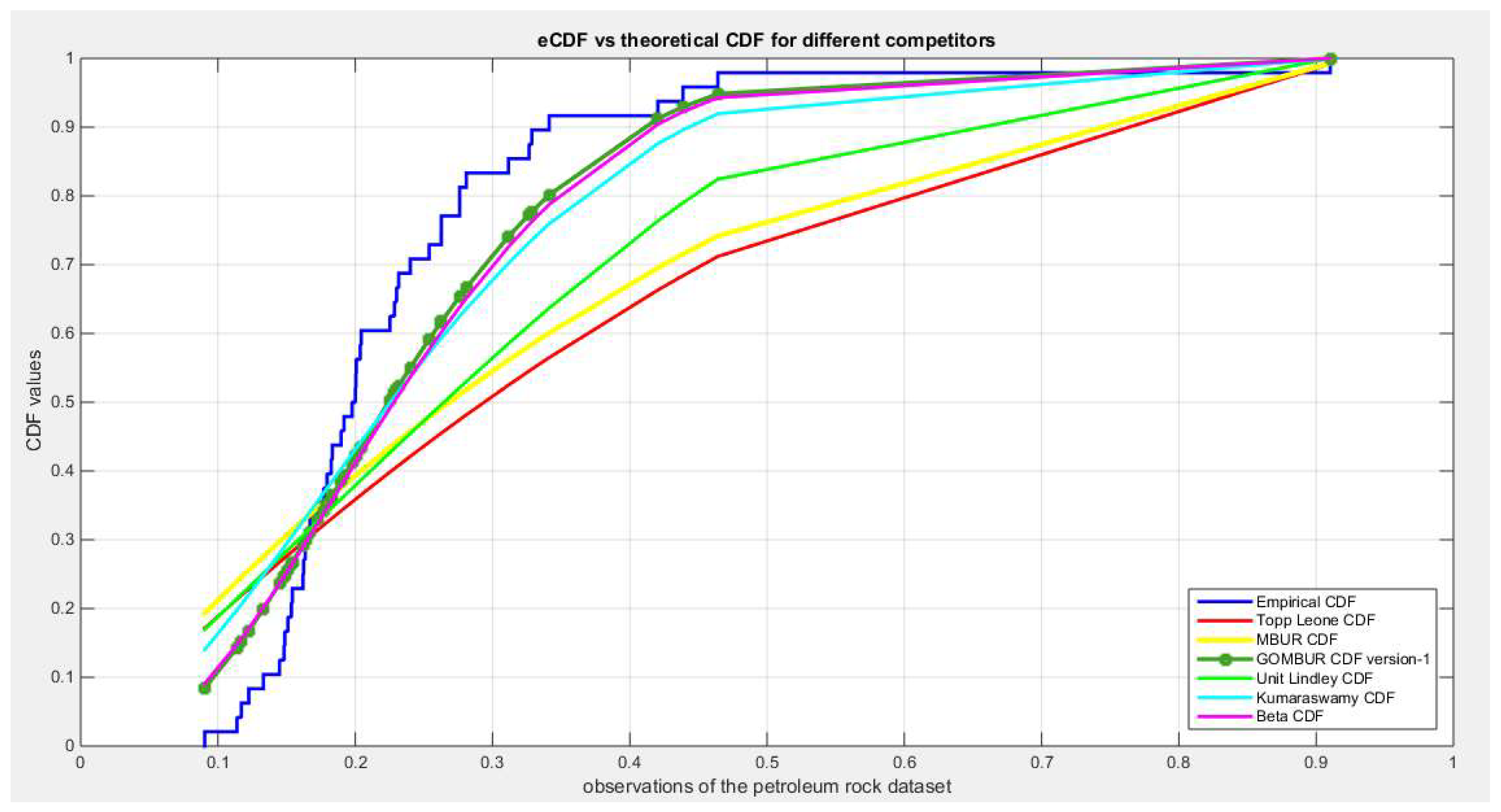
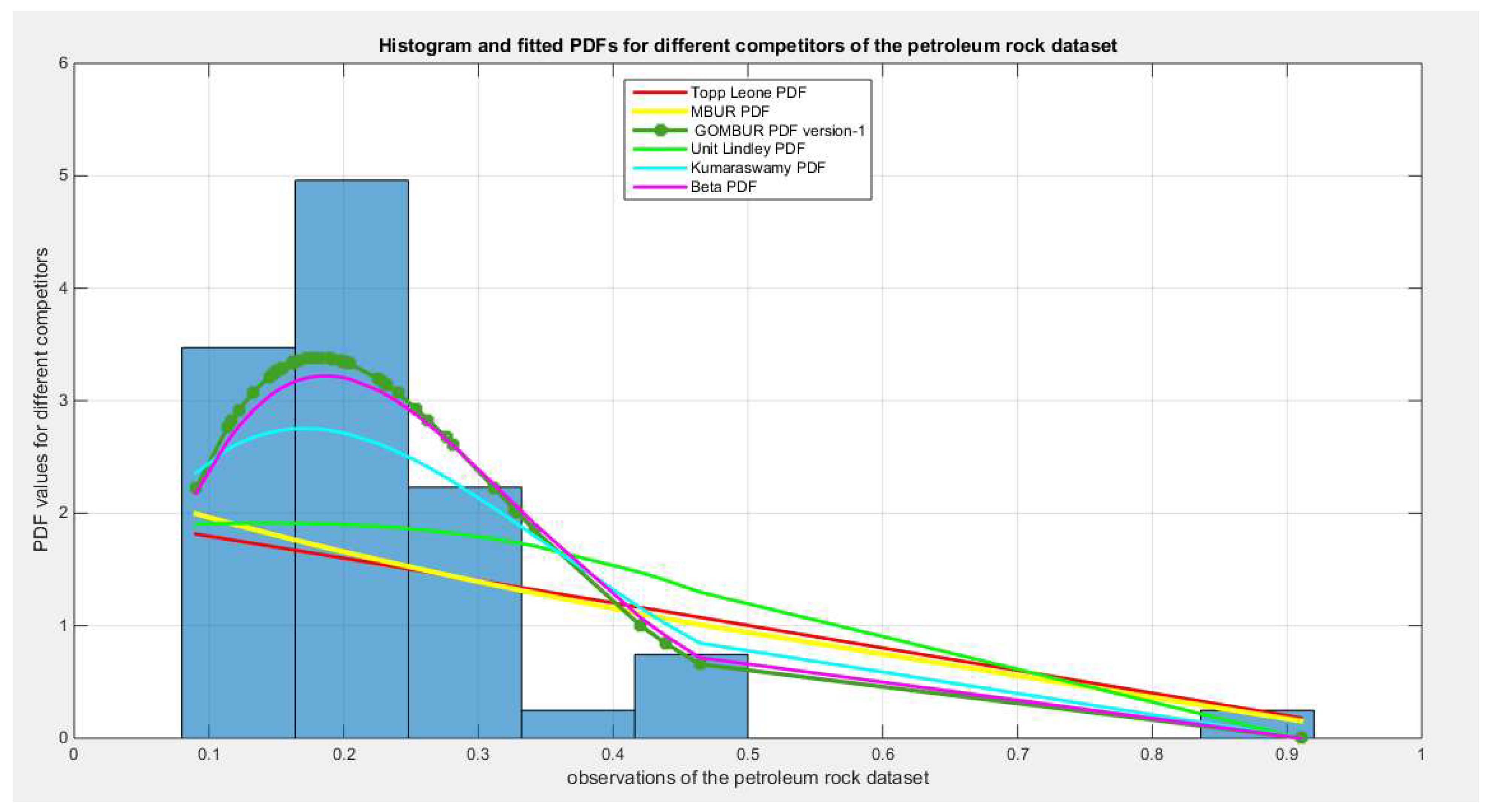
Figure 50.
shows the histogram of the petroleum rock data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 shows near perfect alignments with Beta distribution. Kumaraswamy distribution fits the data. BMUR , Topp Leone, Unit Lindley distributions did not fit the data. .
Figure 50.
shows the histogram of the petroleum rock data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 shows near perfect alignments with Beta distribution. Kumaraswamy distribution fits the data. BMUR , Topp Leone, Unit Lindley distributions did not fit the data. .
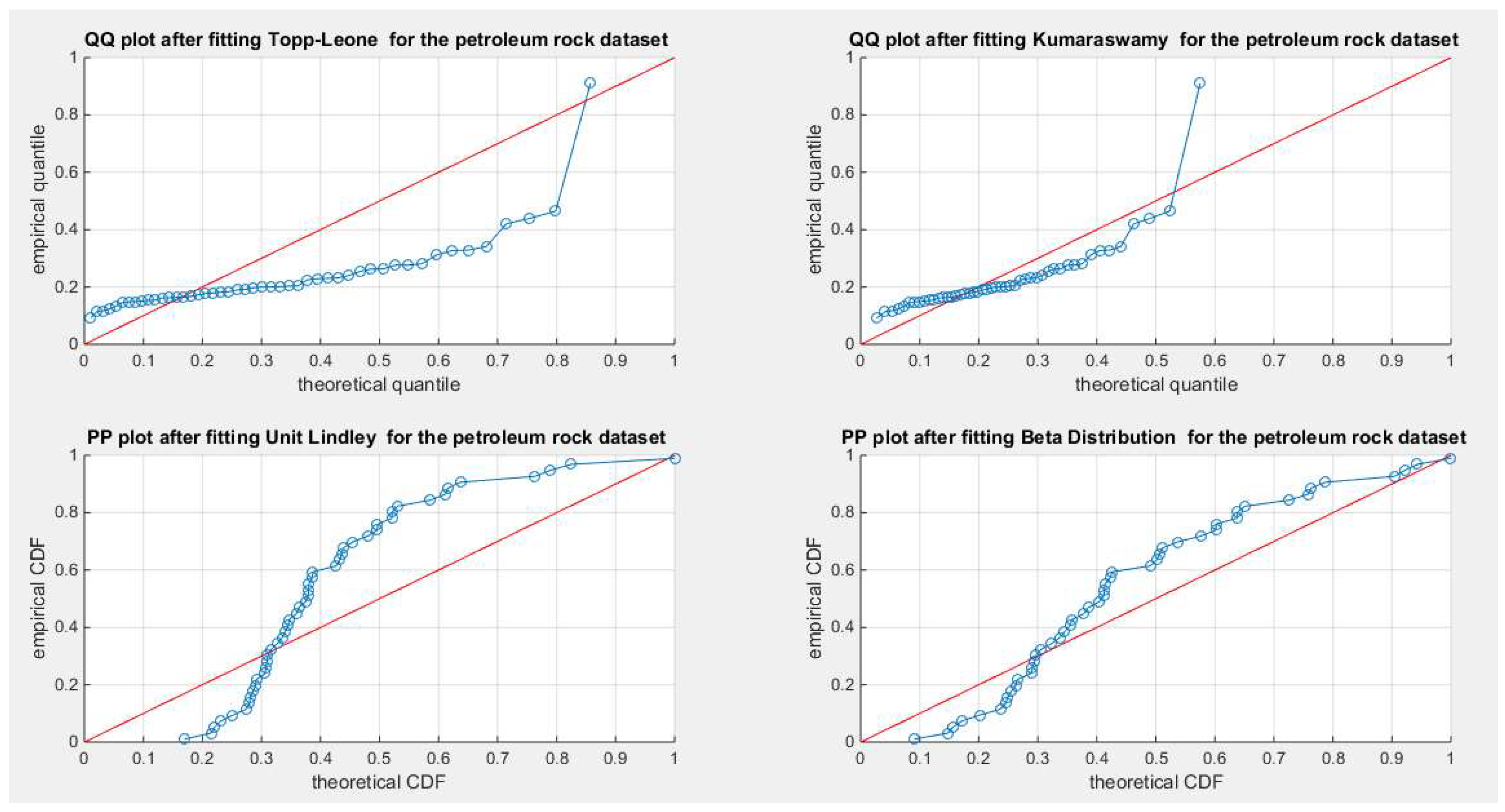
Figure 51.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the petroleum rock dataset.
Figure 51.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the petroleum rock dataset.
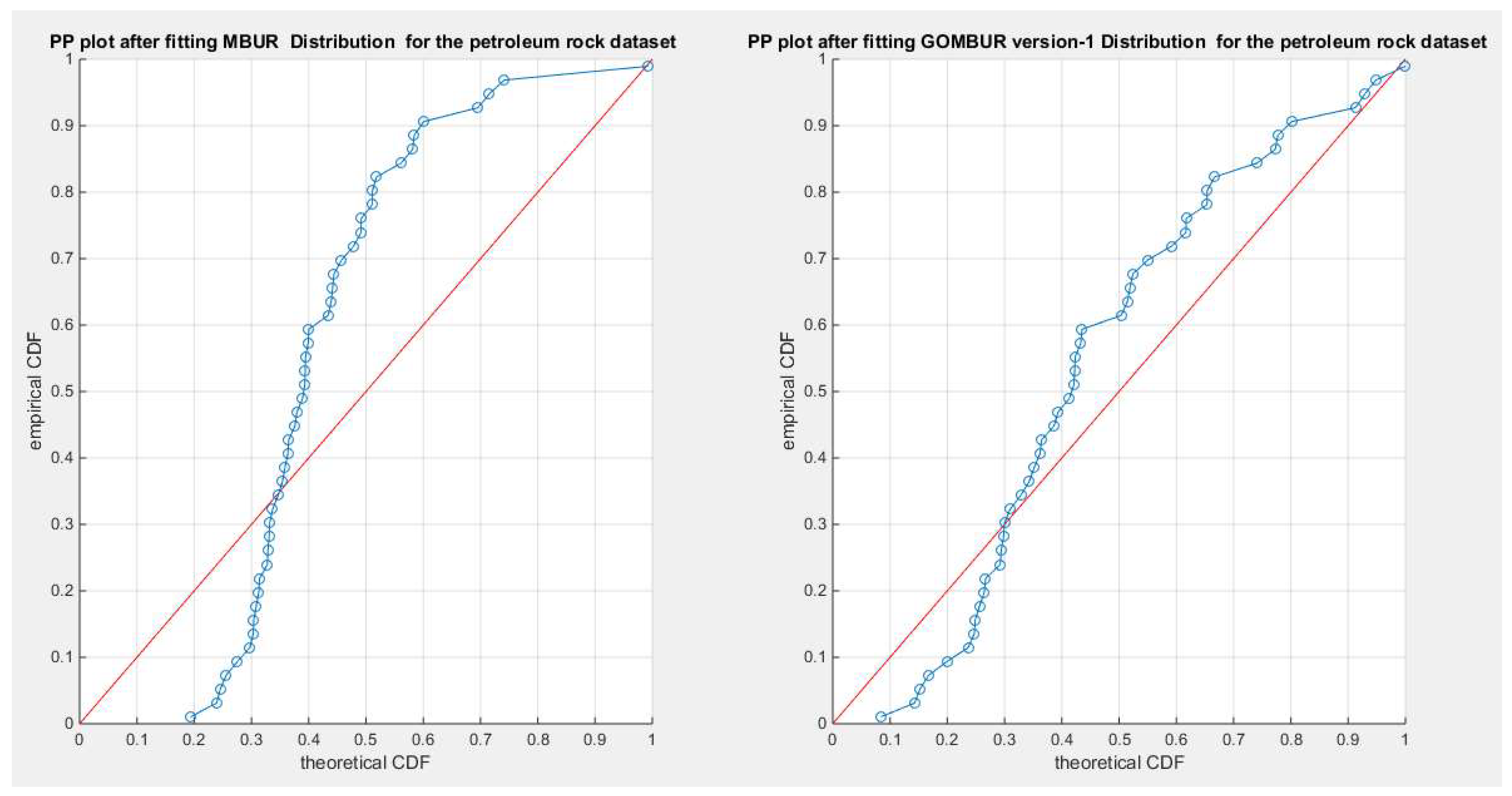
Figure 52.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the petroleum rock dataset. The Generalization of MBUR enhances the diagonal alignment of GOMBUR-1 along both ends and along the center of the distribution.
Figure 52.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the petroleum rock dataset. The Generalization of MBUR enhances the diagonal alignment of GOMBUR-1 along both ends and along the center of the distribution.
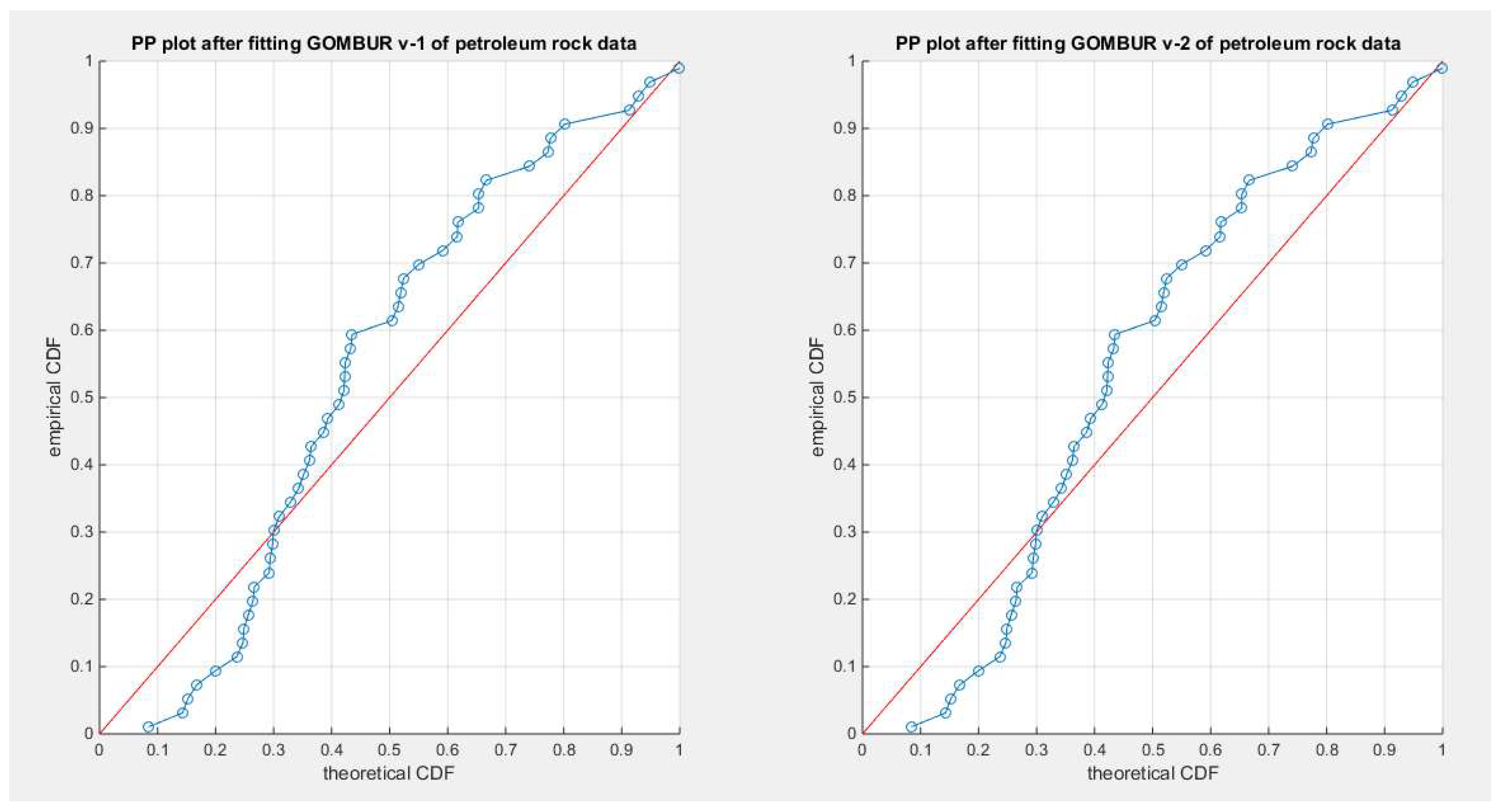
Figure 53.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for petroleum rock dataset. They are identical.
Figure 53.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for petroleum rock dataset. They are identical.
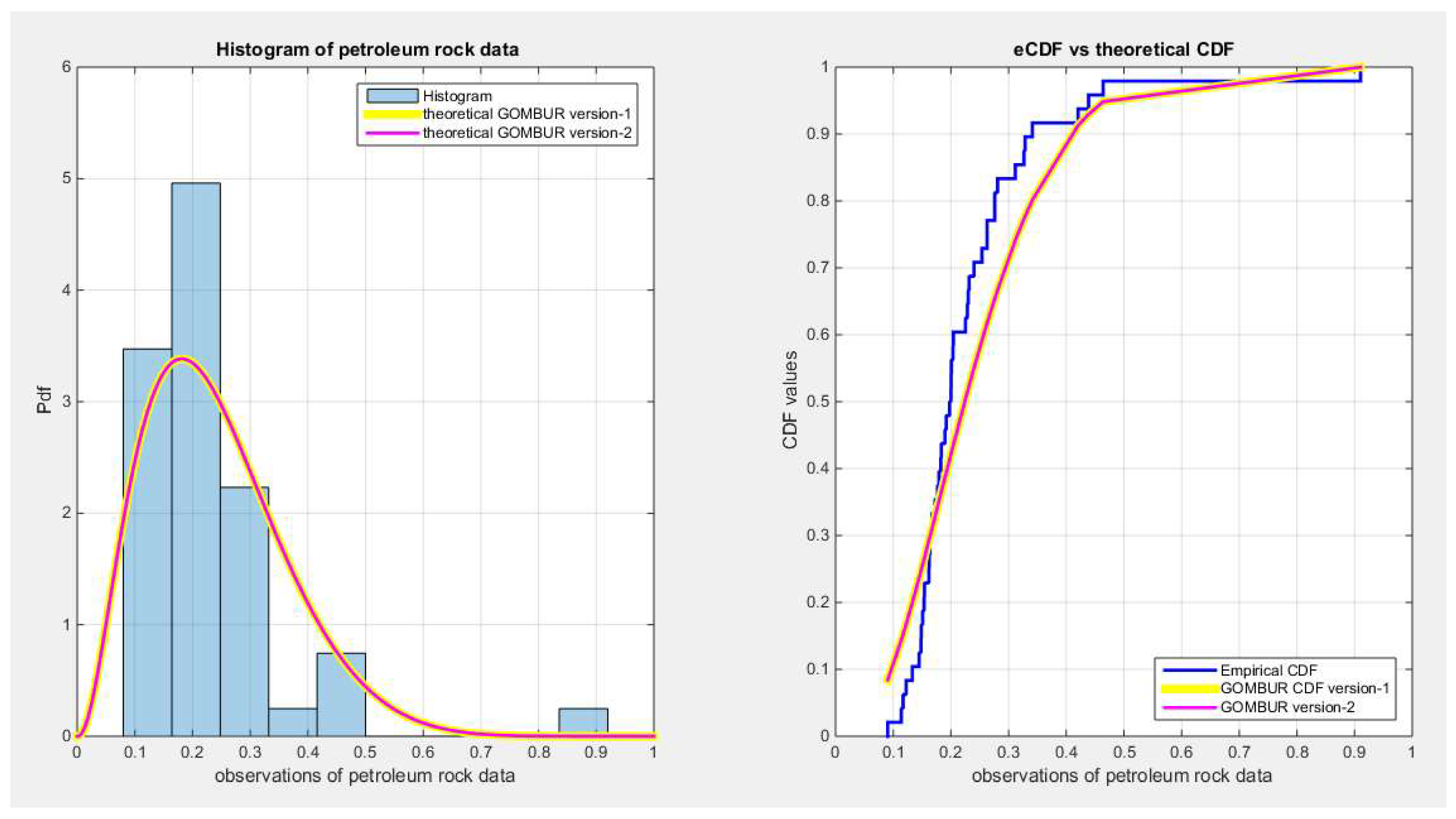
Figure 54.
shows on the left subplot the histogram of the petroleum rock and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical. The PDF curve is right skewed.
Figure 54.
shows on the left subplot the histogram of the petroleum rock and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical. The PDF curve is right skewed.
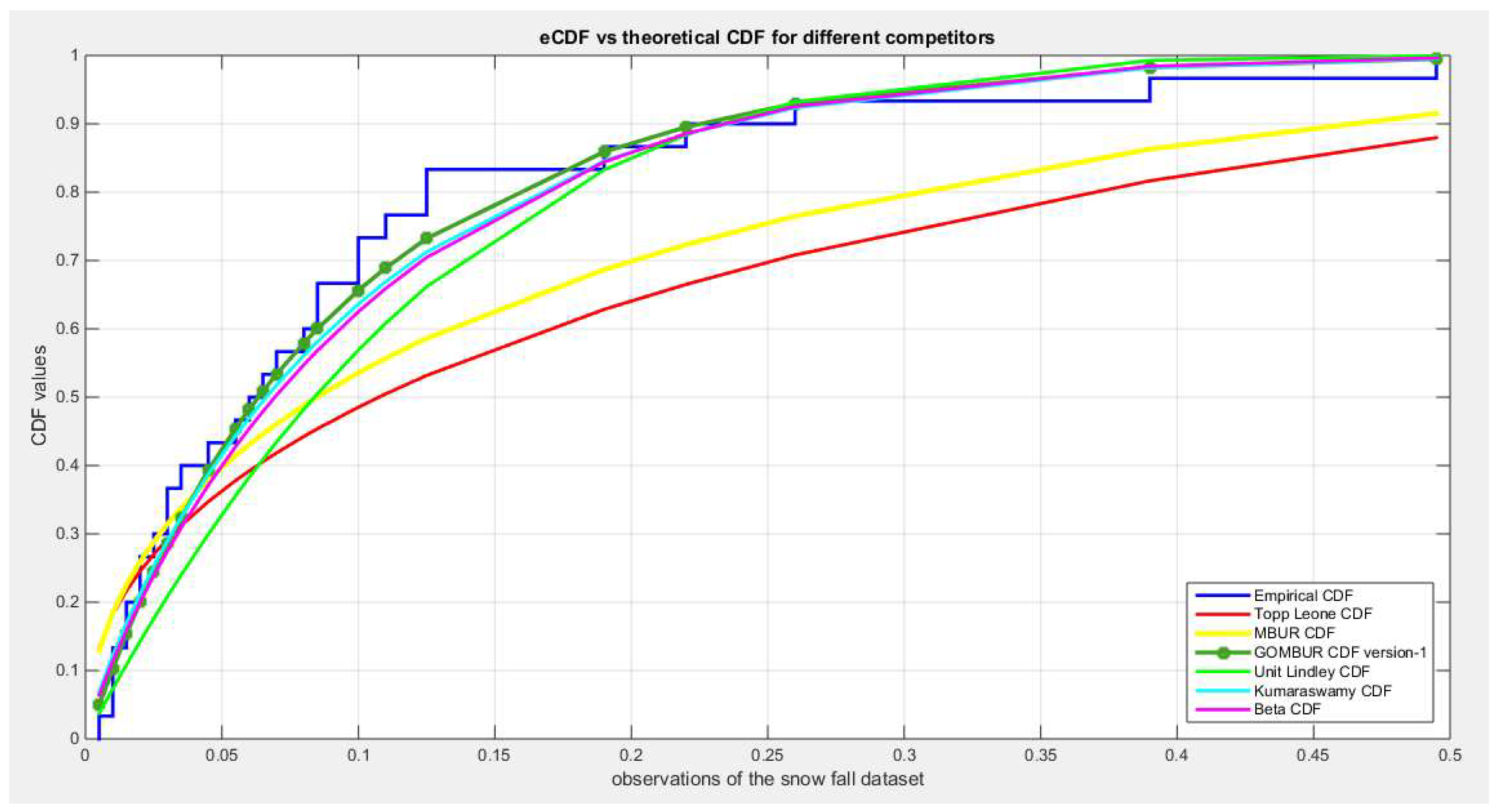
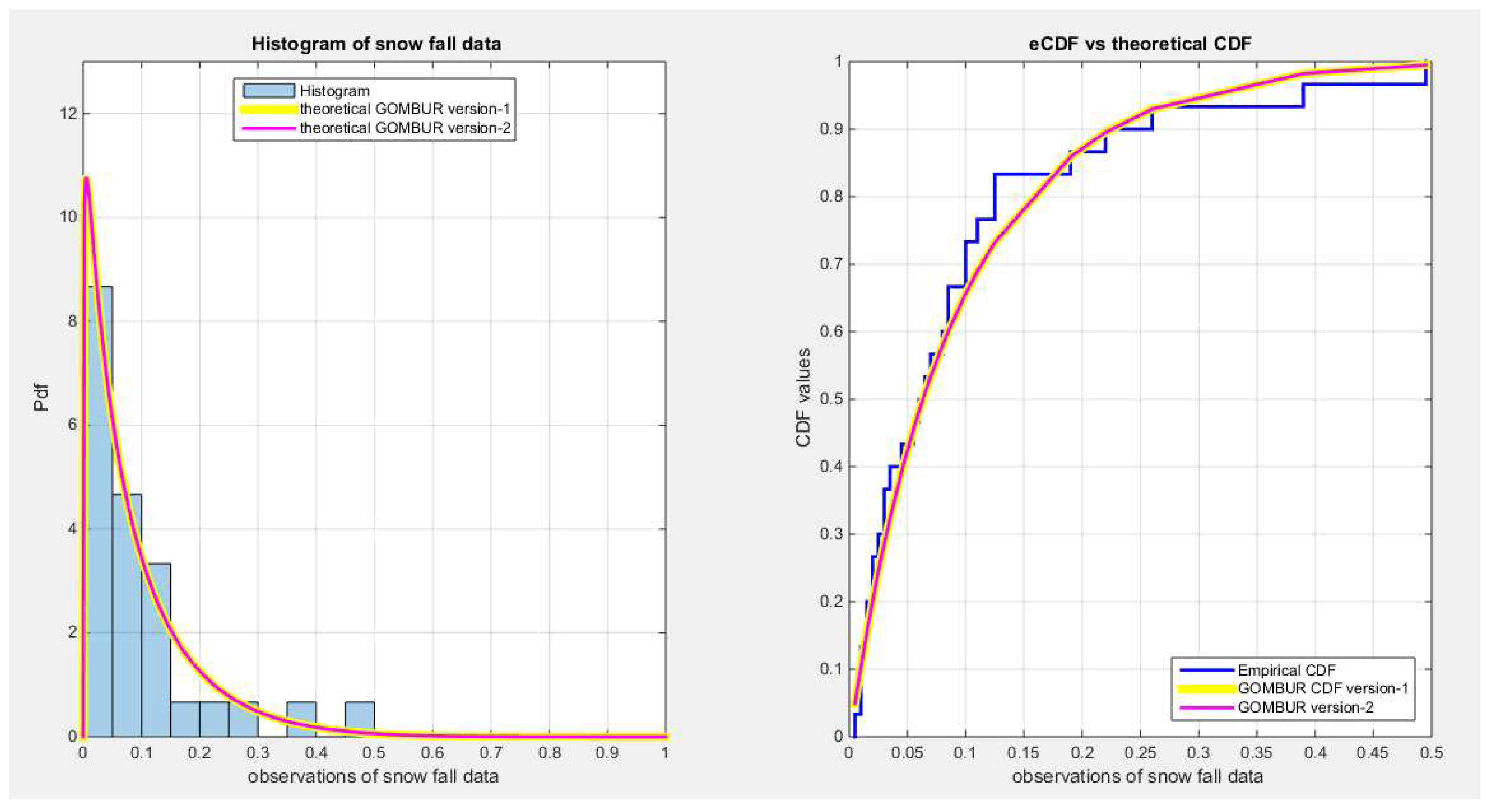
Figure 55.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of snow fall data.
Figure 55.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of snow fall data.
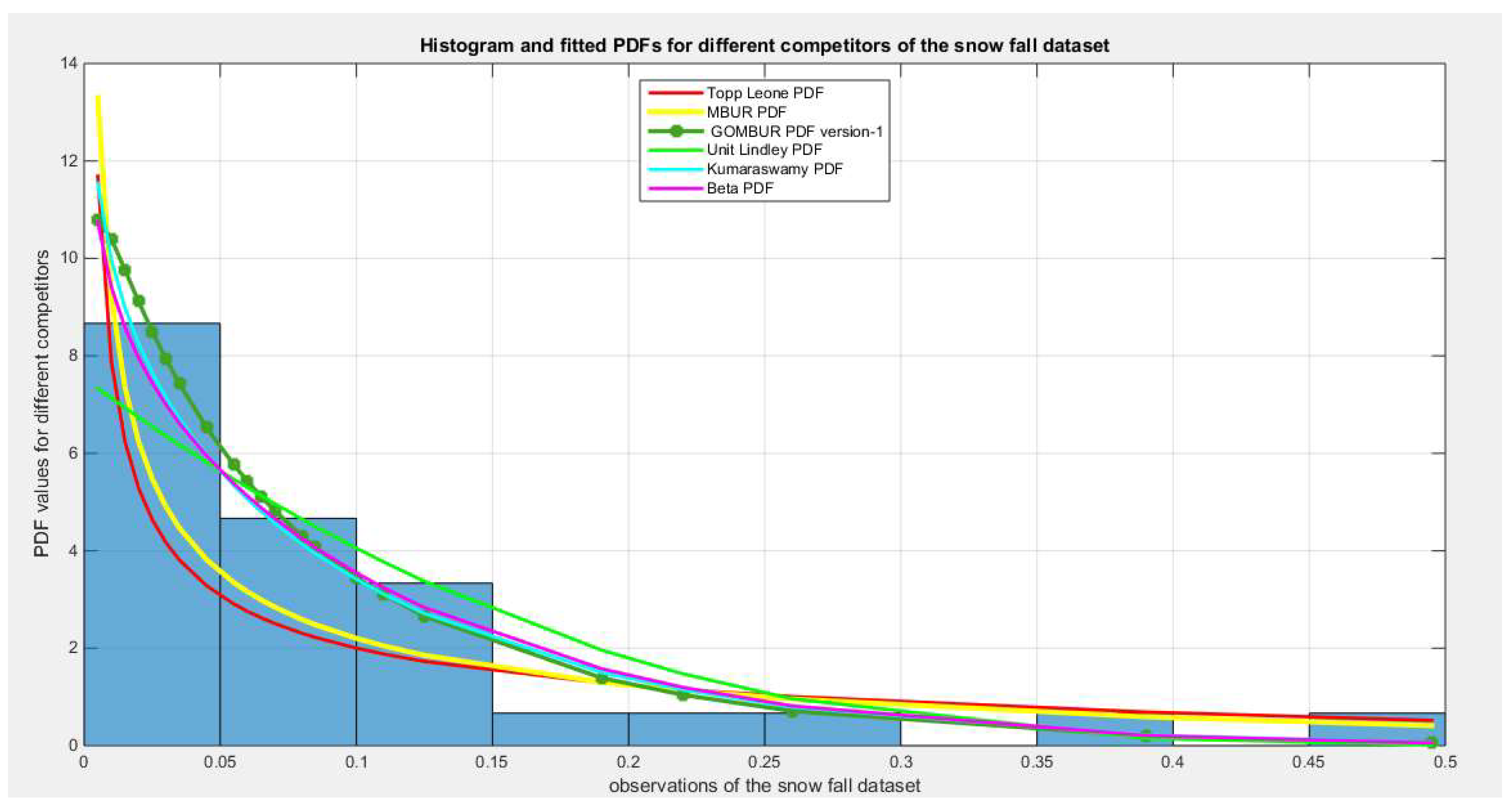
Figure 56.
shows the histogram of the snow fall data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 shows near perfect alignments with Beta distribution. Kumaraswamy distribution fits the data. BMUR and Unit Lindley distributions also fit the data but Topp Leone does not fit the data. .
Figure 56.
shows the histogram of the snow fall data and the theoretical PDFs for the fitted distributions. The GOMBUR-1 shows near perfect alignments with Beta distribution. Kumaraswamy distribution fits the data. BMUR and Unit Lindley distributions also fit the data but Topp Leone does not fit the data. .
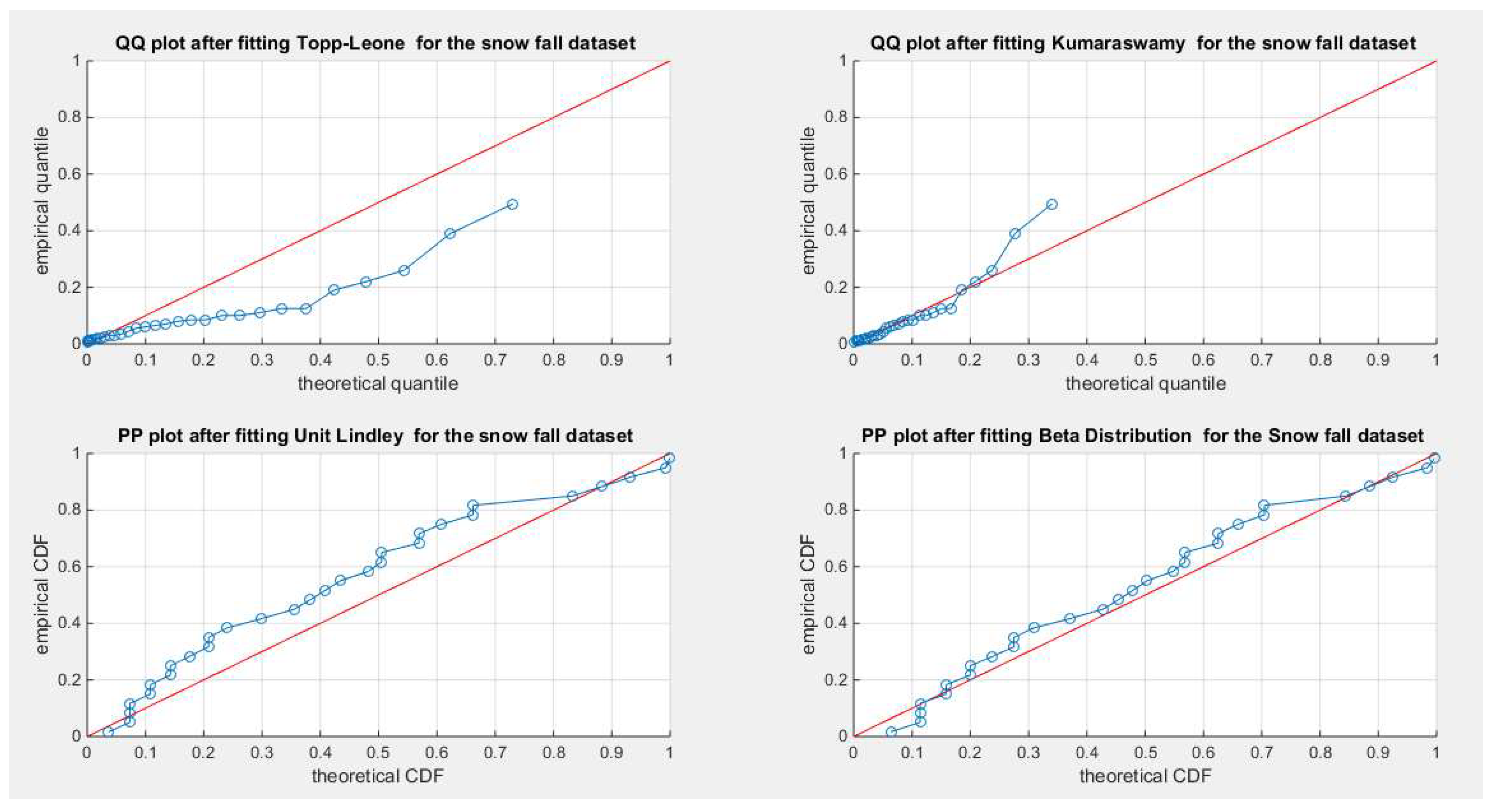
Figure 57.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the snow fall dataset.
Figure 57.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the snow fall dataset.
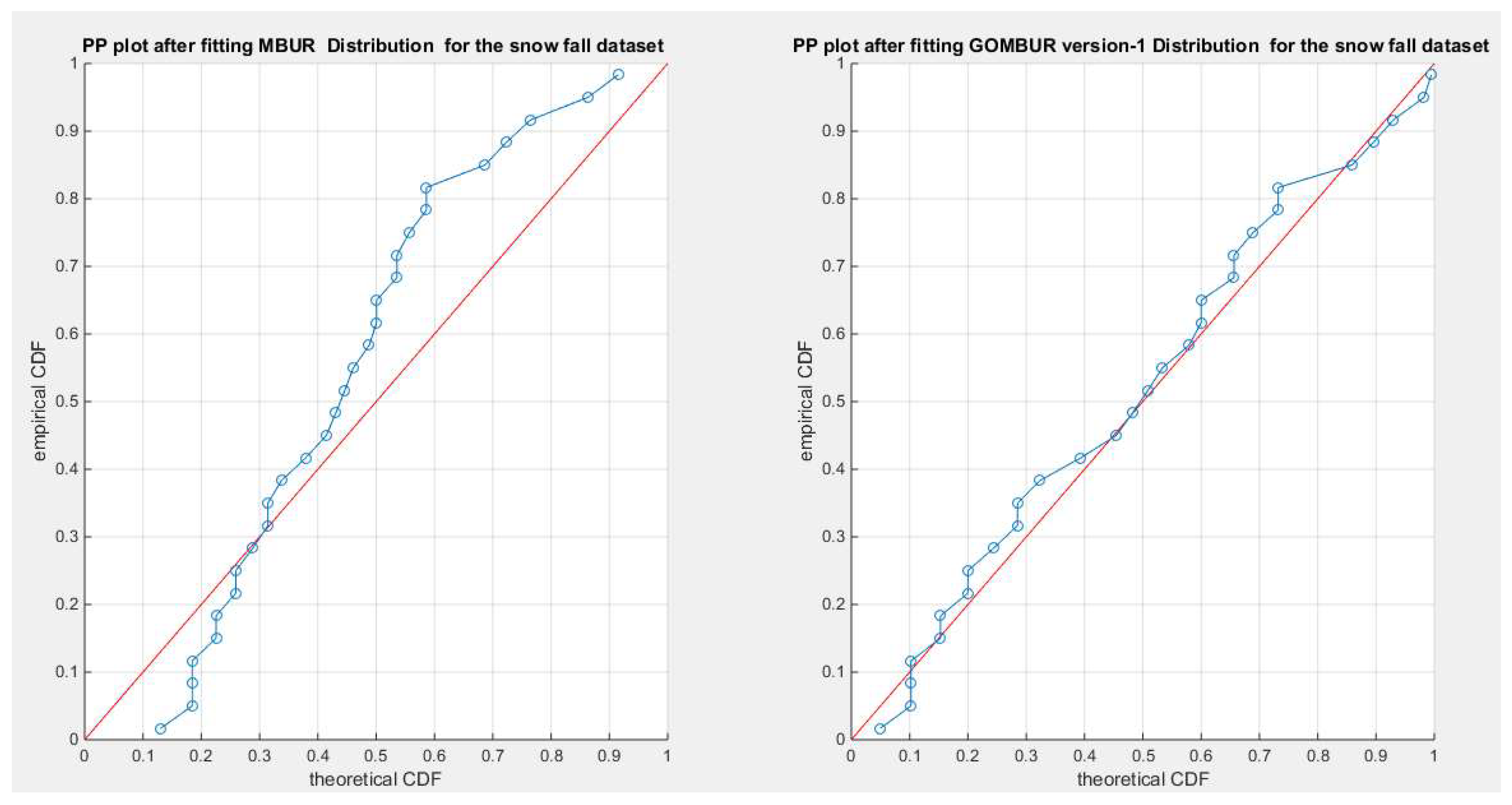
Figure 58.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the snow fall dataset. Although the MBUR fits the data, the generalization of MBUR enhances the diagonal alignment of GOMBUR-1 along both ends and along the center of the distribution.
Figure 58.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the snow fall dataset. Although the MBUR fits the data, the generalization of MBUR enhances the diagonal alignment of GOMBUR-1 along both ends and along the center of the distribution.
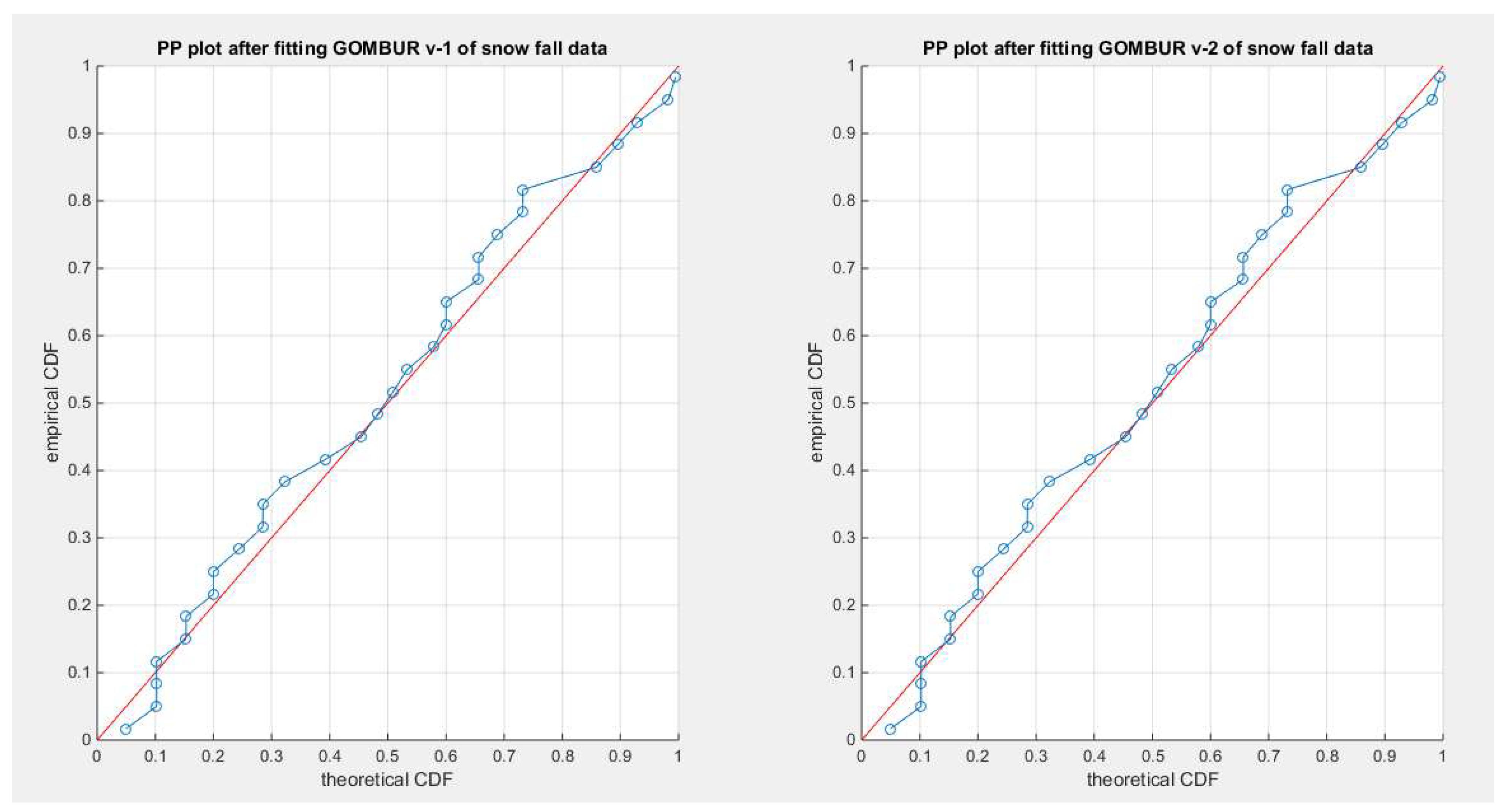
Figure 59.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for snow fall dataset. They are identical.
Figure 59.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for snow fall dataset. They are identical.
Figure 60.
shows on the left subplot the histogram of the snow fall and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical. The PDF curve is highly right skewed.
Figure 60.
shows on the left subplot the histogram of the snow fall and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical. The PDF curve is highly right skewed.
Figure 61.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of the milk production data.
Figure 61.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of the milk production data.
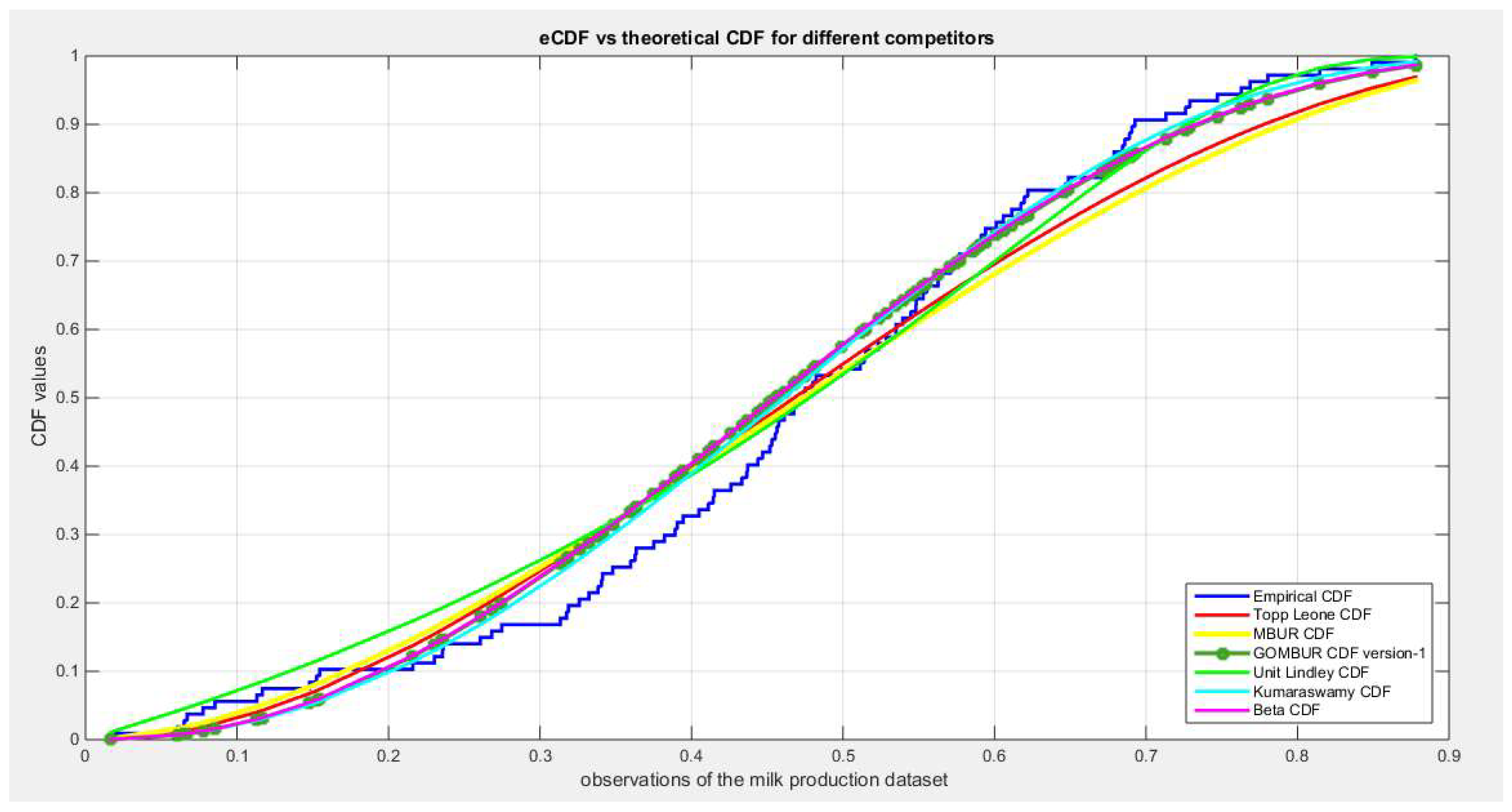
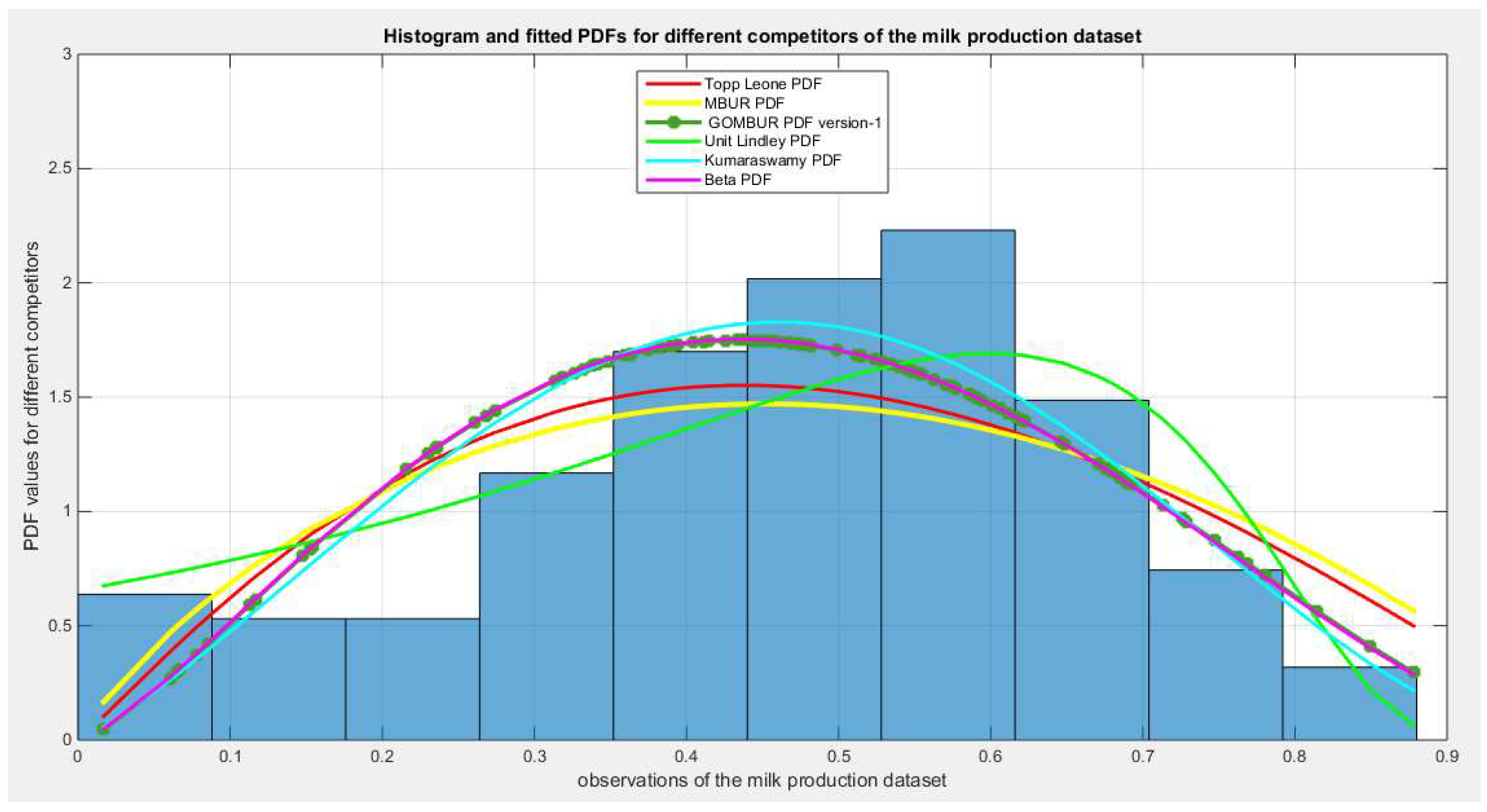
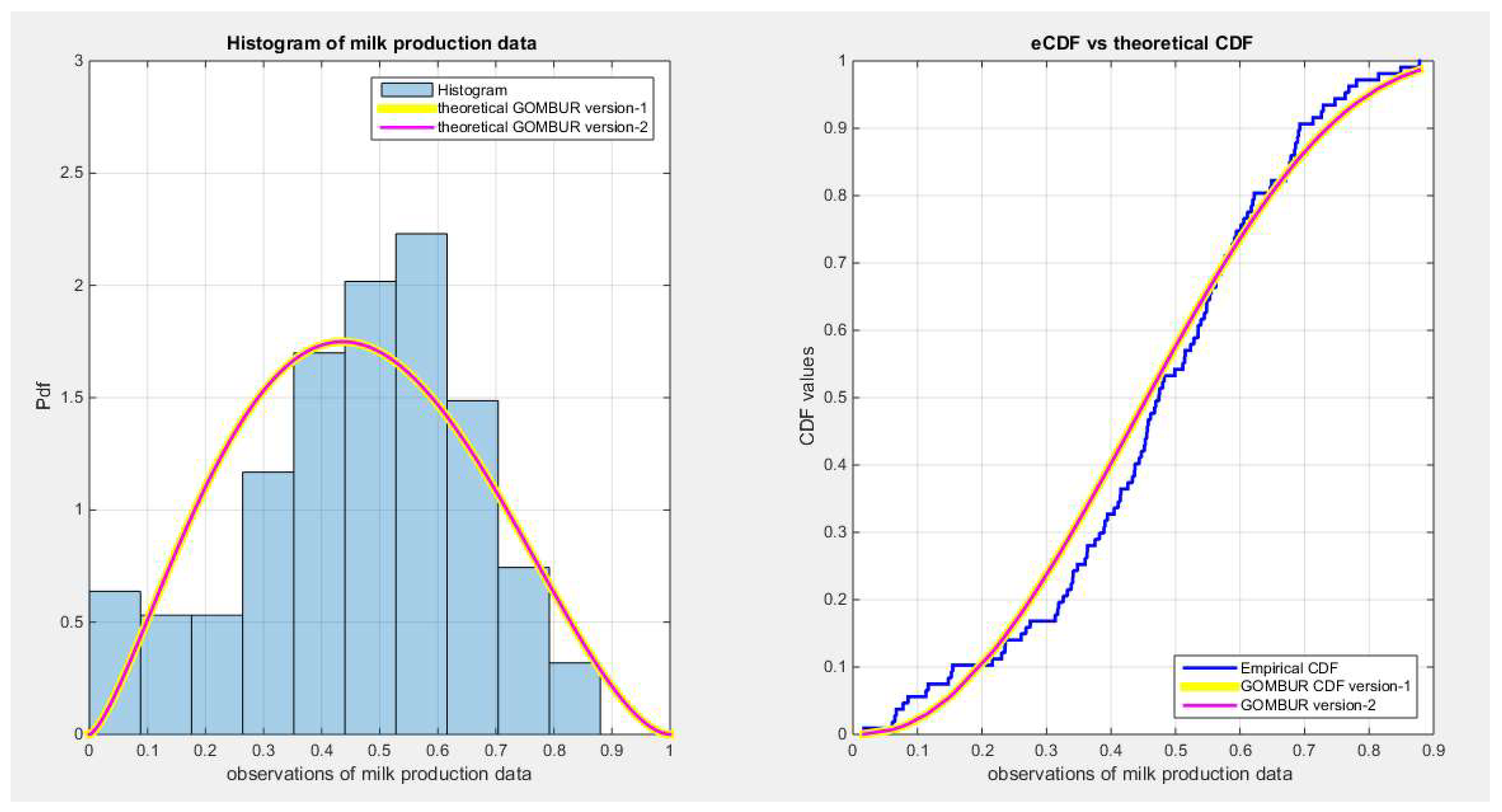
Figure 62.
shows the histogram of the milk production data and the theoretical PDFs for the fitted distributions. All the competitor distributions fit the data well but the Unit Lindley and the Kumaraswamy outperform other competitors. Beta distribution is the third distribution to fit the data, and after generalization of the MBUR , GOMBUR-1 properly aligns with Beta. .
Figure 62.
shows the histogram of the milk production data and the theoretical PDFs for the fitted distributions. All the competitor distributions fit the data well but the Unit Lindley and the Kumaraswamy outperform other competitors. Beta distribution is the third distribution to fit the data, and after generalization of the MBUR , GOMBUR-1 properly aligns with Beta. .
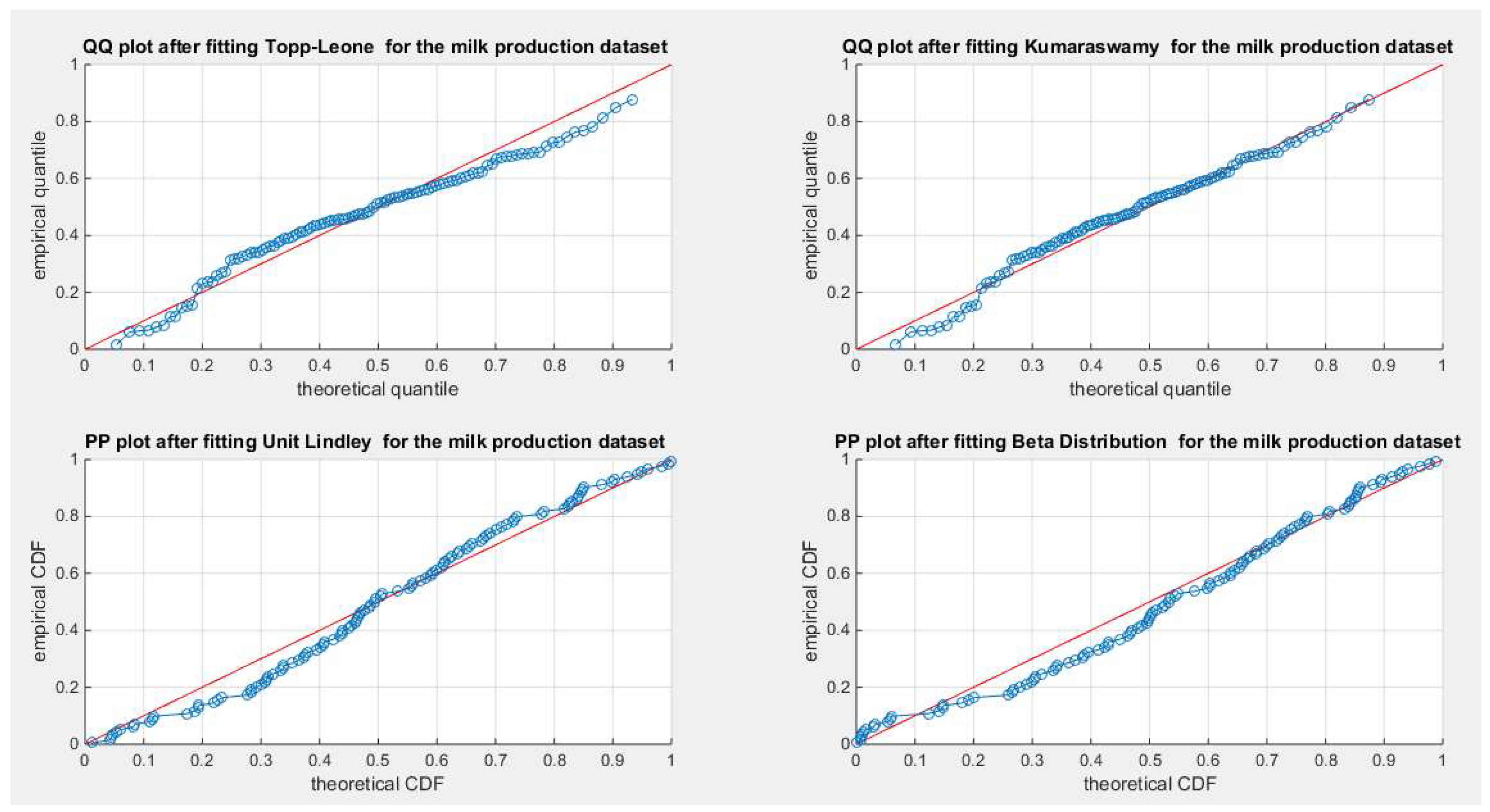
Figure 63.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the milk production dataset.
Figure 63.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the milk production dataset.
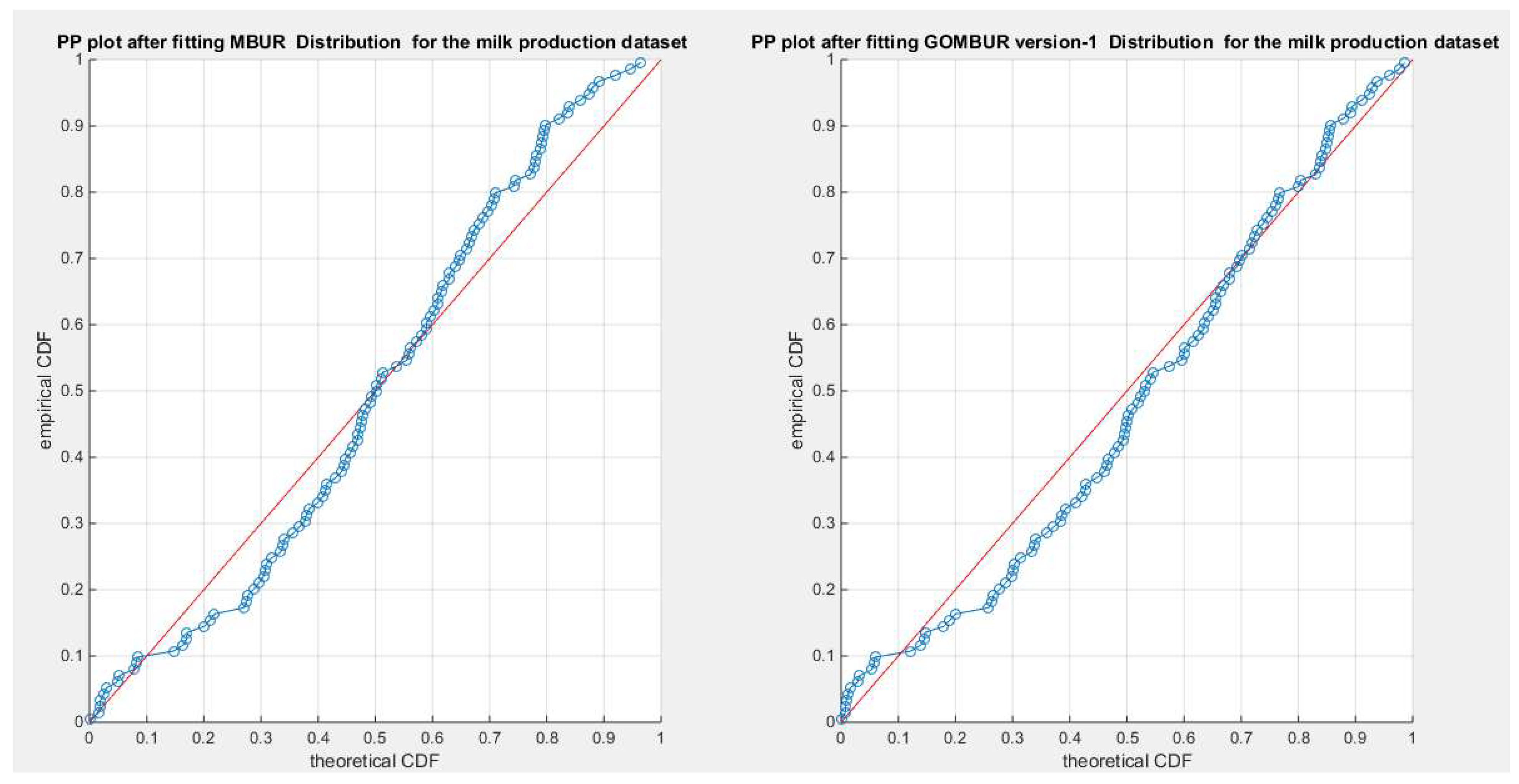
Figure 64.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the milk production dataset. Since the MBUR is the least distribution to fit the data among all other competitors, generalization of MBUR enhances the diagonal alignment of GOMBUR-1 along both ends and along the center of the distribution.
Figure 64.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the milk production dataset. Since the MBUR is the least distribution to fit the data among all other competitors, generalization of MBUR enhances the diagonal alignment of GOMBUR-1 along both ends and along the center of the distribution.
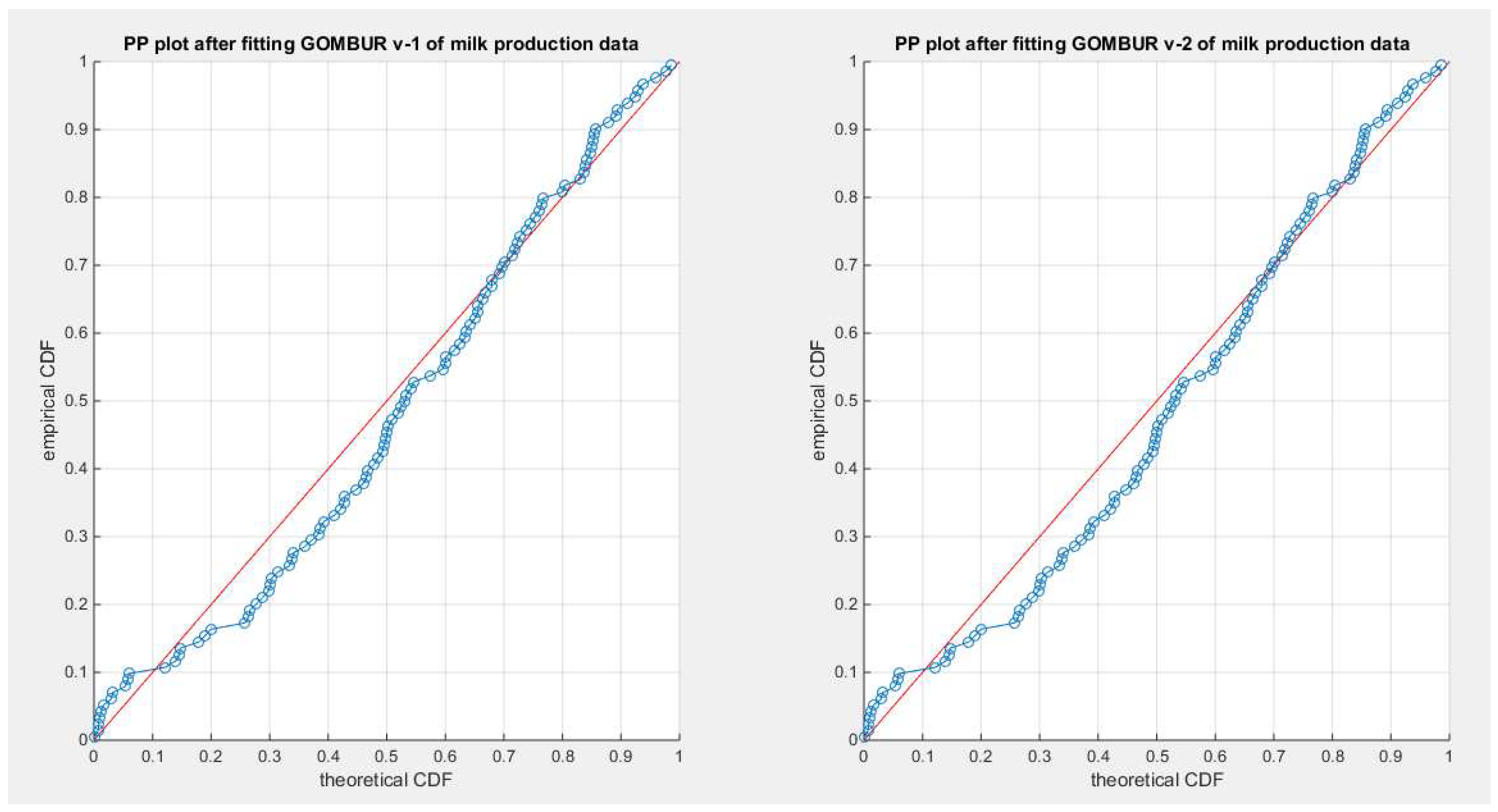
Figure 65.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for milk production dataset. They are identical.
Figure 65.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for milk production dataset. They are identical.
Figure 66.
shows on the left subplot the histogram of the milk production and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Figure 66.
shows on the left subplot the histogram of the milk production and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
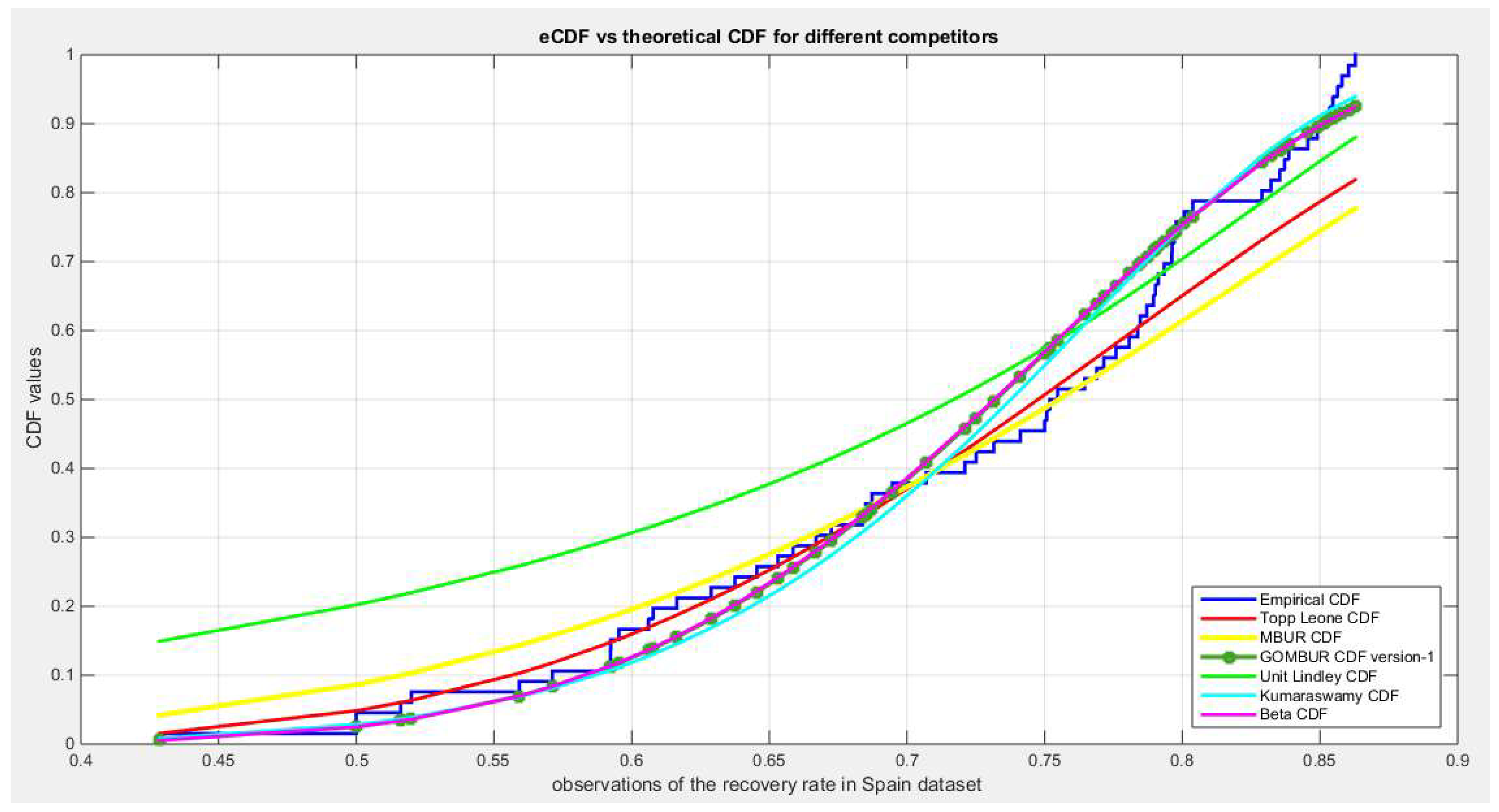
Figure 67.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of the recovery rate in Spain data.
Figure 67.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of the recovery rate in Spain data.
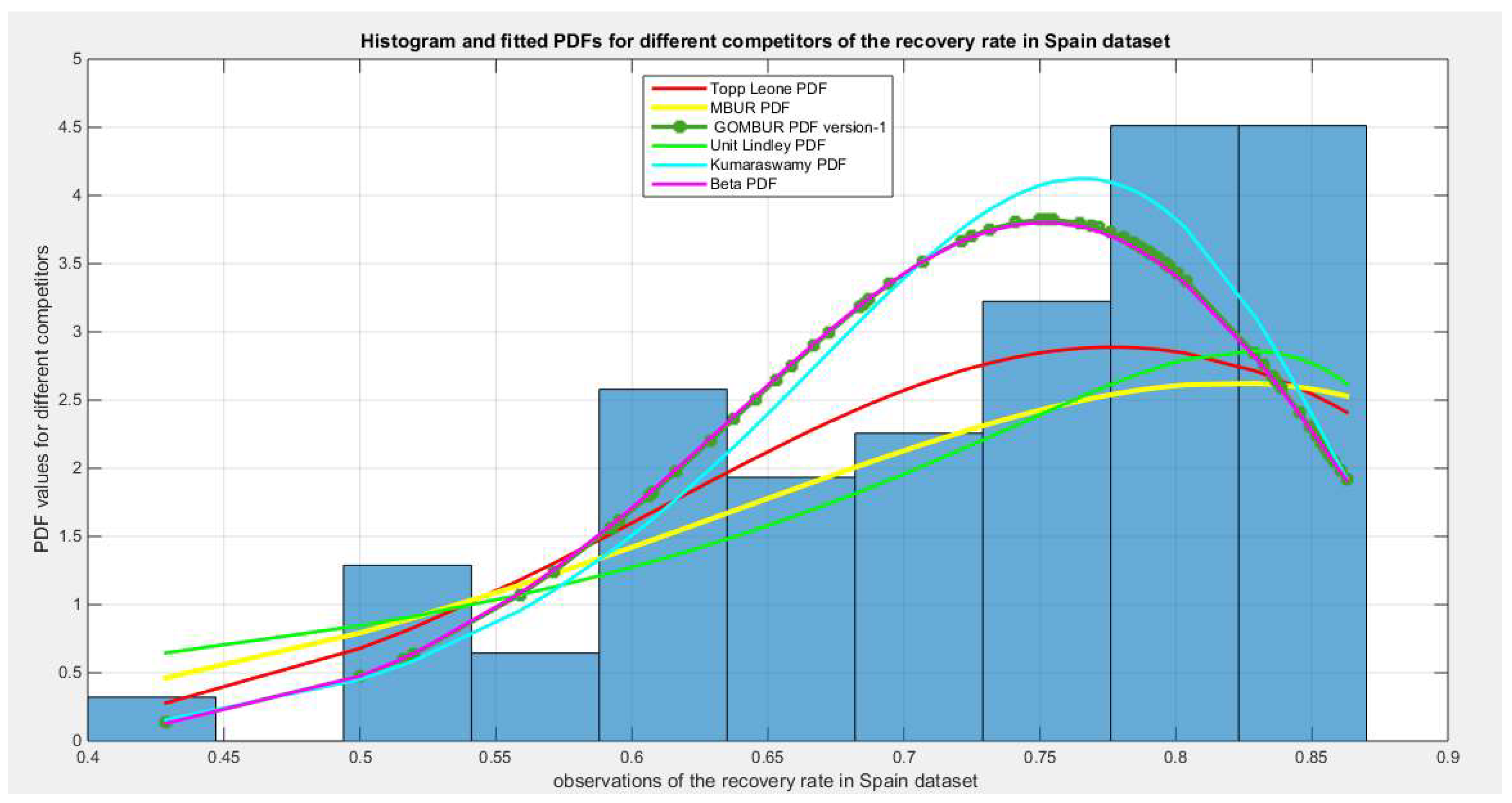
Figure 68.
shows the histogram of the recovery rate in Spain data and the theoretical PDFs for the fitted distributions. Kumaraswamy and Beta fit the data. After generalization the GOMBUR aligns appropriately with the Beta distribution and more or less parallels the Kumaraswamy distribution.
Figure 68.
shows the histogram of the recovery rate in Spain data and the theoretical PDFs for the fitted distributions. Kumaraswamy and Beta fit the data. After generalization the GOMBUR aligns appropriately with the Beta distribution and more or less parallels the Kumaraswamy distribution.
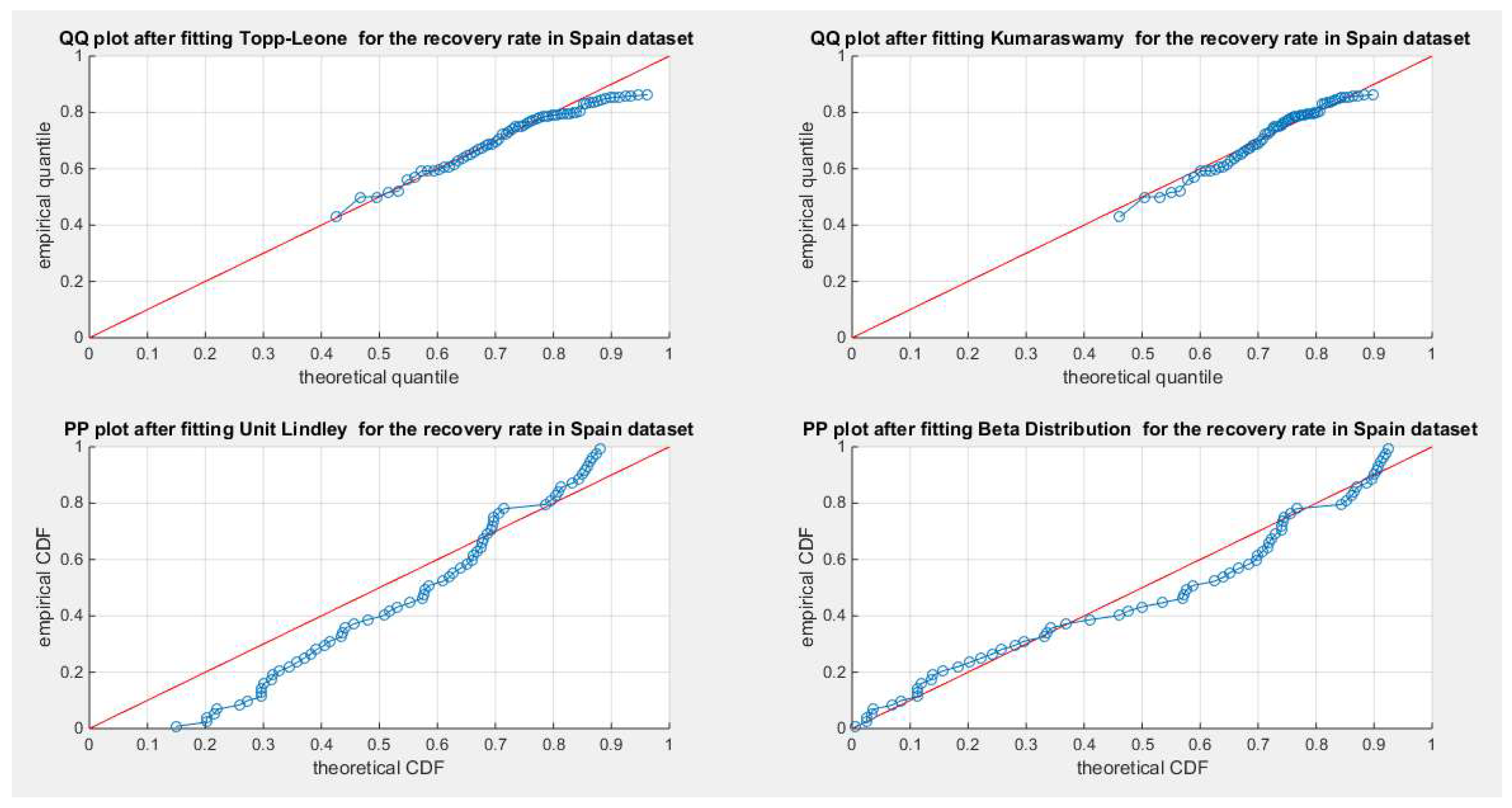
Figure 69.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the recovery rate in Spain dataset.
Figure 69.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the recovery rate in Spain dataset.
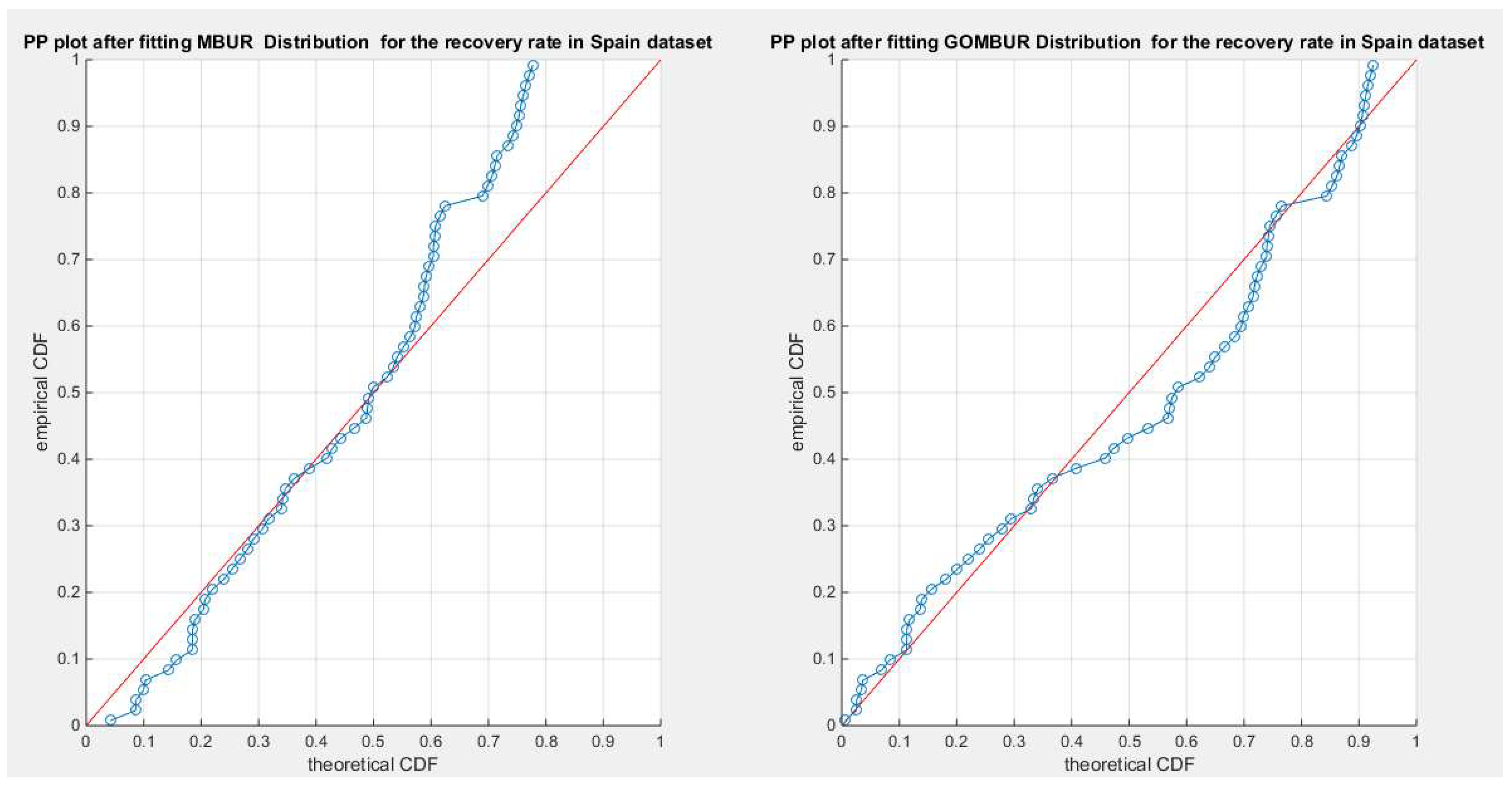
Figure 70.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the recovery rate in Spain dataset. Generalization of the MBUR enhances the diagonal alignment along both ends.
Figure 70.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the recovery rate in Spain dataset. Generalization of the MBUR enhances the diagonal alignment along both ends.
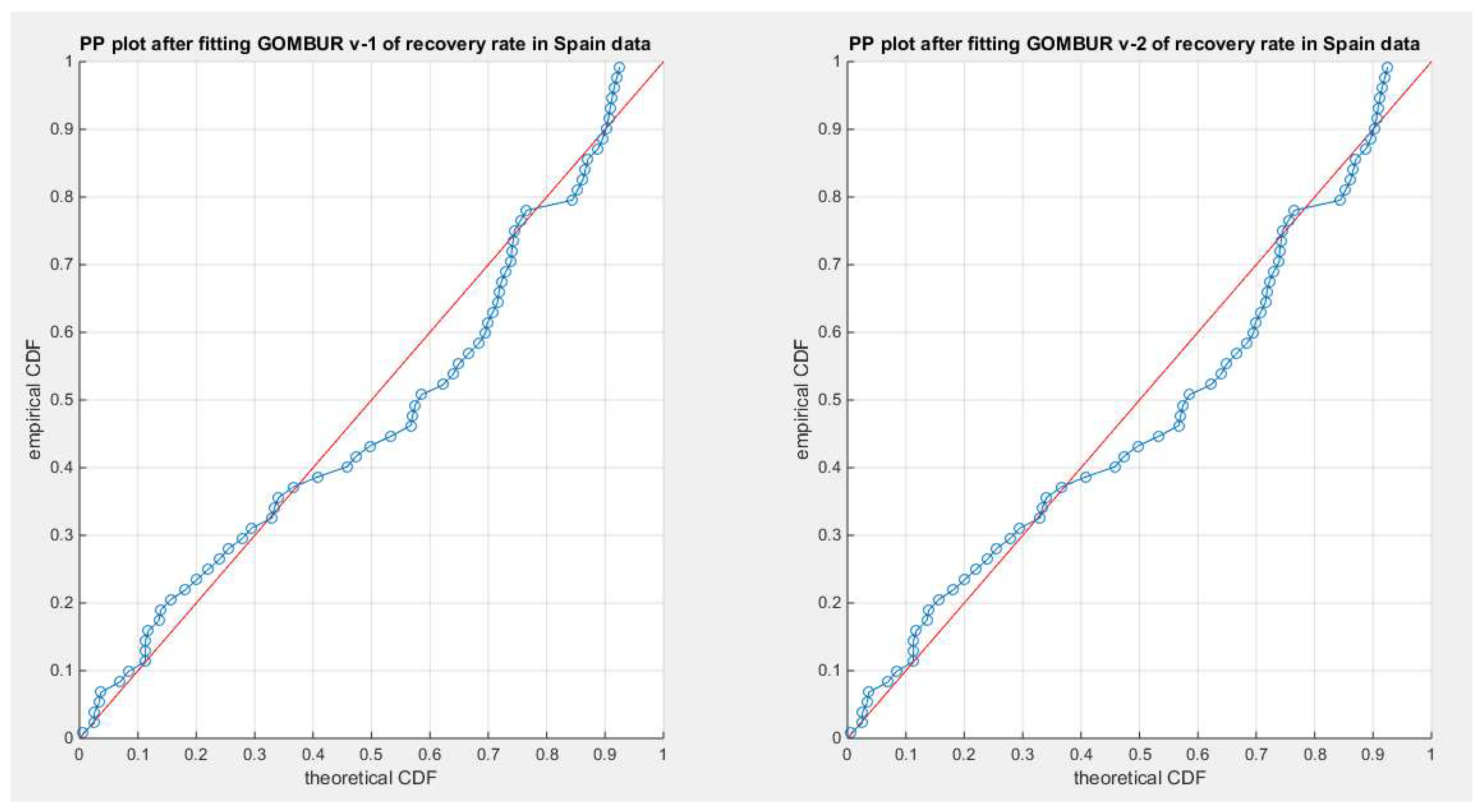
Figure 71.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for recovery rate in Spain dataset. They are identical.
Figure 71.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for recovery rate in Spain dataset. They are identical.
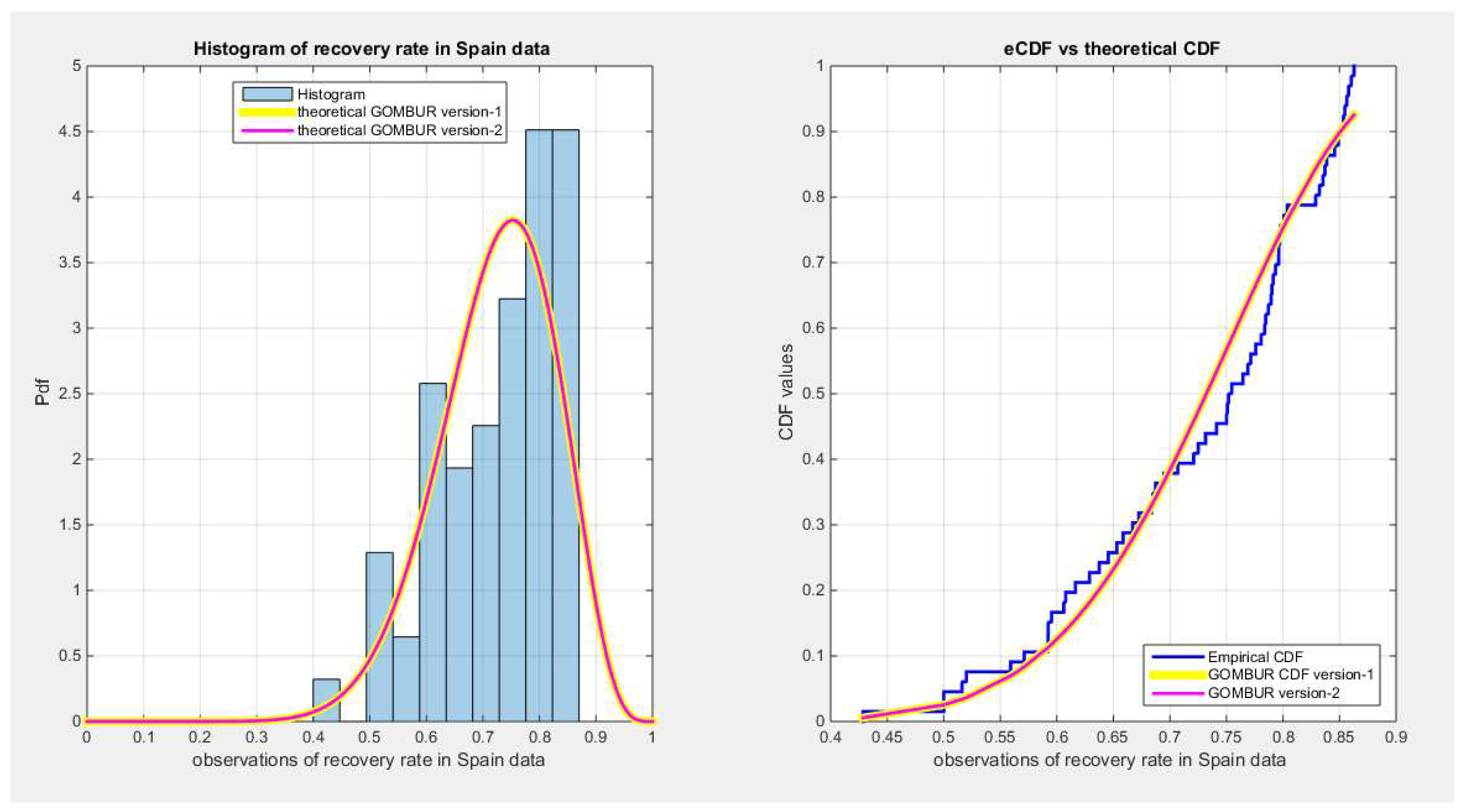
Figure 72.
shows on the left subplot the histogram of the recovery rate in Spain and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Figure 72.
shows on the left subplot the histogram of the recovery rate in Spain and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
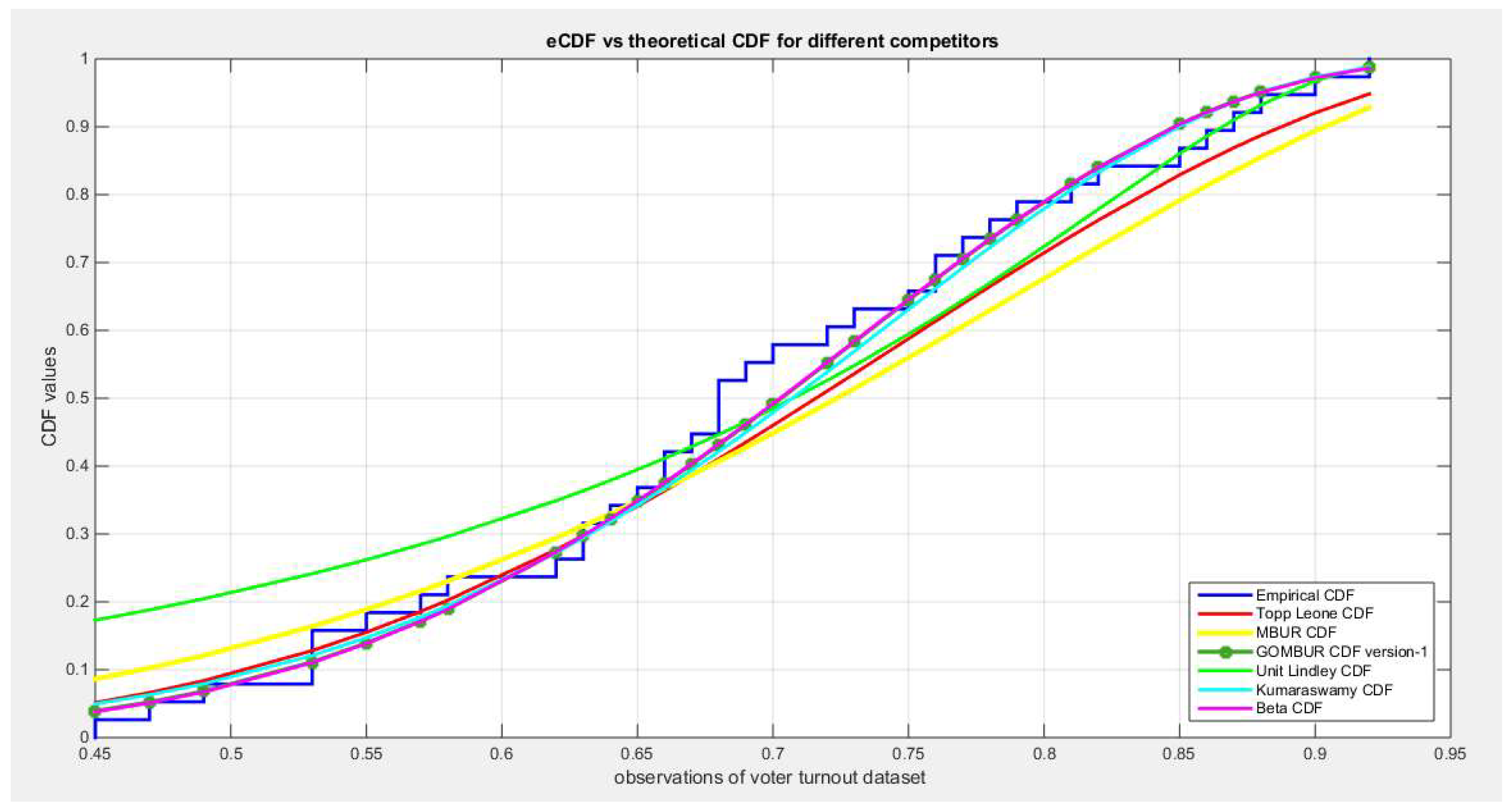
Figure 73.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of the voter turnout data.
Figure 73.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of the voter turnout data.
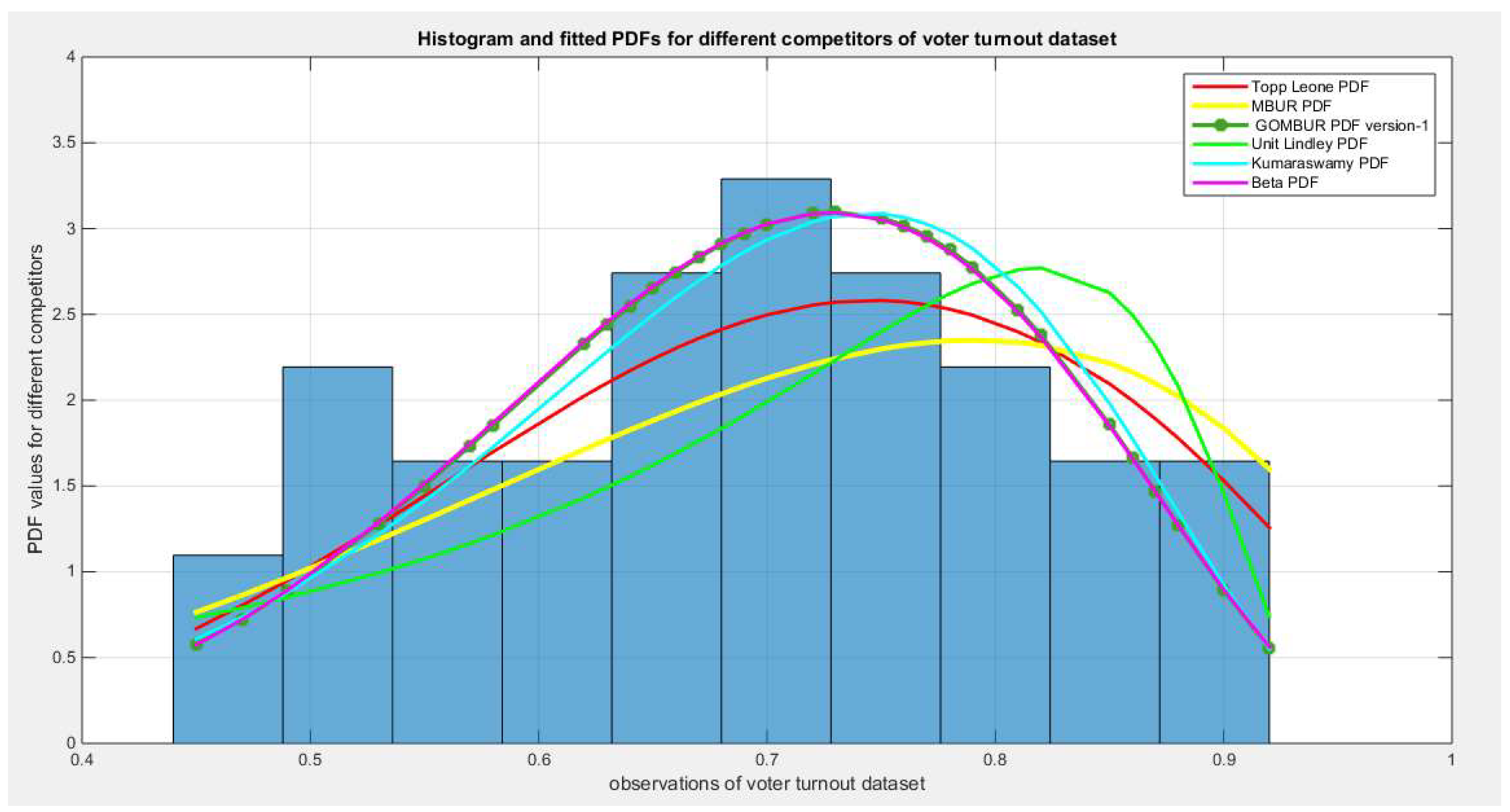
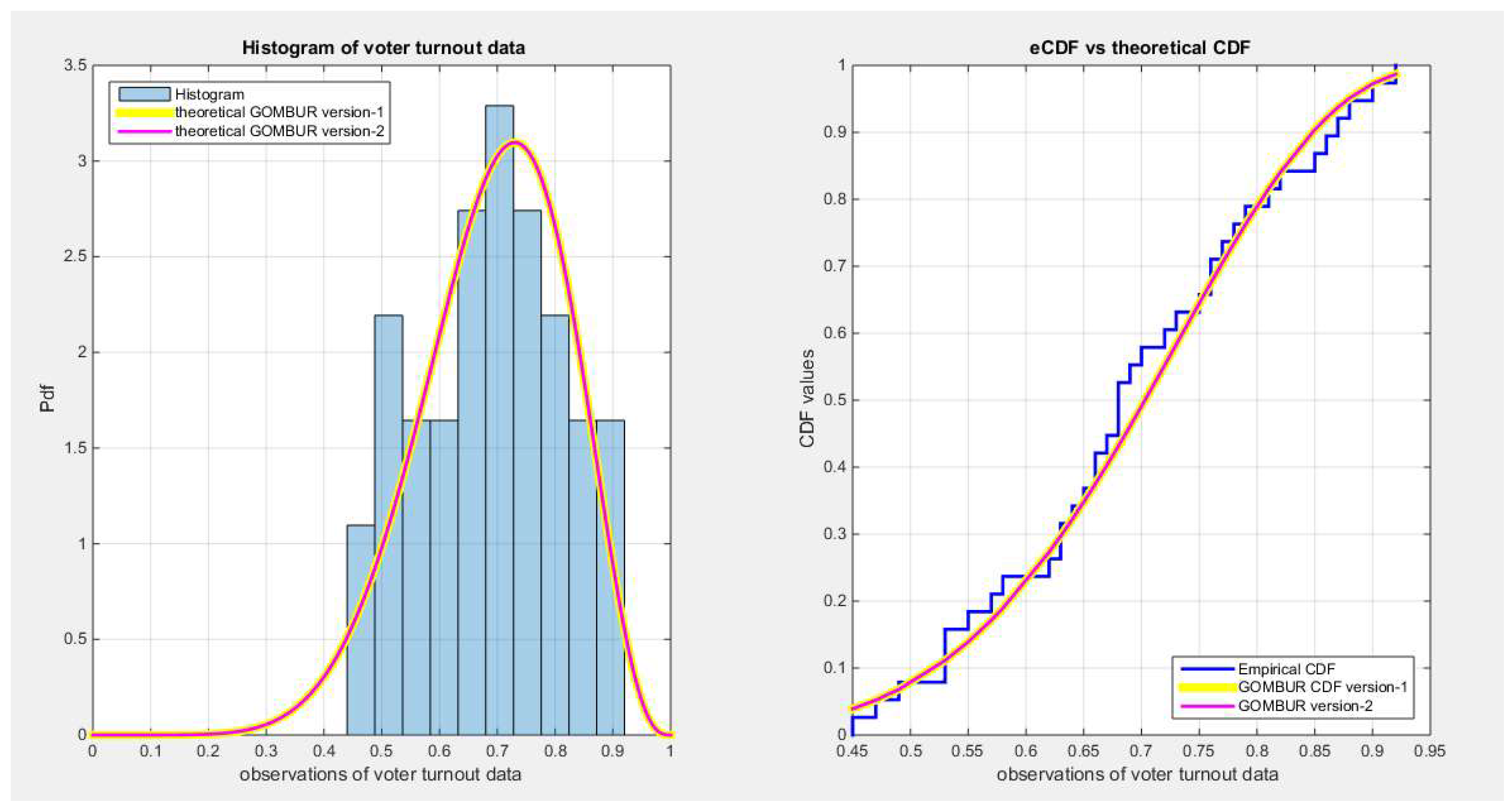
Figure 74.
shows the histogram of the voter turnout data and the theoretical PDFs for the fitted distributions. Beta, Topp Leone, Kumaraswamy, MBUR and lastly Unit Lindley fit the data. After generalization the GOMBUR aligns appropriately with the Beta distribution and more or less parallels the Kumaraswamy distribution.
Figure 74.
shows the histogram of the voter turnout data and the theoretical PDFs for the fitted distributions. Beta, Topp Leone, Kumaraswamy, MBUR and lastly Unit Lindley fit the data. After generalization the GOMBUR aligns appropriately with the Beta distribution and more or less parallels the Kumaraswamy distribution.
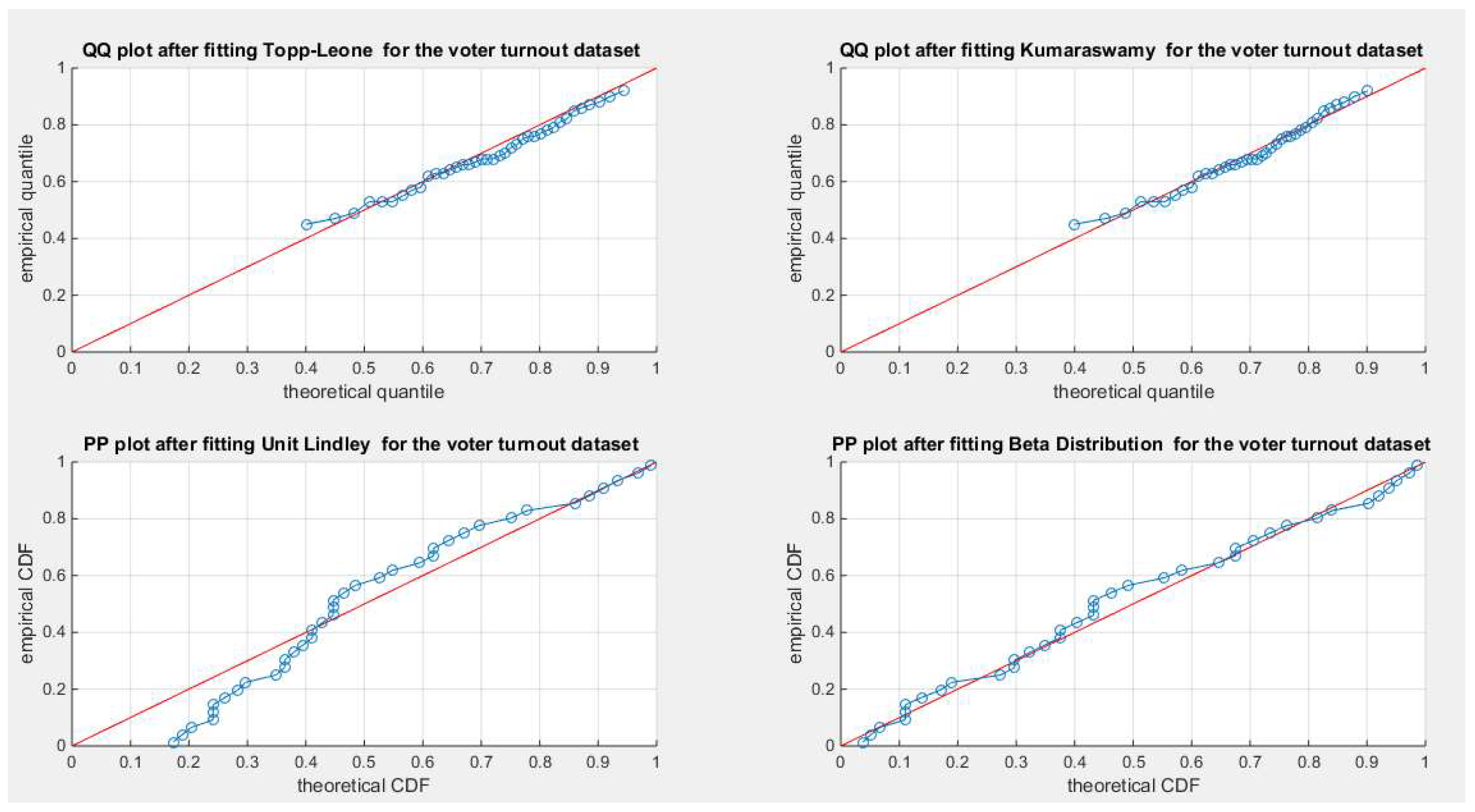
Figure 75.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the voter turnout dataset.
Figure 75.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the voter turnout dataset.
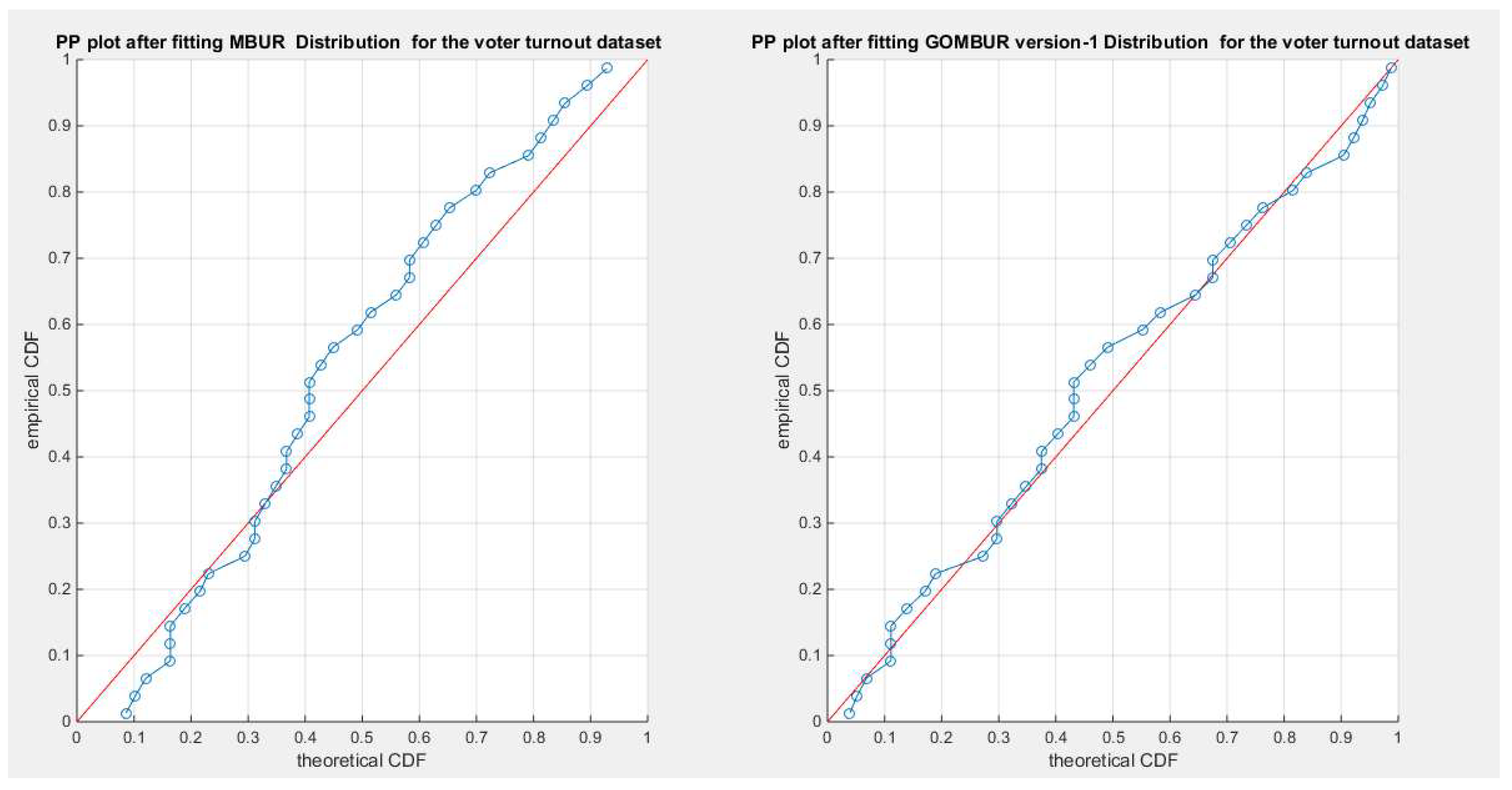
Figure 76.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the voter turnout dataset. Although, MBUR fit the data and the PP plot shows an acceptable diagonal alignment the generalization of the MBUR enhances and refines this diagonal alignment along both ends and along the center of the distribution.
Figure 76.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the voter turnout dataset. Although, MBUR fit the data and the PP plot shows an acceptable diagonal alignment the generalization of the MBUR enhances and refines this diagonal alignment along both ends and along the center of the distribution.
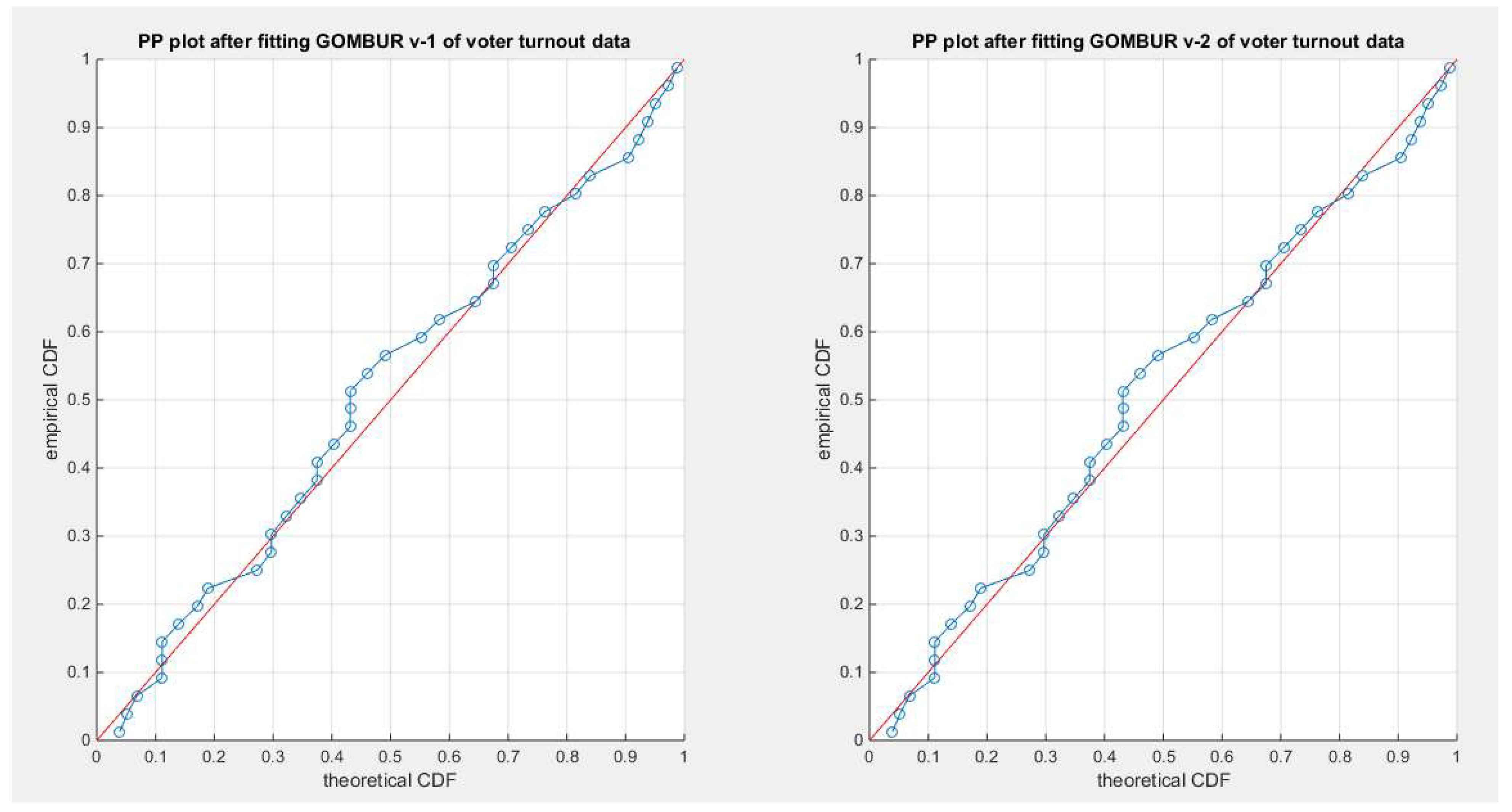
Figure 77.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for voter turnout dataset. They are identical.
Figure 77.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for voter turnout dataset. They are identical.
Figure 78.
shows on the left subplot the histogram of the voter turnout data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Figure 78.
shows on the left subplot the histogram of the voter turnout data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
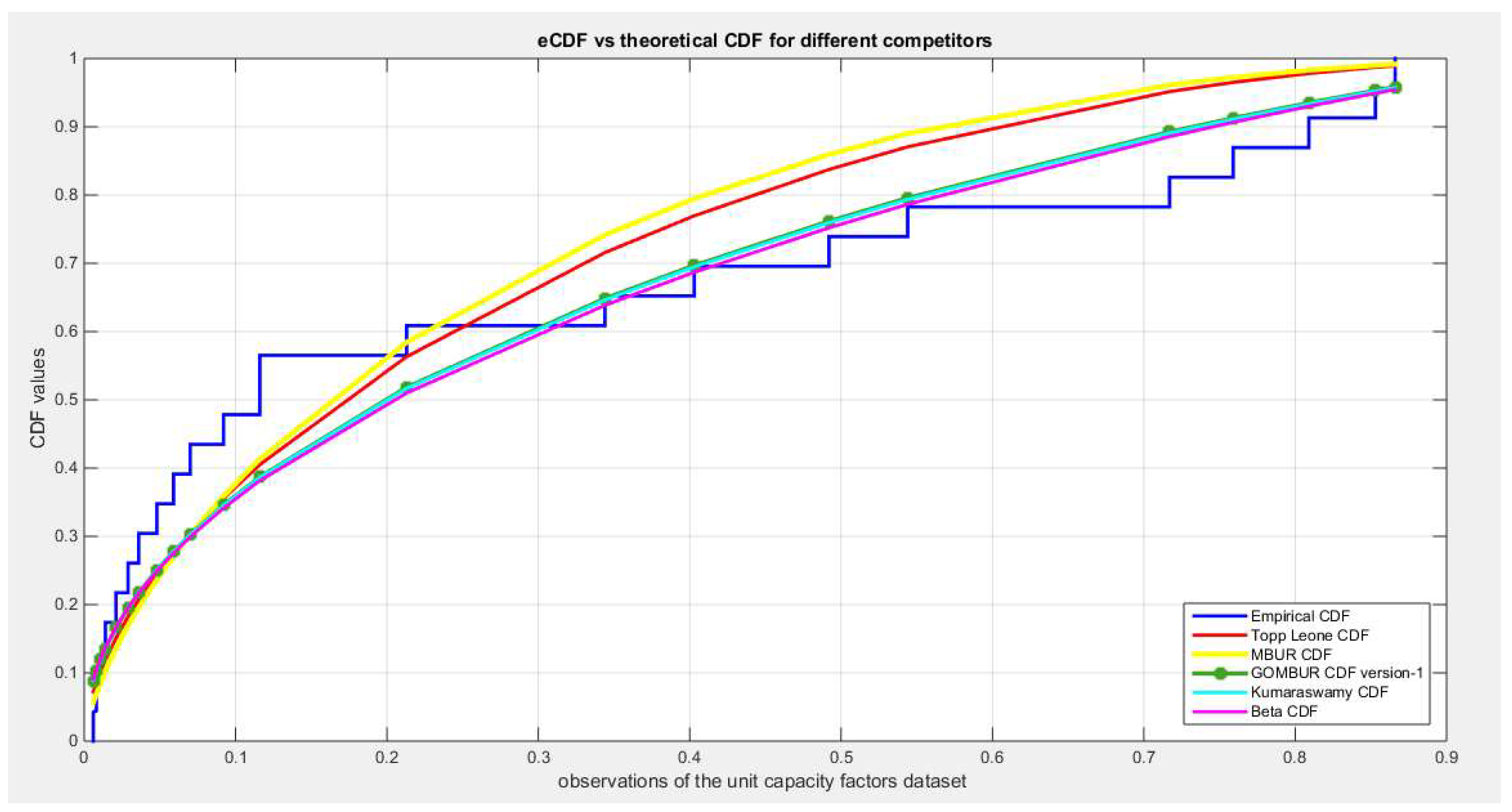
Figure 79.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of the unit capacity factors data.
Figure 79.
shows the e-CDFs and the theoretical CDFs for the fitted distributions of the unit capacity factors data.
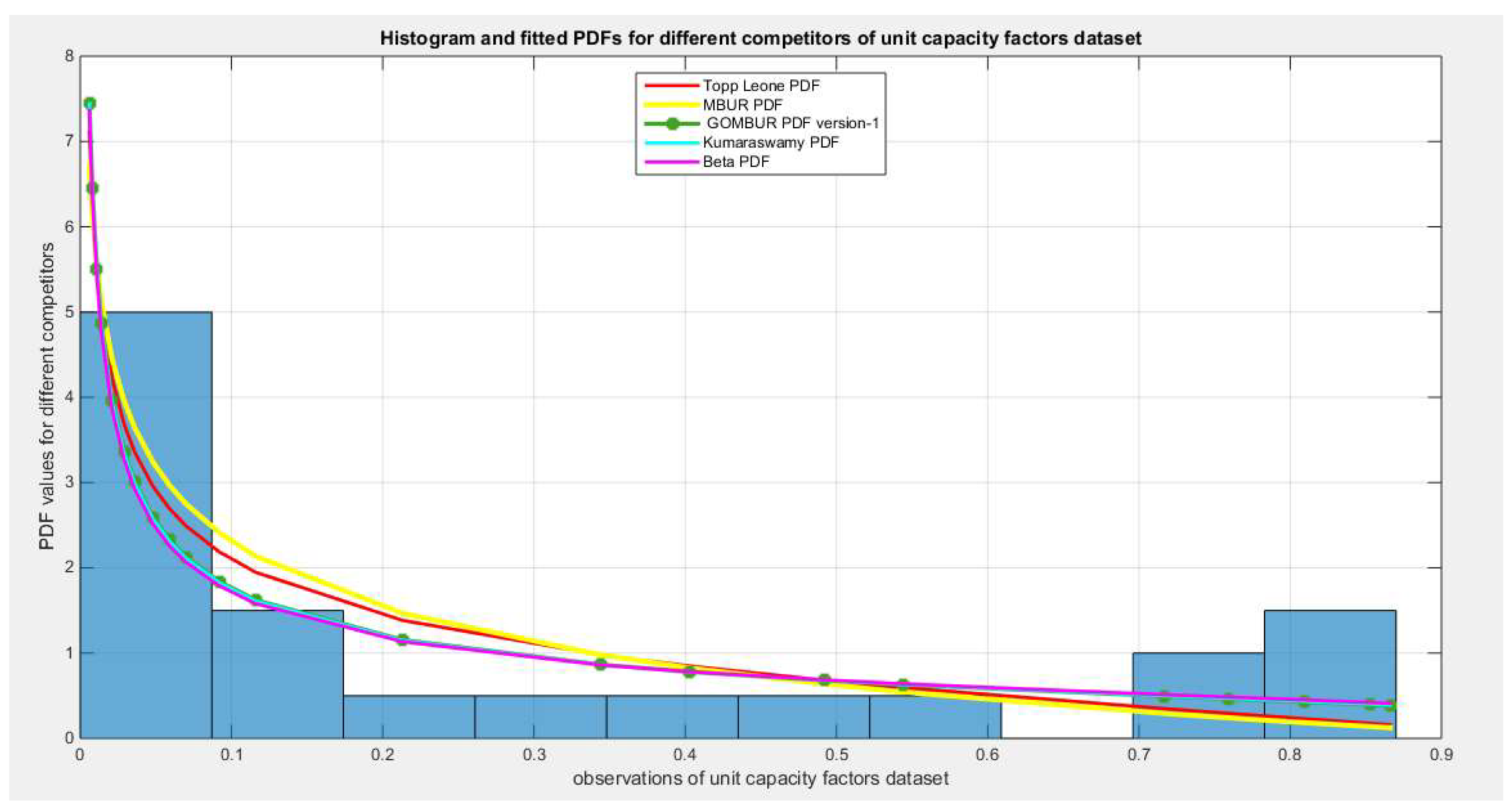
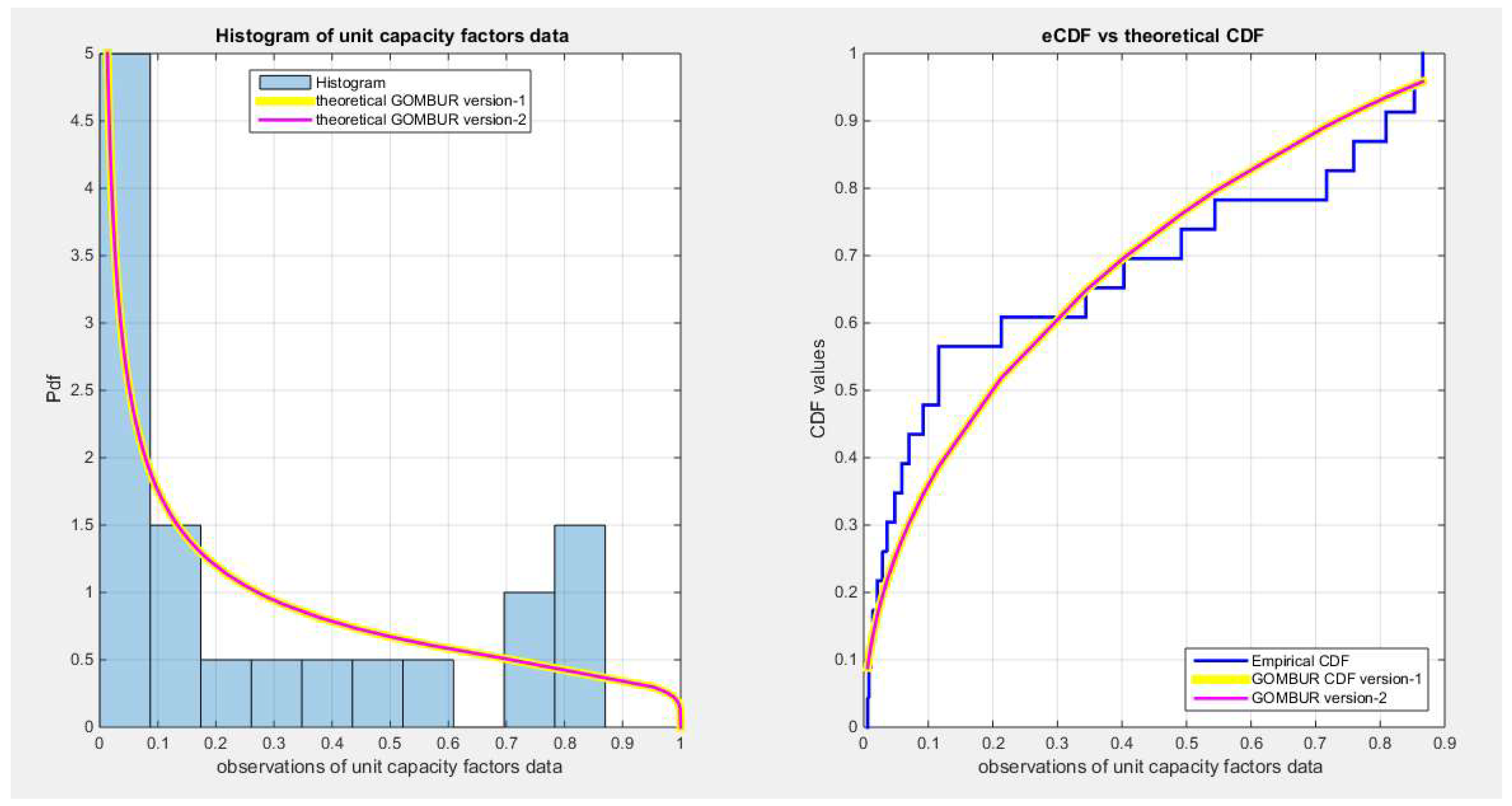
Figure 80.
shows the histogram of the unit capacity factors data and the theoretical PDFs for the fitted distributions. Kumaraswamy, Beta, Topp Leone and lastly MBUR distributions fit the data. After generalization the GOMBUR aligns appropriately with the Beta distribution and more or less parallels the Kumaraswamy distribution.
Figure 80.
shows the histogram of the unit capacity factors data and the theoretical PDFs for the fitted distributions. Kumaraswamy, Beta, Topp Leone and lastly MBUR distributions fit the data. After generalization the GOMBUR aligns appropriately with the Beta distribution and more or less parallels the Kumaraswamy distribution.
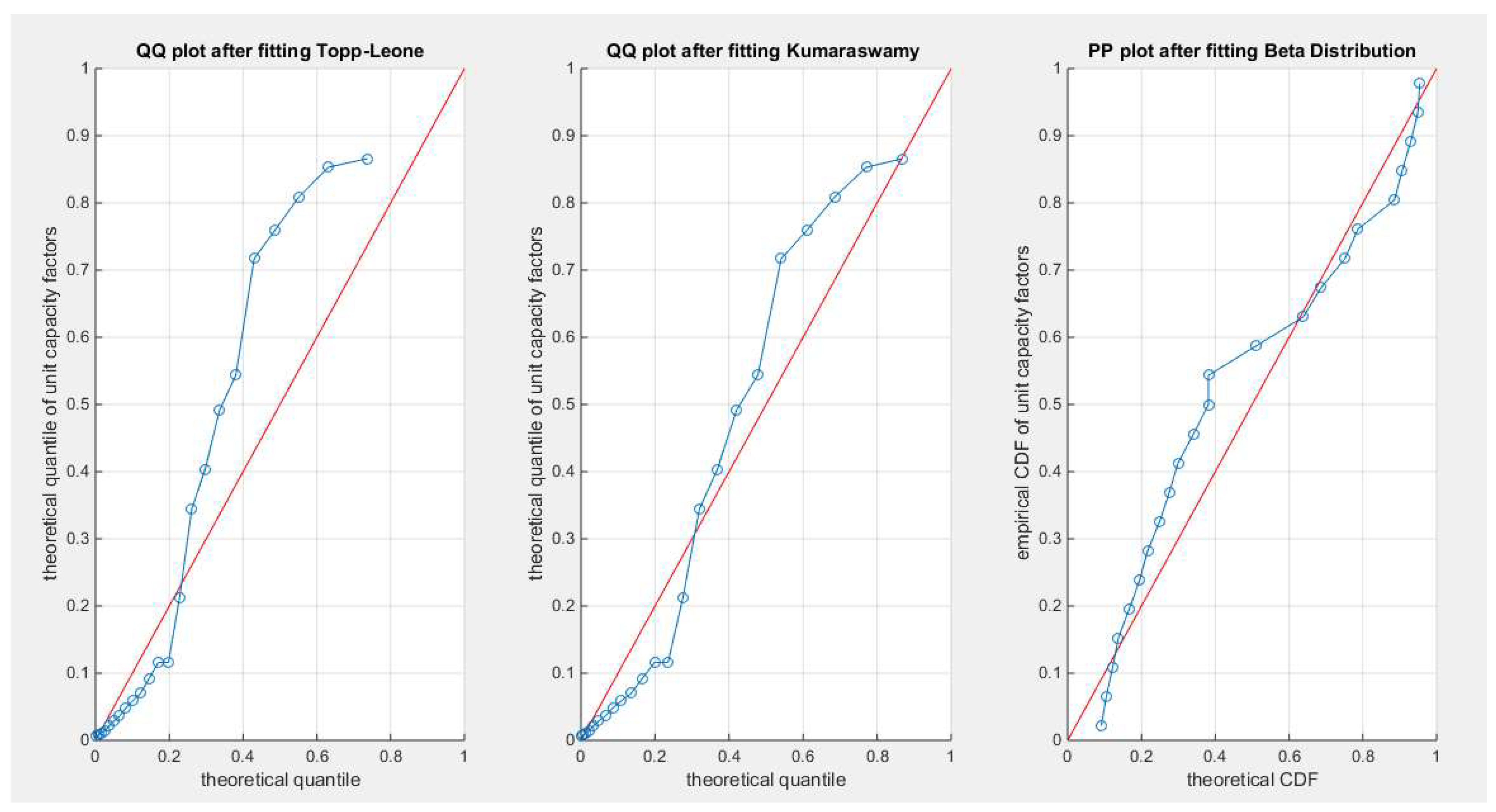
Figure 81.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the unit capacity factors dataset.
Figure 81.
shows the QQ plot for the fitted Topp Leone & Kumaraswamy distributions and the PP plot for the fitted Unit Lindley and Beta distribution for the unit capacity factors dataset.
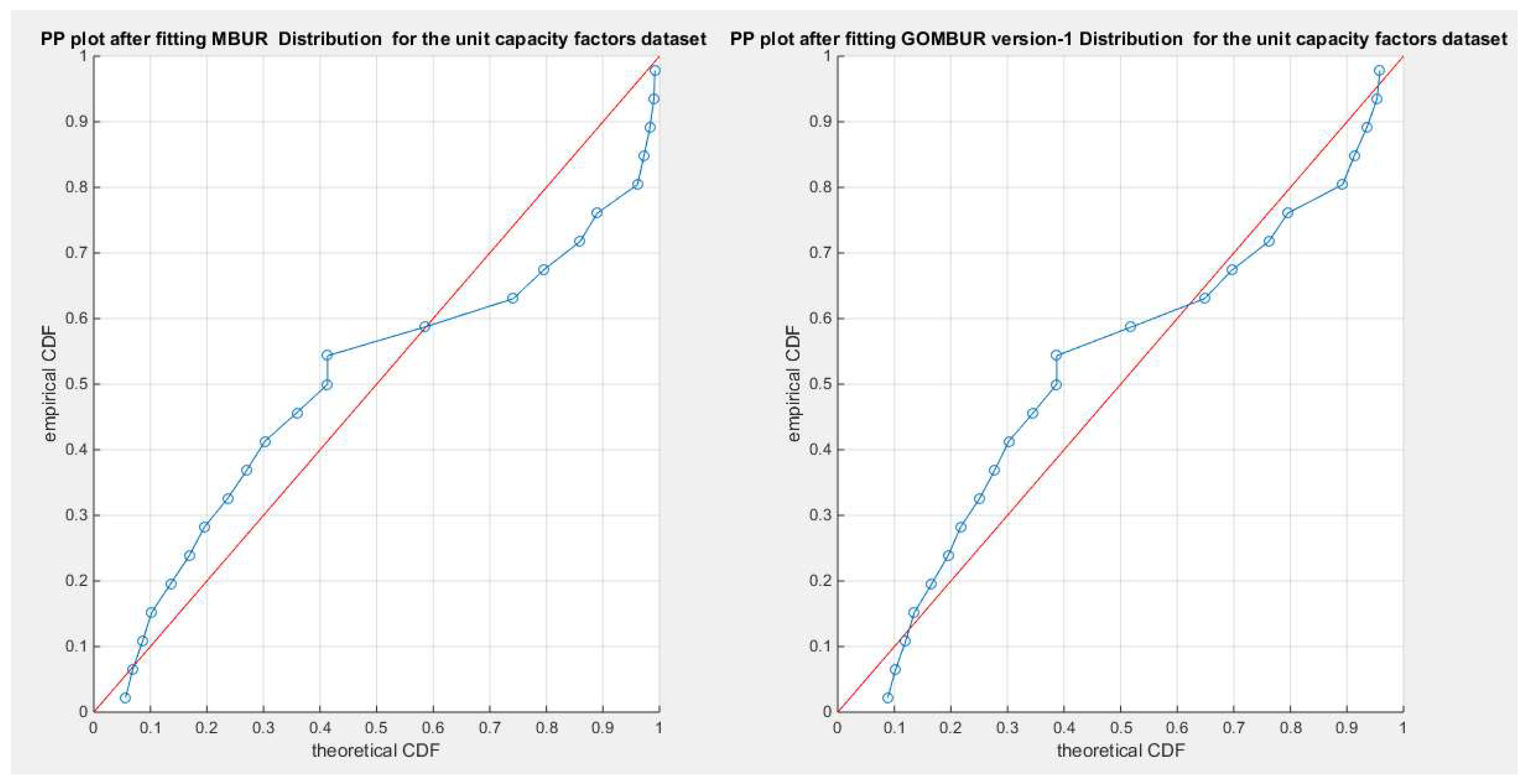
Figure 82.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the voter turnout dataset. Although, MBUR fits the data and the PP plot shows an acceptable diagonal alignment; the generalization of the MBUR enhances and refines this diagonal alignment along the upper end and along the center of the distribution.
Figure 82.
shows the PP plot for the fitted MBUR & GOMBUR-1 for the voter turnout dataset. Although, MBUR fits the data and the PP plot shows an acceptable diagonal alignment; the generalization of the MBUR enhances and refines this diagonal alignment along the upper end and along the center of the distribution.
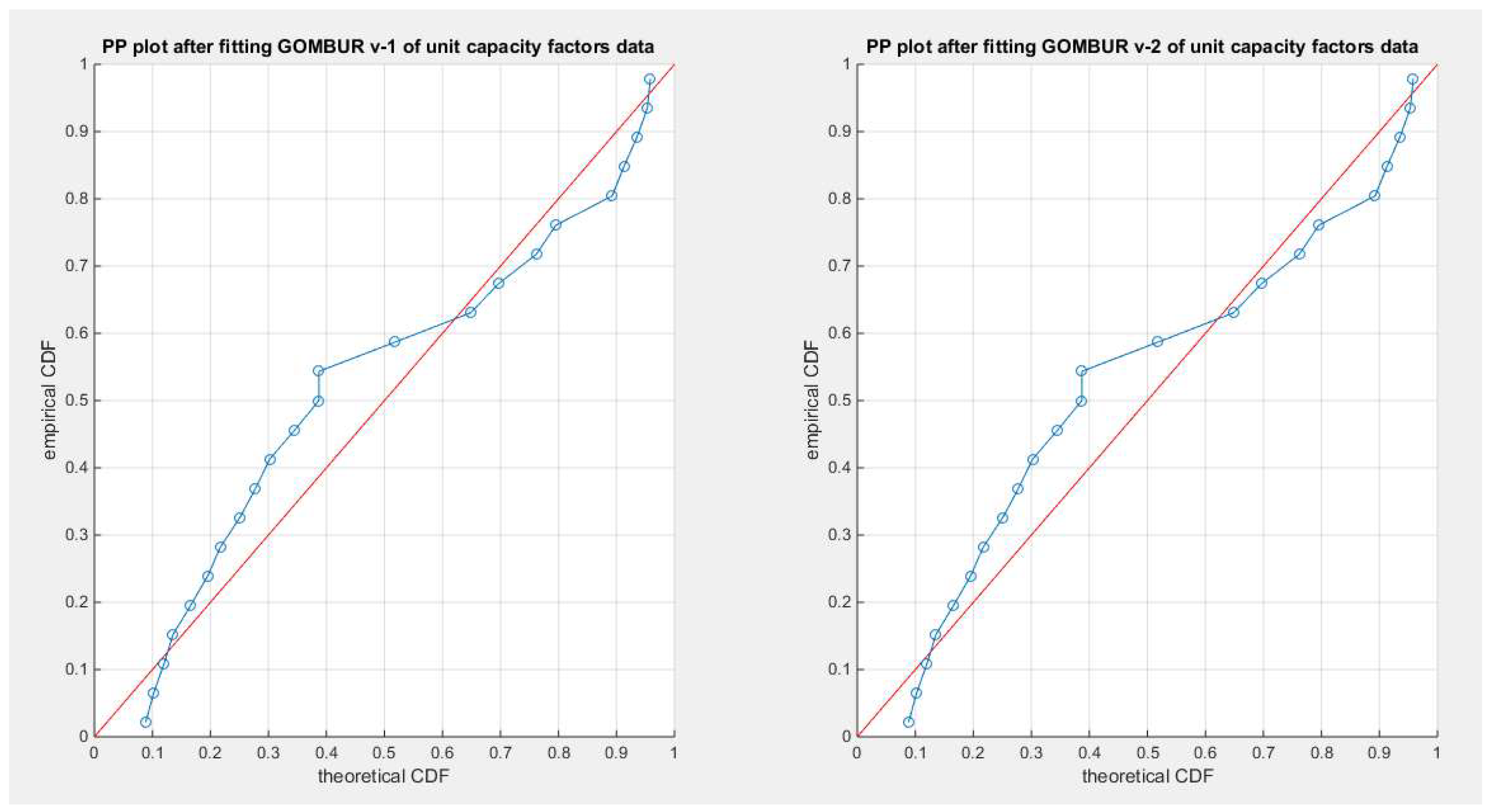
Figure 83.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for unit capacity factors dataset. They are identical.
Figure 83.
shows the PP plot for the fitted GOMBUR-1 & GOMBUR-2 for unit capacity factors dataset. They are identical.
Figure 84.
shows on the left subplot the histogram of the unit capacity factors data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Figure 84.
shows on the left subplot the histogram of the unit capacity factors data and the fitted PDFs of both GOMBUR-1 & GOMBUR-2 and on the right subplot the e-CDFs and the theoretical CDFs for both distributions. Both the fitted CDFs and the fitted PDFs of both versions are identical.
Table 1.
illustrates the descriptive statistics for the above datasets:.
Table 1.
illustrates the descriptive statistics for the above datasets:.
| Data Number |
Min |
Mean |
Std |
Skewness |
Kurtosis |
Q(25) |
Q(50) |
Q(75) |
Max |
| 1 |
0.001 |
0.0345 |
0.0560 |
2.5981 |
10.9552 |
0.0032 |
0.0070 |
0.0455 |
0.2590 |
| 2 |
0.7700 |
0.9005 |
0.0640 |
-0.9147 |
2.6716 |
0.8650 |
0.9200 |
0.9500 |
0.9800 |
| 3 |
0.4200 |
0.7894 |
0.1504 |
-1.3554 |
3.9461 |
0.7500 |
0.8400 |
0.8950 |
0.9400 |
| 4 |
0.2600 |
0.4225 |
0.1244 |
1.1625 |
4.2363 |
0.3300 |
0.4050 |
0.4650 |
0.7400 |
| 5 |
0.0062 |
0.1578 |
0.1931 |
1.4614 |
3.9988 |
0.0292 |
0.0614 |
0.2100 |
0.6560 |
| 6 |
0.1159 |
0.2305 |
0.0520 |
-0.0897 |
2.7360 |
0.2011 |
0.2262 |
0.2678 |
0.3347 |
| 7 |
0.1372 |
0.2760 |
0.1086 |
0.7214 |
2.6670 |
0.2023 |
0.2467 |
0.3545 |
0.5714 |
| 8 |
0.0807 |
0.2888 |
0.1167 |
0.0502 |
1.9766 |
0.1761 |
0.2884 |
0.3879 |
0.5331 |
| 9 |
0.0903 |
0.2310 |
0.1299 |
3.3611 |
18.5254 |
0.1621 |
0.1989 |
0.2627 |
0.9103 |
| 10 |
0.0050 |
0.0962 |
0.1143 |
2.2227 |
8.1749 |
0.0200 |
0.0625 |
0.1100 |
0.4950 |
| 11 |
0.0168 |
0.4689 |
0.1920 |
-0.3401 |
2.7292 |
0.3509 |
0.4741 |
0.5994 |
0.8781 |
| 12 |
0.4286 |
0.7240 |
0.1086 |
-0.7214 |
2.6670 |
0.6455 |
0.7533 |
0.7977 |
0.8628 |
| 13 |
0.4500 |
0.6911 |
0.1251 |
-0.0456 |
2.2538 |
0.6200 |
0.6800 |
0.7800 |
0.9200 |
| 14 |
0.0060 |
0.2881 |
0.3181 |
0.8223 |
2.0246 |
0.0308 |
0.1160 |
0.5310 |
0.8660 |
Table 2.
dwelling data set analysis.
Table 2.
dwelling data set analysis.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
2.3519 |
0.2571 |
26.1445 |
|
|
| Var |
.0323 |
.6661 |
.0086 |
.2424 |
0.023 |
0.0021 |
20.5623 |
| .6661 |
22.1589 |
.2424 |
9.228 |
| SE(a) |
0.03227 |
0.01666 |
0.0272 |
0.0082 |
0.8144 |
| SE(b) |
0.8455 |
0.5456 |
- |
- |
- |
| AIC |
-153.5535 |
-155.8979 |
-143.3057 |
-133.593 |
-140.592 |
| CAIC |
-153.1249 |
-155.4693 |
-143.1678 |
-133.4551 |
-140.454 |
| BIC |
-150.6855 |
-153.0299 |
-141.8717 |
-132.159 |
-139.158 |
| HQIC |
-152.6186 |
-154.963 |
-142.8382 |
-133.1255 |
-140.1243 |
| LL |
78.7767 |
79.9489 |
72.6528 |
67.7965 |
71.2959 |
| K-S Value |
0.2052 |
0.1742 |
0.2034 |
0.2818 |
0.3762 |
| H0
|
Fail to reject |
Fail to reject |
Fail to reject |
reject |
reject |
| P-value |
0.1271 |
0.271 |
0.1336 |
0.0114 |
0.000189 |
| AD |
1.288 |
0.9566 |
2.8789 |
4.6021 |
7.439 |
| CVM |
0.2419 |
0.1659 |
0.4976 |
0.8749 |
1.1683 |
| Determinant |
0.2728 |
0.0205 |
- |
- |
- |
Table 3.
analysis of the quality support network.
Table 3.
analysis of the quality support network.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
0.3591 |
71.2975 |
0.1334 |
|
|
| Var |
86.461 |
9.0379 |
15.7459 |
3.2005 |
0.000837 |
254.1667 |
0.00045 |
| 9.0379 |
1.0646 |
3.2005 |
1.0347 |
| SE(a) |
2.079 |
0.8873 |
0.0063 |
3.565 |
0.0047 |
| SE(B) |
0.231 |
0.2275 |
|
|
|
| AIC |
-56.5056 |
-56.7274 |
-58.079 |
-56.6796 |
-57.3746 |
| CAIC |
-55.7997 |
-56.0215 |
-57.8567 |
-56.4574 |
-57.1523 |
| BIC |
-54.5141 |
-54.7359 |
-57.0832 |
-55.6839 |
-56.3788 |
| HQIC |
-56.1168 |
-56.3386 |
-57.8846 |
-56.4852 |
-57.1802 |
| LL |
30.2528 |
30.3637 |
30.0395 |
29.3398 |
29.6873 |
| K-S |
0.0974 |
0.0995 |
0.1309 |
0.1327 |
0.1057 |
| H0
|
Fail to reject |
Fail to reject |
Fail to reject |
Fail to reject |
Reject to reject |
| P-value |
0.9416 |
0.9513 |
0.8399 |
0.4627 |
0.954 |
| AD |
0.3828 |
0.3527 |
0.3184 |
0.9751 |
0.2749 |
| CVM |
0.0566 |
0.0498 |
0.0407 |
0.1719 |
0.0261 |
| determinant |
10.3649 |
6.0494 |
- |
- |
- |
Table 4.
Educational attainment data analysis results.
Table 4.
Educational attainment data analysis results.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
0.5556 |
13.4254 |
0.2905 |
|
|
| Variance |
3.4283 |
1.0938 |
1.3854 |
0.5232 |
0.0011 |
5.0067 |
0.0012 |
| 1.0938 |
0.416 |
0.5232 |
0.3234 |
| SE |
0.3086 |
0.1962 |
0.0055 |
0.373 |
0.0058 |
| |
0.1075 |
0.0948 |
- |
- |
- |
| AIC |
-46.6152 |
-47.5937 |
-48.8713 |
-40.5725 |
-56.9322 |
| CAIC |
-46.2516 |
-47.23 |
-48.7537 |
-40.4548 |
-56.8145 |
| BIC |
-43.4482 |
-44.4266 |
-47.2878 |
-38.9889 |
-55.3487 |
| HQIC |
-45.5098 |
-46.4883 |
-48.3186 |
-40.0198 |
-56.3795 |
| LL |
25.3076 |
25.7968 |
25.4357 |
21.2862 |
29.4661 |
| K-S |
0.1453 |
0.1390 |
0.1468 |
0.2493 |
0.0722 |
| H0
|
Fail to reject |
Fail to reject |
Fail to reject |
Reject |
Fail to reject |
| P-value |
0.2055 |
0.2411 |
0.1979 |
0.0062 |
0.8300 |
| AD |
1.2191 |
1.1724 |
1.2694 |
4.0059 |
0.2977 |
| CVM |
0.2041 |
0.192 |
0.2133 |
0.7501 |
0.0430 |
| determinant |
0.2299 |
0.1743 |
- |
- |
- |
Table 5.
results of the flood data analysis.
Table 5.
results of the flood data analysis.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
1.0443 |
2.2413 |
1.6268 |
|
|
| Var |
7.22 |
7.2316 |
0.3651 |
2.8825 |
0.007 |
0.2512 |
0.0819 |
| 7.2316 |
8.0159 |
2.8825 |
29.963 |
| SE(a) |
0.6008 |
0.1351 |
0.0187 |
0.1121 |
0.0639 |
| SE(b) |
0.6331 |
1.2239 |
- |
- |
- |
| AIC |
-24.3671 |
-21.9465 |
-10.9233 |
-12.7627 |
-12.3454 |
| CAIC |
-23.6613 |
-21.2407 |
-10.7011 |
-12.5405 |
-12.1231 |
| BIC |
-22.3757 |
-19.9551 |
-9.9276 |
-11.767 |
-11.3496 |
| HQIC |
-23.9784 |
-21.5578 |
-10.7289 |
-12.584 |
-12.151 |
| LL |
14.1836 |
12.9733 |
6.4617 |
7.3814 |
7.1727 |
| K-S |
0.2063 |
0.2175 |
0.3202 |
0.3409 |
0.2625 |
| H0
|
Fail to reject |
Fail to reject |
Fail to reject |
Reject |
Fail to reject |
| P-value |
0.3174 |
0.2602 |
0.0253 |
0.0141 |
0.0311 |
| AD |
0.7302 |
0.9365 |
2.7563 |
2.9131 |
2.3153 |
| CVM |
0.1242 |
0.1653 |
0.531 |
0.5857 |
0.4428 |
| determinant |
5.5784 |
2.6314 |
- |
- |
- |
Table 6.
the results of the analysis of time between failures:.
Table 6.
the results of the analysis of time between failures:.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
1.7886 |
0.4891 |
4.1495 |
|
|
| Var |
0.071 |
0.2801 |
0.0198 |
0.1033 |
0.018 |
0.0104 |
0.5543 |
| 0.2801 |
1.647 |
0.1033 |
0.9135 |
| SE |
0.0555 |
0.0293 |
0.0279 |
0.0213 |
0.1552 |
| |
0.2676 |
0.1993 |
- |
- |
- |
| AIC |
-36.0571 |
-36.6592 |
-37.862 |
-35.5653 |
-27.007 |
| CAIC |
-35.4571 |
-36.0592 |
-37.6712 |
-35.3749 |
-26.8165 |
| BIC |
-33.7861 |
-34.3882 |
-36.7262 |
-34.4298 |
-25.8715 |
| HQIC |
-35.4859 |
-36.0881 |
-37.5764 |
-35.2798 |
-26.7214 |
| LL |
20.0285 |
20.3296 |
19.9310 |
18.7827 |
14.5035 |
| K-S |
0.1541 |
0.1393 |
0.1584 |
0.1962 |
0.3274 |
| H0
|
Fail to reject |
Fail to reject |
Fail to reject |
Fail to Reject |
Reject |
| P-value |
0.5918 |
0.7123 |
0.5575 |
0.2982 |
0.0107 |
| AD |
0.6886 |
0.5755 |
0.6703 |
1.1022 |
4.7907 |
| CVM |
0.1264 |
0.0989 |
0.1253 |
0.2149 |
0.8115 |
| determinant |
0.0385 |
0.0074 |
- |
- |
- |
Table 7.
shows the results of analysis of COVID-19 death rate analysis in Canada.
Table 7.
shows the results of analysis of COVID-19 death rate analysis in Canada.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
1.3479 |
1.0814 |
3.9381 |
|
|
| Variance |
7.839 |
27.531 |
0.2719 |
370.2768 |
0.0042 |
0.0209 |
0.203 |
| 27.531 |
100.6504 |
370.2768 |
523950 |
| SE(a) |
0.3741 |
0.0697 |
0.0086 |
0.0193 |
0.0602 |
| SE(b) |
1.3406 |
96.7273 |
- |
- |
- |
| AIC |
-167.88 |
-169.2 |
-48.8337 |
-46.3748 |
-80.2707 |
| CAIC |
-167.6536 |
-168.9736 |
-48.7596 |
-46.3008 |
-80.1966 |
| BIC |
-163.8293 |
-165.1493 |
-46.8083 |
-44.3495 |
-78.2453 |
| HQIC |
-166.3096 |
-167.6296 |
-48.0485 |
-45.5896 |
-79.4855 |
| LL |
85.94 |
86.6 |
25.4168 |
24.1874 |
41.1353 |
| K-S |
0.0754 |
0.1029 |
0.429 |
0.4685 |
0.359 |
| H0
|
Fail to reject |
Fail to reject |
reject |
reject |
reject |
| P-value |
0.6802 |
0.5583 |
0 |
0 |
0 |
| AD |
0.4398 |
0.369 |
14.0394 |
15.8748 |
12.7087 |
| CVM |
0.0692 |
0.0686 |
2.8621 |
3.3539 |
2.5936 |
| determinant |
31.0432 |
5348.9 |
- |
- |
- |
Table 8.
the results of analysis of COVID-19 death rates in Spain.
Table 8.
the results of analysis of COVID-19 death rates in Spain.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
1.2852 |
1.2218 |
2.9943 |
|
|
| Variance |
1.4278 |
3.2731 |
0.071 |
1.6267 |
0.0032 |
0.0226 |
0.0945 |
| 3.2731 |
8.088 |
1.6267 |
44.6833 |
| SE(a) |
0.1471 |
0.0328 |
0.007 |
0.0185 |
0.0378 |
| SE(b) |
0.3501 |
0.8228 |
- |
- |
- |
| AIC |
-1111486 |
-106.4226 |
-48.5631 |
-47.7193 |
-72.4535 |
| CAIC |
-110.9581 |
-106.2321 |
-48.5006 |
-47.6568 |
-72.391 |
| BIC |
-106.7692 |
-102.0433 |
-46.3734 |
-45.5297 |
-70.2639 |
| HQIC |
-109.4181 |
-104.6921 |
-47.6978 |
-46.8541 |
-71.5883 |
| LL |
57.5743 |
55.2113 |
25.2815 |
24.8597 |
37.2268 |
| K-S |
0.1148 |
0.1271 |
0.2734 |
0.3038 |
0.2896 |
| H0
|
Fail to reject |
Fail to reject |
reject |
reject |
reject |
| P-value |
0.3243 |
0.2172 |
0 |
0 |
0 |
| AD |
1.052 |
1.2437 |
9.1314 |
10.5385 |
6.2515 |
| CVM |
0.0692 |
0.0686 |
2.8621 |
3.3539 |
2.5936 |
| determinant |
0.8345 |
0.5267 |
- |
- |
- |
Table 9.
shows the result of analysis of the COVID-19 death rates in United Kingdom.
Table 9.
shows the result of analysis of the COVID-19 death rates in United Kingdom.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
1.2733 |
1.2462 |
2.8294 |
|
|
| Variance |
0.9001 |
2.3667 |
0.0905 |
1.8019 |
0.0035 |
0.0259 |
0.0918 |
| 2.3667 |
6.8204 |
1.8019 |
42.2606 |
| SE(a) |
0.1225 |
0.0388 |
0.0035 |
0.0259 |
0.0918 |
| SE(b) |
0.3372 |
0.8393 |
|
|
|
| AIC |
-86.7989 |
-87.7288 |
-41.7679 |
-41.3478 |
-62.7546 |
| CAIC |
-86.5884 |
-87.5183 |
-41.6989 |
-41.2788 |
-62.6856 |
| BIC |
-82.6102 |
-83.5401 |
-39.6735 |
-39.2534 |
-60.6602 |
| HQIC |
-85.1605 |
-86.0904 |
-40.9487 |
-40.5285 |
-61.9354 |
| LL |
45.3995 |
45.8644 |
21.8839 |
21.6739 |
32.3773 |
| K-S |
0.0982 |
0.1054 |
0.2786 |
0.3062 |
0.1894 |
| H0
|
Fail to reject |
Fail to reject |
reject |
reject |
reject |
| P-value |
0.5752 |
0.4847 |
0.00013 |
0.0000017 |
0.0103 |
| AD |
0.7351 |
0.6298 |
6.4895 |
7.4679 |
4.4878 |
| CVM |
0.1279 |
0.1047 |
1.1285 |
1.3921 |
0.7574 |
| determinant |
0.5377 |
0.5789 |
- |
- |
- |
Table 10.
result of analysis of the petroleum rock dataset.
Table 10.
result of analysis of the petroleum rock dataset.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
1.3776 |
1.0037 |
2.5672 |
|
|
| Variance |
0.3055 |
0.2942 |
0.0329 |
0.2688 |
0.0051 |
0.021 |
0.0926 |
| 0.2942 |
0.4759 |
0.2688 |
3.3557 |
| SE(a) |
0.0798 |
0.0262 |
0.0103 |
0.0209 |
0.0439 |
| SE(b) |
0.0996 |
0.2644 |
- |
- |
- |
| AIC |
-65.142 |
-58.3691 |
-38.7526 |
-36.1927 |
-19.068 |
| CAIC |
-64.8753 |
-58.1025 |
-38.6056 |
-36.1057 |
-18.9811 |
| BIC |
-61.3996 |
-54.6267 |
-36.8814 |
-34.3215 |
-17.1968 |
| HQIC |
-63.7277 |
-56.9549 |
-38.0455 |
-35.4855 |
-18.3609 |
| LL |
34.571 |
31.1846 |
20.3763 |
19.0963 |
10.534 |
| K-S |
0.1822 |
0.1975 |
0.316 |
0.3518 |
0.3033 |
| H0
|
Fail to reject |
Fail to reject |
reject |
reject |
reject |
| P-value |
0.0723 |
0.0408 |
0 |
0 |
0 |
| AD |
3.0872 |
3.9213 |
8.3144 |
9.6277 |
7.5927 |
| CVM |
0.5351 |
0.6702 |
1.6507 |
1.9901 |
1.4343 |
| determinant |
0.0588 |
0.0381 |
- |
- |
- |
Table 11.
shows the result of analysis of the snow fall dataset.
Table 11.
shows the result of analysis of the snow fall dataset.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
1.8869 |
0.4352 |
8.43 |
|
|
| Variance |
0.0684 |
0.4178 |
0.0189 |
0.2697 |
0.0153 |
0.0063 |
1.9726 |
| 0.4178 |
4.071 |
0.2697 |
5.3991 |
| SE(a) |
0.0478 |
0.0251 |
0.0226 |
0.0145 |
0.2564 |
| SE(b) |
0.3684 |
0.4242 |
- |
- |
- |
| AIC |
-75.1218 |
-75.5952 |
-66.6947 |
-60.8902 |
-72.7696 |
| CAIC |
-74.6773 |
-75.1508 |
-66.5518 |
-60.7473 |
-72.6268 |
| BIC |
-72.3194 |
-72.7928 |
-65.2935 |
-59.489 |
-71.3684 |
| HQIC |
-74.2253 |
-74.6987 |
-66.2464 |
-60.4419 |
-72.3214 |
| LL |
39.5609 |
39.7976 |
34.3474 |
31.4451 |
37.3848 |
| K-S |
0.1288 |
0.1207 |
0.2472 |
0.3015 |
0.1715 |
| H0
|
Fail to reject |
Fail to reject |
Fail to reject |
reject |
Fail to reject |
| P-value |
0.6554 |
0.7294 |
0.0422 |
0.0065 |
0.3045 |
| AD |
0.5715 |
0.4728 |
2.2335 |
3.4324 |
1.6564 |
| CVM |
0.0861 |
0.0646 |
0.396 |
0.6623 |
0.2918 |
| determinant |
0.1040 |
0.0295 |
- |
- |
- |
Table 12.
shows the result of analysis of the milk production dataset.
Table 12.
shows the result of analysis of the milk production dataset.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
1.039 |
2.0802 |
1.2001 |
|
|
| Variance |
0.0631 |
0.0816 |
0.0495 |
0.1063 |
0.0013 |
0.0404 |
0.0079 |
| 0.0816 |
0.1643 |
0.1063 |
0.3388 |
| SE(a) |
0.0243 |
0.0215 |
0.0035 |
0.0194 |
0.0086 |
| SE(b) |
0.0392 |
0.0563 |
- |
- |
- |
| AIC |
-43.5545 |
-46.7894 |
-39.3785 |
-41.0524 |
-48.7609 |
| CAIC |
-43.4391 |
-46.6740 |
-39.3404 |
-41.0143 |
-48.7229 |
| BIC |
-38.2088 |
-41.4437 |
-36.7057 |
-38.3796 |
-46.0881 |
| HQIC |
-41.3874 |
-44.6223 |
-38.2949 |
-39.9689 |
-47.6774 |
| LL |
23.7772 |
25.3947 |
20.6892 |
21.5262 |
25.3805 |
| K-S |
0.0816 |
0.0669 |
0.1080 |
0.093 |
0.1002 |
| H0
|
Fail to reject |
Fail to reject |
Fail to reject |
Fail to reject |
Fail to reject |
| P-value |
0.3189 |
0.5372 |
0.1531 |
0.2473 |
0.1421 |
| AD |
1.3853 |
1.003 |
2.2535 |
1.8813 |
1.3116 |
| CVM |
0.2282 |
0.1522 |
0.3496 |
0.2848 |
0.2286 |
| determinant |
0.0037 |
0.0055 |
- |
- |
- |
Table 13.
shows analysis results of COVID-19 recovery rate in Spain dataset.
Table 13.
shows analysis results of COVID-19 recovery rate in Spain dataset.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
0.6366 |
10.5284 |
0.52 |
|
|
| Variance |
8.088 |
3.2731 |
0.8967 |
1.6853 |
0.00079 |
1.6795 |
0.0022 |
| 3.2731 |
1.4278 |
1.6853 |
4.0747 |
| SE(a) |
0.3501 |
0.1166 |
0.0035 |
0.1595 |
0.0057 |
| SE(b) |
0.1471 |
0.2485 |
- |
- |
- |
| AIC |
-111.1486 |
-113.6686 |
-90.4861 |
-101.1088 |
-90.2298 |
| CAIC |
-110.9581 |
-113.4782 |
-90.4236 |
-101.0463 |
-90.1673 |
| BIC |
-106.7692 |
-109.2893 |
-88.2964 |
-98.9191 |
-88.0402 |
| HQIC |
-109.4181 |
-111.9382 |
-89.6208 |
-100.2435 |
-89.3646 |
| LL |
57.5743 |
58.8343 |
46.243 |
51.5544 |
46.1149 |
| K-S |
0.0996 |
0.0846 |
0.2226 |
0.1813 |
0.1752 |
| H0
|
Fail to reject |
Fail to reject |
reject |
reject |
reject |
| P-value |
0.3243 |
0.4966 |
0.0024 |
0.0227 |
0.0144 |
| AD |
1.052 |
0.9317 |
3.5144 |
2.0475 |
4.2480 |
| CVM |
0.1783 |
0.1519 |
0.5281 |
0.2775 |
0.6736 |
| determinant |
0.8345 |
0.8136 |
- |
- |
- |
Table 14.
analysis results of voter dataset.
Table 14.
analysis results of voter dataset.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
Unit-Lindley |
| theta |
|
|
0.6832 |
8.2339 |
0.5406 |
|
|
| Variance |
6.4427 |
2.3588 |
0.7462 |
0.9005 |
0.0016 |
1.7841 |
0.0041 |
| 2.3588 |
0.9809 |
0.9005 |
1.6212 |
| SE(a) |
0.4118 |
0.1401 |
0.0065 |
0.2167 |
0.0104 |
| SE(b) |
0.1607 |
0.2066 |
|
|
|
| AIC |
-47.9451 |
-46.8575 |
-42.1377 |
-47.4106 |
-36.517 |
| CAIC |
-47.6022 |
-46.5146 |
-42.0266 |
-47.2995 |
-36.4059 |
| BIC |
-44.6699 |
-43.5823 |
-40.5001 |
-45.7731 |
-34.8794 |
| HQIC |
-46.7798 |
-45.6922 |
-41.555 |
-46.828 |
-35.9344 |
| LL |
25.9725 |
25.4287 |
22.0688 |
24.7053 |
19.2585 |
| K-S |
0.0938 |
0.1048 |
0.1364 |
0.119 |
0.1467 |
| H0
|
Fail to reject |
Fail to reject |
Fail to reject |
Fail to reject |
Fail to reject |
| P-value |
0.8605 |
0.7596 |
0.44 |
0.6129 |
0.1828 |
| AD |
0.2721 |
0.3464 |
1.3262 |
0.6861 |
1.4767 |
| CVM |
0.0416 |
0.0559 |
0.2193 |
0.1198 |
0.2266 |
| determinant |
0.7556 |
0.3989 |
- |
- |
- |
Table 15.
analysis results of unit capacity factors dataset.
Table 15.
analysis results of unit capacity factors dataset.
| |
Beta |
Kumaraswamy |
MBUR |
Topp-Leone |
| theta |
|
|
1.6243 |
0.5943 |
|
|
| Variance |
0.0482 |
0.0960 |
0.0166 |
0.0274 |
0.0149 |
0.0154 |
| 0.0960 |
0.2919 |
0.0274 |
0.1066 |
| SE(a) |
0.0458 |
0.0269 |
|
|
| SE(b) |
0.1127 |
0.0681 |
|
|
| AIC |
-15.2149 |
-15.3416 |
-13.2158 |
-14.2302 |
| CAIC |
-14.6149 |
-14.7416 |
-13.0253 |
-14.0398 |
| BIC |
-12.9439 |
-13.0706 |
-12.0803 |
-13.0943 |
| HQIC |
-14.6438 |
-14.7704 |
-12.9302 |
-13.9447 |
| LL |
9.6075 |
9.6708 |
7.6079 |
8.1151 |
| K-S |
0.1836 |
0.179 |
0.1518 |
0.1602 |
| H0
|
Fail to reject |
Fail to reject |
Fail to reject |
Fail to reject |
| P-value |
0.3742 |
0.4051 |
0.4074 |
0.4762 |
| AD |
0.6998 |
0.6975 |
1.9075 |
1.5271 |
| CVM |
0.1189 |
0.1159 |
0.2033 |
0.1735 |
| determinant |
0.0049 |
0.001 |
- |
- |