1. Introduction
Low-dimensional materials exhibiting charge density wave (CDW) orders [
1,
2,
3,
4,
5,
6,
7,
8,
9] have attracted significant attention due to their rich phase diagrams, including superconductivity (SC) [
1,
4], nematicity [
5], and multiple density-wave orders [
4,
5,
6,
7,
8]. Suppression of CDW by external parameters in those low-dimensional materials often leads to emergent novel quantum states, making them an ideal platform for exploring the interplay between the CDW and the competing quantum states. Archetypal examples include the case of transition-metal-dichalcogenides Pd
xTaSe
2, in which intercalating Pd ions between TaSe
2 layers suppresses the CDW and enhances SC near the CDW quantum critical point [
1], and that of the kagome metals AV
3Sb
5 (A = K, Rb, Cs), at which the pressure-induced suppression of the CDW state results in two SC domes [
8,
9]
CuTe represents a prototypical example of exhibiting CDW order from the quasi-one-dimensional (Q1D) electronic structure. Angle-resolved photoemission spectroscopy has confirmed that the CDW transition appearing at
TCDW1=335 K at ambient pressure is driven by the Fermi surface nesting of Te 5
px orbitals [
10]. Under a high pressure condition [
11,
12], CuTe is known to exhibit a complex pressure-temperature phase diagram involving the interplay between the electronic phases of CDW and SC. As pressure increases,
TCDW1 as evidenced by the resistivity
r jump decreases linearly and reaches ~100 K near 6.5 GPa, above which this anomaly vanishes. From the pressure of ~6.7 GPa, another in-plane resistivity anomaly, a peak structure in
dr/
dT curve, appears at ~200 K, signaling stabilization of a second CDW phase (CDW2). With further increase of pressure up to 10 GPa,
TCDW2 gets suppressed, being gradually lowered toward ~150 K; the resistivity anomaly at CDW2 finally vanishes beyond 10 GPa. Moreover, the superconductivity first emerges at a pressure of 4.8 GPa as a small resistivity drop at
TC ≈ 0.5 K.
TC increases with further increase of pressure, showing a maximum at 2.3 K near 6.5 GPa, beyond which,
TC gradually decreases, consequently forming a dome-like phase diagram. Above 10 GPa,
TC becomes below 1 K, indicating significant suppression of SC with increasing pressure. At the pressures exceeding 20 GPa, CuTe undergoes a structural phase transition from the orthorhombic (
Pmmn) to monoclinic (
Cm) phase. In this new structural phase, superconductivity is stabilized with
TC ≈ 2.4 K, persisting across the high-pressure range up to 49 GPa.
However, the nature of pressure-induced SC in CuTe, particularly its relationship with the CDW orders, remains elusive. As a possible mechanism for finding SC in the vicinity of CDW phases, two scenarios have been proposed [
12]. First, a continuous suppression of CDW1 may increase charge fluctuation to enhance the pairing strength for superconductivity. However, this scenario is not applicable to the pristine CuTe as
TCDW1 decreases to only 100 K at 6.5 GPa, thus mitigating the possibility of having quantum fluctuation of the CDW order parameters. Second, a mere competition between CDW and SC may induce the stabilization of SC at the expense of the competing CDW order. As common in a quasi-1D CDW system, the charge density modulation seems to involve significant lattice distortion so that the CDW transition with variation of temperature or pressure is clearly a first-order type. In particular, as a function of pressure, an abrupt first-order transition from CDW1 to CDW2 occurs at ~6.5-6.7 GPa so that SC is not a single competing phase of the CDW1 order. Indeed, SC stabilized at 4.8 ≤
P ≤ 10 GPa also overlaps with the temperature and pressure windows where CDW2 phase stabilized (i.e.,7.5 GPa (
TCDW2= 204 K) £
P £ 10.1 GPa (
TCDW2= 173 K )). Therefore, the SC appears within the electronic structure created by the CDW2 phase rather than appearing directly at the expense of the CDW1 phase.
To address the puzzling question on the relationship between pressure-induced SC with the CDW order, we have investigated a Cu1-δTe (δ=0.016) single crystal using high-pressure studies of Raman spectroscopy, transport, and structural properties. Our study reveals that slight Cu deficiency significantly modifies the phase evolution, leading to TCDW1 ≈ 0 K near 6 GPa and subsequent emergence of SC above 5.2 GPa with the maximum TC ~ 3.2 K at 5.6 GPa. Furthermore, we find that a new structural phase, isostructural to the Cu-deficient rickardite CuTe (r-CuTe), appears above 6 GPa, thereby hosting the CDW2 order around 200 K. These findings suggest that understanding the role of Cu deficiency can be crucial for unraveling the intricate relationship between structural transitions, CDW orders, and superconductivity in the copper telluride system.
3. Results
- A.
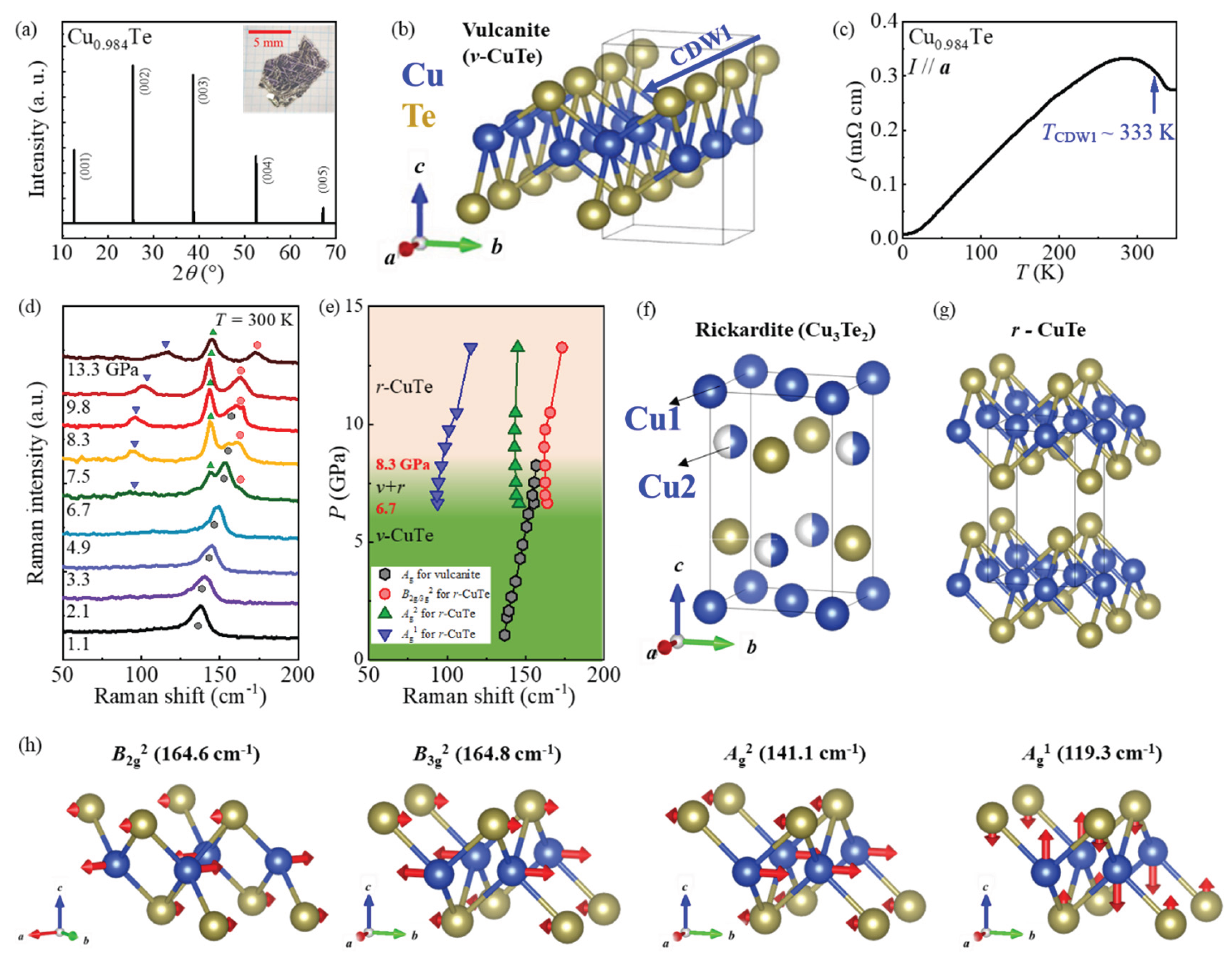
Crystallographic structure and basic physical properties of Cu0.984Te
Figure 1a presents an XRD pattern of a Cu
0.984Te single crystal. Only sharp (00
l) diffraction peaks appear, indicating that the crystallographic
c-axis is perpendicular to the facet of the crystal. The measured (001) peaks match well with those of the vulcanite CuTe (
v-CuTe, space group
Pmmn). Independent XRD experiments on the grounded polycrystals have confirmed the
v-CuTe structure (not shown here). Therefore, the Cu
0.984Te crystal is isostructural to the
v-CuTe structure, as illustrated in
Figure 1b, at ambient pressure and at room temperature. In the
v-CuTe structure, the Te chains are known to exist along the
a-axis and each Cu atom forming a buckled Cu plane is bonded to the four Te atoms located below and above the Cu plane. As a result, the
v-CuTe forms an orthorhombic
Pmmn structure with lattice constants
a = 3.16 Å,
b = 4.08 Å, and
c = 6.93 Å. Wavelength-dispersive x-ray spectroscopy confirmed a Cu:Te ratio 0.984:1.00 (
Figure S1,
Table S1 in the supplemental information [
19]), indicating slight Cu deficiency. We also measured the resistivity along the
a-axis,
ρ, in a Cu
0.984Te single crystal, as shown in
Figure 1c. Despite the slight Cu deficiency, we observe a clear resistivity upturn near 333 K, the feature similar to CuTe at its CDW state [
10,
11].
- B.
Pressure-dependent evolution of Raman phonon modes
To monitor the structural evolution of Cu
0.984Te, we performed high-pressure Raman scattering using diamond anvil cells up to 13.3 GPa at room temperature as presented in
Figure 1d. From the obtained scattering intensity, the pressure dependence of phonon mode frequencies was extracted as summarized in
Figure 1e. Below 6.2 GPa, only one Raman mode was found at 136.6 cm
-1, which seems to be close to a theoretically predicted frequency of the
A1g mode (136.0 cm
-1) in the
v-CuTe [
11,
21]. However, above 6.7 GPa, three new Raman modes, which do not correspond to the reported Raman modes of the
v-CuTe [
12,
20], emerge at 163.8 cm
-1(
mode 1), 145.8 cm
-1(
mode 2), and 93.8 cm
-1(
mode 3). Meanwhile, the original
A1g mode persists up to 8.3 GPa and disappears above the pressure. These spectral changes provide evidence that a new structural phase appearing at 6.7 GPa coexists with the low pressure
v-CuTe up to 8.3 GPa and becomes solely stabilized above 8.3 GPa. Note that in the pristine CuTe, a pressure-induced structural transition has been reported to occur at 20 GPa from an orthorombic (
Pmmn) to a monoclinic structure (
Cm). However, no structural transition has been reported in a low-pressure regime around ~7 GPa [
11,
12].
One might suspect that the newly appearing mode 2 and 3 at the high pressures may have originated from Te clusters [
21] as they are indeed close to those of the
E modes in pristine Te at ambient pressure (140.7 cm⁻¹ and 92.2 cm⁻¹) [
39,
40]. However, if those modes were originated from the Te clusters, the
A₁ mode of Te would have also been observed, since the intensity of the
A1 mode is known to be always stronger than those of the
E modes and its frequency lies around ~120-100 cm⁻¹ in a pressure regime below 15 GPa [
39]. No signal that can be assigned as an
A₁-mode of Te was detected around ~100-120 cm⁻¹ in our experiments performed below 13 GPa. The minimum frequency of the
A₁ mode of Te was previously found at ~100 cm⁻¹ at a pressure of ~8 GPa [
39]; its frequency at high pressures always remains higher than that of mode 3, leading to a conclusion that the mode 3 is not the
A₁ mode of Te. Moreover, the Raman mode of Te has not been reported previously near the frequency region of ~164 cm
-1 (that of mode 1) in a pressure window below 15 GPa, ruling out the possibility that the mode 1 can stem from the possible Te cluster. These observations suggest that the three modes emerging under the pressure above 6.7 GPa are unlikely to originate from possible Te clusters.
According to the previous density functional theory (DFT) calculations on CuTe [
20], it was predicted that the Cu-deficient rickardite structure (
r-CuTe) would have a lower formation energy than the
v-CuTe. In this theoretical
r-CuTe structure plotted in
Figure 1g [
20,
22], the Cu2 sites of the rickardite Cu
3Te
2 (
Figure 1f) located close to the four Te sites become completely vacant and remaining Cu sites form a flat Cu plane. Although the
r-CuTe forms an orthorhombic structure (space group
Pmmn) with lattice constants
a = 3.845 Å,
b = 3.847 Å, and
c = 6.493 Å, it is indeed close to a tetragonal structure as it has similar in-plane lattice constants. However, this theoretical
r-CuTe phase has not been found experimentally in the high-pressure region of CuTe [
11,
12].
We find in
Figure 1d that three Raman modes appearing at the high pressures above 6.7 GPa match relatively well with those predicted for the
r-CuTe in Ref. [
20]; the phonon frequencies of mode 1 (163.8 cm
-1) and mode 2 (145.8 cm
-1) are close to those calculated for the
B2g2/
B3g2 (~164.7 cm-1) and the
Ag2 (141.1 cm
-1) modes, respectively. According to
Figure 1e, the mode 3 frequency shows a drastic increase with pressure from 93.8 cm
-1 at 6.7 GPa to 115.0 cm
-1 at 13.3 GPa. As a result, the predicted
Ag1 mode frequency (~119.28 cm
-1) [
20] is indeed close to the frequency of 115.0 cm
-1 obtained at 13.3 GPa. As this
Ag1 mode involves the vibrational motion along the
c-axis, its frequency can be sensitive to the interlayer distance; consequently, the mode 3 indeed exhibits drastic hardening under pressure. Therefore, the mode 3 can be assigned as the
Ag1 mode predicted in the
r-CuTe structure. On the other hand, we could not identify the additional phonon modes near the theoretically predicted
B2g1/
B3g1 mode (78.4 cm
-1) within our experimental resolution.
- C.
Temperature dependent resistivity under high pressures
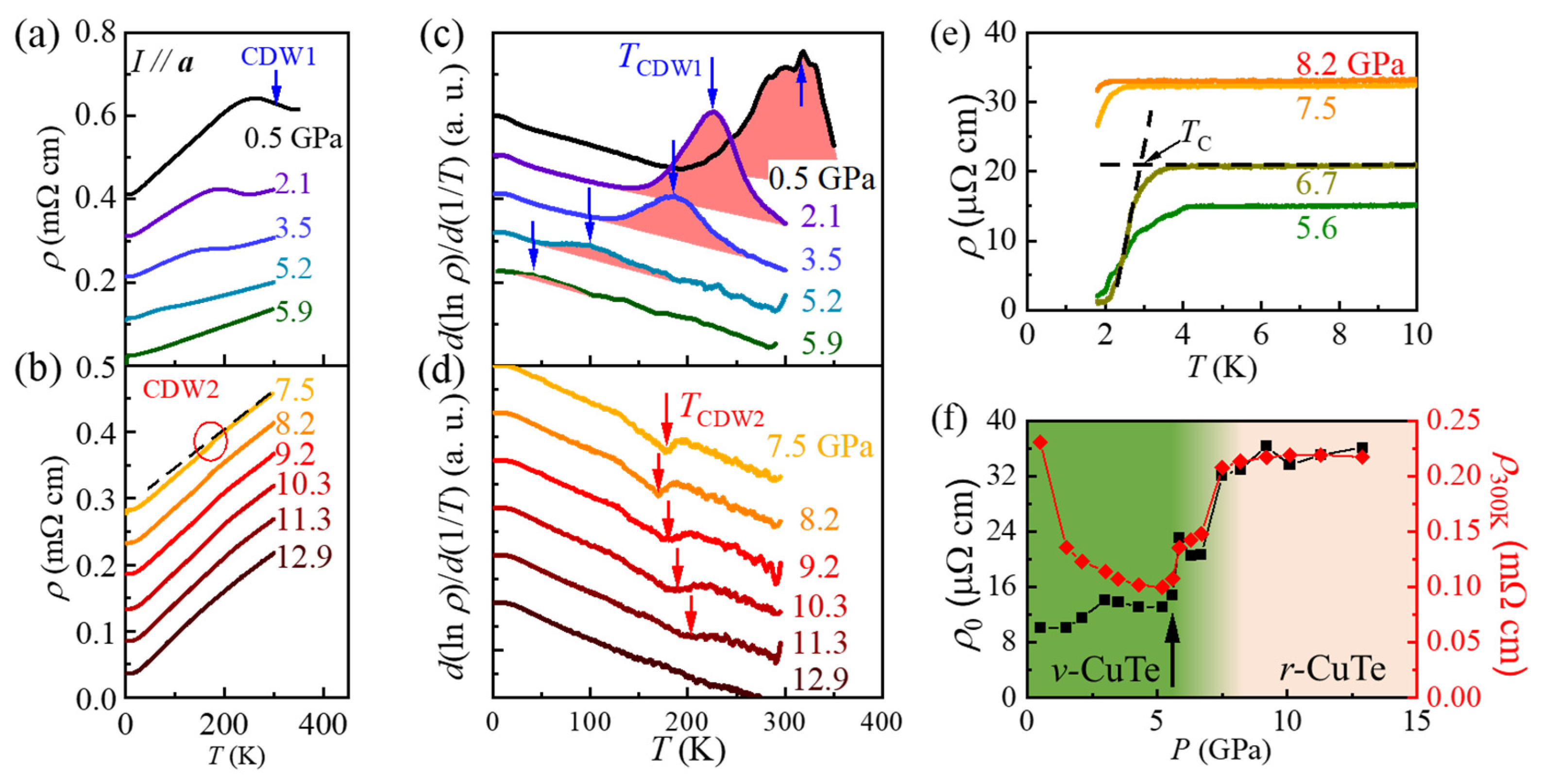
To understand the evolution of electronic orders under external pressure, we have conducted temperature-dependent
r measurements at pressures up to 12.9 GPa using a diamond anvil cell (
Figure 2a,b). In the pressure regime starting from 0.5 GPa, we observe a clear
r upturn around 318 K associated with the CDW1 ordering (a blue arrow). With further increase of pressure, the resistivity upturn is progressively weakened and its location is shifted to lower temperatures. Following a convention in the literature [
23], we determine
TCDW1 at each pressure as the peak temperature in the
d ln(
r)/
d(1/
T) curves (
Figure 2c, blue arrows). As a result,
TCDW1, located at 333 K at ambient pressure, systematically decreases to 40 K at 5.9 GPa. At
P above 6.0 GPa, the peak associated with the CDW1 in the
d ln(
r)/
d(1/
T) curves could not be identified.
With further increase of
P, we find that another kink in the
d ln(
r)/
d(1/
T) curves emerges from 7.5 GPa and remains until ~11.3 GPa (red arrows in
Figure 2d). Those kinks are linked to a weak resistivity drop, as illustrated in
Figure 2b (red circles). Previous studies on the pristine CuTe have similarly found a small positive peak in the
dr/
dT curves [
11]; it was assigned as the onset of the second CDW order (CDW2), based on the observation of the amplitudon mode from Raman scattering measurements [
12]. As the peak feature in the
dr/
dT curves can appear as a dip in the
dln(
r)/
d(1/
T) curve, we attribute the dip in the
dln(
r)/
d(1/
T) curves to the onset of CDW2 order in Cu
0.984Te.
It is found in
Figure 2d that the determined
TCDW2 from the dip of the
dln(
r)/
d(1/
T) curves exhibits non-monotonous changes with pressure; it decreases from 176 K at 7.5 GPa to 170 K at 8.2 GPa, and again increase to 203 K at 11.3 GPa. This behavior is in contrast to that found in a pristine CuTe where
TCDW2, determined from the peak in the
dr/
dT curve, continuously decreases with increase of
P;
TCDW2 ≈ 204 K at 7.5 GPa decreases linearly down to
TCDW2 ≈ 173 K at 10.1 GPa [
12]. Note that the dip feature in the
dln(
r)/
d(1/
T) curve becomes progressively weakened with further
P increase and finally disappears at 12.9 GPa. We also confirmed that the pressure-dependent evolutions of both
TCDW1 and
TCDW2 as revealed in the
dln(
r)/
d(1/
T) curves of Cu
0.984Te (
Figure 2d) align well with those found in the
dr/
dT curves (
Figure S2 in the Supplemental Information [
19]).
At low temperatures, the drop of
r, implying the onset of superconducting transition appears between 5.2 and 8.2 GPa (
Figure 2e). The onset temperature of the superconducting transition (
TC) is determined by a crossing temperature from the two linear extrapolated lines (dashed lines in
Figure 2e). As a result,
TC reaches a maximum of 3.2 K at 5.6 GPa and gradually decreases with increase of
P. Note that this value is significantly higher than the maximum
TC = 2.3 K realized at
P ≈ 5.7 GPa in CuTe [
12].
As depicted in
Figure 2f, we also find that both residual resistivity (
r0) and resistivity at 300 K (
ρ300K) remain small at
P ≤~6 GPa (a black arrow) where the vulcanite structure is dominant. On the other hand, at
P ≥~9 GPa where
r-CuTe structure is dominant, both
r0 and
ρ300K reach the highest value. In an intermediate regime of 6.7 £
P £8.3 GPa, both
r0 and
ρ300K remain in the intermediate values and exhibit gradual increments. At this intermediate
P regime, the Raman scattering results exhibit evidence of structural coexistence in Cu
0.984Te.
- D.
Structural phase transition and the emergence of CDW2
The emergence of CDW2 in Cu
0.984Te and CuTe occurs in a different way. In the Cu
0.984Te,
TCDW2 first appears at 176 K and at
P = 7.5 GPa inside the pressure range where the
r-CuTe structure coexists with
v-CuTe structure (i.e., 6.7≤
P ≤ 8.3 GPa) With the stabilization of the
r- CuTe structure (
P ≥ 8.3 GPa),
TCDW2 decreases to 170 K, and increases again to 203 K as
P increases to 11.3 GPa. In contrast, the pristine CuTe exhibits a sudden appearance of the CDW2 phase at 204 K at
P≥ 6.7 GPa in
v-CuTe structure, and
TCDW2 decreases monotonically with increasing pressure [
11,
12]. It was previously argued that the CDW2 phase in CuTe may stem from electronic correlation effects induced by four hole pockets originating from Te
pz orbitals, because there is no phonon softening or diverging electronic susceptibilities to support either electron-phonon coupling scenario or Fermi-surface nesting picture, respectively [
12]. However, there is no concrete evidence in the theoretical calculations to support the scenario [
12].
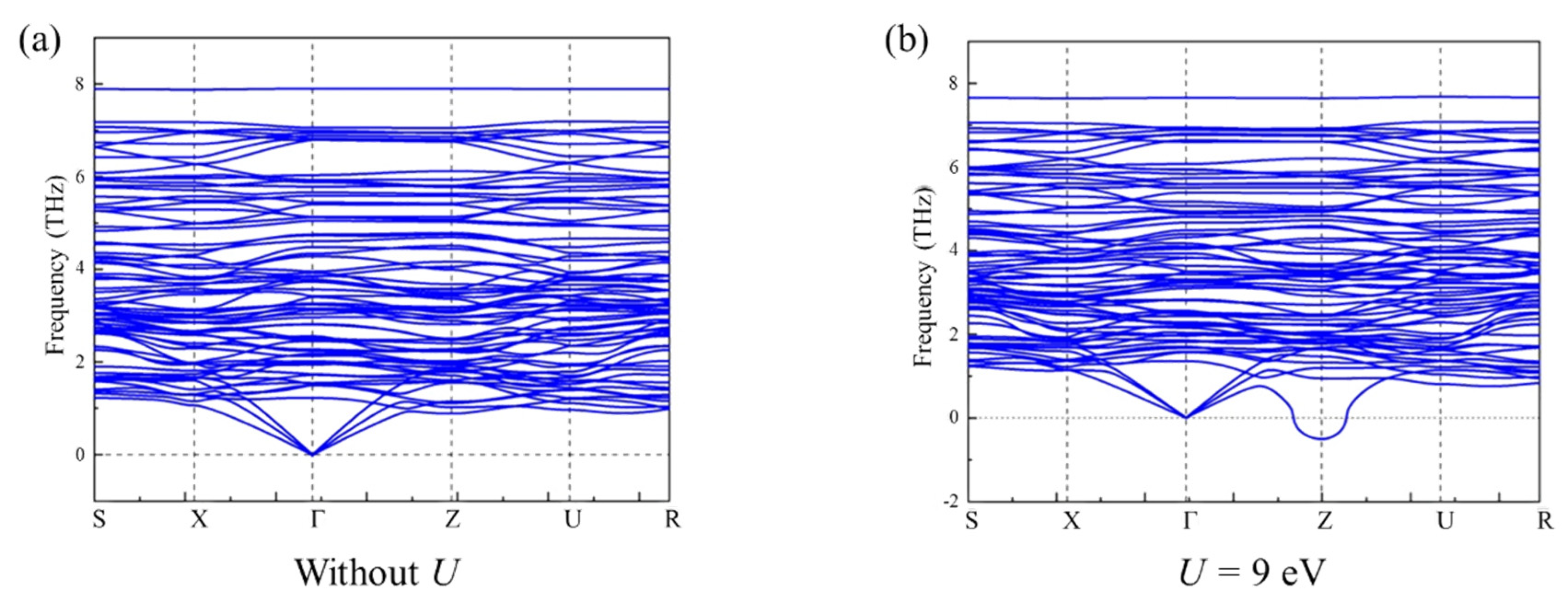
To better understand the origin of stabilizing the CDW2 phase in Cu
0.984Te, we have thus calculated phonon band structures of the
r-CuTe with Cu deficiency, using the Cu
11Te
12 composition at 10 GPa (
Figure 3). For this, the initial atomic positions of the r-CuTe structure, as provided in the supplementary data as a cif file, were used to have Cu deficiency in the Cu sites. Then, at 10 GPa, the atomic positions of
r-CuTe structure with Cu deficiency has been relaxed. Since Coulomb interaction can affect the emergence of CDW2 as argued in CuTe [
24], calculations were performed for the cases with or without Coulomb interaction (
U). Without Coulomb interaction, there was no structural instability. However, the results reveal a negative phonon mode near the
Z point when the Coulomb interaction
U=9 eV is included. When
U is systematically increase, it is found that the phonon mode softening was systematically increased at the Z point (See
Figure S3 in the Supplemental Information [
19]). Our independent calculations of the phonon band structure for the pristine CuTe (
v-CuTe structure) for both with (
U=9 eV) and without (
U=0) Coulomb interaction did not result in any phonon anomaly (See
Figure S4 in the supplemental information [
19]). However, when the chemical potential of the CuTe electronic structure has been shifted toward the hole doped side, the effect of increasing
U has also resulted in a similar negative phonon mode at a different momentum position (
Figure S4). These results suggest that both Cu deficiency making hole-doping and increased Coulomb interactions should be important in the creating CDW2 phase in the high pressure region of Cu
0.984Te.
- E.
Magnetotransport measurements under high pressure
To monitor evolution of electronic structure with pressure, we conducted magnetoresistance (MR) and Hall effects measurements at various pressures.
Figure 4a shows the MR curves, D
ρ(
H)/
ρ(0)
(
ρ(
H)-
ρ(0))/
ρ(0) at 10 K, and at
P ³ 1.5 GPa. For 1.5 ≤
P ≤ 5.6 GPa where CDW1 is stabilized, the MR at 10 K is particularly large, reaching 10- 110% at 9 T. Moreover, at this
P regime, MR shows a crossover from
H-quadratic at m
0H ≤ 2 T (dashed blue line) to linear dependence above m
0H ³ ~3 T (dashed red guide lines). As
P increases from 1.5 to 5.6 GPa, MR at 9 T decreases from 110 to 10%, accompanied by similar decreases of the linear slope (red dashed lines). Therefore, the large MR and the linear slope proportional to the MR value should be attributed to the characteristic features of the CDW1 state.
For
P > 6.3 GPa and at 10 K (
Figure 4b) where the CDW2 state in the
r-CuTe structure is dominantly stabilized, the MR values become less than 10% at m
0H=9 T; they are clearly smaller than those in the lower pressure regime. Moreover, the field-dependence of MR, being proportional to
, exhibits mostly quadratic behavior, i.e.,
with
b »2 at m
0H £ ~6 T (dashed blue lines). Detailed analyses of the d
(
H)/dm
0H curves (
Figure S5 in the Supplemental Information [
19]) are also consistent with such quadratic
H dependence at the region where the CDW2 state in the
r-CuTe structure is realized.
Numerous materials with CDW order have often exhibited large linear MR below their
TCDW’s [
25]. In those cases, the CDW transition can create small electron or hole pockets with sharp curvature, called “sharp corners” in the momentum space. Electrons traveling along these sharply curved trajectories experience abrupt momentum changes, thus strongly influencing the resistivity values. Under magnetic fields, the electrons experience the Lorentz force, causing them to follow the trajectories with a cyclotron frequency proportional to
H. This means that as
H increases, the electrons pass through the trajectory more quickly and thus increases the probability of interaction with the sharp corners. As a result, the number of electrons interacting with such sharp corners can increase linearly with
H, explaining how the CDW state can lead to the linear MR.
Based on the hypothesis that the linear MR in Cu
0.984Te (
Figure 4a) is also caused by the sharp corners in the momentum space as formed inside the CDW1 state [
10], we try to extract the slope
L predicted by the formula of
ρ(
H) =
ρ0 + m
0L|
H|.
Figure 4e shows the resultant
L extracted from the MR data (
Figure 4a, m
0H ≥ 3 T) at each pressure; the MR value at m
0H = 9 T at 10 K is also plotted together. It is found that as
P increases, both
L and MR at 9 T systematically decrease up to 5.9 GPa, at which the CDW1 state is nearly suppressed to become
TCDW1=40 K (not shown). At
P=6.3 GPa, the MR exhibits only linear
H-dependence down to ~2 K. With further increase of
P ≥ 6.3 GPa (
Figure 4b), linear MR behavior disappears (thus
L vanishes) and quadratic
H-dependence becomes dominant in the
ρ(
H) curves as well shown in the three representative curves from 7.5 to 12.9 GPa. Moreover, the MR values at 9 T become saturated at ~10%. These results suggest that the reconstructed electronic structure formed by the CDW1 state produces sharp corners in the momentum space to result in the large linear MR. Moreover, upon pressure being increased to enter the CDW2 state, the sharp corners may have almost disappeared.
Figure 4c,d show the Hall resistivity
rxy at 10 K measured at various
P £ 6.3 and ³ 7.5 GPa, respectively; the evolution of the Hall coefficient
RH extracted at the curves below 1 T is also summarized in
Figure 4f. At
P £ ~5.9 GPa where the CDW1 order is stabilized, the positive
RH values (
Figure 4f) systematically decrease with increase of
P, indicating that effective carrier density increases with the gradual decrease of the electronic gap inside the CDW1 state. However, even at
P ≥ 6.3 GPa where the CDW1 state is no longer stabilized at a finite temperature,
RH keeps decreasing to becomes negative at
P = 7.5 GPa, from which nearly the same negative value is maintained up to
P=12.9 GPa. In addition, followed by the sign change of
RH near 7.5 GPa,
ρxy starts to exhibit nonlinear
H-dependence in the pressure region of ~7.5 £
P £ 12.9 GPa (
Figure 4d). As
RH values (also
ρxy behaviors) are similar at 7.5 £
P £ 12.9 GPa, irrespective of the phase boundaries of CDW2 (7.5 £
P £ 11.3 GPa), it is expected that the
r-CuTe structure, not the CDW2 state, mainly determines the electronic structures.
To analyze the
H-dependence of
rxy under pressure, we used a two-band model with one hole and one electron bands [
26,
27]:
Here,
nh (
ne) represents the hole (electron) density,
μh (
μe) is the hole (electron) mobility,
e is one electron charge, and
B is the magnetic induction. This model was applied to fit the
rxy curve at each pressure (see
Figure S6 in the Supplemental Information [
19]) and the parameters
nh,
ne,
μh, and
μe obtained from the fit are summarized in
Figure 4g,h. It is found that at ~4.3£
P£ 7.5 GPa, both
nh and
ne are sharply increased, forming maximum values at the critical pressure of ~ 5.9 GPa, at which a quantum critical point of the CDW1 state is expected to exist. Simultaneously, both
μh and
μe exhibit nearly two-fold decrease from
P ≈ 3.5 to 6.7 GPa and a slight increase at 7.5 GPa, thus forming a minimum at 6.7 GPa. At
P³ ~7.5 GPa,
μh and
μe remain nearly constant. These observations suggest that a continuous gap closing of the CDW1 state by
P increase up to ~5.9 GPa and associated critical fluctuation of charge amplitude might cause the increase of carrier densities and the decrease of carrier mobilities [
28]. This aligns with the diminishing linear MR as
P approaches ~5.9 GPa, showing that the suppression of the CDW1 order is significantly affecting the transport properties.
When a single CDW state is collapsed within the same crystal structure, thereby closing the CDW gap, it is common to observe the increase of the carrier densities outside the CDW state [
29]. However, our results indicate that near the structure coexistence region of the
v- and
r- CuTe (~6.7 £
P £ 8.3 GPa), the
nh and
ne show abrupt decreases from 6.3 GPa while
μh and
μe increase slightly. This suggests that albeit having the gap closing of the CDW1 state, the creation of different structural phases may have resulted in the abrupt reduction of carrier densities. Besides, possible extra-scattering of carriers at the structural domain walls, if any, may be negligible as compared with the effect of critical fluctuation of the CDW1 order (both CDW amplitude and phase). Furthermore, at
P ≥ 7.5 GPa where the CDW2 state is stabilized, decreasing behavior of
nh and
ne values are saturated to remain nearly same, indicating that the electronic structure, as influenced by the CDW2 state in the
r-CuTe phase, is less sensitive to the pressure-variation.
4. Discussion
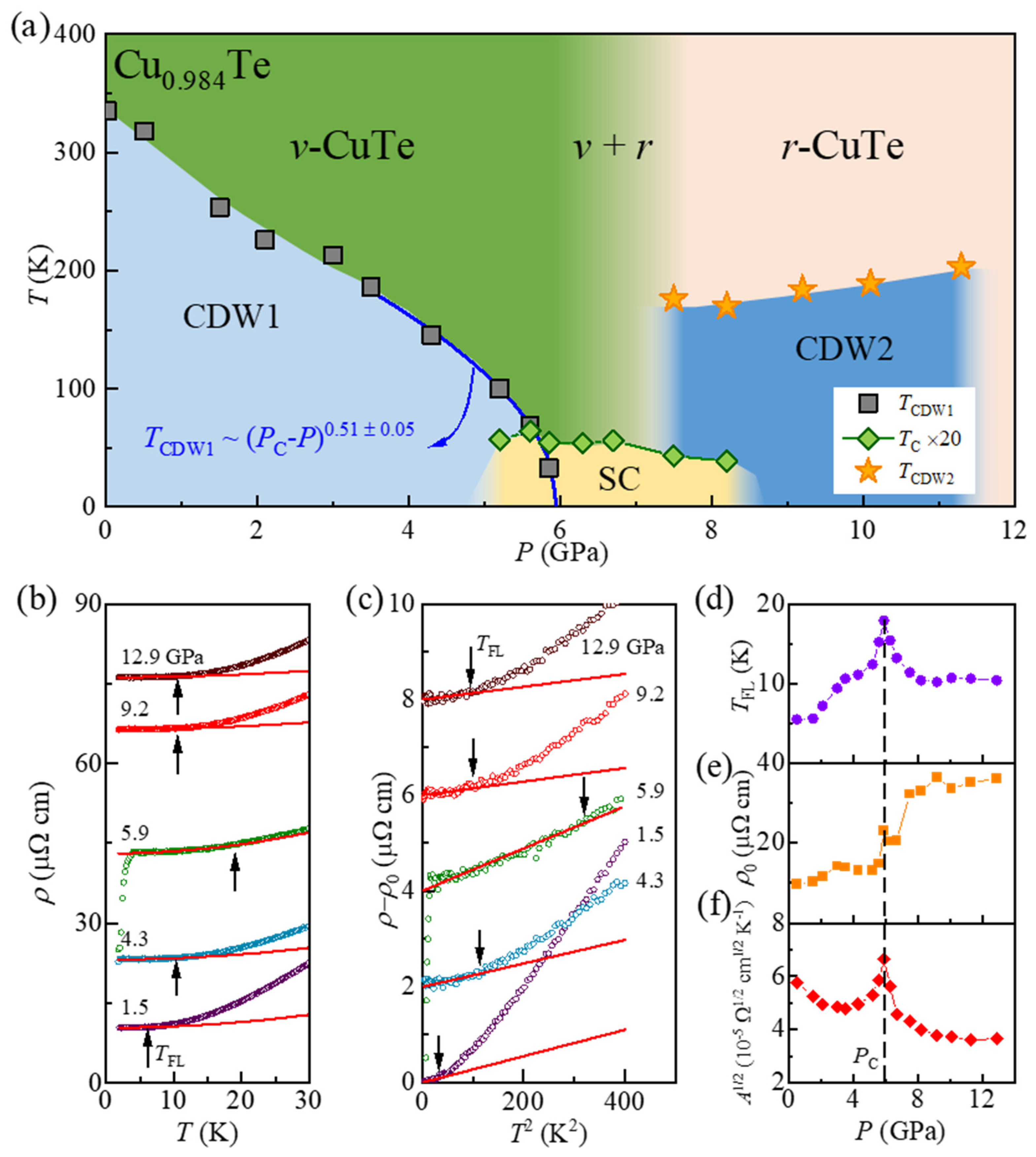
Figure 5a summarizes the pressure-temperature phase diagram of Cu
0.984Te, highlighting distinct regions of structural and electronic phases. Raman spectroscopy, resistivity, and magnetotransport data are used to construct the structural and electronic phase boundaries. The ambient
v-CuTe structure is stabilized below 6.7 GPa within which the CDW1 order emerges at low temperatures below
TCDW1. As described in the Results, the
r-CuTe structure coexists with the
v-CuTe structure between 6.7 and 8.3 GPa. Above 8.3 GPa, the system fully transforms into the
r-CuTe phase. The CDW2 emerges at ~176 K at
P = 7.5 GPa and
TCDW2 is gradually enhanced up to 203 K with pressure increase up to 11.3 GPa. However, above 11.3 GPa, the experimental signature of the CDW2 state (i.e., dip in the
dln(
r)/
d(1/
T) curves in
Figure 2d) disappears.
We should note that the structural/electronic phase evolution of Cu
0.984Te differs significantly from that of the pristine CuTe [
12] in several aspects. Firstly, CDW1 in Cu
0.984Te is continuously suppressed with pressure to reach
TCDW1 =40 K at 5.9 GPa and the signals related to the CDW1 cannot be found in the transport data above 6.0 GPa. In contrast, the CDW1 sate of the pristine CuTe persists up to 6.5 GPa and exhibits
TCDW1 ~100 K near 6.5 GPa. Secondly, in the Cu
0.984Te, we observe a clear structural phase transition into the
r-CuTe structure and the emergence of the CDW2 state within the
r-CuTe structure. This new structure was absent in the pristine CuTe while the CDW2 state in CuTe has been found at 7.5£
P£ 10.3 GPa. This indicates that the high-pressure structure is not an essential part of inducing the CDW2 instability. Thirdly,
TCDW2 in Cu
0.984Te increases with pressure from 170 K at 8.2 GPa to 203 K at 11.3 GPa. However,
TCDW2 in CuTe decreased with pressure increase; it is found at 204 K at 7.5 GPa and 173 K at 10.3 GPa. Therefore, the slight deficiency of Cu significantly affects the both electronic and structural phase boundaries.
The CDW1 state in Cu
0.984Te shows decrease of
TCDW1 with pressure increase. Indeed, we found that
TCDW1 decreases rapidly in the low-
P regime (
P £ 3.5 GPa) (
Figure 5a). On the other hand, above 3.5 GPa, where
P approaches toward 6 GPa,
TCDW1 follows a power-law behavior with
with
PC ~ 5.98 ± 0.05 GPa. This power-law behavior with the exponent 0.5 is a typical behavior expected in a mean-field type phase transition [
30]. This characteristic mean field behavior has been also found in several materials near the quantum critical point (QCP) [
28,
31,
32,
33,
34], including NbSe
3 [
31,
32] and
β-vanadium bronze [
31,
33], which belong to the Q1D materials exhibiting a CDW formation and a charge ordering, respectively. This emergence of power-law behavior in Cu
0.984Te thus strongly suggests that it may undergo a pressure-induced quantum phase transition of the CDW state, and the CDW fluctuation near
PC plays a role in enhancing
TC.
On the other hand, the continuous evolution of
TCDW1 with pressure, following power-law behavior near
PC is distinctly different from that of the pristine CuTe, in which
TCDW1 decreases almost linearly to 100 K at 6.5 GPa and disappears suddenly in a first-order manner above 6.5 GPa [
12]. The different pressure responses suggest that Cu deficiency may allow the continuous decrease of the electronic CDW1 order parameter (i.e., CDW amplitude) to form the pressure-induced CDW-QCP at 5.98 GPa. For this, the structural transition expected in the CDW instability is decoupled so that the associated anomaly in the Te chain occurs at a higher pressure regime (>6.3 GPa). Note that this behavior is clearly different from that observed in a typical 1D-CDW system, in which a first-order CDW transition often occurs together due to the associated large entropy change involved in the lattice modulation.
To investigate the possible effect of charge fluctuations near
PC on transport phenomena, we have studied the pressure-dependent evolution of the Fermi-liquid behavior at low temperatures above
TC (
Figure 5b,c). According to Fermi-liquid theory,
ρ exhibits a quadratic
T-dependence of
ρ = ρ0 +
AT 2, where
ρ0 is a residual resistivity and
A is the coefficient of the quadratic term [
35]. In our data for
P ≤ 1.5 GPa, the quadratic power-law successfully describes the
ρ (
T) behavior below ~ 5 K, defined as an effective Fermi-liquid temperature
TFL. Above
TFL, the results deviate from the Fermi-liquid behavior. This indicats that the electron-electron scattering causing the Fermi liquid behavior is dominant in the transport behavior at ambient and low pressure region (
P ≤ 1.5 GPa) below
TFL, while the other factors, such as electron-phonon coupling, become more important above
TFL.
It is found that the quadratic
T-dependence persists across all the
P ranges studied.
Figure 5c shows the (
ρab –
ρ0) vs.
T2 plots at various pressures, indicating that (
ρab –
ρ0) is linear with
T2 below
TFL. As
P increases,
TFL rises from 5.6 K at 1.5 GPa to 17.9 K at 5.9 GPa, suggesting an enhancement of the effective Fermi-liquid energy scale near
PC. However, after reaching a maximum at
P ~
PC,
TFL drops to ~10 K at 8.2 GPa and remains nearly constant up to 12.9 GPa. (
Figure 5d). This behavior can be interpreted as a modification of the Fermi surface by
P. A larger Fermi surface implies that electrons can maintain a well-defined quasiparticle distribution over a wider
T range, thereby possibly elevating
TFL. Since the suppression of CDW1 often leads to an enlarged Fermi surface, the sharply enhanced
TFL near
PC should be attributed to the increased Fermi surface area. The observed
P-dependent increase of the carrier densities up to 5.9 GPa (
Figure 4g) is also consistent with this picture. However, sharp decreases of both carrier density and
TFL above 5.9 GPa, and their saturated behavior above 8.2 GPa indicates that the full stabilization of the
r-CuTe structure above
P = 8.2 GPa and its resultant electronic band structure limits the increase of carrier density and Fermi surface.
In the Fermi liquid state, it is known that the Kadowaki-Woods relation,
A =
α KW γ02 [
36], where
α KW is the Kadowaki-Woods ratio and
γ0 is the Sommerfeld coefficient, is satisfied, resulting in the relation that
A1/2 ∝
γ0. Moreover,
γ0 can be expressed as
γ0 =
[
37], where
kB is the Boltzmann constant,
(
) is the electron-electron (electron-phonon) coupling constant, and
is the electronic density of states at Fermi level. Based on the experimental data summarized in
Figure 5c, we have extracted the pressure
-dependent evolution of
A1/2 (
Figure 5f). Below 3.0 GPa,
A1/2 decreases from 5.75×10
-5 Ω
1/2cm
1/2K
-1 at 0.5 GPa to 4.79×10
-5 Ω
1/2cm
1/2K
-1 at 3.5 GPa. However, in the range 3.5 - 6.7 GPa near
PC,
A1/2 exhibits a sharp peak reaching a maximum of 6.65×10
-5 Ω
1/2cm
1/2K
-1 at 5.9 GPa. With increasing pressure,
A1/2 gradually decreases again up to 12.9 GPa.
According to the Kadowaki-Woods relation, the evolution of
A1/2 provides insights into changes in
,
, and
. Since the new structural phase in Cu
0.984Te appears above 6.7 GPa,
likely does not change significantly near
PC [
35]. Hence, the increased
A1/2 near
PC seems to arise from the enhancement in
or
. As the effective Fermi surface area is expected to increase upon closing the CDW1 gap, increasing trend of the
TFL and the carrier density across
PC can be reasonably understood. This may be accompanied by gradual decrease of
as the pressure evolution of electronic structure can result in decrease of the effective mass. In our experimental results,
A1/2 indeed exhibits gradually decreases in both low and high pressure regions except near
PC, indicating that the gradual decrease can be explained by the overall decrease of
with pressure. However, to explain the sharp increase of
A1/2 near
PC, where the critical fluctuations of the CDW order parameter is expected, we conjecture that the
increase plays an important role. A similar sharp enhancement of
A1/2 near
PC has been also observed recently in other systems with a CDW-QCP, such as 2
H-Pd
0.05TaSe
2 [
35]. However, it seems quite rare to find the experimental evidence of such enhanced charge fluctuation at the critical pressure in a Q1D material. This seems to be realized because the electronic CDW transition is decoupled with the structural transition in Cu
0.984Te due to the Cu deficiency.
The critical behavior of CDW1 in Cu
0.984Te offers new insights into the relation between SC and CDW1. Near
PC,
TC reaches its maximum value of 3.2 K in Cu
0.984Te. This is much higher than that found in pristine CuTe [
12]. The enhancement of
TC near
PC thus suggests that strong CDW1 fluctuation may also contribute to enhance SC, similar to the recent observations in other systems with the CDW-QCP; Ti-doped CsV
3Sb
5 [
9], Lu(Pt
1-xPd
x)
2In [
38], and 2
H-Pd
0.05TaSe
2 [
35]. In contrast, CDW2 appears to have minimal effect on SC itself because it emerges above 7.5 GPa. Therefore, our observations here underscore the critical role of CDW1 fluctuation in enhancing superconducting pairing strength in Cu
0.984Te, possibly through increased electron-electron interaction.