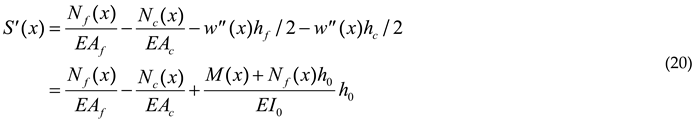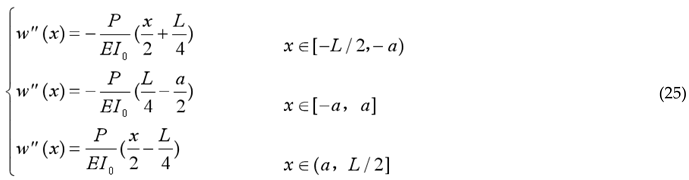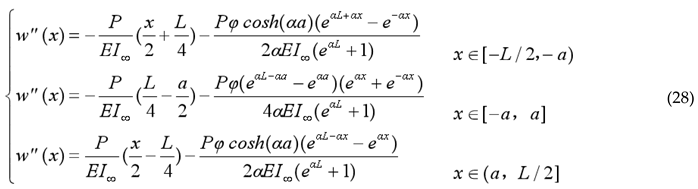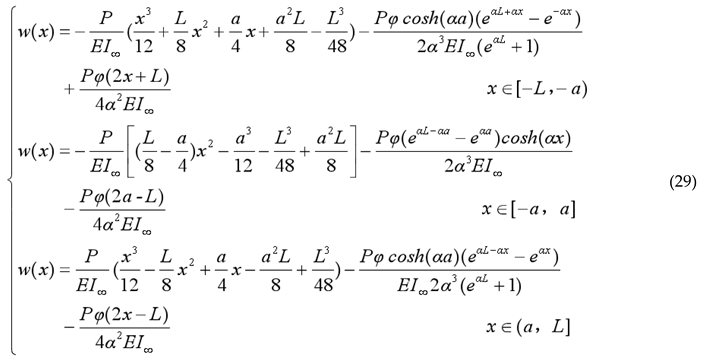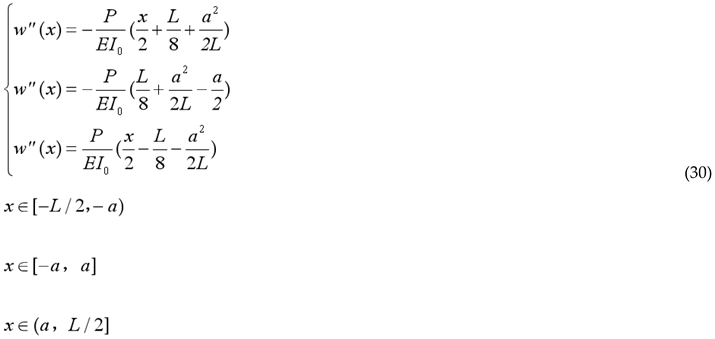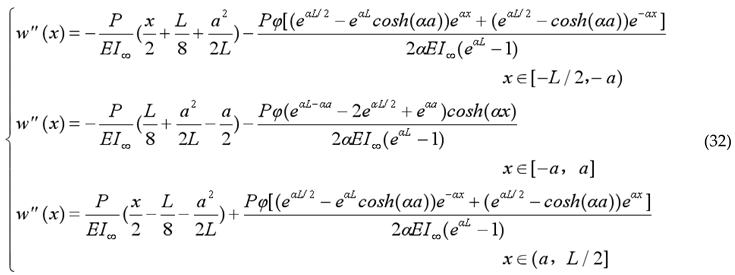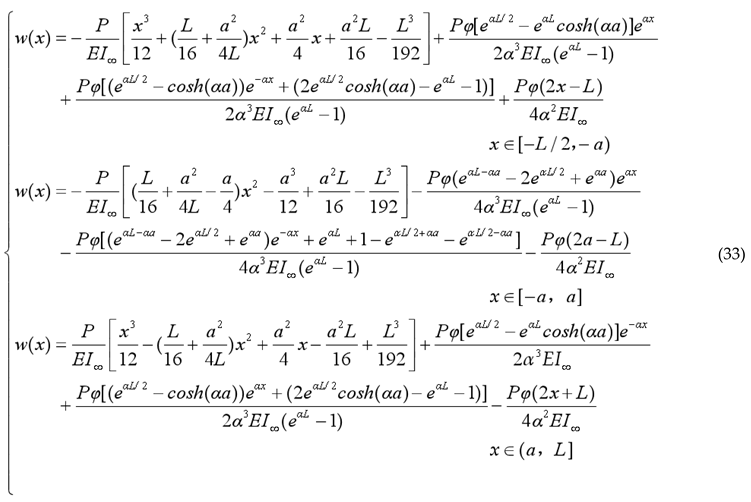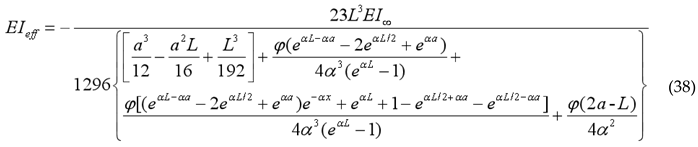Introduction
Modular steel buildings used standardized room modules for design, industrial production, and integrated decoration. The modules were transported to the site for assembly, forming the complete buildings[
1,
2,
3,
4,
5,
6]. This method improved prefabrication rates, shortened construction time, and reduced environmental pollution, meeting the demands of building industrialization[
7,
8,
9,
10,
11,
12,
13]. Due to its construction advantages, the modular steel buildings was widely used in temporary buildings, hospitals, office buildings, and dormitories in recent years.
As for the highly integrated modular steel buildings systems, the coupled connections between modular units exhibited a significant influence on the overall mechanical performance. Traditional modular connection techniques typically assembled modules by welding or bolting at the corner column-to-column joints, with these column-to-column connections responsible for bearing and transferring external loads. Several experts and scholars conducted researches on the mechanical performance of modular steel buildings systems and substructures with only corner constraints. The results indicated that, under seismic loading, the column-to-column connections between modules were prone to stress concentration and the development of plastic hinges, which may ultimately leaded to the loss of overall robustness in the modular structural system. Enhancing the degree of modular joint connection could improved the mechanical coupling between modules; however, the structural ductility still fails to meet the desired design objectives. To improve the overall stability of modular steel buildings, researchers had proposed establishing mechanical connections between adjacent double beams of upper and lower modules. This approach increases the load transfer paths within the modular steel buildings and enhances the mechanical restraint between modular units. Li et al.[
14,
15] designed an interfacial connector for adjacent double beams and conducted two-point concentrated load tests. The experimental results showed that the laminated double beams in modular steel buildings generally conformed to the plane section assumption. Moreover, the overall integrity of the connector's cross-section exhibited superior mechanical performance compared to discontinuous cross-sections, and this advantage became increasingly evident as the applied load increased. Chang et al.[
16] proposed a web-bolted connection for laminated double beams and investigated their flexural mechanical performance. The results indicated that, in laminated steel beams, the floor beam is subjected to compressive bending while the ceiling beam experiences tensile bending. The shear connection between the double beams effectively enhances the overall flexural stiffness and load-bearing capacity of the laminated steel beam. Compared to independent double beams, laminated steel beams can save approximately 15% of steel. By considering the composite effect of adjacent double beams, the cross-sectional dimensions of floor beams and ceiling beams in modular steel buildings can be reasonably reduced. Zhang et al.[
17,
18] enhanced the synergy between horizontally adjacent channel beams in modular steel buildings by installing bolt connections through the webs of back-to-back double channel beams, thereby forming laminated channel beams. They further investigated the overall flexural performance of these laminated channel beams. Cha et al.[
19,
20] investigated the reliability of force transmission in corner joints composed of gusset plates and high-strength bolts in modular prefabricated buildings, and proposed internal force calculation formulas for double-beam and double-column steel frame systems. Zhu Yiyun et al[
21]
. conducted the bending tests on bolted laminated double beams. The experimental results showed that the laminated interface also serves as a longitudinal stiffener, which improved the local stability of the member. In addition, using thinner and higher-strength steel in the tension zone can enhance economic efficiency. Xu et al.[
22,
23,
24,
25,
26] proposed a modular bolted laminated double channel beam structure and conducted studies on its flexural mechanical performance. The results showed that, under mutual mechanical constraints, the laminated double beams exhibit significantly improved the bending capacity and stiffness compared to independent double beams. The existing studies preliminarily investigated the flexural performance of bolted laminated double beams in modular steel buildings and established mechanical models for strength and stiffness. However, they did not conduct theoretical deflection analysis from a mechanical perspective for such non-continuous point-connected composite beams, making it difficult to provide a reliable theoretical basis for their structural design.
This study conducted experimental and theoretical investigations on the mechanical behavior of bolted point-connected laminated beams in modular steel buildings. The cooperative flexural behavior of the composite beams was analyzed. Based on previous work on the fundamental differential equation of double-beam curvature and the interfacial slipping model, a theoretical deflection analysis was carried out. An analytical model for the deflection curve of simply supported composite double beams under typical loading conditions was derived, providing a theoretical basis for the design of such novel laminated beam structures.
1. Design of Laminated Beam Structures in Modular Steel Buildings
According to the
Load Code for the Design of Building Structures[
27], the design loads for the floor beams and ceiling beams in modular steel buildings were determined. Then, the structural design of floor and ceiling beam components was carried out for a standard modular unit with dimensions of 6×3×3.1 (m × m × m), referencing
the Standard for Design of Steel Structures and
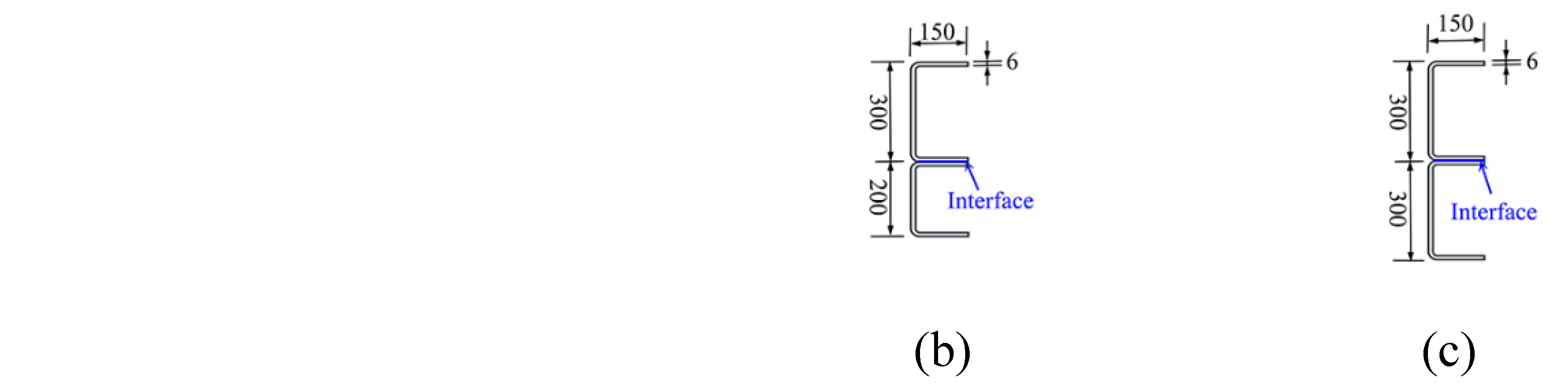
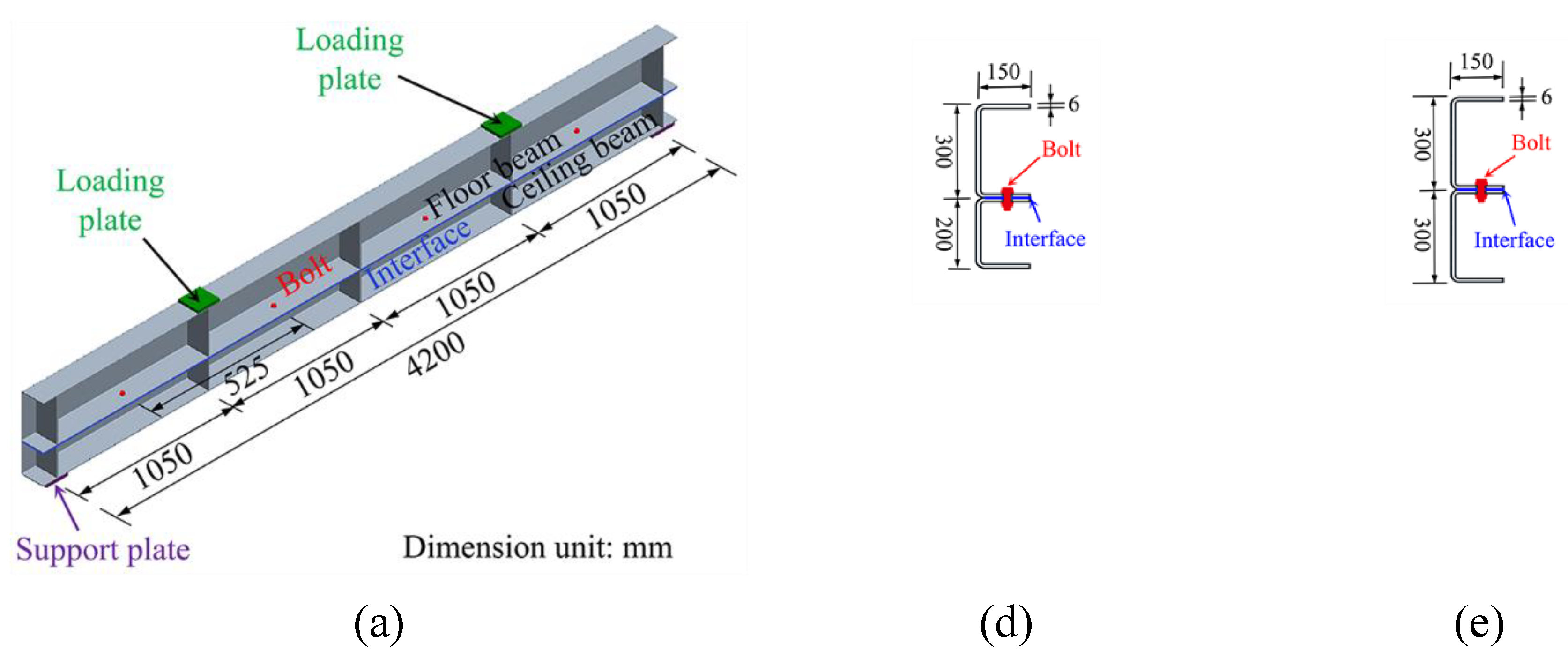
the Handbook for the Design of Modular Structures. As a result, the floor beam (FB) and ceiling beam (CB) were selected as cold-formed channel steel members with cross-sectional dimensions of 300 × 150 × 6 mm and 200 × 150 × 6 mm, respectively, as shown in
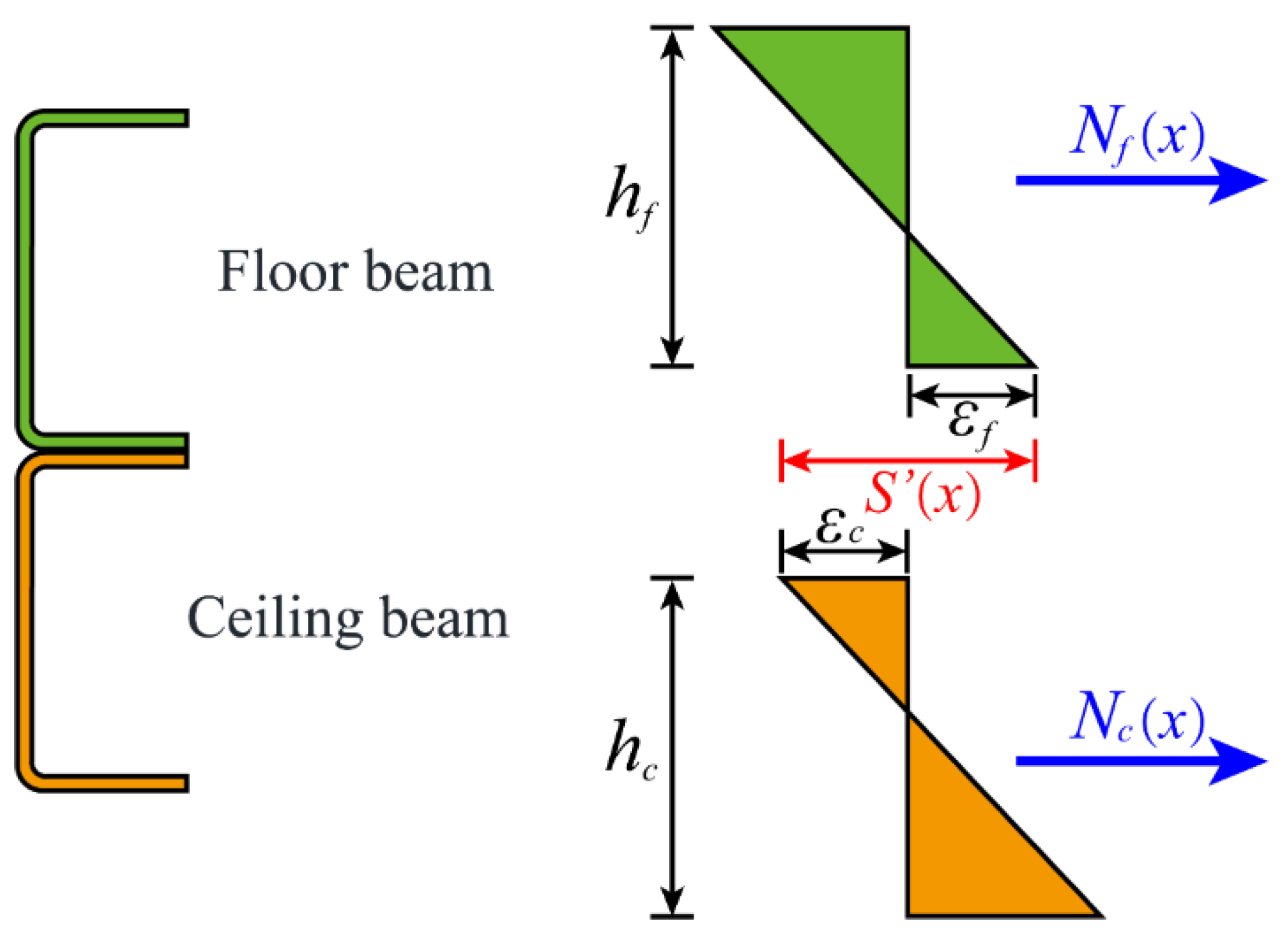
Figure 1. To investigate the flexural performance of laminated steel beams with different interfacial connections, the two friction-laminated beam specimens with only friction restraints and the two bolt-laminated beam specimens were designed. It should be noted that the floor beam (FB) and ceiling beam (CB) were simply superimposed, and only friction acted tangentially at the interface under vertical loading in friction-laminated beam specimens, named as LFCB. Moreover, another friction-laminated double beam specimen with floor beams (FB) of equal height were designed and designated as LFFB, aiming to evaluate the height of single beams. With the same dimensional and structural conditions, the four high-strength bolts were installed at the interface at intervals of 1050 mm to form bolted laminated steel beam specimens, designated as LFCB-4B and LFFB-4B, respectively. The specimen configurations are shown in
Figure 1.
Table 1.
Dimensions of beam specimens (mm).
Table 1.
Dimensions of beam specimens (mm).
| Specimen |
Floor beam
hu×w×tb
|
Ceiling beam
hu×w×tb
|
lc |
l0 |
li |
| LFCB |
300×150×6 |
200×150×6 |
1550 |
4200 |
500 |
| LFFB |
300×150×6 |
300×150×6 |
1550 |
4200 |
600 |
| LFCB-4B |
300×150×6 |
200×150×6 |
1550 |
4200 |
500 |
| LFFB-4B |
300×150×6 |
300×150×6 |
1550 |
4200 |
600 |
Figure 1.
Geometries and dimensions of laminated beam specimens: (a) geometric detail; (b) dimension of LFCB; (c) dimension of LFFB; (d) dimension of LFCB-4B; (e) dimension of LFFB-4B.
Figure 1.
Geometries and dimensions of laminated beam specimens: (a) geometric detail; (b) dimension of LFCB; (c) dimension of LFFB; (d) dimension of LFCB-4B; (e) dimension of LFFB-4B.
2. Theoretical Analysis of the Synergistic Flexural Deflection Curve Laminated Channel Beams in Modular Steel Buildings
2.1. Theoretical Analysis Strategy for the Laminated Beams in Modular Steel Buildings
A theoretical analysis of the deflection curve for modular laminated steel beams was conducted to provide the foundation for practical engineering design. It was noted that during the cooperative bending behaviours of the double-beam structures, the relative slipping occurred between the floor beam and the ceiling beam, which significantly affected the overall mechanical performance of laminated beams in modular steel buildings. Hence, based on the fundamental differential equations of double-beam curvature, the theoretical model for interfacial slip was derived and then the analytical model for the deflection curve of laminated double beams could be further developed. By combining the fundamental differential equation for the flexural behavior of laminated steel beams with the basic physical equation for slip strain at the interfacial surface of double beams, the differential control equation for relative slip in laminated steel beams was derived, thereby establishing theoretical models for relative slip under various loading conditions, boundary conditions, and degrees of interfacial connection. The following fundamental assumptions are made for the composite flexural behavior of double-beam structures: (1) both the floor beam and the ceiling beam are made of linear elastic material, and the deflection and end rotation of the laminated steel beam remain within the small deformation range; (2) the floor beam and ceiling beam exhibit the same curvature in the laminated beam, with no relative vertical displacement between the upper and lower beams; (3) shear deformation of both beams is neglected, and both the upper and lower beams satisfy the plane section assumption; (4) the shear connection at the interface between the floor beam and ceiling beam is uniformly distributed along the beam span, and the tangential distributed load at the interface is proportional to the relative slip between the beams.
Firstly, the the interfacial slip strain s’(x) was analytically calculated and the theoretical expressions for the interfacial slip. By establishing a mathematical expression for the curvature of modular laminated double beams—considering the relative slip between the floor beam and the ceiling beam—was derived. Taken into account the simply supported boundary conditions of the laminated double beams, accurate analytical solutions for the deflection w(x) and rotation w’(x) of the laminated steel beams considering interfacial slip can be obtained. Consequently, theoretical load-deflection models for laminated steel beams under various loading conditions and boundary conditions can be established.
For pure friction laminated double beams, the interlayer effect resulting from friction is not considered in this study. According to assumption (2), the principle of equal curvature, the theoretical stiffness value for pure friction laminated double beams can be expressed as follows:
According to the flexural formula for beams, the curvature distribution of a laminated double beam under bending, neglecting shear deformation, can be expressed as:
For the laminated beams with point-connected, the combination effect resulting from friction was also not considered. The shear stiffness at the interface between the beams was significantly increased, which resulted in the development of axial forces in both the floor beam and the ceiling beam. Consequently, the upper and lower beams were subjected to a combination of axial force and bending moment. Let
N f (
x) denoted the axial force in the floor beam, and
N c (
x) denoted the axial force in the ceiling beam. The static equilibrium equations for the upper and lower beams can thus be expressed as:
The tangential distributed load at the interface was proportional to the relative slip between the beams. According to the sectional internal force equilibrium condition, the following relationship can be obtained:
Based on the internal force equilibrium condition of the cross-section, the internal force equilibrium equation for the laminated steel beam can be established as follows:
Where, M f (x) and M f (x) denotes the bending moments of the floor beam and the ceiling beam, respectively, and h0 represents the distance between the neutral axes of the floor beam and the ceiling beam.
According to assumption (2), the floor beam and ceiling beam in the laminated steel beam exhibit the same curvature. In combination with the relationship between bending moment and curvature, the following expression can be obtained:
The relative slip behavior at the interface was a key factor influencing the composite flexural effect between the floor beam and the ceiling beam. Compared with an integral beam structure, the laminated double-beam structure develops a certain amount of slip strain at the interface, as shown in Figure 2.
Figure 2.
Strain distribution of laminated beam.
Figure 2.
Strain distribution of laminated beam.
According to the internal force–strain relationship of the laminated steel beam cross-section, the following can be obtained:
Furthermore, the analytical equation for the slip strain at the interface can be obtained as follows:
By incorporating the following formula and differentiating the above equation, we have:
Based on the above, the curvature formula for laminated steel beams considering the relative slip between the floor beam and the ceiling beam can be derived as follows:
2.2. Theoretical Model of the Deflection Curve for Laminated Beams with Only Friction Restraints in Modular Steel Buildings
For the laminated beams with only friction restraints in modular steel buildings, the two single layers were simply coupled and undertook the external loads solely, without significant additional axial forces developing in the cross-sections of the upper and lower beams. Therefore, the mathematical expression for the curvature of the double-beam structure was given by Equation (24).
Based on the boundary conditions of the simply supported laminated steel beam, the analytical model for the deflection curve of a simply supported pure friction laminated steel beam under symmetrically applied two-point concentrated loads can be obtained as follows:
2.3. Theoretical Model of the Deflection Curve for Laminated Double Beams with Point-Connected in Modular Steel Buildings
The high-strength bolts effectively enhanced the mutual constraint between the beams, resulting in additional axial forces in the cross-sections of the floor and ceiling beams. Therefore, the mathematical expression for the curvature of laminated beams with point-connected in modular steel buildings was given by Equation (27). Previous studies had systematically analyzed the relative slip of laminated beams in modular steel buildings and established a theoretical slip model for simply supported laminated steel beams with point-connected under symmetrically applied two-point concentrated loads. By substituting the theoretical expression for slip strain into Equation (27), the higher-order differential control equation for the deflection curve of the double-beam structure can be obtained, as shown in Equation (28).

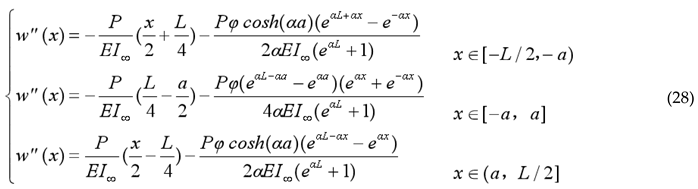
Based on the boundary conditions of the simply supported laminated beam, the analytical model for the load-deflection curve of a simply supported laminated beam in modular steel buildings under symmetrically applied two-point concentrated loads can be obtained as follows:
2.4. Theoretical Model of the Deflection Curve for Pure Friction Laminated Beams with Fixed Supports in Modular Steel Buildings
Under symmetrically applied two-point concentrated loads, the higher-order differential control equation for the relative slip deflection curve of a fixed-end pure friction laminated steel beam is given by Equation (30):
Furthermore, based on the boundary conditions, the analytical model for the load-deflection curve of a fixed-end pure friction laminated steel beam can be derived as follows:
2.5. Theoretical Model of the Deflection Curve for Point-Connected Laminated Beams with Fixed Supports in Modular Steel Buildings
Under symmetrically applied two-point concentrated loads, the higher-order differential control equation for the deflection curve of a fixed-end point-connected laminated steel beam considering interlayer slip is as follows:
Based on the boundary conditions of the fixed-end laminated steel beam, the analytical model for the load-deflection curve of a fixed-end point-connected laminated steel beam under symmetrically applied two-point concentrated loads can be obtained as follows:
3. Equivalent Initial Bending Stiffness Laminated Beams in Modular Steel Buildings
To analyze the composite effect between the floor beam and the ceiling beam, a study on the equivalent initial bending stiffness was carried out based on the theoretical deflection curve of laminated double beams. A theoretical formula for the equivalent initial bending stiffness of laminated steel beams was established, thereby enabled the quantitative evaluation of the cooperative effect in double-beam structures. It was noted that the theoretical models for the deflection curves of pure friction and point-connected laminated beams under various working conditions and symmetrically applied two-point concentrated loads had established. Consequently, the theoretical formulas relating the mid-span deflection and applied load for laminated double beams can be derived. The relationship between the mid-span deflection and the equivalent initial stiffness under symmetrically applied two-point concentrated loads is given by Equation (34). By substituting Equations (3), (6), (8), and (10) into Equation (34), the theoretical formula for the initial flexural stiffness of laminated beams can be obtained.
Under simply supported conditions and symmetrically applied two-point concentrated loads, the theoretical formula for the initial flexural stiffness of pure friction laminated beams was given by:
Under simply supported conditions and symmetrically applied two-point concentrated loads, the theoretical formula for the initial flexural stiffness of point-connected laminated beams was given by:
Under fixed support conditions and symmetrically applied two-point concentrated loads, the theoretical formula for the initial flexural stiffness of pure friction laminated beams was given by:
Under fixed support conditions and symmetrically applied two-point concentrated loads, the theoretical formula for the initial flexural stiffness of pure friction laminated beams was given by:
4. Experimental Investigation of the Bending Performance of Laminated Beams in Modular Steel Buildings
4.1. Set-Up of Bending Tests for the Laminated Beam Specimens
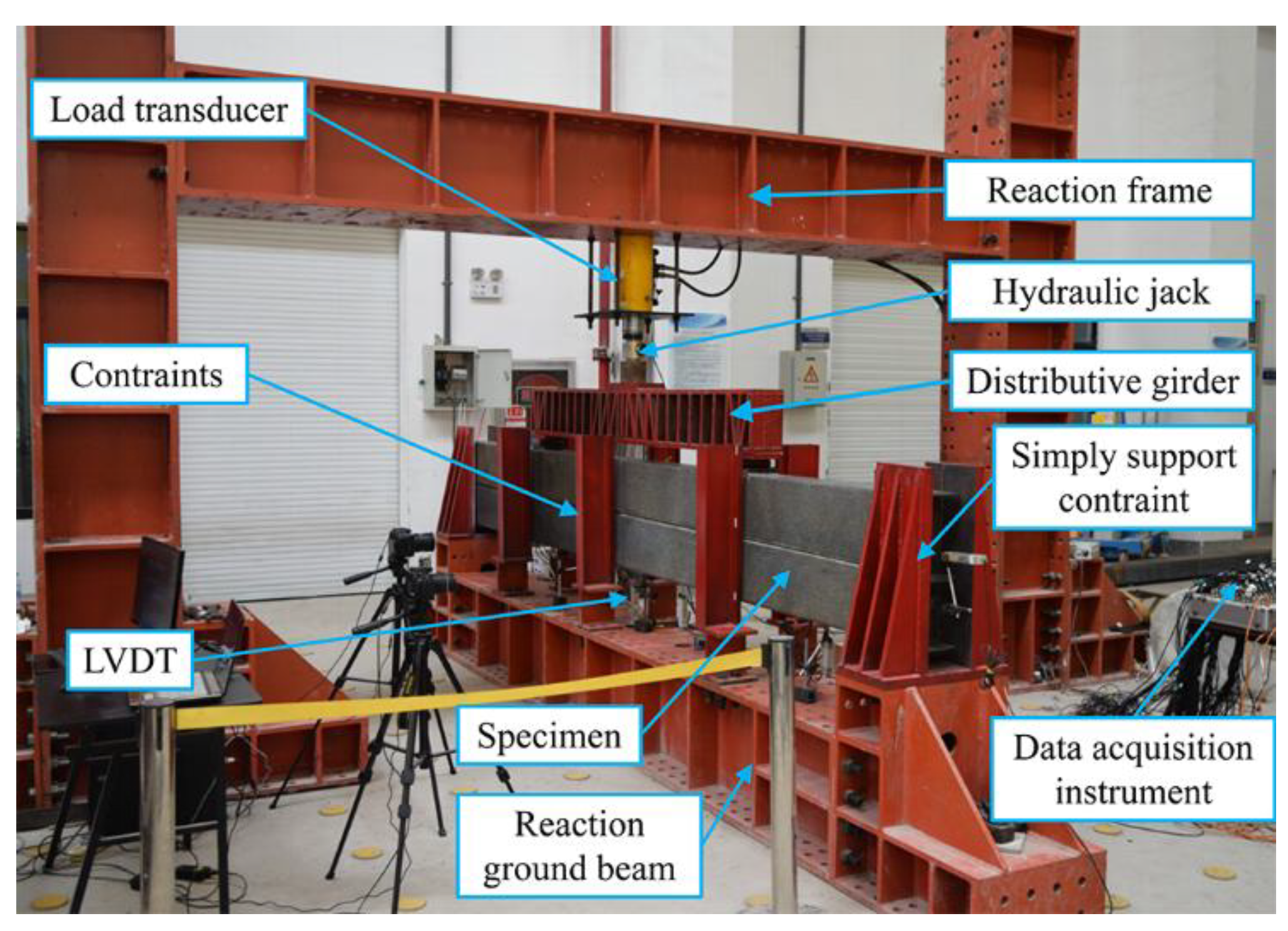
The four-point bending tests were conducted on the full-scale laminated channel beams with only friction interaction and added bolt connections, respectively. The setup for the flexural tests of laminated double beams in modular steel buildings was illustrated in Figure 3. A reaction frame and reaction ground beam were installed to provide counter force and fix constraints for the test loading. Two simply supported bearing devices were positioned at both ends of the reaction ground beam to supply simple supports and out-of-plane constraints for the beam specimens. On each side of the beam specimens, three out-of-plane constraint devices were installed to restrict out-of-plane deformation of the laminated double beam specimens, thereby simulating the out-of-plane and torsional restraints provided by secondary beams, floor slabs, and ceiling slabs in modular steel buildings. A 100-ton hydraulic jack was mounted at the lower flange at mid-span of the reaction frame beam to apply vertical loading in increments of 10 kN. To realize four-point bending tests on the beam specimens, a load distribution beam was installed on the upper part of the specimen, with its supports simply resting on the upper flange of the beam specimen at the quarter-span points. A pressure sensor was arranged between the loading point on the upper flange of the distribution beam and the end of the hydraulic jack to measure the vertical load during the test. Additionally, a rod-type displacement transducer with a range of 100 mm was installed at the lower flange at mid-span of the beam specimen to monitor deflection during the flexural loading process.
Figure 3.
Set-up of bending test.
Figure 3.
Set-up of bending test.
4.2. Flexural Performance of Modular Laminated Beam Specimens
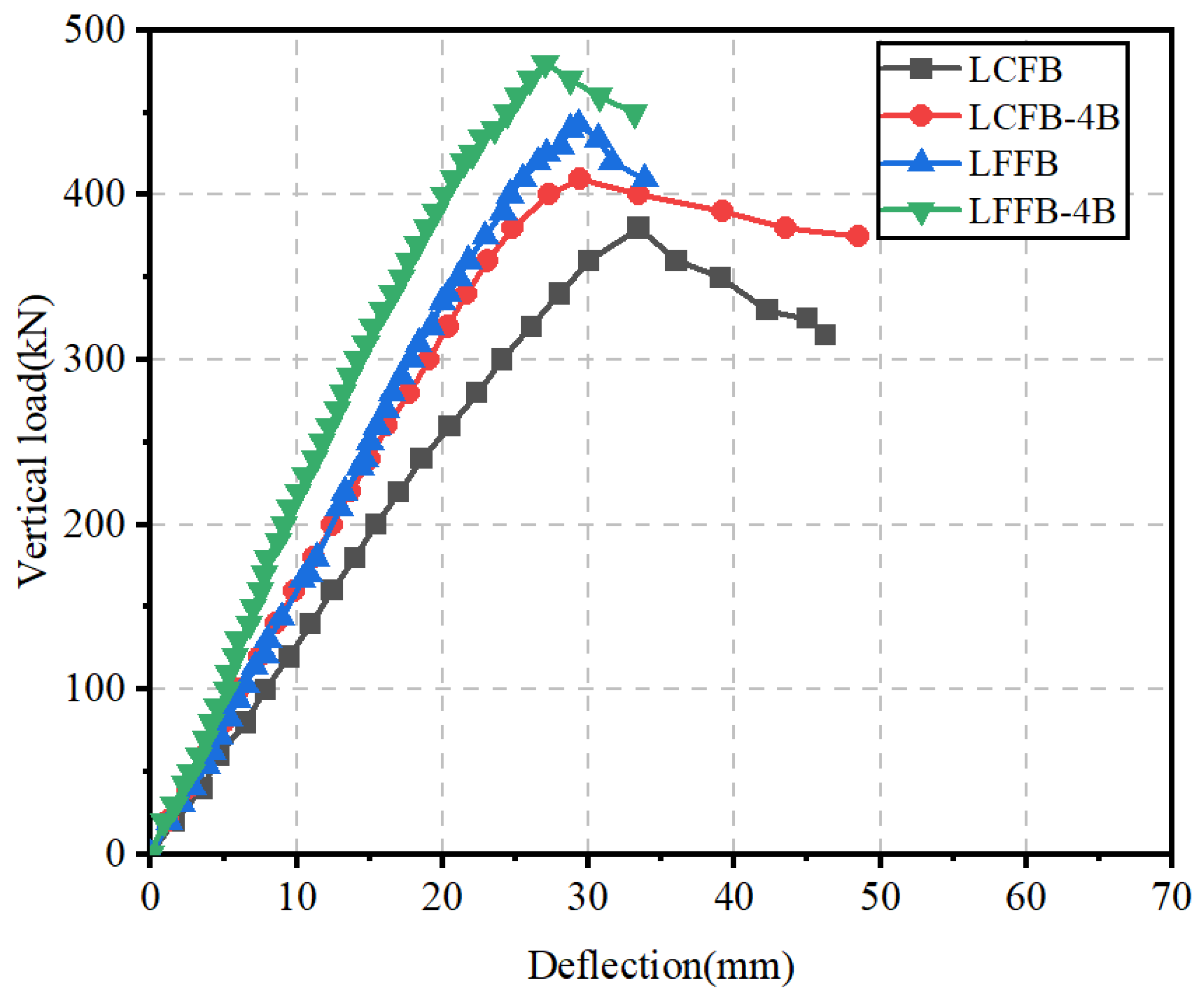
Under the vertical loading, the symmetric flexural deformations about the mid-span section were produced for the laminated beam specimens. By comparatively analyzing the vertical load–deflection curves of the beam specimens, the synergistic effect of the floor beam and the ceiling beam were investigated. As shown in Figure 4, the load–deflection curves of the modular laminated steel beams indicated that the vertical forces were directly transferred in upper and lower beams through normal contact interaction at the interfaces. In specimens LFCB and LFFB, the tangential connection stiffness between the single layers was provided only by the interfacial friction, enabling the coordinated flexural deformations. In specimens LFCB-4B and LFFB-4B, the high-strength bolted connections effectively enhanced the interfacial shear-slipping stiffness, which further improved the overall flexural integrity of the double-beam structures and resulted in the significant increases in both ultimate load-bearing capacities and initial bending stiffness.
Figure 4.
Vertical load-deflection curves.
Figure 4.
Vertical load-deflection curves.
Aiming to quantify the cooperative behaviors of the double beam structures with bolted connections, a detailed comparison was conducted on the ultimate load-bearing capacity, initial bending stiffness, and secant stiffness at the ultimate load state for the modular laminated beam specimens. As shown in
Table 2, the ultimate load-bearing capacity, initial flexural stiffness, and secant stiffness at the ultimate load state for laminated beam specimens with pure friction (LFCB, LFFB) and bolted connections (LFCB-4B, LFFB-4B) were listed, respectively. It was revealed that the ultimate vertical load of the bolted laminated steel beam specimen LFCB-4B increased by 7.89% compared to the pure friction laminated steel beam LFCB, the initial flexural stiffness increased by 27.4%, and the secant stiffness at the ultimate load state increased by 21.9%. For the bolted laminated steel beam specimen LFFB-4B, in which both the upper and lower beams are FB, the ultimate load increased by 8.35%, the initial bending stiffness increased by 27.4%, and the secant stiffness at the ultimate capacity state increased by 16.3% compared to the laminated steel beam specimen LFFB. Compared with the laminated steel beams with only interfacial friction, the interfacial bolted connections further enhanced the shear stiffness at the interface, thereby strengthening the overall flexural integrity of the laminated steel beam specimens LFCB-C-4B and LFFB-C-4B. Considering the superimposition effect of laminated beams with increased ceiling beam height, the flexural capacity of LFFB was significantly higher than that of LFCB. The load-bearing capacity, initial flexural stiffness, and secant stiffness of LFFB are 16%, 56%, and 39% higher than those of LFCB, respectively. Similarly, for bolted connections, the load-bearing capacity, initial flexural stiffness, and secant stiffness of LFFB-4B are 17%, 56%, and 33% higher than those of LFCB-4B, respectively.
Table 2.
Flexural performance of double beams under vertical load.
Table 2.
Flexural performance of double beams under vertical load.
| |
Fexp
(kN) |
Dfal
(mm) |
Sini
(kN·m) |
Ksec
(kN/m) |
Hcap |
Hins |
Hses |
| LFCB |
380 |
33.42 |
1.35×106 |
1.14×103 |
— |
— |
— |
| LFFB |
443 |
27.81 |
2.11×106 |
1.59×103 |
— |
— |
— |
| LFCB-4B |
410 |
29.43 |
1.72×106 |
1.39×103 |
7.89% |
27.4% |
21.9% |
| LFFB-4B |
480 |
25.99 |
2.69×106 |
1.85×103 |
8.35% |
27.4% |
16.3% |
A comparative analysis of the flexural performance between pure friction laminated steel beams and bolted laminated steel beams indicated that the mutual connection between the layered beams has a significant enhancement on the overall flexural mechanical performance of laminated steel beams. Compared with pure friction laminated beams, the bolted connections effectively increase the shear stiffness at the interface, resulting in a further improvement in the vertical load-bearing capacity of bolted laminated steel beams. The bending stiffness was a critical parameter for in-plane flexural performance analysis and structural design of laminated steel beams. It was indicated that the stiffness enhancement was even more pronounced than the improvement in vertical load-bearing capacity. Compared to frictional contact at the interface, the high-strength bolted connections greatly enhanced the interfacial shear stiffness, making the composite effect between the floor beam and the ceiling beam more prominent. As a result, both the initial flexural stiffness and secant stiffness at the ultimate load state for bolted laminated steel beams were further increased relative to pure friction laminated beams. With the increase in tangential connection stiffness—through either interlayer friction or high-strength bolts—the initial flexural stiffness of laminated steel beam specimens increases accordingly. However, once the interfacial shear connection stiffness reached a certain level, further enhancement in the secant stiffness at the ultimate load state did not continue to increase. Overall, laminated steel beams subjected to vertical loads developed the normal contact and tangential shear connections at the interface, which resulted in the coordinated flexural deformation of the upper and lower beams. The structural integrity of the double beams was effectively improved, thus the laminated steel beams exhibited the superior flexural performance compared to independent double beams.
5. Validation of Theoretical Results by Experimental Data
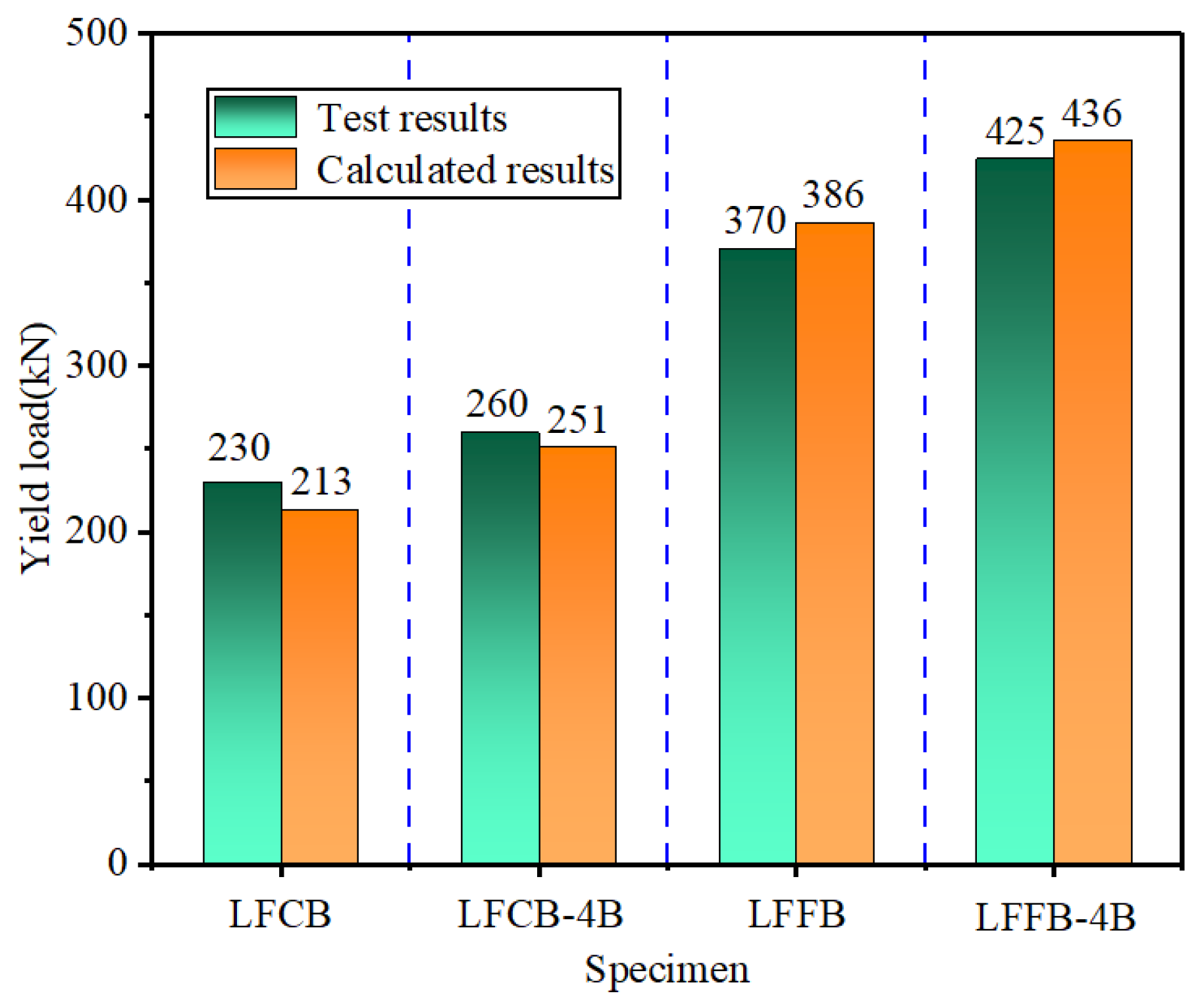
To verify the reliability of the theoretical deflection curve models for the modular laminated steel beams, the analytical results were compared with the experimental data, as shown in
Figure 5. The comparison indicated that, for laminated beams with different interfacial connections, the theoretical values of the yielding loads are in good agreement with the experimental results. The difference between the theoretical and experimental values for the laminated steel beams generally remained within 8%. Overall, the analytical deflection curve model for laminated steel beams demonstrated the satisfied reliability. The analytical models quantitatively described the cooperative effect of the floor beam and ceiling beams and reasonably calculated the overall mechanical performance of modular laminated beams, providing a reliable theoretical foundation for the design of laminated steel beams in modular steel buildings.
6. Conclusions
In this study, the mechanical properties of modular laminated steel beams were thoroughly theoretically evaluated. The deflection curves were analytically predicted for the laminated steel beams with different configurations, demonstrating the excellent agreement with the experimental data. This validation underscores the feasibility and structural integrity of using laminated steel beams in modular construction, offering practical insights for future engineering applications. The conclusions were summarized as follows:
1. Compared with pure friction laminated double beams, bolted laminated double beams in modular steel buildings exhibit significantly improved flexural performance, with load-bearing capacity increased by approximately 8% and initial flexural stiffness increased by 17% to 28%.
1. Based on the fundamental differential equation of the typical double-beam segment, the analytical expressions for interfacial slipping strain were established. Then, the theoretical models of interfacial slippage were respectively developed for the modular laminated steel beams with different connections.
2. By applying the boundary conditions of simply supported beams, the mathematical expressions were derived for the curvature of modular laminated beams, considering the relative slipping behaviors. In this way, the accurate analytical solutions for deflection and rotation were ultimately obtained.
3. More importantly, initial bending stiffness of laminated beams was theoretically calculated and validated by experimental results, which effectively quantitatively characterized the collaborative bending effect of double beam structures and significantly provided the dependable theoretical basis for practical design of modular steel buildings.
References
- C. PASQUIRE, A. GIBB, Considerations for assessing the benefits of standardisation and pre-assembly in construction, Journal of Financial Management of Property & Construction, 7(03): 1-22 (2002),.
- Z. Chen, J. Liu, Y. Yu, Experimental study on interior connections in modular steel buildings, Eng Struct, 147 (2017), 625-638. [CrossRef]
- Z. Chen, J. Wang, J. Liu, K. Khan, Seismic behavior and moment transfer capacity of an innovative self-locking inter-module connection for modular steel building, Eng Struct, 245 (2021), 112978. [CrossRef]
- D.-A. Corfar, K. D. Tsavdaridis, A comprehensive review and classification of inter-module connections for hot-rolled steel modular building systems, J Build Eng, 50 (2022), 104006. [CrossRef]
- E.-F. Deng, Y.-P. Du, J.-D. Gao, Z. Zhang, Y.-B. Wang, Seismic performance of an innovative self-centering and repairable connection with SMA bolts in modular steel construction, Thin-Wall Struct, 205 (2024), 112377. [CrossRef]
- K. Khan, Z. Chen, J. Liu, K. D. Tsavdaridis, Compressive behaviors of corner-supported modular steel sway frames with rotary inter-modular connections, Thin-Wall Struct, 193 (2023), 111245. [CrossRef]
- W. Lacey, W. Chen, H. Hao, K. Bi, Structural response of modular buildings – An overview, J Build Eng, 16 (2018), 45-56. [CrossRef]
- W. Lacey, W. Chen, H. Hao, K. Bi, Review of bolted inter-module connections in modular steel buildings, J Build Eng, 23 (2019), 207-219. [CrossRef]
- R. M. LAWSON, R. G. OGDEN, R. 1: BERGIN, Application of modular construction in high-rise buildings, Journal of Architectural Engineering, 18(02), 2011.
- K. Khan, Z. Chen, J. Liu, K. D. Tsavdaridis, Experimental and analytical investigations on compression behaviors of rotary-connected sway column-supported steel modular interior frames, J Build Eng, 78 (2023), 107692. [CrossRef]
- W. Lacey, W. Chen, H. Hao, K. Bi, New interlocking inter-module connection for modular steel buildings: Experimental and numerical studies, Eng Struct, 198 (2019), 109465. [CrossRef]
- W. Lacey, W. Chen, H. Hao, K. Bi, Lateral behaviour of modular steel building with simplified models of new inter-module connections, Eng Struct, 236 (2021), 112103. [CrossRef]
- W. Lacey, W. Chen, H. Hao, K. Bi, New interlocking inter-module connection for modular steel buildings: Simplified structural behaviours, Eng Struct, 227 (2021), 111409. [CrossRef]
- J. lI, L. DENG, D. SANG, D. WANG, Experimental research on flexural behaviour of laminated steel beams, Industrial Construction, (2015),.
- J. lI, D. SANG, D. WANG, l. LI, Experimental Research on Laminated Steel Beamswith Non-continuous Connectors, Structural Engineers, 29(04): 125-131 (2013),.
- H. Chang, H. Lei, X. SONG, F. Qin, Experimental test and parametric analysis on flexural performance of laminated square tubular beams in steel box module, Journal of China University of Mining & Technology, 52 (2022) (2022),.
- Zhang, J. Liu, Z. Chen, T. Chen, Bending behavior of detachable tapered-head bolt inter-module connection of steel modular structure, J Constr Steel Res, 220 (2024), 108829. [CrossRef]
- Zhang, G. Zhipeng, L. Xuechun, L. Chao, Global stability coefficient of prefabricated beams with dual-channel combined section, Eng Mech, 35 (2018),.
- X. ZHA, X. ZHAI, Q. WANG, Mechanical properties of assembled frame connected bydouble-beam and double-column angle jointswithout on site welding, Journal of Building Structures, 39(S2):8-15 (2018),.
- X. ZHAI, X. ZHA, L. YUAN, Experimental study and numerical simulation on assembled framewith double-beam multi-column joints, Journal of harbin Institute of Technology, 52(08):1-10 (2020),.
- Y. Zhu, J. Zhao, Experimental and numerical study on member classification of I-section plate girders, J Constr Steel Res, 137 (2017), 192-200. [CrossRef]
- Xu, J. Xia, H. Chang, R. Ma, L. Zhang, A comprehensive experimental-numerical investigation on the bending response of laminated double channel beams in modular buildings, Eng Struct, 200 (2019). [CrossRef]
- Xu, J. Xia, H. Chang, R. Ma, L. Zhang, Flexural behaviour of pairs of laminated unequal channel beams with different interfacial connections in corner-supported modular steel buildings, Thin-Wall Struct, 154 (2020). [CrossRef]
- Xu, J. Xia, H. Chang, R. Ma, L. Zhang, Evaluation of superimposed bending behaviour of laminated channel beams in modular steel buildings subjected to lateral load, Thin-Wall Struct, 175 (2022). [CrossRef]
- Xu, J. Xia, H. Chang, R. Ma, L. Zhang, Experimental and numerical investigation on the lateral force resistance of modular steel sub-frames with laminated double beam, J Build Eng, 46 (2022). [CrossRef]
- Xu, J. Xia, R. Ma, H. Chang, C. Yang, L. Zhang, Investigation on interfacial slipping response of laminated channel beams with bolt connections in modular steel buildings, J Build Eng, 63 (2023), 105441. [CrossRef]
- L. M, O. R, G. C. Handbook for the design of modular structures. Monash: CRC press2017.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).